Quantum Systems for Enhanced High Energy Particle Physics Detectors

Developments in quantum technologies in the last decades have led to a wide range of applications, but have also resulted in numerous novel approaches to explore the low energy particle physics parameter space. The potential for applications of quantum technologies to high energy particle physics endeavors has however not yet been investigated to the same extent. In this paper, we propose a number of areas where specific approaches built on quantum systems such as low-dimensional systems (quantum dots, 2D atomic layers) or manipulations of ensembles of quantum systems (single atom or polyatomic systems in detectors or on detector surfaces) might lead to improved high energy particle physics detectors, specifically in the areas of calorimetry, tracking or timing.

1 Introduction

The development of a wide range of highly sensitive technologies based on the manipulations of small numbers of atoms or on quantum effects that arise at ultra-low temperatures has led to the rapid proliferation of a very wide range of quantum devices, many of which are now beginning to see commercial applications. At the same time, the extraordinary sensitivity of these devices, which rely on discrete state changes from one quantum state to another, makes them ideal detectors for probing very weak interactions between putative ultra-light particles or fields and the quantum devices themselves. This has led to their wide uptake in the field of low energy particle physics and the rapid exploration in recent years of the low energy phase space associated with e.g., axions, ALP’s, and many other dark matter candidates (numerous reviews, among them [1–4], have covered these applications).

This same sensitivity would appear to make these devices unsuitable for high energy physics applications, whose detection mechanisms mostly rely on detecting and reconstructing individual particles’ properties through the quasi-continuous effects of their interactions with matter, integrating the charge deposited by the continuous process of multiple ionizations of the atoms of the bulk of a detector by the interacting particle. Forming a usable signal that can be differentiated from thermal and statistical fluctuations requires large numbers of such ionization processes to have taken place. Furthermore, existing detector families are already very well suited to high resolution tracking, calorimetry or particle identification.

In this paper, we discuss a small number of quantum devices or systems in which quantum effects play a major role in view of applying them to the areas of particle tracking, particle identification or calorimetry. We particularly focus on applications that potentially could result in information that is currently difficult to obtain, or where some of the existing technologies’ boundary conditions or limitations might be alleviated or circumvented. These are tied to the need for ever better time resolution to deal with increasing pile-up in high energy collider experiments; to the desire to minimize the material budget of detectors so as to minimize multiple scattering, in particular for vertexing; to the interest in determining electromagnetic shower profiles for better particle identification and energy measurement; to the desire to improve on the existing techniques to avoid detector backgrounds or widen the range of employable materials; or to the potential of providing additional information to particle trajectories that would aid in identifying e.g., particle helicities.

The structure of this paper is built around a handful of selected quantum systems, exploring the potential impact of each of these in different areas of high energy particle detection and reconstruction; in most cases, the proposed detection systems will be hybrids of established technologies and of elements whose quantum nature potentially enhances the functionality of the former. The paper does not claim to be exhaustive, but instead compiles a few of what we consider to be some of the more promising near-term applications, and which are highlighted for each of the investigated families of quantum devices in dedicated sections: low-dimensional materials, nano-engineered semiconducting devices, implementation of polarizable support structures, or manipulation of individual atoms in large volume detectors. Given the rather speculative and often very preliminary nature of the detection schemes described below, it has to be emphasized that significant research and development efforts will be required in validating the concepts proposed here for a range of high energy particle detection approaches and in establishing their viability and usefulness.

2 Low-Dimensional Materials

Low dimensional materials (nanodots, atomically thin monolayers) offer a wide degree of tunability of their parameters, be it through their elemental composition and crystal stucture in the case of 2-D layers, or their composition and geometric size in the case of nanodots. Their properties range from photon emission to modification of surface properties (when used as coatings) to mechanical barriers (differential transmission of electrons and ions).

2.1 Low Dimensional Materials for Scintillating Detectors

Scintillator-based detection systems are in wide use since many years and in many applications ranging from nuclear and particle physics experiments to medical imaging and security. Their physical properties like density, light yield, linearity of the detector response and operational speed, but also their resistance to harsh radiation load, their insensitivity to small changes in operational parameters and the widely available production capabilities make them one of the most popular devices for the detection and the energy measurement of charged and neutral particles interacting with material structures. The need for the above-mentioned ever better timing resolution in particle physics experiments places, however, increasingly stringent requirements on the time measurement performance of scintillator-based detection systems. The timing performance of future particle detector experiments is key to cope with the need to disentangle bunches of colliding particles with ever smaller temporal separation.

2.1.1 Nanomaterial Scintillators

Conventional commonly used scintillators produce an amount of light proportional to the energy deposited by charged or neutral particles. The energy transfer from initial ionisation in the bulk material to the luminescence centers is complex and leads to an intrinsic time-resolution limit in photoproduction due to the stochastic relaxation processes of the hot electron-hole pairs produced by the impact of radiation on the crystal material. This generates irreducible time jitter and limits the time resolution. To go below this intrinsic limitation, which is a characteristic property of conventional scintillation materials, various ways of exploiting faster photon production mechanisms have been investigated [5–12] among which the development of semiconductor nanomaterials represents a promising route towards fast timing; these have thus been extensively studied over the last years see [13–17].

While conventional semiconductor bulk material is characterized by continuous conduction and valence bands, the reduction of the size of a crystal down to a so-called nanocrystal of typically 1–10 nm size, close or below the Bohr radius, results in the energy levels of both conduction and valence band becoming discrete and quantized due to quantum confinement. The variation of the energy gap as a function of the size of nanomaterials and of the density of states as a function of the degree of confinement both offer the possibility of tuning their opto-electronic properties, such as for instance the emission wavelength, which can be varied from red to blue by decreasing the size of a nanocrystal (see Figure 1 left) [18, 19]. Depending on the number of dimensions of the confinement, nanocrystals are classified as quantum wells or ultrathin films (one dimension of confinement resulting in a two-dimensional (2D) object), quantum wires (two dimensional confinement resulting in a remaining one dimensional (1D) object) and quantum dots (confinement in all three directions resulting in a zero dimensional (0D) object [20]. The available energy levels in such objects are discretized as a function of the object dimensionality (0D, 1D, 2D) and their size and shape [20–22].

FIGURE 1

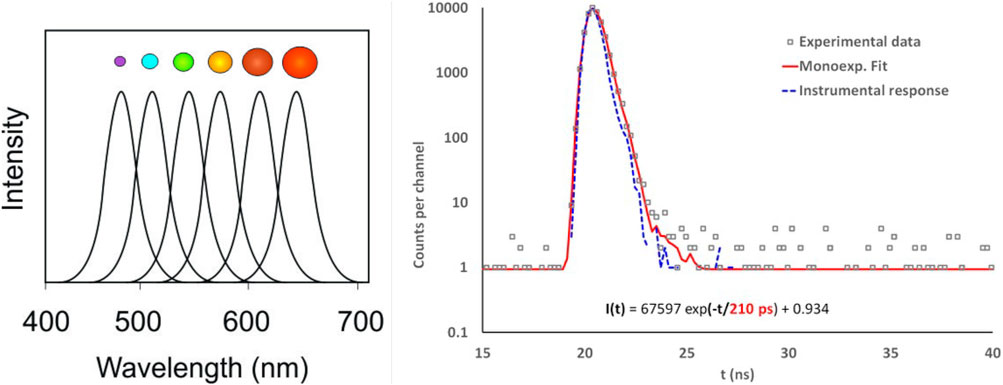
FIGURE 1. Left: Emission spectrum as a function of nanocrystal size (from [22]). Right: decay time spectra of ZnO(Ga) under irradiation by X-rays (from [15]).

In direct-band-gap-engineered semiconductor nanostructures, one effect of quantum confinement consists of a significant enhancement of Coulomb interactions between charge carriers of electron-hole pairs, coherent and multi-exciton states [19, 23, 24]. This plays a significant role in enhancing the transition dipole moment of absorption and emission and can thus increase the rate of fast radiative transitions resulting in scintillation decay times below 1 ns.

The timing resolution of scintillators is to first order proportional to the square root of the photon density (number of produced photons per time interval), which can itself be expressed as the ratio of the emission decay time and the light yield of the scintillator. Therefore, to minimise timing resolution, scintillator development aims at achieving a maximum light yield with the shortest possible decay times. Future scintillator based timing layers or time-of-flight detectors aim at achieving a timing resolution below 30 ps in order to be suitable for pileup rejection at high luminosity colliders and for particle identification, and be competitive with e.g., SPAD’s [25] or LGAD’s [26]. Achieving such timing resolutions with scintillating nanomaterials with a sub-nanosecond decay time would provide flexibility in matching experiment specific performance requirements as well as constraints in terms of costs, radiation hardness and infrastructure needs.

Several types of scintillating nanomaterials with different levels of confinement (nanoplatelet, quantum wire, quantum dots) have been studied over many years. Among them, CdSe and CdSe/CdS [13, 14, 27–29], CdZn/ZnS [30], ZnO quantum dot or nanoplatelets [15, 31–33], InGaN/GaN multi quantum wells [16, 34–36], the Cesium lead halide perovskyte CsPbX3 (X = Cl, Br,I) [17, 37, 38] for instance reach a fast photon emission with characteristic radiative decay times in the range of nanosecond or subnanosecond. An example of the decay time obtained for ZnO(Ga) nanomaterials is given in Figure 1 right.

The very short decay times of such nanocrystals together with the possibility to tune their emission spectra open new prospects for timing detectors for particle physics experiments, such as precision timing layers for time tagging of collision tracks or scintillators for the energy measurement of particles in combination with high time resolution. Furthermore, if the nanocrystal emission spectrum is tuned into the infrared wavelength band between 1 and 5 μm, for which silicon is transparent (or can be made so via surface treatments [39]), any photons emitted away from the scintillating layer can be detected remotely, even through further semiconductor-based tracking layers, thus opening new possibilities in detector design and functionality.

2.1.2 Time Tagging and Calorimetry

In order to exploit the physical and optical properties of nanocrystals for radiation detectors in various particle physics experiments, R & D efforts need to focus on maximizing the energy deposit in the nanomaterial to have a sufficient number of photons with a very fast decay, increasing the Stokes shift to avoid self-absorption and improving the light transport and light collection of the fast emission. While the production of large volumes of pure nano-crystal based detection devices represents a major technical challenge, layers of nano-crystals can be combined in multiple ways with conventional scintillator materials in so-called hetero-structured scintillators or MetaCrystals [40–43], allowing to simultaneously exploit the properties of bulk scintillators, e.g., in terms of absorption power for the measurement of the energy, and the fast light emission of nano-crystals for timing measurement purposes. One possibility could e.g., be to deposit nano-materials as thin layers of several µm thickness on conventional bulk scintillators [37, 43, 44], together building a sample of alternating scintillator/nano-crystal layers. In this approach the standard scintillator and the nano-crystals are optically separated, thus preserving the high-Z scintillator performance and light collection characteristics, while at the same time adding prompt photons to the signal. The performance of such approaches essentially depends on having a minimum thickness and density of nano-crystal layers to allow for the emission of sufficient amount of prompt photons and on having a sufficient transparency to allow prompt photons to reach the photon detection device. The tunable absorption and emission characteristics of nano-crystals may furthermore allow to convert e.g. ultraviolet scintillation light (e.g., cross luminescence material such as BaF2) or Cherenkov light (eg PbF2, Lead glasses) into visible light, which is more efficiently detectable by photo-detectors, thus being functionally similar to a fast wavelength shifter.

Despite the abovementioned difficulties in producing large volumes of nano-crystals, attempts have been made to produce a stack consisting of multiple waveguides of thin 10–50 μm thick epitaxially grown layers of InAs/GaAs quantum dot scintillators [45, 46]. Having a segmented photodetector array for the readout of each waveguide integrated in such stack, one can achieve an impressive detector performance in terms of light yield and timing characteristics. Various assembly technologies are currently under study to overcome the technical challenges related to the separation of the epitaxial layers from its substrate and its combination into a stack.

Another possibility consists of depositing one or more layers of nano-crystals directly on photo-sensitive devices in order to increase the sensitivity of the photo-detector towards X-ray and γ-ray energies or charged particles for time tagging purposes and thus to significantly enhance the range of applications of such devices. Among the issues to be addressed in these approaches figure a detailed understanding of the surface chemistry of nanocrystals in view of their deposition in form of thin layers of nanomaterials on conventional scintillators or photosensitive semiconductor devices and the transport of light.Whereas nano-crystals can currently be added to scintillating crystals only on their surfaces or as layers alternating with conventional crystal materials, they can on the other side be dispersed in liquids or embedded in host materials such as organic materials or glasses in order to enhance or replace the conventional scintillation mechanism of liquid or plastic scintillators or doped glasses by a scintillation with faster emission characteristic, which allows their use as a fast component of the above-mentioned hetero-structure, in the form of shashlik detectors or as integrated (quasi-continuous) wavelength shifters.

However, various aspects and issues have to be addressed and improved in order to bring the performance of nanocrystal composites to that of conventional detectors, such as the optimization of the energy transfer between the host and the nanomaterial. Also the concentration of nanomaterials must be optimized in terms of density and homogeneity, while at the same time having a good transparency and avoiding the scattering of the scintillation light. Several developments in these directions are performed [17, 30–33, 38, 47–49] and some projects have already been proposed. One example consists of the production of plastic scintillators exploiting CsPbBr3 perovskites as high Z sensitizers, resulting in a large Stokes shift, a high emission yield and a fast emission lifetime of few ns [38]. The resulting scintillation performance is comparable to conventional inorganic and plastic scintillators, making such scintillators a usable tool for waveguiding over long optical distances and for the detection of high energy photons and charged particles without absorption losses. The Esquire project [50] proposed to use scintillating quantum dot containing isotope componants such as CdSe/ZnS embedded in a host matrix for the study of rare events such as the neutrinoless Double Beta Decay (0νDBD). More recently AIDAinnova project approved a blue sky project “NanoCal” on the proof of concept of a fine-sampling calorimeter with nanocomposite materials [51, 52].

2.1.3 Chromatic Calorimetry

Recent developments in the tuneability and narrow emission bandwidth (∼ 20 nm) of quantum dots, quantum wells, carbonized polymer dots, monolayer assemblies or perovskite nanocrystals [53–55] opens the door to a novel approach to measuring the development of an electromagnetic or hadronic shower within a scintillator, with the potential of obtaining a longitudinal tomography of the shower profile with a single monolithic device, via the means of chromatic calorimetry. Specifically, a calorimeter module would need to be built from a single high density transparent material that is differentially doped (at high concentrations) along its length with nanodots with different emission wavelengths, those with the longest wavelengths towards the beginning of the module, and those with the shortest wavelengths towards the end. With the currently demonstrated emission bandwidths of 20 nm, and even constraining emissions to take place only in the visible spectrum, overall around twenty different differentiable emission regions can be envisaged, thus providing for fine grained shower development measurements. The radiation tolerance of these specific nanocrystals remains however to be established. Such a device that would function like a polychromatic embedded wave length shifter thus maps the position and local intensity of the stimulating radiation within the overall module onto the wavelength and intensity of the produced fluorescence light; multiple emission regions can be uniquely identified in a single measurement. One major challenge in implementing such a scheme resides in incorporating nanodots in existing dense crystals during their growth; as mentioned earlier, possible alternatives could be to either intercalate thick dense transparent absorber regions with thin, lower-density, radiation resistant, nanodot doped transparent layers; or to embed both nanodots and microsopic high density crystals within the same low density organic or glass bulk material. Another challenge is the radiation resistance of the bulk material, but also of the nanodots: carbonized polymer dots may not reach the expected radiation resistance of e.g., CsPbCl₃ [55], although irradiation tests on triangular carbon nanodots have yet to be carried out.

Naturally, re-absorption (and thus frequency shifting) of light emitted at different points along the cascade has to be avoided: both the bulk material and the subsequent nanodots must be transparent to the photons originating from successively earlier points in the cascade. Positioning of the nanodots emitting the lowest energy photons at the upstream end of the module, and those emitting the most energetic ones at the downstream end (Figure 2, bottom right), together with a nanodot absorption spectrum that only down-converts higher energy photons into lower energy ones, ensures this spectral transparency.

FIGURE 2

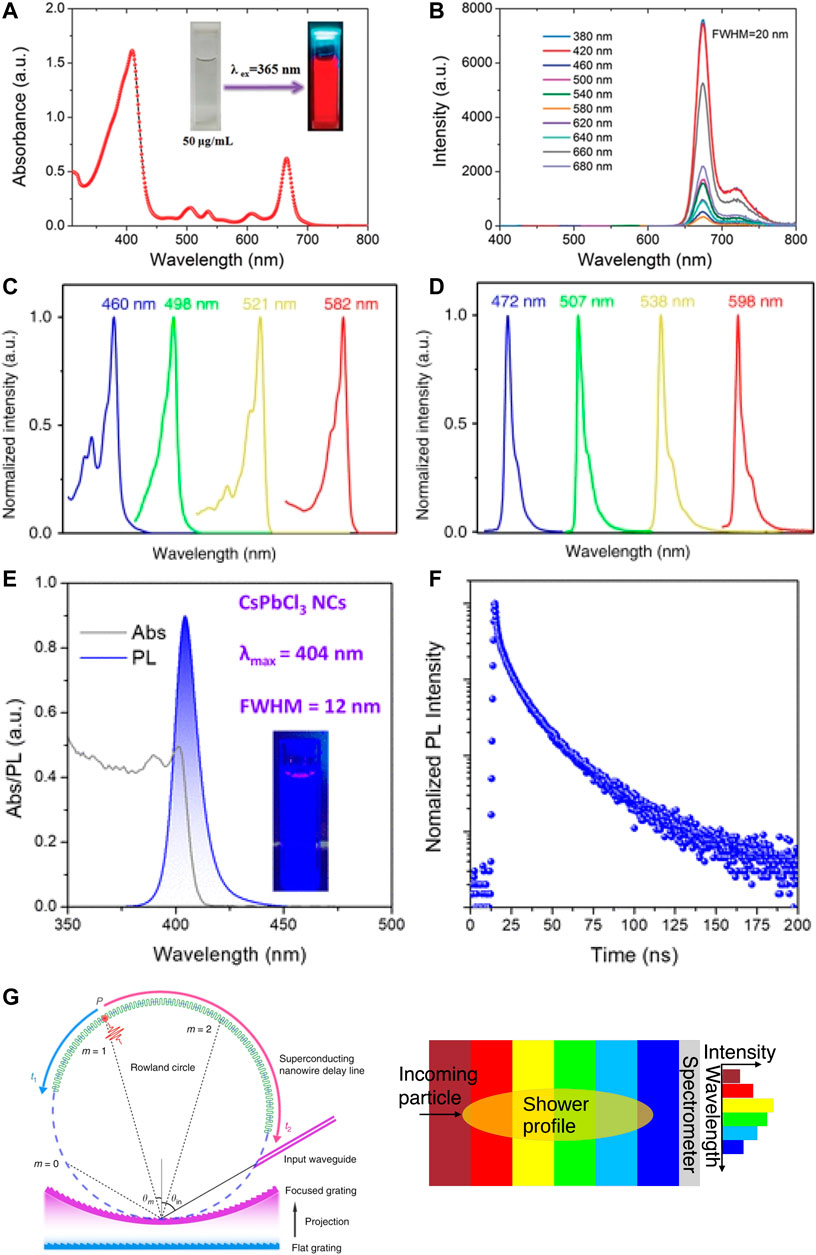
FIGURE 2. Absorption and photoluminescence (PL) emission spectra of selected narrow bandwidth quantum dot emitters. Top row: Carbonized polymer dots (CPD’s): absorption and emission spectra [53]. Second row: triangular Carbon quantum dots. The normalized UV-vis absorption (C) and photoluminescence (D) spectra of B-, G-, Y-, and R-NBE-T-CQDs, respectively [54]. Third row: CsPbCl3 nanocrystals. (E) optical absorption and PL spectra (excitation wavelength 350 nm) (inset: corresponding photograph under UV light), and (F) time-resolved photoluminescence (TRPL) decay curve of the synthesized PhPOCl₂-based CsPbCl₃ nanocrystals [55]. Bottom row: (G) Sketch of a compact nanowire-based spectrometer [56] and (H) of the overall scheme for the positioning of the different emission-wavelength specific nandots. The histogram to the right corresponds to the spectral intensity, and thus the depth profile, of the shower initiated by the incoming particle. Figures by permission.

Figure 2 shows the absorption (left column) and emission (right column) spectra of six different types of nanodots; the emission spectrum of e.g., carbonized polymer dots of around 680 nm lies above the absorption line of the subsequent triangular carbon quantum dot that only absorbs up to 582 nm, while emitting at 593 nm, which itself cannot be absorbed by the yellow-light emitting nanodot, and so forth. The final Perovskite nanocrystal in this example can not absorb any of the wavelengths of the earlier nanodots, since its absorption spectrum lies below 420 nm. In this manner, UV or higher energy light produced by the shower stimulates emission by nanodots at wavelengths that are not absorbed by any of the subsequent nanodots, and whose spectral intensity provides a proxy for the shower energy deposit at the depth corresponding to a specific nanodot emission wavelength. Furthermore, both onset and decay of photoluminescence is at the nanosecond timescale, as shown for CsPbCl₃ nanocrystals in Figure 2, providing for excellent shower timing and, possibly, even determining the temporal evolution of the shower itself.

In order to extract the shower profile from the spectral intensity distribution, the photodetector must be able to resolve the intensities and timings of the individual spectral lines. Very recently, compact moderate-spectral-resolution or narrowband spectrometers based on nanowires [56] or nanodots [57, 58] have been produced or are under active development; more traditional, albeit bulkier, alternatives based on Bragg spectrometers or prismatic structures, coupled to photodiode arrays are also imaginable.

2.2 Low Dimensional Materials for Gaseous Detectors

Gaseous detectors are widely used as large area detection systems in HEP experiments owing to their high gain factors, rate capabilities and compatibility with harsh radiation environments. MicroPattern Gaseous Detectors (MPGDs) feature good granularity and are employed as tracking detectors as well as for the readout of Time Projection Chambers (TPCs) among other applications. State-of-the-art MPGDs achieve high spatial resolution, energy resolution and specific developments of precise timing MPGDs have demonstrated $<$25 ps timing resolution [59].

To enhance the performance of MPGDs in view of future applications, low-dimensional materials are considered for different aspects of detectors: they may be used to tailor the primary charge production process, protect sensitive photocathodes in harsh environments or improve the performance of the amplification stage.

2.2.1 Enhancement of Charge Conversion in Low Dimensional Materials

While gaseous detectors conventionally rely on primary ionisation of gas in the conversion region by incident radiation, solid conversion layers or photocathodes offer a number of advantages by generating primary electrons in a well defined location allowing significantly improved timing resolution. The efficiency and spectral response of conversion layers or photocathodes also directly defines the sensitivity of the detector.

Low dimensional materials and nanostructures can offer new approaches to implement performant conversion layers for radiation detectors and may offer both increased quantum yield as well as access to specific ranges of sensitivity to incident radiation. This can range from exploiting nano-scale geometries to increase the surface available for absorption and photoelectron emission to engineering low dimensional structures to enhance photoemission by resonant processes. Significant improvements of efficiency over thin film or bulk materials as well as tunable work function have been demonstrated in systems such as nanostructured plasmonic surfaces [60], single-wall carbon nanotubes [61], Mg nanodots [62] or graphene layers [63], to name but a few. While some systems target broadband response for versatile detectors with wide spectral sensitivity ranges, other materials offer highly selective and tunable response making them promising conversion layers for particle identification methods. We will suggest possible applications for nanostructures as charge conversion and photocathode layers and highlight their potential for novel radiation detectors.

A key application for photocathodes in gaseous radiation detectors is their use in precise timing detectors where primary charge production needs to occur at a specific time in a well defined location. By converting Cherenkov light from a radiator to primary electrons with a semi-transparent CsI photocathode and using a Micromegas-based amplification stage, the PICOSEC Micromegas detectors have achieved $<$25 ps timing precision [59]. The efficiency of the photocathode directly translates to achievable timing resolution and while metallic or other robust photocathodes would offer resistance against environmental effects and ageing during prolonged operation, their QE is typically too low to be suitable for this detection concept.

An enhancement of photocathode QE by resonant processes in low dimensional structures could offer a possibility to overcome this limitation. Studies on nanodots of different sizes suggest that a significant enhancement of photocathode QE may be achieved by a discretisation of energy levels arising from quantum confinement [62]. Enhancement factors as high as 38 have been shown for Mg nanodots with diameters of 52.2 nm compared to Mg thin films with a strong dependance on dimensions [62]. While the efficiency of metallic photocathodes enhanced by nanostructuring would still be below the QE of semiconductor photocathodes it may be attractive to profit from the robustness of such structures.

Resonance-enhanced multiphoton photoemission processes have also been observed in single-wall carbon nanotubes [61] along with ultrafast emission timescales. In addition to enhanced QE, the high anisotropy of nanotubes also leads to a dependance of their response to different polarisations of incident light as well as a modification of absorption spectra for different geometries, thus providing a high level of flexibility in tuning detector response. In addition to sensitivity enhancements and optimisation to specific wavelength ranges, particle identification (PID) methods can profit from the selectivity of the response of nanomaterials. Tuning the band gap or work function has been demonstrated in a variety of systems, including modifications of graphene layer work function by UV exposure or plasma treatment [63] or the engineering of nanophotonic crystals to cover specific spectral ranges [64]. While nanophotonic crystals provide enhanced sensitivity for narrow spectral ranges and are thus selective for specific particle momenta in PID detectors, stacks of 1D photonic crystals of different periodicities can simultaneously offer high sensitivity to different particle momenta and may allow for efficient PID even in high particle flux environments [65]. Being selective to discrete bands of particle momenta can be a significant advantage in mitigating pileup and preserving PID capabilities in high rate experiments.

2.2.2 Graphene or Other 2D Materials as Photocathodes Encapsulant

The use of photocathodes in gaseous detectors is advantageous in the improvement of both time and spatial resolutions. Semiconducting photocathodes such as CsI provide high quantum efficiency (QE) in the UV range but have a limited lifetime due to 1) environmental condition such as humidity and 2) ion bombardment in gaseous radiation detectors. Surface coatings with 2D materials may enhance the lifetime by blocking incident ions while also modifying surface work function thus increasing QE. Theoretical studies [66, 67], based on ab initio density functional calculations, have been explored showing how a hBN layer on top of alkali-based semiconductive photocathodes should decrease the work function.

Ongoing promising studies demonstrate an increased operational lifetime by encapsulation of semiconductive [68, 69] as well as metallic [70] (i.e., Cu) photocathodes with few layers of graphene (from two up to eight layers) while lowering the QE. The decreased QE is mainly attributed to issues during the transfer process and graphene quality and achieved experimental values are approximately one order of magnitude below theoretical predictions [68].

2.2.3 Tailoring Microscopic Transport Processes

In addition to applications for charge conversion layers and photocathodes, atomically thin layers may be exploited to optimise the operation of gaseous detectors and tailor microscopic transport processes of charges. Gaseous detectors suffer from the back flow of positive ions created during charge amplification to the drift region which can lead to significant distortions of electric fields impacting subsequent events and is of particular importance in gaseous TPCs. Graphene has previously been proposed as selective filter, which could suppress the ion back flow fraction while permitting electrons to pass [71]. Graphene is the thinnest 2D material in nature with single atom thickness composed of sp² hybridized carbon atoms arranged with a honeycomb symmetry. Thanks to its electrical and optical properties it has been used in various applications including ultrafast photodetectors and FETs. Despite being one atom thick, graphene is impermeable to atoms [72] and its mechanical properties as elastic properties and intrinsic breaking strength of free standing layers make it the strongest known material [73]. As shown in [72], carbon’s π-orbitals are delocalized and thus do not allow even to the smallest molecules to pass through the layer. At the same time, graphene is expected to be transparent to electrons traversing the sheet due to its low electron density n $\sim 10^{12}/{\mathrm{c}\mathrm{m}}^2$ in a perpendicular direction, which should hold even for low electron energies in the range of 5–10 eV. Since in gaseous detectors the mean energy of primary electrons cannot be significantly higher than 10 eV because it is limited by the electrons mean free path between subsequent interactions with atoms/molecules of the gas, a good low energy electron transmission through the graphene layer is important in order to apply graphene as a filter for ion back flow.

Freely suspended single or few layer graphene membranes on top of tens of micrometer large holes in Gaseous Electron Multipliers (GEMs) may block ions while permitting electrons to pass and participate in avalanche multiplication. First evaluations of this approach were limited by defects of transferred graphene layers, which degraded electron transparency. Exploiting advances in the growth and transfer of graphene, ion and electron transparency of graphene membranes is being explored and may be used to develop low ion back flow detectors based on GEM technology.

Several theoretical and experimental works were carried out in recent years, investigating electron beam transmission through graphene, by measuring the transparency as a function of the incident electrons’ energy [74–78]. The results of these studies are often contradictory, especially in the very low energy electron range around 5–20 eV. The transverse electron transmission coefficient through graphene is usually measured in vacuum where layers show high transparency almost close to unity to electrons with energies ranging from tens of keV up to 300 keV. These energy values are about three to four orders of magnitude higher than the energies in gaseous detectors and are commonly used for transmission electron microscopy (TEM) where graphene can be used as a sample support for TEM measurements [74, 75]. Transparency for electron energies in the low energy range of tens up to hundreds of eV can be evaluated by the use of electronvolt transmission electron microscopy. Graphene shows a good transparency of about 60–70% for electron energies from 40 to 50 eV up to 100 eV [76, 77]. For low electron energies below 15 eV, experimental results have shown discrepancies which can result from the strong dependence on graphene quality at these low energies ranges [76, 77]. In particular for electrons with energies below 10 eV there is no systematic investigation to date but promising results for this low-energy region, which suggest that the transmission coefficient of electrons with energy less than 10 eV can achieve as high as 99% transparency [78]. In addition to selective ion filtering, freestanding graphene membranes with transparency to primary electrons may also be used to physically separate drift and amplification regions of the detectors working as gas separator [79–81] and profit from additional flexibility in the choice of gas mixtures optimised for high conversion efficiency in the drift region and suitable mixtures for high electron amplification factors.

3 Nanoengineered Semiconducting Devices

3.1 Chromatic Tracking

The position resolution of existing semiconductor pixel or microstrip detectors lies in the region of 10 μm, well suited to the current generation of high energy physics detectors. For future collider experiments, such as FCC-ee, individual hit resolution must be of the order of 3 μm [82] in order to allow achieving a combined vertex resolution of around 5 μm. Particularly, improved position resolution in the first detection plane (first scattering plane) after the primary vertex would allow improved secondary vertex determination, better particle discrimination, and higher jet flavor identification probability. While ultra-thin silicon microstrip and pixel detectors are a very effective approach to address this challenge, their resolution remains limited to the few μm level.

The scintillation properties of quantum dots (section 2), together with their O (10 nm) dimensions, suggest a possibility of improving the hit resolution of these innermost detection planes even further. Tests of InAs/GaAs quantum dots with α particles have provided evidence for a significant photo-electron yield (3 × 10⁴ photoelectrons per 1 MeV of deposited energy) and very rapid luminescence (emission time 0.3 ∼0.6 ns) [83]. Furthermore, due to the mismatch between the differences between the base layer lattice and that of the InAs quantum dots, these self-assemble: in [83], a quantum dot density of about 3.5 × 10¹⁰ cm², with lateral dimensions of 14 ∼18 nm and heights of 5 ∼6 nm was achieved.

It is conceivable to cover the surface of a silicon microstrip or pixel detector, but also of thin intercalated dedicated planes, with thin layers of light-emitting material in form of such semi-conducting quantum dots or quantum wells. While the functionality of existing quantum dots is not subject to external power sources, it may be interesting to consider the possibility that they could be coupled to the power distribution system of the silicon (or GaAs) detectors, perhaps leading to enhanced control over their dynamic properties. Moreover, it might be possible to do this in such a manner that each strip of a silicon microstrip detector is subdivided into a limited number of sub-micron wide bands. Self-assembly of nanodots [84] would appear to ensure that each microstrip zone would contain identical periodically-spaced nanodots, and thus nanodots producing light of the same frequency. If it is possible to affect this self-assembly process, one could effectively introduce a periodic, long-range modulation of the nanodot dimensions within each zone, and thus of the emission wavelengths. While no technology has yet been developed that would allow effectively controlling and modulating the growth of nanodots at the atomic scale over large distances, some possible directions to investigate could be through the moiré-modulated substrate interaction discussed in [84], through interferometric laser annealing of the deposited layer [85] or through careful choice of the lattice mis-match between substrate and few atomic-layer thick additional layer. These could then lead to e.g. periodic changes in the chemical composition of the nanodots [86]).

If feasible, this would result in several distinct sub-bands (or at least a continuous variation of the dimensions of the formed nanodots) on the inter-strip or pixel scale, each concentrating nanodots of a specific size, corresponding to emission of light at a zone-specific frequency range [54]. Detecting the frequency of the light emitted by these nanodots in coincidence with the strip signal would then allow uniquely identifying which band the charged particle traversed, effectively resulting in a sub-micron position resolution. Also here, narrow-band photospectrometers (as in section 2.1.3) will be required.

To enhance and control the photon yield in such layers, an alternative to the passively emitting quantum dots is provided by epitaxially grown intermediate structures between quantum wells and quantum dots [87] which combine the light yield of quantum dots with the active control of quantum wells.

Similar to the above approach, thin layers coated with layer-specific nanodots, thus resulting in light of a layer-specific frequency, can be intercalated between tracking layers. If the emission spectrum of these is chosen in the mid-IR, then the emitted scintillation light will be able to pass through any intermediate silicon-based tracking layers, silicon being mostly transparent for infrared wavelengths between 1 μm and 10μ. A spatially and spectrally resolving IR camera positioned outside of the tracking layers would thus also be able to detect the emitted IR photons, adding spatially (and possibly even temporally) resolved hits to any tracks. This approach can be carried out also inside of the innermost tracking layer by an appropriate coating of the beam pipe at the heart of collider experiments. Naturally, care will need to be taken to minimize absorption through services or silicon-tracker internal structures, by e.g., use of ultrathin (few nm) metallic layers or of IR-transparent conductors.

3.2 Quantum Cascade (Active) Scintillators

While in most widely used scintillators, minimum ionizing particles excite electrons from the valence band into the conduction band, which then emit fluorescence light due to transitions between energy band levels (inorganic scintillators) or through molecular excitation and relaxation processes (organic scintillators), these processes can not be actively enhanced (except for static doping with activators), nor electronically controlled. In other words, there is no possibility of “tuning”, of “switching on” (or “off”), of “priming” the properties of the scintillating material dynamically, nor of benefiting from quantum effects beyond those occurring within the existing crystal lattices or the molecular constituents of the scintillators. In recent years, a number of authors have explored novel types of “custom-built” scintillators, whereby the composition, the structure or the surface of the scintillating material is controlled at the nm scale, with significant potential for dramatic improvements in light yield and temporal resolution [88, 89]. But also these nanostructured scintillators, such as those proposed for chromatic tracking above, as essentially passive devices: the scintillation light they emit is produced by spontaneous de-excitation of the nm-sized structures excited by the passage of a charged particle or the interaction with high energy photons, and its frequency is defined by the chemical composition, geometry and dimensions of the emitting structure.

In contrast, active components should allow—in principle—tuning both frequency and intensity of the emitted light. It is thus tempting to consider systems that would either allow “priming” a detector shortly prior to the passage of charged particles of interest, or that would allow “triggering” optical transitions from excited states after the passage of particles, depending on the intended use. Photo-emitting nano-structures are of wide industrial interest are consequently undergoing very active development. Of particular interest here is F-band photoluminescence (see e.g., [90] for a review). Of particular interest here are quantum cascade lasers (QCL), whose series of wells are carefully tailored to allow a coherent process of photon emission, triggered by the successive tunneling steps of an electron from the central potential well into subsequent wells at lower potential, to take place [91]. A modified QCL with a small number of wells (potentially a single one) would provide the possibility of functioning not as an “amplifier” for the initial electron of a QCL that is converted into a large number of monochromatic photons through the multiple stages of the cascade, but rather as a single stage “converter” of the large number of electrons produced through ionization by the passage of a m.i.p. through the QCL’s central well into the same number of (monochromatic) photons as the electrons tunnel through the single stage cascade structure.

Detection of the photons alone would only result in such modified QCL structures behaving like “active scintillators”; in order for them to function additionally as trackers, a correlation between their position and the frequency of the light produced by each individual active element is required. The tunability of QCL’s can provide this correlation, either by fine-tuning the dimensions or by precise control of the voltages applied to each QCL; in either case, under realistic conditions, only a limited number of differentiable frequencies could be produced. This scheme would thus only work in concert with additional trackers that can disambiguate the specific QCL from which a photon was emitted from the subset of identical QCL’s. Readout of such photonic trackers would, as indicated above, be simplified if the emitted photons were in the infrared regime, as is typical of QCL’s, as the photodetectors could then be remote to the emission region.

4 Nanophotonics, Metamaterials, and Plasmonics

4.1 Nanophotonic Cherenkov Detectors

Nanophotonics, metamaterials and the engineering of plasmon modes in nanostructured materials lies somewhat at the border of quantum sensors, but given that it too represents engineering of materials at the nanometer scale and relies on quantum effects brought forth by the interactions between small numbers of atomic or molecular systems, it makes sense to briefly refer in this paper to opportunities appearing due to recent developments in this field. In addition to the surface treatment of scintillators [92] touched upon in section 2.1.2, and which is being pursued to enhance the light yield in the case of photonic crystal scintillators [93, 94] or plasmonic scintillators [95, 96], recent work on Cerenkov light generation also points towards potentially interesting possibilities.

The material limitations (constraints imposed by the use of low refractive index materials and the concomitant low photon yield, or, in the case of dielectrics, very similar Cerenkov angles for high energy particles) in Cherenkov detectors can be partly overcome by using modern concepts from nanophotonics and metamaterials: longitudinal plasmon modes in nanometallic layered materials [97] can allow achieving continuously-tunable enhanced Cherenkov radiation. In another approach [98] relying on the Brewster effet, structures built of 1D photonic crystals of different periodicities but identical constituent materials, form a broadband angular filter. While this Brewster-Cerenkov scheme is significantly more sensitive to particle velocity than approaches based on the standard Cerenkov angle (albeit at the price of a reduced photon flux), the particle to be identified must travel parallel (within 0.5°) to the surface of this structure, a limitation that will require appropriate detector designs.

This directional limitation is however also an invitation to consider using appropriately-constructed Cerenkov detectors as elements of the charged particle tracker. The nanoscale sensitivity of surface Dyakonov-Cerenkov radiation induced by the motion of charged particles in birefringent crystals [99] (radiation emission is greatly enhanced when the particle is within 200 nm of the surface of the birefringent material) makes it possible to consider very high spatial resolution tracking detectors based on the detection of the Dyakonov surface waves. However, the emission of secondaries through the interaction of the primary within the high-density birefringent material and the concomitant energy loss (which limits the photon yield) present serious challenges towards a concrete realization of such a detector. Nevertheless, it is encouraging that approaches based on engineering scintillator or crystal structures at the nanometer scale might open up completely new functionalities or detector families.

5 Nitrogen-Vacancy Diamonds

Defects in diamonds, which are the reason for the variety in coloration of the jewels, have been studied for decades. One of the most studied is the Nitrogen-Vacancy (NV) defect. Its spin state can be optically prepared and be read out [100–102] using the photoluminescence properties of the crystal [103]. The observed quantum properties at room temperature [104] have attracted intense interest and find applications in the areas of quantum information [105], quantum manipulation [106] and quantum sensing with unprecedented accuracy of absolute nanoscale-resolution measurements of magnetic and electric fields [107], spin [108], strain [109] or temperature [110].

The color center can be in a negative (NV⁻) or neutral (NV⁰) state [111]. The NV⁻ center has a detectable magnetic resonance associated with its ground and excited levels, which is not the case for the NV⁰ center. For this reason, the NV⁻ system is usually preferred. The optical transitions of the defects are far from the conduction and valence band levels of the diamond [112]. The NV⁻ defect can be spin polarized using optical excitation, allowing a precise control of its state. This property allows one to use them as polarimeters. However, their use for direct detection requires to have the probe in the atomic vicinity of the sensed particle: the use of electronic spin reporters on the surface of the diamond allows to read at nanometric distances the spin of single particles [113].

The applications that could potentially incorporate nitrogen vacancies in diamonds benefit from the following intrinsic properties: the vacancies constitute a self-calibrated instrument based on known optical transitions, exhibit fast optical spin-polarization, sensitivity to static and dynamic magnetic fields, long coherence times and coupling to neighboring nuclear and electronic spins, and are reliable in handling and manufacturing. Here, we propose two schemes for tracking and polarimetry using NV’s in diamond as active medium of a new kind of particle detectors. The first scheme introduces the optical polarization of the NV center as the active scattering medium which deflects particles depending on the incoming particle spin orientation; the second scheme is that of an active target, prepared to be operated in close vicinity of the reaction in order to sense the remaining low energy fragments after the collisions have taken place.

5.1 Polarimetry and Tracking: NV in Diamond Arrays as a Polar Tracker

The measurement of observables that can be related to the spin orientation of a particle provides an additional degree of control for understanding the underlying physical processes. In this sense, the internal structure of the nucleon, nucleus, the origin of the spin of hadrons or the spin properties of the deconfined fluids produced in collisions of heavy ions could be explored using particle trackers enhanced with intercalated polarized thin scattering planes for measurement of left-right azimuthal asymmetries along the ϕ angle of the particles impinging on these polarimeters.

Currently, spin physics is limited to facilities with polarized beams [114] and targets [115] or to particles such as the self-resolving weak decays, such as of the Λ baryon [116]. Extending the availability of measurements to other hadrons could bring new insights into their structure and interactions or those from whose decay they stem.

The intrinsic optical polarization properties of the NV defects in diamond can be suitable for construction of thin polarized layers with them. Charged particles undergoing elastic scattering with the polarized centers will have a small anisotropy in the left-right scattering direction. By measuring the process several times, a probabilistic estimate of the polarization of the particle can be reconstructed according to the scheme in Figure 3. The simplest setup would consist of a series of thin pairs of silicons or detectors with similar position sensitivity providing high pointing accuracy and a reduced probability of scattering interleaved with NV’s in diamond planes embedded in guides enabling the polarization of the defects. These defects can be efficiently polarized [102] and slightly modify the helicity-dependent scattering direction probability of a charged particle crossing the polar tracker, thus providing access to determining single particle spin orientations.

FIGURE 3

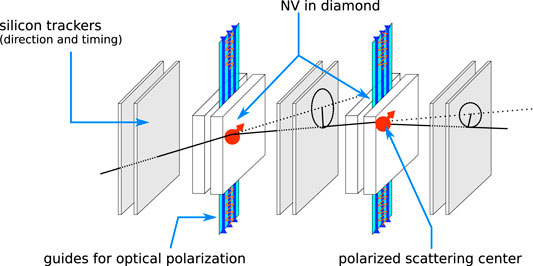
FIGURE 3. Conceptual scheme of a charged particle tracked with incorporated polarimeter based on NV’s in diamond as polarizable scattering medium. The polarization is measured particle-by-particle by using the right-left asymmetry in the scattering probabilities. Two planes of tracking detectors, such as silicon pixel or microstrip detectors, are needed to determine the particle direction before and after the polarized scattering plane. The polarization of the diamonds can be achieved using optical means.

The probability of scattering in a polarized atom is directly proportional to defect abundance in the diamond. The density of defects is one of the parameters that is actively being optimized as the sensitivity as a magnetometer scales with the square root of its number [117]. Several existing approaches using modified deposition schemes [118] or creation of defects with laser radiation [119] can achieve densities of 10^16–18 cm⁻³. In spite of the possibility of locally enhancing this density by another two to three orders of magnitude through hyperpolarization [102] (polarizing the atoms surrounding the defects), an additional increase by two orders of magnitude in the defect abundance (or the size of the locally polarized region surrounding them) will nevertheless be required before such helicity trackers can be realistically contemplated.

5.2 Polarimetry and Tracking: NV in Diamond as Active Targets for Sensing Heavy Fragments

In the previous scheme we have incorporated in the measuring scheme only the optical polarization property of the NV’s in diamond. Diamonds are known for having a high tolerance to ionizing radiation. This makes them suitable beam detectors [120]. Diamonds with defects could however be also used as part of an active target. The high sensitivity of the defects to the presence and spin of even single particles [121] can be used to sense the production and the spin of the remaining highly charged ions (HCI), left after induced fission happens in the interface between the polarized diamond and the target.

The scheme of such an active target is shown in Figure 4. The beam particle hits the target after crossing the first (silicon) tracking section which provides accurate directional and impact location at the position of the diamond target. There, the beam particle interacts with the target producing high momentum particles which are projected in the forward direction. Remnants of the target nucleus might survive and remain in the vicinity of the target with low kinetic energy. The thin silicon trackers provide additional information needed to constraint the locus of the interaction and the vertex and momenta of outgoing particles. The optical readout, which can be synchronized at ns-level with the optical control of the diamond provides background free measurements of the participants and spectators of the collisions. Such a design could also facilitate the measurement of the collision centrality in fixed-target experiments.

FIGURE 4

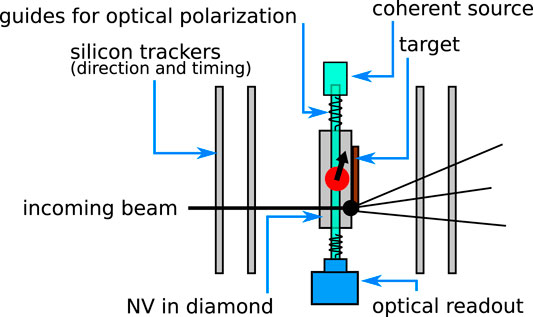
FIGURE 4. Scheme of an active target based on polarized NV’s in diamond used to sense the remaining heavy and slow spectator fragments. The sketch shows the silicon trackers, the target material and the optoelectronic system used to prepare the diamond for the measurement and to perform the readout.

6 Manipulation of Atoms

In recent years, the usage of Rydberg atoms as a key element in many applications has been explored [122]. Their features, related to the precise control of the quantum state, their long lifetime and their size has stimulated their use in quantum computing [123], as sensitive volume [124] or as transducers of electromagnetic radiation of different wavelength [125–127]. The first approaches to produce atomic Rydberg states used collisions, making precise manipulations impossible. Replacing this approach by a laser-based excitation scheme [128] however results in precise control of the accessed energy levels. Rydberg states can be very large, more than 10⁴ times the size of ground state atoms, when they are in high n-states, with n being the principle quantum number. As is the case for many of their properties, their size scales with increasing n, specifically with n². Their lifetime, after including all possible decay modes, scales as n³, being of the order of 10^–5 s for n ∼ 50, making them perfect candidates for long interaction time exposures. Another source of sensitivity is the reduction of the energy needed to strip an electron from a highly excited Rydberg state as compared to starting from ground state atoms. In general, the required energy decreases with n⁻², making them exceptionally sensitive to small changes happening in the medium, be it external electromagnetic fields or the presence of other atomic species or neighbouring Rydberg atoms.

6.1 Optical Tracking TPC’s

High precision charged particle tracking in large volumes requires complex systems, sometimes with more than half a million read-out channels [129]. In addition to collecting charge, recording detector information using electro-optical means is also possible by detecting the fluorescence light produced in the avalanche amplification region [130, 131] of gas-based detectors. This approach has the advantage of providing high accuracy tracking of complex events at a reduced cost [132, 133]. Enhancing tracking detectors with atoms far from the ground state can be interesting in the readout, multiplication or in the ionization regions.

The high sensitivity to electric and magnetic fields of Rydberg atoms makes them ideal candidates for optical transducers [127] for sensing the electron avalanches in the multiplication zone of a projection chamber detector. Sensors based on Rydberg states are not only sensitive to the presence of the fields but also to the incoming direction [134], making it possible to record complex pictures in the visible domain of the amplification region. The scheme of such an optical tracking detector is shown in Figure 5. The scheme shows the typical design of a projection chamber with the large drift volume where the primordial ionization is created along the path of the charged particles. A constant electric field guides the electrons towards the amplification region. Here, a strong electric field accelerates them and electron avalanches are produced. The fast electromagnetic signals in the GHz domain accompanying the electron avalanches can be efficiently transformed into the optical domain using Rydberg states [126]. The excitation of the gas atoms can be done using a two-level laser system tuned to the desired level with sub-ns time synchronization if systems designed for quantum experiments as the Sinara/ARTIQ open hardware and software are used [135, 136]. The highly excited Rydberg atoms in the amplification region also play a second role: their very low and adjustable ionization threshold ensures that electrons in the avalanche can easily ionize them, thus leading to an enhanced avalanche signal.

FIGURE 5

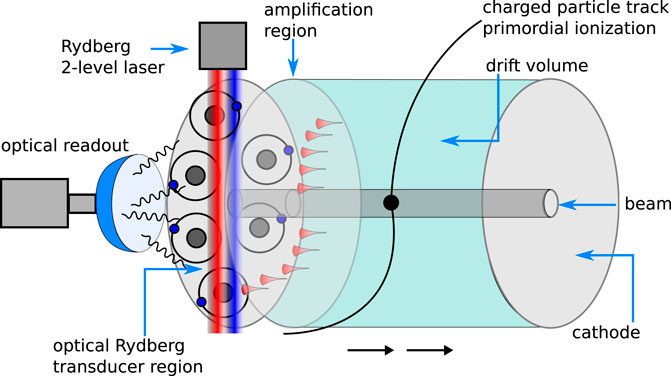
FIGURE 5. Scheme of a projection chamber with a Rydberg transducer of the EM pulses produced in the amplification region and which are upconverted into the visible domain for optical readout. The amplification region furthermore produces an enhanced number of avalanche electrons due to the low ionization threshold of the Rydberg atoms. The atoms are excited by a two-level laser system. The rest of the chamber follows a classical design with a magnetic field to sense the Lorentz force and the homogeneous electric field to transport the electrons and ions from the primordial ionization region to the amplification region.

Alternatively, the concept can be extended to the ionization and drift volume region. If the sensitive volume of the detector can be brought to a highly-excited electronic state, then the immediate benefit is the decrease of the ionization threshold of the medium. This in turn can result in a higher effective ionization along the charged particle’s trajectories, compensating the requirement of a very low gas density to avoid self-ionization (a consequence of the size of Rydberg atoms and their interactions). This would both allow and require a decrease of the current thickness of ∼1% in radiation length [137] by 2 or 3 orders of magnitude, thus reducing the multiple-scattering and energy loss and allowing both the tracking of very low momentum particles and an increase in the momentum resolution and pointing accuracy.

The scheme of a Rydberg Tracking Chamber (RTC) is shown in Figure 6. The optical readout of the signals left by ionizing radiation can be done in 4 steps. In the first one, the low density gas is excited to a low-n Rydberg state with lifetime of 100 ns using a two-level laser system. This process happens synchronously with the expected beam arrival such that the products of the collision find the ionization medium in an excited state, which is the second step. As the excitation cross section dominates over the ionization [138], many low-n Rydberg states can be transferred to high-n states. In the third step, the low-n Rydberg atoms de-excite by emitting photons. However, those atoms that have been excited further have an extended lifetime which can reach μs. These highly excited states can be read out in the last step directly using the electromagnetic induced transparency [139, 140] or the atoms can be photo-detached by electric fields and the resulting supernumerary (with respect to standard ionization) electrons or ions can be detected by conventional means simultaneously with the electrons or ions generated along the same trajectory by standard ionization.

FIGURE 6

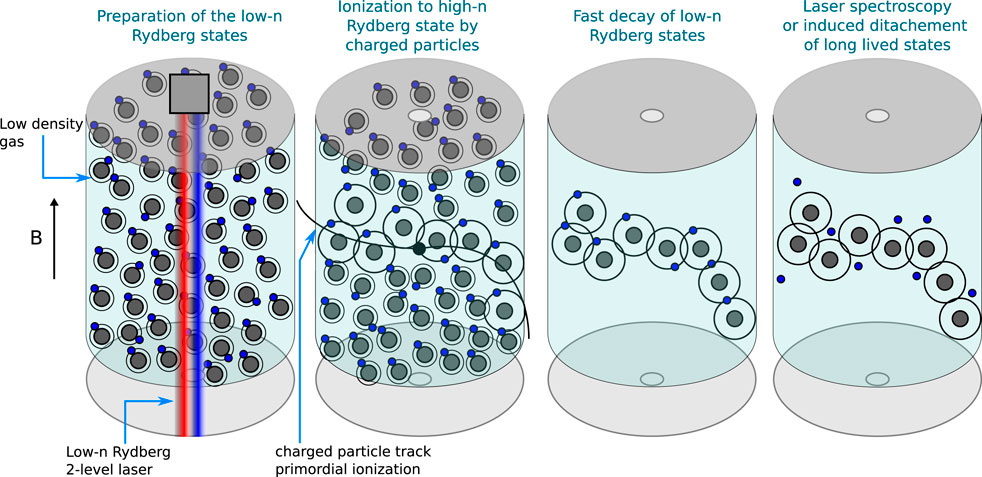
FIGURE 6. Scheme of a tracking chamber using Rydberg atoms as sensing medium. The measurement is performed in four steps. First, via two-level laser excitation, the atoms in the primary ionization region are brought to a low-n Rydberg state synchronously with the collision time. In the second step, the charged particles produced in the reaction ionize or excite the Rydberg atoms along their flight path. After that, the short lived states decay back to the ground state and the highly excited Rydberg states can be read out using opto-electronic means, such as electromagnetic induced transparency. Alternatively, the electrons can be photo-detached and detected as an effective locally increased ionization cloud using standard techniques.

7 Conclusion

While most of the ideas proposed in this paper are very speculative, and much exploratory and developmental work will be required to ascertain their feasibility or usefulness in the context of high energy physics detectors, it is our hope that they could be seen as incentives for further exploration: the problems they address require solutions which these or other quantum sensors may be able to contribute to. It is also clear that these proposed approaches may be neither the optimal, nor the only quantum sensing approaches to some of the challenges of future high energy physics detectors.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors contributed to the paper, writing different sections and correcting the complete document. Specifically, EA, IF, and HH wrote sections on scintilators and nanodots; FB and GO wrote sections related to 2-dimensional materials; GK wrote sections on polarimetry and TPC’s; MD wrote the remaining sections.

Funding

Research was funded by Warsaw University of Technology within the Excellence Initiative: Research University (IDUB) programme and the IDUB-POB-FWEiTE-1 project grant. This work has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 801110. It reflects only the authors’ view; the EU agency is not responsible for any use that may be made of the information it contains.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The work on low dimensional materials for gaseous detectors is conducted within the activities of the CERN EP-DT-DD Gaseous Detector Development (GDD) team and FB and GO would like to thanks and recognise the contribution of the group of Camilla Coletti at Istituto Italiano di Tecnologia (IIT). EA would like to thank her colleagues of Crystal Clear Collaboration.

References

1. Safronova M, Budker De. Focus on Quantum Sensors for New-Physics Discoveries. Quan Sci. Technol. (2022) 6:040401. Available at: https://iopscience.iop.org/journal/2058-9565/page/Focus-on-Quantum-Sensors-for-New-Physics-Discoveries. [Accessed June 10, 2022].

Google Scholar

2. Irastorza IG, Redondo J. New Experimental Approaches in the Search for Axion-like Particles. Prog Part Nucl Phys (2018) 102:89–159. doi:10.1016/j.ppnp.2018.05.003

CrossRef Full Text | Google Scholar

3. Backes KM, Palken DA, Kenany SA, Brubaker BM, Cahn SB, Droster A, et al. A Quantum Enhanced Search for Dark Matter Axions. Nature (2021) 590:238–42. doi:10.1038/s41586-021-03226-7

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Geraci AA, Bradley C, Gao D, Weinstein J, Derevianko A. Searching for Ultralight Dark Matter with Optical Cavities. Phys Rev Lett (2019) 123(Jul):031304. doi:10.1103/PhysRevLett.123.031304

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dujardin C, Auffray E, Bourret-Courchesne E, Dorenbos P, Lecoq P, Nikl M, et al. Needs, Trends, and Advances in Inorganic Scintillators. IEEE Trans Nucl Sci (2018) 65(8):1977–97. doi:10.1109/tns.2018.2840160

CrossRef Full Text | Google Scholar

6. Brunner SE, Schaart DR. BGO as a Hybrid Scintillator/Cherenkov Radiator for Cost-Effective Time-Of-Flight PET. Phys Med Biol (2017) 62:4421–39. doi:10.1088/1361-6560/aa6a49

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gundacker S, Martinez Turtos R, Kratochwil N, Pots RH, Paganoni M, Lecoq P, et al. Experimental Time Resolution Limits of Modern SiPM’s and TOF- PET Detectors Exploring Different Scintillators and Cherenkov Emission. Phys Med Biol (2020) 65(2):025001. doi:10.1088/1361-6560/ab63b4

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kratochwil N, Gundacker S, Lecoq P, Auffray E. Pushing Cherenkov PET with BGO via Coincidence Time Resolution Classification and Correction. Phys Med Biol (2020) 65:115004. doi:10.1088/1361-6560/ab87f9

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Van Eijk CWE. Cross-luminescence. J Lumin (1994) 60-61:936–41. doi:10.1016/0022-2313(94)90316-6

CrossRef Full Text | Google Scholar

10. Pots E, Auffray R, Gundacker S Exploiting Cross-Luminescence in BaF₂ for Ultrafast Timing Applications Using Deep-Ultraviolet Sensitive hpk Silicon Photomultipliers. Front Phys (2020)8:4821. doi:10.3389/fphy.2020.592875

CrossRef Full Text | Google Scholar

11. Gundacker S, Pots RH, Nepomnyashchikh A, Radzhabov E, Shendrik R, Omelkov S, et al. Vacuum Ultraviolet Silicon Photomultipliers Applied to BaF2 Cross-Luminescence Detection for High-Rate Ultrafast Timing Applications. Phys Med Biol (2021) 66:114002. doi:10.1088/1361-6560/abf476

CrossRef Full Text | Google Scholar

12. Omelkov SI, Nagirnyi V, Vasil׳ev AN, Kirm M. New Features of Hot Intraband Luminescence for Fast Timing. J Lumin (2016) 176:309–17. doi:10.1016/j.jlumin.2016.03.039

CrossRef Full Text | Google Scholar

13. Létant SE, Wang T-F. Semiconductor Quantum Dot Scintillation under γ-Ray Irradiation. Nano Lett (2006) 6:2877–80. doi:10.1021/nl0620942

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Turtos RM, Gundacker S, Polovitsyn A, Christodoulou S, Salomoni M, Auffray E, et al. Ultrafast Emission from Colloidal Nanocrystals under Pulsed X-ray Excitation. J Inst (2016) 11:P10015. doi:10.1088/1748-0221/11/10/p10015

CrossRef Full Text | Google Scholar

15. Procházková L, Tomáš G, Václav C, Vítězslav J, Martin N. Fabrication of Highly Efficient ZnO Nanoscintillators. Opt Mater (2015) 47:67–71. doi:10.1016/j.optmat.2015.07.001

CrossRef Full Text | Google Scholar

16. Hospodková A, Martin N, Oliva P, Jiří O, Petr B, Dalibor P, et al. InGaN/GaN Multiple Quantum Well for Fast Scintillation Application: Radioluminescence and Photoluminescence Study. Nanotechnology (2014) 25:455501. doi:10.1088/0957-4484/25/45/455501

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Čuba KV, Brik MG, Mihóková E, Martinez Turtos R, Lecoq P, Auffray E, et al. On the Structure, Synthesis, and Characterization of Ultrafast Blue-Emitting CsPbBr3 Nanoplatelets. APL Mater (2019) 7:011104. doi:10.1063/1.5079300

CrossRef Full Text | Google Scholar

18. Efros AL, Brus LE. Nanocrystal Quantum Dots: From Discovery to Modern Development. ACS nano (2021) 15:6192–210. doi:10.1021/acsnano.1c01399

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Pietryga JM, Park YS, Lim J, Fidler AF, Bae WK, Brovelli S, et al. Spectroscopic and Device Aspects of Nanocrystal Quantum Dots. Chem Rev (2016) 116:10513–622. doi:10.1021/acs.chemrev.6b00169

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Edvinsson T. Optical Quantum Confinement and Photocatalytic Properties in Two-, One- and Zero-Dimensional Nanostructures. R Soc Open Sci (2018) 5:180387. doi:10.1098/rsos.180387

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ooba H. Synthesis of Unique High Quality Fluorescence Quantum Dots for the Biochemical Measurements. AIST TODAY (2006) 6:26–7. Available at: https://www.aist.go.jp/Portals/0/resource_images/aist_e/aist_today/2006_21/pdf/2006_21_p22.pdf. [Accessed June 10, 2022].

Google Scholar

22. Fontes A. Quantum Dots in Biomedical Researchs. In: Biomedical Engineering - Technical Applications in Medicine. London, United Kingdom: IntechOpen. (2012). Available at: https://www.intechopen.com/chapters/38785. [Accessed June 10, 2022].

Google Scholar

23. Klimov VI. Spectral and Dynamical Properties of Multiexcitons in Semiconductor Nanocrystals. Annu Rev Phys Chem (2007) 58:635–73. doi:10.1146/annurev.physchem.58.032806.104537

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Klimov VI. Multicarrier Interactions in Semiconductor Nanocrystals in Relation to the Phenomena of Auger Recombination and Carrier Multiplication. Annu Rev Condens Matter Phys (2014) 5:285–316. doi:10.1146/annurev-conmatphys-031113-133900

CrossRef Full Text | Google Scholar

25. Korzh B, Zhao Q, Allmaras J, Simone F, Travis MA, Eric AB, et al. Demonstration of Sub-3 Ps Temporal Resolution with a Superconducting Nanowire Single-Photon Detector. Nat Photon (2020) 14:250–5.

Google Scholar

26. Onaru K, Hara K, Harada D, Wada S, Nakamura K, Unno Y. Study of Time Resolution of Low-Gain Avalanche Detectors. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2021) 985:164664. doi:10.1016/j.nima.2020.164664

CrossRef Full Text | Google Scholar

27. Grim JQ, Christodoulou S, Di Stasio F, Krahne R, Cingolani R, Manna L, et al. Continuous-wave Biexciton Lasing at Room Temperature Using Solution-Processed Quantum wells. Nat Nanotech (2014) 9:891–5. doi:10.1038/nnano.2014.213

CrossRef Full Text | Google Scholar

28. Christodoulou S, Vaccaro G, Pinchetti V, De Donato F, Grim JQ, Casu A, et al. Synthesis of Highly Luminescent Wurtzite CdSe/CdS Giant-Shell Nanocrystals Using a Fast Continuous Injection Route. J Mater Chem C (2014) 2:3439. doi:10.1039/c4tc00280f

CrossRef Full Text | Google Scholar

29. Meng Z, Mahler B, Houel J, Kulzer F, Ledoux G, Vasil'ev A, et al. Perspectives for CdSe/CdS Spherical Quantum wells as Rapid-Response Nano-Scintillators. Nanoscale (2021) 13:19578–86. doi:10.1039/d1nr04781g

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Liu C, Li Z, Hajagos TJ, Kishpaugh D, Chen DY, Pei Q. Transparent Ultra-high-loading Quantum Dot/Polymer Nanocomposite Monolith for Gamma Scintillation. ACS nano (2017) 11:6422–30. doi:10.1021/acsnano.7b02923

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Procházková L, Cuba V, Mrazek J, Beitlerova A, Jary V, Nikl M. Preparation of Zn(Cd)O:Ga–SiO2 Composite Scintillating Materials. Radiat Meas (2016) 90:59–63. doi:10.1016/j.radmeas.2015.12.040

CrossRef Full Text | Google Scholar

32. Buresova H, Lenka P, Rosana MT, Vítězslav J, Eva M, Alena B, et al. Preparation and Luminescence Properties of ZnO:Ga – Polystyrene Composite Scintillator. Opt Express (2016) 24:15289–98. doi:10.1364/OE.24.015289

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Turtos RM, Gundacker S, Lucchini MT, Procházková L, Čuba V, Burešová H, et al. Timing Performance of ZnO:Ga Nanopowder Composite Scintillators. Phys Status Solidi RRL (2016) 10:843–7. doi:10.1002/pssr.201600288

CrossRef Full Text | Google Scholar

34. Hubáček T, Hospodková A, Kuldová K, Oswald J, Pangrác J, Jarý V, et al. Advancement toward Ultra-thick and Bright InGaN/GaN Structures with a High Number of QWs. CrystEngComm (2019) 21:356–62. doi:10.1039/C8CE01830H Available at: https://pubs.rsc.org/en/content/articlelanding/2019/ce/c8ce01830h/unauth. [Accessed June 10, 2022].

CrossRef Full Text | Google Scholar

35. Tocci G, Leonida GA, Petra K, Baffigi F, Lorenzo F, Luca L, et al. InGaN/GaN Multiple Quantum Well for Superfast Scintillation Application: Photoluminescence Measurements of the Picosecond Rise Time and Excitation Density Effect. J Lumin (2019) 208:119–24. doi:10.1016/j.jlumin.2018.12.034

CrossRef Full Text | Google Scholar

36. Jary V, Hospodkova A, Hubacek T, Hajek F, Blazek K, Nikl M. Optical Properties of InGaN/GaN Multiple Quantum Well Structures Grown on GaN and Sapphire Substrates. IEEE Trans Nucl Sci (2020) 67:974–7. doi:10.1109/tns.2020.2985666

CrossRef Full Text | Google Scholar

37. Decka K, Jan K, František H, Petr P, Vladimir B, Eva M. Scintillation Response Enhancement in Nanocrystalline lead Halide Perovskite Thin Films on Scintillating Wafers. Nanomaterials (2022) 12(1):14. doi:10.3390/nano12010014

CrossRef Full Text | Google Scholar

38. Gandini M, Villa I, Beretta M, Gotti C, Imran M, Carulli F, et al. Efficient, Fast and Reabsorption-free Perovskite Nanocrystal-Based Sensitized Plastic Scintillators. Nat Nanotechnol (2020) 15:462–8. doi:10.1038/s41565-020-0683-8

PubMed Abstract | CrossRef Full Text | Google Scholar

39.Silicon. High Transmission Silicon for Infrared Optical Applications (2019). Available at: https://www.sil-tronix-st.com/en/news/High-transmission-silicon-for-infrared-optical-applications. [Accessed June 10, 2022].

Google Scholar

40. Lecoq P, Metamaterials for Novel X- or γ-ray Detector Designs, 2008 IEEE Nuclear Science Symposium Conference Record. (2008) 1405–9.

Google Scholar

41. Lecoq P. TICAL: 4D Total absorptionTime Imaging CALorimeter, ERC grant 338953 (TICAL) (2014). Available at: https://cordis.europa.eu/project/id/338953/fr. [Accessed June 10, 2022].

Google Scholar

42. Turtos RM, Gundacker S, Auffray E, Lecoq P. Towards a Metamaterial Approach for Fast Timing in PET: Experimental Proof-Of-Concept. Phys Med Biol (2019) 64(18):185018. doi:10.1088/1361-6560/ab18b3

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Turtos R, Gundacker S, Omelkov S. On the Use of Cdse Scintillating Nanoplatelets as Time Taggers for High-Energy Gamma Detection. npj 2D Mater Appl (2019) 3(1):185018. doi:10.1038/s41699-019-0120-8

CrossRef Full Text | Google Scholar

44. Tomanová K, Suchá A, Mihóková E, Procházková L, Jakubec I, Turtos RM, et al. CsPbBr3 Thin Films on LYSO:Ce Substrates. IEEE TRANSACTIONS NUCLEAR SCIENCE (2020) 67(6):933–7. doi:10.1109/TNS.2020.2978581 Available at: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9025189. [Accessed June 10, 2022].

CrossRef Full Text | Google Scholar

45. Oktyabrsky S, Yakimov M, Tokranov V, Murat P. Integrated Semiconductor Quantum Dot Scintillation Detector: Ultimate Limit for Speed and Light Yield. IEEE Trans Nucl Sci (2016) 63:656–63. doi:10.1109/tns.2015.2502426

CrossRef Full Text | Google Scholar

46. Dropiewski K, Minns A, Yakimov M, Tokranov V, Murat P, Oktyabrsky S. Optical Properties of InAs Quantum Dots/GaAs Waveguides for Ultra-fast Scintillators. J Lumin (2020) 220:116952. doi:10.1016/j.jlumin.2019.116952

CrossRef Full Text | Google Scholar

47. Tam AK, Boyraz O, Unangst J, Nazareta P, Schreuder M, Nilsson M. Quantum-dot Doped Polymeric Scintillation Material for Radiation Detection. Radiat Measurements (2018) 111:27–34. doi:10.1016/j.radmeas.2018.02.008

CrossRef Full Text | Google Scholar

48. Delage M-È, Lecavalier M-È, Larivière D, Nì Allen C, Beaulieu L. Characterization of a Binary System Composed of Luminescent Quantum Dots for Liquid Scintillation. Phys Med Biol (2018) 63(17):175012. doi:10.1088/1361-6560/aad9c3

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Delage MÈ, Lecavalier MÈ, Larivière D, Allen CN, Beaulieu L. Dosimetric Properties of Colloidal Quantum Dot-Based Systems for Scintillation Dosimetry. Phys Med Biol (2018) 64:095027. doi:10.1088/1361-6560/ab109b

CrossRef Full Text | Google Scholar

50. Beretta M, Amirkhani A, Brofferio C, Brovelli S, Buonanno L. The ESQUIRE Project: Quantum Dots as Scintillation Detectors. IL NUOVO CIMENTO (2019) 42C:188. doi:10.1393/ncc/i2019-19188-4 Available at: https://www.sif.it/riviste/sif/ncc/econtents/2019/042/04/article/43. [Accessed June 10, 2022]

CrossRef Full Text | Google Scholar

51.AIDAinnova. AIDAinnova Project (2021). Available at: https://aidainnova.web.cern.ch/newsletter. [Accessed June 10, 2022].

Google Scholar

52. Moulson M, NanoCal, Blue Sky Project AIDAinnova, Private Communication.

Google Scholar

53. Liu J, Geng Y, Li D, Yao H, Huo Z, Li Y, et al. Deep Red Emissive Carbonized Polymer Dots with Unprecedented Narrow Full Width at Half Maximum. Adv Mater (2020) 32:1906641. doi:10.1002/adma.201906641

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Yuan F, Yuan T, Sui L, Wang Z, Xi Z, Li Y, et al. Engineering Triangular Carbon Quantum Dots with Unprecedented Narrow Bandwidth Emission for Multicolored LEDs. Nat Commun (2018) 9:2249. doi:10.1038/s41467-018-04635-5

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Zhang C, Wan Q, Ono LK, Liu Y, Zheng W, Zhang Q, et al. Narrow-Band Violet-Light-Emitting Diodes Based on Stable Cesium Lead Chloride Perovskite Nanocrystals. ACS Energ Lett. (2021) 6:3545–54. doi:10.1021/acsenergylett.1c01380

CrossRef Full Text | Google Scholar

56. Cheng R, Zou C-L, Guo X, Wang S, Han X, Tang HX. Broadband On-Chip Single-Photon Spectrometer. Nat Commun (2019) 10:4104. doi:10.1038/s41467-019-12149-x

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Miao J, Zhang F. Recent Progress on Highly Sensitive Perovskite Photodetectors. J Mater Chem C (2019) 7:1741–91. doi:10.1039/C8TC06089D

CrossRef Full Text | Google Scholar

58. Zhou J, Luo J, Rong X, Wei P, Molokeev MS, Huang Y, et al. Lead‐Free Perovskite Derivative Cs 2 SnCl 6− X Br X Single Crystals for Narrowband Photodetectors. Adv Opt Mater (2019) 7:1900139. doi:10.1002/adom.201900139

CrossRef Full Text | Google Scholar

59. Iguaz F, Bortfeldt J, Brunbauer F, David C, Desforge D, Fanourakis G, et al. Charged Particle Timing at Sub-25 Picosecond Precision: The PICOSEC Detection Concept. Nucl Instruments Methods Phy. Res Sect A (2019) 936:515–18.

CrossRef Full Text | Google Scholar

60. Polyakov A, Senft C, Thompson KF, Feng J, Cabrini S, Schuck PJ, et al. Plasmon-enhanced Photocathode for High Brightness and High Repetition Rate X-ray Sources. Phys Rev Lett (2013) 110(Feb):076802. doi:10.1103/PhysRevLett.110.076802

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Green ME, Bas DA, Yao HY, Gengler JJ, Headrick RJ, Back TC, et al. Bright and Ultrafast Photoelectron Emission from Aligned Single-Wall Carbon Nanotubes through Multiphoton Exciton Resonance. Nano Lett (2019) 19:158–64. doi:10.1021/acs.nanolett.8b03564

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Choi HJ, Raghunathan A, Groves TR. Size Dependent Enhancement of Photoelectron Emission Quantum Efficiencies from Magnesium Dots. J Vac Sci Technol B, Nanotechnol Microelectron Mater Process Meas Phenom (2012) 30:06F605. doi:10.1116/1.4766883

CrossRef Full Text | Google Scholar

63. Naghdi S, Sanchez-Arriaga G, Rhee KY. Tuning the Work Function of Graphene toward Application as Anode and Cathode. J Alloys Compounds (2019) 805:1117–34. doi:10.1016/j.jallcom.2019.07.187

CrossRef Full Text | Google Scholar

64. Lin X, Easo S, Shen Y, Chen H, Zhang B, Joannopoulos JD, et al. Controlling Cherenkov Angles with Resonance Transition Radiation”. Nat Phys (2018) 14:816–21. doi:10.1038/s41567-018-0138-4

CrossRef Full Text | Google Scholar

65. Lin X, Hu H, Easo S, Yang Y, Shen Y, Yin K, et al. A Brewster Route to Cherenkov Detectors. Nat Commun (2021) 12. arXiv:2107. doi:10.1038/s41467-021-25822-x

CrossRef Full Text | Google Scholar

66. Wang G, Yang P, Moody NA, Batista ER. Overcoming the Quantum Efficiency-Lifetime Tradeoff of Photocathodes by Coating with Atomically Thin Two-Dimensional Nanomaterials. Npj 2d Mater Appl (2018) 2:17. doi:10.1038/s41699-018-0062-6

CrossRef Full Text | Google Scholar

67. Wang G, Yang P, Batista ER. Computational Screening of Two-Dimensional Coatings for Semiconducting Photocathodes. Phys Rev Mater (2020) 4:024001. doi:10.1103/physrevmaterials.4.024001

CrossRef Full Text | Google Scholar

68. Yamaguchi H, Liu F, DeFazio J, Narvaez Villarrubia CW, Finkenstadt D, Shabaev A, et al. Active Bialkali Photocathodes on Free-Standing Graphene Substrates. Npj 2d Mater Appl (2017) 1:12. doi:10.1038/s41699-017-0014-6

CrossRef Full Text | Google Scholar

69. Liu F, Guo L, DeFazio J, Pavlenko V, Yamamoto M, Moody NA, et al. Photoemission from Bialkali Photocathodes through an Atomically Thin Protection Layer. ACS Appl Mater Inter (2022) 14(1):1710–7. PMID: 34935342. doi:10.1021/acsami.1c19393

CrossRef Full Text | Google Scholar

70. Liu F, Moody NA, Jensen KL, Pavlenko V, Narvaez Villarrubia CW, Mohite AD, et al. Single Layer Graphene Protective Gas Barrier for Copper Photocathodes. Appl Phys Lett (2017) 110(4):041607. doi:10.1063/1.4974738

CrossRef Full Text | Google Scholar

71. Franchino S, Gonzalez-Diaz D, Hall-Wilton R, Jackman RB, Muller H, Nguyen TT, et al. Charge Transfer Properties through Graphene for Applications in Gaseous Detectors. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2016) 824:571–4. doi:10.1016/j.nima.2015.11.077

CrossRef Full Text | Google Scholar

72. Berry V. Impermeability of Graphene and its Applications. Carbon (2013) 62:1–10. doi:10.1016/j.carbon.2013.05.052

CrossRef Full Text | Google Scholar

73. Lee C, Wei X, Kysar JW, Hone J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science (2008) 321:385–8. doi:10.1126/science.1157996

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Sinha S, Warner JH. Recent Progress in Using Graphene as an Ultrathin Transparent Support for Transmission Electron Microscopy. Small Structures (2021) 2(4):2000049. doi:10.1002/sstr.202000049

CrossRef Full Text | Google Scholar

75. Meyer JC, Geim AK, Katsnelson MI, Novoselov KS, Booth TJ, Roth S. The Structure of Suspended Graphene Sheets. Nature (2007) 446:60–3. doi:10.1038/nature05545

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Hassink G, Wanke R, Rastegar I, Braun W, Stephanos C, Herlinger P, et al. Transparency of Graphene for Low-Energy Electrons Measured in a Vacuum-Triode Setup. APL Mater (2015) 3(7):076106. doi:10.1063/1.4927406

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Il’ichev EA, Kuleshov AE, Migunov DM, Nabiev RM, Petrukhin GN, Rychkov GS, et al. Studying the Transparency of Graphene for Low-Energy Electrons. Tech Phys Lett (2018) 44:848–51. doi:10.1134/S1063785018090201

CrossRef Full Text | Google Scholar

78. Srisonphan S, Kim M, Kim HK. Space Charge Neutralization by Electron-Transparent Suspended Graphene. Sci Rep (2014) 4:3764. doi:10.1038/srep03764

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Huang S, Dakhchoune M, Luo W, Oveisi E, He G, Rezaei M, et al. Single-layer Graphene Membranes by Crack-free Transfer for Gas Mixture Separation. Nat Commun (2018) 9:2632. doi:10.1038/s41467-018-04904-3

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Sun PZ, Yang Q, Kuang WJ, Stebunov YV, Xiong WQ, Yu J, et al. Limits on Gas Impermeability of Graphene. Nature (2020) 579:229–32. doi:10.1038/s41586-020-2070-x

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Sun PZ, Yagmurcukardes M, Zhang R, Kuang WJ, Lozada-Hidalgo M, Liu BL, et al. Exponentially Selective Molecular Sieving through Angstrom Pores. Nat Commun (2021) 12:7170. doi:10.1038/s41467-021-27347-9

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Bacchetta N, Collins P, Riedler P. Tracking and Vertex Detectors at FCC-Ee. Eur Phys J Plus (2022) 137:231. doi:10.1140/epjp/s13360-021-02323-w

CrossRef Full Text | Google Scholar

83. Minns A, Dropiewski K, Yakimov M, Tokranov V, Hedges M, Murat P, et al. Parameters of Fast and High-Yield InAs/GaAs Quantum Dot Semiconductor Scintillator. MRS Adv (2021) 6:297–302. doi:10.1557/s43580-021-00019-y

CrossRef Full Text | Google Scholar

84. Camilli L, Jørgensen JH, Tersoff J, Stoot AC, Balog R, Cassidy A, et al. Self-assembly of Ordered Graphene Nanodot Arrays. Nat Commun (2017) 8:47. doi:10.1038/s41467-017-00042-4

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Zheng M, Yu M, Liu Y, Skomski R, Liou SH, Sellmyer DJ, et al. Magnetic Nanodot Arrays Produced by Direct Laser Interference Lithography. Appl Phys Lett (2001) 79:2606–8. doi:10.1063/1.1409948

CrossRef Full Text | Google Scholar

86. Maximov MV, Nadtochiy AM, Mintairov SA, Kalyuzhnyy NA, Kryzhanovskaya NV, Moiseev EI, et al. Light Emitting Devices Based on Quantum Well-Dots. Appl Sci (2020) 10(3):1038. doi:10.3390/app10031038

CrossRef Full Text | Google Scholar

87. Maximov MV, Nadtochiy AM, Mintairov SA, Kalyuzhnyy NA, Kryzhanovskaya NV, Moiseev EI, et al. Light Emitting Devices Based on Quantum Well-Dots. Appl Sci (2020) 10(3). doi:10.3390/app10031038

CrossRef Full Text | Google Scholar

88. Knapitsch A, Auffray E, Fabjan CW, Leclercq J-L, Letartre X, Mazurczyk R, et al. Results of Photonic crystal Enhanced Light Extraction on Heavy Inorganic Scintillators. IEEE Trans Nucl Sci (2012) 59(5):2334–9. doi:10.1109/tns.2012.2184556

CrossRef Full Text | Google Scholar

89. Roques-Carmes C, Rivera N, Ghorashi A, Kooi SE, Yang Y, Lin Z, et al. A General Framework for Scintillation in Nanophotonics (2021). arXiv preprint arXiv:2110.11492.

Google Scholar

90. Canham L. Introductory Lecture: Origins and Applications of Efficient Visible Photoluminescence from Silicon-Based Nanostructures. Faraday Discuss (2020) 222:10–81. doi:10.1039/d0fd00018c

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Faist J, Capasso F, Sivco DL, Sirtori C, Hutchinson AL, Cho AY. Quantum cascade Laser. Science (1994) 264:553–6. doi:10.1126/science.264.5158.553

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Knapitsch A, Lecoq P. Review on Photonic crystal Coatings for Scintillators. Int J Mod Phys A (2014) 29:1430070. doi:10.1142/S0217751X14300701

CrossRef Full Text | Google Scholar

93. Salomoni M, Pots R, Auffray E, Lecoq P. Enhancing Light Extraction of Inorganic Scintillators Using Photonic Crystals. Crystals (2018) 8(2). doi:10.3390/cryst8020078

CrossRef Full Text | Google Scholar

94. Kurman Y, Shultzman A, Segal O, Pick A, Kaminer I. Photonic-Crystal Scintillators: Molding the Flow of Light to Enhance X-Ray and γ-Ray Detection. Phys Rev Lett (2020) 125(Jul):040801. doi:10.1103/PhysRevLett.125.040801

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Liu B, Ouyang X. Optical Improvements of Plastic Scintillators by Nanophotonics. Plast Scintillators (2021) 140. doi:10.1007/978-3-030-73488-6_9

CrossRef Full Text | Google Scholar

96. García-Lojo D, Núñez Sánchez S, Gómez-Graña S, Marek Grzelczak M, Pastoriza-Santos I, Pérez-Juste J, et al. Plasmonic Supercrystals. Acc Chem Res (2019) 52(7):1855–64. doi:10.1021/acs.accounts.9b00213

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Günay M, Chuang Y-L, Tasgin ME. Continuously-tunable Cherenkov-Radiation-Based Detectors via Plasmon index Control. Nanophotonics (2020) 9(6):1479–89. doi:10.1515/nanoph-2020-0081

CrossRef Full Text | Google Scholar

98. Lin X, Hu H, Easo S, Yang Y, Shen Y, Yin K, et al. A Brewster Route to Cherenkov Detectors. Nat Commun (2021) 12:5554. doi:10.103810.1038/s41467-021-25822-x

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Hu H, Lin X, Wong LJ, Yang Q, Liu D, Zhang B, et al. Surface Dyakonov-Cherenkov Radiation. eLight (2022) 2:2. doi:10.1186/s43593-021-00009-5

CrossRef Full Text | Google Scholar

100. Jelezko F, Gaebel T, Popa I, Domhan M, Gruber A, Wrachtrup J. Observation of Coherent Oscillation of a Single Nuclear Spin and Realization of a Two-Qubit Conditional Quantum Gate. Phys Rev Lett (2004) 93:130501. doi:10.1103/PhysRevLett.93.130501

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Jelezko F, Gaebel T, Popa I, Gruber A, Wrachtrup J. Observation of Coherent Oscillations in a Single Electron Spin. Phys Rev Lett (2004) 92:076401. doi:10.1103/PhysRevLett.92.076401

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Álvarez GA, Bretschneider CO, Fischer R, London P, Kanda H, Onoda S, et al. Local And Bulk ¹³C Hyperpolarization in Nitrogen-Vacancy-Centred Diamonds at Variable fields and Orientations. Nat Commun (2015) 6(Sept):8456. arXiv:1412.8635 [quant-ph].

PubMed Abstract | Google Scholar

103. Schirhagl R, Chang K, Loretz M, Degen CL. Nitrogen-Vacancy Centers in Diamond: Nanoscale Sensors for Physics and Biology. Annu Rev Phys Chem (2014) 65(1):83–105. PMID: 24274702. doi:10.1146/annurev-physchem-040513-103659

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Dutt MVG, Childress L, Jiang L, Togan E, Maze J, Jelezko F, et al. Quantum Register Based on Individual Electronic and Nuclear Spin Qubits in Diamond. Science (2007) 316:1312–6. doi:10.1126/science.1139831

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Dolde F, Jakobi I, Naydenov B, Zhao N, Pezzagna S, Trautmann C, et al. Room-temperature Entanglement between Single Defect Spins in diamond. Nat Phys (2013) 9(Feb):139–43. doi:10.1038/nphys2545

CrossRef Full Text | Google Scholar

106. Jelezko F, Wrachtrup J. Single Defect Centres in diamond: A Review. Phys Stat Sol (A) (2006) 203(13):3207–25. doi:10.1002/pssa.200671403

CrossRef Full Text | Google Scholar

107. Budker D, Romalis M. Optical Magnetometry. Nat Phys (2007) 3(Apr):227–34. doi:10.1038/nphys566

CrossRef Full Text | Google Scholar

108. Müller C, Kong X, Cai J-M, Melentijević K, Stacey AD, Markham ML, et al. Nuclear Magnetic Resonance Spectroscopy with Single Spin Sensitivity. Nat Commun (2014) 5. doi:10.1021/acs.accounts.9b00213

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Doherty MW, Struzhkin VV, Simpson DA, McGuinness LP, Meng Y, Stacey A, et al. Electronic Properties and Metrology Applications of the DiamondNV−Center under Pressure. Phys Rev Lett (2014) 112: doi:10.1103/PhysRevLett.112.047601

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Acosta VM, Bauch E, Ledbetter MP, Waxman A, Bouchard LS, Budker D. Temperature Dependence of the Nitrogen-Vacancy Magnetic Resonance in Diamond. Phys Rev Lett (2010) 104(Feb):070801. doi:10.1103/PhysRevLett.104.070801

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Doherty MW, Manson NB, Delaney P, Jelezko F, Wrachtrup J, Hollenberg LCL. The Nitrogen-Vacancy Colour centre in diamond. Phys Rep (2013) 528(Jul):1–45. doi:10.1016/j.physrep.2013.02.001

CrossRef Full Text | Google Scholar

112. Loubser JHN, Wyk JAv. Electron Spin Resonance in the Study of diamond. Rep Prog Phys (1978) 41(aug):1201–48. doi:10.1088/0034-4885/41/8/002

CrossRef Full Text | Google Scholar

113. Sushkov AO, Lovchinsky I, Chisholm N, Walsworth RL, Park H, Lukin MD. Magnetic Resonance Detection of Individual Proton Spins Using Quantum Reporters. Phys Rev Lett (2014) 113(Nov):197601. doi:10.1103/PhysRevLett.113.197601

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Bunce G, Saito N, Soffer J, Vogelsang W. Prospects for Spin Physics at RHIC. Annu Rev Nucl Part Sci (2000) 50:525–75. arXiv:hep-ph/0007218. doi:10.1146/annurev.nucl.50.1.525

CrossRef Full Text | Google Scholar

115. Crabb DG, Meyer W. Solid Polarized Targets for Nuclear and Particle Physics Experiments. Annu Rev Nucl Part Sci (1997) 47:67–109. doi:10.1146/annurev.nucl.47.1.67

CrossRef Full Text | Google Scholar

116. Kharzeev DE, Liao J, Voloshin SA, Wang G. Chiral Magnetic and Vortical Effects in High-Energy Nuclear Collisions-A Status Report. Prog Part Nucl Phys (2016) 88:1–28. arXiv:1511.04050 [hep-ph]. doi:10.1016/j.ppnp.2016.01.001

CrossRef Full Text | Google Scholar

117. Rondin L, Tetienne J-P, Hingant T, Roch J-F, Maletinsky P, Jacques V. Magnetometry with Nitrogen-Vacancy Defects in diamond. Rep Prog Phys (2014) 77(May):056503. doi:10.1088/0034-4885/77/5/056503

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Tallaire A, Brinza O, Huillery P, Delord T, Pellet-Mary C, Staacke R, et al. High NV Density in a Pink CVD diamond Grown with N2O Addition. Carbon (2020) 170:421–9. doi:10.1016/j.carbon.2020.08.048

CrossRef Full Text | Google Scholar

119. Kurita T, Shimotsuma Y, Fujiwara M, Fujie M, Mizuochi N, Shimizu M, et al. Direct Writing of High-Density Nitrogen-Vacancy Centers inside diamond by Femtosecond Laser Irradiation. Appl Phys Lett (2021) 118(21):214001. doi:10.1063/5.0049953

CrossRef Full Text | Google Scholar

120. Pietraszko J, Galatyuk T, Grilj V, Koenig W, Spataro S, Träger M. Radiation Damage in Single crystal CVD diamond Material Investigated with a High Current Relativistic 197Au Beam. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2014) 763:1–5. doi:10.1016/j.nima.2014.06.006

CrossRef Full Text | Google Scholar

121. Sasaki K, Watanabe H, Sumiya H, Itoh KM, Abe E. Detection and Control of Single Proton Spins in a Thin Layer of diamond Grown by Chemical Vapor Deposition. Appl Phys Lett (2020) 117(11):114002. doi:10.1063/5.0016196

CrossRef Full Text | Google Scholar

122. Adams CS, Pritchard JD, Shaffer JP. Rydberg Atom Quantum Technologies. J Phys B: Mol Opt Phys (2019) 53:012002. doi:10.1088/1361-6455/ab52ef

CrossRef Full Text | Google Scholar

123. Wu X, Liang X, Tian Y, Yang F, Chen C, Liu Y-C, et al. A Concise Review of Rydberg Atom Based Quantum Computation and Quantum Simulation*. Chin Phys. B (2021) 30:020305. doi:10.1088/1674-1056/abd76f

CrossRef Full Text | Google Scholar

124. Schmidt J, Münzenmaier Y, Kaspar P, Schalberger P, Baur H, Löw R, et al. An Optogalvanic Gas Sensor Based on Rydberg Excitations. J Phys B: Mol Opt Phys (2020) 53:094001. doi:10.1088/1361-6455/ab728e

CrossRef Full Text | Google Scholar

125. Osterwalder A, Merkt F. Using High Rydberg States as Electric Field Sensors. Phys Rev Lett (1999) 82(Mar):1831–4. doi:10.1103/physrevlett.82.1831

CrossRef Full Text | Google Scholar

126. Sedlacek JA, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer JP. Microwave Electrometry with Rydberg Atoms in a Vapour Cell Using Bright Atomic Resonances. Nat Phys (2012) 8(Nov):819–24. doi:10.1038/nphys2423

CrossRef Full Text | Google Scholar

127. Wade CG, Šibalić N, de Melo NR, Kondo JM, Adams CS, Weatherill KJ. Real-time Near-Field Terahertz Imaging with Atomic Optical Fluorescence. Nat Photon (2016) 11(Nov):40–3. doi:10.1038/nphoton.2016.214

CrossRef Full Text | Google Scholar

128. Gallagher TF. Rydberg Atoms. In: Cambridge Monographs on Atomic, Molecular and Chemical Physics. Cambridge University Press (1994).

Google Scholar

129. Adolfsson J, Ahmed M, Aiola S, Alme J, Alt T, Amend W. The Upgrade of the ALICE TPC with GEMs and Continuous Readout. JINST (2021) 1603:P03022. arXiv:2012.09518 [physics.ins-det]. doi:10.1088/1748-0221/16/03/P03022

CrossRef Full Text | Google Scholar

130. Charpak G, Fabre J-P, Sauli F, Suzuki M, Dominik W. AN OPTICAL, PROPORTIONAL, CONTINUOUSLY OPERATING AVALANCHE CHAMBER. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1987) 258:177–84. doi:10.1016/0168-9002(87)90054-4

CrossRef Full Text | Google Scholar

131. Fonte P, Breskin A, Charpak G, Dominik W, Sauli F. Beam Test of an Imaging High-Density Projection Chamber. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1989) 283:658–64. doi:10.1016/0168-9002(89)91436-8

CrossRef Full Text | Google Scholar

132. Gai M, Ahmed MW, Stave SC, Zimmerman WR, Breskin A, Bromberger B, et al. An Optical Readout TPC (O-TPC) for Studies in Nuclear Astrophysics with Gamma-ray Beams at HIγS1. J Inst (2010) 5:P12004. arXiv:1101.1940 [physics.ins-det]. doi:10.1088/1748-0221/5/12/p12004

CrossRef Full Text | Google Scholar

133. Phan NS, Lauer RJ, Lee ER, Loomba D, Matthews JAJ, Miller EH. GEM-based TPC with CCD Imaging for Directional Dark Matter Detection. Astroparticle Phys (2016) 84:82–96. arXiv:1510.02170 [physics.ins-det]. doi:10.1016/j.astropartphys.2016.08.006

CrossRef Full Text | Google Scholar

134. Robinson AK, Prajapati N, Senic D, Simons MT, Holloway CL. Determining the Angle-Of-Arrival of a Radio-Frequency Source with a Rydberg Atom-Based Sensor. Appl Phys Lett (2021) 118(11):114001. doi:10.1063/5.0045601

CrossRef Full Text | Google Scholar

135. Kasprowicz G, Kulik P, Gaska M, Przywozki T, Pozniak K, Jarosinski J, et al. ARTIQ and Sinara: Open Software and Hardware Stacks for Quantum Physics. In: 2020. OSA Quantum 2.0 Conference (2020). QTu8B.14. doi:10.1364/quantum.2020.qtu8b.14

CrossRef Full Text | Google Scholar

136. Bourdeauducq S, Jördens R, Zotov P, Britton J, Slichter D, Leibrandt D, et al. ARTIQ 1.0 (2016). doi:10.5281/zenodo.51303

CrossRef Full Text | Google Scholar

137. Anderson M, Berkovitz J, Betts W, Bossingham R, Bieser F, Brown R, et al. The Star Time Projection Chamber: A Unique Tool for Studying High Multiplicity Events at RHIC. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2003) 499:659–78. arXiv:nucl-ex/0301015. doi:10.1016/s0168-9002(02)01964-2

CrossRef Full Text | Google Scholar

138. Vrinceanu D. Electron Impact Ionization of Rydberg Atoms. Phys Rev A (2005) 72:022722. doi:10.1103/physreva.72.022722

CrossRef Full Text | Google Scholar

139. Mohapatra AK, Jackson TR, Adams CS. Coherent Optical Detection of Highly Excited Rydberg States Using Electromagnetically Induced Transparency. Phys Rev Lett (2007) 98: doi:10.1103/PhysRevLett.98.113003

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Mauger S, Millen J, Jones MPA. Spectroscopy of Strontium Rydberg States Using Electromagnetically Induced Transparency. J Phys B: Mol Opt Phys (2007) 40:F319–F325. doi:10.1088/0953-4075/40/22/f03

CrossRef Full Text | Google Scholar