- 1School of Physics and Astronomy, China West Normal University, Nanchong, China
- 2School of Physics and Astronomy, Sun Yat-SenUniversity, Zhuhai, China
In this work, we conduct a study regarding the thermodynamic evolution and the phase transition of a black hole in a finite spherical cavity subject to the generalized uncertainty principle. The results demonstrate that both the positive and negative generalized uncertainty principle parameters β0 can significantly affect the thermodynamic quantities, stability, critical behavior, and phase transition of the black hole. For β0 > 0, the black hole forms a remnant with finite temperature, finite mass, and zero local heat capacity in the last stages of evolution, which can be regarded as an elementary particle. Meanwhile, it undergoes one second-order phase transition and two Hawking-Page-type phase transitions. The Gross-Perry-Yaffe phase transition occurs for both large black hole configuration and small black hole configuration. For β0 < 0, the Gross-Perry-Yaffe phase transition occurs only for large black hole configuration, and the temperature and heat capacity of the black hole remnant is finite, whereas its mass is zero. This indicates the remnant is metastable and would be in the Hawking-Page-type phase transition forever. Specifically, according to the viewpoint of corpuscular gravity, the remnant can be interpreted as an additional metastable tiny black hole configuration, which never appears in the original case and the positive correction case.
1 Introduction
The Planck scale is well known as the minimum scale in nature. In the vicinity of it, many works expected that the quantum theory and gravity would merge into a theory of quantum gravity (QG) [1–4]. Therefore, the Planck scale can be regarded as a demarcation line between classical gravity and QG. For a long time, it is believed that the properties of different physical systems would be properly changed at the Planck scale due to the effect of QG. For example, when the Heisenberg uncertainty principle (HUP) approaches the Planck scales, it should be modified to the so-called generalized uncertainty principle (GUP) [5–7]. In this sense, Kempf, Mangano, and Mann [5] proposed one of the most adopted GUP, as follows:
where ℓp is the Planck length, β0 is a dimensionless GUP parameter, while that ℏ corresponds to the reduced Planck constant. Meanwhile, inequality (1) is equivalent to the modified fundamental commutation relation
Despite the GUP with a positive parameter plays an important role in many physical systems, such as gravitational theory and astrophysics [19–24], black hole physics [25–36], cosmology [37–42], quantum physics [43–46]. It is still beneficial to investigate how GUP with the negative parameters affects the classical theories [10, 47–49]. Recently, it has been proposed that the Chandrasekhar limit fails with a positive GUP parameter and leads to the mass of white dwarfs being arbitrarily large [50, 51]. For solving this paradoxical situation, Ong suggests taking a negative GUP parameter, which naturally restores the Chandrasekhar limit [52]. In this regard, to be compatible with the previous works of thermodynamics of black holes, the Hawking temperatures with both positive and negative GUP parameters have been substantively revised in Ref. [53], which can be expressed as follows:
where β0 is the GUP parameter, M is the mass of the Schwarzschild (SC) black hole, whose line element is
where the logarithmic corrections on the right-hand side of Eq. 4 and Eq. 5 are consistent with the expectation of QG theories [49]. The original area law of the entropy
On the other hand, the thermodynamic properties and evolution of black holes can be described not only by the Hawking temperature and the corresponding entropy but also by their phase structures and critical phenomena [54–71, 74–83]. To our knowledge, the study of the thermodynamic phase transition of the black hole started with Hawking and Page, who pointed out the existence of a thermodynamic phase transition (known as “Hawking-Page phase transition”) in the asymptotically anti-de Sitter (AdS) SC black hole when its temperature reaches a certain value. This pioneering work demonstrates the deeper-seated relation between confinement and deconfinement phase transition of the gauge field in the AdS/CFT correspondence [56]. Moreover, this correspondence can be used to investigate the behavior of various condensed matter phenomena [57, 58]. Therefore, inspired by the classical theory of Hawking-Page phase transition, similar investigations were extended to a variety of complicated AdS spacetimes [59–66]. Beyond these achievements, people are also exploring the phase structures and critical phenomena of the non-AdS spacetimes. The biggest obstacle to achieving this is the lack of reflective surfaces (e.g., AdS term), which leads to the thermodynamic instability of non-AdS black holes. To overcome this issue, York suggests placing the non-AdS black holes inside a spherical cavity, so that the boundary of the spherical cavity can ensure the black holes are in a quasi-static thermally stable structure and makes the study of their phase behavior possible. In Ref. [67], York showed that the stable structure of the Schwarzschild black in a spherical cavity is similar to those of the Schwarzschild AdS black hole. Subsequently, the phase behavior of RN black holes in the cavity is shown to have extensive similarity to that of Reissner-Nordström (R-N) AdS black holes in the grand canonical ensemble [68]. In Refs. [69–71], the phase structure and critical phenomena of a class of brane spacetimes in a cavity have been investigated by a similar method. Those results in the existence of Hawking-Page phase transitions in these thermodynamic systems. Moreover, by studying the thermodynamic properties of bosonic stars and hairy black holes in a cavity, it is found that they are very similar to holographic superconductors in AdS gravity [72, 73]. In addition, the author in Ref. [74] found a non-equilibrium second-order phase transition in the charged R-N spacetime. Subsequently, the phenomena of phase transition of the Kerr-Newman black hole were proved by Davies [75]. By using the path-integral formulation of Einstein’s theory, the Gross-Perry-Yaffe (GPY) phase transition, which occurs for a hot flat space decays into the large black hole state [76]. So far, the thermodynamic phase transition and critical phenomena of black holes are still a topic of concern [84–95]. More recently, the quantum gravity corrections to the thermodynamic phase transition and critical behavior of black holes have attracted a lot of attention [96–102]. In particular, when considering the effect of GUP, the modified thermodynamics of black holes in cavities are different from the original case, whereas the corresponding thermodynamic phase transition and critical behavior are similar to those of the AdS black hole [103, 104]. Hence, those results may provide a new perspective on thermodynamic properties and evolution of black holes.
Recently, many works showed that the negative GUP parameters may appear in the nontrivial structures of spacetimes, for example, the discreteness of space [105–108]. This indicates that the spacetimes with negative GUP parameters have different properties from that of positive GUP cases. As we know, the thermodynamic phase transitions and critical behavior of spacetimes are related to their structure. Therefore, it is believed that the negative GUP parameter could lead to many new physical phenomena and results. To this end, the purpose of this study is to explore how the positive/negative GUP effect changes the thermodynamic properties of the SC black hole. However, most investigations pertain to the positive GUP parameters, while the cases of negative GUP parameters case have seen comparatively little development. To this end, we would like to consider this issue and study the local thermodynamic evolution, critical behavior, and phase transition of SC black holes in the framework of GUP with positive/negative parameters, respectively. It turns out that, the positive/negative GUP parameter can change the thermodynamics and phase structure of black holes in varying degrees, which are different from those of the standard cases.
The rest of this article is organized as follows: in Section 2, we investigate the GUP corrected Hawking temperature and the specific heat of the SC black hole in a cavity. Then, the issue of black hole remnants and the corresponding thermodynamic stability are discussed. According to the modified local thermodynamic quantities, the thermodynamic critically and phase transition of SC black hole are analyzed in detail in Section 3. The conclusion and discussion are contained in Section 4. Throughout this article we adopt the convention ℏ = c = kB = 1.
2 The GUP Corrected Thermodynamic Quantities in a Cavity
In order to detect the thermodynamic evolution and the phase transition of a black hole, one should enclose it in a cavity to keep it in a quasilocal thermally stable [105]. Essentially, the boundary of the cavity acts as a reflecting surface to retain the radiation particles in this thermodynamic ensemble. Now, supposing the radius of the cavity is R and using Eqs 2, 3, the GUP corrected local temperature of the SC black hole for an observer on the cavity can be expressed as follows [105]:
The aforementioned equation is implemented by the blue-shifted factor of the metric of the SC black hole. Mathematically, those modifications are not only sensitively dependent on mass M but also the GUP parameters β0. They respect the original local temperature
where mp represents the Planck length. It should be noted that this kind of remnant is consistent with previous works [109–112]. Hence, one can find that the remnant has zero specific heat (see Eq. 13 for more discussions), which means it does not exchange the energy with the surrounding space. In particular, the behavior of the remnant is more likely an elementary particle. Therefore, the temperature of the remnant can be considered as the energy of the particle [53]. However, if β0 < 0, the result shows an “unconventional” black hole remnant, which has no rest mass but only pure temperature
In the aforementioned equation, we setting R = 10 and G = 1, the critical values of GUP parameters, the mass of the black hole, and the local temperature are
It is clear that the critical ratio
Since the phase transition would occurs with
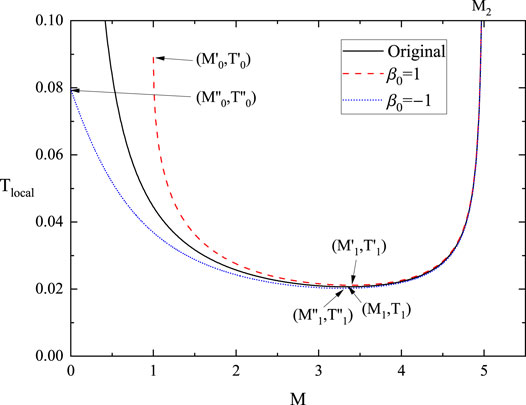
FIGURE 1. The original and GUP corrected local temperature (β0 = ±1) as a function of mass. We set R = 10 and G = 1.
As seen from Figure 1, the black solid curve corresponds to the original local temperature while the red dashed curve and the blue dotted curve represent the GUP corrected cases with β0 = 1 and β0 = −1, respectively. It is obvious that all three kinds of local temperature have the minimum values in the “Tlocal − M” plane, which can be easy numerically obtained if needed (i. e.,
According to the previous works, one can classify the SC black hole as a large black hole and a small black hole depending on the two branches in Figure 1. For confirming this viewpoint, it is necessary to study the thermodynamic stability of the black hole, which is determined by the heat capacity. First, by using the first law of thermodynamics, the local thermal energy is given by
Note that, due to the mass of remnant of black hole, the lower limit of integration for β0 > 0 is
By setting R = 10 and G = 1, the original specific heat and the GUP corrected specific heat as a function of mass for different values of β0 is reflected in Figure 2.
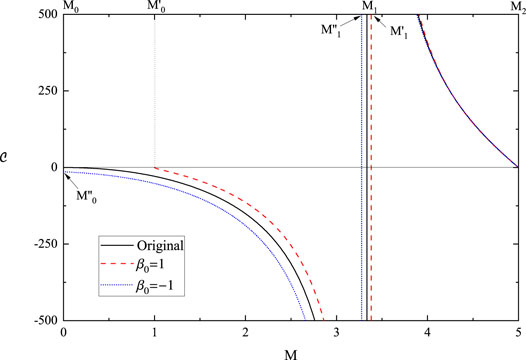
FIGURE 2. The original and GUP corrected local temperature. The original specific heat and GUP corrected specific heat (β0 = ±1) as a function of mass. We set R = 10 and G = 1.
As seen from Figure 2, the black solid curve for the original heat capacity
Now, armed with the discussions on the modified local temperature and heat capacity, one can classify the SC black hole into two configurations depending on its mass scale, namely, the large black hole (LBH) configuration and the small black hole (SBH) configuration. The stability, the region of the heat capacity, and the region of the mass of small/large black holes with the positive and negative GUP parameters are depicted in Table 1.

TABLE 1. Stability and region of the mass of the small/large black hole with different values of GUP parameter.
From Table 1, it is found that whether β0 > 0 or β0 < 0, the system always has one SBH with positive heat capacity and one LBH with negative heat capacity. Obviously, the stability determines that SBH cannot exist for a long time, it would decay into the remnant or the stable LBH. In this process, some interesting thermodynamic phase transitions that never appeared in the original case can be found by analyzing the Helmholtz free energy of LBH and SBH.
3 Helmholtz Free Energy and Phase Transition
In this section, it is necessary to analyze the corrections to thermodynamic criticality and phase transition due to the GUP. To this aim, one needs to calculate the Helmholtz free energy in an isothermal cavity defined as Fon = Elocal − TlocalS. According to Eqs 4–12, the GUP corrected Helmholtz free energy is given by:
where
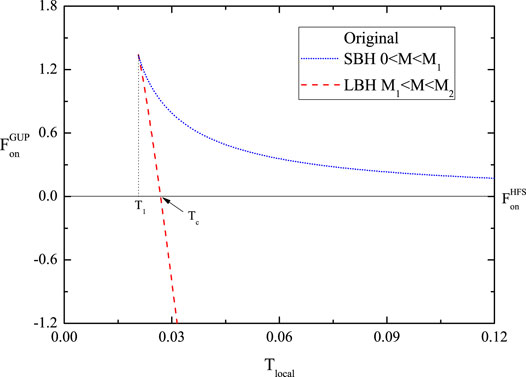
FIGURE 3. The original Helmholtz free energy versus the original local temperature, we take R = 10 and G = 1.
Figure 3 reveals the relationship between the original local free energy and its local temperature. Note that the curve of free energy is not continuous, there is a cusp between the free energies of SBH and LBH, resulting in a second-order phase transition appearing at the critical point T1 corresponding to the mass M1. The horizontal line refers to the Helmholtz free energy of hot flat space (HFS)
Next, let us focus on Figure 4 and Figure 5 for the modified cases with different GUP parameters, for example, β0 = ±1. It is worth noting that spacetime is always curved due to the remnant of the black hole. Hence, there is no HFS in the framework of GUP. In the following discussion, we should use the hot curved (HCS) space to replace the HFS. More specifically, one can find that the free energy of HCS
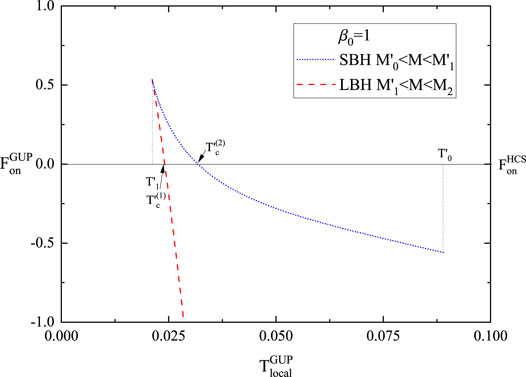
FIGURE 4. The GUP corrected Helmholtz free energy versus the modified temperature for β0 = 1, we take R = 10 and G = 1.
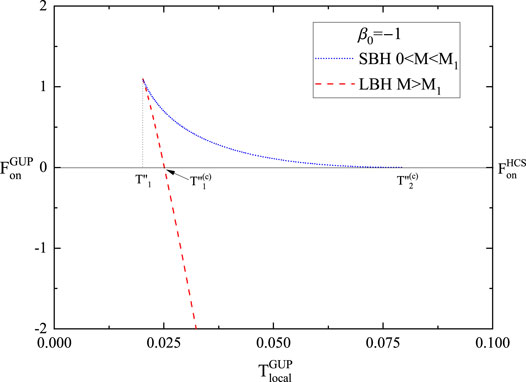
FIGURE 5. The GUP corrected Helmholtz free energy versus the modified temperature for β0 = −1, we take R = 10 and G = 1.
As seen from Figure 4, when the temperature is lower than
1) An additional Hawking-Page-type phase transition can be found at
2) As long as
3) The
Regarding Figure 5, one can observe that:
1) There is a Hawking-Page-type phase transition from
2) The
3) Even more remarkably, the aforementioned results are reminiscent of viewpoints of the black hole in corpuscular gravity (CG), which states that the black holes can be interpreted as a condensate at the critical point of a quantum phase transition [115, 116]. Therefore, along the line of CG theory, the remnant can be interpreted as an additional metastable tiny black hole (TBH) configuration of the system. With this, both the unstable SBH and metastable TBH (or the remnant) would collapse into stable LBH eventually since the relation of free energies obey
4) The Helmholtz free energy of LBH is always lower than those of SBH and HCS for
4 Conclusion
In this study, we have explored how the GUP with positive/negative parameters affects the local thermodynamic quantities, thermal stability, and phase transitions of SC black holes in a cavity. Our results show that the positive/negative corrections have their own unique properties and are unambiguously distinguished from the original case. For β0 > 0, the SC black hole leaves a thermodynamically inert remnant with a finite temperature, a finite mass, and a zero local heat capacity. By analyzing the Fon − Tlocal, it was found two Hawking-Page-type phase transitions and one second-order phase transition, whereas the original case only has one Hawking-Page phase transition. As long as
For a long time, people are focused on the GUP with a positive parameter. However, our work shows that the GUP with a negative parameter is as important as the positive one since it can significantly affect the thermodynamics, stability, and phase structures of a black hole. These results can reasonably and consistently describe the thermodynamic evolution of a black hole, and avoid the information paradox. Specifically, the zero mass remnant can be regarded as a candidate of dark matter (see Refs. [53, 117]), which could be found in further astronomical observations. Therefore, it would be very interesting to explore these phenomena in the context of black holes with the negative GUP. Finally, we only focused on how the GUP with both positive and negative parameters affects the thermodynamic properties and phase transition of the SC black hole in this present work. It should be noted that our work can be applied to more generic black holes, such as SC-AdS black holes. The relevant issues will be discussed in detail in our future work.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
Z-WF and XZ completed all the derivation and manuscript writing. S-QZ checked the errors in equations.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 12105231), the Guiding Local Science and Technology Development Projects by the Central Government of China (Grant No. 2021ZYD0031), and the Sichuan Youth Science and Technology Innovation Research Team (Grant No. 21CXTD0038) the Fundamental Research Funds of China West Normal University (Grant No. 20B009).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Konishi K, Paffuti G, Provero P. Minimum Physical Length and the Generalized Uncertainty Principle in String Theory. Phys Lett B (1990) 234:276–84. doi:10.1016/0370-2693(90)91927-4
2. Maggiore M. The Algebraic Structure of the Generalized Uncertainty Principle. Phys Lett B (1993) 319:83–6. doi:10.1016/0370-2693(93)90785-g
3. Garay LJ. Quantum Gravity and Minimum Length. Int J Mod Phys A (1995) 10:145–65. doi:10.1142/s0217751x95000085
4. Amelino-Camelia G. Relativity in Spacetimes with Short-Distance Structure Governed by an Observer-independent (Planckian) Length Scale. Int J Mod Phys D (2002) 11:35–59. doi:10.1142/s0218271802001330
5. Kempf A, Mangano G, Mann RB. Hilbert Space Representation of the Minimal Length Uncertainty Relation. Phys Rev D (1995) 52:1108–18. doi:10.1103/physrevd.52.1108
6. Scardigli F. Generalized Uncertainty Principle in Quantum Gravity from Micro-black Hole Gedanken experiment. Phys Lett B (1999) 452:39–44. doi:10.1016/s0370-2693(99)00167-7
7. Adler RJ, Santiago DI. On Gravity and the Uncertainty Principle. Mod Phys Lett A (1999) 14:1371–81. doi:10.1142/s0217732399001462
8. Das S, Vagenas EC. Universality of Quantum Gravity Corrections. Phys Rev Lett (2008) 101:221301. doi:10.1103/PhysRevLett.101.221301
9. Ghosh S. Quantum Gravity Effects in Geodesic Motion and Predictions of Equivalence Principle Violation. Class Quan Grav. (2014) 31:025025. doi:10.1088/0264-9381/31/2/025025
10. Scardigli F, Casadio R. Gravitational Tests of the Generalized Uncertainty Principle. Eur Phys J C (2015) 75:425. doi:10.1140/epjc/s10052-015-3635-y
12. Feng Z-W, Yang S-Z, Li H-L, Zu X-T. Constraining the Generalized Uncertainty Principle with the Gravitational Wave Event GW150914. Phys Lett B (2017) 768:81–5. doi:10.1016/j.physletb.2017.02.043
13. Kouwn S. Implications of Minimum and Maximum Length Scales in Cosmology. Phys Dark Universe (2018) 21:76–81. doi:10.1016/j.dark.2018.07.001
14. Bushev P, Bourhill J, Goryachev M, Kukharchyk N, Ivanov E, Galliou S, et al. Phys Rev D (2019) 100:066020. doi:10.1103/physrevd.100.066020
16. Neves JCS. Upper Bound on the GUP Parameter Using the Black Hole Shadow. Eur Phys J C (2020) 80:343. doi:10.1140/epjc/s10052-020-7913-y
17. Ökcü Ö, Aydiner E. Observational Tests of the Generalized Uncertainty Principle: Shapiro Time Delay, Gravitational Redshift, and Geodetic Precession. Nucl Phys B (2021) 964:115324. doi:10.1016/j.nuclphysb.2021.115324
18. Marin F, Marino F, Bonaldi M, Cerdonio M, Conti L, Falferi P, et al. Gravitational Bar Detectors Set Limits to Planck-Scale Physics on Macroscopic Variables. Nat Phys (2013) 9:71–3. doi:10.1038/nphys2503
19. Salah M, Hammad F, Faizal M, Ali AF. Non-singular and Cyclic Universe from the Modified GUP. J Cosmol Astropart Phys (2017) 2017:035. doi:10.1088/1475-7516/2017/02/035
20. Scardigli F, Lambiase G, Vagenas EC. GUP Parameter from Quantum Corrections to the Newtonian Potential. Phys Lett B (2017) 767:242–6. doi:10.1016/j.physletb.2017.01.054
21. Buoninfante L, Luciano GG, Petruzziello L. Generalized Uncertainty Principle and Corpuscular Gravity. Eur Phys J C (2019) 79:663. doi:10.1140/epjc/s10052-019-7164-y
22. Moradpour H, Ziaie AH, Ghaffari S, Feleppa F. The Generalized and Extended Uncertainty Principles and Their Implications on the Jeans Mass. Mon Not R Astron Soc (2019) 488:L69–L74. doi:10.1093/mnrasl/slz098
23. Casadio R, Scardigli F. Generalized Uncertainty Principle, Classical Mechanics, and General Relativity. Phys Lett B (2020) 807:135558. doi:10.1016/j.physletb.2020.135558
24. Chen P, Ong YC, Yeom D-H. Black Hole Remnants and the Information Loss Paradox. Phys Rep (2015) 603:1–45. doi:10.1016/j.physrep.2015.10.007
25. Sakalli I, Övgün A, Jusufi K. GUP Assisted Hawking Radiation of Rotating Acoustic Black Holes. Astrophys Space Sci (2016) 361:330. doi:10.1007/s10509-016-2922-x
26. Feng ZW, Li HL, Zu XT, Yang SZ. Quantum Corrections to the Thermodynamics of Schwarzschild-Tangherlini Black Hole and the Generalized Uncertainty Principle. Eur Phys J C (2016) 76:212. doi:10.1140/epjc/s10052-016-4057-1
27. Scardigli F, Blasone M, Luciano G, Casadio R. Modified Unruh Effect from Generalized Uncertainty Principle. Eur Phys J C (2018) 78:728. doi:10.1140/epjc/s10052-018-6209-y
28. Li H-L, Feng Z-W, Yang S-Z, Zu X-T. The Remnant and Phase Transition of a Finslerian Black Hole. Eur Phys J C (2018) 78:768. doi:10.1140/epjc/s10052-018-6252-8
29. Vagenas EC, Alsaleh SM, Ali AF. GUP Parameter and Black-Hole Temperature. EPL (2018) 120:40001. doi:10.1209/0295-5075/120/40001
30. Kanzi S, Sakallı İ. GUP Modified Hawking Radiation in Bumblebee Gravity. Nucl Phys B (2019) 946:114703. doi:10.1016/j.nuclphysb.2019.114703
31. Barman S. The Hawking Effect and the Bounds on Greybody Factor for Higher Dimensional Schwarzschild Black Holes. Eur Phys J C (2020) 80:50. doi:10.1140/epjc/s10052-020-7613-7
32. Hassanabadi H, Maghsoodi E, Chung WS. Analysis of Black Hole Thermodynamics with a New Higher Order Generalized Uncertainty Principle. Eur Phys J C (2019) 79:358. doi:10.1140/epjc/s10052-019-6871-8
33. Iorio A, Lambiase G, Pais P, Scardigli F. Generalized Uncertainty Principle in Three-Dimensional Gravity and the BTZ Black Hole. Phys Rev D (2020) 101:105002. doi:10.1103/PhysRevD.101.105002
34. Blanchette K, Das S, Rastgoo S. Effective GUP-Modified Raychaudhuri Equation and Black Hole Singularity: Four Models. J High Energ Phys. (2021) 2021:62. doi:10.1007/JHEP09(2021)062
35. Kanzi S, Sakallı İ. GUP-modified Hawking Radiation and Transmission/reflection Coefficients of Rotating Polytropic Black Hole. Eur Phys J Plus (2022) 137:14. doi:10.1140/epjp/s13360-021-02245-7
36. Sakallı İ, Kanzi S. Physical Properties of Brane-World Black Hole Solutions via a Confining Potential. Ann Phys (2022) 439:168803. doi:10.1016/j.aop.2022.168803
39. Zhu T, Ren J-R, Li M-F. Influence of Generalized and Extended Uncertainty Principle on Thermodynamics of FRW Universe. Phys Lett B (2009) 674:204–9. doi:10.1016/j.physletb.2009.03.020
40. Chemissany W, Das S, Ali AF, Vagenas EC. Effect of the Generalized Uncertainty Principle on post-inflation Preheating. J Cosmol Astropart Phys (2011) 2011:017. doi:10.1088/1475-7516/2011/12/017
41. Zeynali K, Darabi F, Motavalli H. Multi-dimensional Cosmology and GUP. J Cosmol Astropart Phys (2012) 2012:033. doi:10.1088/1475-7516/2012/12/033
42. Atazadeh K, Darabi F. Einstein Static Universe from GUP. Phys Dark Universe (2017) 16:87–93. doi:10.1016/j.dark.2017.04.008
43. DasMann SRB, Mann RB. Planck Scale Effects on Some Low Energy Quantum Phenomena. Phys Lett B (2011) 704:596–9. doi:10.1016/j.physletb.2011.09.056
44. Verma H, Mitra T, Prasad Mandal B. Schwinger's Model of Angular Momentum with GUP. Epl (2018) 123:30009. doi:10.1209/0295-5075/123/30009
45. Vagenas EC, Alasfar L, Alsaleh SM, Ali AF. The GUP and Quantum Raychaudhuri Equation. Nucl Phys B (2018) 931:72–8. doi:10.1016/j.nuclphysb.2018.04.004
51. Rashidi R. Generalized Uncertainty Principle and the Maximum Mass of Ideal white Dwarfs. Ann Phys (2016) 374:434–43. doi:10.1016/j.aop.2016.09.005
52. Ong YC. Generalized Uncertainty Principle, Black Holes, and white Dwarfs: a Tale of Two Infinities. J Cosmol Astropart Phys (2018) 2018:015. doi:10.1088/1475-7516/2018/09/015
53. Ong YC. An Effective Black Hole Remnant via Infinite Evaporation Time Due to Generalized Uncertainty Principle. J High Energ Phys (2018) 2018:195. doi:10.1007/jhep10(2018)195
54. Kastor D, Ray S, Traschen J. Enthalpy and the Mechanics of AdS Black Holes. Class Quan Grav. (2009) 26:195011. doi:10.1088/0264-9381/26/19/195011
55. Kastor D, Ray S, Traschen J. Mass and Free Energy of Lovelock Black Holes. Class Quan Grav. (2011) 28:195022. doi:10.1088/0264-9381/28/19/195022
56. Hawking SW, Page DN. Thermodynamics of Black Holes in Anti-de Sitter Space. Commun.Math Phys (1983) 87:577–88. doi:10.1007/BF01208266
57. Hartnoll SA. Lectures on Holographic Methods for Condensed Matter Physics. Class Quan Grav. (2009) 26:224002. doi:10.1088/0264-9381/26/22/224002
60. Wei S-W, Liu Y-X. Insight into the Microscopic Structure of an AdS Black Hole from a Thermodynamical Phase Transition. Phys Rev Lett (2015) 115:111302. doi:10.1103/physrevlett.115.111302
61. Hendi SH, Mann RB, Panahiyan S, Panah BE. Phys Rev D (2017) 95:021501. doi:10.1103/physrevd.95.021501
64. Wei S-W, Liu Y-X. Extended Thermodynamics and Microstructures of Four-Dimensional Charged Gauss-Bonnet Black Hole in AdS Space. Phys Rev D (2020) 101:104018. doi:10.1103/physrevd.101.104018
65. Rostami M, Sadeghi J, Miraboutalebi S. The Static Black Hole in F(R) Gravity with thermal Corrections and Phase Transition. Phys Dark Universe (2020) 29:100590. doi:10.1016/j.dark.2020.100590
66. Rostamia M, Sadeghibac J, Miraboutalebi S. Phys Rev D (2020) 101:044001. doi:10.1103/PhysRevD.101.044001
67. York JW. Black-hole Thermodynamics and the Euclidean Einstein Action. Phys Rev D (1986) 33:2092–9. doi:10.1103/PhysRevD.33.2092
68. Braden HW, Brown JD, Whiting BF, York JW. Charged Black Hole in a Grand Canonical Ensemble. Phys Rev D (1990) 42:3376–85. doi:10.1103/PhysRevD.42.3376
69. Lu JX, Roy S, Xiao Z. Phase Transitions and Critical Behavior of Black Branes in Canonical Ensemble. J High Energ Phys. (2011) 2011:133. doi:10.1007/jhep01(2011)133
72. Peng Y. Scalar Field Configurations Supported by Charged Compact Reflecting Stars in a Curved Spacetime. Phys Lett B (2018) 780:144–8. doi:10.1016/j.physletb.2018.02.068
75. Davies PCW. Thermodynamic phase transitions of Kerr-Newman black holes in de Sitter space. Class Quan Grav. (1989) 6:1909–14. doi:10.1088/0264-9381/6/12/018
76. Gross DJ, Perry MJ, Yaffe LG. Instability of Flat Space at Finite Temperature. Phys Rev D (1982) 25:330–55. doi:10.1103/physrevd.25.330
77. Mandal R, Bhattacharyya S, Gangopadhyay S. Rainbow Black Hole Thermodynamics and the Generalized Uncertainty Principle. Gen Relativ Gravit (2018) 50:143. doi:10.1007/s10714-018-2468-z
79. Kumar N, Bhattacharyya S, Gangopadhyay S. Phase Transitions in Born-Infeld AdS Black Holes in D-Dimensions. Gen Relativ Gravit (2020) 52:20. doi:10.1007/s10714-020-02674-2
80. Haroon S, Hennigar RA, Mann RB, Simovic F. Phys Rev D (2020) 101:084051. doi:10.1103/physrevd.101.084051
81. Promsiri C, Hirunsirisawat E, Liewrian W. Phys Rev D (2021) 104:064004. doi:10.1103/physrevd.104.064004
82. Dehyadegari A, Sheykhi A. Thermodynamic Geometry and Phase Transition of Spinning AdS Black Holes. Phys Rev D (2021) 104:104066. doi:10.1103/physrevd.104.104066
83. Liu Y, Lyu H-D, Raju A. Black Hole Singularities across Phase Transitions. J High Energ Phys. (2021) 2021:140. doi:10.1007/jhep10(2021)140
86. Dolan SR, Ponglertsakul S, Winstanley E. Stability of Black Holes in Einstein-Charged Scalar Field Theory in a Cavity. Phys Rev D (2015) 92:124047. doi:10.1103/physrevd.92.124047
87. Ponglertsakul S, Winstanley E, Dolan SR. Phys Rev D (2016) 94:024031. doi:10.1103/physrevd.94.024031
88. Sanchis-Gual N, Degollado JC, Herdeiro C, Font JA, Montero PJ. Phys Rev D (2016) 94:044061. doi:10.1103/physrevd.94.044061
90. Wang P, Wu H, Yang H. Thermodynamics and Phase Transition of a Nonlinear Electrodynamics Black Hole in a Cavity. J High Energ Phys. (2019) 2019:2. doi:10.1007/jhep07(2019)002
91. Wang P, Wu H, Yang H, Yao F. Extended Phase Space Thermodynamics for Black Holes in a Cavity. J High Energ Phys. (2020) 2020:154. doi:10.1007/jhep09(2020)154
92. Simovic F, Mann RB. Critical phenomena of charged de Sitter black holes in cavities. Class Quan Grav. (2019) 36:014002. doi:10.1088/1361-6382/aaf445
93. Haroon S, Hennigar RA, Mann RB, Simovic F. Phys Rev D (2020) 101:084051. doi:10.1103/physrevd.101.084051
94. Wei S-W, Liu Y-X, Mann RB. Ruppeiner Geometry, Phase Transitions, and the Microstructure of Charged AdS Black Holes. Phys Rev D (2019) 100:124033. doi:10.1103/physrevd.100.124033
95. Simovic F, Mann RB. Critical phenomena of charged de Sitter black holes in cavities. Class Quan Grav. (2019) 36:014002. doi:10.1088/1361-6382/aaf445
96. Gim Y, Kim W. Thermodynamic Phase Transition in the Rainbow Schwarzschild Black Hole. J Cosmol Astropart Phys (2014) 2014:003. doi:10.1088/1475-7516/2014/10/003
97. Gim Y, Kim W. Black Hole Complementarity in Gravity's Rainbow. J Cosmol Astropart Phys (2015) 2015:002. doi:10.1088/1475-7516/2015/05/002
98. Feng Z-W, Yang S-Z. Thermodynamic Phase Transition of a Black Hole in Rainbow Gravity. Phys Lett B (2017) 772:737–42. doi:10.1016/j.physletb.2017.07.057
99. Kim Y-W, Kim SK, Park Y-J. Thermodynamic Stability of Modified Schwarzschild-AdS Black Hole in Rainbow Gravity. Eur Phys J C (2016) 76:557. doi:10.1140/epjc/s10052-016-4393-1
100. Upadhyay S, Hendi SH, Panahiyan S, Panah BE. Prog Theor Exp Phys (2018) 2018:093E01. doi:10.1093/ptep/pty093
102. Feng Z-W, Tang D-L, Feng D-D, Yang S-Z. The Thermodynamics and Phase Transition of a Rainbow Black Hole. Mod Phys Lett A (2020) 35:2050010. doi:10.1142/s0217732320500108
106. Kanazawa T, Lambiase G, Vilasi G, Yoshioka A. Noncommutative Schwarzschild Geometry and Generalized Uncertainty Principle. Eur Phys J C (2019) 79:95. doi:10.1140/epjc/s10052-019-6610-1
107. Nenmeli V, Shankaranarayanan S, Todorinov V, Das S. Maximal Momentum GUP Leads to Quadratic Gravity. Phys Lett B (2021) 821:136621. doi:10.1016/j.physletb.2021.136621
109. Adler RJ, Chen P, Santiago DI. The Generalized Uncertainty Principle and Black Hole Remnants. Gen Relativity Gravitation (2001) 33:2101–8. doi:10.1023/a:1015281430411
111. Chen DY, Jiang QQ, Wang P, Yang H. J. High Energy Phys. (2012) 2013:176. doi:10.1007/JHEP11(2013)176
112. Feng Z, Zhang L, Zu X. The remnants in Reissner-Nordström-de Sitter quintessence black hole. Mod. Phys. Lett. A (2014) 29:1450123. doi:10.1142/S0217732314501235
113. Gunasekaran S, Kubizňák D, Mann RB. Extended Phase Space Thermodynamics for Charged and Rotating Black Holes and Born-Infeld Vacuum Polarization. J High Energ Phys (2012) 2012:110. doi:10.1007/jhep11(2012)110
114. Kim Y-W, Kim SK, Park Y-J. Thermodynamic Stability of Modified Schwarzschild-AdS Black Hole in Rainbow Gravity. Eur Phys J C (2016) 76:557. doi:10.1140/epjc/s10052-016-4393-1
116. Casadio R, Giugno A, Micu O, Orlandi A. Phys Rev D (2014) 90:084040. doi:10.1103/physrevd.90.084040
Keywords: generalized uncertainty principle, black hole, phase transition, thermodynamic evolution, remnant
Citation: Zhou X, Feng Z-W and Zhou S-Q (2022) Impacts of Generalized Uncertainty Principle on the Black Hole Thermodynamics and Phase Transition in a Cavity. Front. Phys. 10:887410. doi: 10.3389/fphy.2022.887410
Received: 01 March 2022; Accepted: 22 April 2022;
Published: 25 May 2022.
Edited by:
Mohamed Chabab, Cadi Ayyad University, MoroccoReviewed by:
Izzet Sakalli, Eastern Mediterranean University, TurkeyAdil Belhaj, Mohammed V University, Morocco
Copyright © 2022 Zhou, Feng and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhong-Wen Feng, endmZW5ncGh5QGN3bnUuZWR1LmNu
 Xia Zhou1
Xia Zhou1 Zhong-Wen Feng
Zhong-Wen Feng