Quantum Droplet in Lower Dimensions

The study of Bose–Einstein condensation (BEC) in lower dimensions plays an important role in understanding the fundamentals of many-body physics as they can be treated theoretically with relative ease and can be verified experimentally. Recently, observation of a liquid-like state in a BEC mixture has been reported along with a theoretical prescription for its observation in the lower dimension. This observation is unique and has serious ramifications in our prevailing conception of the liquid state, which has a deep influence on the van der Waals theory. In explaining the self-bound nature of this state, quantum fluctuation and its fine balance with mean-field (MF) interaction turn out to be playing a key role. Though the experiments are performed predominantly in three dimensions, theoretical studies extend to the lower dimensions. In this brief review, we plan to summarize the recent theoretical advances in droplet research in the lower dimension and elaborate on the description of our contributions. We will mainly focus on analytical results related to this self-bound state in a one-dimension and quasi one-dimension environment. We aim to cover a few results from the family of cnoidal solutions to droplet solutions with smooth transitions between each other, finishing it by carrying a modest discussion on the supersolid phase.

1 Introduction

The first successful experimental realization of the atomic Bose–Einstein condensate (BEC) has paved the way for new research on this unique quantum state theoretically and experimentally [1–3]. Over the last two decades, experimentalists have been able to perform experiments with atomic gases with an unprecedented level of accuracy. The magneto-optic trapping technology is the backbone of such experiments. Moreover, scientists have also been able to tune the interactions between the particles via an external magnetic field. This technique follows from the theory of Fano–Feshbach resonance [4,5]. These unique experimental achievements have enabled multi-facet research in ultra-cold atomic gases [6].

Quantum gas properties are vastly governed by interparticle interactions. For instance, bright solitons are obtained as a solution of the mean-field one-dimensional GP equation for attractive inter-particle interaction, whereas dark solitons result from repulsive interaction [7–16].

Recently, the formation of a liquid droplet-like state in a dipolar BEC [17,18] followed by a BEC mixture [19,20] has been experimentally observed. However, the possibility of the formation of a liquid-like state was first proposed theoretically in the context of binary BEC while describing the collapse of the condensate due to attractive interaction [21] and soon after for dipolar BEC [22]. It was predicted that the collapse in both cases could be arrested by quantum fluctuation.

This is unique because our conception of liquid is highly influenced by the description provided by van der Waals. According to the theory of van der Waals, the liquid state arises at high densities from an equilibrium between attractive inter-atomic forces and short-range repulsion. However, these newly emerged droplets in extremely dilute ultra-cold atomic gases are quite different from the well-known van der Waals liquids [23]. In ultra-cold BEC, the gas is very diluted, and the inter-atomic distances between the particles are larger than the usual classical liquid. At low temperature, a large de-Broglie wavelength associated with atoms interact with interaction potential as contact potential, leading the BEC to exist only in the gaseous phase. However, to make self-bound states like classical liquids, interactions are required to counterbalance each other. In ultra-cold atomic systems, the interplay of quantum fluctuation and effective mean-field interaction allows the formation of self-bound liquid-like states. The underlying theory relies on the Lee–Huang–Yang (LHY) correction [24] to the mean-field Gross–Pitaevskii (GP) equation [25,26].

The GP equation is a well-known non-linear Schrödinger equation (NLSE), used with great effect to describe the ground state behavior of BEC. The solution of NLSE usually comes in a cnoidal form. Cnoidal solutions can be expressed in periodic or solitonic types. Solitons are solitary waves and self-trapped and localized objects, existing in a great variety of physical media due to the interplay of dispersion and non-linearity, which represents the self-attraction of matter [27]. In one-dimensional settings, solitons come in different forms—bright, dark, grey, kink, and antikink—but in two- and three-dimensional settings, the question on stability impedes their progress with time [28].

1.1 Recent Developments

The research on the quantum droplet is enriched via two main tributaries: 1) the quantum droplet in binary BEC and 2) the quantum droplet in dipolar BEC. The latter is the result of balance among the short-range repulsive interaction born from a two-body contact pseudo-potential, namely, the mean-field (MF) interaction, the repulsive beyond mean-field (BMF) effect, which can be noted as a typical attribute of quantum fluctuation, and attractive long-rang dipolar interaction. However, the self-bound nature of the former comes from the opposite nature of MF and BMF effects, where the interplay of inter-species and intra-species plays a crucial role. In three dimensions, the quantum droplet is balanced and shows instability against collapse by attractive effective MF and a repulsive BMF interaction, respectively. However, in the lower dimension, specifically in one dimension, the role is reversed; that is, effective MF energy is repulsive, whereas the BMF energy is attractive. In this review article, we plan to explicate this unique role reversal phenomena and elaborate on the consequences.

Since the experimental observation of the liquid-like state, it has become the subject of intense research activity. In a recent self-consistent theoretical formulation, LHY correction is incorporated in the GP equation via quantum fluctuation [29]. We have also noted theoretical assertions on the collective modes in a droplet-soliton crossover [30], the existence of vortices in droplets [31–34], dynamics of purely one-dimensional droplets [35], its collective excitations [36], and the effect of external artificial coupling [37] along with comprehensive reviews [38]. At this juncture, we also recall a numerical investigation of quantum liquids for the dipolar BEC in quasi-one-dimensional (Q1D) geometry [39]. Apart from that, we have also seen considerable interest in analyzing the origin of the droplets in lower dimensions [33,40]. A contemporary study also notes a possible connection between the droplets and modulational instability in a one-dimensional (1D) system [41].

1.2 Current Objective

The primary focus of this review article is quantum droplets in lower dimensions emerging from a binary condensate. It has already been demonstrated that the coupled equations can be projected into an effective single component equation if both components share the same spatial mode while neglecting the spin excitation [20]. Hence, we start from an extended GP equation, which contains an additional non-linear contribution of the quartic exponent. We then summarize the well-known mathematical prescription to reduce the 3 + 1-dimensional system to 1 + 1-dimension [42]. In this case, the transverse confinement is much stronger than the longitudinal trap frequency. As BEC in one dimension is not realizable, this Q1D geometry is akin to the interest of the experimental community as it can be amenable experimentally. Nevertheless, we summarize the recent theoretical developments in understanding quantum droplets in 1D, and then we move to Q1D. In the 1D system, the GP equation carries an additional quadratic non-linearity, which takes care of the BMF contribution. Therefore, we name this equation quadratic-cubic NLSE or QCNLSE. On the contrary, in Q1D, the governing dynamical equation is cubic quadratic NLSE or CQNLSE. One can also note a unique role reversal of MF and BMF interaction while shifting from Q1D to 1D system geometry.

The review is arranged in the following way: we summarize the theoretical formulation to analyze the liquid-like state in Section 2, which allows us to construct an extended GP equation in 1D. We analyze the existence of the droplets at 1D in Section 3. In Section 4, we present our recent results in Q1D geometry. We brief some of the very recent theoretical developments to describe the recently observed exotic state of the supersolid in Section 5. It has been reported that in between droplet arrays and solitonic state, it is possible to observe phase-coherent periodic waves as if the droplets are immersed in the constant background of a liquid-like state. This kind of paradoxical state of matter that combines the friction-less flow of a superfluid with the crystal-like periodic density modulation of a solid is noted as a supersolid [43]. Experiments were mainly performed using dipolar quantum gases, proving the supersolid nature of arrays of quantum droplets, and establishing the coexistence of spatial order and global phase coherence [44–46]. We also explicate recent theoretical contributions in this aspect in the lower dimension. We draw our conclusion in Section 6.

2 Theoretical Model

Let us consider, at T = 0, a uniform binary mixture of Bose gases with masses m₁ and m₂ condensed in a trap V_trap. They are interacting with intra-atomic, g₁₁ = 4πa₁₁ℏ²/m₁, g₂₂ = 4πa₂₂ℏ²/m₂, and inter-atomic coupling constant, g₁₂ = 2πa₁₂ℏ²/m_r, where m_r = m₁m₂/(m₁ + m₂) is the reduced mass. For this particular case, we consider positive intra-species as a₁₁, a₂₂ and negative inter-species s-wave scattering length as a₁₂. The number of particles in respective species can be written in a normalized form such that ∫n₁dr = N₁ and ∫n₂dr = N₂, where n₁, n₂ are the number densities of the corresponding species, which are expressed in atomic units, $a_B^{-3}$ (a_B is the Bohr radius). The mixture can be characterized by the total number of density, n = n₁ + n₂, and the total number of atoms, N = N₁ + N₂. The energy density functional for this mixture can be written as

$\begin{array}{ll}\hfill \epsilon & ={\epsilon }_{\text{kin}}+{\epsilon }_{\text{trap}}+{\epsilon }_{\text{MF}}+{\epsilon }_{\text{BMF}}\hfill \\ \hfill & =\frac{{\hslash }^2}{2m_1}|\nabla \sqrt{n_1}{|}^2+\frac{{\hslash }^2}{2m_2}|\nabla \sqrt{n_2}{|}^2+\left(n_1+n_2\right)V_{\text{trap}}+\frac{1}{2}{g}_{11}{n}_1^2+\frac{1}{2}{g}_{22}{n}_2^2+g_{12}{n}_1{n}_2+{\epsilon }_{\text{BMF}},\hfill \end{array}(1)$

The kinetic, potential, MF, and BMF contributions are expressed as ɛ_kin, ɛ_trap, ɛ_MF, and ɛ_BMF, respectively. An additional term ɛ_BMF in an extended GP (eGP) equation includes the effect of quantum fluctuations. It has a different form and interaction type depending on the dimension of the mixture. For the three-dimensional case, the BMF term has a repulsive contribution. It includes the renormalization correction [47] to the scattering amplitude within the second Born approximation, and for the homonuclear mixture, it stands as [21]

${\epsilon }_{\text{BMF}}^{3D}=\frac{8m^{3/2}}{15{\pi }^2{\hslash }^3}\sum _{\pm }{\left(g_{11}{n}_1+g_{22}{n}_2\pm \sqrt{{\left(g_{11}{n}_1-g_{22}{n}_2\right)}^2+4g_{12}^2{n}_1{n}_2}\right)}^{5/2}.$

${\epsilon }_{\text{BMF}}^{3D}$ can be expressed for different masses as

${\epsilon }_{\text{BMF}}^{3D}=\frac{8m_1^{3/2}{g}_{11}^{5/2}}{15{\pi }^2{\hslash }^3}F\left(\frac{m_2}{m_1},\frac{g_{12}^2}{g_{11}{g}_{22}},\sqrt{\frac{g_{22}}{g_{11}}}\right)|\sqrt{n_1{n}_2}{|}^{5/2}.$

For a particular case, N₁ = N₂ = N/2, m = m₁ = m₂, g₁₁ = g₂₂ = g₁₂ = g = 4πaℏ²/m, and ${\epsilon }_{\text{BMF}}=\frac{256\sqrt{\pi }{\hslash }^2}{15m}{(na)}^{5/2}$. F > 0 is a dimensionless function and for the case of equal masses, m = m₁ = m₂, it can be written as $F(1,x,y)={\sum }_{\pm }{\left(1+y\pm \sqrt{{(1-y)}^2+4xy}\right)}^{5/2}/4\sqrt{2}$.

In this approach, the spin excitations are neglected [21]. It is also assumed that the two components have identical spatial modes as n_i=1,2 = |Φ|² and in the density ratio such that $n_1/n_2=\sqrt{g_{22}/g_{11}}=\eta$. Now, in the miscible phase but close to the collapse point where the attractive inter-species interactions overwhelm the repulsive interactions on each condensate, that ism $g_{12}>-\sqrt{g_{11}{g}_{22}}$, the following quantities can be defined $g=\sqrt{g_{11}{g}_{22}}$ and $\delta g=g_{12}+\sqrt{g_{11}{g}_{22}}$. δg describes the deviations with respect to g₁₂. The addition of the BMF term close to the MF instability boundary, that is, δg < 0, results in ${\epsilon }_{\text{BMF}}^{3D}$ a complex quantity, which also leads to imaginary sound velocity. To avoid this ill effect created by the imaginary contribution, it is approximated that |δg|≪ g, that is, instability, is very weak. Close to instability boundary imaginary contribution is avoided by setting |δg|∼ 0 just for the BMF term. Then, the energy functional turns out in the following form:

$\begin{array}{ll}\hfill \epsilon & ={\epsilon }_{\text{kin}}+{\epsilon }_{\text{trap}}+{\epsilon }_{\text{MF}}+{\epsilon }_{\text{BMF}}\hfill \\ \hfill & =\frac{{\hslash }^2}{2m}n|\nabla \mathrm{\Phi }{|}^2+V_{\text{trap}}n|\mathrm{\Phi }{|}^2+\delta g\frac{\eta }{{\left(1+\eta \right)}^2}{n}^2|\mathrm{\Phi }{|}^4+\frac{8m^{3/2}}{15{\pi }^2{\hslash }^3}{\left(n\eta g_{11}\right)}^{5/2}|\mathrm{\Phi }{|}^5,\hfill \end{array}(2)$

This energy functional results in the following eGP equation:

$i\hslash \frac{\partial \mathrm{\Phi }}{\partial t}=\left[\left(-\frac{{\hslash }^2}{2m}{\nabla }^2+V_{\text{trap}}\right)+U|\mathrm{\Phi }{|}^2+U^{\prime }|\mathrm{\Phi }{|}^3\right]\mathrm{\Phi },(3)$

where $U=2\delta g\frac{\eta }{{\left(1+\eta \right)}^2}n$, $U^{\prime }=\frac{4m^{3/2}}{3{\pi }^2{\hslash }^3}{(\eta g_{11})}^{5/2}{n}^{3/2}$. For symmetric case where g = g₁₁ = g₂₂, η = 1, U_sym = δgn/2, $U_{\text{sym}}^{\prime }=\frac{4m^{3/2}}{3{\pi }^2{\hslash }^3}{g}^{5/2}{n}^{3/2}$, and $V_{\text{trap}}=\frac{1}{2}m\left[{\omega }_{\perp }^2(y^2+z^2)+{\omega }_0^2{x}^2\right]$. Here, ω_⊥ is the transverse trap frequency and ω₀ describes longitudinal trap frequency. There are two types of non-linearity in Eq. 3, the usual cubic non-linearity results from MF interaction and an additional quartic non-linearity accounting the effect of BMF. In optics, high-order material non-linearities [48] are theorized with the cubic-quintic non-linear Schrödinger equations. Though Eq. 3 bears strong similarities with them, the repulsive term included in Eq. 3 comes with an unusual quartic dependence.

For 1D case, ${\epsilon }_{\text{BMF}}^{1D}$ has an attractive contribution [21], which can be directly obtained from the second-order perturbation theory [49], and ${\epsilon }_{\text{BMF}}^{1D}=-\frac{2\sqrt{m}}{3\pi \hslash }{(g_{11}{n}_1+g_{22}{n}_2)}^{3/2}$ results in the following 1D eGP equation:

$i\hslash \frac{\partial \varphi }{\partial t}=-\frac{{\hslash }^2}{2m}{\varphi }_{xx}+U|\varphi {|}^2\varphi +U^{\prime }|\varphi |\varphi ,(4)$

where $U^{\prime }=-\frac{\sqrt{2m}}{\pi \hslash }{(\eta g_{11})}^{3/2}$ and $U_{\text{sym}}^{\prime }=-\frac{\sqrt{2m}}{\pi \hslash }{g}^{3/2}$.

It is important to note that the nature of the interaction strengths depends on the dimensionality. In the 3D case, the imbalance caused by the negative MF term is balanced by the positive BMF contribution. On the contrary, in the 1D case, a negative BMF imbalance is balanced by a positive MF contribution. Thus, we get a self-bound energy state.

The above-mentioned three-dimensional system can be systematically reduced to an effective dimensional geometry, which we note as Q1D system. Experimentally, this can be obtained by tuning the trapping frequencies discussed in detail in Section 4. Here, we intend to focus solely on these two lower dimensional systems, 1D and Q1D. In the Q1D system, we assume $\sqrt{n{a}^3}<1$ even though $\frac{1}{|\sqrt{n_{1D}{a}_{1D}}|}>1$. Here, n, a, n_1D, and a_1D stands for total number density, s-wave scattering length, and number density on 1D and 1D scattering length, respectively. We must also recall that, in a strict 1D system, $\frac{1}{|\sqrt{n_{1D}{a}_{1D}}|}<1$ [50]. Hence, we plan to summarize the theoretical progresses on both sides of the dimensional crossover where $\frac{1}{|\sqrt{n_{1D}{a}_{1D}}|}\simeq 1$.

3 Analysis of One-Dimensional System

In this section, we review some of the recently reported analytical solutions while describing the effect of BMF contribution and the emergence of a liquid-like state. It must be acknowledged that, in a short span of time, several classes of analytical solutions have already been reported. We note a detailed discussion on droplet formation in the 1D system and its dynamics in [35]. The nature of MF and BMF interaction was systematically studied in [41]. We also note a class of the Cnoidal solution for QCNLSE from there. However, we start our journey from the recently predicted kink–antikink pairs from QCNLSE [51].

3.1 Kink–Antikink Pair

In the 1D setting, for the symmetric case g = g₁₁ = g₂₂ and n = n₁ = n₂, we end up with the following effective energy density [21]:

${\epsilon }_{1D}=\delta g{n}^2-\frac{4\sqrt{2}}{3\pi }{\left(gn\right)}^{3/2},(5)$

From Eq. 5, we can obtain the equilibrium density n₀ = 8mg³/π²ℏ²δg², which denotes a stable liquid when the pressure is zero, and the corresponding chemical potential is noted as ν₀ = −δgn₀/2.

The above energy leads to an eGP equation:

$i\hslash \frac{\partial \varphi }{\partial t}=-\frac{{\hslash }^2}{2m}{\varphi }_{xx}+\delta g|\varphi {|}^2\varphi -\frac{\sqrt{2m}}{\pi \hslash }{g}^{3/2}|\varphi |\varphi ,(6)$

The dynamics of quantum droplets governing Eq. 6 is given by [35]. Eq. 6 can be carried over from weak to strong coupling regime by tunning δg, previously discussed in [52].

Reference [51] explicitly demonstrates kink-like solitons in the droplet regime, that is, 0 < δg ≪ g. The final form of the soliton reads [51] as follows:

${\varphi }_{\pm }=\frac{g_2}{3g_1}{e}^{i\left(kx-\frac{\nu }{\hslash }t\right)}\left[1\pm \tanh \frac{\left(x\pm vt\right)}{\xi }\right],(7)$

Here, g₁ = δg, $g_2=\frac{\sqrt{2m}}{\pi \hslash }{g}^{3/2}$. The healing length is $\xi =\frac{\hslash }{\sqrt{m\delta g}}\frac{1}{A}$ where amplitude $A=\frac{g_2}{3g_1}$. Thus, the sharper the healing, the larger the amplitude larger. These propagating modes share the same phase as the background condensate. A denotes the constant background present in the healing length. It is worth noting that the value of A is exactly one-third of the uniform condensate amplitude $\frac{\sqrt{2m}}{\pi \hslash }{g}^{3/2}/\delta g$. When ϕ₊ has maximum value, then ϕ₋ shows its minimum value and vice versa [51]. These pairs, ϕ_±, vanish asymptotically at one end and connect the normal vacuum with the quantum droplets located at the origin, which is analogous to kink/antikinks in the ϕ⁴-theory [53].

Figure 1 illustrates the density profiles for BMF repulsion g = 5. The blue solid line denotes kink, and the red dashed line describes antikink. These solitons, ϕ_±, travel in the opposite directions with equal velocity. The amplitude of the solitons is directly proportional to the repulsive interaction.

FIGURE 1

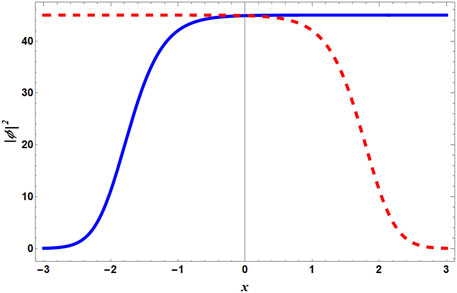
FIGURE 1. (Color Online) Illustration of the kink–antikink solution following Eq. 7 for arbitrary values of g and δ. We have assumed g and δg as 5 and 0.5, respectively. Furthermore, v = 2, t = 1, and ℏ = m = 1. The blue solid line depicts the kink solution, that is, ϕ₊, whereas the red dashed line represents the antikink, that is, ϕ₋.

3.2 Droplet Solution

Eq. 6 can also lead to flat-headed and localized solution as noted in [35]. Here, we can observe a clear transition from a soliton-like state to a liquid-like state from low-to-moderate particle number. This type of solution is noted for τ > 0, where τ = δg/g, as a result of the fine balance between the repulsive MF and attractive BMF interaction:

$\varphi =\frac{A{e}^{-i\nu t}}{1+B\cosh \left(\sqrt{-2\nu }x\right)},(8)$

where $A=\sqrt{n_0}\frac{\nu }{{\nu }_0}$, $B=\sqrt{1-\frac{\nu }{{\nu }_0}}$. The solution in Eq. 8 suggests negative values of the chemical potential and is bound in ν₀ < ν < 0. It features the flat top shape at 0 < ν − ν₀ ≪|ν₀|, with size of the droplet $L\approx {(-2{\nu }_0)}^{-1/2}\ln [{(1-\nu /{\nu }_0)}^{-1}]$ [35,50].

From the norm of Eq. 8 [41],

$N=n_0\sqrt{-\frac{2}{{\nu }_0}}\left[\ln \left(\frac{1+\sqrt{\nu /{\nu }_0}}{\sqrt{1-\nu /{\nu }_0}}\right)-\sqrt{\nu /{\nu }_0}\right],(9)$

In Figure 2, density profiles are plotted for different particle numbers. For N ≪ 1, the kinetic term in Eq. 6 is significant, and a non-uniform localized wave appears. To a certain extent, this profile resembles a bright soliton-like profile where the kinetic energy and the potential energy balance each other. As N increases, for instance, at N = 10, we observe a monotonous growth of the density distribution until it reaches the equilibrium density n₀. Further increase in the particle number does not make any substantial difference as the system has already attained an equilibrium density. This suggests a delocalize wave with uniform density n₀. Adding more particles will lead to special growth of the wave keeping the density of the flat-topped condensate restricted at n₀. The condensate showing this incompressibility may be considered fluid. The situation is analogous to regular liquid, where density remains constant over a wider spatial dimension.

FIGURE 2

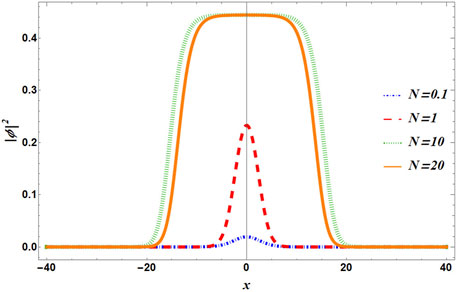
FIGURE 2. (Color Online) Spatial variation of density calculated from Eq. 8 for different particle numbers. A lower particle number yields a localized solution (N = 0.1, 1), whereas the larger number of particles (N = 10, 20) leads to the bulk region described by the flat plateau. The dot-dashed blue line is used for N = 0.1, dashed red line is used for N = 1, dotted green line denotes N = 10, and solid orange line is for N = 20.

3.2.1 Stability

The stability of these solutions was demonstrated through the Vakhitov–Kolokolov (VK) criterion [54]. The VK criterion is involved in calculating the slope between the particle number and the chemical potential, which gives a parameter regime in terms of the chemical potential predicting the exponential growth or decay of the soliton’s amplitude [55–57]. The necessary calculation yields

$\frac{dN}{d\nu }=-\frac{n_0}{{\nu }_0^2}\sqrt{-\frac{\nu }{2}}\frac{1}{1-\nu /{\nu }_0},(10)$

where stability is defined as $\frac{dN}{d\nu }<0$ for ν₀ < 0 and 0 < ν/ν₀ < 1.

The matter-vacuum interface at the right side of the droplet reduces to the kink structure for large N [41]. In the limit of large N, bulk density of the droplets differs from n₀ by an exponentially small correction n = n₀[1 + 4 exp( − 1 − 3N/4)] along with the chemical potential ν = ν₀[1 − 4 exp( − 2 − 3N/2)] [35].

At τ < 0, the exact solution of Eq. 8 is also valid. It is when the MF term in Eq. 6, along with the BMF term, is also self-attractive. In that case, Eq. 8 does not feature a plateau. However, a soliton-like mode exists for all values of ν < 0. Therefore, for small N with τ > 0, we can neglect the MF term, and with the quadratic BMF term, it gives rise to the KdV-soliton shape, that is, ${\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2(\sqrt{-\nu /2}x)$. On the contrary, for large N with τ < 0, we can neglect the BMF term, and with negative cubic MF term, we get bright soliton-like shape, that is, $\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}(\sqrt{-2\nu }x)$. A crossover is observed with the sign change of the MF term in terms of the solitonic shape.

For τ < 0, the N dependence for the soliton family takes the following form [41]:

$N=n_0\sqrt{\frac{2}{{\nu }_0}}\left[\sqrt{\nu /{\nu }_0}-\arctan \left(\sqrt{\nu /{\nu }_0}\right)\right],(11)$

This dependence also satisfies the VK criterion.

3.3 Dynamics of the Droplets

Solitons are in a bound state similar to droplets, except their stabilization process is different. We can distinguish soliton from droplets by analyzing their property while they collide, as the former does not alter its shape upon collision, but the latter behaves differently depending on their momentum, particle number, and phase. We summarize a few recent reports discussing the dynamics theoretically and experimentally [19,35,39].

Dynamical analysis of droplets can be done by simulating Eq. 6 using the split-step method based on the fast-Fourier transform [35]. The initial wave function was taken as ϕ(x, t = 0) = exp(ikx + iφ)ϕ(x + x₀) + exp( − ikx)ϕ(x − x₀), where x₀ is the initial position, k is the initial momentum, and φ is the relative phase.

We note the dynamics in Figure 3, where we observe that the droplets will separate or merge depending on their velocity [19]. For lower initial momentum k = 0.1, droplets with particle numbers N₁ = N₂ = 20 marge into one droplet, and the presence of a sound wave states that the newly formed droplet is in an excited state (Figure 3A). The sound wave can be seen oscillating inside the merged droplet. The effect of the phase is shown in Figures 3B,C. In case the collisions are out-of-phase, that is, φ = π, small excitation can be seen at the time of reflection. On the contrary, population transfer can be seen for phase difference φ = π/2. Population transfer is different for different phase differences. The effect of higher momentum k = 1 leads to fission of the droplet into multiple smaller droplets (Figure 3D), which can be seen occurring in classical liquid [39].

FIGURE 3

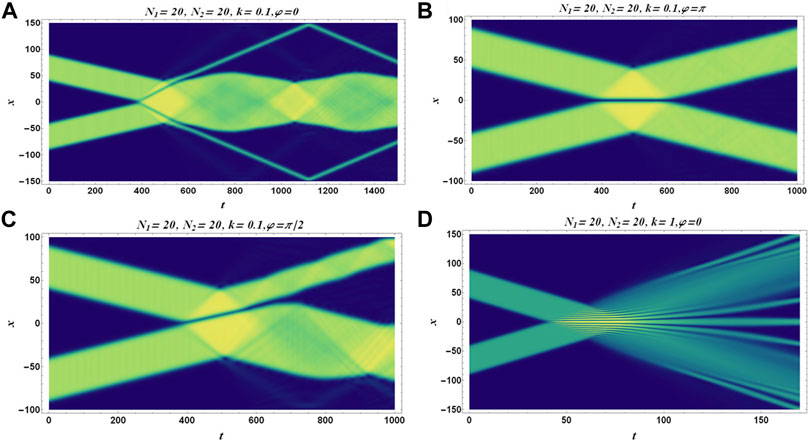
FIGURE 3. (Color Online) Panels cover the time evolution of the droplets under collision between two droplets of the same particle numbers N₁ = N₂ = 20. Their respective momentum and phase are mentioned at the top of each panel.

3.4 Quantum Rabi-Coupled Bosonic Droplets

The exciting developments in droplet formation and recent developments in artificial couplings motivate us to summarize the recent theoretical prediction of droplet formation in Rabi-coupled bosonic atoms in one dimension [37]. We consider the effect of Rabi-coupling between two hyperfine states where effective intra-species interactions are weakly repulsive, whereas the inter-species interaction is attractive. In this scenario, the beyond mean-field interaction and external Rabi coupling play a crucial role in stabilizing the droplets. The transition between the two states is induced by an external coherent Rabi coupling of frequency Ω_R.

The scaled energy density of ultra-dilute with uniform Rabi-coupled mixtures can be written as [37]

${\epsilon }_{Rs}=\frac{1}{2}{\upsilon }_{-}{n}_s^2-{\mathrm{\Omega }}_{Rs}{n}_s-\frac{4\sqrt{2}}{3\pi }{n}_s^{3/2}-\frac{2\sqrt{2}}{\pi }\frac{{\mathrm{\Omega }}_{Rs}}{{\upsilon }_{-}}{n}_s^{1/2},(12)$

Here, υ₋ = 1 − |υ|, $\upsilon =\frac{g_{12}}{g}$, and suffix s denotes scaled form. In the absence of Rabi coupling, that is, Ω_Rs = 0, Eq. 12 becomes analogous to Eq. 5. The shift in the ground state energy density in the presence of Rabi-coupling leads to quantum mechanical instability. Equilibrium density n_0s is [37]

$n_{0s}=\frac{128}{81{\pi }^2{\upsilon }_{-}^2}{\left[\cos \left[\frac{1}{3}\arccos \left[1-\frac{729{\pi }^2{\mathrm{\Omega }}_{Rs}{\upsilon }_{-}}{128}\right]+\frac{1}{2}\right]\right]}^2,(13)$

The mixture is stable for $0<{\mathrm{\Omega }}_{Rs}{\upsilon }_{-}\le \frac{256}{729{\pi }^2}$ as plotted in Figure 4A. The white band shows instability at |υ|∼ 1. Figure 4B shows that local minima in ɛ_Rs disappears above the critical value of ${\mathrm{\Omega }}_{Rs}^c\simeq 0.356$ [37] as predicted by Eq. 13. Beyond ${\mathrm{\Omega }}_{Rs}^c$, the ground state becomes unstable due to effective attraction between atoms.

FIGURE 4

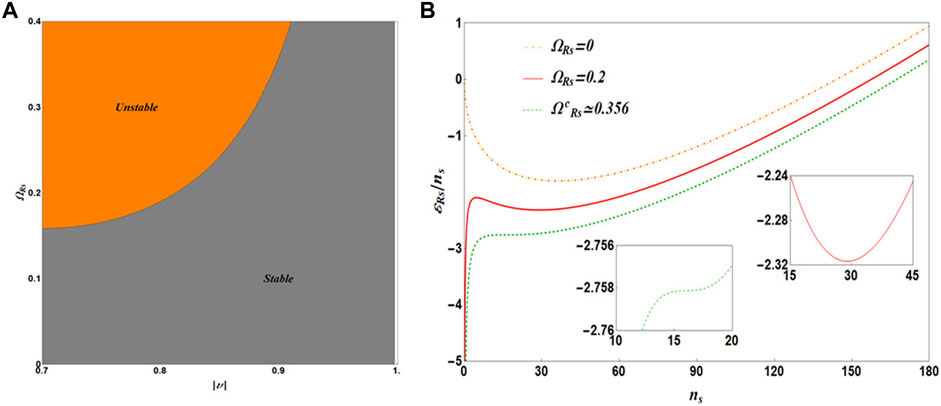
FIGURE 4. (Color Online) (A) Stability diagram of 1D self-bound Rabi-coupled droplets. The white band shows the asymptotic behavior |υ|∼ 1. (B) shows the variation of energy density with density for different Ω_Rs. The dot-dashed orange line represents the droplet phase in the absence of Rabi coupling. The solid red line considers Ω_Rs = 0.2. The dashed green line corresponds to the critical value ${\mathrm{\Omega }}_{Rs}^c\simeq 0.356$ at which the system becomes unstable. Inset: we present the local minimum localization of ɛ_Rs/n_s predicted by Eq. 13. This plot is prepared for |υ| = 0.9.

3.5 Cnoidal Solutions

The NLSE describes a homogeneous second-order non-linear differential equation, which can be mapped to the Jacobi Elliptic equation and solved analytically [58]. This mapping allows us to use the 12 Jacobi elliptic or Cnoidal functions as solutions [59]. The Jacobi elliptic functions can be derived from the amplitude function of Jacobi elliptic integrals [58]. These solutions can be constant, periodic, or localized based on the parameter q as 0 ≤ q ≤ 1. We examine the recently reported cnoidal solutions for QCNLSE with different natures of interaction strength.

3.5.1 τ > 0

In the case of comparable self-attractive BMF term and repulsive MF term in Eq. 6 with δg > 0, exact solutions can be expressed in terms of the Jacobi elliptic sn:

$\varphi \left(x,t\right)=\exp \left(-i{\nu }_{sn}t\right)\left[A+B\mathrm{s}\mathrm{n}\left(\mathrm{\Gamma }x,q\right)\right],(14)$

where $A=\frac{\sqrt{2}}{3\pi }\frac{1}{\tau }>0$, $B=\sqrt{\frac{2}{1+q^2}}A>0$, ν_sn = −2τA² < 0, and ${\mathrm{\Gamma }}^2=\frac{2}{(1+q^2)}\tau A^2$. Eq. 14 goes over into the kink in the limit of q → 1 (the same as found in [60]),

$\varphi \left(x,t\right)=\exp \left(-i{\nu }_{\text{kink}}t\right)\left[A+B\tanh \left(\mathrm{\Gamma }x,q\right)\right],(15)$

where $A=B=\frac{\sqrt{2}}{3\pi }\frac{1}{\tau }>0$, ν_kink = −2τA², Γ² = τA².

3.5.2 τ < 0

In the case when the attractive MF is stronger than the BMF repulsion, resulting in δg < 0, solutions can be expressed in terms of even Jacobi’s elliptic functions, dn(x, q) and cn(x, q). First solution with dn,

$\varphi \left(x,t\right)=\exp \left(-i{\nu }_{\text{dn}}t\right)\left[A+B\mathrm{d}\mathrm{n}\left(\mathrm{\Gamma }x,q\right)\right],(16)$

Here, the elliptic modulus can take all values 0 < q < 1, and the solution parameters are $A=\frac{\sqrt{2}}{3\pi }\frac{1}{\tau }<0$, $B=-\sqrt{\frac{2}{2-q^2}}A>0$, ν_dn = −2τA² > 0, and ${\mathrm{\Gamma }}^2=-\frac{2}{(2-q^2)}\tau A^2$.

The second solution is expressed in terms of cn, with q² > ½:

$\varphi \left(x,t\right)=\exp \left(-i{\nu }_{\text{cn}}t\right)\left[A+B\mathrm{c}\mathrm{n}\left(\mathrm{\Gamma }x,q\right)\right],(17)$

where $A=\frac{\sqrt{2}}{3\pi }\frac{1}{\tau }<0$, $B=-\sqrt{\frac{2}{2q^2-1}}A>0$, ν_cn = −2τA² > 0, and ${\mathrm{\Gamma }}^2=-\frac{2}{(2q^2-1)}\tau A^2$.

Both solutions in Eqs 16, 17 marge into a “bubble” type [61] state in the limit of q → 1, which changes the sign at two points (the same solution was reported as an “W-shaped soliton” in [60]):

$\varphi \left(x,t\right)=\exp \left(-i{\nu }_{\text{bubble}}t\right)\left[A+B\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left(\mathrm{\Gamma }x,q\right)\right],(18)$

where $A=\frac{\sqrt{2}}{3\pi }\frac{1}{\tau }<0$, $B=-\sqrt{2}A>0$, and ν_bubble = −Γ² = −2τA² > 0.

4 Analysis of Quasi-1D System

As promised earlier, this section recaps the recent results where the emergence of droplets and the existence of localized or periodic modes in the Q1D system are discussed. We start from the 3D extended GP equation described in Eq. 3 and summarize the mathematical prescription to yield a Q1D equation of motion [42].

It is possible to reduce a 3 + 1-dimensional system to a 1 + 1 dimension via careful trap engineering. Usually, a 3D trap geometry is realized using isotropic harmonic trapping potentials. However, if we introduce a strong confinement in the transverse directions by tuning the trap frequency, the system can be considered a Q1D system. The Q1D system is quite amenable experimentally and it is possible to observe the condensation in contrast to a 1D geometry. To reduce the dynamical equation from 3 + 1 dimension to 1 + 1 dimension, we use of the following ansatz:

$\mathrm{\Phi }\left(\mathbf{r},t\right)=\frac{1}{\sqrt{2\pi a_B}{a}_{\perp }}\varphi \left(\frac{x}{a_{\perp }},{\omega }_{\perp }t\right)e^{\left(-i{\omega }_{\perp }t-\frac{y^2+z^2}{2a_{\perp }^2}\right)},(19)$

Application of Eq. 19 in Eq. 3 yields the dynamical equation of motion in Q1D [62]:

$i\frac{\partial \varphi \left(x,t\right)}{\partial t}=\left[-\frac{1}{2}\frac{{\partial }^2\varphi \left(x,t\right)}{\partial x^2}+\frac{1}{2}K{x}^2+g|\varphi \left(x,t\right){|}^2+g^{\prime }|\varphi \left(x,t\right){|}^3\right]\varphi \left(x,t\right),(20)$

where g = 2δa/a_B, $g^{\prime }=(64\sqrt{2}/15\pi )\delta a^{\prime }/(a_B^{3/2}{a}_{\perp })$, and $K={\omega }_0^2/{\omega }_{\perp }^2$. The spatio-temporal variables are now in dimensionless units such that x ≡ x/a_⊥ and t ≡ ω_⊥t. From here onward, we will follow this dimensionless notation of x and t.

We realize that the understanding of cubic and quartic non-linearity is quite limited. Hence, we plan to revisit this unique problem on a more mathematical level.

4.1 Cnoidal Solutions

Here, we are interested in discussing the static solutions, and for that purpose, ϕ(x, t) is taken as ψ(x)e^−iνt. Therefore, taking into account the above consideration, Eq. 20 leads to [63]

$\frac{d^2\psi \left(x\right)}{d{x}^2}+\alpha \psi \left(x\right)-\beta |\psi \left(x\right){|}^2\psi \left(x\right)-\gamma |\psi \left(x\right){|}^3\psi \left(x\right)-\delta \left(x\right)\psi \left(x\right)=0,(21)$

where α = 2ν, β = 2g₁, γ = 2g₂, and $\delta (x)=2\mathcal{D}(x)$. $\mathcal{D}(x)$ is the cnoidal potential. At this point, interactions MF and BMF are considered repulsive in nature. However, their exact characteristics can be understood by analyzing the exact solution.

4.1.1 “cn” Solution

Due to the change of the variable to z = ζx and because ζ is the inverse of coherence length, Eq. 21 modifies to [63]

${\zeta }^2\frac{d^2\psi \left(z\right)}{d{z}^2}+\alpha \psi \left(z\right)-\beta |\psi \left(z\right){|}^2\psi \left(z\right)-\gamma |\psi \left(z\right){|}^3\psi \left(z\right)-\delta \left(z\right)\psi \left(z\right)=0,(22)$

Reference [63] takes the ansatz of the form ψ(z) = A + B cn(z, q) with the external potential as δ(z) = V₀ cn³(z, q), where V₀ is the strength of the external potential. The competition between the external potential and the non-linearity allows the system to stabilize. In experiment, one can create such an atmosphere by means to multiple lasers. The solution parameters are $\zeta =\frac{B\sqrt{\beta }}{2\sqrt{q}}$ and $B=\pm \frac{\beta }{\sqrt{4-\frac{2}{q}}\gamma }$. Thus, the strength of optical potential is evaluated as $V_0=\mp \frac{{\beta }^3}{2\sqrt{2}{(\frac{-1+2q}{q})}^{3/2}{\gamma }^2}$. Hence, the solution can be written as

$\psi \left(z\right)=-\frac{\beta }{2\gamma }\left(1\mp \frac{\sqrt{2q}}{\sqrt{2q-1}}\mathrm{c}\mathrm{n}\left(z,q\right)\right),(23)$

However, the solution is acceptable if and only if β³ – 8αγ² = 0. It must be noted that the MF interaction has to be repulsive to avoid complex coherence length. However, there is no such restriction for BMF interaction; it can be repulsive and attractive. This counter-intuitive situation is supported solely by external potential. The solution does not exist for q = ½ and leads to a constant solution for q = 0. Hence, a sinusoidal solution cannot be obtained in this framework. It is possible to obtain a localized solution corresponding to q = 1.

4.1.2 Localized Solution

As mentioned earlier, one can land up to localized modes from the cnoidal “cn” solution for q = 1. In that case, Eq. 23 reduces to

$\psi \left(z\right)=-\frac{\beta }{2\gamma }\left(1\mp \sqrt{2}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left(z\right)\right),(24)$

The existence of the solution is also constrained by the form of the external potential and we find that the potential is $\delta (z)=-\frac{{\beta }^3}{2\sqrt{2}{\gamma }^2}{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^3(z)$. Figure 5 describes the solution along with the potential profile. It is important to acknowledge that the Pöschl–Teller-like potential supports the formation of the localized mode. $B=-\frac{\beta }{\sqrt{2}\gamma }$ leads to bright soliton-like profile, though, contrary to the common perception, the background density remains nonzero. The constant background density in the asymptotic limit turns out as β²/4γ². Because β and γ are related to α (the scaled chemical potential) via β³ = 8αγ², the constant background density is the function of the chemical potential, as noted in [50,55].

FIGURE 5

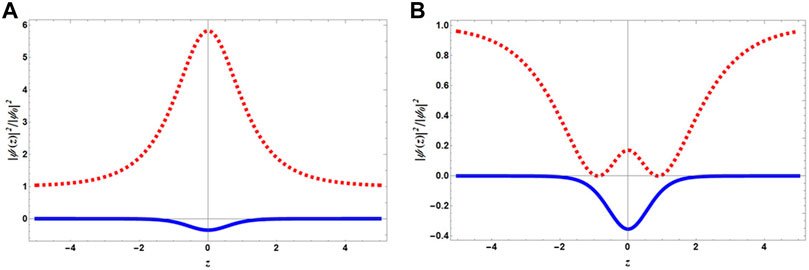
FIGURE 5. (Color Online) Density profiles of Eq. 24 and their potential landscape. (A) Red dashed line depicts the bright soliton-like profile. (B) Red dashed line represents w-soliton. In both the figures, blue solid line represents their potential landscape δ(z)/δ₀. The figure is normalized by ψ₀ = β/2γ, and we find that ${\delta }_0=-\frac{{\beta }^3}{{\gamma }^2}$.

Similarly, we find w-soliton for $B=\frac{\beta }{\sqrt{2}\gamma }$ where the background density is β²/4γ². The existence of w-soliton implies the existence of a deep contest between the interactions and its association with the confinement geometry. Nevertheless, while calculating the particle number from the normalization condition $({\int }_{-\infty }^{\infty }|\psi (z){|}^{2}dz=N)$, we realize that the value of N turns out as negative and thus we ignore the w-soliton. Naturally, the stability analysis via VK criterion (calculating $\frac{\partial N}{\partial \alpha }$) points to the bright soliton as the stable solution. Figures 5A,B describe the bright and w-soliton, respectively.

4.1.3 “sn” Solution

Next, we are interested in exploring other kinds of cnoidal solution and thus we consider ψ(z) = A + B sn(z, q) as ansatz. We modify the cnoidal trap suitably and assume δ(z) = V₀ sn³(z, q) in Eq. 21. After some trivial algebra, this yields A = −β/2γ, $\alpha =\frac{{\beta }^3}{8{\gamma }^2}$, $\zeta =\frac{iB\sqrt{\beta }}{2\sqrt{q}}$, $B=\pm \frac{\beta \sqrt{q}}{2\sqrt{q+1}\gamma }$, and $V_0=\frac{{\beta }^3{q}^{3/2}}{8{(q+1)}^{3/2}{\gamma }^2}$. The solutions clearly indicate that, for q = 0, the coherence length will be zero (as ζ → ∞). Hence, there is no scope for sinusoidal modes under this scheme. Furthermore, one can observe that it is necessary to impose a condition of β < 0 so that the coherence length remains real. Hence, the cnoidal wave solution reads [63]

$\psi \left(z\right)=-\frac{\beta }{2\gamma }\left(1\mp \frac{\sqrt{q}}{\sqrt{q+1}}\mathrm{s}\mathrm{n}\left(z,q\right)\right),(25)$

Contrary to the “cn” solution that “sn” solution yields nontrivial result for all values of q except q = 0 where the solution assimilates in the constant background. Figure 6A describes the behavior of the two solutions for q = ½. The blue solid line corresponds to $1-\frac{\sqrt{q}}{\sqrt{q+1}}\mathrm{s}\mathrm{n}(z,q)$ and the red dashed line depicts $1+\frac{\sqrt{q}}{\sqrt{q+1}}\mathrm{s}\mathrm{n}(z,q)$. We note these two solutions as ψ₋(z) and ψ₊(z), respectively.

FIGURE 6

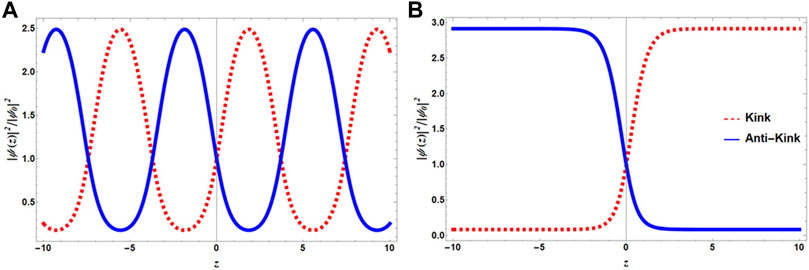
FIGURE 6. (Color Online) The behavior of “sn” solution according to Eq. 25 for different q. (A) The periodic spatial density variation for q = 1/2. (B) Kink and antikink type profiles are reported for q = 1. In both figures, the red dashed line depicts ψ₊(z) solution and the blue solid line corresponds to the ψ₋(z) solution. The density distribution is again normalized by |ψ₀|².

4.1.4 Kink–Antikink Solution

The “sn” solution at q = 1 yields kink–antikink pairs depicted in Figure 6B. Kink and antikink solitons are well-known for the Sine-Gordon (SG) equation. A kink solution can be observed in a ferromagnet where the different spin domains are separated by the domain walls. In these systems, under the influence of external magnetic fields, the Bloch wall can propagate following the dynamical rules governed by the Sine-Gordon equation, and thus the Bloch walls take the shape of kink [63].

4.2 Droplet Solution in Homogeneous System

In the experimental setup of cigar-shaped (Q1D) BEC, ω_⊥ is typically more than 10 times stronger than ω₀. The suitable choice of the transverse (ω_⊥) and longitudinal (ω₀) trapping frequency ensures the interaction energy of the atoms is much less than the kinetic energy in the transverse direction. Since the trapping frequencies can be controlled quite efficiently, it is also possible to tune the transverse confinement much stronger than the longitudinal counterpart (ω₀ ≪ ω_⊥), resulting in K → 0. The system can now be viewed as quasi-homogeneous. Here, we brief the obtained analytical solution for Eq. 20, assuming K = 0.

Using $\varphi (x,t)=\rho (x,t)\exp \left[i\left(\chi (x,t)+\nu t\right)\right]$ where ρ(x, t) leads to the amplitude contribution and χ(x, t) is the non-trivial phase, ν is the chemical potential, and with the required assumptions mentioned in [62], we finally end up with the solution [62]

$\rho \left(\zeta \right)=\frac{1+12{\nu }_g}{1+\sqrt{12{\nu }_g}\cosh \left(\sqrt{-|g|}\zeta \right)}\mathrm{f}\mathrm{o}\mathrm{r}|g|=3g^{\prime }.(26)$

Here, ν_g = ν/g which implies that the localized structures can only be sustained iff g < 0 or the effective MF interaction is attractive and for real solution, ν_g > 0. Hence, the chemical potential must be negative.

We define the relationship between normalization N and chemical potential ν as [62]

$\begin{array}{l}\hfill N=\frac{{\left(1+{\nu }_I\right)}^2}{\sqrt{g}\left(1-{\nu }_I\right)}\left[\ln \left[1-\frac{2}{{\nu }_I}\left(\sqrt{1-{\nu }_I}+1\right)\right]-2\right].\\ \hfill \end{array}(27)$

We have denoted 12ν_g = ν_I. N can also be noted as the number of particles associated with the formation of localized wave and scaled by N₀ where N₀ defines the particle number obtained from the constant background density solution such that $N_0=2a_B{\left(\frac{15\pi a_{\perp }}{64}\right)}^2{\left(\frac{\delta a}{\delta a^{\prime }}\right)}^2$. Solving Eq. 27 numerically for ν, we can create the density profile following Eq. 26. The density profile is presented in Figure 7. It clearly suggests that, for the very low particle number, the system tends to produce localized modes, whereas, for the reasonably large number, we observe the density is constant over a finite spatial dimension, thereby suggesting the formation of a liquid-like state.

FIGURE 7

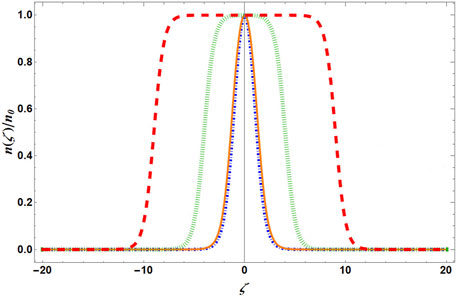
FIGURE 7. (Color online) Spatial variation of the density profile for different particle numbers. The blue dashed-dotted line describes N = 0.1, whereas the orange solid line is prepared for N = 1. The green dotted line and red dashed line depict the density profile for N = 10 and 20, respectively. The density is normalized by the peak density n₀, where n₀ = n(ζ)|_ζ=0.

The droplet formation results from mutual competition between the MF and BMF interaction. It has been argued that, at a lower particle number, the system supports the bright soliton-like modes. In the region where the effective interaction energy (E_eff = E_MF + E_BMF) is negative, the transition from localized to droplet state happens when the effective pressure is nullified (i.e., $P=E_{\mathit{eff}}-n\frac{d{E}_{\mathit{eff}}}{dn}$). The corresponding density is known as equilibrium density. The droplets can sustain below the critical density defined by E_eff = 0. Beyond this point, E_eff > 0 yields gradual evolution of the localized modes. The chemical potential in equilibrium turns out to be −0.02, which is even true for a weakly trapped system, as observed in the following section.

4.3 Droplet to Soliton Transition in Inhomogeneous System

The analytical solution of the CQNLSE motivates us now to examine and validate the result numerically. For that purpose, we implement the imaginary time propagation of the split-step Crank–Nicolson (CN) method [64] over small time steps (5 × 10⁻⁶) for a total of 20,000 steps and solve the homogeneous CQNLSE [62]. Then, we consider K ≠ 0 for several trap frequencies and different BMF interaction strengths κ, where κ is defined as g′/|g|. We use three arbitrary values of κ, as 0.1, 0.5, and 0.9 [65]. Figure 8 depicts the density distribution for K = 0.00001 (blue dashed-dotted line), K = 0.001 (red dotted line), and K = 0.1 (grey dashed-double-dotted line), respectively. The density profile suggests a transition from a droplet-like state to a localized density distribution as we increase the trap frequency. At K = 0.00001, the flat top density distribution is distinctly visible, indicating the droplet-like state, whereas tighter confinement leads to the generation of a bright soliton-like state as described by the grey dashed-double-dotted line. In the intermediate region with moderate trap frequency (say at K = 0.001), a bell-like structure emerges. Though Figure 8 is prepared for κ = 0.1, we do not observe any significant deviation in nature for larger κ values.

FIGURE 8

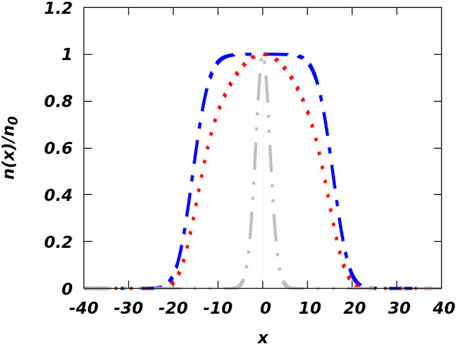
FIGURE 8. (Color online) The density profile of the numerical solution for different K values is depicted here. The blue dashed-dotted line describes the density for K = 0.00001, the red dotted line describes K = 0.001, and the grey dashed-double-dotted line is prepared for K = 0.1. Here, κ = g′/|g| = 0.1 and g is set at 1. The density is normalized by n₀ where n₀ is n(x)|_x = 0.

To understand the possible droplet-soliton transition, we examine the chemical potential. Assuming ϕ(x, t) = ϕ(x)e^−iνt and applying in Eq. 20, we obtain

$\nu \psi \left(x\right)=\left[-\frac{1}{2}\frac{d^2}{d{x}^2}+\frac{1}{2}K{x}^2+g{\psi }^2\left(x\right)+g^{\prime }{\psi }^3\left(x\right)\right]\psi \left(x\right).(28)$

Further incorporating the normalization condition ${\int }_{-\infty }^{\infty }{\psi }^2(x)dx=1$, we yield

$\nu ={\int }_{-\infty }^{\infty }\left[\frac{1}{2}{\left(\frac{d\psi }{dx}\right)}^2+{\psi }^2\left(x\right)\left(\frac{1}{2}K{x}^2+g{\psi }^2\left(x\right)+g^{\prime }{\psi }^3\left(x\right)\right)\right]dx.(29)$

The variation of chemical potential while trap frequency is tuned is noted in Figure 9A. We repeat this calculation for different interaction strengths (κ = 0.1, 0.5, and 0.9). For a quite loos trap, the system can be treated as quasi-homogeneous, leading to the formation of droplets signified by the negative value of the chemical potential. Furthermore, we note that, in this situation, the chemical potential converges to ∼ − 0.02 for different interaction strengths. It must be noted that a similar result has already been reported for κ = 0.33 in the previous section, where we discussed the analytical calculation for a homogeneous system [62]. Figure 9A also reveals that the stronger confinement leads to the solitonic state with ν > 0 (right side of the grey shaded region of Figure 9A). Curiously, we observe a non-monotonic behavior of the chemical potential in the shaded region where the confining potential strength is in the regions 0.001 and 0.1. A comparison with Figure 8 encourages us to consider this frequency window as the transition region.

FIGURE 9

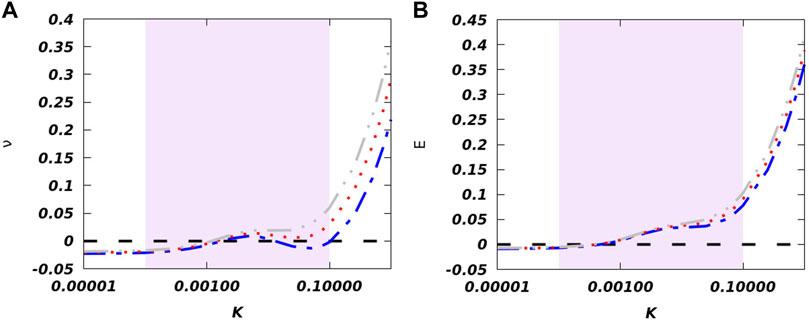
FIGURE 9. (Color online) (A) The variation of chemical potential, while the trapping potential is tuned, is depicted here for different κ values. The grey dashed-double-dotted line corresponds to κ = 0.9, the red dotted and blue dashed-dotted lines describe the variation of chemical potential with trap frequency for κ = 0.5 and 0.1, respectively. The black dashed line indicates ν = 0. The shaded area describes the crossover regime. (B) Change in energy with variation in the trap frequency is plotted here for different BMF interaction strengths. The colors and line styles have the same meaning as previous. The black dashed line indicates E = 0. The light magenta area corresponds to the region of transition from droplet to soliton.

Now, it is important to understand the nature of the transition. The pertaining question is whether the transition is a quantum phase transition (QPT) or a crossover. In QPT, one can identify an abrupt change in the ground state of the system when a Hamiltonian parameter crosses a critical value [66,67]. Here, we recognize K or the square of the longitudinal trapping frequency as the Hamiltonian parameter. Because we do not observe any abrupt change in ν, we calculate the first derivative of the chemical potential with respect to K but again fail to identify any abrupt change. Thus, we conclude the transition to be a crossover rather than a QPT, and we recognize a loose crossover boundary as 0.0001 ≲ K ≲ 0.1 (described in the light-magenta shaded region in the figures).

To verify our analysis, we also calculate the total energy

$E={\int }_{-\infty }^{\infty }\left[\frac{1}{2}{\left(\frac{d\psi }{dx}\right)}^2+{\psi }^2\left(x\right)\left(\frac{1}{2}K{x}^2+\frac{1}{2}g{\psi }^2\left(x\right)+\frac{2}{5}{g}^{\prime }{\psi }^3\left(x\right)\right)\right]dx,(30)$

and capture its variation in Figure 9B. The energy description also supports our assertion as we observe negative energy for weak confinement leading to the accumulation of droplet-like bound pairs. The energy crosses the zero line in the vicinity of K = 0.001, which might point to the breakdown of droplet-like bound pairs. However, the energy flattens in the shaded area might be suggestive of an equilibrium of the dropleton-soliton mixture. Further increase in the trapping potential destroys the bound pairs, and soliton-like state emerges.

We also observe a very smooth transition of root-mean-square (rms) $(\sqrt{⟨x^2⟩})$ size of the condensate, which is depicted in Figure 10. The rms size is normalized by the rms size $(\sqrt{⟨x_0^2⟩})$ for K = 0, and we introduce $⟨X^2⟩=\frac{\sqrt{⟨x^2⟩}}{\sqrt{⟨x_0^2⟩}}$. According to Figure 10fig10, we can conclude that the weak trapping potential allows the larger pair size, suggesting the droplet formation. However, gradually and smoothly, the pair size falls off as we increase the longitudinal frequency. We also observe that the pair size drops much faster in the shaded region, defined as the crossover region. The rms curve flattens thereafter and asymptotically reaches 1/10 of the droplet size for a tightly confined one-dimensional geometry.

FIGURE 10

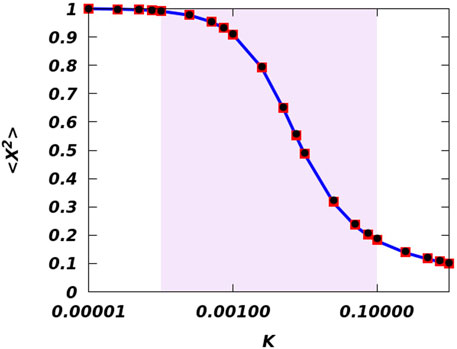
FIGURE 10. (Color online) The variation of the rms size of the droplets with the modulation of the trapping potential. The solid blue line, the red solid squares, and the black solid circles denote κ = 0.1, 0.5, and 0.9, respectively. The shaded region describes the crossover area.

The role of particle number in the transition is also a matter of deep interest. We calculate the energy and chemical potential for different particle numbers (from 25 to 100). We draw a contour phase diagram based on our findings depicted in Figure 11. The bluish region corresponds to the negative energy region, thereby suggesting the existence of the bound pairs and droplet formation. The red region describes the unbound solitonic region, and the greenish region corresponds to the region of crossover where the droplets are breaking down into solitons. Moreover, one can also conclude that the larger particle number hinders the droplet formation even if the confinement is very weak. It is similar to the fact mentioned in the previous section regarding the existence of a critical density beyond which droplets cannot form in a homogeneous system.

FIGURE 11

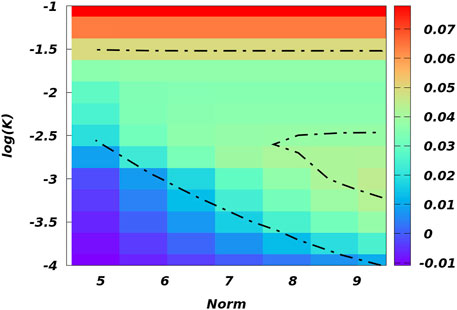
FIGURE 11. (Color online) The contour plot described the energy variation as a function of trap frequency (in log scale) and norm (norm = $\sqrt{N}$). It clearly illustrates the phase boundaries between the droplet-like state (bluish section, mainly bottom and bottom left), soliton-like state (reddish region, in the top), and an intermediate droplet-soliton mixture (greenish region, in the middle).

5 Supersolidity

As quantum liquid remains in its infancy, it is fascinating with new attributes. One such exciting phenomenon is the quantum ferrofluids. It is recently shown that the quantum ferrofluids born from ultracold atomic gases have exhibited supersolid properties [44–46,68]. The investigation has further been extended toward the supersolid to superglass transition [69]. This section covers a couple of theoretical descriptions leading to supersolid formation. The flow of the content will follow the same pattern as the previous; first, we will discuss the 1D system and then we will elaborate on Q1D geometry.

5.1 Supersolidity in 1D

A recent analytical study has highlighted the generation of supersolid-like phase in a self-trapped 1D system [70]. The analysis comes up with several analytical solutions by considering a propagating Bloch function type solutions [71]. The self-trapped dynamical system can be described as

$i\hslash \frac{\partial {\mathrm{\Phi }}^{1D}}{\partial t}=-\frac{{\hslash }^2}{2m}{\mathrm{\Phi }}_{xx}^{1D}+\delta g|{\mathrm{\Phi }}^{1D}{|}^2{\mathrm{\Phi }}^{1D}-\frac{\sqrt{2m}}{\pi \hslash }{g}^{3/2}|{\mathrm{\Phi }}^{1D}|{\mathrm{\Phi }}^{1D},(31)$

Here, Φ^1D defines the wavefunction in a strictly 1D system. For notational convenience let us replace Φ^1D as ϕ, and we assume ϕ represents a propagating Bloch function such that

$\varphi ={\varphi }_0\left(\frac{x-vt}{\xi }\right)\exp \left(ikx-i\frac{\nu }{\hslash }t\right),(32)$

Here, ϕ₀ is taken as a conoidal function with modulus parameter q. We have already noted that, for q = 0, the cnoidal function manifests sinusoidal nature:

${\varphi }_0=A+B\mathrm{s}\mathrm{n}\left(\frac{x-vt}{\xi },q\right),(33)$

where $A=\frac{\sqrt{2m}}{3\pi \hslash }\frac{g^{3/2}}{\delta g}$, $B=\pm \sqrt{\frac{2q}{q+1}}A$, $\xi =\frac{3{\hslash }^2\pi }{2m}\sqrt{\frac{(q+1)\delta g}{g^3}}$, and 0 < q < 1.

It is evident that the existence of the Bloch type solutions with a superfluid background crucially depends upon the MF term, BMF correction, and dispersion. Here, ${\varphi }_{\text{min/max}}=A\pm B=A\left(1\pm \sqrt{\frac{2q}{q+1}}\right)>0$ shows that the quantum supersolid immersed in a residual BEC [44,46,68]. The density of the residual BEC, $n_{\text{res}}=A^2{\left(1-\sqrt{\frac{2q}{q+1}}\right)}^2>0$. This diffused matter-wave density rules out the scenario of one atom per site thereby overtaking the Penrose and Onsager criterion [72–74].

The density of the supersolid phase is shown in Figure 12 in the comoving frame. With increasing repulsive intra-component interaction g, the number of droplets increases and their size decreases to a fixed value of x/ξ. Furthermore, keeping all the physical parameters constant, an increase in the modulus parameter increases the interdroplet spacing [70].

FIGURE 12

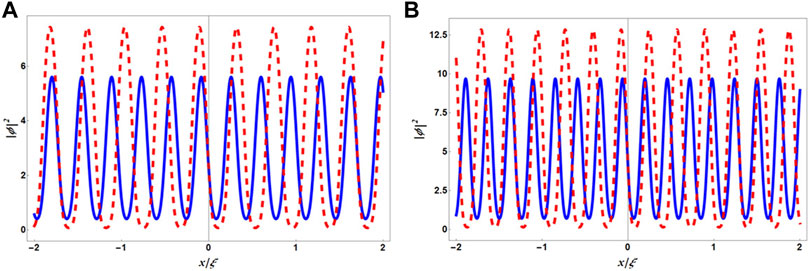
FIGURE 12. (Color Online) Density profiles corresponding to Eq. 33 for different values of g and q. In both the panels, blue solid line and red dashed line are for q = 0.2 and q = 0.5, respectively. (A,B) are prepared for g = 10 and g = 12, respectively. In both figures, δg = 0.1 and |ϕ|² is scaled to 10⁻³.

5.2 Supersolidity in Q1D

Moving toward the Q1D geometry, we recognize that it is impossible to yield any analytical solution from a self-trapped system. Hence, we employ a bi-chromatic lattice in CQNLSE. The application of bi-chromatic lattice was motivated by the recent observations of supersolid-like features in a spin-orbit coupled BEC, where the experiment was performed in the presence of two optical lattices of different frequencies in the same spatial dimension where the effective lattice potential was described as a superlattice [75]. However, the manifestation of supersolidity emerges naturally in a spin-orbit or dipolar BEC. To mimic these additional contributions, we add a driving force that is periodic in nature to compete with the two-body mean-field interaction. The use of external driving force in ultracold atomic systems is not alien [76,77]. There are suggestions for generating and controlling the transport of BEC atoms from a reservoir to the waveguide via a source/driving force [76–79].

The knowledge of Eq. 20 allows us to write a generic time-dependent DCQNLSE as [80]

$-\frac{1}{2}\frac{{\partial }^2\mathrm{\Phi }}{\partial x^2}+\left(V_2\sin \zeta x-V_1{\sin }^3\zeta x\right)\mathrm{\Phi }+g_1|\mathrm{\Phi }{|}^2\mathrm{\Phi }+g_2|\mathrm{\Phi }{|}^3\mathrm{\Phi }-i\frac{\partial \mathrm{\Phi }}{\partial t}{=F}^{\prime }\left(x,t\right).(34)$

Focusing on the static solution we assume, Φ(x, t) = ϕ(x)e^−iνt, where ν is the chemical potential. To extract the static behavior, it is also necessary to lock the temporal phase part of the driving force with the solution ansatz. Also, we assume the spatial variation in sinusoidal in nature. Hence, we denote F′(x, t) = F e^−iνt sin ζx. The resulting time independent DCQNLSE reduces to [80]

$-\frac{1}{2}\frac{d^2\varphi }{d{x}^2}+\left(V_2\sin \zeta x-V_1{\sin }^3\zeta x\right)\varphi +g_1|\varphi {|}^2\varphi +g_2|\varphi {|}^3\varphi -\nu \varphi =\mathcal{F}\sin \zeta x.(35)$

Here, the strength of odd (cubic) and even (quartic) exponents is described via g₁ and g₂, respectively. The coherence length can be recognized as 1/ζ. The bi-chromatic lattice potential depths are described via V₁ and V₂. A suitable modulation of the lattice depth can create a superlattice [75]. As the cubic exponent of the potential can be written in terms of triple angle representation, the wavenumber of one laser is required to be thrice the second laser. $\mathcal{F}$ is the amplitude of the external force. To obtain a sinusoidal mode, we assume an ansatz such that ϕ(x) = A + B sin ζx. From the recent investigation described in [46], we learn that the density distribution of the supersolid phase can be described adequately via the sinusoidal function similar to the ansatz. Applying the ansatz in Eq. 35, we encounter a set of consistency conditions as noted in [80].

The solutions parameters such as A and B can be solved, and we can write the final solution as

$\varphi \left(x\right)={\varphi }_{\mathit{Q1D}}\left(x\right)=-\frac{g_1}{3g_2}+{\left(\frac{V_1}{g_2}\right)}^{1/3}\sin \zeta x.(36)$

Here, A = −g₁/3g₂ and $B={(V_1/g_2)}^{1/3}$. The coherence length shows a function of external driving force as $\zeta =\pm \sqrt{2\mathcal{F}}B$. The expression for B suggests that $B\in \mathbb{R}$, thus avoiding the occurrence of the nonphysical situation such as complex coherence length. This also implies that if V₁ > 0 then g₂ > 0 or vice versa. However, g₁ does not have any such constraints. Therefore, the MF interaction strength can be attractive and repulsive, whereas the nature of BMF will depend on the nature of optical lattice potential amplitude. We also note that it is necessary to apply the driving force in the same direction as the displacement.

Figure 13 depicts the spatial variation of density (|ϕ(x)|²) via a red dashed line. The blue solid line describes the spatial variation of the BOL. As shown in Figure 13, the existence of the density wave is quite evident, with density maxima coinciding with the potential minima.

FIGURE 13

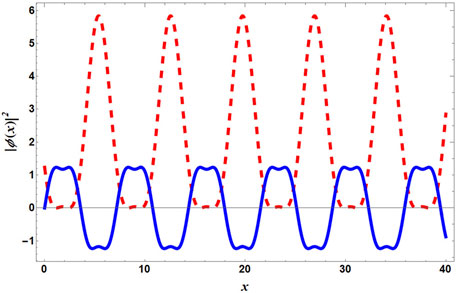
FIGURE 13. (Color Online) The density profile calculated from Eq. 36 is depicted here along with V_BOL. The red dashed line and the blue solid line describe the density variation and V_BOL, respectively. Here, V₁ = 1.0, $V_2=\frac{1}{3}{\left(\frac{V_1}{g_2}\right)}^{1/3}\frac{g_1^2}{g_2}$, g₁ = 1.5, g₂ = 0.3, and $\mathcal{F}$= 0.5.

The stability of these modes can be discussed in the light of the VK criterion [54]. Here, calculating the particle number (N) in a unit cell of length $\mathcal{L}$ we find that $\partial N/\partial \nu =\mathcal{L}/g_1$. Hence, for a stable solution, the MF interaction should be positive, which physically implies a repulsive nature.

5.3 1D, Q1D, and Beyond

Till now, we have discussed the 1D and Q1D systems. The 1D and Q1D systems have already been characterized by the one-dimensional scattering length $(\tilde{a})$ and density $(\tilde{n})$. For a 1D system $\mathrm{\Sigma }=1/|\sqrt{\tilde{n}\tilde{a}}|<1$, whereas Σ > 1 for Q1D geometry. Then, what happens if Σ ∼ 1 or at the dimensional crossover? From a mathematical point of view, we understand that the even exponent in the BMF contribution is two for 1D and four for Q1D. However, we lack the clarity of the dynamical equation at the dimensional crossover. We attempt the problem by assuming a mixture of BMF contributions from 1D and Q1D, which implies that the dynamical equation contains both the quadratic and quartic non-linearities; thus, the NLSE can now be termed as quadratic-cubic-quartic NLSE or QCQNLSE. We solve the dynamical equation following the already described methodology and look for sinusoidal solutions. For brevity, we do not explicate the detailed calculation. Nevertheless, one can easily obtain the analytical results following the same prescription of Section 5.2. If we denote ϕ_1D, ϕ_Q1D as analytically obtained sinusoidal wave functions and ϕ_Q1D−1D describe the wave function in the crossover; then, we observe that ϕ_Q1D = ϕ_Q1D−1D ≠ ϕ_1D. Thus, the continuity of the wave function is retained in the region Σ < 1 and Σ ∼ 1. However, there is a clear discontinuity in moving toward the 1D regime [80]. We have also noted that, for Q1D and dimensional crossover, we require a super lattice-like trapping geometry, whereas a 1D system can be analyzed in a regular optical lattice.

6 Conclusion

This review summarizes the theoretical endeavors to examine the newly observed liquid-like state in ultra-cold atomic gases at a lower dimension. To be precise, we have confined ourselves to Q1D and 1D geometries. It is a well-known fact that condensate formation is not possible in the 1D Bose gas even though, using the Bogoliubov theory, one can correctly predict the ground state energy of a weakly interacting Bose gas. On the contrary, a Q1D geometry is widely used in experiments to create a condensate and study its dynamics.

In order to study the droplets in the lower dimension, it is required to note that the exponent of BMF non-linearity is different for 1D and Q1D. Though in both the cases, the exponents are even. In 1D, it is two, and in Q1D, it is four. Therefore, we attempt to review the recent theoretical advances in 1D systems with quadratic non-linearity (apart from the usual cubic non-linearity, describing the two-body short-range interaction). We summarize the recently reported cnoidal, localized, and kink–antikink type solutions for this system and discuss the interplay of MF and BMF interactions.

In the later half, we study the Q1D geometry and brief the analytically obtained solution for a cubic-quartic NLSE (the governing dynamical equation). In this section, first, we explore the possibility of obtaining a cnoidal solution, and for that, we observe the necessity of cnoidal trapping potential. Subsequently, we present the analytical solution for droplets in a homogeneous CQNLSE, and then we study the effect of harmonic trapping. It comes out that trap modulation can even induce a droplet to soliton transition.

The penultimate chapter briefly discusses the very recent developments related to the observation of the supersolid phase, where one can notice superfluid behavior along with lattice order. The experiments have shown that, in dipolar BEC, there exists a transition from droplet to supersolid phase, which can be characterized by the stripe phases and longer phase coherence. Here, we look back at a very recent report where theoreticians have predicted the existence of a self-trapped supersolid phase in 1D. Apart from that, we also comment on the existence of a supersolid phase through driven CQNLSE in a super lattice. The phenomenological driving force mimics the contribution of the dipolar interaction. At the very end, we examine the dimensional crossover from Q1D to 1D by studying the continuity of the wave function.

As this area of research is still new, we expect our effort in summarizing the recent theoretical developments on the liquid-like state at the lower dimension will be a subject of interest for a wide audience. Moreover, this can stimulate more intense experimental research in the lower dimension, which still requires some grounds to cover.

Author Contributions

AK and AD contributed equally.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

AD thanks A. Trounev for valuable inputs. AK thanks the Department of Science and Technology (DST), India, for the support provided through project no. CRG/2019/000108.

References

1. Dalfovo F, Giorgini S, Pitaevskii LP, Stringari S. Theory of Bose-Einstein Condensation in Trapped Gases. Rev Mod Phys (1999) 71:463–512. doi:10.1103/RevModPhys.71.463

CrossRef Full Text | Google Scholar

2. Giorgini S, Pitaevskii LP, Stringari S. Theory of Ultracold Atomic Fermi Gases. Rev Mod Phys (2008) 80:1215–74. doi:10.1103/RevModPhys.80.1215

CrossRef Full Text | Google Scholar

3. Bloch I, Dalibard J, Zwerger W. Many-body Physics with Ultracold Gases. Rev Mod Phys (2008) 80:885–964. doi:10.1103/RevModPhys.80.885

CrossRef Full Text | Google Scholar

4. Fano U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys Rev (1961) 124:1866–78. doi:10.1103/physrev.124.1866

CrossRef Full Text | Google Scholar

5. Feshbach H. Unified Theory of Nuclear Reactions. Ann Phys (1958) 5:357–90. doi:10.1016/0003-4916(58)90007-1

CrossRef Full Text | Google Scholar

6. Chin C, Grimm R, Julienne P, Tiesinga E. Feshbach Resonances in Ultracold Gases. Rev Mod Phys (2010) 82:1225–86. doi:10.1103/RevModPhys.82.1225

CrossRef Full Text | Google Scholar

7. Burger S, Bongs K, Dettmer S, Ertmer W, Sengstock K, Sanpera A, et al. Dark Solitons in Bose-Einstein Condensates. Phys Rev Lett (1999) 83:5198–201. doi:10.1103/physrevlett.83.5198

CrossRef Full Text | Google Scholar

8. Denschlag J, Simsarian JE, Feder DL, Clark CW, Collins LA, Cubizolles J, et al. Generating Solitons by Phase Engineering of a Bose-Einstein Condensate. Science (2000) 287:97–101. doi:10.1126/science.287.5450.97

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Strecker KE, Partridge GB, Truscott AG, Hulet RG. Formation and Propagation of Matter-Wave Soliton Trains. Nature (2002) 417:150–3. doi:10.1038/nature747

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Khaykovich L, Schreck F, Ferrari G, Bourdel T, Cubizolles J, Carr LD, et al. Formation of a Matter-Wave Bright Soliton. Science (2002) 296:1290–3. doi:10.1126/science.1071021

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Strecker KE, Partridge GB, Truscott AG, Hulet RG. Bright Matter Wave Solitons in Bose-Einstein Condensates. New J Phys (2003) 5:73. doi:10.1088/1367-2630/5/1/373

CrossRef Full Text | Google Scholar

12. Cornish SL, Thompson ST, Wieman CE. Formation of Bright Matter-Wave Solitons during the Collapse of Attractive Bose-Einstein Condensates. Phys Rev Lett (2006) 96:170401. doi:10.1103/physrevlett.96.170401

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Marchant AL, Billam TP, Wiles TP, Yu MM, Gardiner SA, Cornish SL. Controlled Formation and Reflection of a Bright Solitary Matter-Wave. Nat Commun (2013) 4:1865–6. doi:10.1038/ncomms2893

PubMed Abstract | CrossRef Full Text | Google Scholar

14. McDonald GD, Kuhn CC, Hardman KS, Bennetts S, Everitt PJ, Altin PA, et al. Bright Solitonic Matter-Wave Interferometer. Phys Rev Lett (2014) 113:013002. doi:10.1103/PhysRevLett.113.013002

CrossRef Full Text | Google Scholar

15. Lepoutre S, Fouché L, Boissé A, Berthet G, Salomon G, Aspect A, et al. Production of Strongly Bound K 39 Bright Solitons. Phys Rev A (2016) 94:053626. doi:10.1103/physreva.94.053626

CrossRef Full Text | Google Scholar

16. Medley P, Minar MA, Cizek NC, Berryrieser D, Kasevich MA. Evaporative Production of Bright Atomic Solitons. Phys Rev Lett (2014) 112:060401. doi:10.1103/PhysRevLett.112.060401

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ferrier-Barbut I, Kadau H, Schmitt M, Wenzel M, Pfau T. Observation of Quantum Droplets in a Strongly Dipolar Bose Gas. Phys Rev Lett (2016) 116:215301. doi:10.1103/PhysRevLett.116.215301

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kadau H, Schmitt M, Wenzel M, Wink C, Maier T, Ferrier-Barbut I, et al. Observing the Rosensweig Instability of a Quantum Ferrofluid. Nature (2016) 530:194–7. doi:10.1038/nature16485

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ferioli G, Semeghini G, Masi L, Giusti G, Modugno G, Inguscio M, et al. Collisions of Self-Bound Quantum Droplets. Phys Rev Lett (2019) 122:090401. doi:10.1103/PhysRevLett.122.090401

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Cabrera CR, Tanzi L, Sanz J, Naylor B, Thomas P, Cheiney P, et al. Quantum Liquid Droplets in a Mixture of Bose-Einstein Condensates. Science (2018) 359:301–4. doi:10.1126/science.aao5686

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Petrov DS. Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture. Phys Rev Lett (2015) 115:155302. doi:10.1103/PhysRevLett.115.155302

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Wächtler F, Santos L. Quantum Filaments in Dipolar Bose-Einstein Condensates. Phys Rev A (2016) 93:061603. doi:10.1103/PhysRevA.93.061603

CrossRef Full Text | Google Scholar

23. Ferrier-Barbut I. Ultradilute Quantum Droplets. Phys Today (2019) 72:46–52. doi:10.1063/pt.3.4184

CrossRef Full Text | Google Scholar

24. Lee TD, Huang K, Yang CN. Eigenvalues and Eigenfunctions of a Bose System of Hard Spheres and its Low-Temperature Properties. Phys Rev (1957) 106:1135–45. doi:10.1103/PhysRev.106.1135

CrossRef Full Text | Google Scholar

25. Gross EP. Structure of a Quantized Vortex in Boson Systems. Nuovo Cim (1955-1965) (1961) 20:454–77. doi:10.1007/bf02731494

CrossRef Full Text | Google Scholar

26. Pitaevskii L. Vortex Lines in an Imperfect Bose Gas. Sov Phys JETP (1961) 13:451–4.

Google Scholar

27. Dauxois T, Peyrard M. Physics of Solitons. Cambridge: Cambridge University Press (2006).

Google Scholar

28. Malomed B. Multidimensional Self-Trapping in Linear and Nonlinear Potentials. arXiv preprint arXiv:2111.00547 (2021).

Google Scholar

29. Salasnich L. Self-consistent Derivation of the Modified Gross-Pitaevskii Equation with lee-huang-yang Correction. Appl Sci (2018) 8:1998. doi:10.3390/app8101998

CrossRef Full Text | Google Scholar

30. Cappellaro A, Macrì T, Salasnich L. Collective Modes across the Soliton-Droplet Crossover in Binary Bose Mixtures. Phys Rev A (2018) 97:053623. doi:10.1103/PhysRevA.97.053623

CrossRef Full Text | Google Scholar

31. Li Y, Chen Z, Luo Z, Huang C, Tan H, Pang W, et al. Two-dimensional Vortex Quantum Droplets. Phys Rev A (2018) 98:063602. doi:10.1103/PhysRevA.98.063602

CrossRef Full Text | Google Scholar

32. Lin Z, Xu X, Chen Z, Yan Z, Mai Z, Liu B. Two-dimensional Vortex Quantum Droplets Get Thick. Commun Nonlinear Sci Numer Simulation (2021) 93:105536. doi:10.1016/j.cnsns.2020.105536

CrossRef Full Text | Google Scholar

33. Shamriz E, Chen Z, Malomed BA. Suppression of the Quasi-Two-Dimensional Quantum Collapse in the Attraction Field by the lee-huang-yang Effect. Phys Rev A (2020) 101:063628. doi:10.1103/PhysRevA.101.063628

CrossRef Full Text | Google Scholar

34. Zhang X, Xu X, Zheng Y, Chen Z, Liu B, Huang C, et al. Semidiscrete Quantum Droplets and Vortices. Phys Rev Lett (2019) 123:133901. doi:10.1103/physrevlett.123.133901

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Astrakharchik G, Malomed BA. Dynamics of One-Dimensional Quantum Droplets. Phys Rev A (2018) 98:013631. doi:10.1103/physreva.98.013631

CrossRef Full Text | Google Scholar

36. Tylutki M, Astrakharchik GE, Malomed BA, Petrov DS. Collective Excitations of a One-Dimensional Quantum Droplet. Phys Rev A (2020) 101:051601. doi:10.1103/PhysRevA.101.051601

CrossRef Full Text | Google Scholar

37. Chiquillo E. Low-dimensional Self-Bound Quantum Rabi-Coupled Bosonic Droplets. Phys Rev A (2019) 99:051601. doi:10.1103/PhysRevA.99.051601

CrossRef Full Text | Google Scholar

38. Luo Z-H, Pang W, Liu B, Li Y-Y, Malomed BA. A New Form of Liquid Matter: Quantum Droplets. Front Phys (2021) 16:1–21. doi:10.1007/s11467-020-1020-2

CrossRef Full Text | Google Scholar

39. Edmonds M, Bland T, Parker N. Quantum Droplets of Quasi-One-Dimensional Dipolar Bose-Einstein Condensates. J Phys Commun (2020) 4:125008. doi:10.1088/2399-6528/abcc3b

CrossRef Full Text | Google Scholar

40. Malomed BA. The Family of Quantum Droplets Keeps Expanding. Front Phys (2020) 16:22504. doi:10.1007/s11467-020-1024-y

CrossRef Full Text | Google Scholar

41. Mithun T, Maluckov A, Kasamatsu K, Malomed BA, Khare A. Modulational Instability, Inter-component Asymmetry, and Formation of Quantum Droplets in One-Dimensional Binary Bose Gases. Symmetry (2020) 12:174. doi:10.3390/sym12010174

CrossRef Full Text | Google Scholar

42. Atre R, Panigrahi PK, Agarwal GS. Class of Solitary Wave Solutions of the One-Dimensional Gross-Pitaevskii Equation. Phys Rev E Stat Nonlin Soft Matter Phys (2006) 73:056611. doi:10.1103/PhysRevE.73.056611

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Andreev A, Lifshits I. Quantum Theory of Defects in Crystals. Zhur Eksper Teoret Fiziki (1969) 56:2057–68.

Google Scholar

44. Böttcher F, Schmidt J-N, Wenzel M, Hertkorn J, Guo M, Langen T, et al. Transient Supersolid Properties in an Array of Dipolar Quantum Droplets. Phys Rev X (2019) 9:011051.

Google Scholar

45. Chomaz L, Petter D, Ilzhöfer P, Natale G, Trautmann A, Politi C, et al. Long-lived and Transient Supersolid Behaviors in Dipolar Quantum Gases. Phys Rev X (2019) 9:021012. doi:10.1103/physrevx.9.021012

CrossRef Full Text | Google Scholar

46. Tanzi L, Lucioni E, Famà F, Catani J, Fioretti A, Gabbanini C, et al. Observation of a Dipolar Quantum Gas with Metastable Supersolid Properties. Phys Rev Lett (2019) 122:130405. doi:10.1103/physrevlett.122.130405

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Lifshitz E, Pitaevskii L. Statistical Physics, Part 2. oxford: Pergamon Press (1980).

Google Scholar

48. Malomed BA, Mihalache D, Wise F, Torner L. Spatiotemporal Optical Solitons. J Opt B: Quan Semiclass. Opt. (2005) 7:R53–R72. doi:10.1088/1464-4266/7/5/r02

CrossRef Full Text | Google Scholar

49. Lieb EH, Liniger W. Exact Analysis of an Interacting Bose Gas. I. The General Solution and the Ground State. Phys Rev (1963) 130:1605–16. doi:10.1103/physrev.130.1605

CrossRef Full Text | Google Scholar

50. Petrov DS, Astrakharchik GE. Ultradilute Low-Dimensional Liquids. Phys Rev Lett (2016) 117:100401. doi:10.1103/physrevlett.117.100401

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Shukla A, Neeraj PK, Panigrahi PK. Kink-like Solitons in Quantum Droplet. J Phys B: Mol Opt Phys (2021) 54:165301. doi:10.1088/1361-6455/ac1692

CrossRef Full Text | Google Scholar

52. Salasnich L, Parola A, Reatto L. Effective Wave Equations for the Dynamics of Cigar-Shaped and Disk-Shaped Bose Condensates. Phys Rev A (2002) 65:043614. doi:10.1103/physreva.65.043614

CrossRef Full Text | Google Scholar

53.[Dataset] Rajaraman R. An Introduction to Solitons and Instantons in Quantum Field Theory, Solitons and Instantons, Vol. 15. Amsterdam, Netherlands: Elsevier (1987).

Google Scholar

54. Vakhitov NG, Kolokolov AA. Stationary Solutions of the Wave Equation in a Medium with Nonlinearity Saturation. Radiophys Quan Electron (1973) 16:783–9. doi:10.1007/bf01031343

CrossRef Full Text | Google Scholar

55. Roy U, Atre R, Sudheesh C, Kumar CN, Panigrahi PK. Complex Solitons in Bose-Einstein Condensates with Two- and Three-Body Interactions. J Phys B: Mol Opt Phys (2010) 43:025003. doi:10.1088/0953-4075/43/2/025003

CrossRef Full Text | Google Scholar

56. Roy U, Shah B, Abhinav K, Panigrahi PK. Gapped Solitons and Periodic Excitations in Strongly Coupled Becs. J Phys B: Mol Opt Phys (2011) 44:035302. doi:10.1088/0953-4075/44/3/035302

CrossRef Full Text | Google Scholar

57. Das P, Panigrahi PK. Controlled Generation of Nonlinear Resonances through Sinusoidal Lattice Modes in Bose-Einstein Condensate. Laser Phys (2015) 25:125501. doi:10.1088/1054-660x/25/12/125501

CrossRef Full Text | Google Scholar

58. Abramowitz M, Stegun IA. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Vol. 55. Washington, D.C., USA: US Government printing office (1972).

Google Scholar

59. Cervero JM. Unveiling the Solitons Mystery: The Jacobi Elliptic Functions. Am J Phys (1986) 54:35–8. doi:10.1119/1.14767

CrossRef Full Text | Google Scholar

60. Triki H, Biswas A, Moshokoa SP, Belic M. Optical Solitons and Conservation Laws with Quadratic-Cubic Nonlinearity. Optik (2017) 128:63–70. doi:10.1016/j.ijleo.2016.10.010

CrossRef Full Text | Google Scholar

61. Barashenkov IV, Panova EY. Stability and Evolution of the Quiescent and Travelling Solitonic Bubbles. Physica D: Nonlinear Phenomena (1993) 69:114–34. doi:10.1016/0167-2789(93)90184-3

CrossRef Full Text | Google Scholar

62. Debnath A, Khan A. Investigation of Quantum Droplets: An Analytical Approach. Annalen der Physik (2021) 533:2000549. doi:10.1002/andp.202000549

CrossRef Full Text | Google Scholar

63. Debnath A, Khan A. On Solving Cubic-Quartic Nonlinear Schrödinger Equation in a Cnoidal Trap. The Eur Phys J D (2020) 74:1–6. doi:10.1140/epjd/e2020-10364-4

CrossRef Full Text | Google Scholar

64. Muruganandam P, Adhikari SK. Fortran Programs for the Time-dependent Gross-Pitaevskii Equation in a Fully Anisotropic Trap. Comput Phys Commun (2009) 180:1888–912. doi:10.1016/j.cpc.2009.04.015

CrossRef Full Text | Google Scholar

65. Debnath A, Khan A, Basu S. Dropleton-soliton Crossover Mediated via Trap Modulation. arXiv preprint arXiv:2111.12932 (2021).

Google Scholar

66. Khan A, Pieri P. Ground-state Fidelity in the Bcs-Bec Crossover. Phys Rev A (2009) 80:012303. doi:10.1103/physreva.80.012303

CrossRef Full Text | Google Scholar

67. Dey P, Sarkar D, Khan A, Basu S. Participation Ratio and Fidelity Analyses as Tools to Study Bcs-Bec Crossover. Eur Phys J B (2011) 81:95–102. doi:10.1140/epjb/e2011-10907-6

CrossRef Full Text | Google Scholar

68. Roccuzzo SM, Ancilotto F. Supersolid Behavior of a Dipolar Bose-Einstein Condensate Confined in a Tube. Phys Rev A (2019) 99:041601. doi:10.1103/physreva.99.041601

CrossRef Full Text | Google Scholar

69. Hertkorn J, Schmidt J-N, Guo M, Böttcher F, Ng KSH, Graham SD, et al. Pattern Formation in Quantum Ferrofluids: From Supersolids to Superglasses. Phys Rev Res (2021) 3:033125. doi:10.1103/PhysRevResearch.3.033125

CrossRef Full Text | Google Scholar

70. Parit MK, Tyagi G, Singh D, Panigrahi PK. Supersolid Behavior in One-Dimensional Self-Trapped Bose-Einstein Condensate. J Phys B: Mol Opt Phys (2021) 54:105001. doi:10.1088/1361-6455/abf6e0

CrossRef Full Text | Google Scholar

71. Kittel C, McEuen P, McEuen P. Introduction to Solid State Physics, Vol. 8. New York: Wiley (1996).

Google Scholar

72. Penrose O, Onsager L. Bose-einstein Condensation and Liquid Helium. Phys Rev (1956) 104:576–84. doi:10.1103/physrev.104.576

CrossRef Full Text | Google Scholar

73. Chester GV. Speculations on Bose-Einstein Condensation and Quantum Crystals. Phys Rev A (1970) 2:256–8. doi:10.1103/physreva.2.256

CrossRef Full Text | Google Scholar

74. Pomeau Y, Rica S. Dynamics of a Model of Supersolid. Phys Rev Lett (1994) 72:2426–9. doi:10.1103/physrevlett.72.2426

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Li J-R, Lee J, Huang W, Burchesky S, Shteynas B, Top FÇ, et al. A Stripe Phase with Supersolid Properties in Spin-Orbit-Coupled Bose-Einstein Condensates. Nature (2017) 543:91–4. doi:10.1038/nature21431

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Paul T, Richter K, Schlagheck P. Nonlinear Resonant Transport of Bose-Einstein Condensates. Phys Rev Lett (2005) 94:020404. doi:10.1103/PhysRevLett.94.020404

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Yan Z, Zhang X-F, Liu W. Nonautonomous Matter Waves in a Waveguide. Phys Rev A (2011) 84:023627. doi:10.1103/physreva.84.023627

CrossRef Full Text | Google Scholar

78. Pal R, Loomba S, Kumar CN, Milovic D, Maluckov A. Matter Wave Soliton Solutions for Driven Gross-Pitaevskii Equation with Distributed Coefficients. Ann Phys (2019) 401:116–29. doi:10.1016/j.aop.2019.01.002

CrossRef Full Text | Google Scholar

79. Raju TS, Kumar CN, Panigrahi PK. On Exact Solitary Wave Solutions of the Nonlinear Schrödinger Equation with a Source. J Phys A: Math Gen (2005) 38:L271–L276. doi:10.1088/0305-4470/38/16/l02

CrossRef Full Text | Google Scholar

80. Debnath A, Tarun J, Khan A. Signature of Supersolidity in a Driven Cubic-Quartic Nonlinear Schrödinger Equation. J Phys B: Mol Opt Phys (2022) 55:025301. doi:10.1088/1361-6455/ac4c8e

CrossRef Full Text | Google Scholar