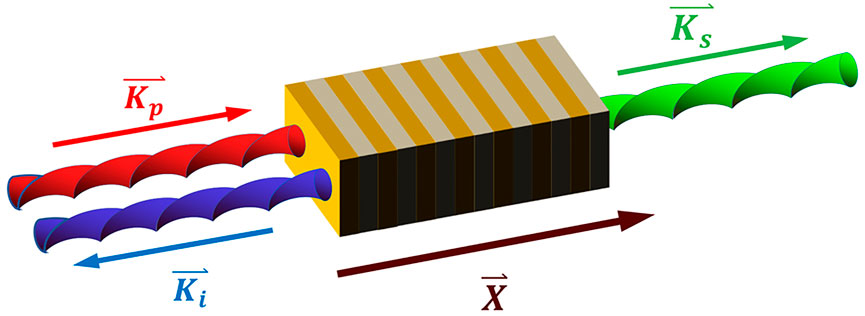
- National Laboratory of Solid State Microstructures, College of Engineering and Applied Sciences, School of Physics, Nanjing University, Nanjing, China
Nonlinear generation and manipulation of vortex beams have emerged as a research hot topic in recent years. During nonlinear frequency conversions, orbital angular momentum will transfer from the fundamental wave to harmonic waves. In this work, we study theoretically the backward optical parametric oscillator pumped by vortex beams. The orbital angular momentum conservation law has been disclosed for the counter propagation nonlinear process. In addition, the oscillation threshold and the conversion efficiency have been investigated in detail. Our results will be helpful for the experimental demonstration of backward optical parametric oscillator pumped by vortex beams.
Introduction
Light beams possessing an azimuthal phase front
Theoretical Model
Theoretically, the backward OPO pumped by vortex beams can be described by the coupled-wave equation. We assume that both the pump and the signal waves travel along the
The electric fields of the interacting waves are given by the following equation:
where
where
Equation 3 is the OAM conservation condition in the backward OPO, which is different from that in conventional OPO due to the reversed propagation direction of the idler wave.
Equation 3 presents the OAM conservation law of the backward OPO, and in principle, there are infinite combinations of the topological charge of the signal and idler waves [
where
According to Eq. 4, the threshold
In the study, we assume that the pump, signal light, and idler light are in the form of the Laguerre–Gaussian mode [1], and have the same confocal parameters [32]:
where
where
Results and Discussions
When OAM conservation in Eq. 3 is satisfied, we use Eq. 6 to calculate the overlapping integrals of all the combinations of
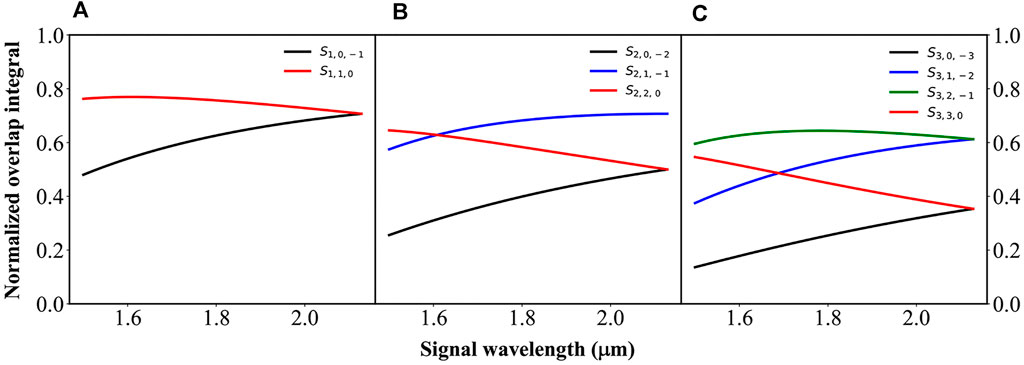
FIGURE 2. Overlapping integral of different combinations
As shown in Figure 2A, when the signal wavelength of the output signal is near the degenerate point, the overlapping integral of
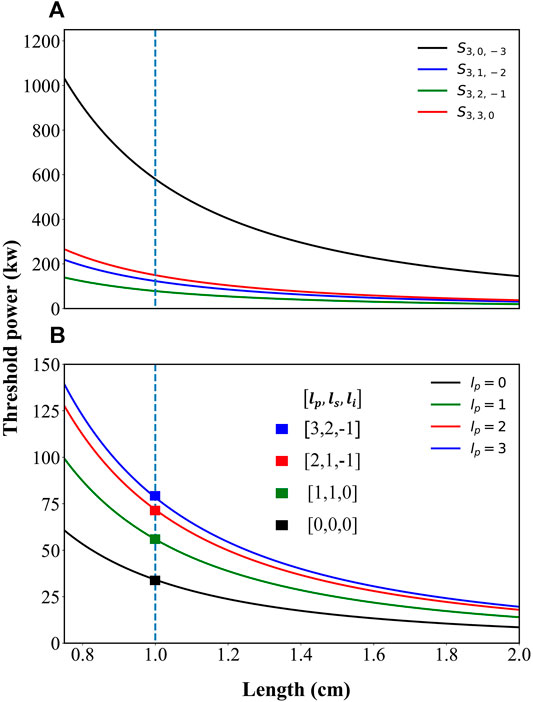
FIGURE 3. Relationship between the OPO threshold and the sample length. (A) Situations for all [
As can be seen from Figure 3A, the oscillation threshold decreases with the increase in the length of the nonlinear crystal. Meanwhile, the difference in the threshold value among the different [
The conversion efficiency
where
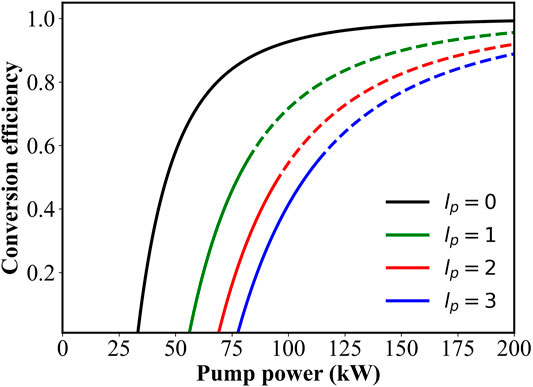
FIGURE 4. Relationship of the conversion efficiency varying with the pump power. The solid lines represent the single mode excitation (the lowest oscillation threshold is reached), and the dotted lines represent the multiple mode excitation.
According to Figure 4, we can see that when the input power of the pump light exceeds the threshold, the conversion efficiency increases rapidly. Since only the [
For practical realization of the backward OPO pumped by vortex beams, a high-energy pulsed laser light source together with a sub-micrometer periodically poled KTP is required. In our theoretical investigations, we choose a long-pulsed laser as the pump rather than ultrashort pulses because oscillation may not be observed due to the appearance of stimulated Raman scattering at pulses shorter than 20 pico-seconds [27]. The main difficulty of the practical demonstration is the nonlinear crystal. For backward OPO, a sub-micrometer QPM structure is required; however, fabrication of such a structure is still a big challenge. Up to now, there are only a few reports on the experimental demonstration of backward OPOs with Gaussian beams as the pump.
Conclusion
In this study, we have investigated the backward OPO pumped by vortex beams using the nonlinear coupled-wave equations. The OAM conservation law was determined to be
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
XH and YC proposed the idea. XZ, JH, and YS performed the theoretical analysis and numerical simulations. XZ, YC, and XH wrote the manuscript with contributions from all co-authors.
Funding
This work was supported by the National Key R&D Program of China (Nos. 2019YFA0705000 and 2017YFA0303700), the National Natural Science Foundation of China (Nos. 12174185, 91950206, 92163216, and 51890861), the Leading-edge Technology Program of Jiangsu Natural Science Foundation (No. BK20192001), and the Key R&D Program of Guangdong Province (No. 2018B030329001).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45(11):8185–9. doi:10.1103/PhysRevA.45.8185
2. Harke B, Keller J, Ullal CK, Westphal V, Schönle A, Hell SW. Resolution Scaling in STED Microscopy. Opt Express (2008) 16(6):4154–62. doi:10.1364/OE.16.004154
3. Gahagan KT, Swartzlander GA. Optical Vortex Trapping of Particles. Opt Lett (1996) 21(11):827–9. doi:10.1364/OL.21.000827
4. Grier DG. A Revolution in Optical Manipulation. Nature (2003) 424(6950):810–6. doi:10.1038/nature01935
5. Trichili A, Rosales-Guzmán C, Dudley A, Ndagano B, Ben Salem A, Zghal M, et al. Optical Communication beyond Orbital Angular Momentum. Sci Rep (2016) 6(1):27674. doi:10.1038/srep27674
6. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical Communications Using Orbital Angular Momentum Beams. Adv Opt Photon (2015) 7(1):66–106. doi:10.1364/AOP.7.000066
7. Hu X, Zhang Y, Zhu S. Nonlinear Beam Shaping in Domain Engineered Ferroelectric Crystals. Adv Mater (2020) 32(27):1903775. doi:10.1002/adma.201903775
8. Chen Y, Ni R, Wu Y, Du L, Hu X, Wei D, et al. Phase-Matching Controlled Orbital Angular Momentum Conversion in Periodically Poled Crystals. Phys Rev Lett (2020) 125(14):143901. doi:10.1103/PhysRevLett.125.143901
9. Xu Z, Lin Z, Ye Z, Chen Y, Hu X, Wu Y, et al. Control the Orbital Angular Momentum in Third-Harmonic Generation Using Quasi-Phase-Matching. Opt Express (2018) 26(13):17563–70. doi:10.1364/OE.26.017563
10. Li Y, Zhou Z-Y, Ding D-S, Shi B-S. Sum Frequency Generation with Two Orbital Angular Momentum Carrying Laser Beams. J Opt Soc Am B (2015) 32(3):407–11. doi:10.1364/JOSAB.32.000407
11. Gauthier D, Ribič PR, Adhikary G, Camper A, Chappuis C, Cucini R, et al. Tunable Orbital Angular Momentum in High-Harmonic Generation. Nat Commun (2017) 8(1):14971. doi:10.1038/ncomms14971
12. Huguenin JAO, Martinelli M, Caetano DP, santos BCd., Almeida MP, Ribeiro PHS, et al. Orbital Angular Momentum Exchange in Parametric Down Conversion. J Mod Opt (2006) 53(5-6):647–58. doi:10.1080/09500340500217548
13. Arlt J, Dholakia K, Allen L, Padgett MJ. Parametric Down-Conversion for Light Beams Possessing Orbital Angular Momentum. Phys Rev A (1999) 59(5):3950–2. doi:10.1103/PhysRevA.59.3950
14. Smith A, Armstrong D. Generation of Vortex Beams by an Image-Rotating Optical Parametric Oscillator. Opt Express (2003) 11(8):868–73. doi:10.1364/OE.11.000868
15. Horikawa M-T, Ogawa A, Miyamoto K, Yusufu T, Omatsu T. Handedness Control in a Tunable Midinfrared (60-125 μm) Vortex Laser. J Opt Soc Am B (2015) 32(12):2406–10. doi:10.1364/JOSAB.32.002406
16. Yusufu T, Tokizane Y, Yamada M, Miyamoto K, Omatsu T. Tunable 2-μm Optical Vortex Parametric Oscillator. Opt Express (2012) 20(21):23666–75. doi:10.1364/OE.20.023666
17. Furuki K, Horikawa M-T, Ogawa A, Miyamoto K, Omatsu T. Tunable Mid-infrared (63-12 μm)optical Vortex Pulse Generation. Opt Express (2014) 22(21):26351–7. doi:10.1364/OE.22.026351
18. Bloch NV, Shemer K, Shapira A, Shiloh R, Juwiler I, Arie A. Twisting Light by Nonlinear Photonic Crystals. Phys Rev Lett (2012) 108(23):233902. doi:10.1103/PhysRevLett.108.233902
19. Liu D, Liu S, Mazur LM, Wang B, Lu P, Krolikowski W, et al. Smart Optically Induced Nonlinear Photonic Crystals for Frequency Conversion and Control. Appl Phys Lett (2020) 116(5):051104. doi:10.1063/1.5141420
20. Toyoda K, Takahashi F, Takizawa S, Tokizane Y, Miyamoto K, Morita R, et al. Transfer of Light Helicity to Nanostructures. Phys Rev Lett (2013) 110(14):143603. doi:10.1103/PhysRevLett.110.143603
21. Toyoda K, Miyamoto K, Aoki N, Morita R, Omatsu T. Using Optical Vortex to Control the Chirality of Twisted Metal Nanostructures. Nano Lett (2012) 12(7):3645–9. doi:10.1021/nl301347j
22. Minor CE, Cudney RS. Mirrorless Optical Parametric Oscillation in Bulk PPLN and PPLT: a Feasibility Study. Appl Phys B (2017) 123(1):38. doi:10.1007/s00340-016-6602-x
23. Harris SE. Proposed Backward Wave Oscillation in the Infrared. Appl Phys Lett (1966) 9(3):114–6. doi:10.1063/1.1754668
24. Strömqvist G, Pasiskevicius V, Canalias C, Montes C. Coherent Phase-Modulation Transfer in Counterpropagating Parametric Down-Conversion. Phys Rev A (2011) 84(2):023825. doi:10.1103/PhysRevA.84.023825
25. Strömqvist G, Pasiskevicius V, Canalias C, Aschieri P, Picozzi A, Montes C. Temporal Coherence in Mirrorless Optical Parametric Oscillators. J Opt Soc Am B (2012) 29(6):1194–202. doi:10.1364/JOSAB.29.001194
27. Canalias C, Pasiskevicius V. Mirrorless Optical Parametric Oscillator. Nat Photon (2007) 1(8):459–62. doi:10.1038/nphoton.2007.137
28. Ding YJ, Khurgin JB. Backward Optical Parametric Oscillators and Amplifiers. IEEE J Quan Electron. (1996) 32(9):1574–82. doi:10.1109/3.535361
29. Aadhi A, Samanta GK, Chaitanya Kumar S, Ebrahim-Zadeh M. Controlled Switching of Orbital Angular Momentum in an Optical Parametric Oscillator. Optica (2017) 4(3):349–55. doi:10.1364/OPTICA.4.000349
30. Abulikemu A, Yusufu T, Mamuti R, Araki S, Miyamoto K, Omatsu T. Octave-band Tunable Optical Vortex Parametric Oscillator. Opt Express (2016) 24(14):15204–11. doi:10.1364/OE.24.015204
31. Sharma V, Chaitanya Kumar S, Samanta GK, Ebrahim-Zadeh M. Orbital Angular Momentum Exchange in a Picosecond Optical Parametric Oscillator. Opt Lett (2018) 43(15):3606–9. doi:10.1364/OL.43.003606
Keywords: vortex beam, optical parametric oscillator, counter propagation nonlinear process, oscillation threshold, coupled-wave equation
Citation: Zhu X, He J, Su Y, Chen Y and Hu X (2022) Theoretical Investigation of Backward Optical Parametric Oscillator Pumped by Vortex Beams. Front. Phys. 10:886962. doi: 10.3389/fphy.2022.886962
Received: 01 March 2022; Accepted: 29 March 2022;
Published: 27 April 2022.
Edited by:
Liangliang Lu, Nanjing Normal University, ChinaReviewed by:
Yan Sheng, Australian National University, AustraliaLina Zhao, Shandong Normal University, China
Copyright © 2022 Zhu, He, Su, Chen and Hu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yan Chen, NDQzOTI4NzE5QHFxLmNvbQ==; Xiaopeng Hu, eHBodUBuanUuZWR1LmNu
 Xiaosi Zhu
Xiaosi Zhu Jianlang He
Jianlang He Yawen Su
Yawen Su Yan Chen
Yan Chen Xiaopeng Hu
Xiaopeng Hu