Synchronization of Traveling Waves in Memristively Coupled Ensembles of FitzHugh–Nagumo Neurons With Periodic Boundary Conditions

Synchronization of traveling waves in two rings of FitzHugh–Nagumo neurons is studied. Coupling between neurons within each ring is dissipative, while one between rings is memristive. Complete synchronization of waves in identical rings in the presence of an initial phase shift between wave processes and partial synchronization of waves in the case of different coupling strengths inside the rings are considered. The influence of the initial states of memristive coupling on the synchronization of wave processes in the case of memristors with an infinitely long memory and with the forgetting effect is investigated.

1 Introduction

An important role in considering synchronization effects is played by the type of coupling of interacting nonlinear systems, which largely determines the possibility of their synchronization, as well as the boundaries and features of synchronization. One of the possible types of coupling that has been of great interest in recent times is a memristive coupling, i.e., interaction through elements such as memristors. The concept of memristors and memristive devices as special two-terminal devices with memory of previous states was proposed in the works of L. Chua [1,2]. According to the generalized definition given in [2], a memristive device (memristive element) is a two-terminal network, which can be described by the following relations:

$y=G_M\left(z,x,t\right)x,\dot{z}=F\left(z,x,t\right),(1)$

where x is the input signal, y is the system response, the variable z (generally a vector) specifies the instantaneous state of the memristor. The function G_M is a characteristic of a memristor (for example, the conductivity or resistance of a two-terminal device) depending on the control variable z. In turn, the instantaneous value z is associated with the input variable x inertially, i.e., depends on the history of the memristor. Currently, real devices based on various materials with memristive properties have been created [3–7]. There are great prospects for the use of memristors in the field of information technology: in the creation of new types of storage devices, data processing devices, supercomputers, etc., [8–13].

An understanding of the features of synchronization and cooperative dynamics of systems with memristive coupling is necessary for effective control of memristive devices. In addition, the concept of memristive connections has been recently used in neurodynamics. There are new models of neural activity that take into account the influence of the electromagnetic field. In this case, the relationship between the field and the membrane potential is of a memristive nature. Taking into account the interaction of neurons through a magnetic field, their connection can be represented as an interaction through memristors [14–17]. Synchronization of periodic and chaotic oscillators connected through memristors was studied in a number of works [18–24]. The effects of frequency locking and complete synchronization of oscillations were established. It was shown that the dynamics of memristively coupled systems is characterized by a special sensitivity of the steady state to the initial state [22–24]. In particular, a significant dependence of the synchronization boundary on the initial state of the memristive coupling elements was established.

Memristive coupling can lead to significant features in the dynamics of ensembles of interacting self-oscillators and excitable oscillators. The study of the behavior of memristively coupled ensembles has been of particular interest in recent years. First of all, this is due to the modeling of processes in neurodynamics using oscillatory and self-oscillating models of neurons. The behavior of oscillatory ensembles with memristive coupling was considered in [25–29]. The influence of memristive bonds on the propagation of waves and the formation of spatial structures was studied. In a number of papers, the problem of synchronization of complex spatio-temporal regimes in interacting layers of a multilayer network of oscillators (models of neurons) was also considered under the assumption of a memristive nature of the connection between layers [22,30,31]. Synchronization effects were established for complex structures including chimera states in memristively interacting layers. Synchronization of chimera structures in case of memristive interaction of layers was also shown using a two-layer homogeneous multiplex network of logistic maps [24], where it was also uncovered that the threshold for complete synchronization of layers depends on the initial states of memristors of coupling.

On the whole, the behavior of oscillatory ensembles with memristive coupling is still relatively little studied. The problem of synchronization of wave processes in interacting ensembles with memristive coupling between them, the influence of initial conditions in the case of ideal memristive couplings and in the presence of the forgetting effect have not been studied. The aim of our work is to study the features of synchronization of traveling waves in memristively coupled ensembles of excitable oscillators. The paper considers the effects of synchronization of traveling waves both in the case of identical ensembles and in the presence of parameter detuning. The influence of the initial states of the coupling memristors on the synchronization effect in the case of ideal memristors and memristors with a limited memory time are analyzed.

2 Model of Memristively Interacting Ensembles of Neurons and Numerical Methods

Let us consider two FitzHugh–Nagumo (FHN) neuron rings [32,33] with dissipative coupling between elements in the ring and memristive coupling between the elements of two rings. The system equations have the form

$\left\{\begin{array}{c}{\dot{x}}_{j,1}=\frac{1}{\epsilon }\left(x_{j,1}-y_{j,1}-\alpha x_{j,1}^3\right)+{\sigma }_1\left(x_{j-\mathrm{1,1}}+x_{j+\mathrm{1,1}}-2x_{j,1}\right)+kM\left(z_j\right)\left[x_{j,2}-x_{j,1}\right],\hfill \\ {\dot{y}}_{j,1}=\gamma x_{j,1}-y_{j,1}+\beta ,\hfill \\ {\dot{x}}_{j,2}=\frac{1}{\epsilon }\left(x_{j,2}-y_{j,2}-\alpha x_{j,2}^3\right)+{\sigma }_2\left(x_{j-\mathrm{1,2}}+x_{j+\mathrm{1,2}}-2x_{j,2}\right)+kM\left(z_j\right)\left[x_{j,1}-x_{j,2}\right],\hfill \\ {\dot{y}}_{j,2}=\gamma x_{j,2}-y_{j,2}+\beta ,\hfill \\ {\dot{z}}_j=x_{j,1}-x_{j,2}-\delta z_j,\hfill \\ M\left(z_j\right)=1+\mu z_j^2,j=\mathrm{1,2},\dots ,N,\hfill \\ x_{j\pm N,i}\left(t\right)=x_{j,i}\left(t\right),y_{j\pm N,i}\left(t\right)=y_{j,i}\left(t\right),i=\mathrm{1,2};\hfill \end{array}\right.(2)$

where j is the number of the element in the ring, i is the number of the ring. Each ring consists of identical FHN oscillators interconnected by a mutually symmetrical internal coupling, which is of a dissipative nature and is characterized by the coefficients σ₁ and σ₂ respectively for the first and second rings. All parameters of the rings are the same except for the internal coupling coefficients. Oscillators with the same numbers j belonging to different rings are locally connected via identical memristive elements. The coupling strength of the rings is characterized by the coefficient k. The characteristic of the coupling memristors M(z_j) is given by the expression $M(z_j)=1+\mu z_j^2$, where μ is the nonlinearity parameter of the memristive element. This characteristic does not describe a specific real device, but is convenient for a qualitative description of memristive systems and is often used [14,21,28]. The dynamics equations for the variables z_j, which specify the instantaneous states of the memristors, contain the parameter δ, which determines the duration of the memristor memory in time (forgetting parameter) [6,34,35].

During the calculations, the following constant parameters were fixed: the number of elements in the ring N = 100; parameters of individual oscillators α = 1/3, β = 0.2, γ = 0.8, ɛ = 0.01 (corresponding to the excitable regime); coefficient of internal coupling in the first ring σ₁ = 4.5; memristor parameters μ = 40. The coefficient of internal coupling in the second ring σ₂ can be equal to the value σ₁ = 4.5 (identical rings) or fixed different from σ₁ (non-identical rings). The calculations were carried out at two fixed values of the forgetting parameter δ: δ = 0 (ideal memristors) and δ = 0.1 (memristors with finite memory). The coupling parameter k between the rings was considered as a control parameter and changed in the course of research. Also, the initial value of the variables z_j is considered as a control parameter and is assumed to be the same for all memristive elements: z_j (0) = z₀.

In this paper, we study the effect of complete synchronization of structures in two identical rings as well as effective partial synchronization when a detuning is introduced into the parameters of the internal coupling of two rings. To diagnose the synchronization effect, we calculate the value

$\mathrm{\Delta }=\frac{1}{N}\sum _{j=1}^N\left({\left[x_{j,2}\left(t\right)-x_{j,1}\right]}^2+{\left[y_{j,2}\left(t\right)-y_{j,1}\right]}^2\right),(3)$

where the brackets $<\dots >$ mean time averaging. In the steady state, Δ characterizes the deviation of the interacting oscillators from complete synchronization; therefore, we will call it the synchronization error. For non-identical rings, in addition to the Δ value, the ratio of the average oscillation periods of the oscillators of two rings in time T₂/T₁ is calculated. The average oscillation period T (average interspike interval) of the considered oscillator is determined using the expression

$T=\underset{p\to \infty }{\lim }\frac{1}{p}\sum _{n=1}^p{\tau }_n,(4)$

where τ_n are the intervals between consecutive transitions of the threshold value x = 1.5 in one direction. The choice of the oscillator within the ring does not matter since the oscillations of all oscillators in the same ring differ only in phase. It should be noted that the model under study (Eq. 2) is not a realistic model of any neural system. It has a simplified topology and a simple nature of coupling. The intensity of coupling between real neurons cannot be chosen arbitrarily, but can be self-adaptive for reaching synchronization within transient period [36]. The FitzHugh–Nagumo neuron itself is also a highly simplified model of a real neuron. However, the choice of a simplified model (Eq. 2) is well suited to the goal of the study. This goal is not to study a real neural system, but to answer the question of what features of synchronization can be caused by the memristive nature of coupling between spatially distributed excitable systems. The choice of the simplest and well-studied model to uncover certain nonlinear effects corresponds to the methods and approaches of nonlinear dynamics. Despite the artificial nature of the model, it can be assumed that the established effects under certain conditions can be observed in real systems of various nature.

3 Complete Synchronization of Waves in Identical Rings

Let us consider two identical rings in the excitable regime at σ₁ = σ₂ = 4.5. We choose the initial conditions for two rings in such a way that in the absence of a connection between the rings (k = 0) traveling excitation waves differing in phases are established in them. Instantaneous spatial profiles and oscillations in time in two non-interacting rings in the steady state regime are shown in Figure 1A. Oscillations of all oscillators both within one ring and in two rings differ only in phases. The values of variables in two non-interacting rings in the steady state were taken as fixed initial states of the rings for further research.

FIGURE 1

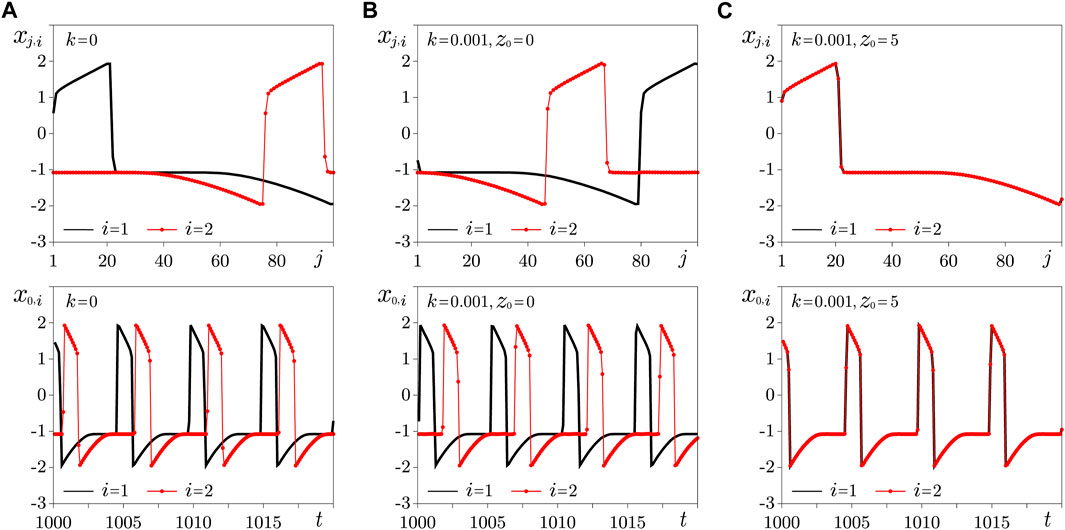
FIGURE 1. Profiles of traveling waves (upper row) and oscillations x_0,i(t) (lower row) in two identical rings (2) in the absence of interlayer coupling k = 0 (A); with coefficient k = 0.001 for different initial values of memristive variables z₀ = 0 (B) and z₀ = 5 (C). Parameters: σ₁ = σ₂ = 4.5, δ = 0.

First, let us consider the connection of rings through ideal memristors (δ = 0). In the steady regime of traveling waves (Figure 1A) at time t = 0 we introduce a mutual memristive coupling of two rings. In this case, we will assume that all coupling memristors were in the same state at that moment z_j (0) = z₀. As the coupling coefficient k increases, let us find out whether phase synchronization of traveling waves is observed and how the value of z₀ affects the behavior of the interacting rings, which will be considered as the control parameter of the memristive coupling together with the coefficient k. Figures 1B,C show illustrations of modes that are established in two rings interacting through ideal memristors with the same value of the ring coupling coefficient k = 0.001 and different initial states of memristors specified by the value of the control variables z₀. It can be seen from the graphs that at z₀ = 0 that the phase shift between the traveling waves is preserved. However, the waves in the rings become completely synchronized with the same coupling coefficient at z₀ = 5.0. Thus, a characteristic property of a memristive connection is manifested: the dependence of the synchronization effect on the initial conditions [23]. In this case, it is the dependence on the initial states of the coupling memristors.

For identical rings connected through ideal memristors, the values of the synchronization error Δ depending on the coupling coefficient k were calculated using the relation (Eq. 3) for different initial values of the memristor state variables zj (0) = z₀. These dependencies for two values of z₀ are shown in Figure 2A. They allow us to conclude that there is an abrupt transition to the regime of complete wave synchronization and that the synchronization threshold depends on z₀.

FIGURE 2

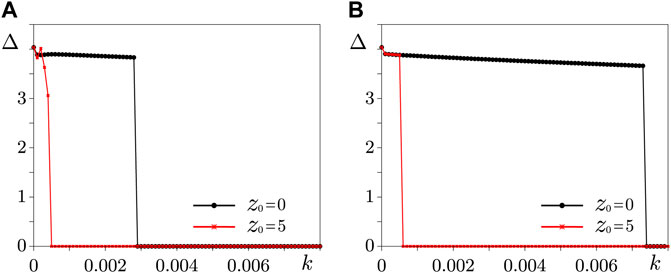
FIGURE 2. Dependencies of the synchronization error Δ of traveling waves on the memristive coupling coefficient k in two identical rings σ₁ = σ₂ = 4.5 obtained for two different values of z₀ in the case of an ideal memristive coupling δ = 0 (A) and in the case of non-ideal memristors with the forgetting parameter δ = 0.1 (B).

Let us consider how the non-ideal nature of the memristive coupling will affect these dependences. Let us fix the value of the forgetting parameter δ = 0.1. This value is quite large since the time constant of the memristive coupling given by the last equation of the system (Eq. 2) τ = 1/δ = 10 is comparable to the oscillation period of the oscillators (approximately 5 units of dimensionless time). In this case, memristors are inertial non-linear elements with a relatively short relaxation time. The dependencies of Δ on the coupling coefficient k for two values z₀ are shown in Figure 2B.

The boundaries of the region of complete synchronization of identical rings were found in the case of an ideal memristive coupling and with the value of the forgetting parameter δ = 0.1. The results are shown in Figure 3. The following condition was chosen as a numerical criterion for complete synchronization

$\mathrm{\Delta }⩽10^{-5}.(5)$

It can be seen that the synchronization threshold strongly depends on the initial state of the coupling memristors, which is set by the value of the control variables z₀. Moreover, this dependence is observed both in the case of ideal memristors (Figure 3A) and non-ideal memristive coupling with the forgetting parameter δ = 0.1 (Figure 3B). In both cases, the boundary of the complete synchronization region has a similar shape. There is some value z_{0 max} at which the synchronization threshold for the link k is maximum. In the case of ideal memristors z_{0 max} = 0.6, at δ = 0.1 z_{0 max} = 0. With distance from the maximum point, the synchronization threshold decreases significantly. In both considered cases (for δ = 0 and δ = 0.1), the threshold value k for z₀ = 5 becomes less than the maximum value approximately by 9 times. One can also note a certain symmetry of the boundary of the synchronization region with respect to the value z_{0 max}. However, the symmetry is not strict, which is especially noticeable at δ = 0.1.

FIGURE 3

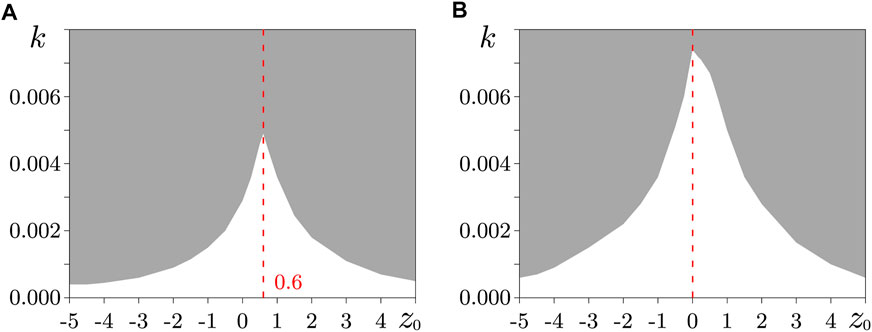
FIGURE 3. The area of complete synchronization of traveling waves (gray area) in identical rings in the case of ideal memristive coupling δ = 0 (A) and in case of coupling through memristors with the forgetting parameter δ = 0.1 (B). The dashed vertical line marks the z_{0 max} value corresponding to the maximum synchronization threshold. Complete synchronization was determined in accordance with the criterion (Eq. 5), the time for calculating the synchronization error was 1,000 units of dimensionless time.

4 Partial Synchronization of Waves in Non-Identical Rings

Let us now consider two non-identical rings in the same regime of excitable dynamics but with different values of the coupling coefficients of the oscillators in the two rings: σ₁ = 4.5, σ₂ = 5.5. In the absence of a connection between the rings (k = 0), traveling waves were established in them differing in the phases and propagation speed of the perturbation (respectively, in the average oscillation periods). Instantaneous spatial profiles and oscillations in time x_0,i(t) in rings without coupling are shown in Figure 4A. The obtained instantaneous values of the variables in the steady state were taken as fixed initial states of the rings for further calculations. First, the connection of the rings through ideal memristors was considered. The regimes established at different values of the coupling coefficient k and the initial values of the state variables of the memristors z₀ were studied. Examples of instantaneous spatial profiles and oscillations in two rings are shown in Figures 4B–F. Based on the presented spatial profiles and time oscillations, it can be concluded that the degree of wave synchronism in two rings undergoes complex changes with increasing coupling, the character of which depends on the choice of z₀.

FIGURE 4

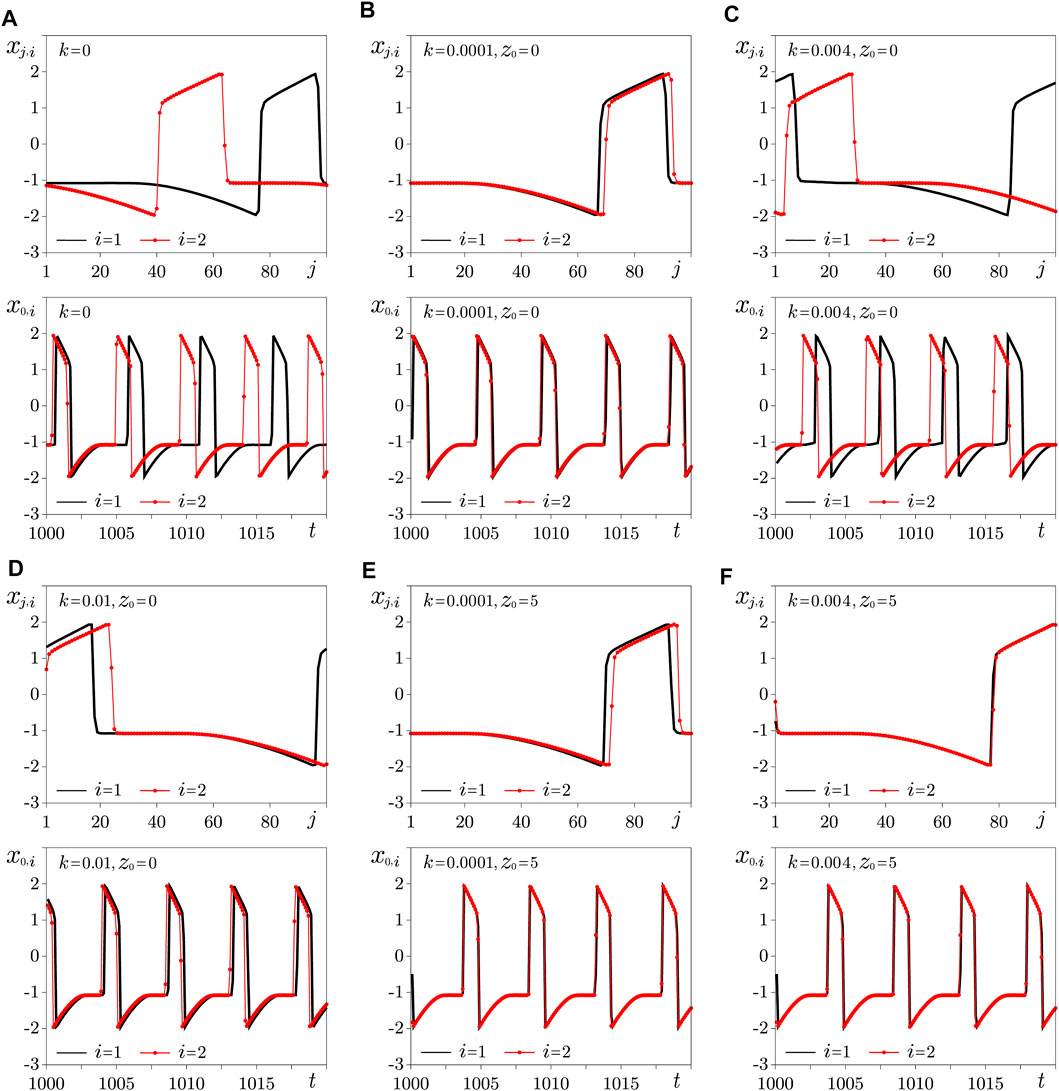
FIGURE 4. Profiles of traveling waves (upper row) and fluctuations x_0,i(t) of oscillators (lower row) in two non-identical rings (Eq. 2) in the absence of interlayer coupling k = 0 (A); in the case of z₀ = 0 with k = 0.0001 (B), k = 0.004 (C), k = 0.01 (D); in the case of z₀ = 5.0 for k = 0.0001 (E) and k = 0.004 (F). Parameters: σ₁ = 4.5, σ₂ = 5.5, δ = 0.

For a more detailed study of the effects of wave synchronization in non-identical rings with an ideal memristive coupling, the dependencies of the ratio of average periods T₂/T₁ and the synchronization error Δ on the coupling coefficient k were calculated. The corresponding plots obtained for two initial values of the control variables z₀ = 0 and z₀ = 5.0 are shown in Figures 5A–C. As the coupling coefficient increases, different behavior of the waves is observed for different z₀. Thus, in the case of z₀ = 0, the ratio of oscillation periods in two rings depends on k in a complicated way (Figure 5A). Although it is close to unity, the periods are still somewhat different. This difference disappears, then reappears. Finally, the periods become equal at k > 0.004. The value of Δ, which characterizes the averaged in time difference in instantaneous spatial profiles, sharply increases and then decreases again at k > 0.007, but remains significant over the entire considered range of changes in the coupling coefficient (Figure 5B). At z₀ = 5.0, the ratio of oscillation periods is almost immediately set equal to unity (Figure 5A) and the value of Δ rapidly decreases with increasing k (Figure 5C). For k = 0.004 and further, Δ does not exceed the order of 10^–2 and one can speak of effective synchronization. A similar behavior is observed at z₀ = −5.0. Figure 5D shows the area of effective synchronization corresponding to the criterion Δ ≤ 10^–2. For small values of z₀, the synchronization boundary goes up sharply. In the figure, the areas of synchronous and non-synchronous modes are calculated up to the value k = 0.1. At z₀ = 0, it is possible to obtain synchronization with the chosen criterion only for k⩾3.03.

FIGURE 5

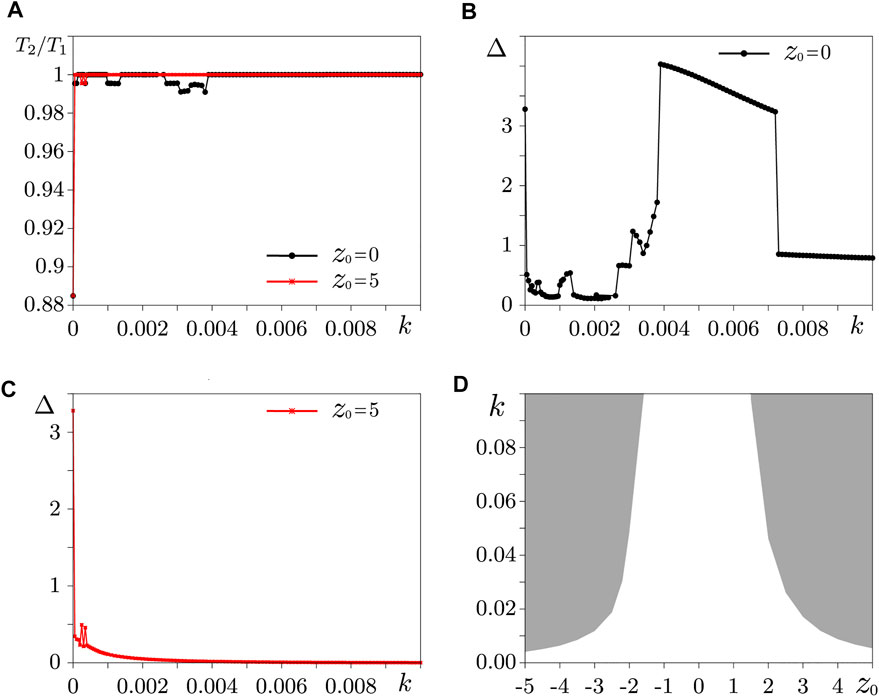
FIGURE 5. Synchronization characteristics in two non-identical rings connected via ideal memristors: dependencies of the ratio of average oscillation periods T₂/T₁ at z₀ = 0 and z₀ = 5.0 (A); dependence of the synchronization error Δ on the coupling coefficient k at z₀ = 0 (B) and z₀ = 5.0 (C); region of effective synchronization of traveling waves determined by the condition Δ ≤ 10^–2 (D). Parameters: σ₁ = 4.5, σ₂ = 5.5, δ = 0.

It becomes clear from the obtained results that in non-identical rings with ideal memristive interaction partial and in some cases almost complete synchronization (Figure 5D) of excitation waves is possible. In the case of the ideal nature of the coupling memristors, the dependence of the synchronization effects on the initial state of the memristors is still clearly visible.

Let us consider the influence of non-ideal nature of memristors by setting the forgetting parameter to be non-zero (δ = 0.1 as in the case of identical rings). In Figure 6 one can see that the results are the same for two values of z₀ within the calculation error. Thus, in the case of a non-ideal memristive coupling, the synchronization of traveling waves in non-identical rings does not depend on the initial states of the memristors.

FIGURE 6

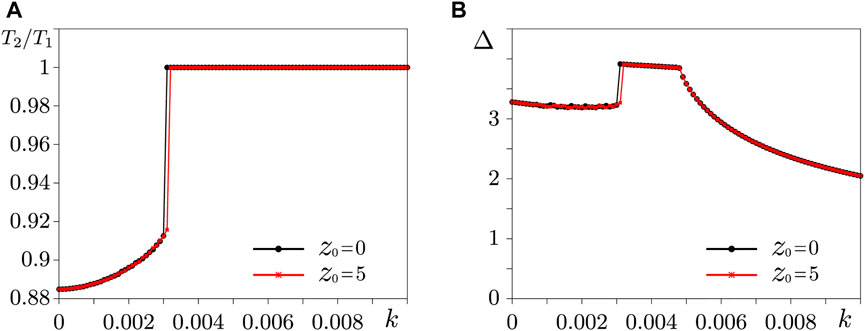
FIGURE 6. Synchronization characteristics in two non-identical rings (σ₁ = 4.5, σ₂ = 5.5) coupled via non-ideal memristors with δ = 0.1: dependencies of the ratio of average oscillation periods T₂/T₁ (A) and synchronization errors Δ (B) on the coupling coefficient k calculated at z₀ = 0, z₀ = 5.0.

The question arises: why the values of |z₀| affect the establishment of identical phases of traveling waves (i.e., complete synchronization) in the case of non-ideal memristive coupling of identical rings, while in the case of non-identical rings, the value of |z₀| does not affect the synchronization effect? To answer this question let us consider how the values of the memristive variables z_j change with time at δ > 0. Integrating the equation for the memristive variable z_j with the initial condition z₀, we obtain

$z_j\left(t\right)=z_0{e}^{-\delta t}+e^{-\delta t}\underset{0}{\overset{t}{\int }}{e}^{-\delta \theta }\left[x_{j,1}\left(\theta \right)-x_{j,2}\left(\theta \right)\right]d\theta .(6)$

Obviously, immediately after switching on the memristive coupling, the influence of the initial value of z₀ on the value of z_j(t) and thus on the strength of the coupling can be great. The larger |z₀|, the stronger the connection between the rings. Over time, the contribution of the initial value to z_j(t) decreases exponentially with the decrement δ. A strong coupling at the initial stage of interaction leads to different consequences in the case of identical and non-identical rings. In identical rings, a strong coupling in a short time interval immediately leads to the establishment of the same phases of the traveling waves, which then remain the same although the coupling decreases. In non-identical rings, a strong short-term coupling cannot affect the synchronization of wave velocities since the coupling strength in the steady state is important for this, and it does not depend on the choice of z₀.

5 Conclusion

Based on the results of the research, the following results were obtained. For identical rings, the effect of complete (in-phase) synchronization of traveling waves, which initially have a phase shift, is established when the interaction of rings through memristors is turned on. For identical rings, the dependence of the boundary of complete wave synchronization on the initial state of the coupling memristors is established, which is fully preserved if the memristors have the forgetting effect. For non-identical rings differing in internal coupling coefficients, the effect of synchronization of the propagation velocities of excitation waves and periods of oscillations of elements in two ensembles is established. It is observed even at weak coupling (k⩽0.0001). In addition, the effect of partial synchronization of wave profiles, which depends on the initial states of the communication memristors, has been revealed. It is shown that when non-identical rings interact through memristors with finite memory, the effects of partial synchronization cease to depend on the initial states of the memristors.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors upon request.

Author Contributions

IAK was involved in the experiment setup, investigation and writing. IRR was involved in the experiment setup and investigation. VVS was involved in the conceptualization, writing and editing. AVS and TEV were involved in writing, editing, conceptualization and project management.

Funding

This work was supported by the Russian Science Foundation, project no. 20-12-00119.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chua L. Memristor-the Missing Circuit Element. IEEE Trans Circuit Theor (1971) 18:507–19. doi:10.1109/tct.1971.1083337

CrossRef Full Text | Google Scholar

2. Chua L, Kang SM. Memristive Devices and Systems. Proc IEEE (1976) 64:209–23. doi:10.1109/proc.1976.10092

CrossRef Full Text | Google Scholar

3. Strukov D, Snider G, Stewart D, Williams R. The Missing Memristor Found. Nature (2008) 453:80–3. doi:10.1038/nature06932

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Berzina T, Smerieri A, Bernabò M, Pucci A, Ruggeri G, Erokhin V, et al. Optimization of an Organic Memristor as an Adaptive Memory Element. J Appl Phys (2009) 105:124515. doi:10.1063/1.3153944

CrossRef Full Text | Google Scholar

5. Jeong H, Kim J, Kim J, Hwang J, Kim J, Lee J, et al. Graphene Oxide Thin Films for Flexible Nonvolatile Memory Applications. Nano Lett (2010) 10:4381–6. doi:10.1021/nl101902k

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Chang T, Jo S-H, Kim K-H, Sheridan P, Gaba S, Lu W. Synaptic Behaviors and Modeling of a Metal Oxide Memristive Device. Appl Phys A (2011) 102:857–63. doi:10.1007/s00339-011-6296-1

CrossRef Full Text | Google Scholar

7. Erokhina S, Sorokin V, Erokhin V. Polyaniline-based Organic Memristive Device Fabricated by Layed-By-Layed Deposition Technique. Electron Mater Lett (2015) 11:801–5. doi:10.1007/s13391-015-4329-1

CrossRef Full Text | Google Scholar

8. Pershin YV, Di Ventra M. Neuromorphic, Digital, and Quantum Computation with Memory Circuit Elements. Proc IEEE (2011) 100:2071–80. doi:10.1109/JPROC.2011.2166369

CrossRef Full Text | Google Scholar

9. Yang J, Strukov D, Stewart D. Memristive Devices for Computing. Nat Nanotechnol (2013) 8:13–24. doi:10.1038/nnano.2012.240

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Vourkas I, Sirakoulis GC. Memristor-Based Nanoelectronic Computing Circuits and Architectures, 19. Heidelberg, New York, Dordrecht, London: Springer (2016).

Google Scholar

11. Prezioso M, Merrikh-Bayat F, Hoskins B, Adam GC, Likharev KK, Strukov DB. Training and Operation of an Integrated Neuromorphic Network Based on Metal-Oxide Memristors. Nature (2015) 521:61–4. doi:10.1038/nature14441

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li C, Hu M, Li Y, Jiang H, Ge N, Montgomery E, et al. Analogue Signal and Image Processing with Large Memristor Crossbars. Nat Electron (2018) 1:52–9. doi:10.1038/s41928-017-0002-z

CrossRef Full Text | Google Scholar

13. Wang Z, Wu H, Burr GW, Hwang CS, Wang KL, Xia Q, et al. Resistive Switching Materials for Information Processing. Nat Rev Mater (2020) 5:173–95. doi:10.1038/s41578-019-0159-3

CrossRef Full Text | Google Scholar

14. Lv M, Wang C, Ren G, Ma J, Song X. Model of Electrical Activity in a Neuron under Magnetic Flow Effect. Nonlinear Dyn (2016) 85:1479–90. doi:10.1007/s11071-016-2773-6

CrossRef Full Text | Google Scholar

15. Wu F, Wang C, Xu Y, Ma J. Model of Electrical Activity in Cardiac Tissue under Electromagnetic Induction. Sci Rep (2016) 6:28. doi:10.1038/s41598-016-0031-2

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Gerasimova SA, Mikhaylov AN, Belov AI, Korolev DS, Gorshkov ON, Kazantsev VB. Simulation of Synaptic Coupling of Neuron-like Generators via a Memristive Device. Tech Phys (2017) 62:1259–65. doi:10.1134/s1063784217080102

CrossRef Full Text | Google Scholar

17. Ma J, Zhang G, Hayat T, Ren G. Model Electrical Activity of Neuron under Electric Field. Nonlinear Dyn (2018) 95:1585–98. doi:10.1007/s11071-018-4646-7

CrossRef Full Text | Google Scholar

18. Volos CK, Kyprianidis I, Stouboulos I, Munoz-Pacheco J, Pham V-T. Synchronization of Chaotic Nonlinear Circuits via a Memristor. J Eng Sci Technol Rev (2015) 8:44–51. doi:10.25103/jestr.082.07

CrossRef Full Text | Google Scholar

19. Ignatov M, Hansen M, Ziegler M, Kohlstedt H. Synchronization of two memristively coupled van der pol oscillators. Appl Phys Lett (2016) 108:084105. doi:10.1063/1.4942832

CrossRef Full Text | Google Scholar

20. Xu Y, Jia Y, Ma J, Alsaedi A, Ahmad B. Synchronization between Neurons Coupled by Memristor. Chaos, Solitons Fractals (2017) 104:435–42. doi:10.1016/j.chaos.2017.09.002

CrossRef Full Text | Google Scholar

21. Xu F, Zhang J, Fang T, Huang S, Wang M. Synchronous Dynamics in Neural System Coupled with Memristive Synapse. Nonlinear Dyn (2018) 92:1395–402. doi:10.1007/s11071-018-4134-0

CrossRef Full Text | Google Scholar

22. Bao H, Zhang Y, Liu W, Bao B. Memristor Synapse-Coupled Memristive Neuron Network: Synchronization Transition and Occurrence of Chimera. Nonlinear Dyn (2020) 100:937–50. doi:10.1007/s11071-020-05529-2

CrossRef Full Text | Google Scholar

23. Korneev I, Semenov V, Vadivasova T. Synchronization of Periodic Self-Oscillators Interacting via Memristor-Based Coupling. Int J bifurcation chaos (2020) 30:2050096. doi:10.1142/s0218127420500960

CrossRef Full Text | Google Scholar

24. Korneev I, Semenov V, Slepnev A, Vadivasova T. Complete Synchronization of Chaos in Systems with Nonlinear Inertial Coupling. Chaos, Solitons Fractals (2021) 142:110459. doi:10.1016/j.chaos.2020.110459

CrossRef Full Text | Google Scholar

25. Pham V-T, Buscarino A, Fortuna L, Frasca M. Autowaves in Memristive Cellular Neural Networks. Int J Bifurcation Chaos (2012) 22:1230027. doi:10.1142/s0218127412300273

CrossRef Full Text | Google Scholar

26. Buscarino A, Corradino C, Fortuna L, Frasca M, Chua L. Turing Patterns in Memristive Cellular Nonlinear Networks. IEEE Trans Circuits Syst (2016) 63:1222–30. doi:10.1109/tcsi.2016.2564738

CrossRef Full Text | Google Scholar

27. Ma J, Wu F, Hayat T, Zhou P, Tang J. Electromagnetic Induction and Radiation-Induced Abnormality of Wave Propagation in Excitable Media. Physica A: Stat Mech its Appl (2017) 486:508–16. doi:10.1016/j.physa.2017.05.075

CrossRef Full Text | Google Scholar

28. Wang C, Lv M, Alsaedi A, Ma J. Synchronization Stability and Pattern Selection in a Memristive Neuronal Network. Chaos: Interdiscip J Nonlinear Sci (2017) 27:113108. doi:10.1063/1.5004234

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Korneev I, Semenov V, Slepnev A, Vadivasova T. The Impact of Memristive Coupling Initial States on Travelling Waves in an Ensemble of the Fitzhugh–Nagumo Oscillators. Chaos, Solitons Fractals (2021) 147:110923. doi:10.1016/j.chaos.2021.110923

CrossRef Full Text | Google Scholar

30. Xu F, Zhang J, Jin M, Huang S, Fang T. Chimera States and Synchronization Behavior in Multilayer Memristive Neural Networks. Nonlinear Dyn (2018) 94:775–83. doi:10.1007/s11071-018-4393-9

CrossRef Full Text | Google Scholar

31. Zhou Q, Wei D. Synchronous Dynamics in Multilayer Memristive Neural Networks: Effect of Electromagnetic Induction. Ieee Access (2020) 8:164727–36. doi:10.1109/access.2020.3022684

CrossRef Full Text | Google Scholar

32. FitzHugh R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys J (1961) 1:445–66. doi:10.1016/s0006-3495(61)86902-6

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Nagumo J, Arimoto S, Yoshizawa S. An Active Pulse Transmission Line Simulating Nerve Axon. Proc IRE (1962) 50:2061–70. doi:10.1109/jrproc.1962.288235

CrossRef Full Text | Google Scholar

34. Chen L, Li C, Huang T, Chen Y, Wen S, Qi J. A Synapse Memristor Model with Forgetting Effect. Phys Lett A (2013) 377:3260–5. doi:10.1016/j.physleta.2013.10.024

CrossRef Full Text | Google Scholar

35. Zhou E, Fang L, Yang B. A General Method to Describe Forgetting Effect of Memristors. Phys Lett A (2019) 383:942–8. doi:10.1016/j.physleta.2018.12.028

CrossRef Full Text | Google Scholar

36. Zhou P, Zhang X, Ma J. How to Wake up the Electric Synapse Coupling between Neurons? Nonlinear Dyn (2022) 108:1681–95. doi:10.1007/s11071-022-07282-0

CrossRef Full Text | Google Scholar