Enhanced Terahertz Generation From the Lithium Niobate Metasurface

The lithium niobate (LiNbO₃) metasurface is an attractive platform for nonlinear frequency conversion due to its excellent nonlinearity, high damage threshold, and strong enhancement of the driving field. Here, we demonstrated the nonlinear metasurface for terahertz (THz) generation from LiNbO₃ on an insulator. The THz electric field from the LiNbO₃ metasurface of 300 nm thickness is enhanced by more than one order of magnitude compared to the unstructured sample. The enhanced terahertz electric field is very selective in the excitation wavelength due to its resonant feature and is highly anisotropic with respect to the excitation polarization. The polarization direction of the THz electric field can be controlled by rotating the optical axis of the LiNbO₃ metasurface. By combining the nanofabrication technology of the LiNbO₃ metasurface and ultrafast nonlinear optics, our work paves the way for the design of new compact terahertz photonic devices that integrate THz emitters into LiNbO₃-based chips with multifaceted capabilities.

Introduction

Terahertz (THz) waves have witnessed an ever-growing number of emerging applications that include advanced biomedical imaging [1], novel security inspection [2, 3], fast wireless communications, [4, 5] and new abilities to study and control matter in all of its phases [6–8]. The blooming of THz technologies and related applications at the current stage demand urgently efficient and compact THz emitters and detectors, yet the development of which remains challenging [9–11]. Regarding broadband THz sources, major recent progress is based on nonlinear optical rectification in inorganic and organic crystals pumped by femtosecond laser pulses [12–14]. Combined with field-resolved detection via electro-optic sampling using similar crystals, THz time-domain spectroscopy is the workhorse of industrial applications [15]. However, the nonlinear optical response of materials is intrinsically weak, especially when the excitation photon energy is much smaller than the bandgap, which is typically the case in THz generation experiments [16, 17]. For efficient THz interaction, a long interaction length and high laser intensity inside crystals are desired. In practice, the subtle phase-matching scheme and strong THz absorption in natural nonlinear crystals limit the accessibility, bandwidth, and conversion efficiency of THz waves [18–21]. A promising solution is designing the nanostructure with materials using resonant nonlinearity and local field enhancement to eliminate the abovementioned common restrictions [22–26]. The strength of this approach is free of phase-matching and phonon absorption in the process of THz emission, while the nonlinear phenomena are boosted by several orders of magnitude when the resonance of the cavity coincides with the fundamental frequency.

Metasurfaces have shown great flexibility in achieving versatile functions in different disciplines [27–32]. Plasmon-enhanced broadband THz generation and spatiotemporal manipulation have been reported from metallic antennas [33, 34]. However, the damage threshold of plasmonic-based metal structures is extremely sensitive to the fabrication quality, and the high degree of confinement at the boundary of the metal/dielectric interface significantly limits the overall signal enhancement [34–36]. Dielectric metasurfaces have emerged as a promising alternative over plasmonic ones due to their lower optical loss and higher damage threshold. Enhanced perturbative third-harmonic generation and nonperturbative high harmonic generation have been observed from an all-dielectric Si metasurface comprising optically resonant dielectric nanostructures [37]. However, these devices generally suffer from low conversion efficiency because of the intrinsic deficiency of Si and a limited volume of nonlinear media. Among the various nonlinear materials for fabricating metasurfaces, lithium niobate (LiNbO₃) is one of the most widely used due to its high second-order nonlinear response [38, 39]. Recently, the platform of LiNbO₃ on the insulator (LNOI) has emerged as a promising candidate for next-generation on-chip wavelength conversion [40]. An enhanced second-harmonic generation has been demonstrated in the LNOI-based nonlinear periodic metasurface excited resonantly [41–44]. Yet compact THz sources based on LNOI have been so far prevented by the nanofabrication challenges.

In this article, for the first time, we report enhanced THz generation from the LNOI-based nonlinear metasurface comprising optically resonant dielectric nanostructures. When the metasurface is resonantly excited, the THz electric field is one order of magnitude higher than an unstructured LiNbO₃ nanofilm at moderate driving intensities. The polarization direction of the THz electric field can be controlled by rotating the optical axis of LNOI. This paves the way for not only the on-chip high-efficient THz sources but also all-optical active THz devices benefiting next-generation THz communications.

Experiment

Sample Characteristics

The platform of LNOI is opening new avenues to optical frequency conversion for its strong second-order nonlinear susceptibility tensor. This platform is formed from nanometer-thick LiNbO₃ films bonded on SiO₂ grown on an insulator (silica) substrate using a smart-cut technique, which results in devices with much increased index contrast (Δn > 0.6) and reduced modal size. The main obstacles are the challenges of the growth of thin crystalline films on low refractive index substrates and the subsequent nanostructuring. Figure 1A shows the schematic representation of the LiNbO₃ metasurface. In order to utilize the largest second-order nonlinear susceptibility d₃₃ maximizing THz generation, an x-cut LNOI wafer of 300 nm thickness bonded on a 4-µm thick SiO₂ is fabricated on a 500-µm thick Si buffer layer (NanoLN, Jinan Jingzheng Electronics Co., Ltd.). We refer to the x-axis of the LiNbO₃ principal crystallographic coordinate and the polarization of laser as the x-axis and z-axis of the experimental coordinate system, respectively. The optical axis of LiNbO₃ lies in the y-z plane and can rotate around the x-axis. Figure 1B shows a scanning electron microscopy image of the realized metasurface with a period constant of 950 nm. The magnified image shows the well-fabricated nanoholes of the LiNbO₃ metasurface with a diameter of 550 nm. The pores are directly drilled by electron-beam lithography.

FIGURE 1

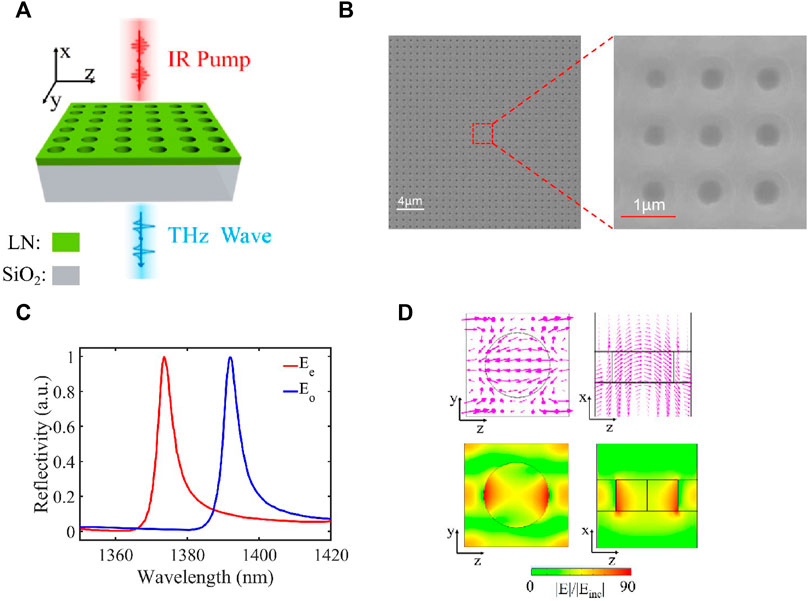
FIGURE 1. Schematic representation of the LiNbO₃ nonlinear metasurface. (A) Metasurfaces are fabricated on an x-cut LNOI film residing on SiO₂. The x- and z-axis of the experimental coordinate system are along the x-axis of the LiNbO₃ principal crystallographic coordinate and the polarization of pump pulses, respectively. The collimated femtosecond pulses excite the metasurface with the normal incidence, and the transmitted THz waves are recorded. (B) Scanning electron microscopy images of the LiNbO₃ metasurface with a period of 950 nm and the magnified image of pores with a diameter of 550 nm. (C) Simulated reflection spectrum of the LiNbO₃ metasurface rotating the optical axis of LiNbO₃ along the z-axis (extraordinary electric field E_e, red) and y-axis (ordinary electric field E_o, blue). The resonant wavelengths are 1,375 and 1,395 nm when the optical axis is parallel and perpendicular to the polarization of the pump pulses, respectively. (D) Distribution of the electric field in the y-z (left) and x-z (right) sections of a LiNbO₃ nanoresonator, respectively. The arrows in the top figures indicate the direction of the electric field. The bottom figures show the amplitude profiles of the electric field.

Periodic pores in the LiNbO₃ film modulate the refractive index of the metasurface, resulting in a guided-mode resonance [45–47] which can couple the normally incident light into the metasurface. The guided-mode resonance is very sensitive to the geometric parameters and the refractive indexes of structured metasurfaces. To design optimized geometry, numerical simulations of the structure are carried out by commercial software (COMSOL Multiphysics) by means of the finite element method. When the collimated light incidents normally onto the LiNbO₃ metasurface, sharp peaks in the simulated reflection spectra are observed, as shown in Figure 1C. When the polarization of the excitation is parallel to the optical axis of LiNbO₃ (extraordinary electric field, E_e), the resonant wavelength is 1,375 nm with a bandwidth of 5 nm. The resonant wavelength shifts to 1,395 nm when the polarization of excitation is perpendicular to the optical axis (ordinary electric field, E_o). The anisotropic refractive indexes of x-cut LiNbO₃ result in the resonant wavelength varying with excitation polarization. The extraordinary refractive index of 2.14 for LiNbO₃ near the resonant wavelength is less than the ordinary refractive index of 2.21, which results in a shorter resonant wavelength [48].

By inducing strong electromagnetic resonances, the electric field intensity is locally enhanced, as compared to unstructured materials. THz waves are mainly contributed by the electric field oriented along the optic axis in LiNbO₃ due to the overwhelmingly dominant d₃₃ coefficient. Figure 1D shows electric fields in the y-z (left) and x-z (right) sections, respectively. The amplitude of electric fields in the bottom of Figure 1D shows a dramatic enhancement in the metasurface compared to the unstructured film. The arrows at the top of Figure 1D show the direction of electric fields and indicate weak components of E_y and E_x. In contrast to the plasmonic enhancement base on the metal metasurface [33, 34], the enhanced electric field extends over a larger region around the pores in the LiNbO₃ metasurface, which will, in general, boost the efficiency of THz generation.

Experimental Setup

Figure 2 schematically illustrates the experimental setup and key elements. The experimental setup is based on a Ti: sapphire amplifier (Coherent, Libra) operating at 800 nm with 4 mJ pulse energy, 100 fs pulse duration, and 1 kHz repetition rate. The laser pulses are split into two beams. The main portion (80%) of the pulse energy is used to pump an optical parametric amplifier (OPA) to generate near-infrared (NIR) light with a pulse duration of approximately 140 fs and a central wavelength tunable from 1,100 nm to 1,610 nm. NIR pulses from the OPA incident normally onto the 300-nm thick LN metasurface with a beam diameter of 5 mm. The generated THz waves are gathered using three 90° off-axis parabolic mirrors and focused on a 1-mm thick ZnTe wafer. The other portion (20%) of pump energy serves as the probe beam for electro-optical (EO) detection. A motorized translation stage is used to change the time delay between THz and probe pulses. A wire grid polarizer is inserted in the collimated THz path to analyze the polarization of the generated THz waves. The experimental coordinate system is defined by the pump pulses. The reverse direction of pump pulses is the x-axis. The polarization direction of pump pulses is fixed to be vertical and regarded as the z-axis. The optical axis of the x-cut LiNbO₃ metasurface lies in the y-z plane, which is rotated to vary the angle φ between the optical axis and y-axis in the experiment. When the optical axis is vertical and parallel to the polarization of the excitation, φ = 90°. Although the optical axis is horizontal and perpendicular to the polarization, φ = 0°.

FIGURE 2

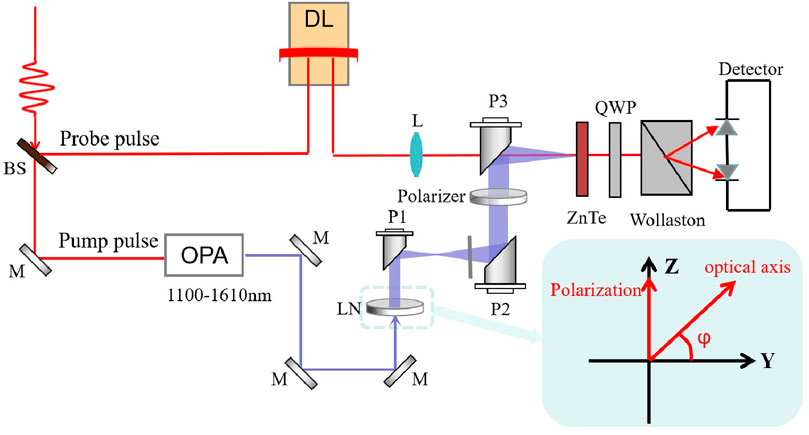
FIGURE 2. Experimental setup for THz electric field generation and detection. BS: beam splitter. OPA: optical parametric amplifier. M: flat laser reflection mirrors. LN: 300-nm thick x-cut lithium niobate metasurface. P₁, P₂, P₃: 90° off-axis parabolic mirrors. Polarizer: thin-film wire-grid THz polarizer. DL: delay line. L: lens with a focal length of 300 mm. ZnTe: 1-mm thick (110)-cut ZnTe crystal. QWP: quarter-wave plate. Wollaston: Wollaston prism. Detector: balanced photodiode detector. The inset shows the optical axis of the x-cut LiNbO₃ metasurface in the experimental coordinate system. The x-axis is the reverse of the propagation direction of pump pulses. z-axis is vertical and along the polarization direction of pump pulses. φ is the angle between the optical axis and horizontal y-axis. The element between P₁ and P₂ is the Teflon board, which is used to transmit the THz waveform and block the pump pulse.

Results and Discussion

Enhanced THz Emission

Figure 3 shows the enhanced THz generation from the LiNbO₃ metasurface. In simulation, the Fano-type resonant wavelength of the LiNbO₃ metasurface is located at 1,375 nm and 1,395 nm, when the optical axis is parallel and perpendicular to the polarization of the pump pulses, respectively. In the experiment, the THz electric field depending on pump wavelength indicates the same result. The THz polarizer ensures that THz polarization is parallel to the pump polarization.

FIGURE 3

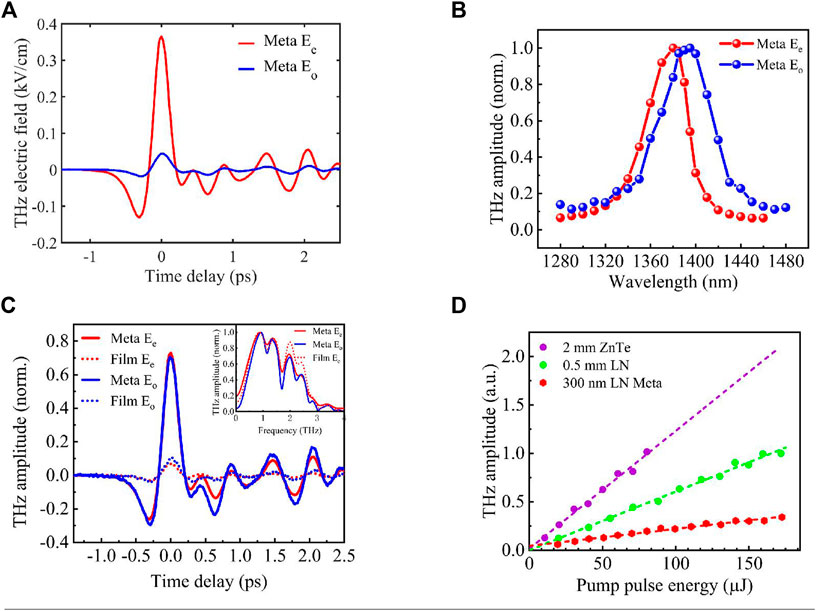
FIGURE 3. Enhanced THz generation from the LiNbO₃ metasurface. The polarization of THz and pump pulses is along the z-axis. (A) Anisotropic THz waves with respect to the orientation of the optical axis. The extraordinary THz waves (E_e, red) with the optical axis are along the z-axis, and the excitation wavelength of 1,375 nm is eight times larger than the amplitude of ordinary THz waves (E_o, blue) with the optical axis along the y-axis and the excitation wavelength of 1,395 nm. (B) Selectivity of the excitation wavelength is due to the resonance in the LiNbO₃ metasurface. Normalized THz peak-to-peak electric field with extraordinary (E_e, red) and ordinary (E_o, blue) polarization by tuning the pump wavelength. (C) Enhancement of THz generation in the LiNbO₃ metasurface (solid line) compared with the unstructured LiNbO₃ nanofilm (dotted) of the same thickness. The extraordinary (E_e, red) and ordinary (E_o, blue) THz waves are generated with the resonant excitation wavelength at 1,375 nm and 1,395 nm, respectively. E_e and E_o are normalized by the resonantly enhanced THz waves from the LiNbO₃ metasurface, respectively. The normalized Fourier contents of the THz electric field are shown in the inset. (D) Dependence of the THz electric field on the pump energy generated from 2-mm thick ZnTe (violet), 0.5-mm thick LiNbO₃ crystal wafer (green), and the 300-nm thick LiNbO₃ metasurface (red). The dashed line is the line fitting the experimental data.

Figure 3A shows the anisotropy of the resonant enhancement of the THz electric field from the LiNbO₃ metasurface, and the pump intensity is 6 GW/cm². When the optical axis of the LiNbO₃ metasurface is rotated in the vertical direction (φ = 90° in Figure 2) and the wavelength is tuned to 1,375 nm, the extraordinary THz waves (E_e) are recorded as the red curve. The detected THz electric field is near 0.4 kV/cm. The conversion efficiency of the THz electric field is estimated to be 5 × 10^–9. When the optical axis is rotated to the horizontal direction (φ = 0° in Figure 2) and the wavelength is tuned to 1,395 nm, the ordinary (E_o) THz waves are recorded as the blue curve. Figure 3A shows that the extraordinary THz electric field is eight times larger than the ordinary counterpart because d₃₃ dominates the second-order nonlinear process [49].

Figure 3B shows the wavelength selectivity of the resonant enhancement for THz generation from the LiNbO₃ metasurface. In the experiment, the wavelength of pump pulses is tuned to search for the resonance wavelength when the optical axis of the LiNbO₃ metasurface is the z- and y-axis in Figure 2. The THz peak-to-peak electric field for extraordinary (φ = 90°) and ordinary (φ = 0°) waves are recorded as red and blue balls in Figure 3B by tuning the wavelength. The central resonant wavelengths of the LiNbO₃ metasurface are 1,375 nm and 1395 nm for E_e and E_o, respectively. This exactly agrees well with our simulation of the designed LiNbO₃ metasurface. At zero detuning, the largest fraction of the excitation pulse spectrum—which is much wider than the width of the resonance—is resonantly coupled to the metasurface, and the THz electric field is strongest. When detuning is slight, the THz electric field decreases monotonically with increasing detuning of the excitation pulse. This is induced by decreasing spectral power overlap between the laser spectrum and the metasurface resonance. This confirms that the THz enhancement is indeed contributed by the resonance-induced electric field enhancement on a metasurface. The full width at half maximum of the THz electric field is about 50 nm in Figure 3B, which is much wider than 5 nm in the simulated reflection spectra, as shown in Figure 1C. It is speculated that the fabrication error and the roughness of the LiNbO₃ metasurface cause the discrepancy.

Figure 3C demonstrates the resonant enhancement of THz generation in the LiNbO₃ metasurface compared with the unstructured LiNbO₃ nanofilm of the same thickness. THz waves are generated at an incident excitation intensity of 6 GW/cm². When the optical axis of the LiNbO₃ metasurface is along the pump polarization and the excitation wavelength is tuned at the resonant wavelength of 1,375 nm, the extraordinary THz electric field (red) is enhanced by a factor of 10 compared to the unstructured LiNbO₃ nanofilm. The ordinary THz electric field (blue) from the resonant metasurface is also ten times larger. The normalized Fourier contents of the THz electric field are the same as shown in the inset. The metasurface only enhances the THz electric field and does not modify the spectral distribution. This demonstrates the THz bandwidth of the metasurface up to 3 THz that is limited mostly by the excitation pulse of duration of ∼140 fs (spectral width ∼13 meV or 3.2 THz) and by the Reststrahlen region of the ZnTe wafer. The enhancement of the THz electric field is one order of magnitude lower than that in the simulation. The spectral width of the pump pulse spectrum (12 nm) is much wider than the width of the resonance (5 nm). The poor overlap of spectral power between the laser spectrum and the metasurface resonance partially explains the obvious discrepancy.

Figure 3D shows the THz electric field as a function of the incident pump power. The pump polarization is parallel to the optical axis of the metasurface. As illustrated in Figure 3D, the THz electric field is linearly proportional to the incident pump power. THz waves from 0.5-mm thick LiNbO₃ or 2-mm thick ZnTe crystal wafers are believed to originate from optical rectification. The enhanced THz electric field originates from the resonant field enhancement in the LiNbO₃ metasurface compared with that in the unstructured LiNbO₃ nanofilm. In the experiment, we used the femtosecond pulses with plane wavefront to excite resonantly the metasurface, which limited the available pump intensity. The THz generation from the metasurface as a function of the excitation intensity is still perturbative and not saturated in the experiment. The measured THz electric field is the same order of magnitude as the ZnTe(110) emitter pumped with the same wavelength and intensity and much higher than plasmon-based metallic nanostructures [33, 34].

Polarization Dependence of the Metasurface THz Emitter

To further investigate the contribution of different nonlinear coefficients to THz generation, the THz peak-to-peak field versus the azimuthal angle $\phi$ is measured by rotating the optical axis of different LiNbO₃ emitters. In the experiment, the THz polarizer can analyze polarization-resolved THz waves, which are excited by polarization along the z-axis. Figure 4 shows the measured (dots) and fitted (lines) THz peak-to-peak fields for a 0.5-mm thick LiNbO₃ crystal wafer and LiNbO₃ metasurface excited with the corresponding resonance wavelength. The first row of Figure 4 is the $E_z^{\text{T}\text{H}\text{z}}$ component of the THz electric field where the THz polarization is parallel to the pump polarization. The middle row of Figure 4 is the $E_y^{\text{T}\text{H}\text{z}}$ component of the THz electric field where the polarization of THz waves is perpendicular to that of excitation. In the polar plots, the azimuthal angles $\phi =90°$ correspond to the optical axis along the z-axis (parallel to pump polarization), and $\phi =0°$ correspond to the optical axis along the y-axis (perpendicular to pump polarization).

FIGURE 4

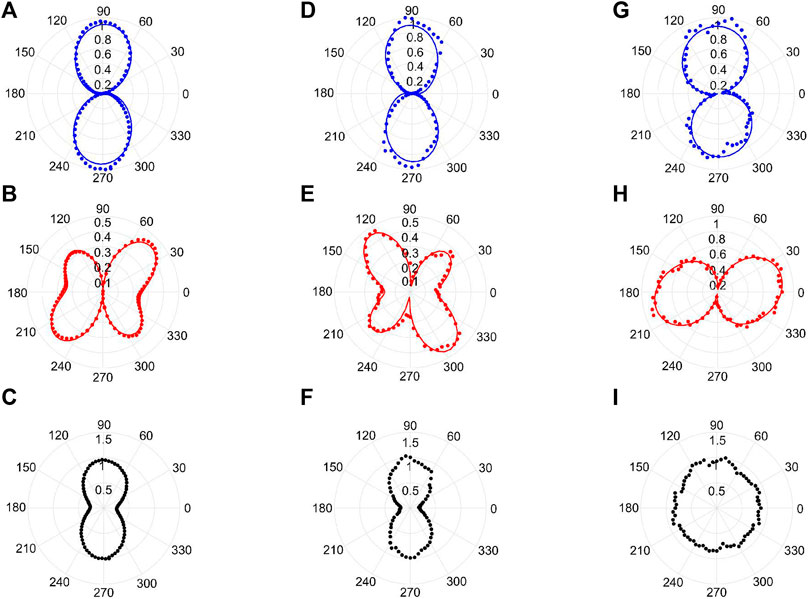
FIGURE 4. Azimuthal dependence of THz generation from LiNbO₃. The polar graph of THz peak-to-peak electric fields as a function of the rotation angle $\phi$ for different emitters. The dots are the experimental data, and the lines are the fittings. The left (A–C), the middle (D–F), and the right (G–I) columns are the azimuthal dependence of the THz electric field generated from 0.5-mm thick LiNbO₃, the LiNbO₃ metasurface excited with the resonance wavelength of 1,375 nm, and the LiNbO₃ metasurface excited with the resonance wavelength of 1,395 nm, respectively. The top (A,D,G), the middle (B,E,H), and the bottom (C,F,I) rows are the azimuthal dependence of the THz electric field with polarization along the z-axis, y-axis, and in total, respectively.

For the 0.5-mm thick LiNbO₃ wafer, Figure 4A shows the $E_z^{\mathrm{T}\mathrm{H}\mathrm{z}}$ component of the THz electric field when THz polarization is parallel to pump polarization. It clearly shows that $E_z^{\mathrm{T}\mathrm{H}\mathrm{z}}$ starting from a maximum at $\phi =90°$ crosses zero at $\phi =180°$ and returns back to a maximum at $\phi =270°$, with a π phase shift from the origin. This eight-like shape is due to the dominating d₃₃ coefficient, which couples z-polarized excitation fields with THz waves. This has been reported in second-harmonic generation from non-resonant LiNbO₃ thin films [49]. The influence of other coefficients can be seen in the $E_y^{\text{T}\text{H}\text{z}}$ component of the THz electric field shown in Figure 4B. Here, the maximal $E_y^{\text{T}\text{H}\text{z}}$ component is about one half of the maximal $E_z^{\text{T}\text{H}\text{z}}$ and is achieved in an azimuthal angle which is approximately $\phi =45°$ and $\phi =225°$ in the y-z plane. This indicates that $E_y^{\text{T}\text{H}\text{z}}$ is generated mostly by the d₃₁ coefficient, which combines z-polarized and y-polarized excitation fields. However, there is an asymmetry in the pattern, which is not exactly along the 45° direction. This can be attributed to the action of the d₂₂ coefficient coupling y-polarized excitation with y-polarized THz waves. This contribution is interfering constructively or destructively with the lobes originating from d₃₁. Comparing the THz electric field with orthogonal polarization in Figures 4A,B, the linearly polarized THz waves are validated even if the polarization plane rotates relative to the orientation of the optical axis. The phase-resolved THz waves allow us to unambiguously determine the second-order nonlinear susceptibility of the LiNbO₃ crystal by fitting the experimental data in Figures 4A,B. If we normalized the largest component d₃₃ of effective second-order nonlinear susceptibility as ‒1, the other two small components d₃₁ and d₂₂ are -0.1879 and 0.0969, respectively [49]. These data agree well with those obtained from second-harmonic generation. Figure 4C shows the total THz electric field. The azimuthal dependence is similar with the eight-shape of $E_z^{\text{T}\text{H}\text{z}}$. However, the THz electric field is not zero at $\phi =0°$ due to the considerable contribution from $E_y^{\text{T}\text{H}\text{z}}$.

The LiNbO₃ metasurface excited in the resonant wavelength of 1,375 nm shows a similar nonlinear behavior as for the LiNbO₃ wafer, as discussed before. However, Figure 4E shows the different azimuthal dependence on the orientation of the optical axis for the $E_y^{\text{T}\text{H}\text{z}}$ component of the THz electric field. The direction of the maximal $E_y^{\text{T}\text{H}\text{z}}$ rotates about $90°$, and there is an isotropic nonzero component compared with Figure 4B. The aforementioned two differences are attributed to the resonant enhancement E_x of the excitation field in the LiNbO₃ metasurface. As shown in Figure 1D, there exist considerable E_x and E_y components when the LiNbO₃ metasurface is resonantly excited with the polarization along the z-axis. Although the THz electric field in Figure 4E is generated mostly by d₃₁, d₂₂ is interfering constructively or destructively with the lobes. The relative values of E_x and E_y of the excitation field in the LiNbO₃ metasurface determine the amplitude and phase of the generated THz electric field $E_y^{\text{T}\text{H}\text{z}}$. There is no E_x of the excitation field in the LiNbO₃ wafer, while E_x is larger than E_y in the resonantly excited LiNbO₃ metasurface. This introduces a π phase shift of $E_y^{\text{T}\text{H}\text{z}}$ in the LiNbO₃ metasurface compared with the wafer. The interference with $E_y^{\text{T}\text{H}\text{z}}$ originated from the d₃₁ coefficient rotates in the maximum direction of $E_y^{\mathrm{T}\mathrm{H}\mathrm{z}}$ to about $\phi =135°$. The E_x of the excitation field in the LiNbO₃ metasurface is independent on the orientation of the optical axis, which contributes isotropic $E_y^{\text{T}\text{H}\text{z}}$, as shown in Figure 4E. The eight-like shape in Figure 4F is more stretched in the direction $\phi =90°$ and $\phi =270°$, indicating a stronger nonlinear response for these polarization angles than in the case of the wafer. This is also due to the resonant electric field enhancement, which increases the THz electric field in this direction but is absent in the orthogonal polarization direction owing to the birefringence.

The LiNbO₃ metasurface excited in the resonant wavelength of 1,395 nm shows two eight-like patterns for $E_z^{\text{T}\text{H}\text{z}}$ and $E_y^{\text{T}\text{H}\text{z}}$ of the THz electric field. As discussed before, $E_z^{\text{T}\text{H}\text{z}}$ is dominantly determined by the d₃₃ coefficient. Due to the resonant enhancement of the E_y excitation field in the LiNbO₃ metasurface, $E_y^{\text{T}\text{H}\text{z}}$ is dominantly determined by the d₂₂ coefficient, which also produces the eight-like pattern, as shown in Figure 4G. The d₃₃ coefficient is ten times larger than the d₂₂ coefficient. By coincidence, the THz electric field is also ten times enhanced when the excitation wavelength is 1,395 nm, and its polarization is perpendicular to the optical axis. These two facts produce the nearly isotropic pattern of THz waves by coincidence, as shown in Figure 4I.

Metasurfaces composed of ensembles of dielectric nanoresonators with subwavelength dimensions have shown great flexibility in achieving versatile functions in THz technologies. The coexistence of resonant nonlinear and local field enhancement in properly designed metasurfaces opens up an alternative route for high-efficiency nonlinear devices. The geometry of the individual meta-atoms along with their crystalline orientation and lattice structure enables one to control the polarization state of the emitted light based on that of the excitation light. In order to explore the polarization of THz waves generated from the LiNbO₃ metasurface, Figure 5 shows the dependence of THz polarization on the orientation of the optical axis. By means of polarization-resolved THz detection, Figure 5A plots THz waves in three-dimension which is resonantly driven at the wavelength of 1,395 nm. It is found that THz waves are linearly polarized. The polarization direction is in accordance with the optical axis. Figure 5B confirms this result at $\text{φ}=10°$ and $\text{φ}=50°$. Combined with the polarization-independent pattern shown in Figure 4I, it provides a simple method to control the polarization direction of THz waves by rotating the optical axis of the LiNbO₃ metasurface. Figure 5C further demonstrates that the polarization of THz waves is determined by the orientation of the optical axis of the LiNbO₃ metasurface due to the prominent contribution of d₃₃. This analysis demonstrates that for high efficient enhancement of THz waves, the excitation field within each nanoresonator should be predominantly polarized along the optical axis.

FIGURE 5

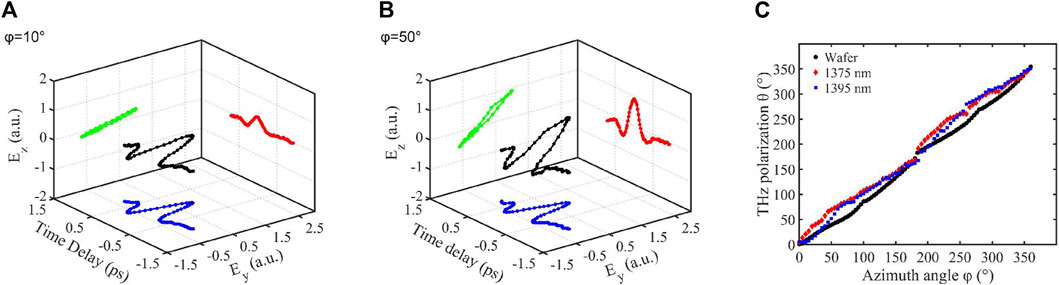
FIGURE 5. Dependence of THz polarization on the orientation of the optical axis. 3D plots of the THz waves generated from the LiNbO₃ metasurface with azimuthal angles $\phi =10°$ (A) and $\phi =50°$ (B) excited in the resonant wavelength of 1,395 nm $E_z^{\text{T}\text{H}\text{z}}$ (red) and $E_y^{\text{T}\text{H}\text{z}}$ (blue) components comprised THz waves (black). The polarization plane of THz waves is projected onto the y-z coordinate plane (green) with the polarization angle θ departing from the y-axis. (C) Dependence of the polarization angle of THz waves on the azimuthal angle of the optical axis of the LiNbO₃ wafer (black) and metasurface excited with 1,375 nm (red) and 1,395 nm (blue).

Conclusion

In summary, we propose a LiNbO₃ metasurface to enhance the THz electric field. The metasurface represents a new platform for revealing artificial Fano-type THz electric field generation. The THz electric field from the LiNbO₃ metasurface is enhanced by more than one order of magnitude compared to unstructured samples. The enhanced THz electric field is highly anisotropic with respect to excitation polarization and is selective by the excitation wavelength due to its resonant nanostructure. Moreover, the polarization state of the THz electric field can be controlled by rotating the optical axis of the LiNbO₃ metasurface with constant amplitude. By combining the nanofabrication technology and ultrafast strong-field physics, our work paves the way for the design of new compact THz photonic devices with enhanced nonlinearities based on LiNbO₃ metasurfaces.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.

Author Contributions

YT, XS, HW, XW, CM, and ZL performed the experiment. XZ and YY helped to process the experimental data. NL, KL, and ZhZ fabricated the metamaterials. DZ and ZeZ conceived the idea and supervised the project.

Funding

This study was funded by the National Key Research and Development Program of China (2019YFA0307704), the NSAF Joint Fund (U1830206), the Major Research plan of the National Natural Science Foundation of China (91850201), and the National Natural Science Foundation of China (11974426 and 11974425).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Pickwell E, Wallace VP. Biomedical Applications of Terahertz Technology. J Phys D: Appl Phys (2006) 39(17):R301–R310. doi:10.1088/0022-3727/39/17/r01

CrossRef Full Text | Google Scholar

2. Tonouchi M. Cutting-edge Terahertz Technology. Nat Photon (2007) 1:97–105. doi:10.1038/nphoton.2007.3

CrossRef Full Text | Google Scholar

3. Jepsen PU, Cooke DG, Koch M. Terahertz Spectroscopy and Imaging-Modern Techniques and Applications. Laser Photon Rev (2011) 5(1):1–43. doi:10.1002/lpor.201000011

CrossRef Full Text | Google Scholar

4. Koenig S, Lopez-Diaz D, Antes J, Boes F, Henneberger R, Leuther A, et al. Wireless Sub-THz Communication System with High Data Rate. Nat Photon (2013) 7(12):977–81. doi:10.1038/nphoton.2013.275

CrossRef Full Text | Google Scholar

5. Hoffmann MC, Fülöp JA. Intense Ultrashort Terahertz Pulses: Generation and Applications. J Phys D: Appl Phys (2011) 44(8):083001. doi:10.1088/0022-3727/44/8/083001

CrossRef Full Text | Google Scholar

6. Huang Y, Meng C, Zhao J, Wang X, Lü Z, Zhang D, et al. High-harmonic and Terahertz Wave Spectroscopy (HATS) for Aligned Molecules. J Phys B: Mol Opt Phys (2016) 49:235601. doi:10.1088/0953-4075/49/23/235601

CrossRef Full Text | Google Scholar

7. Kampfrath T, Tanaka K, Nelson KA. Resonant and Nonresonant Control over Matter and Light by Intense Terahertz Transients. Nat Photon (2013) 7(9):680–90. doi:10.1038/nphoton.2013.184

CrossRef Full Text | Google Scholar

8. Zhang XC, Shkurinov A, Zhang Y. Extreme Terahertz Science. Nat Photon (2017) 11(1):16–8. doi:10.1038/nphoton.2016.249

CrossRef Full Text | Google Scholar

9. Chen M, Wu Y, Liu Y, Lee K, Qiu X, He P, et al. Current-Enhanced Broadband THz Emission from Spintronic Devices. Adv Opt Mater (2019) 7(4):1801608.

Google Scholar

10. Zhang Y, Zhang X, Li S, Gu J, Li Y, Tian Z, et al. A Broadband THz-TDS System Based on DSTMS Emitter and LTG InGaAs/InAlAs Photoconductive Antenna Detector. Sci Rep (2016) 6:26949. doi:10.1038/srep26949

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Schlauderer S, Lange C, Baierl S, Ebnet T, Schmid CP, Valovcin DC, et al. Temporal and Spectral Fingerprints of Ultrafast All-Coherent Spin Switching. Nature (2019) 569:383–7. doi:10.1038/s41586-019-1174-7

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Buchmann TO, Kelleher EJR, Jazbinsek M, Zhou B, Seok JH, Kwon OP, et al. High-power Few-Cycle THz Generation at MHz Repetition Rates in an Organic crystal. APL Photon (2020) 5(10):106103. doi:10.1063/5.0022762

CrossRef Full Text | Google Scholar

13. Vicario C, Jazbinsek M, Ovchinnikov AV, Chefonov OV, Ashitkov SI, Agranat MB, et al. High Efficiency THz Generation in DSTMS, DAST and OH1 Pumped by Cr:forsterite Laser. Opt Express (2015) 23(4):4573–80. doi:10.1364/oe.23.004573

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Lu Y, Zhang Q, Wu Q, Chen Z, Liu X, Xu J. Giant Enhancement of THz-Frequency Optical Nonlinearity by Phonon Polariton in Ionic Crystals. Nat Commun (2021) 12(1):3183. doi:10.1038/s41467-021-23526-w

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Nahata A, Weling AS, Heinz TF. A Wideband Coherent Terahertz Spectroscopy System Using Optical Rectification and Electro‐optic Sampling. Appl Phys Lett (1996) 69:2321–3. doi:10.1063/1.117511

CrossRef Full Text | Google Scholar

16. Fülöp JA, Polónyi G, Monoszlai B, Andriukaitis G, Balciunas T, Pugzlys A, et al. Highly Efficient Scalable Monolithic Semiconductor Terahertz Pulse Source. Optica (2016) 3(10):1075. doi:10.1364/OPTICA.3.001075

CrossRef Full Text | Google Scholar

17. Zhai D, Hérault E, Garet F, Coutaz J-L. Terahertz Generation from ZnTe Optically Pumped above and below the Bandgap. Opt Express (2021) 29(11):17491–8. doi:10.1364/oe.421282

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Ahr F, Jolly SW, Matlis NH, Carbajo S, Kroh T, Ravi K, et al. Narrowband Terahertz Generation with Chirped-And-Delayed Laser Pulses in Periodically Poled Lithium Niobate. Opt Lett (2017) 42(11):2118–21. doi:10.1364/ol.42.002118

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Stepanov AG, Hebling J, Kuhl J. Efficient Generation of Subpicosecond Terahertz Radiation by Phase-Matched Optical Rectification Using Ultrashort Laser Pulses with Tilted Pulse Fronts. Appl Phys Lett (2003) 83(15):3000–2. doi:10.1063/1.1617371

CrossRef Full Text | Google Scholar

20. Zhang B, Ma Z, Ma J, Wu X, Ouyang C, Kong D, et al. 1.4‐mJ High Energy Terahertz Radiation from Lithium Niobates. Laser Photon Rev (2021) 15(3):2000295. doi:10.1002/lpor.202000295

CrossRef Full Text | Google Scholar

21. János HK, Matthias C, Balázs B, Keith AN. Generation of High-Power Terahertz Pulses by Tilted-Pulse-Front Excitation and Their Application Possibilities. J Opt Soc America B (2008) 25(7):B6–B19. doi:10.1364/josab.25.0000b6

CrossRef Full Text | Google Scholar

22. Wang R, Xu L, Wang J, Sun L, Jiao Y, Meng Y, et al. Electric Fano Resonance-Based Terahertz Metasensors. Nanoscale (2021) 13(44):18467–72. doi:10.1039/d1nr04477j

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Ironside DJ, Salas R, Chen P-Y, Le KQ, Alú A, Bank SR. Enhancing THz Generation in Photomixers Using a Metamaterial Approach. Opt Express (2019) 27(7):9481–94. doi:10.1364/oe.27.009481

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Shen YC, Upadhya PC, Linfield EH, Beere HE, Davies AG. Ultrabroadband Terahertz Radiation from Low-Temperature-Grown GaAs Photoconductive Emitters. Appl Phys Lett (2003) 83(15):3117–9. doi:10.1063/1.1619223

CrossRef Full Text | Google Scholar

25. Hafez HA, Kovalev S, Deinert JC, Mics Z, Green B, Awari N, et al. Extremely Efficient Terahertz High-Harmonic Generation in Graphene by Hot Dirac Fermions. Nature (2018) 561(7724):507–11. doi:10.1038/s41586-018-0508-1

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Fan K, Suen JY, Liu X, Padilla WJ. All-dielectric Metasurface Absorbers for Uncooled Terahertz Imaging. Optica (2017) 4(6):601–4. doi:10.1364/optica.4.000601

CrossRef Full Text | Google Scholar

27. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, et al. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science (2011) 334(6054):333–7. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Lin D, Fan P, Hasman E, Brongersma ML. Dielectric Gradient Metasurface Optical Elements. Science (2014) 345(6194):298–302. doi:10.1126/science.1253213

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Lee G-Y, Yoon G, Lee S-Y, Yun H, Cho J, Lee K, et al. Complete Amplitude and Phase Control of Light Using Broadband Holographic Metasurfaces. Nanoscale (2018) 10(9):4237–45. doi:10.1039/c7nr07154j

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Overvig AC, Shrestha S, Malek SC, Lu M, Stein A, Zheng C, et al. Dielectric Metasurfaces for Complete and Independent Control of the Optical Amplitude and Phase. Light Sci Appl (2019) 8(1):92–12. doi:10.1038/s41377-019-0201-7

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Teng S, Zhang Q, Wang H, Liu L, Lv H. Conversion between Polarization States Based on a Metasurface. Photon Res (2019) 7(3):246–50. doi:10.1364/prj.7.000246

CrossRef Full Text | Google Scholar

32. Luo L, Chatzakis I, Wang J, Niesler FB, Wegener M, Koschny T, et al. Broadband Terahertz Generation from Metamaterials. Nat Commun (2014) 5:3055. doi:10.1038/ncomms4055

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Park SG, Choi Y, Oh YJ, Jeong KH. Terahertz Photoconductive Antenna with Metal Nanoislands. Opt Express (2012) 20(23):25530–5.

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Welsh GH, Wynne K. Generation of Ultrafast Terahertz Radiation Pulses on Metallic Nanostructured Surfaces. Opt Express (2009) 17(4):2470–80. doi:10.1364/oe.17.002470

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Ramanandan GKP, Ramakrishnan G, Kumar N, Adam AJL, Planken PCM. Emission of Terahertz Pulses from Nanostructured Metal Surfaces. J Phys D: Appl Phys (2014) 47:374003. doi:10.1088/0022-3727/47/37/374003

CrossRef Full Text | Google Scholar

36. Polyushkin DK, Hendry E, Stone EK, Barnes WL. THz Generation from Plasmonic Nanoparticle Arrays. Nano Lett (2011) 11(11):4718–24. doi:10.1021/nl202428g

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Liu H, Guo C, Vampa G, Zhang JL, Sarmiento T, Xiao M, et al. Enhanced High-Harmonic Generation from an All-Dielectric Metasurface. Nat Phys (2018) 14:1006–10. doi:10.1038/s41567-018-0233-6

CrossRef Full Text | Google Scholar

38. Boyd RW. Nonlinear Optics. Elsevier (2003).

Google Scholar

39. Weis RS, Gaylord TK. Lithium Niobate: Summary of Physical Properties and crystal Structure. Appl Phys A (1985) 37:191–203. doi:10.1007/bf00614817

CrossRef Full Text | Google Scholar

40. Park H, Camper A, Kafka K, Ma B, Lai YH, Blaga C, et al. High-order Harmonic Generations in Intense MIR fields by cascade Three-Wave Mixing in a Fractal-Poled LiNbO₃ Photonic crystal. Opt Lett (2017) 42(19):4020–3. doi:10.1364/ol.42.004020

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Carletti L, Li C, Sautter J, Staude I, De Angelis C, Li T, et al. Second Harmonic Generation in Monolithic Lithium Niobate Metasurfaces. Opt Express (2019) 27(23):33391. doi:10.1364/oe.27.033391

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Ma J, Chen J, Ren M, Wu W, Cai W, Xu J. Second-harmonic Generation and its Nonlinear Depolarization from Lithium Niobate Thin Films. Opt Lett (2020) 45(1):145. doi:10.1364/ol.45.000145

CrossRef Full Text | Google Scholar

43. Shcherbakov MR, Werner K, Fan Z, Talisa N, Chowdhury E, Shvets G. Photon Acceleration and Tunable Broadband Harmonics Generation in Nonlinear Time-dependent Metasurfaces. Nat Commun (2019) 10:1345. doi:10.1038/s41467-019-09313-8

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Ma J, Xie F, Chen W, Chen J, Wu W, Liu W, et al. Nonlinear Lithium Niobate Metasurfaces for Second Harmonic Generation. Laser Photon Rev (2021) 15(5):2000521. doi:10.1002/lpor.202000521

CrossRef Full Text | Google Scholar

45. Wang SS, Moharam MG, Magnusson R, Bagby JS. Guided-mode Resonances in Planar Dielectric-Layer Diffraction Gratings. J Opt Soc Am A (1990) 7(8):1470. doi:10.1364/josaa.7.001470

CrossRef Full Text | Google Scholar

46. Magnusson R, Ko YH. Wideband Dielectric Metamaterial Reflectors: Mie Scattering or Leaky Bloch Mode Resonance. Optica (2018) 5:289–94. doi:10.1364/optica.5.000289

CrossRef Full Text | Google Scholar

47. Tan ZL, Lin K, Xu W, Zhu ZH. Suspended Dielectric Mirrors at Deep Subwavelength Scale. IEEE Photon J (2018) 10(4):4600506. doi:10.1109/jphot.2018.2850883

CrossRef Full Text | Google Scholar

48. Zelmon DE, Small DL, Jundt D. Infrared Corrected Sellmeier Coefficients for Congruently Grown Lithium Niobate and 5 mol.% Magnesium Oxide–doped Lithium Niobate. J Opt Soc America B (1997) 14(12):3319–22. doi:10.1364/josab.14.003319

CrossRef Full Text | Google Scholar

49. Fedotova A, Younesi M, Sautter J, Vaskin A, Löchner FJF, Steinert M, et al. Second-Harmonic Generation in Resonant Nonlinear Metasurfaces Based on Lithium Niobate. Nano Lett (2021) 21:888. doi:10.1021/acs.nanolett.0c03290

PubMed Abstract | CrossRef Full Text | Google Scholar