Effect of Thermal Blooming on the Higher-Order Mode Fiber Laser Array Propagation Through the Atmosphere

The influence of thermal blooming on the propagation properties of higher-order mode (HOM) fiber laser array is studied by using the algorithm for simulating the laser beam propagation in the atmosphere. Based on the multiphase screen method and finite-difference method, the four-dimensional (4D) computer code of time-dependent propagation is designed to simulate the propagation of HOM fiber laser array through the atmosphere. In this study, the laser energy focusability of the LP₁₁ mode beam array is investigated in detail for different beamlet arrangements, transverse wind speed, and the content of LP₀₁ mode under the conditions of thermal blooming. In free space, the focal shape of the LP₁₁ mode beam array depends on the arrangement of the second circle of the initial beam array, whereas the influence of the central beamlets is weak. The number of side lobes can be tailored by changing the arrangement of the beamlets. In contrast, under the conditions of thermal blooming, the central beamlet has a significant effect on focal beam shape. It is demonstrated that the laser energy focusability can be improved by rotating the central beamlet or increasing the transverse wind speed. As the content of the LP₀₁ mode increases, the energy is gradually concentrated from the side lobes to the center lobe. Furthermore, the effects of initial beam array arrangements on the energy focus and focal shape are investigated. The optimal arrangement for obtaining high energy focusability is discussed in detail. These results could provide useful references for applications of the HOM beam array.

Introduction

The large mode area (LMA) fiber is remarkable for its advantages in suppressing a number of nonlinear effects [1–3]. In recent years, higher-order modes (HOMs) with specific spatial intensity, phase, and polarized distributions have been widely applied in many practical applications, such as optical tweezers, optical communication, micro-machining, and material processing [4–8]. Driven by these demanding applications, the methods of generating HOMs in fiber lasers have been demonstrated widely [9–12]. HOMs can be generated based on the active mode control system, and various methods have been successfully demonstrated, including spatial light modulator (SLM) [13], long-period fiber gratings [14, 15], fiber Bragg grating [16], random fiber lasers [17], polarization control [18, 19], and mode-selective couplers (MSCs) [20, 21]. Notably, You et al. demonstrated a kilowatt (kW)-level HOM laser beam based on the master oscillator power amplifier (MOPA) configuration [22]. These advancements of HOMs can be beneficial for further power scaling.

The power scaling of the output laser beyond the kilowatt (kW) level can be achieved by the coherent beam combining (CBC) technology as well [23–25]. In last decades, the coherent combining of laser beams has been widely used in high-power systems and inertial confinement fusion due to the advantages such as efficiency, compactness, and reliability [26–28]. Recently, high output power [29–31] and a large number of channels [32, 33] based on the coherent combining of the fiber amplifier array have been reported. In addition, the structured light beams can also be generated from the beam array [34]. Until now, various structured light beams based on CBC technology have been demonstrated theoretically and experimentally [35–38].

When a high-power laser beam propagates through the atmosphere, the propagation characteristics of the laser beam could be affected by nonlinear effects such as thermal blooming, self-focusing, stimulated Raman scattering, and etc. The thermal blooming effect is one of the most important nonlinear effects, which is caused by the energy of the laser beam absorbed by molecules and aerosols in the atmosphere [39]. Thermal blooming leads to decreasing of the peak irradiance, and the presence of a transverse wind will further cause the shift of the peak irradiance, which will result in the degradation of beam quality and limit the use of high-power laser delivery [40, 41]. Over the last decades, the study of the effect of thermal blooming on high-power laser beams propagating in the atmosphere has gained considerable attention. For example, Gebhardt and Smith developed a theoretical model to predict thermal blooming distortion in the atmosphere [42]. Fleck et al. proposed a four-dimensional (4D) computer code of the time-dependent propagation of high-power laser beams to investigate the thermal blooming effect [43]. Moreover, the effect of thermal blooming on annular beams, airy beams, Hermite–Gaussian beams, and vortex beams has been studied in detail [44–47]. With the development of the CBC technology, the studies of the effect of thermal blooming on the beam array have also been carried out in recent years [48–51]. To the best of our knowledge, the effect of thermal blooming on the HOM beam array has not been investigated yet.

The aim of the study is to study the influence of thermal blooming on the propagation properties of a coherent beam combined with the high-power continuous wave HOM beam array in the atmosphere. The mathematical model of the HOM beam array and 4D computer algorithms are presented in the Theoretical Model section. The LP₁₁ mode beam array is considered in this study. In the Numerical Simulations Results and Analysis section, the changes of focal shape in free space for different beamlet arrangements are studied. In addition, the influence of the beamlet arrangement and content of the LP₀₁ mode on the energy focusability under the conditions of thermal blooming is investigated in detail. In the Conclusion section, the main results obtained in this study are summarized.

Theoretical Model

At present, the step-index fiber is taken as the gain medium for most high-power fiber laser systems. Without loss of generality, the HOMs excited from a step-index fiber is investigated in this study. It is considered that the coordinate z-axis is parallel to the geometrical axis of the fiber with the core radius a. In the weakly guiding approximation, the field distribution of the LP_nm-mode can be expressed as [52].

$E_{nm}\left(r,\varphi \right)=R_{nm}\left(r\right)\cos \left(n\varphi \right),(1)$

where $(r,\varphi )$ are the polar coordinates. The radial dependence of the approximately transverse field amplitude in Eq. 1 is defined as follows

$R_{nm}\left(r\right)=\{\begin{array}{c}{k}_1{J}_n\left(U_m\frac{r}{a}\right)0\le r\le a\\ k_2{K}_n\left(W_m\frac{r}{a}\right)r>a\end{array},(2)$

where $k_1{J}_n\left(U_m\right)=k_2{K}_n\left(W_m\right)$ and J_n and K_n are the n-order Bessel function of the first kind and the modified Bessel function of the first kind, respectively. U_m and W_m are the solutions of the characteristic equations (53).

$\frac{J_n\left(U_m\right)}{U{J}_{n+1}\left(U_m\right)}=\frac{K_n\left(W_m\right)}{W{K}_{n+1}\left(W_m\right)}(3)$

and

$U^2+W^2=V(4)$

The normalized frequency V is defined as

$V=\frac{2\text{π}a}{\lambda }\sqrt{n_{\text{core}}^2-n_{\text{clad}}^2},(5)$

where n_core and n_clad are the core refractive index and cladding refractive index, respectively. The numerical aperture (NA) can be written as $NA=\sqrt{n_{core}^2-n_{clad}^2}$. The exemplary fiber that will be considered here has an ideal step-index profile with a core/inner-cladding diameter of 20/400 μm and an NA of 0.06.

The HOMs excited in the fiber are magnified 200 times by a large diameter collimator and then combined in the beam combiner system. It is assumed that a HOM beam array consists of seven beamlets located as z = 0, which are arranged in a tiled hexagonal architecture by coherent beam combining, as shown in Figure 1. The distance between the centers of neighboring sub-aperture is r₀ and the diameter of the whole beam array is D. The optical field of each beamlet is $E_{nm}^l$. The electric field distribution of the HOM beam array with a hard aperture is expressed as

$E=A_{\text{coe}}{\displaystyle \sum _{l=1}^N{E}_{nm}^l\left[r^2+r_0^2+2r{r}_0\cos (\varphi -{\varphi }_l)\right]}\times circ\left[r^2+R^2+2rR\cos (\varphi -{\varphi }_l)\right],(6)$

where ${\varphi }_l=\pi l/3$. The circ(•) denotes the hard aperture truncated function with a diameter of R. The coefficient A_coe can be obtained according to the well-known relationship between power P and the electric field $E_{nm}^l$ [54].

$P={\displaystyle \underset{0}{\overset{2\pi }{\int }}\text{d}\varphi }{\displaystyle \underset{0}{\overset{\infty }{\int }}{\left|E\right|}^2}r\text{d}r,(7)$

FIGURE 1

FIGURE 1. Schematic diagram of a HOM beam array.

In the parabolic approximation, the electric field E satisfies the Maxwell wave equation (43).

$2\text{i}k\frac{\partial E}{\partial z}={\nabla }_{\perp }^{2}E+k^2\left(\frac{n^2}{n_0^2}-1\right)E,(8)$

where ${\nabla }_{\perp }^2={\partial }^2/\partial x^2+{\partial }^2/\partial y^2$ and n, and n₀ are the refractive indices of the atmosphere with and without disturbance, respectively. $k=2\pi /\lambda$ is the wave number related to the wavelength λ. According to the hydrodynamic equation, the atmospheric density ρ₁ with disturbance caused by thermal blooming can be obtained [43].

$\frac{\partial {\rho }_1}{\partial t}+v\cdot \nabla {\rho }_1=-\frac{\gamma -1}{c_s^2}\alpha I,(9)$

where v, γ, c_s, and α are the wind speed, specific heat, sound speed capacity ratio, and absorption coefficient in the atmosphere, respectively. The intensity I is given by $I={\left|E\right|}^2\exp \left(\alpha z\right)$.

Based on Eqs 1–9, we designed a 4D computer code to simulate the time-dependent propagation of a HOM beam array propagating through the atmosphere by using the multiphase screen method and finite-difference method [43]. A lens with focus z_f = 5 km located at z = 0 is considered in this study. In the following calculations, the parameters are taken as a = 50 μm, R = 4.5 cm, $\lambda =1\text{.}064\text{μm}$, n₀ = 1.00031, v = 2 m/s along x-axis, ρ₀ = 1.30246 kg/m³, c_s = 340 m/s, α = 0.07/km, P = 1 kw, and N = 7, z = 5 km.

Numerical Simulation Results and Analysis

Linear Propagation of the HOM Beam Array

In this section, the propagation properties of the LP₁₁ mode beam array propagating in free space are demonstrated. As we all know, the intensity distribution of the LP₀₁ mode is circular symmetry, and the far field intensity distribution of the LP₀₁ mode coherent beam array is comprises a central lobe with a number of side lobes. But for the LP₁₁ mode, the intensity distribution is axial symmetry, and therefore, the arrangement of the LP₁₁ mode has a significant impact on the focal intensity distributions.

The intensity distributions of the LP₁₁ mode beam array with centrosymmetric arrangement are shown in Figure 2. It is assumed that the angle of the LP₁₁ mode around the central beamlet in Figure 2A is set as θ = 0, and the different rotation angles for the initial beamlet arrangement are shown in Figures 2B–D. It can be seen that the beam shapes of the LP₁₁ mode beam array at the receiver plane are quite different from those of the LP₀₁ mode beam array. The beam shapes of the LP₁₁ mode beam array are a radial spot beam array without a central lobe. As θ changes from 0 to 90°, the number of side lobes gradually changes from 6 to 12. By comparing the beam shapes at the initial plane, it is clearly seen that the focal intensity distributions are consistent with the first ring of the hexagonal mesh of the fiber laser array (see the red circle highlight in Figures 2A–D). These observations indicate that the desired beam shape of the focusing spots can be obtained by simply rotating the surrounding beamlets.

FIGURE 2

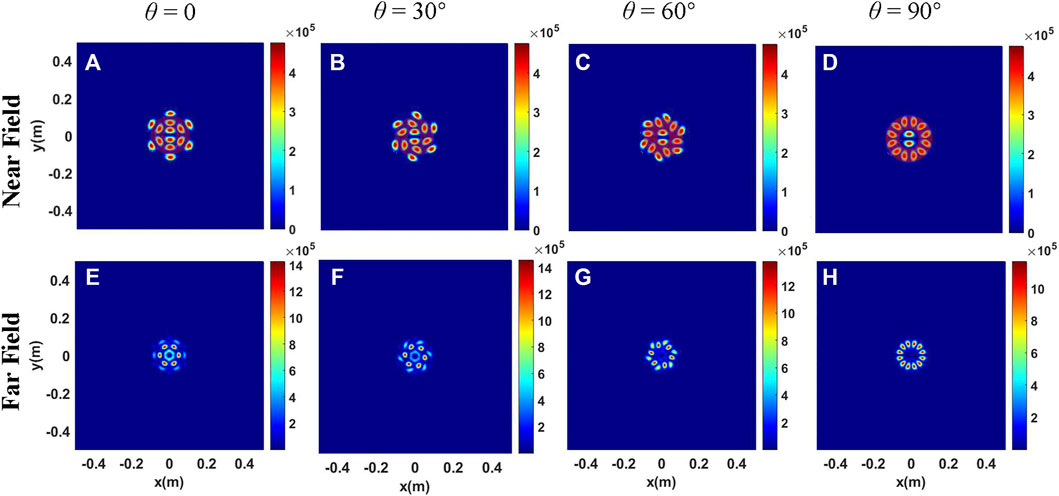
FIGURE 2. Intensity distributions of the LP₁₁ mode beam array for different rotation angles of beamlets. (A–D) Intensity distributions at the initial plane. (E–H) Intensity distributions at the receiver plane in free space.

Effect of Thermal Blooming on the HOM Beam Array

It can be clearly seen that different focal spots can be obtained by changing the initial arrangement of the LP₁₁ mode beam array as mentioned in the Linear propagation of HOMs beam array section. Therefore, the impact of thermal blooming on the LP₁₁ mode beam array can be quite different for different arrangements. In this section, based on the results in the Linear propagation of HOMs beam array section, the effects of thermal blooming on the special arrangements of the LP₁₁ mode beam array are investigated in detail.

The intensity distributions of the LP₁₁ mode beam array for centrosymmetric arrangement under the conditions of thermal blooming are shown in Figures 3, 4. From Figures 4I–L, it can be observed that the influence of thermal blooming on the LP₁₁ mode beam array can be quite different for different rotation angles. In addition, the focal beam shapes are not symmetrical except for the arrangement of Figure 3A. The difference between Figure 3 and Figure 4 is that the initial central beamlets in Figure 4 are rotated by 90 degrees. It can be seen that the focal beam shapes under thermal blooming are quite different, although the focal beam shapes in free space are the same. The phenomena illustrates that the arrangement of the central beamlet has little influence on the focal beam shapes in free space but has a significant effect on the focal beam shapes under thermal blooming.

FIGURE 3

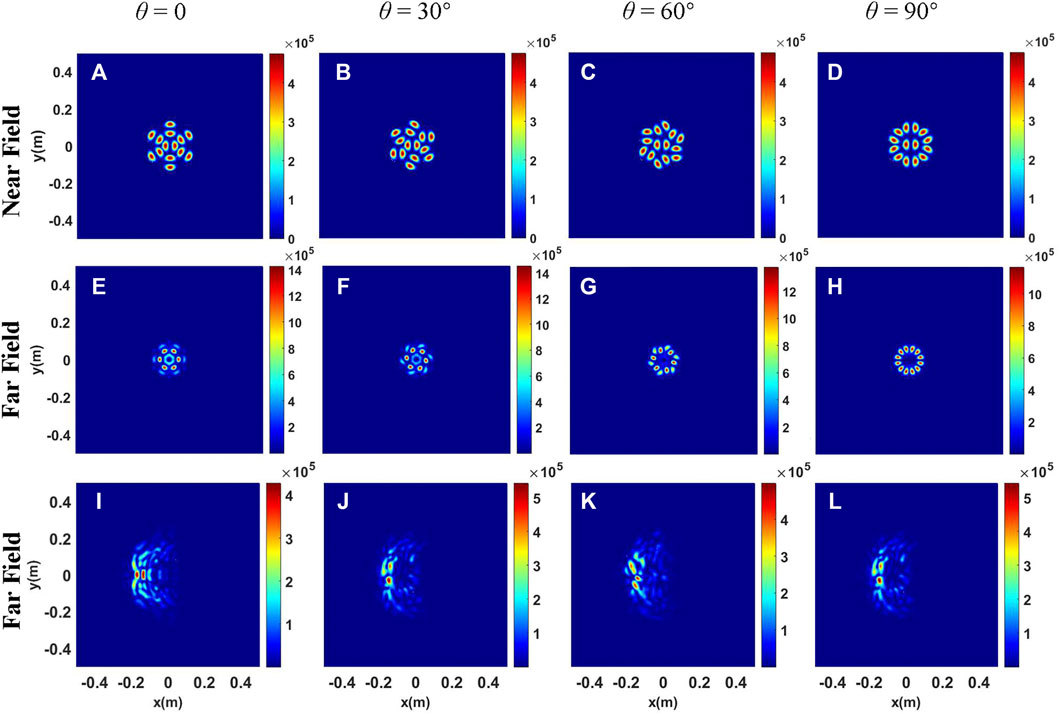
FIGURE 3. Intensity distributions of the LP₁₁ mode beam array for different rotation angles of beamlets. (A–D) Intensity distributions at the initial plane; (E–H) Intensity distributions at the receiver plane in free space; (I–L) Intensity distributions at the receiver plane under thermal blooming.

FIGURE 4

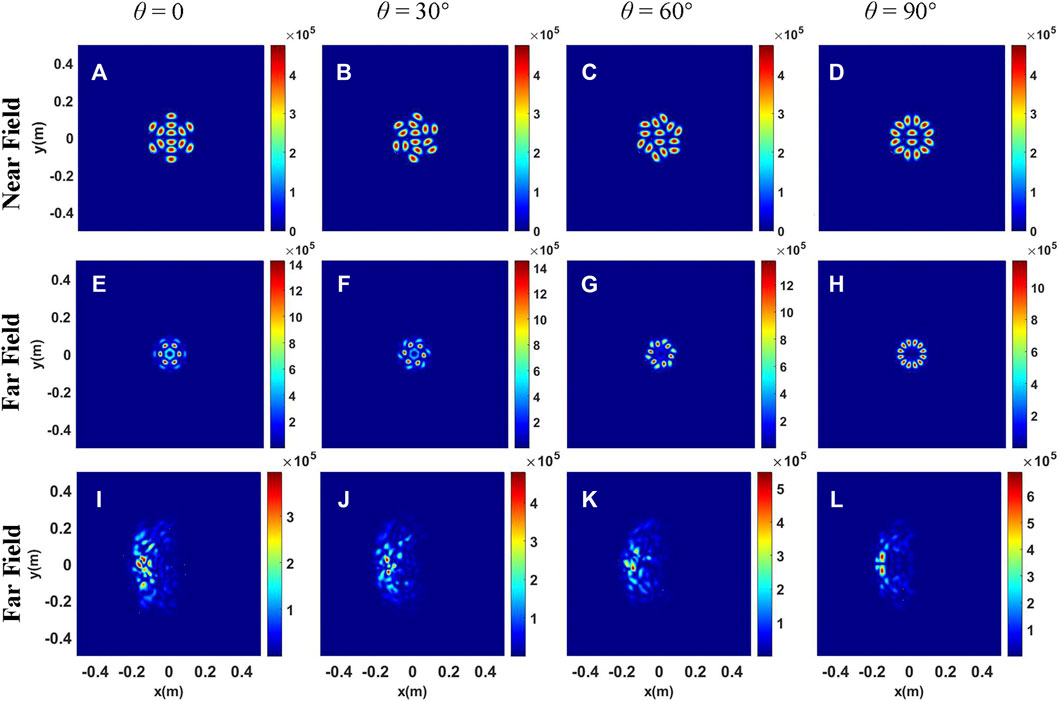
FIGURE 4. Intensity distributions of the LP₁₁ mode beam array with different rotation angles of beamlets. (A–D) Intensity distributions at the initial plane; (E–H) Intensity distributions at the receiver plane in free space; (I–L) Intensity distributions at the receiver plane under thermal blooming.

It is assumed that the directions of the central beamlet in Figures 3A–D are parallel to that of the wind and that in Figures 4A–D are vertical to that of the wind. Generally, the power of the bucket-based beam width is used to describe beam spreading and energy focusability, which is expressed as [55] ${\displaystyle {\int }_0^{w_{\eta }}Ir\text{d}r=}\eta {\displaystyle {\int }_0^{+\infty }Ir\text{d}r}$, where $w_{\eta }$ is the bucket half-width chosen. The beam width $w_{86.5\%}$ is adopted in this study. On the other hand, the beam centroid position is changed due to the effect of thermal blooming, which is defined as [55] $\overline{j}={\displaystyle \iint jI\text{d}x\text{d}y}/{\displaystyle \iint I\text{d}x\text{d}y}$, where j = x and y. The center of the bucket is taken as $\left(\overline{x},\overline{y}\right)$ in the following calculations. The changes of the beam width at the target for different values of rotation angles are shown in Figure 5. It can be seen that the value of beam width $w_{86.5\%}$ of the parallel direction is lower than that of the vertical direction. Thus, the beam focusability of the parallel direction is higher than that of the vertical direction. That means the thermal blooming becomes more severe for the vertical central beamlet arrangement, especially when θ = 20°. As the θ increases, the difference of the beam width $w_{86.5\%}$ between parallel and vertical directions decreases. Thus, the laser energy focusability can be controlled simply by rotating the central beam.

FIGURE 5

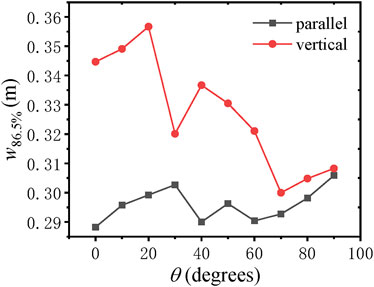
FIGURE 5. Variation of beam width w_86.5% with rotating angle θ for different arrangements of the central beamlet.

Here, we choose four arrangement types of initial beamlets (see Figures 6A–D) to investigate the influence of transverse wind speed on the energy focusability. As can be seen from Figure 6E, the beam width decreases and becomes closer as the wind speed increases. The physical reason is that the absorbed energy in the propagation path is carried away more quickly as the wind speed increases. That is to say, increasing the transverse wind speed can help increase the energy focusability. In addition, the beam width of Figure 6A is the largest for different values of wind speed. Thus, the arrangement of Figure 6A should be avoided in order to improve the energy focusability.

FIGURE 6

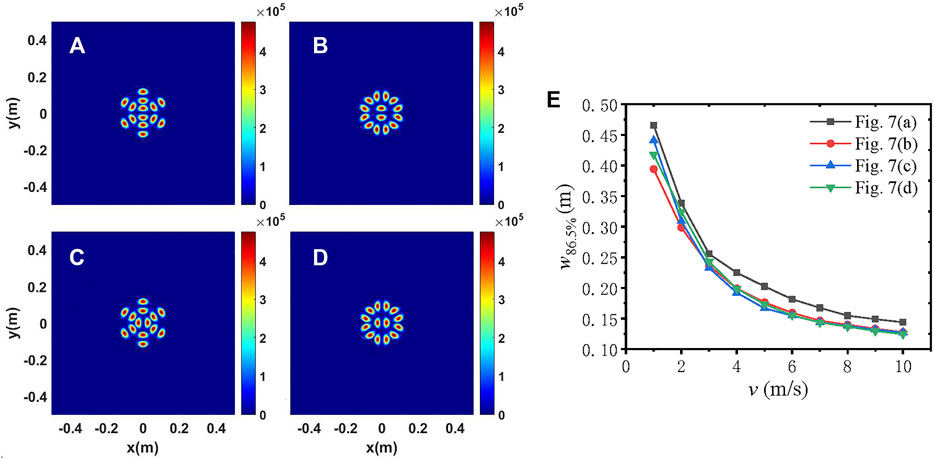
FIGURE 6. (A–D) Intensity distributions of the LP₁₁ mode beam array with different arrangement of beamlets; (E) variation of beam width w_86.5% with wind speed v.

Impact of Fundamental Mode Content on the HOM Beam Array

In practical applications, it is difficult to obtain the pure LP₀₁ mode even at relatively high conversion efficiency. Therefore, the case of the mixture of LP₀₁ and LP₁₁ modes is worth studying. Considering that the model superposition states comprise different admixtures of the LP₀₁ and LP₁₁ modes, the initial field can be expressed as

$E_{\text{mix}}={\displaystyle \sum _{l=1}^N\left\{\sqrt{A_{L{P}_{11}}}{E}_{11}^l\left[r^2+r_0^2+2r{r}_0\cos (\varphi -{\varphi }_l)\right]+\sqrt{1-A_{L{P}_{11}}}{E}_{01}^l\left[r^2+r_0^2+2r{r}_0\cos (\varphi -{\varphi }_l)\right]\right\}},(10)$

where $A_{L{P}_{11}}$ is the power fraction of the LP₁₁ mode and the value of $A_{L{P}_{11}}$ is $0\le A_{L{P}_{11}}\le 1$.

The intensity distributions of the mixed-mode beam array are shown in Figures 7–9. It can be seen from Figures 7–9 that in free space, as the content of the LP₀₁ mode increases, the energy is gradually concentrated from the side lobes to the center lobe. That is to say, the energy distribution between the central lobe and side lobes can be controlled by changing the content of the LP₀₁ mode. The difference in Figures 7–9 is that the initial arrangement of the outer-ring beamlets is different. As can be seen from Figure 7, the focal beam shape of the pure LP₁₁ mode beam array comprises six radial spots, and the energy is concentrated in the central lobe for the pure LP₀₁ mode beam array.

FIGURE 7

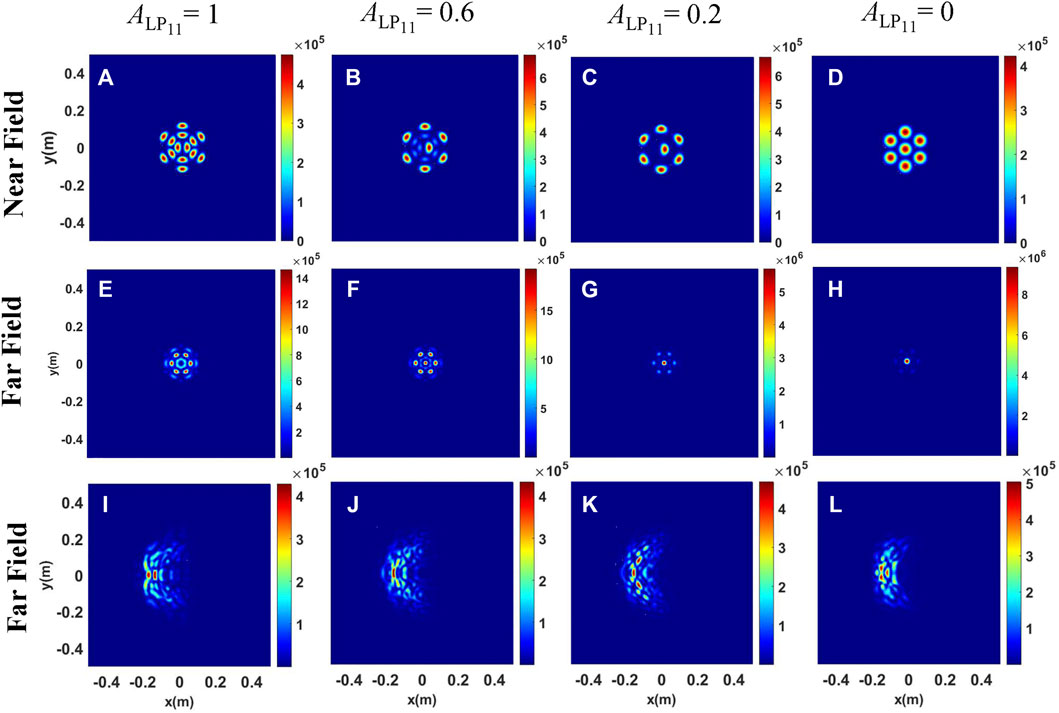
FIGURE 7. Intensity distributions of the mixed-mode beam array for different content of the LP₀₁ mode. (A–D) Intensity distributions at the initial plane; (E–H) Intensity distributions at the receiver plane in free space; (I–L) Intensity distributions at the receiver plane under the conditions of thermal blooming.

FIGURE 8

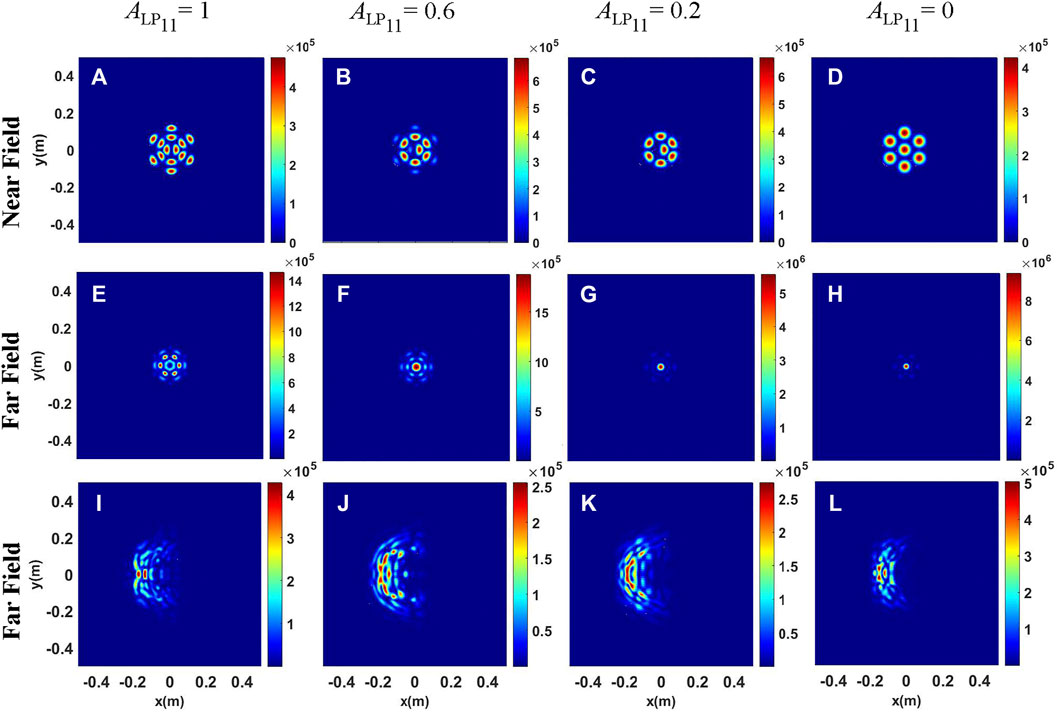
FIGURE 8. Intensity distributions of the mixed-mode beam array for different content of the LP₀₁ mode. (A–D) Intensity distributions at the initial plane; (E–H) Intensity distributions at the receiver plane in free space; (I–L) Intensity distributions at the receiver plane under the conditions of thermal blooming.

FIGURE 9

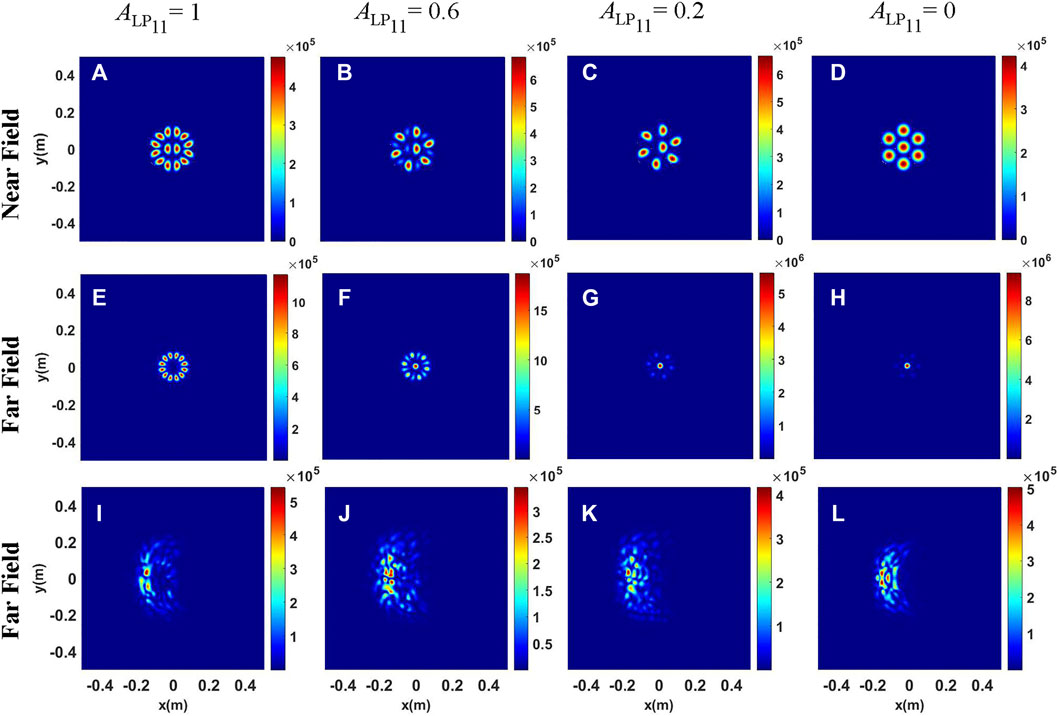
FIGURE 9. Intensity distributions of the mixed-mode beam array for different content of the LP₀₁ mode. (A–D) Intensity distributions at the initial plane; (E–H) Intensity distributions at the receiver plane in free space; (I–L) Intensity distributions at the receiver plane under the conditions of thermal blooming.

As we rotate the outer-ring beamlets 180 degrees on the basis of Figure 7, the intensity distributions of the mixed mode beam array under different conditions are shown in Figure 8. It can be clearly seen that when the mixed-mode beam array propagates in free space, the energy of the central lobe in Figure 8 is more concentrated than that in Figure 7. The physical reason is that the beam distribution at the initial plane is more compact in Figure 8. However, the intensity distributions under thermal blooming in Figure 8 are more dispersive than those in Figure 7. Thus, the arrangements of beamlets at the initial plane in Figure 7 are more resistant to the degrading effect of thermal blooming.

As we rotate the outer-ring beamlets 90 degrees on the basis of Figure 8, the intensity distributions of the mixed-mode beam array under different conditions are shown in Figure 9. As mentioned previously, the focal intensity distribution comprises 12 radial spots when the initial intensity distribution is shown in Figure 9A. However, the number of side lobes decreases as the content of the LP₀₁ mode increases, that is, the side lobes are six when the content of the LP₀₁ mode is 0.6. In order to compare the energy focusability under the three conditions more intuitively, the beam width $w_{86.5\%}$ versus the LP₀₁ fraction for different initial beamlet arrangements is investigated in Figure 10. It can be seen from Figures 10A–C that the beam width decreases as the wind speed increases. Thus, increasing the value of wind speed can be helpful in increasing energy focusability. On the other hand, the beam width in Figure 8 is the smallest under the same wind speed. Thus, the initial beamlet arrangements in Figure 8 can also be helpful in increasing energy focusability. In addition, the beam width in Figure 9 is smaller than that in Figure 10 when the wind speed is small. However, when the wind speed increases, the beam width in Figure 9 is larger than that in Figure 10. It indicates that compared with Figure 9, the effect of wind speed has a greater impact on the focusability of Figure 10.

FIGURE 10

FIGURE 10. Variation of beam width w_86.5% with LP₀₁ fraction for different values of wind speeds.

Conclusion

In this study, the propagation properties of high-power HOM beam arrays propagating in the atmosphere are studied in detail. Based on the multiphase screen method and finite-difference method, a 4D computer code of the HOM beam array propagating through the atmosphere under the conditions of thermal blooming is designed. In particular, the LP₁₁ mode is considered in this study. The propagation characteristics of the pure LP₁₁ mode beam array in free space and in the atmosphere are investigated. It has been found that the focal intensity distributions in free space are consistent with the arrangement of the second circle of the initial beam array. The desired beam shape of focusing spots can be obtained by rotating the surrounding beamlets. In addition, the arrangement of the central beamlet has little influence on the focal beam shapes in free space but has a significant effect on the focal beam shapes under the conditions of thermal blooming. Thus, the energy focusability can be improved by rotating the central beamlet. When the transverse wind speed increases, the thermal blooming effect decreases and the energy focusability increases. Moreover, the influence of the content of the LP₀₁ mode is investigated in this study, and three kinds of arrangement of the initial beam array are considered. The results show that as the content of the LP₀₁ mode increases, the energy is gradually concentrated from the side lobes to the center lobe. The energy ratio of the side lobes to the central lobe is related to the initial arrangement. Meanwhile, the energy distribution between the central lobe and side lobes can be controlled by changing the content of the LP₀₁ mode. The condition for obtaining high energy focusability has been discussed in detail. These results obtained in this study are useful for directed-energy applications in the atmosphere.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the study and approved it for publication.

Funding

National Natural Science Foundation of China (61705265), and Natural Science Foundation of Hunan province, China (2019JJ10005).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Dong L, Kong F, Gu G, Hawkins TW, Jones M, Parsons J, et al. Large-Mode-Area All-Solid Photonic Bandgap Fibers for the Mitigation of Optical Nonlinearities. IEEE J Select Top Quan Electron. (2016) 22(2):316–22. doi:10.1109/jstqe.2015.2451012

CrossRef Full Text | Google Scholar

2. Wang L, He D, Yu C, Feng S, Hu L, Chen D. Very Large-Mode-Area, Symmetry-Reduced, Neodymium-Doped Silicate Glass All-Solid Large-Pitch Fiber. IEEE J Select Top Quan Electron. (2016) 22(2):108–12. doi:10.1109/jstqe.2015.2427746

CrossRef Full Text | Google Scholar

3. Jeong Y, Sahu JK, Payne DN, Nilsson J. Ytterbium-doped Large-Core Fiber Laser with 1.36 kW Continuous-Wave Output Power. Opt Express (2004) 12(25):6088–92. doi:10.1364/opex.12.006088

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Venkatakrishnan K, Tan B. Generation of Radially Polarized Beam for Laser Micromachining. jlmn (2012) 7(3):274–8. doi:10.2961/jlmn.2012.03.0008

CrossRef Full Text | Google Scholar

5. Richardson DJ, Fini JM, Nelson LE. Space-division Multiplexing in Optical Fibres. Nat Photon (2013) 7(5):354–62. doi:10.1038/nphoton.2013.94

CrossRef Full Text | Google Scholar

6. Meier M, Romano V, Feurer T. Material Processing with Pulsed Radially and Azimuthally Polarized Laser Radiation. Appl Phys A (2007) 86(3):329–34. doi:10.1007/s00339-006-3784-9

CrossRef Full Text | Google Scholar

7. Liu Z, Wang L, Liang P, Zhang Y, Yang J, Yuan L. Mode Division Multiplexing Technology for Single-Fiber Optical Trapping Axial-Position Adjustment. Opt Lett (2013) 38(14):2617–20. doi:10.1364/ol.38.002617

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wang J. Advances in Communications Using Optical Vortices. Photon Res (2016) 4(5):B14–B28. doi:10.1364/prj.4.000b14

CrossRef Full Text | Google Scholar

9. Ramachandran S, Kristensen P, Yan MF. Generation and Propagation of Radially Polarized Beams in Optical Fibers. Opt Lett (2009) 34(16):2525–7. doi:10.1364/OL.34.002525

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Mao D, Li M, He Z, Cui X, Lu H, Zhang W, et al. Optical Vortex Fiber Laser Based on Modulation of Transverse Modes in Two Mode Fiber. APL Photon (2019) 4(6):060801. doi:10.1063/1.5094599

CrossRef Full Text | Google Scholar

11. Lin D, Daniel JMO, Gecevičius M, Beresna M, Kazansky PG, Clarkson WA. Cladding-pumped Ytterbium-Doped Fiber Laser with Radially Polarized Output. Opt Lett (2014) 39(18):5359–61. doi:10.1364/OL.39.005359

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Mao D, Zheng Y, Zeng C, Lu H, Wang C, Zhang H, et al. Generation of Polarization and Phase Singular Beams in Fibers and Fiber Lasers. Adv Photon (2021) 3(1):014002. doi:10.1117/1.Ap.3.1.014002

CrossRef Full Text | Google Scholar

13. Lin D, Carpenter J, Feng Y, Jain S, Jung Y, Feng Y, et al. Reconfigurable Structured Light Generation in a Multicore Fibre Amplifier. Nat Commun (2020) 11(1):3986. doi:10.1038/s41467-020-17809-x

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Liu T, Chen S, Qi X, Hou J. High-power Transverse-Mode-Switchable All-Fiber Picosecond MOPA. Opt Express (2016) 24(24):27821–7. doi:10.1364/oe.24.027821

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wang S, Zhang M, Wang H, Hu G. Single- and Dual-Wavelength Fiber Laser with Multi-Transverse Modes. Opt Express (2021) 29(13):20299–306. doi:10.1364/oe.430258

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Li H, Zhang Y, Dong Z, Lv J, Gu C, Yao P, et al. A High‐Efficiency All‐Fiber Laser Operated in High‐Order Mode Using Ring‐Core Yb‐Doped Fiber. Annalen Der Physik (2019) 531(10):1900079. doi:10.1002/andp.201900079

CrossRef Full Text | Google Scholar

17. Lv J, Li H, Zhang Y, Tao R, Dong Z, Gu C, et al. Few-mode Random Fiber Laser with a Switchable Oscillating Spatial Mode. Opt Express (2020) 28(26):38973. doi:10.1364/oe.412234

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Su R, Yang B, Xi X, Zhou P, Wang X, Ma Y, et al. 500 W Level MOPA Laser with Switchable Output Modes Based on Active Control. Opt Express (2017) 25(19):23275–81. doi:10.1364/oe.25.023275

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sun B, Wang A, Xu L, Gu C, Lin Z, Ming H, et al. Low-threshold Single-Wavelength All-Fiber Laser Generating Cylindrical Vector Beams Using a Few-Mode Fiber Bragg Grating. Opt Lett (2012) 37(4):464–6. doi:10.1364/OL.37.000464

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Huang Y, Shi F, Wang T, Liu X, Zeng X, Pang F, et al. High-order Mode Yb-Doped Fiber Lasers Based on Mode-Selective Couplers. Opt Express (2018) 26(15):19171–81. doi:10.1364/oe.26.019171

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Huang P, Cai Y, Wang J, Wan H, Zhang Z, Zhang L. Multiwavelength Mode-Locked Cylindrical Vector Beam Fiber Laser Based on Mode Selective Coupler. Laser Phys Lett (2017) 14(10):105103. doi:10.1088/1612-202X/aa82cd

CrossRef Full Text | Google Scholar

22. You Y, Bai G, Zou X, Li X, Su M, Wang H, et al. A 1.4-kW Mode-Controllable Fiber Laser System. J Lightwave Technol (2021) 39(8):2536–41. doi:10.1109/jlt.2021.3049603

CrossRef Full Text | Google Scholar

23. Zhou P, Liu Z, Wang X, Ma Y, Ma H, Xu X, et al. Coherent Beam Combining of Fiber Amplifiers Using Stochastic Parallel Gradient Descent Algorithm and its Application. IEEE J Select Top Quan Electron. (2009) 15(2):248–56. doi:10.1109/jstqe.2008.2010231

CrossRef Full Text | Google Scholar

24. Fan TY. Laser Beam Combining for High-Power, High-Radiance Sources. IEEE J Select Top Quan Electron. (2005) 11(3):567–77. doi:10.1109/jstqe.2005.850241

CrossRef Full Text | Google Scholar

25. Brignon A. Coherent Laser Beam Combining. Weinheim, Germany: Wiley VCH (2013).

Google Scholar

26. Goodno GD, Asman CP, Anderegg J, Brosnan S, Cheung EC, Hammons D, et al. Brightness-scaling Potential of Actively Phase-Locked Solid-State Laser Arrays. IEEE J Select Top Quan Electron. (2007) 13(3):460–72. doi:10.1109/jstqe.2007.896618

CrossRef Full Text | Google Scholar

27. Hou T, Zhang Y, Chang Q, Ma P, Su R, Wu J, et al. High-power Vortex Beam Generation Enabled by a Phased Beam Array Fed at the Nonfocal-Plane. Opt Express (2019) 27(4):4046–59. doi:10.1364/oe.27.004046

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yu CX, Augst SJ, Redmond SM, Goldizen KC, Murphy DV, Sanchez A, et al. Coherent Combining of a 4 kW, Eight-Element Fiber Amplifier Array. Opt Lett (2011) 36(14):2686–8. doi:10.1364/ol.36.002686

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ma P, Chang H, Ma Y, Su R, Qi Y, Wu J, et al. 7.1 kW Coherent Beam Combining System Based on a Seven-Channel Fiber Amplifier Array. Opt Laser Technology (2021) 140:107016. doi:10.1016/j.optlastec.2021.107016

CrossRef Full Text | Google Scholar

30. Müller M, Aleshire C, Klenke A, Haddad E, Légaré F, Tünnermann A, et al. 104 kW Coherently Combined Ultrafast Fiber Laser. Opt Lett (2020) 45(11):3083–6. doi:10.1364/ol.392843

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Shekel E, Vidne Y, Urbach B. 16kW Single Mode CW Laser with Dynamic Beam for Material Processing. In: Proc. SPIE. L Dong, editor. San Diego, CA: SPIE (2020). doi:10.1117/12.2545900

CrossRef Full Text | Google Scholar

32. Fsaifes I, Daniault L, Bellanger S, Veinhard M, Bourderionnet J, Larat C, et al. Coherent Beam Combining of 61 Femtosecond Fiber Amplifiers. Opt Express (2020) 28(14):20152–61. doi:10.1364/oe.394031

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Chang H, Chang Q, Xi J, Hou T, Su R, Ma P, et al. First Experimental Demonstration of Coherent Beam Combining of More Than 100 Beams. Photon Res (2020) 8(12):1943–8. doi:10.1364/PRJ.409788

CrossRef Full Text | Google Scholar

34. Zhan Q. Cylindrical Vector Beams: from Mathematical Concepts to Applications. Adv Opt Photon (2009) 1(1):1–57. doi:10.1364/aop.1.000001

CrossRef Full Text | Google Scholar

35. Hou T, An Y, Chang Q, Ma P, Li J, Huang L, et al. Deep-learning-assisted, Two-Stage Phase Control Method for High-Power Mode-Programmable Orbital Angular Momentum Beam Generation. Photon Res (2020) 8(5):715–22. doi:10.1364/prj.388551

CrossRef Full Text | Google Scholar

36. Kurti RS, Halterman K, Shori RK, Wardlaw MJ. Discrete Cylindrical Vector Beam Generation from an Array of Optical Fibers. Opt Express (2009) 17(16):13982–8. doi:10.1364/oe.17.013982

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Yu T, Xia H, Xie W, Xiao G, Li H. The Generation and Verification of Bessel-Gaussian Beam Based on Coherent Beam Combining. Results Phys (2020) 16:102872. doi:10.1016/j.rinp.2019.102872

CrossRef Full Text | Google Scholar

38. Chu X, Liu Z, Zhou P. Generation of a High-Power Airy Beam by Coherent Combining Technology. Laser Phys Lett (2013) 10(12):125102. doi:10.1088/1612-2011/10/12/125102

CrossRef Full Text | Google Scholar

39. Spencer MF. Wave-optics Investigation of Turbulence thermal Blooming Interaction: I. Using Steady-State Simulations. Opt Eng (2020) 59(8):1. doi:10.1117/1.Oe.59.8.081804

CrossRef Full Text | Google Scholar

40. Gebhardt FG. High Power Laser Propagation. Appl Opt (1976) 15(6):1479–93. doi:10.1364/ao.15.001479

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Schoen NC, Novoseller DE. Multiple Aperture Laser Systems for thermal Blooming Environments. Appl Opt (1983) 22(21):3366–70. doi:10.1364/AO.22.003366

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Gebhardt FG. Twenty-five Years of thermal Blooming: an Overview. In: Proc. SPIE (1990). doi:10.1117/12.18326

CrossRef Full Text | Google Scholar

43. Fleck JA, Morris JR, Feit MD. Time-dependent Propagation of High Energy Laser Beams through the Atmosphere. Appl Phys (1976) 10(2):129–60. doi:10.1007/BF00896333

CrossRef Full Text | Google Scholar

44. Ji X, Eyyuboğlu HT, Ji G, Jia X. Propagation of an Airy Beam through the Atmosphere. Opt Express (2013) 21(2):2154–64. doi:10.1364/oe.21.002154

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Vorob'ev VV, Murav'ev NI, Sorokin YM, Shemetov VV. Thermal Self-Interaction of Annular Laser Beams in a Moving Medium. Sov J Quan Electron. (1977) 7(11):1333–6. doi:10.1070/qe1977v007n11abeh004119

CrossRef Full Text | Google Scholar

46. Ding Z, Li X, Cao J, Ji X. Influence of thermal Blooming on the Beam Quality of an Array of Hermite-Gaussian Beams Propagating in the Atmosphere. Appl Opt (2020) 59(34):10944–52. doi:10.1364/ao.405980

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Zhao L, Wang J, Guo M, Xu X, Qian X, Zhu W, et al. Steady-state thermal Blooming Effect of Vortex Beam Propagation through the Atmosphere. Opt Laser Technology (2021) 139:106982. doi:10.1016/j.optlastec.2021.106982

CrossRef Full Text | Google Scholar

48. Zhang Y, Hou T, Chang H, Su R, Ma P, Zhou P. Thermal Blooming Effect and the Scaling Laws of Partial Spatially Coherent Beam Array Propagating through the Atmosphere. Results Phys (2021) 26:104444. doi:10.1016/j.rinp.2021.104444

CrossRef Full Text | Google Scholar

49. Spencer MF, Hyde MW. Phased Beam Projection from Tiled Apertures in the Presence of Turbulence and thermal Blooming. In Proc. SPIE (2013). doi:10.1117/12.2022666

CrossRef Full Text | Google Scholar

50. Li X, Cao J, Ding Z, Ji X. Influence of Fill Factors on the thermal Blooming of Array Laser Beams in the Air. Optik (2019) 182:314–23. doi:10.1016/j.ijleo.2018.12.161

CrossRef Full Text | Google Scholar

51. Banakh VA, Falits AV. Numerical Simulation of Propagation of Laser Beams Formed by Multielement Apertures in a Turbulent Atmosphere under thermal Blooming. Atmos Ocean Opt (2013) 26(6):455–65. doi:10.1134/S102485601306002X

CrossRef Full Text | Google Scholar

52. Yoda H, Polynkin P, Mansuripur M. Beam Quality Factor of Higher Order Modes in a Step-index Fiber. J Lightwave Technol (2006) 24(3):1350–5. doi:10.1109/jlt.2005.863337

CrossRef Full Text | Google Scholar

53. Snyder AW, Love JD. Optical Waveguide Theory. London, New York: Boston: Springer MA Press (1983).

Google Scholar

54. Zhang Y, Ji X, Li X, Li Q, Yu H. Self-focusing Effect of Annular Beams Propagating in the Atmosphere. Opt Express (2017) 25(18):21329–41. doi:10.1364/oe.25.021329

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Sean Ross T. Laser Beam Quality Metrics. Bellingham: SPIE Press (2013).

Google Scholar