Entangled Biphoton Enhanced Double Quantum Coherence Signal as a Probe for Cavity Polariton Correlations in Presence of Phonon Induced Dephasing

We theoretically propose a biphoton entanglement-enhanced multidimensional spectroscopic technique as a probe for the dissipative polariton dynamics in the ultrafast regime. It is applied to the cavity-confined monomeric photosynthetic complex that represents a prototypical multi-site excitonic quantum aggregate. The proposed technique is shown to be particularly sensitive to inter-manifold polariton coherence between the two and one-excitation subspaces. It is demonstrated to be able to monitor the dynamical role of cavity-mediated excitonic correlations, and dephasing in the presence of phonon-induced dissipation. The non-classicality of the entangled biphoton sources is shown to enhance the ultra-fast and broadband correlation features of the signal, giving an indication about the underlying state correlations responsible for long-range cavity-assisted exciton migration.

1 Introduction

The quantum aggregates consisting of multiple centers of electronic excitations, e.g., the naturally occurring light-harvesting photosynthetic complexes, artificially designed molecular light-harvesters offer a uniquely favorable testing ground for the entangled photon-induced dynamics. These systems intrinsically host collective excitations, frequently termed as molecular excitons, extending over several excitation centers/sites and often within the coherence domain of the spatial (temporal) length (time) scales. Thus, it provides opportunities for the external modulation of delocalized excitons and testing the limits of coherent dynamics. Further, the vibrational motions associated with these structures often give rise to a collective dephasing mechanism for the delocalized excitons. Additionally, the vibrational motions modulate the energy gradient of the kinetics, leading to situations where coherent excitons undergo inter-site transport and eventually localize. The spectroscopic investigation and control of such exciton kinetics offers insights into the microscopic nature of the coherent energy transfer mechanism and prescribes guidelines for bio-mimetic engineering which builds on the operational equivalence [1–6]. In a separate line of development, there have been a series of studies that have demonstrated the effective role of external electromagnetic cavities in manipulating material excitations. These studies range from the control of electronic excitations [7–16], vibrational modes [17, 18], collective mode responses [19, 20] to the cavity mode-assisted modulation of dynamical resonances [21–25]. Cavity mode interacting resonantly with narrow-band of excitons and off-resonantly with the rest may modulate the excitation dispersal by tuning the delocalization properties and influence the dephasing properties via the spectral weight modulation [26–28]. Hence, combining these two developments to the case of light-harvesting quantum aggregates offers an opportunity to investigate the role of the cavity in controlling a prototypical, extended yet aperiodic system that hosts collective excitons.

Previous spectroscopic studies of the cavity-modulated dynamics [29–35] have increasingly focused their attention on the ultrafast, nonlinear techniques analogs e.g. pump-probe here. In the majority of these studies, participation of the higher-order excitations remain relatively unexplored. The dynamics involving the higher-order nonlinear excitations introduce possibilities for cavity-modulated exciton-exciton annihilation, cavity-assisted exciton fusion, and many more correlated mechanisms of practical interest. On a fundamental level, the external dielectric modification of the Coulomb interaction between different excitons underlies all of these coherent mechanisms. However, the nonlinear spectroscopic signatures studied so far depend dominantly on the associated vibrational (or vibronic) processes [37, 38]. Therefore, in order to explore the complexity of cavity-modulated nonlinear exciton dynamics, it is desirable to combine ultrafast spectroscopic tools that are sensitive to high-order exciton correlations in the presence of collective vibrational dephasing. Among the multi-pulse nonlinear spectroscopic techniques available for mapping out the correlation between two excitons and probing the two-exciton state-specific dephasing in the ultrafast regime, double-quantum multidimensional correlation spectra (DQC) have been proven useful [39–42]. The ultrafast nature of the exciton dynamics in aggregates results in difficulty in measuring the role of energetically-distant states even without the presence of the cavity mode. These delocalized multi-exciton states often participate in dynamics within the same timescale due to dynamical dephasing properties. Associated with the normal exciton-number conserving dephasing process, one encounters a dephasing mechanism that couples the energy-manifolds with the different number of excitons. The presence of cavity adds additional cavity-exciton hybrid states, introduces multiple dynamical timescales, and gives rise to novel cavity-exciton-phonon coupling mechanisms. These excitations are of principal interest in this communication. The investigation of them requires the deployment of probes that specifically excite spectrally narrow-band states (creation of non-linear polarization), allow the associated dynamics to evolve in time in the presence of dephasing (evolution of the polarization), and project them to desired frequency components of interest (projection of polarization to signal components). Robust, correlated state excitation can be controllably achieved by deploying the entangled photon pairs, namely entangled biphotons, via a scheme being referred to as entangled two-photon absorption [43–47]. In comparison to the shaped laser pulses, the entangled biphotons have been shown to improve the spectral resolution while scaling favorably with the intensity of the sources. The non-classical correlation properties can also be utilized to obtain favorable spectral-temporal resolution in the probing via selective state projections of the nonlinear polarization [29, 33, 48–55]. The latter requires the selection of a few states whose correlation properties are of particular interest from a manifold. In this regard, a combination of the aforementioned DQC signal measurement scheme with the entangled photon sources may provide a technique that studies cavity-modulated correlated exciton kinetics in the ultrafast regime with higher spectral resolution.

In what follows, in Section 2, we introduce the Frenkel exciton Hamiltonian and describe the underlying model. It will be used to describe the dissipative exciton-polariton phenomenology and obtain the relevant Green’s functions. Subsequently, in Section 2 we introduce the DQC signal in a modular manner, discuss the nature of the signal and present the simulation results in the relevant parameter regime. Section 4 discusses limitations, the scope of the presented signal within the broader scope of entangled photon-enhanced spectroscopies, and the outlook.

2 Dissipative Exciton-Polariton Phenomenology

Here we present the exciton Hamiltonian concurrently interacting with a cavity mode and the phonon reservoir, which will be used to build up the phenomenology using a quasi-particle picture. It is given by,

$\begin{array}{ll}\hfill H& =\sum _{m,n=1}^{N_s}\left(E_m{\delta }_{mn}+J_{mn}\right)B_m^{†}{B}_n+\sum _{m,n=1}^{N_s}\frac{U_m^{\left(2\right)}}{2}{B}_m^{†}{B}_m^{†}{B}_m{B}_m+\frac{U_{mn}^{\left(2\right)}}{2}{B}_m^{†}{B}_n^{†}{B}_m{B}_n\hfill \\ \hfill & +\sum _{\alpha }{\omega }_c\left(a_{\alpha }^{†}{a}_{\alpha }+1/2\right)+\sum _{m,\alpha }{g}_{c,m,\alpha }\left(a_{\alpha }{B}_m^{†}+a_{\alpha }^{†}{B}_m\right)+\sum _j{\omega }_j\left(b_j^{†}{b}_j+\frac{1}{2}\right)+\sum _{m,j}{g}_{m,j}\left(b_j^{†}+b_j\right)B_m^{†}{B}_m\hfill \end{array}(1)$

where we set the ℏ to unity. The components of the Hamiltonian are explained below.

2.1 Exciton, Cavity and Exciton-Cavity Interactions

The first three terms constitute the bare exciton Hamiltonian where $B_m(B_m^{†})$ are the m-th site exciton creation (annihilation) operators with the respective commutation relation, $[B_m,B_n]=[B_m^{†},B_n^{†}]=0$ and $[B_m,B_n^{†}]={\delta }_{mn}(1-(2-{\kappa }_m^2))B_m^{†}{B}_m^{†}$) (where κ_m = μ₂₁/μ₁₀, is given in terms of ratio of transition dipoles of ij-th level of the m-th site) [56–58]. $E_m^{(1)}$ is the on-site excitation energies and J_mn is the inter-site Coulomb-mediated hopping. The presence of the interacting terms in the exciton Hamiltonian indicates that the single and two exciton states are delocalized over sites. The two-excitation manifold which is composed of permutable composition of pure local and non-local two-exciton, pure two cavity excitations and joint one exciton-one photon excitation is given by, $H_{\mathit{mnkl}}^{(2)}=H_{mn}^{(1)}{\delta }_{kl}+{\delta }_{mn}{H}_{kl}^{(1)}$. The terms $U_m^{(1)},U_{mn}^{(2)}$ further dictates the interaction among higher-order excitonic states which gives rise to static, local energy shifts, exciton-exciton scattering. The values of $U_m^{(1)}$ is taken as $U_m^{(1)}=2({\kappa }_n^{-2}{E}_n^{(2)}-E_n^{(1)})$, with κ = μ₂₁/μ₁₀ which accounts for the local energy shifts for two-exciton states and $U_{mn}^{(2)}=0$. Bare two-exciton energy is given by $E_m^{(2)}=2E_m^{(1)}+{\mathrm{\Delta }}_m$ (where the Δ_m is the two-exciton state anharmonicity from the Harmonic limit). The parameter values for the Hamiltonian are obtained from the semi-empirical simulation in [59–62] where these data-set have been shown to simultaneously fit the spectral data obtained from the linear absorption, fluorescence, and circular dichroism spectra. The combined cavity and the cavity-exciton interaction Hamiltonian is be given by the fourth and fifth term where the g_c;m,α is the cavity-exciton coupling strengths describing the resonant dipolar interaction. The effects arising from the non-resonant cavity-exciton interaction could be significant in the static limit if the exciton-cavity coupling strengths are comparable to the bare Rabi frequencies of the multi-exciton system [63–66]. The cavity-exciton parameter considered in this communication corresponds to moderately weak and within the close to resonant regime which allows this term being neglected. The cavity photonic modes are described in the oscillator basis with the corresponding creation (annihilation) operators denoted as $a_{\alpha }^{†}(a_{\alpha })$, for the α-th mode. Within the scope of this study, a single-mode limit (i.e. α = 1) and two-excitation per-mode (with he fundamental frequency denoted by ω_c) has been considered. Furthermore, we assume an uniform cavity-exciton coupling strengths for all sites, i.e. g_c;m,α = g_c = 100cm⁻¹ is independent of index m, although the analysis presented is not limited by that choice. We note that a detailed estimation of the cavity-exciton couplings requires investigation regarding the mode volume of the cavity and the quality factor which is beyond the scope of the article. The Coulombic origin inter-site hopping in the Hamiltonian is of different magnitude, indicating a different propensity for delocalization in the absence of cavity interaction. The cavity coupling modulates site-delocalization at different extents for one-exciton, local and non-local two-excitons. This gives rise to the possibility of creating a different admixture of cavity-matter excitations. In addition, it offers cavity mediates coupling between these configurations, thereby coupling diverse sets of excitations and inter-site processes. Since the cavity accommodates two-photon excitations, the analysis is capable of describing resonant two-polariton processes.

2.2 Phonon and Exciton-Phonon Interactions

The exciton-phonon interactions originate from the inter and intra-molecular vibrational motions associated with the relative nuclear motions of the aggregate. Normal modes of the low-energy vibrational degrees of freedom related to the collective vibrational coordinates are assigned as phonon modes and are mapped onto an infinite set of Harmonic oscillators. It is given by the free phonon Hamiltonian appearing in the sixth term where υ_k is the mode frequency associated with the k-th normal mode whose creation (annihilation) operators are denoted via $b_j^{†}(b_j)$. The phonon operators follow the free-boson commutation relations, $[b_j,b_{j^{\prime }}]=[b_j^{†},b_{j^{\prime }}^{†}]=0$ and $[b_j,b_{j^{\prime }}^{†}]={\delta }_{j{j}^{\prime }}$. The seventh term presenting the exciton-phonon interactions is taken in the site-uncorrelated, local form and is characterized by the distribution of the corresponding coupling functions, ${\bar{g}}_{m,j}$. These phonon modes are responsible for exciton dephasing, relaxation and exciton-transport phenomena. The extent of these phenomena are governed by the site-dependent exciton-phonon coupling strengths g_m,j which are taken as 1 (1.4) for the sites identified to represent Chl-A (Chl-b). While constructing the two-exciton phonon interaction Hamiltonian these coupling strengths are taken as 0.6 (g_m,j + g_n,j). Due to the differential coupling strengths, the excitations undergo dephasing at different rates, the one and two-exciton transport occur to a different extent over the sites leading to time-windowed interferences at a broader energy window. The inter-band dephasing, a quantity of particular interest in this article has contributions from the elements of the relaxation tensor that also participates in the cavity mediated one-exciton and two-exciton transport. Within this model, the single and the double excitons are coupled to a common set of phonon modes which can be characterized by the discrete distribution function, $J_0(\omega )=\pi {\sum }_j|{\bar{g}}_j{|}^2(\delta (\omega -{\upsilon }_j)-\delta (\omega +{\upsilon }_j))$ from which the spectral density function is obtained in the continuum frequency limit. The spectral density function, presented as, $J(\omega )=2{\lambda }_0({\gamma }_0\omega )/({\omega }^2+{\gamma }_0^2)+{\sum }_{j=1}^{N_b}2{\lambda }_j({\upsilon }_j^2{\gamma }_j\omega )/({({\upsilon }_j^2-{\omega }^2)}^2+{\omega }^2{\gamma }_j^2)$ describes N_b = 48 multi-mode Brownian oscillator modes and one over-damped oscillator mode. The number of multi-mode Brownian oscillators (N_b), the respective spectral shift parameters (λ₀, λ_j = υ_jϒ_j where υ_j and ϒ_j are the j-th oscillator frequencies and Huang-Rhys parameters respectively), and the damping parameter (γ₀, γ_j) which are required to optimally describe the equilibrium spectral density function have been obtained from the work of [35, 59–61]. The numerical values corresponding to those parameters are enlisted in Appendix A2.

2.3 Polariton Manifolds

The polariton states are obtained as number-conserving manifolds via exact-diagonalization of the field-free Hamiltonian subspaces, ${\tilde{H}}_p^{(n)}={\tilde{H}}_s+{\tilde{H}}_c+{\tilde{H}}_{sc}$ by using $T_p^{(n),-1}{\tilde{H}}_p^{(n)}{T}_p^{(n)}=H_p^{(n)}={\sum }_{n=0,1,2}{E}_{p^{(n)}}{X}_{p^{(n)}{p}^{(n)}}$, where we define operators $X_{p^{(n)}{p}^{(n)}}=\left|p^{(n)}\right.⟩\left.⟨p^{(n)}\right|$ as projectors onto the eigenstates of the polariton Hamiltonian $H_p^{(n)}$ (denoted by index n). The three distinct manifolds thus obtained corresponds to ground n = 0, single n = 1 and double n = 2 polariton manifolds with $N_{p^{(0)}}=1$, $N_{p^{(1)}}=15$, $N_{p^{(2)}}=120$ polariton states respectively (Figure 1). The manifolds are composed of the cluster of states which depend on an interplay of the hopping and cavity coupling parameters. The proposed spectroscopic technique utilizing entangled biphotons, in the parameter regime of interest, interact only via two-quantum interactions, which allows the joint-excitation manifold to be truncated at the level of the double polaritons. For the simulation, we have chosen the cavity mode frequency and the coupling strength parameters as ω_c (cm⁻¹) = 15.4 × 10³ and g_c (cm⁻¹) = 0.1 × 10³. The cavity frequency is resonant with the narrow frequency band around the frequency and off-resonant with the rest of the cluster of states in the bare absorption spectra of the excitonic system. The cavity coupling results in the polariton states to encompass a wider range than the cavity-free counterpart with the close-to-resonance states becoming affected to a greater degree. It can also be noted that the two-polariton states accommodate more states within the comparable bandwidth which is determined by the cavity coupling parameter. These two observations, combined, affirm that the exciton-cavity hybridization dominantly takes around the resonances, as expected. The spectral weights of the resultant delocalized polariton states have respective contributions from both the exciton and cavity modes, as determined by the exciton-cavity coupling matrix elements.

FIGURE 1

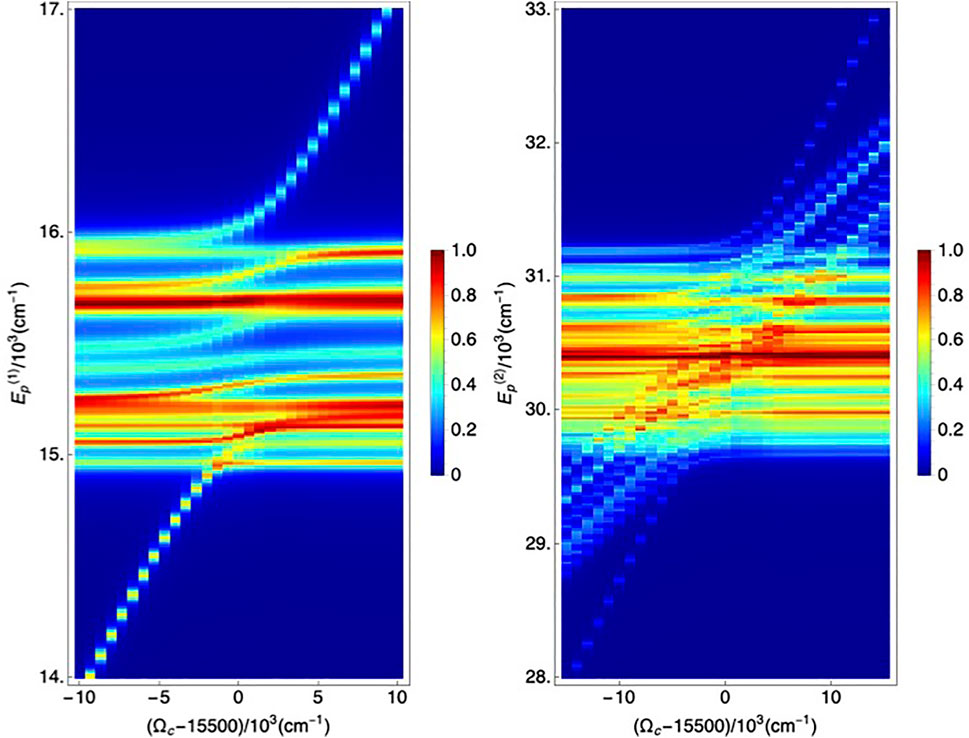
FIGURE 1. The progression of dephasing-broadened bare polariton band with the cavity frequencies and a fixed value of cavity coupling strength are presented. For the dephasing a representative set of values (generated from a random Gaussian distribution of mean and variance of μ₁ = 25, σ₁ = 10 and μ₂ = 35 respectively) are chosen for clarity. In the displayed one-polariton (left panel) and the two-polariton band (right panel), the increase in the density of states in the latter within a comparable energy-window (e.g., $\approx 10,\times ,10^3{\mathrm{c}\mathrm{m}}^{-1}$) is noticeable. The fundamental cavity frequencies along the x-axis are given in terms of detuning from the central region of the one-polariton band.

2.4 Polariton-Laser Interactions

The interaction between the external field i.e. biphoton sources and polaritons are treated within the optical dipolar interaction limit and within the rotating wave approximation. Corresponding Hamiltonian is given by,

$H_{\text{int}}\left(t\right)=\sum _j\sum _{n,n^{\prime }=\mathrm{0,1,2};n\ne n^{\prime }}\left(\sqrt{2\pi {\omega }_j/V}\right)a_j{e}^{-i{\omega }_{j}t}{d}_{p^{\left(n\right)}{p}^{\left(n^{\prime }\right)}}{X}_{p^{\left(n\right)}{p}^{\left(n^{\prime }\right)}}\exp \left(i{\omega }_{p^{\left(n^{\prime }\right)}{p}^{\left(n\right)}}t\right)+\mathrm{h}.\mathrm{c}.(2)$

where external photon mode creation operators a_j and dipole-weighted inter-manifold polariton transition operators, $X_{p^{(n)}{p}^{(n^{\prime })}}$ were defined. Also, the mode quantization volume V and the Fourier expansion frequency ω_j for the photon modes have been introduced. These operators will be used to derive the signal expressions in the next sections. It is notable that in the spirit of the weak laser driving limit suitable for spectroscopy only the one-photon transition operators had been employed.

2.5 Phonon Induced State Broadening and Polariton Green’s Functions

In this section, we introduce the framework to obtain the state-dependent dephasing timescales and obtain the polariton Green’s functions required for the signal expressions. It is carried out by seeking an integral solution of the generalized master equation (written in the multi-polariton basis) obtained in the Markovian and the secular limit (often termed as the Redfield equation). The secular approximation limits the polariton-phonon mode interactions to be describable within the resonant cases only. The latter suffices our treatment of acoustic phonons mediate interactions are mediated by displacive perturbations of exciton states simultaneously dressed by the cavity interactions that are comparatively much stronger. The kinetic equation is given by, ${\dot{\sigma }}^{(n)}(t)=-i{L}_S^{(n)}{\sigma }^{(n)}(t)+{\int }_0^{\infty }d\tau {\mathrm{\Sigma }}^{(n)}(t,\tau ){\sigma }^{(n)}(t)$ where we denote σ⁽ⁿ⁾ as number resolved reduced multi-polariton density operator. We defined the super-operator as, $L_s^{(n)}O=[H_p^{(n)},O]$. The polariton-phonon memory kernel capable of describing the phonon-induced polariton relaxation and dephasing (neglecting the effects of the driving field on the relaxation) is given by, ${\mathrm{\Sigma }}^{(n)}(t,\tau ){\sigma }^{(n)}(t)=-{\lambda }^2\left[X,D(t){\sigma }_s(t)-{\sigma }_s(t)D^{†}(t)\right]$. The kernel contains the dissipation operator D(t) = X (t − t′)C_b(t − t′) where we have the convolution of polariton-phonon coupling operator $X(\tau )={\sum }_{p^{(n)}}{X}_{p^{(n)}{p}^{(n)}}(\tau )$ and time-domain correlation function given by,

$\begin{array}{ll}\hfill C_b\left(\tau \right)& =\left({\lambda }_0{\gamma }_0/2\right)\cot \left(\beta {\gamma }_0/2\right)\exp \left(-{\gamma }_0\tau \right)+\sum _{j=1}^{N_b}\frac{{\lambda }_j}{2{\zeta }_j}\left(\coth \left(i\beta {\varphi }_j^{+}/2\right)\exp \left(-{\varphi }_j^{+}\tau \right)-\coth \left(i\beta {\varphi }_j^{-}/2\right)\exp \left(-{\varphi }_j^{-}\tau \right)\right)\hfill \\ \hfill & +\left(-i{\lambda }_0{\gamma }_0/2\right)\exp \left(-{\gamma }_0\tau \right)+\frac{i{\lambda }_j{\upsilon }_j^2}{2{\zeta }_j}\left(\exp \left(-{\varphi }_j^{+}t\right)-\exp \left(-{\varphi }_j^{-}t\right)\right)-\sum _{n=1}^{\infty }\left(\left(4{\lambda }_j{\gamma }_j{\upsilon }_j^2/\beta \right)\left({\nu }_n/{\left({\upsilon }_j^2+{\nu }_n^2\right)}^2-{\nu }_n^2{\gamma }_j^2\right)\right.\hfill \\ \hfill & +\left.\left(2{\lambda }_0{\gamma }_0/\beta \right)\left({\nu }_n/\left({\nu }_n^2-{\gamma }_0^2\right)\right)\right)\exp \left(-i{\nu }_n\tau \right)\hfill \end{array}(3)$

In the above we have ${\zeta }_j=\sqrt{({\upsilon }_j^2-{\gamma }_j^2/4)}$, ${\varphi }_j^{\pm }=({\gamma }_j/2)\pm i{\zeta }_j$, and, matsubara frequencies, ν_n = n (2π/β) (with n_m = 20). Furthermore, we defined β = 1/κT where the Boltzmann constant κ and temperature T is denoted. The energy domain version of the relaxation kernel was used to extract the dephasing parameters. We define the line-broadening functions as, ${\gamma }_{p_1^{(n)}}(t)=\theta (t){\sum }_{p_2,p_s}{C}_b({\omega }_{p_1{p}_2})T_{p_s{p}_2}^{(n)}{T}_{p_s{p}_2}^{(n)}{T}_{p_s{p}_1}^{(n)}{T}_{p_s{p}_1}^{(n)}$ where we have C_b(Ω) = ∫dt exp iΩtC^±(t) and $C_b^{\pm }(t)=\int (d\omega /2\pi )(\coth \beta \omega /2)\cos \omega t\mp i\sin \omega t$) which can be evaluated using the previous expressions. With the help of the line-broadening functions we estimate the inter-manifold dephasing parameters as, ${\gamma }_{p_1^{(n)}{p}_2^{(m)}}=({\gamma }_{p_1^{(n)}}+{\gamma }_{p_2^{(m)}})/2$. Finally, we obtain the inter-manifold Greens functions relevant for dephasing as, $G_{p_1^{(n)}{p}_2^{(m)}}(\omega )=i{(\omega -{\omega }_{p_1^{(n)}{p}_2^{(m)}}-i{\gamma }_{p_1^{(n)}{p}_2^{(m)}})}^{-1}$. The advanced Green’s functions are defined likewise.

3 Multidimensional Double-Quantum Coherence Signal With Entangled Biphoton Sources

The theoretical development mentioned in the preceding sections provides us the ingredients to introduce the Double Quantum Coherence (DQC) signal. The DQC signal, as hinted earlier, involves excitation of state-selective (or narrow-band around the selected state) two-polariton coherence that is followed by projection of the oscillating polarization components onto two plausible sets of inter-manifold coherence. Provided that the participant two-polariton states are sufficiently correlated with the states onto which they are being projected, the desired nonlinear polarization have dominant component in the phase-matched direction k_s = k₁ + k₂ − k₃. Below we present a modular derivation of the signal starting from the time-dependent dual-perturbation scheme, corroborate the derivation to the Keldysh-Schwinger loop diagrams Figure 2 and introduce the entangled biphoton sources that serves as probe.

FIGURE 2

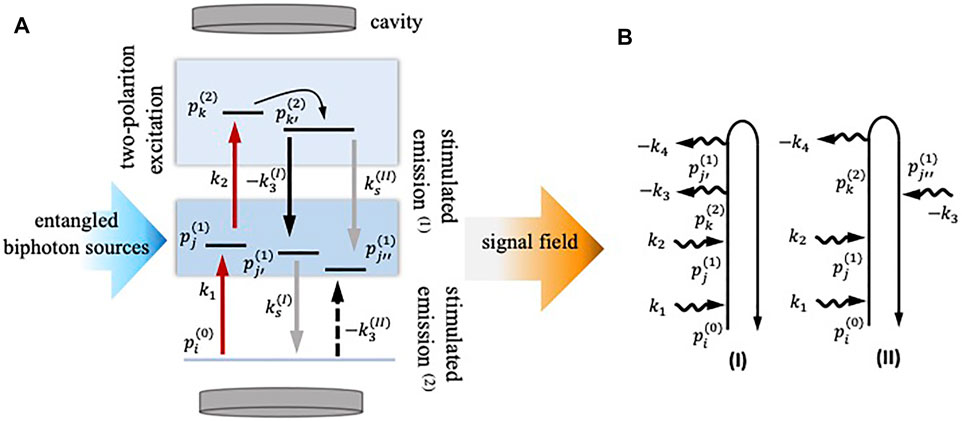
FIGURE 2. (A) Schematic description of the dynamical phenomena (in WMEL diagrammatic convention [36]) that can be addressed by the proposed DQC signal measurement technique. The first two interactions (in red) are common to both the pathways. The last two interactions (in black and gray) are distinguished by two alternative possibilities indicated by $\{k_s^{(I)},-k_3^{(I)}\}$, $\{k_s^{(II)},-k_3^{(II)}\}$ pair. Entangled photons affect both these pair interactions {k₁, k₂} and { − k₃, k_s}. (B) Associated Keldysh-Schwinger diagrams that describe the corresponding dynamical pathways in the multi-polariton basis contributing to the signal and which are distinct in the last two interactions in time.

3.1 Double Quantum Coherence Signal

The DQC signal is typically generated by inducing four external field-matter interactions. In the case of time-domain (frequency-domain) classical field sources, three external fields with controllable delays (relative phases) are allowed to interact with the matter. The radiation field emitted by the time-dependent nonlinear polarization is registered, typically, via suitable heterodyning after another delay (spectrally dispersing) the signal. Typically, the deployment of quantum fields e.g., the biphoton sources to the measurement of DQC signals requires considerable care. These field sources are often parametrically scanned via schemes akin to multi-pulse phase-cycling. An involved discussion regarding the details of the deployment and measurement scheme is beyond the scope of the article [67, 68]. However, we assume that the biphoton generation scheme is capable of producing two sets of entangled photon pairs that lend themselves to external manipulation via central frequencies and delays. Before proceeding further, we introduce the two sets of pathways involved in the DQC signal generation as,

$\begin{array}{cc}\hfill {\mathrm{\Pi }}_a\left({\tau }_4,{\tau }_3,{\tau }_2,{\tau }_1\right)& =d_{p_i^{\left(0\right)}{p}_{j^{\prime }}^{\left(1\right)}}\left({\tau }_4\right)d_{p_{j^{\prime }}^{\left(1\right)}{p}_k^{\left(2\right)}}\left({\tau }_3\right)d_{p_k^{\left(2\right)}{p}_j^{\left(1\right)}}\left({\tau }_2\right)d_{p_j^{\left(1\right)}{p}^{\left(0\right)}}\left({\tau }_1\right)\hfill \\ \hfill {\mathrm{\Pi }}_b\left({\tau }_4,{\tau }_3,{\tau }_2,{\tau }_1\right)& =d_{p_i^{\left(0\right)}{p}_{j^{\prime }}^{\left(1\right)}}\left({\tau }_3^{\prime }\right)d_{p_{j^{\prime }}^{\left(1\right)}{p}_k^{\left(2\right)}}\left({\tau }_4^{\prime }\right)d_{p_k^{\left(2\right)}{p}_j^{\left(1\right)}}\left({\tau }_2^{\prime }\right)d_{p_j^{\left(1\right)}{p}^{\left(0\right)}}\left({\tau }_1^{\prime }\right)\hfill \end{array}(4)$

where the first and the second one have been written in the Heisenberg representation and correspond to diagrams in Figure 2). These pathways, notably, differing in the last two components signify dynamical spectral weights. Interference features between these pathway components depend on the nature of the polariton correlation and dephasing properties. We also introduce the time-domain, four-point external field correlation function as D (τ₄, τ₃, τ₂, τ₁) which is capable of incorporating the generalized nature of the external field. With the help of these definitions, we present the signal expression in the time-domain as, $S=C_{\text{s}}\mathrm{I}\mathrm{m}{\prod }_{i\in a,b}{\int }_{\infty }^{\infty }d{\tau }_4^{(i)}d{\tau }_3^{(i)}d{\tau }_2^{(i)}d{\tau }_1^{(i)}\theta ({\tau }_{43}^{(i)})\theta ({\tau }_{32}^{(i)})\theta ({\tau }_{21}^{(i)})\times D^{(i)}({\tau }_4^{(i)},{\tau }_3^{(i)},{\tau }_2^{(i)},{\tau }_1^{(i)}){\mathrm{\Pi }}_i({\tau }_4^{(i)},{\tau }_3^{(i)},{\tau }_2^{(i)},{\tau }_1^{(i)})$ where C_s represents the coefficients that arises from the perturbative expansion and have been taken as a scaling factor. The Heaviside functions are defined in reference to the interaction times denoted along the loop diagrams. In going forward, the interaction times i.e. the loop time-instance variables were transformed to the loop-delay variables and mapped onto the real-time parameters that are externally tunable using, θ(s₃)θ(s₂)θ(s₁) → θ(t₃)θ(t₂)θ(t₁) for the diagram I and θ(s₃)θ(s₂)θ(s₁) → θ(s₃)θ(s₂ − s₃)θ(s₁) = θ(t₃)θ(t₂)θ(t₁) for the diagram II. These parameters are experimentally realizable. We also use the time-domain phonon-averaged Green’s functions expanded in the multi-polariton basis and write the field correlation function in the frequency domain. Following these exercises, we obtain the generalized signal as,

$\begin{array}{ll}\hfill S& =C_s{\int }_{-\infty }^{\infty }d{T}_{1}d{T}_{2}d{T}_{3}F\left({\mathrm{\Omega }}_3,{\mathrm{\Omega }}_2,{\mathrm{\Omega }}_1;T_3,T_2,T_1\right){\int }_{\infty }^{\infty }\frac{d{\tilde{\omega }}_3}{2\pi }\frac{d{\tilde{\omega }}_2}{2\pi }\frac{d{\tilde{\omega }}_1}{2\pi }{e}^{-i\left(-{\tilde{\omega }}_3+{\tilde{\omega }}_2+{\tilde{\omega }}_1\right)T_3-i\left({\tilde{\omega }}_1+{\tilde{\omega }}_2\right)T_2-i{\tilde{\omega }}_1{T}_1}\hfill \\ \hfill & ⟨E_3^{†}\left({\tilde{\omega }}_3\right)E_4^{†}\left(+{\tilde{\omega }}_1+{\tilde{\omega }}_2-{\tilde{\omega }}_3\right)E_2\left({\tilde{\omega }}_2\right)E_1\left({\tilde{\omega }}_1\right)⟩\sum _{p_j^{\left(1\right)},p_{j^{\prime }}^{\left(1\right)},p_k^{\left(2\right)}}{w}^{\left(1\right)}{G}_{p_k^{\left(2\right)}{p}_{j^{\prime }}^{\left(1\right)}}\left({\tilde{\omega }}_1+{\tilde{\omega }}_2-{\tilde{\omega }}_3\right)G_{p_k^{\left(2\right)}{p}^{\left(0\right)}}\left({\tilde{\omega }}_2+{\tilde{\omega }}_1\right)\hfill \\ \hfill & G_{p_j^{\left(1\right)}{p}^{\left(0\right)}}\left({\tilde{\omega }}_1\right)+⟨E_3^{†}\left({\tilde{\omega }}_3\right)E_4^{†}\left(+{\tilde{\omega }}_1+{\tilde{\omega }}_2-{\tilde{\omega }}_3\right)E_2\left({\tilde{\omega }}_2\right)E_1\left({\tilde{\omega }}_1\right)⟩\sum _{p_j^{\left(1\right)},p_{j^{\prime }}^{\left(1\right)},p_k^{\left(2\right)}}{w}^{\left(2\right)}{G}_{p_{j^{\prime }}^{\left(1\right)}{p}^{\left(0\right)}}\left(-{\tilde{\omega }}_3+{\tilde{\omega }}_2+{\tilde{\omega }}_1\right)\hfill \\ \hfill & G_{p_k^{\left(2\right)}{p}^{\left(0\right)}}\left({\tilde{\omega }}_2+{\tilde{\omega }}_1\right)G_{p_j^{\left(1\right)}{p}^{\left(0\right)}}\left({\tilde{\omega }}_1\right)\hfill \end{array}(5)$

This expression is valid for a general class of DQC signal measurement which may use different kinds of external field sources beyond biphotons and simple Gaussian classical fields. The field correlation function acts as a convolutional probing function for the bare signal. Additional possibilities for the external manipulation of the field correlation function extend the applicability of DQC signals to a wide range of scenarios. Further, we aim to introduce a two-dimensional frequency-domain representation of the signal in order to facilitate a visualization of the correlation features contained in the matter correlation functions. In order to allow such representations to be generated via real-time delay-scanning protocols, we introduce integral transform, $F({\mathrm{\Omega }}_3,{\mathrm{\Omega }}_2,{\mathrm{\Omega }}_1;T_3,T_2,T_1)=\theta (T_3)\theta (T_2)\theta (T_1)e^{i{\mathrm{\Omega }}_3{T}_3}{e}^{i{\mathrm{\Omega }}_2{T}_2}{e}^{i{\mathrm{\Omega }}_1{T}_1}$. We also define the following variable mapping of the parameters, ${\tilde{\tau }}_{21}^0\to T_1,{\tilde{\tau }}_{32}^0\to T_2,{\tilde{\tau }}_{43}^0\to T_3$, for the diagram I and ${\tau }_{21}^0\to T_1,{\tau }_{42}^0-{\tau }_{43}^0\to T_2,{\tau }_{43}^0\to T_3$, for the diagram II (the ${\tau }_{ij}^0$ is the delays between the centering times). Scanning of these set of parameters and obtaining joint Fourier transforms w. r.t the delays generate the desired two-dimensional correlation plots. The final expression can be presented as the following expression.

$\begin{array}{ll}\hfill S\left({\mathrm{\Omega }}_3,{\mathrm{\Omega }}_2,{\mathrm{\Omega }}_1\right)& =C_s\sum _{p^{\left(0\right)}{p}_j^{\left(1\right)}{p}_{j^{\prime }}^{\left(1\right)}{p}_k^{\left(2\right)}}{w}^{\left(1\right)}{\tilde{F}}_{\mathrm{\Omega }}^{\left(1\right)}⟨E_4^{†}\left(z_{p_k^{\left(2\right)}{p}_{j^{\prime }}^{\left(1\right)}}\right)E_3^{†}\left(z_{p_{j^{\prime }}^{\left(1\right)}{p}^{\left(0\right)}}\right)E_2\left(z_{p_k^{\left(2\right)}{p}_j^{\left(1\right)}}\right)E_1\left(z_{p_j^{\left(1\right)}{p}^{\left(0\right)}}\right.)\hfill \\ \hfill & +w^{\left(2\right)}{\tilde{F}}_{\mathrm{\Omega }}^{\left(2\right)}⟨E_4^{†}\left(z_{p_k^{\left(2\right)}{p}_{j^{\prime }}^{\left(1\right)}}\right)E_3^{†}\left(z_{p_{j^{\prime }}^{\left(1\right)}{p}^{\left(0\right)}}\right)E_2\left(z_{p_k^{\left(2\right)}{p}_j^{\left(1\right)}}\right)E_1\left(z_{p_j^{\left(1\right)}{p}^{\left(0\right)}}\right.)\hfill \end{array}(6)$

where the functions are specified as,

$\begin{array}{ll}\hfill {\tilde{F}}_{\mathrm{\Omega }}^{\left(1\right)}& ={\left\{\left({\mathrm{\Omega }}_3-z_{p_2^{\left(1\right)}{p}^{\left(0\right)}}\right)\left({\mathrm{\Omega }}_2-z_{p^{\left(2\right)}{p}^{\left(0\right)}}\right)\left({\mathrm{\Omega }}_1-z_{p_1^{\left(1\right)}{p}^{\left(0\right)}}\right)\right\}}^{-1}\hfill \\ \hfill {\tilde{F}}_{\mathrm{\Omega }}^{\left(2\right)}& ={\left\{\left({\mathrm{\Omega }}_3-z_{p^{\left(2\right)}{p}_{\prime }^{\left(1\right)}}\right)\left({\mathrm{\Omega }}_2-z_{p^{\left(2\right)}{p}^{\left(0\right)}}\right)\left({\mathrm{\Omega }}_1-z_{p^{\left(1\right)}{p}^{\left(0\right)}}\right)\right\}}^{-1}\hfill \end{array}(7)$

These functions encode the polariton dynamical resonances. These resonances show up, as predicted, during the scan of the Fourier transformed parameter. The field correlation function encodes the information about the ability to manipulate the spectral weights of the matter excitations and reveal desired dynamical resonances.

3.2 Entangled Biphoton Properties

The principal aim of using the entangled biphoton sources is to avail the non-classical relation between the joint time of arrival and frequency pairs of the biphotons. This in turn allows one to excite relatively short-lived two-polariton states (i.e., within an ultra-short time window) that are outside the excitation energy window of the classical two-photon laser pulses. These constraints remain difficult to surpass via independent variable manipulation, even in the case of multiple classical pulses. Below we present some basic features of the entangled photon source properties that were used in the simulation and describe their correlation features. The entangled biphoton field is traditionally generated via the spontaneous parametric down-conversion (SPDC) process (in the weak down-conversion limit) by pumping the source material with an ultra-short classical laser. The pump pulse bandwidth and the central frequency determine the correlation properties and time-frequency regime of the generated pairs. An effective Hamiltonian procedure which has been used to derive the correlation properties as outlined previously [47, 69–71] is avoided here for succinctness. Following a similar derivation, the entangled biphoton field correlation function can be obtained as, $⟨E^{†}({\omega }_4)E^{†}({\omega }_4)E({\omega }_2)E({\omega }_1)⟩=F_1^{*}({\omega }_4,{\omega }_3)F_1({\omega }_2,{\omega }_1)$ where we have, $F_1({\omega }_a,{\omega }_b;{\omega }_p)=A_0({\omega }_a,{\omega }_b)\left\{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}[\varphi ({\omega }_a,{\omega }_b)]\exp i\varphi ({\omega }_a,{\omega }_b)+a\leftrightarrow b\right\}.$ The function $\varphi ({\omega }_j,{\omega }_k)=({\omega }_j-{\omega }_p/2){\tilde{T}}_1+({\omega }_k-{\omega }_p/2){\tilde{T}}_2$ and the temporal entanglement parameter of the pairs ${\tilde{T}}_1({\tilde{T}}_2)$, via ${\tilde{T}}_{\text{ent}}={\tilde{T}}_2-{\tilde{T}}_1$, quantifies the spectral-temporal properties of the entangled biphotons [71–73]. The term A₀ denotes the amplitude of the pump. This form of factorization underlies the fact that the signal scales linearly with the intensity. The temporal entanglement parameter can be viewed as an estimator of upper bound of delay between the time of generation of the entangled photon pairs inside the SPDC source material. The entanglement time parameter arises from the phase matching function Δk (ω₁, ω₂) and parametrically depends on the group velocity of propagation inside the SPDC material. The phase mismatching function under the linearization approximation around the central frequencies of the beams, for the collinear case leads to the identification of parameters, T_j = 1/v_p − 1/v_j where j ∈ {1, 2} and v_p/j denotes the group velocity of the pump, and two biphotons inside the material. These values can be estimated from the inverse of the marginal distribution function of the joint spectral amplitude function in the frequency domain [51, 73]. In contrast, the classical field, in a similar weak-field limit factorizes into the product of amplitudes as, $⟨E^{†}({\omega }_4)E^{†}({\omega }_3)E({\omega }_2)E({\omega }_1)⟩=A_4^{*}({\omega }_4)A_3^{*}({\omega }_3)A_1({\omega }_2)A_1({\omega }_1)$ and scales quadratically with the intensity. The biphoton field correlation properties for different typical parameter regimes can be examined by plotting the joint-spectral amplitude which describes the frequency-dependent correlation of the same as shown in Figure 3. The bottom-right plot (i.e., (d)) in Figure 3 corresponds to a classical field scenario. The simulation has the freedom of selecting frequency pairs from the plot region where the function has finite support.

FIGURE 3

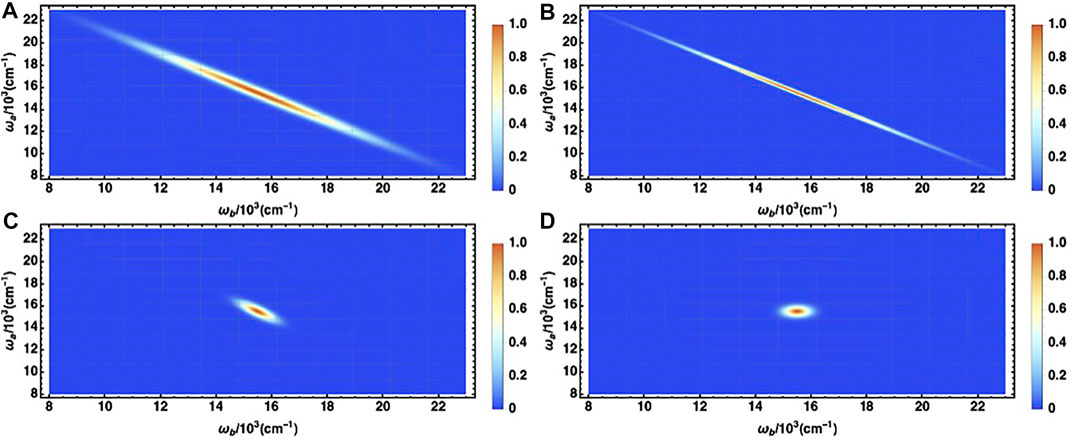
FIGURE 3. Field correlation functions for different entangled photon states corresponding to parameter variation of temporal entanglement parameter T_ent (fs) and pump width τ_p (fs) for uniform pump frequency 31.0, ×, 10³cm⁻¹ and biphoton frequencies ω₁ = ω₂ = 15.5 × 10³cm⁻¹. The bottom right corresponds to the typical case of a classical field two-photon pulse (A) corresponds to the T_ent = 10; τ_p = 20 (B) corresponds to T_ent = 10; τ_p = 50 while (C) assumes values T_ent = 50; τ_p = 20. The (D) corresponds to a Gaussian pair-pulse with τ_g (fs) = 10 with ω_1,g = ω_2,g = 15.5 × 10³cm⁻¹.

3.3 Simulation

The correlated two-polariton excitations via entangled biphoton sources may focus on several experimental configurations which will be of particular interest to the condensed phase spectroscopies. The excitation of specific two-polariton states via higher-energy sectors of the one-polariton manifold and contrasting them with those via the lower-energy sectors may give information about polariton scattering, delocalization, and dephasing. In other words, the specific two-polariton states may have dominant contributions from certain one-polariton states which are distant on the site basis but energetically closer. Alternatively for the same two-polariton excitation, projecting to the higher and lower-energy one-polariton sector offers insights into the state compositions. Combining two strategies may provide important insight into the state resolved polariton correlations. These features can be probed as shown in the upper and lower panel of Figure 4. Particularly the polariton states (e.g., ${\omega }_{p^{(2)}}=30550{\mathrm{c}\mathrm{m}}^{-1}$) that are specifically prone to phonon-induced dephasing (higher dephasing induced broadened) have been excited while the temporal entanglement parameter of the probe, projected one-polariton sector has been varied.

FIGURE 4

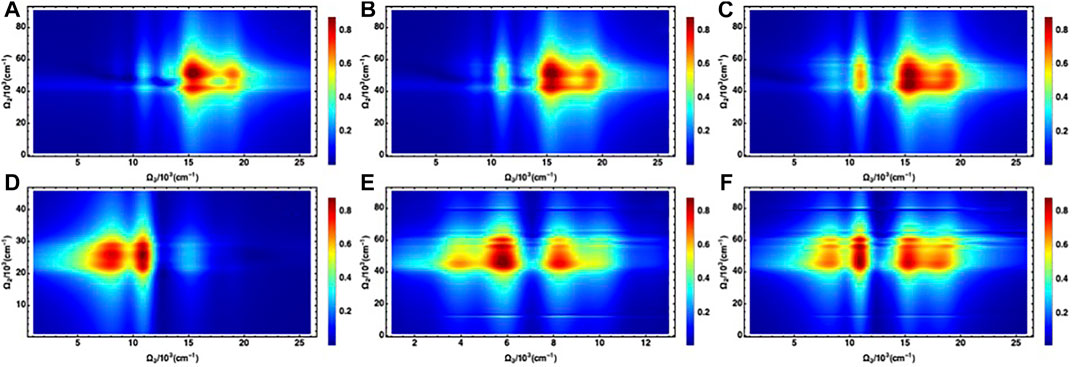
FIGURE 4. Multidimensional correlation plots (A–F) for signal with parametric variation of the frequencies and the temporal entanglement parameters of the entangled biphotons. The short-lived, intermediate one-polariton resonances along the Ω₃ axis can be explored and associated with the two-polariton resonances along the Ω₂ axis. For parameters corresponding to each plot see text.

In the upper panel of Figure 4, we present, along the rows, three sets of results for the variation of the temporal entanglement parameter ${\tilde{T}}_{\text{ent}}\left(\mathrm{f}\mathrm{s}\right.$. Each of them correspond to fixed ${\omega }_{a_1}({\mathrm{c}\mathrm{m}}^{-1})=15500$ and ${\omega }_{b_1}({\mathrm{c}\mathrm{m}}^{-1})=14500$ (therefore exciting the target at ${\omega }_p^{(2)}=30550$) with pump width τ_p (fs) = 20.0. Therefore, the two polariton excitation occurs via the middle sector of the one-polariton band. It also projects the two-polariton coherence to the mixed-energy region of the one-polariton band by choosing the corresponding frequencies as ${\omega }_{a_2}({\mathrm{c}\mathrm{m}}^{-1})={\omega }_p^{(2)}-15800$ and ${\omega }_{b_2}({\mathrm{c}\mathrm{m}}^{-1})=15800$. It is noticed that the strong entanglement between the photon pairs, as we move from (A) to (C) corresponding to ${\tilde{T}}_{\text{ent}}(\mathrm{f}\mathrm{s})$ values 60.0, 50.0, 40.0 respectively, allows correlated signal features to develop. These emergent features may not be visible in the signal obtained by using classical pulse pairs of comparable spectral-temporal properties. Time-frequency correlated excitation gives the freedom of simultaneously choosing the narrow-band target while ensuring that system remains less affected by the high dephasing components of the intermediate states. The latter has the possibility of making the short-time kinetics in the one-polariton manifold more accessible. Even an individually controlled classical field two-pulse scenario may offer less advantage because the temporal and spectral components are bound.

The bottom row ((d) to (f)) accomplishes the aforementioned goal of exploring excitation via different energy sectors of the one-polariton manifold. Here the (d) and (e) allow excitation via middle-sector and (f) lower-sector while projecting all of them to the same mixed-energy sectors as the above panel. With the increase in temporal entanglement parameter in going from (d) to (e) (${\tilde{T}}_{\text{ent}}(\mathrm{f}\mathrm{s})$ values 40.0, 10.0, respectively) we find features shows distinguishable increase. The last panel (f) whose excitation via lower energy sector (excitation via ${\omega }_{a_1}({\mathrm{c}\mathrm{m}}^{-1})=15150$ and ${\omega }_{b_1}({\mathrm{c}\mathrm{m}}^{-1})=$) which reveals many more correlation features. It reveals the higher participation of the particular set of one-polariton states to chosen target in the two-polariton manifold throughout the simulation. The short temporal entanglement parameter also certifies the capability of the biphoton sources to map out correlation involving energetically distant states. The success of the parameter regime and overall strategy of the simulation can be traced back to the ability to choose the frequency pairs from a broader distribution. In addition, the fact that they are also bound by the temporal constraints allow excitation via fast dephasing components in the one-polariton band (during the first time delay i.e., T₁) while simultaneously projecting the resultant two-polariton coherence to short-lived coherences (during the last time delay i.e., T₃).

4 Conclusion and Outlook

In this article, we have proposed a theoretical protocol that is suitable for the investigation of the inter-manifold coherence properties associated with the two-polariton manifold. We observe that the proposal exclusively focused on the cavity control of exciton correlation and modulation of exciton-phonon dephasing via the former. In other words, the cavity affects the exciton transitions directly and redistributes the excitonic spectral weights. The extent to which this redistribution occurs is encoded in the action of the polariton transformation matrices. As a result, the novel hybridized polariton states interact with the phonons rather differently than that of the cavity-free case. We demonstrated that biphoton sources are capable of studying the ultrafast signatures of the related dynamics without losing the state specificity. In the process, it is capable of mapping out the cavity modulated exciton correlation. In this direction, two further extensions namely, the detailed study involving the parametric variation of the cavity-free case and a comparison employing controlled classical fields are worth looking at. They will be part of future communication. However, we note that the signal expressions presented in this communication will be sufficient for such extended analysis.

The role of cavity coupling has been included non-perturbatively with the same quasi-particle excitation picture. Here the real-space coupling variations were neglected for convenience, in the spirit of the first simulation. Also, the role of the mean number of photons in the cavity has not been investigated and the role of the cavity has been confined to the coherence created between the states within the proposed regime of operation.

In comparing and contrasting the present technique to the transmission mode pump-probe measurements several features distinguish the present technique. DQC measures one specific component of the nonlinear polarization of the cavity polariton, unlike the pump-probe analog. The pump-probe technique also includes the pathways analogous to polaritonic Raman scattering pathways. Thus the DQC signal is more specific to the purpose of this article. The two-polariton coherence is explicitly monitored by isolating the signal components as suggested by the plausible implementation via phase-cycling schemes. It can be also highlighted that the present technique works by projecting the two-polariton coherence in two competing coherence components of lower order. The relevant processes leading to the signal occur during the last two time intervals. The degree of discrimination of the pathways, reflected in the associated dynamical spectral weights decides the magnitude of the signal. In contrast to the pump-probe studies, the off-diagonal spectral signatures in the correlation plots required to be interpreted differently. In the latter, the cooperative features appearing in the above-mentioned sector carry less specific information regarding the physical origin of the polaritonic correlation due to non-discrimination between pure two-one polariton coherence and two-polariton-one polariton coherence.

The study can be extended to accommodate the explicit two-polariton transport phenomenology by studying the fluorescence-detected phase cycling protocols [74, 75]. The latter is a four-wave mixing analog but aimed at investigating the longer-time state correlation properties in the presence of phonon-induced dynamical population redistribution. The longer-time dynamical information thereby obtained is complementary to the information provided by the short-time dynamics investigated in this article. An investigation in this direction is on the way. Furthermore, one may combine the interferometric detection schemes to separate the pathways as recently proposed [76, 77].

The theoretical description adopted for describing the dissipative polaritonic matter is formulated at the level of a quasi-particle approach. The quasi-particle Green’s function was chosen to describe the signal [78]. Over the last few years, a host of promising methods have been proposed that can potentially deal with the complexity of the quantum aggregates in near future. These methods have offered several different flavors of treating the matter and the cavity modes. We have, namely, quantum electrodynamics based hybrid (density) functional formulation [79–82], cluster-expansion [21], potential-energy surface-based dynamical calculations combined with the trajectory-based propagation for the cavity quadrature modes [83, 84], path integral based unified framework for nuclear modes and the idealized cavity modes [85–87], first-principles simulations [88–92]. Incorporating these methods to describe the phenomenology described in this article will require a qualified description of exciton formation, a description of exciton-exciton scattering in the presence of a dielectric environment, and nuclear propagation.

We also note that the numerical simulation adopted the analytical expressions which have been derived under the assumption of generalized time-translational invariance. For systems driven out-of-equilibrium via additional laser pulses, one may expect to see more correlation features in the signal. The scope to add additional pulses and using the biphotons as probes, although offers a more complicated scenario, is a promising avenue for future study of nonlinear response in correlated quantum materials [93–97].

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

AD developed the project in consultation with AR. AD performed the research. AD and AR analyzed the results. AD wrote the manuscript with inputs from AR.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge financial support from the European Research Council (ERC-2015-AdG-694097), by the Cluster of Excellence “Advanced Imaging of Matter” (AIM), Grupos Consolidados (IT1249-19) and SFB925 “Light induced dynamics and control of correlated quantum systems.” The Flatiron Institute is a division of the Simons Foundation.

References

1. Boulais É, Sawaya NPD, Veneziano R, Andreoni A, Banal JL, Kondo T, et al. Programmed Coherent Coupling in a Synthetic DNA-Based Excitonic Circuit. Nat Mater (2018) 17:159–66. doi:10.1038/nmat5033

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Romero E, Augulis R, Novoderezhkin VI, Ferretti M, Thieme J, Zigmantas D, et al. Quantum Coherence in Photosynthesis for Efficient Solar-Energy Conversion. Nat Phys (2014) 10:676–82. doi:10.1038/nphys3017

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Scholes GD, Fleming GR, Chen LX, Aspuru-Guzik A, Buchleitner A, Coker DF, et al. Using Coherence to Enhance Function in Chemical and Biophysical Systems. Nature (2017) 543:647–56. doi:10.1038/nature21425

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Schlau-Cohen GS, Ishizaki A, Calhoun TR, Ginsberg NS, Ballottari M, Bassi R, et al. Elucidation of the Timescales and Origins of Quantum Electronic Coherence in LHCII. Nat Chem (2012) 4:389–95. doi:10.1038/nchem.1303

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cao J, Cogdell RJ, Coker DF, Duan H-G, Hauer J, Kleinekathöfer U, et al. Quantum Biology Revisited. Sci Adv (2020) 6:eaaz4888. doi:10.1126/sciadv.aaz4888

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Scholes GDPolaritons and Excitons: Hamiltonian Design for Enhanced Coherence. Proc R Soc A (2020) 476:20200278. doi:10.1098/rspa.2020.0278

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Basov D, Asenjo-Garcia A, Schuck PJ, Zhu X, Rubio APolariton Panorama. Nanophotonics (2021) 10:549.

Google Scholar

8. Ruggenthaler M, Tancogne-Dejean N, Flick J, Appel H, Rubio AFrom a Quantum-Electrodynamical Light–Matter Description to Novel Spectroscopies. Nat Rev Chem (2018) 2:1. doi:10.1038/s41570-018-0118

CrossRef Full Text | Google Scholar

9. Mewes L, Wang M, Ingle RA, Börjesson K, Chergui MEnergy Relaxation Pathways between Light-Matter States Revealed by Coherent Two-Dimensional Spectroscopy. Commun Phys (2020) 3:1. doi:10.1038/s42005-020-00424-z

CrossRef Full Text | Google Scholar

10. Garcia-Vidal FJ, Ciuti C, Ebbesen TWManipulating Matter by strong Coupling to Vacuum fields. Science (2021) 373:eabd0336. doi:10.1126/science.abd0336

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Cao JGeneralized Resonance Energy Transfer Theory: Applications to Vibrational Energy Flow in Optical Cavities. arXiv preprint arXiv:2201.12117 (2022). doi:10.48550/ARXIV.2201.12117

CrossRef Full Text | Google Scholar

12. Engelhardt G, Cao JUnusual Dynamical Properties of Disordered Polaritons in Micocavities. arXiv preprint arXiv:2112.04060 (2021) 105:064205.

Google Scholar

13. Groenhof G, Toppari JJCoherent Light Harvesting through Strong Coupling to Confined Light. J Phys Chem Lett (2018) 9:4848–51. doi:10.1021/acs.jpclett.8b02032

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Latini S, Shin D, Sato SA, Schäfer C, De Giovannini U, Hübener H, et al. The Ferroelectric Photo Ground State of SrTiO ₃: Cavity Materials Engineering. Proc Natl Acad Sci (2021) 118. doi:10.1073/pnas.2105618118

CrossRef Full Text | Google Scholar

15. Lengers F, Kuhn T, Reiter DEPhonon Signatures in Spectra of Exciton Polaritons in Transition Metal Dichalcogenides. Phys Rev B (2021) 104:L241301. doi:10.1103/physrevb.104.l241301

CrossRef Full Text | Google Scholar

16. Autry TM, Nardin G, Smallwood CL, Silverman K, Bajoni D, Lemaître A, et al. Excitation Ladder of Cavity Polaritons. Phys Rev Lett (2020) 125:067403. doi:10.1103/physrevlett.125.067403

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Sidler D, Schäfer C, Ruggenthaler M, Rubio APolaritonic Chemistry: Collective Strong Coupling Implies Strong Local Modification of Chemical Properties. J Phys Chem Lett (2020) 12:508–16. doi:10.1021/acs.jpclett.0c03436

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yang P-Y, Cao JQuantum Effects in Chemical Reactions under Polaritonic Vibrational Strong Coupling. J Phys Chem Lett (2021) 12:9531–8. doi:10.1021/acs.jpclett.1c02210

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Salij A, Tempelaar RMicroscopic Theory of Cavity-Confined Monolayer Semiconductors: Polariton-Induced valley Relaxation and the prospect of Enhancing and Controlling valley Pseudospin by Chiral strong Coupling. Phys Rev B (2021) 103:035431. doi:10.1103/physrevb.103.035431

CrossRef Full Text | Google Scholar

20. Latini S, De Giovannini U, Sie EJ, Gedik N, Hübener H, Rubio APhonoritons as Hybridized Exciton-Photon-Phonon Excitations in a Monolayer H -BN Optical Cavity. Phys Rev Lett (2021) 126:227401. doi:10.1103/physrevlett.126.227401

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Haugland TS, Ronca E, Kjønstad EF, Rubio A, Koch HCoupled Cluster Theory for Molecular Polaritons: Changing Ground and Excited States. Phys Rev X (2020) 10:041043. doi:10.1103/physrevx.10.041043

CrossRef Full Text | Google Scholar

22. Sidler D, Ruggenthaler M, Schäfer C, Ronca E, Rubio A,A Perspective on Ab Initio Modeling of Polaritonic Chemistry: The Role of Non-equilibrium Effects and Quantum Collectivity. arXiv preprint arXiv:2108.12244 (2021).

Google Scholar

23. Schäfer C, Flick J, Ronca E, Narang P, Rubio AShining Light on the Microscopic Resonant Mechanism Responsible for Cavity-Mediated Chemical Reactivity. arXiv preprint arXiv:2104.12429 (2021).

Google Scholar

24. Zhang Z, Scully MO, Agarwal GSQuantum Entanglement between Two Magnon Modes via Kerr Nonlinearity Driven Far from Equilibrium. Phys Rev Res (2019) 1:023021. doi:10.1103/physrevresearch.1.023021

CrossRef Full Text | Google Scholar

25. Zhang Z, Agarwal GS, Scully MOQuantum Fluctuations in the Fröhlich Condensate of Molecular Vibrations Driven Far from Equilibrium. Phys Rev Lett (2019) 122:158101. doi:10.1103/physrevlett.122.158101

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wang D, Kelkar H, Martin-Cano D, Utikal T, Götzinger S, Sandoghdar VCoherent Coupling of a Single Molecule to a Scanning Fabry-Perot Microcavity. Phys Rev X (2017) 7:021014. doi:10.1103/physrevx.7.021014

CrossRef Full Text | Google Scholar

27. Maser A, Gmeiner B, Utikal T, Götzinger S, Sandoghdar VFew-photon Coherent Nonlinear Optics with a Single Molecule. Nat Photon (2016) 10:450–3. doi:10.1038/nphoton.2016.63

CrossRef Full Text | Google Scholar

28. Campos-Gonzalez-Angulo JA, Yuen-Zhou JGeneralization of the Tavis-Cummings Model for Multi-Level Anharmonic Systems: Insights on the Second Excitation Manifold (2022) 156:194308. doi:10.1063/5.0087234

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Debnath A, Rubio AEntangled Photon Assisted Multidimensional Nonlinear Optics of Exciton-Polaritons. J Appl Phys (2020) 128:113102. doi:10.1063/5.0012754

CrossRef Full Text | Google Scholar

30. DelPo CA, Kudisch B, Park KH, Khan S-U -Z, Fassioli F, Fausti D, et al. Polariton Transitions in Femtosecond Transient Absorption Studies of Ultrastrong Light-Molecule Coupling. J Phys Chem Lett (2020) 11:2667–74. doi:10.1021/acs.jpclett.0c00247

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Ribeiro RF, Campos-Gonzalez-Angulo JA, Giebink NC, Xiong W, Yuen-Zhou JEnhanced Optical Nonlinearities under Collective strong Light-Matter Coupling. Phys Rev A (2021) 103:063111. doi:10.1103/physreva.103.063111

CrossRef Full Text | Google Scholar

32. Renken S, Pandya R, Georgiou K, Jayaprakash R, Gai L, Shen Z, et al. Untargeted Effects in Organic Exciton-Polariton Transient Spectroscopy: A Cautionary Tale. J Chem Phys (2021) 155:154701. doi:10.1063/5.0063173

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zhang Z, Peng T, Nie X, Agarwal GS, Scully MODirectional Superradiant Emission from Statistically Independent Incoherent. arXiv preprint arXiv:2106.10988 (2021). doi:10.48550/ARXIV.2106.10988

CrossRef Full Text | Google Scholar

34. Zhang Z, Wang K, Yi Z, Zubairy MS, Scully MO, Mukamel SPolariton-Assisted Cooperativity of Molecules in Microcavities Monitored by Two-Dimensional Infrared Spectroscopy. J Phys Chem Lett (2019) 10:4448–54. doi:10.1021/acs.jpclett.9b00979

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Zhang Z, Saurabh P, Dorfman KE, Debnath A, Mukamel SMonitoring Polariton Dynamics in the LHCII Photosynthetic Antenna in a Microcavity by Two-Photon Coincidence Counting. J Chem Phys (2018) 148:74302. doi:10.1063/1.5004432

CrossRef Full Text | Google Scholar

36. Lee D, Albrecht ACThe Vibronic Theory of Resonance Hyper-Raman Scattering. Adv infrared Raman Spectrosc (1985) 12:179.

Google Scholar

37. Tempelaar R, Jansen TLC, Knoester JExciton-Exciton Annihilation Is Coherently Suppressed in H-Aggregates, but Not in J-Aggregates. J Phys Chem Lett (2017) 8:6113–7. doi:10.1021/acs.jpclett.7b02745

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Gutiérrez-Meza E, Malatesta R, Li H, Bargigia I, Srimath Kandada AR, Valverde-Chávez DA, et al. Frenkel Biexcitons in Hybrid HJ Photophysical Aggregates. Sci Adv (2021) 7:eabi5197. doi:10.1126/sciadv.abi5197

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Mukamel SPrinciples of Nonlinear Optical Spectroscopy, 6. New York: Oxford University Press on Demand (1999).

Google Scholar

40. Lomsadze B, Cundiff STLine-shape Analysis of Double-Quantum Multidimensional Coherent Spectra. Phys Rev A (2020) 102:043514. doi:10.1103/physreva.102.043514

CrossRef Full Text | Google Scholar

41. Gao F, Cundiff ST, Li HProbing Dipole-Dipole Interaction in a Rubidium Gas via Double-Quantum 2D Spectroscopy. Opt Lett (2016) 41:2954. doi:10.1364/ol.41.002954

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Kim J, Mukamel S, Scholes GDTwo-Dimensional Electronic Double-Quantum Coherence Spectroscopy. Acc Chem Res (2009) 42:1375–84. doi:10.1021/ar9000795

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Svozilík J, Peřina J, León-Montiel Rd. JVirtual-state Spectroscopy with Frequency-Tailored Intense Entangled Beams. J Opt Soc Am B (2018) 35:460. doi:10.1364/josab.35.000460

CrossRef Full Text | Google Scholar

44. León-Montiel Rd. J, Svozilík J, Torres JP, U’Ren ABTemperature-Controlled Entangled-Photon Absorption Spectroscopy. Phys Rev Lett (2019) 123:023601. doi:10.1103/physrevlett.123.023601

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Kang G, Nasiri Avanaki K, Mosquera MA, Burdick RK, Villabona-Monsalve JP, Goodson T, et al. Efficient Modeling of Organic Chromophores for Entangled Two-Photon Absorption. J Am Chem Soc (2020) 142:10446–58. doi:10.1021/jacs.0c02808

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Schlawin F, Dorfman KE, Mukamel SEntangled Two-Photon Absorption Spectroscopy. Acc Chem Res (2018) 51:2207–14. doi:10.1021/acs.accounts.8b00173

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Saleh BEA, Jost BM, Fei H-B, Teich MCEntangled-Photon Virtual-State Spectroscopy. Phys Rev Lett (1998) 80:3483–6. doi:10.1103/physrevlett.80.3483

CrossRef Full Text | Google Scholar

48. Richter M, Mukamel SUltrafast Double-Quantum-Coherence Spectroscopy of Excitons with Entangled Photons. Phys Rev A (2010) 82:013820. doi:10.1103/physreva.82.013820

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Roslyak O, Mukamel SMultidimensional Pump-Probe Spectroscopy with Entangled Twin-Photon States. Phys Rev A (2009) 79:063409. doi:10.1103/physreva.79.063409

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Mukamel S, Freyberger M, Schleich W, Bellini M, Zavatta A, Leuchs G, et al. Roadmap on Quantum Light Spectroscopy. J Phys B: Mol Opt Phys (2020) 53:072002. doi:10.1088/1361-6455/ab69a8

CrossRef Full Text | Google Scholar

51. Landes T, Raymer MG, Allgaier M, Merkouche S, Smith BJ, Marcus AHQuantifying the Enhancement of Two-Photon Absorption Due to Spectral-Temporal Entanglement. Opt Express (2021) 29:20022. doi:10.1364/oe.422544

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Bittner ER, Li H, Piryatinski A, Srimath Kandada AR, Silva CProbing Exciton/exciton Interactions with Entangled Photons: Theory. J Chem Phys (2020) 152:071101. doi:10.1063/1.5139197

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Schlawin F, Buchleitner ATheory of Coherent Control with Quantum Light. New J Phys (2017) 19:013009. doi:10.1088/1367-2630/aa55ec

CrossRef Full Text | Google Scholar

54. Li H, Piryatinski A, Srimath Kandada AR, Silva C, Bittner ERPhoton Entanglement Entropy as a Probe of many-body Correlations and Fluctuations. J Chem Phys (2019) 150:184106. doi:10.1063/1.5083613

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Richter M, Singh R, Siemens M, Cundiff STDeconvolution of Optical Multidimensional Coherent Spectra. Sci Adv (2018) 4:eaar7697. doi:10.1126/sciadv.aar7697

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Agranovich V, Toshich BCollective Properties of Frenkel Excitons. Sov Phys JETP (1968) 26:104.

Google Scholar

57. Chernyak V, Zhang WM, Mukamel SMultidimensional Femtosecond Spectroscopies of Molecular Aggregates and Semiconductor Nanostructures: The Nonlinear Exciton Equations. J Chem Phys (1998) 109:9587–601. doi:10.1063/1.477621

CrossRef Full Text | Google Scholar

58. Abramavicius D, Palmieri B, Voronine DV, Šanda F, Mukamel SCoherent Multidimensional Optical Spectroscopy of Excitons in Molecular Aggregates; Quasiparticle versus Supermolecule Perspectives. Chem Rev (2009) 109:2350–408. doi:10.1021/cr800268n

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Novoderezhkin VI, Palacios MA, Van Amerongen H, Van Grondelle RExcitation Dynamics in the LHCII Complex of Higher Plants: Modeling Based on the 2.72 Å Crystal Structure. J Phys Chem B (2005) 109:10493–504. doi:10.1021/jp044082f

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Novoderezhkin VI, Palacios MA, Van Amerongen H, Van Grondelle REnergy-Transfer Dynamics in the LHCII Complex of Higher Plants: Modified Redfield Approach. J Phys Chem B (2004) 108:10363–75. doi:10.1021/jp0496001

CrossRef Full Text | Google Scholar

61. Novoderezhkin V, Marin A, van Grondelle RIntra- and Inter-monomeric Transfers in the Light Harvesting LHCII Complex: the Redfield–Förster Picture. Phys Chem Chem Phys (2011) 13:17093.

PubMed Abstract | CrossRef Full Text | Google Scholar

62. van Amerongen H, van Grondelle RUnderstanding the Energy Transfer Function of Lhcii, the Major Light-Harvesting Complex of green Plants (2001). doi:10.1021/jp0028406

CrossRef Full Text | Google Scholar

63. De Liberato SLight-Matter Decoupling in the Deep Strong Coupling Regime: The Breakdown of the Purcell Effect. Phys Rev Lett (2014) 112:016401. doi:10.1103/physrevlett.112.016401

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Schäfer C, Ruggenthaler M, Rokaj V, Rubio ARelevance of the Quadratic Diamagnetic and Self-Polarization Terms in Cavity Quantum Electrodynamics. ACS Photon (2020) 7:975–90. doi:10.1021/acsphotonics.9b01649

CrossRef Full Text | Google Scholar

65. Keeling JCoulomb Interactions, Gauge Invariance, and Phase Transitions of the Dicke Model. J Phys Condens Matter (2007) 19:295213. doi:10.1088/0953-8984/19/29/295213

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Vukics A, Grießer T, Domokos PElimination of the A-Square Problem from Cavity QED. Phys Rev Lett (2014) 112:073601. doi:10.1103/physrevlett.112.073601

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Dorfman KE, Mukamel SMultidimensional Spectroscopy with Entangled Light: Loop vs Ladder Delay Scanning Protocols. New J Phys (2014) 16:033013. doi:10.1088/1367-2630/16/3/033013

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Raymer MG, Landes T, Marcus AHEntangled Two-Photon Absorption by Atoms and Molecules: A Quantum Optics Tutorial. J Chem Phys (2021) 155:081501. doi:10.1063/5.0049338

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Cutipa P, Chekhova MVBright Squeezed Vacuum for Two-Photon Spectroscopy: Simultaneously High Resolution in Time and Frequency, Space and Wavevector. Opt Lett (2022) 47:465. doi:10.1364/ol.448352

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Andersen UL, Gehring T, Marquardt C, Leuchs G30 Years of Squeezed Light Generation. Phys Scr (2016) 91:053001. doi:10.1088/0031-8949/91/5/053001

CrossRef Full Text | Google Scholar

71. Arzani F, Fabre C, Treps NVersatile Engineering of Multimode Squeezed States by Optimizing the Pump Spectral Profile in Spontaneous Parametric Down-Conversion. Phys Rev A (2018) 97:033808. doi:10.1103/physreva.97.033808

CrossRef Full Text | Google Scholar

72. Schlawin F, Dorfman KE, Fingerhut BP, Mukamel SSuppression of Population Transport and Control of Exciton Distributions by Entangled Photons. Nat Commun (2013) 4:1. doi:10.1038/ncomms2802

CrossRef Full Text | Google Scholar

73. Keller TE, Rubin MHTheory of Two-Photon Entanglement for Spontaneous Parametric Down-Conversion Driven by a Narrow Pump Pulse. Phys Rev A (1997) 56:1534–41. doi:10.1103/physreva.56.1534

CrossRef Full Text | Google Scholar

74. Malỳ P, Mančal TSignatures of Exciton Delocalization and Exciton–Exciton Annihilation in Fluorescence-Detected Two-Dimensional Coherent Spectroscopy. J Phys Chem Lett (2018) 9:5654. doi:10.1021/acs.jpclett.8b02271

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Malỳ P, Brixner TFluorescence-Detected Pump–Probe Spectroscopy. Angew Chem Int Edition (2021) 60:18867. doi:10.1002/anie.202102901

CrossRef Full Text | Google Scholar

76. Dorfman KE, Asban S, Gu B, Mukamel SHong-Ou-Mandel Interferometry and Spectroscopy Using Entangled Photons. Commun Phys (2021) 4:1. doi:10.1038/s42005-021-00542-2

CrossRef Full Text | Google Scholar

77. Asban S, Mukamel SDistinguishability and “Which Pathway” Information in Multidimensional Interferometric Spectroscopy with a Single Entangled Photon-Pair. Sci Adv (2021) 7:eabj4566. doi:10.1126/sciadv.abj4566

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Abrikosov AA, Gorkov LP, Dzyaloshinski IEMethods of Quantum Field Theory in Statistical Physics. New York: Courier Corporation (2012).

Google Scholar

79. Ruggenthaler M, Flick J, Pellegrini C, Appel H, Tokatly IV, Rubio AQuantum-electrodynamical Density-Functional Theory: Bridging Quantum Optics and Electronic-Structure Theory. Phys Rev A (2014) 90:012508. doi:10.1103/physreva.90.012508

CrossRef Full Text | Google Scholar

80. Schäfer C, Buchholz F, Penz M, Ruggenthaler M, Rubio AMaking Ab Initio QED Functional(s): Nonperturbative and Photon-free Effective Frameworks for strong Light-Matter Coupling. Proc Natl Acad Sci (2021) 118. doi:10.1073/pnas.2110464118

CrossRef Full Text | Google Scholar

81. Flick J, Narang PCavity-Correlated Electron-Nuclear Dynamics from First Principles. Phys Rev Lett (2018) 121:113002. doi:10.1103/physrevlett.121.113002

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Yang J, Ou Q, Pei Z, Wang H, Weng B, Shuai Z, et al. Quantum-electrodynamical Time-dependent Density Functional Theory within Gaussian Atomic Basis. J Chem Phys (2021) 155:064107. doi:10.1063/5.0057542

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Hoffmann NM, Lacombe L, Rubio A, Maitra NTEffect of many Modes on Self-Polarization and Photochemical Suppression in Cavities. J Chem Phys (2020) 153:104103. doi:10.1063/5.0012723

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Zhang Y, Nelson T, Tretiak SNon-adiabatic Molecular Dynamics of Molecules in the Presence of strong Light-Matter Interactions. J Chem Phys (2019) 151:154109. doi:10.1063/1.5116550

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Li X, Mandal A, Huo PCavity Frequency-dependent Theory for Vibrational Polariton Chemistry. Nat Commun (2021) 12:1. doi:10.1038/s41467-021-21610-9

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Chowdhury SN, Mandal A, Huo PRing Polymer Quantization of the Photon Field in Polariton Chemistry. J Chem Phys (2021) 154:044109. doi:10.1063/5.0038330

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Mandal A, Li X, Huo PTheory of Vibrational Polariton Chemistry in the Collective Coupling Regime. J Chem Phys (2022) 156:014101. doi:10.1063/5.0074106

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Schäfer C, Ruggenthaler M, Appel H, Rubio AModification of Excitation and Charge Transfer in Cavity Quantum-Electrodynamical Chemistry. Proc Natl Acad Sci U.S.A (2019) 116:4883–92. doi:10.1073/pnas.1814178116

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Flick J, Ruggenthaler M, Appel H, Rubio AAtoms and Molecules in Cavities, from Weak to strong Coupling in Quantum-Electrodynamics (QED) Chemistry. Proc Natl Acad Sci U.S.A (2017) 114:3026–34. doi:10.1073/pnas.1615509114

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Flick J, Welakuh DM, Ruggenthaler M, Appel H, Rubio ALight-Matter Response in Nonrelativistic Quantum Electrodynamics. ACS Photon (2019) 6:2757–78. doi:10.1021/acsphotonics.9b00768

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Welakuh DM, Flick J, Ruggenthaler M, Appel H, Rubio AFrequency-dependent Sternheimer Linear-Response Formalism for Strongly Coupled Light-Matter Systems. arXiv preprint arXiv:2201.08734 (2022). doi:10.48550/ARXIV.2201.08734

CrossRef Full Text | Google Scholar

92. Svendsen MK, Kurman Y, Schmidt P, Koppens F, Kaminer I, Thygesen KSCombining Density Functional Theory with Macroscopic QED for Quantum Light-Matter Interactions in 2D Materials. Nat Commun (2021) 12:1. doi:10.1038/s41467-021-23012-3

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Rostami H, Katsnelson MI, Vignale G, Polini MGauge Invariance and Ward Identities in Nonlinear Response Theory. Ann Phys (2021) 431:168523. doi:10.1016/j.aop.2021.168523

CrossRef Full Text | Google Scholar

94. Parameswaran SA, Gopalakrishnan SAsymptotically Exact Theory for Nonlinear Spectroscopy of Random Quantum Magnets. Phys Rev Lett (2020) 125:237601. doi:10.1103/physrevlett.125.237601

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Rostami H, Cappelluti EDominant Role of Two-Photon Vertex in Nonlinear Response in Two-Dimensional Dirac Systems. npj 2D Mater Appl (2021) 5:1. doi:10.1038/s41699-021-00217-0

CrossRef Full Text | Google Scholar

96. Choi W, Lee KH, Kim YBTheory of Two-Dimensional Nonlinear Spectroscopy for the Kitaev Spin Liquid. Phys Rev Lett (2020) 124:117205. doi:10.1103/physrevlett.124.117205

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Grankin A, Hafezi M, Galitski VMEnhancement of Superconductivity with External Phonon Squeezing. Phys Rev B (2021) 104:L220503. doi:10.1103/physrevb.104.l220503

CrossRef Full Text | Google Scholar

Appendix

In this appendix, we provide two sets of supplementary information that aid the main text. It is composed of a relevant figure of merit for entanglement in the biphoton source and a description of parameters regarding the phonon spectral density.

A1 Singular Value Decomposition of the Biphoton Spectral Function

The singular value decomposition of the joint spectral amplitude of the biphoton sources provides an estimate for the number of effective modes that participated in mode-squeezing. It can be analyzed by obtaining the singular value decomposition of the said function at different parameter regimes. It can be seen in Figure A1 that the cases involving the shorter temporal entanglement parameters increase the number of effectively squeezed modes. Also, a decrease in the pump bandwidth decreases the modal amplitudes for a case with comparable temporal entanglement parameters. The classical two-photon pulse, unsurprisingly, presents a plot reminiscent of the uncorrelated feature.

FIGURE A1

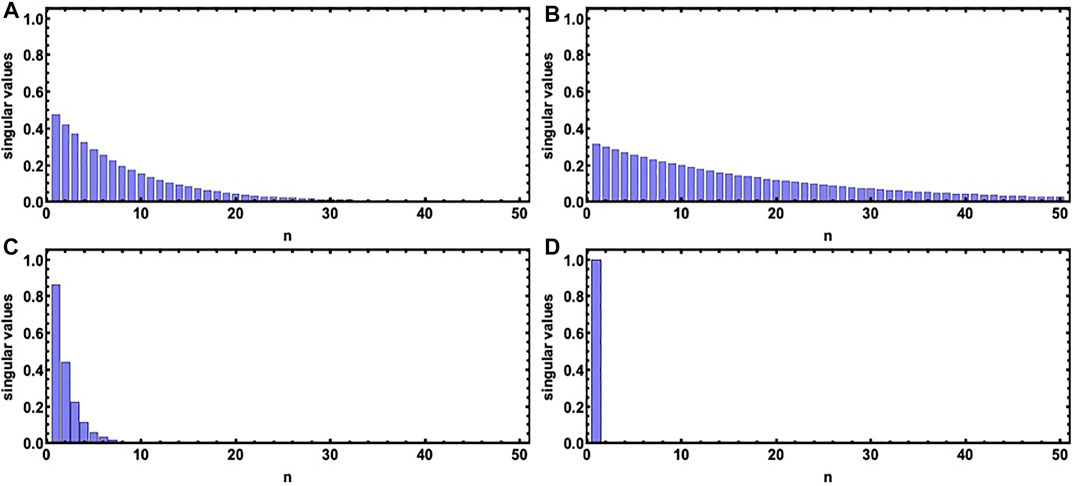
FIGURE A1. Singular values for the three sets of entangled biphoton sources corresponding to a similar parameter regime of the ones used in the simulations of Figure 3. For the first two plots [i.e., in (A,B)] the values are truncated at n_svd = 50, and for the third one [i.e., in (C)], at n = 25 (after normalization). The classical two-photon pulse yields, as expected, n_svd = 1.

A2 Phonon Parameters

The site-independent spectral function is composed of discrete frequencies which primarily induce multiple timescales Markovian dissipation. Here we enlist the parameter values for the 48 structured phonon modes used in the simulation [59–62]. Along with these values, the values of other parameters are given as, γ_j (cm⁻¹) = 30.0 for all the multimode Brownian oscillators. Corresponding Figure A2 illustrates the spectral density distribution. The parameter values for the overdamped oscillator are given by, λ₀ (cm⁻¹) = 37.0 and γ₀ (cm⁻¹) = 30.0.

FIGURE A2

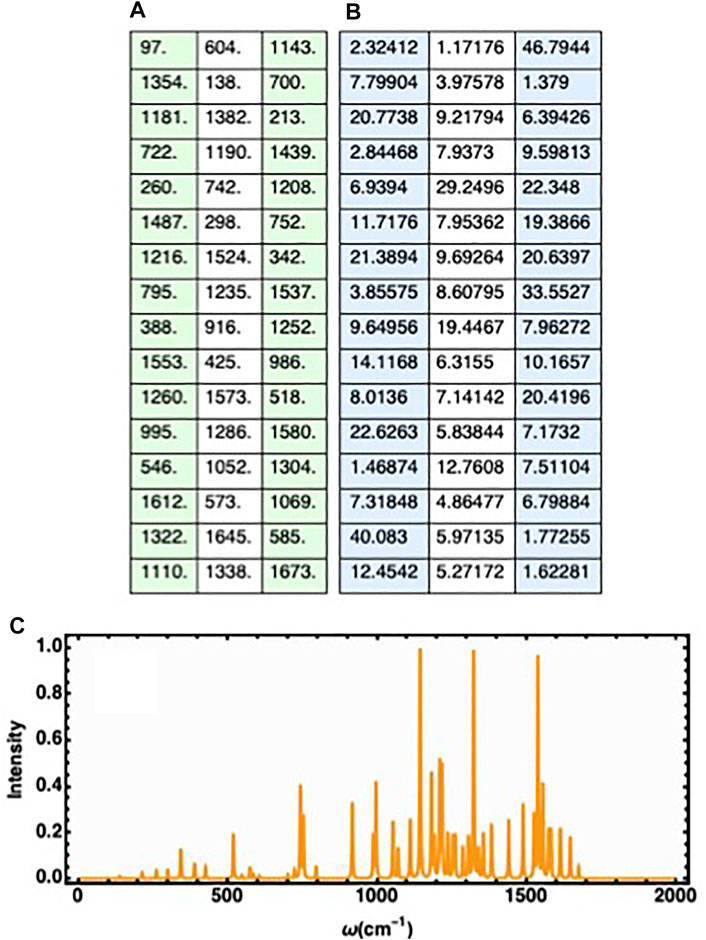
FIGURE A2. (A,B) The list of the υ_j (cm⁻¹) parameters corresponding to the multi-mode Brownian oscillators.The list of the λ_j (cm⁻¹) parameters corresponding to the multi-mode Brownian oscillators. (C) The spectral function of the structured phonon modes (corresponding to the multi-mode Brownian oscillators) used in the simulation.