- 1Department of Physics and Astronomy, University of California, Davis, Davis, CA, United States
- 2Ames Laboratory U.S. DOE and Department of Physics and Astronomy, Iowa State University, Ames, IA, United States
Nuclear magnetic resonance provides a wealth of information about the magnetic and nematic degrees of freedom in the iron-based superconductors. A striking observation is that the spin lattice relaxation rate is inhomogeneous with a standard deviation that correlates with the nematic susceptibility. Moreover, the spin lattice relaxation is strongly affected by uniaxial strain, and in doped samples it depends sensitively upon the history of the applied strain. These observations suggest that quenched strain fields associated with doping atoms induce a nematic glass in the iron pnictide materials.
1 Introduction
Electronic nematic order, in which low energy electronic degrees of freedom drive a crystal to spontaneously break discrete rotational symmetry without simultaneously breaking translational symmetry, has attracted broad interest in correlated electron physics [1]. Much of this interest stems from observations that unconventional superconductivity tends to emerge in materials exhibiting competing ground states with different broken symmetries, including nematic, charge, and/or spin density wave fluctuations [2–6]. Measurements of the nematic susceptibility in the iron based superconductors indicated the presence of a putative nematic quantum critical point under the dome of superconductivity in these materials [7, 8]. These observations have suggested a connection between quantum critical nematic fluctuations and the pairing mechanism for superconductivity [9–13]. It is thus important to understand the nature of the nematic fluctuations and their relationship to the coexisting antiferromagnetism throughout the phase diagram.
Nuclear magnetic resonance (NMR) provides a wealth of information about both the magnetic and nematic degrees of freedom in the iron-based superconductors [14]. Studies under uniaxial strain offer an important new direction in thermodynamic phase space to explore the physics of nematicity. Such experiments can broadly be separated into those that probe the static properties of the magnetic and nematic order, and those that probe the dynamical properties. The latter set of experiments have yielded some important surprises, such as a change in the spin anisotropy as a function of strain [15], and the presence of dynamical inhomogeneity when the materials are doped [16]. Below we discuss how NMR probes these broken symmetries and their fluctuations, and summarize results of experiments under uniaxial strain, both in the undoped and doped materials. These observations are consistent with the emergence of a nematic glass in doped samples, possibly driven by the presence of random strain fields from quenched disorder.
2 Coupling to Nuclear Spins
The 75As nuclei, with 100% abundance and spin I = 3/2, are excellent sensors of both the nematic and magnetic degrees of freedom in the iron pnictide superconductors. Figure 1 shows the unit cell and indicates the hyperfine coupling between the As nuclei and the four nearest neighbor Fe electronic moments. The As also has a significant quadrupolar moment, Q = 3.14 × 10−29 m2, which couples to the surrounding electric field gradient (EFG) [17]. The hyperfine and quadrupolar couplings enable microscopic studies of both the magnetic and nematic susceptibilities of the electronic degrees of freedom.
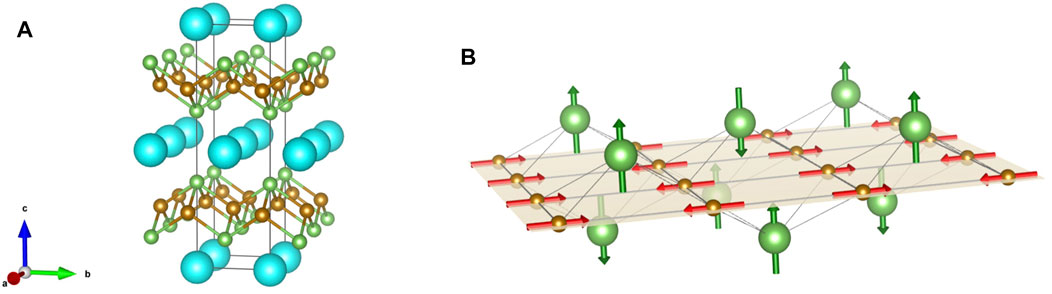
FIGURE 1. (A) BaFe2As2 unit cell. Ba is cyan, Fe is brown and As is green. (B) The hyperfine field (green arrows) at the As sites in the antiferromagnetic state, with the Fe moments (red) oriented in the plane.
2.1 Hyperfine Interaction
The hyperfine coupling is given by:
where
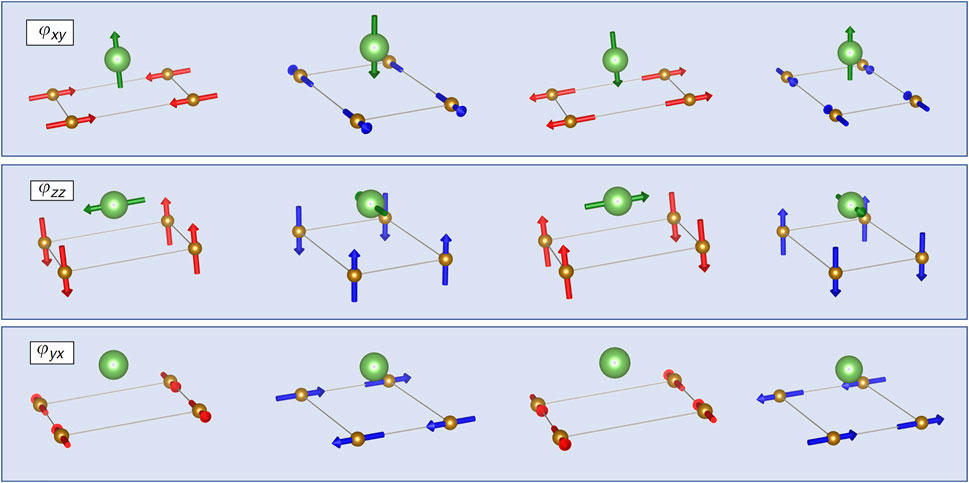
FIGURE 2. The hyperfine field at the As site (green) for the four degenerate domains with in-plane Fe moments oriented parallel to the ordering vector (ϕxy nematic order, upper row), with c-axis Fe moments (ϕzz nematic order, middle row) and with in-plane moments oriented perpendicular to the ordering vector (ϕyx nematic order, bottom row). Red and blue correspond to the two different nematic domains (positive and negative strains). Within each nematic domain, there are two different antiferromagnetic configurations.
Other magnetic orderings can be present in the pnictides, beyond the stripe-type spin density wave illustrated in Figure 2. In particular, the spin-vortex crystal configuration, in which the Fe spins form either loop or hedgehog structures, can be stabilized when a glide symmetry across the Fe planes is broken [20]. This type of order was recently identified in Ni-doped and Co-doped CaKFe4As4 [21]. There are two crystallographically distinct As sites in this structure, and the hyperfine field either vanishes at both sites for loop spin-vortex crystal order, or is aligned along the c axis for one As site and vanishes for the other As site for hedgehog spin-vortex crystal order. In this system, doping induces the latter, which was identified by NMR.
Note that when the Fe is substituted by another transition metal, the symmetry among the hyperfine couplings of the four nearest neighbors is broken, and the hyperfine field vector can acquire a component perpendicular to the c axis [22]. This effect contributes to inhomogeneous broadening in doped samples. In the presence of nematic order, the C4 symmetry of the lattice is broken, and in principle Aaa ≠ Abb. This asymmetry has not been observed directly. In FeSe, the Knight shift tensor becomes anisotropic, with Kaa ≠ Kbb, where Kαα = Aααχαα, and χαα is the static magnetic susceptibility [5]. However, in this case the anisotropy is believed to reflect that of the susceptibility, i.e., χaa ≠ χbb in the nematic phase, rather than an asymmetry in the hyperfine coupling [23]. Curiously, χaa > χbb in FeSe, but χbb > χaa in BaFe2As2, LaFeAsO, and NaFeAs [24–26], which may reflect different natures of the nematic order in these materials [27]. In particular, the nematic order parameter in the latter can be understood in terms of differential occupations between the dyz and dxz orbitals, whereas in the former the nematic order may involve more complex superpositions between 3d orbitals, giving rise to bond-centered nematic order [23, 28, 29]. The sign of the resistivity anisotropies in BaFe2As2 and FeSe match those of the magnetic anisotropies [24, 30], suggesting a common origin for the two.
2.2 Quadrupolar Interaction
For nuclei with spin I > 1/2, the quadrupolar coupling is given by:
where the EFG tensor is given by:
and V is the electrostatic potential at the As site. This quantity is dominated by the occupation of the As 4p orbitals, which in turn are hybridized with the dxz,yz-orbitals of the neighboring Fe atoms [31]. The EFG asymmetry parameter is given by:
This quantity vanishes in the tetragonal phase because the As 4px and 4py orbitals are degenerate, hence νxx = νyy [32]. The EFG tensor is always traceless, thus in this case it can be characterized by a single quantity, νzz. The magnitude of νzz depends on the degree of hybridization of the As 4pz orbital, and is sensitive to the c-axis length of the unit cell [33–35] and also varies with temperature [18, 36–38].
The EFG is strongly affected by doping. Replacing the Fe by another transition metal, or replacing the As by P, will give rise to spatially-varying strain fields that will distort the electrostatic potential and alter the EFG tensor. This effect can lower the symmetry such that νxx ≠ νyy, and create non-zero off-diagonal terms of the tensor. In some cases the effect is sufficiently large that separate resonances can be detected for sites that are adjacent to the substitutional site [31, 39]. This sensitivity to disorder tends to significantly broaden the NMR resonance frequencies in doped samples relative to the parent compound. In doped Ba(Fe,Co)2As2 the width of the quadrupolar satellites is dominated by a variation of η that exhibits a Curie-Weiss temperature dependence, which has been associated with the growth of nematic correlations surrounding the dopant atoms [40]. A similar effect has been observed in FeSe where the magnetic linewidth is broadened by the presence of crystal defects (there is no quadrupolar interaction for Se) [41]. In this case, the Knight shift anisotropy reflects the growth of an Edwards-Anderson order parameter of the nematicity [42].
In the presence of long range nematic order, the C4 symmetry of the EFG tensor is broken and νxx ≠ νyy [43]. In CaFe2As2 η reaches 0.4 at low temperature, but in BaFe2As2 and SrFe2As2, η reaches 1.2 and 1.4, respectively, reflecting the fact that νxx and νyy have opposite signs [33]. Note that it is sometimes customary to define the principal axes of the EFG such that the eigenvalues |Vzz|≥|Vyy|≥|Vxx|, so that 0 ≤ η ≤ 1. Here we do not follow this convention, maintaining the Vzz associated with the crystal c axis as in the tetragonal phase. This choice is the reason that η > 1, which would correspond to a confusing rotation of orientation of the principal axes under the customary definition. These changes reflect a dramatic rearrangement of the charge distribution around the As nucleus below the structural transition, despite an orthorhombicity of only approximately 1%. The EFG tensor is dominated by the occupations of the As 4p orbitals, which in turn are hybridized with the Fe 3dyz and 3dxz orbitals [31, 32]. These orbitals are degenerate in the tetragonal phase, but develop a splitting on the order of 40 meV in the nematic phase [44]. As a result, the relative occupations of the As px and py orbitals change and alter the EFG.
2.3 NMR Spectra
In order to resolve the in-plane asymmetry that emerges in the Knight shift or EFG tensors, it is important to measure the NMR spectra of carefully oriented single crystals. In an external magnetic field, the As nuclear spins experience the sum of three interactions:
where fsat1,2 and fcen are the frequencies of the two satellites and the central transition, θ is the angle between H0 and c, and ϕ is the azimuthal angle of the projection of H0 in the ab plane. The Knight shift is given by:
The second order correction to the central transition is given by:
Measurements of the two satellite transitions as a function of field orientation can be used to extract the Knight shift and EFG tensors.
In the tetragonal phase, there are three distinct resonances for each As in the unit cell (e.g., one As site in AFe2As2). However, in the nematic phase there are multiple domains in an untwinned crystal, giving rise to extra resonances. If the magnetic field is oriented in the plane, then there may be two sets of resonances associated with these two domains because the azimuthal angle, ϕ, differs for each domain, as observed in Figure 3. This behavior is illustrated in Figure 4. In general, there are five distinct transitions (six if the Knight shift is also anisotropic), but in certain directions the spectra from the two domains overlap and three resonances are recovered. Large values of |η| cause the satellites to switch positions from below to above the central transition as the in-plane angle ϕ is rotated.
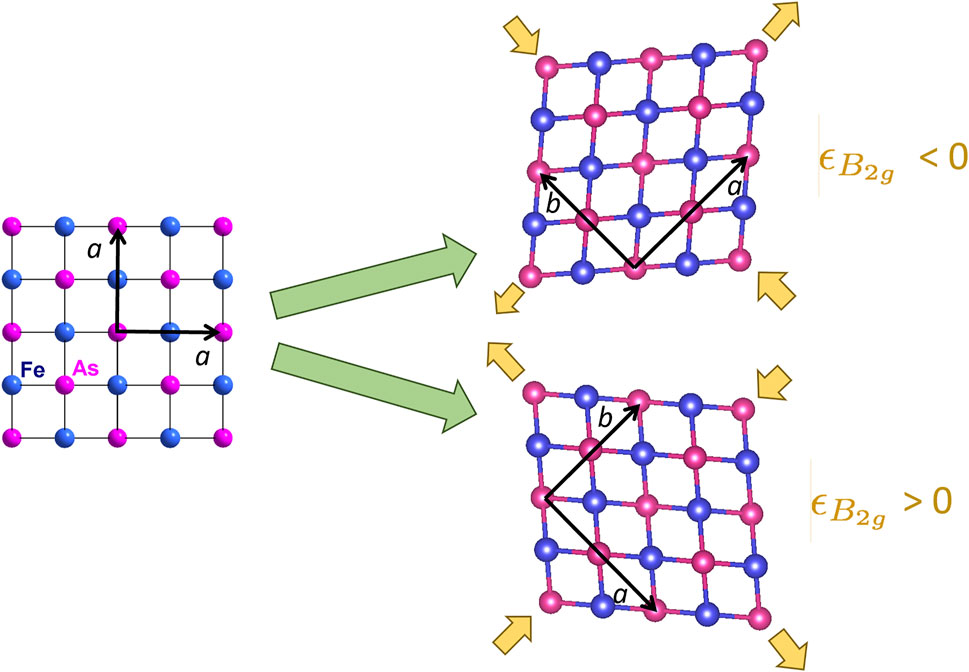
FIGURE 3. Fe-As plane in tetragonal and orthorhombic phase of BaFe2As2. Orange arrows indicate direction of displacements giving rise to two domains with positive and negative B2g strain. Strain is labeled by the unit cell of the tetragonal phase, so uniaxial strain along the [110]T direction of the tetragonal unit cell gives rise to a B2g distortion.
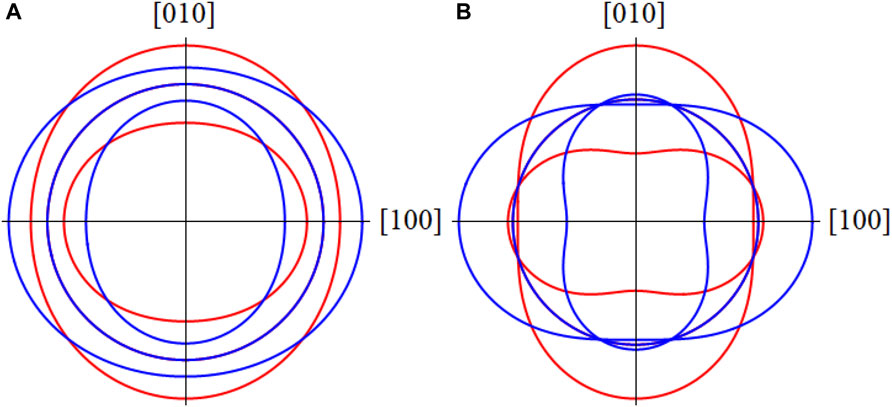
FIGURE 4. Polar plots of the three resonance frequencies of the As for |η| = 0.4 (A) and for |η| = 1.2 (B). Blue and red correspond to two nematic domains with ± η, as a function of in-plane field direction. In this case, we assume Kxx = Kyy. The directions [100] and [010] correspond to the orthorhombic unit cell directions. In general, there are five distinct transitions, but for certain angles the two sets of satellites overlap. When |η| > 1, the two satellites for each domain reverse, crossing the central transition.
When η is non-zero the nuclear spin Hamiltonian does not commute with
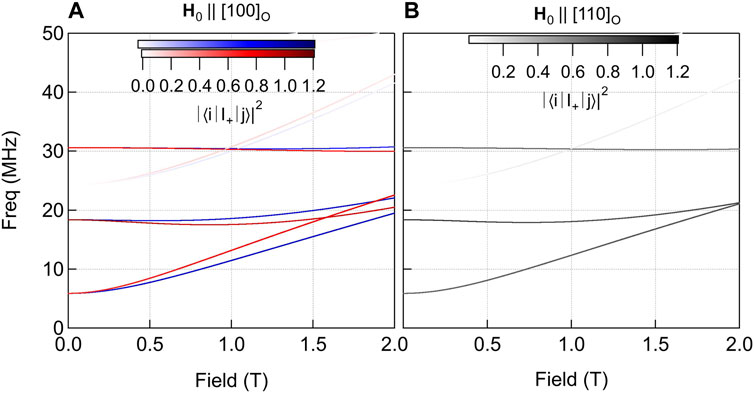
FIGURE 5. Resonance frequencies versus applied magnetic field, H0, oriented either along the orthorhombic [100] (A) or [110] directions (B) assuming an internal field of 2.5 T along c and an EFG of νzz = 12.4 MHz with η = 0.4, corresponding to the case of CaFe2As2. Red and blue correspond to the two nematic domains. The intensity of the transitions are given by the matrix elements |⟨i|I+|j⟩|2, where i, j correspond to eigenstates of the nuclear spin Hamiltonian. Hidden transitions should be visible for certain field ranges.
2.4 Relaxation Rate
The hyperfine field, Hhyp, and the EFG not only give rise to static spectral signatures, but their fluctuations can also drive relaxation of the nuclear spins. The nuclear spin energies are generally several order of magnitude smaller than the relevant electron energies, and thus the nuclear spin ensemble can easily be manipulated to have a non-equilibrium distribution among the energy levels. The nuclear spins will return to thermal equilibrium with the “lattice,” or the electronic spin system, over a time scale, T1, known as the spin-lattice relaxation time. This rate,
where
When the electronic system is close to an thermodynamic instability, critical fluctuations will slow down and may have a dramatic effect on
Usually ωNτc ≪ 1, but close to a phase transition where there is critical slowing down, τc can approach infinity as a power law. As a result,
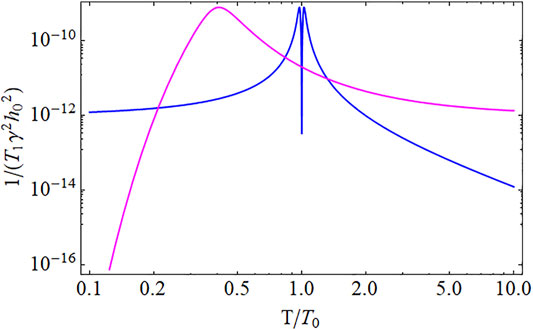
FIGURE 6. Calculated spin lattice relaxation rate versus temperature using Eq. 10 for two different models for the temperature dependence of the autocorrelation time, τc. The blue curve assumes a power law divergence: τc ∝|T − T0|−2, appropriate for critical slowing down at a phase transition. The sharp dip around T0 is usually not observable and there is only a single peak. The purple curve assumes an activated form:
As discussed above in Section 2.3, the nuclear spin eigenstates become superpositions of the Iz states for non-zero values of η. In this case, it is important to consider spectral densities other than those described in Eqs 6, 7 to account for fluctuations in other directions. For example, hyperfine field fluctuations, Hhyp,z, may play a role in relaxing the nuclear spins. In such cases the form of the relaxation function is more complicated, and Eq. 8 will contain more terms.
2.4.1 Quadrupolar Relaxation From Nematic Fluctuations
Although magnetic relaxation is usually dominant, quadrupolar relaxation should also be present in the pnictides because the EFG changes dramatically at the nematic phase transition. This effect has been investigated in BaFe2(As1−xPx)2 by comparing the relaxation of the 75As to 31P [43]. The phosphorus isotope has spin I = 1/2, and does not have a quadrupolar moment. It therefore is only sensitive to magnetic fluctuations, whereas the As probes both magnetic and quadrupolar fluctuations. Importantly, both the As and the P are located in the same crystallographic site, and experience similar hyperfine interactions. In fact, the 75As exhibits a higher relaxation rate, indicating the presence of a second relaxation channel that is, not probed by the 31P. Moreover, the extra relaxation increases with decreasing temperature, and exhibits a peak at the nematic ordering temperature. An analysis of the extra relaxation rate suggests that the nematic susceptibility diverges below TN for the lightly doped system, and below Tc for the optimally doped system. It was not possible to quantitatively disentangle the contributions from the magnetic and quadrupolar channels separately, primarily because the doping introduced inhomogeneous relaxation, as discussed below in Section 4. The three relaxation channels (one magnetic and two quadrupolar) may also be coupled to one another. For example, a nematic fluctuation can give rise spectral densities J (ωN), J(1)(ωN), and J(2)(ωN). Nevertheless, this work provided direct proof of nematic fluctuations that diverge near the superconducting transition temperature, Tc. Theoretical work has suggested that nematic fluctuations may play a role in the superconducting pairing in these materials [9, 11].
3 Response to Uniaxial Strain
In the iron based superconductors, the electronic nematic degrees of freedom couple to lattice strain with B2g symmetry: ɛB2g = (ɛxx − ɛyy)/2, where x and y are defined with respect to the tetragonal unit cell as illustrated in Figure 3 [4]. This coupling gives rise to a linear response of the electronic nematicity to external strain on a crystal. Uniaxial strain can be applied via different techniques, however in recent years piezoelectric-based strain cells have demonstrated excellent properties that enable one to carefully control the level of strain even at cryogenic temperatures [50]. Even though piezoelectric actuators do not have linear response to control voltages, the strain can be controlled through feedback control algorithms for the long periods of time necessary for NMR experiments [51]. The strain is measured by a capacitive dilatometer. Note that even though the device applies a uniaxial stress, σ0, along the x direction, the response of the crystal is not a pure uniaxial strain. Rather, the non-zero stress tensor elements become: ɛxx = σ0/E and ɛyy = ɛzz = −νσ0/E, where E is the Young’s modulus and ν is the Poisson’s ratio of the material. This gives rise to strain in two symmetry channels:
On the other hand, the electronic nematicity has a much stronger response to B2g strain than A1g, thus uniaxial stress is sufficient to probe the intrinsic B2g nematic response [7].
3.1 Spectra
In BaFe2As2, uniaxial strain dramatically alters the EFG tensor and η ∝ɛxx, as illustrated in Figure 7 [32]. In the absence of strain, the crystal remains tetragonal down to the nematic transition temperature Ts = 135 K, in which case the EFG tensor spontaneously develops an asymmetry such that νxx ≠ νyy. However, in the presence of a finite strain field, η becomes finite above Ts. In fact, η ∝ɛxx and the constant of proportionality is the nematic susceptibility. As seen in Figure 7, the response is largest just above Ts, where the nematic susceptibility diverges. This behavior is illustrated in Figure 8, which reveals that dη/dɛxx ≈ 300 at Ts.
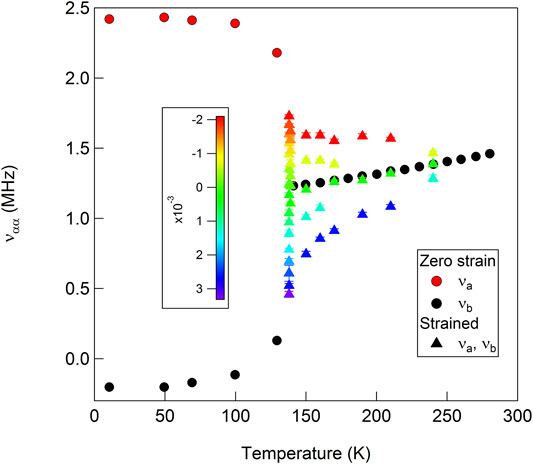
FIGURE 7. The As EFG components, νa = νxx and νb = νyy, as a function of temperature and uniaxial strain. The color bar indicates ɛxx. The circles are the measured values from [18].
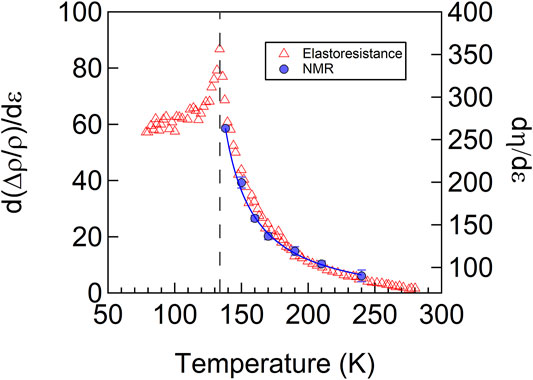
FIGURE 8. The nematic susceptibility measured by the EFG asymmetry parameter, η and via elastoresistance measurements in BaFe2As2. The solid line is a fit to a Curie-Weiss expression. Reproduced from [32].
Uniaxial stress has also been utilized to study the NMR spectra in LaFeAsO and FeSe [23]. In this case, compressive stress on the order of 10–20 MPa was applied by tightening a screw. A similar approach in which a crystal is suspended between the prongs of a horseshoe-shaped device was also utilized for NMR studies under tensile strain [52]. Neither approach directly measures the strain, precluding the possibility for feedback control. Moreover, differential thermal contraction may also give rise to finite strain fields even without applied stresses via the tightening screw. Nevertheless, such approaches can be used to mechanically detwin the crystal in the nematic phase [53]. If the crystal is cooled in a finite strain field, then a single nematic domain should nucleate below the transition. For a twinned crystal, there should be two sets of resonances as discussed above in Section 2.3. In detwinned or partially de-twinned crystals, the relative intensity changes. In FeSe, this approach enabled the identification of which resonance corresponds to which domain [23].
3.2 Relaxation Rate
The spin-lattice-relaxation rate varies strongly with uniaxial strain in BaFe2As2, as shown in Figure 9 [15]. Strain enhances the relaxation rate and the effect is anisotropic: the enhancement is stronger for in-plane fields than for out-of-plane fields. The enhancement can be understood qualitatively by realizing that strain enhances the antiferromagnetic ordering temperature, TN, thus for T > TN, the correlation length should grow with increasing strain. The correlation time τc grows with increasing correlation length, thus enhancing
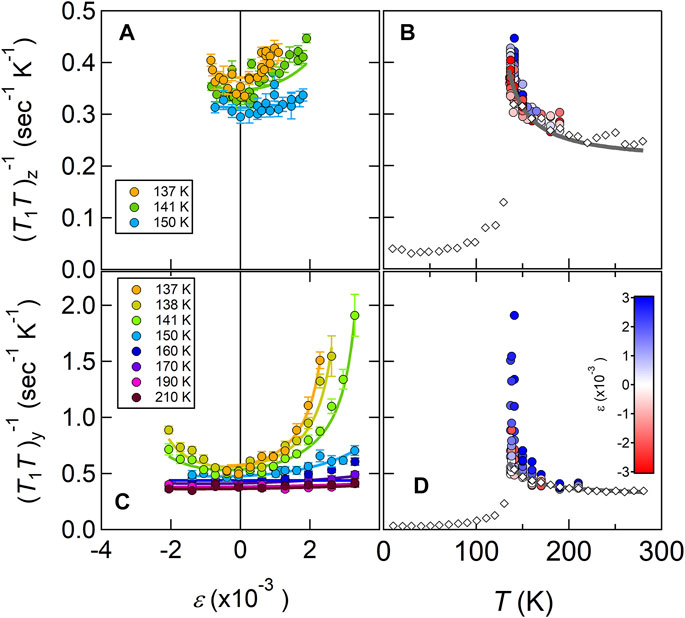
FIGURE 9.
A more complete picture of the nematicity and the antiferromagnetism can be obtained by analyzing the reciprocal-space structure of the spin susceptibility tensor, χαβ(q). In the disordered tetragonal phase, χxx(q) = χyy(q), but in the presence of nematicity these components are no longer equal. In the ordered phase, the susceptibility diverges at the antiferromagnetic ordering wavevectors, Q1 = (π, 0) in one domain, and Q2 = (0, π) in the other domain. A nematic order parameter can defined as
The anisotropy of
4 Glassy Behavior
4.1 Relaxation
Measurements of the doped pnictides under strain are challenging because the doping introduces both static and dynamic inhomogeneities. The quadrupolar linewidths of the satellites broaden significantly with doping, thus it is more difficult to discern static changes in the resonances due to strain. Measurements of the spin-lattice-relaxation rate are more straightforward and do not require sharp resonances, but doping introduces a distribution of local hyperfine fields and autocorrelation times, τc, so that there is no longer a homogeneous
4.1.1 Stretched Relaxation
Heterogeneous spin lattice relaxation is directly manifest in the behavior of the magnetization and leads to a stretching exponent. In this case, the nuclear magnetization is described by:
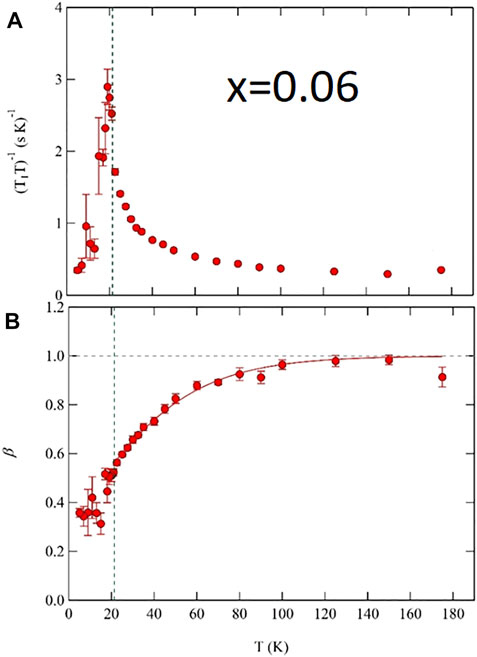
where M0 is the initial magnetization, Meq is the thermal equilibrium magnetization, and 0 < β ≤ 1 is a stretching exponent [55]. β = 1 corresponds to homogeneous relaxation, but in several doped pnictides β ∼ 0.4–0.9 depending on the doping level and temperature [16, 56–60]. A typical temperature dependence is shown in Figure 10 for x = 0.06. For temperatures greater than approximately 100 K, the relaxation is homogeneous, but below this temperature β decreases from unity to approximately 0.4 at TN. The exponent β is a measure of the width of the distribution of local relaxation rates,
4.1.2 Inverse Laplace Transform
Rather than fitting the magnetization with a stretched exponent, as in Eq. 13, it is possible to fit the data assuming a particular form of
In this case the median of the distribution (
An alternative approach is to extract
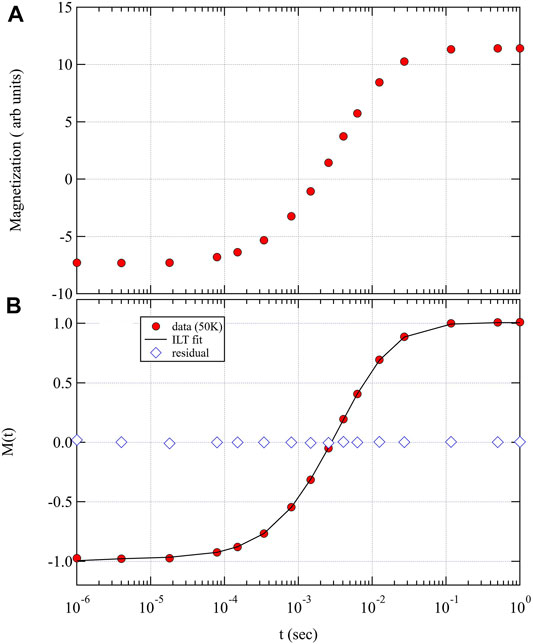
FIGURE 11. Magnetization versus recovery time measured at 50 K in Ba (Fe1−xCox)2As2 with x = 0.06. Panel (A) shows the raw data, and panel (B) shows the data after normalization such that M(∞) = 1 and M(0) = −1. The solid line shows the fit using the ILT algorithm.
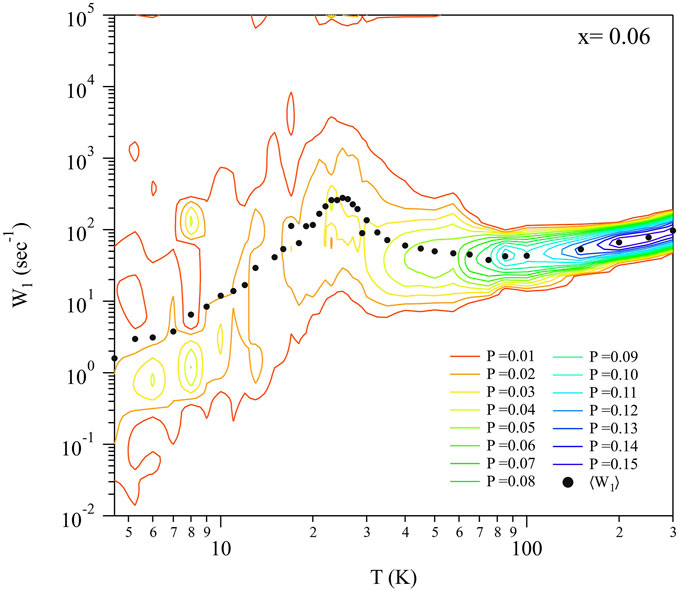
FIGURE 12. Distribution of relaxation rates,
4.1.3 Nematicity and Dynamical Heterogeneity
Similar glassy behavior has been observed in the cuprates and been associated with stripe-glass behavior [65–73]. The cuprates, however, are doped Mott insulators, and the glassy behavior was attributed to intrinsic frustration between the competing effects of Coulomb repulsion and charge segregation [74–76]. The iron arsenides do not exhibit charge ordering and thus a different mechanism must be driving the glassy dynamics. This behavior is present for a range of doping levels, and is most pronounced near optimal doping where Tc reaches a maximum. Figure 13 shows a phase diagram for both Cu and Co doping. Like Co, Cu introduces extra electrons but it also suppresses superconductivity [77]. The color scale indicates the standard deviation of a log-normal distribution fit, σ1. As shown in Figure 13, the distribution exhibits the greatest width in the vicinity of a putative nematic quantum critical point near x ∼ 0.07 if there were no superconductivity. This behavior is striking because it bears a similarity to the divergent nematic susceptibility measured by elastoresistance in these materials [7, 8]. In other words, the width of the distribution of relaxation rates correlates with the magnitude of the nematic susceptibility.
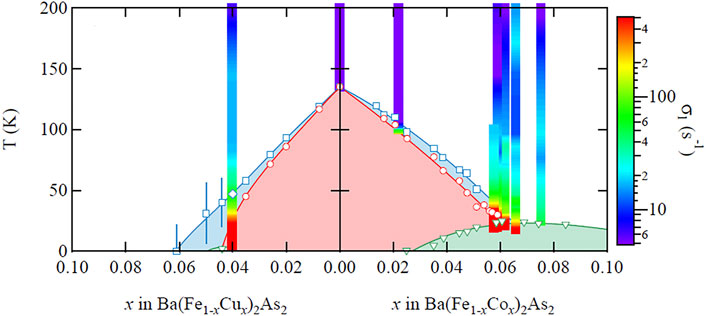
FIGURE 13. Phase diagram of Ba(Fe1−xCux)2As2 and Ba(Fe1−xCox)2As2 with the width of the distribution, σ1 shown as the color scale. The blue diamonds represent Ts, the red circles represent TN, and the green triangles represent Tc. Reproduced from [16].
What is the origin of this glassy behavior, and is there a physical connection with the nematic susceptibility? A compelling hypothesis is that the dopants introduce quenched random strain fields that couple to the nematic order parameter and give rise to a distribution of local correlation times, τc. Local strains can nucleate different nematic domains, even in absence of long range nematic order. The result is a nematic glass, in which a distribution of local nematic domains (with different orientations) exist throughout the sample, each fluctuating with a different correlations times. These nematic fluctuations in turn drive spin fluctuations that are reflected in the distribution
Another hypothesis for the inhomogeneous dynamics is that static inhomogeneity of the EFG and Knight shift tensors induced by the dopants suppresses spin diffusion among the nuclear spins, so that they do not all relax with a common spin temperature. In principle, dipolar interactions between neighboring nuclear spins I1 and I2 may contain terms such as
4.1.4 Edwards-Anderson Parameter
In a recent paper, Wiecki and collaborators pointed out that the NMR linewidth of 77Se in FeSe is directly proportional to the Edwards-Anderson parameter in a random-field Ising model of the nematicity [42]. Crystal defects provide local strain fields, hi, at site i, and the enhanced nematic susceptibility gives rise to large spatial variations of local nematicity, ϕi(hi) (we drop the distinction between ϕxy, ϕyx and ϕzz for simplicity). In this case, the Knight shift is known to vary linearly with ϕ, and the second moment of the NMR spectrum is directly proportional to the Edwards-Anderson parameter:
A similar approach can be utilized to analyze the distribution of relaxation rates,
where α depends the correlation length, and is hence strongly temperature dependent [15]. In the doped system, we can model the distribution of relaxation rates by assuming a distribution of local strain fields, so that:
where pσ(hj) is the disorder distribution [42]. The second moment of
As shown in Figure 13, σ1 is a strong function of temperature and doping. The magnitude of this quantity is given in part by the coefficient α, reflecting the growth of antiferromagnetic fluctuations. Note, however, that σ1 would be zero if qEA = 0. In other words, σ1 is finite because the Edwards-Anderson parameter is non-zero, which indicates the presence of a nematic glass. Higher order corrections to the relationship between W1 and strain, and the presence of other strain channels due the dopant atoms, are likely to modify the quantitative relationship between σ1 and qEA, and these issues should be addressed in future theoretical work.
4.2 Response to Strain
In principle, an external strain field of sufficient magnitude might overcome the local strain fields and give rise to more homogeneous relaxation. This hypothesis was tested in Ba(Fe1−xCox)2As2 with x = 0.048 under tensile strain [52]. Although the magnitude of
4.3 Strain Hysteresis
Although the width of the
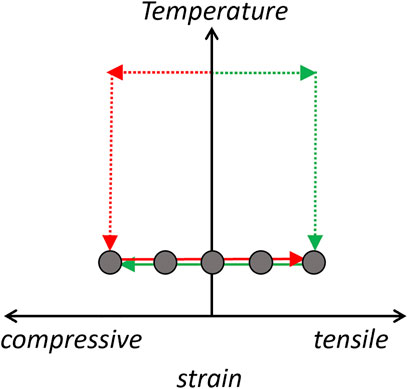
FIGURE 14. Protocol for strain hysteresis measurements. The sample is first cooled (red arrows) in a compressive strain field from room temperature. Spin lattice relaxation measurements are then conducted at several different increasing strain levels as the displacement increases. The sample is then returned to room temperature and zero strain. Finally the sample is strain cooled under tensile strain to the same base temperature and measurements are conducted for several values of decreasing displacement. Figure 15 compares the measured values for both protocols for various temperatures.
Figure 15 shows the results of such a study on Ba(Fe1−xCox)2As2 for four different base temperatures for x = 0.059. As expected, β decreases as temperature is reduced, but remains independent of the applied strain, and is the same for both tensile- and compressive-cooling. On the other hand, the median of the distribution,
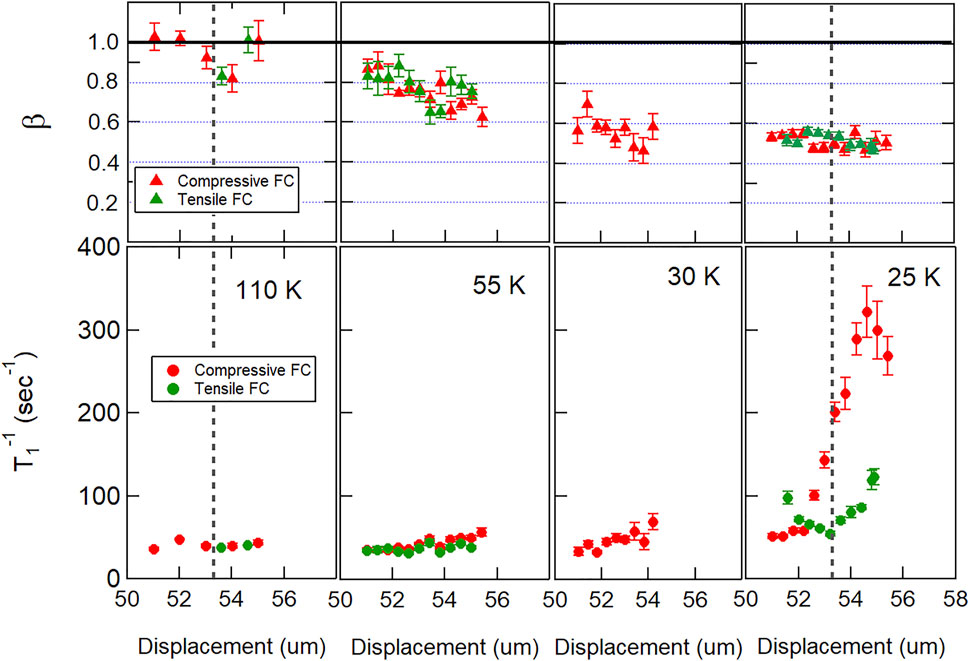
FIGURE 15.
Note that the horizontal axes in Figure 15 are displacement, not strain. Strain is defined as ɛ = (d − d0)/L, where d is the displacement of the capacitative dilatometer, d0 is the equilibrium unstrained displacement, and L is the sample length. d0 can be determined at room temperature, but thermal contractions of both the sample and the strain device make it difficult to determine d0 under cryogenic conditions. It is best to utilize an independent measure of strain, such as the EFG tensor discussed in Section 3.1, to find the displacement corresponding to ɛ = 0. Such a calibration was not possible for the
Despite these complications, these measurements reveal that
4.4 Theoretical Models
A quantitative theory to connect the measured distribution of the spin-lattice-relaxation rate,
On the other hand, the iron pnictides exhibit both antiferromgnetism and nematicity, and there are two types of spin order for each of two possible nematic domains, as illustrated in Figure 2. Recently, a random Baxter-field model was proposed as an alternative to capture both the nematic and antiferromagnetic fluctuations in the presence of quenched random strain fields [84]. In this case, there are two Ising variables at each lattice site associated with the magnetic and the nematic degree of freedom. These two variables are coupled due to the next nearest neighbor coupling, J2, in the J1 − J2 model for the iron pnictides [4]. Random strain fields couple only to the nematic degree of freedom, but the magnetic variable is also affected and consequently the system breaks up into domains of all four configurations illustrated in the top row of Figure 2.
5 Summary and Conclusion
NMR is a powerful tool to investigate nematicity in the iron based superconductors, providing microscopic insight in the local antiferromagnetic and nematic order parameters. Investigations of the NMR response to uniaxial strain in BaFe2As2 and FeSe have revealed important information about the anisotropy of the dynamical and static spin susceptibilities. In particular, the temperature dependence of the spin fluctuations under strain reflect an unusual piezomagnetic response in which the antiferromagnetically ordered spins can change their orientation direction under sufficient strain.
The doped pnictides have been less studied under strain because static and dynamical heterogeneity present in these materials render interpretation of results more difficult. Strain fields surrounding dopants create random fields that couple to the nematic order parameter, which may have a large response at low temperature. As a result, the NMR spectra broaden significantly, reflecting a distribution of static EFGs, some of which may indicate static local nematic order. More importantly, the NMR spin lattice relaxation rate reveals a broad distribution of local spin fluctuations that gradually freeze out at lower temperatures. This distribution likely reflects the correlated nematic fluctuations breaking up into spatial domains in a nematic glass. This distribution depends on the history of the strain field, but remains broad even at the highest uniaxial strain levels applied. These results suggest that quenched disorder creates large random strain fields.
Future studies on other doped materials may shed important light on the nature of the nematic glass. For example, hole doping by substituting Ba with K may introduce milder levels of local strain fields, in which case external strain might be able to induce homogeneous relaxation. Studies of static hysteretic behavior with strain in the ordered nematic phase may also shed important light on the mesoscopic physics of the domain formation, the coercive strain fields, and remnant nematicity. Unfortunately, NMR studies under strain require small crystals, and the NMR signal in doped samples tends to be suppressed due to the same glassy physics giving rise to the stretched relaxation. These effects conspire to make such experiments on doped samples particularly challenging.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
TK acquired the NMR data on crystals grown and characterized by MT, RP, SB and PC, and NC conceived the experiments and wrote the manuscript.
Funding
Work at UC Davis was supported by the NSF under Grant No. DMR-1807889, and the UC Laboratory Fees Research Program (LFR-20-653926). Work at Ames Lab (PC, SB, RP, MT for growth and basic characterization of samples) was supported by the U.S. Department of Energy, Office of Basic Energy Science, Division of Materials Sciences and Engineering. Ames Laboratory is operated for the U.S. Department of Energy by Iowa State University under Contract No. DE-AC02-07CH11358.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Erica Carlson, Karin Dahmen, Stylianos Gregoriou, Lamei Nie and Rafael Fernandes for stimulating discussions.
References
1. Fradkin E, Kivelson SA, Lawler MJ, Eisenstein JP, Mackenzie AP. Nematic Fermi Fluids in Condensed Matter Physics. Annu Rev Condens Matter Phys (2010) 1:153–78. doi:10.1146/annurev-conmatphys-070909-103925
2. Kivelson SA, Fradkin E, Emery VJ. Electronic Liquid-crystal Phases of a Doped Mott Insulator. Nature (1998) 393:550–3. doi:10.1038/31177
3. Vojta M. Lattice Symmetry Breaking in Cuprate Superconductors: Stripes, Nematics, and Superconductivity. Adv Phys (2009) 58:699–820. doi:10.1080/00018730903122242
4. Fernandes RM, Chubukov AV, Schmalian J. What Drives Nematic Order in Iron-Based Superconductors? Nat Phys (2014) 10:97–104. doi:10.1038/nphys2877
5. Baek S-H, Efremov DV, Ok JM, Kim JS, van den Brink J, Büchner B. Orbital-driven Nematicity in FeSe. Nat Mater (2015) 14:210–4. doi:10.1038/nmat4138
6. Comin R, Damascelli A. Resonant X-ray Scattering Studies of Charge Order in Cuprates. Annu Rev Condens Matter Phys (2016) 7:369–405. doi:10.1146/annurev-conmatphys-031115-011401
7. Kuo H-H, Chu J-H, Palmstrom JC, Kivelson SA, Fisher IR. Ubiquitous Signatures of Nematic Quantum Criticality in Optimally Doped Fe-Based Superconductors. Science (2016) 352:958–62. doi:10.1126/science.aab0103
8. Chu J-H, Kuo H-H, Analytis JG, Fisher IR. Divergent Nematic Susceptibility in an Iron Arsenide Superconductor. Science (2012) 337:710–2. doi:10.1126/science.1221713
9. Maier TA, Scalapino DJ. Pairing Interaction Near a Nematic Quantum Critical point of a Three-bandCuO2model. Phys Rev B (2014) 90:174510. doi:10.1103/PhysRevB.90.174510
10. Schattner Y, Lederer S, Kivelson SA, Berg E. Ising Nematic Quantum Critical point in a Metal: A Monte Carlo Study. Phys Rev X (2016) 6:031028. doi:10.1103/PhysRevX.6.031028
11. Lederer S, Schattner Y, Berg E, Kivelson SA. Superconductivity and Non-fermi Liquid Behavior Near a Nematic Quantum Critical point. Proc Natl Acad Sci U.S.A (2017) 114:4905–10. doi:10.1073/pnas.1620651114
12. Malinowski P, Jiang Q, Sanchez JJ, Mutch J, Liu Z, Went P. Suppression of Superconductivity by Anisotropic Strain Near a Nematic Quantum Critical point. Nat Phys (2020) 16:1189–93. doi:10.1038/s41567-020-0983-9
13. Lederer S, Berg E, Kim EA. Tests of Nematic-Mediated Superconductivity Applied to Ba1−xSrxNi2As2. Phys Rev Res (2020) 2:023122. doi:10.1103/physrevresearch.2.023122
14. Carretta P, Prando G. Iron-based Superconductors: Tales from the Nuclei. La Rivista Del Nuovo Cimento (2020) 43:1–43. doi:10.1007/s40766-019-0001-1
15. Kissikov T, Sarkar R, Lawson M, Bush BT, Timmons EI, Tanatar MA, et al. Uniaxial Strain Control of Spin-Polarization in Multicomponent Nematic Order of BaFe2As2. Nat Commun (2018) 9:1058. doi:10.1038/s41467-018-03377-8
16. Dioguardi AP, Lawson MM, Bush BT, Crocker J, Shirer KR, Nisson DM, et al. NMR Evidence for Inhomogeneous Glassy Behavior Driven by Nematic Fluctuations in Iron Arsenide Superconductors. Phys Rev B (2015) 92:165116. doi:10.1103/PhysRevB.92.165116
18. Kitagawa K, Katayama N, Ohgushi K, Yoshida M, Takigawa M. Commensurate Itinerant Antiferromagnetism in BaFe2As2: 75As-NMR Studies on a Self-Flux Grown Single crystal. J Phys Soc Jpn (2008) 77:114709. doi:10.1143/JPSJ.77.114709
19. Smerald A, Shannon N. Angle-resolved NMR: Quantitative Theory of 75As T1 Relaxation Rate in BaFe2As2. Phys Rev B (2011) 84:184437. doi:10.1103/PhysRevB.84.184437
20. O’Halloran J, Agterberg DF, Chen MX, Weinert M. Stabilizing the Spin Vortex crystal Phase in Two-Dimensional Iron-Based Superconductors. Phys Rev B (2017) 95:075104. doi:10.1103/PhysRevB.95.075104
21. Meier WR, Ding QP, Kreyssig A, Bud’ko SL, Sapkota A, Kothapalli K, et al. Hedgehog Spin-Vortex crystal Stabilized in a Hole-Doped Iron-Based Superconductor. npj Quan Mater (2018) 3. doi:10.1038/s41535-017-0076-x
22. Dioguardi AP, apRoberts Warren N, Shockley AC, Bud’ko SL, Ni N, Canfield PC, et al. Local Magnetic Inhomogeneities Observed via 75As NMR in Ba(Fe1−xNix)2As2 with H0 ⊥ C-axis. J Phys Conf Ser (2012) 344:012022. doi:10.1088/1742-6596/344/1/012022
23. Zhou R, Scherer DD, Mayaffre H, Toulemonde P, Ma M, Li Y, et al. Singular Magnetic Anisotropy in the Nematic Phase of FeSe. npj Quan Mater (2020) 5:93. doi:10.1038/s41535-020-00295-1
24. He M, Wang L, Ahn F, Hardy F, Wolf T, Adelmann P, et al. Dichotomy between In-Plane Magnetic Susceptibility and Resistivity Anisotropies in Extremely Strained BaFe2As2. Nat Commun (2017) 8. doi:10.1038/s41467-017-00712-3
25. Zhou R, Xing LY, Wang XC, Jin CQ, Zheng G. Orbital Order and Spin Nematicity in the Tetragonal Phase of the Electron-Doped Iron Pnictides NaFe1−xCoxAs. Phys Rev B (2016) 93:060502. doi:10.1103/PhysRevB.93.060502
26. He M, Wang L, Hardy F, Xu L, Wolf T, Adelmann P, et al. Evidence for Short-Range Magnetic Order in the Nematic Phase of FeSe from Anisotropic In-Plane Magnetostriction and Susceptibility Measurements. Phys Rev B (2018) 97:104107. doi:10.1103/physrevb.97.104107
27. Jiang K, Hu J, Ding H, Wang Z. Interatomic Coulomb Interaction and Electron Nematic Bond Order in FeSe. Phys Rev B (2016) 93:115138. doi:10.1103/PhysRevB.93.115138
28. Christensen MH, Fernandes RM, Chubukov AV. Orbital Transmutation and the Electronic Spectrum of FeSe in the Nematic Phase. Phys Rev Res (2020) 2:013015. doi:10.1103/PhysRevResearch.2.013015
29. Long X, Zhang S, Wang F, Liu Z. A First-Principle Perspective on Electronic Nematicity in FeSe. npj Quan Mater (2020) 5. doi:10.1038/s41535-020-00253-x
30. Bartlett JM, Steppke A, Hosoi S, Noad H, Park J, Timm C, et al. Relationship between Transport Anisotropy and Nematicity in FeSe. Phys Rev X (2021) 11:021038. doi:10.1103/physrevx.11.021038
31. Iye T, Julien MH, Mayaffre H, Horvatic̈ M, Berthier C, Ishida K, et al. Emergence of Orbital Nematicity in the Tetragonal Phase of BaFe2(As1−xPx)2. J Phys Soc Jpn (2015) 84:043705. doi:10.7566/JPSJ.84.043705
32. Kissikov T, Sarkar R, Lawson M, Bush BT, Timmons EI, Tanatar MA, et al. Local Nematic Susceptibility in Stressed BaFe2As2 from NMR Electric Field Gradient Measurements. Phys Rev B (2017) 96:241108. (R). doi:10.1103/physrevb.96.241108
33. Dioguardi AP, Crocker J, Shockley AC, apRoberts Warren N, Lin C, Shirer KR, et al. Angular Dependent 75As NMR Study of the Electric Field Gradient in CaFe2As2. Supercond Sci Technol (2013) 26:025012. doi:10.1088/0953-2048/26/2/025012
34. Kawasaki S, Tabuchi T, Wang XF, Chen XH, qing Zheng G. Pressure-induced Unconventional Superconductivity Near a Quantum Critical point in CaFe2As2. Supercond Sci Technol (2010) 23:054004. doi:10.1088/0953-2048/23/5/054004
35. Ma L, Ji GF, Dai J, Saha SR, Paglione J, Yu W. Quenched Fe Moment in the Collapsed Tetragonal Phase of Ca1−xPrxFe2As2. Chin Phys B (2012) 22:057401. doi:10.1088/1674-1056/22/5/057401
36. Kitagawa K, Katayama N, Ohgushi K, Takigawa M. Antiferromagnetism of SrFe2As2 Studied by Single-crystal 75As-NMR. J Phys Soc Jpn (2009) 78:063706. doi:10.1143/JPSJ.78.063706
37. Baek SH, Curro NJ, Klimczuk T, Bauer ED, Ronning F, Thompson JD. First-order Magnetic Transition in Single-Crystalline CaFe2As2 Detected by As-75 Nuclear Magnetic Resonance. Phys Rev B (2009) 79. doi:10.1103/PhysRevB.79.052504
38. Baek SH, Lee H, Brown SE, Curro NJ, Bauer ED, Ronning F, et al. NMR Investigation of Superconductivity and Antiferromagnetism in CaFe2As2 under Pressure. Phys Rev Lett (2009) 102. doi:10.1103/PhysRevLett.102.227601
39. Ning FL, Ahilan K, Imai T, Sefat AS, McGuire MA, Sales BC, et al. Contrasting Spin Dynamics between Underdoped and Overdoped Ba(Fe1−xCox)2As2. Phys Rev Lett (2010) 104:037001. doi:10.1103/PhysRevLett.104.037001
40. Toyoda M, Ichikawa A, Kobayashi Y, Sato M, Itoh M. In-plane Anisotropy of the Electric Field Gradient in Ba(Fe1−xCox)2As2 NMR. Phys Rev B (2018) 97:174507. doi:10.1103/PhysRevB.97.174507
41. Wiecki P, Nandi M, Böhmer AE, Bud’ko SL, Canfield PC, Furukawa Y. NMR Evidence for Static Local Nematicity and its Cooperative Interplay with Low-Energy Magnetic Fluctuations in FeSe under Pressure. Phys Rev B (2017) 96:180502. doi:10.1103/PhysRevB.96.180502
42. Wiecki P, Zhou R, Julien MH, Böhmer AE, Schmalian J. Edwards-Anderson Parameter and Local Ising Nematicity in FeSe Revealed via NMR Spectral Broadening. Phys Rev B (2021) 104:125134. doi:10.1103/PhysRevB.104.125134
43. Dioguardi AP, Kissikov T, Lin CH, Shirer KR, Lawson MM, Grafe HJ, et al. NMR Evidence for Inhomogeneous Nematic Fluctuations in BaFe2(As1−xPx)2. Phys Rev Lett (2016) 116:107202. doi:10.1103/PhysRevLett.116.107202
44. Yi M, Lu DH, Moore RG, Kihou K, Lee CH, Iyo A, et al. Electronic Reconstruction through the Structural and Magnetic Transitions in Detwinned NaFeAs. New J Phys (2012) 14:073019. doi:10.1088/1367-2630/14/7/073019
45. Suter A, Mali M, Roos J, Brinkmann D. Mixed Magnetic and Quadrupolar Relaxation in the Presence of a Dominant Static Zeeman Hamiltonian. J Phys Condens Matter (1998) 10:5977. doi:10.1088/0953-8984/10/26/022
46. Suter A, Mali M, Roos J, Brinkmann D. Separation of Quadrupolar and Magnetic Contributions to Spin–Lattice Relaxation in the Case of a Single Isotope. J Magn Reson (2000) 143:266–73. doi:10.1006/jmre.1999.1990
47. Suter A, Mali M, Roos J, Brinkmann D. Charge Degree of freedom and the Single-Spin Fluid Model inYBa2Cu4O8. Phys Rev Lett (2000) 84:4938–41. doi:10.1103/physrevlett.84.4938
48. Vinograd I, Shirer KR, Massat P, Wang Z, Kissikov T, Garcia D, et al. Second Order Zeeman Interaction and Ferroquadrupolar Order in TmVO4. arXiv:2112.05859 (2021).
49. Nakai Y, Iye T, Kitagawa S, Ishida K, Ikeda H, Kasahara S, et al. Unconventional Superconductivity and Antiferromagnetic Quantum Critical Behavior in the Isovalent-Doped BaFe2(As1−xPx)2. Phys Rev Lett (2010) 105:107003. doi:10.1103/PhysRevLett.105.107003
50. Hicks CW, Barber ME, Edkins SD, Brodsky DO, Mackenzie AP. Piezoelectric-based Apparatus for Strain Tuning. Rev Sci Instrum (2014) 85:065003. doi:10.1063/1.4881611
51. Kissikov T, Sarkar R, Bush BT, Lawson M, Canfield PC, Curro NJ. Nuclear Magnetic Resonance Probe Head Design for Precision Strain Control. Rev Sci Instrum (2017) 88:103902. doi:10.1063/1.5002631
52. Kissikov T, Dioguardi AP, Timmons EI, Tanatar MA, Prozorov R, Bud’ko SL, et al. NMR Study of Nematic Spin Fluctuations in a Detwinned Single crystal of Underdoped Ba(Fe2−xCox)2As2. Phys Rev B (2016) 94:165123. doi:10.1103/PhysRevB.94.165123
53. Tanatar MA, Blomberg EC, Kreyssig A, Kim MG, Ni N, Thaler A, et al. Uniaxial-strain Mechanical Detwinning of CaFe2As2 and BaFe2As2 Crystals: Optical and Transport Study. Phys Rev B (2010) 81:184508. doi:10.1103/PhysRevB.81.184508
54. Liu P, Klemm ML, Tian L, Lu X, Song Y, Tam DW, et al. In-plane Uniaxial Pressure-Induced Out-Of-Plane Antiferromagnetic Moment and Critical Fluctuations in BaFe2As2. Nat Comm (2020) 11. doi:10.1038/s41467-020-19421-5
55. Johnston DC. Stretched Exponential Relaxation Arising from a Continuous Sum of Exponential Decays. Phys Rev B (2006) 74:184430. doi:10.1103/PhysRevB.74.184430
56. Hammerath F, Gräfe U, Kühne T, Kühne H, Kuhns PL, Reyes AP, et al. Progressive Slowing Down of Spin Fluctuations in Underdoped LaFeAsO1−xFx. Phys Rev B (2013) 88:104503. doi:10.1103/physrevb.88.104503
57. Bossoni L, Carretta P, Halperin WP, Oh S, Reyes A, Kuhns P, et al. Evidence of Unconventional Low-Frequency Dynamics in the normal Phase of Ba(Fe1−xRhx)2As2 Iron-Based Superconductors. Phys Rev B (2013) 88:100503. doi:10.1103/PhysRevB.88.100503
58. Takeda H, Imai T, Tachibana M, Gaudet J, Gaulin BD, Saparov BI, et al. Cu Substitution Effects on the Local Magnetic Properties of Ba(Fe1−xCux)2As2: A Site-Selective 75As and 63Cu NMR Study. Phys Rev Lett (2014) 113:117001. doi:10.1103/physrevlett.113.117001
59. Grafe HJ, Gräfe U, Dioguardi AP, Curro NJ, Aswartham S, Wurmehl S, et al. Identical Spin Fluctuations in Cu and Co Doped BaFe2As2 Independent of Doped Electrons. Phys Rev B (2014) 90:09451. doi:10.1103/PhysRevB.90.094519
60. Dioguardi AP, Crocker J, Shockley AC, Lin CH, Shirer KR, Nisson DM, et al. Coexistence of Cluster Spin Glass and Superconductivity in Ba(Fe1−xCox)2As2 for 0.060 ≤ X ≤ 0.071. Phys Rev Lett (2013) 111:207201. doi:10.1103/PhysRevLett.111.207201
61. Singer PM, Arsenault A, Imai T, Fujita M. NMR Investigation of the Interplay between Lattice, Charge, and Spin Dynamics in the Charge-Ordered High- Tc Cuprate La1.875Ba0.125CuO4. Phys Rev B (2020) 101:174508. doi:10.1103/physrevb.101.174508
62. Arsenault A, Imai T, Singer PM, Suzuki KM, Fujita M. Magnetic Inhomogeneity in Charge-Ordered La1.885Sr0.115CuO4 Studied by NMR. Phys Rev B (2020) 101:184505. doi:10.1103/physrevb.101.184505
63. Wang J, Yuan W, Singer PM, Smaha RW, He W, Wen J, et al. Emergence of Spin Singlets with Inhomogeneous Gaps in the Kagome Lattice Heisenberg Antiferromagnets Zn-Barlowite and Herbertsmithite. Nat Phys (2021) 17:1109–13. doi:10.1038/s41567-021-01310-3
64. Choi H, Vinograd I, Chaffey C, Curro N. Inverse Laplace Transformation Analysis of Stretched Exponential Relaxation. J Magn Reson (2021) 331:107050. doi:10.1016/j.jmr.2021.107050
65. Curro N, Hammel P. The Cu NMR echo Decay in Stripe Ordered La1.65Eu0.2Sr0.15CuO4. In: International Conference on Materials and Mechanisms of Superconductivity High Temperature Superconductors VI; FEB 20-25, 2000; HOUSTON, TEXAS, 341. Phys. C (2000). p. 1797–8. doi:10.1016/S0921-4534(00)01084-4
66. Curro N, Hammel P, Suh B, Hücker M, Büchner B, Ammerahl U, et al. Inhomogeneous Low Frequency Spin Dynamics in La1.65Eu0.2Sr0.15CuO4. Phys Rev Lett (2000) 85:642–5. doi:10.1103/PhysRevLett.85.642
67. Hunt AW, Singer PM, Cederström AF, Imai T. Glassy Slowing of Stripe Modulation in (La,Eu,Nd)2−xSrxCuO4: a 63Cu and 139La NQR Study Down to 350 mK. Phys Rev B (2001) 64:134525. doi:10.1103/PhysRevB.64.134525
68. Hunt A, Singer P, Thurber K, Imai T. 63Cu NQR Measurement of Stripe Order Parameter in La2−xSrxCuO4. Phys Rev Lett (1999) 82:4300–3. doi:10.1103/physrevlett.82.4300
69. Julien MH, Campana A, Rigamonti A, Carretta P, Borsa F, Kuhns P, et al. Glassy Spin Freezing and NMR Wipeout Effect in the High-Tc Superconductor La1.90Sr0.10CuO4 Critical Discussion of the Role of Stripes. Phys Rev B (2001) 63:144508. doi:10.1103/PhysRevB.63.144508
70. Curro NJ. Glassy Spin Dynamics in a Stripe Ordered Cuprate System. Proc SPIE (2004) 5469:114–24. doi:10.1117/12.537625
71. Curro N. Probing Spatial Correlations in the Inhomogeneous Glassy State of the Cuprates by Cu NMR. J Phys Chem Sol (2002) 63:2181–5. doi:10.1016/S0022-3697(02)00231-7
72. Mitrović VF, Julien MH, de Vaulx C, Horvatić M, Berthier C, Suzuki T, et al. Similar Glassy Features in the 139La NMR Response of Pure and Disordered La1.88Sr0.12CuO4. Phys Rev B (2008) 78:014504. doi:10.1103/PhysRevB.78.014504
73. Frachet M, Vinograd I, Zhou R, Benhabib S, Wu S, Mayaffre H, et al. Hidden Magnetism at the Pseudogap Critical point of a Cuprate Superconductor. Nat Phys (2020) 16:1064–8. doi:10.1038/s41567-020-0950-5
74. Schmalian J, Wolynes PG. Stripe Glasses: Self-Generated Randomness in a Uniformly Frustrated System. Phys Rev Lett (2000) 85:836–9. doi:10.1103/PhysRevLett.85.836
75. Westfahl H, Schmalian J, Wolynes PG. Self-generated Randomness, Defect Wandering, and Viscous Flow in Stripe Glasses. Phys Rev B (2001) 64:174203. doi:10.1103/PhysRevB.64.174203
76. Nussinov Z, Vekhter I, Balatsky AV. Nonuniform Glassy Electronic Phases from Competing Local Orders. Phys Rev B (2009) 79:165122. doi:10.1103/PhysRevB.79.165122
77. Canfield PC, Bud’ko SL. FeAs-based Superconductivity: A Case Study of the Effects of Transition Metal Doping on BaFe2As2. Annu Rev Condens Matter Phys (2010) 1:27–50. doi:10.1146/annurev-conmatphys-070909-104041
79. Park K, Louca D, Llobet A, Yan JQ. Evidence of Local Disorder in the Overdoped Regime of Ba(Fe1−xCox)2As2. Phys Rev B (2011) 84:024512. doi:10.1103/PhysRevB.84.024512
80. Carlson EW, Dahmen KA. Using Disorder to Detect Locally Ordered Electron Nematics via Hysteresis. Nat Commun (2010) 2:379. doi:10.1038/ncomms1375
81. Banerjee V, Puri S. Hysteresis Effects in Spin Systems with Quenched Disorder. Phys Rev E (2001) 63:026106. doi:10.1103/physreve.63.026106
82. Loh CEW, Dahmen KA. Noise Predictions for STM in Systems with Local Electron Nematic Order. Phys.Rev B (2010) 81:224207. doi:10.1103/PhysRevB.81.224207
83. Carlson EW, Dahmen KA, Fradkin E, Kivelson SA. Hysteresis and Noise from Electronic Nematicity in High-Temperature Superconductors. Phys Rev Lett (2006) 96:097003. doi:10.1103/PhysRevLett.96.097003
Keywords: nuclear magnetic resonance, nematicity, uniaxial strain, glassy dynamics, spin lattice relaxation, quantum materials
Citation: Curro NJ, Kissikov T, Tanatar MA, Prozorov R, Bud’ko SL and Canfield PC (2022) Nematicity and Glassy Behavior Probed by Nuclear Magnetic Resonance in Iron-Based Superconductors. Front. Phys. 10:877628. doi: 10.3389/fphy.2022.877628
Received: 16 February 2022; Accepted: 21 March 2022;
Published: 14 April 2022.
Edited by:
Laura Fanfarillo, International School for Advanced Studies (SISSA), ItalyReviewed by:
Pietro Carretta, University of Pavia, ItalyKenji Ishida, Kyoto University, Japan
Rui Zhou, Institute of Physics (CAS), China
Copyright © 2022 Curro, Kissikov, Tanatar, Prozorov, Bud’ko and Canfield. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: N. J. Curro, bmpjdXJyb0B1Y2RhdmlzLmVkdQ==
 N. J. Curro
N. J. Curro T. Kissikov
T. Kissikov M. A. Tanatar2
M. A. Tanatar2 R. Prozorov
R. Prozorov