Rydberg Wire Gates for Universal Quantum Computation

Rydberg atom arrays offer flexible geometries of strongly interacting neutral atoms, which are useful for many quantum applications such as quantum simulation and quantum computation. Here, we consider an all-optical gate-based quantum computing scheme for the Rydberg atom arrays, in which auxiliary atoms (wire atoms) are used as a mean of quantum-mechanical remote-couplings among data-qubit atoms, and optical individual-atom addressing of the data and wire atoms is used to construct universal quantum gates of the data atoms. The working principle of our gates is to use the wire atoms for coupling mediation only, while leaving them in noncoupling ground states before and after each gate operation, which allows the double-excited states of data qubits to be accessible by a sequence of π or π/2 pulses addressing the data and wire atoms. Optical pulse sequences are constructed for standard one-, two-, and multi-qubit gates, and the arbitrary two-qubit state preparation is considered for universal computation prospects. We further provide a detailed resource estimate for an experimental implementation of this scheme in a Rydberg quantum simulator.

1 Introduction

Quantum computing is being actively studied as a mean to revolutionize humankind’s computational capability beyond the limits of digital computers [1, 2]. Quantum computing hardware are two-level physical systems, which we refer to as qubits hereafter, and quantum computation performs operations of universal quantum gates on them. Gate-based quantum computations have been demonstrated in many physical systems, including linear optics [3, 4], circuit quantum electrodynamics of superconductor [5–7], trapped ions [8–10], defects in solid-state materials [11, 12], and neutral atoms [13, 14].

Neutral atoms have been considered for gate-based quantum computations using interactions between the Rydberg atoms [15, 16]. The advantages of using Rydberg atoms are strong dipole–dipole interactions that can be switched on and off by fast laser excitation, large-scale atom arrays that can be prepared with almost any desired geometries and topologies [17–19], and stable ground hyperfine states that can be used for long-term quantum information. Quantum gates using Rydberg atoms can utilize the distance-dependent interactions [20] or the Rydberg blockade effect which prohibits adjacent atoms from being excited to a Rydberg state [21, 22]. There are many Rydberg atom schemes for quantum gates and entanglements [23–26] and experimental demonstrations [27–31, 33, 34]. The single-qubit gate fidelity of the recent demonstrations was recorded 0.97 in the alkali atom system [29] and 0.99 in the alkaline-earth atomic system [31]. Many of these previous studies are based on coding quantum information in the stable states, which are the hyperfine-Zeeman substates, requiring a hybrid microwave or Raman excitation scheme in addition to Rydberg atom excitation.

In this article, we consider an all-optical quantum gate scheme in a Rydberg atom array, which does not resort to the ground sublevels and, instead, utilizes auxiliary atoms (wire atoms) to mediate coupling among qubit atoms (data atoms), and single-atom addressing operations. When we use a Rydberg state and ground state to be the two qubit states for a data qubit and use a cluster of data and wire qubits in a Rydberg atom array, in which the wire atoms between the data qubits mediate interactions between the data atoms, by a sequence of single-atom addressing operations. The advantage of this setup comes in twofold. First, the gates are all realized with fast laser excitation of the ground-Rydberg transitions, so that the quantum circuit for a certain computational task (including digital quantum simulation) can be carried out fast. Second, the distance between the data atoms can be large, for which analyses shown later with practical and currently available resources estimates that, for example, a CZ gate between two atoms separated about 19 μm could be created with a high fidelity over 98% within a duration 2π/Ω, where Ω is the Rydberg Rabi frequency.

In the rest of the article, we first outline the main idea of the quantum wire gates based on the Rydberg interaction and single-atom addressing in Section 2, and then construct single- and two-qubit gates in Sections 3, 4. We then discuss the general two-qubit state generation and multi-qubit gates in Sections 5, 6. Experimental implementations, gate performances, and alternative schemes are discussed in Section 7.

2 Single-Atom Addressing in a Rydberg-Atom System

We aim to construct quantum gates with a sequence of individual-atom addressing in an array of atoms. We consider a two-dimensional (2D) array of atoms as shown in Figure 1A. In the Rydberg blockade regime, adjacent two atoms are inhibited from being excited to an antiblockade state, |11⟩, so the computational space of the two atoms is limited to {|00⟩, |01⟩, |10⟩} excluding |11⟩ (the antiblockade two-atom state), when the two-level system, {|0⟩, |1⟩}, is defined with the ground and Rydberg states of each atom. However, because |11⟩ is necessary for general quantum computation, we use the auxiliary atoms (which we refer to as wire atoms, hereafter) to mediate couplings among the data atoms. In Figure 1A, data atoms are illustrated with red spheres and wire atoms are with gray spheres.

FIGURE 1

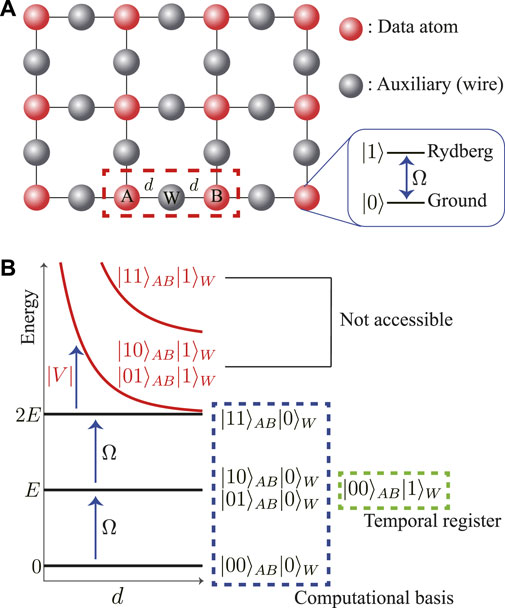
FIGURE 1. The Rydberg wire gate scheme: (A) A 2D atomic array consists of data atoms (red spheres) and auxiliary (wire) atoms (gray spheres). Atomic ground state |0⟩ and Rydberg state |1⟩ are used for the two-level system of each atom. Wire atoms, e.g., W, mediate the couplings between two adjacent data atoms, e.g., A and B which are separated from W by a distance d. (B) The energy level diagram of the three atoms, A, W, and B. We use four computational basis states, |00⟩_AB|0⟩_W, |01⟩_AB|0⟩_W, |10⟩_AB|0⟩_W, and |11⟩_AB|0⟩_W (in the blue dashed rectangle), out of five accessible states including |00⟩_AB|1⟩_W, which is considered as a temporal register (in the light green dashed rectangle). The other states, |10⟩_AB|1⟩_W, |01⟩_AB|1⟩_W, and |11⟩_AB|1⟩_W are not accessible due to the Rydberg blockade.

In the three-atom system, AWB in Figure 1A, A and B are the data atoms and W is the wire atom to couple A and B. When the wire atom is excited to |1⟩, only for data processing of |AB⟩ and otherwise left to be |0⟩_W, there are five computational base states |00⟩_AB|0⟩_W, |01⟩_AB|0⟩_W, |10⟩_AB|0⟩_W, |11⟩_AB|0⟩_W, and |00⟩_AB|1⟩_W. Here, the first four base states are the computational basis for the two-data (AB) system and the last |00⟩_AB|1⟩_W can be considered as a temporal register, as in Figure 1B. There are three available atom addressings:

$\tilde{W}\left(\mathrm{\Theta },\varphi \right)=e^{-\frac{i}{\hslash }\int H_{W}dt},(\mathrm{1a})$

$\tilde{A}\left(\mathrm{\Theta },\varphi \right)=e^{-\frac{i}{\hslash }\int \left(\frac{\hslash \mathrm{\Omega }}{2}{\widehat{n}}_{\varphi }\cdot {\vec{\sigma }}^A+V{n}_W{n}_A\right)dt},(\mathrm{1b})$

$\tilde{B}\left(\mathrm{\Theta },\varphi \right)=e^{-\frac{i}{\hslash }\int \left(\frac{\hslash \mathrm{\Omega }}{2}{\widehat{n}}_{\varphi }\cdot {\vec{\sigma }}^B+V{n}_W{n}_B\right)dt},(\mathrm{1c})$

where Θ and ϕ are the Rabi rotation angle and axis, respectively. H_W is the Hamiltonian of single-addressing of W given by

$H_W=\frac{\hslash \mathrm{\Omega }}{2}{\widehat{n}}_{\varphi }\cdot {\vec{\sigma }}^W+V{n}_W\left(n_A+n_B\right)(2)$

in the Rydberg blockade regime of adjacent atoms, i.e., $d<d_B<\sqrt{2}d$, where d and d_B are the interatom and blockade distances, respectively. Ω is the Rabi frequency, ${\widehat{n}}_{\varphi }$ is the rotational axis defined by a laser phase ϕ, V = C₆/d⁶ is the van der Waals interaction with coefficient C₆, and $\vec{\sigma }=({\sigma }_x,{\sigma }_y,{\sigma }_z)$ is the Pauli vector and n = (1 − σ_z)/2 is the excitation number.

It is noted that the atom-addressing operations in Eqs 1a–c are three-qubit gates. We intend to use them for general quantum computations of the data AB atoms. $\tilde{W}$ changes |00⟩_AB|0⟩_W to |00⟩_AB|1⟩_W and preserves all the other states and their superpositions. Thus, the $\tilde{W}$ operation is the inverted controlled rotation gate, where AB are the control qubits and W is the target qubit. The other three operators are reduced to single- and two-atom rotations in the data-qubit (AB) basis as

${\mathbf{R}}_A\otimes {\mathbf{I}}_B=\langle 0{|}_W\tilde{A}|{0\rangle }_W,(\mathrm{3a})$

${\mathbf{I}}_A\otimes {\mathbf{R}}_B=\langle 0{|}_W\tilde{B}|{0\rangle }_W,(\mathrm{3b})$

${\mathbf{R}}_A\otimes {\mathbf{R}}_B=\langle 0{|}_W\tilde{A}\tilde{B}|{0\rangle }_W,(\mathrm{3c})$

where R is the single-qubit rotation and I is the identity.

3 Standard One-Qubit Gates

With the atom-addressing operations, $\tilde{W}$, $\tilde{A}$, and $\tilde{B}$, in Eqs 1a–c, we construct standard one-qubit gates which include Pauli gates, X, Y, and Z, general rotation R(Θ, ϕ), Hadamard gate H, and phase gate, P.

Pauli gates rotate the quantum state of one atom, while leaving the other atoms unchanged. For the data atoms, A and B, Pauli X-gates are given by

${\mathbf{X}}_A\otimes {\mathbf{I}}_B=e^{i\alpha }\langle 0{|}_W{\tilde{X}}_A|{0\rangle }_W,(\mathrm{4a})$

${\mathbf{I}}_A\otimes {\mathbf{X}}_B=e^{i\alpha }\langle 0{|}_W{\tilde{X}}_B|{0\rangle }_W,(\mathrm{4b})$

where ${\tilde{X}}_A=\tilde{A}(\pi ,0)$, ${\tilde{X}}_B=\tilde{B}(\pi ,0)$, and α = π/2 is the global phase. Likewise, Pauli Y and Z gates are given by

${\mathbf{Y}}_A\otimes {\mathbf{I}}_B=e^{i\alpha }\langle 0{|}_W{\tilde{Y}}_A|{0\rangle }_W,(\mathrm{5a})$

${\mathbf{I}}_A\otimes {\mathbf{Y}}_B=e^{i\alpha }\langle 0{|}_W{\tilde{Y}}_B|{0\rangle }_W,(\mathrm{5b})$

${\mathbf{Z}}_A\otimes {\mathbf{I}}_B=e^{i\alpha }\langle 0{|}_W{\tilde{X}}_A{\tilde{Y}}_A|{0\rangle }_W,(\mathrm{5c})$

${\mathbf{I}}_A\otimes {\mathbf{Z}}_B=e^{i\alpha }\langle 0{|}_W{\tilde{X}}_B{\tilde{Y}}_B|{0\rangle }_W,(\mathrm{5d})$

where ${\tilde{Y}}_{\mathrm{A}}=\tilde{A}(\pi ,\pi /2)$ and ${\tilde{Y}}_{\mathrm{B}}=\tilde{B}(\pi ,\pi /2)$. The general rotations are given by

${\mathbf{R}}_A\left(\mathrm{\Theta },\varphi \right)\otimes {\mathbf{I}}_B=\langle 0{|}_W\tilde{A}\left(\mathrm{\Theta },\varphi \right)|{0\rangle }_W,(\mathrm{6a})$

${\mathbf{I}}_A\otimes {\mathbf{R}}_B\left(\mathrm{\Theta },\varphi \right)=\langle 0{|}_W\tilde{B}\left(\mathrm{\Theta },\varphi \right)|{0\rangle }_W.(\mathrm{6b})$

The Hadamard gate, H, converts the quantum states, |0⟩ and |1⟩, to the superposition states, $|+\rangle =(|0\rangle +|1\rangle )/\sqrt{2}$ or $|-\rangle =(|0\rangle -|1\rangle )/\sqrt{2}$, respectively. The Hadamard gate is identical to $e^{i\pi /4}\mathbf{X}\sqrt{\mathbf{Y}}$, given by

${\mathbf{H}}_A\otimes {\mathbf{I}}_B=e^{i\alpha }\langle 0{|}_W{\tilde{X}}_A\sqrt{{\tilde{Y}}_A}|{0\rangle }_W,(\mathrm{7a})$

${\mathbf{I}}_A\otimes {\mathbf{H}}_B=e^{i\alpha }\langle 0{|}_W{\tilde{X}}_B\sqrt{{\tilde{Y}}_B}|{0\rangle }_W,(\mathrm{7b})$

where $\sqrt{{\tilde{Y}}_A}=\tilde{A}(\pi /2,\pi /2)$ and $\sqrt{{\tilde{Y}}_B}=\tilde{B}(\pi /2,\pi /2)$ are the pseudo-Hadamard gates. α = π/2.

The phase gates, P_A(ϕ) and P_B(ϕ), are given by

${\mathbf{P}}_A\left(\varphi \right)\otimes {\mathbf{I}}_B=e^{i\varphi /2}\langle 0{|}_W{\tilde{X}}_A^{†}\tilde{A}\left(\pi ,\varphi /2\right)|{0\rangle }_W,(\mathrm{8a})$

${\mathbf{I}}_A\otimes {\mathbf{P}}_B\left(\varphi \right)=e^{i\varphi /2}\langle 0{|}_W{\tilde{X}}_B^{†}\tilde{B}\left(\pi ,\varphi /2\right)|{0\rangle }_W.(\mathrm{8b})$

S and T gates are obtained as S_A = P_A(π/2), S_B = P_B(π/2), T_A = P_A(π/4), and T_B = P_B(π/4).

The global phase, α, of the abovementioned gates can be eliminated with a global phase gate. One example is

$\begin{array}{ccc}\hfill \mathbf{P}\mathbf{h}\left(\alpha \right)& =\hfill & \langle 0{|}_W{\tilde{Y}}_B{\tilde{X}}_W^{†}\tilde{W}\left(\pi ,\alpha \right){\tilde{Y}}_{AB}^{†}{\tilde{X}}_W^{†}\tilde{W}\left(\pi ,\alpha \right)\hfill \\ \hfill & \times \hfill & {\tilde{Y}}_B^{†}{\tilde{X}}_W^{†}\tilde{W}\left(\pi ,\alpha \right){\tilde{Y}}_{AB}{\tilde{X}}_W^{†}\tilde{W}\left(\pi ,\alpha \right)|{0\rangle }_W,\hfill \end{array}(9)$

which is a combination of four two-qubit phase rotations, |00⟩ → e^iα|00⟩ which is performed by ${\tilde{X}}_W^{†}\tilde{W}(\pi ,\alpha )$, |01⟩ → e^iα|01⟩ by ${\tilde{Y}}_B{\tilde{X}}_W^{†}\tilde{W}(\pi ,\alpha ){\tilde{Y}}_B^{†}$, |10⟩ → e^iα|10⟩ by ${\tilde{Y}}_A^{†}{\tilde{X}}_W^{†}\tilde{W}(\pi ,\alpha ){\tilde{Y}}_A$, and |11⟩ → e^iα|11⟩ by ${\tilde{Y}}_{AB}^{†}{\tilde{X}}_W^{†}{\tilde{X}}_W(\pi ,\alpha ){\tilde{Y}}_{AB}$, where ${\tilde{Y}}_{AB}$ denotes ${\tilde{Y}}_A{\tilde{Y}}_B$.

4 Standard Two-Qubit Gates

Now, we consider the standard two-qubit gates including the controlled-NOT gate, CNOT, the swap gate, SWAP, and the controlled-phase gate, CP.

The controlled-NOT gate, CNOT, flips the target qubit (the second qubit) only when the control qubit (the first qubit) is in |1⟩, i.e., |AB⟩ → |A, A ⊕ B⟩, which is also the controlled X-gate, i.e., CNOT = CX. With the atom addressing, CX_AB and CX_BA are, respectively, given by

${\mathbf{C}\mathbf{X}}_{AB}=\langle 0{|}_W{\tilde{Y}}_A^{†}\sqrt{{\tilde{Y}}_B^{†}}{\tilde{Y}}_W^2\sqrt{{\tilde{Y}}_B}{\tilde{Y}}_A|{0\rangle }_W,(\mathrm{10a})$

${\mathbf{C}\mathbf{X}}_{BA}=\langle 0{|}_W{\tilde{Y}}_B^{†}\sqrt{{\tilde{Y}}_A^{†}}{\tilde{Y}}_W^2\sqrt{{\tilde{Y}}_A}{\tilde{Y}}_B|{0\rangle }_W,(\mathrm{10b})$

of which the sequence can be understood as follows: In CX_AB, ${\tilde{Y}}_W^2$ at the center works as an inverted-CZ gate, which flips only the sign of the coefficient of |00⟩_AB|0⟩_W. When this is multiplied by ${\tilde{Y}}_{AB}$ from one side and by its Hermitian conjugate from the other side, we get the controlled-Z gate, similarly as in Ref. [32], i.e.,

${\mathbf{C}\mathbf{Z}}_{AB}={\mathbf{C}\mathbf{Z}}_{BA}=\langle 0{|}_W{\tilde{Y}}_{AB}^{†}{\tilde{Y}}_W^2{\tilde{Y}}_{AB}|{0\rangle }_W,(11)$

which is then multiplied by $\sqrt{Y_A}$ and its Hermitian conjugate, to attain CX_AB. The quantum circuit of CX_AB is presented in Figure 2A. Likewise, the controlled-Y gates are given by

${\mathbf{C}\mathbf{Y}}_{AB}=\langle 0{|}_W{\tilde{Y}}_A^{†}\sqrt{{\tilde{X}}_B^{†}}{\tilde{Y}}_W^2\sqrt{{\tilde{X}}_B}{\tilde{Y}}_A|{0\rangle }_W,(\mathrm{12a})$

${\mathbf{C}\mathbf{Y}}_{BA}=\langle 0{|}_W{\tilde{Y}}_B^{†}\sqrt{{\tilde{X}}_A^{†}}{\tilde{Y}}_W^2\sqrt{{\tilde{X}}_A}{\tilde{Y}}_B|{0\rangle }_W.(\mathrm{12b})$

FIGURE 2

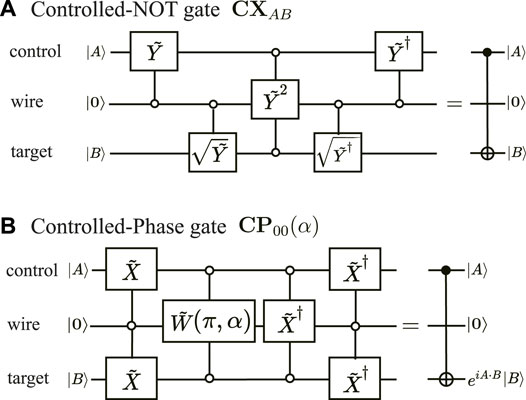
FIGURE 2. Quantum circuits of (A) controlled-NOT gate, CX_AB, and (B) controlled-phase gate, CP₀₀(α).

SWAP gate performs the state swapping of two qubits, i.e., |AB⟩ → |BA⟩, which is also the exchange of the coefficients of |01⟩ and |10⟩. In our atom-addressing scheme, an X-gate version of SWAP gate is given by

$\mathbf{S}\mathbf{W}\mathbf{A}\mathbf{P}=\langle 0{|}_W{\tilde{X}}_A{\tilde{X}}_W{\tilde{X}}_{AB}{\tilde{X}}_W{\tilde{X}}_{AB}^{†}{\tilde{X}}_W{\tilde{X}}_A^{†}|{0\rangle }_W,(13)$

in which the first three-pulse combination, $X_A^{†}{\tilde{X}}_W{\tilde{X}}_A^{†}$, exchanges the coefficients of |10⟩_AB|0⟩_W and |00⟩_AB|1⟩_W. The coefficient of |00⟩_AB|1⟩_W is then exchanged with that of |01⟩_AB|0⟩_W by the second combination, ${\tilde{X}}_B{\tilde{X}}_W{\tilde{X}}_B^{†}$, before the coefficient of |00⟩_AB|1⟩_W is returned to |10⟩_AB|0⟩_W by ${\tilde{X}}_A{\tilde{X}}_W{\tilde{X}}_A$.

The controlled-phase gate, CP(α), puts the local phase of |11⟩ of AB data qubits. In our atom-addressing scheme, W-atom addressing, $\tilde{W}(\pi ,\alpha )$, converts |00⟩_AB|0⟩_W to − ie^iα|00⟩_AB|1⟩_W and $\tilde{W}(\pi ,\pi )\tilde{W}(\pi ,\alpha )$ converts |00⟩_AB to e^iα|00⟩_AB, so CP₀₀(α), which puts the local phase of |00⟩, is given by

${\mathbf{C}\mathbf{P}}_{00}\left(\alpha \right)=\langle 0{|}_W{\tilde{X}}_W^{†}\tilde{W}\left(\pi ,\alpha \right)|{0\rangle }_W.(14)$

The quantum circuit of CP₀₀(α) is presented in Figure 2B. The standard CP(α) = CP₁₁(α) is, therefore, obtained by

$\mathbf{C}\mathbf{P}\left(\varphi \right)=\langle 0{|}_W{\tilde{X}}_{AB}^{†}{\tilde{X}}_W^{†}\tilde{W}\left(\pi ,\varphi \right){\tilde{X}}_{AB}|{0\rangle }_W,(15)$

where the CP₀₀(α) in the middle is multiplied by ${\tilde{X}}_{AB}$ from one side and by the conjugate of ${\tilde{X}}_{AB}$ from the other side, which respectively exchanges and exchanges back the coefficients of |00⟩ and |11⟩. As a result, we get |11⟩ → e^iα|11⟩. Similarly, CP₀₁(ϕ) and CP₁₀(ϕ) are obtained as

${\mathbf{C}\mathbf{P}}_{01}\left(\varphi \right)=\langle 0{|}_{\mathrm{W}}{\tilde{X}}_{\mathrm{B}}^{†}{\tilde{X}}_{\mathrm{W}}^{†}\tilde{W}\left(\pi ,\varphi \right){\tilde{X}}_{\mathrm{B}}|{0\rangle }_{\mathrm{W}},(16)$

${\mathbf{C}\mathbf{P}}_{10}\left(\varphi \right)=\langle 0{|}_{\mathrm{W}}{\tilde{X}}_{\mathrm{A}}^{†}{\tilde{X}}_{\mathrm{W}}^{†}\tilde{W}\left(\pi ,\varphi \right){\tilde{X}}_{\mathrm{A}}|{0\rangle }_{\mathrm{W}}.(17)$

5 Arbitrary Two-Qubit State Generation

The general two-qubit state generation is to find a unitary operation which transforms the initial state |00⟩_AB to an arbitrary two-qubit state, i.e.,

$U|00\rangle =a_0|00\rangle +a_1|01\rangle +a_2|10\rangle +a_3|11\rangle .(18)$

The above U can be in principle constructed with the single- and two-qubit gates. Also, it is sufficient to define the general rotations and at least one inversion operation among the two-qubit base states, {|00⟩, |01⟩, |10⟩, |11⟩} of AB atoms.

Inversion operations are the reflection of the two-qubit state vector about a given plane. For example, CZ inverts the state vector about the plane orthogonal to |11⟩, i.e., ${\tilde{M}}_{11}=\mathbf{C}\mathbf{Z}$. Likewise, ${\tilde{M}}_{00}={\mathbf{C}\mathbf{P}}_{00}(\pi )$, ${\tilde{M}}_{01}={\mathbf{C}\mathbf{P}}_{01}(\pi )$, and ${\tilde{M}}_{10}={\mathbf{C}\mathbf{P}}_{10}(\pi )$.

General rotations are the base-pair rotation between a pair of two-qubit base states, i.e., ${\tilde{R}}_{jk}(\mathrm{\Theta },\varphi )|j\rangle =\cos \frac{\mathrm{\Theta }}{2}|j\rangle -i{e}^{i\varphi }\sin \frac{\mathrm{\Theta }}{2}|k\rangle$ for j, k ∈ {|00⟩, |01⟩, |10⟩, |11⟩}. ${\tilde{R}}_{\mathrm{00,01}}(\mathrm{\Theta },\varphi )$ rotates the quantum information stored in the base pair, |00⟩ and |01⟩, which are, for example, given by

${\tilde{R}}_{\mathrm{00,01}}\left(\mathrm{\Theta },\varphi \right)=\langle 0{|}_W{\tilde{X}}_W{\tilde{X}}_B\tilde{W}\left(\mathrm{\Theta },-\varphi \right){\tilde{X}}_B^{†}{\tilde{X}}_W^{†}|{0\rangle }_W,(19)$

where the first two π-pulse operations, ${\tilde{X}}_B^{†}$ and ${\tilde{X}}_W^{†}$, perform |00⟩_AB|0⟩_W → |00⟩_AB|1⟩_W and |01⟩_AB|0⟩_W → |00⟩_AB|0⟩_W, respectively, which means that the quantum state of B atom is transferred to W atom. Then, the state vector of W atom is rotated by $\tilde{W}(\mathrm{\Theta },-\varphi )$ and transferred back to B atom by the last two π-pulse operations. Similarly, other rotations can be obtained as follows:

${\tilde{R}}_{\mathrm{00,11}}\left(\mathrm{\Theta },\varphi \right)=\langle 0{|}_W{\tilde{X}}_W{\tilde{X}}_{AB}\tilde{W}\left(\mathrm{\Theta },-\left(\varphi +\pi /2\right)\right){\tilde{X}}_{AB}^{†}{\tilde{X}}_W^{†}|{0\rangle }_W,(\mathrm{20a})$

${\tilde{R}}_{\mathrm{01,10}}\left(\mathrm{\Theta },\varphi \right)=\langle 0{|}_W{\tilde{X}}_B{\tilde{X}}_W{\tilde{X}}_{AB}\tilde{W}\left(\mathrm{\Theta },-\left(\varphi +\pi /2\right)\right){\tilde{X}}_{AB}^{†}{\tilde{X}}_W^{†}{\tilde{X}}_B^{†}|{0\rangle }_W,(\mathrm{20b})$

${\tilde{R}}_{\mathrm{01,11}}\left(\mathrm{\Theta },\varphi \right)=\langle 0{|}_W{\tilde{X}}_B{\tilde{X}}_W{\tilde{X}}_A\tilde{W}\left(\mathrm{\Theta },-\varphi \right){\tilde{X}}_A^{†}{\tilde{X}}_W^{†}{\tilde{X}}_B^{†}|{0\rangle }_W,(\mathrm{20c})$

${\tilde{R}}_{\mathrm{10,11}}\left(\mathrm{\Theta },\varphi \right)=\langle 0{|}_W{\tilde{X}}_A{\tilde{X}}_W{\tilde{X}}_B,\tilde{W}\left(\mathrm{\Theta },-\varphi \right){\tilde{X}}_B^{†}{\tilde{X}}_W^{†}{\tilde{X}}_A^{†}|{0\rangle }_W.(\mathrm{20d})$

6 Multi-Qubit Gates

While the multi-qubit gates can be decomposed to a sequence of single- and two-qubit elementary gates, the standard three-qubit gates require many elementary gates. For example, a Toffoli gate needs 15 or 17 elementary gates. In the following, we consider the possibilities of using wire atom arrangements which can reduce the number of gates significantly for the Toffoli and CCZ gates.

If we use the simple linear configuration, as in Figure 3A, of ABC data atoms and two wire atoms W₁ and W₂, their pulse-sequence solutions, e.g., for the Toffoli and CCZ gates, are rather complicated:

$\mathbf{C}\mathbf{C}\mathbf{Z}=\langle 00{|}_{W_{12}}\sqrt{{\tilde{Y}}_C}{\tilde{Y}}_{AB}{\tilde{X}}_{W_2}^{†}{\tilde{Y}}_{W_1}{\tilde{X}}_{BC}^{†}\sqrt{{\tilde{X}}_{W_2}}{\tilde{X}}_{BC}^2,$

$\times \sqrt{{\tilde{X}}_{W_2}^{†}}{\tilde{X}}_{BC}^{†}{\tilde{X}}_{W_{12}}{\tilde{Y}}_{AB}^{†}\sqrt{{\tilde{Y}}_C^{†}}|0{0\rangle }_{W_{12}},(21)$

$\begin{array}{ccc}\hfill \mathbf{T}\mathbf{O}\mathbf{F}\mathbf{F}& =\hfill & \langle 00{|}_{W_{12}}\sqrt{{\tilde{Y}}_B^{†}{\tilde{Y}}_C}{\tilde{Y}}_{AB}{\tilde{X}}_{W_2}^{†}{\tilde{Y}}_{W_1}{\tilde{X}}_{BC}^{†}\sqrt{{\tilde{X}}_{W_2}}{\tilde{X}}_{BC}^2\hfill \\ \hfill & \times \hfill & \sqrt{{\tilde{X}}_{W_2}^{†}}{\tilde{X}}_{BC}^{†}{\tilde{X}}_{W_{12}}{\tilde{Y}}_{AB}^{†}\sqrt{{\tilde{Y}}_C^{†}{\tilde{Y}}_B}|0{0\rangle }_{W_{12}}.\hfill \end{array}(22)$

FIGURE 3

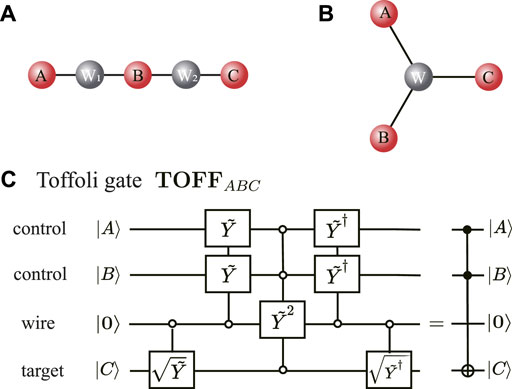
FIGURE 3. (A) A 5-atom chain and (B) an Y-shape atomic array to implement the multi-qubit wire gates. (C) Quantum circuit of the Toffoli gate TOFF_ABC for the control atoms A, B and the target atom C.

Instead, if we use the Y-shape configuration, as shown in Figure 3B, which has one wire atom, W, which couples all the three data atoms, ABC, simultaneously, their solutions are simple, given as the extensions of CX and CZ in Eqs 10a,b, 11. The CCZ utilizes the fact that $\langle 0{|}_W{\tilde{Y}}_W^2|{0\rangle }_W$ is the inverted-CCZ, to attain

$\mathbf{C}\mathbf{C}\mathbf{Z}=\langle 0{|}_W{\tilde{Y}}_{ABC}^{†}{\tilde{Y}}_W^2{\tilde{Y}}_{ABC}|{0\rangle }_W,(23)$

where ${\tilde{Y}}_{ABC}={\tilde{Y}}_A{\tilde{Y}}_B{\tilde{Y}}_C$ and ${\tilde{Y}}_{ABC}^{†}$ are for the bitwise flip and flip-back of the data atoms, applied before and after to change the inverted-CCZ to CCZ. The Toffoli gate of the AB controls and C target is also obtained as

${\mathbf{T}\mathbf{O}\mathbf{F}\mathbf{F}}_{\text{ABC}}=\langle 0{|}_{\mathrm{W}}\sqrt{{\tilde{Y}}_{\mathrm{C}}^{†}}{\tilde{Y}}_{\text{AB}}^{†}{\tilde{Y}}_{\mathrm{W}}^2{\tilde{Y}}_{\text{AB}}\sqrt{{\tilde{Y}}_{\mathrm{C}}}|{0\rangle }_{\mathrm{W}},(24)$

where $\sqrt{{\tilde{Y}}_{\mathrm{C}}^{†}}$ and $\sqrt{{\tilde{Y}}_{\mathrm{C}}}$ on both ends are the pseudo-Hadamard and its inverse acting on the target. The quantum circuit of TOFF_ABC is presented in Figure 3C.

7 Discussion and Conclusion

Experimental implementation: Rydberg wire gates introduced previously can be implemented in optical-tweezer atomic systems, which have been previously demonstrated elsewhere [20, 29, 30]. As an example, we consider three rubidium (⁸⁷Rb) atoms arranged in the linear chain geometry. Once the single atoms are loaded to individual tweezers from magneto-optical trap, the atoms are prepared to one of the magnetic sublevels in hyperfine ground states as the ground state |0⟩ (for example, |0⟩ = |5S_1/2, F = 2, m_F = 2⟩). The states |0⟩ and |1⟩ are coupled by Rydberg state excitation lasers, and in general two-photon excitation is used to transit to |nS⟩ or |nD⟩ Rydberg levels via |5P_3/2⟩ with 780 and 480 nm lights. For |1⟩ = |69S_1/2⟩, the atoms undergo van der Waals interaction, and the interaction strength when the interatomic distance d = 7 μm becomes $V=\left|C_6\right|/d^6=(2\pi )6.2$ MHz, where C₆ = −(2π)732 GHz ⋅ μm⁶. Individual-atom addressing to couple between |0⟩ and |1⟩ can be implemented by diffracting multiple laser beams from an acousto-optic modulator (AOM), then focusing to the individual atoms. The switching of individual beams can be done by controlling the amplitude and frequency of radio-frequency wave to AOM. The individual addressing lasers can be either ground-Rydberg resonant lasers [30] or far-detuned lasers [35], in which the latter suppress the Rydberg state excitation with the additional AC Stark shift combined with global resonant lasers.

Gate performance: the performance of the Rydberg wire gate schemes can be estimated with numerical calculations. In Figure 4, we estimate the average fidelity of CP₀₀(π) gate for all the initial states $\left\{|0{0\rangle }_{AB},|0{1\rangle }_{AB},|1{0\rangle }_{AB},|1{1\rangle }_{AB}\right\}$ using the time-dependent Schrödinger equations. For |1⟩ = |69S_1/2, m_j = 1/2⟩, the results with respect to the interatomic distance are shown with the solid line in Figure 4. For Rabi frequency Ω = (2π)2 MHz, the gate duration is 0.5 μs. It is expected that the maximum fidelity $\mathcal{F}$ can be reached to 94% when the lattice constant is around 6.8 μm.

FIGURE 4

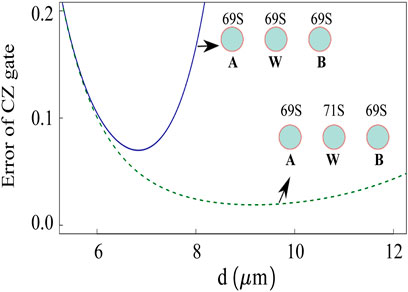
FIGURE 4. Performance estimation of the CZ gate for the present van der Waals scheme (solid line) in comparison with the Förster resonance scheme (dashed line).

Gate imperfection sources: The sources of finite infidelities related to the Rydberg atomic properties can be characterized. The finite lifetime of Rydberg state gives imperfection to the transition to |1⟩. For the lifetime of |1⟩ to be τ, this gives the average gate error $\frac{9\pi }{4\mathrm{\Omega }\tau }$ [36]. Another source of gate infidelity is the Rydberg blockade error: as the Rydberg interaction strength is proportional to 1/d⁶, the interaction strength within the blockade distance d_B is finite, and there is nonzero residual interactions outside. For the interaction strength, V, between a nearest neighbor Rydberg atomic pair, the gate error is given by $\frac{{\hslash }^2{\mathrm{\Omega }}^2}{2V^2}$ for the initial state |10⟩_AB, |01⟩_AB and $\frac{{\hslash }^2{\mathrm{\Omega }}^2}{8V^2}$ for |11⟩_AB [37, 38]. In addition, the phase shift $\frac{2\pi V_2}{\hslash \mathrm{\Omega }}$ occurs for the initial state |11⟩_AB, due to the nonzero interactions between atom A and B. Considering all these error budgets, we estimate the average fidelity error as

$1-\mathcal{F}=\frac{9\pi }{4\mathrm{\Omega }\tau }+\frac{9{\hslash }^2{\mathrm{\Omega }}^2}{32V^2}+\frac{\pi V}{128\hslash \mathrm{\Omega }},(25)$

where the terms denote the Rydberg state decay error, the Rydberg blockade error, and the residual interaction error, respectively. Their estimated infidelity contributions are 4 × 10⁻³, 2.04 × 10⁻² and 9.12 × 10⁻², respectively, at d = 6.8 μm. While our fidelity estimation considers limitedly sub-μs pulsed gate significantly shorter than the typical coherence time of Rydberg atoms, a detailed analysis, for example, in a large-scale quantum circuit requires many-body effects and open quantum system dynamics [39–43].Toward the higher fidelity gates, we discuss methods to improve the gate fidelity to suppress the last two errors in Eq. 25. One approach is to utilize the dipole–dipole interaction by Förster resonance between the nearest neighbor atomic pair. Near the principal quantum number n = 69 discussed previously, there exist two transition channels between the Rydberg pair states, |69S_1/2 + 71S_1/2⟩ ↔|69P_3/2 + 70P_1/2⟩ and |69S_1/2 + 71S_1/2⟩ ↔|69P_1/2 + 70P_3/2⟩ by the dipole–dipole interaction, with Förster defects of 6.6 and 19.7 MHz, respectively [44]. This induces the dipole–dipole interaction with the strength of V′ = C₃/d³, where C₃ = (2π)12.32 GHz ⋅ μm³, with the interatomic distance less than the crossover distance 11 μm [45]. In realizing the CP₀₀(π) gate, the atom W is to be excited to |1′⟩ = |71S_1/2, m_j = 1/2⟩ state, while the data atoms A and B are excited to |1⟩. Then, the interaction strength between A(B) and W is increased due to the Förster resonance, so the interatomic distance can also be increased. This further reduces the long range residual van der Waals interaction between A and B, thus the gate infidelity can be suppressed. In Figure 4, we illustrate the improved performance of the CP₀₀(π) gate of the dipole–dipole interaction (the dashed line). The overall fidelities $\mathcal{F}$ are increased compared to the previous example, and the maximum reached to 98% at d = 9.17 μm.

Weakness of the Rydberg wire gates: The weakness of the present scheme is that the Rydberg states are not stable. There is a constant decay process occurring during the quantum control process. However, for a fast quantum control process, the decay-induced error can be relatively small for the decay error and is proportional to the Rydberg superposition time. Moreover, the quantum error correction can, in principle, be executed by the gates shown in this article, so that the error during the control process can be corrected. Because both the main control process and error correction are fast. Thanks to the fast pulsed operations of quantum wire gates, the overall speed to reach a wanted computational result can still surpass the traditional method of coding information with the stable hyperfine-Zeeman substates.

In summary, the Rydberg wire gates are proposed, which utilize auxiliary atoms to couple the data atoms. By coding the information with a ground-state qubit state and a Rydberg qubit state, the universal gate set can be realized based on the strong, local interactions of the neutral Rydberg atoms. The gates are realized by the fast laser excitation of Rydberg states, so that their speed can be fast, and the well-separated data atoms can be rapidly entangled. Fast entangling operations are important basic elements in a quantum circuit for large-scale quantum computation, and long-distance entanglement can greatly simplify complex operations between distant qubits in the array. The new idea of Rydberg wire gates can bring new prospective in neutral-atom quantum science and technology.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

JA conceived the idea. SJ, XF-S, and MK conducted the research and analysis. All contributed to the manuscript.

Funding

This research was supported by the Samsung Science and Technology Foundation (Grant No. SSTF-BA1301-52), National Research Foundation of Korea (Grant No. 2017R1E1A1A0107430), and Natural Science Foundation of China (Grant No. 12074300).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Feynman RP. Simulating Physics with Computers. Int J Theor Phys (1982) 21:467–88. doi:10.1007/bf02650179

CrossRef Full Text | Google Scholar

2. Nielsen MA, Chuang I. Quantum Computation and Quantum Information. Cambridge: Cambridge Univ. Press (2002).

Google Scholar

3. O’brien JL. Opt Quan Comput Sci (2007) 318:1567.

4. Kok P, Munro WJ, Nemoto K, Ralph TC, Dowling JP, Milburn GJ. Linear Optical Quantum Computing with Photonic Qubits. Rev Mod Phys (2007) 79:135–74. doi:10.1103/revmodphys.79.135

CrossRef Full Text | Google Scholar

5. Arute F, Arya K, Babbush R, Bacon D, Bardin JC, Barends R, et al. Quantum Supremacy Using a Programmable Superconducting Processor. Nature (2019) 574:505–10. doi:10.1038/s41586-019-1666-5

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Krantz P, Kjaergaard M, Yan F, Orlando TP, Gustavsson S, Oliver WD. A Quantum Engineer's Guide to Superconducting Qubits. Appl Phys Rev (2019) 6:021318. doi:10.1063/1.5089550

CrossRef Full Text | Google Scholar

7. Blais A, Grimsmo AL, Girvin SM, Wallraff A. Circuit Quantum Electrodynamics. Rev Mod Phys (2021) 93:025005. doi:10.1103/revmodphys.93.025005

CrossRef Full Text | Google Scholar

8. Kielpinski D, Monroe C, Wineland DJ. Architecture for a Large-Scale Ion-Trap Quantum Computer. Nature (2002) 417:709–11. doi:10.1038/nature00784

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Schindler P, Nigg D, Monz T, Barreiro JT, Martinez E, Wang SX, et al. A Quantum Information Processor with Trapped Ions. New J Phys (2013) 15:123012. doi:10.1088/1367-2630/15/12/123012

CrossRef Full Text | Google Scholar

10. Pogorelov I, Feldker T, Marciniak CD, Postler L, Jacob G, Kriegelsteiner O, et al. Compact Ion-Trap Quantum Computing Demonstrator. PRX Quan (2021) 2:020343. doi:10.1103/prxquantum.2.020343

CrossRef Full Text | Google Scholar

11. van der Sar T, Wang ZH, Blok MS, Bernien H, Taminiau TH, Toyli DM, et al. Decoherence-protected Quantum gates for a Hybrid Solid-State Spin Register. Nature (2012) 484:82–6. doi:10.1038/nature10900

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Childress L, Hanson R. Diamond NV Centers for Quantum Computing and Quantum Networks. MRS Bull (2013) 38:134–8. doi:10.1557/mrs.2013.20

CrossRef Full Text | Google Scholar

13. Weiss DS, Saffman M. Quantum Computing with Neutral Atoms. Phys Today (2017) 70:44–50. doi:10.1063/pt.3.3626

CrossRef Full Text | Google Scholar

14. Henriet L, Beguin L, Signoles A, Lahaye T, Browaeys A, Reymond G-O, et al. Quantum Computing with Neutral Atoms. Quantum (2020) 4:327. doi:10.22331/q-2020-09-21-327

CrossRef Full Text | Google Scholar

15. Saffman M, Walker TG, Mølmer K. Quantum Information with Rydberg Atoms. Rev Mod Phys (2010) 82:2313–63. doi:10.1103/revmodphys.82.2313

CrossRef Full Text | Google Scholar

16. Saffman M. Quantum Computing with Atomic Qubits and Rydberg Interactions: Progress and Challenges. J Phys B: Mol Opt Phys (2016) 49:202001. doi:10.1088/0953-4075/49/20/202001

CrossRef Full Text | Google Scholar

17. Kim M, Song Y, Kim J, Ahn J. Quantum Ising Hamiltonian Programming in Trio, Quartet, and Sextet Qubit Systems. PRX Quan (2020) 1:020323. doi:10.1103/PRXQuantum.1.020323

CrossRef Full Text | Google Scholar

18. Song Y, Kim M, Hwang H, Lee W, Ahn J. Quantum Simulation of Cayley-Tree Ising Hamiltonians with Three-Dimensional Rydberg Atoms. Phys Rev Res (2021) 3:013286. doi:10.1103/PhysRevResearch.3.013286

CrossRef Full Text | Google Scholar

19. Kim M, Kim K, Hwang J, Moon E-G, Ahn J. Rydberg Quantum Wires for Maximum Independent Set Problems. Nat Phys (2022). doi:10.1038/s41567-022-01629-5

CrossRef Full Text | Google Scholar

20. Jo H, Song Y, Kim M, Ahn J. Rydberg Atom Entanglements in the Weak Coupling Regime. Phys Rev Lett (2020) 124:033603. doi:10.1103/PhysRevLett.124.033603

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gaëtan A, Miroshnychenko Y, Wilk T, Chotia A, Viteau M, Comparat D, et al. Observation of Collective Excitation of Two Individual Atoms in the Rydberg Blockade Regime. Nat Phys (2009) 5:115–8. doi:10.1038/nphys1183

CrossRef Full Text | Google Scholar

22. Urban E, Johnson TA, Henage T, Isenhower L, Yavuz DD, Walker TG, et al. Observation of Rydberg Blockade between Two Atoms. Nat Phys (2009) 5:110–4. doi:10.1038/nphys1178

CrossRef Full Text | Google Scholar

23. Jaksch D, Cirac JI, Zoller P, Rolston SL, Côté R, Lukin MD. Fast Quantum Gates for Neutral Atoms. Phys Rev Lett (2000) 85:2208–11. doi:10.1103/physrevlett.85.2208

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Shi X-F. Deutsch, Toffoli, and CNOT Gates via Rydberg Blockade of Neutral Atoms. Phys Rev Appl (2018) 9:051001. doi:10.1103/physrevapplied.9.051001

CrossRef Full Text | Google Scholar

25. Shi X-F. Transition Slow-Down by Rydberg Interaction of Neutral Atoms and a Fast Controlled-Not Quantum Gate. Phys Rev Appl (2020) 14:054058. doi:10.1103/physrevapplied.14.054058

CrossRef Full Text | Google Scholar

26. Saffman M, Beterov II, Dalal A, Páez EJ, Sanders BC. Symmetric Rydberg Controlled-Z gates with Adiabatic Pulses. Phys Rev A (2020) 101:062309. doi:10.1103/physreva.101.062309

CrossRef Full Text | Google Scholar

27. Isenhower L, Urban E, Zhang XL, Gill AT, Henage T, Johnson TA, et al. Demonstration of a Neutral Atom Controlled-Not Quantum Gate. Phys Rev Lett (2010) 104:010503. doi:10.1103/PhysRevLett.104.010503

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Levine H, Keesling A, Omran A, Bernien H, Schwartz S, Zibrov AS, et al. High-Fidelity Control and Entanglement of Rydberg-Atom Qubits. Phys Rev Lett (2018) 121:123603. doi:10.1103/physrevlett.121.123603

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Levine H, Keesling A, Semeghini G, Omran A, Wang TT, Ebadi S, et al. Parallel Implementation of High-Fidelity Multiqubit Gates with Neutral Atoms. Phys Rev Lett (2019) 123:170503. doi:10.1103/physrevlett.123.170503

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Graham TM, Kwon M, Grinkemeyer B, Marra Z, Jiang X, Lichtman MT, et al. Rydberg-Mediated Entanglement in a Two-Dimensional Neutral Atom Qubit Array. Phys Rev Lett (2019) 123:230501. doi:10.1103/physrevlett.123.230501

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Madjarov IS, Covey JP, Shaw AL, Choi J, Kale A, Cooper A, et al. High-fidelity Entanglement and Detection of Alkaline-Earth Rydberg Atoms. Nat Phys (2020) 16:857–61. doi:10.1038/s41567-020-0903-z

CrossRef Full Text | Google Scholar

32. Maller KM, Lichtman MT, Xia T, Sun Y, Piotrowicz MJ, Carr AW, et al. Rydberg-blockade Controlled-Not Gate and Entanglement in a Two-Dimensional Array of Neutral-Atom Qubits. Phys Rev A (2015) 92:022336. doi:10.1103/physreva.92.022336

CrossRef Full Text | Google Scholar

33. Graham TM, Song Y, Scott J, Poole C, Phuttitarn L, Jooya K, et al. Demonstration of Multi-Qubit Entanglement and Algorithms on a Programmable Neutral Atom Quantum Computer (2021). arXiv:2112.14589.

Google Scholar

34. Schine N, Young AW, Eckner WJ, Martin MJ, Kaufman AM. Long-lived Bell States in an Array of Optical Clock Qubits (2021). arXiv:2111.14653.

Google Scholar

35. Omran A, Levine H, Keesling A, Semeghini G, Wang TT, Ebadi S, et al. Generation and Manipulation of Schrödinger Cat States in Rydberg Atom Arrays. Science (2019) 365(6453):570–4. doi:10.1126/science.aax9743

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Shi X-F. Rydberg Quantum gates Free from Blockade Error. Phys Rev Appl (2017) 7:064017. doi:10.1103/physrevapplied.7.064017

CrossRef Full Text | Google Scholar

37. Saffman M, Walker TG. Analysis of a Quantum Logic Device Based on Dipole-Dipole Interactions of Optically Trapped Rydberg Atoms. Phys Rev A (2005) 72:022347. doi:10.1103/physreva.72.022347

CrossRef Full Text | Google Scholar

38. Shi X-F. Quantum Logic and Entanglement by Neutral Rydberg Atoms: Methods and Fidelity. Quan Sci. Technol. (2022) 7:023002. doi:10.1088/2058-9565/ac18b8

CrossRef Full Text | Google Scholar

39. Chen X-Y, Zhang N-N, He W-T, Kong X-Y, Tao M-J, Deng F-G, et al. Global Correlation and Local Information Flows in Controllable Non-markovian Open Quantum Dynamics. Npj Quan Inf (2022) 8:22. doi:10.1038/s41534-022-00537-z

CrossRef Full Text | Google Scholar

40. Tao M-J, Zhang N-N, Wen P-Y, Deng F-G, Ai Q, Long G-L. Coherent and Incoherent Theories for Photosynthetic Energy Transfer. Sci Bull (2020) 65:318–28. doi:10.1016/j.scib.2019.12.009

CrossRef Full Text | Google Scholar

41. Ishizaki A, Fleming GR. Theoretical Examination of Quantum Coherence in a Photosynthetic System at Physiological Temperature. Proc Natl Acad Sci U.S.A (2009) 106:17255–60. doi:10.1073/pnas.0908989106

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Wang B-X, Tao MJ, Ai Q, Xin T, Lambert N, Ruan1 D, et al. Efficient Quantum Simulation of Photosynthetic Light Harvesting. Npj Quan Inf (2018) 4:5625. doi:10.1038/s41534-018-0102-2

CrossRef Full Text | Google Scholar

43. Zhang N-N, Tao M-J, He W-T, Chen X-Y, Kong X-Y, Deng F-G, et al. Efficient Quantum Simulation of Open Quantum Dynamics at Various Hamiltonians and Spectral Densities. Front Phys (2021) 16:51501. doi:10.1007/s11467-021-1064-y

CrossRef Full Text | Google Scholar

44. Weber S, Tresp C, Menke H, Urvoy A, Firstenberg O, Büchler HP, et al. Calculation of Rydberg Interaction Potentials. J Phys B: Mol Opt Phys (2017) 50:133001. doi:10.1088/1361-6455/aa743a

CrossRef Full Text | Google Scholar

45. Walker TG, Saffman M. Consequences of Zeeman degeneracy for the van der Waals blockade between Rydberg atoms. Phys Rev A (2008) 77:032723. doi:10.1103/physreva.77.032723

CrossRef Full Text | Google Scholar