Design of Dual-Functional Metaoptics for the Spin-Controlled Generation of Orbital Angular Momentum Beams

The capability of multiple orbital angular momentum (OAM) modes generation with high resolution and diversified functionalities in the visible and near-infrared regime is challenging for flat and integrated optical devices. Additionally, having a static tiny optical device capable of generating multiple structured spots in space reduces the complexity of optical paths that typically use dynamic optical components and/or many standard elements, leading to unprecedented miniaturization and compactness of optical systems. In this regard, we propose dual-functional transmission dielectric metalenses based on a set of Pancharatnam-Berry phase meta-atoms with different cross-sections, for the combined manipulation of the dynamic and geometric phases. In particular, we present and describe the numerical algorithms for the computation of dual-functional metaoptics and we apply those techniques to the design of optical elements which are able to generate and focus different OAM modes at distinct points in space. In the specific, the designed elements enable the independent or simultaneous manipulation of right-handed and left-handed circularly polarized waves, by acting on the helicity of the input beam to enable or disable a specific optical operation. The theoretical proof-of-concept results highlight the capability of the designed metalenses to generate multiple high-resolution focused OAM modes at different points in space by exploiting the polarization of the incident beam as a degree of freedom, thus providing new integrated optics for applications in the fields of high-resolution microscopy, optical manipulation, and optical communications, both in the classical and single-photon regimes.

Introduction

Since the seminal paper of Allen and coworkers in 1992 [1], structured light ignited a flourishing research area, paving the way for scientific milestones and disruptive applications in an amazing variety of fields [2], including life science, soft and condensed matter, information and communication technology. In particular, orbital angular momentum (OAM) beams [3], also called optical vortices (OVs), offered a new degree of freedom to encode information in classical communications [4] or increase the Hilbert state space in quantum applications [5, 6], while their peculiar intensity and phase distributions enabled innovative and advanced techniques in microscopy [7], micro-manipulation [8], and light-matter interaction [9]. Concurrently, the necessity to tailor and control this spatial property of light inspired the design and engineering of new techniques with different levels of complexity and integration [10–14]. Among all, spiral phase plates (SPPs) [15] represent one of the first optical elements purposely introduced to impart orbital angular momentum to common non-structured beams. Such optical elements are characterized by 3D spiral staircase profiles [16], reproducing the twisting wavefront to impart to the input beam. Their fabrication with high-resolution lithographic techniques [17] has proved the generation of OAM beams with high purity, while the introduction of radial discontinuities [18] in their design enabled the additional control on the radial number and the excitation of higher-order modes. While providing a stable, efficient, and compact method for OAM generation, a strong limitation of SPPs is given by their reduced functionality, which is basically limited to a specific OAM value. q-plates [19] provided a first evolution of standard SPPs, acting on the geometric phase to implement polarization-dependent OAM generators. Instead of spatially changing the local thickness of an isotropic material to tune the optical path, i.e., the dynamic phase, q-plates rely on shaping the wavefront by acting on the polarization state with a 2D birefringent medium. The imparted phase, having a geometric nature, is equal to twice the local angle formed by the extraordinary axis, with a sign depending on the handedness of the circular polarization in input [20]. That is achieved by structuring the optical element at the subwavelength scale in the form of a spatially-variant half-wave plate, by exploiting the inherent anisotropy of liquid crystals [21, 22], or using properly-oriented digital gratings [23] or dielectric resonators [24], the so-called metaunits, to induce an effective form birefringence. Moreover, moving from 3D sculptured surfaces to 2D digital optics, metasurfaces open to the exploitation of semiconductor manufacturing [25], achieving the actual merging between optics and silicon photonics [26]. The metasurface paradigm opens to polarization as an additional degree of freedom, enabling the design of spin-dependent optical elements for the generation of beams with opposite values of OAM. However, it would be extremely advantageous to decouple spin from phase reshaping in order to effectively extend the optical functionality.

The solution is offered by the design of spin-decoupled dual-functional metasurfaces [27–30], which locally combine the dynamic phase from the refractive index profile with the geometric phase from the induced form birefringence. That is achieved by using anisotropic nanopillars with both different orientations and shapes. While the dynamic phases along the main axes of the nanopillars can be adjusted by tailoring their cross-section, an arbitrary geometric phase can be realized by controlling the local fast-axis orientation. The proper combination of the dynamic phase with the polarization-dependent geometric one enables the encoding of two totally different optical operations for the two circular polarization states.

In this work, we focus on the design of dual-functional metasurfaces for the generation of OAM beams. In particular, we provide a numerical recipe for the design of any dual-functional optical element, showing its application to the design of metaoptics enabling the spin-controlled generation of beams with different values of OAM. Moreover, by encoding different focal terms on the two contributions, we show the possibility to control the positions of the two beams independently. The design extends significantly the functionality of standard SPPs and q-plates, providing advanced optical elements for applications in microscopy, optical micromanipulation, and classical and quantum information, with unprecedented potential levels of compactness and integration into today’s technology.

Materials and Methods

In this work, we propose metaoptics which are able to generate and manipulate optical vortices (OVs) with different OAM values at distinct points in space. Mathematically, OVs are wavefront dislocations, with peculiar topological properties, due to phase singularities in the optical field. Light beams carrying OAM are characterized by a dark central region that arises from the destructive interference phenomena leading to the typical doughnut-shaped intensity distribution [31]. In order to generate an OV, the optical element is required to implement an azimuthal phase profile:

$\mathrm{\Omega }\left(r,\theta \right)=\ell \theta ,(1)$

where $\ell$, in units of the reduced Planck constant, is the amount of orbital angular momentum per photon transferred to the impinging beam, $\left(r,\theta \right)$ are polar coordinates on the plane of the optical element.

The metasurface proposed in this work is a dielectric dual-functional metalens (DFML), made of a 2D array of birefringent metaunits that exploit both the Pancharatnam-Berry (geometric) phase and the dynamic one. Our DFML is constituted of subwavelength metaunits (MUs), the so-called metaatoms (MAs), arranged over a square lattice, represented by amorphous silicon nanopillars on a silica substrate, surrounded by air. Each pillar belongs to a subset of nanostructures with different cross sections and orientations but the same height (Figure 1A), and acts as a half-wave plate in order to maximize the polarization conversion and, therefore, the optical efficiency [32–34] . While the pillar orientation allows controlling the geometric phase, by varying the cross section it is possible to act on the dynamic phase. Combining these two properties, the metalens is able to behave in two different ways depending on whether the input beam is right-handed (RCP) or left-handed circularly polarized (LCP) (Figure 1B).

FIGURE 1

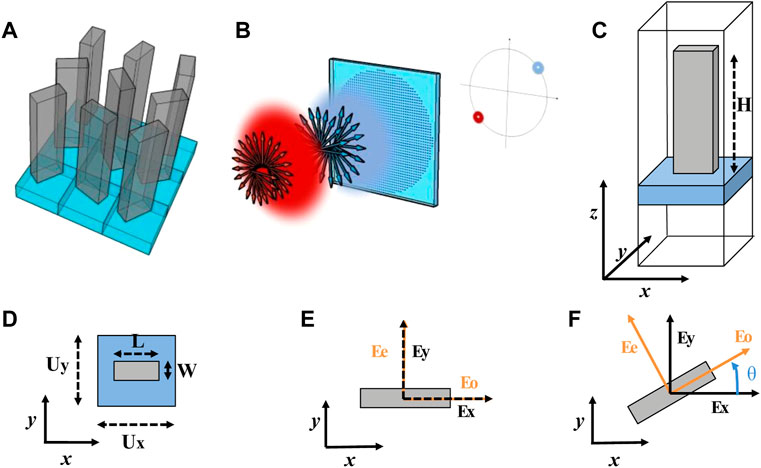
FIGURE 1. (A) Schematic figure representing the 2D array of metaunits composing a metalens. (B) Working principle of a dual-functional metalens: two different structured beams are generated at distinct points in space, depending on the handedness of the circular polarization in input. (C) 3D view of a metaunit. (D) Top view of a metaunit illustrating its geometric features: length (L), width (W), and periods of the 2D array (in our case U_x = U_y = 400 nm). (E) Cross section of a pillar representing the extraordinary and ordinary axes for our simulations. Being E_e the electric field along the extraordinary axis, E_o the electric field along the ordinary axis, E_x the electric field along the x-axis, E_y the electric field along the y-axis, axis and E_0i the input electric field, we consider a TE input polarization when $E_o=Ex=E_{0i}$ and $E_e=E_y=0$. Instead, we assume a TM input polarization when $E_o=E_x=0$ and $E_e=E_y=E_{0i}$. (F) Cross section of a pillar showing a rotation $\theta$ in order to transfer a geometric phase term equal to $2\theta$.

In fact, while a variation on the dynamic phase has the same effects both on LCP or RCP input beams, on the other hand a change in the geometric phase implies symmetrical (opposite) response on a LCP beam compared to on a RCP one. In this way, controlling simultaneously both the shape of the pillars and their rotations, it is possible to generate totally different behaviors under LCP or RCP illumination in input [35, 36].

For the benefit of the reader, we provide in the following the theory underlying the working principle of anisotropic metaunits. As well known, in dual-functional MLs the incident beam is supposed to be either left-handed circularly polarized $|R\rangle ={\left[\begin{array}{cc}1& -i\end{array}\right]}^T$ or right-handed circularly polarized $|L\rangle ={\left[\begin{array}{cc}1& i\end{array}\right]}^T$, where the normalization factor $1/\sqrt{2}$ has been omitted. Then, the transmitted output waves are cross-polarized and carry the spatial phase shifts ${\varphi }^{-}\left(x,y\right)$ or ${\varphi }^{+}\left(x,y\right)$, respectively.

In particular, the Jones matrix $J$ for the metaatom at the coordinates $\left(x,y\right)$ is:

$J\left(x,y\right)=R\left(\theta \left(x,y\right)\right)\left[\begin{array}{cc}{e}^{i{\delta }_x\left(x,y\right)}& 0\\ 0& e^{i{\delta }_y\left(x,y\right)}\end{array}\right]R\left(-\theta \left(x,y\right)\right),(2)$

where $R\left(\theta \right)$ is the unitary rotation matrix:

$R\left(\theta \right)=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right],(3)$

being θ the local orientation of the metaatom fast axis. After straightforward calculations, Eq. 2 can be expressed in the form (the spatial dependence has been omitted to simplify the notation):

$\begin{array}{l}J=e^{i\frac{{\delta }_x+{\delta }_y}{2}}R\left(\theta \right)\left[\begin{array}{cc}{e}^{-i\frac{{\delta }_y-{\delta }_x}{2}}& 0\\ 0& e^{+i\frac{{\delta }_y-{\delta }_x}{2}}\end{array}\right]R\left(-\theta \right)=\\ =e^{i\frac{{\delta }_x+{\delta }_y}{2}}R\left(\theta \right)\left[\begin{array}{cc}\cos \left(\frac{\mathrm{\Delta }}{2}\right)-i\sin \left(\frac{\mathrm{\Delta }}{2}\right)& 0\\ 0& \cos \left(\frac{\mathrm{\Delta }}{2}\right)+i\sin \left(\frac{\mathrm{\Delta }}{2}\right)\end{array}\right]R\left(-\theta \right)=,\\ =e^{i\frac{{\delta }_x+{\delta }_y}{2}}\cos \left(\frac{\mathrm{\Delta }}{2}\right)\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]-i{e}^{i\frac{{\delta }_x+{\delta }_y}{2}}\sin \left(\frac{\mathrm{\Delta }}{2}\right)\left[\begin{array}{cc}\cos \left(2\theta \right)& \sin \left(2\theta \right)\\ \sin \left(2\theta \right)& -\cos \left(2\theta \right)\end{array}\right]\end{array}(4)$

where $\mathrm{\Delta }={\delta }_y-{\delta }_x$ is the phase retardation between the two axes of the metaunit. It is worth noting from Eq. 4 that, under the choice $\mathrm{\Delta }=\pi$, the optical behavior of the metaunit is that of a rotated half-wave plate. Therefore, for circularly-polarized light in input, each metaatom behaves as a polarization converter:

$J|L\rangle =-i{e}^{i\left({\delta }_x+{\delta }_y\right)/2}{e}^{+i2\theta }|R\rangle (5)$

$J|R\rangle =-i{e}^{i\left({\delta }_x+{\delta }_y\right)/2}{e}^{-i2\theta }|L\rangle (6)$

imparting a polarization-independent dynamic phase term equal to $\left({\delta }_x+{\delta }_y\right)/2$, plus a polarization-sensitive geometric phase equal to twice the orientation angle $\theta$, and with sign depending on the input handedness. Therefore, when the condition $\mathrm{\Delta }=\pi$ is satisfied, the cosine term in Eq. 4 representing the zero-order contribution is completely suppressed. Thus, in conclusion, the metaunit acts as a pure half-wave plate and, since the spurious zero-order component has been erased, the diffraction efficiency is optimized.

Then, it is possible to define a spin-decoupled optical response with the following definitions:

${\delta }_x=\frac{{\varphi }^{+}\left(x,y\right)+{\varphi }^{-}\left(x,y\right)}{2}(7)$

${\delta }_y=\frac{{\varphi }^{+}\left(x,y\right)+{\varphi }^{-}\left(x,y\right)}{2}+\pi (8)$

$\theta =\frac{{\varphi }^{+}\left(x,y\right)-{\varphi }^{-}\left(x,y\right)}{4}(9)$

being ${\varphi }^{+}$ and ${\varphi }^{-}$ the phase to impart to left-handed and right-handed circular polarization, respectively. As a matter of fact, it is straightforward to prove that:

$J|L\rangle =e^{i{\varphi }^{+}}|R\rangle (10)$

$J|R\rangle =e^{i{\varphi }^{-}}|L\rangle (11)$

Hence, by accurately selecting a set of nanopillars with different sizes, which satisfy the required phase delays, i.e., $\left({\delta }_x,{\delta }_y\right)$, and rotating each nanopillar of an angle $\theta$ with respect to the x-axis positive direction, it is possible to design a metalens that imparts a phase delay ${\varphi }^{+}\left(x,y\right)$ to an LCP input light and a phase delay ${\varphi }^{-}\left(x,y\right)$ to an RCP input light.

We exploit these properties to design and test DFMLs which are able to generate and focus different orbital angular momentum beams at distinct fixed points in space, depending on the input circularly-polarized state. To implement these functionalities, the spatial phase patterns ${\varphi }^{+}\left(x,y\right)$ or ${\varphi }^{-}\left(x,y\right)$ must be accurately engineered. To this purpose, we suggest a new converging lens profile ϕ, which is able to generate a focused beam carrying OAM at a desired position. In detail:

$\varphi \left(x,y\right)=\ell \arctan \left(\frac{y}{x}\right)-\frac{2\pi }{\lambda }\left(\sqrt{f^2+{\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2}-f\right)(12)$

where $\ell$ is the amount of OAM per photon transferred to the impinging beam, in units of $\hslash$, $\lambda$ is the working wavelength, $f$ is the focal length, and $\left(x_0,y_0\right)$, are the focus coordinates on the focal plane perpendicular to the propagation optical axis (z). The first part of the equation, i.e., $\ell \arctan \left(y/x\right)$ is the azimuthal phase necessary to generate an optical vortex (Eq. 1), while the second part, i.e., $-2\pi /\lambda \left(\sqrt{f^2+{\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2}-\left|f\right|\right)$, is an hyperboloid focusing profile, without spherical aberration if illuminated by a plane-wave [37, 38], mandatory to focus the optical vortex onto a desired point in space.

After defining the theoretical framework for the wavefront engineering, we performed a custom Finite-Element Method (FEM) simulation in the wavelength domain using COMSOL Multiphysics® to extrapolate the set of metaunits which compose the metalens (Figure 2). The geometry of the metaatoms was modelled as an amorphous silicon pillar (n_Si = 3.425) deposited on a glass substrate ($n_{Glass}=1.450$) and surrounded by air ($n_{Air}=1$). Periodic port conditions were set at the base of the substrate (at a distance equal to $\lambda$) and at a distance greater than $\lambda$ in the upper zone simulating air, to ensure the Fraunhofer regime [39]. Perfectly Matched Layers (PML) conditions were imposed in the areas outside the ports in order to absorb the field in the simulation volumes not of interest so to avoid multiple reflections. Finally, periodic boundary conditions were set (along the xz and yz planes) to correctly simulate the interaction between the various metaatoms of the metalens [40]. The period of the metaunits array was fixed at 400 nm in both directions, while the parameters of the pillar cross-section (L, W) were swept during the simulation considering the fabrication limits and the sub-wavelength working regime. In particular, the height (H) was fixed at 500 nm considering the fabrication limits (Figures 1C–F). For a given phase delay along the long axis of the pillar, the final cross-section was selected in order to satisfy the condition $\Delta =\pi$. Concurrently, provided the last condition is satisfied, the transmission values for TE and TM polarizations must be as close as possible, in order guarantee the expected polarization conversion under circularly-polarized light in input. Therefore, previous requirements significantly limit the choice of possible cross-sections for the given thickness and shape. Moreover, in order to increase the degrees of freedom to find the adequate nanostructures to cover the whole 2π range, both rectangular-based and elliptical-based silicon pillars were considered. Finally, a library of 12 different nanopillars has been extrapolated from the simulations, which permits to have a well-distributed 12-level discretization of the phase over the range 0-2π (Figure 3). Conversely, we assumed a continuous rotation of the metaatom, i.e., no discretization on the geometric phase was applied. Then, for given phase patterns ${\varphi }^{+}$ and ${\varphi }^{-}$, we were able to calculate the corresponding maps for the dynamic and geometric phases using Eqs 7–9. Those maps provide the recipe to compute the metaatoms pattern of the desired DFML. While the geometric phase map gives the local orientation of the metaatom, the required dynamic phase delay allows one to select the required cross-section referring to the lookup table in Figure 3.

FIGURE 2

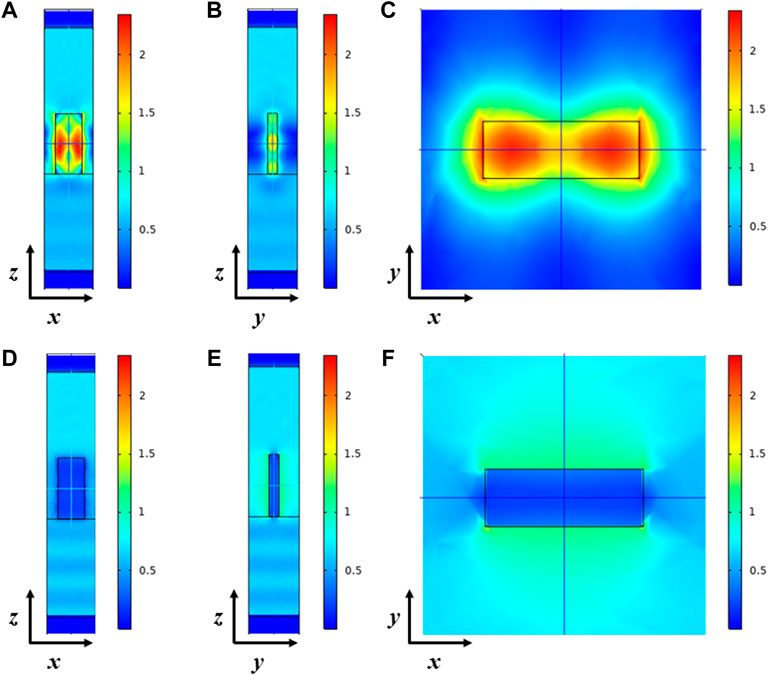
FIGURE 2. Example of FEM simulations of a metaatom ($U_x=U_y=400\mathrm{nm}$) composed by a silicon nanopillar ($L=220\mathrm{nm}$, $W=80\mathrm{nm}$ and $H=500\mathrm{nm}$, i.e., pillar #11 in Figure 3) on a glass substrate under TE (A–C) and TM (D,E) polarization in input from the air side. Lateral cross-sections at y = 0 (A,D) and x = 0 (B,E) and top-view cross-section at z = H/2 (C,F). Input wavelength 775 nm. Colours refer to the intensity of the electric field (a.u.).

FIGURE 3

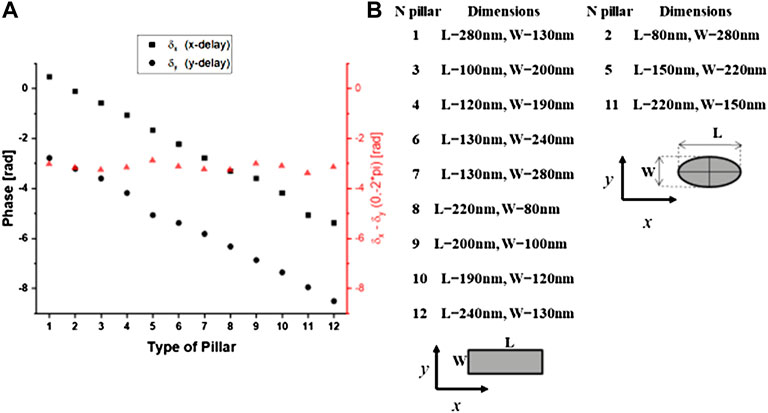
FIGURE 3. (A) Graph showing the library of different pillars working at 775 nm and their phase delays under both TE polarization (x-delay) and TM polarization (y-delay), mandatory to built-up the metalens using the Eqs 7–9. (B) List of pillars composing the library with their corresponding geometric features.

Results

Using a custom code implementing the Fresnel propagation integral [41] in MatLab® environment, we simulated the optical response of several dual functional metalenses designed according to Eq. 12. In particular, we selected different combinations of the parameters $\ell$, $f$, $x_0$, and $y_0$, in such a way to exhibit all the potentialities emerging from the combination of the DFML paradigm Eqs 7–11 with the converging spiral profile of Eq. 12. All the simulations were performed implementing metasurfaces of radius $100\mu m$, with 12 levels of phase discretization, working at $\lambda =775nm$, and illuminated by a Gaussian beam, with a cross-section as given by $\exp \left(-r^2/w_0^2\right)$, being $r=\sqrt{x^2+y^2}$, with $w_0=100\mu m$ chosen to properly illuminate the entire metasurface pattern. The intensities of the simulations have been normalized according to the formula:

$I_{normalized}\left(x,y\right)=\frac{{\left|E\left(x,y\right)\right|}^2}{\max \left({\left|E\right|}^2\right)}(13)$

In the following, we report for each case of interest the phase patterns experienced by the two circular polarization states, and a simulation of their propagation after the optical element. In particular, we show a cross-section of the beam at the focal planes, in order to highlight the expected phase and intensity profiles.

We started implementing a dual-functional metalens able to focus two beams carrying different values of OAM at the same focus along the optical axis, with OAM depending on the input polarization.

Thus, we imposed the following focusing profiles:

${\varphi }^{+}\left(x,y\right)={\ell }_1\arctan \left(\frac{y}{x}\right)-\frac{2\pi }{\lambda }\left(\sqrt{f^2+x^2+y^2}-f\right)(14)$

${\varphi }^{-}\left(x,y\right)={\ell }_2\arctan \left(\frac{y}{x}\right)-\frac{2\pi }{\lambda }\left(\sqrt{f^2+x^2+y^2}-f\right)(15)$

being ${\ell }_1=1$, ${\ell }_2=3$, and $f=500\mu m$. As shown in Figure 4, two structured beams are well generated under both LCP and RCP polarization. From the phase profile (Figure 4), it is clearly observable that the two beams carry different OAM. In particular, a first-order OAM beam is generated with a left-handed helicity, while under a right-handed helicity a third-order OAM beam is produced. In fact, there is only one phase variation from 0 to 2π in the first case, while in the second case 3 phase steps in the range 0-2π appear. That is further confirmed from the singularity size of the generated doughnut, which is larger in the OAM beam with $\ell =3$ with respect to that with $\ell =1$, as expected from the theory [31].

FIGURE 4

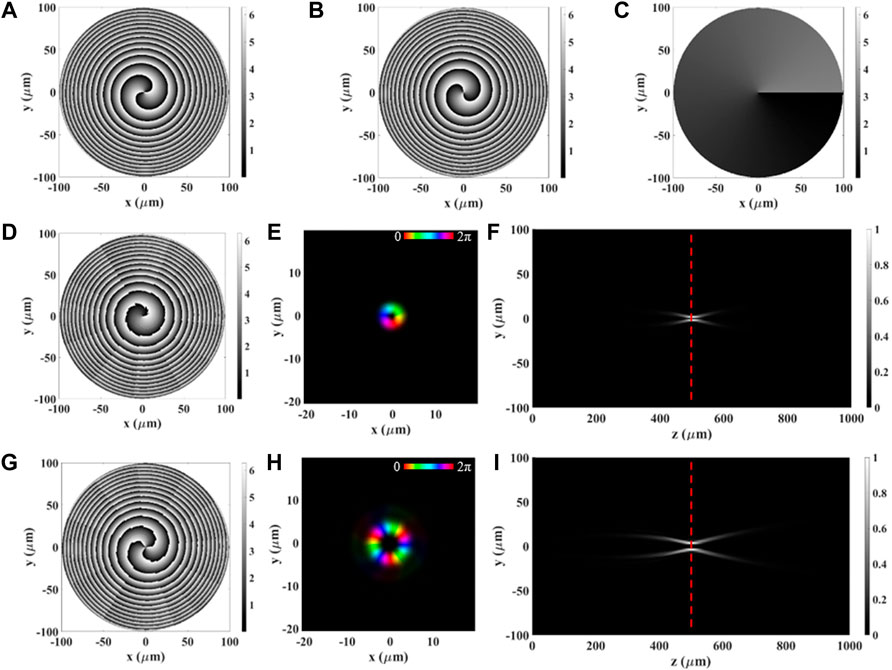
FIGURE 4. Simulations of DFML implementing Eqs 14, 15. (A–C) ML design phase maps of ${\delta }_x$ (A), ${\delta }_y$ (B), and $\theta$ (C) from Eqs 7–9. (D,G) show ${\varphi }^{+}$ and ${\varphi }^{-}$ phase maps, respectively. (E) Intensity and phase of the propagated field under LCP polarization at z = 500 µm. (F) Intensity cross-section (yz-plane, from 0 to 1mm, x = 0)under LCP polarization. (H) Intensity and phase of the propagated field under RCP polarization at z = 500 µm. (I) Intensity cross-section (yz-plane from 0 to 1mm, x = 0) under RCP polarization. In (E,H), brightness and colours refer to intensity and phase, respectively.

Subsequently, we implemented a DFML able to focus two beams carrying different OAM values at different focal lengths along the optical axis, depending on the input helicity. To obtain a metasurface as described above we encoded the following profiles:

${\varphi }^{+}\left(x,y\right)={\ell }_1\arctan \left(\frac{y}{x}\right)-\frac{2\pi }{\lambda }\left(\sqrt{f_1^2+x^2+y^2}-f_1\right)(16)$

${\varphi }^{-}\left(x,y\right)={\ell }_2\arctan \left(\frac{y}{x}\right)-\frac{2\pi }{\lambda }\left(\sqrt{f_2^2+x^2+y^2}-f_2\right)(17)$

being ${\ell }_1=1$, ${\ell }_2=3$, $f_1=500\mu m$, and $f_2=1000\mu m$. As expected, in this case two different doughnut spots are well generated at different focal lengths (Figure 5). Moreover, it can be noticed that the beam carrying OAM with $\ell =3$ and focalized at 1000 µm (d-f)), is bigger than the same beam focalized at $500\mathrm{\mu m}$. This behaviour is also due to the properties of the Fourier transform of a focusing lens [39] .

FIGURE 5

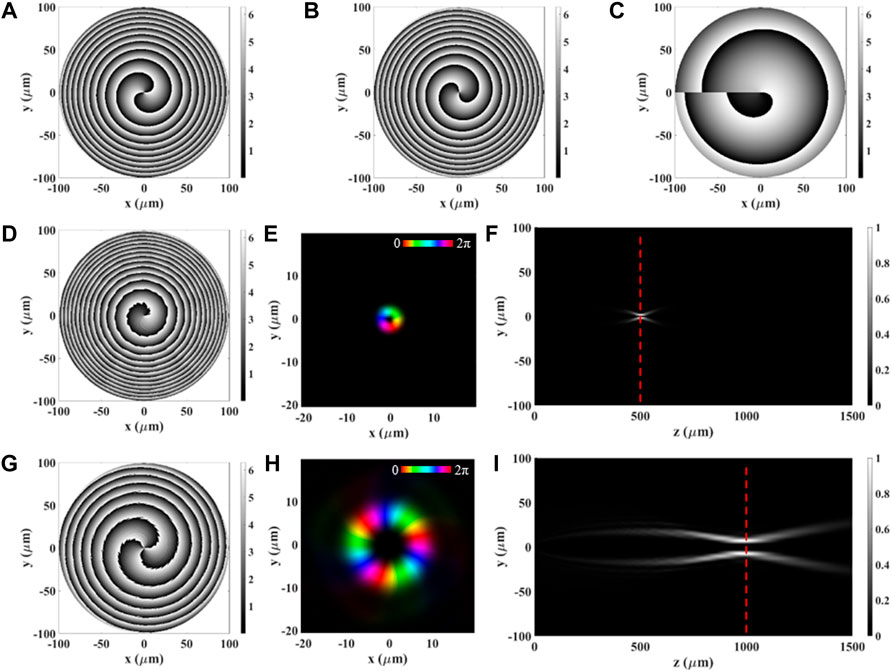
FIGURE 5. Simulations of DFML implementing Eqs 16, 17. (A–C) ML design phase maps of ${\delta }_x$ (A), ${\delta }_y$ (B), and $\theta$ (C) from Eqs 7–9. (D,G) show ${\varphi }^{+}$ and ${\varphi }^{-}$ phase maps, respectively. (E) Intensity and phase of the propagated field under LCP polarization at z = 500 µm. (F) Intensity cross-section (yz-plane, from 0 to 1.5 mm, x = 0) under LCP polarization. (H) Intensity and phase of the propagated field under RCP polarization at $z=1000\mathrm{\mu m}$. (I) Intensity cross-section (yz-plane from 0 to 1.5 mm, x = 0) under RCP polarization. In (E,F), brightness and colours refer to intensity and phase, respectively.

After that, we tried to further extend the focusing on different points in space not located along the propagation axis (z-axis). To this aim, we added two tilting parameters in the focusing formula according to Eq. 12. Initially we propose a DFML able to focus two beams carrying different OAM at the same focal length but onto two distinct points on the same focal plane. To exploit these functionalities the implemented formulas were:

${\varphi }^{+}\left(x,y\right)={\ell }_1\arctan \left(\frac{y}{x}\right)-\frac{2\pi }{\lambda }\left(\sqrt{f_1^2+{\left(x-x_1\right)}^2+{\left(y-y_1\right)}^2}-f_1\right)(18)$

${\varphi }^{-}\left(x,y\right)={\ell }_2\arctan \left(\frac{y}{x}\right)-\frac{2\pi }{\lambda }\left(\sqrt{f_1^2+{\left(x-x_2\right)}^2+{\left(y-y_2\right)}^2}-f_1\right)(19)$

being ${\ell }_1=1$, ${\ell }_2=3$, $f_1=750\mu m$, $x_1=y_1=-50\mu m$, and $x_2=y_2=+50\mu m$.

As shown in Figure 6, the focalized OAM beams are generated at the expected points in space for both the polarizations.

FIGURE 6

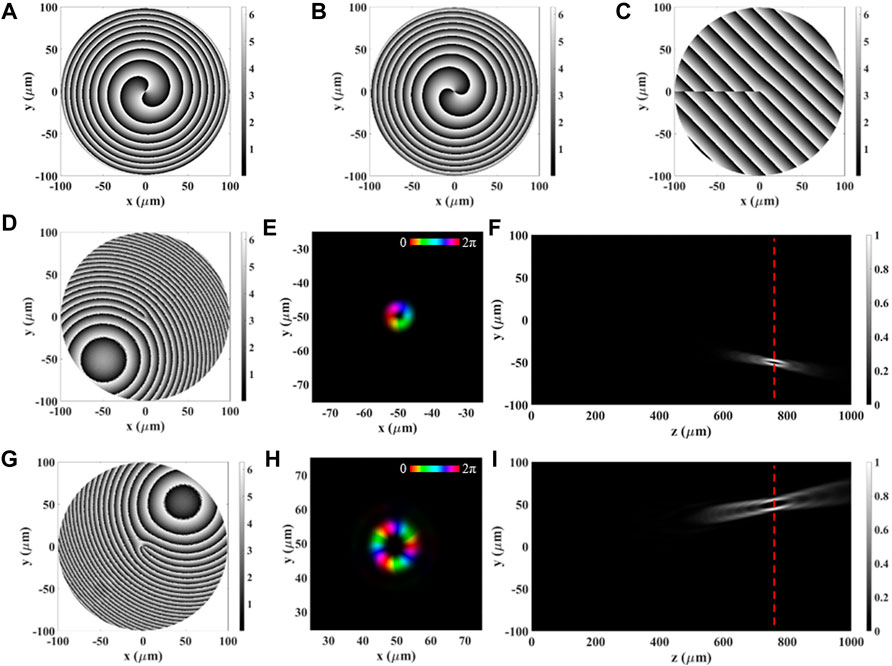
FIGURE 6. Simulations of DFML implementing Eqs 18, 19. (A–C) ML design phase maps of ${\delta }_x$ (A), ${\delta }_y$ (B), and $\theta$ (C) from Eqs 7–9. (D,G) show ϕ⁺ and ϕ⁻ phase maps, respectively. (E) Intensity and phase of the propagated field under LCP polarization at $z=750\mathrm{\mu m}$. (F) Intensity cross-section (yz-plane, from 0 to 1 mm, x = −50 µm) under LCP polarization. (H) Intensity and phase of the propagated field under RCP polarization at $z=\mathrm{750\mu m}$. (I) Intensity cross-section (yz-plane from 0 to 1 mm, x = +50 µm) under RCP polarization. In (E,H), brightness and colours refer to intensity and phase, respectively.

In order to demonstrate the ability to focalize two beams carrying different OAM onto two distinct points in space at different focal lengths, we tried to focalize a spot at the same coordinates xy but at a higher focal length. In this regard, we simulated a DFML implementing the phase profiles:

${\varphi }^{+}\left(x,y\right)={\ell }_1\arctan \left(\frac{y}{x}\right)-\frac{2\pi }{\lambda }\left(\sqrt{f_1^2+{\left(x-x_1\right)}^2+{\left(y-y_1\right)}^2}-f_1\right)(20)$

${\varphi }^{-}\left(x,y\right)={\ell }_2\arctan \left(\frac{y}{x}\right)-\frac{2\pi }{\lambda }\left(\sqrt{f_2^2+{\left(x-x_2\right)}^2+{\left(y-y_2\right)}^2}-f_2\right)(21)$

being ${\ell }_1=1$, ${\ell }_2=3$, $f_1=500\mu m$, $f_2=1000\mu m$, $x_1=y_1=-50\mu m$, and $x_2=y_2=+50\mu m$.

The resulting simulations (Figure 7) show how using the above formulas it is possible to focus different OAM beams in completely different points in space. Accurately choosing the design parameters of a DFML, it is possible to avoid symmetry problems due to both high deviation from the propagation axis and short focal lengths.

FIGURE 7

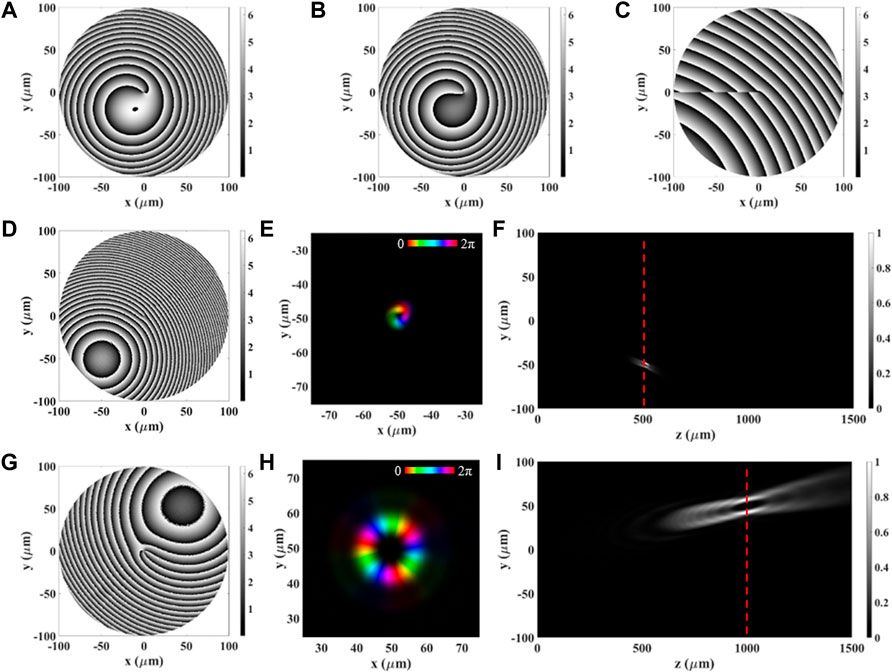
FIGURE 7. Simulations of DFML implementing Eqs 20, 21. (A–C) ML design phase maps of ${\delta }_x$ (A), ${\delta }_y$ (B), and $\theta$ (C) from Eqs 7–9. (D,G) show ϕ⁺ and ϕ⁻ phase maps, respectively. (E) Intensity and phase of the propagated field under LCP polarization at $z=500\mathrm{\mu m}$. (F) Intensity cross-section (yz-plane, from 0 to 1.5 mm, x = −50 µm) under LCP polarization. (H) Intensity and phase of the propagated field under RCP polarization at $z=1000\mathrm{\mu m}$. (I) Intensity cross-section (yz-plane from 0 to 1.5 mm, x = +50 µm) under RCP polarization. In (E,H), brightness and colours refer to intensity and phase, respectively.

Discussion and Conclusions

We have here presented the numerical design and simulation of dual-functional metalenses for the spin-controlled generation of OAM beams. The designed optical elements have been engineered to focus different OAM beams at distinct points in space, depending on the handedness of the circularly polarized state in input. That is achieved by properly selecting the resonant metaunits in order to act both on the dynamic and geometric phase imparted to the input beam, so that the polarization-dependent geometric term combines with the polarization-insensitive dynamic one in order to induce a spin-decoupled functionality. Numerical simulations based on FEM analysis have been performed to define an optimized set of silicon resonators, with fixed thickness and different cross-sections, acting as half-wave plates with different phase delays on two orthogonal optical axes. In such a way, while a rotation of the pillar enables the direct control on the geometric phase, the selection of the proper cross-section is dictated by the specific dynamic phase to be imparted. We provided a set of 12 different nanopillars optimized for the wavelength of 775 nm, which can be used as lookup table for the design of any dual-functional metasurface. In particular, we proved the dual-functional behavior for the specific case represented by the spin-controlled generation of OAM beams, showing the on-demand focusing of beams with different values of OAM at distinct points in space. Such optical elements represent the ultimate optical evolution of standard spiral phase plates and q-plates. While the former optical elements are refractive/diffractive optics restricted to the generation of a specific OAM value, the latter ones are their metaoptics evolution, introducing polarization as an additional degree of freedom to control the helicity of the output twisted wavefronts. Dual-functional metalenses allow to further extend the optical functionality to the generation of any pair of different OAM beams. Moreover, additional functionalities can be added, as the focus onto distinct points in space. Again, that is made possible by the dual-functional behavior, since a standard metalens would focus only one circular polarization in input, while defocusing the orthogonal one. Therefore, the dual-functional implementation could be of extreme interest in total angular momentum analysis, boosting the evolution from diffractive [42] to metasurface [43, 44] optical architectures. Moreover, the possibility to design polarization-switchable optical elements can be of high interest in imaging and microscopy, to enable the compact integration of a high-resolution analysis in the setup. Besides the undoubtful gain in functionality, the metasurface paradigm provides an unprecedented increase in compactness and integration, representing the real merging between lens design and silicon photonics. The designed pattern can be fabricated by transferring a lithographic mask to the silicon substrate by means of etching techniques [45], or chemical vapor deposition [46]. Furthermore, the possibility to select even more complicated metaunits, such as coupled resonant nanofins, opens to the possibility to tune the wavelength dispersion and achieve full achromaticity, as demonstrated for imaging metalenses [47, 48], further extending the working range of the designed metaoptics.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

AV performed FEM numerical analyses, metasurfaces design and optical simulations. GR gave suggestions in numerical simulations and contributed to the algorithms for beam propagation and metasurface computation. FR addressed the aim of the project and defined the design target specs of the optics. All authors discussed the results and the optimization configurations, contributed to the writing of the manuscript, and approved the final version.

Funding

The work was supported by the project LifeLab (CORIS, Veneto Region), by the project VORTEX3 (CEPOLISPE, Italian Ministry of Defence), and by the project STRADA (Italian Government, Presidency of the Council of Ministers).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Allen L., Beijersbergen M. W., Spreeuw R. J. C., Woerdman J. P. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Rubinsztein-Dunlop H., Forbes A., Berry M. V., Dennis M. R., Andrews D. L., Mansuripur M., et al. Roadmap on Structured Light. J Opt (2016) 19:013001. doi:10.1088/2040-8978/19/1/013001

CrossRef Full Text | Google Scholar

3. Padgett M. J. Orbital Angular Momentum 25 Years on [Invited]. Opt Express (2017) 25(10):11265–74. doi:10.1364/oe.25.011265

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wang J. Twisted Optical Communications Using Orbital Angular Momentum. Sci China Phys Mech Astron (2019) 62(3):34201. doi:10.1007/s11433-018-9260-8

CrossRef Full Text | Google Scholar

5. Sit A., Bouchard F., Fickler R., Gagnon-Bischoff J., Larocque H., Heshami K., et al. High-dimensional Intracity Quantum Cryptography with Structured Photons. Optica (2017) 4(9):1006–10. doi:10.1364/optica.4.001006

CrossRef Full Text | Google Scholar

6. De Oliveira M., Nape I., Pinnell J., TabeBordbar N., Forbes A. Experimental High-Dimensional Quantum Secret Sharing with Spin-Orbit-Structured Photons. Phys Rev A (2020) 101(4):042303. doi:10.1103/physreva.101.042303

CrossRef Full Text | Google Scholar

7. Willig K. I., Harke B., Medda R., Hell S. W. STED Microscopy with Continuous Wave Beams. Nat Methods (2007) 4(11):915–8. doi:10.1038/nmeth1108

PubMed Abstract | CrossRef Full Text | Google Scholar

8. MacDonald M. P., Paterson L., Volke-Sepulveda K., Arlt J., Sibbett W., Dholakia K. Creation and Manipulation of Three-Dimensional Optically Trapped Structures. Science (2002) 296:1101–3. doi:10.1126/science.1069571

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Franke-Arnold S. Optical Angular Momentum and Atoms. Phil Trans R Soc A (20172087) 375:20150435. doi:10.1098/rsta.2015.0435

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Fatkhiev D. M., Butt M. A., Grakhova E. P., Kutluyarov R. V., Stepanov I. V., Kazanskiy N. L., et al. Recent Advances in Generation and Detection of Orbital Angular Momentum Optical Beams-A Review. Sensors (2021) 21(15):4988. doi:10.3390/s21154988

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lian Y., Qi X., Wang Y., Bai Z., Wang Y., Lu Z. OAM Beam Generation in Space and its Applications: A Review. Opt Lasers Eng (2022) 151:106923. doi:10.1016/j.optlaseng.2021.106923

CrossRef Full Text | Google Scholar

12. Balthasar Mueller J. P., Rubin N. A., Devlin R. C., Groever B., Capasso F. Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys Rev Lett (2017) 118(11):113901. doi:10.1103/physrevlett.118.113901

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Jin Z., Janoschka D., Deng J., Ge L., Dreher P., Frank B., et al. Phyllotaxis-inspired Nanosieves with Multiplexed Orbital Angular Momentum. eLight (2021) 1(1):1–11. doi:10.1186/s43593-021-00005-9

CrossRef Full Text | Google Scholar

14. Wan C., Rui G., Chen J., Zhan Q. Detection of Photonic Orbital Angular Momentum with Micro- and Nano-Optical Structures. Front Optoelectron (2019) 12:88–96. doi:10.1007/s12200-017-0730-8

CrossRef Full Text | Google Scholar

15. Khonina S. N., Kotlyar V. V., Shinkaryev M. V., Soifer V. A., Uspleniev G. V. The Phase Rotor Filter. J Mod Opt (1992) 39:1147–54. doi:10.1080/09500349214551151

CrossRef Full Text | Google Scholar

16. Turnbull G. A., Robertson D. A., Smith G. M., Allen L., Padgett M. J. The Generation of Free-Space Laguerre-Gaussian Modes at Millimetre-Wave Frequencies by Use of a Spiral Phaseplate. Opt Commun (1996) 127:183–8. doi:10.1016/0030-4018(96)00070-3

CrossRef Full Text | Google Scholar

17. Massari M., Ruffato G., Gintoli M., Ricci F., Romanato F. Fabrication and Characterization of High-Quality Spiral Phase Plates for Optical Applications. Appl Opt (2015) 54(13):4077–83. doi:10.1364/ao.54.004077

CrossRef Full Text | Google Scholar

18. Ruffato G., Massari M., Carli M., Romanato F. Spiral Phase Plates with Radial Discontinuities for the Generation of Multiring Orbital Angular Momentum Beams: Fabrication, Characterization, and Application. Opt Eng (2015) 54(11):111307. doi:10.1117/1.oe.54.11.111307

CrossRef Full Text | Google Scholar

19. Marrucci L., Manzo C., Paparo D. Optical Spin-To-Orbital Angular Momentum Conversion in Inhomogeneous Anisotropic media. Phys Rev Lett (2006) 96:163905. doi:10.1103/physrevlett.96.163905

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Desiatov B., Mazurski N., Fainman Y., Levy U. Polarization Selective Beam Shaping Using Nanoscale Dielectric Metasurfaces. Opt Express (2015) 23(17):22611–8. doi:10.1364/oe.23.022611

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Brasselet E. Tunable High-Resolution Macroscopic Self-Engineered Geometric Phase Optical Elements. Phys Rev Lett (2018) 121(3):033901. doi:10.1103/PhysRevLett.121.033901

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Ruffato G., Brasselet E., Massari M., Romanato F. Electrically Activated Spin-Controlled Orbital Angular Momentum Multiplexer. Appl Phys Lett (2018) 113(1):011109. doi:10.1063/1.5030844

CrossRef Full Text | Google Scholar

23. Ruffato G., Romanato F. Design of Continuously Variant Metasurfaces for Conformal Transformation Optics. Opt Express (2020) 28(23):34201–18. doi:10.1364/oe.400627

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Devlin R. C., Ambrosio A., Wintz D., Oscurato S. L., Zhu A. Y., Khorasaninejad M., et al. Spin-to-orbital Angular Momentum Conversion in Dielectric Metasurfaces. Opt Express (2017) 25(1):377–93. doi:10.1364/oe.25.000377

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Genevet P., Capasso F., Aieta F., Khorasaninejad M., Devlin R. Recent Advances in Planar Optics: from Plasmonic to Dielectric Metasurfaces. Optica (2017) 4:139–52. doi:10.1364/optica.4.000139

CrossRef Full Text | Google Scholar

26. Capasso F. The Future and Promise of Flat Optics: a Personal Perspective. Nanophotonics (2018) 7(6):953–7. doi:10.1515/nanoph-2018-0004

CrossRef Full Text | Google Scholar

27. Devlin R. C., Ambrosio A., Rubin N. A., Mueller J. P. B., Capasso F. Arbitrary Spin-To-Orbital Angular Momentum Conversion of Light. Science (2017) 358(6365):896–901. doi:10.1126/science.aao5392

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Huo P., Zhang C., Zhu W., Liu M., Zhang S., Zhang S., et al. Photonic Spin-Multiplexing Metasurface for Switchable Spiral Phase Contrast Imaging. Nano Lett (2020) 20(4):2791–8. doi:10.1021/acs.nanolett.0c00471

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Li S., Li X., Zhang L., Wang G., Zhang L., Liu M., et al. Efficient Optical Angular Momentum Manipulation for Compact Multiplexing and Demultiplexing Using a Dielectric Metasurface. Adv Opt Mater. (2020) 8(8):1901666. doi:10.1002/adom.201901666

CrossRef Full Text | Google Scholar

30. Guo Y., Zhang S., Pu M., He Q., Jin J., Xu M., et al. Spin-decoupled Metasurface for Simultaneous Detection of Spin and Orbital Angular Momenta via Momentum Transformation. Light: Sci Appl (2021) 10(1):1–12. doi:10.1038/s41377-021-00497-7

PubMed Abstract | CrossRef Full Text | Google Scholar

31.D. L. Andrews, and M. Babiker, editors (2012).The Angular Momentum of Light. Cambridge University Press, Cambridge, United Kingdom.

Google Scholar

32. Lin D., Fan P., Hasman E., Brongersma M. L. Dielectric Gradient Metasurface Optical Elements. science (2014) 345(6194):298–302. doi:10.1126/science.1253213

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Khorasaninejad M., Crozier K. B. Polarization Splitting at Infrared Wavelengths Using Silicon Nanoridges. Nat Commun (2014) 5(1):1–6. doi:10.1364/cleo_si.2014.sf1o.1

CrossRef Full Text | Google Scholar

34. Zheng G., Mühlenbernd H., Kenney M., Li G., Zentgraf T., Zhang S. Metasurface Holograms Reaching 80% Efficiency. Nat Nanotechnol (2015) 10(4):308–12. doi:10.1038/nnano.2015.2

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Zhang K., Yuan Y., Ding X., Ratni B., Burokur S. N., Wu Q. High-efficiency Metalenses with Switchable Functionalities in Microwave Region. ACS Appl Mater Inter (2019) 11(31):28423–30. doi:10.1021/acsami.9b07102

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Ruffato G. OAM-inspired New Optics: the Angular Metalens. Light Sci Appl (2021) 10:96. doi:10.1038/s41377-021-00541-6

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Aieta F., Genevet P., Kats M., Capasso F. Aberrations of Flat Lenses and Aplanatic Metasurfaces. Opt Express (2013) 21(25):31530–9. doi:10.1364/oe.21.031530

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Aieta F., Genevet P., Kats M. A., Yu N., Blanchard R., Gaburro Z., et al. Aberration-free Ultrathin Flat Lenses and Axicons at Telecom Wavelengths Based on Plasmonic Metasurfaces. Nano Lett (2012) 12(9):4932–6. doi:10.1021/nl302516v

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Goodman J. W. (2005). Introduction to Fourier Optics, 3rd ed., by J. W. Goodman. Englewood, CO: Roberts & Co. Publishers p. 1.

Google Scholar

40. Jin J. M. The Finite Element Method in Electromagnetics(2015). John Wiley & Sons. Hoboken, New Jersey, United States.

Google Scholar

41. Li J., Peng Z., Fu Y. Diffraction Transfer Function and its Calculation of Classic Diffraction Formula. Opt Commun (2007) 280:243–8. doi:10.1016/j.optcom.2007.08.053

CrossRef Full Text | Google Scholar

42. Ruffato G., Massari M., Girardi M., Parisi G., Zontini M., Romanato F. Non-paraxial Design and Fabrication of a Compact OAM Sorter in the Telecom Infrared. Opt Express (2019) 27(17):24123–34. doi:10.1364/oe.27.024123

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Ruffato G., Capaldo P., Massari M., Mafakheri E., Romanato F. Total Angular Momentum Sorting in the Telecom Infrared with Silicon Pancharatnam-Berry Transformation Optics. Opt Express (2019) 27(11):15750–64. doi:10.1364/oe.27.015750

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Wang B., Wen Y., Zhu J., Chen Y., Yu S. Sorting Full Angular Momentum States with Pancharatnam-Berry Metasurfaces Based on Spiral Transformation. Opt Express (2020) 28:16342–51. doi:10.1364/oe.393859

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Capaldo P., Mezzadrelli A., Pozzato A., Ruffato G., Massari M., Romanato F. Nano-fabrication and Characterization of Silicon Meta-Surfaces provided with Pancharatnam-Berry Effect. Opt Mater Express (2019) 9(3):1015–32. doi:10.1364/ome.9.001015

CrossRef Full Text | Google Scholar

46. Su V.-C., Chu C. H., Sun G., Tsai D. P. Greg Sun, and Din Ping TsaiAdvances in Optical Metasurfaces: Fabrication and Applications [Invited]. Opt Express (2018) 26(10):13148–82. doi:10.1364/oe.26.013148

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Chen W. T., Zhu A. Y., Capasso F. Flat Optics with Dispersion-Engineered Metasurfaces. Nat Rev Mater (2020) 5:604–20. doi:10.1038/s41578-020-0203-3

CrossRef Full Text | Google Scholar

48. Chen W. T., Zhu A. Y., Sanjeev V., Khorasaninejad M., Shi Z., Lee E.A Broadband Achromatic Metalens for Focusing and Imaging in the Visible. Nat Nanotech (2018) 13:220–6. doi:10.1038/s41565-017-0034-6

CrossRef Full Text | Google Scholar