An Overview of the Director State in Gadolinium Gallate Garnet

In recent years the topic of frustrated magnetism has attracted significant scientific interest that shows little sign of abating. Within the field of frustrated magnetism, the compound Gd₃Ga₅O₁₂ was, for many years, the archetypal frustrated magnet with a ground state that could not be elucidated. Recently an unusual emergent ground state, a director state, has been determined for Gd₃Ga₅O₁₂, which is now also observed for other isostructural compounds. In this review an overview of the director state is given, starting with the basics of rare earth magnetism and leading to a summary of the experimental signatures that led to the insight needed to determine the director state.

1 Introduction

Geometrically frustrated spin systems are widely studied, both theoretically and experimentally, due to the promise of novel and exotic states of matter derived from degenerate ground states. Stunning examples of novel states are magnetic monopoles found in the pyrochlore spin ice compounds [1] and compounds displaying a Kiteav quantum spin liquid state derived from S = 1/2 spins on a honeycomb lattice, for example H₃LiIr₂O₆ [2] and α-RuCl₃ [3].

A particular interest in compounds displaying localised magnetic moments on a triangular lattice was developed after Anderson proposed the, now much sought after, quantum spin liquid state for Heisenberg antiferromagnetic spins on a triangular lattice [5]. The interest in quantum spin liquids is that they offer, unlike their classical counterparts, quantum entanglement and superposition of spins thereby providing unique opportunities in quantum computing. However, it turns out that a quantum spin liquid is not realised on a triangular lattice with Heisenberg spins. Instead an ordered state with 120° ordering of adjacent spins develops. Nevertheless, Anderson’s proposal initiated an intense theoretical and experimental search for magnetically exotic states of matter that continues to this day. The search for spin liquids is matched by the study of geometrically frustrated structures populated with classical spins that, although not quantum in nature, nevertheless develop novel and exotic states of matter that may be of technological importance.

In this review I will focus on the rare earth gallate garnet Gd₃Ga₅O₁₂ (GGG) that has revealed, in recent years, an interesting emergent phenomenon, a director state, derived from the concomitant effect of a three dimensional triangular arrangement of antiferromagnetic localised spins and a perturbative magnetic anisotropy.

The director state, L, is visually represented in Figure 1 and is derived from the net spin structure of the Gd³⁺ ions on a ten-ion loop within the garnet hyperkagome structure, see Figure 1A. A director is represented by the double headed red arrow on the central ion within the ten-ion loop and originates from independently fluctuating spins on each Gd³⁺ ion. The two-fold rotational point symmetry of the loop dictates that the L and–L are equivalent and as such the arrow is double headed. A multipole expansion of the director is a spherical harmonic of order 6 shown by the red and blue bulbous ring at the center of the double headed arrow. The principal direction of the directors are, on average, perpendicular to the plane of the ten-ion loop and therefore the arrow in Figure 1 is shown perpendicular to the plane of the loop with weak contributions in the plane. Although the individual Gd³⁺ spins are independently fluctuating, the directors are correlated throughout the crystal, Figure 1B. The directors are thermally activated and appear to diffuse in a free-energy landscape. The director state is truly an emergent state of matter that cannot be foreseen from the individual parts.

FIGURE 1

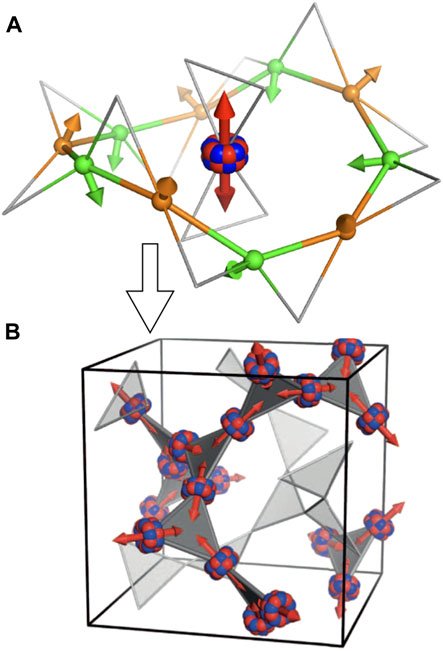
FIGURE 1. (A)Local spin direction on Gd sites of the ten-ion loop and (B) the resultant staggered magnetisation along the loop, L, represented by the director spin in the center. Correlated director state populated on the garnet lattice [4].

2 Rare Earth Magnetism and the Garnet Structure

The rare earth garnet, space group Ia3d, has the general formula A₃B₅O₁₂ where A is a trivalent rare earth ion and B is a non magnetic ion such as Gallium, Aluminium or indeed Indium or Scandium, see Figure 2. It has been possible to synthesise garnets with the complete range of rare earth ions (except Ce and Pm) and Gallium/Aluminium on the B site [6].

FIGURE 2

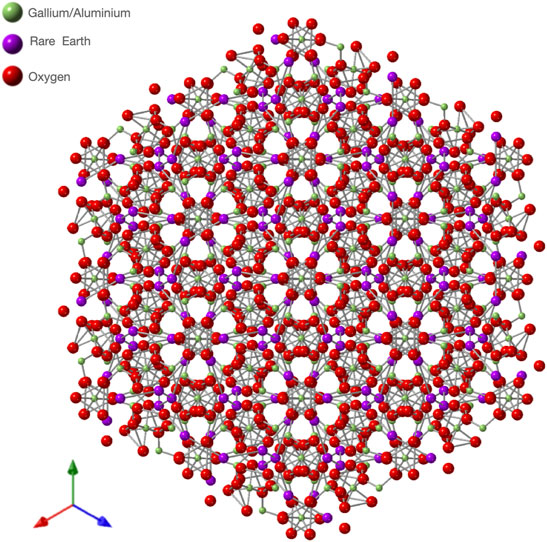
FIGURE 2. (top) Rare earth gallium/alluminate garnet crystal structure viewed along the [1 1 1] direction.

Magnetic ions positioned within the garnet crystal structure, at the Wyckoff position 24c with a 222 point symmetry, form a network derived from two interpenetrating hyperkagome lattices, see Figure 3A. A hyperkagome lattice is a three dimensional structure of corner-sharing triangles that can also be envisaged as a depleted pyrochlore lattice in which only 3 of the 4 vertices on each tetrahedron are occupied by a magnetic ion. The triangles of spins do not lie in a single plane, but lie with an angle of 73.2^o between two adjacent triangles and, as such, the hyperkagome lattice is a highly three dimensional structure. The interest in these compounds stems from the possibility to achieve geometric frustration derived from antiferromagnetically localised ions on a triangular lattice. The highly three dimensional nature of this lattice makes the garnet structure particularly interesting.

FIGURE 3

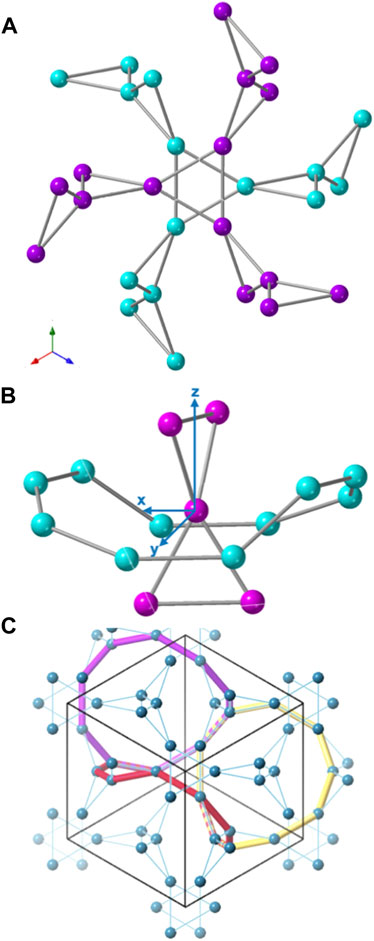
FIGURE 3. (A) Interpenetrating hyperkagome lattice of the rare earth ions on the rare earth garnet lattice along the [1 1 1] direction. (B) Ten ion loop in the garnet surrounding a central rare earth ion. (C) Connected ten-ion loops of rare earth atoms [7].

The garnet structure of rare earth ions can be construed out of loops of rare earth ions with the smallest number in a loop being three followed by a ten ion loop, see Figure 3B, a 12 ion loop and so forth. It is these loops of ions that lie at the origin of the director state. A ten ion loop centers on a rare earth ion of the second hyperkagome lattice with that ion also part of another ten ion loop, see Figure 3B. The local coordinate system for a rare earth ion is shown for the central ion in Figure 3B with x, y defined by the twofold axes of the local 222 (D2) point symmetry and z, perpendicular to x and y, passing through the centers of the two triangles. In Figure 3C I show some examples of connected ten-ion loops of rare earth atoms on the hyperkagome lattice.

Magnetism in the rare earth garnets is clearly derived from the rare earth ions. In the rare earth series the configuration of the valence electrons of the outermost shell is the same for all the ions, La → Lu, while the 4f orbitals are progressively filled with increasing atomic number. Screening of the 4f orbitals leads to extremely similar physical and chemical properties of the elements. Nevertheless, the magnetic properties vary significantly across the series due to anisotropy of, for example, spin-orbit interaction, crystal-field effects of the surrounding ions or the dipolar exchange interaction.

The magnetic ordering and cooperative effects in the rare earths are principally derived from the indirect exchange interaction, through the conduction d-electrons, as the direct exchange between the localised 4f electrons, on adjacent ions, is negligible [8]. Although indirect, this exchange takes the form of the isotropic Heisenberg exchange interaction (−2∑_ijJ_ijS_i ⋅S_j), J_ij is the exchange integral, between the highly localised spins (S_i and S_j) with the exchange interaction originating from a quantum exchange term of the Coulomb interaction between the d electrons on the neighbouring ions.

An intra-atomic repulsive Coulomb interaction hinders the motion of the d-electrons such that, when the Coulomb interaction is large in comparison to the transfer matrix elements between electrons, at adjacent sites, the crystal becomes insulating, an important requirement for the physics of magnetically frustrated compounds. In this work I do not consider the further exchange interactions that lead to metallic states.

The spin orbit interaction is a relativistic effect and is one cause of magnetocrystalline anisotropy. The strength of the spin-orbit coupling is proportional to Z⁴, significant for rare earth ions (Z $>$ 56), and the total angular moment, J = S+L, is thus relevant, in this case L denotes orbital angular momentum, in all other cases L denotes a director state. The 4f moments on the magnetic ions in the hyperkagome lattice are affected by the orthorhombic crystal electric field of the surrounding ions, resulting in strong magnetic anisotropy. In the dodecahedral rare earth site of the garnets the crystal field with D2 symmetry splits the low lying energy levels. The crystal field energies for rare earth ions are often significantly weaker than the spin-orbit coupling.

The dipolar interaction is very weak, typically an order of magnitude less than the indirect exchange between nearest neighbours. It is nevertheless an important perturbation since it is anisotropic and very long range due to the ${\mathbf{r}}_{ij}^{-5}$ term, Eq. (1). The rare earth contraction observed across the rare earth series describes the progressive reduction of ionic radius, from La to Lu, which may have an effect on the dipolar interaction in rare earth garnets as the rare earth ion is exchanged.

3 Gd³⁺ on the Garnet Lattice

GGG has been considered the archetypal geometrically frustrated compound. GGG is intriguing since the Curie-Weiss temperature of GGG, θ_cw = −2.5 K indicates relatively strong antiferromagnetic interactions, yet no long range magnetic order, in the zero field regime, has been observed down to T_N < 0.025 K, [9–11]. Using the frustration index, T_N/θ_cw, it is clear that GGG is highly frustrated with a frustration index greater than 100. In the last few years a considerable body of experimental and theoretical work has been presented revealing the director state of GGG. Here I present an overview on the experimental work.

In GGG the magnetic Gd³⁺ spins S = 7/2 and L = 0 are considered as Heisenberg spins due to a nominal zero single-ion anisotropy, derived from the interplay between spin and orbital angular momentum, which theoretically predicts a negligible crystal field effect. However an admixture of excited states may lead to crystal field anisotropy. An upper limit of 0.04 K has been put on the single ion spin anisotropy [12], a non-negligible perturbation. The dipole exchange is 0.048 K in GGG when limiting D to nearest neighbour interactions: $\mathrm{D}=\frac{{\mu }_{0}m{u}_{\mathit{eff}}^2}{{r_n}_n^3}$. The relevant exchange interactions are J₁, J₂ and J₃, see Figure 3. J₁ and J₂ represent the near and next nearest neighbour exchange while J₃ is the near neighbour inter hyperkagome exchange.

The Hamiltonian for GGG can be thus written as [7, 13]:

$\mathcal{H}=\sum _{ij}{J}_{ij}{\mathbf{S}}_i\cdot {\mathbf{S}}_j+\mathcal{D}\sum _{ij}\frac{{\mathbf{S}}_i\cdot {\mathbf{S}}_j}{r_{ij}^3}-\frac{3\left({\mathbf{S}}_i\cdot {\widehat{\mathbf{r}}}_{ij}\right)\left({\mathbf{S}}_j\cdot {\widehat{\mathbf{r}}}_{ij}\right)}{r_{ij}^5},(1)$

where ${\widehat{\mathbf{r}}}_{ij}$ is a unit vector between atoms i and j.

3.1 Static Experimental Signatures

GGG shows two interesting features in the bulk measurements. First, upon cooling T $<$ 1 K, a broad maxima in the specific heat is observed around 0.8 K [9, 10, 14], T_CP, the cooperative paramagnetic transition. The various specific heat measurements shows very similar features but with a clear sample dependent variation, see Figure 4A.

FIGURE 4

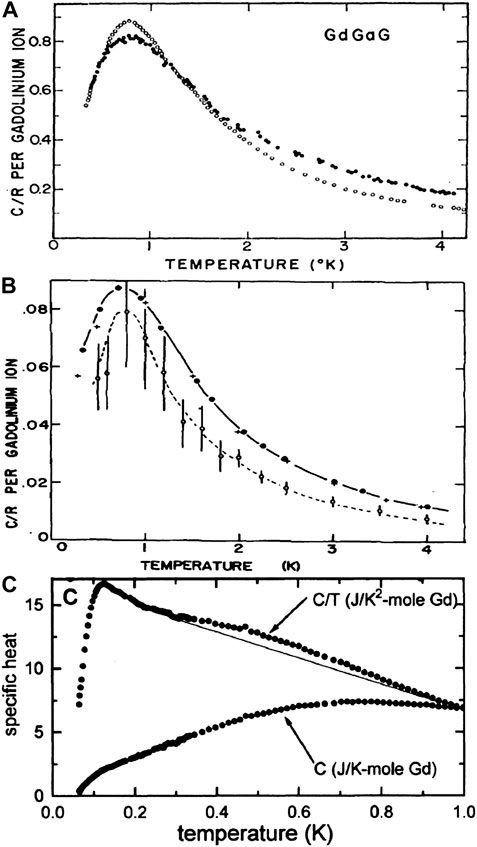
FIGURE 4. (A) Specific heat of two samples of GGG, full marks: Sintered sample, open marks: cluster of single crystals [9]. (B)Temperature dependence of the specific heat of GGG. Solid curve and points are experimental results. Broken curve and points is a Monte Carlo calculation with J₁ = 0.107 K, J₂ = −0.003 K and J₃ = 0.010 K, [10]. (C) Specific heat of a single crystal GGG sample along [1 0 0] direction [15].

This broad maximum could not be reconciled with a Schottky anomaly, since such an interpretation would require a crystal field splitting that is not observed [12]. The exchange interactions, determined from specific heat measurements via Monte Carlo simulations [10], and refined further with a variational mean field theory approach, have been determined to be J₁ = 0.107 K, J₂ = −0.005 K and J₃ = 0.01 K¹³, Figure 4B.

Schiffer et al. remeasured the specific heat of GGG on a single crystal along the [1 0 0] crystallographic direction, see Figure 4C, and noted that, in addition to a broad maximum at T = 0.8 K, a more ordered phase appears for T $<$ 0.2 K, T_SS named the spin-slush transition by Rau et al. [16].

Schiffer et al. measured the temperature dependence of the real component of the magnetic susceptibility in a single crystal, along [1 0 0], revealing a deviation from Curie-Weiss behaviour for T $<$ 0.8 K, see Figure 5A. The linear susceptibility, χ′, Figure 5A, reveals an ordering for T $<$ 0.2 K corroborated by the clear peak in the imaginary component of the susceptibility, Figure 5B. Broad features in the imaginary and non-linear susceptibility indicate a rearrangement of spins beyond that of the development of short range correlations prior to ordering [15]. The peak in χ’ moves to lower temperatures as the measuring frequency decreases, considered originally to be the signature of a spin glass type behaviour but now understood as the spin slush phase, see Figure 5B (inset).

FIGURE 5

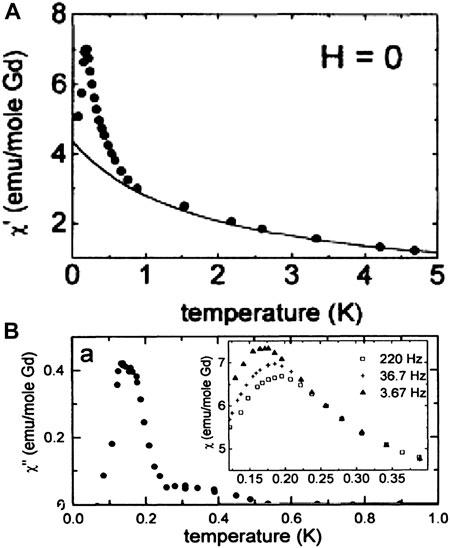
FIGURE 5. (A)The temperature dependence of the real part of the linear susceptibility (H = 0) along with the Curie-Weiss behavior extrapolated from higher temperatures along [1 0 0], [15]. (B) The temperature dependence of the imaginary part of the linear susceptibility, χ”(T). The inset shows the frequency dependence of χ′(T) [15].

Neutron scattering is an ideal tool to probe magnetic correlations and excitations since it provides both spatial and dynamic information on the time and length scale pertinent to magnetic interactions [17]. However, in the case of GGG, neutron scattering is problematic since natural Gd contains 6 isotopes with an average absorbing cross section of 49,700 b (for 1.8 Å neutrons). Neutron scattering of GGG is usually performed on isotope enriched samples with the isotope¹⁶⁰Gd that is only weakly absorbing, 0.77 b (for 1.8 Å neutrons). The majority of the neutron scattering experiments were performed on a single polycrystalline sample containing 99.98% of the non-absorbing isotope¹⁶⁰Gd.

High resolution neutron diffraction revealed a stochiometric sample with an upper limit of 2% site disorder, disorder between the Ga and Gd sites. This is important when considering the behaviour of short range order that may derive from single ion behaviour due to minor chemical disorder. Indeed a low level of chemical disorder was discussed for some time as necessary for the development of the short range order observed [11, 15].

Petrenko et al., employing powder neutron scattering, observed short ranged ordered peaks below 2.9 K, see Figure 6A [11]. Two very broad short ranged ordered and symmetric peaks are found at wavevector transfer, Q, = 1.05 and 2.87 Å⁻¹ for 1.04 $<$ T $<$ 2.9 K. As the temperature is reduced, T_SS < T $<$ T_CP, the first short range ordered peak becomes asymmetric and a third peak develops at 1.82 Å⁻¹. The development of this intermediate peak is consistent with the development of the director state. Longer range ordered incommensurate peaks develop below 0.14 K, T $<$ T$S_S$, and sit on top of the short range order with peaks at Q = 0.64 and 0.85 Å⁻¹, see Figure 6B. At the lowest temperature, 0.043 K, the short range order accounts for 85% of the scattering profile. These results indicate a mixture of longer ranged magnetic correlations, with a correlation length of approximately 100 Å, and a short range cooperative paramagnetic state. The low temperature phase can thus be very aptly described by the term spin slush. The high level of short range order indicates that chemical site disorder is not the origin of this behaviour.

FIGURE 6

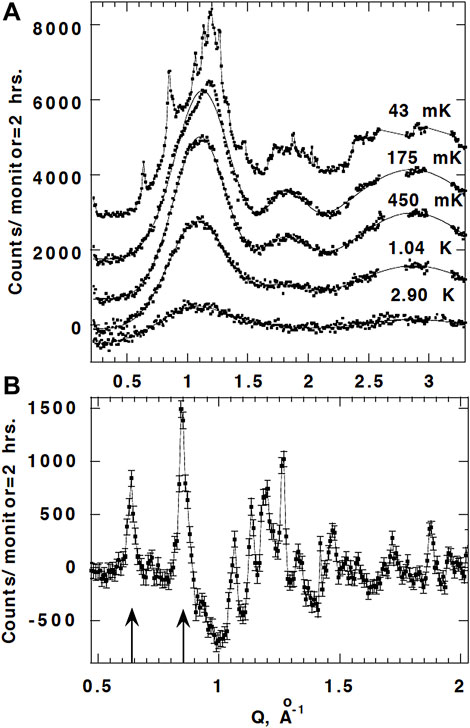
FIGURE 6. (A) Low-temperature neutron diffraction data for GGG after subtracting the 9 K data. The curves for different temperatures are separated by 1,200 counts for clarity. (B) Difference plot for temperatures 0.043 and 0.175 K underlining the appearance of the sharp magnetic peaks at the lowest temperatures [11].

Yavorskii et al. [13] was able to reproduce the fine details of the neutron diffraction profiles, at the mK level, using the Hamiltonian of Eq. 1, with both the longer ranged and short range order represented. Crucially, the long range nature of the dipolar interaction must be treated correctly to provide the sharper peaks seen in neutron diffraction experiments. This indicates that the ground state depends critically on weak perturbations.

The theory by Rau et al. for a spin slush phase, developed for pyrochlore systems but relevant for GGG, provides a phase with both longer range and short range correlations that develops in a structurally clean system through the competition of exchange interactions, J₁, J₂ and J₃ in the case of GGG, in addition to the infinite consideration of the dipolar exchange [16]. The spin slush phase is a ground state manifold with a rich set of states that can include a broad range of spatially extended structures such as, but not exclusively, looped structures. As such a director state would develop prior to the onset of longer range correlations developed from further extended structures.

Further insight can be gained through the application of a magnetic field. The phase diagram centers around a multiphase convergence to a single point at 0.9 T and 0.35 K. Upon the application of a magnetic field, as small as 0.2 T, long range ordered Bragg peaks develop and can be assigned to incommensurate, antiferromagnetic and ferromagnetic structures that develop upon the short range order [18]. The second SRO peak, assigned to scattering from decagon loops is more robust and is unaffected until 0.5 T. This indicates that decagons are resilient to perturbation. The incommensurate Bragg peaks are highly fluid in position and move in reciprocal space as a function of applied field. Long range order is induced through the application of 1 T. The extended (B, T) phase diagram is rather complicated with several additional distinct phase boundaries. The Hamiltonian proposed, see Eq. 1 has not, as yet, been able to reproduce accurately the complete phase diagram. However, spin wave theory is able to reproduce low lying excitations of the high magnetic field (B > 1.8 T) spin wave spectrum and, most interesting, the excitations correspond to the spin waves localised on ten site rings, expected on the basis of nearest neighbour exchange interaction [7], see Figure 12.

A¹⁶⁰Gd isotope enriched single crystal was grown by G. Balakrishnan [19] and revealed a low temperature specific heat profile equivalent to that observed by Schiffer et al. [15] thereby indicating a high quality single crystal sample. An attempt to find the incommensurate peaks for T $<$ T$S_S$, using neutron diffraction with the sample in the [h h l] scattering plane, were not successful. Shortly after, the single crystal was fractured and further single crystal measurements were not possible. No further attempts to grow an isotope enriched single crystal was made due to the prohibitive cost of¹⁶⁰Gd and the complexities associated with the crystal growth.

Instead, a further attempt to measure the magnetic correlations was made by synthesizing a single crystal using natural Gd and studying such a crystal with high energy, low wavelength neutron scattering. The neutron absorption cross section decreases significantly as the neutron wavelength is decreased [17]. In the case of natural Gd a neutron scattering profile can be obtained as λ → 0.5 Å. High energy neutrons, λ → 0.5 Å, reduces the visible range of Q on a wide angle detector and broadens significantly the Q resolution. Nevertheless an instructive scattering profile was obtained for T = 0.05 and 0.175 K. Figure 7 shows (ai) the [h k 0] plane and (aii) the [h k k] plane. S (Q) measured at 0.175 K, T$S_S<$ T $<$ T$C_P$, shows broad but correlated features. The considerable white region in Figure 7A are due to the limitations on neutron scattering with low wavelength neutrons. On the right of Figure 7A are corresponding scattering profiles for the resultant model that was proposed and obtained via Reverse Monte Carlo (RMC) [4]. RMC will be discussed further in the article. S(Q) at 0.05 K, T $<$ T$S_S$, showed no distinct variation from the S(Q) at 0.175 K. This could be due to the poor Q resolution of the experiment.

FIGURE 7

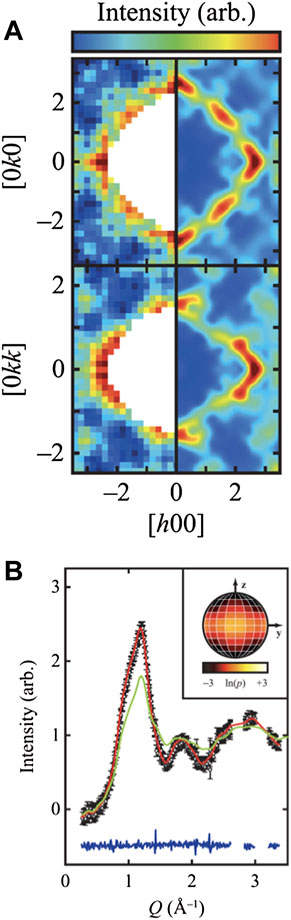
FIGURE 7. (A) Single-crystal magnetic diffuse scattering, S(Q), in two reciprocal-space planes. The upper image, shows the [h k 0] plane, and the lower image shows the [h k k] plane. In each image, the left panel shows experimental data and the right panel shows the calculation from RMC refinements described in the text. Regions where there are no data are shown in white [4]. (B) RMC fit to powder diffuse-scattering data [11]. Data shown as black circles, fit as a red line and difference (fit-data) as a blue line. Green line is a scattering function from an alternative isotropic model [4].

The single crystal results, Figure 7A, prompted a reevaluation using RMC of the neutron powder diffraction data obtained by Petrenko et al., see Figure 6, [11].

RMC is based on Monte Carlo methods first developed by McGreevy et al. who used the technique to study disordered structures [21]. Paddison et al. used RMC to evaluate the spin structure from a magnetic powder diffraction pattern using, initially, a random spin configuration on a supercell, typically nxnxn (n = integer 6–9, n = 6 provides 5,184 spins for GGG), significantly larger than the crystal unit cell. The spin orientations are refined by minimising the sum of the squared residuals between the fit, S(Q) calculated from the derived spin structure, and the neutron scattering data. Typically, 100 independent simulations for each temperature are performed, with 100 steps per Gd ion, resulting in 518,400 steps for each simulation. The final spin structure can then also be used to recalculate the single crystal scattering profile, S(Q), thereby providing multiple checks on the resultant physical model proposed.

RMC is very effective for short range magnetic order in insulating compounds since one can assume the spin is fixed on a lattice site. RMC is therefore a technique for the refinement of spin directions and correlations based on experimental data. Importantly it does not provide a spin Hamiltonian with a predetermined set of magnetic interactions that could bias the results. The validity of the technique has been broadly documented [22].

Excellent agreement between the RMC fit and the powder data is achieved for all temperatures. Figure 7B shows the data and final fit for T = 0.175 K, reproducing accurately the asymmetry of the first and second short range ordered peak. The inset shows a stereographic projection of the logarithmic probability distribution of the local spin orientations, see Figure 7B (inset). The stereographic projection allows one to visualise the dominant spin directions in the local coordinate system of each Gd³⁺ ion. The local coordinate system has been discussed previously, Figure 3B. The stereographic projection, Figure 7B (inset), shows significant spin anisotropy with a preferential spin alignment in the local xy plane. The green line in Figure 7B is the scattering function calculated from an alternative isotropic model that does not capture the data adequately. The RMC derived spin structure enables one to extract further information. The correlations are antiferromagnetic that follow an approximate exponential decay, ⟨S (0) ⋅S(r)⟩ ≈ exp (−r/ξ), with ξ = 4.952 (1) Å (r = distance). ξ does not extend much beyond the near neighbour distance. For near neighbors ⟨S (0) ⋅S(r)⟩ = −0.47. This corresponds to an average angle between near-neighbor spins of 118°, significantly lower than the 120° expected for a pure Heisenberg spin state. This slight deviation from spin isotropy has interesting consequences beyond near neighbour dipole interactions. To highlight this behaviour one can consider the net staggered magnetisation along the ten ion loop, see Figure 1A:

$\mathbf{\text{L}}=\sum _{n=1}^{10}{\left(-1\right)}^n{\mathbf{S}}_n,(2)$

The result of which, the director, is positioned at the center of the ten ion loop coincident with a Gd³⁺ ion. A multipole expansion of the magnetic field due to such a loop of ten antiferromagnetic spins contains contributions from the spherical harmonic of order 6, which contains 5 nodal planes perpendicular to the plane of the loop and one nodal plane parallel to it. The loop director thus describes the multipole orientation associated with a given ten-ion loop. L is dominant along the z-axis. Similar to the spin configuration of Figure 7B (inset) one can now consider L using a stereographic projection of the director directions. The stereographic projection is shown in Figure 8A. Note that L is predominantly along the z-axis.

FIGURE 8

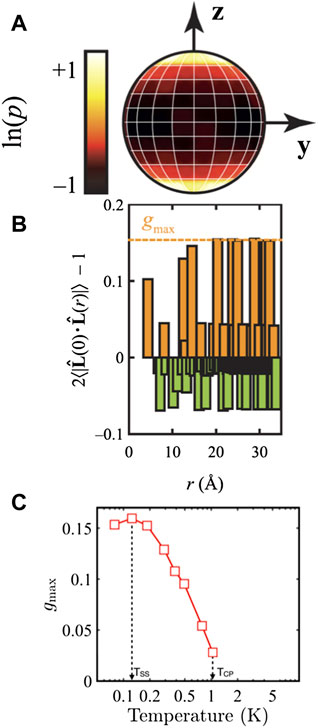
FIGURE 8. (A) Stereographic projection of the logarithmic probability distribution function of the normalized 10-spin directors and (B) the axial correlation function of normalized 10-spin directors calculated from the RMC configurations [4] (C) Temperature dependence of the maximum axial correlation [20].

The axial correlation between directors can be quantified as

$g\left(r\right)=2⟨|\widehat{\mathbf{\text{L}}}\left(0\right)\cdot \widehat{\text{L}}\left(\mathbf{r}\right)|⟩-1,(3)$

where $\widehat{\mathbf{L}}=\mathbf{L}/L$. The director-director correlation is g = 1 for directors that are parallel, and g = −1 for directors that are orthogonal. The correlation function, g_max, Figure 8B, diverges as is to be expected from the axial distribution of 10-spin directors and reveals the long range correlated nature of the director state throughout the crystal, visualised in Figure 1B, and is a key result. The resultant director state does not break crystal symmetry since each director is consistent with a Gd ion position, as the central position in the loop. The temperature dependence of the maximum in the axial correlation shows both transitions, T_CP and T_SS, see Figure 8C, with g_max developing below T_CP and saturating at T_SS. These results support the results by Yavorsk’ii et al. that the director state is an integral precurser to the spin slush phase [13].

Importantly, the results from the RMC fits on neutron powder diffraction data are corroborated by further experimental signatures. First, the deviation from Curie-Weiss behaviour, below 1 K, and the weak signature in the linear susceptibility are signatures of a developing order. Second, the single crystal structure factor, S(Q), derived from the RMC spin structure of the powder diffraction pattern, S(Q), closely matches the data for two different lattice planes, see Figure 7A. Figure 7A shows the [h k 0] plane, and Figure 7A the [h k k] plane. In each image, the left panel shows experimental data and the right panel shows the calculation from RMC refinements. Close agreement between RMC and experiment is found. Finally, the broad temperature evolution of the specific heat anomaly closely matches the evolution of the director state [4] signifying a loss of entropy associated with the developing order.

The spin structure derived from RMC does not have a theoretical basis since RMC provides spin directions only. It is clearly important to understand whether a director state, as opposed to less interested short range correlations, would be derived from the Hamiltonian proposed, Eq. 1, [13]. This is verified by direct Monte Carlo (MC) simulations. Figure 9A shows the spin structure derived via RMC, at 0.45 K, T_SS < T $<$ T_CP, and is compared to the spin structure, at 0.45 K, derived from direct MC simulations of the spin Hamiltonian proposed for GGG, Figure 9B, [4]. In both the RMC and MC simulations a local xy anisotropy is obtained, albeit slightly less well defined in the case of the MC simulations. In the case of the MC simulations the anisotropy is derived from the dipolar term yet this is, as yet, not fully ascertained and it may be possible that the crystal field term provides the relevant anisotropy. Nevertheless these results indicate strongly that the known exchange interactions provide a spin structure consistent with a director state.

FIGURE 9

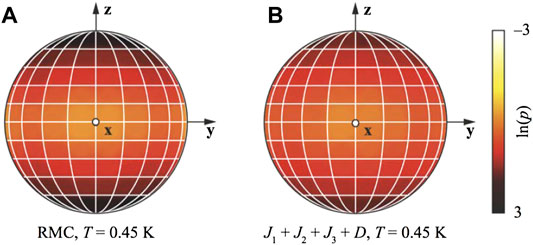
FIGURE 9. Stereographic projections of the logarithmic probability distribution function of spin orientations obtained by (A) RMC refinement against experimental powder neutron-scattering data collected at T = 0.450 K, and (B) direct Monte Carlo simulation of the spin Hamiltonian proposed for GGG at T = 0.45 K¹³, [4].

3.2 Dynamic Experimental Signatures

The dynamic nature of GGG has been studied via the indirect measurements of muon spin rotation (muSR) and neutron scattering and the more direct techniques of AC susceptibility and Mössbauer spectroscopy. Two muSR studies confirmed the absence of long-range order down to 0.025 K, however, these studies disagree on the nature of the slowing down of the spin fluctuations [23, 24], see Figures 10A,B.

FIGURE 10

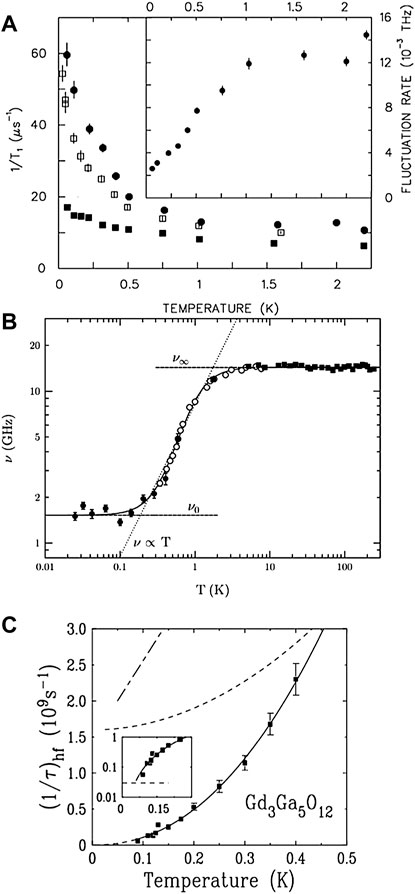
FIGURE 10. (A) The temperature dependence of the root-exponential muon spin relaxation rate 1/T1 in GGG. The filled circles and squares are for single crystal GGG in fields of 0.0011 and 1 T, respectively. The open squares are for GGG powder in a small field of 0.005 T. The inset shows the temperature dependence of the Gd spin fluctuation rate [23]. (B) The inferred fluctuation rate, derived from muon spin relaxation measurements, as a function of temperature [24]. (C) Thermal variation of the fluctuation rate of the correlated Gd³⁺ moments in GGG, obtained from the¹⁵⁵Gd Mssbauer data (black squares). Inset: Low temperature behavior (same units as the main figure), where the horizontal dashed line defines the lower limit of the¹⁵⁵Gd Mossbauer frequency window. The chain and dashed lines schematically represent the data from the muon spin rotation measurements in [23, 24]. [25].

Muon spin relaxation measurements by Dunsiger et al. [23] revealed a linear decrease in the Gd³⁺ spin fluctuation rate below 1 K, see Figure 10A, the fluctuation rate varying from 12 GHz at 1 K to 2 GHz at the lowest temperatures, T = 0.01 K, corresponding to 8.2 μeV at 0 K. However, no significant indication of a change of Gd spin fluctuation rate is observed upon entering the spin slush state for T $<$ 0.14 K. In contrast, Marshall et al. [24] reveals a linear decrease below T $<$ T_CP with a fluctuation rate of 14.5 GHz, down to 0.14 K below which the relaxation rate is temperature independent, 1.2 GHz, 4.9 μeV, see Figure 10B.

A Mssbauer spectroscopy study observed fluctuating Gd³⁺ spins, fluctuating within a plane, down to 0.027 K, with close-to-quadratic thermal dependence, and a decrease in spin fluctuating rate from 11.9 μeV at 0.4 K to 0.12 μeV at 0.09 K²⁵, see Figure 10C.

Ghosh et al. pointed to a different dynamical phenomena for the lowest temperature phase, T $<$ T_SS, via magnetic optical hole burning, in which fluctuating uncompensated moments coexist with an unsaturated AF order and defect centered clusters [26]. The experimental technique revealed a temperature independent behaviour of the spin clusters which led to an interpretation of the spin clusters as quantum objects.

Inelastic neutron scattering, again on the isotopically enhanced powder sample, revealed three gapped magnetic excitations at energies 0.04(1), 0.14(2), and 0.58(3) meV [27], see Figure 11A. The three excitations are soft modes, flat in energy, with integrated intensities that do not conform to crystal field levels but moreso to magnetic correlations. Inelastic neutron scattering revealed that 82% of the total scattering at 60 mK was static within the energy resolution of the instrument, 50 μeV [27].

FIGURE 11

FIGURE 11. (A) Powder-averaged scattering function S (Q, ω) of GGG at 0.06 K with incident E_i = 1.94 meV. Insert is a cut at wave-vector transfer of Q = 0.5 $\mathring{A}-1$ showing the elastic lineshape and two low-lying excitations with the corresponding fits. (B) Q-dependent integrated intensity of INS3. The dashed lines correspond to a model of short-range AF correlation with only near neighbor interactions. The inset shows the integrated intensities of INS1 and INS2 [27].

The lowest and highest energy excitations show spatial dependencies indicative of dimerized short-range antiferromagnetic correlations, comparable to the nearest-neighbor exchange interactions Figure 11B. These excitations are unaffected by the ordering at T = 0.14 K, T $<$ T_SS, and survive to high temperatures T = 1.2 K, T $>$ T_CP. The second excitation, at 0.14(2) meV, shows a spatial dependence that does not correspond to near neighbour exchange. Following this excitation upon the application of magnetic field indicates that it is derived from the ten-ion looped spin structure^?, although more experimental and theoretical work is needed to determine this absolutely for H = 0 T.

Higher energy resolution measurements, using neutron backscattering with μeV energy resolution, reveals that for T $<$ T_SS the signal appears almost entirely elastic. A broad quasielastic broadening is observed around 0.045 K, T_SS < T $<$ T_CP, with a peak in intensity near Q = 1.1 Å⁻¹. This feature was assigned to diffusive dynamics of the director state consistent with loops diffusing in an entropically dominated free-energy landscape [28].

The director state is a highly robust state and this is exemplified by the behaviour of neutron diffraction and inelastic neutron scattering of GGG under an applied polarising magnetic field. Figure 12B compares S(Q, ω) at 0.06 K under an applied field of 2.5 T and the theoretical simulation under the same conditions, Figure 12A. The Hamiltonian for the theoretical simulation includes J₁, J₃ and the dipole exchange, D. The inclusion of J₂ did not yield any significant variation in the profiles. In the experimental plot a powder diffraction profile is also added for 0.06 K and 2.5 T. Previous results indicate that 2.5 T will fully polarise the magnetic moments in GGG [15] and as such the (2 0 0) reflection, clearly observed in Figure 12B, is forbidden. Instead the theoretical analysis indicates that dipolar interactions cant the moments even in the polarised state. As stated previously, the inelastic scattering profiles, Figure 12B, in the polarised state, is closely reproduced by linear spin wave theory Figure 12B and correspond to spin waves localised on the ten ion loop.

FIGURE 12

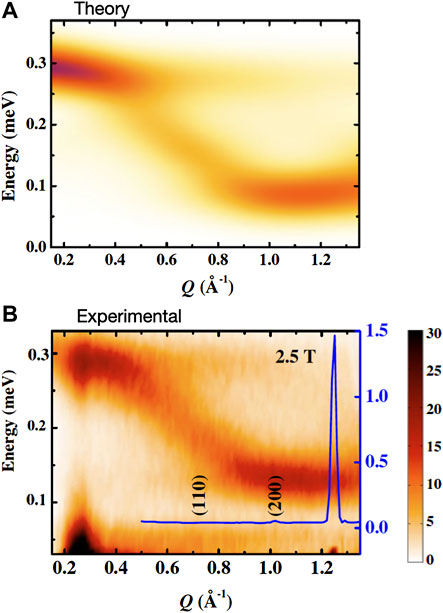
FIGURE 12. (A) Theoretically calculated, Holstein-Primakoff transformation, neutron scattering intensity for GGG under B = 2.5 T and T = 0.06 K shown as a function of momentum transfer, Q, and energy transfer, E. (B) Inelastic neutron scatering S (Q, ω) (Ei = 1.28 meV) of GGG with B = 2.5 T and T = 0.06 (K). The feature at 0.25 Å⁻¹ is an experimental spurion.

The neutron scattering results led to further AC susceptibility measurements with a particular focus on low temperature and frequency dynamics, see Figure 13. The temperature dependence of the imaginary susceptibility for single crystal GGG displays an unusual double-peaked structure. The frequency dependence of each peak follows an Arrhenius law, see Figure 14, thus indicating the presence of two distinct thermally activated processes with energy barriers, E = 0.11(1) and 0.33(2) meV, close in energy to those observed in inelastic neutron scattering. The fluctuation rate extracted are τ_0,1 = 3 × 10^–14 s and τ_0,2 = 6 × 10^–8. Single spin magnetization precession is typically on the ps time scale indicating that the first process in GGG, τ_0,1, could be related to single spin processes and τ_0,2 probes the dynamics of larger structures. These larger structure can reasonably be assumed to be the director state.

FIGURE 13

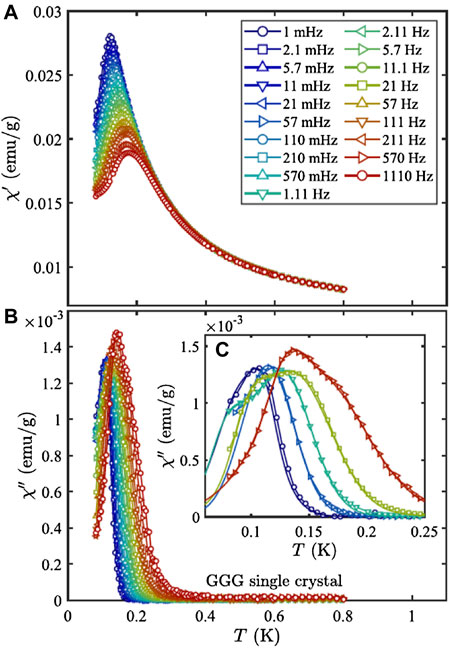
FIGURE 13. Temperature and frequency dependence of (A) the real (χ′ and (B) imaginary (χ′′) AC susceptibliity on a single crystal of GGG measured along the (110) direction. The frequencies, 1 mHz$<f<1110$ Hz, are indicated by color (inset) Detailed view of χ′′ for selected frequencies.

FIGURE 14

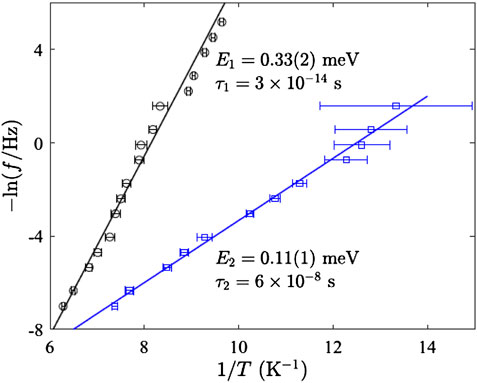
FIGURE 14. Arrhenius plot for the two peaks in χ′′ for the single crystal of GGG. The straight lines are fits to the Arrhenius law.

4 Conclusion

This review paper has brought together the experimental results leading to the determination of correlated directors as emergent magnetic behaviour in GGG. Condensed matter physics is replete with examples of emergent behaviour with some high levels examples being superfluidity, superconductivity and spin liquid phases with exotic quasiparticles such as Majorana fermions [29, 30]. The emergent behaviour in GGG is more closely linked to skyrmions [31] and spiral spin liquids [32]. In all these examples the resultant macroscopic behaviour is strongly emergent in the sense that the phenomena is derived from the underlying microscopic interactions but not in an obvious manner, unlike the weak emergent cases of ferromagnetic and antiferromagnetic order for which the macroscopic phenomena can be discerned from the microscopic exchange interactions.

Recent results on the isotructural compounds Gd₃Al₅O₁₂ and Yb₃Ga₅O₁₂ reveal that the director state in GGG is not unique [20, 33, 34]. All three compounds reveal a broad feature in the temperature dependence of the specific heat as a precurser to a longer ranged ordered state. The second signature is the three low lying non-dispersive magnetic excitations representing the single ion spin fluctuations. Broad, beyond the instrumental resolution, neutron diffraction profiles can be modelled with a director state derived from a preferential local spin direction with the director direction perpendicular to the ten ion loop plane for all three compounds. The director state is derived from near neighbour antiferromagnetic exchange with some anisotropy, a J₁-D model. The details of the broad energy scales, anisotropy and correlation lengths vary from compound to compound and will provide a means to manipulate these unusual states of matter. Further studies across the rare earth gallate and aluminate garnet series should help to establish the nature of the director state in these compoundss and allow further exploration.

In addition to a director state in the garnet series, a director state has been uncovered in the spinel compound ZnCr₂O₄ [35]. Hexagon spin loops form protected clusters in the cooperative paramagnet regime above the antiferromagnetic transition temperature [35]. Groups of six antiferromagnetically coupled Heisenberg spins self-organise into weakly interacting antiferromagnetic loops, whose directors are parallel or antiparallel to a principal direction. The hexagon loops with their derivative directors are decoupled from each other unlike the correlated director state in GGG and GAG. The antiferromagnetic exchange is strongly suppressed upon the introduction of structural disorder as ZnCr₂O₄ is doped with Ga antiferromagnetic near neighbour exchange is weakened and a ferromagnetic next nearest neighbour exchange interaction is induced [36]. It is not entirely clear how such disorder affects the director state in ZnCr₂O₄ and this would be an informative experimental study.

Other Heisenberg spinel chalcogenides antiferromagnets with the general structure ARE₂X₄ in which A = Cd or Mg, RE denotes a rare earth and X = Se, S are also interesting candidates for unusual magnetic behaviour in the cooperative paramagnetic regime. The rare earth ion in the spinel chalcogenides form a pyrochlore lattice with local environments that are distinctly different from the rare earth titanates. A combination of complex crystal field states, strong anisotropy and enhanced geometric magnetic frustration can give rise to unusual magnetic behaviours [37]. In particular, spinel chalcogenides with Yb³⁺ on the pyrochlore site, AYb₂X₄ (A = Cd, Yb, X = Se, S), are great candidates for Heisenberg antiferromagnets on a looped lattice. All four ytterbium spinels develop long-range antiferromagnetic order between 1 and 2 K with strong frustration indexes. The ordered moment is very much reduced with respect to theoretical expectation and, as such, strong quantum fluctuations are predicted. A broad feature in the specific heat, in the cooperative paramagnet state above the second order transition, of all four compounds signifies unusual cooperative behaviour such as a director state [38]. In this series of compounds it is possible to replace Cd with the slightly larger ion Mg to study changes in the dipolar interaction.

In this review I present an overview of the experimental results with links to theoretical insight. The experimental results provide rather great confidence in the Hamiltonian. There is a close similarity between the measured neutron scattering profiles, S(Q), S(Q) and S (Q, ω), with S(Q) determined from the Hamiltonian, Eq. 1, in the spin slush phase, in addition to S (Q, ω) derived from linear spin wave theory. Finally the direct MC results reveal a spin structure very similar to the RMC result again providing confidence in the Hamiltonian. These results are, crucially, backed up bulk specific heat and susceptibility measurements. Subtle spin pattern such as looped or vortex structures are not directly obtained from the Hamiltonian and required the detailed data analysis I present in this review. Future works should attempt to unify these unusual states of matter across complex phase diagrams for a broad range of materials. In particular it is important to clarify the role of anisotropy in developing the director state and moreso how these small anisotropies perturb a large degenerate manifold to develop a long range ordered ground state. With this in mind the role of structural disorder, both uncorrelated and correlated, should be considered as a means to manipulate these exotic magnetic states of matter [39]. Extended structures are found across many scientific disciplines. Experimentalists can, in the case of magnetic systems, tune various degrees of freedom, such as exchange parameters, dipolar exchange, crystal field levels, to probe the effect on the extended structures that typify these states of matter and thus provide insight into emergent behaviours in other scientific fields.

The work presented in this overview is the work across many decades and of many groups. What is particularly interesting is the need to reexamine, continuously, previous data in the light of new results. Continuous technical improvements in experimental techniques have been essential for the determination of small changes in experimental signatures. Equally essential is access to high quality single crystal samples. Any compound that displays anisotropic and weak exchange interactions can only be fully understood through investigations on high quality single crystals. Of course these do not materialise without adequate financial support and staffing levels.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bramwell ST, Harris MJ. The History of Spin Ice. J Phys Condens Matter (2020) 32:374010. doi:10.1088/1361-648x/ab8423

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Takayama KT, Kato YA, Kishimoto RY, Dinnebier SR, Jackeli GH, Dinnebier R, et al. A Spin-Orbital-Entangled Quantum Liquid on a Honeycomb Lattice. Nature (2018) 554:341–5. doi:10.1038/nature25482

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Bertinshaw J, Ueda K, Kim H, Laha S, Weber D, Yang Z, et al. Proximate Ferromagnetic State in the Kitaev Model Material α-rucl₃. Nat Commun (2021) 12:4512. doi:10.1038/s41467-021-24722-4

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Petrenko OA, Fernandez-Diaz MR, Deen PP, Paddison JAM, Jacobsen H, Goodwin AL. Hidden Order in Spin Liquid gd₃ga₅o₁₂. Science (2015) 350:179. doi:10.1126/science.aaa5326

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Anderson PW. Resonating Valence Bonds: A New Kind of Insulator? Mater Res Bull (1973) 8:153–60. doi:10.1016/0025-5408(73)90167-0

CrossRef Full Text | Google Scholar

6. Pauthenet R, Neel L, Dreyfus B. In: CJ Gorter, editor. Progress in Low-Temperature Physics, Volume 4. Amsterdam: North-Holland Publishing Company (1965).

Google Scholar

7. d’Ambrumenil N, Petrenko OA, Mutka H, Deen PP. Dispersionless Spin Waves and Underlying Field-Induced Magnetic Order in Gadolinium Gallium Garnet. Phys Rev Lett (2015) 114:227203.

PubMed Abstract | Google Scholar

8. Jensen J, Mackintosh AR. Rare Earth Magnetism. Oxford, UK: Oxford University Press (1981). p. 1991.

Google Scholar

9. Onn DG, Meyer H, Remeika JP. Calorimetric Study of Several Rare-Earth Gallium Garnets. Phys Rev (1967) 156:663–70. doi:10.1103/physrev.156.663

CrossRef Full Text | Google Scholar

10. Kinney WI, Wolf WP. Magnetic Interactions and Short Range Order in Gadolinium Gallium Garnet. J Appl Phys (1979) 50:2115–7. doi:10.1063/1.326954

CrossRef Full Text | Google Scholar

11. Petrenko OA, Ritter C, Yethiraj M, McK Paul D. Investigation of the Low-Temperature Spin-Liquid Behavior of the Frustrated Magnet Gadolinium Gallium Garnet. Phys Rev Lett (1998) 80:4570–3. doi:10.1103/physrevlett.80.4570

CrossRef Full Text | Google Scholar

12. Overmeyer J, Giess EA, Freiser MJ, Calhoun BA. Paramagnetic Resonance. New York: Academic Press (1963).

Google Scholar

13. Yavors’kii T, Enjalran M, Michel J, Gingras P. Spin Hamiltonian, Competing Small Energy Scales, and Incommensurate Long-Range Order in the Highly Frustrated gd₃ga₅o₁₂ Garnet Antiferromagnet. Phys Rev Lett (2006) 97:267203. doi:10.1103/PhysRevLett.97.267203

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Hornung EW, Fisher RA, Brodale GE, Giauque WF. Magnetothermodynamics of Gadolinium Gallium Garnet. I. Heat Capacity, Entropy, Magnetic Moment from 0.5 to 4.2 K, with fields to 90 Kg along the [100] axis. J Chem Phys (1973) 59:4652. doi:10.1063/1.1680677

CrossRef Full Text | Google Scholar

15. Schiffer P, Ramirez AP, Huse DA, Gammel PL, Yaron U, Bishop DJ, et al. Frustration Induced Spin Freezing in a Site-Ordered Magnet: Gadolinium Gallium Garnet. Phys Rev Lett (1995) 74:2379–82. doi:10.1103/physrevlett.74.2379

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Rau JG, Gingras MJP. Spin Slush in an Extended Spin Ice Model. Nat Commun (2016) 7:12234. doi:10.1038/ncomms12234

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Boothroyd AT. Principles of Neutron Scattering from Condensed Matter. Oxford, UK: Oxford University Press (2020).

Google Scholar

18. Deen PP, Florea O, Lhotel E, Jacobsen H. Updating the Phase Diagram of the Archetypal Frustrated Magnet gd₃ga₅o₁₂. Phys Rev B (2015) 91:014419. doi:10.1103/physrevb.91.014419

CrossRef Full Text | Google Scholar

19. McK Paul D, Yethiraj M, McIntyre GJ, Petrenko OA, Balakrishnan G, Wills AS. Field Induced Magnetic Order in the Frustrated Magnet Gadolinium Gallium Garnet. J Phys Conf Ser (2009) 145:012026. doi:10.1088/1742-6596/145/1/012026

CrossRef Full Text | Google Scholar

20. Jacobsen H, Florea O, Lhotel E, Kim L, Petrenko OA, Knee CS, et al. Spin Dynamics of the Director State in Frustrated Hyperkagome Systems. Phys Rev B (2021) 104:054440. doi:10.1103/physrevb.104.054440

CrossRef Full Text | Google Scholar

21. McGreevy RL, Pusztai L. Reverse Monte Carlo Simulation: A New Technique for the Determination of Disordered Structures. Mol Simulation (1988) 1:359–67. doi:10.1080/08927028808080958

CrossRef Full Text | Google Scholar

22. Stewart JAJR, Paddison AL, Goodwin AL. Spinvert: a Program for Refinement of Paramagnetic Diffuse Scattering Data. J Phys Condens Matter (2013) 25:454220. doi:10.1088/0953-8984/25/45/454220

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Dunsiger SR, Gardner JS, Chakhalian JA, Cornelius AL, Jaime M, Kiefl RF, et al. Low Temperature Spin Dynamics of the Geometrically Frustrated Antiferromagnetic GarnetGd3Ga5O12. Phys Rev Lett (2000) 85:3504–7. doi:10.1103/physrevlett.85.3504

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Marshall IM, Blundell SJ, Pratt FL, Husmann A, Steer CA, Coldea AI, et al. A Muon-Spin Relaxation (μSR) Study of the Geometrically Frustrated Magnets gd3ga5o12and ZnCr2o4. J Phys Condensed Matter (2002) 14:157. doi:10.1088/0953-8984/14/6/104

CrossRef Full Text | Google Scholar

25. Bonville P, Hodges JA, Sanchez JP, Vulliet P. Planar Spin Fluctuations with a Quadratic Thermal Dependence Rate in Spin LiquidGd3Ga5O12. Phys Rev Lett (2004) 92:167202. doi:10.1103/physrevlett.92.167202

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Ghosh S, Rosenbaum TF, Aeppli G. Macroscopic Signature of Protected Spins in a Dense Frustrated Magnet. Phys Rev Lett (2008) 101:157205. doi:10.1103/physrevlett.101.157205

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Deen PP, Petrenko OA, Balakrishnan G, Rainford BD, Ritter C, Capogna L, et al. Spin Dynamics in the Hyperkagome compoundGd3Ga5O12. Phys Rev B (2010) 82:174408. doi:10.1103/physrevb.82.174408

CrossRef Full Text | Google Scholar

28. Henley CL, Moessner R, Taillefumier M, Robert J, Canals B. Semiclassical Spin Dynamics of the Antiferromagnetic Heisenberg Model on the Kagome Lattice. Phys.Rev.B (2014) 90:064419. doi:10.1103/PhysRevB.90.064419

CrossRef Full Text | Google Scholar

29. Yoshitake J, Nasu J, Motome Y, Seung Kwon Y, Adroja DT, Voneshen DJ, et al. Majorana Fermions in the Kitaev Quantum Spin System α-rucl₃. Nat Phys (2017) 13:1079. doi:10.1038/nphys4264

CrossRef Full Text | Google Scholar

30. Savary L, Balents L. Quantum Spin Liquids: a Review. Rep Prog Phys (2016) 80:016502. doi:10.1088/0034-4885/80/1/016502

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Everschor-Sitte K, Masell J, Reeve RM, Klaui M. Perspective: Magnetic Skyrmions—Overview of Recent Progress in an Active Research Field. J Appl Phys (2018) 124:240901. doi:10.1063/1.5048972

CrossRef Full Text | Google Scholar

32. Gao S, Zaharko O, Tsurkan V, Su Y, White JS, Tucker GS, et al. Spiral Spin-Liquid and the Emergence of a Vortex-like State in MnSc₂S₄. Nat Phys (2017) 13:157. doi:10.1038/nphys3914

CrossRef Full Text | Google Scholar

33. Sandberg LØ, Edberg R, Berg Bakke IM, Pedersen KS, Ciomaga Hatnean M, Balakrishnan G, et al. Emergent Magnetic Behavior in the Frustrated yb₃ga₅o₁₂ Garnet. Phys Rev B (2021) 104:064425. doi:10.1103/physrevb.104.064425

CrossRef Full Text | Google Scholar

34. Lhotel E, Mangin-Thro L, Ressouche E, Steffens P, Bichaud E, Knebel G, et al. Spin Dynamics of the Quantum Dipolar Magnet yb₃ga₅o₁₂ in an External Field. Phys Rev B (2021) 104:024427. doi:10.1103/physrevb.104.024427

CrossRef Full Text | Google Scholar

35. Broholm SHC, Gasparovic WG, Kim QTH, Kim SW, Lee S, Broholm C, et al. Emergent Excitations in a Geometrically Frustrated Magnet. Nature (2002) 418:856–8. doi:10.1038/nature00964

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Ying Y, Zheng J, Li W, Qiao L, Cai W, Li J, et al. Magnetic Exchange Interactions in Geometrically Frustrated Antiferromagnet of Zncr2xgaxo4. J Supercond Nov Magn (2019) 32:1095–8. doi:10.1007/s10948-019-5132-2

CrossRef Full Text | Google Scholar

37. Reig-i Plessis D, Alannah M. Hallas. Frustrated Magnetism in Fluoride and Chalcogenide Pyrochlore Lattice Materials. Phys Rev Mater (2021) 5:030301. doi:10.1103/physrevmaterials.5.030301

CrossRef Full Text | Google Scholar

38. Higo T, Iritani K, Halim M, Higemoto W, Ito TU, Kuga K, et al. Frustrated Magnetism in the Heisenberg Pyrochlore Antiferromagnets AYb2X4 (A=Cd, Mg; X=S, Se). Phys Rev B (2017) 95:174443. doi:10.1103/physrevb.95.174443

CrossRef Full Text | Google Scholar

39. Keen DA, Goodwin AL. The Crystallography of Correlated Disorder. Nature (2015) 521:303–9. doi:10.1038/nature14453

PubMed Abstract | CrossRef Full Text | Google Scholar