- 1School of Physical Science and Technology, Guangxi Normal University, Guilin, China
- 2School of Physical Science and Technology and Collaborative Innovation Center of Suzhou Nano Science and Technology, Soochow University, Suzhou, China
Topological photonics is an emergent field at the cross of photonics and topological physics which opens our eyes to novel topological phenomena and versatile photonic effects. Photonic crystals (PhCs) are the optical analogs of conventional crystals that have proven to be an excellent photonic platform to explore topological physics. Here, we present a brief review of the all-dielectric topological PhCs by focusing on several prominent milestones of topological phases, such as the Su-Schrieffer–Heeger model, topological insulators, topological semimetals, and higher order topological phases. For each topological phase, the topological invariants and the intriguing topological properties as well as the potential applications are discussed. We conclude with the current challenge and the prospect of all-dielectric topological PhCs.
Introduction
Photonic crystals (PhCs), originally proposed by Yablonovitch [1] and John [2], are periodic structures of electromagnetic materials in which the electromagnetic wave propagates in a similar way as electrons move inside the conventional crystals (Figures 1A–C). Actually, many natural structures, such as the colorful wings of butterflies (Figures 1D, E) [3, 4] and the skin of chameleons (Figures 1F,G) [5], have PhC origins. PhCs not only decorate nature brilliantly but also provide a powerful means to manipulate and control the propagation of light. For example, PhCs with complete band gaps, which serve as light semiconductors, are highly desirable in controlling and manipulating light [6–8]. Thanks to the Bloch band theory for the periodic systems, the photonic band structure can be designed and tuned conveniently, making PhCs a key platform for studying a broad spectrum of energy band-related physics [9].
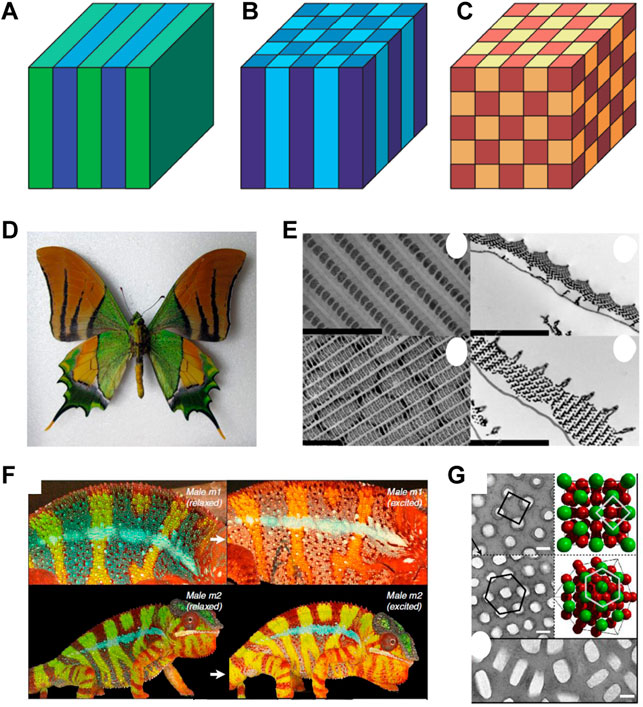
FIGURE 1. All-dielectric PhCs in nature [3–5, 9]. Schematic model of (A) one-dimensional (1D), (B) two-dimensional (2D), and (C) three-dimensional (3D) PhCs Reproduced permission from Ref. [9]. (D) Image of butterfly. (E) Electron micrographs of the scale on the wings of the butterfly, which exhibit long-range order. Reproduced Permission from Ref. 3. (F) Reversible color change in chameleons. (G) Transmission electron microscopy images of guanine nanocrystals and the 3D PhC model. Reproduced permission from Ref. 5.
The past decades also witnessed the birth of various topological phases of electrons in condensed matter systems, such as topological insulators, superconductors, and semimetals [10–12]. One of the well-known topological phases is the integer quantum Hall effect (IQHE), which is a quantized version of the Hall effect discovered by Klitzing [13]. He found that two-dimensional (2D) electron gas in a strong magnetic field with low temperatures has a quantized Hall conductance. The most significant feature of IQHE is that electrons are localized in the bulk but unidirectionally propagate along the boundaries without any backscattering, even in the presence of large defects. An invariant called Chern number (or TKNN number) is employed to characterize the topological property of IQHE [14, 15]. Haldane [16] later on proposed a toy model based on the honeycomb lattice for supporting IQHE and demonstrated that the essential element to obtain IQHE is not a net magnetic field but the breaking of time-reversal symmetry (T), which paves a way to realize IQHE in the periodic lattice systems. Moreover, because the nontrivial topological phases can survive in the non-interacting systems, the topology studies later on transferred to the photonics and directly led to the birth of topological photonics [17–23]. Generally, topological photonics aims to explore the physics of topological phases of matter, which was originally discovered in condensed matter physics, in a novel optical context. The first case of topological photonics is proposed by Haldane and Raghu [24, 25], who transferred IQHE to the realm of photonics in PhCs made with nonreciprocal media. Subsequently, Haldane and Raghu’s idea was experimentally demonstrated by Wang et al. [26, 27] in the gyromagnetic PhCs in the microwave regime. In the literature, the photonic analogs of IQHE with nonzero Chern number and unidirectional and backscattering immunity edge states (also known as chiral edge states) are generically termed photonic Chern insulators (PCIs).
Although chiral edge states featured with unidirectional and backscattering immunity are highly desirable in light guiding, the use of PCIs in optical devices remains a challenge mainly because magneto-optical responsive materials hardly exist in the optical frequency. It is natural to explore the photonic analog of the quantum spin Hall insulator (QSHI) [also known as a photonic topological insulator (PTI)] with T, which makes it more suitable for practical applications. In the context of condensed matter physics, the QSHI can be regarded as two copies of Chern insulators with opposite spin, where the spin-up and spin-down electrons propagate in opposite directions [28–31]. Therefore, a topological invariant named spin Chern number can be employed to characterize the QSHI in some situations. The sign of the group velocity of the edge states is locked by the spin. The edge states featured with spin–momentum locking are termed helical edge states. Thanks to the Kramers theorem, the edge states of spin-up and spin-down cross each other at k = 0 without opening a gap, making it a pair of topologically protected edge states. However, the Kramers theorem is no longer valid in photonics due to the distinct nature between electrons and photons. Therefore, to realize the photonic Kramers degeneracy is at the heart of the design of PTIs. At the early stage of the development of topological photonics, the optical polarization such as TE/TM [32, 33], TE + TM/TE-TM [34], and LCP/RCP [35] are utilized to act as the spin degree of freedom (DoF) in realizing PTIs. Nevertheless, these schemes extremely rely on the metamaterial with special electromagnetic properties, such as the electromagnetic duality, which hardly exist in the optical frequency. It was not until 2015 that Wu et al. [36] proposed a scheme of PTI via crystalline symmetry, which goes beyond the material limitation and largely promotes the development of the all-dielectric topological photonics.
In addition, it is also deserved to mention the photonic analog of valley Hall insulator that preserve T but lacks the parity inversion symmetry (P). In the context of electronics, the valley labels the degenerate energy extrema of bands in the momentum space, which can be employed to process information in modern electronic devices. By employing the valley DoF, a number of intriguing phenomena such as valley filters [37] and valley-selective Hall transport [38, 39] have been achieved due to the valley-contrasting physics. Taking the honeycomb lattice as an example, gapping the Dirac point via staggering the sublattice potential results in the K and K′ valleys. Electrons at different valleys (K and K′) propagate along the boundaries in the opposite directions. Similar to the helical edge states in QSHI, the edge states dispersion of a valley Hall insulator exhibits opposite signs of the group velocity. In the view of topological physics, the Berry curvature around K(K′) is nonzero, giving rise to the valley-dependent edge state as local topological effects. However, the Berry curvature at K and K′ is of opposite value, which leads to a total Chern number of zero. Inspired by the valley Hall effect in the valleytronics, Ma et al. [40] first bring the valley DoF into photonic realms, leading to the studies of photonic valley Hall insulators (PVHIs).
Very recently, a new class of topological insulators, called the higher-order topological insulators (HOTIs) that are characterized by higher-order bulk-boundary correspondence, were discovered [41–44]. The higher-order topology manifests itself with nontrivial boundary states that are more than one dimension lower than bulk states. For example, a 2D HOTI hosts one-dimensional (1D) edge states at the edge boundaries as well as zero-dimensional (0D) corner states at the corner boundaries. Prototype HOTIs include quadrupole and octupole topological insulators [41, 45, 46], three-dimensional (3D) HOTIs in electronic systems with topological hinge states [42, 47–49], and HOTIs with quantized Wannier centers [43]. Although the concept of HOTI was first proposed in electronics, the experimental confirmations of most HOTIs are still absent. By contrast, HOTIs and the emergent higher-order topological states have been realized in acoustic and photonic systems, thanks to their versatile performance. To the best of our knowledge, Li et al. [50] first reported the photonic HOTI in the kagome lattice that exhibits topological bulk polarization.
In addition to the aforementioned 2D topological systems, it is also deserved to pay attention to other topological systems associated with their photonic counterparts. For example, the 1D Su-Schrieffer–Heeger (SSH) model, originally proposed for polyacetylene [51], describes spinless fermions hopping on a diatomic chain with staggered hopping amplitude. Remarkably, exchanging the hopping amplitudes within a unit cell yields two topologically distinct phases. A topological invariant named Zak phase [62] for the SSH model can be defined, which is an integer related to the ratio of the two hopping amplitudes. The study of the 1D SSH model also attracts much attention since it provides a concise physical picture to understand the topological phenomena [52–54]. To the best of our knowledge, Xiao et al. [55] first studied the photonic analog of the SSH model based on 1D all-dielectric PhCs. For 3D topological systems, both topological gapless and topological gapped systems should be highlighted, where the former includes the Dirac semimetal, Weyl semimetal, nodal line semimetal, and so on, while the latter includes 3D topological insulators and 3D HOTIs. It is natural to extend QSHI to 3D version, which led to the study of 3D topological insulators. However, the 3D topological gapless phase has no 2D counterpart. A typical 3D topological gapless phase is the Weyl semimetal, of which the band structure contains Weyl points that corresponding to the solution of the massless Dirac equations. The topological invariant of a Weyl point is called topological charge (or chirality), which can be obtained by integrating the Berry curvature over a small sphere enclosing the Weyl point. When two Weyl points with opposite signs of chirality merge, a 3D Dirac point featured with Z2 topological charge appeared [12]. As a manifestation of topology, the surface dispersion of Weyl (Dirac) semimetal map to helicoid (double-helicoid) structure, of which the isoenergy contours are Fermi arcs [56, 57]. To the best of our knowledge, the 3D all-dielectric topological insulator are initially proposed by Lu et al. [58] and Slobozhanyuk et al. [59], respectively, while the first report of topological semimetal is implemented by Lu et al. [60, 61] in the all-dielectric gyroid PhCs.
In this review, we focus on the topological photonics that is made of all-dielectric PhCs. We first review various topological phases and point out the initial proposals of the all-dielectric topological photonics. Then, we introduce several milestones of topological phases based on all-dielectric topological photonics, from 1D to 3D, by discussing topological invariants, intriguing properties, and potential applications. Finally, we conclude by providing the outlooks for the future development direction of the all-dielectric topological photonics.
1D All-Dielectric Topological Photonic Crystals and Their Interface States
We start from the 1D all-dielectric topological photonics based on the SSH model. The topological invariant for the SSH model is the Zak phase [62], which is defined as follows:
where Λn,k = i〈ψn,k(r)|∇kψn,k(r)〉 is the Berry connection for the nth band and ψn,k(r) is the periodic part of the k-dependent Bloch wavefunction. Note that we set the lattice constant to be unity in Eq. 1.
In systems with P, the Zak phase can only be 0 (trivial) or π (nontrivial). The integral of the Berry connection can be obtained by dividing the Brillouin zone (BZ) into many small segments and approximating the integral as the summation of the contribution from each small segment. For example, if the BZ is divided into N segments, then the Zak phase is given by [63].
The aforementioned method to calculate the Zak phase is termed the Wilson loop approach, which is a gauge invariant and compatible with numerical implementations [63, 64]. In addition, in the systems with P, the bulk states at the high symmetry points are either even or odd. Therefore, the Zak phase can also be determined via the parity inversion picture, which is given by
where ξ(k = 0) and ξ(k = π) are the parity at k = 0 and π, respectively. The nontrivial Zak phase manifested itself in the topological edge mode as the most significant feature of the SSH model. Therefore, it is expected that the interface states exist when the Zak phase of the occupied band on the one side of 1D PhCs is different from that on the other side. In 2014, Xiao et al. [55] theoretically demonstrated a rigorous relation between the surface impedance of a 1D PhC and the Zak phases of the bulk bands, which is given by
Here, θn is the Zak phase of the nth bulk band, and φn and φn−1 are the reflection phase of the nth gap and (n−1)th gap, respectively. Soon after this work, Wang et al. [65] experimentally demonstrated Eq. 4 by implementing a reflection measurement. Figure 2A presents the structure of the measurement setups, which are composed of a silver film and a binary PhC. The values of the Zak phases can be acquired via either numerical calculation or the parity inversion picture, which are labeled in Figure 2B. In particular, the numerically calculated reflection phase in Figure 2C shows that the Zak phase of a specific band depends on the ratio of the reflection phase of its upper and lower band gaps, which is in good agreement with Eq. 4. Moreover, in Figure 2D, the experimental reflection spectra of the PhCs (black lines) and silver/PhCs (red) reveal that interface state only exists in the band gap with the nontrivial Zak phase, which matches well with the numerical simulation in Figure 2E. Remarkably, Eq. 4 unveils an inner connection between the topology and optical property of a 1D PhC, which provides an effective method to calculate the Zak phase in order to avoid the cumbersome calculation [66], as well as to generate PhC interface states for various applications [67]. Note that Eq. 4 is even applicable to explain the origin of some geometric-induced interface states, such as 2D PhC possessing Dirac-like cone at k = 0 [68], mutually inverted PhCs [69], and self-complementary checkerboard PhCs [70].
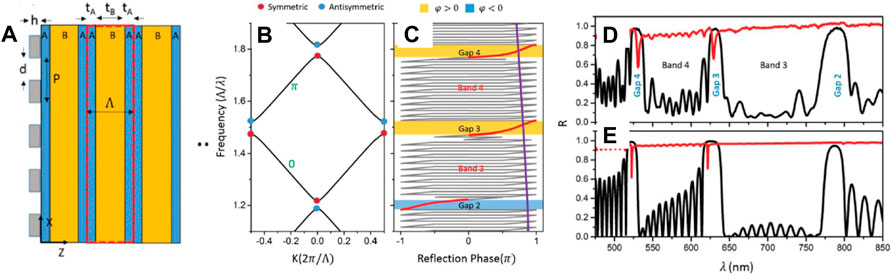
FIGURE 2. One-dimensional all-dielectric topological PhCs [65]. (A) Schematic structure of the silver films/PhC systems. (B, C) Inner connection between Zak phase and the sign of reflection phase, where (B) gives the photonic band structure with Zak phase and (C) displays the reflection phases of the 1D PhCs. (D) Experimental and (E) numerical reflection spectra of the PhC (black line) and the silver film/PhC (red line). Reproduced permission with Ref. 65.
2D Topological Gapped Phases Based on All-Dielectric Photonic Crystals
Photonic Analog of Chern Insulator
As a landmark of topological photonics, Wang et al. [27] first experimentally demonstrated unidirectional electromagnetic wave featured with backscattering immunity in the 2D magneto-optical square-lattice PhCs that made of yttrium iron garnet (YIG). When an external DC magnetic field is applied, the YIG produces strong magnetic anisotropy, making the PhC a magnetic insulator. The breaking of T via an external applied magnetic field is essential to realize the PCI. Figure 3A presents the band structure of PhCs with T breaking adopted from Wang’s scheme. The primitive unit cell is shown in the inset. The nontrivial band topology can be demonstrated via the first-principle calculation of band Chern number, which can be implemented through the integral of Berry curvature in the discretized Brillouin zone [71] or the Wilson loop approach [63]. Here, we introduce the main idea of the Wilson loop approach to calculate the band Chern number. Note that the Chern number that is related to the Berry phase can be calculated using the following relations [72]:
where
is the Berry phase for the nth band along the loop kx ∈ [−π,π] for a fixed ky which is obtained by the integration over the Berry connection through Eq. 2 for the Wilson loop along kx. Note that the 2D BZ is equivalent to a torus under the periodic boundary condition for the Bloch states. Therefore, in numerical calculations, the Chern number Cn is obtained by counting the winding phase of when ky goes from −π to π. The Chern numbers of the first three bands are determined by plotting the Berry phase θn,kx (n = 1, 2, and 3) as functions of kx. For the first photonic band, the Berry phase remains zero for all kx, leading to a zero Chern number, while for the second (third) photonic band, the Berry phase has a winding number of 1 (-2), corresponding to a Chern number C2 = 1(C3 = −2), as shown in Figures 3B–D. The Chern numbers calculated here from the Wilson loop approach agree with the Chern numbers inferred from the chiral edge states in using the bulk-edge correspondence [73]. As shown in Figure 3E, the projected band structure (light blue areas) with a chiral edge state (red line) is calculated in finite systems. A typical field distribution of the chiral edge state is also displayed in Figure 3F. To characterize the chiral edge states, the transmission measurement is implemented. From Figure 3G, it is shown that a strong forward transmission with the second band gap approximately 50 dB greater than the backward transmission at frequencies was observed at mid-gap frequencies. After this milestone of work, a series of work related to the PCIs made of gyromagnetic PhCs are implemented, such as cladding-free guiding of topologically protected edge states [74, 75], steering of multiple edge states along domain walls with large Chern numbers [76, 77], designing of one-way slow-light PhC waveguide [78–81], and antichiral edge states [82, 83]. It is evident that the unidirectional backscattering immunity edge states are expected to have a deep impact on the designing of new optical devices. However, owing to the weak magnetic response in optical materials and the difficulty in device integration, the use of PCIs in optical devices remains a challenge. To date, there is an urgent need to achieve one-way waveguides at optical wavelength.
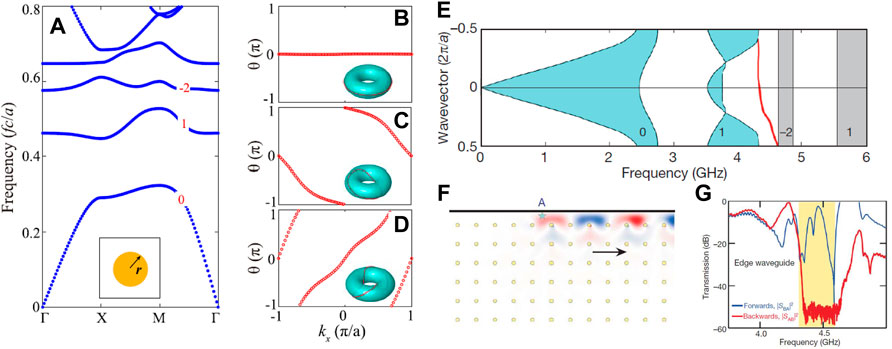
FIGURE 3. Photonic analog of Chern insulators [27, 63]. (A) Photonic band structure with applied magnetic field. The Chern number of each band is labeled in red. (B–D) The evolution of the Berry phase of (B) the first, (C) the second, and (D) the third photonic band as the functions of kx. The winding number of the Berry phase gives the Chern number. Reproduced permission from Ref. 27. (E) Calculated projected photonic band structure with the chiral edge state exits at the interface between the metal cladding and the PhC. (F) Chiral edge state field distribution, which radiates only to the right along metal cladding. (G) Measure transmission spectra of the chiral edge states. Reproduced permission from Ref. 63.
Photonic Analog of Quantum Spin-Hall Insulator
In 2015, Wu et al. [36] proposed a scheme for achieving PTI by using the all-dielectric PhC, which paves a way for the practical application of PTI. In their seminal work, they start with an expanded cell of photonic honeycomb lattice. Based on the band folding mechanism, the well-known Dirac cone at K and K′ points are folded at Γ point, giving rise to the deterministic double Dirac cone. By either stretching or compressing the expanded unit cell, the double Dirac cone lifted into a trivial or nontrivial band gap. Such a scheme for realizing PTI was later demonstrated by observing the momentum–pseudospin locking in the microwave experiment [84]. Inspired by Wu’s work, a large number of studies of all-dielectric PTI are implemented based on the photonic honeycomb lattice [85–96] and other specific PhC structures, such as core–shell PhCs [97], Stampfli-triangle PhCs [98], and moon-shaped PhCs [99].
Actually, to construct all-dielectric PTI, two issues should be highlighted: one is to create the fourfold-degeneracy double Dirac cone, which is the mother state of PTI, the other one is to find out the photonic analog spin–orbit coupling terms. Guided by these two principles, Xu et al. [97] systematically studied accidental band degeneracy in an all-dielectric core–shell PhC (Figure 4A), where the Mie resonance can be regarded as atomic orbits for photonic bands [100]. Those atomic orbits can be of s, p, d, and f nature and have well-defined parities at Γ point [see a typical band structure of the core–shell PhCs in Figure 4B]. Note that due to the C6 crystalline symmetry, both the photonic p-orbit and d-orbit are double degenerate. Figure 4C gives the electric field patterns of the p doublets (px and py) and d doublets (dxy and dx2−y2). In particular, these four states can be linearly combined into p± = (px ± ipy)/√2 and d± = (dx2−y2 ±idxy)/√2, where subscript + (−) refers to pseudospin-up (pseudospin-down). Apparently, the spin DoF here is synthesized by the orbital angular momentum [89]. By tuning the inner and outer radii of the core–shell PhCs, the phase diagram with multiple accidental degeneracies can be acquired (Figure 4D).
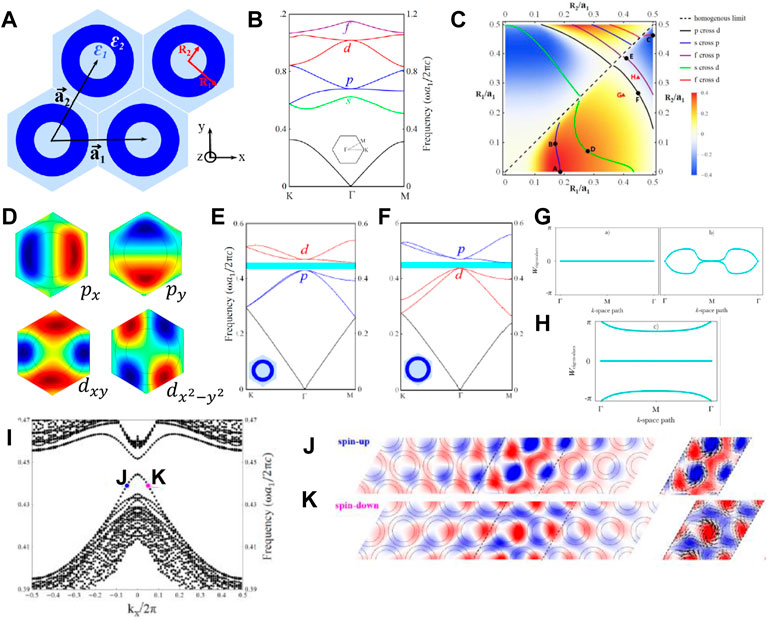
FIGURE 4. Photonic analog of quantum spin Hall insulator [97, 101]. (A) Schematic configuration of a triangular PhC using core–shell dielectric. (B) Typical band structure of the core–shell PhCs, where the photonic-like orbits are labeled. (C) Phase diagram of the p − d inversion induced photonic topological insulator in the geometric parameter spaces. (D) Eigen modes of p doublets (px, py) and d doublets (dxy, dx2−y2), which served as the photonic pseudospin DoF. (E, F) Band structure of core–shell PhCs with (E) trivial and (F) nontrivial band gaps. (G, H) Wannier center positions of the bands below the (G) trivial and (H) nontrivial band gap. Reproduced permission from Ref. 101. (I) Projected band structure of two PhCs with helical edge states. (J) and (K) are the Ez field pattern in (I). Reproduced permission from Ref. 97.
Importantly, the double Dirac cone formed by the p and d doublets plays a vital role in the phase transition between PTI and a normal insulator. When the p band is below the d band (Figure 4E), the gap exhibits a trivial phase, while flipping the order of the p and d photonic bands results in a nontrivial band gap (Figure 4F). Such a parity inversion (also known as p-d inversion) picture is at the heart of the quantum spin Hall effect in electronic systems [31]. The topological invariant of PTI can be also acquired via the Wilson loop approach [63]. Considering the Berry phase calculation for multiple bands, the inner product
where the band indices n and n′ go over all the bands below the concerned band gaps. Then, the Berry phase for a loop in the BZ can be obtained by the matrix product of the Berry connection matrix through the following form,
To evaluate the topological invariant, one needs the eigenvalues of the above Berry phase matrix, which can be written as follows:
where wn is the nth eigenvalues of the matrix
Typical Berry phase calculations for a trivial insulator and PTI via the Wilson loop approach are displayed in Figures 4G,H. For the trivial case, the Wilson loop of the first band has a constant value equal to 0 (see left panel in Figure 4G), while that of the set of the second and third bands does not exhibit any winding properties (see right panel in Figure 4G). For the nontrivial case, it is necessary to take the three lowest bands as a set since there is a band crossing between the first and second bands. As shown in Figure 4H, there is no winding but the Wannier centers are localized at the edge of the unit cell, in contrast to that in the trivial case. In the literature, such a topological insulator with non-winding values of Wilson loop is called the photonic obstructed atomic limit [101, 102], which is easily confusing with the concept of fragile topological insulator [96, 99, 102, 103]. Parallel to the topological invariant calculation, a typical calculation of the edge state using two PhCs with distinct topology is presented in Figure 4I. Note that the helical edge states are gapped, which originate from the C6 symmetry breaking at the boundary between the two different PhCs. The size of the gap depends on the strength of the perturbation induced by the symmetry breaking. However, the helical feature of the edge states is still clearly demonstrated. As shown in Figures 4J,K, the edge states at the J(K) point are mostly pseudospin-down (pseudospin-up) as recognized from the real space distribution of the Poynting vector with the negative (positive) group velocity.
Utilizing the robust transport properties of the topological PhC interface, many intriguing physical systems are explored, including unidirectional electromagnetic waveguide [84], topological all-optical logic gates [104], topological whispering gallery modes [105], coupled cavity-waveguide system [106], topological converter [95], topological bulk laser [93], Dirac vortex cavity [107], and Dirac vortex fiber [108]. Additionally, all-dielectric PTIs also open an avenue to quantum optics. In 2018, Barik et al. [86] proposed an all-dielectric topological PhC slab with 2D helical edge states confined in a dielectric slab, which is highly desirable to achieve out-of-plane confinement without the use of metal [85, 86, 90, 94]. They also demonstrate the strong interface between the single quantum emitters and topological photonic states [94]. Since all-dielectric PTIs take full advantage of crystalline symmetry and thus go beyond the material limitation, more in-depth research based on all-dielectric PTIs is foreseen.
Photonic Analog of Valley Hall Insulator
Another kind of topology-related gapped systems with T is PVHIs [40, 109–135]. Following the idea of valleytronics in the graphene, Chen et al. [119] proposed a PVHI based on the modified honeycomb PhCs, as shown in Figure 5A, where the radii of the two rods are different in a unit cell. Note that most PVHI studies are based on the modified honeycomb lattice [110, 111, 113, 116, 117, 119, 122, 123] since it provides a concise physical picture. Other proposals, including detuning the refractive index [124, 125] and specific geometric designs without P [40, 109, 112, 114, 115, 118, 120, 121, 126], are also adopted to study valley physics. From the point of view of the symmetry, these PVHIs broke the C6 symmetry of the structure while preserved the C3 symmetry. A typical band structure of PVHI is presented in Figure 5B, where two inequivalent but T valleys (K and K′) with vortex-valley locking (Figures 5C,D) are observed.
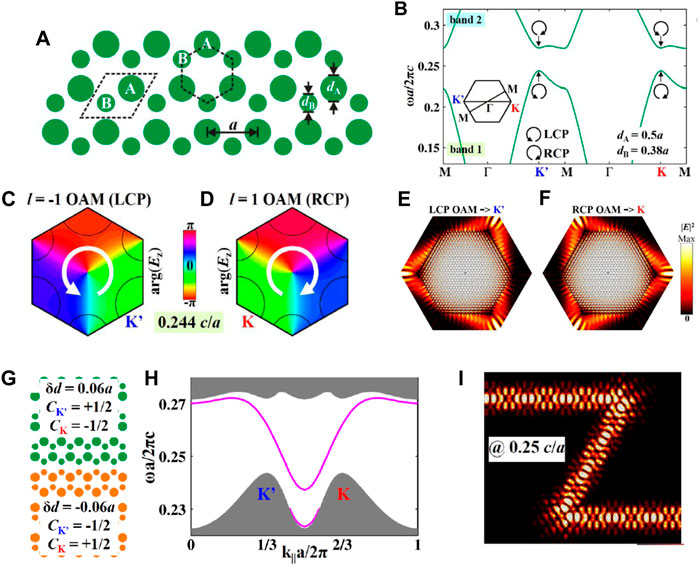
FIGURE 5. Photonic analog of valley Hall insulator [119]. (A) Schematic of valley PhCs based on honeycomb lattice, where the radii of the two rods are different in a unit cell. (B) Photonic band structure for transverse magnetic modes, in which four valley states are marked. (C,D) Valley-contrasting chiral orbital angular momentum and the phase distributions of Ez at K and K′ valleys. (E, F) Electric intensity of the excited. (E) K′ and (F) K valley states. (G) Schematic of the edge constructed by two distinct valley PhCs. (H) Valley-dependent edge states. (I) Electric field intensity at a specific frequency, illustrating the smooth propagating wave through the Z sharp corners. Reproduced permission from Ref. 119.
Using the valley as a binary DoF, the unidirectional excitation of the valley chirality bulk states can be realized either by sources carrying orbital angular momentum with proper chirality (Figures 5E,F) [119] or by a point-like chiral source based on the azimuthal phase matching condition [120]. Similar to the pseudospin–momentum locking effect in PTIs, there also exist valley pseudospin–momentum locking edge states at the interface of two valley Hall PhCs (Figures 5G,H). Most studies hold that the different valley topological index between two of the valley Hall PhCs gives a nonzero valley Chern number and lead to the emergence of the valley-dependent edge states. However, the valley Chern number cannot be used as a topological invariant because it is not a quantized value. Yang et al. [117] addressed that the chiral vortex-valley locking plays a fundamental role in the emergence of the valley-dependent edge states, rather than the valley Chern number. Thanks to the chiral vortex-valley locking, valley PhCs with valley-dependent edge states exhibit robust transportation against sharp corners (Figure 5I).
For applications, many intriguing photonic devices, including energy beam splitters [127, 131, 132, 135], logic gates [127], switches [132], fiber [134], and filter [132] are created via PVHIs [131, 132]. Based on valley edge states, the electrically pumped terahertz quantum cascade laser is also realized [128]. Xie et al. [133] constructed a topological cavity based on slow-light valley Hall edge states, which exhibit a greatly enhanced Purcell factor. Moreover, it is also desirable to realize PVHIs with a large Chern number, which can support multimode topological transmission [114, 118].
Photonic Higher-Order Topological Insulators
The recent advances in higher-order topology deepen our knowledge of the topology physics. The first HOTI proposed by Benalcazar et al. [41] is a quadrupole topological insulator (QTI), in which the bulk dipole is absent while the quantized, fractional electric multipole moments emerged in the bulk. The key to realize a QTI is to generate both positive and negative nearest-neighbor couplings in a single physical system. In order to meet such requirements, Chen et al. [136] proposed a scheme to realize QTI in plasmon-polaritonic systems by utilizing the sign-reversal mechanism for the coupling between the plasmon-polaritonic cavities. In addition, He et al. [137] extended the idea of QTI from tight-binding models to continuum theories. They demonstrated that the quadrupole topological phase survived in a gyromagnetic PhC, of which the quadrupole moment is quantized by the simultaneous presence of crystalline symmetry and broken T. Since the realization of photonic QTI is limited to some specific systems, most studies focus on the photonic HOTIs with quantized Wannier centers. In 2018, Ezawa [43] constructed a tight-binding model on the breathing kagome lattice, in which both gapped edge states and corner states are observed. In his proposal, the bulk polarization is served as a topological index, which can be defined as the integral of the Berry connection. Intuitively, the bulk polarization characterizes the displacement of the average position of the Wannier center from the center of the unit cell, giving rise to the emergence of corner states in a finite system.
Inspired by Ezawa’s proposal, the studies on the HOTI based on the kagome lattice are later transferred to various classical systems [50, 138–143]. In particular, all-dielectric PhCs provide an excellent platform to study HOTI with quantized Wannier centers and thus have been extensively studied [50, 144–154]. Wang et al. [154] systematically studied the multiple higher-order phase transition in a 2D hexagonal PhC with C3 symmetry, where each unit cell consists of three dielectric rods, as illustrated in Figure 6A. By moving the three dielectric rods along three symmetry lines, the PhCs undergo a continuous geometry transformation that includes three triangular lattice configurations and three kagome lattice configurations. Typical band structures for the triangular and kagome lattices are presented in Figures 6B,C. Accompanying with the geometry transformation, the first photonic band experiences multiple phase transitions (Figure 6D). To characterize the higher order topology, one can calculate the bulk polarization (Wannier center positions) via the Wilson loop approach, as depicted in Figures 6E–G, or use the symmetry indicators [155], which can be achieved from C3 eigenvalues at high symmetry points.
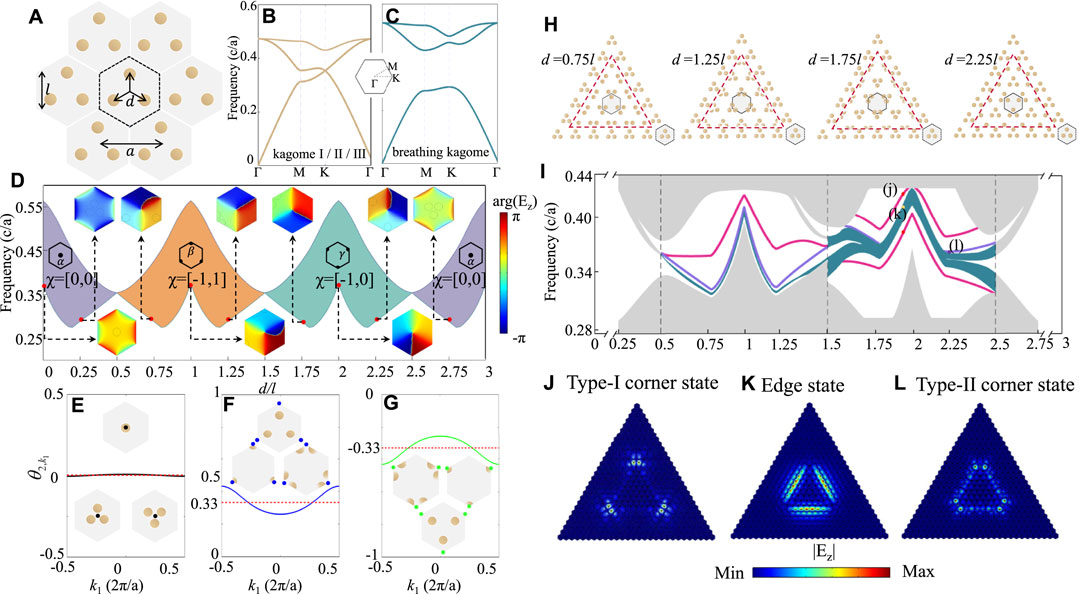
FIGURE 6. Photonic higher order topological insulator [154]. (A) 2D PhCs with C3 symmetry, where the primitive cell is indicated by hexagonal dotted lines. (B, C) Typical band structure for (B) triangular PhCs and (C) kagome lattice. (D) Eigenfrequencies of the first and second photonic bands at the K point as a function of geometric parameter d. (E–G) The calculated Berry phase for PhCs with (E) the phase [0,0], (F) the phase [−1,1], and (G) the phase [−1,0]. The bulk polarization is shown in red dots. The corresponding Wannier center configuration is also displayed in the insets. (H) Schematic illustration of large triangular supercell with two types of PhCs with distinct higher order topology. (I) Eigenfrequencies of the photon as functions of the geometric parameter d. (J–L) Typical electric field pattern for (J) type-I corner state, (K) edge state, and (L) type-II corner state. Reproduced permission from Ref. 154.
As a direct manifestation of the higher-order band topology, one may expect that corner states appear in a finite system with C3 symmetry. However, the emergence of corner states also depends on the geometric configurations [141, 156]. We remark that often the photonic bands do not have the chiral symmetry and the corner states may shift into the bulk continuum and disappear without the chiral symmetry. To avoid this, it is necessary to place two all-dielectric PhCs with distinct higher topological phases together in a finite system. Along with the geometry transformation, various cases of the calculated supercell are realized, where outside PhCs are of trivial phase, while the insider PhCs are dependent. Several prototype geometries of the calculated supercell are presented in Figure 6H. The eigen solutions are displayed systematically in Figure 6I. Figures 6J,K give the electric field |Ez| distributions of the eigenstates of the corner and edge states. In particular, two types of corner states emerge, as revealed in Refs. 50, 142, 154: type-I corner states due to the nearest neighbor couplings and type-II corner states originating from the next nearest-neighbor coupling.
In addition to the kagome lattice with C3 symmetry, the nontrivial bulk polarization and corner states can also appear in the expanded C4 symmetric lattice. A typical case is the 2D Su-Schrieffer–Heeger model, which has been extensively studied [151–153]. The 2D Zak phase is employed to characterize the higher-order topology. The photonic HOTIs have been found promising applications in high-quality nanocavities [157], cavity quantum electrodynamics [158], topological nanolasers [159, 160], and multi-channel system fibers [161]. Since HOTIs set up examples with multidimensional topological physics going beyond the bulk-edge correspondence in conventional topological insulators and semimetals, it opens a new avenue toward exploring novel topological phenomena and optical device applications.
Before proceeding, let us comment on the 1D and 2D all-dielectric topological PhCs. Since all-dielectric PhCs are the optical analogs of conventional crystals, it is natural to explore different topological phases as well as to find the potential applications based on all-dielectric PhCs. For 1D topological photonics, the 1D PhC consists of a dielectric AB layered structure that is regarded as a photonic analog of the SSH model. Since the 1D binary PhC supports the Tamm mode, which originates from the lack of translation symmetry, there is a need to clarify the difference as well as a connection between the topological interface states and Tamm modes [162]. For 2D cases, topological phases in all-dielectric PhCs are more diverse, including PCI, PTI, PVHI, and HOTI. We notice that most studies focus on the topological phase transition between trivial and nontrivial phases, while that between two nontrivial phases is very few [163–165]. It is expected that all-dielectric PhCs will become more versatile if two topological phases coexist in a single system. In addition, it is also interesting to introduce other ingredients into the all-dielectric PhCs, such as layer DoF [111, 166].
3D Topological Phases Based on All-Dielectric Photonic Crystals
In the previous sections, we have reviewed the 2D topological phases. It is natural to extend 2D topological phases to 3D cases. In what follows, we give a brief review on several milestone works of 3D topological insulators and topological semimetals that are made of all-dielectric PhCs.
3D All-Dielectric Photonic Topological Insulator
Generally, 3D topological insulators can be realized in both T-broken and T-invariant system. A typical T-broken case is the 3D quantum Hall phase [also known as a strong topological insulator (STI)], which can be regarded as a 3D extended version of the 2D quantum Hall phase. To the best of our knowledge, Lu et al. [58] first proposed the photonic analog of 3D STI by using PhCs composed of ferrimagnetic materials (Figure 7A). A magnetic field bias breaks T and produces a nontrivial band gap that hosts a single-surface Dirac cone (Figures 7B,C), which is protected by the nonsymmorphic glide reflections. Such a gapless surface state is fully robust against the random disorder of any type. The evolution of Wannier centers is calculated via the Wilson loop approach to characterize the bulk topological invariant (Figure 7D).
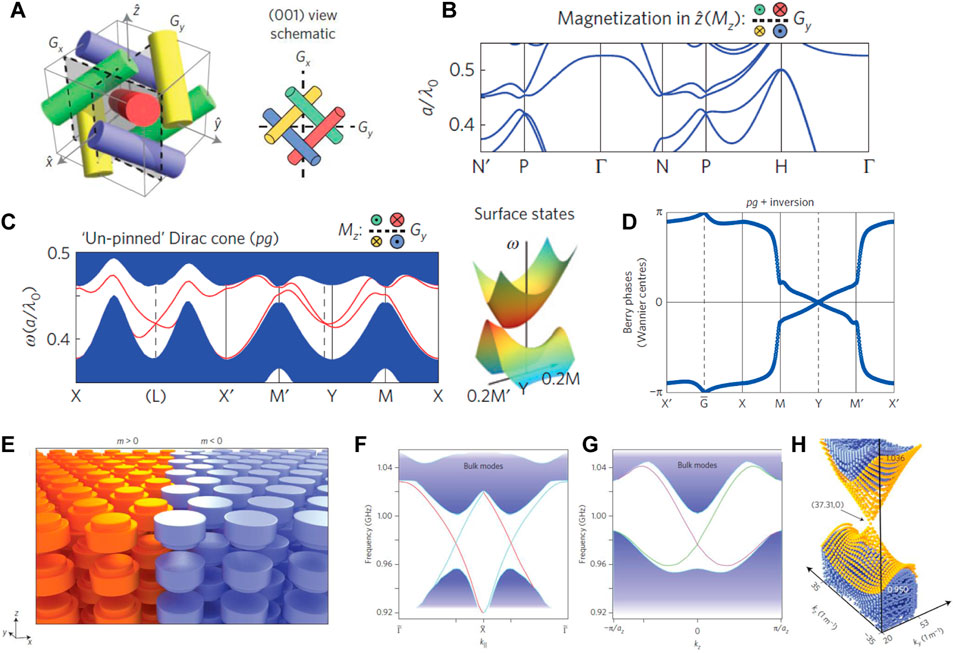
FIGURE 7. Three-dimensional photonic topological insulators [58, 59]. (A) Three-dimensional all-dielectric PhCs with topological band gap. (B) Bulk band structure when magnetization is applied. (C) Single-surface Dirac cone in the M′ − M line. (D)) Gapless hybrid Wannier centers corresponding to the nontrivial surface states in (C). (E) Schematics of the domain wall formed by the two 3D PTIs. (F, G) Band diagrams of topological surface states supported by the domain wall in (E) with 2D cut-planes (F) ω-k|| and (G) ω-kz, respectively. (H) Conical Dirac-like dispersion of the surface states. Reproduced permission from Refs. 58, 59.
Similarly, the 3D quantum spin Hall phase [also known as a weak topological insulator (WTI)] can be viewed as a generalization of the 2D quantum spin Hall phase and corresponds to the T-invariant case. In 2011, Yannopapas [167] proposed a scheme for realizing a 3D photonic analog of WTI. A tetragonal lattice of uniaxial dielectric cavities in a lossless metallic host was investigated using a coupled dipole method, which is the photonic counterpart of topological crystalline insulators in an electronic system [168]. This system with T and point-group symmetry exhibit a complete 3D band gap and gapless topological surface states. Topological photonics with 3D band gaps also have been proposed by using 3D bianisotropic structures [59, 169]. As shown in Figure 7E a stacked layer of triangular arrays of mirror-symmetry-broken dielectric rods (Figure 7F) supports a conical dispersion of topological surface states (Figures 7G,H) and backscattering immunity propagation of the surface modes. The scheme for achieving 3D photonic WTI paves a way to various optical devices, such as topological lasers and circuits in previously inaccessible 3D geometries.
3D All-Dielectric Photonic Topological Semimetals
As one of the earliest studies of topological semimetals, Lu et al. theoretically [60] and experimentally [61] demonstrated the existence of Weyl points in gyroid PhCs. The Weyl point refers to the 3D linear point between two bands, of which the dispersions are governed by the Weyl Hamiltonian. Unlike the 2D Dirac point, which is protected by PT symmetry, the 3D Weyl point only exists on the systems that lack T or P or both [170–176]. Such a character makes a single Weyl point absolutely robust to any perturbations. The only way to eliminate and create Weyl points is through pair annihilations and pair generations of Weyl points with opposite chirality. It seems the emergence of Weyl points is somehow accidental, nevertheless, one can have a 3D topological phase with symmetry protection first and then have the Weyl points by symmetry reduction (Figure 8A) [170–173]. From this point of view, Wang et al. [170, 171] systematically studied the 3D Z2 Dirac point, which can be viewed as a pair of Weyl points with opposite chirality, based on all-dielectric PhCs. Usually, the 3D Dirac points are unstable when two Weyl points annihilate each other and form a gap. Nevertheless, Wang et al. [170, 171] pointed out that 3D Z2 Dirac can survive stably via certain crystalline symmetry, and split into the Weyl points when the P is broken.
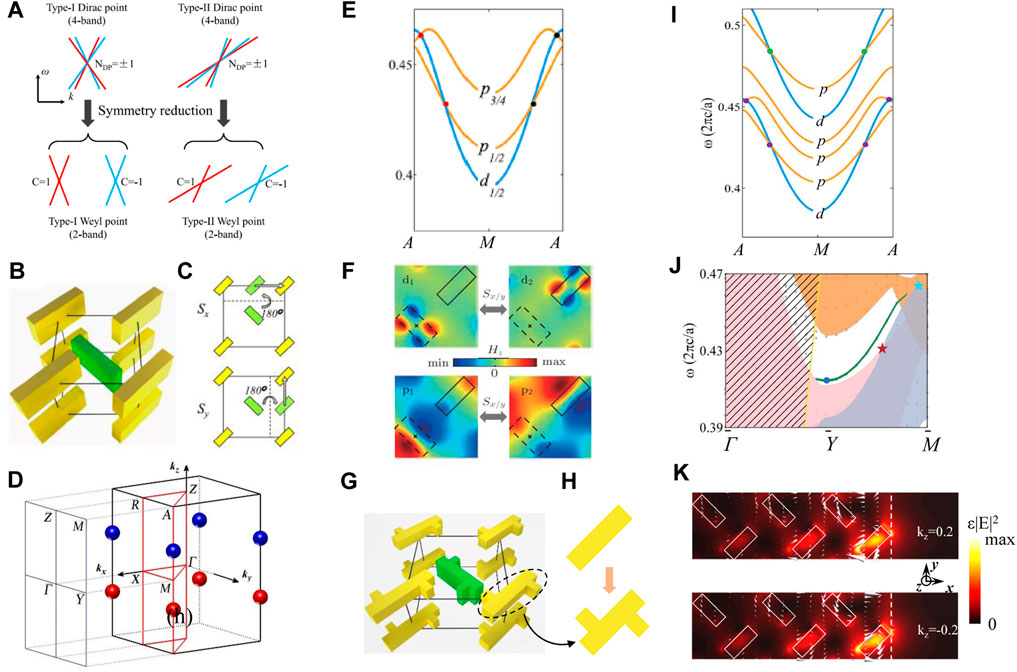
FIGURE 8. Photonic topological semimetals [171]. (A) Relationship between type-I/type-II Dirac points and Weyl points. (B) Three-dimensional structure of a unit cell, where the boundaries are indicated by black lines. (C) Illustration of the two screw symmetry Sx and Sy in top-down view. (D) The bulk and surface Brillouin zone, with the distribution of the Dirac points. (E) Parity inversion induced type-I and type-II Dirac points on the MA line. (F) Magnetic field profiles of the p- and d-wave doublets, p1/2 and d1/2, respectively. The doubly degenerate states are connected by the screw symmetries. (G) Unit cell structure of the symmetry-broken PhCs. (H) Three-dimensional view with zoom-in illustration of structure deformations. (I) Band structure on the MA line for part of the first six photonic bands indicates, which the crossings are identified as type-I and type-II Weyl points. (J) Surface band and projected bulk band on PhC–air surface. (K) Energy density and Poynting vector profiles for the topological surface states at two opposite wavevectors. Reproduced permission from Ref. 171.
As an illustration, Figure 8B presents a kind of 3D all-dielectric PhCs with nonsymmorphic symmetry. In each unit cell, there are two dielectric blocks of the same shape and permittivity, which are connected via screw symmetry Sx and Sy (Figure 8C). To realize the Z2 photonic Dirac point, both Kramers double degeneracy and parity-inversion should be synthesized, in which the crystalline symmetry plays a key role in realizing these two elements. On the one hand, anti-unitary operators that combine the screw symmetry with T symmetry are created to simulate the photonic Kramers degenerate pairs. On the other hand, the eigenvalue of a two-fold rotation symmetry operator is employed to define the parity of photonic states. The distribution of 3D Z2 Dirac points in the BZ is displayed in Figure 8D.
The 3D Dirac point emerges from the band crossing of two doublets with distinct parities (Figures 8E,F). The spit–orbit physics of the Dirac points can be understood via a symmetry-based ∼k⋅p ∼ theory. When the space symmetry is reduced, it is expected that the Dirac point will split into Weyl points. As shown in Figures 8G,H, by transforming the dielectric blocks into other shapes, namely, breaking the screw symmetry while keeping the two-fold rotation symmetry, the crossing between the band with distinct parities (i.e., p and d bands) result in Weyl points (Figure 8I). Following this idea, the Weyl point is also realized in the metasurface [172] and twisted 1D dielectric PhCs [173]. Because the 3D Dirac point acts as the mother state of the Weyl points, it is interesting to explore the properties of surface states according to the bulk-edge correspondence principle. Figure 8J shows a gapless surface band traversing the projected photonic band gap. The topological surface states carry finite total angular momentum as indicated in Figure 8K by the winding profile of the Poynting vectors. The sign of the photonic total angular moment is changed when the wavevector is reversed. This property is similar to the “spin–wavevector locking” on the edges of topological insulators. Based on such a salient feature, one can further study frequency-, angle-, wavevector-, and angular momentum-selective transmission in Weyl/Dirac PhCs. In addition, note that the topological surface states are below the light-line and hence can form cavity states on the PhC–air interfaces with no need for additional cladding. Last but not least, the conical dispersions in Dirac/Weyl all-dielectric PhCs provide a new mechanism to realize unconventional optical properties, such as anomalous refraction [171].
Conclusion and Outlook
The past decade has witnessed the rapid development of topological photonics, which is beneficial for both electronics and photonics. Although many exotic topological phenomena have been demonstrated, the aid of metamaterials hinders the application of topological photonics. Therefore, it is highly desirable to realize all-dielectric topological PhCs, which take full advantage of the crystalline symmetry and get rid of the limitation of the material. In this review, we give a brief review on several milestones of all-dielectric topological PhCs by discussing their topological invariants, intriguing properties, and potential applications. A summary of all-dielectric topological PhCs mentioned in this review is provided in Table 1. We conclude that all-dielectric PhCs served as a common photonic system have achieved great success in both emulating various topological phases and finding potential application in light manipulation.
All-dielectric topological PhCs will continue to evolve in the coming years, as in the past decade. The scope of all-dielectric topological PhCs is becoming diverse and can be further expanded by combing nonlinearity [177–181], non-hermiticity [182–186], real space topology (such as dislocation [187] and disinclination [188–190]), and synthesis dimension [196–206]. In particular, it was reported recently that non-hermiticity fundamentally changes the topological band theory, leading to exotic phenomena like non-Hermitian skin effect, as confirmed in the 1D SSH model [191–195]. By adding gain and loss into the all-dielectric PhCs, one can study non-Hermitian topological photonics in a direct way [182–185]. Alternatively, as an open system, topological waveguide-cavity coupled structure made of all-dielectric, offers an excellent platform to study non-Hermitian topological physics [186]. In addition to non-hermiticity, it also deserves to study the all-dielectric topological PhCs with the ingredient of synthesis dimension. It is generally believed that the dimension of a physical system cannot be larger than its geometric dimensionality. However, with the introduction of synthetic frequency dimension, and combined with the intrinsic geometric dimension, one can investigate higher dimensional physics. These studies may sustain further developments of all-dielectric topological photonics and offer novel methods for light manipulations.
Author Contributions
H-XW conceived the idea and prepared the draft. All authors contributed to the discussion and revision of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (11904060, 12074279, and 12125504).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Yablonovitch E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys Rev Lett (1987) 58:2059–62. doi:10.1103/physrevlett.58.2059
2. John S. Strong Localization of Photons in Certain Disordered Dielectric Superlattices. Phys Rev Lett (1987) 58:2486–9. doi:10.1103/physrevlett.58.2486
3. Biró LP, Kertész K, Vértesy Z, Márk GI, Bálint Z, Lousse V, et al. Living Photonic Crystals: Butterfly Scales - Nanostructure and Optical Properties. Mater Sci Eng C (2007) 27:941–6. doi:10.1016/j.msec.2006.09.043
4. Proietti Zaccaria R. Butterfly wing Color: A Photonic crystal Demonstration. Opt Lasers Eng (2016) 76:70–3. doi:10.1016/j.optlaseng.2015.04.008
5. Teyssier J, Saenko SV, van der Marel D, Milinkovitch MC. Photonic Crystals Cause Active Colour Change in Chameleons. Nat Commun (2015) 6:6368. doi:10.1038/ncomms7368
6. Ishizaki K, Noda S. Manipulation of Photons at the Surface of Three-Dimensional Photonic Crystals. Nature (2009) 460:367–70. doi:10.1038/nature08190
7. Ma T-X, Wang Y-S, Zhang C. Photonic and Phononic Surface and Edge Modes in Three-Dimensional Phoxonic Crystals. Phys Rev B (2018) 97:134302. doi:10.1103/PhysRevB.97.134302
8. Cersonsky RK, Antonaglia J, Dice BD, Glotzer SC. The Diversity of Three-Dimensional Photonic Crystals. Nat Commun (2021) 12:2543. doi:10.1038/s41467-021-22809-6
9.JD Joannopoulos, editor. Photonic Crystals: Molding the Flow of Light. 2nd ed. Princeton: Princeton University Press (2008).
10. Qi X-L, Zhang S-C. Topological Insulators and Superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/RevModPhys.83.1057
11. Hasan MZ, Kane CL. Colloquium: Topological Insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/RevModPhys.82.3045
12. Armitage NP, Mele EJ, Vishwanath A. Weyl and Dirac Semimetals in Three-Dimensional Solids. Rev Mod Phys (2018) 90:015001. doi:10.1103/RevModPhys.90.015001
13. Klitzing Kv., Dorda G, Pepper M. New Method for High-Accuracy Determination of the fine-structure Constant Based on Quantized Hall Resistance. Phys Rev Lett (1980) 45:494–7. doi:10.1103/physrevlett.45.494
14. Thouless DJ, Kohmoto M, Nightingale MP, den Nijs M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys Rev Lett (1982) 49:405–8. doi:10.1103/PhysRevLett.49.405
15. Kohmoto M. Topological Invariant and the Quantization of the Hall Conductance. Ann Phys (1985) 160:343–54. doi:10.1016/0003-4916(85)90148-4
16. Haldane FDM. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the "Parity Anomaly". Phys Rev Lett (1988) 61:2015–8. doi:10.1103/physrevlett.61.2015
17. Lu L, Joannopoulos JD, Soljačić M. Topological Photonics. Nat Photon (2014) 8:821–9. doi:10.1038/nphoton.2014.248
18. Khanikaev AB, Shvets G. Two-dimensional Topological Photonics. Nat Photon (2017) 11:763–73. doi:10.1038/s41566-017-0048-5
19. Wu Y, Li C, Hu X, Ao Y, Zhao Y, Gong Q. Applications of Topological Photonics in Integrated Photonic Devices. Adv Opt Mater (2017) 5:1700357. doi:10.1002/adom.201700357
20. Xie B-Y, Wang H-F, Zhu X-Y, Lu M-H, Wang ZD, Chen Y-F. Photonics Meets Topology. Opt Express (2018) 26:24531. doi:10.1364/OE.26.024531
21. Ozawa T, Price HM, Amo A, Goldman N, Hafezi M, Lu L, et al. Topological Photonics. Rev Mod Phys (2019) 91:015006. doi:10.1103/RevModPhys.91.015006
22. Kim M, Jacob Z, Rho J. Recent Advances in 2D, 3D and Higher-Order Topological Photonics. Light Sci Appl (2020) 9:130. doi:10.1038/s41377-020-0331-y
23. Liu H, Xie B, Cheng H, Tian J, Chen S. Topological Photonic States in Artificial Microstructures [Invited]. 中国光学快报 (2021) 19:052602. doi:10.3788/COL202119.052602
24. Raghu S, Haldane FDM. Analogs of Quantum-Hall-Effect Edge States in Photonic Crystals. Phys Rev A (2008) 78:033834. doi:10.1103/PhysRevA.78.033834
25. Haldane FDM, Raghu S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys Rev Lett (2008) 100:013904. doi:10.1103/physrevlett.100.013904
26. Wang Z, Chong YD, Joannopoulos JD, Soljacić M. Reflection-free One-Way Edge Modes in a Gyromagnetic Photonic crystal. Phys Rev Lett (2008) 100:013905. doi:10.1103/PhysRevLett.100.013905
27. Wang Z, Chong Y, Joannopoulos JD, Soljačić M. Observation of Unidirectional Backscattering-Immune Topological Electromagnetic States. Nature (2009) 461:772–5. doi:10.1038/nature08293
28. Kane CL, Mele EJ. Quantum Spin Hall Effect in Graphene. Phys Rev Lett (2005) 95:226801. doi:10.1103/PhysRevLett.95.226801
29. Kane CL, Mele EJ. Z2Topological Order and the Quantum Spin Hall Effect. Phys Rev Lett (2005) 95:146802. doi:10.1103/PhysRevLett.95.146802
30. Bernevig BA, Zhang S-C. Quantum Spin Hall Effect. Phys Rev Lett (2006) 96:106802. doi:10.1103/PhysRevLett.96.106802
31. Bernevig BA, Hughes TL, Zhang S-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science (2006) 314:1757–61. doi:10.1126/science.1133734
32. Chen W-J, Jiang S-J, Chen X-D, Zhu B, Zhou L, Dong J-W, et al. Experimental Realization of Photonic Topological Insulator in a Uniaxial Metacrystal Waveguide. Nat Commun (2014) 5:5782. doi:10.1038/ncomms6782
33. Ma T, Khanikaev AB, Mousavi SH, Shvets G. Guiding Electromagnetic Waves Around Sharp Corners: Topologically Protected Photonic Transport in Metawaveguides. Phys Rev Lett (2015) 114:127401. doi:10.1103/physrevlett.114.127401
34. Khanikaev AB, Hossein Mousavi S, Tse W-K, Kargarian M, MacDonald AH, Shvets G. Photonic Topological Insulators. Nat Mater (2013) 12:233–9. doi:10.1038/nmat3520
35. He C, Sun X-C, Liu X-P, Lu M-H, Chen Y, Feng L, et al. Photonic Topological Insulator with Broken Time-Reversal Symmetry. Proc Natl Acad Sci U.S.A (2016) 113:4924–8. doi:10.1073/pnas.1525502113
36. Wu L-H, Hu X. Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material. Phys Rev Lett (2015) 114:223901. doi:10.1103/PhysRevLett.114.223901
37. Rycerz A, Tworzydło J, Beenakker CWJ. Valley Filter and valley Valve in Graphene. Nat Phys (2007) 3:172–5. doi:10.1038/nphys547
38. Xiao D, Yao W, Niu Q. Valley-contrasting Physics in Graphene: Magnetic Moment and Topological Transport. Phys Rev Lett (2007) 99:236809. doi:10.1103/PhysRevLett.99.236809
39. Yao W, Xiao D, Niu Q. Valley-dependent Optoelectronics from Inversion Symmetry Breaking. Phys Rev B (2008) 77:235406. doi:10.1103/PhysRevB.77.235406
40. Ma T, Shvets G. All-Si valley-Hall Photonic Topological Insulator. New J Phys (2016) 18:025012. doi:10.1088/1367-2630/18/2/025012
41. Benalcazar WA, Bernevig BA, Hughes TL. Quantized Electric Multipole Insulators. Science (2017) 357:61–6. doi:10.1126/science.aah6442
42. Schindler F, Cook AM, Vergniory MG, Wang Z, Parkin SSP, Bernevig BA, et al. Higher-order Topological Insulators. Sci Adv (2018) 4:eaat0346. doi:10.1126/sciadv.aat0346
43. Ezawa M. Higher-Order Topological Insulators and Semimetals on the Breathing Kagome and Pyrochlore Lattices. Phys Rev Lett (2018) 120. doi:10.1103/PhysRevLett.120.026801
44. Xie B, Wang H-X, Zhang X, Zhan P, Jiang J-H, Lu M, et al. Higher-order Band Topology. Nat Rev Phys (2021) 3:520–32. doi:10.1038/s42254-021-00323-4
45. Benalcazar WA, Bernevig BA, Hughes TL. Electric Multipole Moments, Topological Multipole Moment Pumping, and Chiral Hinge States in Crystalline Insulators. Phys Rev B (2017) 96:245115. doi:10.1103/PhysRevB.96.245115
46. Franca S, van den Brink J, Fulga IC. An Anomalous Higher-Order Topological Insulator. Phys Rev B (2018) 98:201114. doi:10.1103/PhysRevB.98.201114
47. Langbehn J, Peng Y, Trifunovic L, von Oppen F, Brouwer PW. Reflection-Symmetric Second-Order Topological Insulators and Superconductors. Phys Rev Lett (2017) 119:246401. doi:10.1103/PhysRevLett.119.246401
48. Song Z, Fang Z, Fang C. (d−2) -Dimensional Edge States of Rotation Symmetry Protected Topological States. Phys Rev Lett (2017) 119:246402. doi:10.1103/PhysRevLett.119.246402
49. Schindler F, Wang Z, Vergniory MG, Cook AM, Murani A, Sengupta S, et al. Higher-order Topology in Bismuth. Nat Phys (2018) 14:918–24. doi:10.1038/s41567-018-0224-7
50. Li M, Zhirihin D, Gorlach M, Ni X, Filonov D, Slobozhanyuk A, et al. Higher-order Topological States in Photonic Kagome Crystals with Long-Range Interactions. Nat Photon (2019) 14:89. doi:10.1038/s41566-019-0561-9
51. Su WP, Schrieffer JR, Heeger AJ. Soliton Excitations in Polyacetylene. Phys Rev B (1980) 22:2099–111. doi:10.1103/physrevb.22.2099
52. Lang L-J, Cai X, Chen S. Edge States and Topological Phases in One-Dimensional Optical Superlattices. Phys Rev Lett (2012) 108:220401. doi:10.1103/PhysRevLett.108.220401
53. Li L, Xu Z, Chen S. Topological Phases of Generalized Su-Schrieffer-Heeger Models. Phys Rev B (2014) 89:085111. doi:10.1103/PhysRevB.89.085111
54. Chen H-T, Chang C-H, Kao H-c. Connection between the Winding Number and the Chern Number. Chin J Phys (2021) 72:50–68. doi:10.1016/j.cjph.2020.12.025
55. Xiao M, Zhang ZQ, Chan CT. Surface Impedance and Bulk Band Geometric Phases in One-Dimensional Systems. Phys Rev X (2014) 4:021017. doi:10.1103/PhysRevX.4.021017
56. Fang C, Lu L, Liu J, Fu L. Topological Semimetals with Helicoid Surface States. Nat Phys (2016) 12:936–41. doi:10.1038/nphys3782
57. Yang B, Guo Q, Tremain B, Liu R, Barr LE, Yan Q, et al. Ideal Weyl Points and Helicoid Surface States in Artificial Photonic crystal Structures. Science (2018) 359:1013–6. doi:10.1126/science.aaq1221
58. Lu L, Fang C, Fu L, Johnson SG, Joannopoulos JD, Soljačić M. Symmetry-protected Topological Photonic crystal in Three Dimensions. Nat Phys (2016) 12:337–40. doi:10.1038/nphys3611
59. Slobozhanyuk A, Mousavi SH, Ni X, Smirnova D, Kivshar YS, Khanikaev AB. Three-dimensional All-Dielectric Photonic Topological Insulator. Nat Photon (2017) 11:130–6. doi:10.1038/nphoton.2016.253
60. Lu L, Fu L, Joannopoulos JD, Soljačić M. Weyl Points and Line Nodes in Gyroid Photonic Crystals. Nat Photon (2013) 7:294–9. doi:10.1038/nphoton.2013.42
61. Lu L, Wang Z, Ye D, Ran L, Fu L, Joannopoulos JD, et al. Experimental Observation of Weyl Points. Science (2015) 349:622–4. doi:10.1126/science.aaa9273
62. Zak J. Berry's Phase for Energy Bands in Solids. Phys Rev Lett (1989) 62:2747–50. doi:10.1103/physrevlett.62.2747
63. Wang H-X, Guo G-Y, Jiang J-H. Band Topology in Classical Waves: Wilson-loop Approach to Topological Numbers and Fragile Topology. New J Phys (2019) 21:093029. doi:10.1088/1367-2630/ab3f71
64. Yu R, Qi XL, Bernevig A, Fang Z, Dai X. Equivalent Expression ofZ2topological Invariant for Band Insulators Using the Non-abelian Berry Connection. Phys Rev B (2011) 84:075119. doi:10.1103/PhysRevB.84.075119
65. Wang Q, Xiao M, Liu H, Zhu S, Chan CT. Measurement of the Zak Phase of Photonic Bands through the Interface States of a Metasurface/photonic crystal. Phys Rev B (2016) 93:041415. doi:10.1103/physrevb.93.041415
66. Gao WS, Xiao M, Chan CT, Tam WY. Determination of Zak Phase by Reflection Phase in 1D Photonic Crystals. Opt Lett (2015) 40:5259. doi:10.1364/ol.40.005259
67. Gao W, Xiao M, Chen B, Pun EYB, Chan CT, Tam WY. Controlling Interface States in 1D Photonic Crystals by Tuning Bulk Geometric Phases. Opt Lett (2017) 42:1500. doi:10.1364/OL.42.001500
68. Huang X, Xiao M, Zhang ZQ, Chan CT. Sufficient Condition for the Existence of Interface States in Some Two-Dimensional Photonic Crystals. Phys Rev B (2014) 90:075423. doi:10.1103/physrevb.90.075423
69. Huang X, Yang Y, Hang ZH, Zhang Z-Q, Chan CT. Geometric Phase Induced Interface States in Mutually Inverted Two-Dimensional Photonic Crystals. Phys Rev B (2016) 93:085415. doi:10.1103/PhysRevB.93.085415
70. Chen X-D, Zhao D, Zhu X-S, Shi F-L, Liu H, Lu J-C, et al. Edge States in Self-Complementary Checkerboard Photonic Crystals: Zak Phase, Surface Impedance, and Experimental Verification. Phys Rev A (2018) 97:013831. doi:10.1103/PhysRevA.97.013831
71. Fukui T, Hatsugai Y, Suzuki H. Chern Numbers in Discretized Brillouin Zone: Efficient Method of Computing (Spin) Hall Conductances. J Phys Soc Jpn (2005) 74:1674–7. doi:10.1143/JPSJ.74.1674
72. Weng H, Yu R, Hu X, Dai X, Fang Z. Quantum Anomalous Hall Effect and Related Topological Electronic States. Adv Phys (2015) 64:227–82. doi:10.1080/00018732.2015.1068524
73. Hatsugai Y. Chern Number and Edge States in the Integer Quantum Hall Effect. Phys Rev Lett (1993) 71:3697–700. doi:10.1103/PhysRevLett.71.3697
74. Ao X, Lin Z, Chan CT. One-way Edge Mode in a Magneto-Optical Honeycomb Photonic crystal. Phys Rev B (2009) 80:033105. doi:10.1103/physrevb.80.033105
75. Poo Y, Wu R-x., Lin Z, Yang Y, Chan CT. Experimental Realization of Self-Guiding Unidirectional Electromagnetic Edge States. Phys Rev Lett (2011) 106:093903. doi:10.1103/physrevlett.106.093903
76. Skirlo SA, Lu L, Soljačić M. Multimode One-Way Waveguides of Large Chern Numbers. Phys Rev Lett (2014) 113:113904. doi:10.1103/physrevlett.113.113904
77. Skirlo SA, Lu L, Igarashi Y, Yan Q, Joannopoulos J, Soljačić M. Experimental Observation of Large Chern Numbers in Photonic Crystals. Phys Rev Lett (2015) 115:253901. doi:10.1103/physrevlett.115.253901
78. Yang Y, Poo Y, Wu R-x., Gu Y, Chen P. Experimental Demonstration of One-Way Slow Wave in Waveguide Involving Gyromagnetic Photonic Crystals. Appl Phys Lett (2013) 102:231113. doi:10.1063/1.4809956
79. Chen J, Liang W, Li ZY. Strong Coupling of Topological Edge States Enabling Group-Dispersionless Slow Light in Magneto-Optical Photonic Crystals. Phys Rev B (2019) 99:014103. doi:10.1103/physrevb.99.014103
80. Chen J, Liang W, Li Z-Y. Switchable Slow Light Rainbow Trapping and Releasing in Strongly Coupling Topological Photonic Systems. Photon Res (2019) 7:1075. doi:10.1364/PRJ.7.001075
81. Chen J, Liang W, Li Z-Y. Broadband Dispersionless Topological Slow Light. Opt Lett (2020) 45:4964. doi:10.1364/OL.401650
82. Chen J, Liang W, Li Z-Y. Antichiral One-Way Edge States in a Gyromagnetic Photonic crystal. Phys Rev B (2020) 101:214102. doi:10.1103/PhysRevB.101.214102
83. Zhou P, Liu G-G, Yang Y, Hu Y-H, Ma S, Xue H, et al. Observation of Photonic Antichiral Edge States. Phys Rev Lett (2020) 125:263603. doi:10.1103/PhysRevLett.125.263603
84. Yang Y, Xu YF, Xu T, Wang H-X, Jiang J-H, Hu X, et al. Visualization of a Unidirectional Electromagnetic Waveguide Using Topological Photonic Crystals Made of Dielectric Materials. Phys Rev Lett (2018) 120:217401. doi:10.1103/PhysRevLett.120.217401
85. Zhu X, Wang H-X, Xu C, Lai Y, Jiang J-H, John S. Topological Transitions in Continuously Deformed Photonic Crystals. Phys Rev B (2018) 97:085148. doi:10.1103/physrevb.97.085148
86. Barik S, Miyake H, DeGottardi W, Waks E, Hafezi M. Two-dimensionally Confined Topological Edge States in Photonic Crystals. New J Phys (2016) 18:113013. doi:10.1088/1367-2630/18/11/113013
87. Huang H, Huo S, Chen J. Reconfigurable Topological Phases in Two-Dimensional Dielectric Photonic Crystals. Crystals (2019) 9:221. doi:10.3390/cryst9040221
88. Jin M-C, Gao Y-F, Ma Q-L, Zhang W, Song H, Sun J-P. Regularly Multiple Double Dirac Cones in Photonic Bands and Topological Transitions of All-Dielectric Photonic Crystals. Phys Rev Mater (2021) 5:024204. doi:10.1103/PhysRevMaterials.5.024204
89. Deng W-M, Chen X-D, Zhao F-L, Dong J-W. Transverse Angular Momentum in Topological Photonic Crystals. J Opt (2018) 20:014006. doi:10.1088/2040-8986/aa9b06
90. Parappurath N, Alpeggiani F, Kuipers L, Verhagen E. Direct Observation of Topological Edge States in Silicon Photonic Crystals: Spin, Dispersion, and Chiral Routing. Sci Adv (2020) 6. doi:10.1126/sciadv.aaw4137
91. Gorlach MA, Ni X, Smirnova DA, Korobkin D, Zhirihin D, Slobozhanyuk AP, et al. Far-field Probing of Leaky Topological States in All-Dielectric Metasurfaces. Nat Commun (2018) 9. doi:10.1038/s41467-018-03330-9
92. Slobozhanyuk A, Shchelokova AV, Ni X, Hossein Mousavi S, Smirnova DA, Belov PA, et al. Near-field Imaging of Spin-Locked Edge States in All-Dielectric Topological Metasurfaces. Appl Phys Lett (2019) 114:031103. doi:10.1063/1.5055601
93. Shao Z-K, Chen H-Z, Wang S, Mao X-R, Yang Z-Q, Wang S-L, et al. A High-Performance Topological Bulk Laser Based on Band-Inversion-Induced Reflection. Nat Nanotechnol (2020) 15:67–72. doi:10.1038/s41565-019-0584-x
94. Barik S, Karasahin A, Flower C, Cai T, Miyake H, DeGottardi W, et al. A Topological Quantum Optics Interface. Science (2018) 359:666–8. doi:10.1126/science.aaq0327
95. Kagami H, Amemiya T, Okada S, Nishiyama N, Hu X. Topological Converter for High-Efficiency Coupling between Si Wire Waveguide and Topological Waveguide. Opt Express (2020) 28:33619. doi:10.1364/OE.398421
96. Wei Y, Yan B, Peng Y, Shi A, Zhao D, Peng R, et al. Fragile Topology in Double-Site Honeycomb Lattice Photonic crystal. Opt Lett (2021) 46:3941. doi:10.1364/OL.434502
97. Xu L, Wang H-X, Xu Y-D, Chen H-Y, Jiang J-H. Accidental Degeneracy in Photonic Bands and Topological Phase Transitions in Two-Dimensional Core-Shell Dielectric Photonic Crystals. Opt Express (2016) 24:18059. doi:10.1364/OE.24.018059
98. Yan B, Xie J, Liu E, Peng Y, Ge R, Liu J, et al. Topological Edge State in the Two-Dimensional Stampfli-Triangle Photonic Crystals. Phys Rev Appl (2019) 12:044004. doi:10.1103/physrevapplied.12.044004
99. Li Z, Chan H-C, Xiang Y. Fragile Topology Based Helical Edge States in Two-Dimensional Moon-Shaped Photonic Crystals. Phys Rev B (2020) 102:245149. doi:10.1103/PhysRevB.102.245149
100. Lidorikis E, Sigalas MM, Economou EN, Soukoulis CM. Tight-binding Parametrization for Photonic Band gap Materials. Phys Rev Lett (1998) 81:1405–8. doi:10.1103/PhysRevLett.81.1405
101. Blanco de Paz M, Devescovi C, Giedke G, Saenz JJ, Vergniory MG, Bradlyn B, et al. Tutorial: Computing Topological Invariants in 2D Photonic Crystals. Adv Quan Tech (2020) 3:1900117. doi:10.1002/qute.201900117
102. de Paz MB, Vergniory MG, Bercioux D, García-Etxarri A, Bradlyn B. Engineering Fragile Topology in Photonic Crystals: Topological Quantum Chemistry of Light. Phys Rev Res (2019) 1:032005. doi:10.1103/physrevresearch.1.032005
103. Alexandradinata A, Höller J, Wang C, Cheng H, Lu L. Crystallographic Splitting Theorem for Band Representations and Fragile Topological Photonic Crystals. Phys Rev B (2020) 102:115117. doi:10.1103/PhysRevB.102.115117
104. He L, Zhang WX, Zhang XD. Topological All-Optical Logic gates Based on Two-Dimensional Photonic Crystals. Opt Express (2019) 27:25841. doi:10.1364/oe.27.025841
105. Yang Y, Hang ZH. Topological Whispering Gallery Modes in Two-Dimensional Photonic crystal Cavities. Opt Express (2018) 26:21235. doi:10.1364/OE.26.021235
106. Ji C-Y, Liu G-B, Zhang Y, Zou B, Yao Y. Transport Tuning of Photonic Topological Edge States by Optical Cavities. Phys Rev A (2019) 99:043801. doi:10.1103/PhysRevA.99.043801
107. Gao X, Yang L, Lin H, Zhang L, Li J, Bo F, et al. Dirac-vortex Topological Cavities. Nat Nanotechnol (2020) 15:1012–8. doi:10.1038/s41565-020-0773-7
108. Lin H, Lu L. Dirac-vortex Topological Photonic crystal Fibre. Light Sci Appl (2020) 9:202. doi:10.1038/s41377-020-00432-2
109. Deng W-M, Chen X-D, Chen W-J, Zhao F-L, Dong J-W. Vortex index Identification and Unidirectional Propagation in Kagome Photonic Crystals. Nanophotonics (2019) 8:833–40. doi:10.1515/nanoph-2019-0009
110. He X-T, Liang E-T, Yuan J-J, Qiu H-Y, Chen X-D, Zhao F-L, et al. A Silicon-On-Insulator Slab for Topological valley Transport. Nat Commun (2019) 10:872. doi:10.1038/s41467-019-08881-z
111. Chen XD, He XT, Dong JW. All‐Dielectric Layered Photonic Topological Insulators. Laser Photon Rev (2019) 13:1900091. doi:10.1002/lpor.201900091
112. Wong S, Saba M, Hess O, Oh SS. Gapless Unidirectional Photonic Transport Using All-Dielectric Kagome Lattices. Phys Rev Res (2020) 2:012011. doi:10.1103/PhysRevResearch.2.012011
113. Xu Z, Kong X, Davis RJ, Bisharat Da., Zhou Y, Yin X, et al. Topological valley Transport under Long-Range Deformations. Phys Rev Res (2020) 2:013209. doi:10.1103/physrevresearch.2.013209
114. Xi X, Ye K-P, Wu R-X. Topological Photonic crystal of Large valley Chern Numbers. Photon Res (2020) 8:B1. doi:10.1364/prj.396872
115. Tang G-J, Chen X-D, Shi F-L, Liu J-W, Chen M, Dong J-W. Frequency Range Dependent Topological Phases and Photonic Detouring in valley Photonic Crystals. Phys Rev B (2020) 102:174202. doi:10.1103/PhysRevB.102.174202
116. Arora S, Bauer T, Barczyk R, Verhagen E, Kuipers L. Direct Quantification of Topological protection in Symmetry-Protected Photonic Edge States at Telecom Wavelengths. Light Sci Appl (2021) 10:9. doi:10.1038/s41377-020-00458-6
117. Yang J-K, Hwang Y, Oh SS. Evolution of Topological Edge Modes from Honeycomb Photonic Crystals to Triangular-Lattice Photonic Crystals. Phys Rev Res (2021) 3:L022025. doi:10.1103/physrevresearch.3.l022025
118. Yan B, Peng Y, Xie J, Peng Y, Shi A, Li H, et al. Multifrequency and Multimode Topological Waveguides in Stampfli-triangle Photonic crystal with Large valley Chern Numbers. arXiv:2104.14142[physics] (2021).
119. Chen X-D, Zhao F-L, Chen M, Dong J-W. Valley-contrasting Physics in All-Dielectric Photonic Crystals: Orbital Angular Momentum and Topological Propagation. Phys Rev B (2017) 96. doi:10.1103/PhysRevB.96.020202
120. Ye L, Yang Y, Hong Hang Z, Qiu C, Liu Z. Observation of valley-selective Microwave Transport in Photonic Crystals. Appl Phys Lett (2017) 111:251107. doi:10.1063/1.5009597
121. Han Y, Fei H, Lin H, Zhang Y, Zhang M, Yang Y. Design of Broadband All-Dielectric valley Photonic Crystals at Telecommunication Wavelength. Opt Commun (2021) 488:126847. doi:10.1016/j.optcom.2021.126847
122. Yang Y, Jiang H, Hang ZH. Topological Valley Transport in Two-Dimensional Honeycomb Photonic Crystals. Sci Rep (2018) 8. doi:10.1038/s41598-018-20001-3
123. Chen XD, Shi FL, Liu H, Lu JC, Deng WM, Dai JY, et al. Tunable Electromagnetic Flow Control in Valley Photonic Crystal Waveguides. Phys Rev Appl (2018) 10:044002. doi:10.1103/physrevapplied.10.044002
124. Wu Y, Hu X, Gong Q. Reconfigurable Topological States in valley Photonic Crystals. Phys Rev Mater (2018) 2:122201. doi:10.1103/PhysRevMaterials.2.122201
125. Noh J, Huang S, Chen KP, Rechtsman MC. Observation of Photonic Topological Valley Hall Edge States. Phys Rev Lett (2018) 120:063902. doi:10.1103/PhysRevLett.120.063902
126. Chan H-C, Guo G-Y. Tuning Topological Phase Transitions in Hexagonal Photonic Lattices Made of Triangular Rods. Phys Rev B (2018) 97:045422. doi:10.1103/physrevb.97.045422
127. He L, Ji HY, Wang YJ, Zhang XD. Topologically Protected Beam Splitters and Logic gates Based on Two-Dimensional Silicon Photonic crystal Slabs. Opt Express (2020) 28:34015. doi:10.1364/OE.409265
128. Zeng Y, Chattopadhyay U, Zhu B, Qiang B, Li J, Jin Y, et al. Electrically Pumped Topological Laser with valley Edge Modes. Nature (2020) 578:246–50. doi:10.1038/s41586-020-1981-x
129. He L, Zhang H, Zhang W, Wang Y, Zhang X. Topologically Protected Vector Edge States and Polarization Beam Splitter by All-Dielectric valley Photonic crystal Slabs. New J Phys (2021) 23:093026. doi:10.1088/1367-2630/ac20eb
130. Ji C-Y, Zhang Y, Zou B, Yao Y. Robust Fano Resonance in the Photonic valley Hall States. Phys Rev A (2021) 103:023512. doi:10.1103/PhysRevA.103.023512
131. Makwana M, Craster R, Guenneau S. Topological Beam-Splitting in Photonic Crystals. Opt Express (2019) 27:16088. doi:10.1364/OE.27.016088
132. Makwana MP, Craster RV. Designing Multidirectional Energy Splitters and Topological valley Supernetworks. Phys Rev B (2018) 98:235125. doi:10.1103/PhysRevB.98.235125
133. Xie X, Yan S, Dang J, Yang J, Xiao S, Wang Y, et al. Topological Cavity Based on Slow-Light Topological Edge Mode for Broadband Purcell Enhancement. Phys Rev Appl (2021) 16:014036. doi:10.1103/PhysRevApplied.16.014036
134. Makwana M, Wiltshaw R, Guenneau S, Craster R. Hybrid Topological Guiding Mechanisms for Photonic crystal Fibers. Opt Express (2020) 28:30871. doi:10.1364/oe.398559
135. Makwana MP, Chaplain G. Tunable Three-Way Topological Energy-Splitter. Sci Rep (2019) 9:18939. doi:10.1038/s41598-019-55485-0
136. Chen Y, Lin Z-K, Chen H, Jiang J-H. Plasmon-polaritonic Quadrupole Topological Insulators. Phys Rev B (2020) 101:041109. doi:10.1103/PhysRevB.101.041109
137. He L, Addison Z, Mele EJ, Zhen B. Quadrupole Topological Photonic Crystals. Nat Commun (2020) 11:3119. doi:10.1038/s41467-020-16916-z
138. Ezawa M. Higher-order Topological Electric Circuits and Topological Corner Resonance on the Breathing Kagome and Pyrochlore Lattices. Phys Rev B (2018) 98:201402. doi:10.1103/PhysRevB.98.201402
139. Yang H, Li Z-X, Liu Y, Cao Y, Yan P. Observation of Symmetry-Protected Zero Modes in Topolectrical Circuits. Phys Rev Res (2020) 2:022028. doi:10.1103/PhysRevResearch.2.022028
140. Xue H, Yang Y, Gao F, Chong Y, Zhang B. Acoustic Higher-Order Topological Insulator on a Kagome Lattice. Nat Mater (2019) 18:108–12. doi:10.1038/s41563-018-0251-x
141. Ni X, Weiner M, Alù A, Khanikaev AB. Observation of Higher-Order Topological Acoustic States Protected by Generalized Chiral Symmetry. Nat Mater (2019) 18:113–20. doi:10.1038/s41563-018-0252-9
142. Shen S-l., Li C, Wu J-F. Investigation of Corner States in Second-Order Photonic Topological Insulator. Opt Express (2021) 29:24045. doi:10.1364/OE.426691
143. Wakao H, Yoshida T, Araki H, Mizoguchi T, Hatsugai Y. Higher-order Topological Phases in a spring-mass Model on a Breathing Kagome Lattice. Phys Rev B (2020) 101:094107. doi:10.1103/PhysRevB.101.094107
144. Phan HT, Liu F, Wakabayashi K. Valley-dependent Corner States in Honeycomb Photonic Crystals without Inversion Symmetry. Opt Express (2021) 29:18277. doi:10.1364/OE.427222
145. Wu S, Jiang B, Liu Y, Jiang J-H. All-dielectric Photonic crystal with Unconventional Higher-Order Topology. Photon Res (2021) 9:668. doi:10.1364/PRJ.418689
146. Yang Y, Jia Z, Wu Y, Xiao R-C, Hang ZH, Jiang H, et al. Gapped Topological Kink States and Topological Corner States in Honeycomb Lattice. Sci Bull (2020) 65:531–7. doi:10.1016/j.scib.2020.01.024
147. Proctor M, Huidobro PA, Bradlyn B, de Paz MB, Vergniory MG, Bercioux D, et al. Robustness of Topological Corner Modes in Photonic Crystals. Phys Rev Res (2020) 2:042038. doi:10.1103/physrevresearch.2.042038
148. Liu F, Deng H-Y, Wakabayashi K. Helical Topological Edge States in a Quadrupole Phase. Phys Rev Lett (2019) 122:086804. doi:10.1103/PhysRevLett.122.086804
149. Li M, Wang Y, Lu M, Sang T. Two Types of Corner States in Two-Dimensional Photonic Topological Insulators. J Appl Phys (2021) 129:063104. doi:10.1063/5.0039586
150. Chen Y, Meng F, Kivshar Y, Jia B, Huang X. Inverse Design of Higher-Order Photonic Topological Insulators. Phys Rev Res (2020) 2:023115. doi:10.1103/PhysRevResearch.2.023115
151. Xie B-Y, Wang H-F, Wang H-X, Zhu X-Y, Jiang J-H, Lu M-H, et al. Second-order Photonic Topological Insulator with Corner States. Phys Rev B (2018) 98:205147. doi:10.1103/PhysRevB.98.205147
152. Xie B-Y, Su G-X, Wang H-F, Su H, Shen X-P, Zhan P, et al. Visualization of Higher-Order Topological Insulating Phases in Two-Dimensional Dielectric Photonic Crystals. Phys Rev Lett (2019) 122:233903. doi:10.1103/PhysRevLett.122.233903
153. Chen X-D, Deng W-M, Shi F-L, Zhao F-L, Chen M, Dong J-W. Direct Observation of Corner States in Second-Order Topological Photonic Crystal Slabs. Phys Rev Lett (2019) 122:233902. doi:10.1103/PhysRevLett.122.233902
154. Wang H-X, Liang L, Jiang B, Hu J, Lu X, Jiang J-H. Higher-order Topological Phases in Tunable C3 Symmetric Photonic Crystals. Photon Res (2021) 9:1854. doi:10.1364/PRJ.433188
155. Benalcazar WA, Li T, Hughes TL. Quantization of Fractional Corner Charge in Cn -symmetric Higher-Order Topological Crystalline Insulators. Phys Rev B (2019) 99:245151. doi:10.1103/physrevb.99.245151
156. Chen Z-G, Wang L, Zhang G, Ma G. Chiral Symmetry Breaking of Tight-Binding Models in Coupled Acoustic-Cavity Systems. Phys Rev Appl (2020) 14:024023. doi:10.1103/PhysRevApplied.14.024023
157. Ota Y, Liu F, Katsumi R, Watanabe K, Wakabayashi K, Arakawa Y, et al. Photonic crystal Nanocavity Based on a Topological Corner State. Optica (2019) 6:786. doi:10.1364/OPTICA.6.000786
158. Xie X, Zhang W, He X, Wu S, Dang J, Peng K, et al. Cavity Quantum Electrodynamics with Second‐Order Topological Corner State. Laser Photon Rev (2020) 14:1900425. doi:10.1002/lpor.201900425
159. Kim H-R, Hwang M-S, Smirnova D, Jeong K-Y, Kivshar Y, Park H-G. Multipolar Lasing Modes from Topological Corner States. Nat Commun (2020) 11:5758. doi:10.1038/s41467-020-19609-9
160. Zhang W, Xie X, Hao H, Dang J, Xiao S, Shi S, et al. Low-threshold Topological Nanolasers Based on the Second-Order Corner State. Light Sci Appl (2020) 9:109. doi:10.1038/s41377-020-00352-1
161. Gong R, Zhang M, Li H, Lan Z. Topological Photonic crystal Fibers Based on Second-Order Corner Modes. Opt Lett (2021) 46:3849. doi:10.1364/ol.430579
162. Henriques JCG, Rappoport TG, Bludov YV, Vasilevskiy MI, Peres NMR. Topological Photonic Tamm States and the Su-Schrieffer-Heeger Model. Phys Rev A (2020) 101:043811. doi:10.1103/physreva.101.043811
163. Chen Z-G, Mei J, Sun X-C, Zhang X, Zhao J, Wu Y. Multiple Topological Phase Transitions in a Gyromagnetic Photonic crystal. Phys Rev A (2017) 95:043827. doi:10.1103/PhysRevA.95.043827
164. Chen MLN, Jiang LJ, Lan Z, Sha WEI. Coexistence of Pseudospin- and valley-Hall-like Edge States in a Photonic crystal with C3v Symmetry. Phys Rev Res (2020) 2:043148. doi:10.1103/PhysRevResearch.2.043148
165. Liu G-G, Zhou P, Yang Y, Xue H, Ren X, Lin X, et al. Observation of an Unpaired Photonic Dirac point. Nat Commun (2020) 11:1873. doi:10.1038/s41467-020-15801-z
166. Wu X, Li Z, Chen J, Li X, Tian J, Huang Y, et al. Interlayer Topological Transport and Devices Based on Layer Pseudospins in Photonic Valley‐Hall Phases. Adv Opt Mater. (2019) 7:1900872. doi:10.1002/adom.201900872
167. Yannopapas V. Gapless Surface States in a Lattice of Coupled Cavities: A Photonic Analog of Topological Crystalline Insulators. Phys Rev B (2011) 84. doi:10.1103/PhysRevB.84.195126
168. Fu L. Topological Crystalline Insulators. Phys Rev Lett (2011) 106:106802. doi:10.1103/physrevlett.106.106802
169. Ochiai T. Gapless Surface States Originating from Accidentally Degenerate Quadratic Band Touching in a Three-Dimensional Tetragonal Photonic crystal. Phys Rev A (2017) 96:043842. doi:10.1103/physreva.96.043842
170. Wang H, Xu L, Chen H, Jiang J-H. Three-dimensional Photonic Dirac Points Stabilized by point Group Symmetry. Phys Rev B (2016) 93:235155. doi:10.1103/PhysRevB.93.235155
171. Wang H-X, Chen Y, Hang ZH, Kee H-Y, Jiang J-H. Type-II Dirac Photons. Npj Quant Mater (2017) 2:54. doi:10.1038/s41535-017-0058-z
172. Guo Q, Yang B, Xia L, Gao W, Liu H, Chen J, et al. Three Dimensional Photonic Dirac Points in Metamaterials. Phys Rev Lett (2017) 119:213901. doi:10.1103/PhysRevLett.119.213901
173. Chen Y, Wang H-X, Bao Q, Jiang J-H, Chen H. Ideal Type-II Weyl Points in Twisted One-Dimensional Dielectric Photonic Crystals. Opt Express (2021) 29:40606. doi:10.1364/OE.444780
174. Bravo-Abad J. Weyl Points in Photonic-crystal Superlattices. 2D Mater (2015) 8:034013. doi:10.1088/2053-1583/2/3/034013
175. Chang ML, Xiao M, Chen WJ, Chan CT. Multiple Weyl Points and the Sign Change of Their Topological Charges in Woodpile Photonic Crystals. Phys Rev B (2017) 95. doi:10.1103/physrevb.95.125136
176. Wang L, Jian S-K, Yao H. Topological Photonic crystal with Equifrequency Weyl Points. Phys Rev A (2016) 93:061801. doi:10.1103/PhysRevA.93.061801
177. Jürß C, Bauer D. High-harmonic Generation in Su-Schrieffer-Heeger Chains. Phys Rev B (2019) 99:195428. doi:10.1103/PhysRevB.99.195428
178. Smirnova D, Kruk S, Leykam D, Melik-Gaykazyan E, Choi D-Y, Kivshar Y. Third-Harmonic Generation in Photonic Topological Metasurfaces. Phys Rev Lett (2019) 123:103901. doi:10.1103/PhysRevLett.123.103901
179. Smirnova DA, Smirnov LA, Leykam D, Kivshar YS. Topological Edge States and Gap Solitons in the Nonlinear Dirac Model. Laser Photon Rev (2019) 13:1900223. doi:10.1002/lpor.201900223
180. Lan Z, You JW, Panoiu NC. Nonlinear One-Way Edge-Mode Interactions for Frequency Mixing in Topological Photonic Crystals. Phys Rev B (2020) 101:155422. doi:10.1103/PhysRevB.101.155422
181. Smirnova D, Leykam D, Chong Y, Kivshar Y. Nonlinear Topological Photonics. Appl Phys Rev (2020) 7:021306. doi:10.1063/1.5142397
182. Jiang J-R, Chen W-T, Chern R-L. Parity-time Phase Transition in Photonic Crystals with $$C_{6v}$$ Symmetry. Sci Rep (2020) 10:15726. doi:10.1038/s41598-020-72716-x
183. Zhou X, Wu J, Wu Y. Topological Corner States in Non-hermitian Photonic Crystals. Opt Commun (2020) 466:125653. doi:10.1016/j.optcom.2020.125653
184. Chen MLN, Jiang LJ, Zhang S, Zhao R, Lan Z, Sha WEI. Comparative Study of Hermitian and Non-hermitian Topological Dielectric Photonic Crystals. Phys Rev A (2021) 104:033501. doi:10.1103/PhysRevA.104.033501
185. Jiang J, Yan B, Peng Y, Xie J, Shi A, Liu J. Multiband Topological States in Non-hermitian Photonic Crystals. Opt Lett (2022) 47:437. doi:10.1364/ol.449733
186. Dong J, Hu Q, Ji C-Y, Zou B, Zhang Y. Exceptional Points in a Topological Waveguide-Cavity Coupled System. New J Phys (2021) 23:113025. doi:10.1088/1367-2630/ac3441
187. Li F-F, Wang H-X, Xiong Z, Lou Q, Chen P, Wu R-X, et al. Topological Light-Trapping on a Dislocation. Nat Commun (2018) 9. doi:10.1038/s41467-018-04861-x
188. Liu Y, Leung S, Li F-F, Lin Z-K, Tao X, Poo Y, et al. Bulk-disclination Correspondence in Topological Crystalline Insulators. Nature (2021) 589:381–5. doi:10.1038/s41586-020-03125-3
189. Wang Q, Xue H, Zhang B, Chong YD. Observation of Protected Photonic Edge States Induced by Real-Space Topological Lattice Defects. Phys Rev Lett (2020) 124:243602. doi:10.1103/physrevlett.124.243602
190. Peterson CW, Li T, Jiang W, Hughes TL, Bahl G. Trapped Fractional Charges at Bulk Defects in Topological Insulators. Nature (2021) 589:376–80. doi:10.1038/s41586-020-03117-3
191. Yao S, Wang Z. Edge States and Topological Invariants of Non-hermitian Systems. Phys Rev Lett (2018) 121:086803. doi:10.1103/PhysRevLett.121.086803
192. Imura K-I, Takane Y. Generalized Bulk-Edge Correspondence for Non-hermitian Topological Systems. Phys Rev B (2019) 100:165430. doi:10.1103/PhysRevB.100.165430
193. Yokomizo K, Murakami S. Non-Bloch Band Theory of Non-hermitian Systems. Phys Rev Lett (2019) 123:066404. doi:10.1103/PhysRevLett.123.066404
194. Helbig T, Hofmann T, Imhof S, Abdelghany M, Kiessling T, Molenkamp LW, et al. Generalized Bulk-Boundary Correspondence in Non-hermitian Topolectrical Circuits. Nat Phys (2020) 16:747–50. doi:10.1038/s41567-020-0922-9
195. Zhang K, Yang Z, Fang C. Correspondence between Winding Numbers and Skin Modes in Non-hermitian Systems. Phys Rev Lett (2020) 125:126402. doi:10.1103/physrevlett.125.126402
196. Yuan L, Fan S. Bloch Oscillation and Unidirectional Translation of Frequency in a Dynamically Modulated Ring Resonator. Optica (2016) 3:1014. doi:10.1364/OPTICA.3.001014
197. Yuan L, Shi Y, Fan S. Photonic Gauge Potential in a System with a Synthetic Frequency Dimension. Opt Lett (2016) 41:741. doi:10.1364/OL.41.000741
198. Lin Q, Xiao M, Yuan L, Fan S. Photonic Weyl point in a Two-Dimensional Resonator Lattice with a Synthetic Frequency Dimension. Nat Commun (2016) 7. doi:10.1038/ncomms13731
199. Lin Q, Sun X-Q, Xiao M, Zhang S-C, Fan S. A Three-Dimensional Photonic Topological Insulator Using a Two-Dimensional Ring Resonator Lattice with a Synthetic Frequency Dimension. Sci Adv (2018) 4:eaat2774. doi:10.1126/sciadv.aat2774
200. Ozawa T, Price HM, Goldman N, Zilberberg O, Carusotto I. Synthetic Dimensions in Integrated Photonics: From Optical Isolation to Four-Dimensional Quantum Hall Physics. Phys Rev A (2016) 93:043827. doi:10.1103/PhysRevA.93.043827
201. Yuan L, Xiao M, Lin Q, Fan S. Synthetic Space with Arbitrary Dimensions in a Few Rings Undergoing Dynamic Modulation. Phys Rev B (2018) 97:104105. doi:10.1103/PhysRevB.97.104105
202. Yuan L, Lin Q, Zhang A, Xiao M, Chen X, Fan S. Photonic Gauge Potential in One Cavity with Synthetic Frequency and Orbital Angular Momentum Dimensions. Phys Rev Lett (2019) 122:083903. doi:10.1103/PhysRevLett.122.083903
203. Qin C, Wang B, Wong ZJ, Longhi S, Lu P. Discrete Diffraction and Bloch Oscillations in Non-hermitian Frequency Lattices Induced by Complex Photonic Gauge fields. Phys Rev B (2020) 101:064303. doi:10.1103/PhysRevB.101.064303
204. Qin C, Yuan L, Wang B, Fan S, Lu P. Effective Electric-Field Force for a Photon in a Synthetic Frequency Lattice Created in a Waveguide Modulator. Phys Rev A (2018) 97:063838. doi:10.1103/physreva.97.063838
205. Qin C, Liu Q, Wang B, Lu P. Photonic Weyl Phase Transition in Dynamically Modulated brick-wall Waveguide Arrays. Opt Express (2018) 26:20929–43. doi:10.1364/oe.26.020929
Keywords: all-dielectric, photonic crystals, crystalline symmetry, topological phases, higher-order topology
Citation: Wang H-X and Jiang J-H (2022) A Short Review of All-Dielectric Topological Photonic Crystals. Front. Phys. 10:866552. doi: 10.3389/fphy.2022.866552
Received: 31 January 2022; Accepted: 23 March 2022;
Published: 28 April 2022.
Edited by:
Xiaoyong Hu, Peking University, ChinaCopyright © 2022 Wang and Jiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hai-Xiao Wang, aHh3YW5nQGd4bnUuZWR1LmNu; Jian-Hua Jiang, amlhbmh1YWppYW5nQHN1ZGEuZWR1LmNu
 Hai-Xiao Wang
Hai-Xiao Wang Jian-Hua Jiang
Jian-Hua Jiang