- 1Wenzhou Key Laboratory of Micro-Nano Optoelectronic Devices, Wenzhou University, Wenzhou, China
- 2Key Laboratory of Optoelectronic Materials Chemistry and Physics, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, China
Optical vortices are optical fields that possess a helical phase and orbital angular momentum, which have found the application in micromanipulation, optical communication, orbital angular momentum entanglement, super-resolution imaging, metrology, etc. The urgent need for the wide spreading applications of vortex lasers is to increase the wavelength versatility. In this study, the nonlinear frequency conversion of vortex lasers with a focus on sum frequency generation stimulated Raman scattering, and optical parametric oscillators were meticulously reviewed. The characteristics of the topological charge transfer and output beam profiles of different frequency conversion were discussed. As the precise tuning of optical fields in both temporal and spatial domains shall be the trend of future studies, it is our hope that this review shall serve as a reference for future research. Combining these techniques with the streaming methods to produce optical vortices, i.e., annular pump, off-axis pump, reflection mirror with defect spots, spherical aberration, and birefringence, it is advisable to expand the wavelength and fill the wavelength gap in the ultraviolet, visible, and infrared bands.
Introduction
Optical vortex is a beam with doughnut shape intensity profile—characterizing a dark region in the center and a helical phase [1]. Its concept was first introduced by Coullet et al. [2] in 1989. It has an azimuthal phase term
Optical vortices were later found to be extremely useful. Early works have demonstrated its availability to facilitate particle-trapping [5, 6]. Compared with conventional optical tweezers, the LG beam can create stronger adherence and produce no dissipative force. Another application of optical vortices is quantum communication since Zeilinger et al. [7] realized high-order OAM entanglement in 2001. In 2008, Barreiro et al. [8] successfully beat the capacity limit in quantum communication by taking advantage of an OAM-carrying beam. Furthermore, over 10,000
The study of optical vortices could benefit astronomical observations as well. In 2003, Harwit [12] made a theoretical work to associate optical vortex generation with the astronomical process. Further analysis of this information told additional properties of the stellar object. In 2011, Fabrizio et al. [13] made an observation of twisted light in rotating blackhole. Due to the rotational Doppler effect [14–16], it is advantageous in remote sensing, image restoration, super-resolution imaging, metrology, and so on [17–23]. Researchers found that due to the low diffraction limit, the vortex beam could replace the trivial Gaussian beam to improve the resolution of imaging, e.g., stimulated emission depletion, which can be of great use to biological and clinical medicine research [24]. Other recent applications in 2021 point to high-dimension OAM-entanglement, and phase-gradient protection was also reported [25–28]. Many other exciting applications with regard to optical vortices are yet to be found. Methods to characterize optical vortices have been developed including using interference fringes such as the Mach–Zehnder interferometer, or using diffraction methods such as by using a triangular aperture [29, 30].
Nevertheless, much like the lasers in its early stage of development, the widespread use of this twisted photon source requires it to cover a wide spectrum. Thankfully, nonlinear frequency conversion techniques have provided numerous possibilities to achieve this objective. This study summarizes some of the most prestigious vortex laser designs and their results. Frequency conversion techniques such as second harmonic generation (SHG), sum frequency generation (SFG), high-order harmonic generation (HHG), stimulated Raman scattering (SRS), and optical parametric oscillation (OPO) are investigated and presented as detailed as possible. Furthermore, some proposals will be put forward with respect to the problems that still need to be addressed.
Vortex Beam Generation
Optical vortex could refer to any beam with singularities and intrinsic OAM. For beams with OAM, wavefront dislocations are presented. In general term, the OAM beam could be written in the following expression:
The phase term is expressed as follows:
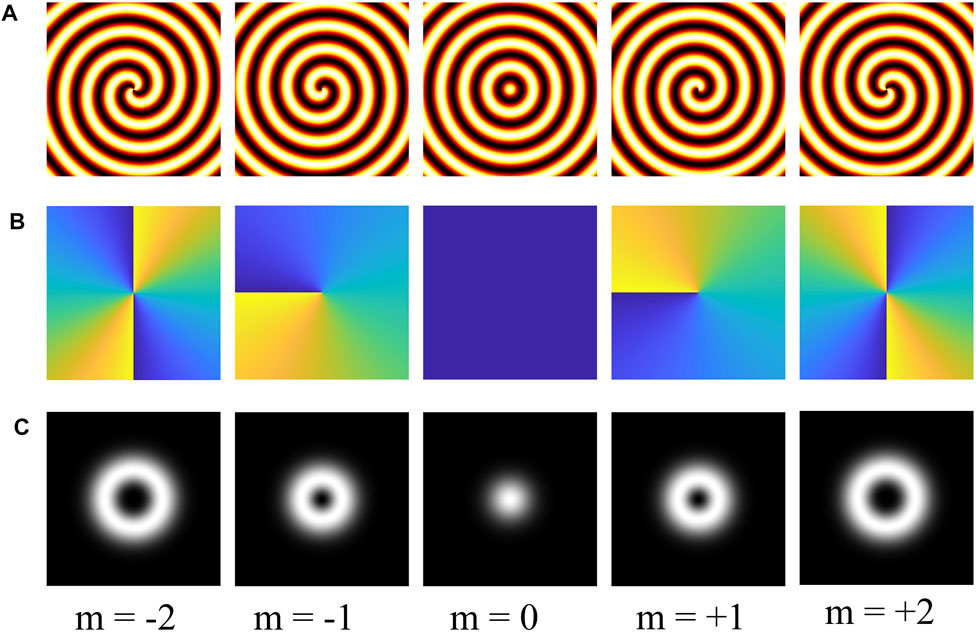
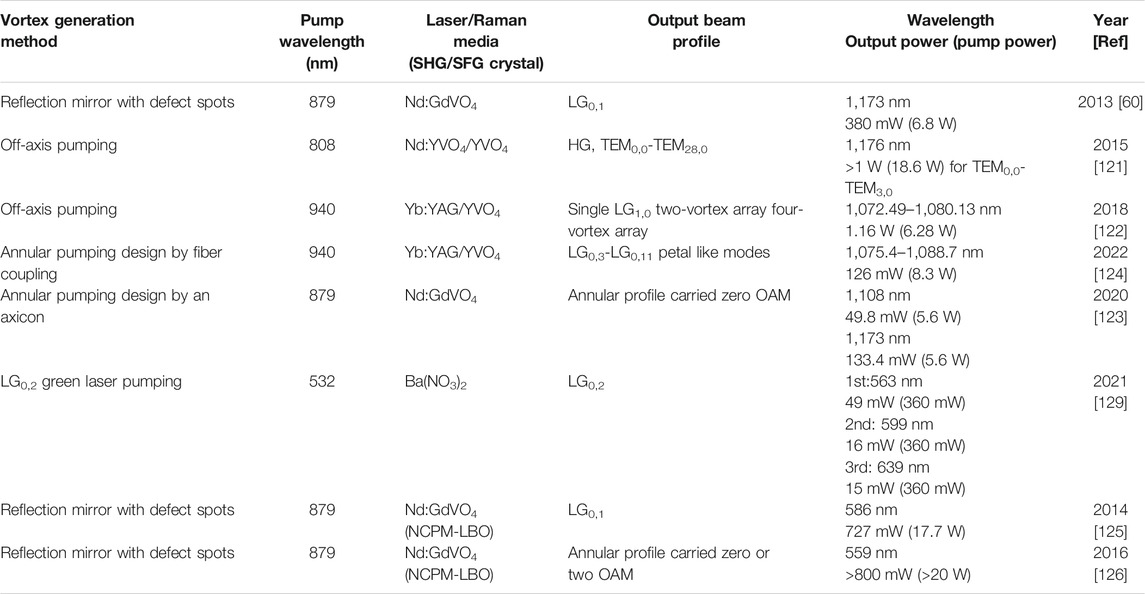
FIGURE 1. (A) Illustration of corkscrew wavefronts of a vortex beam (m = 2, 1, 0, −1, and −2, respectively); (B) the corresponding phase information of the vortex beam with the topological order m = 2, 1, 0, −1, and −2, respectively; (C) the corresponding intensity distribution profile of the vortex beam with topological order m = 2, 1, 0, −1, and −2.
Following the scalar Helmholtz equation under the paraxial condition gave a set of eigenmodes, such as Hermite–Gaussian, Laguerre–Gaussian, and Bessel. Conventional lasers are Gaussian beams TEM0,0. For high-order modes TEMm,n, m and n being the indices of x and y axes, the diffraction loss is severe. So to keep the lasing condition favorable for high-order modes, a certain mechanism to inhabit the fundamental transverse patterns is required.
Nowadays, several ways are already developed to obtain optical vortices. They can be categorized into two types—extra-cavity and intracavity. For extra-cavity, the most common way is forked pattern grating with a spatial light modulator [31, 32], digital macrodevices [33], etc. The spiral phase plate, q-plate, and metasurface materials can be used to produce vortex beam as well. For all the apparent benefits of these methods, they do have one fatal flaw—the lack of flexibility. Once manufactured, the operable range of these components was fairly limited. Even though tremendous efforts have been put to it, metasurface materials still have a long way to go. For the intracavity approach, which can directly produce optical vortices without additional components, the lay-out is usually configured very compact and robust when compared to the extra-cavity approach, reducing the cost for space, and hence reducing the spatial loss since there is no need of additional optical elements. Therefore, it is easier to obtain a beam with high beam quality. In light of these advantages, the intracavity method may be the apt choice for the production of vortex laser.
In general, the basic principle to directly produce such tailored optical fields is by breaking the lasing symmetry to enable the oscillator of high-order modes. The methods to produce intracavity OAM-carrying beams mainly include the following: annular pump, off-axis pump, reflection mirror with defect spots, and inserting lens with high spherical aberrations.
The annular pump approach is based on a central-null pumping configuration, which was usually obtained through axicons [34–37], capillary fiber [38–41], or center-punched mirror [42–46]. In 2017, Zhang et al [47] achieved a direct LG0,1 vortex output in a Yb:MgWO4 laser, which manifested handedness control without additional elements. In 2021, they realized a tunable topological charge as high as 18th with an axicon [48]. Off-axis pumping [49–55] is to achieve the asymmetric pumping condition, which can efficiently hinder the oscillation of low-order modes. It is realized mainly by tilting the crystal or shifting the position of the pump spot on the crystal. It tends to produce high-order Hermite–Gaussian (HG) modes and is in need of an additional astigmatism converter [56–58] to be transformed to the vortex mode. The defect spot approach [59–62] is to choose a defect mirror as the output coupler or as rear mirror. If the defect spot radius to mode radius is kept within a reasonable range, then the corresponding mode will be produced. Intracavity lens with short focus can introduce large spherical aberrations, which were said to be an effective mechanism for mode separation. Intracavity lens were yet another method [63–70]. Early in 2009, Senatsky et al. [63] realized circular LG0,m modes by inserting the intracavity lens. Recently in 2021, Wang et al. [69] developed this method by using a plano-concave cavity and a long-focus lens followed by a short focus lens. LG0,l doughnut beams were produced with l ranging from ±10 to ±33. Apart from a real lens, the thermal lensing effect could also be utilized for the same purpose, which were already explicitly demonstrated by Okida et al. in 2009 [65, 66] and 2011 [67].
These methods are constantly developing over the years. In Figure 2, we presented a summary concerning intracavity generation of vortex beams. Other unconventional approaches such as using volume Bragg grating and other diffractive elements have also been developed over these years [71–86]. Many reports have already performed a thorough review of the development of optical vortex lasers concerning its generation, tunability, and control of vortex handedness. In 2011, Sensky et al. [87] reviewed LG mode selection in diode-pumped solid-state lasers. In 2018, Wang et al. [88] gave a review on the progresses of optical vortex generation with a focus on the development of optical devices. In 2019, at the 30th anniversary since the start of the topic, Shen et al. [89] reviewed the advances of optical vortices and its many applications. In 2021, Fu et al. [90] reviewed the measurement of the OAM-spectrum and its application in various fields. These reviews have given the generation, tunability, and improvement of power performance of optical vortices, as well as the potential application, a thorough investigation. Nevertheless, another technique for filling in the wavelength gap is by nonlinear frequency conversion. In 2017, Omatsu et al. [91] and Lee at al [92] have respectively made reviews in this regard, with special attention to their work in this area. However, in the last 5 years, there have been many new achievements in nonlinear frequency conversion of OAM-carrying optical vortices. Therefore, in the following section, we will summarize latent results and introduce some of the most interesting phenomena during the nonlinear process. An extended discussion for their potential applications will also be given.
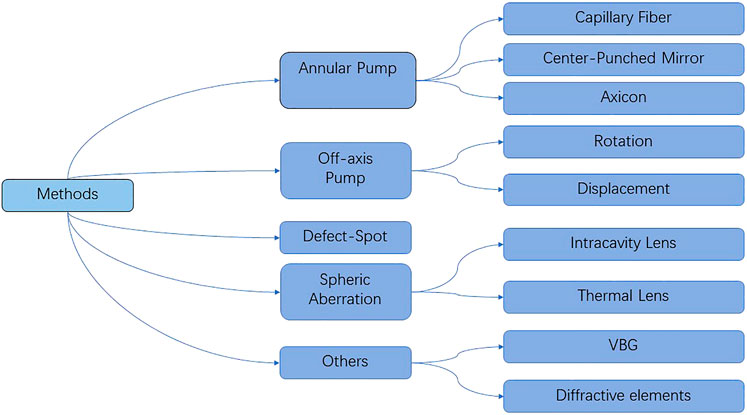
FIGURE 2. Generalization of various methods that gives rise to a direct vortex mode without extra-cavity components.
Frequency Conversion of Vortex Beams
The urgent need for the wide spreading applications of vortex lasers is to increase the wavelength versatility. For instance, in communication systems, 1.5 μm light can achieve low crosstalk. By detecting the OAM spectrum of a visible beam, contrast enhancement of imaging is possible.
SHG/SFG/HHG
In this section, details would cover the SHG, SFG, and HHG. SHG is a
As early as 1996, Padgett et al. [98], who were among the earliest pioneers who studied optical vortices, reported SHG of an LG mode vortex beam by deploying a pair of cylindrical lenses as the mode converter. The fundamental HG mode was converted into the LG mode which contains the OAM, at the work of the
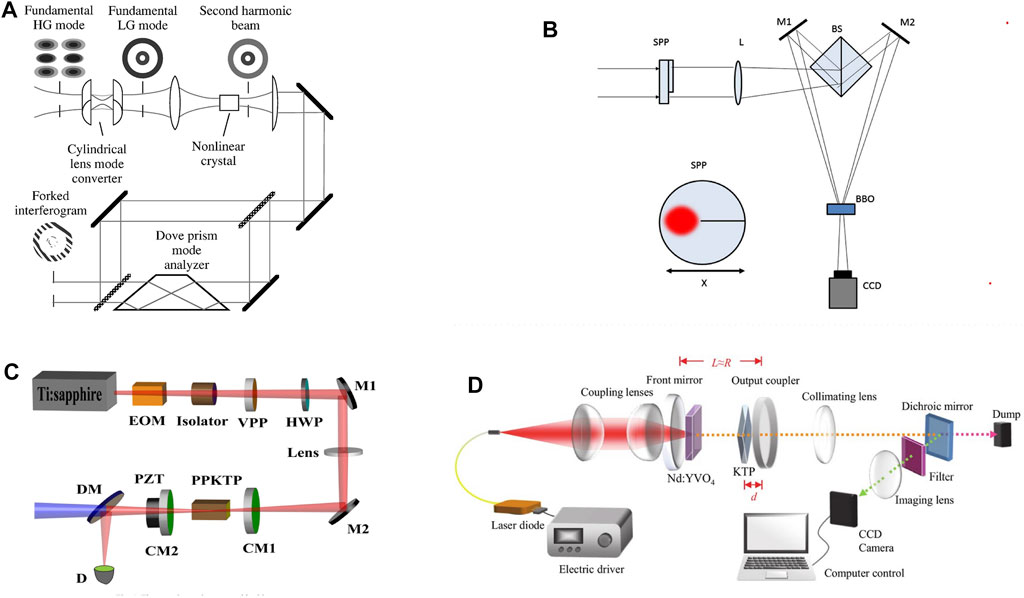
FIGURE 3. (A) SHG of the LG beam converted from a HG mode by a mode converter; [99] (B) Off-axis SHG where the topological charge was introduced by a half-integer spiral phase plate; [101] (C) quasi-phase-matched SHG of the vortex beam with a periodic-poled KTP [104]; (D) intra-cavity SHG of the bottle beam by an intra-cavity KTP [109].
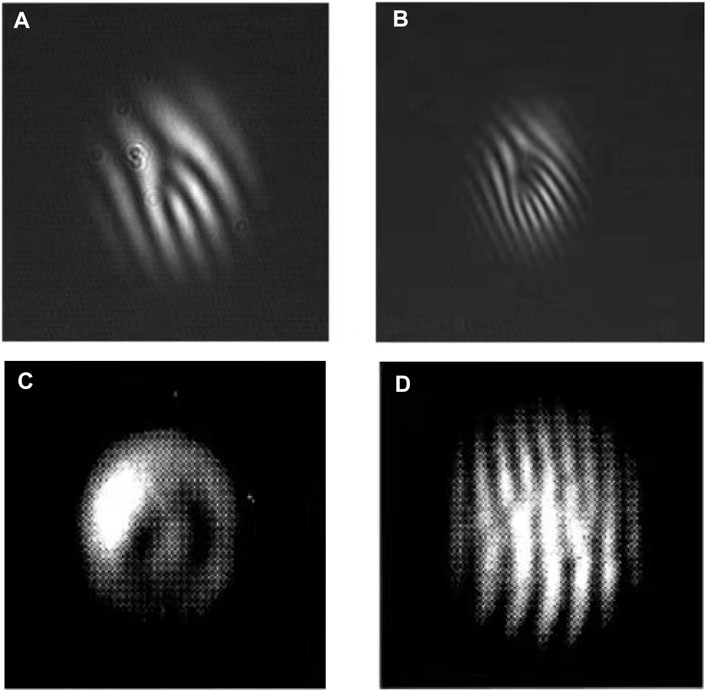
FIGURE 4. Forked interference fringes [99] of (A) fundamental wave (B) SHG wave; and (C) Spatial distribution and interference patterns (D) of the SHG wave with the influence of walk-off [100].
Photonic crystals were suggested to produce twisted light by Bloch in 2012 [102]. In 2014, Zhou et al. [103] conducted an SHG experiment using periodically poled KTP (PPKTP) and successfully produced an ultraviolet beam with the OAM higher to 100
In 2012, Ding et al. [107] experimentally displayed an infrared light with the OAM being up converted into visible light through four-wave-mixing via a ladder-type configuration in 85Rb atoms in a vapor cell. Two pump beams were imprinted with the OAM by a computer-generated hologram. Regardless of the different topological charges the two pump beam carries, all results remain identical apart from the conversion efficiency and the temperature of the vapor cell. In 2017, Zhao et al. [108] observed the frequency doubling effect of the topological charge with a composite vortex beam. A 2-f system was built while a laser at the wavelength 1,064 nm after alignment and magnification were separated by a beam split, then to form a composite vortex beam after passing through a vortex phase plate. Two beams were then converged to the KTP crystal for frequency doubling. A filter (T532nm > 85%, T1064nm < 1%) was used to filter out the fundamental light. They observed that for an input composite vortex, the frequency-doubled beam was also composite (coherent superposition of the pure LG mode). Tung et al. [109] also reported a frequency-doubled vortex beam in 2018, which they designated as the bottle beam. The experimental configuration is in Figure 3D. The KTP crystal was placed inside the fundamental cavity, with some small distance d from the output coupler. As d varied from 1.8 to 3 mm, the recorded transverse pattern changes drastically. The green bottle beam was generated with a narrow 3-D dark core. This suggested that shortening the distance between the SHG-crystal and the output coupler can be a possible route toward mode tunability. It was interesting to observe that while the wave remained perfectly a central-dark spatial profile in the near field, for the far field, it propagated; however, it resembles a circular beam with a shining spot in the middle. Such a beam was said to have a unique advantage when both the doughnut shaped beam and the ordinary Gaussian beam are required because they can be tailored, respectively.
In 2021, Gui et al. [110] demonstrated the SHG of a beam with spatiotemporal orbital angular momentum (ST-OAM). ST-OAM is a form of structured electromagnetic field recently identified. It features a space-time spiral phase structure and a transverse OAM which were perpendicular to the energy-density flow. They observed the modification of the OAM pulse by complex spatiotemporal astigmatism, in conjunction with multiple phase singularities. A 400-nm second-harmonic and an ST-OAM pulse with undetermined charge
In 2017, Gauther et al. [113] studied HHG for producing the XUV beam with tunable OAM. Their configuration is shown in Figure 5A, where a femtosecond pump beam at the wavelength of 805 nm is frequency-doubled by a BBO crystal; then, they were separated, and the
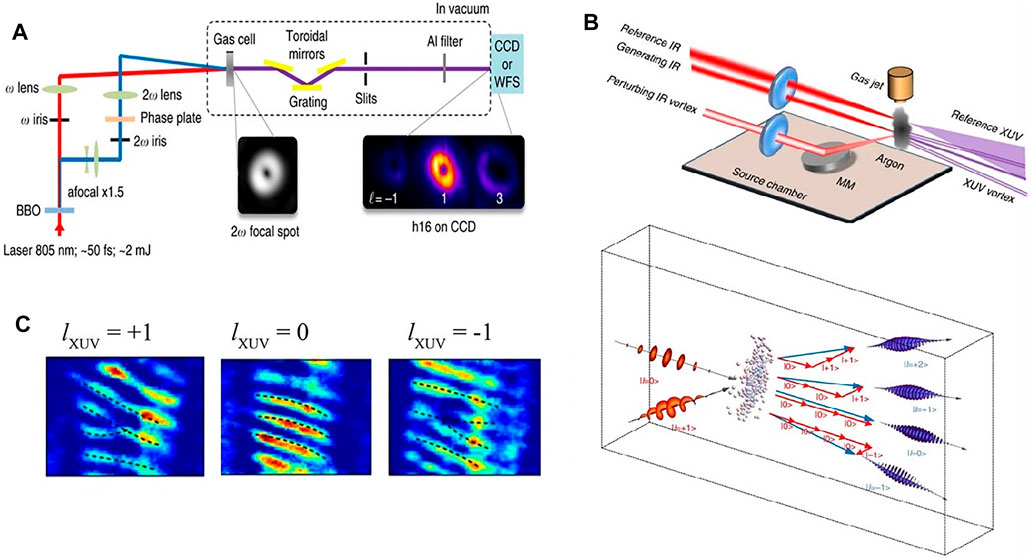
FIGURE 5. (A) HHG for XUV with tunable OAM [113] (B) HHG for extreme based on the Argon gas jet [114] (C) interferogram of (B) with a plane-wave as reference beam, recorded in the CCD camera.
Overall, we have summarized the important results concerning SHG, SFG, and HHG. First, extensive works have explicitly confirmed that during such process, the change of the topological charge abided by the laws of conservation. Second, the walk-off on frequency conversion with critical phase-matching leads to the collapse of vortex field distribution; therefore, the noncritical phase matching and quasi-phase matching crystals are excellent candidates for SHG/SFG of the vortex beam. Finally, SHG, THG, and HHG are efficient to obtain visible and ultraviolet beam with the OAM. For n-order high harmonic generation, if the OAM of the fundamental beam is 1, the HHG beam should naturally have
Stimulated Raman Scattering
Stimulated Raman Scattering, or SRS in short, is a third-order nonlinear effect. Many materials with Raman configuration were used for Stokes output, such as vanadates, tungstates, molybdates, and KTP family crystals [116–121]. Self-Raman experiments are most popular because it can ensure the compactness and attribute to versatile wavelength operation.
Vanadate laser crystals have a unique structure that enables the relatively low threshold output. In 2014, Lee et al. [60] used Nd:GdVO4 self-Raman to achieve the first Stokes line at 1,173 nm with the experimental configuration shown in Figure 6A, corresponding to the Raman shift of 882 cm−1. At the incident pump power of 6.8 W, the fundamental and the Stokes output were both produced with the output power at 400 and 380 mW, respectively. The LG0,1 mode was observed, and the transfer of its topological charge to the Stokes field was also recorded. The vortex output was attributed to the annular gain profile and the Fresnel diffraction loss by the defect spot mirror. To improve the compactness, a microchip laser might be the choice. In 2015, Lee et al. reported a YVO4/Nd:YVO4 self-Raman laser with off-axis pumping for the high-order Hermite–Gaussian beam generation. The HG mode order of the first Stokes wave can be up to TEM28,0. The output power was higher than 1.0 W from TEM0,0 to TEM3,0 at a pump power of 18.6 W [121]. In 2018, Dong et al. [122] designed a Raman microchip laser with the combination of the Yb:YAG and YVO4 crystals; the overall length was 2.2 mm. The corresponding design is shown in Figure 6B. The optical vortices realized by tilting the laser crystal with off-axis pumping geometry. Different frequency combs were obtained as the pump power increased, and it remained perfectly a doughnut-shaped intensity profile. The vortex characteristics were identified by using an interferogram. In 2020, Ma et al. [123] came up with the annular pumping scheme by an axicon. Figure 6C is a portrait of their experimental design. Nd: GdVO4 was used to serve both as the laser medium and the Raman medium. The annular beam output carried zero OAM for both the first Stokes of 1,108 nm and 1,173 nm were achieved. Figure 7 shows the spatial intensity profiles of the fundamental and Stokes waves, as well as the interferogram of the Stokes waves. Compared between the spatial intensity profiles of the fundamental and Stokes waves, obvious beam-cleaning phenomena could be observed. More recent, Miao et al. reported the petal-like Raman laser in a Yb:YAG/YVO4 microchip laser with annular pumped with the setup shown in Figure 6D. The LG0,n mode petal-like lasers with order of n tuning from 3 to 11 had been obtained. [124].
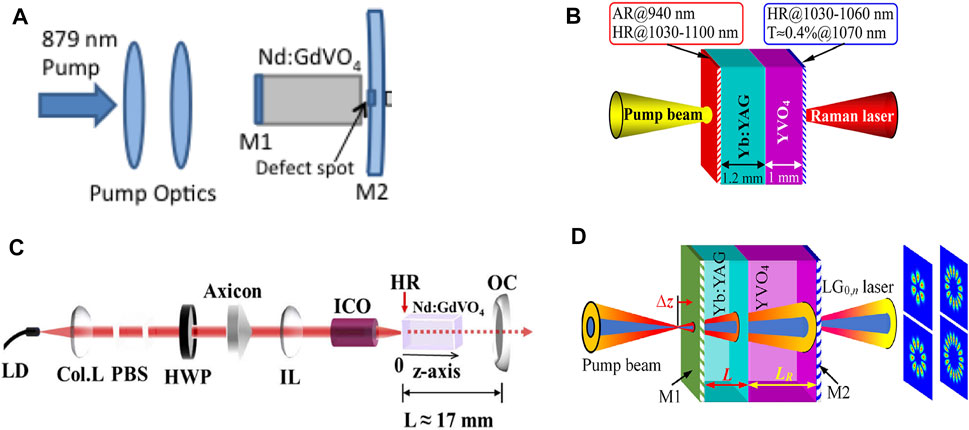
FIGURE 6. (A) Nd:GdVO4 self-Raman vortex laser with defect spot mirror for first Stokes output [60] (B) Yb:YAG/YVO4 microchip Raman vortex laser with off-axis pumping for the frequency-comb output [122] (C) Nd:GdVO4 self-Raman vortex laser with annular pumping design by an axicon for multi-Stokes output [123] (D) microchip Raman vortex laser based on annular pumping for LG0,n petal-mode generation [124].
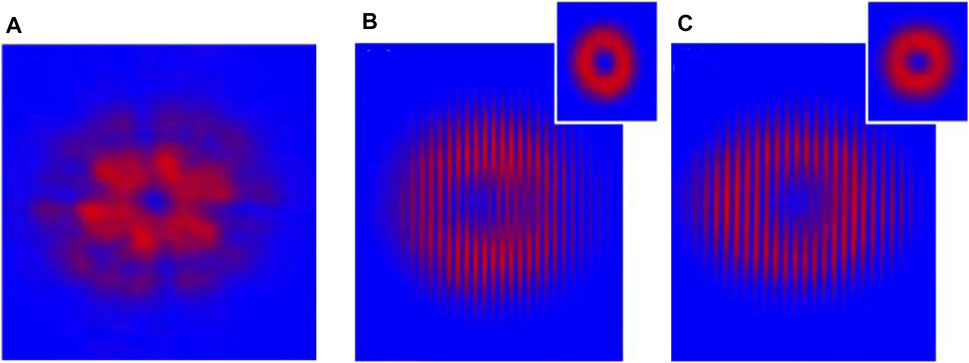
FIGURE 7. (A) Spatial profile of the fundamental beam; (B) spatial profile (top right) and the interference fringes of the 1,108 nm Stokes output; (C) spatial profile (top right) and the interference fringes of the 1,173 nm Stokes output [123].
The aforementioned self-Raman lasers had expanded the optical vortices in the near-infrared waveband. If the Raman combined with SHG and SFG, the optical vortices in the visible waveband also could be expanded. In 2014, Lee et al. [125] also combined this vortex Raman laser design with the LBO crystal for the SHG of both the fundamental and the first Stokes waves to produce the 532/586 nm laser. The experimental configuration is depicted in Figure 8A. Figure 9 shows the fork interferogram of the first Stokes wave and its SHG with yellow light. The OAM has been transferred to Stokes field in the Raman process and then doubled in the SHG process. In 2016, the SFG of the fundamental and the first Stokes wave for 559 nm vortex laser generation was also reported by his team [126] with the experimental configuration shown in Figure 8B. The jointing of self-Raman effects and an LBO crystal, along with the defect spot mirror cavity design, has enabled the multi-wavelength operation. If the wavelength selection mechanism based on vanadate crystals be introduced [127, 128], it will put forward the application of a selective multi-wavelength vortex laser. It is natural to include our future work in the areas of vortex Raman operation, particularly to introduce vortex characteristics into the visible band laser.
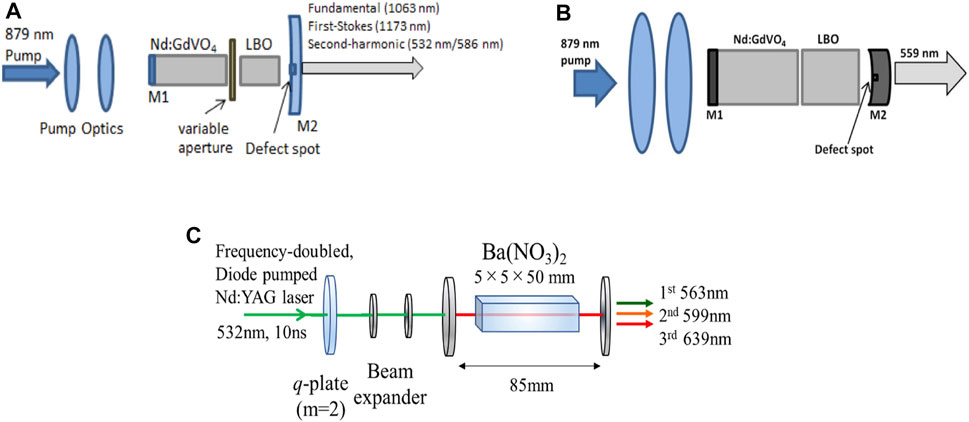
FIGURE 8. (A) SHG of Nd:GdVO4 self-Raman for 532/586 nm vortex output [125] (B) SFG of Nd:GdVO4 self-Raman for 559 nm vortex output [126] (C) cascaded Ba(NO3)2 Raman for 563/599/639 nm vortex output with extra-cavity configuration [129].

FIGURE 9. Forked interference fringes of (A) 1,173 nm Stokes fields and (B) SHG of the first Stokes (1,173 nm) for 586-nm yellow beam [125].
During the Raman process, it is evident to see that the transfer of a topological process occurs as a result of the superposition of fundamental modes, HG1,0, HG0, 1. It is modeled by Lee et al. [60] They also observed an interesting phenomenal for the SFG field: it possesses a +2 or 0 topological charge while an annular profile is retained in the near field but only to degrade into a bright spot in the far field. The SFG field was different in the near and far fields. They explained this because the SFG field was not resonated by the laser cavity and not an eigenmode of the resonator.
In addition to expanding visible optical vortices through SHG of the Raman laser, the cascade Raman excited by the 532 nm laser also had been reported to fill the gap in the visible waveband of optical vortices. In 2021, Omatsu et al. [129] realized the cascaded Raman output with a 5 mm × 5 mm×50 mm Ba(NO3)2 (Raman shift 1,046 cm-1). A 10 ns green pulse at wavelength 532 nm served as the pump beam. A topological charge of 2 was introduced to the pump via a q-plate. The design is shown in Figure 8C. Wavelengths of first, second, and third Stokes at 563 nm, 599 nm, and 639 nm, respectively, had been achieved.
Table 1 lists performance data of aforementioned experiments for Raman vortex generation. According to the research progress of the Raman vortex laser, intracavity Raman is popular and has been widely reported. Compact configuration can be easily achieved as the fundamental laser and the Raman output shared the same cavity. It is also concluded as follows: first, the topological charge used to transfer to the Stokes waves in the Raman process according to the published work. Second, the Raman vortex laser was ideal to maintain a better beam quality than the fundamental laser, due to the Raman beam cleanup effect. Third, stimulated Raman scattering and its combination with second-order nonlinear optical frequency conversion can expand the wavelength of vortex light in infrared and visible bands.
Optical Parametric Oscillator
Optical parametric oscillators, or OPO in short, are a useful nonlinear technique known for the application of tunable and mid-infrared laser generation [130–132]. For a given pump frequency
One interesting property to be investigated during an OPO process of a vortex beam is the possible mechanism for the topological charges to be transferred from the pump beam to the signal beam. In 1999, Maleev et al. [133] reported the violation of the conservation law for topological charge transfer in parametric down conversion. No further reports have followed that conclusion. Usually speaking, a
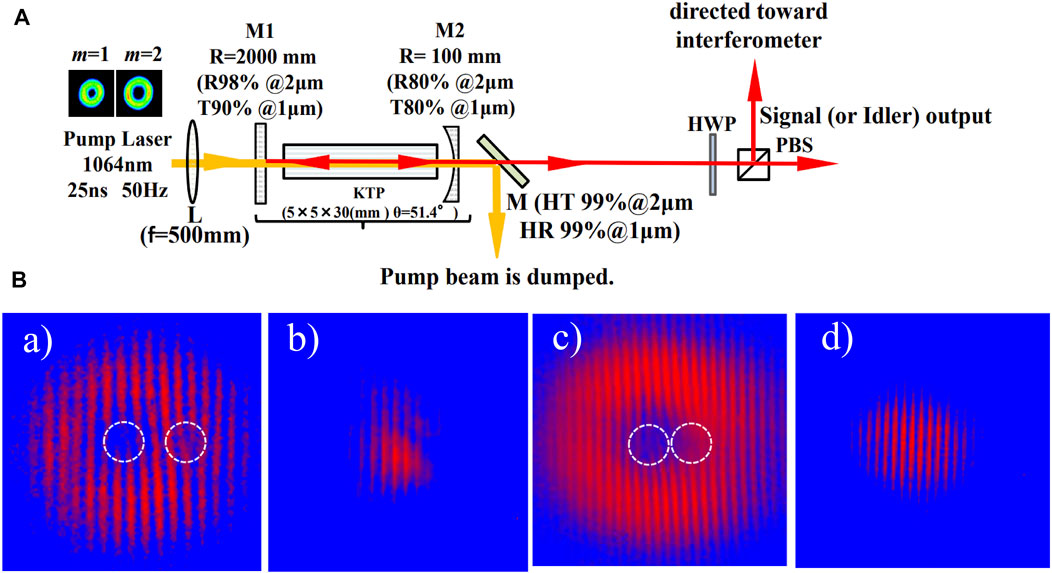
FIGURE 10. (A) Configurations of a 2-μm tunable optical parametric oscillator with vortex characteristics based on a KTP cut along θ = 51.4°; (B) a)∼d) interference fringes of a) signal wave and b) idler wave obtained when pumped by the first-order vortex beam; and c) signal wave and d) idler wave obtained when pumped by the second-order vortex beam. [134].
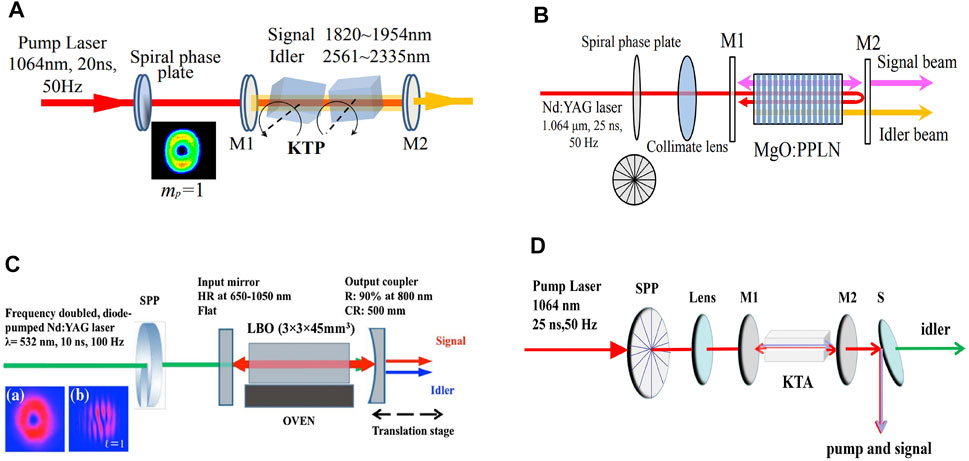
FIGURE 11. (A) setups of mid-infrared (6.3–12
Apart from compensating the walk-off effect with two cascaded crystals, the quasi-phase matching and non-critical phase matching without walk-off were widely used. For the quasi-phase matching, Yusufu et al. [136] reported a tunable vortex laser based on the parametric source with a periodically poled crystal MgO: PPLN. A 1064 nm Nd: YAG laser was chosen as the seed light, and a spiral phase plate was adopted for tailing the pump light into a vortex beam. They obtained the milli-joule-level 3 μm output (2.14 mJ maximum output with a conversion efficiency of 10.2%). They observed the transfer of the topological charge from the pump to the idler. The experimental configuration is shown in Figure 11B. In 2019, Sharma et al. [137] reported the vortex mode at order
For the non-critical phase matching, Mamuti et al. [140] reported the superposition of laser modes that carried orbital angular momentum by a parametric process with the use of NCPM-LBO, which is illustrated in Figure 11C The tunability of the topological charge was realized mainly by two mechanisms: 1) the shortening of the laser cavity provided a change in mode spatial overlapping, which caused the lasing conditions favorable for certain modes. 2) the non-critical phase matching not only avoided large the walk-off effect, but it also provided the favorable mode-overlapping condition; therefore, the tunable topological charges were realized at different frequencies. Depicted in Figure 12A is the spatial profile and the interference fringes of the signal and the idler wave from a compact cavity. The selective OAM transferred to either the signal or the idler was also realized simply by shortening the extended cavity. Since the mode radius at the plano-concave cavity changes while the cavity length extended, the spatial overlapping thus changes as well. This combined with the NCPM-LBO for tunable frequencies create a condition for separating the signal wave from the idler wave. When the cavity length was suited for the lasing condition of the signal or the idler wave, the topological charge will be transferred to it simultaneously. From Figure 11A a∼f) is the spatial profile, and the corresponding interference fringes of the signal wave at the lasing signal frequency of 930 nm; g)∼l) are the spatial profile and the corresponding interference fringes of the idler wave at frequency 1,243 nm. The tunable OAM ranging from
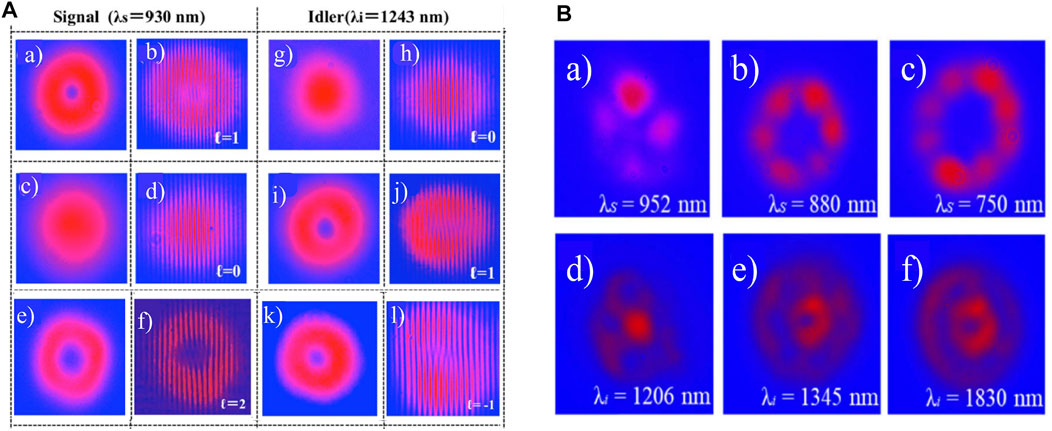
FIGURE 12. (A) a), c), and e) (the first row) are the spatial profiles of the signal wave with the topological charge to be
According to the above results, all the reported OPO vortex lasers were extra-cavity pumped. Compensating the walk-off effect with two cascaded crystals, quasi-phase matching crystals and non-critical phase-matching crystals were used to avoid the walk-off effect. More importantly is the selective transfer of the topological charge and the tunability of OAM and wavelength, which have been reported. OPO has been used for mid-infrared widely tunable laser generation. The high-order vortex beam and anisotropic transfer of the topological charge to signal and idler waves were possible in OPO with a reasonable design.
Summary and Outlook
To summarize, we presented introduction to the research on frequency conversion techniques for the optical vortices, such as sum frequency generation, scatted Raman scattering, and optical parametric oscillation for the expanding of wavelength versatility from the XUV region to the middle-infrared region. Some of those methods were found to be privy to real applications, such as the applications in free space communication, optical machining, and super-resolution imaging. Some important issues have reviewed including the topological transfer during nonlinear frequency conversion. During the SHG process, OAM is doubled. As for the high-order harmonics, if n is the order, l is the topological charge of the fundamental wave; then, the HHG wave should have a topological charge of
Furthermore, the development of the optical vortex, with particular respect to the tunability of its handedness and selective transfer of its topological charges, has made many applications possible. Although there have been sufficient studies on both the generation of optical vortices and the expanding of the tunable wavelength via techniques of nonlinear optics, most of them were driving by an extra-cavity vortex source. Intra-cavity direct generation approaching has not yet been able to produce an optical beam with sufficient power to surpass the yield. Further research should focus on pulse-sharpening via Q-switching or mode-locking [147]. An ultra-short optical vortex will prove more useful, in combination with nonlinear frequency conversion. The compactness needs to be improved as well. Future attention might be given to the combination of both intracavity optical vortex generation and the nonlinear frequency expansion for the efficient generation of tunable optical vortices in the wavelength, OAM value, and the helicities. The diffractive method for the efficient means of tailoring the optical field should also be considered and developed with an improved accuracy.
The purpose of this yet comprehensive review is to provide some clarity concerning the development of optical vortices and the corresponding frequency conversion techniques and the involved OAM transfer dynamics. We have summarized some of those key components and important results. Further research both computational and experimental should be conducted to achieve selective frequency-mixing, selective topological charge transfer, or the tunability of OAM-related properties.
Author Contributions
JL, YD, and HZ prepared the draft. All authors contributed to the discussion and revision of the manuscript. HZ was responsible for the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (62075167 and 61875199) and the Wenzhou Basic Scientific Research Project (G2020013).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Coullet P, Gil L, Lega J. Defect-mediated Turbulence. Phys Rev Lett (1989) 62:1619–22. doi:10.1103/physrevlett.62.1619
3. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/physreva.45.8185
4. He H, Friese MEJ, Heckenberg NR, Rubinsztein-Dunlop H. Direct Observation of Transfer of Angular Momentum to Absorptive Particles from a Laser Beam with a Phase Singularity. Phys Rev Lett (1995) 75(5):826–9. doi:10.1103/physrevlett.75.826
5. Sinclair G, Leach J, Jordan P, Gibson G, Yao E, Laczik ZJ, et al. Interactive Application in Holographic Optical Tweezers of a Multi-Plane Gerchberg-Saxton Algorithm for Three-Dimensional Light Shaping. Opt Express (2004) 12:1665–70. doi:10.1364/OPEX.12.001665
6. Zhao Y, Shapiro D, Mcgloin D, Chiu DT, Marchesini S. Direct Observation of the Transfer of Orbital Angular Momentum to Metal Particles from a Focused Circularly Polarized Gaussian Beam. Opt Express (2009) 17:23316–22. doi:10.1364/OE.17.023316
7. Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the Orbital Angular Momentum States of Photons. Nature (2001) 412(6844):313–6. doi:10.1038/35085529
8. Barreiro JT, Wei T-C, Kwiat PG. Beating the Channel Capacity Limit for Linear Photonic Superdense Coding. Nat Phys (2008) 4:282–6. doi:10.1038/nphys919
9. Fickler R, Campbell G, Buchler B, Lam PK, Zeilinger A. Quantum Entanglement of Angular Momentum States with Quantum Numbers up to 10,010. Proc Natl Acad Sci USA (2016) 113(48):13642–7. doi:10.1073/pnas.1616889113
10. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical Communications Using Orbital Angular Momentum Beams. Adv Opt Photon (2015) 7:66–106. doi:10.1364/AOP.7.000066
11. Yao AM, Padgett MJ. Orbital Angular Momentum: Origins, Behavior and Applications. Adv Opt Photon (2011) 3:161. doi:10.1364/aop.3.000161
12. Harwit M. Photon Orbital Angular Momentum in Astrophysics. ApJ (2003) 597(2):1266–70. doi:10.1086/378623
13. Tamburini F, Thidé B, Molina-Terriza G, Anzolin G. Twisting of Light Around Rotating Black Holes. Nat Phys (2011) 7:195–7. doi:10.1038/nphys1907
14. Zhang W, Gao J, Zhang D, He Y, Xu T, Fickler R, et al. Free-space Remote Sensing of Rotation at the Photon-Counting Level. Phys Rev Appl (2018) 10:044014. doi:10.1103/physrevapplied.10.044014
15. Qiu S, Liu T, Ren Y, Li Z, Wang C, Shao Q. Detection of Spinning Objects at Oblique Light Incidence Using the Optical Rotational Doppler Effect. Opt Express (2019) 27:24781–92. doi:10.1364/OE.27.024781
16. Emile O, Emile J, Brousseau C. Rotational Doppler Shift upon Reflection from a Right Angle Prism. Appl Phys Lett (2020) 116(22):221102. doi:10.1063/5.0009396
17. Qin H, Zhao W, Zhao W, Zhang C, Liu Y, Wang G, et al. Evaluation of Saturation Intensity Based on the FWHM of CW Stimulated Emission Depletion Microscopy. Optik (2018) 166:219–26. doi:10.1016/j.ijleo.2018.04.036
18. Liu X, Qiao S, Ma Y. Highly Sensitive Methane Detection Based on Light-Induced Thermoelastic Spectroscopy with a 2.33 µm Diode Laser and Adaptive Savitzky-Golay Filtering. Opt Express (2022) 30(2):1304–13. doi:10.1364/OE.446294
19. Ma Y, Hong Y, Qiao S, Lang Z, Liu X. H-shaped Acoustic Micro-resonator-based Quartz-Enhanced Photoacoustic Spectroscopy. Opt Lett (2022) 47(3):601–4. doi:10.1364/OL.449822
20. Zhuang YY, Zhang YJ, Zhu HY. Enhancing Near-Field Photolithography by Surface Plasmon Polaritons Excited from Negative-Refractive-index Nanofilms. J Russ Laser Res (2011) 32:120–4. doi:10.1007/s10946-011-9196-0
21. Fang C, Zhang Y, Zhu H. Optimizing the Optical Field Distribution of Near-Field SIL Optical Storage System Using Five-Zone Binary Phase Filters. Opt Commun (2012) 285:3042–5. doi:10.1016/j.optcom.2012.02.070
22. Ma Y, Hu Y, Qiao S, Lang Z, Liu X, He Y, et al. Quartz Tuning forks Resonance Frequency Matching for Laser Spectroscopy Sensing. Photoacoustics (2022) 25:100329. doi:10.1016/j.pacs.2022.100329
23. Liu X, Ma Y. Sensitive Carbon Monoxide Detection Based on Light-Induced Thermoelastic Spectroscopy with a Fiber-Coupled Multipass Cell [Invited]. Chin Opt Lett (2022) 20:031201. doi:10.3788/COL202220.031201
24. Moneron G, Medda R, Hein B, Giske A, Westphal V, Hell SW. Fast STED Microscopy with Continuous Wave Fiber Lasers. Opt Express (2010) 18:1302–9. doi:10.1364/OE.18.001302
25. Chen YF, Hsieh MX, Ke HT, Yu YT, Liang HC, Huang KF. Quantum Entanglement by a Beam Splitter Analogous to Laser Mode Transformation by a Cylindrical Lens. Opt Lett (2021) 46:5129–32. doi:10.1364/OL.439322
26. Chen Y, Wang J, Wang C, Zhang S, Cao M, Franke-Arnold S, et al. Phase Gradient protection of Stored Spatially Multimode Perfect Optical Vortex Beams in a Diffused Rubidium Vapor. Opt Express (2021) 29:31582–93. doi:10.1364/OE.439716
27. Asadpour SH, Kirova T, Qian J, Hamedi HR, Juzeliūnas G, Paspalakis E. Azimuthal Modulation of Electromagnetically Induced Grating Using Structured Light. Sci Rep (2021) 11:20721. doi:10.1038/s41598-021-00141-9
28. Sun Z, Xu B, Wu B, Wang X, Ying H. High Efficiency Focusing and Vortex Generator Based on Polarization-Insensitive Gallium Nitride Metasurface. Nanomaterials (2021) 11:2638. doi:10.3390/nano11102638
29. Hickmann JM, Fonseca EJS, Soares WC, Chávez-Cerda S. Unveiling a Truncated Optical Lattice Associated with a Triangular Aperture Using Light's Orbital Angular Momentum. Phys Rev Lett (2011) 105:053904. doi:10.1103/PhysRevLett.105.053904
30. de Araujo LEE, Anderson ME. Measuring Vortex Charge with a Triangular Aperture. Opt Lett (2011) 36:787–9. doi:10.1364/OL.36.000787
31. Ostrovsky AS, Rickenstorff-Parrao C, Arrizón V. Generation of the "perfect" Optical Vortex Using a Liquid-crystal Spatial Light Modulator. Opt Lett (2013) 38:534–6. doi:10.1364/OL.38.000534
32. Heckenberg NR, Mcduff R, Smith CP, White AG. Generation of Optical Phase Singularities by Computer-Generated Holograms. Opt Lett (1992) 17:221. doi:10.1364/OL.17.000221
33. Gong L, Ren Y, Liu W, Wang M, Zhong M, Wang Z, et al. Generation of Cylindrically Polarized Vector Vortex Beams with Digital Micromirror Device. J Appl Phys (2014) 116:183105. doi:10.1063/1.4901574
34. Arlt J, Dholakia K. Generation of High-Order Bessel Beams by Use of an Axicon. Opt Commun (2000) 177:297–301. doi:10.1016/s0030-4018(00)00572-1
35. Endo M. Generation of Doughnut-like Beams by Means of a W-Axicon Resonator with a Movable Axicon Element. Quan Electron Laser Sci Conf (2005) 2005:1591–3. doi:10.1109/QELS.2005.1549217
36. Bisson JF, Li J, Ueda K, Senatsky Y. Radially Polarized Ring and Arc Beams of a Neodymium Laser with an Intra-cavity Axicon. Opt Express (2006) 14:3304–11. doi:10.1364/OE.14.003304
37. Ma Y, Lee AJ, Pask HM, Miyamoto K, Omatsu T. Direct Generation of 1108 nm and 1173 nm Laguerre-Gaussian Modes from a Self-Raman Nd:GdVO4 Laser. Opt Express (2020) 28(16):24095–103. doi:10.1364/OE.400007
38. Kim JW, Mackenzie JI, Hayes JR, Clarkson WA. High Power Er:YAG Laser with Radially-Polarized Laguerre-Gaussian (LG01) Mode Output. Opt Express (2011) 19:14526–31. doi:10.1364/OE.19.014526
39. Kim DJ, Kim JW, Clarkson WA. High-power Master-Oscillator Power-Amplifier with Optical Vortex Output. Appl Phys B (2014) 117:459–64. doi:10.1007/s00340-014-5855-5
40. Kim DJ, Kim JW. Direct Generation of an Optical Vortex Beam in a Single-Frequency Nd:YVO4 Laser. Opt Lett (2015) 40:399–402. doi:10.1364/OL.40.000399
41. Lin D, Daniel JMO, Clarkson WA. Controlling the Handedness of Directly Excited Laguerre-Gaussian Modes in a Solid-State Laser. Opt Lett (2014) 39:3903–6. doi:10.1364/OL.39.003903
42. Zhao Y, Liu Q, Zhou W, Shen D. ∼1 mJ Pulsed Vortex Laser at 1645 nm with Well-Defined Helicity. Opt Express (2016) 24:15596. doi:10.1364/OE.24.015596
43. Liu Q, Zhang B, Qi S, Li Y, Fan X, Zhao Y, et al. Integration of Helicity-Control and Pulse-Modulation for Vortex Laser Based on a Black Phosphorus Plate. Opt Express (2016) 24:30031. doi:10.1364/OE.24.030031
44. Liu Q, Zhao Y, Zhou W, Shen D. Vortex Operation in Er:LuYAG crystal Laser at ∼1.6 μm. Opt Mater (2017) 71:31–4. doi:10.1016/j.optmat.2016.06.034
45. Ding M, Chen Y, Wang J, Yin D, Wang Y, Liu P, et al. 2.7 μm Optical Vortex Beam Directly Generated from an Er:Y2O3 Ceramic Laser. Opt Lett (2019) 44(20):4973–6. doi:10.1364/OL.44.004973
46. Chen Y, Ding M, Wang J, Wang L, Liu Q, Zhao Y, et al. High-energy 2 µm Pulsed Vortex Beam Excitation from a Q-Switched Tm:LuYAG Laser. Opt Lett (2020) 45(3):722–5. doi:10.1364/ol.384201
47. Lu J, Lin H, Zhang G, Li B, Zhang L, Lin Z, et al. Direct Generation of an Optical Vortex Beam from a Diode-Pumped Yb:MgWO4laser. Laser Phys Lett (2017) 14:085807. doi:10.1088/1612-202X/aa7878
48. Li K, Tang K, Lin D, Wang J, Li B, Liao W, et al. Direct Generation of Optical Vortex Beams with Tunable Topological Charges up to 18th Using an Axicon. Opt Laser Technol (2021) 143:107339. doi:10.1016/j.optlastec.2021.107339
49. Dong JS, Ma J, Ren YY, Xu G, Kaminskii A. Generation of Ince–Gaussian Beams in Highly Efficient, Nanosecond Cr, Nd: YAG Microchip Lasers. Laser Phys Lett (2013) 10(8):085803. doi:10.1088/1612-2011/10/8/085803
50. Lee CY, Chang CC, Cho CY, Tuan PH, Chen YF. Generation of Higher Order Vortex Beams from a YVO4/Nd:YVO4 Self-Raman Laser via off-Axis Pumping with Mode Converter. IEEE J Select Top Quan Electron. (2015) 21(1):318–22. doi:10.1109/jstqe.2014.2324754
51. Dong J, Bai S-C, Liu S-H, Ueda K-I, Kaminskii AA. A High Repetition Rate Passively Q-Switched Microchip Laser for Controllable Transverse Laser Modes. J Opt (2016) 18:055205. doi:10.1088/2040-8978/18/5/055205
52. Shen Y, Meng Y, Fu X, Gong M. Wavelength-tunable Hermite-Gaussian Modes and an Orbital-Angular-Momentum-Tunable Vortex Beam in a Dual-Off-axis Pumped Yb:CALGO Laser. Opt Lett (2018) 43(2):291–4. doi:10.1364/OL.43.000291
53. Huang X, Xu B, Cui S, Xu H, Cai Z, Chen L. Direct Generation of Vortex Laser by Rotating Induced off-Axis Pumping. IEEE J Select Top Quan Electron. (2018) 24(5):1601606. doi:10.1109/jstqe.2018.2814789
54. He H-S, Chen Z, Li H-B, Dong J. Low-threshold, Nanosecond, High-Repetition-Rate Vortex Pulses with Controllable Helicity Generated in Cr,Nd:YAG Self-Q-Switched Microchip Laser. Laser Phys (2018) 28:055802. doi:10.1088/1555-6611/aaad4c
55. Yuan Y, Tong L, Cai F, Zhang W, Cai Y, Zhao L. Direct Generation of Optical Vortex Arrays by Rotating in an All-Solid-State Yb:CALGO Laser. Opt Mater Express (2021) 11(6):1594–602. doi:10.1364/OME.425827
56. Beijersbergen MW, Allen L, van der Veen HELO, Woerdman JP. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt Commun (1993) 96(1):123–32. doi:10.1016/0030-4018(93)90535-D
57. Tung JC, Liang HC, Lu TH, Huang KF, Chen YF. Exploring Vortex Structures in Orbital-Angular-Momentum Beams Generated from Planar Geometric Modes with a Mode Converter. Opt Express (2016) 24(20):22796–805. doi:10.1364/OE.24.022796
58. Tung JC, Omatsu T, Liang HC, Huang KF, Chen YF. Exploring the Self-Mode Locking and Vortex Structures of Nonplanar Elliptical Modes in Selectively End-Pumped Nd:YVO_4 Lasers: Manifestation of Large Fractional Orbital Angular Momentum. Opt Express (2017) 25(9):22769–79. doi:10.1364/OE.25.022769
59. Ito A, Kozawa Y, Sato S. Generation of Hollow Scalar and Vector Beams Using a Spot-Defect Mirror. J Opt Soc Am A (2010) 27(9):2072–7. doi:10.1364/JOSAA.27.002072
60. Lee AJ, Omatsu T, Pask HM. Direct Generation of a First-Stokes Vortex Laser Beam from a Self-Raman Laser. Opt Express (2013) 21(10):12401–9. doi:10.1364/OE.21.012401
61. Qiao Z, Xie G, Wu Y, Yuan P, Ma J, Qian L, et al. Generating High-Charge Optical Vortices Directly from Laser up to 288th Order. Laser Photon Rev (2018) 12(8):1800019. doi:10.1002/lpor.201800019
62. Wang S, Zhao Z, Ito I, Kobayashi Y. Direct Generation of Femtosecond Vortex Beam from a Yb:KYW Oscillator Featuring a Defect-Spot Mirror. OSA Continuum (2019) 2(3):523–30. doi:10.1364/OSAC.2.000523
63. Senatsky Y, Bisson J-F, Shelobolin A, Shirakawa A, Ueda K. Circular Modes Selection in Yb:YAG Laser Using an Intracavity Lens with Spherical Aberration. Laser Phys (2009) 19(5):911–8. doi:10.1134/S1054660X09050028
64. Thirugnanasambandam MP, Senatsky Y, Ueda K-i. Generation of Radially and Azimuthally Polarized Beams in Yb:YAG Laser with Intra-cavity Lens and Birefringent crystal. Opt Express (2011) 19(3):1905. doi:10.1364/OE.19.001905
65. Okida M, Hayashi Y, Omatsu T, Hamazaki J, Morita R. Characterization of 1.06 μm Optical Vortex Laser Based on a Side-Pumped Nd:GdVO4 Bounce Oscillator. Appl Phys B (2009) 95(1):69–73. doi:10.1007/s00340-009-3438-7
66. Chard SP, Shardlow PC, Damzen MJ. High-power Non-astigmatic TEM00 and Vortex Mode Generation in a Compact Bounce Laser Design. Appl Phys B (2009) 97(2):275–80. doi:10.1007/s00340-009-3642-5
67. Okida M, Huang JY, Chen YF, Omatsu T. Controllable Direction Switching of Vortex Output in a Nd: YVO4 Bounce Laser. In: Conference on Lasers and Electro-Optics Europe and 12th European Quantum Electronics Conference (CLEO EUROPE/EQEC) (2011). p. 1. doi:10.1109/CLEOE.2011.5942477
68. Thirugnanasambandam MP, Senatsky Y, Ueda K-i. Generation of Radially and Azimuthally Polarized Beams in Yb:YAG Laser with Intra-cavity Lens and Birefringent crystal. Opt Express (2011) 19(3):1905–14. doi:10.1364/OE.19.001905
69. Wang M, Ma Y, Sheng Q, He X, Liu J, Shi W, et al. Laguerre-Gaussian Beam Generation via Enhanced Intracavity Spherical Aberration. Opt Express (2021) 29(17):27783–90. doi:10.1364/oe.436110
70. Omatsu T, Okida M, Lee A, Pask HM. Thermal Lensing in a Diode-End-Pumped Continuous-Wave Self-Raman Nd-Doped GdVO4 Laser. Appl Phys B (2012) 108(1):73–9. doi:10.1007/s00340-012-4919-7
71. Bisson J-F, Senatsky Y, Ueda K-I. Generation of Laguerre-Gaussian Modes in Nd:YAG Laser Using Diffractive Optical Pumping. Laser Phys Lett (2005) 2(7):327–33. doi:10.1002/lapl.200510008
72. Liu Q, Zhao Y, Ding M, Yao W, Fan X, Shen D. Wavelength- and OAM-Tunable Vortex Laser with a Reflective Volume Bragg Grating. Opt Express (2017) 25(19):23312–9. doi:10.1364/OE.25.023312
73. Geberbauer JWT, Kerridge-Johns WR, Damzen MJ. >30 W Vortex LG01 or HG10 Laser Using a Mode Transforming Output Coupler. Opt Express (2021) 29(18):29082–94. doi:10.1364/OE.432674
74. Otsuka K, Chu S-C. Generation of Vortex Array Beams from a Thin-Slice Solid-State Laser with Shaped Wide-Aperture Laser-Diode Pumping. Opt Lett (2009) 34(1):10–2. doi:10.1364/ol.34.000010
75. Tung JC, Hsieh YH, Omatsu T, Huang KF, Chen YF. Generating Laser Transverse Modes Analogous to Quantum Green's Functions of Two-Dimensional Harmonic Oscillators. Photon Res (2017) 5(6):733–9. doi:10.1364/PRJ.5.000733
76. Li N, Xu B, Cui S, Qiu X, Luo Z, Xu H, et al. High-Order Vortex Generation from CW and Passively Q-Switched Pr:YLF Visible Lasers. IEEE Photon Technol Lett (2019) 31(17):1457–60. doi:10.1109/lpt.2019.2931907
77. Chen YF, Lan YP, Wang SC. Generation of Laguerre-Gaussian Modes in Fiber-Coupled Laser Diode End-Pumped Lasers. Appl Phys B (2001) 72:167–70. doi:10.1007/s003400000433
78. Naidoo D, Aït-Ameur K, Brunel M, Forbes A. Intra-cavity Generation of Superpositions of Laguerre-Gaussian Beams. Appl Phys B (2012) 106:683–90. doi:10.1007/s00340-011-4775-x
79. Zhang W, Wei K, Huang L, Mao D, Jiang B, Gao F, et al. Optical Vortex Generation with Wavelength Tunability Based on an Acoustically-Induced Fiber Grating. Opt Express (2016) 24:19278–85. doi:10.1364/oe.24.019278
80. Shen Y, Ren G, Yang Y, Yao S, Xiao S, Jiang Y, et al. Generation of the Tunable Second-Order Optical Vortex Beams in Narrow Linewidth Fiber Laser. IEEE Photon Technol Lett (2017) 29(19):1659–62. doi:10.1109/lpt.2017.2742519
81. Liu Q, Zhao Y, Ding M, Yao W, Fan X, Shen D. Wavelength- and OAM-Tunable Vortex Laser with a Reflective Volume Bragg Grating. Opt Express (2017) 25:23312–9. doi:10.1364/OE.25.023312
82. Zhao Y, Wang T, Mou C, Yan Z, Liu Y, Wang T. All-Fiber Vortex Laser Generated with Few-Mode Long-Period Gratings. IEEE Photon Technol Lett (2018) 30(8):752–5. doi:10.1109/lpt.2018.2815041
83. Yan R, Li M, Li X, Zhao C, Zhou Y, Jiang Y. Vortex Laser Generation and Chirality Control in a LD End Pumped Nd:YVO4 Laser. Optik (2021) 236:166669. doi:10.1016/j.ijleo.2021.166669
84. Tian B, Yu J, Zhang B. A Method for Generating LG0l Vortex Beams with Tunable Topological Charges Based on Tube Lasers. Opt Commun (2021) 491:126939. doi:10.1016/j.optcom.2021.126939
85. Liu G, Fu S, Zhang X, Yin H, Li Z, Chen Z. Geometric Control of Vector Vortex Light Beams via a Linear Coupling System. Opt Express (2021) 29:30694–705. doi:10.1364/OE.435152
86. Srinivasa Rao A, Miike T, Miamoto K, Omatsu T. Direct Generation of 523 nm Orbital Poincaré Mode from a Diode-Pumped Pr3+:LiYF4 Laser with an off-axis Optical Needle Pumping Geometry. Opt Express (2021) 29:30409–18. doi:10.1364/OE.439491
87. Senatsky Y, Bisson J-F, Li J, Shirakawa A, Thirugnanasambandam M, Ueda K-i. Laguerre-gaussian Modes Selection in Diode-Pumped Solid-State Lasers. Opt Rev (2012) 19(4):201–21. doi:10.1007/s10043-012-0032-8
88. Wang X, Nie Z, Liang Y, Wang J, Li T, Jia B. Recent Advances on Optical Vortex Generation. Nanophotonics (2018) 7(9):1533–56. doi:10.1515/nanoph-2018-0072
89. Shen Y, Wang X, Xie Z, Min C, Fu X, Liu Q, et al. Optical Vortices 30 Years on: OAM Manipulation from Topological Charge to Multiple Singularities. Light Sci Appl (2019) 8:90. doi:10.1038/s41377-019-0194-2
90. Fu SY, Huang L, Lv YL, Gao CQ Advances on the Measurement of Orbital Angular Momentum Spectra for Laser Beams. Infrared Laser Eng (2021) 50(9):20210145. doi:10.3788/IRLA20210145
91. Omatsu T, Miyamoto K, Lee AJ. Wavelength-versatile Optical Vortex Lasers. J Opt (2017) 19:123002. doi:10.1088/2040-8986/aa9445
92. Lee AJ, Omatsu T. Direct Generation of Vortex Laser Beams and Their Non-linear Wavelength Conversion. Vortex Dyn Opt Vortices (2017) 2:57–82. doi:10.5772/66425
93. Duan Y-M, Zhou Y-M, Sun Y-L, Li Z-H, Zhang Y-J, Wang H-Y, et al. Frequency Doubling of Acousto-Optic Q-Switched Nd:YVO4 Cascaded Raman Laser for Narrow Pulse-Width 657 nm Laser. Acta Phys Sin (2021) 70:224209. doi:10.7498/aps.70.20210695
94. Chen S, Cheng M, Zhu H, Mao T, Zhang X, Zhou Q, et al. Orange, Yellow and green Emissions Generated in Q-Switched Nd:YALO3/YVO4 Raman Laser. J Lumin (2019) 214:116555. doi:10.1016/j.jlumin.2019.116555
95. Mao T, Duan Y, Chen S, Chen M, Zhang X, Zhou Q, et al. Yellow and Orange Light Selectable Output Generated by Nd:YAP/YVO4/LBO Raman Laser. IEEE Photon Technol Lett (2019) 31(13):1112–5. doi:10.1109/lpt.2019.2920145
96. Fang X, Kuang Z, Chen P, Yang H, Li Q, Hu W, et al. Examining Second-Harmonic Generation of High-Order Laguerre-Gaussian Modes through a Single Cylindrical Lens. Opt Lett (2017) 42:4387–90. doi:10.1364/OL.42.004387
97. Zhang Y, Duan Y, Wang Z, Zhang D, Zhang J, Zhang Y, et al. Continuous-Wave Widely Tunable MgO:PPLN Optical Parametric Oscillator with Compact Linear Cavity. IEEE Photon Technol Lett (2018) 30(20):1756–9. doi:10.1109/lpt.2018.2868736
98. Dholakia K, Simpson NB, Padgett MJ, Allen L. Second-harmonic Generation and the Orbital Angular Momentum of Light. Phys Rev A (1996) 54:R3742–R3745. doi:10.1103/physreva.54.r3742
99. Courtial J, Dholakia K, Allen L, Padgett MJ. Second-harmonic Generation and the Conservation of Orbital Angular Momentum with High-Order Laguerre-Gaussian Modes. Phys Rev A (1997) 56(5):4193–6. doi:10.1103/PhysRevA.56.4193
100. Berzanskis A, Matijosius A, Piskarskas A, Smilgevicius V, Stabinis A. Sum-frequency Mixing of Optical Vortices in Nonlinear Crystals. Opt Commun (1998) 150:372–80. doi:10.1016/S0030-4018(97)00591-9
101. Bovino FA, Braccini M, Giardina M, Sibilia C. Orbital Angular Momentum in Noncollinear Second-Harmonic Generation by off-axis Vortex Beams. J Opt Soc Am B (2011) 28:2806–11. doi:10.1364/JOSAB.28.002806
102. Bloch NV, Shemer K, Shapira A, Shiloh R, Juwiler I, Arie A. Twisting Light by Nonlinear Photonic Crystals. Phys Rev Lett (2012) 108(23):233902. doi:10.1103/PhysRevLett.108.233902
103. Zhou Z-Y, Ding D-S, Jiang Y-K, Li Y, Shi S, Wang X-S, et al. Orbital Angular Momentum Light Frequency Conversion and Interference with Quasi-phase Matching Crystals. Opt Express (2014) 22:20298–310. doi:10.1364/oe.22.020298
104. Zhou Z-Y, Li Y, Ding D-S, Zhang W, Shi S, Shi B-S, et al. Highly Efficient Second Harmonic Generation of a Light Carrying Orbital Angular Momentum in an External Cavity. Opt Express (2014) 22:23673–8. doi:10.1364/OE.22.023673
105. Xu Z, Lin Z, Ye Z, Chen Y, Hu X, Wu Y, et al. Control the Orbital Angular Momentum in Third-Harmonic Generation Using Quasi-Phase-Matching. Opt Express (2018) 26:17563–70. doi:10.1364/OE.26.017563
106. Wang H, Wei D, Xu X, Wang M, Cui G, Lu Y, et al. Controllable Generation of Second-Harmonic Vortex Beams through Nonlinear Supercell Grating. Appl Phys Lett (2018) 113:221101. doi:10.1063/1.5050423
107. Ding D-S, Zhou Z-Y, Shi B-S, Zou X-B, Guo G-C. Linear Up-Conversion of Orbital Angular Momentum. Opt Lett (2012) 37:3270–2. doi:10.1364/OL.37.003270
108. Zhao YL, Li FS, Qiu XD, Zhang WH, Lu QH, Chen LX Frequency Doubling Effect of Topological Charge of Composite Vortex in Frequency Doubling Process. Laser Optoelectron Prog (2017) 54:051901. doi:10.3788/LOP54.051901
109. Tung JC, Ma YY, Miyamoto K, Chen YF, Omatsu T. Bottle Beam Generation from a Frequency-Doubled Nd:YVO4 Laser. Sci Rep (2018) 8:16576. doi:10.1038/s41598-018-34783-z
110. Gui G, Brooks NJ, Kapteyn HC, Murnane MM, Liao C-T. Second-harmonic Generation and the Conservation of Spatiotemporal Orbital Angular Momentum of Light. Nat Photon (2021) 15:608–13. doi:10.1038/s41566-021-00841-8
111. Li H, Liu H, Chen X. Nonlinear Generation of Airy Vortex Beam. Opt Express (2018) 26:21204–9. doi:10.1364/OE.26.021204
112. Liu Y, Chen W, Tang J, Xu X, Chen P, Ma CQ, et al. Switchable Second‐Harmonic Generation of Airy Beam and Airy Vortex Beam. Adv Opt Mater. (2021) 9(4):2001776. doi:10.1002/adom.202001776
113. Gauthier D, Ribič PR, Adhikary G, Camper A, Chappuis C, Cucini R, et al. Tunable Orbital Angular Momentum in High-Harmonic Generation. Nat Commun (2017) 8:14971. doi:10.1038/ncomms14971
114. Kong F, Zhang C, Bouchard F, Li Z, Brown GG, Ko DH, et al. Controlling the Orbital Angular Momentum of High Harmonic Vortices. Nat Commun (2017) 8:14970. doi:10.1038/ncomms14970
115. Fan X, Liang H-J, Shan L-Y, Yan B, Gao Q-H, Ma R, et al. Extreme Ultraviolet Polarization Vortex Beam Based on High Harmonic Generation. Acta Phys Sin (2020) 69:044203. doi:10.7498/aps.69.20190834
116. Ma Y, Yu X, Li X. Performance Improvement in a Directly 879 nm Dual-End-π-Polarized-Pumped CW and Pulsed GdVO4/Nd:GdVO4 Laser. Appl Opt (2012) 51(5):600–3. doi:10.1364/AO.51.000600
117. Zhang L, Duan Y, Mao X, Li Z, Chen Y, Zhang Y, et al. Passively Q-Switched YVO4 Raman Operation with 816 and 890 cm−1 Shifts by Respective Raman Configurations. Opt Mater Express (2021) 11:1815–23. doi:10.1364/OME.427483
118. Duan Y, Zhang J, Zhu H, Zhang Y, Xu C, Wang H, et al. Compact Passively Q-Switched RbTiOPO4cascaded Raman Operation. Opt Lett (2018) 43:4550–3. doi:10.1364/OL.43.004550
119. Duan Y, Zhu H, Wang H, Zhang Y, Chen Z. Comparison of 115 Μm Nd:YAG\KTA Raman Lasers with 234 and 671 cm−1 Shifts. Opt Express (2016) 24:5565–71. doi:10.1364/OE.24.005565
120. Pask HM. The Design and Operation of Solid-State Raman Lasers. Prog Quan Electron (2003) 27(1):3–56. doi:10.1016/S0079-6727(02)00017-4
121. Lee CY, Chang CC, Cho CY, Tuan PH, Chen YF. Generation of Higher Order Vortex Beams from a YVO4/Nd:YVO4 Self-Raman Laser via off-Axis Pumping with Mode Converter. IEEE J Sel Top Quan Electron (2015) 21(1):318–22. doi:10.1109/JSTQE.2014.2324754
122. Dong J, Wang X, Zhang M, Wang X, He H. Structured Optical Vortices with Broadband Comb-like Optical Spectra in Yb:Y3Al5O12/YVO4 Raman Microchip Laser. Appl Phys Lett (2018) 112:161108. doi:10.1063/1.5024051
123. Ma Y, Lee AJ, Pask HM, Miyamoto K, Omatsu T. Direct Generation of 1108 nm and 1173 nm Laguerre-Gaussian Modes from a Self-Raman Nd:GdVO4 Laser. Opt Express (2020) 28(16):24095–103. doi:10.1364/OE.400007
124. Miao Y, Zhang L, Dong J. Broadband Petal‐Like Raman Laser. Annalen der Physik (2022) 2022:2100476. doi:10.1002/andp.202100476
125. Lee AJ, Zhang C, Omatsu T, Pask HM. An Intracavity, Frequency-Doubled Self-Raman Vortex Laser. Opt Express (2014) 22:5400–9. doi:10.1364/OE.22.005400
126. Lee AJ, Pask HM, Omatsu T. A Continuous-Wave Vortex Raman Laser with Sum Frequency Generation. Appl Phys B (2016) 122:64. doi:10.1007/s00340-016-6334-y
127. Duan Y, Zhou Y, Zhu H, Li Z, Jin X, Tang D. Selective Frequency Mixing in a Cascaded Self-Raman Laser with a Critical Phase-Matched LBO crystal. J Lumin (2022) 244:118698. doi:10.1016/j.jlumin.2021.118698
128. Duan Y, Sun Y, Zhu H, Mao T, Zhang L, Chen X. YVO4 Cascaded Raman Laser for Five-Visible-Wavelength Switchable Emission. Opt Lett (2020) 45:2564–7. doi:10.1364/OL.392566
129. Nishigata Y, Sasaki S, Miyamoto K, Omatsu T. Cascaded Vector Vortex Mode Generation from a Solid-State Raman Laser. Appl Opt (2021) 60:10638–42. doi:10.1364/AO.443596
130. Duan Y, Zhang J, Guo J, Zhu H, Zhang Y, Xu C, et al. Potassium Titanyl Arsenate Based Cascaded Optical Parametric Oscillator Emit at 2.5µm Derived by Neodymium-Doped Yttrium Lithium Fluoride Laser. JPN J Appl Phys (2018) 57:040304. doi:10.7567/JJAP.57.100311
131. Zhu H, Duan Y, Wang H, Shao Z, Zhang Y, Zhang G, et al. Compact Nd:YAlO3/RbTiOPO4 Based Intra-Cavity Optical Parametric Oscillator Emit at 1.65 and 3.13 µm. IEEE J Sel Top Quan Electron (2015) 21(1):1600105. doi:10.1109/jstqe.2014.2302352
132. Duan Y, Zhu H, Ye Y, Zhang D, Zhang G, Tang D. Efficient RTP-Based OPO Intracavity Pumped by an Acousto-Optic Q-Switched Nd:YVO_4 Laser. Opt Lett (2014) 39(5):1314–7. doi:10.1364/OL.39.001314
133. Maleev ID, Deykoon AM, Swartzlander GA, Soskin MS, Sergienko AV. Violation of Conservation of Topological Charge in Optical Down Conversion. Technical Digest. In: Summaries of Papers Presented at the Quantum Electronics and Laser Science Conference (1999). p. 99. doi:10.1109/QELS.1999.807359
134. Yusufu T, Tokizane Y, Yamada M, Miyamoto K, Omatsu T. Tunable 2-μm Optical Vortex Parametric Oscillator. Opt Express (2012) 20:23666–75. doi:10.1364/OE.20.023666
135. Furuki K, Horikawa M-T, Ogawa A, Miyamoto K, Omatsu T. Tunable Mid-infrared (6.3-12 μm)optical Vortex Pulse Generation. Opt Express (2014) 22:26351–7. doi:10.1364/OE.22.026351
136. Yusufu T, Niu S, Tuersun P, Tulake Y, Miyamoto K, Omatsu T. Tunable 3 Μm Optical Vortex Parametric Oscillator. Jpn J Appl Phys (2018) 57:122701. doi:10.7567/JJAP.57.122701
137. Sharma V, Aadhi A, Samanta GK. Controlled Generation of Vortex and Vortex Dipole from a Gaussian Pumped Optical Parametric Oscillator. Opt Express (2019) 27:18123–30. doi:10.1364/OE.27.018123
138. Tong H, Xie G, Qiao Z, Qin Z, Yuan P, Ma J, et al. Generation of a Mid-infrared Femtosecond Vortex Beam from an Optical Parametric Oscillator. Opt Lett (2020) 45:989–92. doi:10.1364/ol.388096
139. Sharma V, Chaitanya Kumar S, Samanta GK, Ebrahim-Zadeh M. Tunable, High-Power, High-Order Optical Vortex Beam Generation in the Mid-infrared. Opt Express (2022) 30:1195–204. doi:10.1364/OE.443345
140. Mamuti R, Araki S, Nishida S, Miyamoto K, Omatsu T. Tunable Near-Infrared Optical Vortex Parametric Laser with Versatile Orbital Angular Momentum States. Appl Opt (2018) 57:10004–8. doi:10.1364/AO.57.010004
141. Mamuti R, Goto S, Miyamoto K, Omatsu T. Generation of Coupled Orbital Angular Momentum Modes from an Optical Vortex Parametric Laser Source. Opt Express (2019) 27:37025–33. doi:10.1364/OE.27.037025
142. Ababaike M, Wang S, Aierken P, Omatsu T, Yusufu T. Near and Mid-infrared Optical Vortex Parametric Oscillator Based on KTA. Sci Rep (2021) 11:8013. doi:10.1038/s41598-021-86945-1
143. Zhu H, Duan Y, Feng Z, Zhang G, Xu C, Zhang Y, et al. Generation of 2-µm Light Based on a Noncritical Phase Matching OPO Technique. IEEE Photon Technol Lett (2013) 25(7):690–3. doi:10.1109/lpt.2013.2247395
144. Duan Y, Zhu H, Xu C, Ruan X, Cui G, Zhang Y, et al. Compact Self-Cascaded KTA-OPO for 2.6 μm Laser Generation. Opt Express (2016) 24:26529–35. doi:10.1364/OE.24.026529
145. Zhu H, Guo J, Duan Y, Zhang J, Zhang Y, Xu C, et al. Efficient 1.7 μm Light Source Based on KTA-OPO Derived by Nd:YVO_4 Self-Raman Laser. Opt Lett (2018) 43:345–8. doi:10.1364/OL.43.000345
146. Murray JT, Austin WL, C. Powell R. Intracavity Raman Conversion and Raman Beam Cleanup. Opt Mater (1999) 11(4):353–71. doi:10.1016/S0925-3467(98)00033-0
Keywords: optical vortex, solid-state laser, frequency conversion, orbital angular momentum, Laguerre–Gaussian
Citation: Liu J, Duan Y, Li Z, Zhang G and Zhu H (2022) Recent Progress in Nonlinear Frequency Conversion of Optical Vortex Lasers. Front. Phys. 10:865029. doi: 10.3389/fphy.2022.865029
Received: 29 January 2022; Accepted: 14 February 2022;
Published: 07 March 2022.
Edited by:
Yufei Ma, Harbin Institute of Technology, ChinaCopyright © 2022 Liu, Duan, Li, Zhang and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haiyong Zhu, aHl6aHUub3B0QGdtYWlsLmNvbQ==
†These authors have contributed equally to this work and share first authorship
 Jie Liu
Jie Liu Yanmin Duan1†
Yanmin Duan1† Haiyong Zhu
Haiyong Zhu