Neural Network Model Based on the Tensor Network for Audio Tagging of Domestic Activities

1 Introduction

The world is facing the problem of population aging. It is estimated that by 2050, the number of people over 64 years will exceed 20% of the world’s population. According to the survey, 40% of the elderly will live alone at home [1]. This will lead to many social problems, such as the increase in diseases and healthcare costs, the shortage of nursing staff, and the increase in the number of people unable to live independently. Therefore, it is imperative to develop ambient intelligence-assisted living tools to help the elderly live independently at home [2]. The first task is to detect what is happening at home. Audio tagging is very suitable when the visual data are unavailable due to the interference from light and the environment. Audio tagging associate tags with the audio and identifies the events that generate the audio. Audio tagging of domestic activities has important applications in smart home robots, monitoring of domestic activities, and the lives of the elderly [3]. For the problem of audio tagging, Gong [4] proposed PSLA, a collection of model-agnostic training techniques. It includes ImageNet pre-training, balanced sampling, data augmentation, label augmentation, and model aggregation. The results we obtained outstripped the best previous systems. Puy [5] proposed a model based on separable convolutions, which uses separable convolutions in channel, time, and frequency dimensions to control the complexity of the network and achieved good results in terms of effect and complexity. The widely used dataset for audio signals is DCASE (Detection and Classification of Acoustic Scenes and Events). DCASE 2018 Challenge Task 5 [6] is specifically used for audio tagging for domestic activities. This tagging task provides the development and validation datasets and baseline system and requires identifying nine classes of events in domestic activities within 10-s clips. The audio data are collected by four linearly arranged microphones. There are many ways to process microphone array audio, among which Wang [7] proposed a modeling method that uses the channel mode, time mode, and frequency mode as the three dimensions to construct a three-dimensional tensor space, which has achieved good results. In the tensor completion method proposed by Yang [8], tensor modeling of multi-channel audio signals with the missing data has achieved good results.

Among the submitted systems in DCASE 2018 Challenge Task 5, the baseline system of this task trains a single classifier model that takes a single channel as the input. The learner in the baseline system is based on a neural network architecture using convolutional and dense layers. As input, log Mel-band energies are provided to the network for each microphone channel separately [9]. Inoue [10] put forward a combination method of a data-enhanced front-end module and a back-end module based on the CNN classification method. First, it enhances the input data by shuffling and mixing the sound clips. Its data enhancement method helped increase the variation of training samples and reduce the impact of unbalanced datasets. Then, the input of the CNN, as a classifier, is the log-Mel spectrogram of the enhanced data. The system proposed by Tanabe [11] is a combination of the front-end modules based on blind signal processing and the back-end modules based on machine learning. The front-end modules employ blind dereverberation and blind source separation. They use spatial cues without machine learning to avoid overfitting. The back-end modules employ one-dimensional convolutional neural network (1DCNN)-based architecture and VGG16-based architecture for the individual front-end modules. All of the probability outputs are ensembled. In addition, through mix-up-based data augmentation, overfitting is avoided in the back-end modules. TC2DCNN [12] is extended by operating the convolutions along the two dimensions of time and channel, not along the frequency axis, since similar patterns in different frequency bands do not necessarily belong to the similar audio event. INRC_2D [13] combines a deep neural network with a scattering transform. Each audio segment is first represented by two layers of scattering transform. The four denoised transforms of each of the two layers are combined together. Each of the fused layers is processed in parallel by two neural network (NN) architectures, RESNET, and a long short-term memory (LSTM) network, with a joint fully connected layer. The VGGish model proposed by Kong [14], which has an AlexNetish 8-layer CNN with global max pooling, has achieved good results.

The tensor network is a sparse data structure designed for the efficient representation and manipulation of the ultra-high dimensional data to achieve better interpretability of the data. It is similar to the kernel method in machine learning [15]. Through feature mapping, the original linearly inseparable data are converted to a high-dimensional space. In this space, a hyperplane can be linearly separable. But the number of parameters will be very large. Tensor train decomposition (also called the matrix product state) is a kind of tensor decomposition specifically for high-dimensional data. Wang [16] uses tensor train decomposition in a compressed HRTF, which is closer to the original HRTF than other methods. Therefore, tensor train decomposition is used to approximate the tensor networks. Matrix product state is the first tensor network to be discovered and used, which can be efficiently used in the simulation of the ground state of an infinite one-dimensional system. In recent years, tensor networks based on matrix product states have shown good performance in classification. For example, Stoudenmire [17] encoded the MNIST data into a tensor network, and the tensor network was trained to obtain the probability of each class to complete the classification. Efthymiou [18] proposed a new contraction method for Fashion-MNIST, which realizes the parallel compression of the horizontal edges, and then the vertical compression, which further accelerates the training speed. Selvan [19] proposed a lonet tensor network, which overcomes the shortcomings of the MPS tensor network, that is, the loss of spatial correlation when used for large resolutions. It is used for the two-dimensional classification of medical images and has achieved good results. While achieving good results, compared with other models, the GPU usage is significantly lower than that of the other models. PEPS [20] is a two-dimensional extension of the matrix product state. Although it has achieved great success, its algorithmic complexity is much higher than that of the matrix product state. MERA [20] is an experimental state of the ground state of a one-dimensional quantum system, which is inherently scale-invariant. In the MERA, tensors are connected to reproduce the holographic geometry. There are also other kinds of tensor network structures which have higher complexity than the MPS and can be used in other applications such as applied mathematics, chemistry, physics, machine learning, and many other fields.

In the article, a neural network model based on the tensor network is proposed for audio tagging of domestic activities. This article draws on the research results of the simplest and most mature matrix product state in the tensor network, hoping to achieve a balance between the complexity and effectiveness of the network model. An end-to-end tensor network-based neural network model is constructed and trained with the Mel spectrograms. After going through the convolutional layers, important features are extracted. Then, the MPS tensor network further extracts the features and gives the tagging results. This can not only achieve good tagging results but also compresses the network through tensor train decomposition, which has a smaller number of parameters than the traditional CNN. The F1-score is used to evaluate the performance of the proposed method. In terms of tagging performance, the performance of the proposed model is compared with other models. Compared with the results of the development dataset and the validation dataset of DCASE 2018 challenge task 5, the proposed method achieved better results. This article is a beneficial attempt to combine the tensor networks and neural networks and can also be extended to other deep learning sound signal processing fields.

The rest of this article is organized as follows: Section 2 introduces the neural network model based on the tensor network proposed in this article in detail. Section 3 introduces the parameter settings and experimental results of the proposed method, which are analyzed in terms of precision, recall, and F1-score, respectively. This article is concluded in Section 4.

2 Neural Network Model Based on Tensor Network

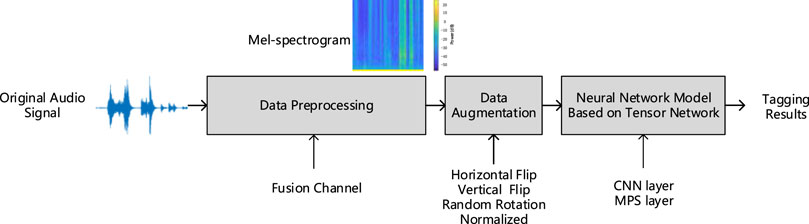
As the experimental flowchart shows in Figure 1, the proposed audio tagging method consists of three main stages, namely, data preprocessing, data augmentation, and neural network model based on the tensor network. Data preprocessing first performs channel fusion [21] on the audio, then takes the log after FFT, and then the Mel spectrogram is obtained by mapping the Mel frequency.

FIGURE 1

FIGURE 1. Flow chart of audio tagging.

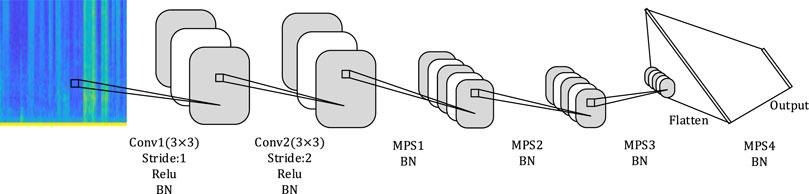
The structure of the neural network model based on the tensor network is shown in Figure 2. Convolutional layers are used for extracting deeper feature representations. Important spatial structure and time information will be retained in the middle MPS layers. Finally, the retained information enters the MPS decision layer after being flattened to obtain the audio tagging results.

FIGURE 2

FIGURE 2. Structure of the neural network model based on the tensor network.

2.1 Data Preprocessing and Augmentation

The Mel spectrogram as the audio feature of the original signal is used in the proposed method. The Mel spectrogram converts the ordinary frequency scale of the spectrogram into the Mel frequency scale. After framing, the fbank feature is extracted through the Mel filter bank [22]. The energy value distribution range is summarized and is then linearly corresponded to blue-yellow [23]. In this article, 128 triangular filters are used to form a Mel filter bank, which corresponds to the objective law that the higher the frequency, the duller the human ear is.

Data augmentation uses horizontal flip, vertical flip, and random rotation to enlarge the training data, avoid overfitting, and enhance the robustness of the model.

2.2 Neural Network Model Based on the Tensor Network

2.2.1 CNN Feature Extraction

CNN [24] is used to process the multi-dimensional data, such as the two-dimensional images with many channels. CNN uses shared weights, local connections, pooling, and other layers to organize the attributes of natural signals. The convolutional layer, ReLU layer, and pooling layer are the most commonly used CNN layers.

The basic purpose of the convolutional layer is to determine the local connections between the features and map their information to a specific feature map. The convolution of the input $I$ with filter $F\in {\mathbf{R}}^{2a_1+2a_2}$ is given as follows:

${\left(I\mathrm{\ast }F\right)}_{n,m}={\displaystyle \sum _{k=-a_1}^{a_1}{\displaystyle \sum _{l=-a_2}^{a_2}{F}_{k,l}{I}_{n-k,m-l}}},(1)$

where $a_1$ and $a_2$ determine the size of the convolution kernel along the x and y directions. ReLU $(g\left(z\right)=\max (0,z))$ [25] is a non-linear function which is applied to feature mapping created by the convolutional layer. The BN [26] layer normalizes each mini batch throughout the entire network, reducing the internal covariate shift caused by the progressive transforms. The BN layer is used to reduce the training time of the CNN and the sensitivity of network initialization. Therefore, this layer is used for normalization in the proposed network model.

2.2.2MPS Tensor Network

The tensor network notation is a brief graphical representation of the high-dimensional tensors. It not only makes it easier and more intuitive to process the high-dimensional tensors but also provides an insight into how to achieve more efficient operations. For a more comprehensive introduction to the tensor networks, references in [27]can be referred.

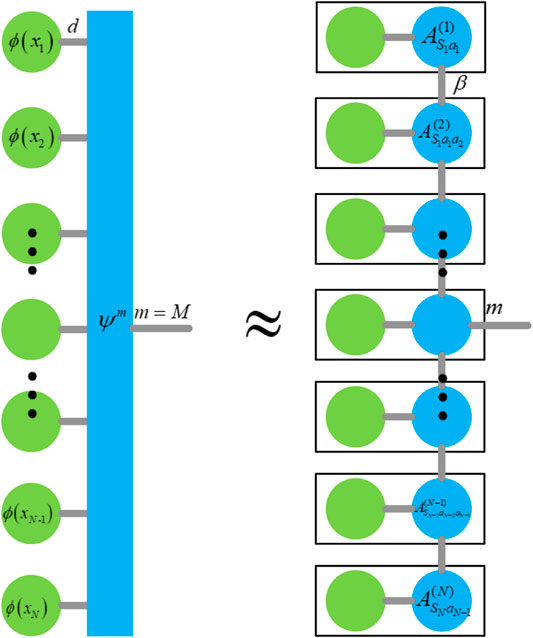
The MPS (matrix product state) [17, 18] is a one-dimensional tensor network structure, which is based on tensor train decomposition [28]. It uses chain-connected small tensors to represent the high-dimensional tensors.

For a neural network model based on the tensor network, the generated Mel spectrograms must first be mapped to the high-dimensional space corresponding to the tensor network. According to Eq. 2, each pixel of the Mel spectrogram is mapped to a two-dimensional space.

$|x_n^{\left[l\right]}\rangle =\cos \frac{x_n^{\left[l\right]}\pi }{2}|0\rangle +\sin \frac{x_n^{\left[l\right]}\pi }{2}|1\rangle ,(2)$

where $|\rangle$ is the Dirac symbol in physics, representing the state vector. $|0\rangle$ means blue with low energy, and $|1\rangle$ means yellow with high energy, where $l$ represents the order of the Mel spectrogram, and $n$ represents the pixel order in the Mel spectrogram. The function with cos(πx/2) and sin(πx/2) is one of the mapping methods. After inputting the spectrogram, the data of each pixel are normalized to be between 0 and 1; using cos(πx/2) and sin(πx/2) can accurately represent the information in the pixel. After mapping, $|x_n^{\left[l\right]}\rangle$ can represent all the magnitudes of energy in the Mel spectrogram. After all the pixels are mapped, Mel spectrograms can be expressed as Eq. 3 and also be expressed as Eq. 4 using the tensor network notation.

$|X^{\left[l\right]}\rangle =|x_1^{\left[l\right]}\rangle \otimes |x_2^{\left[l\right]}\rangle \otimes \mathrm{...}\otimes |x_N^{\left[l\right]}\rangle ,(3)$

$\mathbf{\Phi }\left(x\right)=\mathbf{\varphi }\left(x_1\right)\otimes \mathbf{\varphi }\left(x_2\right)\otimes \mathrm{...}\otimes \mathbf{\varphi }\left(x_N\right),(4)$

where $\otimes$ represents the tensor product. $x$ represents the Mel spectrogram of each input, and $N$ is the total number of pixels in the Mel spectrogram. $\mathit{\varphi }\left(x_1\right)$ is the representation of the first pixel in the Mel spectrogram mapped to a two-dimensional space, and $\Phi \left(x\right)$ is the high-dimensional mapping form of the Mel spectrogram. Given the high-dimensional features, for the input Mel spectrogram, the decision function of the event tagging can be expressed as

$f^m\left(x\right)={\mathit{\psi }}^m\cdot \mathbf{\Phi }\left(x\right),(5)$

$m=\arg \max f^m\left(x\right).(6)$

Here, $m$ represents M categories, $m=\left[\mathrm{0,1},\mathrm{...},M-1\right]$, where ${\mathit{\psi }}^m$ is the trainable weight tensor. The model of the decision module in audio tagging is shown on the left of Figure 3 and in Eq. 5. ${\mathit{\psi }}^m$ is a weight tensor, and its dimension is as high as $M\cdot 2^N$, which is difficult to be calculated. After decomposing ${\mathit{\psi }}^m$ into the chained small tensors through the MPS, the two-dimensional space that can be mapped with each pixel can be contracted with the weight tensor ${\mathit{\psi }}^m$. In this way, the calculation can only be carried out between the small tensors, without directly calculating the weight tensors with high dimensionality. Figure 3 is a linear model of the decision module in audio tagging represented by the tensor network notation. For details on the tensor network notation, reference in [27]can be referred. As shown by the small green tensor in Figure 3, $\mathrm{\Phi }\left(x\right)$ is the form in which the two-dimensional space mapped by each pixel is connected to the weight tensor ${\mathit{\psi }}^m$. The nodes in the first column are the pixels of each Mel spectrogram after being mapped to the two-dimensional space. They are connected to the weight tensor obtained after the training. There is an index $m$ on the right side of ${\mathit{\psi }}^m$, whose dimension is the number of the final tagging classes.

FIGURE 3

FIGURE 3. Linear model of the decision module in audio tagging.

This mapping method will result in a huge number of parameters in the weight tensor. The matrix product state is the name for tensor train decomposition in physics. It approximates a large tensor to the product form of several second-order and third-order tensors. In this way, the contraction can be performed in the way on the right side of Figure 3, to avoid the direct calculation of the ultra-high dimensional tensor, and the calculation amount will be greatly reduced. A high-dimensional tensor $T$ is decomposed into an approximate tensor $\stackrel{\sim }{T}$ by the tensor train [28], as shown in Eq. 7.

$\stackrel{\sim }{T}={\displaystyle \sum _{a_1{a}_2\mathrm{...}{a}_{N-1}}{A}_{S_1{a}_1}^{\left(1\right)}}{A}_{S_1{a}_1{a}_2}^{\left(2\right)}\mathrm{...}{A}_{S_{N-1}{a}_{N-2}{a}_{N-1}}^{\left(N-1\right)}{A}_{S_N{a}_{N-1}}^{\left(N\right)}.(7)$

The weight tensor ${\mathit{\psi }}^m$ is approximated by the product form of some two-dimensional and three-dimensional tensors according to Eq. 7. The approximated weight tensor is shown in Eq. 8 and on the right of Figure 3.

${\mathit{\psi }}^{m,i_1,i_2,\mathrm{...},i_N}={\displaystyle \sum _{{\alpha }_1,{\alpha }_2,\mathrm{...}{\alpha }_N}{A}_{{\alpha }_1}^{i_1}}{A}_{{\alpha }_1{\alpha }_2}^{i_2}{A}_{{\alpha }_2{\alpha }_3}^{i_3}\mathrm{...}{A}_{{\alpha }_j{\alpha }_{j+1}}^{m,i_j}\mathrm{...}{A}_{{\alpha }_N}^{i_N},(8)$

where$A$ is the decomposed second-order and third-order tensors. The subscript $i_j$ is called the free index, and the free index $m$ corresponds to the right side of Figure 3, and its dimension is the number of tagging classes. The subscript $a_j$ is an auxiliary indicator, and its dimension is called the bond dimension, which controls the quality of the approximation. The size of the bond dimension determines the size of the tensor. The components of the tensor $A$ are the variational parameters determined through the training.

2.2.3 Local Orderless Operation

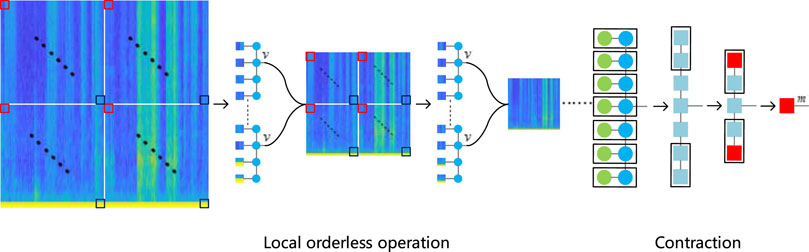
Since MPS is a one-dimensional tensor network, the neighboring pixels in the spectrogram are usually highly correlated. Therefore, directly flattening and inputting the Mel spectral feature into the MPS layer will cause the loss of spatial information. Spatial information includes the information of a single frame in the vertical direction, as well as the information between the frames in the horizontal direction, which is very important for audio tagging. In order to solve this problem, the local orderless operation according to the local orderless theory is used in the tensor network [29, 30]. The local orderless operation divides a large patch into many small patches. After the small patches are contracted, the dimension of the output vector is $\mathit{v}$ , and $\mathit{v}$ is set to the same size as the bond dimension. This step can be interpreted as using a vector of dimension $\mathit{v}$ to represent small patches of information, similar to feature extraction. Each small patch contains global features, which can better preserve the spatial information.

First, the Mel spectrogram is divided into four parts, as shown in Figure 4. The first pixel of each part is taken out and combined into a $2\times 2$ local orderless small patch, as shown in the red box in Figure 4. Then, the pixels of each part are combined according to this step, until the last pixel in the black box, as shown in Figure 4. The pixel order in the patch is shown in Eq. 9.

${{\rm P}}^K=\left(\begin{array}{c}\mathit{K},\mathit{K}+\frac{\mathrm{W}}{2}\\ K+\frac{\mathrm{H}\times \mathrm{W}}{2},K+\frac{\left(\mathrm{H}+1\right)\times \mathrm{W}}{2}\end{array}\right)\forall K=1,\mathrm{...},\left(\mathrm{H}\times \mathrm{W}\right)/4,(9)$

where $P^K$ represents the local orderless small patch, the superscript K represents the sequential number of small patches, and H and W represent the height and width of the Mel spectrogram, respectively.

FIGURE 4

FIGURE 4. Local orderless operation and contraction.

Then the small patches are flattened and input into the MPS layer to contract. Then all the output vectors $\mathit{v}$ are reshaped into images. The converted graph has a smaller resolution than the previous Mel spectrogram, but the important information will be preserved. This operation is repeated on the converted image. After the three MPS layers, the resolution of the generated image is already very small, but the features and spatial information of the original Mel spectrogram are well-preserved.

2.2.4 Contraction and Optimization

After the three MPS layers of contraction, a small size image has been generated. It has spatial structure information and important features of the Mel spectrogram. It is flattened into the last MPS layer, as shown in Figure 4. In line with the implementation method from the MPS in Miller [31], the horizontal edges are first contracted in parallel to get the contracted tensors, and then, these tensors are contracted vertically. The output is generated by connecting the free indicators of the tensor. A recent work has proposed a more effective calculation method [32, 33], which is expected to further accelerate the calculation speed.

3 Experiments

3.1 Datasets

In the experiment, development and validation datasets of DCASE 2018 challenge task 5 are used to evaluate the audio tagging for domestic activities. DCASE 2018 challenge task 5 is a derivative of the SINS dataset. It contains a continuous recording of one person living in a holiday home over a period of 1 week. It was collected using a network of 13 microphone arrays distributed over the entire home. The microphone array consisted of four linearly arranged microphones. For this task, seven microphone arrays are used in the living room and kitchen area combined. The continuous recordings are split into audio segments of 10 s. These audio segments are provided as individual files along with the ground truth. The dataset contains 72,984 audio files. Each audio segment contains four channels. It is organized with nine class labels consisting of absence, cooking, dishwashing, eating, social activity, vacuum cleaning, watching TV, and working. The audio files are recorded with 16 kHz sampled frequency, and the number of files in each class are not the same.

3.2 Evaluation Method

In this experiment, the development dataset and validation dataset are divided into the training set, validation set, and test set with a ratio of 8:1:1, respectively. The evaluation criteria include the precision rate, recall rate, and F1-score. Precision is the ratio of real positive samples to samples that are predicted to be positive, which is specific to the predicted samples. Recall is the ratio of the correct predictions to the positive cases in the sample, which is specific to the actual samples. The F1 score is calculated based on recall and precision. The experimental results in this article are the results of the development and the validation datasets in the divided test set, respectively. These criteria are obtained by calculating the confusion matrix given by Eqs 10–12.

$\mathit{Pr}ecision=\frac{TP}{TP+FP},(10)$

$\mathit{Re}call=\frac{TP}{TP+FN},(11)$

$F1-Score=\frac{2\times \mathit{Pr}ecision\times \mathit{Re}call}{\mathit{Pr}eci\mathrm{si}on+\mathit{Re}call}=\frac{2TP}{2TP+FP+FN},(12)$

where TP is the number of true positive results, TN is the number of true negative results, FP is the number of false positive results, and FN is the number of false negative results.

3.3 Experimental Setup and Result

There are four channels $(C_1,C_2,C_3,C_4)$ within one audio signal. The four channels are manually averaged [21] to yield $C_5$, where $C_5=(C_1+C_2+C_3+C_4)/4$ so as to better fuse the four channels and augment the dataset. The audio signal is converted to a Mel spectrogram, as described in Section 2. The window type, window size, overlap, and FFT size parameters are set to Hamming, 480, 240, and 480, respectively. The Hamming window is adopted for signal framing as it can effectively overcome the leakage phenomenon [34]. The dimension of the Mel spectrogram is $336\times 336\times 3$ as the input of the neural network model based on the tensor network, which is composed of the two convolutional layers and four MPS layers. It is then the horizontal flip, vertical flip, and random rotation that enlarge the training data, avoid overfitting, and enhance the robustness of the model. The batch size is set to 256, bond dimension is set to 5, and the initial learning rate is 0.001. The optimizer and loss function used in the training are Adam and cross-entropy loss function. The structure of the neural network model based on the tensor network is shown in Figure 2, and the states of TP, TN, FP, and FN in the test set of the development dataset are shown for each class on the confusion matrix in Figure 5.

FIGURE 5

FIGURE 5. Confusion matrix for the test set of the development dataset.

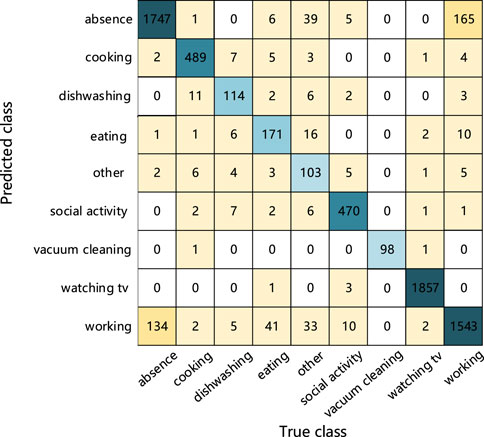
As can be seen from the confusion matrix in Figure 5, the abscissa is the true class, and the ordinate is the predicted class. The blue square indicates that the predicted class is the same as the true class. The color intensity corresponds to the number of audio tagging. It can be found from Figure 5 that the proposed model judges 165 working audios as absence and 134 absence audios as working. Because people may make very small noises at work, it is easy to confuse it with the absence class. In addition, the model judges 39 and 33 other class audios as absence and working class, and many labels for other class audios cannot be distinguished since the other class is not a class of specific activities. There are many types of features extracted from the other class audio, and the common features of other class are difficult to learn. As a result, a lot of audio signals are near the decision boundary, and it is easy to be misjudged as absence, working, and eating. But for the prediction results, it can be found from Figure 5 that the prediction results for the other class are more accurate, proving the better learning ability of the tensor network model.

In order to compare with other models more intuitively, other performance criteria including precision, recall, and F1-score are separately given in Table 1 for each class of DCASE 2018 challenge task 5. It can be seen from the Table 1 that the precision rate of the other class is much higher than the recall rate. This shows that the prediction of the other class is more accurate, but many other class audios are prone to judgment errors. Since the other class is not a class of specific activities, the tensor network can better learn the common features of the class. But for the other class audio with less commonality, it is less possible to identify the deeper rules.

TABLE 1

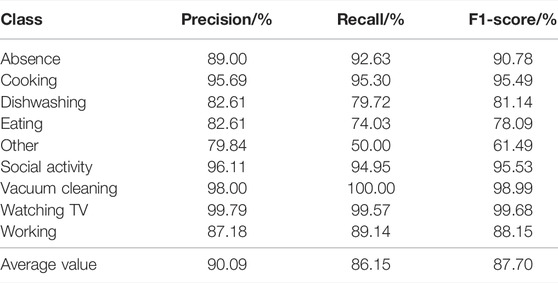
TABLE 1. Neural network model based on the tensor network performance criteria in the test set of the development dataset.

Table 2 is a comparison between the proposed model and other models, which represent several typical and commonly used networks, including the CNN, RESNET, and LSTM. This experiment selected the three models to compare with the neural network model based on tensor network (NNMBTN) model, namely, the baseline system [9], TC2DCNN [12], and INRC_2D [13]. The baseline system uses a neural network architecture based on the convolutional layers and dense layers. TC2DCNN is extended by operating the convolutions along the two dimensions of time and channel. INRC_2D is processed in parallel by RESNET and long short-term memory (LSTM) network, with a fully joint connected layer.

TABLE 2

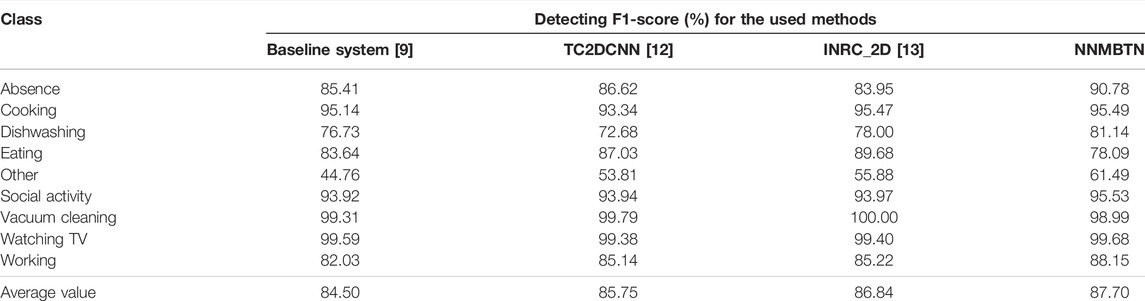
TABLE 2. Comparison of the neural network model based on the tensor network with other models in the test set of the development dataset.

It can be seen from Table 2 that the F1-score of the proposed method on the test set of the DCASE 2018 challenge task 5 development set is 87.70%, which is 3.2% higher than the baseline system, 1.95% higher than the TC2DCNN system, and 0.86% higher than INRC_2D system. The proposed method has five classes that are higher than the baseline, TC2DCNN, and INRC_2D. This shows that the tensor network model can identify the important features well after obtaining the features extracted by the convolutional layer. At the same time, the spatial information of the audio is well-preserved. Compared with the other models, the tensor network has powerful representation ability in the high-dimensional space and can separate the different classes of audio with hyperplane. There is little difference in the F1-score performance on cooking, vacuum cleaning, and working. The score advantage of other classes is more obvious, 5.61% higher than the INRC_2D system, which shows that for classes of not specific activities, the tensor network can also learn the features better.

The data provided in the evaluation set are based on the sensor nodes that do not exist in the development set and can provide data from the same nodes in the development set. The F1-scores of each model in the test set of the validation set are shown in Table 3.

TABLE 3

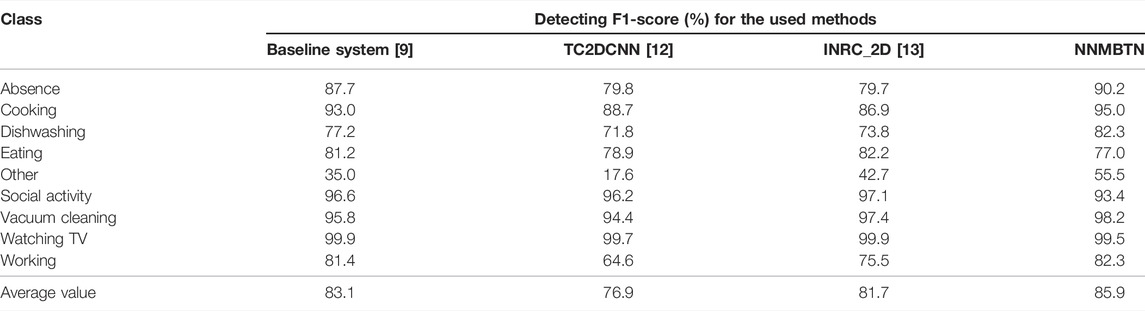
TABLE 3. Comparison of the neural network model based on the tensor network with other models in the test set of the validation dataset.

Compared with the results on the development set, it can be seen from Table 3 that the proposed model in the test set of the validation set is lower than the other models in the two categories of eating and social activities and higher than the other models in both categories of dishwashing and vacuuming. The advantages of the other categories are still obvious. The average F1-score reaches 85.9%, which is 9.0% higher than TC2DCNN, 4.2% higher than INRC2D, and 2.8% higher than the baseline. The F1-scores of the neural network model based on the tensor network are relatively stable, which proves that the proposed network has a good generalization ability. On the whole, the proposed model has better ability to extract and learn the important features of the data.

In order to better demonstrate the compression ability of the MPS to the network, the MPS layer in the proposed model is replaced by the convolutional layer, max pooling layer, and fully connected layer. We compared the proposed model (NNMBTN: 2CNN+4MPS) with the traditional CNN-based model which is composed of four CNNs, Maxpool, and a fully connected layer. The model comparison results are shown in Table 4.

TABLE 4

TABLE 4. Performance and parameter comparison between the proposed model and the traditional neural network.

It can be seen from Table 4 that the parameters of the proposed model are one quarter smaller than that of the traditional neural network after replacement, and the effect is also better than that of the traditional neural network, which shows that the MPS layer has better compression ability for the network.

To further investigate the effect of combining the proposed model with the state-of-the-art model, separable convolutions network [5] are used to verify the feasibility of the proposed model. Separable convolutions network consists of four convolutional layers using $5\times 5$ filters, followed by a global pooling layer and a final MLP (Multilayer Perceptron). The separate convolution network structure is improved to be combined with the MPS tensor network in which only two layers of separate convolutions network are retained. In the comparison experiments, only the network structure was changed, and the rest remained unchanged. The experimental results are shown in Table 5.

TABLE 5

TABLE 5. Performance comparison between the separable convolution model and the separable convolution model combined with tensor networks.

It can be seen from Table 5 that the GPU occupancy in the training procedure is reduced by 55% after combining with the tensor network under the same conditions except for the network structure. This shows that the tensor network can better reduce the redundancy of the network during the training. In terms of parameter quantity, the parameter quantity of the separate convolution is slightly smaller than that of ordinary convolution. The F1-score is slightly lower than the split convolutional network. Compared with the state-of-the-art model, the combination of the tensor network can reduce the redundancy of the network to achieve a balance between efficiency and accuracy. In the future, more research practices could be carried out to find a better way when combining the tensor network with the new neural network approaches.

4 Conclusion

In this article, the neural network model based on the tensor network is proposed for audio tagging of domestic activities, which takes the advantage of the CNN in extracting spatial features and the MPS tensor network for better interpretability and the ability to compress the network with tensor train decomposition. The MPS is one-dimensional tensor network structure, which is based on tensor train decomposition. It uses the chain-connected small tensors to represent the high-dimensional tensors. The proposed model is composed of two convolutional layers and four MPS layers. The function of the first three MPS layers is to extract the features, and the last MPS layer is used as a classifier. The DCASE 2018 challenge task 5 datasets are considered in the experiment, and the F1-score is calculated for performance evaluation. The experimental results show that the neural network model based on the tensor network proposed in this article has a good learning ability. The results show that the average F1-Score of the proposed neural network model based on the tensor network in the test set of the development dataset and validation dataset of DCASE 2018 challenge task 5 reached 87.7 and 85.9%, which were 3.2 and 2.8% higher than the baseline system, respectively. When compared with the state-of-the-art model, the combination of the tensor network can reduce the redundancy of the network to achieve a balance between the efficiency and accuracy. It is verified that the proposed model can function better for the task of audio tagging of domestic activities.

In the future, it is necessary to extract more representative audio features in the face of a huge database. There are some other structures of tensor networks, such as PEPS and MERA, and the combination of these models with the neural networks deserves a further in-depth study. In addition, the classes of the sound events in household activities are more complex, so expanding the dataset and improving the audio tagging accuracy are also necessary.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

L-DY and R-BY mainly carried out topic selection, experiments, and completion of the first draft. JW mainly checked the logical structure and writing of the manuscript. ML was mainly responsible for the revision and polishing of the manuscript.

Funding

The Central Government Guides Local Science and Technology Development Fund Project of China (grant number: 2021ZY0004). This work was supported by the National Natural Science Foundation of China (Grant Nos. 62071039 and 62161040), the Natural Science Foundation of Inner Mongolia (Grant No. 2021MS06030), and the Science and Technology Major Project of Inner Mongolia (Grant No. 2021GG0023).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rafferty J, Nugent CD, Liu J, Chen L. From Activity Recognition to Intention Recognition for Assisted Living within Smart Homes. IEEE Trans Human-mach Syst (2017) 47(3):368–79. doi:10.1109/thms.2016.2641388

CrossRef Full Text | Google Scholar

2. Erden F, Velipasalar S, Alkar AZ, Cetin AE. Sensors in Assisted Living: A Survey of Signal and Image Processing Methods. IEEE Signal Process Mag (2016) 33(2):36–44. doi:10.1109/msp.2015.2489978

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Phan H, Hertel L, Maass M, Koch P, Mazur R, Mertins A. Improved Audio Scene Classification Based on Label-Tree Embeddings and Convolutional Neural Networks. Ieee/acm Trans Audio Speech Lang Process (2017) 25(6):1278–90. doi:10.1109/taslp.2017.2690564

CrossRef Full Text | Google Scholar

4. Gong Y, Chung Y-A, Glass J. Psla: Improving Audio Tagging with Pretraining, Sampling, Labeling, and Aggregation. Ieee/acm Trans Audio Speech Lang Process (2021) 29:3292–306. doi:10.1109/taslp.2021.3120633

CrossRef Full Text | Google Scholar

5. Bursuc A, Puy G, Jain H. Separable Convolutions and Test-Time Augmentations for Low-Complexity and Calibrated Acoustic Scene Classification. Barcelona, Spain: Detection and Classification of Acoustic Scenes and Events 2021 (2021).

Google Scholar

6. Dekkers G, Lauwereins S, Thoen B, Adhana MW, Brouckxon H, Van den Bergh B, et al. The Sins Database for Detection of Daily Activities in a Home Environment Using an Acoustic Sensor Network. Munich, Germany: Detection and Classification of Acoustic Scenes and Events 2017 (2017). p. 1–5.

Google Scholar

7. Wang J, Xie X, Kuang J. Microphone Array Speech Enhancement Based on Tensor Filtering Methods. China Commun (2018) 15(4):141–52. doi:10.1109/cc.2018.8357692

CrossRef Full Text | Google Scholar

8. Yang L, Liu M, Wang J, Xie X, Kuang J. Tensor Completion for Recovering Multichannel Audio Signal with Missing Data. China Commun (2019) 16(4):186–95. doi:10.12676/j.cc.2019.04.014

CrossRef Full Text | Google Scholar

9. Dekkers G, Vuegen L, van Waterschoot T, Vanrumste B, Karsmakers P. Dcase 2018 Challenge-Task 5: Monitoring of Domestic Activities Based on Multi-Channel Acoustics. Surrey, United Kingdom: arXiv preprint arXiv:180711246 (2018).

Google Scholar

10. Inoue T, Vinayavekhin P, Wang S, Wood D, Greco N, Tachibana R. Domestic Activities Classification Based on Cnn Using Shuffling and Mixing Data Augmentation. Surrey, United Kingdom: DCASE 2018 Challenge (2018).

Google Scholar

11. Tanabe R, Endo T, Nikaido Y, Ichige T, Nguyen P, Kawaguchi Y, et al. Multichannel Acoustic Scene Classification by Blind Dereverberation, Blind Source Separation, Data Augmentation, and Model Ensembling. Surrey, United Kingdom: DCASE 2018 Challenge (2018).

Google Scholar

12. Tiraboschi M. Monitoring of Domestic Activities Based on Multi-Channel Acoustics: A Time-Channel {2d}-Convolutional Approach. Surrey, United Kingdom: DCASE 2018 Challenge (2018).

Google Scholar

13. Raveh A, Amar A. Multi-Channel Audio Classification with Neural Network Using Scattering Transform. Surrey, United Kingdom: Tech. Rep. DCASE (2018).

Google Scholar

14. Kong Q, Iqbal T, Xu Y, Wang W, Plumbley MD. Dcase 2018 Challenge Surrey Cross-Task Convolutional Neural Network Baseline. Surrey, United Kingdom: arXiv preprint arXiv:180800773 (2018).

Google Scholar

15. Hofmann T, Schölkopf B, Smola AJ. Kernel Methods in Machine Learning. Ann Stat (2008) 36(3):1171–220. doi:10.1214/009053607000000677

CrossRef Full Text | Google Scholar

16. Wang J, Liu M, Xie X, Kuang J. Compression of Head-Related Transfer Function Based on Tucker and Tensor Train Decomposition. IEEE Access (2019) 7:39639–51. doi:10.1109/access.2019.2906364

CrossRef Full Text | Google Scholar

17. Stoudenmire EM, Schwab DJ. Supervised Learning with Quantum-Inspired Tensor Networks. Barcelona, Spain: arXiv preprint arXiv:160505775 (2016).

Google Scholar

18. Efthymiou S, Hidary J, Leichenauer S. Tensornetwork for Machine Learning. Ithaca, New York: arXiv preprint arXiv:190606329 (2019).

Google Scholar

19.R Selvan, and EB Dam, editors. Tensor Networks for Medical Image Classification. Montreal, QC: Medical Imaging with Deep Learning (2020).

Google Scholar

20. Evenbly G, Vidal G. Tensor Network States and Geometry. J Stat Phys (2011) 145(4):891–918. doi:10.1007/s10955-011-0237-4

CrossRef Full Text | Google Scholar

21. Liu H, Wang F, Liu X, Guo D. An Ensemble System for Domestic Activity Recognition. Surrey, United Kingdom: DCASE2018 Challenge, Tech Rep (2018).

Google Scholar

22.SK Kopparapu, and M Laxminarayana, editors. Choice of Mel Filter Bank in Computing Mfcc of a Resampled Speech. In: Proceedings of the 10th International Conference on Information Science, Signal Processing and their Applications (ISSPA 2010); 2010 May 10; Kuala Lumpur, Malaysia. IEEE (2010).

CrossRef Full Text | Google Scholar

23.K Yanai, and Y Kawano, editors. Food Image Recognition Using Deep Convolutional Network with Pre-training and Fine-Tuning. In: Proceedings of the 2015 IEEE International Conference on Multimedia & Expo Workshops (ICMEW); 2015 June 29; Turin, Italy. IEEE (2015).

CrossRef Full Text | Google Scholar

24. Kalchbrenner N, Grefenstette E, Blunsom P. A Convolutional Neural Network for Modelling Sentences. Ithaca, New York: arXiv preprint arXiv:14042188 (2014).

Google Scholar

25. Schmidt-Hieber J. Nonparametric Regression Using Deep Neural Networks with Relu Activation Function. Ann Stat (2020) 48(4):1875–97. doi:10.1214/19-aos1875

CrossRef Full Text | Google Scholar

26. Sigtia S, Benetos E, Dixon S. An End-To-End Neural Network for Polyphonic Piano Music Transcription. Ieee/acm Trans Audio Speech Lang Process (2016) 24(5):927–39. doi:10.1109/taslp.2016.2533858

CrossRef Full Text | Google Scholar

27. Bridgeman JC, Chubb CT. Hand-Waving and Interpretive Dance: An Introductory Course on Tensor Networks. J Phys A: Math Theor (2017) 50(22):223001. doi:10.1088/1751-8121/aa6dc3

CrossRef Full Text | Google Scholar

28. Oseledets IV. Tensor-Train Decomposition. SIAM J Sci Comput (2011) 33(5):2295–317. doi:10.1137/090752286

CrossRef Full Text | Google Scholar

29. Koenderink JJ, Van Doorn AJ. The Structure of Locally Orderless Images. Int J Comput Vis (1999) 31(2):159–68. doi:10.1023/a:1008065931878

CrossRef Full Text | Google Scholar

30. Oron S, Bar-Hillel A, Levi D, Avidan S. Locally Orderless Tracking. Int J Comput Vis (2015) 111(2):213–28. doi:10.1007/s11263-014-0740-6

CrossRef Full Text | Google Scholar

31. Miller J. Torchmps (2019). Available from: https://githubcom/jemisjoky/torchmps (Accessed March 1, 2019).

Google Scholar

32. Fishman M, White SR, Stoudenmire EM. The Itensor Software Library for Tensor Network Calculations. Ithaca, New York: arXiv preprint arXiv:200714822 (2020).

Google Scholar

33. Novikov A, Izmailov P, Khrulkov V, Figurnov M, Oseledets IV. Tensor Train Decomposition on Tensorflow (T3f). J Mach Learn Res (2020) 21(30):1–7.

PubMed Abstract | Google Scholar

34.W Astuti, W Sediono, A Aibinu, R Akmeliawati, and M-JE Salami, editors. Adaptive Short Time Fourier Transform (Stft) Analysis of Seismic Electric Signal (Ses): A Comparison of Hamming and Rectangular Window. In: Proceedings of the 2012 IEEE Symposium on Industrial Electronics and Applications; Bandung, Indonesia; 2012 September 23. IEEE (2012).

CrossRef Full Text | Google Scholar