Fundamentals and Applications of Topological Polarization Singularities

Wang , Feifan; Yin, Xuefan; Zhang, Zixuan; Chen, Zihao; Wang, Haoran; Li, Peishen; Hu, Yuefeng; Zhou, Xinyi; Peng, Chao

doi:10.3389/fphy.2022.862962

REVIEW article

Front. Phys., 28 March 2022

Sec. Optics and Photonics

Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.862962

This article is part of the Research Topic Topological Photonics View all 15 articles

Fundamentals and Applications of Topological Polarization Singularities

Feifan Wang ¹

Xuefan Yin²

Zixuan Zhang¹

Zihao Chen¹

Haoran Wang³

Peishen Li¹

Yuefeng Hu^3,4

Xinyi Zhou¹

Chao Peng^1,3*

¹State Key Laboratory of Advanced Optical Communication Systems and Networks, School of Electronics and Frontiers Science Center for Nano-optoelectronics, Peking University, Beijing, China
²Department of Electronic Science and Engineering, Kyoto University, Kyoto, Japan
³Peng Cheng Laboratory, Shenzhen, China
⁴Peking University Shenzhen Graduate School, Shenzhen, China

Radiations towards the continuum not only brings non-Hermicity to photonic systems but also provides observable channels for understanding their intrinsic physics underneath. In this article, we review the fundamental physics and applications of topological polarization singularities, which are defined upon the far-field radiation of photonic systems and characterized by topological charges as the winding numbers of polarization orientation around a given center. A brief summarizing of topological charge theory is presented. A series of applications related to topological polarization singularities are then discussed.

1 Introduction

Waves are ubiquitous phenomena in the nature. Serving as one of the most fundamental concepts in modern physics and applications, the examples range from electromagnetic waves, acoustic waves, to matter waves. Ever since the discovery of the transverse nature of some waves, the study of the polarization properties of those vector waves has attracted a great deal of attention, and varieties of novel mathematical concepts have been introduced. Among them, the most direct representation of polarization is the elliptically polarized state. For a generic plane wave, its field vector can be traced from the evolution of amplitudes and phases along two orthogonal directions, and correspondingly, the wave motion becomes a rotating vector that follows an ellipse path. In addition, the complicated polarization states can be projected onto the Poincaré sphere for better visualization, by using the Stokes’ parameters [1]. Such a geometric representation shed lights upon deeper understanding of polarization from topological perspectives [2].

From a topological point of view, the objects of interest are some special points or regions on the Poincaré sphere, known as the singularities, such as lines where the polarization gets linear (“L lines”), points with circular polarization (“C points”), and centers of polarization vortices (“V points”) [2–6]. At these regions, one or two components that compose the polarization, namely amplitude and phase, are ill-defined, so that the waves may exhibit some abnormal behavior, leading to exotic and potential useful physical phenomena. In particular, a special attention has been paid to the realization of singularities in optical domain [2, 6–9]. Examples include optical vortex beam generation [10–12], cylindrically polarized laser beams for tighter focusing [13–16], and the bound states in the continuum (BICs) [17–20]. It is noteworthy to highlight the BICs. Although the BICs have been developed from different contexts in history, their nature was found to be topological. Since first proposed in 1929 by von Neumann and Wigner [21], the BICs are understood as an elimination of radiation in the case that radiation is allowed. After the first photonic realization [22], the BICs had been intensively investigated in various systems from a picture of destructive interference of waves [17, 18, 23, 24].

Later, the topological picture regarding BICs was established: they are interpreted as the vortex centers in far-field polarization orientation field where the polarization is ill-defined and all the radiation is forbidden [25]. In other words, BICs are a type of V-points in k-momentum space. By counting on the winding times of polarization direction around a specific center in momentum space, a conserved quantity called “topological charge” was defined, which was proved to be a topological invariant. It is found that the BICs possess integer topological charges [25]. Besides, the circularly-polarized states (CPs) carry half-integer topological charges, as a type of C-points. Furthermore, the topological charges defined on polarization are connected to the non-trivial band topology of non-Hermitian systems: half charges have been observed from a bulk Fermi arc encircling paired exceptional points (EPs) [26]. These findings built a framework to understand the polarization singularities, and utilize them for many applications.

In this article, we review the fundamental physics and applications of the research field of topological polarization singularities. We start from briefly summarizing the general principles and theory framework, and then present a comprehensive review on a series of applications related to polarization singularities. At last, we give our prospect and summary.

2 Principles and Theory

The concept of optical singularities provide vivid and useful representations to understand the exotic phenomena of light, and thus they are applied in a series of investigation for different purposes. To keep the review focused, we concentrate on topological polarization singularities in this article. Specifically, we review the theoretical framework of polarization topological charges in this section, including their definitions, origins, and the methods for manipulating them. More information and connections regarding related topics can be found in other review articles, including topological photonics [27–29], singular optics [2, 6, 7], non-Hermitian topology [30–36], BICs [37–39], and orbital angular momentum of light (OAM) [40–42].

2.1 Theory of Polarization Topological Charges

Polarization topological charge was firstly proposed to depict the topological nature of BICs. In 2014, Zhen et al. [25] pointed out that the BICs are V-points in the far-field polarization vector field, carrying integer topological charges in momentum space. At the vortex center, the radiation is eliminated since the far-field polarization cannot be defined. Figure 1A illustrates the basic concepts of BICs. A resonance turns into a BIC if and only if c_x = c_y = 0, where (c_x, c_y) is the projection on the x-y plane of electric field $< u_{k} >$ of the radiative wave. The polarization field winds according to the topological charge, and Q diverges at BICs. An explicit definition of the polarization topological charge is given by:

q = \frac{1}{2 π} \oint_{C} d k \cdot \nabla_{k} ϕ (k) (1)

in which ϕ(k) is the angle of the polarization vector arg [c_x(k) + ic_y(k)] describing the orientation of polarization major axis, k is the in-plane wavevector, and C is a closed simple path in momentum space that goes around a specific point along the counterclockwise direction. Eq. 1 describes the number of times that the polarization vector winds around the specific point in momentum space. Encircling the BICs, namely the vortex centers, the polarization vector has to come back to itself after travelling through a closed loop, upon which the topological charge q must be an integer. Besides, according to the definition, we readily check that the CPs carry half-integer charges as q = ±1/2 from a topological view. Figure 1B gives a possible configuration of the polarization field near a CP, giving rise to a topological charge q = +1/2. Both the BICs and CPs are types of topological polarization singularities.

FIGURE 1

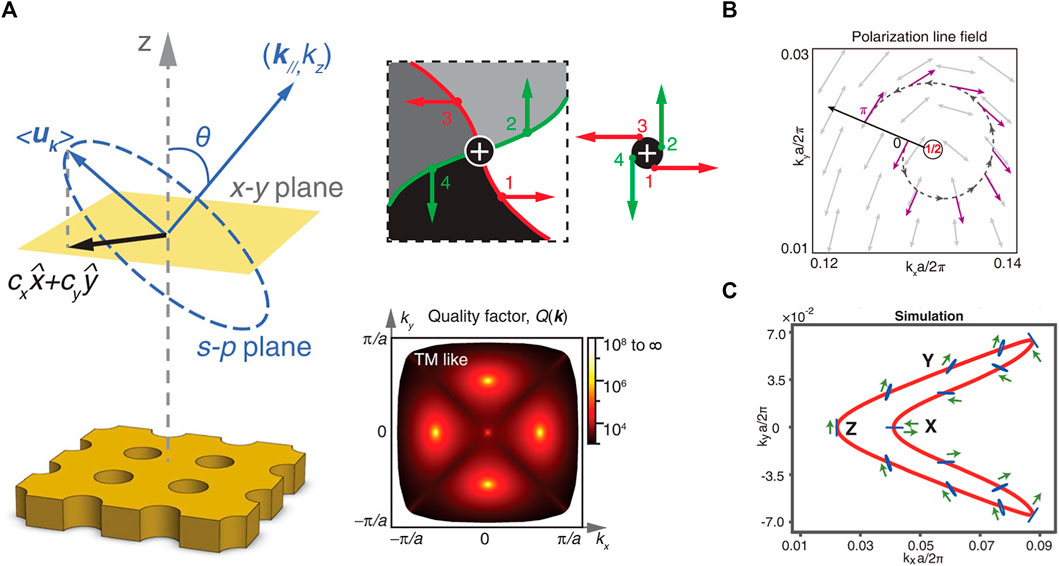
FIGURE 1. Definitions and properties of different types of polarization singularities, (A) BICs [25] copyright American Physical Society; (B) a CP with charge +1/2 [43] copyright Springer Nature Ltd., and (C) a bulk Fermi arc connecting paried EPs [26] Copyright AAAS.

Note that the polarization topological charge is defined upon the far-field polarization in momentum space, which may connect, or say project the intrinsic band topology to the radiation field. For example, half-integer charges was observed around the bulk Fermi arc (Figure 1C), as a direct consequence of paired EPs [26] revealing the non-Hermitian topology of the bulk bands. However, the connection between band topology and radiation topology may not be obvious. For instance, the BICs and CPs are polarization singularities in radiation field, but they are topologically trivial upon the energy band. Further explorations are for sure interesting topics.

As a topological invariant, topological charges are conserved quantities: they continuously evolve in the momentum space and cannot suddenly disappear unless one charge drops out of the light cone or annihilates with another charge with the opposite sign. Besides, a pair of half charges can merge to an integer charge, or annihilate to nothing according to their signs. Consequently, the topological charge evolution offers an abstract but essential view to understand the radiation characteristics, as well as new methods to manipulate it. Examples and consequences of charge evolution will be presented in the following section.

Topological charge is actually a quite general concept that can quantitatively depict the winding of any arbitrary attributes. Although sharing the same terminology, the term “topological charge” are not only defined on the polarization, but also on phase, or other attributes of wave, in the real space, momentum space or parameter space. It is worthy to pay extra attention to distinguish the definitions. For instance, the term has been applied to phase singularities [44–51] that are related to vortex beam generations, and singularities on transmissions or reflections [52–55]. Other definitions utilizing the concept of winding are also reported in electromagnetic [19, 56–58], phononic [59] and mechanical systems [60].

2.2 Origins of Integer Topological Charge

The BICs, which are polarization singularities carrying integer charges, have been an attractive topic for several decades. The history, origins and results of BICs have been comprehensively reviewed by Hsu et al. [37] in 2016. In this section, we will summarize the new advances and understandings developed in recent years. Given that the investigations upon the BICs are diverse and extensive, we organize our review from different aspects.

From the aspect of physics origins, Friedrich and Wintgen presented a fundamental picture of interfering resonances to create the BICs [61]. Their original work pointed out that, the coupling between any two or more leaky resonances could eliminate the radiation of particular hybridized resonances, if the coupling strengths were well chosen. Although the term “FW BIC” is currently usually specialized to a BIC raised from interband coupling, other types of BICs can also be interpreted from Friedrich and Wintger’s picture, if one appropriately defines the “resonances”. For instance, for a photonic crystal (PhC) slab or gratings system, such resonances are guided-mode resonances [62–67]; for nanoparticles, dielectric spheres or tight-binding metasurfaces, the resonances are Mie resonances or other localized states [68–70]; for metallic systems, they are plasmonics resonances [20, 71]. Accordingly, BICs can be explained as the hybridization of different bases (i.e. unperturbed resonances) equivalently from a mathematical point of view. Examples include the coupled-wave theory that uses quasi-plane waves as the bases in periodic structures [17, 23, 24], and the multipole-expansion theory for Mie resonances in which the shape of a single resonator matters [72–74].

From the aspect of system symmetry, the BICs are classified into “symmetry-protected BICs”, and “symmetry-incompatible BICs” [17, 37]. Since the radiation elimination originates from the high symmetry, the symmetry-protected BICs usually reside at the symmetry center in momentum space (for instance the Γ point). It is noteworthy that the symmetry-protected BICs have been independently developed in different photonic fields in history and described by different terminologies, such as band-edge modes in distributed-feedback lasers (DFB) [75–79], and photonic-crystal surface emitting lasers (PCSELs) [78, 80–83]. On the other hand, the symmetry-incompatible BICs also have many alias names, such as tunable BICs [24], off-Γ BICs [23], resonance trapping BICs [84], and topology-protected BICs [25, 85]. Since the creation of symmetry-incompatible BICs doesn’t rely on the in-plane symmetry, they can move off the symmetry center in momentum space, which is distinguishable from the symmetry-protected ones.

From the aspect of platforms, the BICs are realized in both periodic and non-periodic structures. PhC is an easy-to-fabricate, optical-friendly platform to investigate BICs and other polarization singularities, in which the lattice periodicity offers naturally well-defined Bloch bases to depict the wave interactions [20, 86, 87]. Compared with PhCs, metasurfaces [68–70], coupled arrays of rods [19, 88, 89] and spheres [85, 90] share some similarities in their geometries: both of them are periodic and planar. The major difference might be—while the PhC supports long-range interactions, the wave interactions in metasurfaces are likely short-ranged and dominated by a few of adjacent unit cells. Alternatively, another type of systems is single resonators [18, 91, 92]. Although in principle a perfect BIC cannot be realized in a three-dimensional compact volume [37, 93], the single resonators can support quasi-BICs with considerably high-Q and extremely small modal volume V, thus they are promising for nonlinear optic application and sensing.

It is noteworthy that, the BICs with high-order topological charges |q| > 1 are also reported. The vortices with q = −2 were found in a triangular latticed PhC slab [20] owing to the high in-plane symmetry of the lattice at the high-order Γ point although not been explicitly mentioned. In 2020, Yoda et al. [94] reported a symmetry-protected BIC with charge q = −2 in a C₆ symmetric lattice. It was found that two BICs each with q = −1 spawned from the q = −2 charge when the in-plane symmetries were broken from C₆ to C₂.

Another interesting fact is, although the BICs are usually isolated points, they can appear as a line in momentum space when involving extra dimensions. In 2019, Cerjan et al. [95] proposed a method called the environmental design for this purpose, in which the environment worked as new degree of freedom. Recently, this line of BICs was observed in a slab by altering the surrounding radiative environment with a 3D PhC [96].

Moreover, the topological polarization singularities are found in other systems such as disordered or quasi-crystal systems, and parity-time-symmetric (PT-symmetric) systems. In 2019, De Angelis et al. [97] reported the random vortices in a chaotic cavity composed of 2D PhCs. In 2021, Che et al. [98] experimentally observed the quasi-BICs in 2D photonic quasi-crystals. In 2020, Song et al. [99] reported the emergence of two types of modes with divergence of Q in a PT-symmetric system, named as a “PT-BIC” and a “lasing threshold mode”.

2.3 Emergence of Half-Integer Topological Charge

Another type of polarization singularities, namely CPs, can also emerge in momentum space by tuning material or structural parameters. According to the definition of topological charges, the CPs carry half-integer charges that obey the conservation law of topological charge together with the integer charges. Several methods are reported to create these half charges.

One method is to split integer charges to paired half charges following the conservation law, for instance q = 1 → 1/2 + 1/2, by breaking the in-plane symmetry. As reported by Liu et al. [100], it was observed that a symmetry-protected BIC split into a pair of CPs with opposite helicity but carrying topological charges of the same sign. Similar phenomenon was observed by Chen et al. [71]. The CPs can also originate from symmetry-incompatible BICs. For instance, Ye et al. [101] reported two CPs with identical topological charges of q = −1/2 but different handedness originating from a BIC with charge q = −1 at the K point in a honeycomb-lattice PhC. As mentioned above, Yoda et al. [94] showed that the BIC with high order charge q = −2 split to integer charges following q = −2 → (−1) + (−1) by breaking the symmetry from C₆ to C₂. By further breaking the C₂ symmetry, the integer charge split to paired half charges as q = −1 → (−1/2) + (−1/2). It is noteworthy that all the evolution followed the conservation law.

An alternative method for creating half charges is to spawn the CPs from trivial polarization field, namely q = 0. Recently, Zeng et al. [102] built a two-layered 1D PhC with an offset between the layers. Two CPs emerged from a given k point where the far-field polarization is trivial, carrying opposite signed half charges as q = 0 → 1/2 + (−1/2). Apparently, the conservation law still held.

Besides, polarization half charges are related to another important type of singularities in non-Hermitian system, namely EPs. In 2018, Zhou et al. [26] reported a pair of EPs connected by so-called bulk Fermi arc. A flip of the polarization major axis was observed in experiment along one closed loop around the EP pair connected by bulk Fermi arc, showing a clear signature of polarization half charge. It is noteworthy that the EPs belonged to the singularities upon the non-Hermitian band, while the polarization half charges represented the singularities upon the radiation. It is still vague that how the band topology connects to the radiation topology. Nevertheless, as reported by Chen et al. [103], a conservation law of global charge was still valid.

2.4 Consequences of Topological Charge Evolution

The conservation law of topological charges allows the continuous evolution of charges in momentum space, namely moving, merging, splitting and annihilating with the summation of all charge numbers remaining constant. Since the topological charges are related to the far-field radiation characteristics, it was found that interesting and useful consequences could be obtained from the topological charge evolution.

One of the example is the merging of multiple integer topological charges, i.e. the BICs, which strongly suppresses the out-of-plane scattering and leads to a class of robust ultra-high-Q resonances. Although the BICs completely forbid the radiation and own infinite photon lifetime in theory, their experimental realizations had suffered from a limited Q in a level of 10⁴ [17], due to the energy leakage from the inevitable out-of-plane scattering originated from fabrication imperfections. To address this problem, Jin et al. [104] reported a method of merging BICs in a C₄ symmetric PhC slab where existed eight off-Γ BICs with q = ±1 charges around one symmetry-protected BIC at the Γ point. By continuously tuning the lattice periodicity a, the eight BICs kept moving until merging at Γ, and further annihilated into one isolated BIC with charge q = +1. (Figure 2A).

FIGURE 2

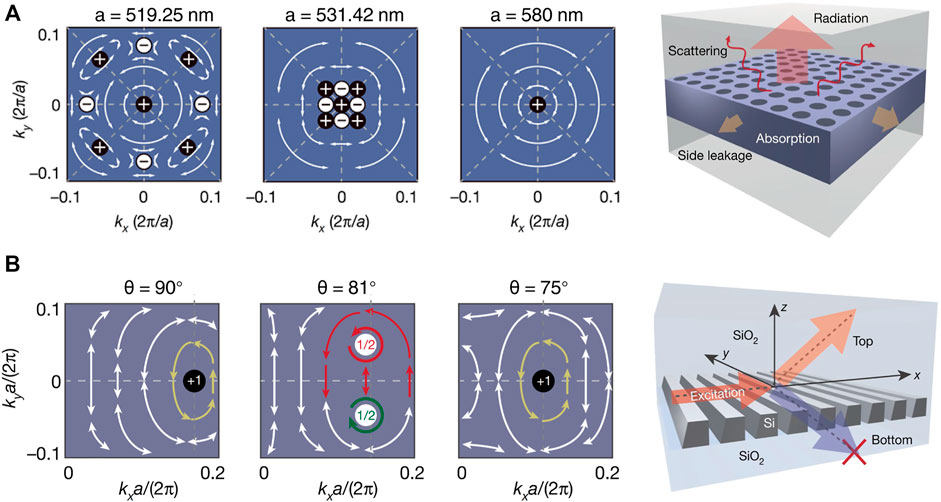
FIGURE 2. Consequences of topological charge evolution. (A) A high-Q cavity robust of out-of-plane scatterings constructed by the merging of multiple integer charges [104]. (B) The merged half-charges in downward radiation leading to a unidirectional radiation [43]. Copyright Springer Nature Ltd.

As mentioned, the configuration of topological charges implies the radiation capabilities of nearby resonances, and further determines the observable Qs in samples by taking into account the scattering losses. Near an isolated BIC with charge q = ±1, the Q scales quadratically (1/k²) as the distance k away from the BIC. However, the scaling law dramatically changes to 1/k⁶ when nine BICs just merge, as shown in Jin’s work. As a result, the scattering loss was significantly suppressed, and a record-high Q of 4.9 × 10⁵ was experimentally observed.

Recently, Kang et al. [105] took a further step and realized a merging BIC at off-high symmetry points, namely the merging behavior of integer charges were not restricted to the Brillouin zone (BZ) center. The in-plane C₄ and mirror symmetries were broken, resulting in the merging of an FW-BIC and a tunable-BIC at a nearly arbitrary point in momentum space.

Another example of topological charge evolution is related to an interplay with half charges and integer charges, leading to the realization of unidirectional guided resonances (UGRs) (Figure 2B), reported by Yin et al. [43]. The evolution started from an off-Γ BIC in a 1D silicon PhC slab, carrying a topological charge of q = +1 upon both up- and downwards radiation. By tilting the sidewall that broke the in-plane C₂ symmetry and up-down mirror symmetry simultaneously, the BIC split into a pair of CPs carrying q = +1/2 upon both the top and bottom sides of the slab. Further, paired CPs evolved following different trajectories in the upward and downward radiation fields due to the breaking of up-down mirror symmetry. At a specific angle, the paired CPs in downward radiation merged into an integer charge while upward CPs remained departing. Therefore, the downward radiation was totally eliminated while the upward radiation channel was still open, thus generating a resonance with directional emission named UGR. The experimental results demonstrated 99.8% of the energy radiated through the upward channel at UGR.

Recently, Zeng et al. [102] reported a similar phenomenon from theory in a two-layered 1D PhC with an offset between the two layers which broke the up-down-mirror symmetry. Two pairs of CPs with q = ±1/2: one left-handed pair and another right-handed pair, emerged at a specific value of the offset. By continuously varying the offset, the CPs evolved in momentum space, and merged to integer charges at different k points upon up- and downward radiation, which created two UGRs.

3 Applications

Topological charge provides not only a convenient mathematical tool in theory, but also flexible and rich methods for manipulating lights, thus paving the way to a variety of applications. In particular, topological charges can be tuned to selectively eliminate or suppress the radiation, which leads to the realization of optical modes with ultra-long lifetime and desired radiation patterns in intensity, phase and polarization. Consequently, topological charges have been applied in many scenarios, boosting the development of light trapping, lasing, light-matter interaction enhancement, nonlinear optics, wave-front control, polarization conversion, photonic integration and others. In this section, we review the recent progresses of applications related to the topological charges.

3.1 Trapping of Light and Optical High-Q Cavities

From a scientific or technological point of view, the importance of light-trapping is self-evident. The BICs are interpreted as vortices in far-field polarization, thus providing novel methods for light-trapping other than conventional optical cavities such as bound states under light-cone [108–110].

Early efforts was paid to inhibit out-of-plane radiations in large-area 2D systems. In 2012, Lee et al. [106] reported observation of a unique high-Q resonance near zero wavevector in large-area 2D PhC slab by using angular resolved analysis. Q of 1 × 10⁴ was found near the symmetry-protected BIC at Γ point (Figure 3A). In 2013, Hsu et al. [17] reported the off-Γ BICs for the first time, in which the Qs of resonances diverge to infinity at seemly insignificant wavevectors on certain bands. The structure is shown in Figure 3B. A radiative quality factor Q_r of 1 × 10⁶ was measured at a direction angle ∼ 35° of the reflection. Such BICs can stably exist in a general class of geometries and can move to a different k point by continuously tuning the system parameters.

FIGURE 3

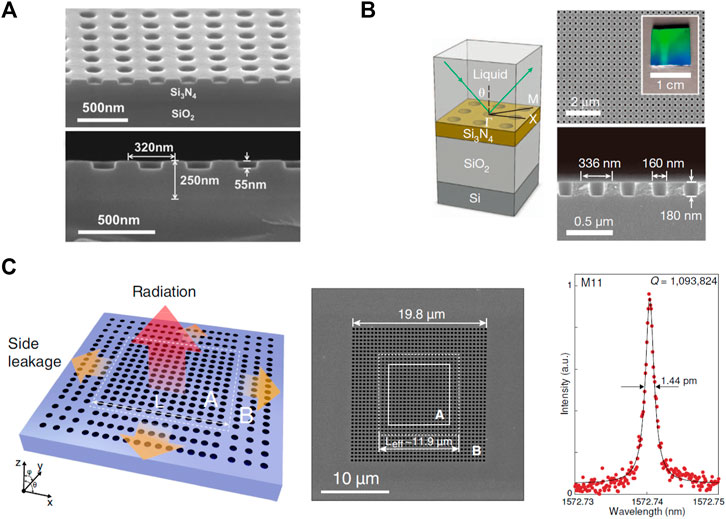
FIGURE 3. (A) Macroscopic photonic crystal [106] for observing symmetry-protected BICs, copyright American Physical Society. (B) The observation of symmetry-incompatible off-Γ BICs [17], copyright Springer Nature Ltd. (C) Miniaturized BICs [107], copyright Science China Press.

Subsequently, Zhen et al. [25] proposed the topological interpretation of the BICs in 2014 as elaborated in previous sections. The BICs’ capability of trapping light are further promoted. In 2019, Jin et al. [104] proposed and realized a class of ultra-high-Q resonances by merging multiple off-Γ BICs carrying topological charges towards the center of Brillouin zone (BZ). As a direct consequence of topological charge manipulation, Qs as high as 4.9 × 10⁵ were observed in an SOI PhC slab, as mentioned in Section 2.4. The merging-BIC designs strongly suppressed out-of-plane-scattering losses caused by fabrication imperfections, thus paved the way to realistic applications of BICs.

Strictly speaking, all the above examples belong to high-Q resonances but not high-Q cavities. According to the continuity of electromagnetic field, it was proved that fully 3D compact BIC does not exist in theory [37, 93]. In addition, the periodic conditions of PhC imply that the structure extends infinitely in the lateral direction, which is not practically feasible. The high-Q resonances in PhC slabs only localize in the vertical direction but remain de-localized in transverse direction across the slab.

The most straightforward method for achieving 3D light-trapping is to simply truncate the PhC slab laterally. Such method reduces modal volume V but also drastically degrades the quality factor Q because it introduces leakage in both lateral and vertical directions. A common relationship between Q and V for truncated BICs was derived [111] and verified experimentally [112]. In 2019, Liu et al. [69] observed a truncated BIC with Q of 18,511 and footprint of 19 × 19 μm². In 2021, a long-lifetime mode with Q of 7,300 was reported in InGaAsP PhC slab for low-threshold lasing in a footprint of 22.4 × 22.4 μm² [113]. In addition to simply truncating the PhC, the light can be confined transversely by applying lateral hetero-structures as reflective perimeters. For example, a mode with Q of 2 × 10⁴ has been measured in footprint of 215 μm² [114]. In these designs, although the hetero-structure suppress the lateral energy leakage effectively, the leakage toward out-of-plane direction raised by truncation remains unresolved.

Recently, Chen et al. [107] reported a new method of light trapping combining lateral mirrors and BIC in a cooperative way (Figure 3C). Light was confined in the vertical direction by manipulating the constellation of topology charges, matching them with the finite-size radiation channel. In the transverse direction, the light was trapped by the near-perfectly reflective photonic bandgap of the lateral hetero-structure, with the radiative and scattering losses of the boundary region being greatly suppressed, at the same time, the radiation in cavity region becomes highly directional. The coworking of the topological-charges covered a larger area in momentum space that protects the scattered waves from radiation. Since the boundary region shared similar geometries with the cavity region, they also benefit from the protection of topological constellation for a smaller radiation loss. As a result, light-trapping in all three dimensions was achieved. Miniaturized BICs with Qs of 1.09 × 10⁶ was measured experimentally with a footprint of ∼ 20 μm × 20 μm. Benefiting from the protection of topological constellations that are composed by topological charges, the microcavity exhibited excellent robustness to fabrication imperfections.

3.2 Lasing and Vortex Beam Generation

Since the integer topological charges carried by BICs are good candidates for realizing high-Q resonances, their most direct application is for lasing. Historically, the band-edge modes were widely adopted for semiconductor lasers such as DFB lasers [75–79] and distributed Bragg reflector (DBR) lasers [115–117]. Although it is not explicitly mentioned, the grating modes that operate at the band-edge of second-order Γ point are actually the symmetry-protected BICs. Later, the periodicity of one-dimensional gratings was extended to two-dimensional PhC slabs, leading to the invention of photonic-crystal surface-emitting lasers (PCSELs) [80]. The PCSELs also operate near the band edge residing in the continuum, supporting coherent oscillations in large areas. In the case that the periodic lattice and unit cells of PCSELs respect C₂ or higher in-plane symmetry, the lasing band-edge modes are found to be symmetry-protected BICs, too [118, 119].

In the past two decades, PCSELs have experienced dramatically developments and become a promising laser architecture as the successor of DFB lasers which had already made tremendous successes in industry. With a comprehensive review of PCSELs presented elsewhere [120], here we just list several major milestones: the first lasing action of PCSELs was observed in 1999 [80], as illustrated in Figure 4A; room-temperature, continuous-wave operation, current-injected lasing was achieved in 2004 [81]. Later, the abilities of tailoring beam patterns were reported in 2006 [121]; the lasing wavelength was extended to blue-violet region in 2008 [78]; a beam-steering functionality was demonstrated in 2010 [118]. What’s more, much efforts have been paid to promote the lasing power, and watt-class lasing was achieved (shown in Figure 4B) in 2014 [82] and 10-W-class lasing in 2019 [83]. Recently, PCSELs with a peak power of 20 W and pulse width of 35 ps were realized [122] and on-chip beam scanning lasers were first achieved [123] as illustrated in Figure 4C. It is noteworthy that, in the early age of PCSELs, circular shaped holes were adopted to pattern the PhC, so that the lasing modes were the BICs with infinite Qs in theory. Although the high Q factor lowered the lasing threshold, it was not good for high-efficient power extraction which was critical for high-power lasers. Therefore, the in-plane C₂ symmetries were broken on purpose, which turned the BICs with infinite Qs to quasi-BICs with high but finite Q values in carefully controlled manners [82, 83].

FIGURE 4

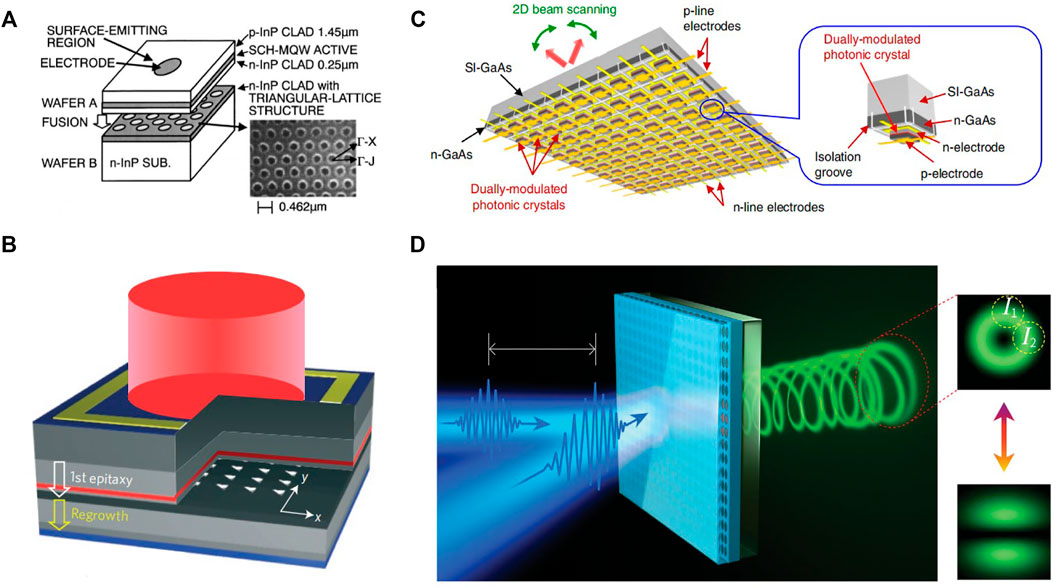
FIGURE 4. (A) Early PCSEL based on wafer fusion technique [80], copyright AIP publishing. (B) A W-class high-power PCSEL [82], copyright Springer Nature Ltd. (C) The on-chip beam scanning laser [123], copyright Springer Nature Ltd. (D) All-optical switching from the vortex microlaser [124], copyright AAAS.

Besides the PCSELs, the lasing action utilizing the BICs have also been developed in a parallel lane motivated from physics curiosity. In 2017, Kodigala et al. [84] demonstrated the optical-pumped lasing in an array of suspended cylindrical nanoresonators consisting of In_xGa_1−xAs_yP_1−y multiple quantum wells, claimed as the first lasing action of the BICs. In 2018, Ha et al. [125] reported directional lasing in resonant semiconductor nanoantenna arrays, that is, arrays of GaAs nanopillars. On the other hand, lasing action has been reported in Mie-resonant BICs, too. For instance, combining colloidal CdSe/CdZnS core-shell nanoplatelets with square-latticed TiO₂ nanocylinders, Wu et al. [126] reported the lasing from in-phased out-of-plane magnetic dipoles in 2020.

It is worthy to mention that, the polarization singularities accompanied with the BICs can be adopted to generate rich and exotic beam patterns. Some early experiments of PCSELs showed such possibility of creating tailored vectorial beams [121]. Recently, vortex beam generation has attracted huge attention, particularly owing to its great potentials in escalating the optical communication systems to higher level of multiplexing. In 2020, Wang et al. [12] reported optical vortex generation in a PhC slab with i-fold (i > 2) rotational symmetry related to the BICs, in which spin-to-orbit angular momentum conversion was realized and the vortex beam was proved to be a diffraction resistant high-order quasi-Bessel beam. Also in 2020, Huang et al. [124] reported that the BICs enabled ultra-fast control of vortex micro-lasers based on a perovskite metasurface, as shown in Figure 4D. Through modifying the two-beam-pumping configuration, ultra-fast switching between a vortex beam and regular linearly polarized beam was demonstrated with a transition time of only 1.5 ps.

3.3 Light-Matter Interaction Enhancement and Nonlinear Optics

As elaborated in Section 3.1, ultra-high Qs and small modal volume Vs can be achieved by arranging the topological charges, leading to dramatic enhancement of Purcell effect that favors the light-matter interactions and nonlinear optics. In 2019, Xu et al. [127] experimentally demonstrated third-harmonic generation (THG) in silicon metasurfaces and observed a conversion efficiency of 5 × 10⁶ at 100 mW. Later, Liu et al. [69] promoted the Q to a record-high value of 18,511 in the metasurface, and reported that the THG conversion efficiency was five orders of magnitude higher than the former silicon metasurfaces. Even the second-harmonic generation (SHG) was also observed in silicon in their work. Moreover, Kang et al. [128] observed the high-order vortices, namely, high-order topological charges upon the harmonic waves generated from optical nonlinearity.

To enhance the efficiency of the nonlinear processes, several considerations were taken into account. Firstly, the excitation and emission of the resonances under critical-coupling condition would maximize the field strength in the cavity. As reported, by slightly breaking the in-plane symmetry that shifted the resonance away from the complete dark BIC, the energy exchange between the external excitation and the resonance became more efficient, thus promoting the conversion efficiency [127, 130]. Besides, the process benefited a lot from a doubly-resonant design, namely both the excitation and its harmonics were resonances supported by the same cavity. For example, Wang et al. [114] realized a GaN photonic cavity from this concept, in which the fundamental frequency matched with a defect mode and its second-harmonics operated upon a quasi-BIC. As a result, the intrinsic conversion efficiency was 10 times larger than singly resonant cavities with similar materials.

Besides the periodic structures including PhCs and metasurfaces, single Mie resonators provide another promising platform for nonlinear optics. Although the Qs of single resonators are lower than that of periodic structures, single resonators have particular advantages in small modal volume V to promote the strength of light-matter interaction. In 2018, Carletti et al. [91] predicted that the conversion efficiency of SHG in an isolated AlGaAs nano-antenna could be two orders of magnitude stronger than that in conventional designs. In 2020, Koshelev et al. [18] experimentally implemented such design, as illustrated in Figure 5A. They found a quasi-BIC in a particle with a diameter of 930 nm and height of 635 nm. Owing to the mutual interference of several Mie modes, Q of 188 was realized. Combining with doubly-resonant strategy, two orders of magnitude higher conversion efficiency was achieved as expected.

FIGURE 5

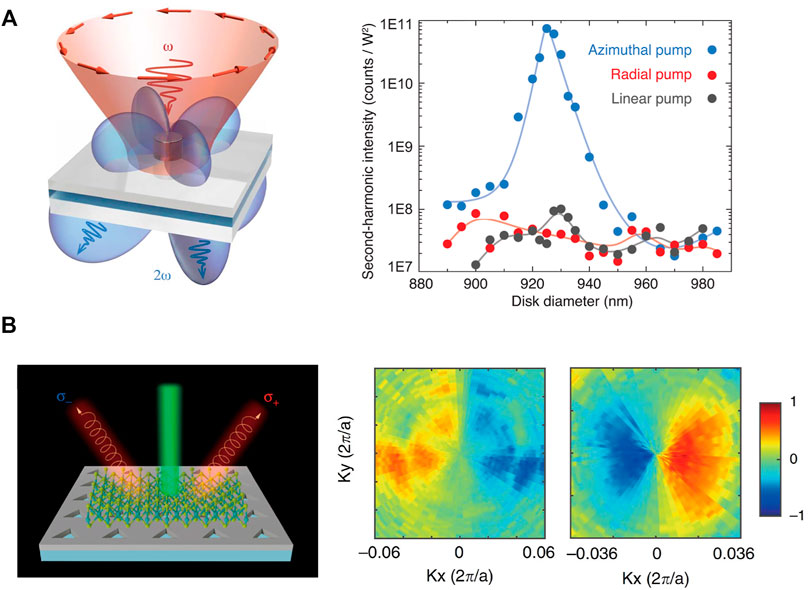
FIGURE 5. Light-matter interaction enhancement and nonlinear optics. (A) SHG in an isolated antenna, the SH intensity vs nano-resonator diameter was measured at different pump polarizations [18], copyright AAAS. (B) Routing of valley photons with different chiralities by coupling to CPs, measured valley polarization in momentum space at 615 nm (left) and 628 nm (right) [129], copyright Springer Nature Ltd.

In addition to those dielectric nonlinear materials, thin-film materials such as 2D transitional metal dichalcogenides (TMDCs) were specifically cooperated with the BICs to investigate the light-matter interaction. In 2018, Koshelev et al. [131] achieved a strongly-coupled exciton-photon system in which PhC was covered by a WSe₂ monolayer. Two years later, Kravtsov et al. [132] demonstrated a BIC-based polaritonic excitation with MoSe₂ upon PhCs, in which strong exciton-fraction-dependent optical nonlinearities were exhibited. Besides, as reported by Yu et al. [133], the decoupling from the continuum could confine light in a low-dielectric waveguide upon high-dielectric substrate, which contributed to new graphene device designs.

Besides the V-points (BICs), the C points (CPs) can also be involved in the light-matter interactions since they provide extra selectivity in chirality. In 2020, Wang et al. [129] generated paired CPs with different chirality. Owing to the valley-dependent selection rules in WSe₂, the photons radiated from inequivalent valleys could couple to the two CPs, as illustrated in Figure 5B. Accordingly, a maximum degree of valley polarization over 80% was observed.

3.4 Intensity and Phase Modulation

Amplitudes and phases are fundamental attributes depicting the characteristics of light. By cooperating with the resonances associated with topological charges, these attributes can be manipulated thus leading to a series of applications.

As a directly-observable attribute, the intensity of light can be controlled for a variety of purposes. Specifically, in 2019, Yu et al. [133] realized a BIC-waveguide-integrated modulator in which the electro-absorption effect of graphene was adopted and a bandwidth of 5 GHz was achieved. In 2020, Tian et al. [134] theoretically proposed that a near-unity absorption could happen on an all-dielectric metasurface with quasi-BICs, when the material absorption rate matched with the radiative decay rate (Figure 6A). Dai et al. [53] proposed a mechanism for perfect reflection called coherent perfect reflection (CPR), which was raised from interband coupling between two propagating modes so the forward transmission of light could be eliminated under appropriate complex coupling coefficients. Besides, Wong et al. [55] conceived an idea for perfect isolation of light from topological theory, upon a nonreciprocal metasurface composed of dimer unit cells interacting with a static magnetic field.

FIGURE 6

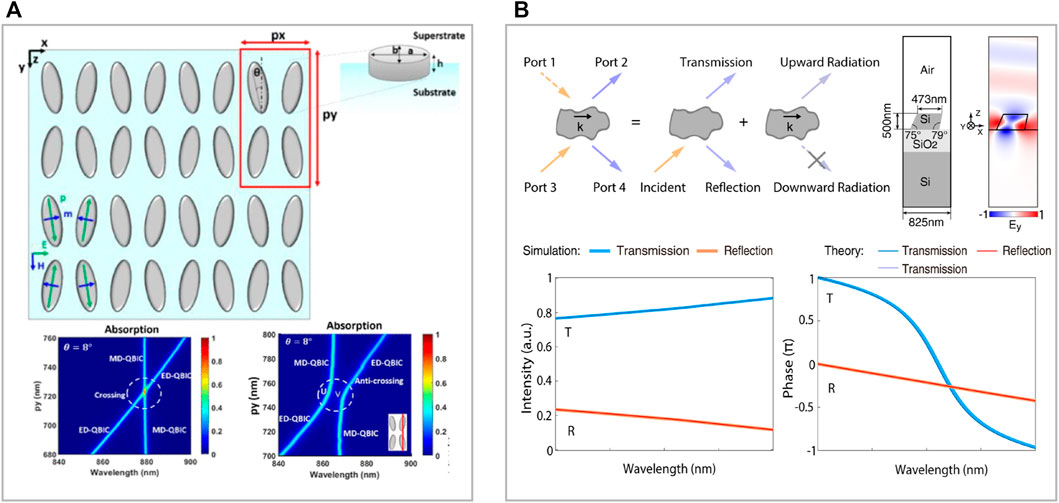
FIGURE 6. Light manipulation in intensity and phase. (A) High-Q silicon metasurface and its absorption spectra [134], copyright American Chemical Society. (B) Intensity flatten phase shifting based on the unidirectional radiation resonance [135], copyright De Gruyter.

Besides, phase is also a key attribute of light that plays important roles in many scenarios. The modulation of phase is as straightforward as intensity, since both of them are related to the tuning of the resonances themselves. As an example, a thermo-optic phase-shifter utilizing the high-Q quasi-BICs was reported [136]. However, phase-only modulation, namely the phase modulation without the change of intensity, is even more important for applications ranging from three-dimensional video projection, flat metalens optics, to optical phased arrays and light detection and ranging.

Although perfect phase-only modulation is difficult, much effort was devoted for intensity-flatten phase modulation, with the key concept of making the resonance operating under over-coupled status. For instance, Kwon et al. [137] experimentally demonstrated nano-electromechanical tuning of gratings associated with quasi-BICs in the telecom wavelength. They realized a spectral shift over 5 nm, with absolute intensity modulation over 40%, modulation speed exceeding 10 kHz, and a phase shift of 144° with a bias of 4 V. Salary et al. [138] proposed an electro-optically tunable all-dielectric metasurface composed of elliptical silicon nanodisks for the same purpose. By applying bias voltage, the electro-optical driven Huygens mode produced a dynamic phase span of 240° while maintaining an average transmission amplitude of 0.77, giving rise to a unevenness of about 25%.

Recently, it was reported by Zhang et al. [135] that perfect phase-only modulation was possible in theory with the assistance of the UGRs (Figure 6B). As mentioned, UGRs are connected to single-sided topological polarization singularities. A UGR mandates the light transmitting to only one out-going port without other choices, which creates perfect phase-shifting upon the transmission if nonradiative loss is negligible. The unevenness of transmission intensity could be lower than 10% with nonradiative Q > 8,000 which was feasible in state-of-art fabrication process.

3.5 Polarization Conversion

Polarization is a critical and fundamental attribute of electromagnetic waves and the polarization control has been widely used in optical communications [139], nonlinear optics [140], imaging [141], etc. Besides cascading polarizers and waveplates to regulate the polarization, periodic structures including the metasurfaces and PhC slabs are promising platforms to achieve the polarization conversion [52, 139, 142–146], by manipulating the polarization singularities in radiation.

To be specific, Khan et al. [142] reported a single-layer, mirror-symmetric anisotropic metasurface constructed of fish-like unit cells to demonstrate both the linear cross-polarization conversion and linear-to-circular polarization conversion in X-band, as illustrated by Figure 7A. Besides, broadband linear-to-circular polarization conversion in the terahertz region with almost unity conversion efficiency was demonstrated by Chang et al. [144] based on the birefringent metasurface. In 2021, Wang et al. [145] proposed a monolayer all-dielectric metasurface composed of dimerized nanopillars shown in Figure 7B, which generated arbitrary polarization on the Poincaré sphere from the unpolarized input light. This effect was equivalent to an “all-in-one” full Poincaré sphere polarizer. In addition, Yu et al. [143] reported a dynamic control of polarization conversion depending on the metasurfaces with electrically tunable refractive indices for the metasurface antennas.

FIGURE 7

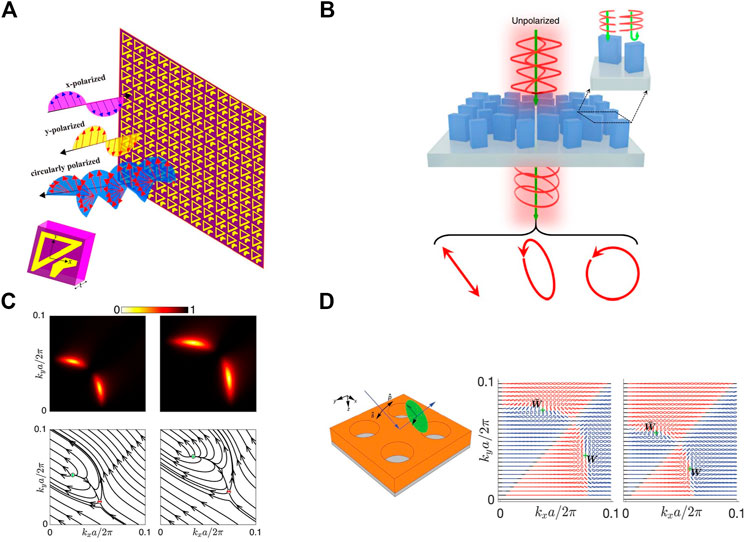
FIGURE 7. (A) fish-like metasurface converting linear polarization to orthogonal-linear and circular polarization [142], copyright Springer Nature Ltd. (B) Dimerized nanopillars generating linear, elliptical and circular polarization regardless of input polarization [145], copyright Springer Nature Ltd. (C) Maps of reflection coefficient and vector field of reflection in momentum space in the polarization conversion [52], copyright American Physical Society. (D) PhC slab manipulating incident polarization to arbitrary polarization in reflection [146], copyright Wiley-VCH GmbH, Weinheim.

Recently, 2D PhC slab structures were employed to manipulate the polarization without tuning the structural parameters [52, 146]. In particular, Guo et al. [52] achieved complete polarization conversion between linear polarizations, indicating the full energy exchange between p- and s-polarized incident lights; in addition, they proved such polarization conversion was topologically protected owing to the winding vector of the complex reflection coefficient. Complete polarization conversion happened at the vortex center, where a nonzero winding number (+1 or −1) in momentum space gave rise to a zero reflection coefficient, which is shown in Figure 7C. More interestingly, they revealed the relationship between the complete polarization conversion and the integer topological charges, namely the BICs. Given that the BICs correspond to the vanishing points of out-going coupling coefficients, they always appeared on the curves that supported complete polarization conversion in momentum space, thus bridging the phenomena with topological singularities.

Furthermore, arbitrary polarization conversion was proposed in a lossless 2D PhC slab [146]. Namely, by tuning the incident light with any given polarization towards a given direction that fell into a wide range of frequency, the polarization of the reflected light could cover the whole Poincaré sphere. Figure 7D shows the result of the reflected polarization under s-polarized incidence for frequency 0.402 × 2πc/a and 0.405 × 2πc/a, in which a is the lattice constant. Complete polarization conversion occurred at W point where all the s-polarized incidence converted to p-polarized, related with the topological property of the scattering matrix [52]. Moreover, with losses, the 2D PhC slab system could still generate arbitrary output polarization if the input was p- or s-polarized.

3.6 Spectral and Chiral Sensing

Given that topological polarization singularities possess exotic characteristics upon the radiation fields, it is reasonable to utilize them for sensing the surrounding environment. In particular, the high-Q nature of integer charges (BICs), and the chiral responses of half charges (CPs) are two promising features. In a perturbated environment, the ideal BICs transform to quasi-BICs with shifted resonance wavelengths while remaining considerably high Qs, thus providing the capability of sensing small refractive-index changes from spectral observation. High sensitivity refractive index (RI) sensing in chemical and biological processes has been realized in many high-Q resonators [147–157]. The RI sensors based on BICs realized by dielectric metasurfaces and PhC slabs have also shown promising performances in figure-of-merit (FOM) and detection-limit (DL) [158, 159]. On the other hand, since chiral responses observed from the reflected or transmitted light can be used to distinguish the chirality of targets, chiral sensing were realized accordingly [160]. In addition, although not directly utilizing the polarization singularities, it is noteworthy to mention a class of novel methods that use the EPs to improve sensing performance [161–170], given by the underlying connections to the polarization singularities.

For instance, in 2017, Liu et al. [158] experimentally demonstrated RI sensing in a wavelength range of 1,400, −, 1,600 nm by applying the BICs in PhCs, which showed great potential for label-free optical biosensors. To further promote the sensing performance, it was important to suppress the out-of-plane scattering loss caused by fabrication imperfections to improve the Qs. Following this strategic, Lv et al. [159] adopted the merging BIC design to RI sensing, which significantly promoted the DL performances in practice owing to the higher Qs (Figure 8A). However, the sensitivity of RI sensors are also related to the field overlap between the optical resonances and the targets embedded in surrounding environment. Methods such as breaking the in-plane symmetry or using low-contrast materials have been developed on PhC slabs [171] and metasurfaces [172] platforms for high-sensitivity hyper-spectral bio-molecular detection.

FIGURE 8

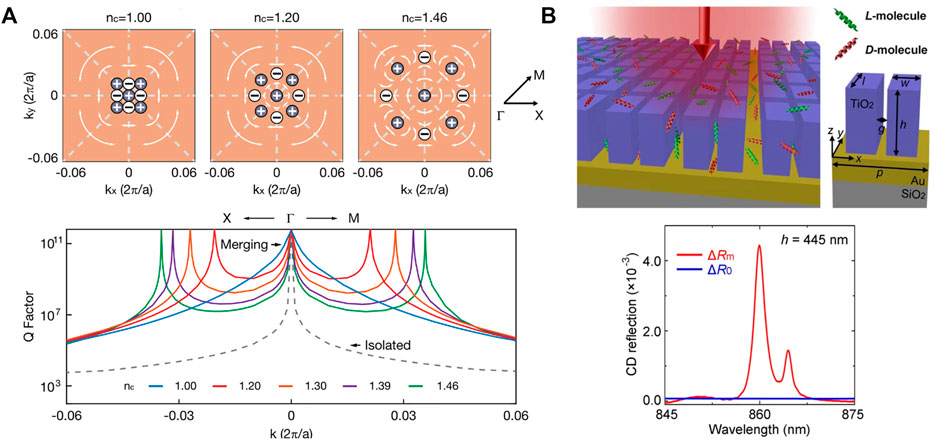
FIGURE 8. Refractive index and chiral sensing applications. (A) Topological charge evolution of merging BICs and the Qs with refractive index variation [159], copyright IEEE. (B) Comparison of CD reflection spectrum of the BICs metasurface enhanced chiral layer and the bare chiral layer [160], copyright American Chemical Society.

On the other hand, chiral sensing is desired in medical and biological applications. Since many biochemical compounds are chiral in nature, circular dichroism (CD) spectroscopy is utilized for the enantiomer-specific analysis of chiral samples. It is noteworthy that certain resonant nanostructures can significantly enhance the circular dichroism responses and improve the sensitivity of spectroscopy as well as photochemical, and thus ehannce the sensitivity of chiral sensing [173]. In 2019, Koshelev et al. [174] investigated the effect of detuning between the electrical and magnetic dipole resonances in silicon nano-cylinders in which the optical chirality at the nanoscale could be greatly enhanced. Later in 2020, Chen et al. [160] demonstrated the acquisition of CD spectrum and molar concentration over an individual metasurface with a high sensitivity (Figure 8B). Owing to the high-Q resonances, a hyperchiral field enhancement of the CD signal by a factor of 59 was observed, together with a large FOM of 80.6 in the detection of molar concentration, and thus it became a promising mythology in food industry, medical diagnostics, and drug development.

The EPs belong to a type of topologically non-trivial diabolic points. In 2017, for the first time, Chen et al. [170] proposed the scheme of using the micro-cavities operated at non-Hermitian spectral degeneracies for sensing. Owing to the complex-square-root dependency near an EP, the frequency splitting scaled as the square root of the perturbation strength, and hence, led to larger responses from small perturbation than that from traditional dispersion relations. This method paved the way for the sensors with unprecedented sensitivity. It is noteworthy that as mentioned in Section 2.1, the EPs are accompanied with polarization singularities, namely half-charges. Although not reported yet, we are optimistic to see the polarization singularity raised from EPs being utilized for sensing in the future.

3.7 Photonic Integration

Topological polarization singularities provide a vivid picture for light manipulation, which is useful in eliminating radiations, suppressing scatterings, and creating directional emitting, and thus shed light on the possibilities of photonic integration. Specifically, the superior photon confinement ability of the BICs leads to the ultra-high Q, ultra-narrow linewidth and low propagation loss, and the merging of half charges upon a single-side may boost the applications requiring unidirectional emission. Hereby we introduce some devices as examples, including waveguides [175–178], filters [179], couplers [43] and lasers [180].

By using BICs to confine light vertically, Zhang et al. [176] and Lin et al. [177] demonstrated waveguiding in PhC slabs. These works demonstrated the possibility to manipulate the radiation lifetime and spatial dispersion of BIC in a cooperative way. The BIC-based in-plane waveguiding was also utilized in the topological edge state in Zhang et al.'s work [175].

Recently, a new photonic platform with a low-refractive index material (Polymer) patterned on a high-refractive-index substrate (LiNbO₃) was demonstrated for integrated BIC-based devices including waveguides, microcavities, directional couplers, and modulators [178, 181]. This platform overcame the challenge of fabricating nano-scale structures upon high-refractive-index dielectric materials. The schematic of the platform in [178] is shown in Figure 9A. Specifically, the waveguide width was optimized and a BIC was observed by tuning the coupling strength between the TM bound mode and TE continuous mode. Benefiting from the BIC, the propagation loss of a straight waveguide was reduced to almost zero. For bent waveguides, the bending loss was suppressed in a similar way by changing the bend radius and waveguide width. Besides, the BICs also provided an ultra-high Q, showing an intrinsic Q over 10⁶ in microdisk cavities.

FIGURE 9

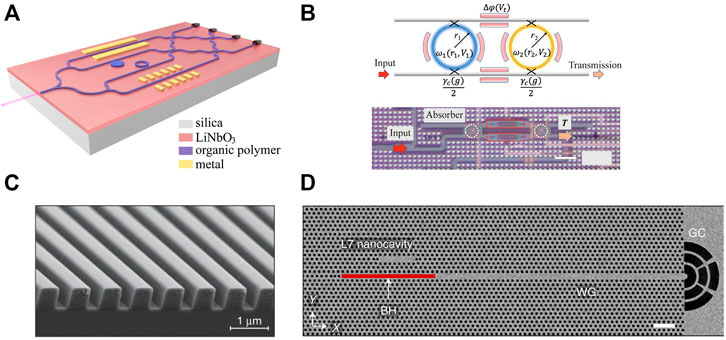
FIGURE 9. BIC-based photonic integrated components, including (A) photonic circuit where low-refractive index material was patterned on a high-refractive-index substrate. Adapted with permission from [178] copyright The Optical Society, (B) filter [179], copyright American Physical Society. (C) Grating coupler [43], copyright Springer Nature Ltd. and (D) laser [180], copyright Springer Nature Ltd.

Gong et al. [179] implemented a BIC filter based on silicon photonic integrated circuits (PICs). The BIC filter was composed of two cascaded ring resonators side-coupled to two bus waveguides, as illuatrated in Figure 9B, with the two resonance frequencies ω₁and ω₂ both tunable. By tuning the phase delay between the two rings to a multiple of π, the working state approached a near-FP-BIC [37] point, resulting in a filter performance with a near-unity transmission at $ω_{0} = \frac{ω_{1} + ω_{2}}{2}$ and a near-zero transmission at ω₁ and ω₂.

On the other hand, unidirectional guided resonances (UGRs) proposed by Yin et al. [43] paves the way to energy-efficient grating couplers. The UGRs only radiate toward one side of the PhC slab with the radiation at the other side eliminated (Figure 9C). The asymmetry ratio of the directional radiation reached 27.7 dB which indicated 99.8% of the power radiated toward the target direction. Moreover, the effect was maintained within a reasonably broad bandwidth (over 90% within a 26 nm bandwidth), and was proved to be effective for a coupling angle ranging from 5 to 11°.

The ultra-narrow linewidth of the BICs also facilitates the on-chip integrated lasers. Yu et al. experimentally an demonstrated a Fano BIC laser with a 5.8 MHz linewidth based on InP PhC slab buried within Si wafer [180](Figure 9D). Fano interference occurred between the discrete mode of a nanocavity and the continuum modes of a waveguide. The propagating modes in the waveguide destructively interfered with the nanocavity mode at the BIC wavelength, thereby turning the ordinary leaky mode into a BIC. Assuming an ideal BIC, a Fano mirror with total reflection would be formed in the waveguide region. Therefore, the light would be confined in the nanocavity and the region within the Fano mirror. The Q of the Fano BIC was significantly increased because photons were generated in the active region but stored in the passive region. Furthermore, the long lifetimes of the photons in the passive area can offset part of the quantum fluctuations caused by spontaneous radiation in the active area. The Fano BIC laser showed good mode selectivity and its lasing linewidth met the requirement of coherent optical communication.

4 Discussion

In previous sections, we have reviewed the fundamentals and applications of polarization singularities that are defined upon the far-field radiations. As elaborated, the polarization singularities are topological in nature, with their existence and continuous evolution robust in the momentum space. From the view of science, polarization singularities reflect the “inside information” of a system which becomes observable since the escaping photons carry it out. On the other hand, polarization singularities establish abstract and primitive concepts for depicting, and further manipulating lights, and then pave the way to many applications as discussed.

For an outlook, several points might be noteworthy. From theoretical point of view, it is essential to build up a comprehensive connection between radiation topology, where polarization singularities are defined, and non-Hermitian topology, where generic topological band theory is developed upon. Given that radiation raises non-Hermiticity, it is expected that non-trivial intrinsic band topology might lead to observable manifestation in radiation field, that bridges to polarization singularities. Given that many exotic phenomena were discovered in non-Hermitian systems, it is necessary to study how the radiation raises and represents unique topology landscapes for deeper understanding of the physics. For instance, both the BICs and EPs carry topological charges in their far-field radiation, but only the latter are associated with nontrivial Chern numbers. Besides, from the view of technology, there’s still much to explore about extending the idea of polarization singularity manipulation to more materials, devices, scenarios and applications. We are optimistic to foresee that the utilization of polarization singularities will be boosted by the methodology of topological photonics, thus bring essential promotion to many key applications, including optical communication, LIDAR, AR/VR, and bio-sensing.

Author Contributions

CP organized the article. FW, CP, and XY composed Section 1, 2, and 4. All the authors contributed to Section 3.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 61922004 and 62135001), China Postdoctoral Science Foundation funded project (Grant No. 2021M690239), National Key Research and Development Program of China (2020YFB1806405), and Major Key Project of PCL (PCL2021A14, PCL2021A04).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Poincaré H. Théorie mathématique de la lumière: cours de Physique Mathématique. Paris: Georges Carré Editeur (1889).

Google Scholar

2. Soskin MS, Vasnetsov MV. Singular Optics. Prog Opt (2001) 42:219–76. doi:10.1016/S0079-6638(01)80018-4