Multidimensional Discrete Chaotic Maps

In this paper, the general concept of multidimensional discrete maps is presented. Moreover, new and fundamental results show the invariance of the bifurcation points from periodic to chaotic behavior. Numerical examples regarding the multidimensional cases of the logistic map, the complex-valued Ikeda map, and the multivariable Henon map are reported.

1 Introduction

The role of iterative nonlinear maps has been fundamental both regarding the possibility to explain complex nonlinear dynamics and their elegant attractors in more detail [1, 2] and regarding their practical applications [3–6]. In fact, in [5, 6], the possibility of using logistic maps to make computations and the actual, timely use of them to generate secure code numbers are discussed. Discrete maps are easily handled by computers and can be processed by powerful available microcontrollers. Therefore, today, their use in less expensive applications is becoming possible starting from the previous considerations. As an example, chaos computing is a timely topic as it consists in using chaotic systems for computation. In particular, chaotic discrete-time systems can be designed to reproduce all types of logic gates [7–9]. This suggests the actual interest in exploring iterative maps for real-world advanced applications.

It is, therefore, of particular interest to discover new high-dimensional iterative chaotic maps. Under this perspective, the idea that is proposed in this contribution is the introduction of multidimensional discrete maps. The term “multidimensional” must not be considered as the classical multidimensional systems theory [10] in this context, but rather refers to the cases discussed in previous works [11, 12], where a two-dimensional matrix logistic map has been reported, discussing the not-explosivity condition referred to the choice of the initial conditions. Besides these results, the intriguing topic of multidimensional chaotic maps is quite absent in the literature.

Referring to this class of systems, a particular property regarding the so-called bifurcation parameter invariance is shown in this contribution. This means that the bifurcation points are invariants in the multidimensional system with respect to the scalar one. Moreover based on some combinatory considerations, the concept of “almost similarity” of the bifurcation diagrams, in periodic windows, is introduced.

The paper is organized as follows. In Section 2, the main concepts of iterative maps are reported also including some mathematical preliminaries. The core of the paper is concentrated in Section 3, where the main definitions and facts regarding the multidimensional nonlinear maps are dealt with. In order to clearly explain the concepts included in the previous section, extensive numerical results are reported in Section 4, even if the theory is quite general, the numerical results are related to the logistic map, the Ikeda map, and the Henon map. The conclusive Section 5 will draw a summary of the presented results and defines the perspectives of the research.

2 Iterative Maps and Mathematical Preliminaries

Definition 1. An iterative 1D discrete map is defined as a map of the form

$x\left(k+1\right)=f\left(x\left(k\right),\mathrm{\alpha }\right)(1)$

Where $x\in \mathbb{C}$ is a scalar quantity, f is a nonlinear analytic function, and $\alpha \in {\mathbb{C}}^m$ is the parameters vector. The function is the said map, moreover, x is assumed to belong to the complex set.

Of course, if $\mathrm{x}\in {\mathbb{C}}^{m\times 1}$, the map is called an mD discrete map. The dynamical behavior of the map is characterized both by the parameter vector and by the initial condition x₀.

Definition 2. The 1D discrete map:

$x\left(k+1\right)=ax\left(k\right)\left(1-x\left(k\right)\right)(2)$

where $a\in {\mathbb{R}}^{+}$ with a ≤ 4 and $x(k)\in \mathbb{R}$ is the logistic map [1].

The behavior of the logistic map (2) is synthesized thanks to the bifurcation diagram reported in Figure 1.

FIGURE 1

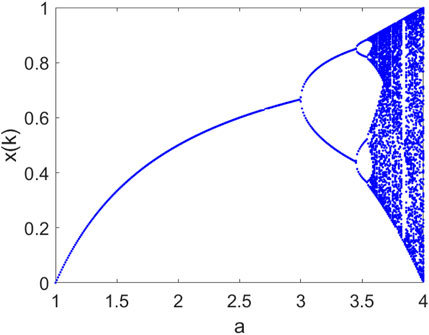
FIGURE 1. Bifurcation diagram of the logistic map in Eq. 2 with respect to a.

The logistic map represents the easiest map with the stereotyped behavior of a complex system [1].

The bifurcation diagram includes, by varying the parameter a, fixed points, oscillatory behavior, intermittency, and chaos. The various studies about logistic 1D maps make us consider them both as a reference example for further study in discrete maps and a paradigm of complex behavior to take into account in more complex continuous-time systems. Moreover, it is literature, it is considered a reference point in the generation of complex lattices by coupling more logistic maps [13].

Due to the importance of the logistic map, attention is devoted in particular to the case of multidimensional discrete maps generated by the logistic map. In the literature, in fact, attention has been devoted to the iterative logistic map of matrices [11, 12] for matrices belonging to ${\mathbb{R}}^{2\times 2}$. In the following, we will expand the research on multidimensional maps based on logistic maps but show that the main results referring to the bifurcation invariance are quite general, and also the multidimensional case considering the Ikeda map, defined in the complex domain, and the Henon map in the multivariable domain will be discussed.

Definition 3. The complex-valued Ikeda map is represented by the following equation:

$z\left(k+1\right)=p+Bz\left(k\right)e^{\frac{j\rho }{a\left(|z\left(k\right){|}^2+1\right)}}(3)$

where $z\in \mathbb{C}$, $p\in {\mathbb{R}}^{+}$, $B\in {\mathbb{R}}^{+}$, and $\rho \in {\mathbb{R}}^{+}$ are system parameters [14].

It is also considered an analytic function in the complex domain of the logistic map. The onset of chaos can be observed by varying the parameter p, while fixing B = 0.76, ρ = 0.4, and a = 6, as shown in the bifurcation diagram reported in Figure 2.

FIGURE 2

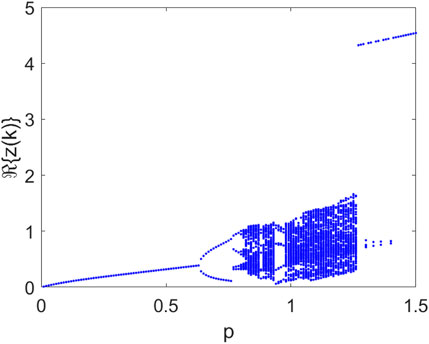
FIGURE 2. Bifurcation diagram of the Ikeda map in Eq. 3 with respect to p. Other parameters: B = 0.76, ρ = 0.4, and a = 6.

Definition 4. The Henon map is a two-variable nonlinear map described by the following equations:

$\begin{array}{c}\hfill x\left(k+1\right)=1+y\left(k\right)-a{x}^2\left(k\right)\hfill \\ \hfill y\left(k+1\right)=bx\left(k\right)\hfill \end{array}(4)$

where $a\in \mathbb{R}$ and $b\in \mathbb{R}$ are parameters [15]. Its behavior can be derived from the bifurcation diagram obtained by varying a with b = 0.3 as reported in Figure 3.

FIGURE 3

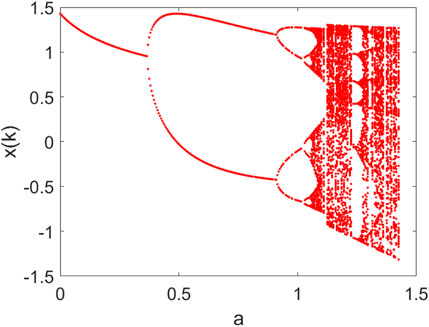
FIGURE 3. Bifurcation diagram of the Henon map in Eq. 4 with respect to a. Other parameters: b = 0.3.

3 Multidimensional Nonlinear Discrete Maps

Let us consider the scalar 1D map in Eq. 2. If, instead of x being a scalar, a matrix $\mathrm{X}\in {\mathbb{C}}^{N\times N}$ is considered in the vectorial function F, it is

$\mathrm{X}\left(k+1\right)=\mathrm{F}\left(\mathrm{X}\left(k+1\right),\alpha \right)(5)$

which is called a multidimensional discrete map. Therefore, the matrix

$\mathrm{X}\left(k\right)=\left[\begin{array}{cccc}\hfill x_{11}\left(k\right)\hfill & \hfill x_{12}\left(k\right)\hfill & \hfill \dots \hfill & \hfill x_{1N}\left(k\right)\hfill \\ \hfill x_{21}\left(k\right)\hfill & \hfill x_{22}\left(k\right)\hfill & \hfill \dots \hfill & \hfill x_{2N}\left(k\right)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill x_{N1}\left(k\right)\hfill & \hfill x_{N2}\left(k\right)\hfill & \hfill \dots \hfill & \hfill x_{NN}\left(k\right)\hfill \end{array}\right](6)$

contains N × N elements which vary according to the function F.

Moreover, the concept is generalized to the case of mD maps, i.e., maps with more variables. In fact, in this case, F is a function whose arguments are instead of the scalars x₁, x₂, and x_m, respectively the matrices X₁, X₂, and X_m, each belonging to the set ${\mathbb{C}}^{N\times N}$.

Easily speaking the multidimensional map is generated by a scalar iterative maps where, instead of the original scalar variable, square matrices are considered. Moreover, if the function f is analytic, the multidimensional iterative map achieves particular properties.

Definition 5. An iterative map is said to be explosive if it does occur

$\underset{k\to +\infty }{\lim }\Vert x\left(k\right)\Vert \to \infty (7)$

being ‖⋅‖ a matrix norm if the map is multidimensional, the Euclidean norm if it is considered an mD map, the absolute value if a 1D map is considered.

Theorem 1. The iterative multidimensional map is not explosive if the matrix X(0) has eigenvalues belonging to the basin of attraction of the scalar map f with an analytic function.Proof. In fact, let x(0) be in the basin of attraction of f being

$x\left(k+1\right)=f\left(\alpha ,x\left(k\right)\right)(8)$

Let us consider the corresponding multidimensional map defined as

$\mathrm{X}\left(k+1\right)=\mathrm{F}\left(\alpha ,\mathrm{X}\left(k\right)\right)(9)$

with X(0) = TX_D(0)T⁻¹, X_D(0) being a diagonal matrix containing the eigenvalues of X(0), and $\mathrm{T}\in {\mathbb{R}}^{N\times N}$ being the matrix of its eigenvectors.Therefore, it is

$\begin{array}{c}\mathrm{X}\left(1\right)=\mathrm{F}\left(\alpha ,\mathrm{T}{\mathrm{X}}_D\left(0\right){\mathrm{T}}^{-1}\right)\hfill \\ \mathrm{X}\left(2\right)=\mathrm{F}\left(\alpha ,\mathrm{T}{\mathrm{X}}_D\left(1\right){\mathrm{T}}^{-1}\right)\hfill \\ ⋮\hfill \\ \mathrm{X}\left(k+1\right)=\mathrm{F}\left(\alpha ,\mathrm{T}{\mathrm{X}}_D\left(k\right){\mathrm{T}}^{-1}\right)\hfill \end{array}(10)$

due to the fact that F is analytic and therefore with the peculiarity to be expressed in a polynomial form, it does result in

$\mathrm{X}\left(k+1\right)={\mathrm{T}}^{-1}{\mathrm{F}}_D\left(\alpha ,{\mathrm{X}}_D\left(k\right)\right)\mathrm{T}(11)$

where F_D is a diagonal matrix made by N maps f_i(α, x_i(k)), with x_i(0) = X_D(i, i) and i = 1, … , N.Therefore, from the last consideration, if the eigenvalues of X(0) that include the quantities X_D(i, i) are chosen in the basin of attraction of f, the multidimensional map is not explosive. □.Example. Let us consider the logistic map

$x\left(k+1\right)=ax\left(k\right)\left(1-x\left(k\right)\right)(12)$

The associated multidimensional map is given by

$\mathrm{X}\left(k+1\right)=a\mathrm{X}\left(k\right)\left(\mathrm{I}-\mathrm{X}\left(k\right)\right)(13)$

Let X(0) = TX_D(0)T⁻¹, we have

$\begin{array}{c}\mathrm{X}\left(k+1\right)=a\mathrm{T}{\mathrm{X}}_D\left(k\right){\mathrm{T}}^{-1}\left[\mathrm{I}-\mathrm{T}{\mathrm{X}}_D\left(k\right){\mathrm{T}}^{-1}\right]=\hfill \\ \mathrm{T}\left[a{\mathrm{X}}_D\left(k\right)\left(\mathrm{I}-{\mathrm{X}}_D\left(k\right)\right)\right]{\mathrm{T}}^{-1}\hfill \end{array}(14)$

It is therefore

${\mathrm{F}}_D\left(\alpha ,{\mathrm{X}}_D\left(k\right)\right)=a{\mathrm{X}}_D\left(k\right)\left(\mathrm{I}-{\mathrm{X}}_D\left(k\right)\right)(15)$

which is a diagonal matrix where each term represents the scalar map (12). Therefore, if each λ_i = X_D(i, i) belongs to the interval $\left]\mathrm{0,1}\right[$ that is the basin of attraction of the logistic map, the multidimensional map is not explosive.Definition 6. Given a dynamical nonlinear system s₁ with a defined bifurcation diagram, we say that a dynamical nonlinear system s₂ has an almost equal bifurcation diagram if it exists a set of initial conditions leading to the same bifurcation points of s₁ with non-null probability.

Theorem 2. Let us consider the multidimensional map as previously defined and the relationship (11). If the map is not explosive, under the conditions given in Theorem 1, the multidimensional map related to it assumes for each variable a chaotic behavior exactly at the same parameter values.Proof. We are guaranteed that each term of the diagonal matrix F_D has a diagonal trend. The real trend of X(k + 1) is therefore the linear combination of the n chaotic signal by the matrices T and T⁻¹ and therefore the general matrix is made by n² chaotic signals [16]. □Remark 1. Let us consider a multidimensional iterative map of dimension N × N. Assuming the same conditions of Theorem 1, the bifurcation diagram is almost equal to that of the generating map as regards the entire bifurcation route to chaos.

4 Numerical Results

In this section, numerical investigations on the behavior of multidimensional chaotic maps are reported. We will consider the paradigmatic case of the logistic map and the cases of the two-dimensional Henon map and the complex-valued Ikeda map. In the following, without lack of generality, initial conditions are chosen as symmetric matrices; similar results can be gained with non-symmetrical initial conditions.

4.1 Logistic Map

The multidimensional logistic map is described by

$\mathrm{X}\left(k+1\right)=a\mathrm{X}\left(k\right)\left(\mathrm{I}-\mathrm{X}\left(k\right)\right)(16)$

where $\mathrm{X}\in {\mathbb{R}}^{N\times N}$ and $\mathrm{I}\in {\mathbb{R}}^{N\times N}$ is the identity matrix. We refer the reader to the Appendix 1 for the explicit equations of the multidimensional map. Let us consider the bifurcation diagrams obtained varying parameter a for the cases N = 2, N = 3, N = 4, and N = 5 reported in Figure 4. As it can be observed by comparison with the bifurcation diagram of the scalar logistic map, shown in Figure 1, the bifurcation points are consistent. The Lyapunov exponents for the case N = 2 when a = 4 are λ₁ = 0.7113, λ₂ = 0.6812, λ₃ = 0.6732, and λ₄ = 0.6728. We recall that the Lyapunov exponent for the scalar logistic map when a = 4 is λ = 0.6722. A suitably defined return map for the multidimensional Logistic map with N = 2 and a = 4 is introduced in the Appendix 2.

FIGURE 4

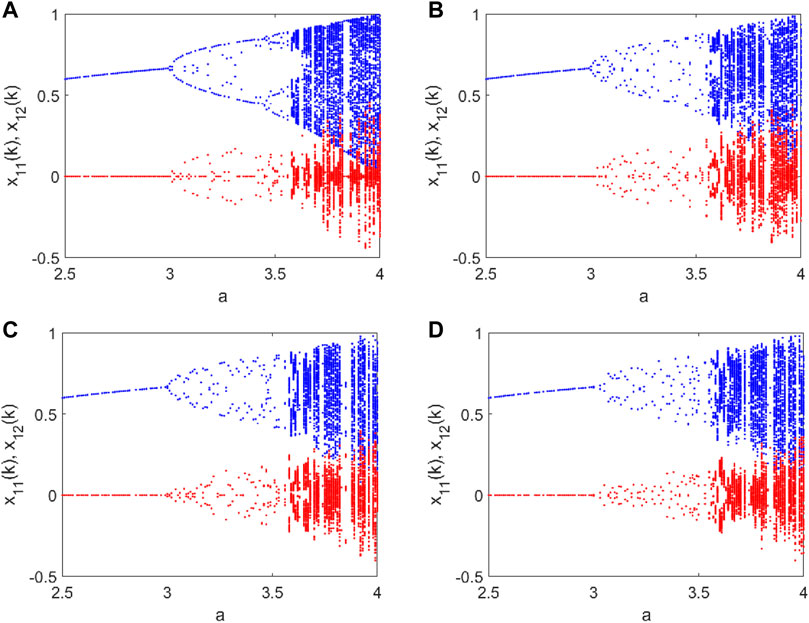
FIGURE 4. Bifurcation diagram of the multidimensional logistic map in Eq. 16 with respect to a: (A) N = 2; (B) N = 3; (C) N = 4; and (D) N = 5.

The different behavior of the branches in the periodic windows is due to the role of initial conditions. Let us consider the period-2 window, fixing parameter a = 3.1. Two possible behaviors can arise as the maps in the diagonal of X can show an in-phase period-2 or a counter-phase period-2. This leads to the two plots reported in Figure 5. As it can be seen, in the first case, the off-diagonal maps converge to zero since the two contributions of the diagonal map make the off-diagonal map converge.

FIGURE 5

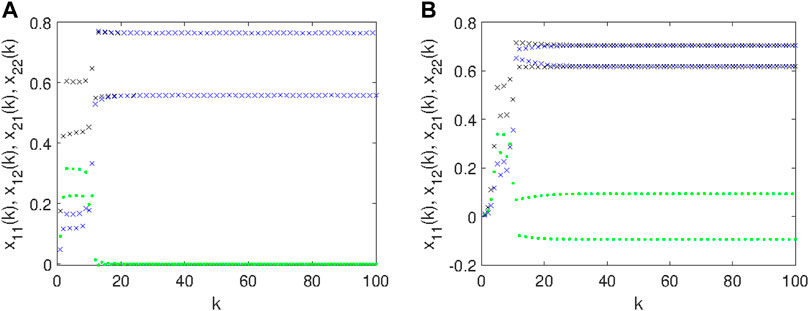
FIGURE 5. Different periodic behavior of the multidimensional logistic map in Eq. 16 with N = 2 and a = 3.1: (A) In-phase periodicity of the diagonal maps x₁₁(k) and x₂₂(k) leading to convergent off-diagonal maps x₁₂(k) and x₂₁(k); (B) anti-phase periodicity of the diagonal maps x₁₁(k) and x₂₂(k) leading to period-2 behavior also in the off-diagonal maps x₁₂(k) and x₂₁(k).

A similar condition occurs for the period-4 window, fixing a = 3.5, as four possible behaviors emerges with one leading to off-diagonal maps converging to zero, as reported in Figure 6.

FIGURE 6

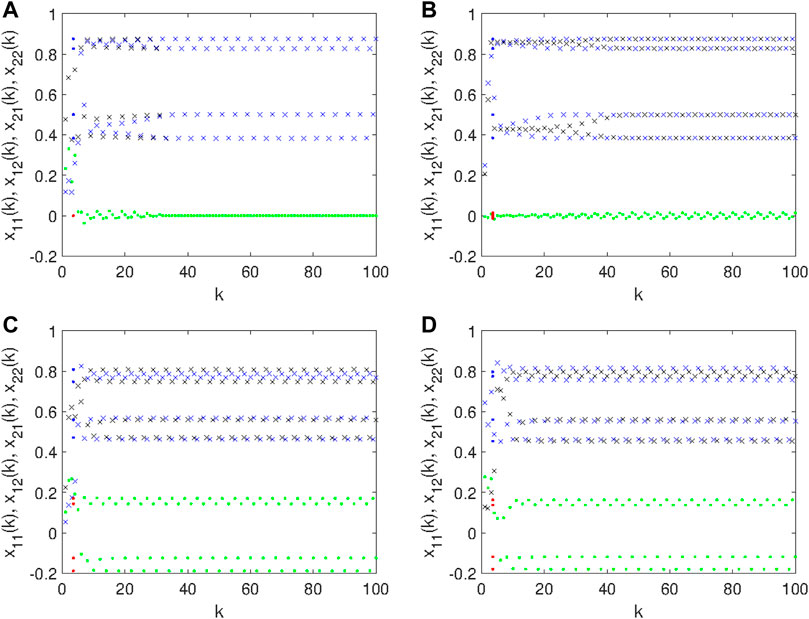
FIGURE 6. Different periodic behavior of the multidimensional logistic map in Eq. 16 with N = 2 and a = 3.5: (A) In-phase periodicity of the diagonal maps x₁₁(k) and x₂₂(k) leading to convergent off-diagonal maps x₁₂(k) and x₂₁(k); (B–D) not in-phase periodicity of the diagonal maps x₁₁(k) and x₂₂(k) leading to period-4 behavior also in the off-diagonal maps x₁₂(k) and x₂₁(k).

This allows us to determine the probability of having off-diagonal maps converging to zero as $p_{o\mathit{ff}}=\frac{r}{r^N}$, where r is the periodicity. In Figure 7, the probability p_off to obtain off-diagonal converging maps from periodic behavior is reported as a function of N over 100,000 different initial conditions in the periodic windows r = 2 and r = 4, respectively.

FIGURE 7

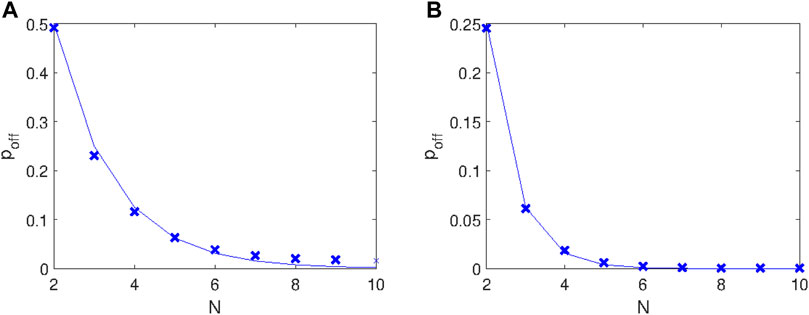
FIGURE 7. Probability of having off-diagonal maps converging to zero in the multidimensional logistic map with N = 2: (A) Period-2 window (r = 2); (B) period-4 window (r = 4). The continuous lines refer to the exact formula $p_{o\mathit{ff}}=\frac{r}{r^N}$, while the markers indicate the probability calculated over 100,000 different initial conditions.

It appears evident that the initial conditions play a crucial role in multidimensional maps, also when the global behavior is periodic. Thus a strong multi-stable behavior is elicited by the multidimensionality of the system. In Figure 8, we reported the bifurcation diagram for N = 4 limited to the period-2 window for 100 different initial conditions. As can be observed, the two branches of the scalar logistic map enclose all the admissible periodic states. The initial conditions, thus, also play a role in the amplitude of the observed states. We remark also that the symmetry of the matrix X(0), chosen as initial conditions, leads to synchronized symmetric off-diagonal variables, as derived directly from Theorem 1.

FIGURE 8

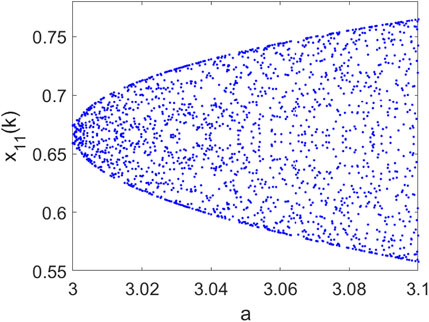
FIGURE 8. Bifurcation diagram of the multidimensional logistic map in Eq. 16 with respect to a, for N = 4, in the period-2 window. Points represent the steady state for 100 different realizations for each value of a.

We remark that the invariance of the bifurcation points is independent from N, as expressed by Theorem 2. Therefore, considering a multidimensional map with a higher values of N, we observe that the bifurcation diagram maintains the bifurcation points of the scalar map, as shown in Figure 9, where the bifurcation diagram for N = 100 and N = 1 are compared in the parameter range $a\in \left[3.7,4\right]$, thus confirming that the results are mathematically well posed.

FIGURE 9

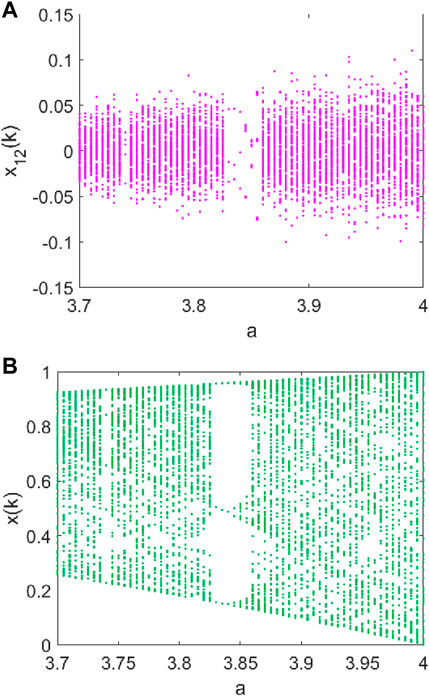
FIGURE 9. Invariance of the bifurcation points for higher values of N: (A) Bifurcation diagram for the multidimensional logistic map with N = 100; (B) bifurcation diagram for the scalar logistic map. Diagrams are evaluated with respect to $a\in \left[3.7,4\right]$.

The parameter range $a\in \left[3.7,4\right]$ contains an odd-periodic window. The scalar logistic map, in fact, presents a period-3 behavior for $a=1+\sqrt{8}$. For values of the parameter a near the odd-periodicity, the scalar logistic map displays an intermittent behavior [3]. This behavior consists of chaotic bursting, interleaved with period-3 behavior. The presence of chaotic bursting for $a=1+\sqrt{8}-10^{-6}$ in the multidimensional logistic map with N = 100 is reported in Figure 10, where the variable x₁₁ is shown, thus further confirming the invariant properties of multidimensional maps. All the other variables in X show a similar bursting behavior.

FIGURE 10

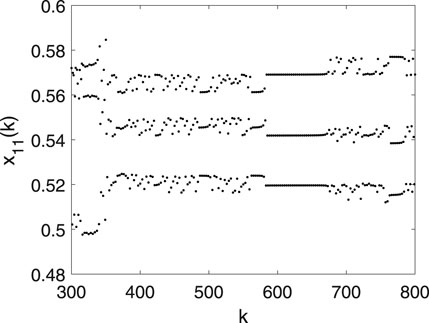
FIGURE 10. Chaotic bursting in the intermittent behavior of x₁₁ shown by the multidimensional logistic map with N = 100 for $a=1+\sqrt{8}-10^{-6}$.

4.2 Ikeda Map

Let us consider the multidimensional extension of the Ikeda map as:

$\mathrm{Z}\left(k+1\right)=p\mathrm{I}+B\mathrm{Z}\mathrm{(k)}{e}^{j\left(\rho \mathrm{I}/a{\left(\mathrm{I}+{\mathrm{Z}}^T\mathrm{Z}\right)}^{-1}\right)}(17)$

where $\mathrm{Z}\in {\mathbb{C}}^{N\times N}$ and $\mathrm{I}\in {\mathbb{R}}^{N\times N}$ is the identity matrix. The bifurcation diagrams obtained for both N = 2 and N = 3 varying the parameter p with B = 0.76, ρ = 0.4, and a = 6, report the real parts of the complex variables for one map of the diagonal elements and one of the off-diagonal elements. As shown in Figure 11, the bifurcation points are invariant with respect to N, while the irregular appearance is given by the sensitivity to initial conditions, still confirming the periodicity windows and the onset of chaos.

FIGURE 11

FIGURE 11. Bifurcation diagram of the multidimensional Ikeda map in Eq. 17 with respect to p: (A) N = 2; (B) N = 3. Other parameters: B = 0.76, ρ = 0.4, and a = 6.

4.3 Henon Map

Let us consider the multidimensional Henon map as

$\begin{array}{c}\mathrm{X}\left(k+1\right)=\mathrm{I}+\mathrm{Y}\left(k\right)-a{\mathrm{X}}^2\left(k\right)\hfill \\ \mathrm{Y}\left(k+1\right)=b\mathrm{X}\left(k\right)\hfill \end{array}(18)$

where $\mathrm{X}\in {\mathbb{R}}^{N\times N}$ and $\mathrm{Y}\in {\mathbb{R}}^{N\times N}$. In order to obtain the bifurcation diagram, we have to recall the proof of Theorem 2. The condition to maintain the invariance of the bifurcation points is the possibility to diagonalize the matrices X and Y with the same eigenvector matrix T. In Figure 12, the bifurcation diagram obtained by choosing two matrices X(0) and Y(0) as initial conditions with the same eigenvector set and with different eigenvector sets are reported for the case N = 2. It is possible to notice that the chaotic window vanishes in this latter case, as the hypothesis of Theorem 2 is not satisfied. Conversely, appropriately choosing the initial matrices allows us to verify the invariance of the bifurcation points also in this case.

FIGURE 12

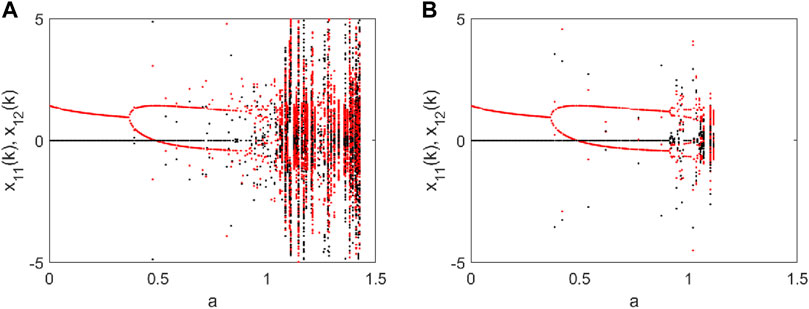
FIGURE 12. Bifurcation diagram of the multidimensional Henon map in Eq. 18 with respect to a: (A) N = 2 and X(0) and Y(0) with the same eigenvector set; (B) N = 2 and X(0) and Y(0) with different eigenvectors. Other parameters: b = 0.3.

5 Conclusions

The multidimensional maps allow us to directly interconnect more signals with similar characteristics. In particular, this aspect is evident referring to the consideration related to the chaotic behavior remarked in the bifurcation diagrams. Moreover, the definition of almost similar bifurcation diagrams gives us strong assurances that the same bifurcation points are observed for the periodic behavior of the multidimensional maps.

The interest in further considering multidimensional maps is also motivated by the fact that nonlinear discrete maps with a higher number of variables are less frequent in literature with respect to scalar discrete maps. The possibility to build matrix-based high-order chaotic systems in discrete-time domain is therefore opened with this paper. This means considering a low-order dynamical system as a gene. From it, the use of matrices instead of scalar state variables should be considered. Even if in the discrete case that a chaotic map is generated from a multidimensional system with the same strange characteristics, in the case of continuous-time multidimensional systems, it is conjectured that hyperchaotic behavior arises.

From an application point of view, the multidimensional discrete maps will be very useful in encryption systems generating instead of one scalar quantity, N² signals that can be changed in real-time varying the multidimensional size. For these applications, a physical implementation of multidimensional maps must be taken into account. An analog implementation is not convenient since it includes more couplings and the use of several analog multipliers. Indeed, the difficulties of the practical realization of the logistic map with analog components discussed in previous work [17] are further amplified. For these reasons, to obtain a straightforward, flexible, and reliable implementation, a digital approach based on microcontrollers or hybrid analog/digital solutions [3] is preferable.

Regarding the Lyapunov exponents, a direct correlation does not exist between the gene scalar map and the corresponding multidimensional map. In fact, in the multidimensional maps, the increase of the variables leads to the use of standard algorithms for computing Lyapunov exponents that are highly computationally demanding. Moreover, from our experiments we can conjecture that the maximum Lyapunov exponent of the multidimensional case is always greater than that of the generating scalar or multivariable map.

The multidimensional maps introduced in this paper can be further generalized by considering networks of multidimensional maps and exploring them for collective behavior and chaos synchronization between two or more coupled multidimensional maps. In this case, the synchronization strategy can be approached by using nonlinear discrete-time Luenberger observers where the observer gains can be designed by using Lyapunov functions in order to guarantee an asymptotically converging error [18]. Another idea is to linearize the error dynamics and to use linear Luenberger observers. Moreover, a Master-Slave strategy can be considered as the nonlinear feedback introduced in a previous study [19], even if it is desirable to achieve the synchronization via lower levels of energy.

As a final remark deriving from the main results of this paper, we can affirm that maintaining the bifurcation points, the multidimensional map confirms the occurrence of the Figenbaum sequence of the original generating scalar map.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Peitgen HO, Jürgens H, Saupe D, Feigenbaum MJ. Chaos and Fractals: New Frontiers of Science, 106. New York, NY: Springer (2004).

Google Scholar

2. Sprott JC. Elegant Chaos: Algebraically Simple Chaotic Flows. Singapore: World Scientific (2010).

Google Scholar

3. Buscarino A, Fortuna L, Frasca M. Essentials of Nonlinear Circuit Dynamics with MATLAB® and Laboratory Experiments. Boca Raton, FL: CRC Press (2017).

Google Scholar

4. Stoyanov B. Double Ikeda Map as a Source of Pseudorandom Numbers. In: AIP Conference Proceedings, 2333. AIP Publishing LLC (2021). p. 070004. doi:10.1063/5.0041614

CrossRef Full Text | Google Scholar

5. Meranza-Castillón MO, Murillo-Escobar MA, López-Gutiérrez RM, Cruz-Hernández C. Pseudorandom Number Generator Based on Enhanced Hénon Map and its Implementation. AEU - Int J Electro Commun (2019) 107:239–51. doi:10.1016/j.aeue.2019.05.028

CrossRef Full Text | Google Scholar

6. Wang L, Cheng H. Pseudo-random Number Generator Based on Logistic Chaotic System. Entropy (2019) 21:960. doi:10.3390/e21100960

CrossRef Full Text | Google Scholar

7. Sinha S, Ditto WL. Computing with Distributed Chaos. Phys Rev E (1999) 60:363–77. doi:10.1103/physreve.60.363

CrossRef Full Text | Google Scholar

8. Ditto WL, Murali K, Sinha S. Chaos Computing: Ideas and Implementations. Phil Trans R Soc A (2008) 366:653–64. doi:10.1098/rsta.2007.2116

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Rogers A, Keating J, Shorten R, Heffernan DM. Chaotic Maps and Pattern Recognition - the XOR Problem. Chaos, Solitons & Fractals (2002) 14:57–70. doi:10.1016/s0960-0779(01)00181-3

CrossRef Full Text | Google Scholar

10. Bose NK. Applied Multidimensional Systems Theory. New York, NY: Springer (1982).

Google Scholar

11. Navickas Z, Smidtaite R, Smidtaite R, Vainoras A, Ragulskis M. The Logistic Map of Matrices. Discrete & Continuous Dynamical Systems-B (2011) 16:927–44. doi:10.3934/dcdsb.2011.16.927

CrossRef Full Text | Google Scholar

12. Navickas Z, Ragulskis M, Vainoras A, Smidtaite R. The Explosive Divergence in Iterative Maps of Matrices. Commun Nonlinear Sci Numer Simulation (2012) 17:4430–8. doi:10.1016/j.cnsns.2012.03.018

CrossRef Full Text | Google Scholar

13. Kaneko K. Theory and Applications of Coupled Map Lattices. In: Nonlinear Science: Theory and Applications. Hoboken, NJ: John Wiley and Sons. (1993).

Google Scholar

14. Ikeda K. Multiple-valued Stationary State and its Instability of the Transmitted Light by a Ring Cavity System. Opt Commun (1979) 30:257–61. doi:10.1016/0030-4018(79)90090-7

CrossRef Full Text | Google Scholar

15. Hénon M. A Two-Dimensional Mapping with a Strange Attractor. In: The Theory of Chaotic Attractors. New York, NY: Springer (1976). p. 94–102. doi:10.1007/978-0-387-21830-4_8

CrossRef Full Text | Google Scholar

16. Baptista MS. Chaos for Communication. Nonlinear Dyn (2021) 105:1821–41. doi:10.1007/s11071-021-06644-4

CrossRef Full Text | Google Scholar

17. McGonigal G, Elmasry M. Generation of Noise by Electronic Iteration of the Logistic Map. IEEE Trans Circuits Syst (1987) 34:981–3. doi:10.1109/tcs.1987.1086230

CrossRef Full Text | Google Scholar

18. Ciccarella G, Dalla Mora M, Germani A. A Luenberger-like Observer for Nonlinear Systems. Int J Control (1993) 57:537–56. doi:10.1080/00207179308934406

CrossRef Full Text | Google Scholar

19. Morgül Ö. On the Synchronization of Logistic Maps. Phys Lett A (1998) 247:391–6. doi:10.1016/s0375-9601(98)00576-3

CrossRef Full Text | Google Scholar

Appendix 1: Explicit Equations of the Multidimensional Map

The multidimensional extension of discrete-time maps leads to a high dimension discrete-time system. In this Appendix, we report the explicit equation for the multidimensional logistic map in Eq. 16 for N = 2. The equations of the multidimensional map are

$\begin{array}{c}\mathrm{X}\left(k+1\right)=a\mathrm{X}\left(k\right)\left(\mathrm{I}-\mathrm{X}\left(k\right)\right)=a\left[\begin{array}{cc}\hfill x_{11}\left(k\right)\hfill & \hfill x_{12}\left(k\right)\hfill \\ \hfill x_{21}\left(k\right)\hfill & \hfill x_{22}\left(k\right)\hfill \end{array}\right]\cdot \left[\begin{array}{cc}\hfill 1-x_{11}\left(k\right)\hfill & \hfill -x_{12}\left(k\right)\hfill \\ \hfill -x_{21}\left(k\right)\hfill & \hfill 1-x_{22}\left(k\right)\hfill \end{array}\right]=\hfill \\ =a\left[\begin{array}{cc}\hfill x_{11}\left(k\right)\left(1-x_{11}\left(k\right)\right)-x_{12}\left(k\right)x_{21}\left(k\right)\hfill & \hfill x_{12}\left(k\right)\left(1-x_{22}\left(k\right)\right)-x_{11}\left(k\right)x_{12}\left(k\right)\hfill \\ \hfill x_{21}\left(k\right)\left(1-x_{11}\left(k\right)\right)-x_{21}\left(k\right)x_{22}\left(k\right)\hfill & \hfill x_{22}\left(k\right)\left(1-x_{22}\left(k\right)\right)-x_{12}\left(k\right)x_{21}\left(k\right)\hfill \end{array}\right]\hfill \end{array}(19)$

which can be rendered as a vector as

$\left[\begin{array}{c}\hfill x_{11}\left(k+1\right)\hfill \\ \hfill x_{12}\left(k+1\right)\hfill \\ \hfill x_{21}\left(k+1\right)\hfill \\ \hfill x_{22}\left(k+1\right)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill x_{11}\left(k\right)\left(1-x_{11}\left(k\right)\right)-x_{12}\left(k\right)x_{21}\left(k\right)\hfill \\ \hfill x_{12}\left(k\right)\left(1-x_{22}\left(k\right)\right)-x_{11}\left(k\right)x_{12}\left(k\right)\hfill \\ \hfill x_{21}\left(k\right)\left(1-x_{11}\left(k\right)\right)-x_{21}\left(k\right)x_{22}\left(k\right)\hfill \\ \hfill x_{22}\left(k\right)\left(1-x_{22}\left(k\right)\right)-x_{12}\left(k\right)x_{21}\left(k\right)\hfill \end{array}\right](20)$

This representation allows us to represent the dynamics of multidimensional maps through phase portraits. In Figure 13, we report the phase portraits x₁₁ − x₁₂, x₁₁ − x₂₁, and x₁₁ − x₂₂.

FIGURE 13

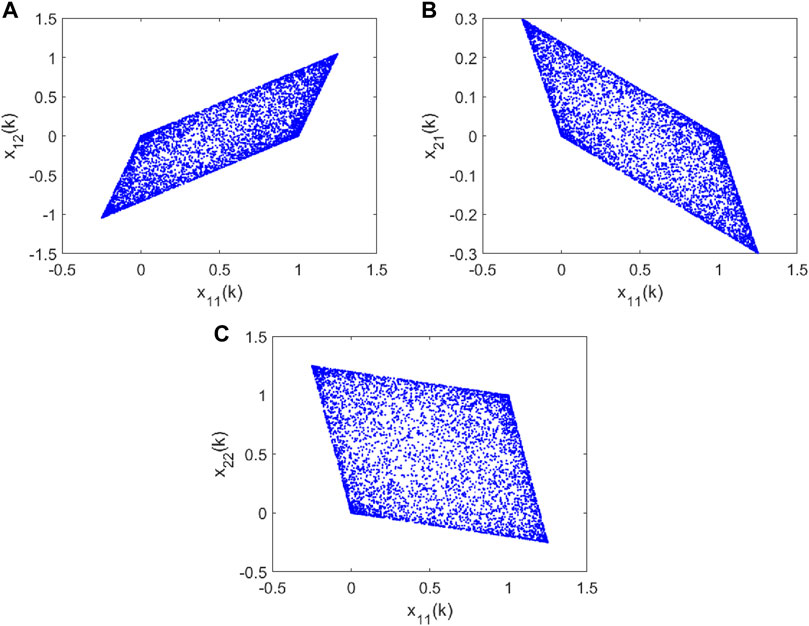
FIGURE 13. Phase portraits of the multidimensional logistic map with N = 2: (A) x₁₁ − x₁₂, (B) x₁₁ − x₂₁, and (C) x₁₁ − x₁₂.

Appendix 2: Return Maps for Multidimensional Discrete Chaotic Maps

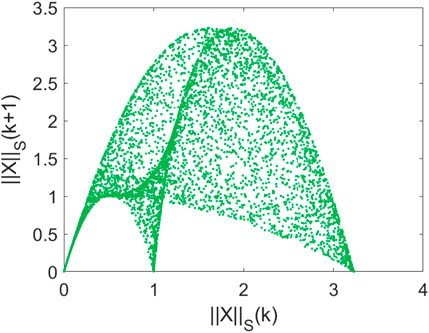
The scalar discrete chaotic maps are often represented, instead of using phase portraits, through the so-called return maps, i.e., plots reporting x(k) vs. x(k + 1). In the case of multidimensional maps, we have matrices instead of scalar quantities, therefore to construct the return map we refer to the spectral norm of the matrix X, that is the maximum singular value. In Figure 14, we report as an example the return map ‖X(k)‖_S − ‖X(k + 1)‖_S for the multidimensional logistic map with N = 2 for a = 4, in which the classical logistic map parabolic shape can be identified.

FIGURE 14

FIGURE 14. Return ‖X(k)‖_S − ‖X(k + 1)‖_S map for the multidimensional logistic map with N = 2 for a = 4.