Modulating the Band Alignments of Two-Dimensional In2Se3/InSe Heterostructure via Ferroelectric Polarization and Interlayer Coupling

Two-dimensional (2D) ferroelectric materials with robust polarization down to atomic thicknesses provide novel building blocks for functional heterostructures. The effects of ferroelectric polarization on the electronic properties of 2D ferroelectric heterostructures are rarely investigated. Here, based on the first-principles calculations, we study the effect of ferroelectric polarization and interlayer coupling on the electronic properties of the 2D In₂Se₃/InSe ferroelectric heterostructure. It is found that the ferroelectric polarization of In₂Se₃ can effectively tune the band alignments of the In₂Se₃/InSe heterostructure. When the direction of ferroelectric polarization is reversed (i.e., from up to down), the band alignments of In₂Se₃/InSe heterostructures transition from type I to type II. Meanwhile, we find that the transition between type I and type II band alignments can be induced by means of interlayer coupling (i.e., varying interlayer distances). The results demonstrate that ferroelectric polarization and interlayer coupling are effective methods to modulate the band alignments of In₂Se₃/InSe heterostructures.

Introduction

2D materials have attracted considerable attention due to their promising mechanical, electrochemical, electronic, and optical characteristics as well as great potential applications in the next generation of nanoelectronic and optoelectronic devices [1–4]. Owing to weak van der Waals interaction between different layers of 2D materials, 2D materials can be isolated from their layered bulk counterparts [5–7]. Accordingly, we can stack different 2D materials on top of each other layer by layer to fabricate van der Waals heterostructures [8–11]. van der Waals heterostructures with two or more layered materials demonstrate many new properties which are absent in respective materials while preserving the intrinsic properties of individual constituents [12–15]. For instance, Tan et al [16] reported that the CrI₃/NiCl₂ van der Waals heterostructure showed a nearly perfect thermal spin-filtering effect in each layer while generating a well-defined spin-Seebeck effect in the whole system.

The band alignment is crucial for the stability and transport of electrons and holes in the van der Waals heterostructure. An intensive understanding of the material intrinsic band alignment properties is necessary for the optimization and design of effective and high-capacity micro–nano devices. From the view of band alignment, the band alignments of van der Waals heterostructures usually can be divided into three types, i.e., straddling (type I), staggered (type II), and broken (type III) [17]. Type I heterostructures consist of two layer materials whereby the conduction band minimum (CBM) and valence band maximum (VBM) of one material are localized within the band gap of the other material; consequently, electrons and holes accumulate on the same material [18]. Type II heterostructures denote the staggered alignment with the CBM and VBM of one material is higher than that of the other material, resulting in an effective electron–hole separation [19–21]. For type III heterostructures, the VBM of one material is higher than the CBM of the other material which gives a broken alignment. However, the van der Waals heterostructure with a fixed band alignment cannot realize multifunctional applications. To broaden the application range, the tuning of band alignment in a heterostructure by the external electric field has been studied extensively [22–24]. Studies show that applying the external electric field is usually low-efficiency and high-energy consumption. Alternatively, 2D ferroelectric materials with a non-volatile remanent polarization electric field can be used for modulating the band alignment.

Recently, monolayer In₂Se₃ has been proposed as a new member of 2D ferroelectric material, and the room temperature ferroelectricity has been confirmed experimentally [25, 26]. The crystal structures of layered In₂Se₃ are composed of sets of quintuple layers, Se–In–Se–In–Se, with each atomic layer containing only one elemental species arranged in a triangular lattice. Within the quintuple layers, the atoms form strong covalent/ionic bonds, while the interactions between neighboring quintuple layers are weak and of the van der Waals type. The most studied phases of layered In₂Se₃ are the α phase. In the α-In₂Se₃ structure, space group R3m, the Se–In–Se–In–Se atomic layers are stacked in the ABBCA sequence, where one of the In atoms is fourfold coordinated in a tetrahedral environment and the other is sixfold coordinated in an octahedral environment. Zhou et al [26] reported that the polarization is potentially switchable for α-In₂Se₃ nanoflakes with thicknesses down to ∼10 nm. Different from other 2D and conventional ferroelectrics, In₂Se₃ demonstrates intrinsically intercorrelated out-of-plane and in-plane polarization, where the reversal of the out-of-plane polarization by a vertical electric field also induces the rotation of the in-plane polarization [27]. The polarization in In₂Se₃ provides a non-volatile remanent built-in electric field, which can tune the band alignment of the 2D ferroelectric heterostructure consisting of In₂Se₃ and other materials. In particular, ferroelectric In₂Se₃-based vdW heterostructures have attracted a great deal of attention.

On the contrary, InSe [28, 29] is suitable to form van der Waals heterostructures with In₂Se₃ due to the similar hexagonal lattices and the close lattice constants. InSe crystals are anisotropic layered materials comprising covalently bonded layers stacked together by van der Waals forces. Each layer consists of four atomic planes (Se–In–In–Se) arranged in a hexagonal atomic lattice. In bulk, a hexagonal β-structure belongs to the ${\text{D}}_{6\text{h}}^4$ space group. In this paper, we construct In₂Se₃/InSe heterostructures and study their electronic properties. The results show that the band alignments of In₂Se₃/InSe heterostructures transition from type I to type II when the direction of ferroelectric polarization is reversed (i.e., from up to down). Moreover, the transition between type I and type II band alignments can be induced by means of interlayer coupling (i.e., varying interlayer distances). The results indicate that ferroelectric polarization and interlayer coupling are effective methods to modulate the band alignments of In₂Se₃/InSe heterostructures.

Computational Methods

The first-principles calculations are performed by means of the Vienna Ab initio Simulation Package (VASP) with the projector-augmented wave (PAW) pseudopotentials [30, 31] and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional [32]. Since the PBE functional usually underestimates the band gap, the band structures are calculated by the hybrid Heyd–Scuseria–Ernzerhof (HSE06) functional [33]. To describe the van der Waals interactions between In₂Se₃ and InSe, the DFT-D3 method within the Grimme scheme is adopted [34]. The plane-wave cutoff energy is set to be 500 eV. All atoms are fully relaxed till the atomic Hellmann–Feynman forces are less than 0.01 eV/Å, and the energy convergence threshold is selected to be 10⁻⁵ eV between two steps. The Brillouin zone was sampled with a fine grid of 9 × 9 × 1 for structure optimization and electronic structures. A 20 Å vacuum spacing is chosen to avoid interactions between the adjacent slabs. Moreover, a dipole correction is employed to cancel the errors of electrostatic potential, atomic forces, and total energy under periodic boundary conditions.

Results and Discussion

Geometry Structure and Stability of the In₂Se₃/InSe Heterostructure

First of all, we explore the structural parameters of In₂Se₃ and InSe. The optimized lattice constants of monolayers In₂Se₃ and InSe are 4.05 and 4.09 Å, respectively, which are in excellent agreement with those in previous studies [35, 36]. The In₂Se₃ monolayer has been prepared by using the physical vapor deposition (PVD) method [37], which indicates that the In₂Se₃ monolayer is stable in reality. Thus, the integration of In₂Se₃ and InSe has feasibility and research value. Owing to the close lattice constants of In₂Se₃ and InSe, In₂Se₃/InSe heterostructures are fabricated with a 1 × 1 supercell of In₂Se₃ and a 1 × 1 supercell of InSe, leading to a lattice mismatch of 0.9%. A spontaneous polarization electric field exists in monolayer In₂Se₃. We construct In₂Se₃/InSe heterostructures considering two different polarization electric field directions, namely, In₂Se₃/InSe (up) and In₂Se₃/InSe (down), as shown in Figure 1.

FIGURE 1

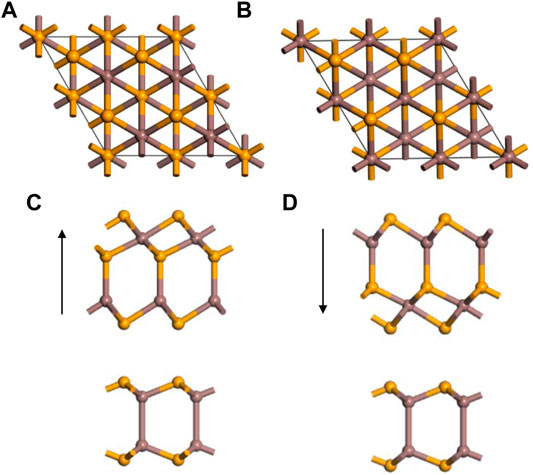
FIGURE 1. (A) Top view and (C) side view of In₂Se₃/InSe heterostructures with the up polarization electric field. (B) Top view and (D) side view of In₂Se₃/InSe heterostructures with the down polarization electric field. The black arrow denotes the direction of polarization electric field.

To evaluate the stability of In₂Se₃/InSe (up) and In₂Se₃/InSe (down), the binding energies E_b of In₂Se₃/InSe (up) and In₂Se₃/InSe (down) heterostructures are calculated, which can be defined as

$E_b=E_H-E_{I{n}_{2}S{e}_3}-E_{InSe},(1)$

where $E_H$, $E_{I{n}_{2}S{e}_3}$, and $E_{InSe}$ represent the total energy of the heterostructure and In₂Se₃ and InSe monolayers, respectively. The results demonstrate that the binding energies of In₂Se₃/InSe (up) and In₂Se₃/InSe (down) heterostructures are −0.161 eV and −0.172 eV, respectively. In₂Se₃/InSe (down) has more negative binding energy than In₂Se₃/InSe (up), which indicates that In₂Se₃/InSe (down) is more stable than In₂Se₃/InSe (up). The binding energies of In₂Se₃/InSe (up) and In₂Se₃/InSe (down) heterostructures are both negative, which shows that both heterostructures are easy to fabricate in experiments.

Electronic Properties of In₂Se₃/InSe Heterostructures

In order to understand electronic properties of In₂Se₃/InSe heterostructures, firstly, the band structures of monolayers In₂Se₃ and InSe calculated by the HSE06 hybrid functional are given in Figure 2. As can be seen from Figure 2, the VBM of In₂Se₃ and InSe is located at the Γ point, while the CBM of In₂Se₃ and InSe is located at a point between M and Γ points, indicating monolayers In₂Se₃ and InSe are both indirect band gap semiconductors. The band gaps of In₂Se₃ and InSe are 1.59 and 2.34 eV, respectively.

FIGURE 2

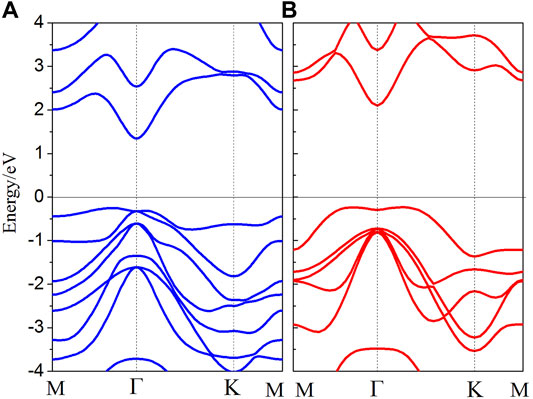
FIGURE 2. Band structures of monolayers (A) In₂Se₃ and (B) InSe calculated by the HSE06 hybrid functional.

The projected band structures of In₂Se₃/InSe (up) and In₂Se₃/InSe (down) heterostructures are plotted in Figure 3. The size of the circles denotes the proportion of In₂Se₃ and InSe. As can be seen form Figures 2, 3, the band structures of In₂Se₃/InSe heterostructures are equal to the simple sum of In₂Se₃ and InSe due to weak van der Waals interlayer interaction. The In₂Se₃/InSe (up) heterostructure has an indirect band gap of 1.35 eV with the CBM located at the Γ point and VBM located at a point between M and Γ points. The CBM and VBM of In₂Se₃/InSe (up) are both dominated by In₂Se₃; therefore, In₂Se₃/InSe (up) is a type I heterostructure, which indicates that the excited electrons and holes are confined inside the In₂Se₃ layer and results in the formation of direct excitons. The excited electrons and holes will recombine quickly in the heterostructure, which indicates In₂Se₃/InSe (up) is suitable for applications in the light-emitting diode. For the In₂Se₃/InSe (down) heterostructure, the CBM comes from the contribution of In₂Se₃, while the VBM arises from InSe; consequently, a type II band alignment is formed in the In₂Se₃/InSe (down) heterostructure. Therefore, the InSe layer can be used as the electron donor and the In₂Se₃ layer can be used as the electron acceptor, resulting in an effective electron–hole separation. Such a band alignment makes the In₂Se₃/InSe (down) heterostructures attractive candidates for the potential application in photovoltaic devices owing to the separated photogenerated electrons and holes at the interface. The band alignments of In₂Se₃/InSe heterostructures transition from type I to type II when the direction of ferroelectric polarization is reversed (i.e., from up to down), which demonstrates that the ferroelectric polarization can effectively tune the band alignments of the In₂Se₃/InSe heterostructure. The above results show that the In₂Se₃/InSe heterostructure is a potential candidate for multifunctional devices.

FIGURE 3

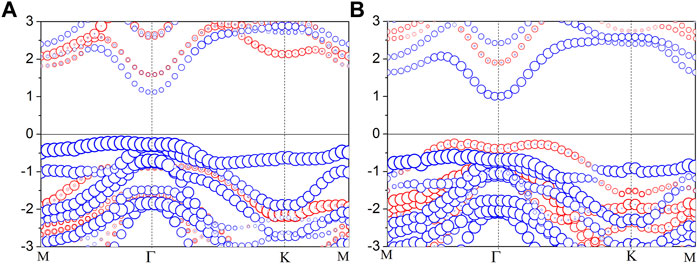
FIGURE 3. Projected band structures of (A) In₂Se₃/InSe (up) and (B) In₂Se₃/InSe (down) heterostructures calculated by the HSE06 hybrid functional. The blue and red circles represent In₂Se₃ and InSe components, respectively. The Fermi level is set to zero.

To obtain further insight, the electrostatic potentials of In₂Se₃, InSe, In₂Se₃/InSe (up), and In₂Se₃/InSe (down) heterostructures are plotted and shown in Figure 4. For In₂Se₃, the difference of electrostatic potential ($\Delta \varphi$) between two surfaces is 1.41 eV, and an intrinsic ferroelectric field is introduced into In₂Se₃ due to ferroelectric polarization. As can be seen from Figure 4, the differences of electrostatic potential($\Delta \varphi$) between In₂Se₃ and InSe are 1.41 eV for In₂Se₃/InSe (up) and 1.31 eV for In₂Se₃/InSe (down), respectively; therefore, built-in electric fields are induced at the interfaces of both In₂Se₃/InSe (up) and In₂Se₃/InSe (down). The electrostatic potential difference in In₂Se₃/InSe (down) is smaller than that of In₂Se₃/InSe (up), which can be attributed to the screening effects due to the charge transfer and depolarizing electrostatic field between In₂Se₃ and InSe in the heterostructure.

FIGURE 4

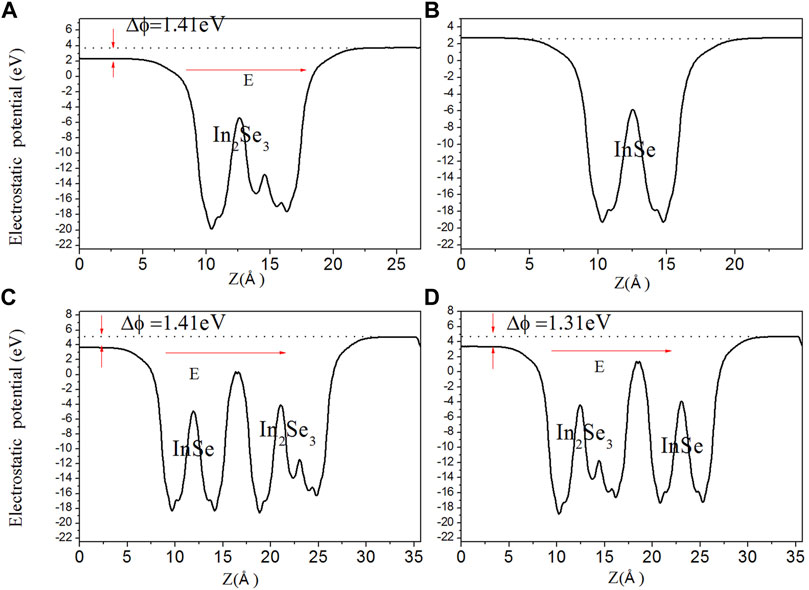
FIGURE 4. Electrostatic potentials of (A) monolayer In₂Se₃, (B) monolayer InSe, and (C) In₂Se₃/InSe (up) and (D) In₂Se₃/InSe (down) heterostructures. The dotted lines and the red arrows represent the vacuum level and the direction of the built-in electric field, respectively.

The band alignments are very important in designing multifunctional devices. Thus, the band alignments of monolayer In₂Se₃, monolayer InSe, and In₂Se₃/InSe (up) and In₂Se₃/InSe (down) heterostructures are plotted in Figure 5. It can be seen that the work functions of monolayer In₂Se₃, monolayer InSe, and In₂Se₃/InSe (up) and In₂Se₃/InSe (down) heterostructures are 7.25, 6.34, 7.37, and 6.79 eV, respectively. The work function of InSe is smaller than that of In₂Se₃; therefore, the electrons transfer from InSe to In₂Se₃. Eventually, InSe will gather positive holes, and In₂Se₃ will accumulate negative electrons. A built-in electric field occurs at the interface of the In₂Se₃/InSe heterostructure, which will hinder the diffusion of electrons and holes, and finally, the built-in electric field force and the diffusion force exactly balance each other. Meanwhile, the Fermi level of InSe moves downward, while that of In₂Se₃ shifts upward, and the two Fermi levels reach the same level at last. The intrinsic ferroelectric field induced by In₂Se₃ has an external electric field–like tuning effect on the electronic properties of In₂Se₃/InSe (up) and In₂Se₃/InSe (down) heterostructures. Thus, under the influence of the intrinsic ferroelectric field induced by In₂Se₃, the band edge of InSe moves downward gradually, and the band edge shift of InSe in In₂Se₃/InSe (up) is larger than that of InSe in In₂Se₃/InSe (down), which leads to type I and type II band alignments in In₂Se₃/InSe (up) and In₂Se₃/InSe (down), respectively.

FIGURE 5

FIGURE 5. Band alignments of monolayer In₂Se₃, monolayer InSe, and In₂Se₃/InSe (up) and In₂Se₃/InSe (down) heterostructures. The horizontal dashed lines represent the Fermi level.

Interlayer Coupling Modulations of Band Structures in the In₂Se₃/InSe Heterostructure

In fact, the interlayer coupling effect has an important impact on the band structures of two-dimensional van der Waals heterostructures. By means of varying interlayer distances, we can tune the interlayer coupling effects of monolayer In₂Se₃ and monolayer InSe in the heterostructure. In order to understand the interlayer coupling effects on the band structures of the heterostructures, the projected band structures of the In₂Se₃/InSe heterostructures with different interlayer distances are shown in Figure 6. It is obvious at a glance that the band gaps of both In₂Se₃/InSe (up) and In₂Se₃/InSe (down) are driven continuously to zero with decreasing interlayer distances. Nevertheless, the band gaps of In₂Se₃/InSe (up) and In₂Se₃/InSe (down) change slightly when interlayer distances are increased. We note that both In₂Se₃/InSe (up) and In₂Se₃/InSe (down) have the indirect band gap feature with varying interlayer distances. It is clearly found that the CBM and VBM of In₂Se₃/InSe (up) are both dominated by In₂Se₃; therefore, In₂Se₃/InSe (up) is a type I heterostructure. By decreasing interlayer distances, we find that the CBM and VBM of InSe shift down continuously, inducing a transition from type I to type II heterostructure. For In₂Se₃/InSe (down), the CBM comes from the contribution of In₂Se₃, while the VBM arises from InSe, and a type II band alignment is formed in the In₂Se₃/InSe (down) heterostructure. When the interlayer distance is decreased, eventually the CBM and VBM of In₂Se₃/InSe (down) are both attributed from In₂Se₃, which results in the transition from type II to type I band alignment. Interestingly, In₂Se₃/InSe (up) maintains type I band alignment and In₂Se₃/InSe (down) retains type II band alignment when interlayer distances are increased. The results indicate that interlayer coupling is an effective method to modulate the band structures of In₂Se₃/InSe heterostructures. Charge transfer between In₂Se₃ and InSe is enhanced as interlayer distances decrease, which may induce the modulation of the band alignments of In₂Se₃/InSe heterostructures.

FIGURE 6

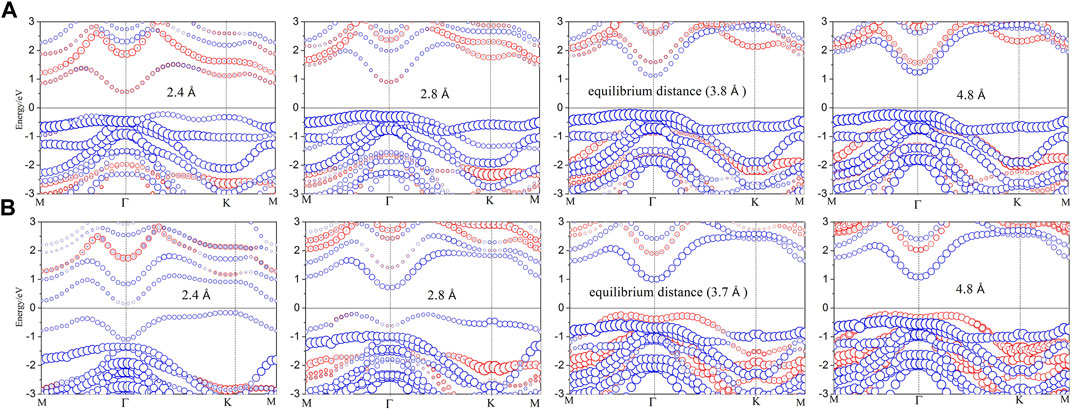
FIGURE 6. Projected band structures of (A) In₂Se₃/InSe (up) and (B) In₂Se₃/InSe (down) heterostructures with different interlayer distances. The blue and red circles represent In₂Se₃ and InSe components, respectively. The Fermi level is set to zero.

To shed more light on the charge transfer with different interlayer distances, the Bader charge analysis is performed. The results show that there are 0.034, 0.021, 0.0022, and 0.0003 electrons transferring from In₂Se₃ to InSe at 2.4 Å, 2.8 Å, 3.8 Å, and 4.8 Å for In₂Se₃/InSe (up), respectively. Similarly, for the In₂Se₃/InSe (down) heterostructure, there are 0.0568, 0.0284, 0.0119, and 0.0013 electrons transferring from InSe to In₂Se₃ at 2.4 Å, 2.8 Å, 3.7 Å, and 4.8 Å, respectively. The amount of charge transfer increases with decreasing interlayer distances, no matter what In₂Se₃/InSe (up) or In₂Se₃/InSe (down). More charge transfer between In₂Se₃ and InSe leads to the shift of band edges, which results in the modulation of band gap and band alignment.

Conclusion

In summary, we have studied the electronic properties of the In₂Se₃/InSe heterostructures based on the first-principle calculations. Our results indicate that the ferroelectric polarization of In₂Se₃ can effectively tune the band alignments of the In₂Se₃/InSe heterostructure. When the direction of ferroelectric polarization is reversed (i.e., from up to down), the band alignments of In₂Se₃/InSe heterostructures transition from type I to type II, and the band gap changes slightly from 1.35 to 1.25 eV. The band gaps of both In₂Se₃/InSe (up) and In₂Se₃/InSe (down) are driven continuously to zero with decreasing interlayer distances. In particular, interlayer coupling (i.e., varying interlayer distances) can effectively modify the band edges of both In₂Se₃/InSe (up) and In₂Se₃/InSe (down); eventually, the transition between type I and type II band alignments is realized. Our results provide interesting guidelines for using the In₂Se₃/InSe heterostructure in future optoelectronic devices and open the path for further theoretical and experimental studies of this system.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the study and approved it for publication.

Funding

This study was supported by the National Natural Science Foundation of China (Grant No. 62074053) and the Key R&D and Promotion Program of Hunan Province (Grant No. 212102210172).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank the support from the High Performance Computing Center of Henan Normal University.

References

1. Song D., Chen X., Lin Z., Tang Z., Ma W., Zhang Q, et al. Usability Identification Framework and High-Throughput Screening of Two-Dimensional Materials in Lithium Ion Batteries. ACS Nano (2021) 15:16469–77. doi:10.1021/acsnano.1c05920

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yadav A., Kangsabanik J., Singh N., Alam A. Novel Two-Dimensional MA2N4 Materials for Photovoltaic and Spintronic Applications. J Phys Chem Lett (2021) 12:10120–7. doi:10.1021/acs.jpclett.1c02650

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Velický M. Electrolyte versus Dielectric Gating of Two-Dimensional Materials. J Phys Chem C (2021) 125:21803–9. doi:10.1021/acs.jpcc.1c04795

CrossRef Full Text | Google Scholar

4. Chung Y. K., Lee J., Lee W.-G., Sung D., Chae S., Oh S, et al. Theoretical Study of Anisotropic Carrier Mobility for Two-Dimensional Nb2Se9 Material. ACS Omega (2021) 6:26782–90. doi:10.1021/acsomega.1c03728

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Barrera D., Wang Q., Lee Y.-J., Cheng L., Kim M. J., Kim J, et al. Solution Synthesis of Few-Layer 2H MX2 (M = Mo, W; X = S, Se). J Mater Chem C (2017) 5:2859–64. doi:10.1039/C6TC05097B

CrossRef Full Text | Google Scholar

6. Wang F., Wang J., Guo S., Zhang J., Hu Z., Chu J. Tuning Coupling Behavior of Stacked Heterostructures Based on MoS2, WS2, and WSe2. Sci Rep (2017) 77:44712. doi:10.1038/srep44712

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yao Q.-F., Cai J., Tong W.-Y., Gong S.-J., Wang J.-Q., Wan X, et al. Manipulation of the Large Rashba Spin Splitting in Polar Two-Dimensional Transition-Metal Dichalcogenides. Phys Rev B (2017) 95:165401. doi:10.1103/PhysRevB.95.165401

CrossRef Full Text | Google Scholar

8. Iqbal S., Pan Z., Zhou K. Enhanced photocatalytic hydrogen evolution from In Situ formation of few-layered MoS2/CdS nanosheet-based van der Waals heterostructures. Nanoscale (2017) 9:6638–42. doi:10.1039/C7NR01705G

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Guo H., Zhang Z., Huang B., Wang X., Niu H., Guo Y, et al. Theoretical study on the photocatalytic properties of 2D InX(X = S, Se)/transition metal disulfide (MoS2 and WS2) van der Waals heterostructures. Nanoscale (2020) 12:20025–32. doi:10.1039/D0NR04725B

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Din H. U., Idrees M., Albar A., Shafiq M., Ahmad I., Nguyen C. V, et al. Rashba spin splitting and photocatalytic properties of GeC−MSSe ( M=Mo , W) van der Waals heterostructures. Phys Rev B (2019) 100:165425. doi:10.1103/PhysRevB.100.165425

CrossRef Full Text | Google Scholar

11. Xiang R., Inoue T., Zheng Y., Kumamoto A., Qian Y., Sato Y, et al. One-dimensional van der Waals heterostructures. Science (2020) 367:537–42. doi:10.1126/science.aaz2570

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Fowler-Gerace L. H., Choksy D. J., Butov L. V. Voltage-controlled long-range propagation of indirect excitons in a van der Waals heterostructure. Phys Rev B (2021) 104:165302. doi:10.1103/PhysRevB.104.165302

CrossRef Full Text | Google Scholar

13. Li X., Su Y., Zhu M., Zheng F., Zhang P., Zhang J, et al. Current-Perpendicular-to-Plane Giant Magnetoresistance Effect in van der Waals Heterostructures. Phys Rev Appl (2021) 16:034052. doi:10.1103/PhysRevApplied.16.034052

CrossRef Full Text | Google Scholar

14. Liu Z., Han Y., Ren Y., Niu Q., Qiao Z. Van der Waals heterostructure Pt2HgSe3/CrI3 for topological valleytronics. Phys Rev B (2021) 104:L121403. doi:10.1103/physrevb.104.l121403

CrossRef Full Text | Google Scholar

15. Ye H., Wang X., Bai D., Zhang J., Wu X., Zhang G. P, et al. Significant enhancement of magnetic anisotropy and conductivity in GaN/CrI3 van der Waals heterostructures via electrostatic doping. Phys Rev B (2021) 104:075433. doi:10.1103/PhysRevB.104.075433

CrossRef Full Text | Google Scholar

16. Tan X., Ding L., Du G.-F., Fu H.-H. Spin caloritronics in two-dimensional CrI3/NiCl2 van der Waals heterostructures. Phys Rev B (2021) 103:115415. doi:10.1103/PhysRevB.103.115415

CrossRef Full Text | Google Scholar

17. Moniz S. J. A., Shevlin S. A., GuoMartin Z.-X., Tang J., Tang J. W. Visible-light Driven Heterojunction Photocatalysts for Water Splitting - a Critical Review. Energy Environ. Sci. (2015) 8:731–59. doi:10.1039/c4ee03271c

CrossRef Full Text | Google Scholar

18. Do T.-N., Idrees M., Binh N. T. T., Phuc H. V., Hieu N. N., Hoa L. T, et al. Type-I band alignment of BX-ZnO (X = As, P) van der Waals heterostructures as high-efficiency water splitting photocatalysts: a first-principles study. RSC Adv (2020) 10:44545–50. doi:10.1039/D0RA09701B

CrossRef Full Text | Google Scholar

19. Rao Y., Zhang F., Zhu B., Li H., Zheng K., Zou Y, et al. A C2N/ZnSe Heterostructure with Type-II Band Alignment and Excellent Photocatalytic Water Splitting Performance. New J Chem (2021) 45:13571–8. doi:10.1039/D1NJ02366G

CrossRef Full Text | Google Scholar

20. Do T.-N., Idrees M., Amin B., Hieu N. N., Phuc H. V., Hieu N. V, et al. Electronic and photocatalytic properties of two-dimensional boron phosphide/SiC van der Waals heterostructure with direct type-II band alignment: a first principles study. RSC Adv (2020) 10:32027–33. doi:10.1039/D0RA05579D

CrossRef Full Text | Google Scholar

21. Zhou B.-X., Ding S.-S., Wang Y., Wang X.-R., Huang W.-Q., Li K, et al. Type-II/type-II Band Alignment to Boost Spatial Charge Separation: a Case Study of G-C3n4 Quantum Dots/a-TiO2/r-TiO2 for Highly Efficient Photocatalytic Hydrogen and Oxygen Evolution. Nanoscale (2020) 12:6037–46. doi:10.1039/d0nr00176g

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Wang Z., Sun F., Liu J., Tian Y., Zhang Z., Zhang Y, et al. Electric Field and Uniaxial Strain Tunable Electronic Properties of the InSb/InSe Heterostructure. Phys Chem Chem Phys (2020) 22:20712–20. doi:10.1039/D0CP02721A

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Nguyen C. Q., Ang Y. S., Nguyen S.-T., Hoang N. V., Hung N. M., Nguyen C. V. Tunable Type-II Band Alignment and Electronic Structure of C3N4/MoSi2N4 Heterostructure: Interlayer Coupling and Electric Field. Phys Rev B (2022) 105:045303. doi:10.1103/PhysRevB.105.045303

CrossRef Full Text | Google Scholar

24. Rahimi K. Tunable Electronic Properties of the Novel G-ZnO/1T-TiS2 vdW Heterostructure by Electric Field and Strain: Crossovers in Bandgap and Band Alignment Types. Phys Chem Chem Phys (2020) 22:7412–20. doi:10.1039/d0cp00524j

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Rashid R., Ling F. C.-C., Wang S.-P., Xiao K., Cui X., Chan T. H, et al. Shape-control Growth of 2D-In2Se3 with Out-Of-Plane Ferroelectricity by Chemical Vapor Deposition. Nanoscale (2020) 12:20189–201. doi:10.1039/c9nr10207h

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Zhou Y., Wu D., Zhu Y., Cho Y., He Q., Yang X, et al. Out-of-Plane Piezoelectricity and Ferroelectricity in Layered α-In2Se3 Nanoflakes. Nano Lett (2017) 17:5508–13. doi:10.1021/acs.nanolett.7b02198

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Cui C., Hu W.-J., Yan X., Addiego C., Gao W., Wang Y, et al. Intercorrelated In-Plane and Out-Of-Plane Ferroelectricity in Ultrathin Two-Dimensional Layered Semiconductor In2Se3. Nano Lett (2018) 18:1253–8. doi:10.1021/acs.nanolett.7b04852

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Alidoosti M., Esfahani D. N., Asgari R. Charge Density Wave and Superconducting Phase in Monolayer InSe. Phys Rev B (2021) 103:035411. doi:10.1103/PhysRevB.103.035411

CrossRef Full Text | Google Scholar

29. Kumar A. S., Premasiri K., Gao M., Kumar U. R., Sankar R., Chou F.-C, et al. Electron-electron Interactions in the Two-Dimensional Semiconductor InSe. Phys Rev B (2020) 102:121301. doi:10.1103/PhysRevB.102.121301

CrossRef Full Text | Google Scholar

30. Kresse G., Furthmüller J. Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys Rev B (1996) 54:11169–86. doi:10.1103/physrevb.54.11169

CrossRef Full Text | Google Scholar

31. Blöchl P. E. Projector Augmented-Wave Method. Phys Rev B (1994) 50:17953–79. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

32. Perdew J. P., Burke K., Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Krukau A. V., Vydrov O. A., Izmaylov A. F., Scuseria G. E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J Chem Phys (2006) 125:224106. doi:10.1063/1.2404663

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Grimme S. Semiempirical GGA-type Density Functional Constructed with a Long-Range Dispersion Correction. J Comput Chem (2006) 27:1787–99. doi:10.1002/jcc.20495

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Zhou B., Jiang K., Shang L., Zhang J., Li Y., Zhu L, et al. Enhanced carrier separation in ferroelectric In2Se3/MoS2 van der Waals heterostructure. J Mater Chem C (2020) 8:11160–7. doi:10.1039/D0TC02366C

CrossRef Full Text | Google Scholar

36. Ren C., Wang S., Tian H., Luo Y., Yu J., Xu Y, et al. First-principles Investigation on Electronic Properties and Band Alignment of Group III Monochalcogenides. Sci Rep (2019) 9:13289. doi:10.1038/s41598-019-49890-8

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Li X.-Z., Wang Y.-F., Xia J., Meng X.-M. Growth of Vertical Heterostructures Based on Orthorhombic SnSe/hexagonal In2Se3 for High-Performance Photodetectors. Nanoscale Adv (2019) 1:2606–11. doi:10.1039/c9na00120d

CrossRef Full Text | Google Scholar