Bubble Dynamics in Stationary Two-phase Flow Through Disordered Porous Media

Two-phase flow through porous media leads to the formation of drops and fingers, which eventually break and merge or may be trapped behind obstacles. This complex dynamical behavior highly influences macroscopic properties such as the effective permeability and it also creates characteristic fluctuations in the velocity fields of the two phases, as well as in their relative permeability curves. In order to better understand how the microscopic behavior of the flow affects macroscopic properties of two phases, we simulate the velocity fields of two immiscible fluids flowing through a two-dimensional porous medium. By analyzing the fluctuations in the velocity fields of the two phases, we find that the system is ergodic for large volume fractions of the less viscous phase and high capillary numbers Ca. We also see that the distribution of drop sizes m follows a power-law scaling, $\mathcal{P}(m)\propto m^{-\xi }$. The exponent ξ depends on the capillary number. Below a characteristic capillary number, namely Ca* ≈ 0.046, the drops are large and cohesive with a constant scaling exponent ξ ≈ 1.23 ± 0.03. Above the characteristic capillary number Ca*, the flow is dominated by many small droplets and few finger-like spanning clusters. In this regime the exponent ξ increases approaching 2.05 ± 0.03 in the limit of infinite capillary number. Our analysis also shows that the temporal mean velocity of the entire mixture can be described by a generalization of Darcy’s law of the form ${\bar{v}}^{(m)}\propto {(\nabla P)}^{\beta }$ where the exponent β is sensitive to the surface tension between the two phases. In the limit of infinite capillary numbers the mobility term increases exponentially with the saturation of the less viscous phase. This result agrees with previous observations for effective permeabilities found in dissolved-gas-driven reservoirs.

1 Introduction

Due to its technological application, two-phase flows in porous media have been an active subject of research for decades [1–4]. It is well known, for instance, that the flow of a water/oil mixture through a porous rock strongly depends on the volume ratio of the two fluids, the surface tension between the two phases and their wetting interactions with the solid walls [5–8]. Phenomenologically, this behavior has been described by relative permeability curves, which need to be determined experimentally. Over the years, many models have been proposed to explain those experimental measurements, or to approximate them when experimental gauging curves are not available [9–11]. Most of these studies focused on the displacement of an interface moving in a transient regime, such as in gas/oil drainage or water/oil imbibition. Understanding this process is of great practical relevance in petroleum engineering where the main goal is to increase production by delaying the breakthrough of the injected fluid, i.e., to increase the amount of the displaced fluid by extending the time the injected fluid takes to reach the producing well [12].

Immiscible two-phase flows in porous media commonly exhibit intriguing phenomena that arise due to the competition between capillary and viscous effects. Generally speaking, the resulting interface formation is controlled by two dimensionless numbers, namely, the capillary number Ca, which describes the balance of viscous forces to capillary forces, and the ratio of the two viscosities. By carrying out multiple experiments, Lenormand classified the emerging patterns in two-phase flow into three major regimes, depending on these two dimensionless parameters. This classification is today known as the so-called Lenormand’s phase-diagram [13], which was recently extended including effects of surface adhesion, namely, also considering contact angles [14]. While the general partitioning of the different flow regimes is characterized by Lenormand’s phase diagram, the transitions at which one regime changes to another are not universal and depend on the particular pore geometry and the dimensionality of the system [7, 15, 16]. Low capillary numbers and high viscosity ratios are frequently associated with a “capillary fingering” regime, while high capillary numbers and high viscosity ratios to a “stable displacement.” In addition, when a low viscous fluid displaces a high viscous one (low viscosity ratio), the resulting interface forms unstable patterns, known as “viscous fingering” [17–19], which can be obtained for any value of the capillary number. This flow regime can be described in terms of a Laplacian growth problem [20], which is also equivalent to diffusion-limited-aggregation (DLA) systems [21]. Experimental studies have also revealed that the capillary number influences the effective permeability of two immiscible phases in terms of a power-law k_eff ∼Ca^α [22, 23] and numerical studies suggest that the exponent α depends on the relative fraction of the two phases in the mixture [24].

The description of two-phase flow at the Darcy scale as an effective medium has a long history [25, 26], but the dynamics of the interface between the different phases at the pore scale still represents a challenging and scientifically important problem. In this case, the geometric properties of the substrate create heterogeneous flow paths which can be invaded by one fluid or the other or both. In such mixing flows, drops of many sizes and shapes naturally emerge. These drops may split and re-merge while they are dragged by the flow through the porous medium or maybe trapped behind obstacles for some time. Numerical simulations [5] and micro-tomography [6, 27] have been used to understand the interplay between two phases inside a porous medium on the scale of individual pores, but the connection between this micro-dynamic behavior and macroscopic quantities such as permeability or displacement efficiency is still poorly understood [28]. Over time, the dynamic of a two-phase flow inside a heterogeneous medium eventually reaches a stationary regime, where certain variables fluctuate around a long-time averaged value [8]. In this regime the application of novel techniques from non-equilibrium statistical physics [29] proved to be very helpful in establishing a proper connection between micro and macro scale. Recent studies of fluctuations in mesoscopic properties, such as relative permeability and flow velocity, paved the way to a new perspective on the conceptual description for two-phase flow at low Reynolds numbers [30–32] with focus on its statistical properties. Here, we study through two-dimensional simulations the characteristic fluctuations in the velocity time series of two immiscible fluids flowing through an irregular porous medium.

The paper is organized as follows: In Section 2, we present the details of our pore geometry, the mathematical model and numerical technique used to calculate the velocity fields of the two phases. Section 3 covers the analysis of the numerical results. More specifically, we analyze temporal correlations in the spatially averaged time series of the velocity fields of the different phases and the mixture in the stationary regime and apply Onsager’s reciprocal relations in order to investigate time reversibility. Moreover, we show that the drop size distribution follows a power-law scaling and propose a generalization of Darcy’s law with a non-linear coupling between flow rate and pressure drop in Section 3.4. We close our analysis with discussions and conclusions in Section 4.

2 Mathematical Model

The pore geometry of our system consists of a two-dimensional “Swiss cheese” type of porous medium [33–35], which is made of circular obstacles that can overlap with each other. More specifically, the porous domain is composed of a 50 mm × 50 mm square, which is iteratively filled with randomly placed discs of 1 mm in diameter until a desired porosity ϱ is reached. For all simulations performed here, ϱ = 0.8. Periodic boundary conditions are applied in both directions in order to avoid finite-size effects. The pore space is filled with two immiscible Newtonian fluids with a surface tension, γ, acting at the interface between them. A global pressure gradient, ∇P, in the horizontal direction (x-direction) drives the flow. Figure 1A shows the initial condition of the system, where the filling fraction S₁ of the low viscous phase (blue) is set to 0.2. The two phases flowing through the pore space are solved numerically by a Volume-of-Fluid (VoF) formalism [5, 36], which is an adaptation of the Navier-Stokes equations for multi-phase flow as implemented in the Ansys Fluent™ software [37]. This numerical technique has been previously validated in several studies through numerous distinct applications [38–44]. In particular, the surface tension and contact angle in the model of Fluent’s VoF scheme have been successfully applied to quantitatively describe the droplet pinch-off dynamics in a microfluidic step emulsification device [45].

FIGURE 1

FIGURE 1. Time evolution of the two-phase flow starting from an initial condition (A) where the filling fraction of the lower viscous phase is set to S₁ = 0.2. (B–D) describe the case for Ca → ∞ while the case for Ca = 0.006 is shown in (E–G). In both cases, the pressure drop is ∇P = 1.0 kPa/m and the viscosity ratio is M = 10. The time series of the averaged x-component velocity for phase 1 (blue curves), phase 2 (red curves), and the mixture (black curves), computed with Eqs 3–5, are shown in (B,E). (C,F) show typical configurations of the two-phase flow in the stationary regime. For high capillary numbers, (B) phase 1 is scattered into several small droplets and few fingers (long and thin clusters), while for small capillary numbers, (F) phase 1 forms large drops. The corresponding velocity fields of the mixture are shown in (D,G), with velocities ranging from 0.0 to 4.0 mm/s. Brighter colors represent regions of high speeds. Large bubbles, of the order of the system size, can be trapped and cause large fluctuations as shown in (E).

In the Volume-of-Fluid formalism, the Navier-Stokes and continuity equations describe the conservation of linear momentum and mass of the entire mixture,

$\begin{array}{ccc}\hfill \rho \frac{\partial \mathbf{u}}{\partial t}+\rho \nabla ·\left(\mathbf{u}\otimes \mathbf{u}\right)& =\hfill & -\nabla p+\nabla ·\left[\mu \left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^T\right)\right]+\gamma \kappa \nabla s,\hfill \\ \hfill \nabla ·\mathbf{u}& =\hfill & 0,\hfill \end{array}(1)$

where ρ, μ, p and u are density, viscosity, pressure, and the fluid velocity, respectively. The term u ⊗ u is an outer product, and s(x) is the fraction function of phase 1 in a given control volume. Due to mass conservation, the fraction of phase 2 is given by 1 − s(x). Because Eq. 1 describes the motion of both phases, ρ and μ are not constants, but scalar fields, which depend on the fraction function s(x). More specifically, a linear mixing rule μ(x) = μ₁ ⋅ s(x) + μ₂ ⋅ [1 − s(x)] is used to define a local effective viscosity of the mixture, where the constants μ₁ and μ₂ stand for the viscosities of phase 1 and 2, respectively. The same holds for the density in case of phases with different densities, ρ₁ and ρ₂. The term γκ∇s in Eq. 1 describes the interfacial tension force and is proportional to the gradient of s normal to the interface. Here, the variable κ = ∇·n is the curvature of the interface. Because ∇s is nonzero only along the interface, interfacial tension forces vanish in the bulk of phase 1 and phase 2, where s is constant. As boundary conditions on the solid walls, we limit our study to neutral wettability (contact angle α = 90°) and no slip. The fraction function s(x) has a sharp interface at the border between the two phases, and is advected by the flow via

$\frac{\partial s}{\partial t}+\mathbf{u}·\nabla s=0.(2)$

In this analysis, we keep the density of the two fluids equal ρ₁ = ρ₂ = 1.0 kg/m³, to avoid disturbance by inertial effects. Moreover, we set μ₂ = 1.0 Pa·s and keep the viscosity ratio M = μ₂/μ₁ at either 1 or 10. During a simulation, the integration time step dt is kept fixed and small enough to avoid high Courant numbers, generally dt ≈ 10⁻⁴ s. If not mentioned otherwise, our fluid mixture consists of 20% of phase 1 (blue, lower viscous phase) and 80% of phase 2 (red, high viscous phase). Initially, the two phases are placed in vertical strips (see Figure 1A) in the fluid domain with their interface perpendicular to the pressure gradient. Different initial configurations have been tested in multiple simulations to ensure that the stationary regime does not depend on this initial condition. Using this setup, we study the behavior of the mixture as we change the two major interactions between the phases, namely, the viscous forces, which is controlled here by the global pressure gradient, ∇P, and interfacial forces, which depends on surface tension, γ. We also ran simulations with vanishing surface tension and equal viscosities in order to test whether our two-phase model recovers the properties of a single-phase flow. Simulation data are only analyzed after the stationary state is reached, in order to produce statistically meaningful time series. This highly increases the computational costs as the initial transient part of the calculation has to be discarded.

3 Results

Shear and surface tension exert forces on the fluid while it flows through the porous medium. These forces eventually lead to the breakup of connected components of a phase and, thus, to the generation of drops. These drops may flow separately through the porous channels or may be trapped for some time by the porous matrix. Moreover, colliding drops may also merge with each other forming larger clusters. This complex dynamics of merging and disconnecting drops dominates the flow’s microscopic behavior in the stationary state. As a result, the velocity fields of the two phases show typical transient fluctuations.

3.1 Velocity Time Series

In the VoF method, the volumetric average velocity of a phase, at time t, may be written in terms of the fluid velocity, u, and the fraction function s(x, t). For the x-component of phase 1’s velocity we find

$v^{\left(1\right)}\left(t\right)=\frac{1}{{\mathrm{\Omega }}_1}{\int }_{\mathrm{\Omega }}{u}_x\left(\mathbf{x},t\right)\cdot s\left(\mathbf{x},t\right)\mathrm{d}\mathrm{\Omega },(3)$

where Ω₁ = ∫_Ωs(x)dΩ is the domain occupied by phase 1, Ω is the total porous space occupied by the fluid mixture and u_x(x, t) is the x-component of u, solved with Eqs 1, 2. Equivalently, the mean x-velocity of phase 2 is given by

$v^{\left(2\right)}\left(t\right)=\frac{1}{{\mathrm{\Omega }}_2}{\int }_{\mathrm{\Omega }}{u}_x\left(\mathbf{x},t\right)\cdot \left[1-s\left(\mathbf{x},t\right)\right]\mathrm{d}\mathrm{\Omega },(4)$

with ${\mathrm{\Omega }}_2={\int }_{\mathrm{\Omega }}\left[1-s(\mathbf{x})\right]\mathrm{d}\mathrm{\Omega }$. Since the two phases are incompressible and mass is conserved, Ω₁ and Ω₂ are constants. Finally the mean x-velocity of the entire mixture is given by

$v^{\left(m\right)}\left(t\right)=\frac{1}{\mathrm{\Omega }}{\int }_{\mathrm{\Omega }}{u}_x\left(\mathbf{x},t\right)\mathrm{d}\mathrm{\Omega }.(5)$

The temporal mean values of these time series are computed through ${\bar{v}}^{(j)}=1/T{\int }_{t_0}^{t_0+T}{v}^{(j)}\mathrm{d}t$, where j = 1, 2, m stands for the two phases (1,2) or the mixture (m). The variable T corresponds to the time window spanning the stationary regime. The capillary number describes the ratio between viscous forces and surface tension being defined here in terms of the mean mixture velocity as

$\mathrm{C}\mathrm{a}={\bar{v}}^{\left(m\right)}{\mu }_2/\gamma .(6)$

Figure 1 shows the influence of the capillary number on the two-phase flow in the stationary regime. The initial configuration is shown in panel (A), where the volume fraction of phase 1 is set to S₁ = 0.2. Panels (B-D) show the case of Ca → ∞ while panels (E-G) the case for Ca = 0.006. The velocity time series computed through Eqs 3–5 are presented in panels (B) and (E) where phase 1, phase 2, and the mixture are marked by blue, red and black lines, respectively. Note that, although the pressure drop is constant, the flow rate can actually vary due to the fluctuations in hydraulic resistance. These inherent fluctuations in the velocity time series reflect the dynamics of the drops and their interactions with the pore geometry. When drops get trapped in a region of the porous medium, the average velocity is slowed down. Conversely, when drops are released at a later time, the flow accelerates resulting in one or multiple peaks appearing in the time series.

The snapshots in panels Figures 1C,F show the distribution of phase 1 (blue) and phase 2 (red) in the pore space for the two cases Ca → ∞ (equivalent to γ = 0) and Ca = 0.006. At high capillary number, the flow is characterized by a large number of small droplets with a highly active merging and splitting dynamics. In some of these cases, the formation of one or more finger-like cluster spanning from left to right along a major flow path can be observed. In the case with low capillary number, the phases stick together and create more cohesive drops, preventing split-merging events. In cases of very small capillary numbers, the pressure gradient may even not be sufficient to overcome the interfacial forces and thus the formation and motion of drops may be suppressed. In this situation, permanently trapped drops are observed in the porous medium. The velocity maps corresponding to the snapshots shown in (C) and (F) are plotted in panels (D) and (G). Darker colors represent regions with low velocities, while brighter colors indicate fast flowing regions.

3.2 Time Correlations in Two-phase Flow

In order to develop a description of the flow as a stochastic dynamical system, it is important to know whether the system is ergodic or not. Although originally applied to thermal fluctuations on the molecular scale, Onsager symmetries [46, 47] have been successfully applied to describe the behavior of multi-phase flows in macroscopic porous media [48] and in pore-network models [30–32]. For this purpose, we apply Onsager’s reciprocal relations in order to study ergodicity. Onsager’s reciprocal relations are based on time correlations which can be calculated as follows

$C_{AB}\left(\tau \right)=\frac{1}{T}{\int }_0^{T-\tau }\frac{\mathrm{\Delta }A\left(t\right)\mathrm{\Delta }B\left(t+\tau \right)}{{\sigma }_A{\sigma }_B}\mathrm{d}t.(7)$

Here $\mathrm{\Delta }A(t)=A(t)-\bar{A}$ are the fluctuations of the time series A(t) and ΔB(t + τ) are the corresponding fluctuations of B(t) shifted by τ. The mean values, $\bar{A}$ and $\bar{B}$, and the variances, σ_A and σ_B, are all computed over the time window, $\left[0,T-\tau \right]$, shared by both time series. If A(t) and B(t) are identical, then Eq. 7 recovers the autocorrelation function, otherwise the cross-correlation function is calculated. Accordingly, a dynamical process is considered to be time reversible if the cross correlation function is symmetric, thus the integrals of C_AB and C_BA are equal [49]. This condition is satisfied when C_AB(τ) collapses on C_BA(τ) at all times, except for some very small timescales in which the contribution to the integral is negligible [32]. Autocorrelations, on the other hand, measure the randomness in the time series and the rate at which fluctuations change with respect to the time scale τ. It can also be interpreted as the memory of a stochastic process, determining whether successive observations are independent or not.

In the following, we analyze the correlations in the time series of the spatially averaged x-velocity of phase 1, phase 2, and the entire fluid as defined through Eqs 3–5. Here, C₁₂(τ) and C₂₁(τ) describe the cross-correlation between phase 1 (2) and phase 2 (1), where the evolution of phase 2 (1) is shifted forward in time relative to phase 1 (2). C_mm(τ) is the autocorrelation of the mixture. Figure 2 shows C₁₂(τ), C₂₁(τ), and C_mm(τ) for ∇P = 1.0 kPa/m and M = 10. Generally, for small delays, phase 1 and phase 2 tend to be anti-correlated and weakly correlated for increasing τ, i.e., if one phase speeds up (comparing to its average velocity) the other phase slows down. In the limit of very large delays, the cross correlations of C₁₂(τ) and C₂₁(τ) both vanish. Conversely, the autocorrelation functions show the opposite behavior with strong correlations for small delays, slight anti-correlations in a intermediate range, and vanishing correlations for τ → ∞.

FIGURE 2

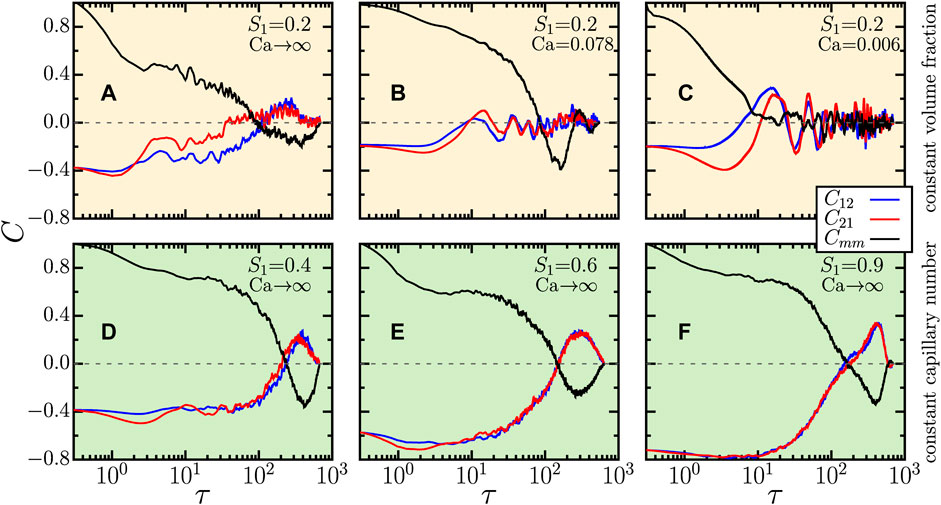
FIGURE 2. Time correlation functions computed with the velocity time series of the two phases and the mixture, like those shown in Figures 1B,E, for M = 10 and ∇P = 1.0 kPa/m. C₁₂ is the cross-correlation function between the velocity time series of phase 1 and phase 2, where the evolution of phase 2 is shifted forward in time by τ relative to phase 1, while C₂₁ is the opposite case. C_mm is the autocorrelation of the velocity of the entire fluid. The top panels show the effect of decreasing the capillary number from Ca → ∞ in (A) to 0.078 in (B), and to 0.006 in (C), while the volume fraction of phase 1 is kept at S₁ = 0.2. In (D–F) we keep Ca → ∞, as in (A), but increase the saturation of the less viscous phase systematically from S₁ = 0.4 to 0.6, and to 0.9, respectively.

Figure 2 shows how the filling fraction of phase 1 and the capillary number affect the different correlations in the flow. Panels (A), (B), and (C) show the cross-correlation functions for decreasing Ca, keeping a constant filling fraction of S₁ = 0.2. For Ca → ∞ and S₁ = 0.2, C₁₂(τ) and C₂₁(τ) seem to collapse only for large values of τ. As Ca decreases, the cross-correlation functions approach zero more rapidly, but the fluctuations also increase and thus the collapse of C₁₂ with C₂₁ is not completely clear for small Ca. For capillary-dominant systems, Ca → 0, time-reversibility is less clear, similar to a recent experiments with two-phase flows in three-dimensional heterogeneous systems [30]. The figure also shows the effect of increasing filling fraction of the less viscous phase. Here S₁ is varied from 0.2 in panel (A) to 0.4 in (D), to 0.6 in (E), and to 0.9 in (F) while all other parameters are kept fixed. For filling fractions of 0.4, 0.6, and 0.9 the cross correlation functions almost perfectly collapse onto each other suggesting a more time reversal dynamics compared to the case with only 0.2 filling fraction, as shown in panel (A). In fact, by varying the saturation S₁ from 0.1 to 0.9, a good collapse of the two cross-correlation function is observed for S₁ ≥ 0.4 at all time scales. Regarding the autocorrelation functions (black lines in Figure 2), our results show that they slowly become decorrelated, which is similar to Brownian motion [50]. However, as the surface tension increases, C_mm(τ) vanishes sooner, at smaller values of τ.

3.3 Drop Size Distribution

In order to study how the agglomerates of drops may influence the mesoscopic behavior of the two-phase flow, we determine the sizes of the different drops for every time step during the stationary regime and then calculate their distributions. Figure 3A shows the drop size distribution $\mathcal{P}(m)$ as a function of capillary number for ∇P = 2.0 kPa/m and M = 10, where m is the drop size normalized by the whole fluid volume. The distribution follows a power law, $\mathcal{P}(m)\propto m^{-\xi }$, whose exponent ξ depends on the capillary number. For Ca ≲ 0.046, the exponent ξ is roughly constant with a value of ξ ≈ 1.23 ± 0.03. In this capillary range, the drops are mostly large and the split-merging events (as well as the spanning channels) are rarely observed. For Ca > 0.046, however, the drops are shattered into many smaller droplets and few fingers (thin elongated clusters) along higher speed channels. In this regime, ξ increases from 1.73 ± 0.06 to 1.92 ± 0.06 for Ca = 0.078 and 0.150, respectively, and then converging to 2.05 ± 0.03 as Ca approaches infinity. The characteristic capillary number, Ca* ≈ 0.046, separates the two regimes, which are marked by light blue and cream background in Figure 3. The heavy-tail scaling of the drop sizes in the large capillary regime may be associated with the emergence of long-range correlations, similar to those found in anomalous diffusion [51].

FIGURE 3

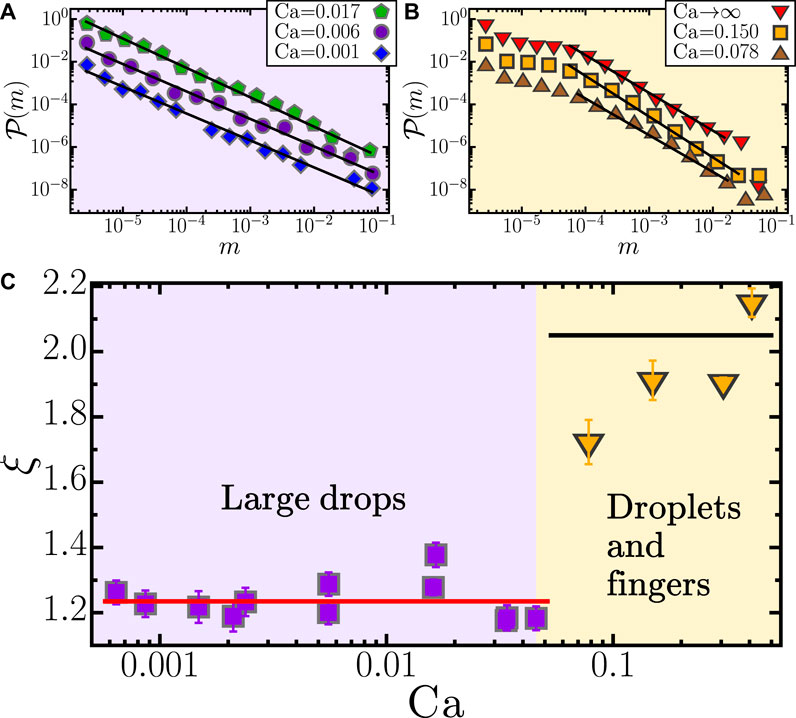
FIGURE 3. (A,B) show the distributions of drop sizes, normalized by the amount of total fluid, in the stationary regime for different values of Ca. The solid lines correspond to the best fit of a power law to the data, $\mathcal{P}(m)\propto m^{-\xi }$, whose exponent ξ depends on the capillary number. For better visibility, the different power laws are shifted by one order of magnitude with respect to each other, vertically. The (A) shows cases for small values of Ca, while (B) for high values of Ca. In (C), ξ is plotted in terms of Ca. The exponent remains approximately constant for Ca ≲ 0.046, with average given by 1.23 ± 0.03, as indicated by the red line. Above this value, ξ increases quickly. In the limiting case of Ca → ∞, the exponent is $\approx 2.05\pm 0.03$, as indicated by the black line.

3.4 Generalized Darcy Law

Next, we analyze the stationary state from a single-phase Darcy flow perspective, namely, how the averaged fluid velocity depends on the pressure gradient. Figure 4 shows the x-velocity of the mixture averaged over space and time, ${\bar{v}}^{(m)}$, as a function of the applied pressure drop ∇P. As depicted, the temporal average velocity follows a power-law scaling, ${\bar{v}}^{(m)}\propto {(\nabla P)}^{\beta }$, for different values of the surface tension γ. This equation can be interpreted as a non-linear form of Darcy’s law for two-phase flows. A similar generalization between flux and pressure drop has been successfully applied to non-Newtonian flows in pipes and pore networks [52, 53]. The exponent β varies as a function of surface tension. As expected, the case γ = 0 and M = 1 (green markers) recovers the traditional linear relation predicted by Darcy for a single phase, with β = 0.99 ± 0.01 ≈ 1.

FIGURE 4

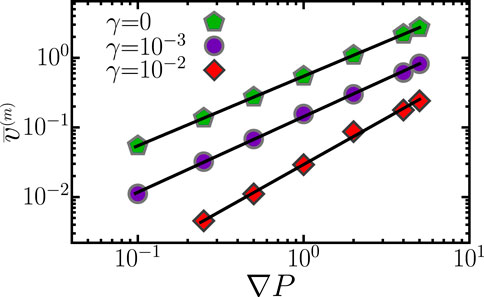
FIGURE 4. Temporal average velocity of the mixture in the stationary regime as a function of the pressure gradient, for different values of surface tension. Each point on the graph correspond to a specific capillary number. For better visibility, the curves for different values of γ were shifted vertically by one order of magnitude with respect to each other. The velocity can be described as a generalized Darcy’s law, ${\bar{v}}^{(m)}\propto {(\nabla P)}^{\beta }$, where the exponent increases with the surface tension. Green markers present the traditional Darcy’s law with β = 0.99 ± 0.01, obtained for γ = 0 and M = 1, while β = 1.09 ± 0.02, for γ = 10⁻³ N/m, and β = 1.34 ± 0.03, for γ = 10⁻² N/m. The cases where drops are permanently trapped in the pore matrix are not plotted in the graphs.

In regimes of very high capillary numbers, the flow behavior is dominated by the presence of many small droplets. Figure 5 shows how the filling fraction of the less viscous phase (phase 1) impacts the average velocity for ∇P = 1 kPa/m and M = 10. The plot shows that ${\bar{v}}^{(m)}$ increases exponentially with filling fraction ${\bar{v}}^{(m)}\propto e^{(\delta S_1)}$ with an exponent δ = 2.34 ± 0.07, where $e^{(\delta S_1)}$ is a mobility coefficient for the mixture [54]. In a single phase flow, the mobility term is the ratio between the permeability and the viscosity. In a two-phase flow system, the mobility term is related to relative permeability curves [10]. The effective permeability in the form of an exponential increase with saturation fits particularly well with measurements of gas percolation in dissolved gas-driven reservoirs [55], where the oil phase is saturated with dispersed small bubbles, the so-called “foamy oil” [56, 57], in order to enhance the recovery rates. Despite the complexity involved in the two-phase flow dynamics, our results suggest that the mean flow velocity of the mixture can be described by a simple function of the saturation and the gradient of pressure.

FIGURE 5

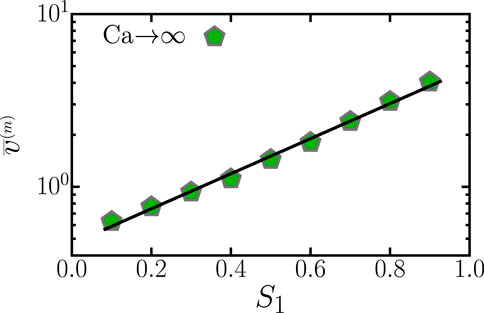
FIGURE 5. Log-linear graph showing that, for Ca → ∞, the behavior of the temporal average velocity can be described by an exponential function of the filling fraction, ${\bar{v}}^{(m)}\propto e^{(\delta S_1)}$, where S₁ is the saturation of phase 1 (the less viscous phase) with exponent δ = 2.34 ± 0.07, for M = 10 and ∇P = 1.0 kPa/m.

4 Discussion and Conclusion

We investigated the stationary flow regime of two immiscible and incompressible Newtonian fluids in porous media by solving Navier-Stokes equations in multi-phase flow in two dimensions. The behavior of the time series of the fluid’s velocity is influenced by the complex dynamics of drops which form as the two phases interact with each other and the heterogeneous pore space. Despite the apparent disorder, in the stationary regime, the drop size distribution follows a well-defined power law, $\mathcal{P}(m)\propto m^{-\xi }$, whose exponent ξ depends on the capillary number. This exponent is roughly constant ξ ≈ 1.23 for Ca ≲ 0.046, where the drops are mostly large and cohesive, and splitting and merging are less common. For Ca > 0.046, however, ξ increases systematically, reaching 2.05 ± 0.03 for Ca → ∞. This regime is characterized by the presence of a large number of small droplets and few finger-like clusters. Fluctuations in the time series are analyzed via cross-correlation functions between the x-velocities of the two phases showing that Onsager’s reciprocal relations and time reversal symmetry are fulfilled for volume fraction above 0.4 and high capillary number. At lower capillary numbers Ca the time reversibility of the flow is less clear which is consistent with observations made in three dimensional two-phase experiments. Finally, we study the macroscopic scaling of the average velocity. Our results show that two-phase flows can be modeled by an effective Darcy type of description, namely, ${\bar{v}}^{(m)}\propto {(\nabla P)}^{\beta }$. In this generalization of Darcy’s law, the exponent β depends on the surface tension between the phases (and, thus, on the capillary number). When the surface tension is neglected and the viscosity ratio is unity, the traditional Darcy relation is recovered, β = 1. For Ca → ∞, when the systems is dominated by the presence of many small droplets, the averaged fluid velocity increases exponentially with the filling fraction of the lower viscous phase, ${\bar{v}}^{(m)}\propto e^{(\delta S_1)}$, where this term represents the mobility coefficient and δ is a constant. This behavior is similar to effective permeabilities found in dissolved-gas-driven reservoirs. We believe that our results have direct applications in the behavior of the mesoscopic flow (at the level of the pore) in several real situations, and can help in the description of the macroscopic propagation of the invasion front in oil reservoirs.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

HS, CO, and JA designed the research. JS performed the simulations with input from HS and CO. All authors contributed to the discussion and interpretation of the results. HS, CO, and JA wrote the paper with input from JS. All authors approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge financial support from the Brazilian agencies CNPq, CAPES, and FUNCAP, and Petrobras (“Física do Petróleo em Meios Porosos”, Project Number: F0185).

References

1. McNutt MK, Camilli R, Crone TJ, Guthrie GD, Hsieh PA, Ryerson TB, et al. Review of Flow Rate Estimates of the Deepwater Horizon Oil Spill. Proc Natl Acad Sci (2012) 109:20260–7.doi:10.1073/pnas.1112139108

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Berkowitz B. Characterizing Flow and Transport in Fractured Geological media: a Review. Adv Water Resour (2002) 25:861–84. doi:10.1016/S0309-1708(02)00042-8

CrossRef Full Text | Google Scholar

3. Bloch S, Lander RH, Bonnell L. Anomalously High Porosity and Permeability in Deeply Buried sandstone Reservoirs: Origin and Predictability. Bulletin (2002) 86:301. doi:10.1306/61EEDABC-173E-11D7-8645000102C1865D

CrossRef Full Text | Google Scholar

4. Ortner F, Mazzotti M. Two-phase Flow in Liquid Chromatography, Part 1: Experimental Investigation and Theoretical Description. Ind Eng Chem Res (2018) 57:3274–91. doi:10.1021/acs.iecr.7b05153

CrossRef Full Text | Google Scholar

5. Raeini AQ, Blunt MJ, Bijeljic B. Modelling Two-phase Flow in Porous media at the Pore Scale Using the Volume-Of-Fluid Method. J Comput Phys (2012) 231:5653–68. doi:10.1016/j.jcp.2012.04.011

CrossRef Full Text | Google Scholar

6. Raeini AQ, Blunt MJ, Bijeljic B. Direct Simulations of Two-phase Flow on Micro-CT Images of Porous media and Upscaling of Pore-Scale Forces. Adv Water Resour (2014) 74:116–26. doi:10.1016/j08.012.advwatres.2014

CrossRef Full Text | Google Scholar

7. Armstrong RT, Georgiadis A, Ott H, Klemin D, Berg S. Critical Capillary Number: Desaturation Studied with Fast X‐ray Computed Microtomography. Geophys Res Lett (2014) 41:55–60. doi:10.1002/2013GL058075

CrossRef Full Text | Google Scholar

8. Avraam DG, Payatakes AC. Flow Regimes and Relative Permeabilities during Steady-State Two-phase Flow in Porous media. J Fluid Mech (1995) 293:207–36. doi:10.1017/S0022112095001698

CrossRef Full Text | Google Scholar

9. Corey AT, Rathjens CH. Effect of Stratification on Relative Permeability. Trans AIME (1956) 207:358. doi:10.2118/744-G

CrossRef Full Text | Google Scholar

10. Chierici GL. Novel Relations for Drainage and Imbibition Relative Permeabilities. Soc Pet Eng J (1984) 24:275–6. doi:10.2118/10165-PA

CrossRef Full Text | Google Scholar

11. BergUnsalDijk SEH, Unsal E, Dijk H. Non-uniqueness and Uncertainty Quantification of Relative Permeability Measurements by Inverse Modelling. Comput Geotechnics (2021) 132:103964. doi:10.1016/j.compgeo.2020.103964

CrossRef Full Text | Google Scholar

12. Oliveira CLN, Araújo AD, Lucena LS, Almeida MP, Andrade JS. Post-breakthrough Scaling in Reservoir Field Simulation. Physica A: Stat Mech its Appl (2012) 391:3219–26. doi:10.1016/j01.017.physa.2012

CrossRef Full Text | Google Scholar

13. Lenormand R, Touboul E, Zarcone C. Numerical Models and Experiments on Immiscible Displacements in Porous media. J Fluid Mech (1988) 189:165–87. doi:10.1017/S0022112088000953

CrossRef Full Text | Google Scholar

14. Primkulov BK, Pahlavan AA, Fu X, Zhao B, MacMinn CW, Juanes R. Wettability and Lenormand's Diagram. J Fluid Mech (2021) 923:A34.doi:10.1017/jfm.2021.579

CrossRef Full Text | Google Scholar

15. Hilfer R, Oeren PE. Dimensional Analysis of Pore Scale and Field Scale Immiscible Displacement. Transp Porous Med (1996) 22:53–72. doi:10.1007/BF00974311

CrossRef Full Text | Google Scholar

16. Hilfer R, Armstrong RT, Berg S, Georgiadis A, Ott H. Capillary Saturation and Desaturation. Phys Rev E (2015) 92:063023. doi:10.1103/PhysRevE.92.063023

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Homsy GM. Viscous Fingering in Porous media. Annu Rev Fluid Mech (1987) 19:271–311. doi:10.1146/annurev.fl.19.010187.001415

CrossRef Full Text | Google Scholar

18. Oliveira CLN, Wittel FK, Andrade JS, Herrmann HJ. Invasion Percolation with a Hardening Interface under Gravity. Int J Mod Phys C (2010) 21:903–14. doi:10.1142/S0129183110015555

CrossRef Full Text | Google Scholar

19. Oliveira CL, Andrade JS, Herrmann HJ. Oil Displacement through a Porous Medium with a Temperature Gradient. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 83:066307.doi:10.1103/PhysRevE.83.066307

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ben Amar M. Viscous Fingering: A Singularity in Laplacian Growth Models. Phys Rev E (1995) 51:R3819–R3822(R).doi:10.1103/PhysRevE.51.R3819

CrossRef Full Text | Google Scholar

21. Witten TA, Sander LM. Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon. Phys Rev Lett (1981) 47:1400–3. doi:10.1103/PhysRevLett.47.1400

CrossRef Full Text | Google Scholar

22. Tallakstad KT, Knudsen HA, Ramstad T, Løvoll G, Måløy KJ, Toussaint R, et al. Steady-state Two-phase Flow in Porous media: Statistics and Transport Properties. Phys Rev Lett (2009) 102:074502. doi:10.1103/PhysRevLett.102.074502

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Tallakstad KT, Løvoll G, Knudsen HA, Ramstad T, Flekkøy EG, Måløy KJ. Steady-state, Simultaneous Two-phase Flow in Porous media: An Experimental Study. Phys Rev E (2009) 80:036308. doi:10.1103/PhysRevE.80.036308

CrossRef Full Text | Google Scholar

24. Grøva M, Hansen A. Two-phase Flow in Porous media: Power-Law Scaling of Effective Permeability. J Phys Conf Ser (2011) 319:012009. doi:10.1088/1742-6596/319/1/012009

CrossRef Full Text | Google Scholar

25. Bear J. Dynamics of Fluids in Porous Media. New York: Dover publications (1972).

Google Scholar

26. Whitaker S. Flow in Porous media I: A Theoretical Derivation of Darcy's Law. Transp Porous Med (1986) 1:3–25. doi:10.1007/BF01036523

CrossRef Full Text | Google Scholar

27. Berg S, Ott H, Klapp SA, Schwing A, Neiteler R, Brussee N, et al. Real-time 3D Imaging of Haines Jumps in Porous media Flow. Proc Natl Acad Sci (2013) 110:3755–9. doi:10.1073/pnas.1221373110

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gu H, Duits MHG, Mugele F. Droplets Formation and Merging in Two-phase Flow Microfluidics. Ijms (2011) 12:2572–97. doi:10.3390/ijms12042572

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Kjelstrup S, Bedeaux D. Non-Equilibrium Thermodynamics of Heterogeneous Systems. Singapore: World Scientific (2008).

Google Scholar

30. McClure JE, Berg S, Armstrong RT. Thermodynamics of Fluctuations Based on Time-And-Space Averages. Phys Rev E (2021) 104:035106. doi:10.1103/PhysRevE.104.035106

PubMed Abstract | CrossRef Full Text | Google Scholar

31. McClure JE, Berg S, Armstrong RT. Capillary Fluctuations and Energy Dynamics for Flow in Porous media. Phys Fluids (2021) 33:083323. doi:10.1063/5.0057428

CrossRef Full Text | Google Scholar

32. Winkler M, Gjennestad MA, Bedeaux D, Kjelstrup S, Cabriolu R, Hansen A. Onsager-Symmetry Obeyed in Athermal Mesoscopic Systems: Two-phase Flow in Porous Media. Front Phys (2020) 8:60. doi:10.3389/fphy.2020.00060

CrossRef Full Text | Google Scholar

33. Morais AF, Seybold H, Herrmann HJ, Andrade JS. Non-Newtonian Fluid Flow through Three-Dimensional Disordered Porous media. Phys Rev Lett (2009) 103:194502. doi:10.1103/PhysRevLett.103.194502

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Lorenz CD, Ziff RM. Precise Determination of the Critical Percolation Threshold for the Three-Dimensional "Swiss Cheese" Model Using a Growth Algorithm. J Chem Phys (2001) 114:3659–61. doi:10.1063/1.1338506

CrossRef Full Text | Google Scholar

35. Seybold HJ, Eberhard U, Secchi E, Cisne RLC, Jiménez-Martínez J, Andrade RFS, et al. Localization in Flow of Non-newtonian Fluids through Disordered Porous Media. Front Phys (2021) 9:635051. doi:10.3389/fphy.2021.635051

CrossRef Full Text | Google Scholar

36. Hirt CW, Nichols BD. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J Comput Phys (1981) 39:201–25. doi:10.1016/0021-9991(81)90145-5

CrossRef Full Text | Google Scholar

37. Ansys A. Workbench User Manual. Canonsburg: ANSYS (2019).

Google Scholar

38. Ban S, Pao W, Nasif MS. Numerical Simulation of Two-phase Flow Regime in Horizontal Pipeline and its Validation. Hff (2018) 28:1279–314. doi:10.1108/HFF-05-2017-0195

CrossRef Full Text | Google Scholar

39. Ambekar AS, Mattey P, Buwa VV. Pore-resolved Two-phase Flow in a pseudo-3D Porous Medium: Measurements and Volume-Of-Fluid Simulations. Chem Eng Sci (2021) 230:116128. doi:10.1016/j.ces.2020.116128

CrossRef Full Text | Google Scholar

40. Ambekar AS, Mondal S, Buwa VV. Pore-resolved Volume-Of-Fluid Simulations of Two-phase Flow in Porous media: Pore-Scale Flow Mechanisms and Regime Map. Phys Fluids (2021) 33:102119. doi:10.1063/5.0064833

CrossRef Full Text | Google Scholar

41. Gopala VR, van Wachem BGM. Volume of Fluid Methods for Immiscible-Fluid and Free-Surface Flows. Chem Eng J (2008) 141:204–21. doi:10.1016/j.cej.2007.12.035

CrossRef Full Text | Google Scholar

42. Renardy M, Renardy Y, Li J. Numerical Simulation of Moving Contact Line Problems Using a Volume-Of-Fluid Method. J Comput Phys (2001) 171:243–63. doi:10.1006/jcph.2001.6785

CrossRef Full Text | Google Scholar

43. Piller M, Casagrande D, Schena G, Santini M. Pore-scale Simulation of Laminar Flow through Porous media. J Phys Conf Ser (2014) 501:012010. doi:10.1088/1742-6596/501/1/012010

CrossRef Full Text | Google Scholar

44. Carlson A, Kudinov P, Narayanan C. Prediction of Two-phase Flow in Small Tubes: A Systematic Comparison of State-Of-The-Art CMFD Codes. Netherlands: 5th European Thermal-Sciences Conference (2008). p. 126.

Google Scholar

45. Eggersdorfer ML, Seybold H, Ofner A, Weitz DA, Studart AR. Wetting Controls of Droplet Formation in Step Emulsification. Proc Natl Acad Sci USA (2018) 115:9479–84. doi:10.1073/pnas.1803644115

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Onsager L. Reciprocal Relations in Irreversible Processes. I. Phys Rev (1931) 37:405–26. doi:10.1103/PhysRev.37.405

CrossRef Full Text | Google Scholar

47. Onsager L. Reciprocal Relations in Irreversible Processes. II. Phys Rev (1931) 38:2265–79. doi:10.1103/PhysRev.38.2265

CrossRef Full Text | Google Scholar

48. Flekkøy EG, Pride SR. Reciprocity and Cross Coupling of Two-phase Flow in Porous media from Onsager Theory. Phys Rev E (1999) 60:4130–7. doi:10.1103/PhysRevE.60.4130

CrossRef Full Text | Google Scholar

49. de Groot SR, Mazur P. Non-equilibrium Thermodynamics. New York, NY: Dover (1984).

Google Scholar

50. Chakraborty D. Velocity Autocorrelation Function of a Brownian Particle. Eur Phys J B (2011) 83:375–80. doi:10.1140/epjb/e2011-20395-3

CrossRef Full Text | Google Scholar

51. Combe G, Richefeu V, Stasiak M, Atman APF. Experimental Validation of a Nonextensive Scaling Law in Confined Granular Media. Phys Rev Lett (2015) 115:238301. doi:10.1103/PhysRevLett.115.238301

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Lenk RS. Polymer Rheology. London: Applied Science Publishers LTD (1978).

Google Scholar

53. Eberhard U, Seybold HJ, Floriancic M, Bertsch P, Jiménez-Martínez J, Andrade JS, et al. Determination of the Effective Viscosity of Non-newtonian Fluids Flowing through Porous Media. Front Phys (2019) 7:71. doi:10.3389/fphy.2019.00071

CrossRef Full Text | Google Scholar

54. Craft BC, Hawkins MF. Applied Petroleum Reservoir Engineering. 2nd ed. New Jersey: Prentice-Hall (1991).

Google Scholar

55. Smith GE. Fluid Flow and Sand Production in Heavy-Oil Reservoirs under Solution-Gas Drive. SPE Prod Eng (1988) 3:169–80. doi:10.2118/15094-PA

CrossRef Full Text | Google Scholar

56. Sarma H, Maini B. Role of Solution Gas in Primary Production of Heavy Oils. Proc Latin Am Petro Eng Conf Caracas, Venezuela (1992). doi:10.2118/23631-MS

CrossRef Full Text | Google Scholar

57. Lv W, Du D, Yang J, Jia N, Li T, Wang R. Experimental Study on Factors Affecting the Performance of Foamy Oil Recovery. Energies (2019) 12:637. doi:10.3390/en12040637

CrossRef Full Text | Google Scholar