Theory of Spin-Excitation Anisotropy in the Nematic Phase of FeSe Obtained From RIXS Measurements

Recent resonant inelastic x-ray scattering (RIXS) experiments have detected a significant high-energy spin-excitation anisotropy in the nematic phase of the enigmatic iron-based superconductor FeSe, whose origin remains controversial. We apply an itinerant model previously used to describe the spin-excitation anisotropy as measured by neutron scattering measurements, with magnetic fluctuations included within the RPA approximation. The calculated RIXS cross section exhibits overall agreement with the RIXS data, including the high energy spin-excitation anisotropy.

1 Introduction

Identifying the dominant interaction channels, and pinpointing the correct microscopic origin of preferred electronic ordering tendencies in strongly-correlated materials, constitute a challenge to the theoretical description of materials. This is particularly relevant in systems where spin, charge, orbital, and lattice degrees of freedom all strongly couple with one another. For the iron-based superconductors, the main relevant players are spin-density waves, nematic order, and unconventional superconductivity. In this regard, iron selenide, FeSe, has played a leading role in recent years since its superconducting phase condenses directly from a nematic state without concomitant broken time-reversal symmetry breaking (magnetic order) at lower temperatures [1–3]. In addition, FeSe has been in the spotlight due to its superconducting transition temperature T_c, which is tunable by intercalation, pressure, or dimensional reduction (monolayer FeSe on STO) [3].

Since FeSe enters an orthorhombic phase below T_n ∼ 90K it exhibits 90° rotational symmetry breaking in all measured quantities (of detwinned crystals). However, from comparisons to theoretical calculations the degree of measured rotational symmetry breaking is much too large to be ascribed solely to the bare electronic structure of the orthorhombic phase. Therefore, several theoretical works have explored the possibility of various interaction-driven feedback effects that enhance the symmetry breaking [4–10] and strongly influence the shape and orbital content of the Fermi pockets [7, 8, 11–13]. A particularly simple theoretical framework which includes such effects is the so-called orbital-selective scenario, where the low-energy self-energy is approximated by orbital-dependent, but energy- and momentum-independent, quasi-particle weight factors [6, 7, 14–19]. While this is clearly a crude simplification of the full interacting multi-orbital problem, it was shown to provide overall agreement with a series of different experiments [3].

More recently, spectroscopic probes have revealed that the Fermi surface of FeSe is exceedingly anisotropic; it appears to be missing an entire electron pocket at the Y-point of the Brillouin zone (BZ), as shown in Figure 1 [20, 21]. This Fermi surface topology does not naturally arise from DFT band structure calculations, even with additional nematic order added to the description [3]. This finding has reinvigorated the discussion of nematicity and the origin of the large electronic anisotropy in FeSe. For example, the lifting of the Y-pocket imposes new constraints on the nature of the nematic order, leading to studies of the importance of d_xy-orbital contributions [13, 22–27], and important inter-orbital components in the nematic order [28–30]. The latter were shown recently to arise naturally from longer-range Coulomb interactions [29]. Additionally, the possible non-existence of the Y-pocket has important consequences for superconductivity and the need for anisotropy-enhancing self-energy feedback effects. For example, as shown in Ref. [29], the highly anisotropic superconducting gap structure of FeSe follows immediately from standard spin-fluctuation mediated pairing without additional self-energy effects applied to the Fermi surface without any electron pocket at the Y-point. This conclusion, however, is mainly a direct consequence of the missing Y-pocket itself, and does not eliminate the need for self-energy feedback more generally in the theoretical description of FeSe. This is seen, for example, in theoretical modelling of the neutron response of FeSe, where a prominent momentum anisotropy seems only consistent with calculations incorporating self-energy feedback effects [29] since the possible lifting of the Y pocket alone only yields a very weak anisotropy of the susceptibility between (π, 0) and (0, π) as also presented in Ref. [27].

FIGURE 1

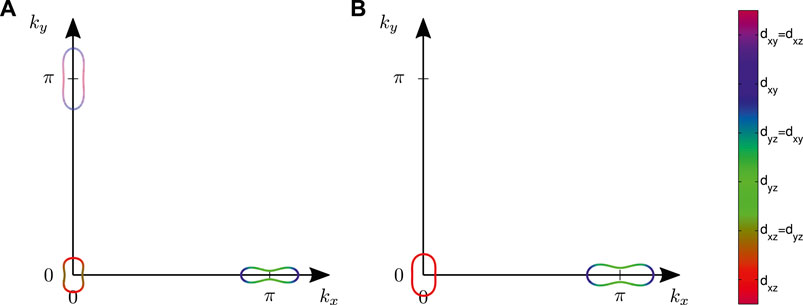
FIGURE 1. Fermi surface of nematic FeSe with orbital content as indicated by colorbar. (A) Model of an electronic structure exhibiting a Fermi surface pocket at the Y point which, however, carries incoherent electronic states (sketched by fading colors) [6, 7]. Note that the model in Eq. 1 is a three dimensional electronic structure. For the full corresponding Fermi surface we refer to Figure 1A of Ref. [7]. (B) Fermi surface of a model including d_xy orbital order as proposed in Ref. [27] where the Y pocket is lifted; similar topology of the Fermi surface was also discussed in [29] with a different orbital order parameter.

Therefore, further experiments probing the momentum anisotropy of detwinned FeSe are highly desirable. In this respect, Chen et al. [31] succeeded in measuring the inelastic neutron scattering response from a mosaic of single FeSe crystals glued on to BaFe₂As₂, detwinned at low temperatures by the single domain stripe magnetism of the (uniaxially strained) substrate BaFe₂As₂ material. This experiment revealed highly anisotropic low-energy (≲ 10 meV) magnetic fluctuations in (detwinned) FeSe with the main scattering taking place near the (π, 0) position of the BZ. In the superconducting phase, a similarly momentum-anisotropic resonance peak was additionally identified [31]. These results can be explained by itinerant models that include self-energy effects that 1) suppress d_xy orbital contributions to the spin susceptibility predominantly near (π, π), and 2) favor (π, 0) d_yz over (0, π) d_xz orbital contributions in the nematic phase [32, 33]. Only by allowing for such orbital-selective self-energy effects can a standard RPA-like itinerant scenario be made compatible with the neutron data. We stress that this remains true irrespective of whether or not the Y-pocket is present at the Fermi surface.

Recently, the spin excitations were measured to higher energies in detwinned FeSe by RIXS measurements at the Fe-L₃ edge [34]. The RIXS energy spectra revealed clear dispersive broad spin modes. It was found that the spin-excitation anisotropy, as seen by comparing the scattering cross section along the perpendicular H and K high-symmetry directions, remains to high energies ($\sim 200$ meV). This energy scale is substantially larger than the orbital splitting associated with the nematicity, and as pointed out in Ref. [34], the amplitude of the spin-excitation anisotropy in nematic FeSe is comparable to that obtained from the spin-wave anisotropy in the magnetically ordered stripe (π, 0) phase of BaFe₂As₂ [34, 35].

The RIXS results for detwinned FeSe provide new testing ground for theories of FeSe. At present the origin of nematicity and the degree of localization and correlation is still being discussed. In particular, theoretical works have both applied models based on fully localized or itinerant electrons, in order to explain the peculiar electronic ordering tendencies of FeSe [3]. Here, we compute the RIXS cross section within an itinerant RPA procedure with nematicity included in the bare band structure [6]. The applied RIXS framework is similar to that used in Ref. [36] where second order perturbation theory involving the absorption and emission process is used to calculate the RIXS intensity from the generalized spin-susceptibility. The latter is then calculated within a random phase approximation (RPA) where additional reduced coherence of the electronic structure [33] is taken into account. We find that the RIXS cross section as calculated for the fully coherent electronic structure exhibits relatively sharp modes, but remains nearly isotropic when comparing the intensity along the (π, 0) and (0, π) directions, irrespective of whether the Y pocket is present or not at the Fermi level. A strong spin-excitation anisotropy inherent in the sharp paramagnons of the itinerant system can be found if self-energy effects in the nematic state are taken into account. Furthermore, we note that this anisotropy persists to high energies much larger than the energy scale of the nematic order parameter of a few tens of meV, similar to the experimental findings in a recent RIXS experiment [34]. The spin-excitation anisotropy in the theoretical intensity at low energies depends sensitively on the orbital content of the Fermi surface. We discuss implications for our general understanding of magnetic fluctuations and electronic structure of FeSe by comparison to the experimentally determined RIXS data from Ref. [34].

2 Model and Method

The following calculations are based on a tight-binding parametrization for iron-based superconductors [37] with values of the hopping parameters used earlier [6, 7, 33], that closely matches the electronic structure measured in spectroscopic probes. The Fermi surface of this band structure contains an electron Fermi pocket at the Y-point of the BZ, but its presence is largely irrelevant for the RIXS results discussed below, compare Figure 1A of Ref. [7] and Figure 1 for a simplified two dimensional plot of the Fermi surface. Thus, we start from the Hamiltonian

$H=\sum _{\mathbf{k}\sigma \ell {\ell }^{\prime }}{t}_{\mathbf{k}}^{\ell {\ell }^{\prime }}{c}_{\ell \sigma }^{†}\left(\mathbf{k}\right)c_{{\ell }^{\prime }\sigma }\left(\mathbf{k}\right),(1)$

where $c_{\ell \sigma }^{†}(\mathbf{k})$ is the Fourier amplitude of an operator $c_{i\ell \sigma }^{†}$ that creates an electron in Wannier orbital ℓ with spin σ ∈ {↑, ↓} and $t_{\mathbf{k}}^{\ell {\ell }^{\prime }}$ is the Fourier transform of the hoppings connecting the Fe 3d orbitals $(d_{xy},d_{x^2-y^2},d_{xz},d_{yz},d_{3z^2-r^2})$. This term includes an on-site spin-orbit coupling of type S^zL^z, giving rise to imaginary hopping elements [38], which yield a splitting of the two hole-like bands along the Γ-Z line in the BZ. The nematic state at low temperatures is modelled by including an onsite and nearest neighbor bond order term with an energy scale of $\approx 10\text{meV}$ [6, 33] arising from Coulomb interactions [22, 23, 29, 39]. While other types of orbital order terms have been proposed in the literature [27, 40], we do not examine these possibilities in this work.

The Bloch Hamiltonian can be diagonalized by a unitary transformation with the matrix elements $a_{\mu }^{\ell }(\mathbf{k})$, such that it reads $H={\sum }_{\mathbf{k}\sigma \mu }{\tilde{E}}_{\mu }(\mathbf{k})c_{\mu \sigma }^{†}(\mathbf{k})c_{\mu \sigma }(\mathbf{k})$, where ${\tilde{E}}_{\mu }(\mathbf{k})$ are the eigenenergies closely matching the maxima of the spectral function as deduced experimentally [6, 15, 41–44]. $c_{\mu \sigma }^{†}(\mathbf{k})$ is the Fourier amplitude of electrons in band μ and momentum k. Furthermore, we adopt an ansatz for the Green’s function in orbital space incorporating correlations via quasiparticle weights Z_ℓ in orbital ℓ,

$\begin{array}{ll}\hfill {\tilde{G}}_{\ell {\ell }^{\prime }}\left(\mathbf{k},{\omega }_n\right)& =\sqrt{Z_{\ell }{Z}_{{\ell }^{\prime }}}\sum _{\mu }\frac{a_{\mu }^{\ell }\left(\mathbf{k}\right)a_{\mu }^{{\ell }^{\prime }*}\left(\mathbf{k}\right)}{i{\omega }_n-{\tilde{E}}_{\mu }\left(\mathbf{k}\right)}\hfill \\ \hfill & =\sqrt{Z_{\ell }{Z}_{{\ell }^{\prime }}}\sum _{\mu }{a}_{\mu }^{\ell }\left(\mathbf{k}\right)a_{\mu }^{{\ell }^{\prime }*}\left(\mathbf{k}\right){\tilde{G}}^{\mu }\left(\mathbf{k},{\omega }_n\right).\hfill \end{array}(2)$

Here ${\tilde{G}}^{\mu }(\mathbf{k},{\omega }_n)={[i{\omega }_n-{\tilde{E}}_{\mu }(\mathbf{k})]}^{-1}$ is the coherent Green’s function in band space which in the paramagnetic state is diagonal in spin space, i.e., proportional to δ_σ,σ′. This ansatz does not include the actual incoherent spectral weight, and should therefore only describe the low energy properties of the electronic structure. While the quasiparticle weights are phenomenological parameters, these can also be calculated e.g., by using fluctuation exchange approach [16], or slave-boson methods or dynamical mean field theory [14, 45–50], qualitatively giving similar trends for the quasiparticle weights, but in detail yielding different band renormalizations and Fermi surfaces, i.e., exhibiting a low-energy Green’s function that is not expected to describe the physical properties accurately at low energies. Here, we adopt the values $\{\sqrt{Z_l}\}=[0.2715,0.9717,0.4048,0.9236,0.5916]$ as used in previous investigations [6, 7, 33]; conclusions are robust as long as the quasiparticle weights are chosen within the range presented in Ref. [33].

To obtain two-particle responses as measured by a RIXS experiment, we adopt a standard Hubbard-Hund Hamiltonian for local interactions

$H=U\sum _{i,\ell }{n}_{i\ell \uparrow }{n}_{i\ell \downarrow }+U^{\prime }\sum _{i,{\ell }^{\prime }<\ell }{n}_{i\ell }{n}_{i{\ell }^{\prime }}+J\sum _{i,{\ell }^{\prime }<\ell }\sum _{\sigma ,{\sigma }^{\prime }}{c}_{i\ell \sigma }^{†}{c}_{i{\ell }^{\prime }{\sigma }^{\prime }}^{†}{c}_{i\ell {\sigma }^{\prime }}{c}_{i{\ell }^{\prime }\sigma }+J^{\prime }\sum _{i,{\ell }^{\prime }\ne \ell }{c}_{i\ell \uparrow }^{†}{c}_{i\ell \downarrow }^{†}{c}_{i{\ell }^{\prime }\downarrow }{c}_{i{\ell }^{\prime }\uparrow },(3)$

where the parameters U, U′, J, J′ are given in the notation of Kuroki et al. [51]. Imposing spin-rotational invariance, i.e., U′ = U − 2J, J = J′, there are only two parameters U and J/U left to specify the interactions which we set to values used previously [33].

Within the ansatz of Eq. 2, the paramagnetic orbital susceptibility is given by

${\tilde{\chi }}_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^0\left(q\right)=-\sum _{k,\mu ,\nu }{\tilde{M}}_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^{\mu \nu }\left(\mathbf{k},\mathbf{q}\right){\tilde{G}}^{\mu }\left(k+q\right){\tilde{G}}^{\nu }\left(k\right),(4)$

where we have adopted the shorthand k ≡ (k, ω_n) and defined the abbreviation

${\tilde{M}}_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^{\mu \nu }\left(\mathbf{k},\mathbf{q}\right)=\sqrt{Z_{{\ell }_1}{Z}_{{\ell }_2}{Z}_{{\ell }_3}{Z}_{{\ell }_4}}{a}_{\nu }^{{\ell }_4}\left(\mathbf{k}\right)a_{\nu }^{{\ell }_2,*}\left(\mathbf{k}\right)a_{\mu }^{{\ell }_1}\left(\mathbf{k}+\mathbf{q}\right)a_{\mu }^{{\ell }_3,*}\left(\mathbf{k}+\mathbf{q}\right).$

After performing the internal frequency summation analytically, we calculate ${\tilde{\chi }}_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^0$ by integrating over the full BZ, which is just the susceptibility ${\chi }_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^0$ of a fully coherent Green’s function multiplied by the quasiparticle weights

${\tilde{\chi }}_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^0\left(\mathbf{q},\omega \right)=\sqrt{Z_{{\ell }_1}{Z}_{{\ell }_2}{Z}_{{\ell }_3}{Z}_{{\ell }_4}}{\chi }_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^0\left(\mathbf{q},\omega \right).(5)$

Two-particle correlation functions of the interacting system with the interacting Hamiltonian of Eq. 3 can be calculated in the random-phase approximation (RPA) by summing a subset of diagrams (see, e.g., Ref. [52]) such that the spin part of the RPA susceptibility, ${\tilde{\chi }}_1^{\text{RPA}}$, is given by

${\tilde{\chi }}_{1{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^{\text{RPA}}\left(\mathbf{q},\omega \right)={\left\{{\tilde{\chi }}^0\left(\mathbf{q},\omega \right){\left[1-{\bar{U}}^s{\tilde{\chi }}^0\left(\mathbf{q},\omega \right)\right]}^{-1}\right\}}_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}.(6)$

The interaction matrix ${\bar{U}}^s$ in orbital space is composed of linear combinations of U, U′, J, J′. For its detailed form, we refer to e.g., Ref. [53].

The total physical spin susceptibility as, for example, measured in inelastic neutron scattering experiments is then given by the sum

$\chi \left(\mathbf{q},\omega \right)=\frac{1}{2}\sum _{\ell {\ell }^{\prime }}{\tilde{\chi }}_{1\ell \ell {\ell }^{\prime }{\ell }^{\prime }}^{\text{RPA}}\left(\mathbf{q},\omega \right).(7)$

For discussion purposes, and to illustrate the differences to the RIXS cross section, we present results for FeSe of this quantity in Figure 2. This is the same calculation as in Ref. [33], but with focus on the small q regions, Figures 2A,B.

FIGURE 2

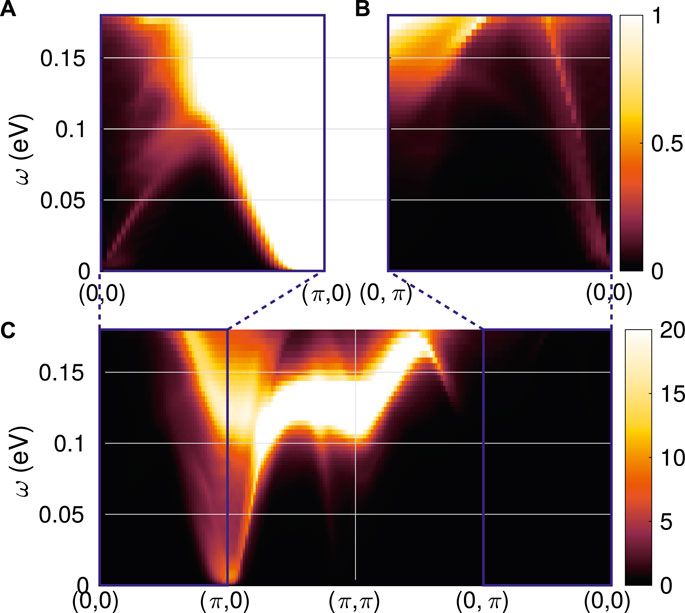
FIGURE 2. Spin susceptibility: − Imχ(q, ω). (A,B) Zoom-in to the details of the spin susceptibility as calculated using the modified RPA approach for U = 0.57 eV and J = U/6, compare Figure 9C of Ref. [33]. Close to q = (0, 0) paramagnon modes are dispersing linearly up as seen towards the X point (A), and towards the Y point (B). The overall intensity close to q = (π, 0) is much larger and exhibits a dispersion with broad maximum around ω ≥ 0.1 eV (C) compared to the relatively sharp paramagnon dispersion close to q = (0, 0).

To calculate the RIXS spectra we follow the approach presented in Ref. [36], where it is calculated as a second-order perturbation from the Kramers-Heisenberg equation in the fast-collision approximation [54]. The transition operator in the dipole approximation, $D_{\mathbf{k}}\approx {\sum }_{j,j_z,\ell ,\sigma ,{\mathbf{k}}^{\prime }}{c}_{\ell ,\sigma }^{j,j_z}(\mathit{\epsilon })c_{\ell \sigma }^{†}(\mathbf{k})p{(\mathbf{k}+{\mathbf{k}}^{\prime })}_{j,j_z}+\mathrm{H}.\mathrm{c}.$ is written using the fermionic operator of the Fe 2p electrons, $p{(\mathbf{k})}_{j,j_z}$ for momentum k and total angular momentum j and z-projection j_z. The dipole transition matrix elements $c_{\ell ,\sigma }^{j{j}_z}(\mathit{\epsilon })=⟨3d;\ell ,\sigma |\mathit{\epsilon }\cdot \mathbf{r}|2p;j,j_z⟩$, depend on the unit vector of the polarization of the x-rays involved in the process.

Considering the Fe-L₃ edge absorption, we restrict to the intermediate j = 3/2 states of the 2p electrons, and calculate the matrix elements assuming wavefunctions with pure hydrogen-like symmetries, i.e., ignoring the deviations of the true Wannier states due to the lower crystal symmetry. The contribution from the radial integration of these wavefunctions will be just a constant (when assuming the same radial dependence for all Fe 3d and 2p orbitals) while the angular part is given by integrals of trigonometric functions on the unit sphere. Having calculated the matrix elements, one can then obtain the RIXS spectrum from the calculated orbital susceptibility as a sum over internal spin and orbital degrees of freedom via [36].

$I_{\text{RIXS}}\left(\mathbf{q},\omega \right)\propto -\mathrm{I}\mathrm{m}\{\sum _{\left\{{\sigma }_i\right\}}\sum _{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}{\chi }_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^{\left({\sigma }_1,{\sigma }_1^{\prime }\right)\left({\sigma }_2,{\sigma }_2^{\prime }\right)}\left(\mathbf{q},\omega \right)\times [\sum _{j_z,j_z^{\prime }}{c}_{{\ell }_1,{\sigma }_1}^{j{j}_z}{\left({\mathbf{\epsilon }}_{\text{o}}\right)}^{*}{c}_{{\ell }_2,{\sigma }_1^{\prime }}^{j{j}_z}\left({\mathbf{\epsilon }}_{\text{i}}\right)c_{{\ell }_3,{\sigma }_2}^{j{j}_z^{\prime }}{\left({\mathbf{\epsilon }}_{\text{i}}\right)}^{*}{c}_{{\ell }_4,{\sigma }_2^{\prime }}^{j{j}_z^{\prime }}\left({\mathbf{\epsilon }}_{\text{o}}\right)]\},(8)$

where ɛ_i and ɛ_o are the polarization vectors of the incoming and outgoing x-rays. As discussed in Ref. [36], the spin-orbit coupling allows spin-flip processes as mediated by the Clebsh-Gordan coefficients when writing the 2p states in the basis for the total angular momentum j = 3/2. However, since there is no magnetism and we ignore the transverse part of the spin-orbit coupling, the susceptibility turns out to be diagonal, ${\chi }_{{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^{({\sigma }_1,{\sigma }_1^{\prime })({\sigma }_2,{\sigma }_2^{\prime })}(\mathbf{q},\omega )={\delta }_{{\sigma }_1,{\sigma }_2}{\delta }_{{\sigma }_1^{\prime },{\sigma }_2^{\prime }}{\tilde{\chi }}_{1{\ell }_1{\ell }_2{\ell }_3{\ell }_4}^{\text{RPA}}(\mathbf{q},\omega )$.

Following the experimental details given in Ref. [34], i.e., setting the scattering angle β = 50°, considering the energy of the resonance as ω₀ = 707 eV, we calculate the polarization vector for incoming π polarization as

${\mathit{\epsilon }}_{\text{i}}=\sin \alpha {\mathbf{e}}_{\parallel }+\cos \alpha {\mathbf{e}}_z,(9)$

where the in plane vector is defined as e_∥ = q/q. The polarization vectors for the two outgoing polarization directions are

$\begin{array}{ccc}\hfill {\mathit{\epsilon }}_{\text{o},\sigma }& =\hfill & \sin \left(\alpha +\beta \right){\mathbf{e}}_{\parallel }+\cos \left(\alpha +\beta \right){\mathbf{e}}_z,\hfill \end{array}(10)$

$\begin{array}{ccc}\hfill {\mathit{\epsilon }}_{\text{o},\pi }& =\hfill & {\mathbf{e}}_{\perp }\hfill \end{array}(11)$

with the perpendicular in – plane vector, i.e. e_⊥⋅ q = 0, where the angle α between wavevector k_i = ω₀/(ℏc) of the incoming and the outgoing k_o x-ray is obtained from solving the equation for momentum conservation along the surface, q = k_i cos α + k_o cos (α + β) for fixed angle β = 50° and approximating k_o ≈ k_i. Finally, we note that the energy resolution of the RIXS experiment in Ref. [34] is given as 80 meV. Below, we focus the theory discussion on the as-calculated (non-broadened) computed results.

3 Results

For convenience, and to contrast expected intensity measured in an inelastic neutron scattering experiment and a RIXS measurement, we start by presenting the spin susceptibility as obtained from Eq. 7 for the case with reduced coherence [33]. In Figure 2C the susceptibility along a high symmetry cut is presented exhibiting large intensity together with a broad dispersive feature close to (π, 0), and, in contrast, essentially no intensity at (0, π). At higher energies, there is also spectral weight close to (π, π). Due to the restricted momentum transfer from the photons, RIXS experiments are only able to access the momentum transfer close to (0, 0). Therefore the susceptibility in these regions will contribute to the summation given in Eq. 8, weighted by the dipole transition matrix elements, shown in Figure 2A,B (note different color scale). Already at the level of the (summed) susceptibility, one can see a dispersive and relatively sharp magnetic mode emanating from (0, 0) with different slopes along the q_x and q_y directions.

Next, we present our results for the RIXS intensity along high symmetry cuts as detailed in Figure 3C, where the sum over the perpendicular polarizations has been performed. It turns out that there is a sharp mode along (0, 0) → (π/2, 0) that presumably originates from the coherent small q-scattering at the Γ-pocket, which occurs from the d_yz orbital component; panel (A). In contrast, there is only a very broad mode along the (0, π/2) direction also coming from scattering of the d_yz orbital, but at the X-pocket. Scattering contributions from the other orbital components are strongly suppressed due to a reduced quasiparticle weight Z_ℓ < 1. Along the diagonal direction both modes are present, giving rise to two relatively sharp features; panel (B). Note that the black area is due to the mentioned kinematic RIXS constraint, i.e. the respective q-vectors cannot be reached.

FIGURE 3

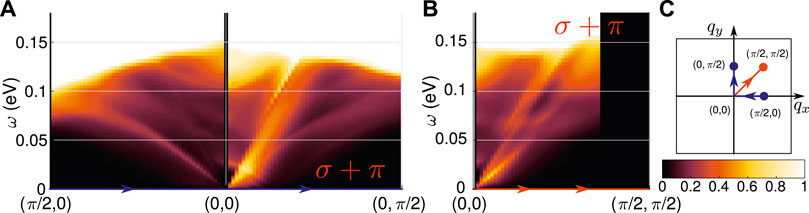
FIGURE 3. RIXS intensity with orbital-selective quasiparticle weight reduction. The RIXS intensity (see common colorbar) at the accessible momentum transfer exhibits sharp paramagnon-like modes towards q = (π/2, 0), while towards q = (0, π/2) a broad intensity and a much weaker paramagnon mode is visible (A). Along the diagonal in the BZ, there are multiple quasi-sharp paramagnon modes visible (B). Calculated for U = 0.57 eV, J = U/6. Geometry of the paths along the diagonal (orange) and along the coordinate axis (blue) as shown in the other panels (C).

We can disentangle the polarization dependence by looking at each polarization separately. As shown in Figure 4A the σ polarization yields a much weaker intensity along the q_x and q_y directions as compared to the π polarization, while along the diagonal both polarizations have similar structure and magnitude. One notes also that the broad feature along the q_y cut is only present in the π polarization. Indeed, there are strong effects on the anisotropy of the RIXS intensity which are mediated by orbitally selective coherence of the electronic structure, leading to the presence of a sharp mode only along the q_x direction as also detected experimentally; the broad mode along the q_y direction is, however, enhanced due to orbital selectivity. The experimental measurement of the polarization dependence might be able to disentangle scattering contributions from the Γ- and the X-pockets.

FIGURE 4

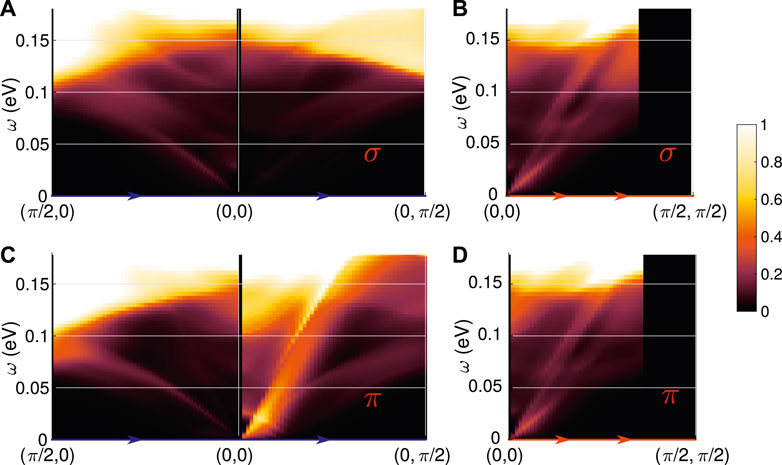
FIGURE 4. Polarization dependence of RIXS intensity. Expected RIXS spectra decomposed in the intensities from σ (A,B) and π polarization of the outgoing photons (C,D) along the paths defined in Figure 3B; U = 0.57 eV, J = U/6.

In contrast, a calculation using a fully coherent electronic structure where self-energy corrections are not taken into account, Z_l = 1, yields a RIXS cross section that is almost isotropic, as shown in Figure 5A. This result is calculated with the band structure which exhibits a Y-pocket at the Fermi level. Except for the very lowest energies $<20meV$, the same conclusions remain within an electronic structure where the Y-pocket has been lifted by nematic order from nearest neighbor Coulomb interactions [29], or from including d_xy nematicity [27]. The reasons for this almost isotropic result are similar to the spin susceptibility discussion [7], whereby the missing Y-pocket only reduces scattering contributions at very low energies corresponding to the nematic energy scale, while interband contributions and scattering at larger energies are almost identical to the ones from a model with a Y-pocket present at the Fermi level.

FIGURE 5

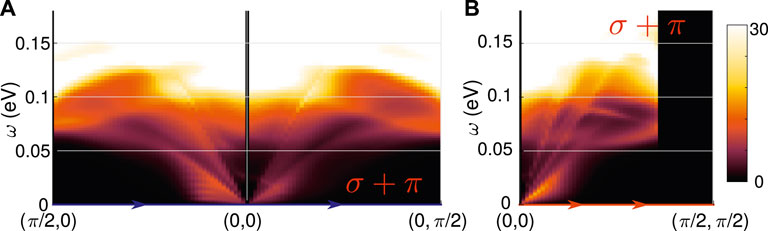
FIGURE 5. RIXS intensity without orbital incoherence. Same as Figure 3, but calculated using Z_l = 1 and by setting U = 0.36 eV, J = U/6 as discussed in Ref. [33].

To complete our understanding of the origin of the different spectral features in the RIXS intensity, we present in Figure 6 a separation of the intensities in orbitally diagonal components, i.e., considering in the sum of Eq. 8 only the terms with ℓ₁ = ℓ₂ = ℓ₃ = ℓ₄, panels (a-e), and extracting the off-diagonal contributions by subtracting diagonal components from the full intensity for the case of Z_l = 1. One clearly sees that the $d_{x^2-y^2}$ and the $d_{z^2}$ orbitals do not contribute to the intensity in the energy range at all. The d_xy orbital yields an almost isotropic contribution along the q_x and the q_y cuts which, however, should be suppressed given the correlated nature of that orbital. Finally, the d_yz orbital contributes to a branch along q_y from scattering within the X-pocket, while the d_xz orbital contributes with a slightly larger intensity along the q_x direction. Again, these conclusions remain similar for models without the Y-pocket with the exception of reduced weight from the d_xz orbital at and below the nematic energy scale of $\approx 20$ meV (not shown). Figure 6F demonstrates that the orbitally off-diagonal contributions are quite sizeable; we also note that different from the susceptibility extracted from inelastic neutron scattering experiments, the sum in Eq. 8 contains elements of the susceptibility tensor with all four orbitals being different. Interestingly, the sharp dispersive mode along q_x as seen in Figure 3A and also Figure 4A,C does not originate from orbitally diagonal contributions, but rather appears as blue mode in the subtracted intensity of Figure 6F. Hence the orbitally off-diagonal contributions give rise to this intensity, and it is less affected by reduced coherence and therefore more visible in Figure 3A compared to Figure 5A.

FIGURE 6

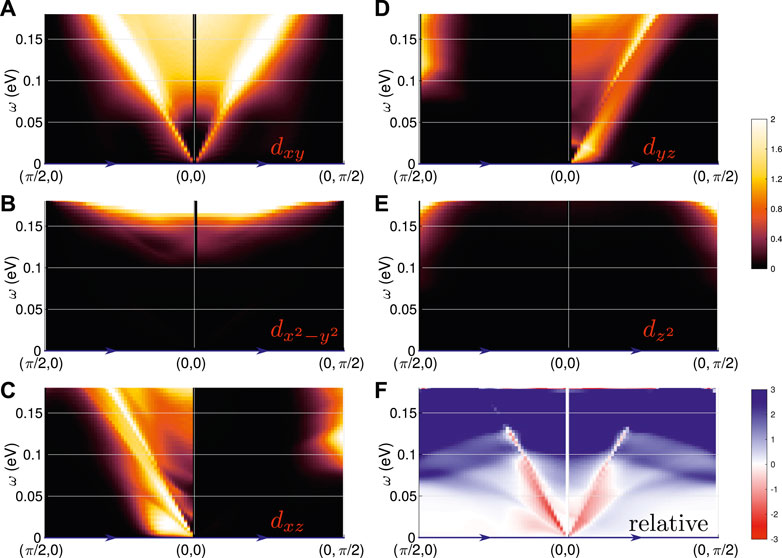
FIGURE 6. RIXS intensity from single orbital components. Intensity calculated by setting Z_l = 0, except for one orbital component, where $Z_{l^{*}}=1$ (A–E), i.e., in the sum in Eq. 8 only the fully diagonal components of the susceptibility contribute. The off-diagonal contributions are sizeable as showin in panel (F) where the results of panels (A–E) multiplied by the number of orbitals are subtracted from the full RIXS intensity as shown in Figure 5A.

Since the RIXS experiment is kinematically constrained to momentum space close to (0, 0) the dispersive modes are less affected by the particular choice of the bare interaction Eq. 3, i.e., no shift of intensity to lower energy is visible as the magnetic instability is approached, U → U_c. This is unlike the dispersive modes close to (π, 0) or (π, π) whose bandwidth is strongly governed by the denominator in the RPA equation for the susceptibility, Eq. 6, i.e., the spectral position of the high energy weight presented in Figure 2C is sensitive to the value of the bare interaction U.

In Ref. [34] the RIXS data was analyzed in terms of a phenomenological model where the RIXS spectra were fitted to a general damped harmonic oscillator model, and discussed in terms of an anisotropic Heisenberg Hamiltonian. In addition, it was concluded without explicit calculations that itinerant models are at variance with the RIXS data due to expected Landau-damped high-energy excitations. The current calculations invalidates this argumentation since we find highly dispersive magnetic excitations persisting to high energies. Indeed, the sharp dispersive mode is visibly strongest along the q_x direction, see Figure 3A. In general, we find a spin-excitation anisotropy with larger intensity along the q_x-directions, similar to experiments [34]. At the lowest energies, however, the current band structure produces a larger intensity in the q_y direction; a property which is not seen experimentally [34]. The reason for this discrepancy is the “boosted” d_zy orbital due to the particular choice of quasiparticle weight factors. This hints at more d_xz-orbital content present at the Fermi level than included in the present modelling.

4 Summary and Conclusion

We have provided a microscopic calculation of the RIXS and neutron response relevant for nematic FeSe. The model is based on itinerant electrons with additional interaction-generated self-energy effects, crudely approximated by simple energy- and momentum independent quasi-particle weight factors. This approach offers a consistent picture of spin fluctuations as detected in inelastic neutron scattering and the recent RIXS experiments, in addition to other experiments, without further tuning of parameters. Specifically, the calculations yield overall agreement with the momentum and energy structure of the low-energy modes, and their momentum anisotropy. We have also discussed quantitative discrepancies between the current calculation, and the recent RIXS measurement by Lu et al. [34]. The microscopic calculation allowed us to explore orbital- and band-dependence of the RIXS scattering cross section, revealing 1) an insensitivity of the RIXS spin-excitation anisotropy response to the presence or absence of a Y-pocket at the Fermi level, and 2) a sensitivity of the low-energy anisotropy to the detailed balance of d_xz- and d_yx-orbital content present on the Γ- and X-pockets of the Fermi surface.

While the RPA approach to itinerant spin excitations is expected to break down at sufficiently high energies, where exactly this occurs is not clear; the crossover to a more localized description is expected in the range of 100s of meV. Here we have shown that for intermediate energies of up to ∼ 150 meV this approach appears to reproduce qualitative features, and that well-defined spin excitations are not overdamped by electron-hole scattering. Of course the theory is not complete in the sense that the quasiparticle weights are not derived properly from a self-energy, nor are vertex corrections included. Nevertheless the current framework appears to be a useful phenomenology to describe the low-energy physics of this unusual material.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

AK performed the calculations, and all authors contributed to writing the manuscript.

Funding

BA acknowledges support from the Independent Research Fund Denmark grant number 8021-00047B. PH was supported by the U.S. Department of Energy under Grant No. DE-FG02-05ER4623.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge useful discussions with A. Kemper and X. Lu.

References

1. Böhmer AE, Kreisel A. Nematicity, Magnetism and Superconductivity in FeSe. J Phys Condens Matter (2018) 30:023001. doi:10.1088/1361-648X/aa9caa

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Coldea AI, Watson MD. The Key Ingredients of the Electronic Structure of FeSe. Annu Rev Condens Matter Phys (2018) 9:125–46. doi:10.1146/annurev-conmatphys-033117-054137

CrossRef Full Text | Google Scholar

3. Kreisel A, Hirschfeld P, Andersen B. On the Remarkable Superconductivity of FeSe and its Close Cousins. Symmetry (2020) 12:1402. doi:10.3390/sym12091402

CrossRef Full Text | Google Scholar

4. Fanfarillo L, Cortijo A, Valenzuela B. Spin-Orbital Interplay and Topology in the Nematic Phase of Iron Pnictides. Phys Rev B (2015) 91:214515. doi:10.1103/PhysRevB.91.214515

CrossRef Full Text | Google Scholar

5. Mukherjee S, Kreisel A, Hirschfeld PJ, Andersen BM. Model of Electronic Structure and Superconductivity in Orbitally Ordered FeSe. Phys Rev Lett (2015) 115:026402. doi:10.1103/PhysRevLett.115.026402

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Sprau PO, Kostin A, Kreisel A, Böhmer AE, Taufour V, Canfield PC, et al. Discovery of Orbital-Selective Cooper Pairing in FeSe. Science (2017) 357:75–80. doi:10.1126/science.aal1575

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kreisel A, Andersen BM, Sprau PO, Kostin A, Davis JCS, Hirschfeld PJ. Orbital Selective Pairing and gap Structures of Iron-Based Superconductors. Phys Rev B (2017) 95:174504. doi:10.1103/PhysRevB.95.174504

CrossRef Full Text | Google Scholar

8. Benfatto L, Valenzuela B, Fanfarillo L. Nematic Pairing from Orbital-Selective Spin Fluctuations in FeSe. Npj Quant Mater (2018) 3:56. doi:10.1038/s41535-018-0129-9

CrossRef Full Text | Google Scholar

9. Hu H, Yu R, Nica EM, Zhu J-X, Si Q. Orbital-Selective Superconductivity in the Nematic Phase of FeSe. Phys Rev B (2018) 98:220503. doi:10.1103/PhysRevB.98.220503

CrossRef Full Text | Google Scholar

10. Bhattacharyya S, Björnson K, Zantout K, Steffensen D, Fanfarillo L, Kreisel A, et al. Nonlocal Correlations in Iron Pnictides and Chalcogenides. Phys Rev B (2020) 102:035109. doi:10.1103/PhysRevB.102.035109

CrossRef Full Text | Google Scholar

11. Liu D, Li C, Huang J, Lei B, Wang L, Wu X, et al. Orbital Origin of Extremely Anisotropic Superconducting gap in Nematic Phase of FeSe Superconductor. Phys Rev X (2018) 8:031033. doi:10.1103/PhysRevX.8.031033

CrossRef Full Text | Google Scholar

12. Fanfarillo L, Mansart J, Toulemonde P, Cercellier H, Le Fèvre P, Bertran F, et al. Orbital-Dependent Fermi Surface Shrinking as a Fingerprint of Nematicity in FeSe. Phys Rev B (2016) 94:155138. doi:10.1103/PhysRevB.94.155138

CrossRef Full Text | Google Scholar

13. Christensen MH, Fernandes RM, Chubukov AV. Orbital Transmutation and the Electronic Spectrum of FeSe in the Nematic Phase. Phys Rev Res (2020) 2:013015. doi:10.1103/PhysRevResearch.2.013015

CrossRef Full Text | Google Scholar

14. de’ Medici L, Giovannetti G, Capone M. Selective Mott Physics as a Key to Iron Superconductors. Phys Rev Lett (2014) 112:177001. doi:10.1103/PhysRevLett.112.177001

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Kostin A, Sprau PO, Kreisel A, Chong YX, Böhmer AE, Canfield PC, et al. Imaging Orbital-Selective Quasiparticles in the Hund's Metal State of FeSe. Nat Mater (2018) 17:869–74. doi:10.1038/s41563-018-0151-0

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Björnson K, Kreisel A, Rømer AT, Andersen BM. Orbital-Dependent Self-Energy Effects and Consequences for the Superconducting gap Structure in Multiorbital Correlated Electron Systems. Phys Rev B (2021) 103:024508. doi:10.1103/PhysRevB.103.024508

CrossRef Full Text | Google Scholar

17. Cercellier H, Rodière P, Toulemonde P, Marcenat C, Klein T. Influence of the Quasiparticle Spectral Weight in FeSe on Spectroscopic, Magnetic, and Thermodynamic Properties. Phys Rev B (2019) 100:104516. doi:10.1103/physrevb.100.104516

CrossRef Full Text | Google Scholar

18. Biswas PK, Kreisel A, Wang Q, Adroja DT, Hillier AD, Zhao J, et al. Evidence of Nodal gap Structure in the Basal Plane of the FeSe Superconductor. Phys Rev B (2018) 98:180501. doi:10.1103/PhysRevB.98.180501

CrossRef Full Text | Google Scholar

19. Zhou R, Scherer DD, Mayaffre H, Toulemonde P, Ma M, Li Y, et al. Singular Magnetic Anisotropy in the Nematic Phase of Fese. Npj Quan Mater. (2020) 5:93. doi:10.1038/s41535-020-00295-1

CrossRef Full Text | Google Scholar

20. Yi M, Pfau H, Zhang Y, He Y, Wu H, Chen T, et al. Nematic Energy Scale and the Missing Electron Pocket in FeSe. Phys Rev X (2019) 9:041049. doi:10.1103/PhysRevX.9.041049

CrossRef Full Text | Google Scholar

21. Huh SS, Seo JJ, Kim BS, Cho SH, Jung JK, Kim S, et al. Absence of Y-Pocket in 1-Fe Brillouin Zone and Reversed Orbital Occupation Imbalance in FeSe. Commun Phys (2020) 3:52. doi:10.1038/s42005-020-0319-1

CrossRef Full Text | Google Scholar

22. Jiang K, Hu J, Ding H, Wang Z. Interatomic Coulomb Interaction and Electron Nematic Bond Order in FeSe. Phys Rev B (2016) 93:115138. doi:10.1103/PhysRevB.93.115138

CrossRef Full Text | Google Scholar

23. Scherer DD, Jacko AC, Friedrich C, Şaşıoğlu E, Blügel S, Valentí R, et al. Interplay of Nematic and Magnetic Orders in FeSe under Pressure. Phys Rev B (2017) 95:094504. doi:10.1103/PhysRevB.95.094504

CrossRef Full Text | Google Scholar

24. Xing R-Q, Classen L, Khodas M, Chubukov AV. Competing Instabilities, Orbital Ordering, and Splitting of Band Degeneracies from a Parquet Renormalization Group Analysis of a Four-Pocket Model for Iron-Based Superconductors: Application to FeSe. Phys Rev B (2017) 95:085108. doi:10.1103/PhysRevB.95.085108

CrossRef Full Text | Google Scholar

25. Eugenio PM, Vafek O. Classification of Symmetry Derived Pairing at the M point in FeSe. Phys Rev B (2018) 98:014503. doi:10.1103/PhysRevB.98.014503

CrossRef Full Text | Google Scholar

26. Christensen MH, Kang J, Fernandes RM. Intertwined Spin-Orbital Coupled Orders in the Iron-Based Superconductors. Phys Rev B (2019) 100:014512. doi:10.1103/PhysRevB.100.014512

CrossRef Full Text | Google Scholar

27. Rhodes LC, Böker J, Müller MA, Eschrig M, Eremin IM. Non-Local D_xy Nematicity and the Missing Electron Pocket in FeSe. Npj Quan Mater. (2021) 6:45. doi:10.1038/s41535-021-00341-6

CrossRef Full Text | Google Scholar

28. Long X, Zhang S, Wang F, Liu Z. A First-Principle Perspective on Electronic Nematicity in FeSe. Npj Quan Mater. (2020) 5:50. doi:10.1038/s41535-020-00253-x

CrossRef Full Text | Google Scholar

29. Steffensen D, Kreisel A, Hirschfeld PJ, Andersen BM. Interorbital Nematicity and the Origin of a Single Electron Fermi Pocket in FeSe. Phys Rev B (2021) 103:054505. doi:10.1103/PhysRevB.103.054505

CrossRef Full Text | Google Scholar

30. Yamada T, Tohyama T. Multipolar Nematic State of Nonmagnetic FeSe Based on DFT+U. Phys Rev B (2021) 104:L161110. doi:10.1103/PhysRevB.104.L161110

CrossRef Full Text | Google Scholar

31. Chen T, Chen Y, Kreisel A, Lu X, Schneidewind A, Qiu Y, et al. Anisotropic Spin Fluctuations in Detwinned FeSe. Nat Mater (2019) 18:709–16. doi:10.1038/s41563-019-0369-5

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Kreisel A, Mukherjee S, Hirschfeld PJ, Andersen BM. Spin Excitations in a Model of FeSe with Orbital Ordering. Phys Rev B (2015) 92:224515. doi:10.1103/PhysRevB.92.224515

CrossRef Full Text | Google Scholar

33. Kreisel A, Andersen BM, Hirschfeld PJ. Itinerant Approach to Magnetic Neutron Scattering of FeSe: Effect of Orbital Selectivity. Phys Rev B (2018) 98:214518. doi:10.1103/PhysRevB.98.214518

CrossRef Full Text | Google Scholar

34. Lu X, Zhang W, Tseng Y, Liu R, Tao Z, Paris E, et al. Spin-Excitation Anisotropy in the Nematic State of Detwinned FeSe. arXiv e-prints arXiv:2108.04484 (2021).

Google Scholar

35. Lu X, Scherer DD, Tam DW, Zhang W, Zhang R, Luo H, et al. Spin Waves in Detwinned BaFe₂As₂. Phys Rev Lett (2018) 121:067002. doi:10.1103/PhysRevLett.121.067002

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Kaneshita E, Tsutsui K, Tohyama T. Spin and Orbital Characters of Excitations in Iron Arsenide Superconductors Revealed by Simulated Resonant Inelastic X-ray Scattering. Phys Rev B (2011) 84:020511. doi:10.1103/PhysRevB.84.020511

CrossRef Full Text | Google Scholar

37. Eschrig H, Koepernik K. Tight-Binding Models for the Iron-Based Superconductors. Phys Rev B (2009) 80:104503. doi:10.1103/PhysRevB.80.104503

CrossRef Full Text | Google Scholar

38. Kreisel A, Wang Y, Maier TA, Hirschfeld PJ, Scalapino DJ. Spin Fluctuations and Superconductivity in K_xFe_2−ySe₂. Phys Rev B (2013) 88:094522. doi:10.1103/physrevb.88.094522

CrossRef Full Text | Google Scholar

39. Wu X, Liang Y, Fan H, Hu J. Nematic Orders and Nematicity-Driven Topological Phase Transition in FeSe. ArXiv e-prints ArXiv:1603.02055 (2016).

Google Scholar

40. Yu R, Zhu J-X, Si Q. Orbital Selectivity Enhanced by Nematic Order in FeSe. Phys Rev Lett (2018) 121:227003. doi:10.1103/PhysRevLett.121.227003

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Terashima T, Kikugawa N, Kiswandhi A, Choi E-S, Brooks JS, Kasahara S, et al. Anomalous Fermi Surface in FeSe Seen by Shubnikov-De Haas Oscillation Measurements. Phys Rev B (2014) 90:144517. doi:10.1103/PhysRevB.90.144517

CrossRef Full Text | Google Scholar

42. Audouard A, Duc F, Drigo L, Toulemonde P, Karlsson S, Strobel P, et al. Quantum Oscillations and Upper Critical Magnetic Field of the Iron-Based Superconductor FeSe. Europhys Lett (2015) 109:27003. doi:10.1209/0295-5075/109/27003

CrossRef Full Text | Google Scholar

43. Watson MD, Kim TK, Haghighirad AA, Davies NR, McCollam A, Narayanan A, et al. Emergence of the Nematic Electronic State in FeSe. Phys Rev B (2015) 91:155106. doi:10.1103/PhysRevB.91.155106

CrossRef Full Text | Google Scholar

44. Watson MD, Kim TK, Rhodes LC, Eschrig M, Hoesch M, Haghighirad AA, et al. Evidence for Unidirectional Nematic Bond Ordering in FeSe. Phys Rev B (2016) 94:201107. doi:10.1103/PhysRevB.94.201107

CrossRef Full Text | Google Scholar

45. Yu R, Si Q. U(1) Slave-Spin Theory and its Application to Mott Transition in a Multiorbital Model for Iron Pnictides. Phys Rev B (2012) 86:085104. doi:10.1103/PhysRevB.86.085104

CrossRef Full Text | Google Scholar

46. Georges A, Medici Ld., Mravlje J. Strong Correlations from Hund's Coupling. Annu Rev Condens Matter Phys (2013) 4:137–78. doi:10.1146/annurev-conmatphys-020911-125045

CrossRef Full Text | Google Scholar

47. van Roekeghem A, Richard P, Ding H, Biermann S. Spectral Properties of Transition Metal Pnictides and Chalcogenides: Angle-Resolved Photoemission Spectroscopy and Dynamical Mean-Field Theory. Comptes Rendus Physique (2016) 17:140–63. doi:10.1016/j.crhy.2015.11.003

CrossRef Full Text | Google Scholar

48. Yi M, Zhang Y, Shen Z-X, Lu D. Role of the Orbital Degree of freedom in Iron-Based Superconductors. Npj Quant Mater (2017) 2:57. doi:10.1038/s41535-017-0059-y

CrossRef Full Text | Google Scholar

49. Guterding D, Backes S, Tomić M, Jeschke HO, Valentí R. Ab Initioperspective on Structural and Electronic Properties of Iron-Based Superconductors. Phys Status Solidi B (2017) 254:1600164. doi:10.1002/pssb.201600164

CrossRef Full Text | Google Scholar

50. de’ Medici L. The Physics of Correlated Insulators, Metals, and Superconductors (Modeling and Simulation). In: Hund’s Metals Explained, 7. Juelich: Forschungszentrum Juelich (2017). p. 377–98.

Google Scholar

51. Kuroki K, Onari S, Arita R, Usui H, Tanaka Y, Kontani H, et al. Unconventional Pairing Originating from the Disconnected Fermi Surfaces of Superconducting LaFeAsO_1−xF_x. Phys Rev Lett (2008) 101:087004. doi:10.1103/PhysRevLett.101.087004

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Graser S, Maier TA, Hirschfeld PJ, Scalapino DJ. Near-Degeneracy of Several Pairing Channels in Multiorbital Models for the Fe Pnictides. New J Phys (2009) 11:025016. doi:10.1088/1367-2630/11/2/025016

CrossRef Full Text | Google Scholar

53. Kemper AF, Maier TA, Graser S, Cheng H-P, Hirschfeld PJ, Scalapino DJ. Sensitivity of the Superconducting State and Magnetic Susceptibility to Key Aspects of Electronic Structure in Ferropnictides. New J Phys (2010) 12:073030. doi:10.1088/1367-2630/12/7/073030

CrossRef Full Text | Google Scholar

54. Ament LJP, van Veenendaal M, Devereaux TP, Hill JP, van den Brink J. Resonant Inelastic X-ray Scattering Studies of Elementary Excitations. Rev Mod Phys (2011) 83:705–67. doi:10.1103/RevModPhys.83.705

CrossRef Full Text | Google Scholar