- Hunan University of Finance and Economics, Changsha, China
In view of the dynamics of the dam safety monitoring data, the sensitivity to time and space, and the nonlinearity, it has been proposed to use the firefly algorithm to search to determine the delay order and the number of hidden layer units and combine them with nonlinear autoregressive algorithms. The algorithms are combined to obtain the FA-NAR algorithm dam deformation prediction model, which is compared with the traditional BP algorithm prediction results, combined with the Xiaolangdi dam deformation monitoring data for prediction, and the dam deformation data predicted by the dynamic neural network have a better convergence effect and a more accurate prediction result. It provides a certain reference basis for perfecting dam safety monitoring.
Introduction
As one of the representatives of water conservancy projects, dams play a vital role in the development and utilization of water resources. Once a dam break occurs, it will bring immeasurable losses to the life and safety of the people. The occurrence of dam breaks is mostly due to the lack of necessary monitoring technologies and better monitoring equipment [1]. It can be seen that analyzing the dam prototype monitoring data and studying the dam safety monitoring model are essential to ensure the safe operation of the dam. Therefore, it is necessary to choose an efficient, fast, and accurate method for analyzing and processing observational data in order to grasp the safe operation of the dam in real time [2] and realize the automation of dam monitoring, thereby reducing the possibility of dam breaks.
In recent years, neural networks as a new and powerful information processing method, especially its unique nonlinear dynamics, powerful function approximation ability, self-learning, and self-adaptive ability, in the analysis and processing of dam observation data can also be applied. At present, the research on the dam monitoring neural network model is in the development stage. It is a newly developed, very important, and very active frontier research field in the research of dam safety monitoring.
Some scholars have done a lot of useful work in this field of exploration and achieved certain results [2]; XingLi, ZhipingWen, HuaizhiSu, and so forth proposed random forest intelligent algorithms to build dam safety monitoring model methods [3]; Wang Lirong, Zheng Dongjian, and so forth proposed to use CNN to identify dam safety monitoring data anomaly modes in order to reduce the data processing pressure of dam safety monitoring data anomaly identification and solve the problem that traditional methods find it difficult to identify non-maximum abnormal points [4]; SiyuChen, ChongshiGu, and so forth used RBF neural networks and kernel main component analysis to establish a safety monitoring model for ultra-high concrete dams [5]; FeiKang, AMASCE, and JunjieLi proposed a Gaussian process regression model for the health monitoring of concrete gravity dams [6]; BoDai et al. proposed to use statistical models and random forest regression (RFR) models to predict the deformation of concrete dams [7]; Dowrueng A, Thongthamchart C, Raphitphan N, and so forth describe decision-making based on the civil engineering expertise of the dam safety remote monitoring system: DS-RMS, which can make action-based recommendations based on everyday scenarios and special events such as earthquakes and floods. The key benefits include quick and reliable access to current information about the dam and relief for dam managers in critical situations. Also, in further development, some real-time dam information is selected and made available to the public automatically and continuously through a mobile app along with the dam safety assessment results [8]; Li, X, Wen, Z., Su, H, and so forth analyze the mechanism of the dam safety monitoring model; for the dam system affected by multiple factors, the mapping relationship between the influencing factors and the dam behavior effect domain is usually nonlinear. Taking the actual monitoring data as the evaluation factor, a dam safety monitoring model based on the random forest (RF) intelligent algorithm was constructed to predict the uplift pressure. The results show that the reservoir water level and daily rainfall have a significant impact on the lifting pressure, and the impact of other factors on the dam deformation is unstable and varies with the external environment [9]; Y. Su, K. Weng, C. Lin, Z. Zheng, and so forth propose an improved RF model for dam displacement prediction analysis combined with a sliding time window strategy. This article takes the Chinese masonry arch dam as an example and takes the horizontal displacement recorded by the global navigation satellite system (GNSS) as the research object. Based on the evaluation criteria, the accuracy and effectiveness of the proposed model are verified and evaluated. Simulation results show that the proposed model can capture long-term features and provide better predictions based on short-term monitoring data [10]; Wang, L, Mao, Y, Cheng, Y, and Liu, Y propose a single-node evaluation model based on the multiple correlation sequence (SAM) to improve the accuracy of single-node evaluation. At the same time, LREA can evaluate the operational status of dams by considering changes in credibility and multi-node coordination. Finally, it is concluded that LREA can timely and accurately reveal the trend of monitoring value changes and improve the accuracy of dam safety evaluation results [11].
Although these scholars have achieved certain results in this field, most of them tend to study static models. Therefore, according to the time characteristics of the external deformation of the dam, the NAR dynamic neural network algorithm is applied to the dam safety monitoring. There are many studies on the NAR dynamic neural network algorithm model, but its delay order and the number of hidden layer units will affect the prediction results of the model. However, most scholars only use empirical formulas or obtain them through multiple experiments, which are difficult to apply to practical engineering. Therefore, in view of the nonlinear time series characteristics of the external deformation of the dam, this study proposes a combined algorithm model of the firefly algorithm and nonlinear autoregressive dynamic neural network and uses the global search of the firefly algorithm to automatically determine the characteristics of the delay order and the number of hidden layer units to solve the problem of blindly inputting network parameters and optimize the algorithm, thereby improving the network learning efficiency and prediction ability [12]. At the same time, the prediction and analysis of the external deformation of the Xiaolangdi dam are carried out, and the combined algorithm and the BP algorithm prediction results are compared and analyzed to verify the effectiveness and reliability of this method in the field of external deformation monitoring of the dam. This will directly improve the accuracy of automatic monitoring of dams and provide a direct basis for timely prevention before dam failure occurs. On one hand, it can alleviate the worries and panics of the state and society due to engineering safety issues, thereby maintaining social stability. On the other hand, it can reduce the unnecessary expenditure of the national finance due to dam safety issues, reduce the burden on the people, and thus promote the smooth operation of the economy.
NAR Dynamic Network and Firefly Algorithm
Because the research on dam safety monitoring in this study is based on the NAR algorithm and firefly algorithm, it will be introduced separately in the second part.
NAR Dynamic Network
The NAR algorithm is a kind of dynamic network, and its algorithm model [13, 14] is expressed as
In this formula,
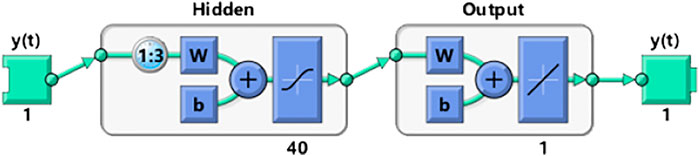
The NAR algorithm has processing time series-related delay variables in its structure. The structure is shown in Figure 1.
From the NAR algorithm structure in Figure 1, y(t) on the left represents the input of the NAR algorithm, and y(t) on the right represents the output of the NAR algorithm. 1:3 represents the delay order, w is the weight, b is the threshold, and 40 is the number of hidden layer units.
Now, the NAR neural network is combined with the dam deformation monitoring, that is, by monitoring the external deformation of the dam to obtain a nonlinear time series related to time changes and then train this time series and find the nonlinear relationship between the amount of deformation at the time and the amount of deformation at time n before time t. It is expressed as
It can be seen from the above formula that it is basically consistent with the algorithm structure of the NAR neural network. This also shows that the NAR neural network is very suitable for processing time-related nonlinear time series. However, in order to solve that the NAR neural network cannot determine the parameters autonomously, the firefly algorithm will be introduced next to optimize the NAR neural network.
Firefly Algorithm
The firefly algorithm is a typical bionic intelligent algorithm proposed by X.S. Yang. It is based on the principle of simulating fireflies to perceive the brightness of other fireflies within a certain range to achieve the purpose of attracting each other and to achieve the optimization process in the algorithm. The specific principle [15–17] is to regard the feasible solutions in the search space as individual fireflies, and the process of searching and optimizing to get the best solution represents the mutual attraction between individual fireflies and the update of positional movement. Finally, the best solution of the objective function is transformed into finding the firefly with the highest brightness. Each search and optimization will update the individual position of the firefly so as to realize the optimization process.
The implementation of the firefly algorithm is also based on the following three principles:
• All fireflies have no gender distinction, and the mutual attraction factor is only related to brightness.
• Attractiveness is proportional to brightness, that is, the brighter the brightness, the stronger the attractiveness.
• The brightness of the fireflies is determined by the objective function, and the distance between any two fireflies i and j is defined as
where d is the coordinate dimension,
The attraction function is expressed as
In the formula,
The fluorescence brightness is expressed as
In the formula,
In the formula,
Experiments
Data Analysis
Data Preprocessing
Due to the interference of many external factors at the monitoring point and the complexity of the dam construction, expansion, reinforcement, and environmental impacts on the structure and material parameters, the dam safety monitoring information has greater uncertainty, so first, preprocessing is adopted for the observation data of the dam, that is, the system error is judged, and the gross errors in the modeling data are eliminated so as to improve the reliability and accuracy of the data used in the modeling. In this study, we intend to use the µ test method to distinguish the systematic errors and use the Laida criterion to eliminate the influence of gross errors [18].
Data Selection
The actual data of the deformation monitoring of the Xiaolangdi Dam is confidential, so this article uses the experimental data simulated according to the nature of the monitoring data. Among them, the data accounting for 70% of the total data volume are selected as the sample for training, and the data accounting for 30% of the total data volume are selected as the forecast data.
Experiment Analysis
According to the algorithm flow chart of the NAR algorithm combination model, a Matlab program is compiled for the training and prediction of the FA-NAR algorithm. Also, the BP algorithm is used to train the same data and make predictions, and the results are compared with the prediction results of the FA-NAR algorithm to verify the high prediction accuracy of the FA-NAR algorithm.
In the process, according to the empirical data, the number of fireflies N is set to 10, the maximum number of iterations is 50, the maximum attraction is 0.5, the step factor a is 0.2, and the light intensity absorption coefficient γ is 1.
After optimization by the firefly algorithm, the delay order of the NAR algorithm is 1:3, and the number of hidden layer units is 40. The structure of the BP neural network is 9-16-1, that is, there are nine input variables, 16 hidden layer units, and one output variable.
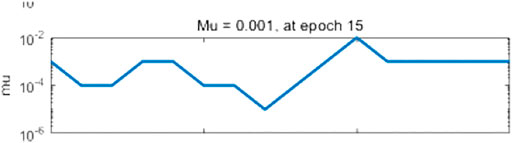
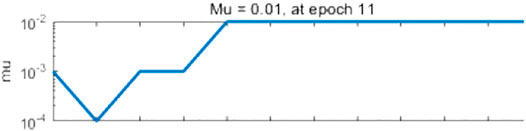
Figures 2, 3 show the Mu values of BP and FA-NAR, respectively. The larger the Mu value, the better the convergence effect of the algorithm. From the comparison, it is found that the convergence of FA-NAR is better than that of BP.
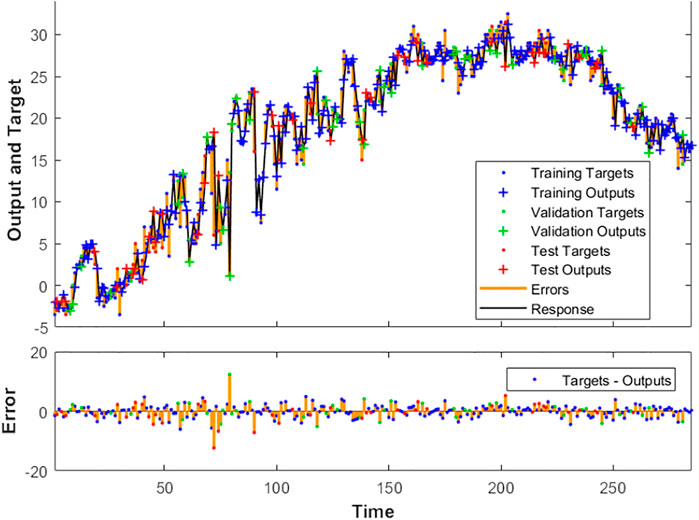
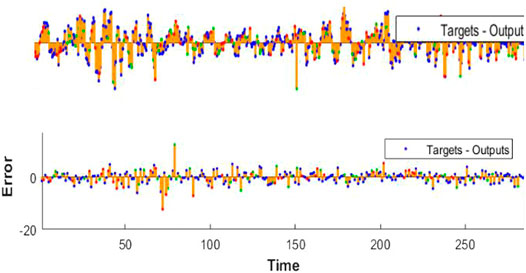
Figure 4 shows the network effect error graph. The vertical line segment represents the error between the actual measured value and the predicted value. The smaller the line segment, the better the network prediction effect. It can be seen from the three that the maximum error does not exceed 0.2 (the data in the figure is expanded by 100 on the original basis, times); the error basically remains at about 0 after the later stabilization, indicating that the FA-NAR algorithm has high prediction accuracy and is suitable for long-term prediction and analysis of dam deformation.
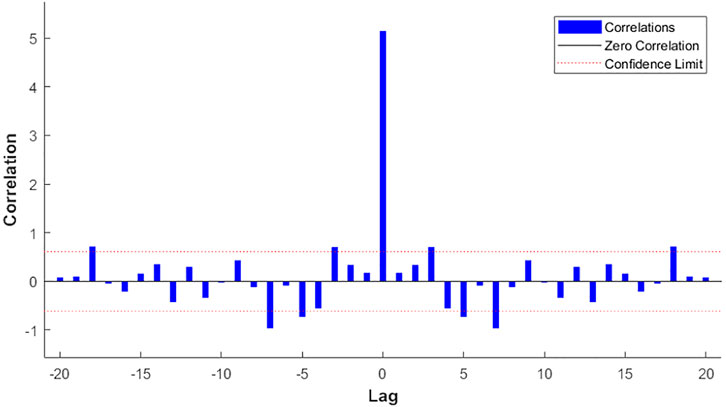
The autocorrelation of the network error in Figure 5 is within the confidence interval, indicating that the correlation of the prediction error between the steps of the algorithm model at each time is nonlinear, and the degree of correlation is small, and it will not be caused by the large prediction error at the previous time. The prediction error at this moment is large, and the prediction effect of this algorithm model is better.
Figure 6 is the effect diagram of training. The closer R is to 1, the better the fitting effect. The training data, prediction data, and overall effect in the figure have reached more than 95%, indicating that the prediction of this algorithm model is of higher accuracy.
Figure 7 shows that the FA-NAR algorithm has higher prediction accuracy than the BP neural network. When the later stage is in the stable stage, the prediction accuracy of the two algorithms is improved. In the later stage, the FA-NAR algorithm is in the stable stage. The prediction accuracy of the algorithm is still higher than that of the BP algorithm.
Conclusion
This study compares the FA-NAR algorithm with the classic BP algorithm and finds that the BP algorithm exists in the monitoring of dam safety. The learning process often requires thousands of iterations, and as the number of learning samples increases, the performance of the algorithm will deteriorate. Using the algorithm model combining the NAR dynamic neural network and firefly algorithm, due to its own learning ability, it not only reduces the blindness of manual input of network parameters but also improves the learning ability and prediction accuracy of the network, so the convergence effect is better than that of the BP algorithm, and it is more suitable for the prediction of dam deformation.
However, the FA-NAR algorithm is not perfect. When the fireflies are attracted by the lack of outstanding individuals, the algorithm will be terminated, or when super individuals appear, it will converge rapidly and lose diversity, and the distance between outstanding individuals is very close to the same position; if the step size is greater than the distance, the search ability will be reduced, oscillation will occur near the peak value, and the local optimal solution cannot be jumped out. It will affect the determination of the number of delay layers and the number of hidden unit layers, and the performance of the algorithm will decrease. Ultimately, it will have an impact on the accuracy of dam deformation predictions.
The experimental data simulated in this study are in good agreement with the FA-NAR algorithm, so it is not affected by the limitations of the algorithm, and the convergence effect of the results is better. Because the experimental data are simulated according to the actual situation of the dam, the model is still effective in predicting the deformation of the dam in the actual situations. However, instability may also occur, so the FA-NAR algorithm can be further optimized in the future to eliminate the limitations of the algorithm as much as possible, making the model more stable in predicting the deformation of the dam.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
Conceptualization, ZQ; methodology, XH; formal analysis, GS and BP.
Funding
The research was co-completed by the School of Journalism and Communication of Hunan Normal University and Financial Big-data Research Institute of Hunan University of Finance and Economics. This research was funded by the National Natural Science Foundation of China (No. 72073041); the Open Foundation for the University Innovation Platform in Hunan Province (No. 18K103); the 2011 Collaborative Innovation Center for Development and Utilization of Finance and Economics Big Data Property, Universities of Hunan Province, Open Project (Nos. 20181901CRP03, 20181901CRP04, and 20181901CRP05); the 2020 Hunan Provincial Higher Education Teaching Reform Research Project (Nos. HNJG-2020-1130 and HNJG-2020-1124); and the 2020 General Project of Hunan Social Science Fund (No. 20B16).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
References
1. Chen W. Research on Application of Genetic Algorithm and Neural Network in Dam Safety Monitoring D, 12. Xi’an: Changan University (2009). p. 66.
2. Fang W. Comprehensive Discussion on Safety Monitoring of Earth-Rock Dam. J.Hongshuihe (2002) 04:pp64–67.
3. Li X, Wen Z, Su H. An Approach Using Random forest Intelligent Algorithm to Construct a Monitoring Model for Dam Safety. J.Engineering Comput (2021) 37:pp39–56. doi:10.1007/s00366-019-00806-0
4. Wang L, Zheng D. Anomaly Recognition of Dam Safety Monitoring Data Based on Convolutional Neural Network. J.Journal Yangtze River Scientific Res Inst (2021) 38:pp72–77.
5. Chen S, Gu C. Safety Monitoring Model of a Super-high Concrete Dam by Using RBF Neural Network Coupled with Kernel Principal Component Analysis J. Hindawi. Math Probl Eng 2018 (2018).
6. Kang F, Li J. Displacement Model for Concrete Dam Safety Monitoring via Gaussian Process Regression Considering Extreme Air Temperature J. J Struct Eng (2020) 146. doi:10.1061/(asce)st.1943-541x.0002467
7. Bo D, Gu C, Zhao E, Qin X. Statistical Model Optimized Random forest Regression Model for concrete Dam Deformation Monitoring. J.Structural Control Health Monit (2018) 25.
8. Dowrueng A, Thongthamchart C, Raphitphan N. Decision Support System in Thailand's Dam Safety with a Mobile Application for Public Relations: DS-RMS (Dam Safety Remote Monitoring System). J Int J Decis Support Syst Tech (Ijdsst) (2022) 14(1):pp1–35. doi:10.4018/ijdsst.286183
9. Li X, Wen Z, Su H. An Approach Using Random forest Intelligent Algorithm to Construct a Monitoring Model for Dam Safety. J Eng Comput (2021) 37:pp39–56. doi:10.1007/s00366-019-00806-0
10. Su Y, Weng K, Lin C, Zheng Z. An Improved Random Forest Model for the Prediction of Dam Displacement. J.IEEE Access (2021) 9:pp9142–9153. doi:10.1109/access.2021.3049578
11. Wang L, Mao Y, Cheng Y, Liu Y. Deep Learning-Based Diagnosing Structural Behavior in Dam Safety Monitoring System J. Sensors (2021) 21:pp1171. doi:10.3390/s21041171
12. Cai S, Li E, Chen L. Time Series Prediction of Tunnel Surrounding Rock Deformation Based on FA-NAR Dynamic Neural Network. J Chin J Rock Mech Eng (2019) 38(S2):pp3346–3353.
13. Yuan L. Vehicle Speed Prediction and Application Based on NAR Neural Network D. Dalian: Dalian University of Technology (2016).
14. Li X, Wang N, Mei Y. Application and Test of NAR Neural Network——Taking Urban Residents' Water Demand Quota as an Example. J.Journal of Irrigation and Drainage (2017) 36(11):pp122–128.
15. Yang XS. Firefly algorithms for multimodal optimization. J Math (2009) 5792:pp169–178. doi:10.1007/978-3-642-04944-6_14
16. Yang XS. DEB S. Eagle strategy using Lévy walk and firefly algorithms for stochastic optimization. J Stud Comput Intelligence (2010) 284:pp101–111.
17. Chen K, Chen F, Dai M. Fast image segmentation with two-dimensional entropy and multi-threshold based on firefly algorithm. J Opt Precision Eng (2014) 22(2):pp517–523. doi:10.3788/ope.20142202.0517
Keywords: dig data, FA-NAR dynamic neural network, dam safety, model integration, monitor safety
Citation: Pan B, Quan Z, Huang X and Sun G (2022) Using the FA-NAR Dynamic Neural Network Model and Big Data to Monitor Dam Safety. Front. Phys. 10:859172. doi: 10.3389/fphy.2022.859172
Received: 04 February 2022; Accepted: 07 April 2022;
Published: 08 June 2022.
Edited by:
Lev Shchur, Landau Institute for Theoretical Physics, RussiaReviewed by:
Venkatesan Rajinikanth, St. Joseph’s College of Engineering, IndiaKaibo Shi, Chengdu University, China
Copyright © 2022 Pan, Quan, Huang and Sun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhitong Quan, MjcxMTcxNjczNUBxcS5jb20=; Guang Sun, c3VuZ3VhbmdAaHVmZS5lZHUuY24=
 Bin Pan
Bin Pan Zhitong Quan
Zhitong Quan Xueli Huang
Xueli Huang