FeSe and the Missing Electron Pocket Problem

The nature and origin of electronic nematicity remains a significant challenge in our understanding of the iron-based superconductors. This is particularly evident in the iron chalcogenide, FeSe, where it is currently unclear how the experimentally determined Fermi surface near the M point evolves from having two electron pockets in the tetragonal state, to exhibiting just a single electron pocket in the nematic state. This has posed a major theoretical challenge, which has become known as the missing electron pocket problem of FeSe, and is of central importance if we wish to uncover the secrets behind nematicity and superconductivity in the wider iron-based superconductors. Here, we review the recent experimental work uncovering this nematic Fermi surface of FeSe from both ARPES and STM measurements, as well as current theoretical attempts to explain this missing electron pocket of FeSe, with a particular focus on the emerging importance of incorporating the d_xy orbital into theoretical descriptions of the nematic state. Furthermore, we will discuss the consequence this missing electron pocket has on the theoretical understanding of superconductivity in this system and present several remaining open questions and avenues for future research.

1 Introduction

One of the reasons for the huge interest in FeSe over the past decade has been the sense that it holds the key to the wider understanding of the whole Fe-based superconductor family [1–3]. With its minimalistic crystal structure and alluringly simple band structure in the tetragonal phase, alongside the prevalence of high-quality single crystals, it seemed like the ideal test bed to examine in detail the themes that were emerging in the field: strong orbital-dependent correlations [4–6], spin fluctuation pairing [7, 8], and most pertinently for this review, the so-called “nematic” phase [9–11], where C₄ rotational symmetry is spontaneously broken below 90 K.

Spontaneous breaking of rotational symmetry of the underlying lattice due to electronic correlations, the signature of nematic order, is known to occur via many mechanisms, such as via a high field FFLO state, which has been proposed for various materials including FeSe [12–14]. However, whereas a clear theory for FFLO order exists, the precise microscopic origin of the zero field nematicity in FeSe is still an important open question. Part of the challenging in understanding this nematic state arises due to the formation of antiferromagnetism that often accompanies the onset of the nematic state in many systems, although not FeSe. FeSe is therefore the perfect candidate to uncover the origin of the nematic state, as well as elucidate the effect nematicity has on the superconducting properties of the iron-based superconductors.

The measurement of the momentum-dependence of the superconducting gap in FeSe, between 2016 and 2018, was a particular experimental triumph. The data from both scanning tunneling microscopy (STM) [15] and multiple angle-resolved photoemission spectroscopy (ARPES) measurements [16–20] revealed a clear conclusion: the gap structure is extremely anisotropic, and broadly follows the d_yz orbital weight around the Fermi surface. While a twofold-symmetric gap is of course symmetry-allowed in an orthorhombic system, the fact that such a strong anisotropy was observed implied that the nematic state must also induce a profound anistropic effect on the Fermi surface of FeSe. However due to significant uncertainty as to the correct description of the low-temperature electronic structure, multiple theoretical explanations for the anisotropic gap structure were proposed [15, 19, 21–24].

A critical question required to understand this anisotropic superconducting gap is how does the nematic state influence the low temperature Fermi surface and electronic structure of FeSe? Given that we have a second-order phase transition [25], and that the lattice distortion $\frac{|a-b|}{(a+b)}$ is only ∼0.2%, the natural assumption, from an ab-initio perspective [26], would be that nematicity should only weakly distort the established Fermi surface of the high-temperature tetragonal phase, which ARPES measurements have shown contains two hole pockets and two electron pockets [26–33]. Yet ARPES measurements in the nematic state have revealed sizeable band shifts, of the order of 10–50 meV [33], much larger that what would be predicted from ab-initio calculations [26].

Unfortunately, the precise identification of specific parts of the band structure, the nematic energy scales and even the Fermi surface of FeSe has been complicated by the formation of orthorhombic domains upon entering the nematic state. In an orthorhombic crystal, conventional ARPES experiments measure a superposition of two perpendicularly orientated crystallographic domains, which doubles the number of bands observed in the experimental data and creates ambiguity about which bands arise from which domain. For this reason, a recent focal point of research has involved overcoming this technical challenge of orthorhombic domains, for example by applying uniaxial strain [28, 34–40] or using NanoARPES [41] or scanning tunneling microscopy [14, 15, 42, 43]. The conclusion from these measurements have been unanimous, and have revealed that within the nematic state the Fermi surface of FeSe consists of one hole pocket and one electron pocket.

This finding, however, is very surprising and presents a fundamental theoretical conundrum that is at the heart of understanding the nematic and superconducting properties of FeSe. The bands that generate the two electron pockets observed in the tetragonal state form saddle points at the high symmetry M point close to the Fermi level. It is therefore not trivial to deform or shift these saddle points to lift one of these electron pockets away from the Fermi level upon entering the nematic state. This current theoretical challenge has become known as the “missing electron pocket problem” of FeSe and resolving this problem promises deeper insight into the nematic state, and a wider understanding of superconductivity in the iron-based superconductors.

In this review we will overview the recent experimental and theoretical work uncovering the Fermi surface of FeSe in the nematic state and tackling the missing electron pocket problem. In Section 2 we will briefly introduce the experimental electronic structure of FeSe in the tetragonal state, to use as the foundation for understanding the nematic electronic structure. In Section 3 we will discuss the recent experimental data uncovering the electronic structure in the nematic state, in particular focusing on measurements which overcome the technical problems associated with orthorhombic crystals, including ARPES measurements under uniaxial strain, NanoARPES measurements and Scanning tunneling microscopy (STM) measurements. In Section 4 we will review the latest theoretical attempts to resolve this missing electron pocket problem, highlighting the necessity of considering the d_xy orbital in the phenomenological description of the nematic state. And in Section 5 we will discuss the consequence the updated Fermi surface has on the understanding of the superconducting properties of FeSe. A summary of the electronic structure and missing electron pocket problem of FeSe is presented in Figure 1.

FIGURE 1

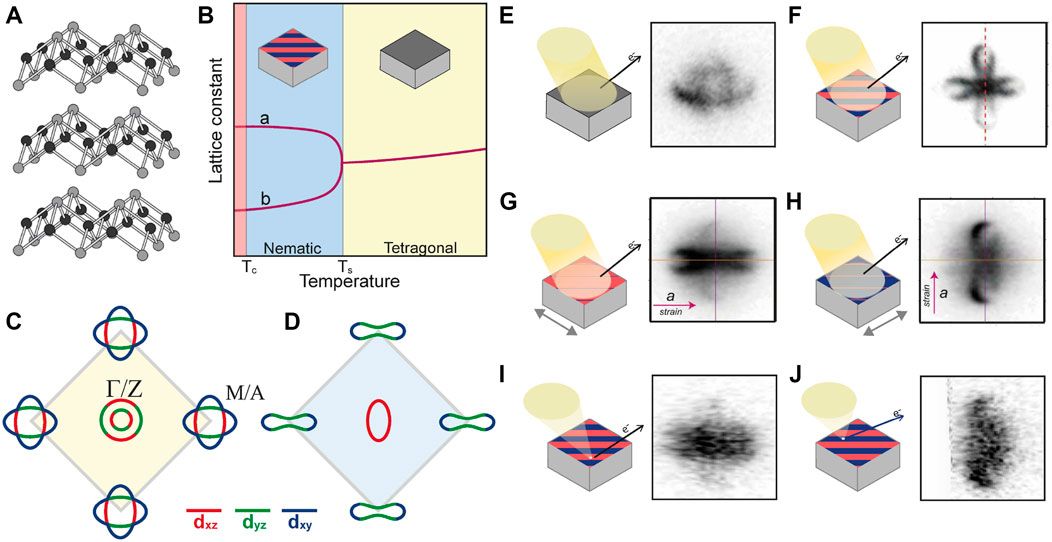
FIGURE 1. Summary of the Fermi surface of FeSe and photoemission measurements of a single electron pocket. (A) Crystal structure of FeSe, Fe (black), Se (grey). (B) Sketch of the temperature evolution of the lattice constants in FeSe, as described in Ref. [44], highlighting the evolution from a tetragonal (dark grey surface) to orthorhombic system with differently orientated domains (red and blue striped surface). (C) Sketch of the experimentally determined Fermi surface of FeSe in the tetragonal state and (D) in the nematic state. (E–J) Summary of the Fermi surface of FeSe measured around the M/A point via different photoemission techniques. (E) Measurement in the tetragonal state (100 K, LV hν = 56 eV [32]) showing two electron pockets, (F) ARPES Measurement in the nematic state (10 K, LV, hν = 56 eV [32]) arising from a superposition of two orthorhombic domain orientations (red and blue regions), referred to as a “twinned” measurement. (G,H) ARPES measurement of a detwinned crystal in the nematic state (10 K, hν = 56 eV [34], where tensile strain is applied either along the a or b crystallographic axis and predominately probes a single domain orientation. (I,J) NanoARPES measurement using a photon beamspot of $<1$ μm (30 K, hν = 56 eV [41]) in individual orthorhombic domains.

2 Electronic Structure in the Tetragonal State

From both a theoretical and experimental point of view, the electronic structure of the tetragonal state is relatively well understood. Prior to the onset of nematicity at T_s = 90 K, FeSe exhibits tetragonal symmetry with a P4/nmm crystal structure [44]. This structure consists of layers of Fe atoms, in a 2D square lattice configuration, bridged by staggered out-of-plane Se atoms, giving rise to a crystallographic unit cell containing two Fe atoms and two Se atoms. The two Fe atoms are related by a glide-mirror symmetry, which can theoretically half the number of bands and allows for an unfolding to a 1-Fe Brillouin zone used by some authors [45], but here we use the 2-Fe unit cell notation for comparison with ARPES measurements.

The low energy electronic properties are governed by the partially-filled 3d_xz, 3d_yz and 3d_xy orbitals of the two Fe atoms, which in momentum space gives rise to three hole bands around the Γ point and two symmetry-protected saddle point van-Hove singularities around the M point [46] as shown in Figure 2A.

FIGURE 2

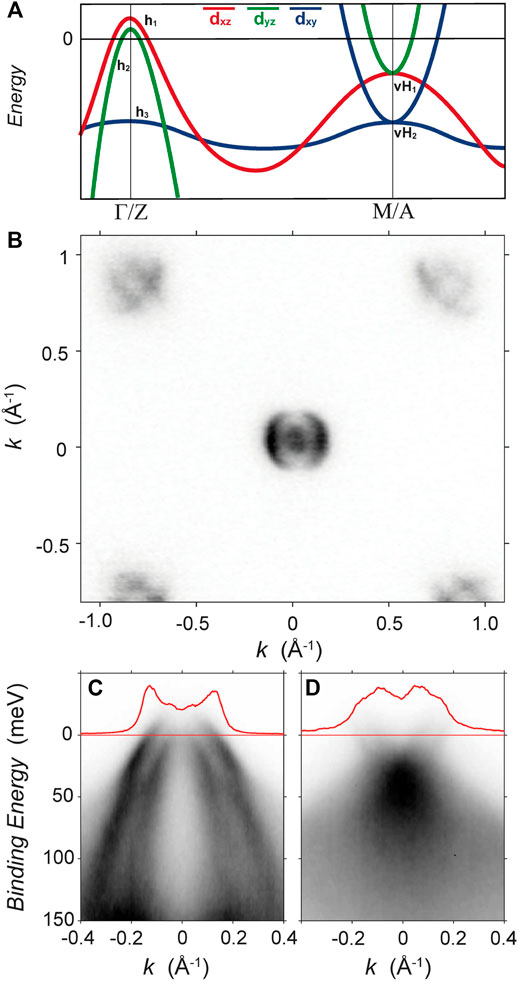
FIGURE 2. Electronic structure in the tetragonal state of FeSe. (A) Sketch of the low-energy band structure of a typical P4/nmm Fe-based superconductor along the Γ − M (k_z = 0) or Z − A (k_z = π) high symmetry points. The colours indicate the dominant orbital character of the bands. (B) Fermi surface in the tetragonal state measured at 100 K close to k_z = π (hν = 56 eV). (C) Cut along the Z − A direction (equivalent to Γ − M but at k_z = π) direction for the hole bands around the Z point for the same photon energy (hν = 56 eV). (D) Cut along the Z − A direction for the electron bands around the A point. Figures adapted from [29, 32].

Of the three hole bands, two exist as a C₄ symmetric pair exhibiting predominantly d_xz and d_yz orbital weight (labelled h₁ and h₂ in Figure 2A) and the third is dominated by d_xy orbital character (h₃). h₁ and h₂ would be energy degenerate at the high symmetry point, however spin orbit coupling lifts this degeneracy [47]. As for the van-Hove singularities around the M point, one is a saddle point connecting bands of majority d_xz and d_yz weight (vH₁) and the other is a saddle point connecting two d_xy dominated bands (vH₂). This general structure is broadly applicable to all P4/nmm Fe-based superconductors (e.g., Fe(Te,Se,S), LiFeAs, NaFeAs, LaFeAsO), with some modifications for the 122 family due to the I-centering of the lattice.

The experimentally measured Fermi surface of FeSe at 100 K (or more precisely, a map of the experimental spectral function at the chemical potential) at approximately k_z = π is shown in Figure 2B, revealing a two-hole pocket and two electron pocket Fermi surface. Measurements around the center of the Brillouin zone show that both h₁ and h₂ cross the chemical potential at 100 K, as shown in Figure 2C. Their band maximas are separated by ∼20 meV due to spin-orbit coupling [47–49]. At k_z = 0 these bands have a maxima at approximately h₂ = −13 meV and h₁ = + 7 meV [48], and at k_z = π (shown in Figure 2C) the bands have maxima of approximately h₂ = + 5 meV and h₁ = + 30 meV. The second smaller hole pocket of FeSe is thus only present at finite k_z, which highlights an important property of this system. Even though FeSe has a “quasi-2D” structure, i.e. the energy shift of the bands as a function of k_z is only on the order of 20 meV, this energy scale is actually on the same order of magnitude as the total Fermi energy of this system, and therefore is non-negligible in quantitative descriptions of the physical properties of FeSe. We note in passing that, due to the small Fermi energy of this system, the electronic structure is subject to substantial temperature-dependence of the chemical potential, and the appearance of the “Fermi surface” changes substantially between 100 and 300 K [50], although without any change of the symmetry.

The third d_xy hole band, h₃, is observed to be much flatter and cross both h₁ and h₂ at an energy of approximately −50 meV. In most ARPES data sets, this band has a much lower intensity than the h₁ and h₂ bands, which is a consequence of photoemission-based matrix element effects, which ensures the intensity of photoelectrons originating from d_xy states with momentum near |k| = 0 will be suppressed [51]. Nevertheless, h₃ can be identified most clearly near where it hybridises with h₁ and h₂, and thus acquires some d_xz and d_yz orbital weight as shown in Figure 2C.

Near the corner of the Brillouin zone, both the d_xy dominated electron band, connected to vH₂, and the d_xz/d_yz electron band, connecting to vH₁, are observed to cross the Fermi level. Here the outer four-fold symmetric electron pocket is dominated by d_xy orbital character while the inner pocket is dominated by d_xz and d_yz orbital weight [52]. As this is a compensated system, the total Fermi volume of these electron pockets should be equal to that of the hole pockets [29].

These two sets of electron bands connect to the saddle points which have an energy of approximately vH₁ = − 20 meV and vH₂ = − 40 meV at the high symmetry point. The exact position of these stationary points, however, are masked by the presence of self-energy interactions which give rise to a broadening of the electronic states around the M point. This broadening is also captured in theoretical simulations involving spin and charge fluctuations [53].

The ARPES data presented in Figure 2 is taken from our own works [29, 32], however multiple data sets are available in the literature and are all consistent with the interpretation presented here [26–28, 30, 33, 54]. Indeed, the electronic structure must be constrained by the symmetry based arguments of Figure 2A [46, 52, 55] and each of the bands observed in the measurements can be mapped to corresponding bands calculated from ab-initio techniques such as density functional theory (DFT) [26, 29, 52] of the paramagnetic tetragonal phase.

There are, however, serious quantitative issues with DFT-based calculations, which severely limit its use in describing the low energy properties of FeSe. First, DFT-based calculations overestimate the bandwidth of the Fe 3d-bands by a factor of ∼3 [29, 56]. This is a generic finding across all Fe-based superconductors [57], and derives from the fact that electronic correlations are inadequately treated in DFT. It has been often argued that the correlation effects are orbital-dependent and particularly strong for the d_xy orbital [29, 57, 58]. More advanced theoretical simulations, such as DFT + DMFT [59] and QSGW + DMFT [53], have had some success in capturing the global electronic structure on the eV scale [59, 60], finding strongly incoherent spectral weight at 1–3 eV below E_F and sharp quasiparticles only in the near vicinity of E_F. However ab-initio efforts still usually overestimate the size of the hole and electron Fermi surfaces, which are much smaller in experiment [29, 59]. Most DFT-based simulations additionally predict that the d_xy hole band also crosses the Fermi level, suggesting a three hole pocket and two electron pocket Fermi surface [29, 52]. Finally, typical DFT-based calculations also suggest that a stripe or staggered-stripe antiferromagnetic ground state is the most stable configuration [57, 61], when in reality FeSe remains paramagnetic (albeit with strong antiferromagnetic fluctuations [62–64]). Current research is attempting to resolve this discrepancy from a pure ab-initio perspective. Wang. et. al. [64] were able to reproduce the band structure around the Gamma point using a polymorphus network of local structural distortions. The use of hybrid exchange correlation functionals and Hubbard-Hund correlations have recently been shown to also produce a substantial improvement on the tetragonal structure [65].

Due to the current limitations in ab-initio modelling however, a substantial amount of work has gone into developing quantitatively accurate tight binding models of FeSe [8, 50, 52, 66, 67]. These models bypass the limitations in our current ab-initio theories, allowing for an accurate, albeit phenomenological, description of the single-particle electronic structure to be defined, which we can compare with experimental measurements. Several hopping parameters sets have been developed, which have been obtained by directly comparing the numerical band dispersion with experimental ARPES data in the tetragonal state [21, 50, 66, 67]. These models have been shown to reproduce the single-particle electronic properties of tetragonal FeSe much better than conventional DFT-based approaches [50, 52, 66]. In particular these models accurately capture the small Fermi energy of FeSe, which has been shown to lead to strong chemical potential renormalising effects as a function of temperature and nematic ordering [33, 50, 68–70]. By construction, such models allow for a quantitative description of the band positions of the hole and electron bands such that a comparison of the electronic structure in the nematic state can take place.

3 Experimental Evidence for a Missing Electron Pocket in the Nematic State

We now focus on the electronic structure in the nematic state. Here experimental measurements encounter a major challenge. The nematic state is accompanied by a tetragonal to orthorhombic structural transition, at which point multiple orthorhombic domains form in the crystal. It has been identified that these domains are typically on the order of 1–5 μm in size [41, 71–73], which is much smaller than the cross section of the photon beam used in most high resolution synchrotron-based ARPES measurements ($>50\mu$m [74]), as sketched in Figure 3A. Most of the initial photoemission data of FeSe in the nematic phase was collected on “twinned” crystals. In such measurements, the band dispersion measured along the experimental k_x axis contains contributions from domains with the orthorhombic a axis both along, or perpendicular to, this direction, i.e. one measures a superposition of the spectral function arising from both domains. This creates an apparent C₄ symmetry in the measurements even at low temperatures (in the sense that the measured spectra are invariant under 90° rotation of the sample; the as-measured spectra are not generally fourfold-symmetric due to the ARPES matrix elements [75, 76]). This can lead to ambiguity about which band arises from which domain.

FIGURE 3

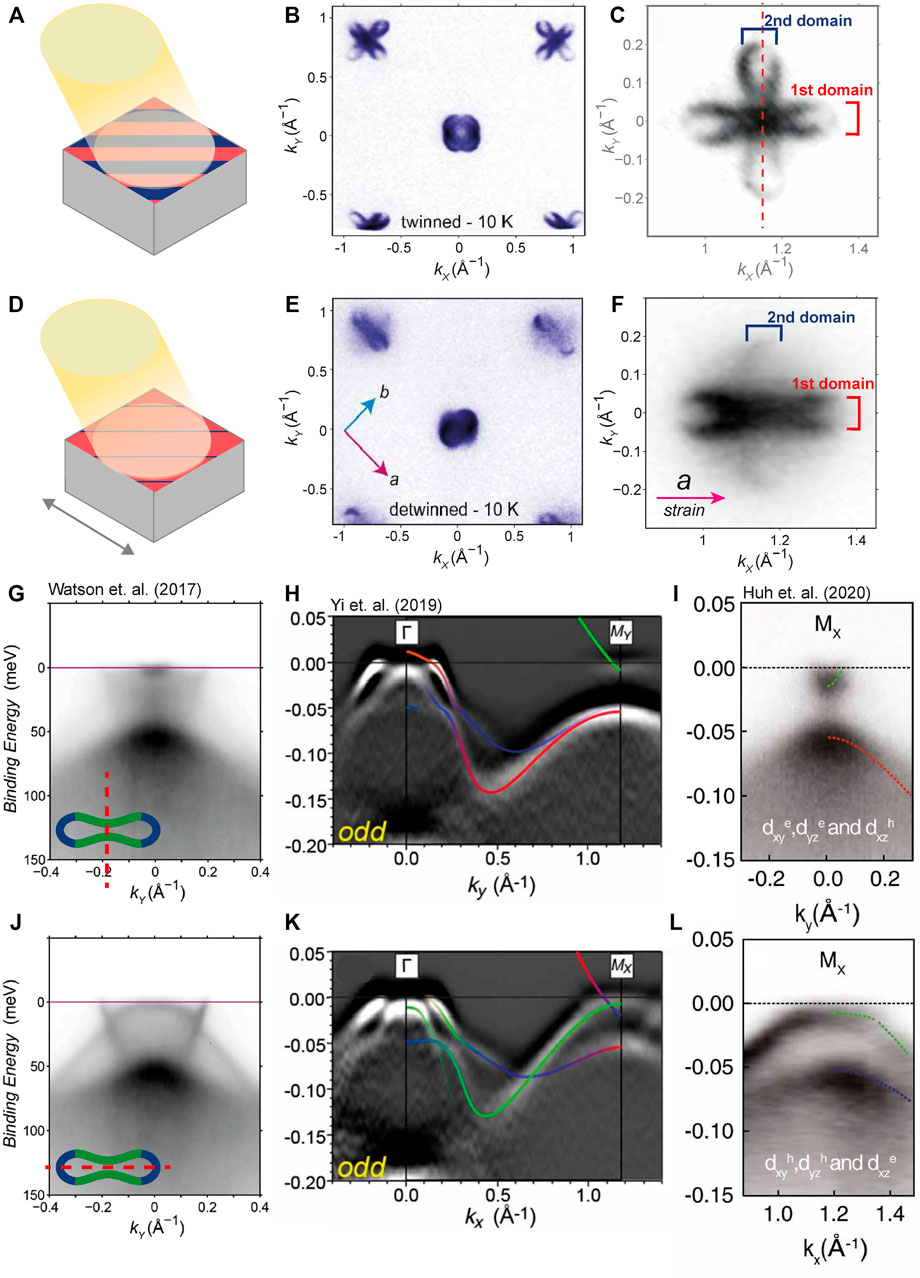
FIGURE 3. Summary of ARPES measurements on FeSe in the nematic state. (A) Sketch of a photoemission setup on a twinned crystal, showing equal coverage of both red and blue orthorhombic domains. (B) Fermi surface measured from a measurement on a twinned crystal (hν = 56 eV). Taken from Watson et. al. [34] (C) Close up of the electron pocket near the A point from Watson et. al. [32] (hν = 56 eV). (D–F) Equivalent sketch and measurement for a detwinned crystal of FeSe, which probes a majority of orthorhombic domains aligned in one direction. (G) Band dispersion of a detwinned crystal centered at the electron pocket. The insert shows the band path, from Watson et. al. [34]. (H) Second derivative band dispersions of a detwinned crystal along the same path as (G) but extended from Z to A, taken from Yi. et. al. [35]. (I) Band dispersion of a detwinned crystal along the same path as (G) from Huh. et. al. [36]. (J–L) Equivalent measurements but taken along the length of the electron pocket. (H,K) reproduced from Ref. [35] under the Creative Commons Attribution 4.0 International License. (I,J) reproduced from Ref. [36] under the Creative Commons Attribution 4.0 International License.

3.1 ARPES Measurements on Twinned Crystals

Multiple ARPES measurements on twinned crystals of FeSe have been reported [19, 20, 26–32, 54, 68, 77] and have been extensively reviewed [1, 10, 33, 78]. We present a representative Fermi surface obtained from a twinned crystal in Figure 3B from Ref. [32]. The hole pockets appear as two overlapping ellipses. Meanwhile, at the corner of the Brillouin zone, measurements reveal two electron pockets, which have been pinched in to produce what looks like two overlapping “peanuts”.

The challenge now lies in identifying which of these pockets, comes from which domain. The two hole pockets can be easily understood as one ellipse from each orthorhombic domain. Measurements of the band dispersion around the hole pocket reveal that the inner hole band (h₂) undergoes a Lifshitz transition as a function of temperature and resides below the Fermi level at 10 K, whilst the outer hole band (h₁) elongates into an elliptical shape. As all three hole bands can be tracked as a function of temperature from the tetragonal to nematic state, there is little ambiguity about the shape of the hole pocket Fermi surface at low temperatures. However, it is not possible to identify the orientation of the elliptical hole pocket from a single domain, i.e. to identify whether it elongates along the orthorhombic a or b axis simply from these twinned measurements.

For the electron pocket, however, the understanding was less clear, and historically several distinct band structures have been interpreted from nearly identical data sets [19, 20, 29, 30, 32]. As can be seen in Figure 3C, two electron pockets can be observed which look like overlapping “peanuts” in the twinned data. As the tetragonal state also exhibits two electron pockets, this may not appear that surprising. Indeed one interpretation was that the two oval shaped electron pockets in the tetragonal state simply pinched in at the sides, due to raising the binding energy of vH₁ [26, 32]. In other words, the electron pockets could retain approximate fourfold symmetry around the M point, and the pockets from each domain simply overlapped in twinned data sets [20]. However, other interpretations, particularly those attempting to understand the nematic band shifts from theoretical grounds, believed that the nematic state should have two differently shaped electron pockets [29, 30]. It was also equally plausible, experimentally at least, that only one electron pocket existed per domain [19, 28, 34]. Distinguishing between these scenarios was particularly challenging due to the broadness of the spectral weight around the M point in the tetragonal state (see Figure 2D), which made a precise interpretation of the temperature evolution of the two van-Hove singularities ambiguous.

3.2 ARPES Measurements on Detwinned Crystals

Compared to the measurements on twinned data, a much more preferable method to study the Fermi surface of FeSe would be to experimentally overcome the limitation imposed by these orthorhombic domains, and directly measure the electronic structure from a single crystallographic orientation. There are two strategies to overcome the twinning issue faced by ARPES measurements. Either 1) generate a sample with macroscopic ordering of the orthorhombic domains on length scales larger than the photon beam cross section, or 2) make the photon beam much smaller than the size of an orthorhombic domain. It has been known from earlier work on the 122 family of Fe-based superconductors that upon the application of “uniaxial” strain along the Fe-Fe direction, it becomes energetically favourable for a majority of the orthorhombic domains to align along that axis [79]. While the resulting domain population is unlikely to be 100% pure, measurements on strained, or “detwinned”, samples, as sketched in Figure 3D, allows one to distinguish between the intense spectral weight arising from the majority domain and the weak spectral weight arising from the 90° rotated minority domain.

The first ARPES measurements on uniaxial strained samples of FeSe were performed in 2014 by Shimojima et. al. [28], where it was shown that the single hole pocket was elongated along the k_y axis. Later, in 2017, Watson et. al. [34] was additionally able to resolve the detail of the electron pockets, as shown in Figure 3E. These measurements on detwinned crystals confirmed that the Fermi surface consisted of one elliptical hole-pocket, as expected from interpretation of the twinned measurements, but additionally revealed only one electron-pocket around the M point. This is shown in Figure 3F, where the majority of the spectral weight intensity now comes from one domain, and only a weak residual intensity comes from the minority domain. Unlike in the tetragonal state, at low temperatures, the electronic band structure around the M point produces sharp quasiparticle bands, a saddle point can be observed at −5 meV, which is electron like along the minor length of the electron pocket (as shown in Figure 3G), but hole-like when rotated by 90° (Figure 3J). Additionally, along the major length of the electron pocket, a deeper electron band and saddle point at ∼ − 60 meV can be observed. This gap between the upper and lower saddle points, is approximately 50 meV, and has been previously quoted as a “nematic energy scale” [29, 35, 39]. However, as we will discuss in the theoretical section below, the exact energy scale of nematic shifts and splittings is slightly more complex and requires a linear combination of order parameters of different energy scales [67].

This finding of only a single electron pocket at the Fermi level was not the expected theoretical result [66], but nevertheless Yi et. al. [35] and Huh et. al. [36] have since then reported additional measurements on detwinned crystals of FeSe, with a slightly larger degree of detwinning than what was achieved by Watson et. al.. These measurements further confirmed that the residual intensity observed in Figure 3G was due to the minority orthorhombic domain, which is nearly absent in Figures 3H,I. Further measurements on sulphur doped FeSe_1−xS_x crystals under uniaxial strain by Cai et. al. [37, 38] have also reported very similar Fermi surfaces.

Polarised light analysis of the matrix elements of FeSe has also been used to identify the orbital content of the bands. If one uses Linear Vertical polarised light (LV also known as odd, or s-polarised light) and measures through the M point parallel to k_y as in Figures 3G–I, only bands with orbital character symmetric to the yz plane of the crystal should be detected [51]. Hence the electron-like dispersion with a very small k_F (i.e., the narrow part of the peanut-shaped pocket) is identified as having d_yz orbital character. Similarly, if one uses the same LV polarised light but with the sample rotated by 90°, as was performed Figures 3J–l), the orbital characters that will be detected will be antisymmetric with respect to the xz plane, which along the momentum dispersion shown in Figures 3J–l) is true for both the d_yz orbital and the d_xy orbital [51]. From this logic, the larger deeper electron dispersion that has a minima around − 50 meV, is attributed to d_xy orbital character. Equally the hole-like dispersion that has a maxima near the Fermi level and is a saddle point connecting to the electron-like dispersion in Figures 3G–I has been identified as having d_yz orbital weight. In both orientations, the most intense contribution is a broad feature located at − 60 meV. From comparison with theoretical models, this band is likely to have a mixture of d_xz and d_xy orbital character, although the precise identification remains challenging. As well as these polarisation-based arguments, one can also assign the orbital character of the bands based on comparison to DFT or tight-binding calculations, at least in the tetragonal phase.

3.3 Temperature Dependence ARPES Measurements of the Electron Pocket

So far we have only discussed the electronic structure of FeSe at either high temperature (e.g., 100 K, where two electron pockets exists) or low temperature (e.g., 10 K, where only one electron pocket exists). However, a natural question to ask is how does the electronic structure of the electron pockets evolve as a function of temperature? In principle, this data should be able to identify the mechanism responsible for the removal of an electron pocket at the Fermi level. Many temperature dependent studies on twinned samples exist (e.g., [26–32, 54, 68, 77] and reviewed e.g., by Coldea and Watson [33]), but due to the complication of orthorhombic domains as well as the broadness of the spectral weight around the M point at high temperatures, there was no obvious signature of the disappearance of an electron pocket in such data sets. To illustrate this, we present a representative temperature-dependent data set on twinned crystals, taken from Ref. [32], in Figures 4A–D. The evolution of these bands from twinned data has been interpreted in different ways by different groups over the years, with a key feature being the appearance of a 50 meV energy scale at the M point, emerging from a broadened “blob” at higher temperatures. Some manuscripts have claimed that the 50 meV energy scale directly corresponds to lifting of the d_xz/d_yz degeneracy [27–30], which was claimed to be consistent with earlier theoretical interpretations [9]. However other analysis [26, 32, 33] instead found an increase in the separation of the two van Hove singularities, from 20 to 50 meV, in which case the 50 meV scale is linked to nematicity but not a direct probe of d_xz − d_yz splitting. However both of these interpretations would imply a ground stat Fermi surface consisting of two electron pockets, in disagreement with the experimental results.

FIGURE 4

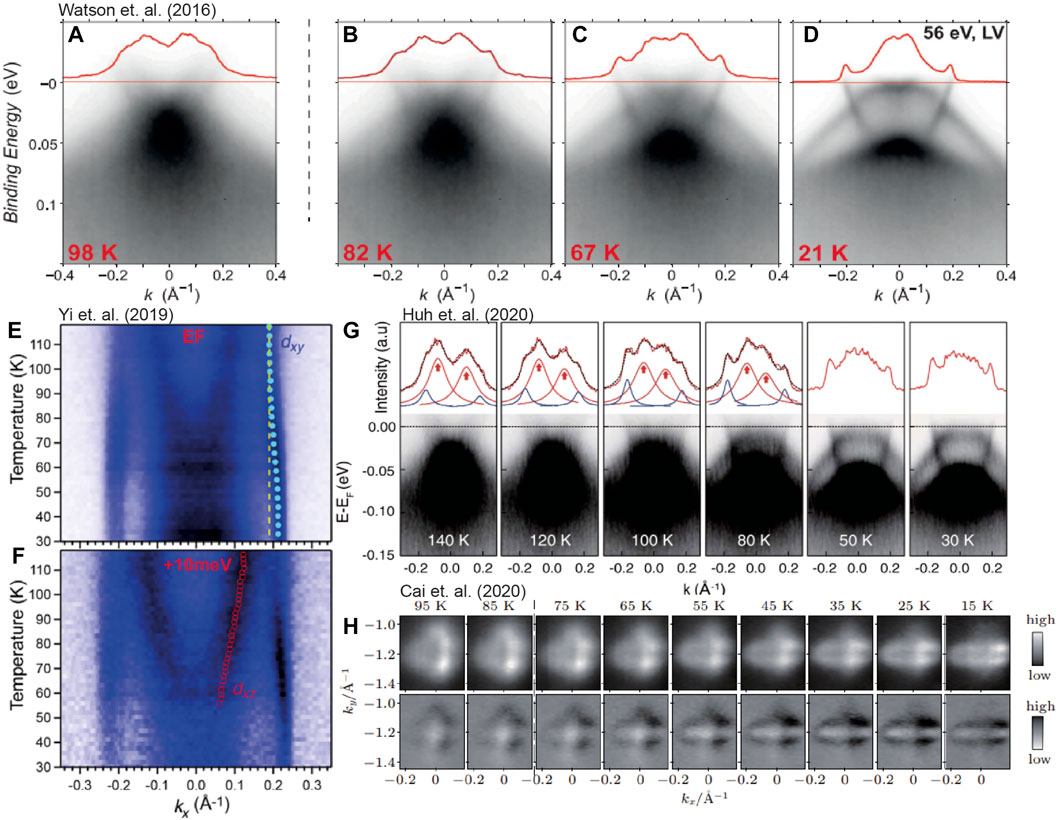
FIGURE 4. Summary of the temperature dependent ARPES measurements of the electron pocket of FeSe (A–D) measurements from twinned crystals of the electron bands near the A point (hν = 56 eV), as a function of temperature, taken from Watson et. al. [32]. (E,F) Spectral intensity at the Fermi energy (E) and 10 meV above the Fermi energy (F), as a function of temperature on a detwinned crystal of FeSe, taken from Yi et. al. [35]. (G) Temperature dependence of the bands near the A point (hν = 56 eV) for a detwinned crystal of FeSe, taken from Huh et. al. [36]. (H) Fermi surface maps as a function of temperature on detwinned crystals of 9% Sulphur doped FeSe, taken from Cai et. al. [38]. (E,F) reproduced from Ref. [35] under the Creative Commons Attribution 4.0 International License. (G) reproduced from Ref. [36] under the Creative Commons Attribution 4.0 International License. (H) Reproduced from Ref. [38] with permission from Chinese Physics B.

More recently, technically challenging temperature dependent measurements on detwinned crystals have been accomplished. This highly necessary data ensures that the bands are easier to track than those taken on twinned samples. Huh et. al. [36] have measured the temperature dependent evolution of the detwinned ARPES measurements around the A point (Figure 4G), which shows the formation of clear sharp quasiparticle bands corresponding to one electron pocket, emerging from the high temperature phase with two electron pockets and much broader features. It was argued that this data was consistent with a Lifshitz transition of a second electron pocket as a function of temperature.

Yi et. al, [35] performed a detailed analysis of the momentum distribution curves along the major axis of the electron pocket as a function of temperature, both at the Fermi level and 10 meV above it (Figures 4E,F). In principle, this analysis enables the identification of any Lifshitz transitions as a function of temperature. Focusing on the data at + 10 meV in Figure 4F, they observe a reduction in the k_F for an inner electron band, which appears to close at around 60 K, indicating that this band becomes completely unoccupied and therefore not observed at low temperatures. This is the most compelling data so far in support of a Lifshitz transition of the electron pocket as a function of temperature.

This evidence for a Lifshitz transition has however been challenged by Cai et. al. [38] who reported temperature dependent Fermi surface measurements of the electron pocket for detwinned crystals of 9% sulphur-substituted FeSe, as shown in Figure 4H. They claim that the spectral weight of the second electron pocket simply decreases in intensity, rather than moving above the Fermi level. This would be indicative of a more complex, self energy evolution, rather than a single-particle Lifshitz transition.

We conclude by noting that the analysis of data, even for detwinned samples, remains challenging. The k_F magnitudes and energy separation of bands are small, challenging the resolution of ARPES instrumentation, and the spectral broadening at high temperatures and deeper energies frustrates the clear identification of the bands at around the M point. While performing the temperature-dependent measurements on detwinned samples, such measurements come with numerous complications, such as temperature-dependent domain populations and spectral contribution from the minority domain. Moreover it is known that samples with over 90% detwinning may experience changes to the underlying electronic properties [80, 81], which may be a concern if strain is altered as a function of temperature. However in our view the results obtained by Yi et. al, [35] make an important contribution by detecting a Lifshitz transition, which would be impossible to determine from twinned data alone, and which provides a plausible route between the two-electron Fermi surface at high temperature and the one-electron pocket Fermi surface in the ground state.

3.4 NanoARPES

There are experimental complications with performing ARPES measurements on uniaxially strained crystals, which may leave doubt as to the validity of the conclusions presented above. First, it is hard to fully exclude if the application of uniaxial strain has actually perturbed the underlying electronic structure of the crystal you are measuring. For example in the tetragonal material Sr₂RuO₄, uniaxial strain on the order of 1% shifts the position of the vHs by nearly 20 meV [83]. In order to fully support the conclusions from these ARPES measurements on detwinned crystals, complementary techniques must be employed and their results compared. To this end, nanoARPES has also been performed on crystals of FeSe. In these technically demanding measurements, the photon beam is focused to sub-micrometer spatial resolution using a focusing optic close to the sample [84]. The reduction of the spot size comes at the cost of dramatically reducing the photon flux, and thus the energy and angular resolutions are typically relaxed (compared to the earlier high-resolution results presented) in order to have a reasonable signal of photoelectrons. Nevertheless, the technique has been improved over the past 10 years to allow for energy resolution better than 20 meV [85]. This sub-micrometer spot size is smaller than a single orthorhombic domain, allowing for a spatial map of the sample from which the two orthorhombic domains can be distinguished by analysing their differing ARPES spectra, shown as red and blue stripes in Figures 5A,B. Measurements of the Fermi surface and band dispersion around the electron pocket in both domains (Figures 5C–F) reveal an electronic structure totally consistent with that extracted from the ARPES measurements under uniaxial strain. In summary, the nanoARPES results fully support the conclusion of a Fermi surface in the nematic state consisting of a single hole pocket and a single electron pocket.

FIGURE 5

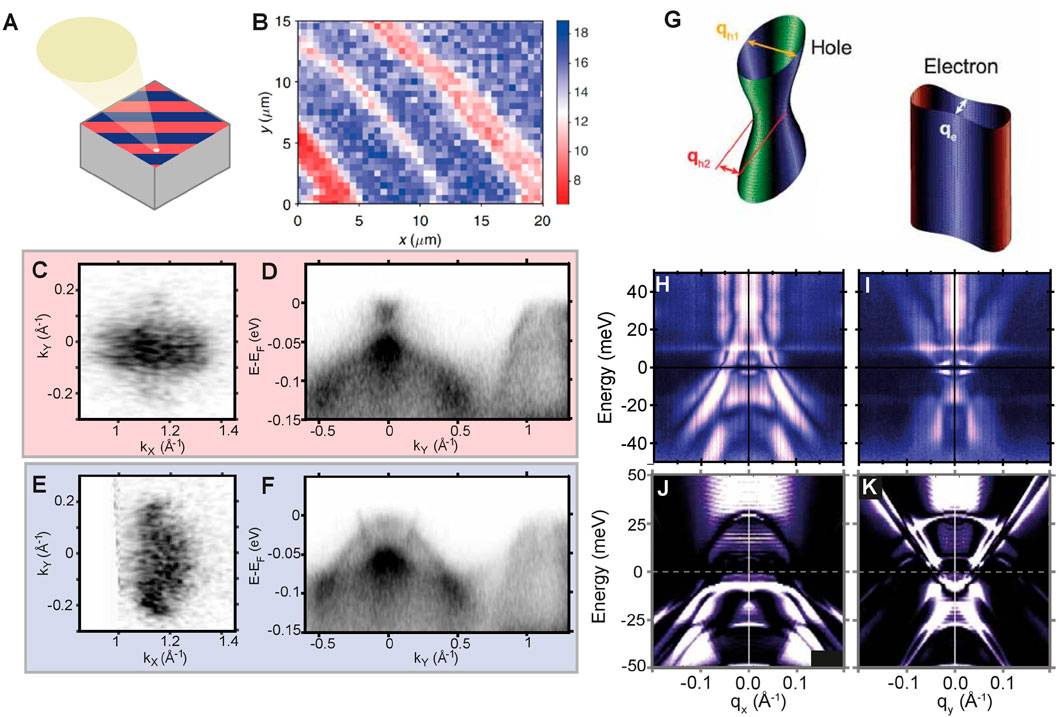
FIGURE 5. Electronic structure within a single domain without the application of uniaxial strain. (A) Sketch of a NanoARPES measurement, where the beam is focused to have a cross section $<1\mu$m. (B) Experimental spatial map of FeSe where the colour corresponds to the orthorhombic domains of FeSe, reproduced from Ref. [41]. (C,D) Fermi surface around the electron pocket (hν = 56 eV, 30 K) and A_y − Z cut taken within a single orthorhombic domain [41]. (E,F) Fermi surface around the electron pocket and A_y − Z cut taken in an adjacent orthorhombic domain [41]. (G) Sketch of the Fermi surface scattering vectors inferred from STM measurements, as suggested by Ref. [42]. (H,I) STM measurements of the QPI scattering dispersions as a function of energy along the q_x and q_y high symmetry axes respectively, reproduced from Ref. [42]. (J,K) Simulated QPI scattering dispersion from a model of FeSe which described the band structure shown in Figure 3, from Ref. [82]. (G–I) are reproduced under the Creative Commons Attribution 4.0 International License.

3.5 STM Measurements

An entirely independent method to study the momentum resolved electronic structure within a single domain is to use scanning tunneling microscopy (STM). STM utilises quantum tunnelling, between the surface of a material and an atomically sharp tip, to study the electronic structure on the sub-nanometer scale. Information about the electronic structure can then be extracted in two ways. The first is by studying the differential conductance (dI/dV) to obtain a quantity proportional to the local density of states of the system. The second is to measure quasiparticle interference (QPI), to measure the perturbations to the local density of states generated by the presence of defects such as impurities or atomic vacancies. The wavelength associated with this perturbation contains direct information about the allowed momentum dependent scattering vectors associated with an electronic structure at a constant energy via q = k − k′.

Multiple STM measurements have been reported for FeSe, and information regarding the nematic [14, 15, 43] and superconducting state [14, 15, 42, 86] have been determined, tetragonal state information has also been obtained from studies of isoelectronic sulphur doped crystals [42]. These measurements all contain a plethora of information regarding the local structure of the surface of FeSe, as well as information on defects [87, 88]. Here, however, we focus on what the STM measurements can tell us about the low energy electronic structure in the nematic state, and whether this is consistent with the ARPES measurements discussed above. Although measuring QPI is an indirect method to measuring the electronic structure of a material, it is particularly powerful in determining band minimas and maximas, especially above the Fermi level, as well identifying whether bands have hole or electron scattering characteristics within a certain energy range.

The scattering vector vs. energy dispersion along the q_x and q_y directions, taken from Ref. [42], are presented in Figures 5H,I. In agreement with other data sets [14, 43], several hole-like scattering vectors can be observed predominately along the q_x axis, with a narrower hole-like dispersion along the q_y direction. Also along the q_y axis, one very clear electron-like scattering vector can be detected, which has a minima at ∼ − 5 meV, and has been identified as a scattering vector that connects the d_yz parts of the electron pocket in FeSe (Figure 5G) [14, 42, 43, 82]. No corresponding electron-like dispersion can be observed along the q_x direction, which should be the case in a two electron pocket scenario where all bands scatter equally. This was therefore interpreted as further evidence, from an independent technique to ARPES, that the Fermi surface of FeSe only consists of one hole pocket and one electron pocket, as sketched in Figure 5G.

We note that due to the indirect nature of QPI measurements, there is a degree of interpretation and uncertainty about the assignment of the electronic states and often it is necessary to directly simulate the QPI dispersion from a theoretical assumption of the electronic structure and compare the agreement. Due to the intrinsic broadness of the experimentally measured scattering vectors, this can lead to differing conclusions based on initial assumptions. For example, Kostin et. al. [43], assuming that two electron pockets must be present at the Fermi level, interpreted a weak spectral feature as evidence for a second electron pocket, with a greatly reduced scattering intensity. Whereas Rhodes et. al. [82], assuming that only one electron pocket was present at the Fermi level, interpreted this weak feature as an artifact of the Feenstra function, used in the experimental processing [89]. Importantly however, both theoretical simulations agree that a Fermi surface consisting of one hole pocket and two electron pockets can not independently reproduce the observed data without some additional form of anisotropy, which implies that ARPES and STM are probing the same underlying electronic structure. We present the numerical simulations from Ref. [82] in Figures 5J,K.

As an aside, it is interesting to note that the hole band maxima in 5(h) extends to + 25 meV [42]. It is known from ARPES that only one hole-like scattering vector at this energy can exist, and specifically must be generated by the k_z = π states [33]. This reveals that QPI measurements are sensitive to states with different k_z. From arguments about the group velocity of electrons scattering off of defects [90, 91], and the short range nature of quantum tunneling, it actually implies that QPI measurements will exhibit a k_z-selectivity rule [82], such that all stationary points along the k_z axis will contribute to scattering vectors that will be detected by STM measurements, this has recently been realised in the fully 3D system, PbS [92].

3.6 Points of Contention

While we have so far presented a unified picture of the electronic structure of FeSe and have focused on points where broad agreement is found in the recent literature, historically there have been many points of disagreement surrounding the identification of bands and the nature of the Fermi surface, and there remain some points of contention.

Regarding the hole pockets, an outlying report is a recent claim from laser-ARPES measurements that there is additional splitting, most prominently resulting in two hole pockets at the Fermi level instead of one [93]. The implication is that the Kramer’s degeneracy of the bands is lifted, i.e., that either time-reversal or inversion symmetry is broken. However, it is worth noting that at low photon energies used the k_z is not well-defined as the final states are not free electron-like, and the two Fermi contours identified appear to be fairly close to the known Fermi contours at k_z = 0 and k_z = π. Moreover, synchrotron-ARPES measurements with equally high energy resolution and better angular resolution (due to better definition of k_z) do not identify any additional splitting either in the Γ or Z planes [19], and neither has any comparable splitting been observed for the electron pockets. Finally, there is no supporting evidence for time-reversal symmetry breaking from other techniques. Thus it remains our view that the Kramer’s degeneracy holds for all states and that there is only one hole pocket crossing EF, which is significantly warped along the k_z axis.

Regarding the electron pockets, while several groups have now coalesced around the one electron pocket scenario, it has previously been claimed that the ARPES data on twinned crystals is consistent with four features in the EDC at the M point [26] such that there are two electron pockets per domain, with each domain contributing a pair of crossed peanuts with slightly differing shapes [20]. This scenario is perhaps the most natural, as it is based on DFT predictions, and comes down to somewhat technical questions of whether asymmetric lineshapes at the M point contain one or two peaks, and whether the proposed small splittings can be resolved. Some of this groups data on twinned samples does indeed seem to show a splitting, which at face value would support their scenario. However, neither our group nor other groups have observed these claimed features and peak splittings in comparable data on twinned samples. Moreover, the detwinned data shows a complete absence of any spectral weight aside from the peanut along the a direction, in multiple experimental geometries, which cannot easily be explained away by matrix element effects in ARPES (and similarly in QPI). We encourage all groups to continue to push for higher resolution data which could finally settle the controversy, especially on detwinned samples.

4 Theoretical Explanations for the Missing Electron Pocket

As we have discussed, the low energy electronic structure of the tetragonal state of FeSe can be qualitatively understood just from symmetry based arguments regarding the crystal structure and the d_xz, d_yz and d_xy orbitals of the Fe atoms. This band structure can be explained both from the framework of tight-binding modelling [8, 50, 52, 66] as well as DFT-based simulations. All of this implies that, although a true quantitative explanation describing the renormalisation of the band structure from correlation effects may be missing, our understanding of the single-particle physics is complete.

Within the nematic state, however, this is not the case. Following the previous logic, it would be assumed that the orthorhombic distortion produces a negligible change to the electronic structure, such that two hole pockets and two electron pockets should be present in the nematic state, which as the experimental data has revealed is clearly not the case. It is for this reason that the nematic state is believed to be of electronic or magnetic origin, yet the microscopic details still remain unclear. To address this, there has been a great deal of focus on trying to model how the nematic state evolves the electronic structure of a tetragonal-based model of FeSe, such as that shown in Figures 6A–C originally presented in Ref. [67]. Specifically, theoretical research has attempted to develop a nematic order parameter which.

• Lowers the symmetry from C₄ to C₂ whilst still preserving mirror symmetry.

• Generates an elliptical hole pocket dominated by d_xz orbital weight.

• Removes one of the two electron pockets from the Fermi surface.

FIGURE 6

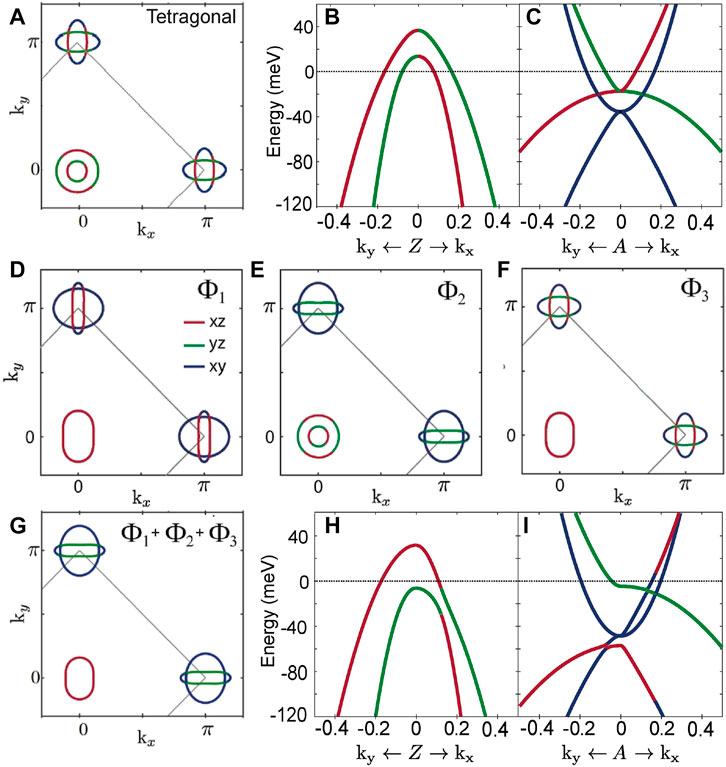
FIGURE 6. Limitations of d_xz/d_yz nematic ordering and origin of the missing electron pocket problem. (A,B,C) Fermi surface and band dispersions around the Z and A point, for a tetragonal state model of the electronic structure from Ref. [67] in quantitative agreement with ARPES measurements. (D,E,F) The individual effect of the three symmetry breaking d_xz/yz nematic order terms on the Fermi surface of the tetragonal state model. (D) Ferro orbital order (Φ₁ = 26 meV) (E) d-wave bond order (Φ₂ = −26 meV) (F) Extended s-wave bond order (Φ₃ = 15 meV). (G,H,I) Fermi surface and band dispersions around the Z and A point, using a combination of Φ₁, Φ₂ and Φ₃ as is often used in the literature. No matter what linear combination of these order parameters are used, a Fermi surface in agreement with the experimental data can not be produced.

Historically, the first attempt to describe such a mechanism assumed that the C₄ symmetry breaking was governed by a lifting of the energy degeneracy of the d_xz and d_yz orbitals [94].

${\mathrm{\Phi }}_1\left(n_{xz}-n_{yz}\right),(1)$

where $n_{xz/yz}=c_{A,xz/yz}^{†}{c}_{A,xz/yz}+c_{B,xz/yz}^{†}{c}_{B,xz/yz}$ is the number operator for the xz or yz orbital respectively on atom A and B in a two atom unit cell model of FeSe, and Φ₁ is a scalar value used to describe the magnitude of the nematic order, which can in principle be fit to experiment.

This term, referred to in the literature as ferro-orbital ordering, is the simplest form of C₄ symmetry breaking possible in this system. It acts in a momentum independent fashion to raise the binding energy of the d_xz bands and lower the binding energy of the d_yz band, similar to a Jahn-teller distortion [95]. In this scenario, the electronic structure would evolve to produce a Fermi surface as shown in Figure 6D, which despite producing the correct elliptical hole pocket, does not generate the one-electron-pocket Fermi surface determined from experiment.

Following the train of thought that the phenomenology of the nematic state may be captured by a degeneracy breaking of the d_xz and d_yz states, it was also noted that there are two additional B_1g symmetry breaking terms that can be defined and are equally valid in the nematic state [55, 66].

${\mathrm{\Phi }}_2\left(n_{xz}^{\prime }+n_{yz}^{\prime }\right)\left(\cos \left(k_x\right)-\cos \left(k_y\right)\right)(2)$

${\mathrm{\Phi }}_3\left(n_{xz}^{\prime }-n_{yz}^{\prime }\right)\left(\cos \left(k_x\right)+\cos \left(k_y\right)\right)(3)$

Here, $n_{xz/yz}^{\prime }=c_{A,xz/yz}^{†}{c}_{B,xz/yz}+c_{B,xz/yz}^{†}{c}_{A,xz/yz}$ describes a hopping from an xz or yz orbital on atom A (B) to a xz or yz orbital on atom B (A). These two terms, referred to as d-wave nematic bond order (Φ₂) and extended-s wave bond order (Φ₃) respectively, in combination with the ferro orbital order (Φ₁) are the only possible nematic order parameters that can be defined for the d_xz and d_yz orbitals up to nearest neighbour hopping [55], and have been extensively used in previous theoretical descriptions of the nematic state of FeSe [15, 18, 19, 23, 24, 32, 43, 82, 96–104]. The individual consequences of these order parameters are shown in Figures 6E,F.

However, despite this vast amount of literature assuming these three d_xz/d_yz nematic order parameters as the starting point for theoretical analysis, there lies one big problem. No matter what values of Φ₁, Φ₂ and Φ₃ are chosen, a Fermi surface consisting of one hole pocket and a single electron pocket can not be produced, at least not starting from a quantitatively accurate ARPES-based model of FeSe in the tetragonal state [67]. The best attempts to describe the ARPES data within this limitation result in a Fermi surface consisting of the correct elliptical hole pocket, a first electron pocket, of correct shape and size, and a second large electron pocket, dominated by d_xy orbital character, as shown in Figures 6G–I.

There is no experimental evidence for this large second electron pocket in the nematic state, and this discrepancy between theory and experiment has posed a major challenge for our theoretical understanding of nematicity. This is the central origin of the missing electron pocket problem. It has now become clear that a theory of nematicity only involving the physics captured in Eqs 1–3, i.e., nematicity derived solely from d_xz and d_yz orbital ordering, is insufficient to reproduce our experimental measurements, and additional explanations for this discrepancy have had to be developed.

4.1 Orbital Selective Quasiparticle Weights

The earliest attempt to explain this discrepancy came from attempts to understand local spin fluctuations in tetragonal FeSe, such as those incorporated by DFT + dynamic mean field theory (DMFT). Within this framework it has been shown that the self-consistently determined quasiparticle weight (Z) of the d_xy orbital was significantly smaller than the quasiparticle weight of the d_xz/yz orbitals [53, 57, 105], approximately half. As the spectral function intensity measured by ARPES is directly proportional to the quasiparticle weight, the contribution of d_xy dominated bands should be significantly reduced, compared to the d_xz and d_yz dominated bands in ARPES measurements. It was thus argued that ARPES measurements may not be able to observe the d_xy orbital, and thus would not detect the second d_xy dominated electron pocket in the nematic state, e.g., in Ref. [100], shown in Figures 7A,B.

FIGURE 7

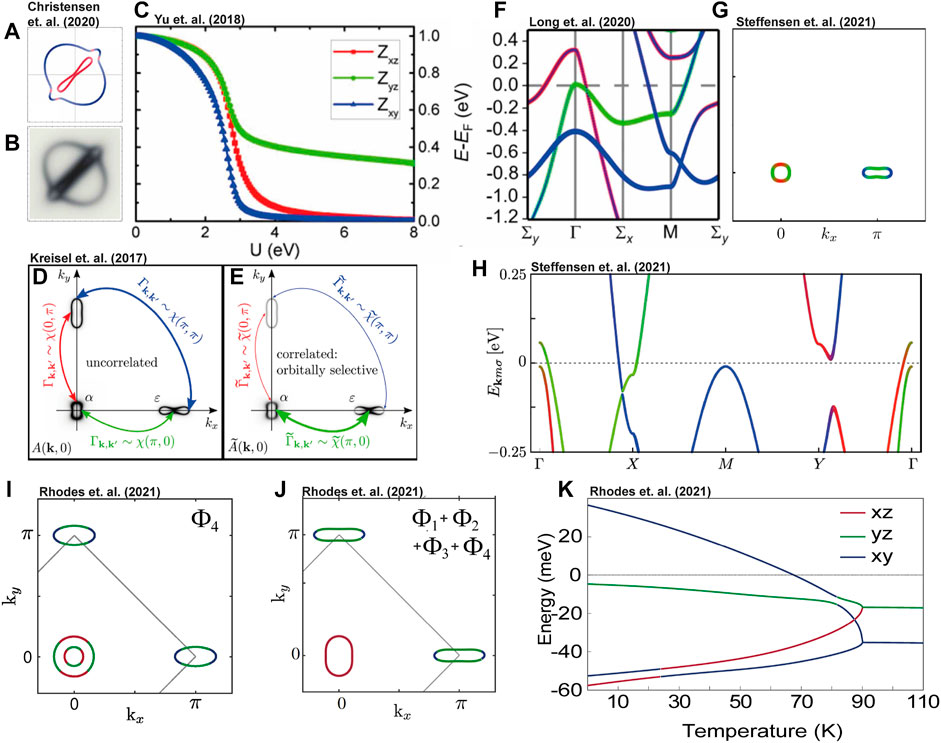
FIGURE 7. Theoretical attempts to resolve the missing electron pocket problem. (A) Fermi surface of the electron pockets in the nematic state proposed by Christensen et. al. [100]. The spectral function is argued to have an increased decoherence of d_xy weight, which is argued would not be observed by experiment and is simulated in (B). (C) Slave-spin calculations from Yu et. al. [24], revealing the possibility of highly anisotropic quasiparticle weights with local Coulomb repulsion. (D,E) Spectral function of the 1-Fe unit cell tight binding model from Kreisel et. al. [21], with and without orbital-selective quasiparticle weights, highlighting the possible suppression of the second electron pocket via incoherent d_xz and d_xy spectral weight. (F) Band dispersion of FeSe obtained from a DFT + U calculation with symmetry preconditioned wavefunctions from Long et. al. [106], highlighting the band hybridisation obtained if an E-type nematic order parameter is considered. (G) Fermi surface of the 1-Fe unit cell model from Steffensen et. al. [108] taking into account a self consistently obtained E-type nematic order parameter. (H) Band dispersion from the model used by Steffensen et. al. [108] showing a band hybridisation of the d_xz (red) and d_xy (blue) bands around the Y point (1-Fe unit cell), gapping out the second electron pocket. (I) Fermi surface obtained from the 2-Fe unit cell tetragonal model from Figure 6A assuming dominant d_xy nematic ordering, as suggested by Rhodes et. al. [67]. (J) Equivalent Fermi surface including all four symmetry allowed nematic order parameters of FeSe and a symmetry allowed Hartree shift. (K) Mean-field temperature evolution of the electronic states at the high symmetry M point, highlighting a Lifshitz transition of the d_xy band and removal of the second electron pocket as proposed by Rhodes. et. al. [67]. (A,B) Reproduced from Ref. [100] under the Creative Commons Attribution 4.0 International License. (C) Reproduced from Ref. [24] with permission from the American Physical Society. (D,E) Reproduced from Ref. [21] with permission from the American Physical Society. (F) Reproduced from Ref. [106] under the Creative Commons Attribution 4.0 International License.

This argument, however, is not supported by experimental measurements. Both in the tetragonal and nematic state, bands of d_xy orbital character have been identified, particularly around the M point [33]. And although it is true that the d_xy orbital appears to exhibit a larger effective mass renormalisation than the d_xz and d_yz orbitals [29], this extra renormalisation appears to not be enough to mask d_xy spectral weight from ARPES-based measurements.

A similar, more phenomenological, approach was later employed by Kreisel et. al. [21] and popularised by Sprau et. al. [15]. Here the values of the nematic order parameters (Φ₁ − Φ₃) were adjusted such that two similar shaped electron pockets were generated (Figure 7D), one dominated by d_xz orbital weight and one dominated by d_yz orbital weight, with the tips retaining significant d_xy orbital character. Specifically, starting from an ARPES-based tetragonal model of FeSe [21] values of Φ₁ = 9.6 meV, Φ₂ = − 8.9 meV and Φ₃ = 0 meV were used. It was then assumed that the nematic state could exhibit a significant reduction in the d_xz quasiparticle weight compared to the d_yz weight and, following the same argument as before, hidden from ARPES measurements of the spectral function. This is shown in Figure 7E. Following this logic, Sprau et. al. attempted to determine which values of Z by fitting them to experimental measurements of the angular dependence of the superconducting gap (discussed in Section 5) and the quasiparticle weight values chosen were Z_xy = 0.1 Z_xz = 0.2 and Z_yz = 0.8, which in a later study was refined to Z_xy = 0.073, Z_xz = 0.16 and Z_yz = 0.86 [43]. In order to reproduce experimental data, it was also necessary to strongly suppress the quasiparticle weight of the d_xy orbital, which as a consequence effectively fully suppressed one of the two electron pockets at the Fermi level. Slave-spin calculations, starting from a DFT-based tight binding model and varying the contributions of Φ₁ − Φ₃ have also been performed and found that similar anisotropic ratios of the quasiparticle weights can be obtained [24], as shown in Figure 7C. A review of the slave-spin approach can be found in Ref. [98].

This formalism of “orbital selective quasiparticle weights”, i.e., suppressing the contribution of electronic states with d_xz and d_xy orbital character in the nematic state, has received the most traction out of the potential theories of the missing electron pocket of FeSe. It has been claimed to be in agreement with STM and QPI measurements of the electronic structure [43], the superconducting gap properties [15], the spin susceptibility measured by inelastic neutron scattering [63], μSR measurements of spin relaxations [102] and thermodynamic based-measurements [99]. A recent review on the topic can be found in Ref. [1].

In our view, however, the success of this approach is due to accurately generating a Fermi surface of FeSe that has the correct one hole pocket and one electron pocket structure, and not necessarily due to the underlying assumptions behind the ansatz of highly anisotropic quasiparticle weights. Indeed, a change in spectral weight, on the order of magnitude as proposed by this theory, is something that should be directly observable with ARPES based measurements. In the tetragonal state, the quasiparticle weight of the d_xz and d_yz orbitals must be equivalent by symmetry, and thus, under this assumption, there would be a strong sudden suppression of the d_xz dominated bands upon entering the nematic state. This is not what is observed in experimental measurements, bands of d_xz dominated weight are detected at all temperatures within the nematic state, with no obvious reduction to the spectral intensity [17–20, 30, 40]. It is also not clear how this interpretation would account for the observed band shifts as shown in Figure 4E [35], and Figure 4G [36]. Additionally, alternate explanations of the STM data and superconducting gap data, that do not rely on the assumption of orbital-selective quasiparticle weights, have been presented [19, 22, 42, 82].

4.2 E-Type Order Parameters

More recent attempts to explain the missing electron pocket have gone back to studying the single-particle physics of FeSe. A recent DFT + U calculation by Long et. al. [106], involving symmetry preconditioned wavefunctions, found a lower energy configuration of FeSe by breaking the E symmetry via a multipole nematic order, as shown in Figure 7F. This has been further studied by Yamada et. al. [107]. This symmetry breaking essentially generates a tetragonal to monolclinic distortion by generating an overlap between a d_xy orbital and either d_xz or d_yz orbital, which as a bi-product also breaks C₄ symmetry. This consequentially generates a hybridisation between the d_xy dominated electron band and either the d_xz or d_yz dominated electron band and was shown to produce a one-electron pocket Fermi surface within a certain parameter regime.

A stable E-type nematic order parameter was equally identified, within a tight-binding framework using parameters extracted from LDA-based calculations, by Steffensen et. al. [108]. Here it was shown that including nearest-neighbour Coloumbic repulsion, the self consistently calculated mean-field nematic order parameter that had the largest magnitude was an inter-orbital term hybridising the d_xz and d_xy orbitals (or d_yz and d_xy). This order parameter was equally able to generate a one-electron pocket Fermi surface, via a similar hybridisation mechanism as the DFT-based calculation as shown in Figures 7G,H.

This appears to suggest that long-range Coulomb repulsion can stabilise a C₄ symmetry breaking ground state in FeSe. However, in this scenario, the E-type order parameter would also reduce the crystal symmetry of FeSe from tetragonal to monoclinic. Currently, the experimental evidence suggesting a tetragonal to monoclinic structural distortion in FeSe is lacking. However, upon $>85$% Te doping of the Se sites, a tetragonal to monoclinic transition has been realised [109]. This could hint that the known monoclinic structure of FeTe is actually stabilised by electron interactions [110], however whether this mechanism can describe the physics of FeSe will require further experimental investigation.

4.3 Non-Local d_xy Nematic Order Parameter

When considering the relevant d_xz, d_yz and d_xy orbitals of tetragonal FeSe within a tight binding framework, there are only four order parameters that can be defined which break the B_1g rotational symmetry of the material within a single unit cell. The first three, described in Eqs 1–3, involve breaking the degeneracy of the d_xz and d_yz orbitals. However, a fourth equally valid order parameter involving the d_xy orbital can also be defined as,

${\mathrm{\Phi }}_4\left(n_{xy}^{\prime }\right)\left(\cos \left(k_x\right)-\cos \left(k_y\right)\right).(4)$

This term acts as a hopping anisotropy for nearest neighbour d_xy orbitals, in a similar manner as Eq. 2 for the d_xz and d_yz orbitals. It was initially defined by Fernandes et. al. [55], however in subsequent works it was assumed that this d_xy nematic term would be much smaller, or negligible, compared to Eqs 1–3 [55]. Renormalisation group theory [111–113] additionally found, that whilst Eq. 4 was symmetry allowed, nematic symmetry breaking only had stable RG flow in either the d_xz/d_yz channel or the d_xy channel, implying that finite Φ₁ − Φ₃ and Φ₄ would not both be present simultaneously [111]. However a weakly unstable trajectory suggested that this may not be the case [112].

In Ref. [67] Rhodes et. al. looked at the qualitative effect Φ₄ has on the electronic structure. They showed that a one-electron pocket Fermi surface could be generated from a ARPES-based tight binding model of FeSe solely using the Φ₄ term, as shown in Figure 7I. It was shown that Φ₄ has the effect of breaking the degeneracy of the d_xy vHs (vH₂ in Figure 2A), which if made large enough (∼50 meV) would induce a Lifshitz transition of the d_xy band, and thus reduce the total number of electron pockets crossing the Fermi level to one. This is shown in Figure 7K. In combination with Φ₁ to Φ₃, the addition of Φ₄ made it possible to generate a Fermi surface in agreement with the ARPES measurements, as shown in Figure 7J. One recent study has also found this ordering to be consistent with specific heat measurements [114], and a second independent study has found that this order parameter can explain the dc resistivity anisotropy within the framework of elastic scattering at low temperatures [115].

However, in order to get quantitative agreement with the Fermi surface and low-energy electronic structure using Eqs 1–4, it was observed that the splitting of the d_xy van-Hove singularity must be asymmetric. Specifically, ARPES measurements as a function of temperature find that the lower part of the d_xy vHs around the M point remains approximately at the same energy [30, 32, 35]. This is not captured by the Φ₄ term that assumes a symmetric splitting of the bands. To account for this, Rhodes et. al. [67] included a d_xy-specific Hartree shift, a constant energy shift of the d_xy orbital at the M point, that although allowed by symmetry, did not have an obvious origin. Additionally, in order to generate a Lifshitz transition of the electron pocket, and obtain quantitative agreement with experimental data as a function of temperature both d_xy terms, Φ₄ and the Hartree shift, had to be significantly larger than the d_xz/d_yz terms (Φ₁ − Φ₃). Specifically, in order to reproduce the ARPES measurements Φ₁ + Φ₃ = 15 meV, Φ₁ + Φ₂ = − 26 meV and Φ₄ = Δ_Hartree = 45 meV [67]. It is also worth noting that the mean-field analysis by Steffensen et. al. [108] equally found that the Φ₄ nematic order parameter should be finite, but found it to be of approximately equal magnitude as Φ₁-Φ₃ rather than twice as large, as suggested by Rhodes et. al. [67].

4.4 Importance of the d_xy Orbital in Theories of Nematicity

Each theory proposed to describe the low-energy electronic structure of the nematic state of FeSe has it is relative strengths and weaknesses. Nevertheless a common theme in these different attempts has begun to emerge. In all methods used to theoretically remove an electron pocket from the Fermi level, it has been necessary to modify the d_xy orbital in some way. Whether that’s suppressing its contribution via quasiparticle weights, gapping out the d_xy band via hybridisation, or rigidly shifting the d_xy band above the Fermi level. What we can gleam from this analysis therefore, is that we should view the nematic state in a new light, not originating from a specific orbital ordering mechanism of d_xz and d_yz states, but rather as a symmetry breaking phenomena which couples to every orbital at the Fermi level. Further theoretical investigations are required in order to elucidate the origin of the nematic state. The importance of the d_xy orbital has also been recently noted from NMR measurements [116] and angular dependent magnetoresistance [117].

5 Consequences for the Superconducting Gap Symmetry

One of the most striking properties of FeSe is it is highly tuneable superconducting transition temperature, ranging from 8 K in bulk crystals [44], 36.7 K under pressure [118], and up to 65 K when a monolayer is placed on SrTiO₃ [119], and hence the nature of superconductivity in FeSe is an important question that attracted a lot of attention.

From an experimental point of view, the momentum dependence of the superconducting gap of bulk FeSe, has been extensively determined from ARPES [16–20], STM [15, 42, 86], Spectific heat [120, 121] and muSR measurements [102], with surprisingly near unanimous agreement as to the angular dependence of the gap structure around both the hole and electron pocket. This achievement provided the perfect opportunity to directly compare theories of superconductivity with experimental measurements.

In this section, we will review the experimental data of the momentum dependence of the superconducting gap, particularly from ARPES measurements, and discuss the theoretical consequence the updated Fermi surface topology has on the theoretical understanding of superconductivity in FeSe.

5.1 Experimental Measurements of the Superconducting Gap

The key findings from the multiple ARPES and QPI measurements are presented in Figure 8. For the gap situated on the hole pocket, a highly two-fold anisotropic momentum dependence of the gap was measured, as shown from QPI analysis by Sprau et. al. in Figure 8A. The angular dependence of the hole pocket using ARPES was first reported in 2016 by Xu et. al. [16] on 7% sulphur doped FeSe measured at 6.3 K, as shown in Figure 8F. It was found that the angular dependence at both k_z = 0 (using a photon energy of hν = 37 eV) and k_z = π (hν = 21 eV) produced near identical momentum distributions. This sulphur doped system has a very similar electronic structure to undoped FeSe, albeit with a slightly reduced nematic transition temperature [122] and slightly higher superconducting transition temperature (9.8 K [16]). Later, in 2018, Liu et. al. [18] and Hashimoto et. al. [17] used laser ARPES, with hν = 6.994 eV, on FeSe at 1.6 K and observed the same highly anistropic angular dependence of the gap at the hole pocket, as shown in Figures 8B,C. By using such a low photon energy and temperature these authors ensured the greatest possible energy resolution for resolving the gap of the hole pocket. However the trade-off here is that information about states with large angular momentum, e.g., the electron pockets, as well as the k_z-dependence of the hole pocket, can not be obtained. Kushnirenko et. al. [20], as well as Rhodes et. al. [19], were able to resolve the three dimensional gap structure of both the hole and electron pockets using synchrotron radiation, as shown in Figures 8D,E. In these manuscripts, it was again confirmed that the gap structure of the hole pocket at both k_z = 0 and k_z = π exhibited the same highly anisotropic two-fold angular dependence of the gap as determined in the Sulphur doped sample of Xu. et. al. [16]. Kushnirenko et. al. claimed that the superconducting gap that was larger at k_z = π and smaller at k_z = 0, however Rhodes et. al. suggested the opposite: the gap was observed to be larger at k_z = 0 and smaller at k_z = π. We note that in order to reach the k_z = 0 hole pocket, a higher photon energy of 37 eV is required, which makes the measurement of the gap at the Γ point exceedingly challenging, and the measurements are at the cutting edge of what is currently achievable by synchrotron-based ARPES measurements.

FIGURE 8

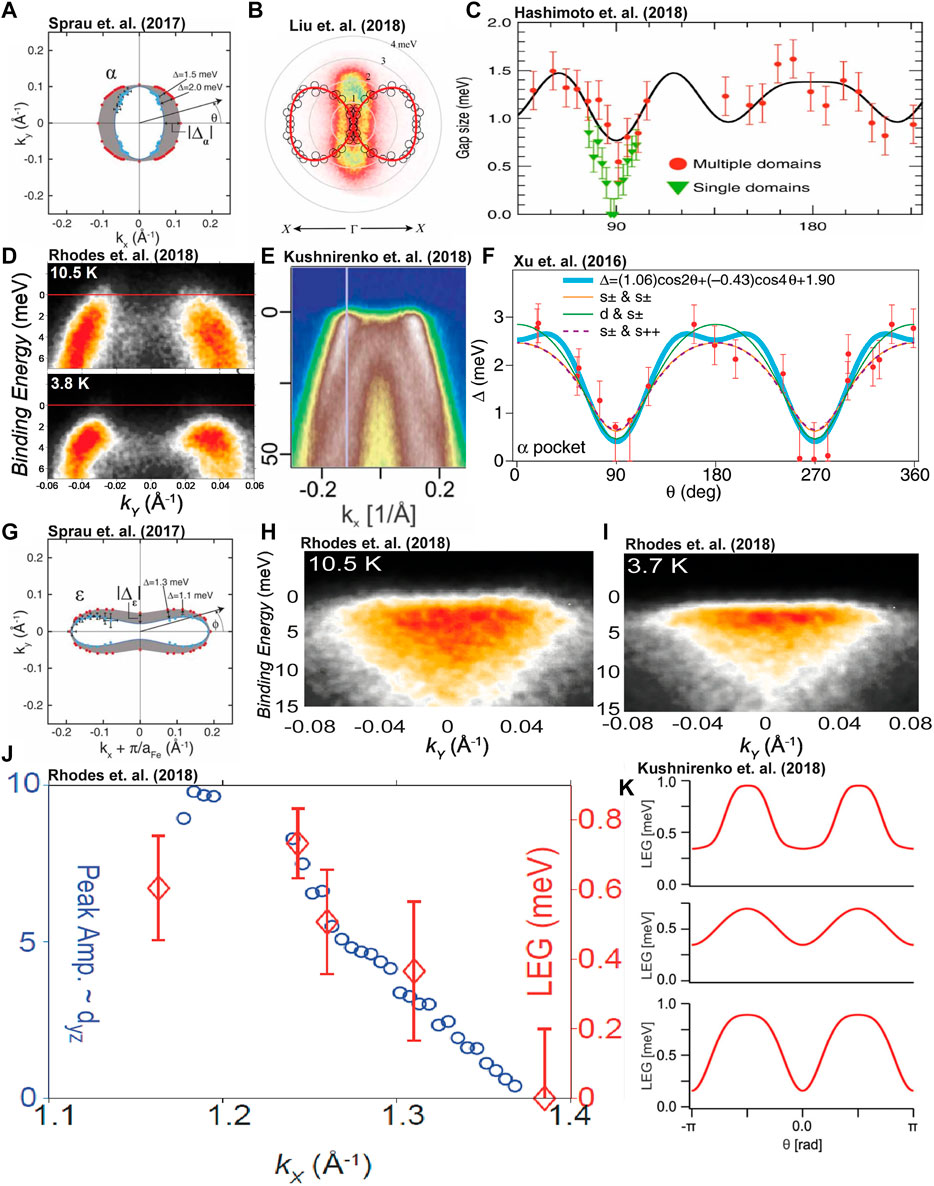
FIGURE 8. Experimental measurements of the superconducting gap of FeSe. (A) Angular dependence of the gap around the hole pocket as extracted from BQPI measurements from Sprau et. al. [15]. (B) Angular dependence of the gap around the hole pocket as extracted from Laser ARPES measurements from Liu et. al [18]. (C) Angular dependence of the gap around the hole pocket from Hashimoto et. al. [17]. Red dots are data from a twinned sample, whereas green data was measured on an accidentally strained sample. (D) Band dispersion of the k_z = 0 hole band (hν = 37 eV) from Rhodes et. al. [19] taken along the direction where the hole band gap is largest, above and below T_c. (E) Equivalent band dispersion of the k_z = π hole band (hν = 21 eV) below T_c from Kushnirenko et. al. [20]. (F) Angular dependence of the hole band of FeSe_0.93S_0.07 from Xu et. al. [16], showing equivalent momentum dependence as the undoped sample. (G) Angular dependence of the gap around the electron pocket as extracted from BQPI measurements from Sprau et. al. [15]. (H,I) Band dispersion along the minor length of the electron pocket above and below T_c, along the high symmetry axis from Rhodes et. al. [19]. (J) Comparison of the gap magnitude (Leading Edge Gap - LEG) and the intensity of the spectral weight from Linear Vertical polarised light as a function of k_x, which is directly correlated to the amplitude of d_yz orbital weight. The gap is observed to decrease with decreasing d_yz weight. Taken from Rhodes et. al. [19]. (K) Sketch of the angular dependence of the electron pocket at k_z = 0 (bottom) $k_z=\frac{\pi }{2}$ (middle) and k_z = π (top) from Kushirenko et. al. [20]. (A,G) Reproduced from Ref. [15] with permission from the AAAS. (B) Reproduced from Ref. [18] under the Creative Commons Attribution 4.0 International License. (C) b) Reproduced from Ref. [17] under the Creative Commons Attribution 4.0 International License. (F) Reproduced from Ref. [16] with permission from the American Physical Society. (E,K) Reproduced from Ref. [20] with permission from the American Physical Society.

Hashimoto et. al. additionally claimed that the gap structure produced a different behaviour with and without the presence of uniaxial strain. Without strain, they observed a cos (8θ) behaviour [17], which when accidentally detwinned via uniaxial strain, yielded a gap structure that is consistent with the other measurements. So far this cos (8θ) dependence of the gap has not been reproduced.

As for the electron pocket, the angular dependence of the gap from QPI measurements is presented in Figure 8G. Revealing a particularly constant gap magnitude across the length of the ellipse, which quickly decays towards zero at the tips of the pocket. This is where the orbital character of the pocket transforms from predominantly d_yz weight to d_xy weight. ARPES measurements by Kushnirenko et. al [20], and Rhodes et. al. [19], were also able to resolve the angular dependence of the superconducting gap at the electron pocket. ARPES measurements along the minor length of the electron pocket, above and below T_c, are shown in Figures 8H,I. Thanks to the orbital sensitivity of ARPES-based measurements, Rhodes et. al. found a direct correlation between the intensity of d_yz orbital weight and the size of the superconducting gap, establishing a direct link between orbital character and gap magnitude (Figure 7J). Kushnirenko et. al. [20] also observed that the rate that the gap decreased as a function of momentum was slightly different for intermediate k_z values (Figure 8K).

This extremely aniostropic gap structure for both the hole and electron pocket raises a question as to whether FeSe is a nodal or nodeless superconductor, which could have a profound effect on our understanding of the gap symmetry in this system. For example, neglecting the electron pocket, it was argued by Hashimoto et. al. that a nodal gap structure of the hole pocket would be consistent with p-wave superconductivity [17] (This is not consistent once the gap structure of the electron pocket is additionally taken into account). It is not possible to clearly distinguish between a nodal gap or a very small gap in ARPES measurements, due to the limitations of energy resolution arising from thermal broadening and the choice of photon energy. Alternate techniques, such as STM and specific heat measurements, do have sufficient energy and thermal resolution to tackle this issue, but here STM measurements of the density of states by Sprau et. al. [15] suggest a fully gapped, nodeless, superconducting ground state, whereas specific heat measurements have argued that the measured data is consistent with a nodal superconducting gap [120]. It is still unclear whether FeSe exhibits nodes or very small superconducting gaps, however as we will discuss below, theoretical arguments appear to suggest that if any nodes do exist, they would be accidental in nature.

5.2 Theoretical Understanding of the Superconducting Gap

The most striking result from the experimentally determined gap structure of FeSe, is the clear realisation that the size of the superconducting gap at the Fermi level is correlated with the magnitude of d_yz orbital weight. This tells us that the superconducting pairing mechanism is sensitive to orbital character, and is evidence for superconductivity mediated by Coulomb interactions, such as via a spin-fluctuation mechanism of superconductivity.

Although the idea that spin fluctuations govern the Cooper pairing in the iron-based superconductors, was originally proposed back when superconductivity in these materials were first discovered [7], the evidence for this has often been inferred from gap symmetry arguments, such as a sign-changing s^± order parameter [15], or from the general argument that FeSe is close to a magnetic instability. FeSe, being such a clean system, has enabled a direct comparison between theoretical simulations and experimental data.

Indeed many theoretical simulations of the angular dependence of the superconducting gap in FeSe have been performed [15, 19, 21–24, 67, 108]. However, as the formation of Cooper pairs are directly sensitive to the states at the Fermi level, the starting model used to describe FeSe is very important. Numerical simulations have shown that models of FeSe which do not account for the missing electron pocket of the nematic state, i.e. a model Fermi surface which describes two electron pockets around the M point, can not reproduce the experimentally observed gap structure [15, 19, 22, 23].

Initially, this was a confusing result, but with hindsight it is not that surprising. The presence of an extra electron pocket in the simulations would naturally influence the superconducting pairing. Due to the local nature of Coulomb repulsion, the pairing between electrons in real space will be largest for electrons located on the same atom in the same orbital. It follows from this argument, that the pairing of electrons in momentum space would be favoured if a spin scattering process occurs which couples electronic states of the same orbital character. In the nematic state of FeSe, spin-fluctuations are strongest when connecting the hole and electron pocket [63, 123, 124]. In a one-electron pocket scenario, the only common orbital content between the two pockets are the d_yz orbital weight, as shown in Figures 9A–D, and thus this would dominate the superconducting gap magnitude. This would not be the case in a two-electron pocket scenario, where scattering with d_xz electrons between the hole and electron pocket would also contribute.

FIGURE 9

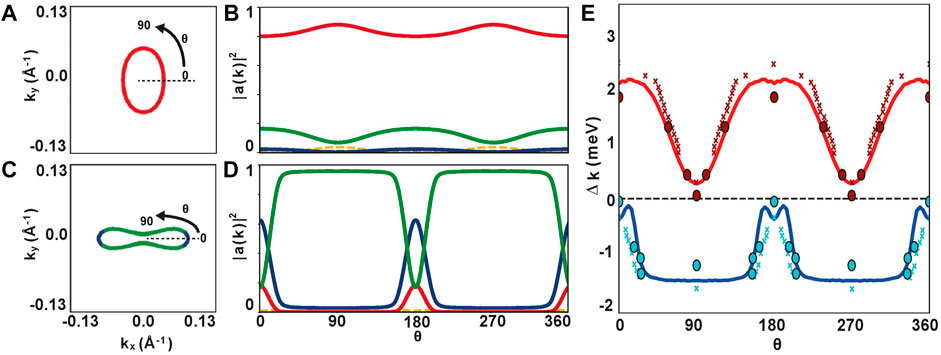
FIGURE 9. Theoretical simulation of the momentum dependence of the superconducting gap from Rhodes et. al. [19]. Here, a Fermi surface consisting of one hole pocket a single electron pocket were considered and a spin fluctuation pairing mechanism was assumed. (A,B) Fermi surface of the hole pocket and angular dependence of the orbital content of the hole pocket. (C,D) Fermi surface of the one electron pocket and angular dependence of the orbital content of the electron pocket. The colour labels are red d_xz, green d_yz and blue d_xy. (E) Simulated angular dependence of the superconducting gap for the hole pocket (red) and electron pocket (blue), revealing a direct correlation with the d_yz weight shown in (B) and (D). The crosses and dots are experimental data extracted from STM [15] and ARPES [19] measurements respectively.

It has now been shown that irregardless of the theoretical mechanism employed to remove this second electron pocket from the superconducting calculation, whether that’s orbital selective quasiparticle weights [15, 21, 24], orbital selective spin fluctuations [22], E-type nematic ordering [108], a non-local d_xy nematic order parameter [67] or simply ignoring it from simulations of the superconducting pairing outright [19] (as shown in Figure 9), the correct momentum dependence of the gap structure can be naturally captured assuming weak-coupling spin fluctuation mediated pairing.

This is a remarkable finding, not only does it further support the theory of spin-fluctuation mediated superconductivity in the iron-based superconductors, but it provides another independent piece of evidence for a single electron pocket around the M point in the nematic state of FeSe. This result highlights the incredible importance of correctly accounting for the missing electron pocket in the nematic state, as without it we can not begin to understand the superconducting properties of this material.

6 Discussion

This review has been wholly focused on what at first glance might appear to be an esoteric point of discussion, namely, the characterisation and modelling of the Fermi surface of FeSe in the nematic state. However, we propose that after the hundreds of papers and many years of debate and controversy on the subject, that there are very important conclusions to be drawn, which have wider implications for our understanding of both nematic ordering and superconductivity across the wider family of Fe-based superconductors.

The first conclusions surround nematic ordering, where the results establish.

• That nematic ordering affects all bands at the Fermi level, with the d_xy derived bands playing as significant a role as the d_xz and d_yz derived bands.

• That nematic order manifests in the band structure through a combination of all allowed symmetry-breaking terms, primarily anisotropic hopping terms, and cannot be exclusively treated by on-site orbital ordering.

• That nematic ordering does not cause a minor perturbation of the electronic structure, but can lift an entire electron pocket away from the Fermi level.

We believe that these conclusions should be widely applicable across other Fe-based superconductors. While these conclusions do not yet constitute a self-consistent microscopic mechanism of nematic order, they do present strong constraints to any proposed microscopic models.

The second set of conclusions relate to the superconductivity:

• The superconducting gap of FeSe is remarkably anisotropic.

• The fact that the gap follows the d_yz orbital character is strong experimental evidence that the pairing mechanism is sensitive to local orbital degrees of freedom, i.e., for spin-fluctuation pairing.

• The superconducting gap of FeSe can be naturally reproduced by spin-fluctuation calculations assuming only one electron pocket at the Fermi level.

There has long been a consensus that the superconductivity in the Fe-based systems is mediated by spin-fluctuation pairing, but we argue that FeSe provides some of the most direct experimental support for this. As long as one starts with the one-electron pocket Fermi surface, the further details of the calculation are not critical, because in this scenario the only orbital component which is present on both the hole and electron pockets is the d_yz character, and so this channel dominates the structure of the gap. The success of this result justifies the use of similar spin-fluctuation pairing calculations on other Fe-based superconductors, although we emphasize the importance of starting with an experimentally accurate Fermi surface.

Importantly this insight has only been unlocked once we understand that the true Fermi surface of FeSe consists of one hole pocket and a single electron pocket, rather than one hole pocket and two electron pockets as was initially believed. However, despite us emphasizing how the one electron pocket scenario is key to the understanding of the unusual properties of FeSe, we believe it is still an open question as to what mechanism really drives this modification of the electronic structure. The models of describing the electronic structure in the nematic state have grown more accurate and more sophisticated, yet there is a lack of intuition about what is the real driving force for the evolution of the electronic structure that we observe. In our opinion it remains a delicate and important open question, but solving it in the case of FeSe could unlock a wider understanding of nematicity in the iron-based superconductors.

Additionally, whilst the experimental challenge imposed by measuring the electronic structure of orthorhombic crystals has always been present, the focus on an answer to the origin of nematicity in FeSe has particularly emphasised the continued development of detwinning methods in ARPES [28, 34–40, 85, 125], as well as showcasing the potential of NanoARPES for strongly correlated materials with local domain structures [67, 85].

The anisotropic Fermi surface of the nematic state also has important consequences for the understanding of the spin excitation spectrum of FeSe, which has also been shown to be highly anisotropic [63], revealing a dominant scattering vector at (π, 0) in the nematic state but not (0, π). From an itinerant magnetism perspective, this can be intuitively understood, the only allowed scattering vectors at the Fermi level are the one hole pocket and one electron pocket, seperated by (0, π), thus the imaginary part of the spin susceptibility should also be highly anisotropic [67, 97, 108]. This has so far mainly been discussed within the weak coupling- RPA approximation for the spin fluctuation, within the concext of orbital selective quasiparticle weights [97, 126], however it would be interesting to explore how well this weak coupling calculations agrees with the inelastic neutron scattering data applied the other descriptions of the missing electron pocket.

7 Outlook and Conclusion

With an outlook to the future, there are still multiple open questions regarding the missing electron pocket problem, nematicity and superconductivity in FeSe. Firstly, can we experimentally identify the exact conditions when one of the electron pockets in the tetragaonal state appears or disappears from the Fermi level? So far, this has remained slightly ambiguous, with some experiments claiming a gradual disappearance of the electron pocket [37] and others claiming a Lifshitz transition around 70 K [35, 36, 67].

Another open question is how the missing electron pocket scenario can be reconciled with the QPI measurements as a function of sulphur doping [42] or Tellurium doping [2], each providing an isoelectronic tuning parameter to control the evolution of the Fermi surface. The systematic evolution of the Fermi surface has been studied by Quantum Oscillations [127], however due to the tiny size of the Fermi energy in this system, the unambiguous assignment of the quantum oscillation frequencies is challenging [67]. Equally, twinned ARPES measurements on sulphur doped FeSe have already been performed [54, 77], as well as several studies on detwinned crystals for 9% sulphur doping [37, 38]. So far it is unclear when the missing electron pocket reappears, and so further measurements of detwinned FeSe_1−xS_x are desirable, although by 18% the system is tetragonal once more and two electron pockets are certainly observed [77].

Finally, an important avenue of research is how does the momentum-dependence of the superconducting gap change as nematicity is supressed, e.g., as a function of sulphur doping. The momentum dependence of the superconducting gap for undoped FeSe has now been extensively characterised, and theoretical predictions of how the gap should evolve as nematicity is suppressed have been proposed [67]. This much needed experimental data would again place important constraints on our theories of nematicity and superconductivity in these systems.

As the study of the Fe-based superconductors has matured since they exploded onto the scene in 2008, the emphasis has shifted from basic characterisation of a wide variety of superconducting families, to detailed examination of particular cases. FeSe has been the subject of particularly focused attention, and the effort has been worthwhile, with two remarkable results emerging: the one electron pocket Fermi surface, and the highly anisotropic superconducting gap structure. We have argued that these two, taken together, provide strong evidence for spin-fluctuation pairing in FeSe, which is presumably applicable to the wider family of Fe-based superconductors. However, the extent to which the one electron pocket phenomenology may be applicable to the nematic phase of other material systems is a large open question; as well as FeSe_1−xS_x and FeSe_1−xTe_x, we propose NaFeAs [125] as a candidate worthy of re-examination. Thus as this review of FeSe concludes, we propose it is time to take the experimental and theoretical tools developed for case of FeSe, and apply them with renewed vigour to the wider field of Fe-based superconductors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

LR acknowledges funding from the royal commission for the exhibition for the 1851.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kreisel A, Hirschfeld P, Andersen B. On the Remarkable Superconductivity of FeSe and its Close Cousins. Symmetry (2020) 12(9):1402. doi:10.3390/sym12091402

CrossRef Full Text | Google Scholar

2. Shibauchi T, Hanaguri T, Matsuda Y. Exotic Superconducting States in FeSe-Based Materials. J Phys Soc Jpn (2020) 89(10):102002. doi:10.7566/jpsj.89.102002

CrossRef Full Text | Google Scholar

3. Fernandes RM, Coldea AI, Ding H, Fisher IR, Hirschfeld PJ, Kotliar G. Iron Pnictides and Chalcogenides: a New Paradigm for Superconductivity. Nature (2022) 601(7891):35–44. doi:10.1038/s41586-021-04073-2

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Georges A, de' Medici L., Mravlje J. Strong Correlations from Hund's Coupling. Annu Rev Condens Matter Phys (2013) 4(1):137–78. doi:10.1146/annurev-conmatphys-020911-125045

CrossRef Full Text | Google Scholar

5. de’ Medici L, Giovannetti G, Capone M. Selective Mott Physics as a Key to Iron Superconductors. Phys Rev Lett (2014) 112:177001. doi:10.1103/physrevlett.112.177001

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lanatà N, Strand HUR, Giovannetti G, Hellsing B, de’ Medici L, Capone M. Orbital Selectivity in Hund’s Metals: The Iron Chalcogenides. Phys Rev B (2013) 87:045122. doi:10.1103/physrevb.87.045122

CrossRef Full Text | Google Scholar

7. Mazin II, Singh DJ, Johannes MD, Du MH. Unconventional Superconductivity with a Sign Reversal in the Order Parameter of LaFeAsO_1−xF_x. Phys Rev Lett (2008) 101:057003. doi:10.1103/physrevlett.101.057003

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Graser S, Maier TA, Hirschfeld PJ, Scalapino DJ. Near-degeneracy of Several Pairing Channels in Multiorbital Models for the Fe Pnictides. New J Phys (2009) 11:025016. doi:10.1088/1367-2630/11/2/025016

CrossRef Full Text | Google Scholar

9. Fernandes RM, Chubukov AV, Schmalian J. What Drives Nematic Order in Iron-Based Superconductors? Nat Phys (2014) 10(2):97–104. doi:10.1038/nphys2877

CrossRef Full Text | Google Scholar

10. Böhmer AE, Kreisel A. Nematicity, Magnetism and Superconductivity in FeSe. J Phys Condens Matter (2017) 30(2):023001. doi:10.1088/1361-648x/aa9caa

CrossRef Full Text | Google Scholar

11. Coldea AI. Electronic Nematic States Tuned by Isoelectronic Substitution in Bulk FeSe_1−xS_x. Front Phys (2021) 8:528. doi:10.3389/fphy.2020.594500

CrossRef Full Text | Google Scholar

12. Ptok A, Kapcia KJ, Piekarz P, Oleś AM. The ab-initio Study of Unconventional Superconductivity in CeCoIn₅ and FeSe. New J Phys (2017) 19(6):063039. doi:10.1088/1367-2630/aa6d9d

CrossRef Full Text | Google Scholar

13. Kasahara S, Sato Y, Licciardello S, Čulo M, Arsenijević S, Ottenbros T, et al. Evidence for an Fulde-Ferrell-Larkin-Ovchinnikov State with Segmented Vortices in the BCS-BEC Crossover Superconductor FeSe. Phys Rev Lett (2020) 124:107001. doi:10.1103/physrevlett.124.107001

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kasahara S, Watashige T, Hanaguri T, Kohsaka Y, Yamashita T, Shimoyama Y, et al. Field-induced Superconducting Phase of FeSe in the BCS-BEC Cross-Over. Proc Natl Acad Sci U.S.A (2014) 111(46):16309–13. doi:10.1073/pnas.1413477111

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Sprau PO, Kostin A, Kreisel A, Böhmer AE, Taufour V, Canfield PC, et al. Discovery of Orbital-Selective Cooper Pairing in FeSe. Science (2017) 357:75–80. doi:10.1126/science.aal1575

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Xu HC, Niu XH, Xu DF, Jiang J, Yao Q, Chen QY, et al. Highly Anisotropic and Twofold Symmetric Superconducting Gap in Nematically Ordered FeSe_0.93S_0.07. Phys Rev Lett (2016) 117:157003. doi:10.1103/physrevlett.117.157003

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hashimoto T, Ota Y, Yamamoto HQ, Suzuki Y, Shimojima T, Watanabe S, et al. Superconducting gap Anisotropy Sensitive to Nematic Domains in FeSe. Nat Commun (2018) 9(1):282. doi:10.1038/s41467-017-02739-y

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Liu D, Li C, Huang J, Lei B, Wang L, Wu X, et al. Orbital Origin of Extremely Anisotropic Superconducting Gap in Nematic Phase of FeSe Superconductor. Phys Rev X (2018) 8:031033. doi:10.1103/physrevx.8.031033

CrossRef Full Text | Google Scholar

19. Rhodes LC, Watson MD, Haghighirad AA, Evtushinsky DV, Eschrig M, Kim TK. Scaling of the Superconducting gap with Orbital Character in FeSe. Phys Rev B (2018) 98(18):180503. doi:10.1103/physrevb.98.180503

CrossRef Full Text | Google Scholar

20. Kushnirenko YS, Fedorov AV, Haubold E, Thirupathaiah S, Wolf T, Aswartham S, et al. Three-dimensional Superconducting gap in FeSe from Angle-Resolved Photoemission Spectroscopy. Phys Rev B (2018) 97:180501. doi:10.1103/physrevb.97.180501

CrossRef Full Text | Google Scholar

21. Kreisel A, Andersen BM, Sprau PO, Kostin A, Davis JCS, Hirschfeld PJ. Orbital Selective Pairing and gap Structures of Iron-Based Superconductors. Phys Rev B (2017) 95:174504. doi:10.1103/physrevb.95.174504

CrossRef Full Text | Google Scholar

22. Benfatto L, Valenzuela B, Fanfarillo L. Nematic Pairing from Orbital-Selective Spin Fluctuations in FeSe. Npj Quant Mater (2018) 3(1):56. doi:10.1038/s41535-018-0129-9

CrossRef Full Text | Google Scholar

23. Kang J, Fernandes RM, Chubukov A. Superconductivity in FeSe: The Role of Nematic Order. Phys Rev Lett (2018) 120:267001. doi:10.1103/physrevlett.120.267001

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Yu R, Zhu J-X, Si Q. Orbital Selectivity Enhanced by Nematic Order in FeSe. Phys Rev Lett (2018) 121:227003. doi:10.1103/physrevlett.121.227003

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Böhmer AE, Hardy F, Eilers F, Ernst D, Adelmann P, Schweiss P, et al. Lack of Coupling between Superconductivity and Orthorhombic Distortion in Stoichiometric Single-Crystalline FeSe. Phys Rev B (2013) 87:180505. doi:10.1103/physrevb.87.180505

CrossRef Full Text | Google Scholar

26. Fedorov A, Yaresko A, Kim TK, Kushnirenko Y, Haubold E, Wolf T, et al. Effect of Nematic Ordering on Electronic Structure of FeSe. Sci Rep (2016) 6:36834. doi:10.1038/srep36834

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Nakayama K, Miyata Y, Phan GN, Sato T, Tanabe Y, Urata T, et al. Reconstruction of Band Structure Induced by Electronic Nematicity in an FeSe Superconductor. Phys Rev Lett (2014) 113:237001. doi:10.1103/physrevlett.113.237001

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Shimojima T, Suzuki Y, Sonobe T, Nakamura A, Sakano M, Omachi J, et al. Lifting Of xz/yz Orbital Degeneracy at the Structural Transition in Detwinned FeSe. Phys Rev B (2014) 90:121111. doi:10.1103/physrevb.90.121111

CrossRef Full Text | Google Scholar

29. Watson MD, Kim TK, Haghighirad AA, Davies NR, McCollam A, Narayanan A, et al. Emergence of the Nematic Electronic State in FeSe. Phys Rev B (2015) 91:155106. doi:10.1103/physrevb.91.155106

CrossRef Full Text | Google Scholar

30. Fanfarillo L, Mansart J, Toulemonde P, Cercellier H, Le Fèvre P, Bertran F, et al. Orbital-dependent Fermi Surface Shrinking as a Fingerprint of Nematicity in FeSe. Phys Rev B (2016) 94:155138. doi:10.1103/physrevb.94.155138

CrossRef Full Text | Google Scholar

31. Maletz J, Zabolotnyy VB, Evtushinsky DV, Thirupathaiah S, Wolter AUB, Harnagea L, et al. Unusual Band Renormalization in the Simplest Iron-Based Superconductor FeSe_1−x. Phys Rev B (2014) 89:220506. doi:10.1103/physrevb.89.220506

CrossRef Full Text | Google Scholar

32. Watson MD, Kim TK, Rhodes LC, Eschrig M, Hoesch M, Haghighirad AA, et al. Evidence for Unidirectional Nematic Bond Ordering in FeSe. Phys Rev B (2016) 94:201107. doi:10.1103/physrevb.94.201107

CrossRef Full Text | Google Scholar

33. Coldea AI, Watson MD. The Key Ingredients of the Electronic Structure of FeSe. Annu Rev Condens Matter Phys (2018) 9(1):125–46. doi:10.1146/annurev-conmatphys-033117-054137

CrossRef Full Text | Google Scholar

34. Watson MD, Haghighirad AA, Rhodes LC, Hoesch M, Kim TK. Electronic Anisotropies Revealed by Detwinned Angle-Resolved Photo-Emission Spectroscopy Measurements of FeSe. New J Phys (2017) 19:103021. doi:10.1088/1367-2630/aa8a04

CrossRef Full Text | Google Scholar

35. Yi M, Pfau H, Zhang Y, He Y, Wu H, Chen T, et al. Nematic Energy Scale and the Missing Electron Pocket in FeSe. Phys Rev X (2019) 9:041049. doi:10.1103/physrevx.9.041049

CrossRef Full Text | Google Scholar

36. Huh SS, Seo JJ, Kim BS, Cho SH, Jung JK, Kim S, et al. Absence of Y-Pocket in 1-Fe Brillouin Zone and Reversed Orbital Occupation Imbalance in FeSe. Commun Phys (2020) 3:52. doi:10.1038/s42005-020-0319-1

CrossRef Full Text | Google Scholar

37. Cai C, Han TT, Wang ZG, Chen L, Wang YD, Xin ZM, et al. Momentum-resolved Measurement of Electronic Nematic Susceptibility in the FeSe_0.9S_0.1 Superconductor. Phys Rev B (2020) 101:180501. doi:10.1103/physrevb.101.180501

CrossRef Full Text | Google Scholar

38. Cai C, Han TT, Wang ZG, Chen L, Wang YD, Xin ZM, et al. Anomalous Spectral Weight Transfer in the Nematic State of Iron-Selenide Superconductor. Chin Phys. B (2020) 29:077401. doi:10.1088/1674-1056/ab90ec

CrossRef Full Text | Google Scholar

39. Pfau H, Chen SD, Yi M, Hashimoto M, Rotundu CR, Palmstrom JC, et al. Momentum Dependence of the Nematic Order Parameter in Iron-Based Superconductors. Phys Rev Lett (2019) 123:066402. doi:10.1103/PhysRevLett.123.066402

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Pfau H, Yi M, Hashimoto M, Chen T, Dai P-C, Shen Z-X, et al. Quasiparticle Coherence in the Nematic State of FeSe. Phys Rev B (2021) 104:L241101. doi:10.1103/physrevb.104.l241101

CrossRef Full Text | Google Scholar

41. Rhodes LC, Watson MD, Haghighirad AA, Evtushinsky DV, Kim TK. Revealing the Single Electron Pocket of FeSe in a Single Orthorhombic Domain. Phys Rev B (2020) 101:235128. doi:10.1103/physrevb.101.235128

CrossRef Full Text | Google Scholar

42. Hanaguri T, Iwaya K, Kohsaka Y, Machida T, Watashige T, Kasahara S, et al. Two Distinct Superconducting Pairing States Divided by the Nematic End point in FeSe_1−xS_x. Sci Adv (2018) 4(5):eaar6419. doi:10.1126/sciadv.aar6419

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Kostin A, Sprau PO, Kreisel A, Chong YX, Böhmer AE, Canfield PC, et al. Imaging Orbital-Selective Quasiparticles in the Hund's Metal State of FeSe. Nat Mater (2018) 17:869–74. doi:10.1038/s41563-018-0151-0

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Margadonna S, Takabayashi Y, McDonald MT, Kasperkiewicz K, Mizuguchi Y, Takano Y, et al. Crystal Structure of the New FeSe_1−x Superconductor. Chem Commun (Camb) (2008) 4(8):5607–9. doi:10.1039/b813076k

CrossRef Full Text | Google Scholar

45. Andersen OK, Boeri L. On the Multi-Orbital Band Structure and Itinerant Magnetism of Iron-Based Superconductors. Annalen der Physik (2011) 523(1-2):8–50. doi:10.1002/andp.201000149

CrossRef Full Text | Google Scholar

46. Eugenio PM, Vafek O. Classification of Symmetry Derived Pairing at the M point in FeSe. Phys Rev B (2018) 98:014503. doi:10.1103/physrevb.98.014503

CrossRef Full Text | Google Scholar

47. Borisenko SV, Evtushinsky DV, Liu Z-H, Morozov I, Kappenberger R, Wurmehl S, et al. Direct Observation of Spin-Orbit Coupling in Iron-Based Superconductors. Nat Phys (2016) 12(4):311–7. doi:10.1038/nphys3594

CrossRef Full Text | Google Scholar

48. Watson MD, Haghighirad AA, Takita H, Mansuer W, Iwasawa H, Schwier EF, et al. Shifts and Splittings of the Hole Bands in the Nematic Phase of FeSe. J Phys Soc Jpn (2017) 86(5):053703. doi:10.7566/jpsj.86.053703

CrossRef Full Text | Google Scholar

49. Day RP, Levy G, Michiardi M, Zwartsenberg B, Zonno M, Ji F, et al. Influence of Spin-Orbit Coupling in Iron-Based Superconductors. Phys Rev Lett (2018) 121:076401. doi:10.1103/PhysRevLett.121.076401

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Rhodes LC, Watson MD, Haghighirad AA, Eschrig M, Kim TK. Strongly Enhanced Temperature Dependence of the Chemical Potential in FeSe. Phys Rev B (2017) 95:195111. doi:10.1103/physrevb.95.195111

CrossRef Full Text | Google Scholar

51. Zhang Y, He C, Ye ZR, Jiang J, Chen F, Xu M, et al. Symmetry Breaking via Orbital-dependent Reconstruction of Electronic Structure in Detwinned NaFeAs. Phys Rev B (2012) 85:085121. doi:10.1103/physrevb.85.085121

CrossRef Full Text | Google Scholar

52. Eschrig H, Koepernik K. Tight-binding Models for the Iron-Based Superconductors. Phys Rev B (2009) 80(10):104503. doi:10.1103/physrevb.80.104503

CrossRef Full Text | Google Scholar

53. Acharya S, Pashov D, Jamet F, van Schilfgaarde M. Electronic Origin of Tc in Bulk and Monolayer FeSe. Symmetry (2021) 13(2):169. doi:10.3390/sym13020169

CrossRef Full Text | Google Scholar

54. Watson MD, Kim TK, Haghighirad AA, Blake SF, Davies NR, Hoesch M, et al. Suppression of Orbital Ordering by Chemical Pressure in FeSe_1−xS_x. Phys Rev B (2015) 92:121108. doi:10.1103/physrevb.92.121108

CrossRef Full Text | Google Scholar

55. Fernandes RM, Vafek O. Distinguishing Spin-Orbit Coupling and Nematic Order in the Electronic Spectrum of Iron-Based Superconductors. Phys Rev B (2014) 90:214514. doi:10.1103/physrevb.90.214514

CrossRef Full Text | Google Scholar

56. Yi M, Zhang Y, Shen Z-X, Lu D. Role of the Orbital Degree of freedom in Iron-Based Superconductors. Npj Quant Mater (2017) 2(1):57. doi:10.1038/s41535-017-0059-y

CrossRef Full Text | Google Scholar

57. Yin ZP, Haule K, Kotliar G. Kinetic Frustration and the Nature of the Magnetic and Paramagnetic States in Iron Pnictides and Iron Chalcogenides. Nat Mater (2011) 10(12):932–5. doi:10.1038/nmat3120

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Yi M, Liu Z-K, Zhang Y, Yu R, Zhu J-X, Lee JJ, et al. Observation of Universal strong Orbital-dependent Correlation Effects in Iron Chalcogenides. Nat Commun (2015) 6(1):7777. doi:10.1038/ncomms8777

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Watson MD, Backes S, Haghighirad AA, Hoesch M, Kim TK, Coldea AI, et al. Formation of Hubbard-like Bands as a Fingerprint of strong Electron-Electron Interactions in FeSe. Phys Rev B (2017) 95:081106. doi:10.1103/physrevb.95.081106

CrossRef Full Text | Google Scholar

60. Evtushinsky DV, Aichhorn M, Sassa Y, Liu Z-H, Maletz J, Wolf T, et al. Direct Observation of Dispersive Lower Hubbard Band in Iron-Based Superconductor FeSe (2017). arXiv:1612.02313.

Google Scholar

61. Glasbrenner JK, Mazin II, Jeschke HO, Hirschfeld PJ, Fernandes RM, Valentí R. Effect of Magnetic Frustration on Nematicity and Superconductivity in Iron Chalcogenides. Nat Phys (2015) 11(11):953–8. doi:10.1038/nphys3434

CrossRef Full Text | Google Scholar

62. He M, Wang L, Hardy F, Xu L, Wolf T, Adelmann P, et al. Evidence for Short-Range Magnetic Order in the Nematic Phase of FeSe from Anisotropic In-Plane Magnetostriction and Susceptibility Measurements. Phys Rev B (2018) 97:104107. doi:10.1103/physrevb.97.104107

CrossRef Full Text | Google Scholar

63. Chen T, Chen Y, Kreisel A, Lu X, Schneidewind A, Qiu Y, et al. Anisotropic Spin Fluctuations in Detwinned FeSe. Nat Mater (2019) 18(7):709–16. doi:10.1038/s41563-019-0369-5

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Wang Z, Zhao X-G, Koch R, Billinge SJL, Zunger A. Understanding Electronic Peculiarities in Tetragonal FeSe as Local Structural Symmetry Breaking. Phys Rev B (2020) 102:235121. doi:10.1103/physrevb.102.235121

CrossRef Full Text | Google Scholar

65. Gorni T, Villar Arribi P, Casula M, de’ Medici L. Accurate Modeling of FeSe with Screened Fock Exchange and Hund Metal Correlations. Phys Rev B (2021) 104:014507. doi:10.1103/physrevb.104.014507

CrossRef Full Text | Google Scholar

66. Mukherjee S, Kreisel A, Hirschfeld PJ, Andersen BM. Model of Electronic Structure and Superconductivity in Orbitally Ordered FeSe. Phys Rev Lett (2015) 115(2):026402. doi:10.1103/PhysRevLett.115.026402

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Rhodes LC, Böker J, Müller MA, Eschrig M, Eremin IM. Non-local d_xy Nematicity and the Missing Electron Pocket in FeSe. Npj Quan Mater. (2021) 6(1):45. doi:10.1038/s41535-021-00341-6

CrossRef Full Text | Google Scholar

68. Kushnirenko YS, Kordyuk AA, Fedorov AV, Haubold E, Wolf T, Büchner B, et al. Anomalous Temperature Evolution of the Electronic Structure of FeSe. Phys Rev B (2017) 96:100504. doi:10.1103/physrevb.96.100504

CrossRef Full Text | Google Scholar

69. Pustovit YV, Bezguba VV, Kordyuk AA. Temperature Dependence of the Electronic Structure of FeSe. Metallofiz Noveishie Tekhnol (2017) 39:709–18. doi:10.15407/mfint.39.06.0709

CrossRef Full Text | Google Scholar

70. Pustovit YV, Brouet V, Chareev DA, Kordyuk AA. Temperature Evolution of Charge Carrier Density in the Centre of the Brillouin Zone of Fe(Se,Te) Superconductor. Metallofiz Noveishie Tekhnol (2018) 40:139–46. doi:10.15407/mfint.40.02.0139

CrossRef Full Text | Google Scholar

71. Schwier EF, Takita H, Mansur W, Ino A, Hoesch M, Watson MD, et al. Applications for Ultimate Spatial Resolution in LASER Based μ - ARPES: A FeSe Case Study. AIP Conf Proc (2019) 2054(1):040017. doi:10.1063/1.5084618

CrossRef Full Text | Google Scholar

72. Shimojima T, Motoyui Y, Taniuchi T, Bareille C, Onari S, Kontani H, et al. Discovery of Mesoscopic Nematicity Wave in Iron-Based Superconductors. Science (2021) 373(6559):1122–5. doi:10.1126/science.abd6701

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Tanatar MA, Böhmer AE, Timmons EI, Schütt M, Drachuck G, Taufour V, et al. Origin of the Resistivity Anisotropy in the Nematic Phase of FeSe. Phys Rev Lett (2016) 117:127001. doi:10.1103/physrevlett.117.127001

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Hoesch M, Kim TK, Dudin P, Wang H, Scott S, Harris P, et al. A Facility for the Analysis of the Electronic Structures of Solids and Their Surfaces by Synchrotron Radiation Photoelectron Spectroscopy. Rev Sci Instrum (2017) 88:013106. doi:10.1063/1.4973562

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Brouet V, Fuglsang Jensen M, Lin P-H, Taleb-Ibrahimi A, Le Fèvre P, Bertran F, et al. Impact of the Two Fe Unit Cell on the Electronic Structure Measured by ARPES in Iron Pnictides. Phys Rev B (2012) 86:075123. doi:10.1103/physrevb.86.075123

CrossRef Full Text | Google Scholar

76. Day RP, Zwartsenberg B, Elfimov IS, Damascelli A. Computational Framework chinook for Angle-Resolved Photoemission Spectroscopy. npj Quan Mater (2019) 4(1):54. doi:10.1038/s41535-019-0194-8

CrossRef Full Text | Google Scholar

77. Reiss P, Watson MD, Kim TK, Haghighirad AA, Woodruff DN, Bruma M, et al. Suppression of Electronic Correlations by Chemical Pressure from FeSe to FeS. Phys Rev B (2017) 96:121103. doi:10.1103/physrevb.96.121103

CrossRef Full Text | Google Scholar

78. Pustovit YV, Kordyuk AA. Metamorphoses of Electronic Structure of FeSe-Based Superconductors. Low Temperature Phys (2016) 42(11):995–1007. doi:10.1063/1.4969896

CrossRef Full Text | Google Scholar

79. Fisher IR, Degiorgi L, Shen ZX. In-plane Electronic Anisotropy of Underdoped ‘122’ Fe-Arsenide Superconductors Revealed by Measurements of Detwinned Single Crystals. Rep Prog Phys (2011) 74(12):124506. doi:10.1088/0034-4885/74/12/124506

CrossRef Full Text | Google Scholar

80. Bartlett JM, Steppke A, Hosoi S, Noad H, Park J, Timm C, et al. Relationship between Transport Anisotropy and Nematicity in FeSe. Phys Rev X (2021) 11:021038. doi:10.1103/physrevx.11.021038

CrossRef Full Text | Google Scholar

81. Ghini M, Bristow M, Prentice JCA, Sutherland S, Sanna S, Haghighirad AA, et al. Strain Tuning of Nematicity and Superconductivity in Single Crystals of FeSe. Phys Rev B (2021) 103:205139. doi:10.1103/physrevb.103.205139

CrossRef Full Text | Google Scholar

82. Rhodes LC, Watson MD, Kim TK, Eschrig M. K_z Selective Scattering within Quasiparticle Interference Measurements of FeSe. Phys Rev Lett (2019) 123:216404. doi:10.1103/physrevlett.123.216404

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Sunko V, Abarca Morales E, Marković I, Barber ME, Milosavljević D, Mazzola F, et al. Direct Observation of a Uniaxial Stress-Driven Lifshitz Transition in Sr₂RuO₄. npj Quan Mater (2019) 4(1):46. doi:10.1038/s41535-019-0185-9

CrossRef Full Text | Google Scholar

84. Iwasawa H. High-resolution Angle-Resolved Photoemission Spectroscopy and Microscopy. Electron Struct (2020) 2(4):043001. doi:10.1088/2516-1075/abb379

CrossRef Full Text | Google Scholar

85. Watson MD, Dudin P, Rhodes LC, Evtushinsky DV, Iwasawa H, Aswartham S, et al. Probing the Reconstructed Fermi Surface of Antiferromagnetic BaFe₂As₂ in One Domain. npj Quan Mater (2019) 4(1):36. doi:10.1038/s41535-019-0174-z

CrossRef Full Text | Google Scholar

86. Jiao L, Huang C-L, Rößler S, Koz C, Rößler UK, Schwarz U, et al. Superconducting gap Structure of FeSe. Scientific Rep (2017) 7(1):44024. doi:10.1038/srep44024

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Choubey P, Berlijn T, Kreisel A, Cao C, Hirschfeld PJ. Visualization of Atomic-Scale Phenomena in Superconductors: Application to FeSe. Phys Rev B (2014) 90:134520. doi:10.1103/physrevb.90.134520

CrossRef Full Text | Google Scholar

88. Bu K, Wang B, Zhang W, Fei Y, Zheng Y, Ai F, et al. Study of Intrinsic Defect States of FeSe with Scanning Tunneling Microscopy. Phys Rev B (2019) 100:155127. doi:10.1103/physrevb.100.155127

CrossRef Full Text | Google Scholar

89. Macdonald AJ, Tremblay-Johnston Y-S, Grothe S, Chi S, Dosanjh P, Johnston S, et al. Dispersing Artifacts in FT-STS: a Comparison of Set point Effects across Acquisition Modes. Nanotechnology (2016) 27(41):414004. doi:10.1088/0957-4484/27/41/414004

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Weismann A, Wenderoth M, Lounis S, Zahn P, Quaas N, Ulbrich RG, et al. Seeing the Fermi Surface in Real Space by Nanoscale Electron Focusing. Science (2009) 323(5918):1190–3. doi:10.1126/science.1168738

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Lounis S, Zahn P, Weismann A, Wenderoth M, Ulbrich RG, Mertig I, et al. Theory of Real Space Imaging of Fermi Surface Parts. Phys Rev B (2011) 83:035427. doi:10.1103/physrevb.83.035427

CrossRef Full Text | Google Scholar

92. Marques CA, Bahramy MS, Trainer C, Marković I, Watson MD, Mazzola F, et al. Tomographic Mapping of the Hidden Dimension in Quasi-Particle Interference. Nat Comm (2021) 12(1):6739. doi:10.1038/s41467-021-27082-1

CrossRef Full Text | Google Scholar

93. Li C, Wu X, Wang L, Liu D, Cai Y, Wang Y, et al. Spectroscopic Evidence for an Additional Symmetry Breaking in the Nematic State of FeSe Superconductor. Phys Rev X (2020) 10:031033. doi:10.1103/physrevx.10.031033

CrossRef Full Text | Google Scholar

94. Lee C-C, Yin W-G, Ku W. Ferro-Orbital Order and Strong Magnetic Anisotropy in the Parent Compounds of Iron-Pnictide Superconductors. Phys Rev Lett (2009) 103:267001. doi:10.1103/physrevlett.103.267001

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Pradhan B, Parida PK, Sahoo S. Superconductivity and Jahn-Teller Distortion in S±-Wave Iron-Based Superconductors. Braz J Phys (2021) 51(3):393–400. doi:10.1007/s13538-020-00827-x

CrossRef Full Text | Google Scholar

96. Kreisel A, Mukherjee S, Hirschfeld PJ, Andersen BM. Spin Excitations in a Model of FeSe with Orbital Ordering. Phys Rev B (2015) 92:224515. doi:10.1103/physrevb.92.224515

CrossRef Full Text | Google Scholar

97. Kreisel A, Andersen BM, Hirschfeld PJ. Itinerant Approach to Magnetic Neutron Scattering of FeSe: Effect of Orbital Selectivity. Phys Rev B (2018) 98:214518. doi:10.1103/physrevb.98.214518

CrossRef Full Text | Google Scholar

98. Yu R, Hu H, Nica EM, Zhu J-X, Si Q. Orbital Selectivity in Electron Correlations and Superconducting Pairing of Iron-Based Superconductors. Front Phys (2021) 9(92). doi:10.3389/fphy.2021.578347

CrossRef Full Text | Google Scholar

99. Cercellier H, Rodière P, Toulemonde P, Marcenat C, Klein T. Influence of the Quasiparticle Spectral Weight in FeSe on Spectroscopic, Magnetic, and Thermodynamic Properties. Phys Rev B (2019) 100:104516. doi:10.1103/physrevb.100.104516

CrossRef Full Text | Google Scholar

100. Christensen MH, Fernandes RM, Chubukov AV. Orbital Transmutation and the Electronic Spectrum of FeSe in the Nematic Phase. Phys Rev Res (2020) 2:013015. doi:10.1103/physrevresearch.2.013015

CrossRef Full Text | Google Scholar

101. Jiang K, Hu J, Ding H, Wang Z. Interatomic Coulomb Interaction and Electron Nematic Bond Order in FeSe. Phys Rev B (2016) 93(11):115138. doi:10.1103/physrevb.93.115138

CrossRef Full Text | Google Scholar

102. Biswas PK, Kreisel A, Wang Q, Adroja DT, Hillier AD, Zhao J, et al. Evidence of Nodal gap Structure in the Basal Plane of the FeSe Superconductor. Phys Rev B (2018) 98:180501. doi:10.1103/physrevb.98.180501

CrossRef Full Text | Google Scholar

103. Xing R-Q, Classen L, Chubukov AV. Orbital Order in FeSe: The Case for Vertex Renormalization. Phys Rev B (2018) 98:041108. doi:10.1103/physrevb.98.041108

CrossRef Full Text | Google Scholar

104. Kang J, Chubukov AV, Fernandes RM. Time-reversal Symmetry-Breaking Nematic Superconductivity in FeSe. Phys Rev B (2018) 98:064508. doi:10.1103/physrevb.98.064508

CrossRef Full Text | Google Scholar

105. Mandal S, Zhang P, Ismail-Beigi S, Haule K. How Correlated Is the FeSe/SrTiO₃ System? Phys Rev Lett (2017) 119:067004. doi:10.1103/PhysRevLett.119.067004

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Long X, Zhang S, Wang F, Liu Z. A First-Principle Perspective on Electronic Nematicity in FeSe. npj Quan Mater (2020) 5(1):50. doi:10.1038/s41535-020-00253-x

CrossRef Full Text | Google Scholar

107. Yamada T, Tohyama T. Multipolar Nematic State of Nonmagnetic FeSe Based on DFT + U. Phys Rev B (2021) 104:L161110. doi:10.1103/physrevb.104.l161110

CrossRef Full Text | Google Scholar

108. Steffensen D, Kreisel A, Hirschfeld PJ, Andersen BM. Interorbital Nematicity and the Origin of a Single Electron Fermi Pocket in FeSe. Phys Rev B (2021) 103:054505. doi:10.1103/physrevb.103.054505

CrossRef Full Text | Google Scholar

109. Rodriguez EE, Stock C, Zajdel P, Krycka KL, Majkrzak CF, Zavalij P, et al. Magnetic-crystallographic Phase Diagram of the Superconducting Parent Compound Fe_1+xTe. Phys Rev B (2011) 84:064403. doi:10.1103/physrevb.84.064403

CrossRef Full Text | Google Scholar

110. Trainer C, Yim C-M, Heil C, Giustino F, Croitori D, Tsurkan V, et al. Manipulating Surface Magnetic Order in Iron telluride. Sci Adv (2019) 5(3):eaav3478. doi:10.1126/sciadv.aav3478

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Chubukov AV, Khodas M, Fernandes RM. Magnetism, Superconductivity, and Spontaneous Orbital Order in Iron-Based Superconductors: Which Comes First and Why? Phys Rev X (2016) 6:041045. doi:10.1103/physrevx.6.041045

CrossRef Full Text | Google Scholar

112. Xing R-Q, Classen L, Khodas M, Chubukov AV. Competing Instabilities, Orbital Ordering, and Splitting of Band Degeneracies from a Parquet Renormalization Group Analysis of a Four-Pocket Model for Iron-Based Superconductors: Application to FeSe. Phys Rev B (2017) 95:085108. doi:10.1103/physrevb.95.085108

CrossRef Full Text | Google Scholar

113. Classen L, Xing R-Q, Khodas M, Chubukov AV. Interplay between Magnetism, Superconductivity, and Orbital Order in 5-Pocket Model for Iron-Based Superconductors: Parquet Renormalization Group Study. Phys Rev Lett (2017) 118:037001. doi:10.1103/PhysRevLett.118.037001

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Islam KR, Böker J, Eremin IM, Chubukov AV. Specific Heat and gap Structure of a Nematic Superconductor: Application to FeSe. Phys Rev B (2021) 104:094522. doi:10.1103/physrevb.104.094522

CrossRef Full Text | Google Scholar

115. Marciani M, Benfatto L. Resistivity Anisotropy from Multiorbital Boltzmann Equation in Nematic FeSe. (2022). arXiv:2202.12070.

Google Scholar

116. Li J, Lei B, Zhao D, Nie LP, Song DW, Zheng LX, et al. Spin-Orbital-Intertwined Nematic State in FeSe. Phys Rev X (2020) 10:011034. doi:10.1103/physrevx.10.011034

CrossRef Full Text | Google Scholar

117. Liu S, Yuan J, Ma S, Lu Z, Zhang Y, Ma M, et al. Magnetic-Field-Induced Spin Nematicity in FeSe_1−xS_x and FeSe_1−yTe_y Superconductor Systems. Chin Phys. Lett. (2021) 38:087401. doi:10.1088/0256-307x/38/8/087401

CrossRef Full Text | Google Scholar

118. Medvedev S, McQueen TM, Troyan IA, Palasyuk T, Eremets MI, Cava RJ, et al. Electronic and Magnetic Phase Diagram of β-Fe_1.01Se with Superconductivity at 36.7K under Pressure. Nat Mater (2009) 8(8):630–3. doi:10.1038/nmat2491

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Huang D, Hoffman JE. Monolayer FeSe on SrTiO₃. Annu Rev Condens Matter Phys (2017) 8(1):311–36. doi:10.1146/annurev-conmatphys-031016-025242

CrossRef Full Text | Google Scholar

120. Hardy F, He M, Wang L, Wolf T, Schweiss P, Merz M, et al. Calorimetric Evidence of Nodal Gaps in the Nematic Superconductor FeSe. Phys Rev B (2019) 99:035157. doi:10.1103/physrevb.99.035157

CrossRef Full Text | Google Scholar

121. Sun Y, Kittaka S, Nakamura S, Sakakibara T, Irie K, Nomoto T, et al. Gap Structure of FeSe Determined by Angle-Resolved Specific Heat Measurements in Applied Rotating Magnetic Field. Phys Rev B (2017) 96:220505. doi:10.1103/physrevb.96.220505

CrossRef Full Text | Google Scholar

122. Matsuura K, Mizukami Y, Arai Y, Sugimura Y, Maejima N, Machida A, et al. Maximizing Tc by Tuning Nematicity and Magnetism in FeSe_1−xS_x Superconductors. Nat Commun (2017) 8(1):1143. doi:10.1038/s41467-017-01277-x

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Wang Q, Shen Y, Pan B, Zhang X, Ikeuchi K, Iida K, et al. Magnetic Ground State of FeSe. Nat Comm (2016) 7(1):12182. doi:10.1038/ncomms12182

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Wang Q, Shen Y, Pan B, Hao Y, Ma M, Zhou F, et al. Strong Interplay between Stripe Spin Fluctuations, Nematicity and Superconductivity in FeSe. Nat Mater (2016) 15(2):159–63. doi:10.1038/nmat4492

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Watson MD, Aswartham S, Rhodes LC, Parrett B, Iwasawa H, Hoesch M, et al. Three-dimensional Electronic Structure of the Nematic and Antiferromagnetic Phases of NaFeAs from Detwinned Angle-Resolved Photoemission Spectroscopy. Phys Rev B (2018) 97:035134. doi:10.1103/physrevb.97.035134

CrossRef Full Text | Google Scholar

126. Chen T, Yi M, Dai P. Electronic and Magnetic Anisotropies in FeSe Family of Iron-Based Superconductors. Front Phys (2020) 8:314. doi:10.3389/fphy.2020.00314

CrossRef Full Text | Google Scholar

127. Coldea AI, Blake SF, Kasahara S, Haghighirad AA, Watson MD, Knafo W, et al. Evolution of the Low-Temperature Fermi Surface of Superconducting FeSe_1−xS_x across a Nematic Phase Transition. npj Quan Mater (2019) 4(1):2. doi:10.1038/s41535-018-0141-0

CrossRef Full Text | Google Scholar