Generation of Magnon Orbital Angular Momentum by a Skyrmion-Textured Domain Wall in a Ferromagnetic Nanotube

1 Introduction

Magnons are quanta of spin waves which are low-energy collective excitations of ordered magnets [1–3]. Due to fundamental curiosity and potential technical applicability, magnons have received significant attention both theoretically and experimentally [4–10]. A magnon carries a spin angular momentum and thus it can apply torque to magnetic textures such as a domain wall and a Skyrmion, as an electron does through spin-transfer torque [11–14]. Since a magnon current does not involve electron transport, magnons can be used to transport information even in insulators, enabling magnon-based information technology free from Joule heating [15]. Because of this potential utility for low-power devices, it is important to investigate the dynamics of magnons, spawning the rising fields of magnonics or magnon spintronics in condensed matter physics [16–19].

Over the past decades, magnonics has been mainly focused on flat geometry. Recently, magnonics in curved geometry has emerged [20–24]. One of the simplest curved geometries is a nanotube. In the magnetic nanotube, orbital angular momenta, as well as spin angular momenta, are keys to understanding the dynamics of magnetic textures and particles in the system [25, 26]. In particular, in a ferromagnetic nanotube, a magnon can carry orbital angular momentum, which can be exploited to magnonic computing [20, 27, 28]. A domain wall with non-trivial magnetic texture has the Skyrmion charge and has been recently shown to possess an orbital angular momentum [25, 29]. An electron also can carry orbital angular momentum and the exchange of orbital angular momenta between electrons and the domain wall can be interpreted as a current-induced torque. Current-induced domain wall motion and interaction between electrons and the Skyrmion-textured domain wall in a nanotube have been studied [25, 30].

Waves carrying orbital angular momentum have been intriguing physicists throughout various fields. For example, orbital angular momenta of photons [31–36], phonons [37–39], neutrons [40, 41], electrons [42, 43], and gravitational waves [44, 45] have been investigated. Orbital angular momentum exchange between photons and magnetic Skyrmions has also been studied [46]. These waves and particles with orbital angular momentum can offer novel functionalities. In particular, it has been proposed that a magnon carrying an orbital angular momentum can be used to construct a topology-protected logic gate [27].

In this paper, we propose a way to generate a twisted magnon current that carries orbital angular momentum by using a domain wall. In a two-dimensional magnet, a domain wall on the magnet is a line and spin-textures on the domain wall can spatially vary [47]. When the magnet is curved, the domain wall line can also be curved. In particular, when the magnet has the cylindrical geometry, the domain wall become a circle. Figure 1 for the illustration of a domain wall with the nontrivial texture in a nanotube. Due to the periodicity of the nanotube along the azimuthal direction, spin textures through the domain wall circle can have integer winding number and this winding number determines the system’s Skyrmion charge $Q=\frac{1}{4\pi }\int dzd\phi \mathbf{m}\cdot \left({\partial }_{\phi }\mathbf{m}\times {\partial }_z\mathbf{m}\right)=0,\pm 1,\pm 2,\cdots$. The Skyrmion-textured domain wall can be classified by its Skyrmion charge and the Skyrmion charge characterizes the emergent magnetic field of the domain wall. We find that the emergent magnetic field exerts the Lorentz force for the magnon beam and thereby the beam is bent, one can tune the orbital motion of the magnon by the domain wall. In other words, one can generate the magnon orbital angular momentum by a domain wall. In order to solve the problem analytically, we use a method of supersymmetric quantum mechanics (SUSY QM) [48, 49]. We obtain the exact solutions for the magnon on the domain wall possessing a finite Skyrmion charge. We solve the scattering problem and also find the bound states. Our work deals with the exchange of the angular momenta of magnets and their fluctuations, similar to that the Einstein-de Haas effect [50] deals with the exchange of angular momenta of the magnets and the lattice. We hope that our study paves the way for the understanding of angular momentum conservation.

FIGURE 1

FIGURE 1. A ferromagnetic nanotube with a domain wall possessing finite Skyrmion charge and magnetic textures with spin-wave fluctuations. The arrows represent magnetizations of spin-wave excitations. The transparent cones represent swapped regions by fluctuations of the magnetizations. The black curve lines the heads of the arrows. The axis of the nanotube is the z-axis.

Our paper is organized as follows. In Section 2.1, we introduce the general formalism to obtain the magnon on top of the Skyrmion-textured domain wall in a ferromagnetic nanotube. The equation of motion for the magnon which we obtain can be interpreted as “Schrödinger” equation with the “Hamiltonian” for the charged particle in an electromagnetic field. In Section 2.2, orbital angular momentum exchange between the magnon and the domain wall is calculated by the Lorentz force. In Section 2.3, we define the SUSY partner Hamiltonian and potential. In Section 2.4, we discuss magnon-bound states. In Section 2.5, precise reflection probability is obtained. Also, the result from Section 2.2 is reproduced. Section 3 is devoted to the dynamics of the domain wall. Due to the Skyrmion charge, critical behavior of the domain wall velocity occurs. In Section 4, we summarized main results and discuss potential future outlook.

2 Exact Solution of a Spin Wave on Top of the Domain Wall

In this section, we construct the equation of motion for the magnon on top of the Skyrmion-textured domain wall and solve the equation analytically with the aid of SUSY QM. To this end, we introduce the general formalism of the dynamics of the magnetization and obtain the “Schrödinger” equation and the “electromagnetic” gauge field for the magnon.

2.1 General Formalism

To investigate the low-energy dynamics of magnetizations in a ferromagnetic nanotube, we take the continuum limit. The normalized magnetization m is considered as a field with two spatial variables z and φ, which are the axial coordinate and the azimuth, and a temporal variable t. The axis of the nanotube is chosen to be the z-axis. For theoretical description of a ferromagnetic nanotube, we use the continuum Heisenberg model with easy-axis anisotropy, whose potential energy density is given by

$\mathcal{U}=\frac{A}{2}\left[{\left({\partial }_z\mathbf{m}\right)}^2+\frac{1}{{\rho }^2}{\left({\partial }_{\phi }\mathbf{m}\right)}^2\right]-\frac{K}{2}{m}_z^2,(1)$

where ρ is the radius of the nanotube, A is the exchange constant, and K > 0 is the anisotropy constant [25]. The dynamics of the magnetization stems from the kinetic part of the Lagrangian density $\mathcal{L}={\mathcal{L}}_{\text{kin}}-\mathcal{U}$, which is given by ${\mathcal{L}}_{\text{kin}}=-s\cos \theta {\partial }_t\varphi$, and the Rayleigh dissipation $\mathcal{R}=(\alpha s/2)|{\partial }_t\mathbf{m}{|}^2$, where α is the Gilbert damping coefficient. The variational principle with respect to m yields the Landau-Lifshitz-Gilbert equation [51]

$s{\partial }_t\mathbf{m}-\alpha s\mathbf{m}\times {\partial }_t\mathbf{m}={\mathbf{h}}_{\text{eff}}\times \mathbf{m},(2)$

where s is the spin density and h_eff is the effective magnetic field conjugate to m given by

${\mathbf{h}}_{\text{eff}}=-\frac{\delta U}{\delta \mathbf{m}}=A{\partial }_z^2\mathbf{m}+\frac{A}{{\rho }^2}{\partial }_{\phi }^2\mathbf{m}+K{m}_z\widehat{z},(3)$

where $U=\int dzd\phi \rho \mathcal{U}$. Solving Eq. 2 for the case of ∂_tm = 0, we can obtain static solutions. We will consider a set of solutions of the Skyrmion-textured domain wall as a family of the slow modes with an angle representation m₀ = (sin θ₀ cos ϕ₀, sin θ₀ sin ϕ₀, cos θ₀),

$\cos {\theta }_0=\tanh \left[\frac{z-Z}{\lambda }\right],{\varphi }_0=Q\left(\phi -\mathrm{\Upsilon }\right)+\mathrm{\Phi },(4)$

where $\lambda \equiv {\lambda }_0/\sqrt{1+Q^2{\lambda }_0^2/{\rho }^2}$ and ${\lambda }_0\equiv \sqrt{A/K}$ [25]. Here, Z, ϒ, Φ and Q are the position of the domain wall, the angle of the Skyrmionic texture, the global rotation angle, and the Skyrmion charge, respectively. Since the system is invariant under translations along the z axis, orbital rotations about the axis of the nanotube, and spin rotations about the easy-axis, linear momentum, orbital angular momentum, and spin angular momentum are conserved. The domain-wall solution (4) breaks these three symmetries and the three collective coordinates Z, ϒ, Φ represent corresponding zero-energy modes. We decompose the magnetization into a slow mode m₀ (z, φ) and a perturbative fast mode δm (z, φ, t) which are orthogonal. The magnetization can be written as

$\mathbf{m}\left(z,\phi ,t\right)=\sqrt{1-|\delta \mathbf{m}{|}^2}{\mathbf{m}}_0\left(z,\phi \right)+\delta \mathbf{m}\left(z,\phi ,t\right).(5)$

With this decomposition, the equation of motion for the fast mode can be derived from the expansion of the Landau-Lifshitz equation up to linear order of the fast mode δm,

$\begin{array}{cc}\hfill s\left(1-\alpha \mathbf{m}\times \right){\partial }_t\delta \mathbf{m}=& \left(A{\nabla }^2{\mathbf{m}}_0+K\left({\mathbf{m}}_0\cdot \widehat{z}\right)\widehat{z}\right)\times \delta \mathbf{m}\hfill \\ \hfill & +\left(A{\nabla }^2\delta \mathbf{m}+K\left(\delta \mathbf{m}\cdot \widehat{z}\right)\widehat{z}\right)\times {\mathbf{m}}_0,\hfill \end{array}(6)$

where ${\nabla }^2={\partial }_z^2+{\partial }_{\phi }^2/{\rho }^2$. To obtain magnon modes on top of the domain wall, we neglect the Gilbert damping by following previous literature on the interaction of magnons with magnetic textures, e.g., Refs. [52–54], which allows us to invoke the conservation of angular momentum to understand the interaction with transparent physical picture. Note that the effect of the damping on magnons can be captured simply by introducing a finite lifetime, τ ∝ (αω)⁻¹ with ω the magnon frequency as has been done in, e.g., Refs. [13, 52, 55]. Plugging the domain-wall solution (4) into Eq. 6, the equation of motion for the fast mode on top of the Skyrmion-textured domain wall becomes

$\begin{array}{cc}\hfill s{\partial }_t\delta \mathbf{m}=& {\mathbf{m}}_0\times \left[-A{\nabla }^2\delta \mathbf{m}-K\left(\delta \mathbf{m}\cdot \widehat{z}\right)\widehat{z}\right.\hfill \\ \hfill & \left.+\left(A/{\lambda }_0^2\right)\left[1-{\left({\lambda }_0/\lambda \right)}^{2}2{\sin }^2\theta \right]\delta \mathbf{m}\right].\hfill \end{array}(7)$

It is convenient to use the following as an orthonormal basis $\{{\widehat{e}}_1,{\widehat{e}}_2,{\widehat{e}}_3\}$

$\begin{array}{cc}\hfill & {\widehat{e}}_1=\widehat{\theta }=\left(\cos {\theta }_0\cos {\varphi }_0,\cos {\theta }_0\sin {\varphi }_0,-\sin {\theta }_0\right),\hfill \\ \hfill & {\widehat{e}}_2=\widehat{\varphi }=\left(-\sin {\varphi }_0,\cos {\varphi }_0,0\right),\hfill \\ \hfill & {\widehat{e}}_3={\mathbf{m}}_0={\widehat{e}}_1\times {\widehat{e}}_2.\hfill \end{array}(8)$

The magnetic texture of the spin-wave excitation with the solution (4) is illustrated in Figure 1. For the convenience, we define a complex field Ψ = δm₁ − iδm₂, where $\delta m_j=\delta \mathbf{m}\cdot {\widehat{e}}_j\text{and\hspace{0.17em}}j=\mathrm{1,2}$. The complex filed Ψ contains full information of the spin wave. Reassembling the equations of motion for each component δm_j yields the equation of motion for the complex filed Ψ. The complex field Ψ obeys the “Schrödinger” equation ¹

$is{\partial }_t\mathrm{\Psi }=H\mathrm{\Psi }(9)$

with the “Hamiltonian”

$H=\frac{A}{{\hslash }^2}{\left(\frac{\hslash }{i}\nabla -\mathbf{a}\right)}^2+V,(10)$

with vector potential $\mathbf{a}=a_{\phi }\widehat{\phi },a_{\phi }=Q\hslash \cos {\theta }_0/\rho$ and scalar potential $V=A[1/{\lambda }_0^2-(2/{\lambda }^2-Q^2/{\rho }^2){\sin }^2{\theta }_0]$. The independency of the Hamiltonian (Eq. 10) on the spin azimuthal angle ϕ₀ is due to the spin rotational symmetry. The independency on the spatial azimuthal angle φ is due to the orbital rotational symmetry. Conservation of spin and orbital angular momenta of the system stems from these two rotational symmetries.

2.2 Emergent Magnetic Field

Before solving the Hamiltonian (Eq. 10) exactly, we can invoke the following simple argument to compute orbital angular momentum change of magnons. Magnons on the Skyrmion-textured domain wall experience an emergent magnetic field [56] $\mathbf{b}=\nabla \times \mathbf{a}=-\frac{Q\hslash }{\lambda \rho }{\text{sech}}^2(\frac{z-Z}{\lambda })\widehat{\rho }$. For the magnetic field which is a curl of a, we only take its surface-normal component, since the nanotube is considered as a two-dimensional surface ². The orbital angular momentum change of each magnon can be evaluated from the Lorentz force, $\mathrm{\Delta }{l}_z=\mathrm{\Delta }(\rho p_{\phi })=\int \rho (\mathbf{v}\times \mathbf{b})\cdot \widehat{\phi }dt=-2Q\hslash$, where v is the magnon velocity and p_φ is momentum in the azimuthal direction. Since the total orbital angular momentum of the domain wall and magnons is a conserved quantity, an orbital transfer torque to the domain wall per magnon is 2Qℏ. Figure 2 depicts the bent trajectory of the magnon due to the surface-normal emergent magnetic field. In this classical viewpoint, we can calculate the orbital angular momentum transfer, but it does not offer concise reflection property. In the section below we solve the reflection problem exactly.

FIGURE 2

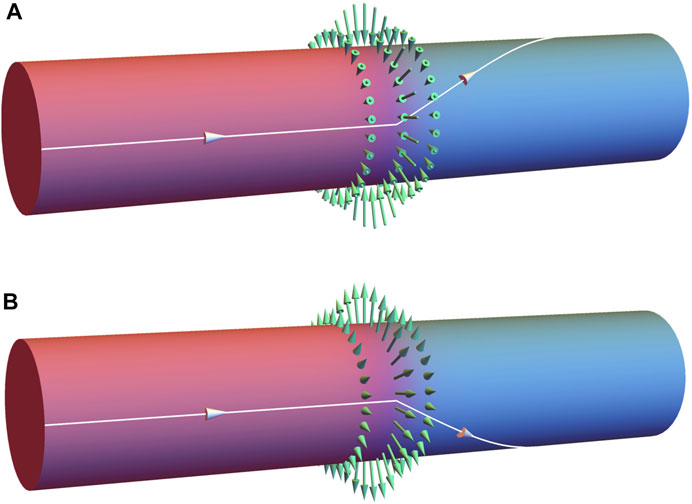
FIGURE 2. Schematic illustrations of magnon trajectory on the ferromagnetic nanotube in the presence of the Skyrmion-textured domain wall. The red and blue regions represent the domains whose background magnetizations are ${\mathbf{m}}_0=-\widehat{z}$ and ${\mathbf{m}}_0=\widehat{z}$, respectively. The green arrows perpendicular to the surface express the emergent magnetic field associated with the Skyrmion charge (A) Q = 1 and (B) Q = −1. The white curves indicate the trajectories of magnons.

2.3 SUSY QM

Since the field θ₀ of the domain-wall solution (4) has z-dependence only, the “Hamiltonian” H (Eq. 10) is invariant under global translation of the azimuthal angle φ → φ + δφ. Therefore we can write the wavefunction as an eigenmode Ψ (z, φ, t) = ψ (z)e^i(lφ−ωt), l = 0, ±1, ±2, ⋯. The equation of motion for ψ (z) is written as a time independent Schrödinger equation sωψ (z) = H_effψ (z) with the effective Hamiltonian $H_{\text{eff}}=-A{\partial }_z^2+V_{\text{eff}}$, where the effective potential is

$\begin{array}{cc}\hfill V_{\text{eff}}=& A\left[\frac{l^2}{{\rho }^2}-2\frac{Ql}{{\rho }^2}\tanh \left(\frac{z-Z}{\lambda }\right)\right.\hfill \\ \hfill & \left.+\frac{1}{{\lambda }^2}\left[1-2{\text{sech}}^2\left(\frac{z-Z}{\lambda }\right)\right]\right].\hfill \end{array}(11)$

Then the original two-dimensional problem is simplified as a one-dimensional quantum mechanics. The effective potential is also known as the Rosen-Morse potential [57]. The tanh term plays role of an energy barrier which reduce longitudinal momentum of incoming magnon. The sech² term represents a potential well, which gives us possibility of existence of bound modes.

The problem can be solved by using a method of SUSY QM [48, 49]. In terms of creation and annihilation operators $a={\partial }_z+\tanh \left[\left(z-Z\right)/\lambda \right]/\lambda +\beta ,a^{†}=-{\partial }_z+\tanh \left[\left(z-Z\right)/\lambda \right]/\lambda +\beta$, the effective Hamiltonian and its SUSY partner Hamiltonian can be written as

$H_{\text{eff}}=A\left[a^{†}a-{\beta }^2+\frac{l^2}{{\rho }^2}\right]=-A{\partial }_z^2+V_{\text{eff}},(12)$

${\tilde{H}}_{\text{eff}}=A\left[a{a}^{†}-{\beta }^2+\frac{l^2}{{\rho }^2}\right]=-A{\partial }_z^2+{\tilde{V}}_{\text{eff}},(13)$

where β = −Qlλ/ρ² and

${\tilde{V}}_{\text{eff}}=A\left[-\frac{2Ql}{{\rho }^2}\tanh \left(\frac{z-Z}{\lambda }\right)+\frac{1}{{\lambda }^2}+\frac{l^2}{{\rho }^2}\right].(14)$

Note that, in the case of Q = 0, the partner potential ${\tilde{V}}_{\text{eff}}$ is a constant potential so that there is no reflection of magnons and the linear momentum is preserved. Also, the original potential V_eff becomes the Pöschl-Teller potential [58, 59] which is a well known reflectionless potential as shown in Figure 3. Here, we can conclude that, for moving magnons, the Skyrmionic texture of the domain wall generates the potential barrier. Since ${\tilde{H}}_{\text{eff}}=H_{\text{eff}}+A\left[a,a^{†}\right]$, the commutation relation

$\left[a,a^{†}\right]=\frac{2}{{\lambda }^2}{\text{sech}}^2\left(\frac{z-Z}{\lambda }\right)(15)$

eliminate the ${\text{sech}}^2\left(\left(z-Z\right)/\lambda \right)$ term in Eq. 11 and yields Eq. 14. The problem with the potential V_eff is simplified to the problem with ${\tilde{V}}_{\text{eff}}$. Eigenfunctions of the two Hamiltonians are easily transformed into each other’s ones by annihilation and creation operators:

${\tilde{H}}_{\text{eff}}a\psi \left(z\right)=a{H}_{\text{eff}}\psi \left(z\right)=s\omega a\psi \left(z\right),(16)$

$H_{\text{eff}}{a}^{†}\tilde{\psi }\left(z\right)=a^{†}{\tilde{H}}_{\text{eff}}\tilde{\psi }\left(z\right)=s\tilde{\omega }{a}^{†}\tilde{\psi }\left(z\right),(17)$

where $s\tilde{\omega }\tilde{\psi }={\tilde{H}}_{\text{eff}}\tilde{\psi }$. Since the a (a^†) operation on the eigenfunction of $H_{\text{eff}}({\tilde{H}}_{\text{eff}})$ is the eigenfunction of ${\tilde{H}}_{\text{eff}}(H_{\text{eff}})$, we can switch the problem to its SUSY partner which turn out to be easier to tackle than the original one.

FIGURE 3

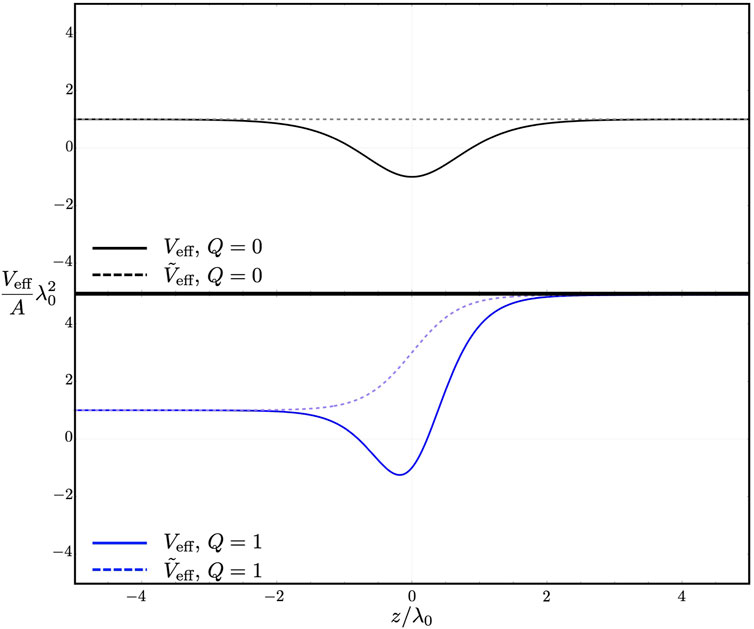
FIGURE 3. The effective potentials V_eff and their SUSY partners ${\tilde{V}}_{\text{eff}}$ for an incoming magnon through the z-axis. The solid (dashed) lines represent the effective potential $V_{\text{eff}}({\tilde{V}}_{\text{eff}})$. The black lines represent the cases of Q = 0 and the blue lines represent the cases of Q = −1. Here, we assume that ρ = λ₀.

2.4 Bound Magnon Modes

One can obtain the bound state solution by solving aψ (z) = 0, which is given by

$\psi {\left(z\right)}_b=\text{sech}\left(\frac{z-Z}{\lambda }\right)e^{\frac{Ql\lambda }{{\rho }^2}z},(18)$

${\omega }_b=\frac{A{l}^2}{s{\rho }^2}\left[1-\frac{Q^2{\lambda }^2}{{\rho }^2}\right],(19)$

where ω_b is the frequency of the bound solution. The condition of normalizability is |l| < ρ²/(|Q|λ²). This mode is local [60, 61] and the magnon position δ obeys

$\tanh \left(\frac{\delta -Z}{\lambda }\right)=\frac{Ql{\lambda }^2}{{\rho }^2},(20)$

where the position is defined as the maximum position of wavefunction’s amplitude. Figure 4 shows the positions of bound magnons schematically, the white lines are trajectories of bound magnon. Note that, for the non-zero Skyrmion charge, the bound modes with different l are separated [47, 53, 62–65] unlike the bound modes with Q = 0 [66, 67].

FIGURE 4

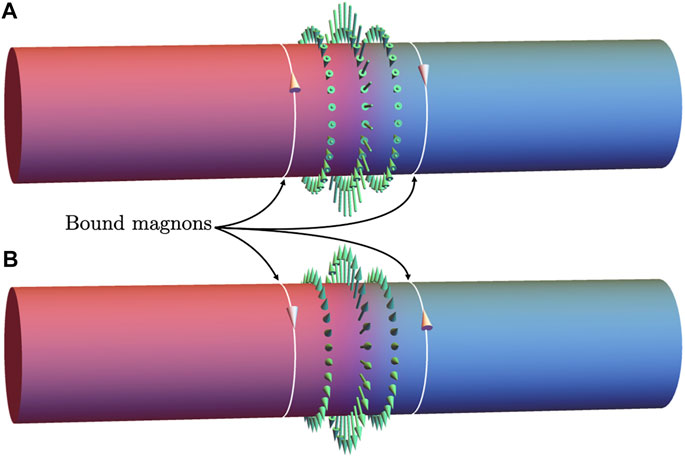
FIGURE 4. Bound magnon modes on the Skyrmion-textured domain walls whose Skyrmion charges are (A) Q = 1 and (B) Q = −1. The red and blue regions represent the domains whose background magnetizations are ${\mathbf{m}}_0=-\widehat{z}$ and ${\mathbf{m}}_0=\widehat{z}$, respectively. White lines represent the bound modes and green arrows represent the emergent magnetic field.

2.5 Propagating Magnon Modes

Let us consider a scattering problem of the spin wave. We now can write the wavefunction ψ (z) as

$\psi \left(z\to -\infty \right)\sim e^{i{k}_{-}z}+r{e}^{-i{k}_{-}z},(21)$

$\psi \left(z\to +\infty \right)\sim t{e}^{i{k}_{+}z},(22)$

where

$k_{+}=\sqrt{k_{-}^2-4\frac{|Ql|}{{\rho }^2}}(23)$

and k₋ is the wavenumber of the incoming magnon. Because of the asymmetric potential, wavenumbers of incoming and outgoing magnons are different. Using the relations (Eqs 16, 17), we can obtain asymptotic behaviors of the corresponding partner wavefunction:

$\begin{array}{ll}\hfill a\psi \left(z\to -\infty \right)& \sim \left[i{k}_{-}-\frac{1}{\lambda }+\beta \right]e^{i{k}_{-}z}\hfill \\ \hfill & +r\left[-i{k}_{-}-\frac{1}{\lambda }+\beta \right]e^{-i{k}_{-}z},\hfill \end{array}(24)$

$a\psi \left(z\to +\infty \right)\sim t\left[i{k}_{+}+\frac{1}{\lambda }+\beta \right]e^{i{k}_{+}z}.(25)$

Then we can check the fact that the reflection probabilities of original and partner potentials are equivalent:

${\tilde{R}}_k={\left|\frac{-i{k}_{-}-\frac{1}{\lambda }+\beta }{i{k}_{-}-\frac{1}{\lambda }+\beta }\right|}^2|r{|}^2=|r{|}^2=R_k,(26)$

where $R_k({\tilde{R}}_k)$ is the reflection probability of the original (partner) potential. Now the problem is simplified as a hyperbolic-tangent-potential-barrier problem which is exactly solvable. The reflection probability of the SUSY partner is given by

$R_k=\left\{\begin{array}{cc}\frac{{\sinh }^2\left(\frac{\pi \lambda }{2}\left(k_{-}-k_{+}\right)\right)}{{\sinh }^2\left(\frac{\pi \lambda }{2}\left(k_{-}+k_{+}\right)\right)},\hfill & \text{if\hspace{0.17em}}{k}_{-}>\frac{2}{\rho }\sqrt{|Ql|}\hfill \\ 1,\hfill & \text{if\hspace{0.17em}}{k}_{-}<\frac{2}{\rho }\sqrt{|Ql|}\hfill \end{array}\right.(27)$

[68–71]. Here, we use the Euler’s reflection formula [72] to simplify the reflection probability. We can assume that l is negative and Q is positive, without loss of generality, since the reflection probability is symmetric under the exchange of k₋, k₊. The transmission probability is determined by T_k = 1−R_k for both Hamiltonians. Figure 5 illustrates trajectories of reflected, transmitted, and incoming spin waves.

FIGURE 5

FIGURE 5. Magnon scattering due to the Skyrmion-textured domain wall. The red and blue regions represent the domains whose background magnetizations are ${\mathbf{m}}_0=-\widehat{z}$ and ${\mathbf{m}}_0=\widehat{z}$, respectively. The spin wave coming from z = −∞ with non-zero l scatters with the Skyrmion-textured domain wall. Finite amount of the incoming spin wave is reflected.

The wavefuntion Ψ is defined in the spatially varying local frame $\{\widehat{\theta },\widehat{\varphi },{\mathbf{m}}_0\}$ (Eq. 8). Thus, to see scattering properties of the magnon in the laboratory frame, we obtain wavefunction in the laboratory frame. Since there are two domains, local axis of a moving magnon is flipped passing by the domain wall and it makes difference between functional forms of incoming and outgoing wavefunctions:

$\begin{array}{cc}\hfill {\psi }_{\text{Lab}}^{\text{in}}& =\delta \mathbf{m}\cdot \left(\widehat{x}+i\widehat{y}\right)=\left(-1\right)\mathrm{\Psi }{e}^{i{\varphi }_0}\text{as}z\to -\infty \hfill \\ \hfill & \sim \psi \left(z\right)e^{i\left(\left(l+Q\right)\phi -\omega t\right)},\hfill \\ \hfill {\psi }_{\text{Lab}}^{\text{out}}& =\delta \mathbf{m}\cdot \left(\widehat{x}-i\widehat{y}\right)=\mathrm{\Psi }{e}^{-i{\varphi }_0}\text{as}z\to +\infty \hfill \\ \hfill & \sim \psi \left(z\right)e^{i\left(\left(l-Q\right)\phi -\omega t\right)},\hfill \end{array}(28)$

up to constant phase factors ³. Since Φ₀ = Q (φ−ϒ) + Φ, orbital wavenumbers of incoming and outgoing magnons are different. An orbital angular momentum of a transmitted magnon is changed from ℏ (l + Q) to ℏ (l−Q). Hence the change of magnon’s orbital angular momentum after passing the domain wall is Δl_z = −2ℏQ and orbital-transfer torque applying to the domain wall per magnon is 2ℏQ. The resultant torque derived from the calculation by SUSY QM is consistent with the result from the emergent field dynamics of Section 2.2. This is one of our main results: By using a Skyrmion-textured domain wall, we can generate an orbital angular momentum of a magnon.

3 Magnon-Driven Domain Wall Dynamics

Here, we study the dynamics of a skyrmion-textured domain wall driven by a magnon current. As shown in Section 2.5, the orbital angular momentum of a magnon on the domain wall varies due to the interaction of the magnon and the background domain wall. Analogous to Newton’s third law, which is also known as the action-reaction law, the domain-wall position is shifted to compensate the change of angular momentum of magnon traversing the domain wall. In order to describe the low energy dynamics of the domain wall, we introduce the two variables Z, Ξ ≡Φ−Qϒ as collective coordinates. The linear momentum, spin angular momentum and orbital angular momentum are expressed as linear functions of the collective coordinates [25, 73].

$P_z=-4\pi \rho s\mathrm{\Xi },(29)$

$S_z=4\pi \rho sZ,(30)$

$L_z=-4\pi \rho sQZ.(31)$

Note that angular momenta are linearly dependent on the domain wall position Z and the orbital angular momentum is proportional to the Skyrimon charge Q.

The continuity equation of the magnon wavefunction can be written as

$\frac{\partial }{\partial t}\left({\mathrm{\Psi }}^{*}\mathrm{\Psi }\right)+\nabla \cdot \mathbf{j}=0,(32)$

where j is the corresponding current. From the Eq. 9 and Eq. (10), we obtain the z-component of j

$j_z=\frac{2Ak}{s}|\mathcal{A}{|}^2,(33)$

where $\mathcal{A}$ and k are the amplitude and wavenumber of a plane wave Ψ. To connect |Ψ|² to the magnon number density, we see the longitudinal fluctuation of m (Eq. 5), the reduction of the longitudinal component due to the magnon is given by

$\mathrm{\Delta }{m}_l=1-\sqrt{1-|\delta \mathbf{m}{|}^2}\approx \frac{1}{2}|\delta \mathbf{m}{|}^2=\frac{1}{2}|\mathcal{A}{|}^2.(34)$

Then the reduction of spin density is sΔm_l and it must be the ℏ times magnon number density. Consequently, plugging the relation sΔm_l = ℏσ into the Eq. 34, the magnon number density σ_m is given by

${\sigma }_m=\frac{s}{2\hslash }|\mathcal{A}{|}^2.(35)$

Finally, we obtain the z-component of the number density current

$j_m=j_z\frac{s}{2\hslash }=\frac{Ak}{\hslash }|\mathcal{A}{|}^2.(36)$

Since we know the angular momentum exchange per magnon, we can obtain the torque using the magnon number density current (Eq. 36). The magnonic orbital-transfer torque for the given number density current j_m and magnon wavenumber k is given by

$F_L={\int }_0^{2\pi }d\phi \rho j_m{T}_{k}2\hslash Q=4\pi \rho Ak|\mathcal{A}{|}^2{T}_{k}Q,(37)$

where T_k is the transmission probability and 2ℏQ is the orbital-transfer torque per magnon. Here, the factor T_k is present since only the magnons passing through the domain wall exert the torque. Similarly, the magnonic force and the magnonic spin-transfer torque are given by

$F_P=4\pi \rho Ak|\mathcal{A}{|}^2\left[\frac{T_k}{2}\left(k-k^{\prime }\right)+R_{k}k\right],(38)$

$F_S=-4\pi \rho Ak|\mathcal{A}{|}^2{T}_k,(39)$

where k′ is the wavenumber of the transmitted magnon. Including the Rayleigh dissipation, Euler-Lagrange equations for the collective coordinates are given by [25].

$4\pi \rho s\dot{Z}+4\pi \rho \alpha s\lambda \dot{\mathrm{\Xi }}=F_s,(40)$

$-4\pi \rho sQ\dot{Z}-4\pi \rho \alpha s\lambda Q\dot{\mathrm{\Xi }}=F_L,(41)$

$-4\pi \rho s\dot{\mathrm{\Xi }}+4\pi \rho \alpha s\frac{1}{\lambda }\dot{Z}=F_P.(42)$

Solving these equations, the magnon-driven domain-wall velocity is expressed as

$\dot{Z}=-\frac{Ak}{s\left(1+{\alpha }^2\right)}|\mathcal{A}{|}^2\left[T_k+\alpha \lambda \left(\frac{T_k}{2}\left(k-k^{\prime }\right)+R_{k}k\right)\right],(43)$

where k and k′ are wavenumbers of incoming and outgoing magnons, respectively.

In Figure 6, we consider the velocity of the domain wall driven by the magnon beam which is coming from the left end (z = −∞) and moving parallel to the z-axis. Here, we assume α = 0.1, $|\mathcal{A}|=0.1,\rho ={\lambda }_0$ and use material constants of Co: A = 31 pJ/m, K = 410 kJ/m³, and s = 8.23 × 10⁻⁶ J⋅s/m³ [74]. Note that the magnon whose wavenumber is smaller than $2\sqrt{|Ql|}/\rho$ is totally reflected. The orbital angular momentum and spin angular momentum of the totally reflected magnon are unchanged by the scattering and thus the domain wall maintains its position.

FIGURE 6

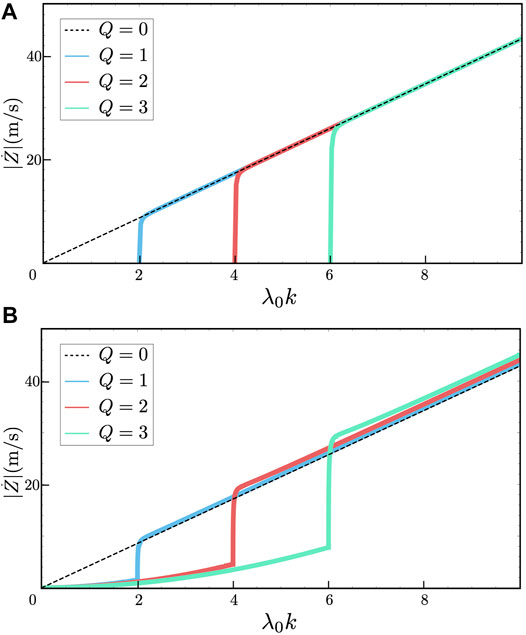
FIGURE 6. Domain-wall velocity $\dot{Z}$ as a function of wavenumber λ₀k in the (A) absence of the damping α = 0 and in the (B) presence of the damping α = 0.1. The dashed line represents the domain-wall velocity without considering reflection which is equivalent to the case of Q = 0. The blue (red, green) line is the velocity (Eq. 43) with Q = 1 (Q = 2, Q = 3).

4 Summary and Discussion

We have shown that a magnon moving in a curved geometry can exchange its orbital angular momentum with the background magnetic texture. In particular, the Skyrmion-textured domain wall in the ferromagnetic nanotube generates the Lorentz force on the moving magnon, whereby we have verified the orbital-angular-momentum exchange between the magnon and the domain wall by solving the Hamiltonian with the aid of SUSY QM. We have investigated the reflection property of the magnon-domain-wall scattering. An analytic form of the reflection probability is obtained. We have also shown that a magnon whose wavenumber is lower than the critical wavenumber is totally reflected. The critical wavenumber is discretized by the Skyrmion charge of the domain wall.

An orbital angular momentum of a magnon can be used to carry additional information. Since the orbital angular momentum of the magnon can be generated and tuned by the domain wall with the Skyrmion-charge, the Skyrmion-textured domain wall may find its role in magnon-based devices. Due to the orbital symmetry, the domain wall with a non-zero Skyrmion charge interacts weakly with an external magnetic field in comparison to an ordinary domain wall [25]. Moreover, the domain wall with the Skyrmion charge is topologically stable in the cylindrical geometry. These properties support the technological utility of the Skyrmion-textured domain wall.

Magnons have been known to pass through the domain wall without reflection in a quasi-one-dimensional wire. We have shown that this does not hold for a domain wall with the Skyrmion charge. The Skyrmion-textured domain wall induces the effective potential for magnons and it is reflective. The magnon whose wavenumber is below the critical value is totally reflected and the critical wavenumber is proportional to the Skyrmion charge. Therefore the domain wall can play a role of a magnon filter.

In this work, we have neglected the effects of the thermal noise that are present at finite temperatures [75–78] and the effects of the Dzyaloshinskii-Moriya interaction that can exist if the inversion symmetry of the system is broken [79, 80]. The former can affect the stabilization of the Skyrmion-textured domain wall at elevated temperatures and the latter can also modify our results appreciably. The investigation of these effect is beyond the scope of the current work. We would also like to mention that we neglect the spin-inertia effects that add the second-order time derivative term to the LLG equation [81–85], which has been generally thought to be important only at the ultrafast time scales of the order of THz and beyond, but has recently been shown to be able to significantly affect the GHz-scale switching behavior of nanoscale ferromagnets via the long-term nutation dynamics [86]. We leave the investigation of the effects of the spin inertia on our results as a future research topic.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SL and SKK conceived the idea of the research, conducted theoretical analysis, and wrote the manuscript.

Funding

SL and SKK were supported by Brain Pool Plus Program through the National Research Foundation of Korea funded by the Ministry of Science and ICT (NRF-2020H1D3A2A03099291), by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2021R1C1C1006273), and by the National Research Foundation of Korea funded by the Korea Government via the SRC Center for Quantum Coherence in Condensed Matter (NRF-2016R1A5A1008184).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge the enlightening discussions with Gyungchoon Go.

Footnotes

¹Considering the Gilbert damping, the wave equation is modified as (i−α) s∂_tΨ = HΨ.

²The potential V is ignored while we calculate the Lorentz force, because the potential V is symmetric with respect to sign-change of z so that the global contribution to orbital angular momentum change is zero. The validity of this approach is confirmed by the result of Section 2.5.

³We notice that the case of l = 0 is not the case of a magnon whose wavevector is parallel to z-axis in the laboratory frame.

References

1. Bloch F. Zur Theorie des Ferromagnetismus. Z Physik (1930) 61:206–19. doi:10.1007/BF01339661

CrossRef Full Text | Google Scholar

2. Holstein T, Primakoff H. Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet. Phys Rev (1940) 58:1098–113. doi:10.1103/PhysRev.58.1098

CrossRef Full Text | Google Scholar

3. Dyson FJ. General Theory of Spin-Wave Interactions. Phys Rev (1956) 102:1217–30. doi:10.1103/PhysRev.102.1217

CrossRef Full Text | Google Scholar

4. Chumak AV, Serga AA, Hillebrands B. Magnon Transistor for All-Magnon Data Processing. Nat Commun (2014) 5:1–8. doi:10.1038/ncomms5700

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Chumak AV, Vasyuchka VI, Serga AA, Hillebrands B. Magnon Spintronics. Nat Phys (2015) 11:453–61. doi:10.1038/nphys3347

CrossRef Full Text | Google Scholar

6. Serga AA, Chumak AV, Hillebrands B. YIG Magnonics. J Phys D: Appl Phys (2010) 43:264002. doi:10.1088/0022-3727/43/26/264002

CrossRef Full Text | Google Scholar

7. Demidov VE, Urazhdin S, Anane A, Cros V, Demokritov SO. Spin-orbit-torque Magnonics. J Appl Phys (2020) 127:170901. doi:10.1063/5.0007095

CrossRef Full Text | Google Scholar

8. Khitun A, Bao M, Wang KL. Magnonic Logic Circuits. J Phys D: Appl Phys (2010) 43:264005. doi:10.1088/0022-3727/43/26/264005

CrossRef Full Text | Google Scholar

9. Chumak AV, Serga AA, Hillebrands B. Magnonic Crystals for Data Processing. J Phys D: Appl Phys (2017) 50:244001. doi:10.1088/1361-6463/aa6a65

CrossRef Full Text | Google Scholar

10. Csaba G, Papp Á, Porod W. Perspectives of Using Spin Waves for Computing and Signal Processing. Phys Lett A (2017) 381:1471–6. doi:10.1016/j.physleta.2017.02.042

CrossRef Full Text | Google Scholar

11. Berger L. Emission of Spin Waves by a Magnetic Multilayer Traversed by a Current. Phys Rev B (1996) 54:9353–8. doi:10.1103/PhysRevB.54.9353

CrossRef Full Text | Google Scholar

12. Slonczewski JC. Current-driven Excitation of Magnetic Multilayers. J Magnetism Magn Mater (1996) 159:L1–L7. doi:10.1016/0304-8853(96)00062-5

CrossRef Full Text | Google Scholar

13. Jiang W, Upadhyaya P, Fan Y, Zhao J, Wang M, Chang L-T, et al. Direct Imaging of Thermally Driven Domain wall Motion in Magnetic Insulators. Phys Rev Lett (2013) 110:1–5. doi:10.1103/PhysRevLett.110.177202

CrossRef Full Text | Google Scholar

14. Han J, Zhang P, Hou JT, Siddiqui SA, Liu L. Mutual Control of Coherent Spin Waves and Magnetic Domain walls in a Magnonic Device. Science (2019) 366:1121–5. doi:10.1126/science.aau2610

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Tu KN, Liu Y, Li M. Effect of Joule Heating and Current Crowding on Electromigration in mobile Technology. Appl Phys Rev (2017) 4:011101. doi:10.1063/1.4974168

CrossRef Full Text | Google Scholar

16. Yu H, Xiao J, Schultheiss H. Magnetic Texture Based Magnonics. Phys Rep (2021) 905:1–59. doi:10.1016/j.physrep.2020.12.004

CrossRef Full Text | Google Scholar

17. Lenk B, Ulrichs H, Garbs F, Münzenberg M. The Building Blocks of Magnonics. Phys Rep (2011) 507:107–36. doi:10.1016/j.physrep.2011.06.003

CrossRef Full Text | Google Scholar

18. Kruglyak VV, Demokritov SO, Grundler D. Magnonics. J Phys D: Appl Phys (2010) 43:264001. doi:10.1088/0022-3727/43/26/264001

CrossRef Full Text | Google Scholar

19. Yan P, Wang XS, Wang XR. All-magnonic Spin-Transfer Torque and Domain wall Propagation. Phys Rev Lett (2011) 107:1–5. doi:10.1103/PhysRevLett.107.177207

CrossRef Full Text | Google Scholar

20. Jia C, Ma D, Schäffer AF, Berakdar J. Twisted Magnon Beams Carrying Orbital Angular Momentum. Nat Commun (2019) 10:2077. doi:10.1038/s41467-019-10008-3

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Streubel R, Fischer P, Kronast F, Kravchuk VP, Sheka DD, Gaididei Y, et al. Magnetism in Curved Geometries. J Phys D: Appl Phys (2016) 49:363001. doi:10.1088/0022-3727/49/36/363001

CrossRef Full Text | Google Scholar

22. Hertel R. Ultrafast Domain wall Dynamics in Magnetic Nanotubes and Nanowires. J Phys Condens Matter (2016) 28:483002. doi:10.1088/0953-8984/28/48/483002

PubMed Abstract | CrossRef Full Text | Google Scholar

23. González AL, Landeros P, Núñez ÁS. Spin Wave Spectrum of Magnetic Nanotubes. J Magnetism Magn Mater (2010) 322:530–5. doi:10.1016/j.jmmm.2009.10.010

CrossRef Full Text | Google Scholar

24. Yan M, Andreas C, Kákay A, García-Sánchez F, Hertel R. Fast Domain wall Dynamics in Magnetic Nanotubes: Suppression of Walker Breakdown and Cherenkov-like Spin Wave Emission. Appl Phys Lett (2011) 99:122505–11. doi:10.1063/1.3643037

CrossRef Full Text | Google Scholar

25. Lee S, Kim SK. Orbital Angular Momentum and Current-Induced Motion of a Topologically Textured Domain wall in a Ferromagnetic Nanotube. Phys Rev B (2021) 104:L140401. doi:10.1103/PhysRevB.104.L140401

CrossRef Full Text | Google Scholar

26. Landeros P, Núñez ÁS. Domain wall Motion on Magnetic Nanotubes. J Appl Phys (2010) 108:033917. doi:10.1063/1.3466747

CrossRef Full Text | Google Scholar

27. Jia C, Chen M, Schäffer AF, Berakdar J. Chiral Logic Computing with Twisted Antiferromagnetic Magnon Modes. Npj Comput Mater (2021) 7:101. doi:10.1038/s41524-021-00570-0

CrossRef Full Text | Google Scholar

28. Jiang Y, Yuan HY, Li Z-X, Wang Z, Zhang HW, Cao Y, et al. Twisted Magnon as a Magnetic Tweezer. Phys Rev Lett (2020) 124:217204. doi:10.1103/PhysRevLett.124.217204

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang X, Wang XS, Wang C, Yang H, Cao Y, Yan P. Current-induced Skyrmion Motion on Magnetic Nanotubes. J Phys D: Appl Phys (2019) 52:225001. doi:10.1088/1361-6463/ab0c64

CrossRef Full Text | Google Scholar

30. Hurst J, De Riz A, Staňo M, Toussaint J-C, Fruchart O, Gusakova D. Theoretical Study of Current-Induced Domain wall Motion in Magnetic Nanotubes with Azimuthal Domains. Phys Rev B (2021) 103:1–13. doi:10.1103/physrevb.103.024434

CrossRef Full Text | Google Scholar

31. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Molina-Terriza G, Torres JP, Torner L. Twisted Photons. Nat Phys (2007) 3:305–10. doi:10.1038/nphys607

CrossRef Full Text | Google Scholar

33. Marrucci L, Manzo C, Paparo D. Optical Spin-To-Orbital Angular Momentum Conversion in Inhomogeneous Anisotropic Media. Phys Rev Lett (2006) 96:163905. doi:10.1103/PhysRevLett.96.163905

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Tamburini F, Thidé B, Molina-Terriza G, Anzolin G. Twisting of Light Around Rotating Black Holes. Nat Phys (2011) 7:195–7. doi:10.1038/nphys1907

CrossRef Full Text | Google Scholar

35. Elias NM. Photon Orbital Angular Momentum in Astronomy. A&A (2008) 492:883–922. doi:10.1051/0004-6361:200809791

CrossRef Full Text | Google Scholar

36. Karakhanyan V, Eustache C, Lefier Y, Grosjean T. Inverse Faraday Effect from the Orbital Angular Momentum of Light. Phys Rev B (2021) 105:045406. doi:10.1103/PhysRevB.105.045406

CrossRef Full Text | Google Scholar

37. Nakane JJ, Kohno H. Angular Momentum of Phonons and its Application to Single-Spin Relaxation. Phys Rev B (2018) 97:174403. doi:10.1103/PhysRevB.97.174403

CrossRef Full Text | Google Scholar

38. Garanin DA, Chudnovsky EM. Angular Momentum in Spin-Phonon Processes. Phys Rev B (2015) 92:024421. doi:10.1103/PhysRevB.92.024421

CrossRef Full Text | Google Scholar

39. Rückriegel A, Streib S, Bauer GEW, Duine RA. Angular Momentum Conservation and Phonon Spin in Magnetic Insulators. Phys Rev B (2020) 101:1–14. doi:10.1103/PhysRevB.101.104402

CrossRef Full Text | Google Scholar

40. Cappelletti RL, Jach T, Vinson J. Intrinsic Orbital Angular Momentum States of Neutrons. Phys Rev Lett (2018) 120:090402. doi:10.1103/PhysRevLett.120.090402

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Clark CW, Barankov R, Huber MG, Arif M, Cory DG, Pushin DA. Controlling Neutron Orbital Angular Momentum. Nature (2015) 525:504–6. doi:10.1038/nature15265

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Verbeeck J, Tian H, Schattschneider P. Production and Application of Electron Vortex Beams. Nature (2010) 467:301–4. doi:10.1038/nature09366

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Uchida M, Tonomura A. Generation of Electron Beams Carrying Orbital Angular Momentum. Nature (2010) 464:737–9. doi:10.1038/nature08904

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Bialynicki-Birula I, Bialynicka-Birula Z. Gravitational Waves Carrying Orbital Angular Momentum. New J Phys (2016) 18:023022. doi:10.1088/1367-2630/18/2/023022

CrossRef Full Text | Google Scholar

45. Baral P, Ray A, Koley R, Majumdar P. Gravitational Waves with Orbital Angular Momentum. Eur Phys J C (2020) 80:326. doi:10.1140/epjc/s10052-020-7881-2

CrossRef Full Text | Google Scholar

46. Yang W, Yang H, Cao Y, Yan P. Photonic Orbital Angular Momentum Transfer and Magnetic Skyrmion Rotation. Opt Express (2018) 26:8778. doi:10.1364/OE.26.008778

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Kim SK, Nakata K, Loss D, Tserkovnyak Y. Tunable Magnonic Thermal Hall Effect in Skyrmion Crystal Phases of Ferrimagnets. Phys Rev Lett (2019) 122:057204. doi:10.1103/PhysRevLett.122.057204

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Cooper F, Khare A, Sukhatme U. Supersymmetry and Quantum Mechanics. Phys Rep (1995) 251:267–385. doi:10.1016/0370-1573(94)00080-M

CrossRef Full Text | Google Scholar

49. Sukumar CV. Supersymmetric Quantum Mechanics of One-Dimensional Systems. J Phys A: Math Gen (1985) 18:2917–36. doi:10.1088/0305-4470/18/15/020

CrossRef Full Text | Google Scholar

50. Einstein A, de Haas WJ. Experimenteller Nachweis der Ampèreschen Molekularströme. Dtsch Phys Gesellschaft (1915) 17:152–70.

Google Scholar

51. Landau LD, Lifshitz E. On the Theory of the Dispersion of Magnetic Permeability in Ferromagnetic Bodies. Phys Z Sowjet (1935) 8:153.

Google Scholar

52. Kovalev AA, Tserkovnyak Y. Thermomagnonic Spin Transfer and Peltier Effects in Insulating Magnets. EPL (2012) 97:67002. doi:10.1209/0295-5075/97/67002

CrossRef Full Text | Google Scholar

53. Schütte C, Garst M. Magnon-skyrmion Scattering in Chiral Magnets. Phys Rev B (2014) 90:094423. doi:10.1103/PhysRevB.90.094423

CrossRef Full Text | Google Scholar

54. Qaiumzadeh A, Kristiansen LA, Brataas A. Controlling Chiral Domain walls in Antiferromagnets Using Spin-Wave Helicity. Phys Rev B (2018) 97:020402. doi:10.1103/PhysRevB.97.020402

CrossRef Full Text | Google Scholar

55. Nakata K, Ohnuma Y. Magnonic thermal Transport Using the Quantum Boltzmann Equation. Phys Rev B (2021) 104:1–8. doi:10.1103/physrevb.104.064408

CrossRef Full Text | Google Scholar

56. Nagaosa N, Tokura Y. Emergent Electromagnetism in Solids. Phys Scr (2012) T146:014020. doi:10.1088/0031-8949/2012/T146/014020

CrossRef Full Text | Google Scholar

57. Rosen N, Morse PM. On the Vibrations of Polyatomic Molecules. Phys Rev (1932) 42:210–7. doi:10.1103/PhysRev.42.210

CrossRef Full Text | Google Scholar

58. Pöschl G, Teller E. Bemerkungen zur Quantenmechanik des anharmonischen Oszillators. Z Physik (1933) 83:143–51. doi:10.1007/BF01331132

CrossRef Full Text | Google Scholar

59. Lekner J. Reflectionless Eigenstates of the Sech2 Potential. Am J Phys (2007) 75:1151–7. doi:10.1119/1.2787015

CrossRef Full Text | Google Scholar

60. Sheka DD, Ivanov BA, Mertens FG. Internal Modes and Magnon Scattering on Topological Solitons in Two-Dimensional Easy-axis Ferromagnets. Phys Rev B (2001) 64:024432. doi:10.1103/PhysRevB.64.024432

CrossRef Full Text | Google Scholar

61. Ivanov BA, Sheka DD. Local Magnon Modes and the Dynamics of a Small-Radius Two-Dimensional Magnetic Soliton in an Easy-axis Ferromagnet. Jetp Lett (2005) 82:436–40. doi:10.1134/1.2142872

CrossRef Full Text | Google Scholar

62. Díaz SA, Klinovaja J, Loss D. Topological Magnons and Edge States in Antiferromagnetic Skyrmion Crystals. Phys Rev Lett (2019) 122:187203. doi:10.1103/PhysRevLett.122.187203

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Díaz SA, Hirosawa T, Klinovaja J, Loss D. Chiral Magnonic Edge States in Ferromagnetic Skyrmion Crystals Controlled by Magnetic fields. Phys Rev Res (2020) 2:013231. doi:10.1103/PhysRevResearch.2.013231

CrossRef Full Text | Google Scholar

64. Van Hoogdalem KA, Tserkovnyak Y, Loss D. Magnetic Texture-Induced thermal Hall Effects. Phys Rev B (2013) 87:1–7. doi:10.1103/PhysRevB.87.024402

CrossRef Full Text | Google Scholar

65. Lin S-Z, Batista CD, Saxena A. Internal Modes of a Skyrmion in the Ferromagnetic State of Chiral Magnets. Phys Rev B (2014) 89:1–7. doi:10.1103/PhysRevB.89.024415

CrossRef Full Text | Google Scholar

66. Zhang B, Wang Z, Cao Y, Yan P, Wang XR. Eavesdropping on Spin Waves inside the Domain-wall Nanochannel via Three-Magnon Processes. Phys Rev B (2018) 97:94421. doi:10.1103/PhysRevB.97.094421

CrossRef Full Text | Google Scholar

67. Wang XS, Wang XR. Thermodynamic Theory for thermal-gradient-driven Domain-wall Motion. Phys Rev B (2014) 90:1–4. doi:10.1103/PhysRevB.90.014414

CrossRef Full Text | Google Scholar

68. Gadella M, Kuru Ş, Negro J. The Hyperbolic Step Potential: Anti-bound States, SUSY Partners and Wigner Time Delays. Ann Phys (2017) 379:86–101. doi:10.1016/j.aop.2017.02.013

CrossRef Full Text | Google Scholar

69. Boonserma P, Visserb M. Quasi-normal Frequencies: Key Analytic Results. J High Energ Phys. (2011) 2011. doi:10.1007/JHEP03(2011)073

CrossRef Full Text | Google Scholar

70. Kim SK, Tserkovnyak Y, Tchernyshyov O. Propulsion of a Domain wall in an Antiferromagnet by Magnons. Phys Rev B (2014) 90:1–15. doi:10.1103/PhysRevB.90.104406

CrossRef Full Text | Google Scholar

71. Khare A. Supersymmetry in Quantum Mechanics. Pramana - J Phys (1997) 49:41–64. doi:10.1007/BF02856337

CrossRef Full Text | Google Scholar

72. Dence TP, Dence JB. A Survey of Euler's Constant. Maths Mag (2009) 82:255–65. doi:10.4169/193009809X468689

CrossRef Full Text | Google Scholar

73. Tatara G, Kohno H, Shibata J. Microscopic Approach to Current-Driven Domain wall Dynamics. Phys Rep (2008) 468:213–301. doi:10.1016/j.physrep.2008.07.003

CrossRef Full Text | Google Scholar

74. Coey JMD. Magnetism and Magnetic Materials. Cambridge: Cambridge University Press (2001). doi:10.1017/CBO9780511845000

CrossRef Full Text | Google Scholar

75. Kubo R, Hashitsume N. Brownian Motion of Spins. Prog Theor Phys Suppl (1970) 46:210–20. doi:10.1143/ptps.46.210

CrossRef Full Text | Google Scholar

76. García-Palacios JL, Lázaro FJ. Langevin-dynamics Study of the Dynamical Properties of Small Magnetic Particles. Phys Rev B (1998) 58:14937–58. doi:10.1103/PhysRevB.58.14937

CrossRef Full Text | Google Scholar

77. Kim SK, Tchernyshyov O, Tserkovnyak Y. Thermophoresis of an Antiferromagnetic Soliton. Phys Rev B (2015) 92:020402. doi:10.1103/PhysRevB.92.020402

CrossRef Full Text | Google Scholar

78. Kovalev AA. Skyrmionic Spin Seebeck Effect via Dissipative Thermomagnonic Torques. Phys Rev B (2014) 89:241101. doi:10.1103/PhysRevB.89.241101

CrossRef Full Text | Google Scholar

79. Dzyaloshinsky I. A Thermodynamic Theory of “Weak” Ferromagnetism of Antiferromagnetics. J Phys Chem Sol (1958) 4:241–55. doi:10.1016/0022-3697(58)90076-3

CrossRef Full Text | Google Scholar

80. Moriya T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys Rev (1960) 120:91–8. doi:10.1103/PhysRev.120.91

CrossRef Full Text | Google Scholar

81. Ciornei M-C, Rubí JM, Wegrowe J-E. Magnetization Dynamics in the Inertial Regime: Nutation Predicted at Short Time Scales. Phys Rev B (2011) 83:020410. doi:10.1103/PhysRevB.83.020410

CrossRef Full Text | Google Scholar

82. Wegrowe J-E, Ciornei M-C. Magnetization Dynamics, Gyromagnetic Relation, and Inertial Effects. Am J Phys (2012) 80:607–11. doi:10.1119/1.4709188

CrossRef Full Text | Google Scholar

83. Mondal R, Kamra A. Spin Pumping at Terahertz Nutation Resonances. Phys Rev B (2021) 104:214426. doi:10.1103/PhysRevB.104.214426

CrossRef Full Text | Google Scholar

84. Böttcher D, Henk J. Significance of Nutation in Magnetization Dynamics of Nanostructures. Phys Rev B (2012) 86:020404. doi:10.1103/PhysRevB.86.020404

CrossRef Full Text | Google Scholar

85. Neeraj K, Awari N, Kovalev S, Polley D, Zhou Hagström N, Arekapudi SSPK, et al. Inertial Spin Dynamics in Ferromagnets. Nat Phys (2021) 17:245–50. doi:10.1038/s41567-020-01040-y

CrossRef Full Text | Google Scholar

86. Rahman R, Bandyopadhyay S. An Observable Effect of Spin Inertia in Slow Magneto-Dynamics: Increase of the Switching Error Rates in Nanoscale Ferromagnets. J Phys Condens Matter (2021) 33:355801. doi:10.1088/1361-648X/ac0cb4

CrossRef Full Text | Google Scholar