A Numerical Investigation of Thermal-Induced Explosive Spalling Behavior of a Concrete Material Using Cohesive Interface Model

Thermal-induced spalling is a typical failure behavior of concrete materials exposed to high temperatures. This study uses Abaqus to establish a numerical model of concrete material comprising aggregates and mortar matrix. Cohesive elements considering heat conduction are embedded into this numerical model to simulate the thermal-induced explosive spalling failure process of the concrete material. Simulation results show that the heat gradually transfers from the outer boundaries to the inner areas with increasing temperature. Thermal stresses concentrate in the aggregates-mortar interfaces, where thermal-induced cracks initiate and propagate. The occurrence of thermal-induced cracks reduces the heat conductivity of mortar, reduces thermal stresses and leads to severe spalling failure in the concrete material. This research provides a practical scheme for the numerical simulation of the thermal-induced spalling behavior of concrete materials.

Introduction

Thermal-induced cracking is the explosive-spalling failure occurred in concrete materials under the high-temperature environment such as fire [1, 2]. Many tests [3–5] show that concrete’s thermal-induced explosive spalling behavior is mainly controlled by two processes [6, 7].

One is the thermal-hydro process [8]. Under high-temperature conditions, free water or crystalline water existing in the concrete pores vaporizes to form vapor pressure. When the accumulated vapor pressure exceeds the tensile strength of mortar material, thermal-induced cracks initiate and propagate to form failure. The other is the thermal-mechanical process [2, 7]. Under high-temperature conditions, the difference of thermal expansion of materials constituting concrete will cause thermal stress concentration. When the concentrated thermal stresses exceed the strength of concrete, it will lead to the failure of concrete materials [7].

Based on the conservation equations [9, 10], scholars have proposed constitutive models to describe high-temperature spalling failure behaviors of concretes. Some researchers considered the thermal-hydro process [11] and proposed thermo-elastoplastic models of concretes [2, 12]. Other scholars have established the coupled thermal-hydro-mechanical constitutive model and formed the multi-physical field coupling theories [13, 14]. These coupled multi-physical constitutive models can better describe the high-temperature spalling failure of concrete and are applied in some engineering practices [2, 15].

Some of these constitutive models are incorporated within the finite element method (FEM) and applied in engineering practices [2, 15]. Scholars [16–18] built the governing equations to describe the high-temperature spalling failure of concretes. In this field, Zhao et al. [16] established a finite element model of two-phase materials (aggregate and mortar), considering the mesostructure characteristics of concrete aggregate. They simulated the temperature, thermal stress, vapor pressure and water transportation in concrete under high-temperature conditions. However, this traditional FEM can only simulate continuous deformation of concretes caused by high temperatures. It is difficult to simulate the thermal-induced fracturing behaviors of concretes.

To simulate thermal-induced cracking behaviors of concretes, the cohesive element-based FEM considering thermal-mechanical coupling process was developed by [19–21]. The cohesive element-base FEM can realistically simulate the discontinuous failure behaviors of concretes during the thermal-induced fracturing process. It can better simulate the thermo-mechanical process of concrete spalling failure at high temperatures. Therefore, this method has good development potential.

In this study, a numerical model of two-phase heterogeneous medium of concrete material is established using Abaqus finite element software. Then, in this numerical model, the cohesive element is embedded. The thermal-mechanical coupling equation is considered in the cohesive element, and the damage model is used to simulate the crack propagation behavior of the cohesive element. The numerical simulation of the high-temperature spalling failure process of concrete is realized.

Theories

Constitutive Model of Cohesive Interface

The crack propagation process at the crack tip of solid material is schematically illustrated in Figure 1A. Accordingly, the mechanical behavior of crack propagation can be described using a cohesive interface model, which is usually abstracted as a cohesive element (see Figure 1B). The stress-displacement relationship of a cohesive interface can be described using the bilinear traction-separation constitutive model, as shown in Figure 1C. This constitutive model is divided into linear stress growth and damage softening stages divided by peak strength. In the two-dimensional problem, Eq. 1 can be used to describe the traction-separation behavior in the pre-peak stage [22]:

$\left\{\begin{array}{c}{\sigma }_{\text{n}}\\ {\tau }_{\text{s}}\end{array}\right\}=\left[\begin{array}{cc}{E}_{\text{nn}}& 0\\ 0& E_{\text{ss}}\end{array}\right]\left\{\begin{array}{c}{\epsilon }_{\text{n}}\\ {\epsilon }_{\text{s}}\end{array}\right\}=\frac{1}{T_0}\left[\begin{array}{cc}{E}_{\text{nn}}& 0\\ 0& E_{\text{ss}}\end{array}\right]\left\{\begin{array}{c}{\delta }_{\text{n}}\\ {\delta }_{\text{s}}\end{array}\right\},(1)$

where ${\sigma }_{\text{n}}$ and ${\tau }_{\text{s}}$ are the nominal traction components: normal and shear stresses, respectively. ${\epsilon }_{\text{n}}$ and ${\epsilon }_{\text{s}}$ are the two components of the nominal strains, respectively. ${\delta }_{\text{n}}$ and ${\delta }_{\text{s}}$ are the separation components: normal and shear displacements, respectively. $T_0$ denotes the original thickness of the cohesive element. $E_{\text{nn}}$ and $E_{\text{ss}}$ are the initial normal and shear stiffness of the interface, respectively.

FIGURE 1

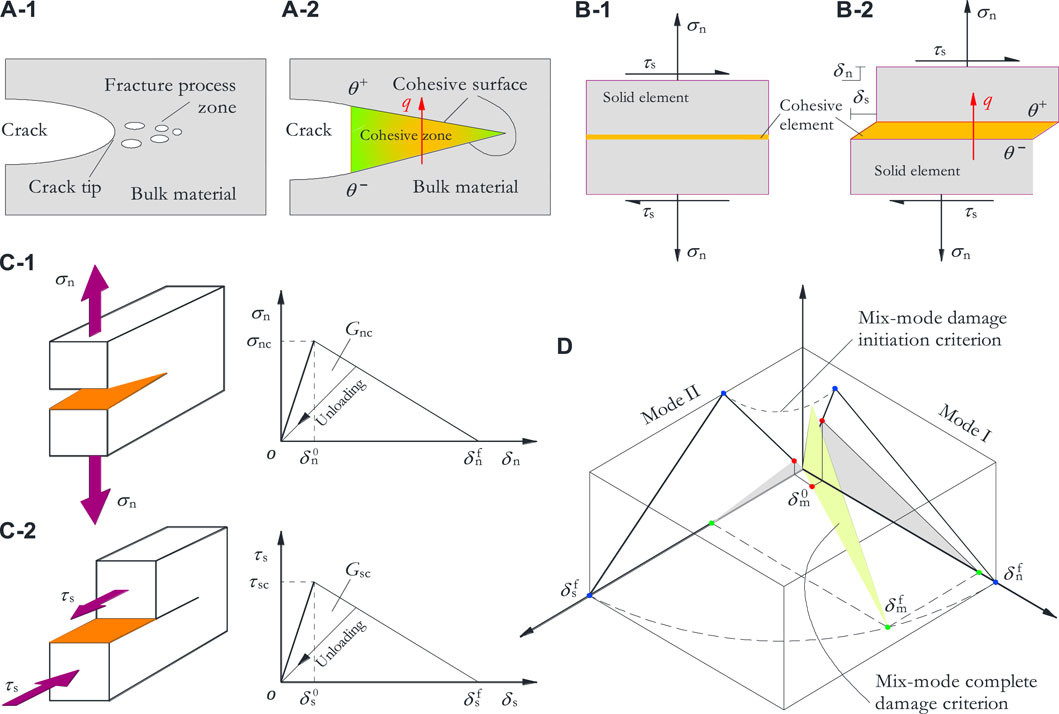
FIGURE 1. (A-1) Fracture process zone; (A-2) Equivalent cohesive interface model [23, 24]; (B) Schematical illustration of thermal-mechanical behavior of cohesive interface model; (C) Bi-linear traction-separation law under Mode I and Mode II fracture of a cohesive interface [25]; (D) Mixed-mode bi-linear traction-separation law of a cohesive interface [25].

When the interface displacement increases to ${\delta }_{\text{n}}^0$ and ${\delta }_{\text{s}}^0$, the interface model is damaged. According to Eq. 1, the displacements of damage initiation can be calculated as follows:

${\delta }_{\text{n}}^0=\frac{{\sigma }_{\text{nc}}}{K_{\text{nn}}}and{\delta }_{\text{s}}^0=\frac{{\tau }_{\text{sc}}}{K_{\text{ss}}},(2)$

where ${\sigma }_{\text{nc}}$ and ${\tau }_{\text{sc}}$ are normal and shear stresses when the cohesive interface reaches the Mode I and Mode II fracture, respectively.

According to the bilinear traction-separation constitutive law shown in Figure 1C, the complete separation displacements ${\delta }_{\text{n}}^{\text{f}}$ and ${\delta }_{\text{s}}^{\text{f}}$ of the cohesive interface can be calculated using the following formula:

${\delta }_{\text{n}}^{\text{f}}=\frac{2G_{\text{n}}}{{\sigma }_{\text{nc}}}and{\delta }_{\text{s}}^{\text{f}}=\frac{2G_{\text{s}}}{{\tau }_{\text{sc}}}(3)$

where $G_{\text{n}}$ and $G_{\text{s}}$ are the critical fracture energy of Mode I and Mode II fracture at the cohesive interface, respectively.

When the traction nominal stress on the cohesive interface meets the maximum stress criterion, it can be considered that the cohesive interface is damaged. The maximum nominal stress criterion of the cohesive interface is used to represent the damage initiation condition, which can be written as:

$\max \left\{\frac{\langle {\sigma }_{\text{n}}\rangle }{{\sigma }_{\text{nc}}},\frac{\langle {\tau }_{\text{s}}\rangle }{{\tau }_{\text{sc}}}\right\}=1,(4)$

where $\langle \rangle$ is the Macaulay bracket. When $x\ge 0$, $\langle x\rangle =x$. When $x<0$, $\langle x\rangle =0$.

When the damage condition described in Eq. 4 are met, the traction stress on the cohesive interface enters the post-peak linear softening stage. A scalar damage variable is used to describe the linear reduction of traction stress at the cohesive interface, which is expressed as follows:

${\sigma }_{\text{n}}=\left(1-D\right){\overline{\sigma }}_{\text{n}}and{\tau }_{\text{s}}=\left(1-D\right){\overline{\tau }}_{\text{s}}(5)$

where ${\overline{\sigma }}_{\text{n}}$ and ${\overline{\tau }}_{\text{s}}$ are nominal traction normal and shear stresses predicted using the traction-separation law without damage.

For the mixed fracture failure mode, as shown in Figure 1D, the bilinear traction-separation law of the cohesive interface is described by the effective relative displacement ${\delta }_{\text{m}}$, which is defined as:

${\delta }_{\text{m}}=\sqrt{{\langle {\delta }_{\text{n}}\rangle }^2+{\delta }_s^2}.(6)$

For linear damage softening, the damage variable can be expressed using the following formula [23]:

$D=\frac{{\delta }_{\text{m}}^{\text{f}}\left({\delta }_m-{\delta }_{\text{m}}^0\right)}{{\delta }_m\left({\delta }_{\text{m}}^{\text{f}}-{\delta }_{\text{m}}^0\right)},(7)$

where ${\delta }_{\text{m}}^0$ and ${\delta }_{\text{m}}^{\text{f}}$ are the effective displacements at damage initiation and complete debonding, respectively.

For the mixed-mode fracture, the mode combination of the cohesive interface can be quantified by defining the relative ratio of normal fracture and shear fracture energies. The fracture energy $G_{\text{n}}$ represents the corresponding traction nominal stress work to its corresponding separation displacement. Thus, the mixed fracture energy $G_{\text{t}}=G_{\text{n}}+G_{\text{s}}$ can be defined. Therefore, the ratios $m_1$ and $m_2$ of normal fracture energy $G_{\text{n}}$ to shear fracture energy $G_{\text{s}}$ can be defined as:

$m_1=\frac{G_{\text{n}}}{G_{\text{t}}}and{m}_2=\frac{G_{\text{s}}}{G_{\text{t}}}.(8)$

The damage evolution of the cohesive interface can be defined according to the fracture energy, which is equal to the area of the geometric region under the traction-separation curve, which can be expressed by $G_{\text{n}}$ and $G_{\text{s}}$, respectively. Based on the power-law fracture criterion, the dependence of fracture energy on mixed-mode can be defined. The power-law fracture criterion is expressed as:

${\left\{\frac{G_{\text{s}}}{G_{\text{n}}^{\text{c}}}\right\}}^{\alpha }+{\left\{\frac{G_{\text{s}}}{G_{\text{s}}^{\text{c}}}\right\}}^{\alpha }=1,(9)$

where $G_{\text{n}}^{\text{C}}$, $G_{\text{s}}^{\text{C}}$ and $\alpha$ are the material constants for describing the fracture behavior of the cohesive interface.

Heat Conduction Crossing Cohesive Interface

The heat conduction between the upper and lower surfaces of the cohesive interface can be considered as a function of the temperature difference between the upper and lower interfaces, which is defined by the following formula:

$q=k_{\text{cz}}\left({\theta }^{+}-{\theta }^{-}\right),(10)$

where $q$ is the heat flux per unit area crossing the cohesive interface. ${\theta }^{+}$ and ${\theta }^{-}$ are the temperatures on the top and bottom surfaces of the cohesive interface. $k_{\text{cz}}$ is the gap conductance of the cohesive zone. Its value depends on the normal separation displacement, i.e. $k_{\text{cz}}=k_{\text{cz}}\left({\delta }_{\text{n}}\right)$. In this study, it is considered that the relationship between gap conductance $k_{\text{cz}}$ and normal separation displacement ${\delta }_{\text{n}}$ can be described using the following piecewise function.

$k_{\text{cz}}=\{\begin{array}{c}{k}_{\text{cz0}}-k{\delta }_{\text{n}},{\delta }_{\text{n}}<k_{\text{cz0}}/k\\ 0,{\delta }_{\text{n}}\ge k_{\text{cz0}}/k\end{array},(11)$

where $k_{\text{cz0}}$ is the thermal conductivity of cohesive interface without any normal separation displacement (${\delta }_{\text{n}}$ = 0), which can be considered to have the same value as the thermal conductivity of surrounding solid material. $k$ is the coefficient that the thermal conductivity of the cohesive region decreases with the increase of separation displacement ${\delta }_{\text{n}}$. When the separation displacement ${\delta }_{\text{n}}$ exceeds the maximum crack width $k_{\text{cz0}}/k$, $k_{\text{cz}}=0$. It is considered that there is no heat conduction between the open cohesive interfaces.

Models

Geometric Model of Concrete Material

Concrete is a heterogeneous composite material. When studying its mechanical behavior, the heterogeneity of concrete can be simplified as a two-phase medium constituting aggregate and mortar matrix. Figure 2A shows the geometric plane model of the concrete specimen, a square area with a side length of 150 mm. The model’s right horizontal and vertical-up directions are the positive x-axis and y-axis, respectively.

FIGURE 2

FIGURE 2. (A) Geometric plane model of a concrete specimen; (B) Numerical model of the concrete specimen; (C) Elements of the cement mortar matrix (element type: CPE3T); (D) Elements of the aggregates (element type: CPE3T); (E) Cohesive elements embedded into the cement mortar matrix (element type: COH2D4T).

In this plane area of the geometric model, as shown in Figure 2A, the computer reconstruction technology proposed in the articles [26, 27] is used to generate aggregates randomly. This study uses polygons to reconstruct the geometric model of aggregates. In order to control the calculation scale, the equivalent diameter of the simulated minimum aggregate particle is greater than 2.36 mm. Aggregates smaller than this size are considered part of the mortar matrix.

In this model, the aggregates are divided into five groups according to the size range in the generated geometric model. The total volume fraction of aggregates in the whole model area is 30%. The aggregate size ranges are (26.5,19.0) with volume fraction of 2.37% (19.0,16.0) with volume fraction of 6.78% (16.0,9.5) with volume fraction of 12.96% (9.5,4.75) with volume fraction of 6.66% and (4.75, 2.36) with volume fraction of 1.23%.

Numerical Model of Concrete Material

In this study, Abaqus is used to carry out coupled thermal-displacement analysis to simulate the thermal-induced spalling failure of the concrete specimen in the high-temperature furnace. The geometric plane model is meshed using the first-order linear plane strain quadrilateral element with a temperature degree of freedom, as shown in Figures 2B,C. The element type is CPE3T. This numerical model has 4244 CPE3T elements and 10,708 nodes.

This study uses the first-order cohesive element, including temperature degrees of freedom, to simulate the spalling failure behavior caused by the thermal stress of concrete under high temperatures. The aggregates are rock particles whose strengths are significantly higher than the mortar matrix. Thus, it is reasonable to consider that the high-temperature spalling failure of concrete occurs only in the cement mortar matrix. Therefore, the cohesive elements are embedded into the area of the cement mortar matrix, as shown in Figure 2D. This model embeds 5,193 cohesive elements, including 10,517 nodes. The cohesive element type is COH2D4T.

Thermal and Mechanical Parameters

In this numerical model, three materials are involved. They are aggregate, cement mortar and cohesive interfaces. The thermal and mechanical behaviors of aggregate and cement mortar are described using a thermo-elastic model, which contains six material parameters: density $\rho$, elastic modulus $E$, Poisson’s ratio $\nu$, thermal expansion coefficient $\alpha$, thermal conductivity $\lambda$ and specific heat capacity $c_{\text{p}}$.

In this study, the high-temperature experiments of concrete materials were not carried out. By referring to the research results of the articles [16, 17, 19, 28], the thermal and mechanical parameters for the numerical simulation are obtained. For aggregate, they are $\rho =2650\text{kg}\cdot {\text{m}}^{-3}$, $E=45\text{GPa}$, $\nu =0.2$, $\alpha =2.0\times {10}^{-5}$, $\lambda =3.0\text{W}\cdot {\text{m}}^{-1}\cdot {\text{K}}^{-1}$ and $c_{\text{p}}=750\text{J}\cdot {\text{kg}}^{-1}\cdot {\text{K}}^{-1}$. For cement mortar, they are $\rho =2200\text{kg}\cdot {\text{m}}^{-3}$, $E=22\text{GPa}$, $\nu =0.22$, $\alpha =1.5\times {10}^{-5}$, $\lambda =1.5\text{W}\cdot {\text{m}}^{-1}\cdot {\text{K}}^{-1}$ and $c_{\text{p}}=1200\text{J}\cdot {\text{kg}}^{-1}\cdot {\text{K}}^{-1}$.

The mechanical behavior of the cohesive interface is described using the traction-separation constitutive model. This model has two elastic parameters: normal traction modulus $E_{\text{nn}}=0.5\text{GPa}$ and tangential traction modulus $E_{\text{ss}}=0.2\text{GPa}$, and five damage parameters: nominal traction normal stress ${\sigma }_{\text{nc}}=1.8\text{MPa}$, nominal traction shear stress ${\tau }_{\text{sc}}=5.2\text{MPa}$, critical fracture energy $G_{\text{n}}=150\text{N}/\text{m}$ for Mode I fracture, critical fracture energy $G_{\text{s}}=1500\text{N}/\text{m}$ for Mode II fracture, and the power exponent $\eta =0.97$ for the power-law fracture criterion. The cohesive interface model has two thermal parameters: initial gap thermal conductivity $k_{\text{cz0}}=1.5\text{W}\cdot {\text{m}}^{-1}\cdot {\text{K}}^{-1}$ and gap thermal conductivity reduction coefficient $k=0.3$.

Boundary Conditions and Computation Setup

In order to simulate the thermal expansion deformation, two nodes, A and B, are selected in the central area of the numerical model. Constrain the displacement in the x-axis direction of point A and the displacement in the y-axis direction of point B.

In this study, ISO834 standard fire curve is used as the temperature load, which is described using the following formula:

$\theta ={\theta }_0+345{\log }_{10}\left(8t/60+1\right)(12)$

where ${\theta }_0$ is the initial ambient temperature. In this study, ${\theta }_0=20{}^{\circ }\text{C}$. $t$ is the heating time in second. $\theta$ is the temperature at the current time.

An initial temperature field ${\theta }_0=20{}^{\circ }\text{C}$ is applied on the nodes of all elements in the numerical model. The temperature load of the standard fire curve is applied on the nodes in the four boundaries of the model.

In this study, the simulation time is 1800 s. That is, the concrete specimen is heated for 30 min. The numerical calculation cannot converge when the heating time reaches 1,399 s. This shows that the concrete specimen exhibits a severe thermal-induced explosive spalling failure at this time.

Simulation Results and Analysis

Thermal-Induced Explosive Spalling Characteristics

Figure 3 shows the deformations of the concrete specimen under high temperatures and the damage states of cohesive elements. It can be seen that the deformation of the concrete material increases gradually. At the same time, the damage of cohesive elements in mortar increases, and the thermal-induced damage gradually extends from the outer boundaries to the interior of the model. The damage evolution of the cohesive elements shows that the thermal cracks originate at the aggregate boundaries. Thermal cracks are easier to sprout at aggregates-mortar interfaces due to different thermal expansion coefficients. The initiated thermal cracks propagate along with the interfaces.

FIGURE 3

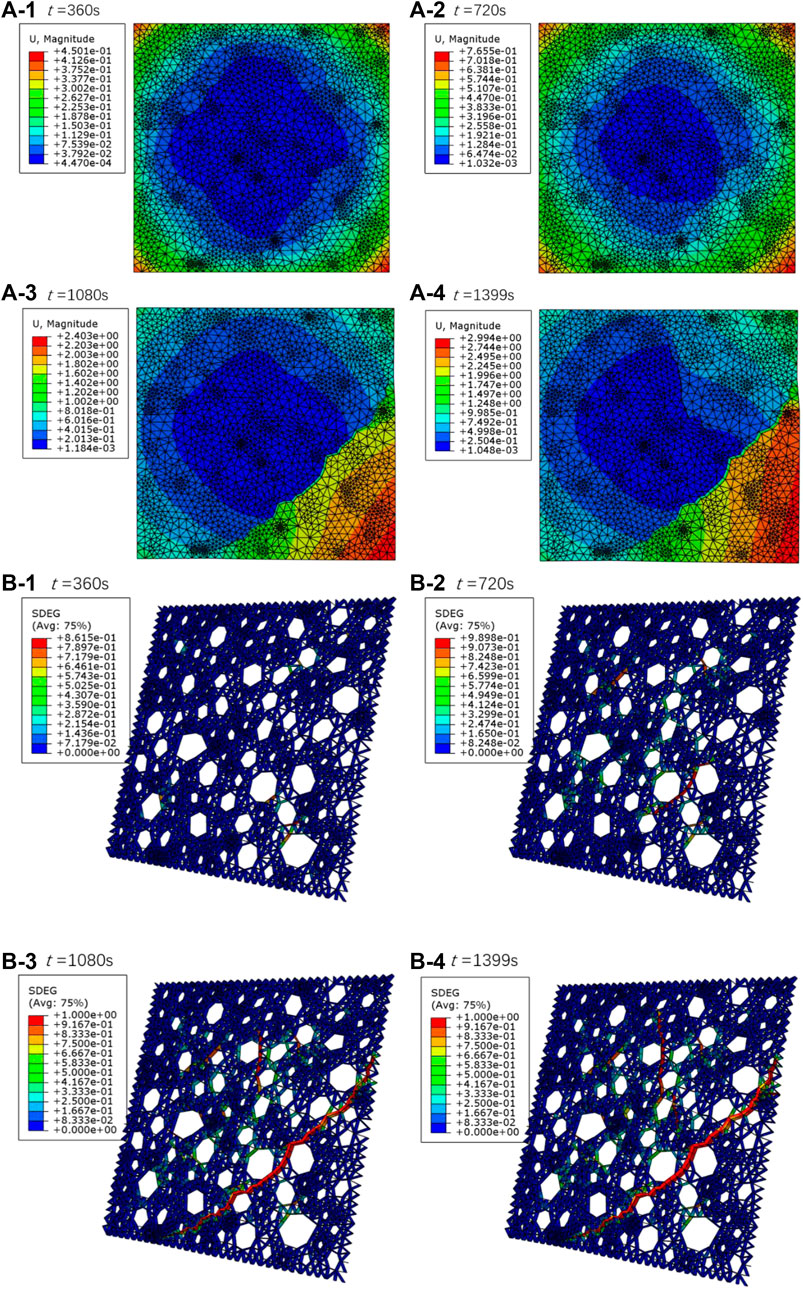
FIGURE 3. (A) Numerical simulation results of thermal-induced deformation; (B) Numerical simulation results of thermal-induced damage in the cohesive elements.

When t = 360 s, as shown in Figure 3A-1, the displacement field of the concrete material is roughly centrosymmetric. Nevertheless, the aggregate distribution affects the centrosymmetry of the displacement field. At the four corners, the thermal-induced displacement values are in a range of 0.38–0.45 mm. Figure 3B-1 shows that, in the local areas about 2–5 cm away from the four corners, the values of damage variable D are about 0.57–0.86. It shows that the cohesive elements in these local areas have been damaged and deteriorated, and thermal cracks begin to propagate.

Figure 3A-2 shows that, when t = 720 s, the centrosymmetry of the displacement field is weakened by the distribution of aggregates. The displacement values at the four corners increased to 0.64–0.77 mm. The displacements in the upper-left and lower-left corners increase rapidly, related to the damage states of the cohesive elements, as shown in Figure 3B-2. It can be seen that the damaged area gradually extends from the four corners towards the depths of about 4–6.5 cm. The fractured cohesive elements were observed at three positions: 6.6 cm-depth from the upper-left corner, 5.8 cm-depth from the upper-right corner and 6.5 cm-depth from the lower-right corner. The damage variable values of cohesive elements at these three positions are 0.90, 0.91 and 0.98, respectively. It can be seen that the cohesive elements at these three positions have been completely destroyed to form thermal cracks. These crack lengths are about 13.6, 8.9 and 39.8 cm, respectively.

When t = 1080 s, as shown in Figure 3A-3, the displacements are in a range of 0.85–1.00 mm observed in the upper-left, lower-left and upper-right corners. The maximum displacement appears in the lower-right corner, and its value is about 2.0–2.4 mm. The thermal-induced displacement of the concrete specimen has completely lost its centrosymmetry. The reason is related to the propagation and evolution of thermal cracks, as shown in Figure 3B-3. It can be seen that when the time reaches 1080 s, some thermal cracks gradually form in the model. The longest thermal crack appears in the lower-right corner, and its middle is about 6.5 cm away from the lower-right corner. The two ends of this crack are 4.5 cm away from the lower-left corner and 4.0 cm away from the upper-right corner, respectively. This crack length is about 14.8 cm, and its maximum width is about 1.7 mm. The damage variable of cohesive elements on this thermal-induced spalling crack ranges from 0.91 to 1.00.

When t = 1399 s, as shown in Figure 3A-3, the thermal deformations increase to 0.93–1.35 mm in the upper-left, lower-left and upper-right corners. The maximum displacement appears in the lower-right corner, and its value is about 3.0 mm. It can be seen from Figure 3B-3 that when the time reaches 1399 s, the high-temperature spalling damage of the concrete material is more severe. The numerical calculation has been unable to converge. It can be observed that many large thermal cracks have penetrated into the middle of the specimen. An obvious longitudinal thermal crack penetrates from the position 1.4 cm away from the upper boundary to the center of the specimen. This longitudinal thermal crack is about 7.8 cm long, and the maximum width in the middle part is about 0.4 mm. The damage variable on this thermal crack ranges from 0.80 to 1.00. It shows that the cohesive elements on this damage zone have been destroyed. These destroyed cohesive elements formed a thermal crack penetrating the specimen. At this time, the length of the largest thermal crack that appeared in the lower-right corner increases to 15.5 cm, and its maximum width is about 2.2 mm. The high temperature has caused the lower-right corner to be completely destroyed and spalled from the concrete specimen.

Temperature and Thermal Stress Fields

Figure 4A shows the temperature field in the concrete material at different times. It can be seen that the temperature continues to rise with increasing of time. Heat is gradually transferred from the outer boundaries to the interior of the concrete specimen. The temperature growth at the outer boundaries meets the predictions of the standard fire curve. The minor and major principal thermal stress fields are shown in Figures 4B,C. It is found that the thermal stresses change with increasing temperature. However, the overall distributions of the thermal stress fields do not change significantly with increasing temperature.

FIGURE 4

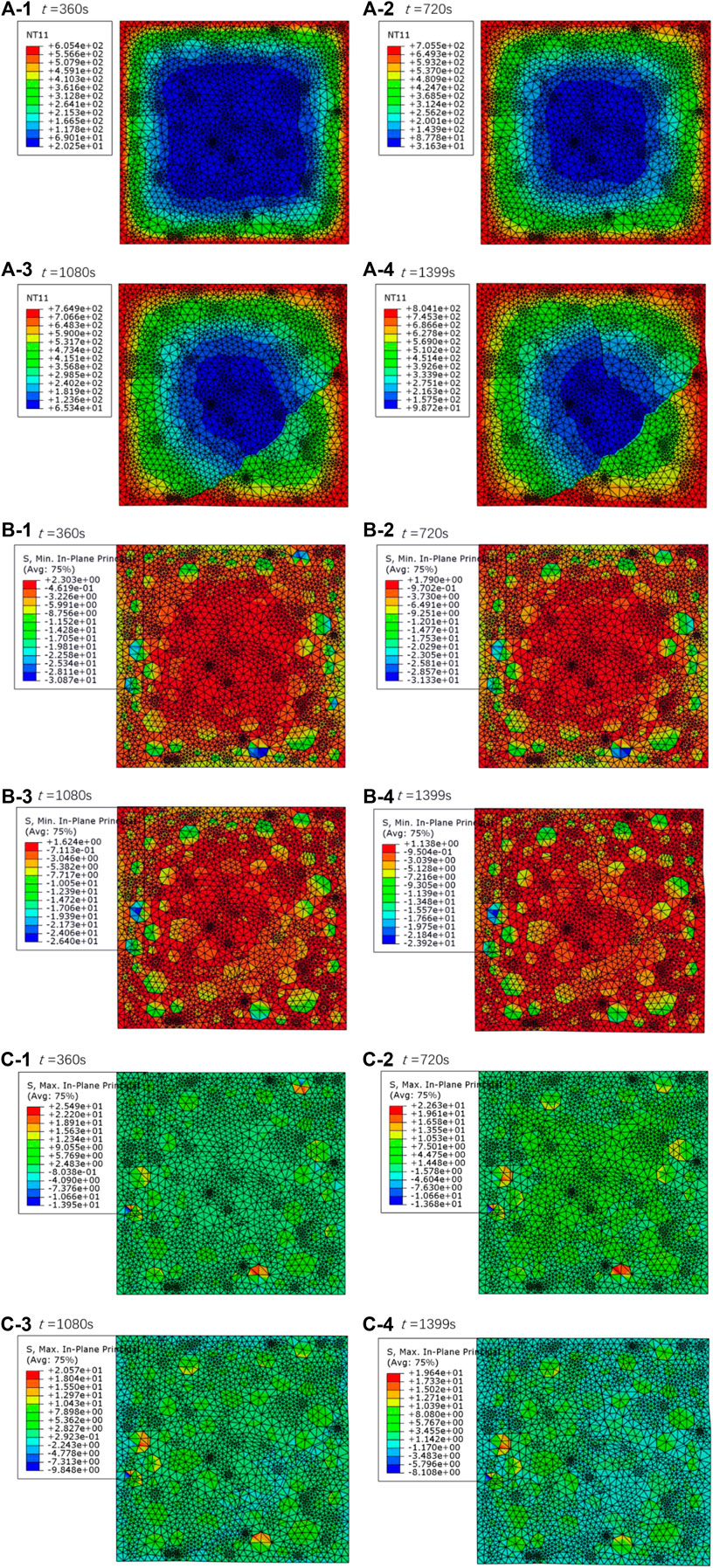
FIGURE 4. (A) Numerical simulation results of temperature field; (B) Numerical simulation results of minor principal thermal stress field; (C) Numerical simulation results of major principal thermal stress field.

When t = 360 s, as shown in Figure 4A-1, the temperature at the outer boundaries of the model reaches 605.4°C. The temperature in the central area is slightly higher than the initial temperature of 20°C. The corresponding minor and major principal thermal stresses are shown in Figures 4B-1,C-1. The thermal stresses caused by high temperature are in a tensile state. Large aggregates greatly influence the thermal stress fields. In the areas 0.5–2.0 cm away from the boundaries, the temperature ranges from 210 to 370°C, where some large aggregates exhibit thermal stress concentrations. The minor principal thermal stresses are in a compressive state, ranging from −25.34 MPa to −30.87 MPa. The major principal thermal stresses are in a tensile state, ranging from 19.91 to 25.49 MPa.

As shown in Figure 4A-2, when t = 720 s, the temperature reaches 705.5 and 31.63°C at the outer boundaries and in the central area, respectively. The temperature field is roughly centrosymmetric. The aggregate distribution has little effect on the temperature field. Figures 4B-2,C-2 show that, at the same time, the thermal stresses are in a tensile state. At a distance of 0.5–2.0 cm away from the boundaries, the temperature rises to a range of 290–510°C. It is observed that thermal stresses concentrate around some large aggregates. Compared with t = 360 s, the values of major principal thermal stresses increase to a range from −25.81 MPa to −31.33 MPa. However, on the same aggregates, the values of major principal thermal stresses decrease to a certain extent due to the initiation and propagation of thermal cracks.

Figure 4A-3 shows that when t = 1080 s, the temperature at the boundaries increases to 964.9°C, and the temperature in the central area increases to 65.3°C. By referring to Figure 3, it is found that the initiation and propagation of a large number of thermal cracks cause the temperature field at t = 1080 s to be no longer symmetrical. There is an obvious temperature difference on both sides of the thermal crack in the lower-right corner. This indicates that large thermal cracks weaken the heat conductance towards the central region. The thermal stress fields at this time are shown in Figures 4B-3,C-3. It can be seen that, compared with t = 360 s and t = 720 s, the minor and major principal thermal stresses are still in compressive and tensile states, respectively. However, their values are reduced to a certain extent. This indicates that the initiation and propagation of thermal-induced spalling cracks lead to the damage of concrete material and then reduce the values of thermal stresses.

Figure 4A-4 shows that t = 1399 s, the concrete specimen is destroyed. On the boundaries and in the central areas, the temperature rises to 804.1 and 98.7°C, respectively. Compared with t = 1080 s, the high-temperature spalling failure is more severe. By referring to Figure 3, it is found that many thermal-induced spalling cracks propagate to the center of the specimen, which greatly affects the temperature distribution. Figure 4B-2,C-2 show that the propagation of thermal cracks reduces the values of minor and major principal thermal stresses. However, thermal-induced explosive spalling damage is relatively lower in the middle area, about 0.5–1.5 cm away from the left boundary. Some large aggregates in this area still exhibit a certain degree of thermal stress concentration.

Conclusion and Discussions

This study uses Abaqus to establish a numerical model of the concrete specimen composed of aggregates and cement mortar. Cohesive elements are embedded in the numerical model to simulate the high-temperature spalling failure of the concrete material. There are some conclusions and discussions in the application of this numerical method, as follows:

Because of differences in thermal expansion coefficient, the thermal-induced spalling cracks are easier to initiate at the aggregate-mortar interfaces. The initiated thermal cracks expand alongside the interfaces and form penetrating cracks with increasing temperature. Large aggregates contribute more to the thermal spalling cracks than small ones.

There is an obvious difference in concrete temperature on both sides of large thermal-induced spalling cracks. This indicates that the large thermal cracks greatly affect the temperature distributions in the concrete material. The reason is that the large thermal cracks form a gap, which reduces the thermal conductivity, failing ineffective heat transfer from the outer boundaries to the center areas.

This study validates that in Abaqus, cohesive elements considering heat conduction can simulate the continuous-discontinuous thermal-induced spalling failure behavior of concrete materials. However, this study only simulates the thermal-mechanical spalling failure process, but cannot simulate the spalling failure caused by vapor pressure under high temperature. To solve this problem, the authors believe in two feasible solutions.

1) Based on the existing experimental research, the physical relationship between high temperature and vapor pressure should be obtained. The field variable can be adopted to simulate the effect of high temperature on vapor pressure. Then, the thermal-hydro-mechanical process of spalling failure under high temperature can be simulated using the heat-transferring cohesive element with a degree of freedom considering pore pressure.

2) Based on experimental investigations, establish a traction-separation constitutive model for cohesive interface considering the effects of heat conduction and vapor pressure. On the Abaqus platform, use UMAT (user-defined material) and UEL (user-defined element) subroutines to implement this model for simulating the thermal-hydro-mechanical coupling deformation and failure process of concrete materials under high temperatures.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conception and design of study was contributed by RZ and RG. Numerical simulations were contributed by JC and JZ. Drafting the manuscript was contributed by JZ.

Funding

This research was financially supported by China Postdoctoral Science Foundation (Grant No. 2020M673589XB) and National Natural Science Foundation of China (Grant No. 12062026).

Conflict of Interest

JC is employed by Sany Heavy Industry Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zeiml M, Lackner R, Mang HA. Experimental Insight into Spalling Behavior of concrete Tunnel Linings under Fire Loading. Acta Geotech. (2008) 3:295–308. doi:10.1007/s11440-008-0069-9

CrossRef Full Text | Google Scholar

2. Zhang Y, Zeiml M, Pichler C, Lackner R. Model-based Risk Assessment of concrete Spalling in Tunnel Linings under Fire Loading. Eng Structures (2014) 77:207–15. doi:10.1016/j.engstruct.2014.02.033

CrossRef Full Text | Google Scholar

3. Li L, Shi L, Wang Q, Liu Y, Dong J, Zhang H, et al. A Review on the Recovery of Fire-Damaged concrete with post-fire-curing. Construction Building Mater (2020) 237:117564. doi:10.1016/j.conbuildmat.2019.117564

CrossRef Full Text | Google Scholar

4. Zheng WZ, Hou XM, Shi DS, Xu MX. Experimental Study on Spalling of concrete of Prestressed Slabs in Fire. Fire Saf J. 2010;45:283–297. doi:10.1016/j.firesaf.2010.06.001

CrossRef Full Text | Google Scholar

5. Novak J, Kohoutkova A. Mechanical Properties of concrete Composites Subject to Elevated Temperature. Fire Saf J (2018) 95:66–76. doi:10.1016/j.firesaf.2017.10.010

CrossRef Full Text | Google Scholar

6. Hertz KD. Limits of Spalling of Fire-Exposed Concretefire-Exposed concrete. Fire Saf J (2003) 38:103–16. doi:10.1016/s0379-7112(02)00051-6

CrossRef Full Text | Google Scholar

7. Ulm F-J, Coussy O, Bazant Z. The “Chunnel” Fire. I: Chemoplastic Softening in Rapidly Heated Concrete. J Eng Mechanics-ASCE (1999) 125:3. doi:10.1061/(asce)0733-9399(1999)125:3(272)

CrossRef Full Text | Google Scholar

8. Kalifa P, Menneteau F-D, Quenard D. Spalling and Pore Pressure in HPC at High Temperatures. Cement Concrete Res (2000) 30:1915–27. doi:10.1016/s0008-8846(00)00384-7

CrossRef Full Text | Google Scholar

9. Othman MIA, Said S, Marin M. A Novel Model of Plane Waves of Two-Temperature Fiber-Reinforced Thermoelastic Medium under the Effect of Gravity with Three-Phase-Lag Model. Int. J. Numer. Methods Heat Fluid Flow (2019) 29:4788–806. doi:10.1108/hff-04-2019-0359

CrossRef Full Text | Google Scholar

10. Marin M, Othman MA, Abbas I. An Extension of the Domain of Influence Theorem for Generalized Thermoelasticity of Anisotropic Material with Voids. J Comput Theor Nanosci (2015) 12:1594–8. doi:10.1166/jctn.2015.3934

CrossRef Full Text | Google Scholar

11. Chung JH, Consolazio GR, McVay MC. Finite Element Stress Analysis of a Reinforced High-Strength concrete Column in Severe Fires. Comput Structures (2006) 84:1338–52. doi:10.1016/j.compstruc.2006.03.007

CrossRef Full Text | Google Scholar

12. Gawin D, Pesavento F, Schrefler BA. Modelling of Hygro-thermal Behaviour of concrete at High Temperature with Thermo-Chemical and Mechanical Material Degradation. Computer Methods Appl Mech Eng (2003) 192:1731–71. doi:10.1016/s0045-7825(03)00200-7

CrossRef Full Text | Google Scholar

13. Gawin D, Pesavento F, Schrefler BA. Towards Prediction of the thermal Spalling Risk through a Multi-phase Porous media Model of concrete. Computer Methods Appl Mech Eng (2006) 195:5707–29. doi:10.1016/j.cma.2005.10.021

CrossRef Full Text | Google Scholar

14. Schrefler BA, Majorana CE, Khoury GA, Gawin D. Thermo‐hydro‐mechanical Modelling of High Performance concrete at High Temperatures. Eng Computations (2002) 19:787–819. doi:10.1108/02644400210444320

CrossRef Full Text | Google Scholar

15. Zeiml M, Lackner R, Pesavento F, Schrefler BA. Thermo-hydro-chemical Couplings Considered in Safety Assessment of Shallow Tunnels Subjected to Fire Load. Fire Saf J (2008) 43:83–95. doi:10.1016/j.firesaf.2007.05.006

CrossRef Full Text | Google Scholar

16. Zhao J, Zheng J-j., Peng G-f., van Breugel K. A Meso-Level Investigation into the Explosive Spalling Mechanism of High-Performance concrete under Fire Exposure. Cement Concrete Res (2014) 65:64–75. doi:10.1016/j.cemconres.2014.07.010

CrossRef Full Text | Google Scholar

17. Fu Y, Li L. Study on Mechanism of thermal Spalling in concrete Exposed to Elevated Temperatures. Mater Struct (2011) 44:361–76. doi:10.1617/s11527-010-9632-6

CrossRef Full Text | Google Scholar

18. Zhang HL, Davie CT. A Numerical Investigation of the Influence of Pore Pressures and Thermally Induced Stresses for Spalling of concrete Exposed to Elevated Temperatures. Fire Saf J (2013) 59:102–10. doi:10.1016/j.firesaf.2013.03.019

CrossRef Full Text | Google Scholar

19. Caggiano A, Etse G. Coupled Thermo-Mechanical Interface Model for concrete Failure Analysis under High Temperature. Computer Methods Appl Mech Eng (2015) 289:498–516. doi:10.1016/j.cma.2015.02.016

CrossRef Full Text | Google Scholar

20. Caggiano A, Schicchi DS, Etse G, Ripani M. Meso-scale Response of concrete under High Temperature Based on Coupled Thermo-Mechanical and Pore-Pressure Interface Modeling. Eng Fail Anal (2018) 85:167–88. doi:10.1016/j.engfailanal.2017.11.016

CrossRef Full Text | Google Scholar

21. Caggiano A, Said Schicchi D. A Thermo-Mechanical Interface Model for Simulating the Bond Behaviour of FRP Strips Glued to concrete Substrates Exposed to Elevated Temperature. Eng Structures (2015) 83:243–51. doi:10.1016/j.engstruct.2014.10.017

CrossRef Full Text | Google Scholar

22. Abaqus UM. Abaqus Analysis User's Guide Version 6. Rhode Island, USA: Dassault Systemes Simulia Corp (2012).

Google Scholar

23. Ibrahim GR, Albarbar A. A New Approach to the Cohesive Zone Model that Includes thermal Effects. Composites B: Eng (2019) 167:370–6. doi:10.1016/j.compositesb.2019.03.003

CrossRef Full Text | Google Scholar

24. Jousset P, Rachik M. Comparison and Evaluation of Two Types of Cohesive Zone Models for the Finite Element Analysis of Fracture Propagation in Industrial Bonded Structures. Eng Fracture Mech (2014) 132:48–69. doi:10.1016/j.engfracmech.2014.10.018

CrossRef Full Text | Google Scholar

25. Zhang C, Curiel-Sosa JL, Bui TQ. A Novel Interface Constitutive Model for Prediction of Stiffness and Strength in 3D Braided Composites. Compos Structures (2017) 163:32–43. doi:10.1016/j.compstruct.2016.12.042

CrossRef Full Text | Google Scholar

26. Meng Q-X, Xu W-Y, Wang H-L, Zhuang X-Y, Xie W-C, Rabczuk T. DigiSim - an Open Source Software Package for Heterogeneous Material Modeling Based on Digital Image Processing. Adv Eng Softw (2020) 148:102836. doi:10.1016/j.advengsoft.2020.102836

CrossRef Full Text | Google Scholar

27. Meng QX, Wang HL, Xu WY, Cai M. A Numerical Homogenization Study of the Elastic Property of a Soil-Rock Mixture Using Random Mesostructure Generation. Comput Geotechnics (2018) 98:48–57. doi:10.1016/j.compgeo.2018.01.015

CrossRef Full Text | Google Scholar

28. Štefan R, Foglar M, Fládr J, Horníková K, Holan J. Thermal, Spalling, and Mechanical Behaviour of Various Types of Cementitious Composites Exposed to Fire: Experimental and Numerical Analysis. Construction Building Mater (2020) 262:119676. doi:10.1016/j.conbuildmat.2020.119676

CrossRef Full Text | Google Scholar