Phase-Dependent Epitaxy for Antimonene Growth on Silver Substrate

Antimonene is a novel two-dimensional topological semiconductor material with a strain-driven tunable electronic structure for future electronic devices, but the growth of clean antimonene is not fully understood. In this work, the growth process of antimonene on the silver substrate has been studied in detail by using the density functional theory and particle swarm optimization algorithms. The results show that, in addition to the experimental reported flat honeycomb and β-phase antimonene, α-phase antimonene was observed to be able to grow on the substrates, and the phases of antimonene were deeply dependent on the reconstructed supercells and surface alloys. It has been demonstrated that the surface alloys on the substrate play an active role in the growth of antimonene.

1 Introduction

Antimonene, one of the novel monoelemental class of two-dimensional (2D) material, has been extensively studied from theory to experiment [1–4], since it was first reported by Zhang et al. [5] in 2015. As a member of the 2D group-V family [6], the freestanding monolayer antimonene, either puckered (α-phase) or buckled (β-phase) structure, is a semiconductor. Compared to α-phase antimonene (α-Sb), β-phase antimonene (β-Sb) with a buckled honeycomb structure similar to black phosphorus [7] is more thermodynamically stable. It was reported to have a strain-tunable energy gap and high carrier mobility [5, 7–12]. Recently, Zhao et al. [13] achieved band inversion by applying a large stretching strain on the lattice, and β-Sb was transferred from a trivial semiconductor to a nontrivial quantum spin hall insulator. Unlike β-Sb, the structure of α-Sb is a structural analog of blue phosphorus, with four atoms in the unitcell, which are arranged in a rectangular lattice in puckered shape with two distorted sublayers. It was found to be a kind of 2D topological insulator when the in-plane anisotropic strain was applied [14]. Applying the in-plane strain is a very important method to tune the electronic structure of antimonene, and how to obtain strained antimonene becomes critical.

To obtain monolayer antimonene, scientists have done experiments with different synthesis methods, including micromechanical exfoliation (MME), liquid-phase exfoliation (LPE), and molecular beam epitaxy (MBE). By applying the MME method, which is used to obtain graphene [15]. Ares et al. [16] have successfully obtained few-layer antimonene, but it is hard to obtain monolayer antimonene. Some other works have reported successes in the preparation of antimonene using the LPE method [17–19], while the samples obtained were mostly freestanding antimonene. It usually does not meet the requirements for obtaining topological properties. By using the MBE method, it may be possible to obtain strain-stretched antimonene. In 2016, Ji et al. [20] synthesized high-quality, few-layer β-Sb polygons on mica substrate through van der Waals epitaxy. Some works have reported successful epitaxial growth of β-Sb on various types of substrates, such as layered materials, transition metals, and transition metal-oxides. According to our collection, layered material substrates include PdTe₂ [21], MoS₂ [22], graphene [23], Bi₂Se₃ [24], and WSe₂ [25]; transition metal substrates include Ag (111) [26–28], Cu(111) [29], and Au (111) [30] surfaces; transition metal-oxide substrates include Cu₃O₂ [31] and sapphire [32]. During the epitaxial growth of antimonene, the substrate played a very important role. With the lower mismatch between the selected substrates and antimonene, the lattice parameters of the grown antimonene were closer to that of the freestanding antimonene. For example, the lattice constant of antimonene on PdTe₂ was 4.13Å [21], and 4.1 Å [24] on Bi₂Se₃. The lattice parameter of antimonene grown on transition metals was much larger than that of the freestanding antimonene. It was 4.43 Å on Cu(111) surface [29] and 5.0 Å on Ag (111) surface [26, 27]. Thus, transition metals may be good substrates for the epitaxial growth of antimonene with stress tensile.

The Density Functional Theory (DFT) based simulations have played an increasingly important role in assisting experimental efforts to synthesize and analyze two-dimensional (2D) materials in these years. The structural analysis of 2D materials is one of the main functions. In this article, the structural analysis of antimonene on Ag (111) substrate, on which antimonene could have about 20% stretching of lattice, was carried out with the DFT calculations based on the following fundamental questions: 1) How do the structures evolve with an increasing Sb coverage? 2) What is the most stable phase of antimonene on substrates? Our results demonstrated that the antimonene phase was strongly affected by the structure of the substrate and reconstructed supercell.

2 Computation Methods

To find the most stable configuration of antimonene on the Ag (111) substrate, we have selected different sizes of Ag (111) supercells. Then, the surface reconstruction search under various Sb coverage using the particle swarm optimization (PSO) algorithm, which is well-designed in the software package CALYPSO [33–35], was applied. Our calculations were based on the fact that antimony atoms were sufficiently contracting with the substrate and distributed uniformly. Therefore, the evolution of the most stable structures at different coverages was able to describe the continuous deposition of Sb on the Ag (111) surface theoretically.

The coverage of antimony (C_Sb) on the substrate was the key parameter in this work. Usually, we describe it in terms of C_Sb = N_Sb/N_Sb-sheet. In this equation, the N_Sb-sheet would not be constant for different phases of the substrate with the same reconstructed area. Therefore, for the ease to describe C_Sb, we defined it as follows:

$C_{\text{Sb}}=\frac{N_{\text{Sb}}}{N_{\text{Sub}}},(1)$

where N_Sb is the number of Sb atoms adsorbed on substrate, and N_Sub is the number of atoms in a monolayer of the substrate. For the supercells in type of $\mathcal{A}(\sqrt{3}\times \sqrt{3})$, $\mathcal{B}(3\times \sqrt{3})$ and $\mathcal{C}(3\times 3)$ of Ag (111), N_Sub = 3, 6, and 9, respectively.

To measure the structural stability, the formation energy of Sb adsorbed onto the substrates is defined by the following formula:

$E_{\text{form}}=\frac{1}{N_{\text{Sb}}}\left(E_{\text{tot}}-E_{\text{sub}}\right)-E_{\text{bulk}}^{\text{Sb}},(2)$

where E_tot is the total energy of the substrate with the Sb atoms adsorbed, E_sub is the total energy of the substrate, $E_{\text{bulk}}^{\text{Sb}}$ is the bulk total energy per atom of bulk Sb (space group: R-3m, No.166). Under this definition, the lower the formation energy, the more stable is the structure, and a negative value of energy indicates that the growth is prone to occur.

To the best of our knowledge, the formation of surface alloy on the substrate is crucial for the epitaxial growth of two-dimensional materials. It has been reported that when being deposited on the Ag (111) surface, the Sb atoms react with the surface and form Ag₂Sb surface alloy, which is combined by a monolayer of a 1 × 1 Ag₂Sb matching with a $\sqrt{3}\times \sqrt{3}$ R 30°supercell of Ag (111) [36–38]. Therefore, a transition state search calculation was done to verify the possibility of the existence of surface alloy and to identify their structures. After confirming the surface alloy structure, we extended these types of supercells with and without surface alloy. To facilitate the description, we ignored the intermediate alloy layer, and all the reconstructed structure labels are based on Ag (111).

All the PSO calculations were energetically converged with a population size of 20 and a max step of 10 (for saving compute resources, five steps for N_Sb = 1–4, 10 or 15 steps for N_Sb ≥ 5) to meet the global optimization required. Then, the possible stable surface structures with lower entropy and different structural symmetry were collected to do the next step of high precision structure optimization. After all the DFT calculations had been done, the energetically favorable structures of all the coverages were obtained to characterize the most probable structural evolution path.

All the DFT calculations were carried out as implemented in the Vienna ab-initio simulation package (VASP) [39–41]. The electron–ion interaction was described by the projector augmented-wave potentials [42], and the exchange-correlation function was given by generalized gradient approximation parametrized by Perdew, Burke, and Ernzerhof [43, 44]. The van der Waals corrections were treated by the semi-empirical DFT-D3 method [45] in the surface reconstruction calculations. The cutoff energy was set to 400 eV for all calculations. The vacuum layer was set to be at least 15 Å to eliminate the interaction between the layers. All the structures were fully relaxed until the force on each atom was less than 0.02 eV/Å, and the energy convergence criterion was met to 10^–8 eV. The substrates were built on the basis of the bulk structure of FCC Ag, and the Ag bulk lattice constant obtained by structural optimization was 4.137 Å, which was well converged in the VASP. The total number of layers in the substrate was set to three ( four for the substrate with surface alloy), and the atom positions in the bottom layer were fixed during the geometry optimization.

3 Results and Discussion

3.1 Antimonene on a Pure Ag(111) Surface

In this section, we have carried out the structural search for the most stable configuration with different coverage of Sb atoms on pure Ag (111) substrate. In Figure 1A, we depicted the variation of formation energies with C_Sb on Ag (111) substrate. There are formation energy valleys at the corresponding coverages of C_Sb = 2/3, 2/3, 4/9 for type $\mathcal{A}$, $\mathcal{B}$, and $\mathcal{C}$ substrates, respectively. The configuration with the lowest formation energy is at C_Sb = 2/3 on $\mathcal{B}$-type Ag (111) substrate, in which the Sb atoms are arranged in a zigzag shape on the substrate, which is consistent with the half layer of α-Sb, as shown in Figure 4 (4/6).

FIGURE 1

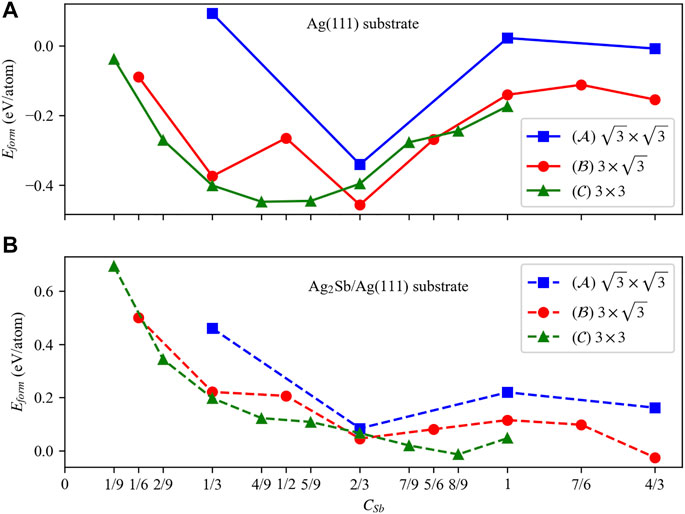
FIGURE 1. The formation energies of the Sb atoms adsorbed on different types of pure Ag (111) and Ag₂Sb/Ag (111) substrates. (A) and (B) show the evolution curves of the formation energy, where blue, red, and green represent $\sqrt{3}\times \sqrt{3}$, $3\times \sqrt{3}$, and 3×3 superstructure, and solid and dashed lines represent Ag (111) and Ag₂Sb/Ag (111) substrates, respectively.

The upper four subfigures in Figure 2 show the structures with the lowest energy at different coverage of antimony on an $\mathcal{A}$-type of pure Ag (111) substrate. Overall, as C_Sb increased from 1/3 to 4/3, there were two kinds of antimony sheets present, one with the flat honeycomb lattice at C_Sb = 2/3, and the other with the buckled honeycomb lattice at C_Sb = 3/3 and 4/3. At C_Sb = 1/3, the Sb atoms sit on the fcc-hollow sites, which is the most favorable adsorbed site. According to our tests, the fcc- and hcp-hollow sites have very similar adsorbed energies, about a difference of 0.04 eV/atom. Therefore, both the fcc- and hcp-hollow sites could be stable during actual production. At C_Sb = 2/3, the Sb atoms of the lowest energy configuration sit on the hcp-hollow sites, and formed a flat honeycomb lattice with a 23.1% stretched lattice constant of a = 5.067 Å compared to the freestanding β-Sb(4.117 Å). This configuration is the most stable on $\mathcal{A}$-type Ag (111) substrate and well agreed with the results of the work by Shao et al. [27]. It is interesting to note that the C_Sb = 3/3 structure is split into two layers, with the upper layer being a buckled honeycomb lattice and the discrete Sb atoms in the lower layer sitting almost on the bridge sites. When the deposition of antimony atoms increased to more than a single layer, the structure did not grow from the bottom to the up, layer by layer, like building blocks. The flat honeycomb lattice was no longer available and has been replaced by the buckled honeycomb ones. When C_Sb increased to 4/3, a two-layer buckling honeycomb lattice with AB stacks of different buckling heights was formed. The buckling height of the upper layer is 0.968 Å and that of the lower layer is 0.712 Å. The electron localization function of C_Sb from 2/3 to 4/3 in Figure 3 showed that the electrons were localized around the Sb atoms. The interaction between Ag–Sb was weaker than Sb–Sb. The stronger Sb–Sb interaction from the z-direction leads to the fact that the antimonene no longer maintains the flat structure when the number of layers is more than one.

FIGURE 2

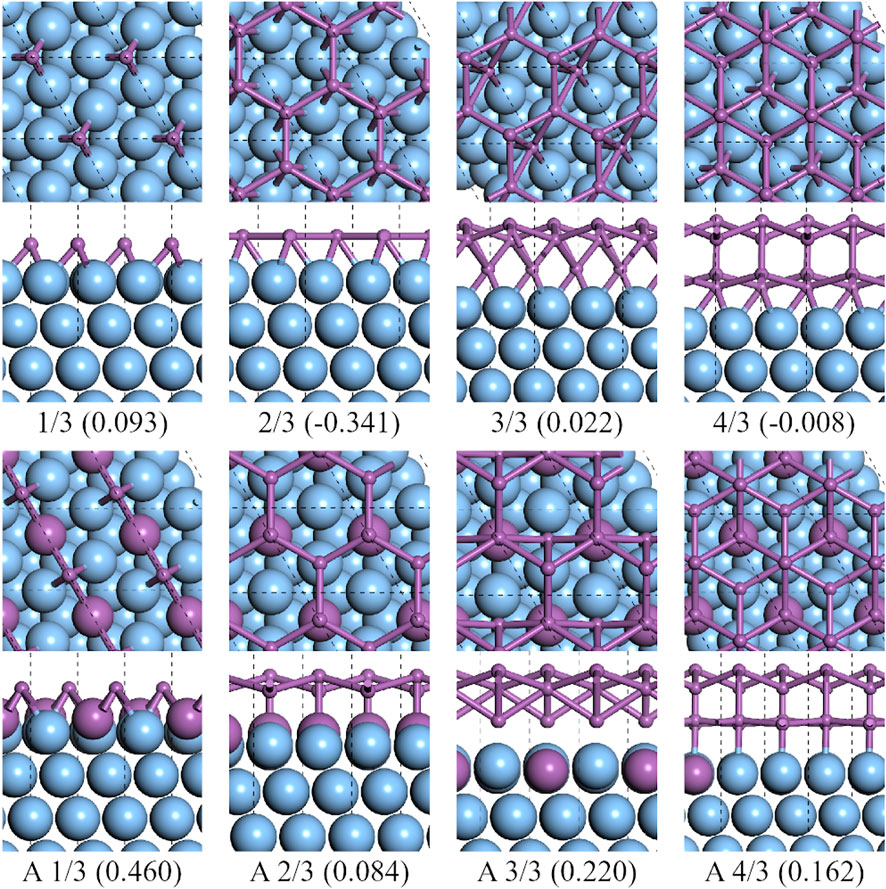
FIGURE 2. Top and side views of the lowest formation energy favorable configurations of antimony adsorbed on the $\sqrt{3}\times \sqrt{3}$ Ag (111) and Ag₂Sb/Ag (111) substrate. The four subfigures above correspond to the pure Ag (111) substrate, and the last four subfigures labeled with “A” correspond to the Ag₂Sb/Ag (111) substrate. The fractions under each subfigure correspond to the coverage of antimony C_Sb, and the decimals in brackets represent the formation energies E_form. The purple and blue balls represent the Sb and Ag atoms, respectively.

FIGURE 3

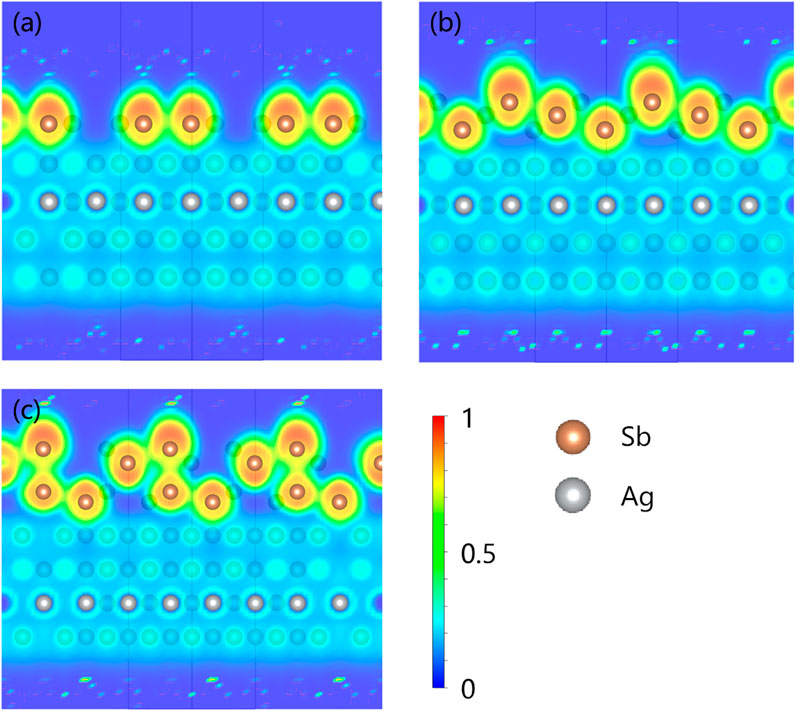
FIGURE 3. 2D contour plot of the electron localization function (ELF) of the Sb atoms on a pure Ag (111) substrate at C_Sb = (A) 2/3, (B) 3/3, and (C) 4/3 along the cut of the Miller index (110). The minimum ELF value is 0.0 (blue) and the maximum value is 1.0 (red). The brown and silver balls represent Sb and Ag, respectively.

As it is shown in Figure 4, from C_Sb = 1/6 to 4/6, there existed a clear pathway to form a half layer of α-Sb on $\mathcal{B}$-type Ag (111) substrate. From C_Sb = 5/6 to 8/6, all the configurations were based on C_Sb = 4/6, and as the Sb atoms continued to be deposited, the atoms were regularly arranged on this half-layer structure, and when C_Sb = 8/6, a full layer of α-Sb was formed. The lattice constants of α-Sb on Ag (111) substrate are a = 4.388 Å and b = 5.067 Å, which have a stretch of 0.9 and 6.6% along each of the a (Zigzag) and b (Armchair) directions compared to the freestanding α-Sb. The thickness of α-Sb was 2.95 Å and its sublayers were almost flat.

FIGURE 4

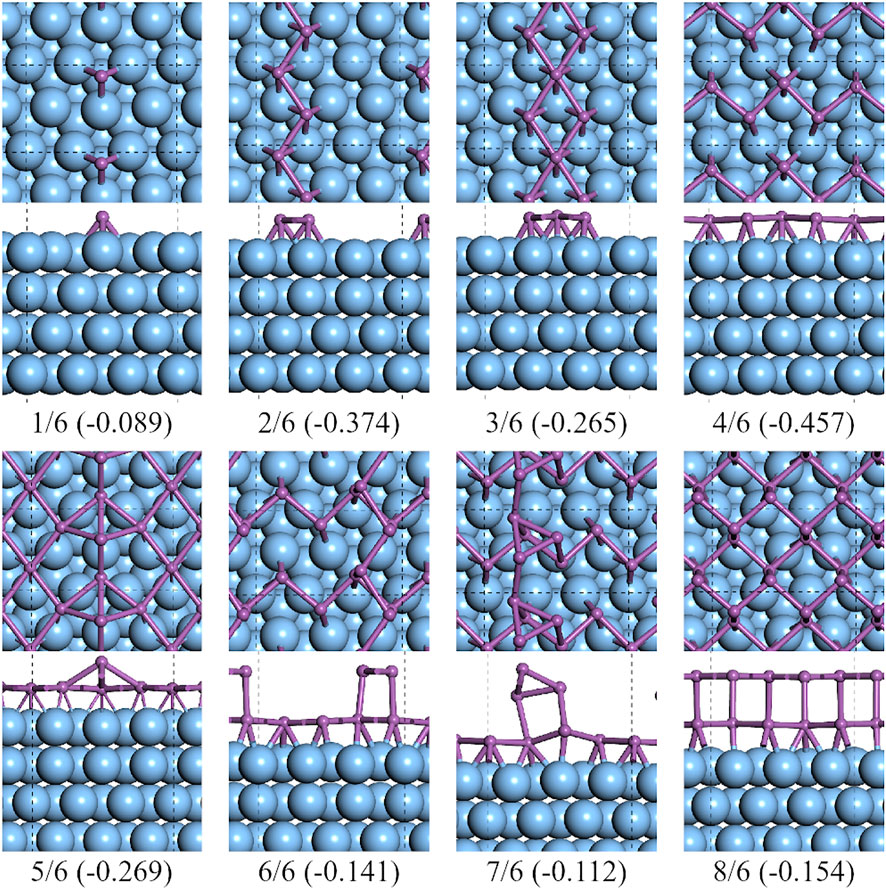
FIGURE 4. Top and side views of the lowest formation energy favorable configurations of antimony adsorbed on the $3\times \sqrt{3}$ Ag (111) surface.

On $\mathcal{C}$-type Ag (111) substrates, we did the calculations for Sb coverage from 1/9 to 9/9, a range that contains a monolayer of antimony sheet, as shown in Figure 5. Same as $\mathcal{A}$- and $\mathcal{B}$-type Ag (111) substrates, the single Sb sits on the hollow sites. From C_Sb = 3/9 to 6/9, the most stable structures of each coverage are triangular, quadrilateral, pentagonal, and hexagonal lattices, respectively. This is quite different from the results of the other two types of substrate. Small flat polygonal Sb clusters seem to dominate in the early stages of growth, and the formation energy of the quadrilateral structure is the lowest. With the increase of C_Sb from 4/9, the formation energy shows an overall increasing trend, and the Sb atoms did not spread over the entire surface until C_Sb = 7/9. A valley point appears at C_Sb = 8/9, which indicates that the structure is more stable at that coverage. However, the lowest energy structure of C_Sb = 8/9 we obtained from the structural search is a bilayer structure shown in Figure 5. It was an irregular mesh of seven atoms in the bottom layer and an additional atom located at the top site of the center of a square of four atoms in the bottom layer. We also obtained the structure of β-Sb at C_Sb = 8/9 with the lattice constant of about 4.390 Å and thickness of 1.552 Å (see Supplementary Figure S3, its formation energy is 0.035 eV/atom higher than that of the lowest one.) These results indicated that C_Sb = 8/9 maybe a magic coverage.

FIGURE 5

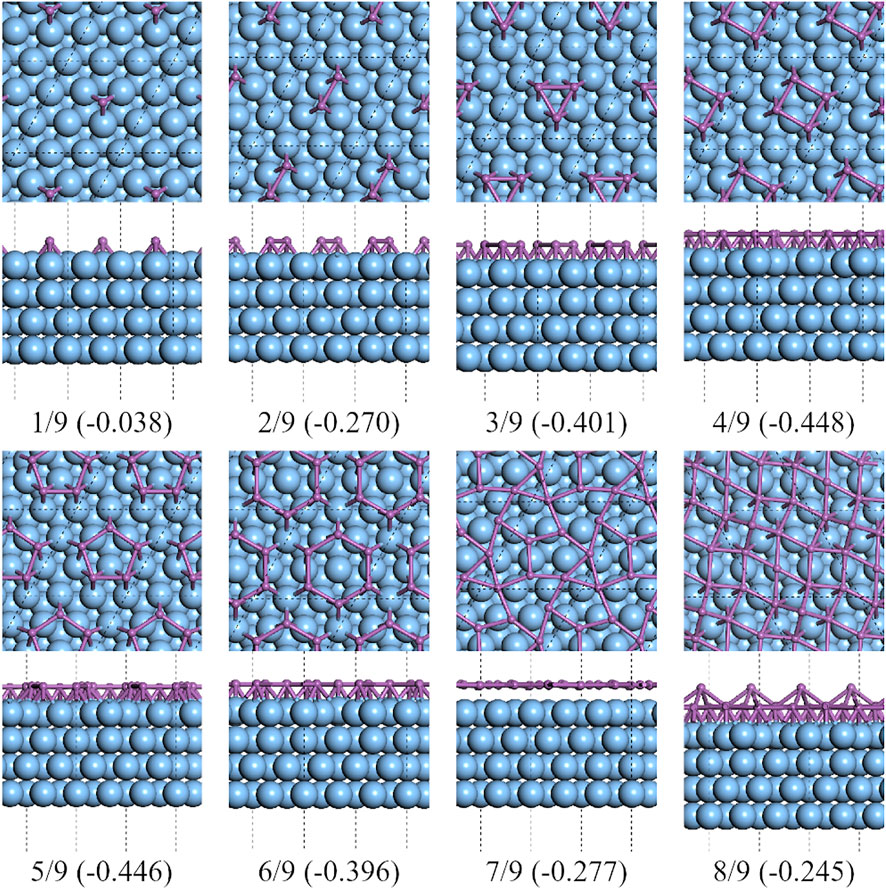
FIGURE 5. Top and side views of the lowest formation energy favorable configurations of the antimony adsorbed on 3×3 Ag (111) substrate.

To further examine the structure of antimony clusters grown on the surface of Ag (111), we calculated the various structures of 1-3 Sb₄ clusters falling on the Ag (111) surface by using ab initio molecular dynamics (AIMD) embedded in the package of CP2K [46]. The substrate of Ag (111) was set to three layers with the bottom layer fixed, and the orthogonal lattice parameter was set to a = 26.327 Å, b = 25.333 Å, and c = 32.314 Å to avoid the interaction between the periodic clusters. The AIMD results showed the process of how small Sb₄ clusters spread over the Ag 111) substrate into the flat ones after 5 ps at 300 K. Figure 6A plots the total energy of the systems as a function of time for three Sb₄ clusters on a pure Ag (111) surface. Two of these clusters disintegrate and rapidly tile to the substrate after 0.7 ps of simulations. About 4.2 ps, the atoms in all the clusters spread out. We found that the flat tetragonal structures, which have the same structure as the C_Sb = 4/9 on pure Ag (111) surface, exhibit unusual stability during the simulation. To analyze the interaction between the Sb and Ag atoms, we have drawn the curve of radial distribution function (RDF), as shown in Figure 7. The curve shows that the average distance between Sb–Sb stays within 2.935 Å, and the Sb–Ag bond increases slightly with the increase of the number of Sb atoms, from about 2.815 to 2.885 Å. As the Sb_N cluster gets larger, the distance between Sb_N and the substrate gets farther, indicating that the interaction between Sb and Sb is much stronger than that between Sb and Ag. Thus, the growth of small clusters is much easier than that of Ag–Sb alloys. The results of the other two configurations are plotted in Supplementary Figure S1 and Supplementary Figure S2. We have also examined the integration curve of RDF. The average coordination number of these three systems increases from 1 to 2 with the increasing number of Sb₄ clusters. It can be seen from its structural variations, where dimer, chain, and polygonal structures occupy the majority of conformations. For more visual observation of the structural changes, we exported the animations of the AIMD trajectory, as shown in the MP4 files in SI. The flat square Sb₄ clusters are very stable in this simulation. This is consistent with the fact that the most stable configuration on $\mathcal{C}$-type Ag (111) substrate in Figure 1 is Sb₄ at C_Sb = 4/9.

FIGURE 6

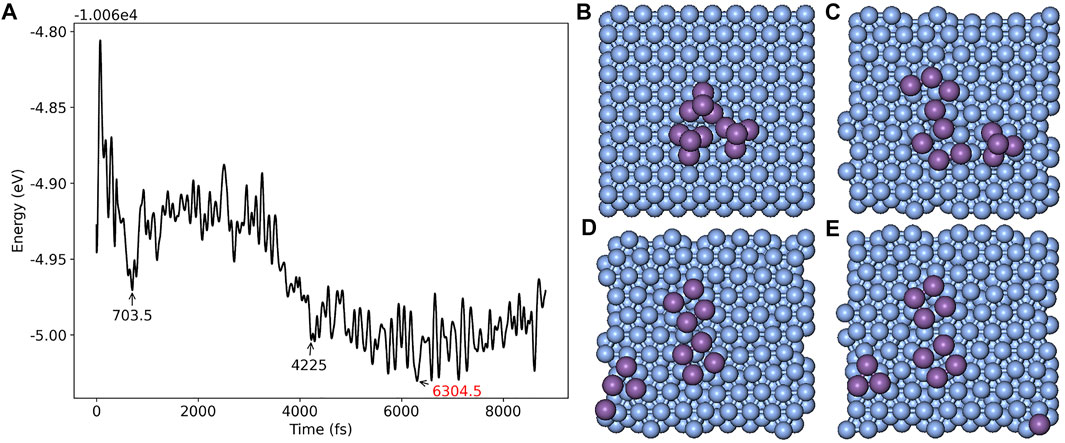
FIGURE 6. (A) Total energy of the system as a function of time from the AIMD simulation for three Sb₄ clusters on pure Ag (111) surface at 300K and zero pressure; System structures at (B) 0 fs (initial configuration), (C) 703.5 fs (two of Sb₄ clusters collapse to planar configuration), (D) 4,225 fs (all three Sb₄ clusters collapse to planar configuration), and (E) 6,304.5 fs (the configuration with the lowest energy) are listed at right, respectively.

FIGURE 7

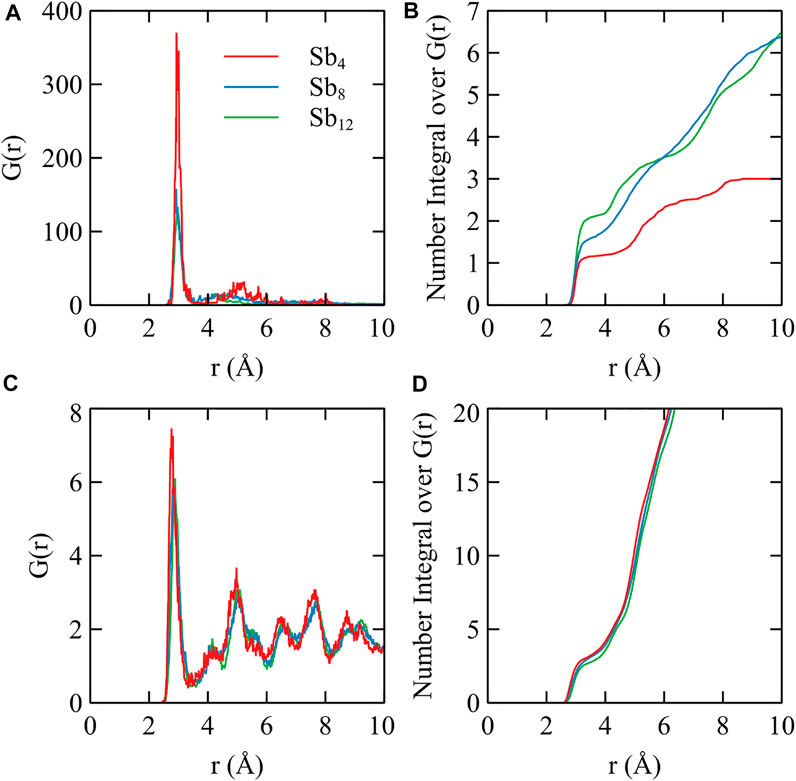
FIGURE 7. (A) and (C) are the radial distribution function for Sb–Sb and Sb–Ag, respectively. (B) and (D) are integration curve of (A) and (C). The line in red, blue, and green correspond to one, two, and three Sb₄ clusters on the Ag (111) substrate, respectively.

Theoretically, the larger the substrate, the closer the results are to reality. Combining the results of these three substrates, it can be seen that at lower coverages, flat 2D clusters occupy the major part, and when the antimony atoms increase enough to spread over the substrate or even more, it is quite possible to grow the so-called β- and α-Sb structures. However, in terms of energy comparison, the most stable configuration is the flat half layer of α-Sb.

3.2 Antimonene on Ag(111) With Ag₂Sb Surface Alloy

Before calculating the deposition of Sb atoms on the Ag₂Sb/Ag (111) substrate, the climbing image nudged elastic band (cNEB) method [47] was applied to search the transition state to analyze the process of penetration and replacement of Sb to Ag on the Ag (111) surface. We started with modeling the Sb/Ag (111) interface by adding a single Sb atom onto 3 × 3 supercell Ag (111) surface (see Figure 8 (a), the structure diagram on the left). The adsorption energy was calculated by the formula: $E_{\text{ads}}^{\text{Sb}}=E^{\text{Ag}\left(111\right)}+E_{\text{atom}}^{\text{Sb}}-E_{\text{tot}}^{\text{Sb/Ag}\left(111\right)},$ where, $E_{\text{atom}}^{\text{Sb}}$ is the total energy of per Sb atom in bulk. The calculated $E_{\text{ads}}^{\text{Sb}}$ value is 0.037 eV on the 3 × 3 Ag (111) surface. The minimum energy path (MEP) of the penetration of one Sb atom into the Ag (111) surface plotted in Figure 8A, it shows a forward energy barrier of $\overrightarrow{E_a}$ = 0.779 eV, and a reverse energy barrier of $\stackrel{⃖}{E_a}$ = 0.672 eV. The $\overrightarrow{E_a}$ is much higher than $E_{\text{ads}}^{\text{Sb}}$. Therefore, the replacement process should not occur unless the system is in a heat-absorbing state. The environment provides enough energy to make it cross this energy barrier.

FIGURE 8

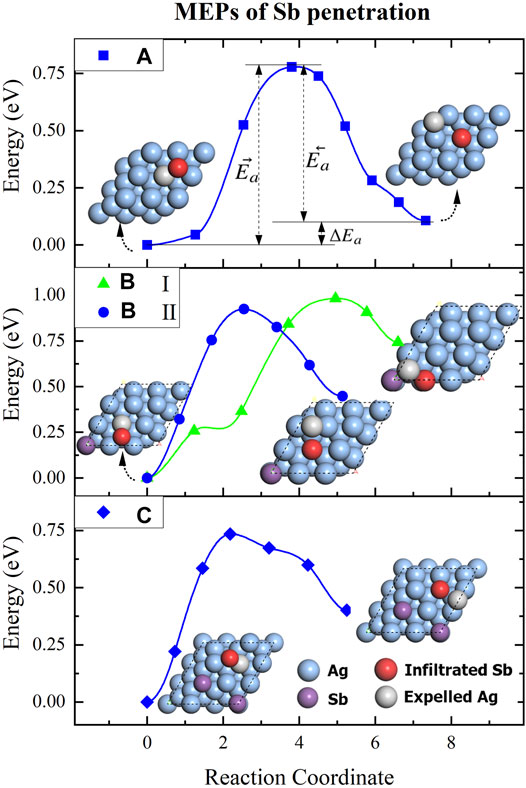
FIGURE 8. The MEPs of the Sb atoms continuously replace the Ag atoms in surface of Ag(111) substrate. (A) is the first step of one Sb atom penetrating into Ag(111) surface. B (I) and B (II) are the second step of another Sb atom penetrate into the final state of step A at neighbor and sub-neighbor sites, respectively. C is the third step of Sb atom penetrate into the final state of step B (II) at sub-neighbor site. The purple and blue balls represent the Ag and Sb atoms, the red and gray balls represent the infiltrated Sb atom and expelled Ag atoms, respectively.

Next, we added the second Sb atom to the substrate while removing the Ag atom that was expelled. Since there was already a penetrated Sb atom after step (A), so we chose to calculate the MEPs for the penetration at the neighbor and subneighbor site separately, see Figure 8B. From the results, it is clear that path B (II) is more favorable than path B (I), with a lower energy of the final state and a relatively shorter reaction path. Based on this, we continued to add a 3rd Sb atom to the final state of path B (II) and made it penetrate at the subneighbor site, and the MEP of this process was plotted in Figure 8C. All the energies of MEPs are listed in Table 1, the ΔE_a are all positive, which proves that Sb penetration is a heat absorption process. Such subneighbor atomic arrangement characteristics predetermine the impossibility of continuous replacement of Ag by Sb, and with Sb penetration occurring all over the surface, and an Ag₂Sb alloy monolayer is formed. Till now, we have confirmed that if a surface alloy could be formed, it would be Ag₂Sb.

TABLE 1

TABLE 1. Forward energy barrier $\overrightarrow{E_a}$, reverse energy barrier $\stackrel{⃖}{E_a}$, and energy difference ΔE_a of the processes described in Figure 8.

Then, we continued to study the adsorption of Sb atoms on the Ag₂Sb/Ag (111) substrate. Same as pure Ag (111) substrates, three types of substrates were constructed, and the curve of the formation energies vs C_Sb were plotted in Figure 1B. Overall, the formation energies on 3 × 3 substrates were generally lower than on the other two types of substrates. Unlike pure Ag (111) substrates, Sb exhibits different growth characteristics on the Ag₂Sb monolayer, the small antimony clusters are no longer more stable, and the formation energy continues to decline until at coverage of 8/9. At C_Sb = 8/9, the Sb layer shows a 2 × 2 reconstructed β-phase structure with a minor deformation on $\mathcal{C}$-type Ag₂Sb alloy monolayer. One of the Sb atoms in the lower sublayer is affected by the Sb atom of the substrate and shifts upward, causing the original double sublayers structure to split into three sublayers from the side view. The lattice constant is a = 4.388 Å, with about 6.58% stretching compared to the free state of antimonene (4.117 Å). The layer height is about 4.377 Å. This structure is in good agreement with the results of Sun et al.‘s work [28].

For A-type of Ag₂Sb/Ag (111) substrates, the results of single Sb on Ag₂Sb/Ag (111) shows that the Ag–Ag bridge site was the most favorable, but a monolayer of β-Sb with a layer height of 0.736 Å formed at C_Sb = 2/3 and Sb atoms occupy the top sites of both the Ag and Sb atoms in the substrate, see Figure 2A 2/3). At C_Sb = 3/3, the bilayer structure consisted of a layer of β-Sb and intercalated atoms, while the intercalated atoms were located at the Ag–Ag bridge-sites of the substrate. At C_Sb = 4/3, the bilayer structure consisted of two layers of β-Sb with AB stacking, the bottom layer was almost flat, and the top layer was a buckled honeycomb lattice with buckling higher the 1.022 Å. On such substrates, the flat honeycomb antimonene cannot be stabilized due to the surface alloy, but is replaced by a honeycomb structure with buckling. The interaction between the Ag and Sb atoms affects the structures of antimonene layers. It is worth mentioning that the formation energies of $\mathcal{A}$-type is the highest one of the three types.

The lowest formation energy on the $\mathcal{B}$-type Ag₂Sb/Ag (111) substrates was at C_Sb = 8/6, and a full-layer of α-Sb formed, see Figure 9. It was almost the same structural evolution path compared to the pure Ag (111) substrates, but, the formation energy of the full-layer of α-Sb is much lower than that of the half-layer, which means that the full-layer α-Sb is energetically stable on such substrate. The adsorbed Sb atoms first formed a half layer of α-Sb, which then grow to a full layer. Unlike on the pure Ag (111) substrate, the bottom layer of α-Sb was no longer flat. One of the Sb atoms in the unit cell sits on the top site of the Sb atom in the surface alloy, while the other Sb atoms sit on the bridge sites of the Ag–Ag pair. The difference in the strength of the interactions of Ag–Sb and Sb–Sb makes the interatomic spacing different.

FIGURE 9

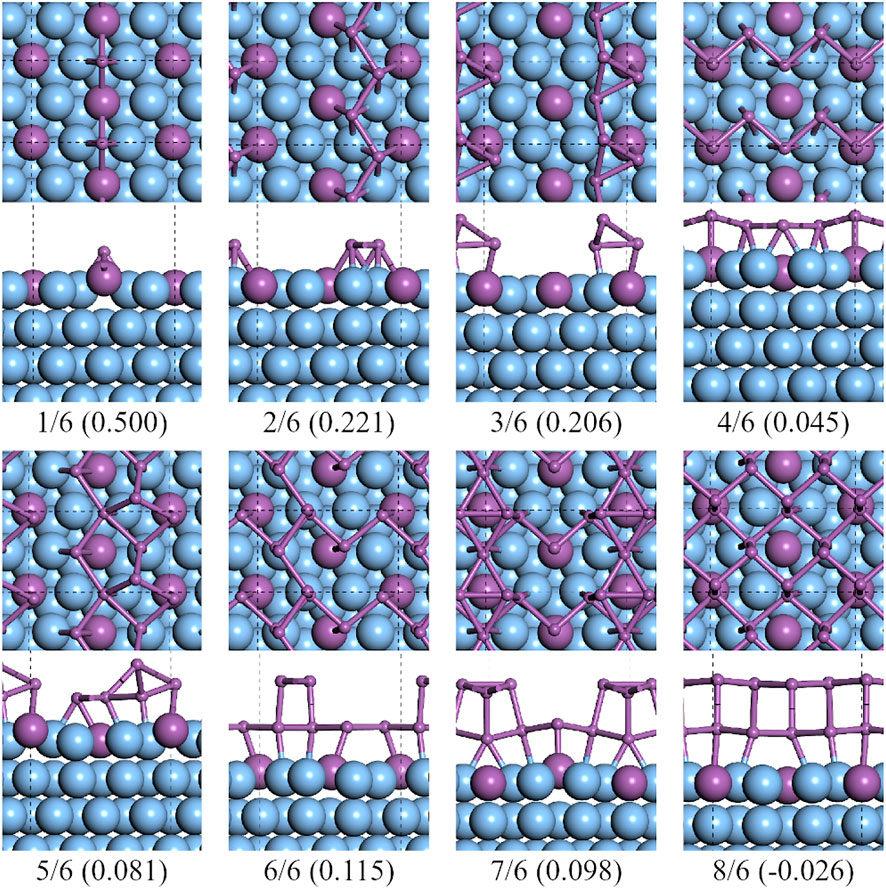
FIGURE 9. Top and side views of the lowest formation energy favorable configurations of antimony adsorbed on the $3\times \sqrt{3}$ Ag₂Sb/Ag (111) substrate.

On C-type Ag₂Sb/Ag (111) substrates, the lowest formation energy was at C_Sb = 8/9 of a reconstructed 2 × 2 supercell of β-Sb, see Figure 10. The reconstructed supercell contains eight Sb atoms, divided into two sublayers, with three of the four Sb atoms in the bottom layer at the bridge site of the Ag–Ag pair and the other Sb atom at the top site of the Sb atom in the surface alloy. This structure is highly consistent with that in Sun’s work [28]. It can be seen from the green dashed line in Figure 1 that the formation energy decreases with the increase of C_Sb. The existence of the alloy surface changes the potential energy surface of the Ag (111) substrate. Under its impact, the flat polygonal clusters, that appear on the pure silver substrate, are no longer the more stable configurations.

FIGURE 10

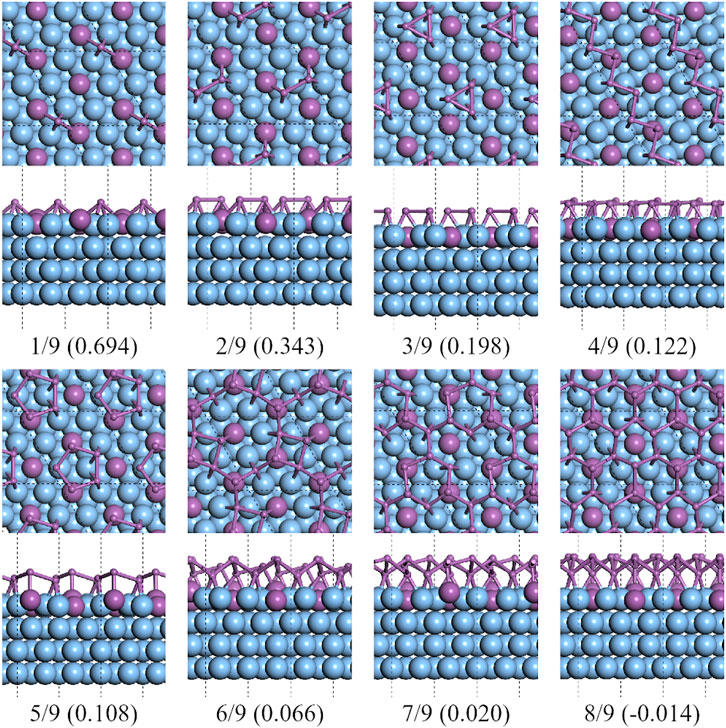
FIGURE 10. Top and side views of the lowest formation energy favorable configurations of antimony adsorbed on the 3×3 Ag₂Sb/Ag (111) substrate.

From the calculation results of the abovementioned three substrates, we can see that the presence of the surface alloy changes the adsorption site. The Sb–Sb interaction is somewhat stronger than that of Sb–Ag, so the presence of Sb atoms in the surface alloy can affect the growth of antimonene, especially in the earlier stage. The energetically stable adsorption sites change from the hollow sites to the Ag–Ag bridge sites. Moreover, unlike the pure silver substrate, the Sb top site is also a more stable adsorption site.

Our calculation shows that the formation energies of β-Sb (-0.014 eV/atom) and α-Sb (-0.026 eV/atom) on the Ag₂Sb/Ag (111) substrates are very close. Since both α- and β-Sb monolayers are stable in ambient conditions, we need to compare their structural stability and find their structural growth paths to determine which phrase is easier to grow on and which one is relatively stable. Therefore, we carefully examined all the structures, including the substable ones, from the half-layer to the full layer and found two evolutionary paths for each phrase on the Ag₂Sb/Ag (111) substrate. In Figure 11A, the formation energies increased and then decreased with the increasing coverage, where the two relatively stable configurations were half- and full-layer α-Sb at C_Sb = 4/6 and 8/6, respectively. The structures from C_Sb = 5/6 to 8/6 were all grown based on the stable structure at C_Sb = 4/6. It is clear that α-Sb is grown half-layer by half-layer on this substrate. Although, there exists a small energy barrier of 0.069 eV/atom along this path. For 3 × 3 Ag₂Sb/Ag (111) substrate in Figure 11B, at C_Sb = 4/9 and 5/9, there were quadrilateral and pentagonal rings with pucker, in which the Sb₅ is a very special one, two of the five atoms are sitting on the top site of the Sb atoms in the substrate, and the other three are on the top site of the Ag atoms. This pucker structure is exactly a part of the β-Sb at C_Sb = 8/9. The continuously deposited Sb atoms placed in their gap positions can form the structures of C_Sb = 6/9 and 7/9, and the structure of C_Sb = 7/9 is exactly β-Sb with a Sb vacancy. The formation energy decreases with the increasing concentration of the adsorbed Sb atoms, which indicates that the deposition process is exothermic and can react autonomously. The growth of β-Sb is more advantageous under lower-temperature, while at a high-temperature, there exists a competition between the two phases. Therefore, we believe that it should be possible to observe the growth of both the structures simultaneously during a given experiment.

FIGURE 11

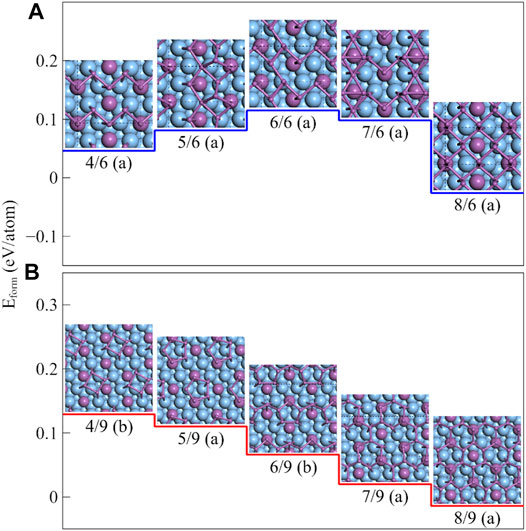
FIGURE 11. Structural evolution paths of $3\times \sqrt{3}$ and 3×3 supercell surface reconstructions of Sb on the Ag₂Sb/Ag (111) substrates. (A): $3\times \sqrt{3}$ substrate, culminating in α-Sb; (B): 3×3 substrate, culminating in β-Sb. The fractions marked below each structure represent their coverages, and (a) and (b) correspond to the most stable and meta-stable structures, respectively.

Considering the results of all the types of substrates together, both the size of reconstructed supercells and the surface alloy have a significant effect on growth. No matter with or without the surface alloy, the structure of antimonene on the $\mathcal{A}$-type of substrates always show a large stretch whether forming the flat honeycomb antimonene or low-buckled honeycomb antimonene. On the $\mathcal{B}$-type of substrates, the α-Sb occupy the main structures, and there exists a very clear evolutionary path of growing half-layer by half-layer. The half layer α-Sb has high stability, regardless of the deformation by the substrates. On the largest substrates in this work, the β-Sb exhibits excellent stability on the substrate with surface alloy and much less stability on the pure Ag (111) substrates compared to the flat honeycomb and half-layer α-phase antimonene. It can be seen that the phase of antimonene is deeply influenced by the size of the reconstructed supercells. Especially, all the configurations are at lower energy levels at the coverage of 2/3, which is included in all types of substrates, and the structures of antimonene are significantly modulated by the size of the reconstructed supercells. When adsorbed on the smaller substrates ($\mathcal{A}$ and $\mathcal{B}$), the Sb atoms could fully cover the substrates, but not for the larger ones $(\mathcal{C})$. The direct factor, which determines the different phases, is the size of the reconstructed supercells. If we can control the size of the reconstructed supercells, the phase of antimonene will be determined.

The existence of the surface alloy of Ag₂Sb has also played an important role in the growth of antimonene. At lower coverages (C_Sb < 2/3), clusters of Sb_N (N = 3, 4, and 5), although present, are no longer the most stable structures. On the other hand, at higher coverages (C_Sb > 2/3), the formation energies of α- and β-Sb shift from the higher to the lowest levels with the presence of the surface alloy. This has a positive effect on the formation of a stable monolayer of α-antimonene.

Note that the minimum value of the required coverage to form a monolayer are 2/3, 2/3, and 7/9 for the substrates of $\mathcal{A}$, $\mathcal{B}$, and $\mathcal{C}$ types, respectively. Our simulations are based on the complete relaxation of the Sb atoms on the substrate, and if the speed of the process of atomic relaxation can be controlled, then the phase of the antimonene should also be controllable. In the molecular beam epitaxy experiments, the control of relaxation is usually multifactorial, such as temperature, pressure, and source evaporation rate. Which one is the main factor affecting the relaxation speed remains to be finely verified.

4 Conclusion

In summary, we have simulated the growth process of antimonene on the Ag (111) substrate with and without Ag₂Sb surface alloy using the DFT and PSO methods. According to the results, in addition to the experimental reported flat honeycomb and β-phase antimonene, α-phase antimonene had also been observed to grow on the substrates and showed a highly stable topological structure with low puckering. In the comparison of the silver substrates with and without the surface alloys, it can be seen that the presence of surface alloys does not hinder the growth of antimonene, but rather promotes the stabilization of antimonene. On the substrates with Ag₂Sb surface alloy, both α-Sb and β-Sb have been observed to grow. The core of phase modulation engineering lies in the control of the relaxation rate of the antimony deposited atoms. Our work provides a more comprehensive theoretical insight into the growth of antimonene on silver substrates, complementing the possible omissions in experiments that may provide some basis for antimonene synthesis on such kind of metal substrate.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

LK, BK, and WJ contributed to conception and design of the study. LK carried out the computations and organized the database. BK and WJ performed the statistical analysis. SJ and LY contributed to the computational methods. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 12174084, 11904075, and 11874139), the National Postdoctoral Program for Innovative Talents (Grant No. BX20190104), the Scientific and Technological Research Foundation of Hebei Province (Grant No. ZD2021065), and the Key Program of Natural Science Foundation of Hebei Province (Grant No. A2021205024).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.856526/full#supplementary-material

References

1. Ares P, Palacios JJ, Abellán G, Gómez-Herrero J, Zamora F. Recent Progress on Antimonene: A New Bidimensional Material. Adv Mater (2018) 30:1703771. doi:10.1002/adma.201703771

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zhang S, Guo S, Chen Z, Wang Y, Gao H, Gómez-Herrero J, et al. Recent Progress in 2D Group-VA Semiconductors: From Theory to experiment. Chem Soc Rev (2018) 47:982–1021. doi:10.1039/c7cs00125h

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Wang X, Song J, Qu J. Antimonene: From Experimental Preparation to Practical Application. Angew Chem Int Ed (2019) 58:1574–84. doi:10.1002/anie.201808302

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Xue C-L, Li S-C. Recent Progress on Antimonene: From Theoretical Calculation to Epitaxial Growth. Jpn J Appl Phys (2021) 60:SE0805. doi:10.35848/1347-4065/abf74e

CrossRef Full Text | Google Scholar

5. Zhang S, Yan Z, Li Y, Chen Z, Zeng H. Atomically Thin Arsenene and Antimonene: Semimetal-Semiconductor and Indirect-Direct Band-Gap Transitions. Angew Chem Int Ed (2015) 54:3112–5. doi:10.1002/anie.201411246

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Meng Y-X, Zhao Y-F, Li S-C. Research Progress of Puckered Honeycomb Monolayers. Acta Phys Sin (2021) 70:148101. doi:10.7498/aps.70.20210638

CrossRef Full Text | Google Scholar

7. Wang G, Pandey R, Karna SP. Atomically Thin Group V Elemental Films: Theoretical Investigations of Antimonene Allotropes. ACS Appl Mater Inter (2015) 7:11490–6. doi:10.1021/acsami.5b02441

CrossRef Full Text | Google Scholar

8. Wang Y, Ding Y. Electronic Structure and Carrier Mobilities of Arsenene and Antimonene Nanoribbons: A First-Principle Study. Nanoscale Res Lett (2015) 10:254. doi:10.1186/s11671-015-0955-7

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Aktürk OÜ, Özçelik VO, Ciraci S. Single-layer Crystalline Phases of Antimony: Antimonenes. Phys Rev B (2015) 91:235446. doi:10.1103/physrevb.91.235446

CrossRef Full Text | Google Scholar

10. Wang S, Wang W, Zhao G. Thermal Transport Properties of Antimonene: An Ab Initio Study. Phys Chem Phys (2016) 18:31217–22. doi:10.1039/c6cp06088a

CrossRef Full Text | Google Scholar

11. Zhao M, Zhang X, Li L. Strain-driven Band Inversion and Topological Aspects in Antimonene. Sci Rep (2015) 5:16108. doi:10.1038/srep16108

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Kripalani DR, Kistanov AA, Cai Y, Xue M, Zhou K. Strain Engineering of Antimonene by a First-Principles Study: Mechanical and Electronic Properties. Phys Rev B (2018) 98:085410. doi:10.1103/physrevb.98.085410

CrossRef Full Text | Google Scholar

13. Zhao A, Wang B. Two-dimensional Graphene-like Xenes as Potential Topological Materials. APL Mater (2020) 8:030701. doi:10.1063/1.5135984

CrossRef Full Text | Google Scholar

14. Cheung C-H, Fuh H-R, Hsu M-C, Lin Y-C, Chang C-R. Spin Orbit Coupling Gap and Indirect Gap in Strain-Tuned Topological Insulator-Antimonene. Nanoscale Res Lett (2016) 11:459. doi:10.1186/s11671-016-1666-4

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, et al. Electric Field Effect in Atomically Thin Carbon Films. Science (2004) 306:666–9. doi:10.1126/science.1102896

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ares P, Aguilar-Galindo F, Rodríguez-San-Miguel D, Aldave DA, Díaz-Tendero S, Alcamí M, et al. Mechanical Isolation of Highly Stable Antimonene under Ambient Conditions. Adv Mater (2016) 28:6332–6. doi:10.1002/adma.201602128

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Gibaja C, Rodriguez-San-Miguel D, Ares P, Gómez-Herrero J, Varela M, Gillen R, et al. Few-Layer Antimonene by Liquid-phase Exfoliation. Angew Chem Int Ed (2016) 55:14345–9. doi:10.1002/anie.201605298

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wang X, He J, Zhou B, Zhang Y, Wu J, Hu R, et al. Bandgap‐Tunable Preparation of Smooth and Large Two‐Dimensional Antimonene. Angew Chem (2018) 130:8804–9. doi:10.1002/ange.201804886

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Gibaja C, Assebban M, Torres I, Fickert M, Sanchis-Gual R, Brotons I, et al. Liquid Phase Exfoliation of Antimonene: Systematic Optimization, Characterization and Electrocatalytic Properties. J Mater Chem A (2019) 7:22475–86. doi:10.1039/c9ta06072c

CrossRef Full Text | Google Scholar

20. Ji J, Song X, Liu J, Yan Z, Huo C, Zhang S, et al. Two-dimensional antimonene single crystals grown by van der Waals epitaxy. Nat Commun (2016) 7:13352. doi:10.1038/ncomms13352

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wu X, Shao Y, Liu H, Feng Z, Wang Y-L, Sun J-T, et al. Epitaxial Growth and Air-Stability of Monolayer Antimonene on PdTe₂. Adv Mater (2017) 29:1605407. doi:10.1002/adma.201605407

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chen H-A, Sun H, Wu C-R, Wang Y-X, Lee P-H, Pao C-W, et al. Single-Crystal Antimonene Films Prepared by Molecular Beam Epitaxy: Selective Growth and Contact Resistance Reduction of the 2D Material Heterostructure. ACS Appl Mater Inter (2018) 10:15058–64. doi:10.1021/acsami.8b02394

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Sun X, Lu Z, Xiang Y, Wang Y, Shi J, Wang G-C, et al. Van der Waals Epitaxy of Antimony Islands, Sheets, and Thin Films on Single-Crystalline Graphene. ACS Nano (2018) 12:6100–8. doi:10.1021/acsnano.8b02374

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Flammini R, Colonna S, Hogan C, Mahatha SK, Papagno M, Barla A, et al. Evidence Of β-Antimonene at the Sb/Bi2Se3 Interface. Nanotechnology (2018) 29:065704. doi:10.1088/1361-6528/aaa2c4

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zhang Y-W, Li J-Y, Wu C-H, Chang C-Y, Chang S-W, Shih M-H, et al. Tungsten Diselenide Top-Gate Transistors with Multilayer Antimonene Electrodes: Gate Stacks and Epitaxially Grown 2D Material Heterostructures. Sci Rep (2020) 10:5967. doi:10.1038/s41598-020-63098-1

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Mao Y-H, Zhang L-F, Wang H-L, Shan H, Zhai X-F, Hu Z-P, et al. Epitaxial Growth of Highly Strained Antimonene on Ag(111). Front Phys (2018) 13:138106. doi:10.1007/s11467-018-0757-3

CrossRef Full Text | Google Scholar

27. Shao Y, Liu Z-L, Cheng C, Wu X, Liu H, Liu C, et al. Epitaxial Growth of Flat Antimonene Monolayer: A New Honeycomb Analogue of Graphene. Nano Lett (2018) 18:2133–9. doi:10.1021/acs.nanolett.8b00429

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Sun S, Yang T, Luo YZ, Gou J, Huang Y, Gu C, et al. Realization of a Buckled Antimonene Monolayer on Ag(111) via Surface Engineering. J Phys Chem Lett (2020) 11:8976–82. doi:10.1021/acs.jpclett.0c02637

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Niu T, Zhou W, Zhou D, Hu X, Zhang S, Zhang K, et al. Modulating Epitaxial Atomic Structure of Antimonene through Interface Design. Adv Mater (2019) 31:1902606. doi:10.1002/adma.201902606

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Zhou D, Si N, Jiang B, Song X, Huang H, Ji Q, et al. Interfacial Effects on the Growth of Atomically Thin Film: Group VA Elements on Au(111). Adv Mater Inter (2019) 6:1901050. doi:10.1002/admi.201901050

CrossRef Full Text | Google Scholar

31. Niu T, Meng Q, Zhou D, Si N, Zhai S, Hao X, et al. Large‐Scale Synthesis of Strain‐Tunable Semiconducting Antimonene on Copper Oxide. Adv Mater (2020) 32:1906873. doi:10.1002/adma.201906873

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Gu M, Li C, Ding Y, Zhang K, Xia S, Wang Y, et al. Direct Growth of Antimonene on C-Plane Sapphire by Molecular Beam Epitaxy. Appl Sci (2020) 10:639. doi:10.3390/app10020639

CrossRef Full Text | Google Scholar

33. Wang Y, Lv J, Zhu L, Ma Y. Crystal Structure Prediction via Particle-Swarm Optimization. Phys Rev B (2010) 82:094116. doi:10.1103/PhysRevB.82.094116

CrossRef Full Text | Google Scholar

34. Wang Y, Lv J, Zhu L, Ma Y. CALYPSO: A Method for crystal Structure Prediction. Comput Phys Commun (2012) 183:2063–70. doi:10.1016/j.cpc.2012.05.008

CrossRef Full Text | Google Scholar

35. Lu S, Wang Y, Liu H, Miao M-s., Ma Y. Self-assembled Ultrathin Nanotubes on diamond (100) Surface. Nat Commun (2014) 5:3666. doi:10.1038/ncomms4666

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Oppo S, Fiorentini V, Scheffler M. Theory of Adsorption and Surfactant Effect of Sb on Ag(111). Phys Rev Lett (1993) 71:2437–40. doi:10.1103/PhysRevLett.71.2437

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Soares EA, Bittencourt C, Nascimento VB, de Carvalho VE, de Castilho CMC, McConville CF, et al. Structure Determination of Ag(111) (3×3) R30°−Sb by Low-Energy Electron Diffraction. Phys Rev B (2000) 61:13983–7. doi:10.1103/PhysRevB.61.13983

CrossRef Full Text | Google Scholar

38. Quinn PD, Brown D, Woodruff DP, Bailey P, Noakes TCQ. Structural Study of the Adsorption of Sb on Ag( 111 ) Using Medium Energy Ion Scattering. Surf Sci (2002) 511:43–56. doi:10.1016/S0039-6028(02)01488-7

CrossRef Full Text | Google Scholar

39. Kresse G, Hafner J. Ab Initiomolecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium. Phys Rev B (1994) 49:14251–69. doi:10.1103/PhysRevB.49.14251

CrossRef Full Text | Google Scholar

40. Kresse G, Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput Mater Sci (1996) 6:15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

41. Kresse G, Furthmüller J. Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys Rev B (1996) 54:11169–86. doi:10.1103/PhysRevB.54.11169

CrossRef Full Text | Google Scholar

42. Blöchl PE. Projector Augmented-Wave Method. Phys Rev B (1994) 50:17953–79. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

43. Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, et al. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys Rev B (1992) 46:6671–87. doi:10.1103/PhysRevB.46.6671

CrossRef Full Text | Google Scholar

44. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Grimme S, Antony J, Ehrlich S, Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J Chem Phys (2010) 132:154104. doi:10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Kühne TD, Iannuzzi M, Del Ben M, Rybkin VV, Seewald P, Stein F, et al. CP2K: An Electronic Structure and Molecular Dynamics Software Package - Quickstep: Efficient and Accurate Electronic Structure Calculations. J Chem Phys (2020) 152:194103. doi:10.1063/5.0007045

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Sheppard D, Xiao P, Chemelewski W, Johnson DD, Henkelman G. A Generalized Solid-State Nudged Elastic Band Method. J Chem Phys (2012) 136:074103. doi:10.1063/1.3684549

PubMed Abstract | CrossRef Full Text | Google Scholar