Abstract
Self-propelled objects, which exhibit characteristic features of motion, are proposed based on nonlinear science. At first, a self-propelled object with length like undulatory swimming is designed, i.e., the phase of oscillation at several points on the object is propagated in the opposite direction of motion. Second, the vertical oscillation of a camphor disk is created at an amphiphilic molecular layer developed on water. The proposed systems suggest that nonlinearity can enhance the autonomy of self-propelled objects as multidimensional motion.
Introduction
Several types of inanimate self-propelled objects such as nano wires and Janus particles have been developed for environmental, industrial, and medical applications [1–4]. In general, self-propelled objects exhibit random motion or unidirectional motion which is determined by their shape or the external force [1–7]. On the other hand, animate self-propelled objects such as bacteria exhibit characteristic features of motion depending on the information of the environment. These facts suggest that the autonomy of animate self-propelled objects is significantly higher than that of the inanimate ones [5–7].
We introduced nonlinear science into systems to enhance their autonomy, and as a result, characteristic nonlinear phenomena such as oscillation, bifurcation, synchronization, hysteresis, and pattern formation could be reproduced experimentally [5–7]. Several types of self-propelled objects, which exhibit characteristic features of motion from the viewpoint of nonlinear science, have been reported [5–18]. Among them, the objects composed of camphor or camphor derivatives, of which the driving force is the difference in surface tension, have been investigated as a simple experimental system [5–7, 19–35]. For example, a camphor disk placed on a linear water channel, reciprocating motion along the channel, was observed [5, 6]. When a camphor disk attached to the bottom of a larger plastic circular plate was placed on water, oscillatory motion between rest and motion was observed, and the bifurcation between the continuous and oscillatory motion was determined by the location of the camphor disk [5, 6, 23, 27]. The period of oscillatory motion and bifurcation between continuous and oscillatory motion was observed coupled with chemical reactions [5–8, 36, 37]. When two or more camphor disks or boats were placed in the same circular water channel, synchronized swimming or collective motion was observed [5–7]. Motion with memory, i.e., future motion expected by previous motion, could be realized by using a camphor disk and plastic plate [22, 28, 35]. Recently, the catch and release type of chemotaxis was realized using 6-methylcoumarin as a self-propelled object and sodium phosphate as a chemical stimulus [38]. These characteristic features of motion could be qualitatively reproduced by numerical calculations based on reaction–diffusion equations and the equation of motion [5–7, 28, 31–35, 39].
In this article, we propose novel self-propelled objects which exhibit multidimensional motion at the air–water interface under nonequilibrium: one is a self-propelled object with length like undulatory swimming and the other exhibits vertical oscillation of a camphor disk on an amphiphilic molecular layer developed on water. The proposed systems suggest that nonlinearity can further enhance the autonomy of self-propelled objects.
Self-Propelled Filament Like Undulatory Swimming
In this section, we introduce a self-propelled filament placed on water. The filament is produced from a commercial adhesive (consisting mainly of nitrocellulose and acetone), and the energy source is acetone and the driving force of motion is the difference in the surface tension around the filament since acetone reduces the surface tension. As the shape of the filament is deformed and oscillated periodically, information of wave propagation along the filament is added as characteristic features of motion in addition to information of mass movement [40]. When one of the end points of the single filament is fixed on the edge of the chamber, periodic pendulum motion is produced and the phase of the filament near the fixed edge progresses faster in comparison with the phase of the free edge for the pendulum motion. When two filaments are coupled together, in-phase and out-phase synchronizations are produced depending on the distance between them and the initial floating state.
We propose a self-propelled filament of which one of the end points is adhered to the free plastic film with V-shape to introduce heterogeneity. Figure 1 shows (a) snapshots of the filament and (b) outline of points a, b, c, and d on the filament. The filament moves in the direction of the plastic film while oscillating except for point a, i.e., the head of the filament. The phase of oscillation was propagated from b to d, i.e., in the opposite direction of the motion. The propagation of the phase oscillation in the animate undulatory swimming is the same as the direction of motion. Thus, the direction of the phase propagation of our inanimate meandering filament is opposite to the animate undulatory swimming like “moon walk” by MJ. The opposite direction of phase propagation suggests that our inanimate filament is passive on the motion since the Marangoni flow occurs in the opposite direction of motion. The shape and size of the head of the filament should be improved to make the direction of the phase propagation the same as animate undulatory swimming.
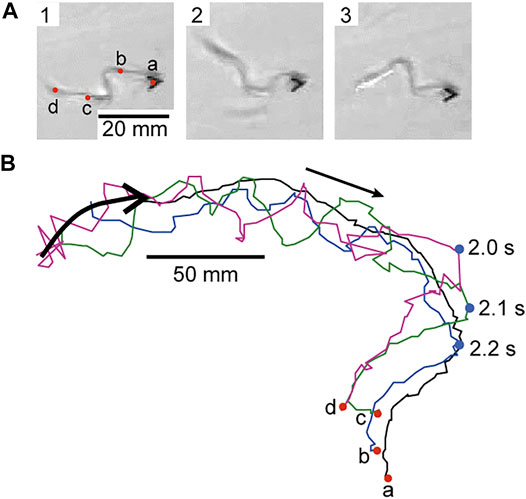
FIGURE 1
(A) Snapshots of the self-propelled filament (time interval: 0.2 s) and (B) outline of the points a, b, c, and d on the filament from top view. The arrow around the middle of the outline denotes the direction of motion. The object around the left side of the outline denotes the schematic illustration of the filament. [See the actual movies in the supporting information as Supplementary Movie S1 (10× speed)]. 2.2, 2.1, and 2.0 s on the blue circles in (A) denote the time at one of the maximum values of the oscillation on the outlines of the points b, c, and d.
Vertical Oscillatory Motion of a Camphor Disk Placed on an Amphiphilic Molecular Layer Developed at the Air–Water Interface
In this chapter, we introduce vertical oscillatory motion of a camphor disk placed on an amphiphilic molecular layer developed at the air–water interface. Here, nervonic acid is used as an amphiphilic substance [24]. The surface pressure vs. area isotherm exhibits a transition point corresponding to a phase transition between the fluid and fluid/condensed phases of nervonic acid. The characteristic features of motion, i.e., no motion, oscillatory motion, and continuous motion, are determined by not only the value of the surface pressure but also the nature of the phase in the nervonic acid molecular layer. These results suggest that the characteristic features of motion can be designed based on the chemical structure of an amphiphilic molecule.
We propose vertical oscillation of a camphor disk (diameter: 3 mm, thickness: 1 mm) placed at the air–water interface. Here, nervonic acid which is developed on water is in the fluid/condensed phase. Figure 2 shows (a1) snapshots of one cycle of vertical oscillation and (a2) time-variation of the lateral location of a camphor disk. The camphor disk exhibited not only lateral oscillation but also vertical oscillation even at the air–water interface. The vertical oscillation may be generated by the following mechanism. As the surface pressure of the nervonic acid molecular layer (Πna ∼ 8 mN m−1 at 293 K and 40 Å molecule−1) is similar to that of the camphor (Πc, the saturated value of Πc ∼ 17 mN m−1), repetition between the resting and motion states is possible since no motion at Πna ≥ Πc and motion at Πna ≤ Πc occur. The periodicity and nonlinearity of the oscillation were observed as the fundamental frequency (∼0.3 Hz) and the higher harmonics in the linear spectrum of the fast Fourier transformation (FFT) for Figure 2A2, respectively (see Figure 2A3). Vertical oscillation may occur due to the repetition of fluid and fluid/condensed phases since the development and sublimation of the camphor molecules at the air–water interface induces the phase transition from the fluid/condensed to the fluid phase and vice versa, respectively. No oscillation was observed at 298 K and 40 Å molecule−1, i.e., the fluid phase, as shown in Figure 2B. The change in the surface pressure around the disk induces the change in the meniscus at the camphor solid/water interface including nervonic acid, and as a result, the vertical oscillation occurs.
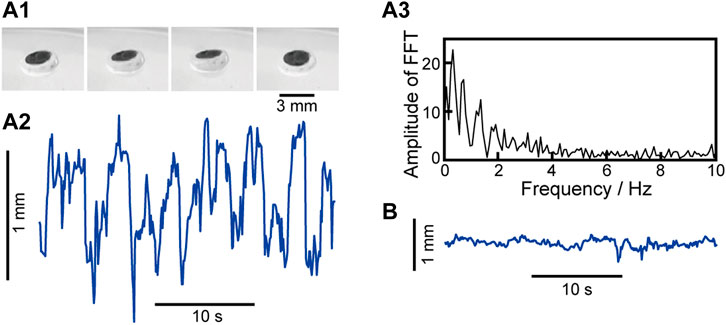
FIGURE 2
(A1) Snapshots of vertical oscillation of a camphor disk (time interval: 0.2 s, view from an angle) and (A2) time-variation of the location of the camphor disk on the vertical axis, (A3) linear spectrum of FFT for (A2) at 293 K and 40 Å molecule−1 and (B) time-variation of the location of the camphor disk on the vertical axis at 298 K and 40 Å molecule−1. A black circle on the camphor disk was marked to measure the vertical location using the laser displacement meter. [See the actual movies in the supporting information as Supplementary Movie S2 (10× speed)].
Conclusion and Outlook
In this article, we proposed novel types of self-propelled objects which exhibit multidimensional motion from the viewpoint of nonlinear science. Further multidimensional motion, such as translation including rotation like drill and pattern formation coupled with motion like collective motion, will be created in the near future by enhancing autonomy.
Statements
Data availability statement
The data that support the findings of this study are available from the corresponding author, SN, upon reasonable request.
Author contributions
RF performed the examination, analyzed the experimental results, and prepared the manuscript. MM analyzed the data and edited the manuscript. SN planned the experimental system and edited the manuscript.
Funding
This study was supported by JSPS KAKENHI (Grant Nos. JP20H02712, JP20H01871, and JP21H00996), the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” (No. 20211061) to SN, JSPS Bilateral Joint Research Project between Japan and the Polish Academy of Sciences (JPJSBP120204602), and JSPS Japan–Hungary Bilateral Joint Research Project (JPJSBP120213801).
Acknowledgments
We acknowledge Mr. Katsuhiko Kayahara for his technical support on the examination.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.854892/full#supplementary-material
References
1.
Soto F Karshalev E Zhang F Esteban Fernandez de Avila B Nourhani A Wang J . Smart Materials for Microrobots. Chem Rev (2021). 10.1021/acs.chemrev.0c00999
2.
Wang H Pumera M . Coordinated Behaviors of Artificial Micro/Nanomachines: From Mutual Interactions to Interactions with the Environment. Chem Soc Rev (2020) 49:3211–30. 10.1039/c9cs00877b
3.
Huang Z Chen P Zhu G Yang Y Xu Z Yan L-T . Bacteria-Activated Janus Particles Driven by Chemotaxis. ACS Nano (2018) 12(7):6725–33. 10.1021/acsnano.8b01842
4.
Bechinger C Di Leonardo R Löwen H Reichhardt C Volpe G Volpe G . Active Particles in Complex and Crowded Environments. Rev Mod Phys (2016) 88(4):45006–150. 10.1103/RevModPhys.88.045006
5.
Nakata S Pimienta V Lagzi I Kitahata H Suematsu NJ . Self-Organized Motion, Physicochemical Design Based on Nonlinear Dynamics. Cambridge: RSC-ebook (2018). 10.1039/9781788013499
6.
Nakata S Nagayama M Kitahata H Suematsu NJ Hasegawa T . Physicochemical Design and Analysis of Self-Propelled Objects that Are Characteristically Sensitive to Environments. Phys Chem Chem Phys (2015) 17:10326–38. 10.1039/C5CP00541H
7.
Suematsu NJ Nakata S . Evolution of Self-Propelled Objects: From the Viewpoint of Nonlinear Science. Chem Eur J (2018) 24:6308–24. 10.1002/chem.201705171
8.
Suematsu NJ Mori Y Amemiya T Nakata S . Spontaneous Mode Switching of Self-Propelled Droplet Motion Induced by a Clock Reaction in the Belousov-Zhabotinsky Medium. J Phys Chem Lett (2021) 12(31):7526–30. 10.1021/acs.jpclett.1c02079
9.
Kitahata H Yoshinaga N Nagai KH Sumino Y . Spontaneous Motion of a Droplet Coupled with a Chemical Wave. Phys Rev E (2011) 84(1):015101. 10.1103/PhysRevE.84.015101
10.
Tanaka S Nakata S Nagayama M . A Surfactant Reaction Model for the Reciprocating Motion of a Self-Propelled Droplet. Soft Matter (2021) 17:388–96. 10.1039/d0sm01500h
11.
Banno T Asami A Ueno N Kitahata H Koyano Y Asakura K et al Deformable Self-Propelled Micro-object Comprising Underwater Oil Droplets. Sci Rep (2016) 6:31292–19. 10.1038/srep31292
12.
Banno T Kuroha R Toyota T . pH-Sensitive Self-Propelled Motion of Oil Droplets in the Presence of Cationic Surfactants Containing Hydrolyzable Ester Linkages. Langmuir (2012) 28(2):1190–5. 10.1021/la2045338
13.
Ban T Matsumoto K Nanzai B Mori Y Nabika H . Bifurcation of Chemically Driven Self-Propelled Droplets on a Surfactant-Adsorbed Surface Based on Spreading Coefficients. Colloids Surf A: Physicochemical Eng Aspects (2021) 620(5):126563. 10.1016/j.colsurfa.2021.126563
14.
Sharma J Tiwari I Das D Parmananda P Akella VS Pimienta V . Rotational Synchronization of Camphor Ribbons. Phys Rev E (2019) 99(1):012204. 10.1103/PhysRevE.99.012204
15.
Čejková J Novák M Štěpánek F Hanczyc MM . Dynamics of Chemotactic Droplets in Salt Concentration Gradients. Langmuir (2014) 30(40):11937–44. 10.1021/la502624f
16.
Zhou C Chen X Han Z Wang W . Photochemically Excited, Pulsating Janus Colloidal Motors of Tunable Dynamics. ACS Nano (2019) 13(4):4064–72. 10.1021/acsnano.8b08276
17.
Holló G Suematsu NJ Ginder E Lagzi I . Electric Field Assisted Motion of a Mercury Droplet. Sci Rep (2021) 11:2753–111. 10.1038/s41598-020-80375-1
18.
Yamamoto D Maeno J Manabe Y Okamoto Y Nawa-Okita E Shioi A . Mode Bifurcation on Contact Line Dynamics at Oil/Water Interface Depending on the Contact Line Length. Front Chem (2021) 9:708633–18. 10.3389/fchem.2021.708633
19.
Tomlinson C . On the Motions of Camphor on the Surface of Water. Proc R Soc Lond (1860) 11:575–7.
20.
Rayleigh L . Measurements of the Amount of Oil Necessary in Order to Check the Motions of Camphor upon Water. Proc R Soc Lond (1890) 47:364–7.
21.
Nakata S Iguchi Y Ose S Kuboyama M Ishii T Yoshikawa K . Self-Rotation of a Camphor Scraping on Water: New Insight into the Old Problem. Langmuir (1997) 13(16):4454–8. 10.1021/la970196p
22.
Fujita R Matsufuji T Matsuo M Nakata S . Alternate Route Selection of Self-Propelled Filter Papers Impregnated with Camphor for Two-Branched Water Channels. Langmuir (2021) 37(23):7039–42. 10.1021/acs.langmuir.1c00644
23.
Xu Y Takayama N Er H Nakata S . Oscillatory Motion of a Camphor Object on a Surfactant Solution. J Phys Chem B (2021) 125(6):1674–9. 10.1021/acs.jpcb.0c09314
24.
Nakata S Fujita R . Self-Propelled Motion of a Camphor Disk on a Nervonic Acid Molecular Layer and its Dependence on Phase Transition. J Phys Chem B (2020) 124(26):5525–9. 10.1021/acs.jpcb.0c03044
25.
Nakata S Matsufuji T Gorecki J Kitahata H Nishimori H . Inversion Probability of Three-Bladed Self-Propelled Rotors after Forced Stops of Different Durations. Phys Chem Chem Phys (2020) 22:13123–8. 10.1039/d0cp00746c
26.
Nakata S Nasu K Irie Y Hatano S . Self-Propelled Motion of a Camphor Disk on a Photosensitive Amphiphilic Molecular Layer. Langmuir (2019) 35(12):4233–7. 10.1021/acs.langmuir.8b04285
27.
Tenno R Gunjima Y Yoshii M Kitahata H Gorecki J Suematsu NJ et al Period of Oscillatory Motion of a Camphor Boat Determined by the Dissolution and Diffusion of Camphor Molecules. J Phys Chem B (2018) 122(6):2610–5. 10.1021/acs.jpcb.7b11903
28.
Nakata S Kayahara K Yamamoto H Skrobanska P Gorecki J Awazu A et al Reciprocating Motion of a Self-Propelled Rotor Induced by Forced Halt and Release Operations. J Phys Chem C (2018) 122(6):3482–7. 10.1021/acs.jpcc.7b12089
29.
Matsuo M Hashishita H Nakata S . Self-Propelled Motion Sensitive to the Chemical Structure of Amphiphilic Molecular Layer on an Aqueous Phase. Membranes (2021) 11(11):885. 10.3390/membranes11110885
30.
Löffler RJG Hanczyc MM Gorecki J . A Hybrid Camphor-Camphene Wax Material for Studies on Self-Propelled Motion. Phys Chem Chem Phys (2019) 21:24852–6. 10.1039/C9CP04722K
31.
Koyano Y Kitahata H Nakata S Gorecki J . On a Simple Model that Explains Inversion of a Self-Propelled Rotor under Periodic Stop-And-Release-Operations. Chaos (2020) 30:023105–1. 10.1063/1.5140626
32.
Nagayama M Nakata S Doi Y Hayashima Y . A Theoretical and Experimental Study on the Unidirectional Motion of a Camphor Disk. Physica D: Nonlinear Phenomena (2004) 194:151–65. 10.1016/j.physd.2004.02.003
33.
Koyano Y Gryciuk M Skrobanska P Malecki M Sumino Y Kitahata H et al Relationship between the Size of a Camphor-Driven Rotor and its Angular Velocity. Phys Rev E (2017) 96:012609. 10.1103/PhysRevE.96.012609
34.
Koyano Y Suematsu NJ Kitahata H . Rotational Motion of a Camphor Disk in a Circular Region. Phys Rev E (2019) 99:022211. 10.1103/PhysRevE.99.022211
35.
Nakata S Hata M Ikura YS Heisler E Awazu A Kitahata H et al Motion with Memory of a Self-Propelled Object. J Phys Chem C (2013) 117(46):24490–5. 10.1021/jp409172m
36.
Nakata S Irie Y Suematsu NJ . Self-Propelled Motion of a Coumarin Disk Characteristically Changed in Couple with Hydrolysis on an Aqueous Phase. J Phys Chem B (2019) 123(19):4311–7. 10.1021/acs.jpcb.8b11534
37.
Xu Y Ji L Izumi S Nakata S . pH‐Sensitive Oscillatory Motion of a Urease Motor on the Urea Aqueous Phase. Chem Asian J (2021) 16(13):1762–6. 10.1002/asia.202100336
38.
Yasugahira Y Tatsumi Y Yamanaka O Nishimori H Nagayama M Nakata S . Catch and Release Chemotaxis. ChemSystemsChem (2021) 3:e202100031–16. 10.1002/syst.202100031
39.
Kim M Okamoto M Yasugahira Y Tanaka S Nakata S Kobayashi Y et al A Reaction-Diffusion Particle Model for Clustering of Self-Propelled Oil Droplets on a Surfactant Solution. Physica D: Nonlinear Phenomena (2021) 425:132949–113. 10.1016/j.physd.2021.132949
40.
Nakata S Kayahara K Kuze M Ginder E Nagayama M Nishimori H . Synchronization of Self-Propelled Soft Pendulums. Soft Matter (2018) 14:3791–8. 10.1039/c8sm00517f
Summary
Keywords
nonlinear, oscillation, self-propelled object, camphor, nonequilibrium, autonomy
Citation
Fujita R, Matsuo M and Nakata S (2022) Multidimensional Self-Propelled Motion Based on Nonlinear Science. Front. Phys. 10:854892. doi: 10.3389/fphy.2022.854892
Received
14 January 2022
Accepted
04 February 2022
Published
07 March 2022
Volume
10 - 2022
Edited by
Rabih Sultan, American University of Beirut, Lebanon
Reviewed by
Charles Reichhardt, Los Alamos National Laboratory (DOE), United States
Updates
Copyright
© 2022 Fujita, Matsuo and Nakata.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Satoshi Nakata, nakatas@hiroshima-u.ac.jp
This article was submitted to Physical Chemistry and Chemical Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.