Abstract
Two-dimensional generalized XY spin model on a triangular lattice is studied by means of Monte-Carlo simulations. The critical temperatures of Berezinskii-Kosterlitz-Thouless (BKT) phase transition are obtained by the method of helicity modulus. It is found that the results are consistent with those obtained by other methods. The vortex density and the vortex-antivortex pair formation energy are also obtained. The result shows that the critical temperature decreases with the increase of the generalization parameter . While the vortex-antivortex pair formation energy increases with the increase of when .
Introduction
The critical phase transition behavior of two-dimensional spin models has been the subject of intense study in recent years. The two-dimensional (2D) XY spin model is one of the most intensively studied due to it’s a paradigmatic example of phase transitions mediated by topological defects [1–4]. It is well known that there is a Berezinskii-Kosterlitz-Thouless (BKT) phase transition in the XY spin model. The BKT phase transition is caused by the unbinding of vortex-antivortex pairs [3, 4]. The XY model has a rich variety of applications in condensed matter physics and statistical physics. For example, it can be used to describe magnetic films with planar anisotropy, two-dimensional solids, thin-film super fluids or superconductors [5, 6].
Besides the two-dimensional XY model, transitions of the BKT type exist in other models such as the classical Heisenberg antiferromagnet model [7], spin model of Long-Range ferromagnetic interactions [8], the ice-type F model [9], 2D spin models with nonmagnetic impurities [10–12] and even spin model with anisotropic interaction [13]. Thus a thorough and quantitative understanding of XY model is very important for the expansion of theoretical physics knowledge. Recently, a generalized XY model has been proposed and attracted a lot of interest [14]. The generalized XY model Hamiltonian is described bywhere spin vector consists of three spin components parameterized by usual spherical angles, defined as . is the generalization parameter. is a ferromagnetic interaction of nearest neighbours. Notice that the case corresponds to the usual XY model and the case is the planar rotator model with two-component spins. In this model, an ordering transition taking place at finite temperature for is supported by mean field and two-site cluster approaches [14]. In turn, different techniques, such as self-consistent harmonic approximation (SCHA) and Monte Carlo (MC) simulation, had been used to investigate this transition for all values of . It is found that the phase transition temperature of this phase transition decreases with the increase of , and it is confirmed that this second-order phase transition is similar to XY type, that is, it belongs to BKT type phase transition [15–17]. Using Monte Carlo simulation, some physical quantities such as vortex density, specific heat, energy and critical temperature are obtained on different lattices [15, 18]. Moreover, a first-order phase transition is also proved to exist when the value of is large [15, 17]. However, most of the previous work did not discuss the helicity modulus and vortex in detail. In particular, vortex density and the vortex-antivortex pair formation energy have an extremely important reference for the study of BKT phase transition. In this paper, we further expand research content and discuss in detail the vortex density and helicity modulus.
Method and Results
A hybrid MC approach that includes Wolff cluster [19] and Metropolis single spin updates [20] has been used to calculate some thermodynamic quantities for the model defined by Eq. 1. The initial spin configuration is constructed by randomly assigning a spin value to each lattice point. The simulations were performed on a triangular lattice with periodic boundary conditions for system size , where the largest size of lattice is considered as . During the simulation, MC steps are used for equilibration and about MC steps are used to get thermal averages at each temperature. The thermodynamic quantities have been discussed in detail in our previous work [18, 21]. In the present work, we mainly focus on discussion of vortex density and helicity modulus in the case of different . For simplicity, we set during the simulation. It should be noted that in this paper, when the statistical errors are less than the symbols, the error bars are not shown in the figures.
In the process of Monte Carlo simulation, different methods are often used to determine the phase transition temperature (or critical temperature) , such as finite size scaling method of susceptibility, Binder fourth-order cumulant method, helicity modulus method and so on. The helicity modulus, , obtained by a measure of the resistance to an infinitesimal spin twist across the system along one coordinate, is an efficient method to calculate the BKT phase-transition temperature [22]. The difference between the internal energy obtained under periodic and antiperiodic boundary conditions yields the temperature derivative of helicity modulus [23]. An expression applicable to any general model Hamiltonian is [24].where is the inverse temperature and for simplicity. is infinitesimal spin twist. For the generalized XY model, defined by Eq. 1, following the derivation process of Ref. [25], the expression of helicity modulus (in limit ) on a triangular lattice can be written as
Here is the unite vector pointing from site to site . is a selected basis vector in one coordinate. According to the renormalization-group theory [2], there is a universal relation between the helicity modulus and the phase-transition temperature. The BKT transition is characterized by a jump in the helicity modulus from to zero at the critical temperature. That is, the critical temperature can be estimated from the intersection of the helicity modulus and the straight line . Taking and 10 as an example, Figure 1 shows the results of helicity modulus as a function of temperature. The lattice size is . Through the intersection of the two lines, the critical temperatures are estimated to be 0.804 () and 0.892 (), respectively. Because the finite lattice sizes give rise to a smoothing of the jump in helicity modulus, so the critical temperatures of this method are often estimated higher than the real values. Therefore, it is necessary to find more effective methods to avoid the influence of finite-size effect. Through the solution of the renormalization group equation, it is obtained that at the critical temperature the helicity modulus can be described by the following relationship with the lattice size [3].where C is an undetermined fitting constant. According to finite-size scaling formula of helicity modulus in Eq. 4, the critical temperature can be obtained by fitting the data under different sizes.
FIGURE 1
Helicity modulus as a function of temperature for different . The lattice size is .
Figures 2, 3 show the finite-size scaling plot of helicity modulus for and . The lines are fits to the scaling relation of Eq. 4. Here, the lattice sizes are taken as L = 16, 24, 32, 48, 64, and 80 respectively. Eq. 4 indicates that the equation is valid only at the critical temperature point, that is, the equation is not valid at other temperatures. According to Eq. 4, the fitting curves at different temperatures can be obtained by adjusting the value of parameter C. If the simulated value at a certain temperature is in good agreement with the fitting line, it indicates that the temperature is the critical temperature. It can be seen from the figure that the critical temperature can be directly obtained by fitting the curve. For example, as shown in Figure 2, the data at is in good agreement with Eq. 4, except for the data point of the smallest lattice L = 16. The data at other temperatures are not consistent with Eq. 4. Therefore, the critical temperature can be determined as . The critical temperatures are 0.79 () and 0.88 (), respectively, which are lower than the values 0.804 and 0.892 obtained by the intersection acquisition method mentioned above. () is consistent with the result obtained from the finite scaling relation of susceptibility [21]. In order to further verify the effectiveness, we apply this method to the planar rotator model (i.e., ) and obtain the critical temperature is (), which is consistent with the previous Monte Carlo simulation result [27]. This shows the method of estimating the critical temperature by the finite-size scaling formula of helictiy modulus is very effective.
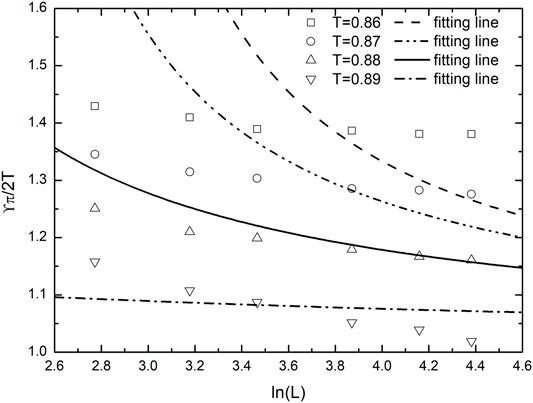
FIGURE 2
Application of the finite-size scaling of to estimate the critical temperature for . The lines are fits to the finite-size scaling relation of Eq. 4.
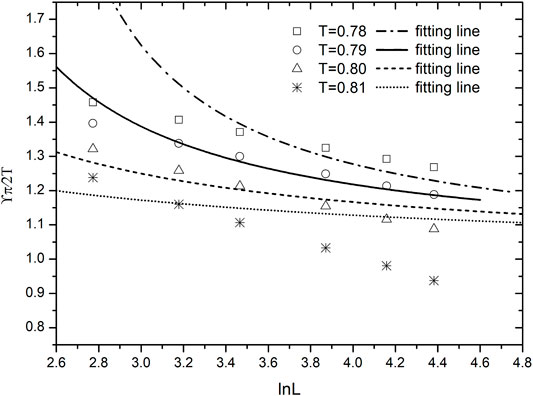
FIGURE 3
Application of the finite-size scaling of to estimate the critical temperature for . The lines are fits to the finite-size scaling relation of Eq. 4.
It is well known that the XY model supports topological excitation and shows a BKT phase transition related to the unbinding of vortex–antivortex pairs. However, whenever the BKT transition temperature is reached, the bound pairs appear to dissociate. In the present work, each vortex or antivortex was counted with L = 80. Each vortex core consists of three spins on each unit triangular lattice. When the sum of all spin angles on the unit lattice is equal to , the vortex increases by one. The vortex density is obtained by dividing all the vortex numbers by N. Figure 4 shows the variation of vortex density with temperature for and . Obviously, the vortex density increases with the increase of temperature, especially when it is close to the critical temperature. Vortex pairs do not appear out of thin air, but are formed under the action of so-called vortex-antivortex pair formation energy. The vortex-antivortex pair formation energy is the energy required to create a pair of vortices. Around the critical temperature, the vortex density and vortex-antivortex pair formation energy satisfy the following relationship [26].where is the vortex-antivortex pair formation energy. As an example, Figure 5 shows as a function of for . In order to calculate the vortex-antivortex pair formation energy, according to the previous work [26], taking the temperature corresponding to the critical temperature and ( is the temperature of the maximum specific heat) as the reference point, the temperature is divided into three regions: high temperature (), intermediate temperature (), and low temperature () regions. Using a linear fit to the data of intermediate temperature, we obtain . Using the same method, we obtain the value for . The value is higher than that at . We also calculated the vortex-antivortex pair formation energy when without dilution, and its value is . The corresponding critical temperature is 1.05, which is higher than the critical temperature of the planar rotator model of two spin components (). The vortex-antivortex pair formation energy of the planar rotator model is . This result is consistent with the result of Ref. [26]. The last result of the relation between vortex-antivortex pair formation energy with is shown in Figure 6. It can be seen from the figure that the vortex-antivortex pair formation energy gradually increases with the increase of when . Figure 7 shows the critical temperature for different . The critical temperature decreases with the increase of .
FIGURE 4
Vortex density for .
FIGURE 5
The vortex density vs. 1/T for . The solid line is linear fit for .
FIGURE 6
The vortex-antivortex pair formation energy for different .
FIGURE 7
The critical temperature for different .
There has been great interest in the discussion of the first-order phase transition of the model. The previous work shows that the 2D generalized XY model has both BKT phase transition and first-order phase transition. When is small, the first-order phase transition phenomenon is not obvious, or even there may be no first-order phenomenon. When is large enough, such as , the first-order phase transition becomes more and more obvious [14–17]. We know that the BKT phase transition is caused by the release of vortex anti-vortex pairs at the critical temperature point. The change of phase transition properties at large may be related to a large number of almost instantaneous vortices at the transition point. For small , with the increase of temperature T, vortex and vortex gradually enter the system. At the BKT point, a continuous transition occurs through the separation of vortex anti-vortex pairs. For large , the increase of vortex density at low temperature is not enough to make the dissociation mechanism work. However, with the increase of temperature, at a certain temperature, they will suddenly appear in large numbers and undergo a first-order phase transition. As shown in Figure 4, the vortex density increases almost precipitously with the increase of . These two kinds of phase transitions occur at almost the same temperature point, so it is difficult to accurately judge the phase transition properties [15, 16]. How to accurately determine the first-order phase transition temperature may be an interesting research in the future.
Conclusion
In this paper, with the application of MC simulation, the helicity modulus and vortex density of a 2D generalized XY model on a triangular lattice is discussed. The helicity modulus and vortex density were obtained as a function of temperature for and . The critical temperature obtained by the finite-size scaling relation of the helicity modulus is consistent with the values obtained in our previous work. It is found that the vortex-antivortex pair formation energy increases with the increase of , while the critical temperature decreases with the increase of .
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding authors.
Author contributions
Y-ZS conceived this idea and provided most of the calculations. QW and QA made the overall modification of the article and assigned some calculation tasks. L-YZ and QC provided their help for the calculation of the vortex part, and X-LY and YZ provided help in algorithm and calculation.
Acknowledgments
The authors thank the three reviewers for their constructive comments.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
BerezinskiiVL. Destruction of Long-Range Order in One-Dimensional and Two-Dimensional Systems Possessing a Continuous Symmetry Group. II. Quantum Systems. Sov Phys JEPT (1972) 34:610–6.
2.
KosterlitzJMThoulessDJ. Ordering, Metastability and Phase Transitions in Two-Dimensional Systems. J Phys C: Solid State Phys (1973) 6:1181–203. 10.1088/0022-3719/6/7/010
3.
WeberHMinnhagenP. Monte Carlo Determination of the Critical Temperature for the Two-dimensionalXYmodel. Phys Rev B (1988) 37:5986–9. 10.1103/physrevb.37.5986
4.
EvertzHGLandauDP. Critical Dynamics in the Two-Dimensional classicalXYmodel: A Spin-Dynamics Study. Phys Rev B (1996) 54:12302–17. 10.1103/PhysRevB.54.12302
5.
NelsonDR. Defects, Geometry in Condensed Matter Physics. Cambridge: University Press (2002).
6.
ChamatiHRomanoSMólLASPereiraAR. Three-dimensional Generalized Xy Models: A Monte Carlo Study. Europhys Lett (2005) 72:62–8. 10.1209/epl/i2005-10197-8
7.
RomanoS. Computer Simulation Evidence for Berezhinskiǐ-kosterlitz-thouless-like Transitions in One Dimension. Int J Mod Phys B (1997) 11:2043–56. 10.1142/s0217979297001052
8.
CapriottiLVaiaRCuccoliATognettiV. Phase Transitions Induced by Easy-Plane Anisotropy in the Classical Heisenberg Antiferromagnet on a Triangular Lattice: A Monte Carlo Simulation. Phys Rev B (1998) 58:273–81. 10.1103/PhysRevB.58.273
9.
WeigelMJankeW. The Square-latticeFmodel Revisited: a Loop-Cluster Update Scaling Study. J Phys A: Math Gen (2005) 38:7067–92. 10.1088/0305-4470/38/32/002
10.
WysinGM. Vacancy Effects in an Easy-Plane Heisenberg Model: Reduction of Tc and Doubly Charged Vortices. Phys Rev B (2005) 71:094423. 10.1103/PhysRevB.71.094423
11.
SunY-ZYiLWysinGM. Berezinskii-Kosterlitz-Thouless Phase Transition for the Dilute Planar Rotator Model on a Triangular Lattice. Phys Rev B (2008) 78:155409. 10.1103/PhysRevB.78.155409
12.
PaulaFMPereiraARWysinGM. Contribution of Impurity-Pinned Vortices to the Response Function in a Randomly Diluted Easy-Plane Ferromagnet on a Square Lattice. Phys Rev B (2005) 72. 10.1103/PhysRevB.72.094425
13.
SunY-ZYiLWangJ-S. Effects of Dzyaloshinsky-Moriya Interaction on Planar Rotator Model on Triangular Lattice. Commun Comput Phys (2012) 11:1169–81. 10.4208/cicp.100410.020211s
14.
RomanoSZagrebnovV. On the Xy Model and its Generalizations. Phys Lett A (2002) 301:402–7. 10.1016/s0375-9601(02)01077-0
15.
MólLASPereiraARChamatiHRomanoS. Monte Carlo Study of 2D Generalized XY-Models. Eur Phys J B (2006) 50:541–8. 10.1140/epjb/e2006-00172-3
16.
MólLASPereiraARMoura-MeloWA. On Phase Transition and Vortex Stability in the Generalized XY Models. Phys Lett A (2003) 319:114–21. 10.1016/j.physleta.2003.10.009
17.
Van EnterACDRomanoSZagrebnovVA. First-order Transitions for Some Generalized XY Models. J Phys A: Math Gen (2006) 39. 10.1088/0305-4470/39/26/l03
18.
SunYZWuQLiJYChenQ. Thermodynamic Quantities and Phase Transition of a Generalized XY Model on Triangular Lattice. IOP Conf Series: Earth Environ Sci (2018) 128. 10.1088/1755-1315/128/1/012106
19.
WolffU. Collective Monte Carlo Updating for Spin Systems. Phys Rev Lett (1989) 62:361–4. 10.1103/physrevlett.62.361
20.
MetropolisNRosenbluthAWRosenbluthMNTellerAHTellerE. Equation of State Calculations by Fast Computing Machines. J Chem Phys (1953) 21:1087–92. 10.1063/1.1699114
21.
SunY-ZLiangJ-CXuS-LYiL. Berezinskii-Kosterlitz-Thouless Phase Transition of 2D Dilute Generalized Model. Physica A: Stat Mech its Appl (2010) 389:1391–9. 10.1016/j.physa.2009.12.023
22.
OlssonP. Two Phase Transitions in the Fully FrustratedXYModel. Phys Rev Lett (1995) 75:2758–61. 10.1103/physrevlett.75.2758
23.
LeeKWLeeCEKimI-m.Helicity Modulus and Vortex Density in the Two-Dimensional Easy-Plane Heisenberg Model on a Square Lattice. Solid State Commun (2005) 135:95–8. 10.1016/j.ssc.2005.03.054
24.
WysinGMPereiraARMarquesIALeonelSACouraPZ. Extinction of the Berezinskii-Kosterlitz-Thouless Phase Transition by Nonmagnetic Disorder in Planar Symmetry Spin Models. Phys Rev B (2005) 72. 10.1103/physrevb.72.094418
25.
LeeDHJoannopoulosJDNegeleJWLandauDP. Symmetry Analysis and Monte Carlo Study of a Frustrated Antiferromagnetic Planar (XY) Model in Two Dimensions. Phys Rev B (1986) 33:450–75. 10.1103/physrevb.33.450
26.
GuptaRBaillieCF. Critical Behavior of the Two-dimensionalXYmodel. Phys Rev B (1992) 45:2883–98. 10.1103/PhysRevB.45.2883
27.
ButeraPComiM. High-temperature Study of the Kosterlitz-Thouless Phase Transition in theXYmodel on the Triangular Lattice. Phys Rev B (1994) 50:3052–7. 10.1103/PhysRevB.50.3052
Summary
Keywords
Monte—Carlo method, XY model, vortex density, phase transition, helicity modulus
Citation
Sun Y-Z, Wu Q, Yang X-L, Zhou Y, Zhu L-Y, Chen Q and An Q (2022) Numerical Studies of Vortices and Helicity Modulus in the Two-Dimensional Generalized XY Model. Front. Phys. 10:851322. doi: 10.3389/fphy.2022.851322
Received
09 January 2022
Accepted
14 February 2022
Published
04 March 2022
Volume
10 - 2022
Edited by
Guoying Gao, Huazhong University of Science and Technology, China
Reviewed by
Zhongbing Huang, Hubei University, China
Weibin Li, University of Nottingham, United Kingdom
Updates
Copyright
© 2022 Sun, Wu, Yang, Zhou, Zhu, Chen and An.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qin Wu, nue-qinwu@qq.com; Qing An, 490756729@qq.com
This article was submitted to Condensed Matter Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.