Determination of Static and Dynamic Yield Stress of Chengdu Clay Slurry

The yield stress of mud is one key to analyze the initiation and deposition of debris flow. Taking Chengdu clay as the experimental material, slurries with different solid volume concentrations were prepared. Using the blade rotor system of mcr301 rheometer and the continuous shear experimental method, the dynamic change process of shear stress of slurries with different solid volume concentrations was obtained with the shear rate increasing and decreasing continuously. According to the experimental results, the static and dynamic yield stress of Chengdu clay slurry is determined, and the influence of solid volume concentration on the yield stress is analyzed. The following conclusions are obtained: Chengdu clay slurry is a non-Newtonian fluid with yield stress. In the process of accelerated shear, for Chengdu clay slurry with solid volume concentration exceeding 35%, the shear rate is in the range of 0.01–1 s⁻¹, and the shear stress increases rapidly to the maximum. When the shear rate exceeds 1 s⁻¹, the shear stress decreases rapidly and finally tends to be stable. The shear rate appears stress overshoot near 1s⁻¹. However, in the process of increasing shear rate, for Chengdu clay slurry with solid volume concentration of no more than 35%, the shear stress increases rapidly in the range of shear rate of 0.01–0.1 s⁻¹, and the shear rate exceeds 0.1 s⁻¹. The shear rate has little effect on the shear stress, and the stress overshoot disappears. In the process of deceleration shear, for all solid volume concentrations in the semi logarithmic coordinate system, the mud shear stress decreases steadily with the decrease of shear rate. The static and dynamic yield stress of slurry increases exponentially with particle concentration.

1 Introduction

Debris flow disasters induced by heavy rainfall occur from time to time all over the world. Reasonable risk zoning has always been one of the basic problems in the study of such disasters. Risk zoning should not only consider the factors such as altitude, topographic slope, rainfall and distance of the disaster source area [1], but also consider the physical vulnerability of residents and buildings in the area [2]. However, from the material composition of landslide and debris flow, mud (mixture of fine-grained soil and water) is the basic component of landslide and debris flow. Mud moves together with coarse particles, which makes it have the characteristics of strong impact and great destruction [3]. [4] pointed out that the flow behavior of landslide and debris flow is controlled by the rheological properties of mud matrix. The cognition of mud rheological characteristics is very important for understanding and analyzing debris flow movement. It is the basis for determining debris flow velocity, impact force and outflow distance, and is helpful to evaluate the risks related to debris flow movement. The rheological properties of mud will help to better understand the flow characteristics of such events. The rheological model thus obtained can indeed be input into the numerical simulation to predict the characteristics of debris flow events and draw the dangerous area map [5,6]. The yield stress of mud is one key.

Mud is a thixotropic non-Newtonian fluid with yield stress [7, 8]. The correlation between thixotropy and yield stress of such fluids and time has been widely studied by relevant scholars. [9] described the physical behavior of such materials in detail, summarized the experimental techniques that can be used for yield stress test, and discussed the latest progress in the application of micro theory. A new concept is proposed to divide it into simple yield stress fluid without time-dependent tolerance and thixotropic yield stress fluid with obvious time-dependent tolerance. For thixotropic fluids, yield stress is closely related to time, and the scheme used to obtain yield stress, especially for aging systems, depends on its precise definition [10]. For such materials, the yield stress depends on the nature of the test - there is a consensus on distinguishing between the yield stress measured by the solid to liquid (or yield) transition and the yield stress measured during the liquid to solid transition. Most yield stress fluids have microstructure, which is destroyed by flow in the shear process, so that the viscosity decreases reversibly with time, which is called thixotropy of fluids [11]. [12] summarized the research results of thixotropy in detail and analyzed the differences between thixotropy and shear hardening, aging and other phenomena. [13] emphasized that this time-varying rheological property makes it difficult to find a reliable method to determine the true yield stress. [14] proposed a practical definition of yield stress, that is, “any critical stress below which flow cannot be observed under experimental conditions.” At present, how to determine the yield stress of debris flow mud according to the starting movement and deposition process of debris flow and apply it to the analysis and prevention of debris flow disaster is still not clearly defined.

The yield stress of clay slurry comes from the microstructure of particle network formed by colloidal interaction or direct contact [15], which is related to the stress history [16,17]. According to the precise experimental scheme, the estimated yield stress can be described as static or dynamic [18,19]. The static yield stress can be determined by increasing the amplitude of oscillation scanning (stress or strain control) [9]. It can also be determined according to the actual shear rate (continuous shear or oscillatory shear test). In this case, the stress with deviation of stress response from linearity or maximum stress can be considered. The static yield stress thus determined depends on the shear rate applied and the “sample age” [20,21]. For dynamic yield stress, it is theoretically the shear stress value when the shear rate approaches zero, which represents that the material gradually enters the solid state from the flowing liquid state. In the experiment, the flow curve is usually measured by applying stable shear and gradually reducing the shear rate to reach the limit. The stress extrapolation within the vanishing shear rate limit (the intercept from the shear stress axis) is usually called the stress value of dynamic yield stress.

Debris flow movement includes three processes: initiation, migration and accumulation of debris flow. In the start-up stage, the debris flow fluid changes from static state to stable motion state in a short time, and the shear rate acting on the debris flow slurry increases rapidly from zero to a large value. The accumulation process of debris flow is the process of debris flow fluid changing from moving state to static state. The shear rate acting on debris flow mud gradually decreases from a large value of maintaining stable movement to zero. According to the above method for determining the dynamic and static yield stress, combined with the shear rate change process of debris flow slurry in the start-up and accumulation stages of debris flow, taking Chengdu clay as the experimental material and considering the actual situation of material source supply during the movement of debris flow (the addition of solid substances increases the slurry concentration, and the supplement of water source decreases the slurry concentration), prepare slurries with different volume concentrations, Using the blade rotor system of mcr301 rheometer, the rheological experiments of continuous shear (increasing shear and decreasing shear) were carried out. According to the experimental results, the effects of mud dynamic and static yield stress and solid volume concentration on dynamic and static yield stress are analyzed and determined. In addition, the influence of filling mud on the determination of yield stress is not considered.

2 Experimental Materials and Sample Preparation

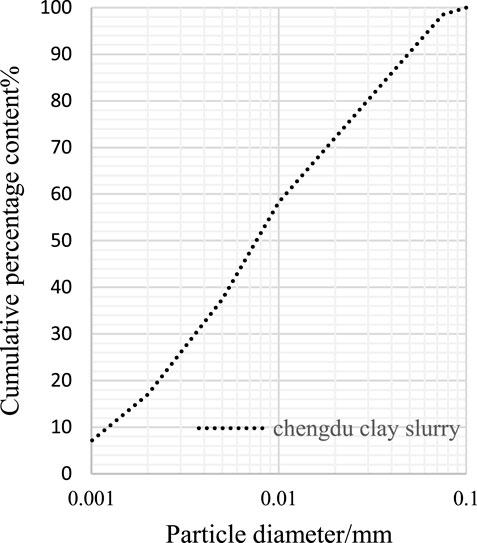
Chengdu clay is widely distributed in the second and third terraces of Minjiang River, the eastern suburb of Chengdu and Longquanyi area. It is brownish yellow, brownish yellow and grayish yellow. It is hard plastic, contains iron and manganese nodules, has strong viscosity and weak ∼ medium expansibility. The experimental materials in this paper are taken from Longquan District, Chengdu. The particle composition of the sample is analyzed by Mastersizer 3,000 laser diffraction particle size analyzer (measuring particle size range: 0.01–3500 um). The particle composition of Chengdu clay is shown in Figure 1. According to the experimental measurement method of liquid plastic limit of cohesive soil, the liquid plastic limit is measured by photoelectric liquid plastic limit joint measuring instrument. The liquid limit water content of Chengdu clay is 66.5% (the water content corresponding to the cone sinking depth of 17 mm) and the plastic limit water content is 24.5% (the water content corresponding to the cone sinking depth of 2 mm) [22]. Plasticity index: 42, >17. The density of clay particles in Chengdu is determined by volumetric flask method, which is ds = 2.7 g/cm³.

FIGURE 1

FIGURE 1. Grain size distribution of the chengdu clay materials.

Take some Chengdu clay, soak it in the container with water for more than 48 h, mix it manually, and fully saturate it for spare. The initial water content was determined by drying method ($w_0$:Percentage of water mass and dry soil mass per unit volume). Take a certain amount of standby mud and place it in 10 measuring cups. Add different amounts of distilled water into each measuring cup respectively, and calculate the water content ($w_1$) after adding water according to the initial water content ($w_0$). Calculate mud solid volume concentration ($C_{\mathrm{s}}$):

$C_{\mathrm{s}}=\frac{V_s}{V}\times 100\%=\frac{V_s}{V_s+V_v}\times 100\%$

$V_s$Is the solid volume, $V$is the total volume ($V$ = $V_s$+$V_v$), $V_v$is the water volume.

According to water content (ω1) And particle density (ds), calculate the slurry solid volume concentration in each measuring cup (see Table 1).

TABLE 1

TABLE 1. Miosture content and solid volume concentration of the Chengdu clay mud.

3 Rheological Instruments and Experimental Methods

3.1 Experimental Instrument

The geometry of viscometer commonly used for yield stress fluid measurement includes concentric cylinder, cone and plate, blade shape, etc. [23] comprehensively introduced the principle and application of the above viscometers with different geometry used for viscosity measurement, and fully analyzed the source of experimental error. In hard particle suspensions, wall slip is a common main problem affecting rheological measurement [24]. Relevant scholars have adopted local measurement techniques (light scattering velocimetry in Couette geometry [25] and particle tracking velocimetry in cones and plates [26‐28] and flat plate geometry [29], It provides direct evidence for the wall slip of materials with different yield stress, and puts forward the quantitative measurement of sliding velocity. In the presence of wall slip, the measured apparent shear rate overestimates the true shear rate inside the material [9]. The vane viscometer consists of four blades arranged at an equal angle. Compared with other geometries, the vane viscometer has the advantages of minimal interference to the material structure during insertion, and can minimize the problem of wall slip. Although magnetic resonance imaging technology has found that wall slip phenomenon still exists [30], it is still widely used to study in gel and thixotropic materials; [31‐35].

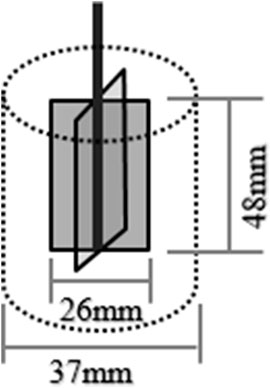
According to the above analysis, the blade rotor system of mcr301 rotary rheometer in antonpa, Austria is used in this study- It is a stress-controlled rheometer by Anton Paar. The rheometer adopts modular and intelligent design and is composed of temperature control system, fixture system and test system. It consists of four thin blades arranged equiangularly around the axis of a small cylinder; Blade diameter d1 = 13 mm, blade height h = 48 mm; Cup mouth diameter d2 = 37 mm (see Figure 2). The rheometer adopts air bearing, and the minimum torque is 0.002 μNm, maximum torque: 200 mnm, deflection angle (preset): 0.1 to ∞ μRad, minimum speed (CSS): 10⁻⁷ rpm, minimum speed (CSR): 10⁻⁶ rpm, maximum speed: 3000 rpm, minimum frequency: 10⁻⁵ Hz, maximum frequency: 100 Hz, normal stress range: 0.01–50 N, normal stress accuracy: 0.002 N, temperature range: 150–1,000°C.

FIGURE 2

FIGURE 2. Schematic diagram of blade rotor system.

Assuming no inertia effect and ignoring the normal stress difference, the shear stress ($\tau$) and shear rate ($\dot{\gamma }$) are calculated as follows:

$\tau =\frac{T}{2\pi R_1^{2}L};\dot{\gamma }=\frac{\omega R_1}{R_2-R_1}$

Where $T$is the torque applied to the blade and $\omega$ is the angular velocity of the blade rotor.

3.2 Experimental Method

In the past, many methods have been developed to measure yield stress, mainly including stress relaxation, creep/recovery test, stress growth test, continuous shear test and so on. The yield stress of stress relaxation experiment is defined as the residual ultimate stress after the fluid stops flowing. Creep/recovery test is to apply a constant shear stress to the fluid, the shear stress is higher than the yield stress, the material flows, the stress is lower than the yield stress, and the material behaves as a solid. The stress growth experiment is to shear the fluid at a constant shear rate during the rheological experiment, obtain the change process of shear stress with time, and determine the yield stress according to the change curve of stress with time. Continuous shear test is a process in which the shear rate continuously increases from zero to the set value (accelerated shear) or decreases from the set value to zero (decelerated shear) during the rheological experiment to obtain the variation of shear stress with the shear rate (increase or decrease). [36] summarized the advantages and disadvantages of each method. Although some methods are widely used, because the yield stress depends on its measurement method, especially whether it is determined during the solid-liquid transition or the opposite transition [9], no method is considered as a standard procedure for determining the yield stress. Aiming at the start-up and deposition process of debris flow, in the start-up process of debris flow, the debris flow fluid develops from static state to stable motion state in a short time, and the shear rate of debris flow slurry increases from zero to a large value; In the process of debris flow deposition, the moving debris flow fluid changes from moving state to static state, and the shear rate of debris flow slurry decreases from large value to zero. According to the field observation of field debris flow disasters by [3] and [37], it is estimated that the shear rate of moving debris flow slurry is usually between 0.1 and 20 S⁻¹ [38]. In order to explore the variation process of shear stress with shear rate during the start-up and accumulation of debris flow slurry, the rheological experiments of increasing shear (representing the start-up process of debris flow) and decreasing shear (representing the deposition process of debris flow) were carried out continuously by using the blade rotor of mrc301 rheometer and the method of continuous shear experiment. At the beginning of the test, the slurry with different solid volume concentrations is fully stirred, and then take an appropriate amount of prepared mud into the fixed outer cylinder of the blade rheometer, and immerse the blade rotor into the mud. In the test, the shear rate (blade rotor rotation rate) continuously increased from 0 to 30s⁻¹ (accelerated shear) in a logarithmic growth mode, and then the shear rate continuously decreased from 30 s to 1 to 0 (deceleration shear) in the same path. There is no time interval between increasing shear and decreasing shear. The dynamic change process of shear stress with the increase and decrease of shear rate was recorded. Although this process is not complicated, the scheme combines the complex transient response of the sample and the shear induced solid-liquid phase transition [39], but largely reflects the rheological process of debris flow slurry during debris flow initiation and accumulation. In the whole experimental process, the test temperature of the sample is constant at 20°C through the water circulation system.

4 Experiment Results and Discussion

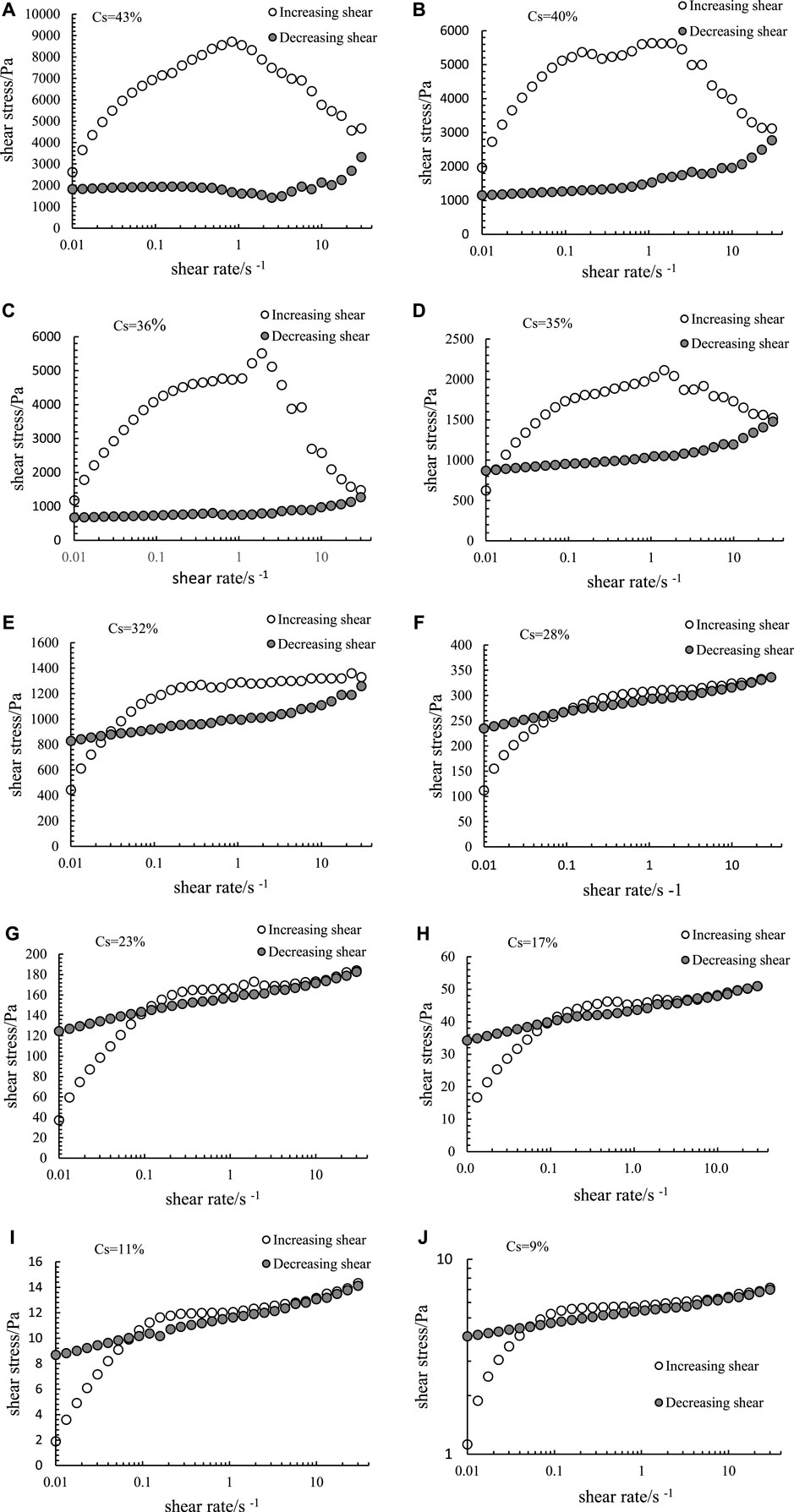
According to the above experimental methods, using the blade rotor system of Anton Paar mcr301 rheometer, the dynamic process of shear stress increasing with shear rate (unfilled ○) and decreasing with shear rate (filled • (see Figure 3).

FIGURE 3

FIGURE 3. (Continued).

4.1 Dynamic Response of Shear Stress With Shear Rate

The dynamic change process of shear stress 1) of Chengdu clay mud with shear rate 2) is shown in semi logarithmic coordinate system (Figure 3A–J). Figure 3 shows that Chengdu mud with all solid volume concentrations shows non-Newtonian behavior. At the same shear rate, the shear stress increases with the increase of mud solid concentration. The change of shear stress is completely different in the process of increasing shear and decreasing shear. In the process of increasing shear rate, the influence of solid volume concentration on the dynamic change of shear stress is obviously different. The main manifestations are: When the volume concentration of mud solid exceeds 35% and the shear rate is in the range of 0.01-1s-1, the shear stress increases rapidly to the maximum; When the shear rate exceeds 1s-1, the shear stress decays rapidly and tends to be stable (Figure 4A, B). For example, for the slurry with a solid volume concentration of 43%, when the shear rate is in the range of 0.01–1 s⁻¹, the shear stress increases rapidly from 2650 pa to nearly 9000 pa (Figure 4A, and then decreases to less than 4700 pa (Figure 4. b). When the solid volume concentration is less than 35% and the shear rate is less than 0.1 s⁻¹, the shear stress increases rapidly with the shear rate; When the shear rate exceeds 0.1 s⁻¹, although the shear stress increases with the increase of shear rate, the increase range is small. For example, when the solid volume concentration is 28%, the shear rate is in the range of 0.01–0.1 s⁻¹, and the shear stress increases rapidly from nearly 110 pa to nearly 270 pa. The shear rate is in the range of 0.1 s^–1 to 30 s⁻¹, and the shear stress increases slowly from 270 to 310 pa (Figure 3F). As the results of Jeong et al. 2010 on bentonite and illite natural clay, its flow behavior depends not only on the shear rate, but also on the particle concentration[40]. This result is consistent with the results of similar laboratory tests ([41,42]; Sueng won [43]). This result shows that Chengdu clay slurry is a typical non-Newtonian fluid with yield stress. In the process of decelerating shear, in the semi logarithmic coordinate system, the shear stress decreases steadily with the decrease of shear rate (filled with ● in Figure 3).

FIGURE 4

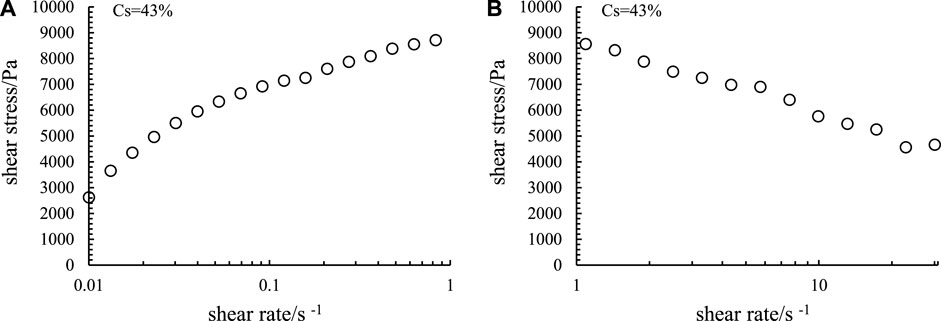
FIGURE 4. Relationship between shear stress and shear rate of Chengdu clay slurry with solid volume concentration of 43% (A) Shear stress with shear rate in the range of 0.01–1 s⁻¹; (B) Shear stress with shear rate in the range of 1–30 s⁻¹).

In the process of accelerated shear and decelerated shear, although the same shear rate change path is adopted, the increase (accelerated shear) and decrease (decelerated shear) of shear stress are completely inconsistent. The shear stress forms a hysteresis loop with the increase and decrease of shear rate (Figure 3), and the area of hysteresis loop decreases with the decrease of solid volume concentration. It shows that Chengdu clay mud has thixotropy, which decreases with the decrease of solid volume concentration. Relevant studies have shown that the response of thixotropic yield stress fluid will depend on the rate of stress rise and fall and the rest time between subsequent scans [8]. For the slurry with solid volume concentration lower than 35%, there is an intersection between the increasing shear stress curve and the decreasing shear stress curve (Figures 3E–J). [44] also observed similar behavior, and [45] reviewed the hysteresis loop in thixotropic fluid.

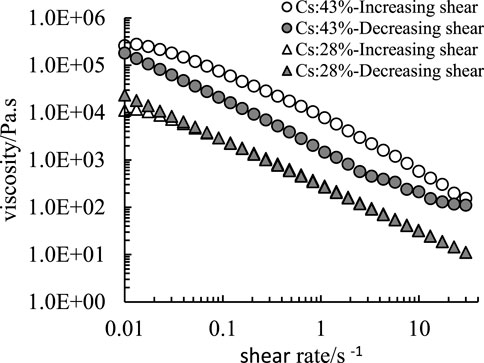
In addition, in order to analyze the viscosity change in the shear process, the viscosity change of Chengdu clay slurry with solid volume concentration of 43% and 28% respectively in the process of increasing and decreasing shear is plotted in Figure 5. Unfilled ○ in the figure represents the increasing shear process of slurry with solid volume concentration of 43%, and filled • presents its decreasing shear process; Unfilled △ represents the increasing shear process of slurry with solid volume concentration of 28%, and filled ▲ represents the decreasing shear process. Figure 5 shows that the viscosity of Chengdu clay slurry decreases with the increase of shear rate and increases with the decrease of shear rate, with typical shear thinning characteristics [46,47].

FIGURE 5

FIGURE 5. Variation process of mud viscosity with shear rate.

4.2 Determination of Static and Dynamic Yield Stress of Mud

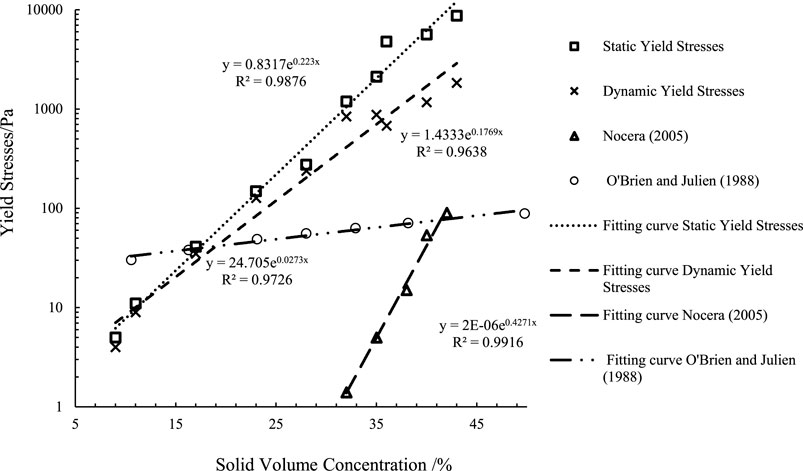
According to the experimental results and 4.1 analysis, the variation process of shear stress of mud with different concentrations with shear rate is not consistent. When the solid volume concentration is greater than 35%, the shear stress increases rapidly, then decreases gradually, and finally tends to be stable. This change process is more clearly shown by plotting the change of shear stress with shear rate in semi logarithmic coordinate system (Figure 4A, B). [48,49] described this change process: in viscoelastic thixotropic fluid or nonlinear viscoelastic fluid, there will be stress growth first, then stress attenuation, and then the stress change tends to be stable (equilibrium flow). Although the static yield stress of thixotropic fluid depends on the applied shear rate and sample age [20,21], it is one of the common methods to use the stress overshoot as the static yield stress of mud. In this paper, for the slurry with solid volume concentration greater than 35%, the peak stress (stress overshoot) in the process of accelerated shear is taken as its static yield stress. For the slurry with solid volume concentration less than 35%, the growth range of shear stress before the shear rate is less than 0.1 s⁻¹ and after the shear rate is greater than 0.1 s⁻¹ is obviously different. Therefore, the shear stress value with shear rate of 0.1 s^–1 is taken as its static yield stress. Combined with the start-up process of debris flow, the static yield stress value of mud with different solid volume concentration represents the minimum stress value that needs to be overcome when debris flow enters the flow state from start-up.

The dynamic yield stress value represents the stress threshold of the material gradually entering the solid state from the flowing liquid state. The shear stress value is measured by gradually reducing the shear rate to reach the limit. The stress value obtained by extrapolating the stress within the disappearance limit of the shear rate (the intercept from the shear stress axis) is usually called the stress value of dynamic yield stress. According to the variation process curve of shear stress with shear rate obtained from the deceleration shear rheological experiment of mud with different solid volume concentration (filled with ● Figure 3), the shear stress value with shear rate of 0.01 s^–1 is taken as the dynamic yield stress of mud.

4.3 Effect of Solid Concentration on Yield Stress

Table 2 confirms that the solid volume concentration has a strong effect on the yield stress. For slurries with solid volume concentration greater than 35%, the dynamic yield stress is much smaller than the static yield stress [30,37,50–52], and this difference decreases with the decrease of concentration. The yield stress increases exponentially with particle concentration (Figure 4). [38] expressed the relationship between yield stress and solid volume concentration as: ${\tau }_c=\alpha \bullet e^{\beta \bullet C_s}$, where α,βis an empirical coefficient, depending on sediment characteristics. eonardo. [53] used a rotary rheometer equipped with a blade rotor system, adopted the same experimental scheme, conducted rheological experiments on the slurry composed of fine pyroclastic particles with solid concentrations of 32%, 35%, 38%, 40% and 42% respectively, analyzed the influence of solid volume concentration on its static and dynamic yield stress, and obtained the conclusion consistent with this paper. The research results of Leonardo [53] on Nocera debris flow and [54] on Colorado debris flow are drawn in the same semi logarithmic coordinate diagram (Figure 6), and the influence of solid concentration on yield stress is compared. Empirical coefficient of static yield stress of Chengdu clay slurry varying with solid volume concentration α, β is 0.8317 and 0.223, respectively Empirical coefficient of dynamic yield stress with solid volume concentration α, β They are 1.433 and 0.1769 respectively. Empirical coefficient of variation of mud yield stress of Nocera debris flow and Colorado debris flow with solid volume concentration α,β See the fitting data in Figure 6. This result shows that due to the difference of mud composition, the effect of solid concentration on yield stress is quite different.

TABLE 2

TABLE 2. Summarizes the static yield stress and dynamic yield stress values of slurries with different solid volume concentrations (see Table 2). Table 2 Miosture content and solid volume concentration of the Chengdu clay mud.

FIGURE 6

FIGURE 6. Yield stress versus Solid Volume Concentration.

5 Conclusion

In this paper, Chengdu clay is used as experimental material to prepare slurries with different solid volume concentrations. Based on the preliminary analysis of the experimental method, the application of experimental equipment and the determination of static and dynamic yield stress, combined with the movement characteristics in the process of debris flow startup and accumulation, using the blade rotor system of mcr301 rheometer and the experimental methods of continuous increasing shear and decelerating shear, the dynamic change process curve of mud shear stress with different solid volume concentration with the increase/decrease of shear rate is obtained. According to the experimental results, the static and dynamic yield stress of Chengdu clay mud is determined, and the influence of solid volume concentration on the dynamic and static yield stress of mud is analyzed. The following conclusions are obtained:

Chengdu clay slurry is a non-Newtonian fluid with yield stress. At the same shear rate, the shear stress increases with the increase of mud solid concentration. The change of shear stress is completely different in the process of increasing shear and decreasing shear. In the process of increasing shear rate, when the volume concentration of mud solid exceeds 35% and the shear rate is in the range of 0.01–1 s⁻¹, the shear stress increases rapidly to the maximum value; When the shear rate exceeds 1 s⁻¹, the shear stress decays rapidly and tends to be stable, and the stress overshoot occurs near the shear rate of 1 s⁻¹. When the solid volume concentration is less than 35%, when the shear rate is less than 0.1 s⁻¹, the shear stress increases rapidly with the shear rate; When the shear rate exceeds 0.1 s⁻¹, although the shear stress increases with the increase of shear rate, the increase range is small, and the stress overshoot disappears. Chengdu clay mud is thixotropic. Thixotropy decreases with the decrease of solid volume concentration. The viscosity decreases with the increase of shear rate and increases with the decrease of shear rate. The static and dynamic yield stress of slurry increases exponentially with particle concentration.

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Author Contributions

Conceptualization, writing—original draft preparation, XJ; formal analysis, YL. methodology, WC; resources, KS; data curation PS. All authors have read and agreed to the published version of the manuscript.

Funding

We gratefully wish to acknowledge the Natural Science Foundation (Grant Nos. 41672357), and the Henan Provincial Department of Science and Technology Research Project(Grant Nos. 162102310253; 182102310779).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rafiei Sardooi E, Azareh A, Mesbahzadeh T, Soleimani Sardoo F, Parteli EJR, Pradhan B. A hybrid model using data mining and multi-criteria decision-making methods for landslide risk mapping at Golestan Province, Iran. Environ Earth Sci (2021) 80:487. doi:10.1007/s12665-021-09788-z

CrossRef Full Text | Google Scholar

2. Guillard-Gonçalves C, Zêzere JL. Combining social vulnerability and physical vulnerability to analyse landslide risk at the municipal scale. Geosciences (2018) 8(8):294. doi:10.3390/geosciences8080294

CrossRef Full Text | Google Scholar

3. Ochiai H, Okada Y, Furuya G, Okura Y, Matsui T, Sammori T, et al. A fluidized landslide on a natural slope by artificial rainfall. Landslides (2004) 1(3):211–9. doi:10.1007/s10346-004-0030-4

CrossRef Full Text | Google Scholar

4. Forterre Y, Pouliquen O. Flows of Dense Granular Media[J]. Annu. Rev. Fluid Mech. (2008) 40(1):1–24. doi:10.1146/annurev.fluid.40.111406.102142

CrossRef Full Text | Google Scholar

5. Laigle D, Hector AF, Hubl J, Rickenmann D. Comparison of Numerical Simulation of Muddy Debris-Flow Spreading to Records of Real Events. 3rd Int. Conf. on Debris-Flow Hazards Mitigation: Mechanics, Prediction and Assessment, Davos (2003)635–46.

Google Scholar

6. Rickenmann D, Laigle D, McArdell BW, Hubl J. Comparison of 2D Debris-Flow Simulation Models With Field Events. Comput. Geosci. (2006) 10 (2):241–64. doi:10.1007/s10596-005-9021-3

CrossRef Full Text | Google Scholar

7. Barnes HA, Nguyen QD. Rotating vane rheometry - a review. J Non-Newtonian Fluid Mech (2001) 98:1–14. doi:10.1016/s0377-0257(01)00095-7

CrossRef Full Text | Google Scholar

8. Moller P, Fall A, Chikkadi V, Derks D, Bonn D. An attempt to categorize yield stress fluid behaviourfluid behaviour. Phil Trans R Soc A (2009) 367:5139–55. doi:10.1209/0295-5075/87/38004

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Bonn D, Denn MM, Berthier L, Divoux T, Manneville S. Yield stress materials in soft condensed matter. Rev Mod Phys (2017) 89(3):035005. doi:10.1103/revmodphys.89.035005

CrossRef Full Text | Google Scholar

10. Joshi YM. Yield stress fluids and ageing. Rheologica Acta Int J Rheology (2018) 57:521–49. doi:10.1007/s00397-018-1096-6

CrossRef Full Text | Google Scholar

11. Mewis J, Wagner NJ. Thixotropy. Adv Colloid Interf Sci (2009) 147-148:214–27. doi:10.1016/j.cis.2008.09.005

CrossRef Full Text | Google Scholar

12. Larson RG, Wei Y. A review of thixotropy and its rheological modeling. J Rheology (2019) 63(3):477–501. doi:10.1122/1.5055031

CrossRef Full Text | Google Scholar

13. Bingham EC. Fluidity and plasticity. McGraw-Hill Book Compny, Incorporated (1922).

Google Scholar

14. Blair G. On the Nature of “Yield‐Value”[J]. Physics (1933) 4 (3):113–8. doi:10.1016/s0377-0257(97)00004-9

CrossRef Full Text | Google Scholar

15. Ye Q, Kawashima S. Distinguishing Dynamic and Static Yield Stress of Fresh Cement Mortars Through Thixotropy[J]. Cement Concrete Composites (2018) 86:288–96.

Google Scholar

16. Barnes HA. A review of the slip (wall depletion) of polymer solutions, emulsions and particle suspensions in viscometers: Its cause, character and cure. J Non-Newtonian Fluid Mech (1995) 56:221–51. doi:10.1016/0377-0257(94)01282-m

CrossRef Full Text | Google Scholar

17. Wallevik JE. Rheological properties of cement paste: Thixotropic behavior and structural breakdown. Cem Concr Res (2009) 39:14–29. doi:10.1016/j.cemconres.2008.10.001

CrossRef Full Text | Google Scholar

18. Bonnecaze RT, Brady JF. Dynamic Simulation of an Electrorheological Fluid[J]. J. Chem. Phy. (1992) 96 (3):2183–202. doi:10.1063/1.462070

CrossRef Full Text | Google Scholar

19. Pham GT, Park YB, Liang Z. Processing and Modeling of Conductive Thermoplastic/Carbon Nanotube Films for Strain Sensing[J]. Composites Part B: Eng. (2008) 39 (1):209–16. doi:10.1016/j.compositesb.2007.02.024

CrossRef Full Text | Google Scholar

20. Benzi R, Divoux T, Barentin C. Stress overshoots in simple yield stress fluids. Phys Rev Lett (2021) 10: 127. doi:10.1103/PhysRevLett.127.148003

CrossRef Full Text | Google Scholar

21. Benzi R, Divoux T, Barentin C. Continuum modeling of shear startup in soft glassy materials. Phys Rev E (2021) 9: 104. doi:10.1103/PhysRevE.104.034612

PubMed Abstract | CrossRef Full Text | Google Scholar

22.Ministry of Communications of the People's Republic of China. Test methods of soils for highway engineering(JTG 3430-2020). China Communications Press (2020).

Google Scholar

23. Nguyen Q, Boger DV. Measuring the flow properties of yield stress fluids. Annu Rev Fluid Mech (1992) 24(1):47–88. doi:10.1146/annurev.fl.24.010192.000403

CrossRef Full Text | Google Scholar

24. Cloitre , Michel , Bonnecaze . A Review on Wall Slip in High Solid Dispersions[J]. Rheologica Acta: An Inter J Rheol (2017). doi:10.1007/s00397-017-1002-7

CrossRef Full Text | Google Scholar

25. Salmon JB, Bécu L, Manneville S. Towards Local Rheology of Emulsions Under Couette Flow Using Dynamic Light Scattering[J]. European Phy J (2003) 10(3):209–21. doi:10.1140/epje/i2002-10110-5

CrossRef Full Text | Google Scholar

26. Ballesta P, Besseling R, Isa L, Petekidis G. Slip and Flow of Hard-Sphere Colloidal Glasses[J]. Phy Rev Let (2008) 101(25):258301. doi:10.1103/PhysRevLett.101.258301

CrossRef Full Text | Google Scholar

27. Ballesta P, Petekidis G, Isa L, Poon W. Wall Slip and Flow of Concentrated Hard-Sphere Colloidal Suspensions[J]. J Rheeol (2012) 56(5):1005–37. doi:10.1122/1.4719775

CrossRef Full Text | Google Scholar

28. José , Paredes , Noushine . Wall Slip and Fluidity in Emulsion Flow[J]. Phys Review E (2015) 92(4):042313. doi:10.1103/PhysRevE.92.042313

CrossRef Full Text | Google Scholar

29. Seth JR, ClémentineLocatelli-Champagne , Fabrice M, Bonnecaze RT. How do Soft Particle Glasses Yield and Flow Near Solid Surfaces?[J]. Soft Matter (2011) 8(1):140–8. doi:10.1039/C1SM06074K

CrossRef Full Text | Google Scholar

30. Ovarlez G, Mahaut F, Bertrand F, Chateau X. Flows and heterogeneities with a vane tool: Magnetic resonance imaging measurements. J Rheology (1978) 55(2):197–223. doi:10.1122/1.3526349

CrossRef Full Text | Google Scholar

31. Stokes JR, Telford JH. Measuring the Yield Behaviour of Structured Fluids[J]. J Nonnewton Fluid Mech (2004) 124 (1–3):137–146. doi:10.1016/j.jnnfm.2004.09.001

CrossRef Full Text | Google Scholar

32. Koehler EP, Fowler DW, Ferraris CF, Amziane SA. New, Portable Rheometer for Fresh Self-Consolidating Concrete. ACI Mater J (2006) 233:97–116.

Google Scholar

33. Patrice Estellé , Lanos C, Perrot A. Processing the Vane Shear Flow Data From Couette Analogy[J]. Appl Rheol (2008) 18(3):34037. doi:10.3933/ApplRheol-18-34037

CrossRef Full Text | Google Scholar

34. Wallevik JE. Thixotropic investigation on cement paste: Experimental and numerical approach. J Nonnewton Fluid Mechfluid Mech (2005) 132:86–99. doi:10.1016/j.jnnfm.2005.10.007

CrossRef Full Text | Google Scholar

35. Jau WC, Yang CT. Development of a Modified Concrete Rheometer to Measure the Rheological Behavior of Conventional and Self-Consolidating Concretes[J]. Cement Concrete Composites (2010) 32(6):450–60. doi:10.1016/j.cemconcomp.2010.01.001

CrossRef Full Text | Google Scholar

36. Nguyen QD, Boger DV. Direct yield stress measurement with the vane method. J Rheol (N Y N Y) (1985) 29:335–47. doi:10.1122/1.549794

CrossRef Full Text | Google Scholar

37. Struble LJ, Schultz MA. Using creep and recovery to study flow behavior of fresh cement pasteflow behavior of fresh cement paste. Cem Concr Res (1993) 23:1369–79. doi:10.1016/0008-8846(93)90074-j

CrossRef Full Text | Google Scholar

38. Parsons J, Whipple K, Simoni A. Experimental Study of the Grain Flow, Fluid-Mud Transition in Debris Flow. J Geol (2001) 109 (4):427–47. doi:10.1086/320798

CrossRef Full Text | Google Scholar

39. Divoux T, Grenard V, Manneville S. Rheological Hysteresis in Soft Glassy Materials[J]. Phys Rev Lett (2013) 110(1):018304. doi:10.1103/PhysRevLett.110.018304

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Jeong SW, Locat J, Leroueil S. Rheological Properties of Fine-Grained Sediment: The Roles of Texture and Mineralogy[J]. Canadian Geotech J (2010) 47(10):1085–1100. doi:10.1139/T10-012

CrossRef Full Text | Google Scholar

41. Major JJ, Pierson TC. Debris flow rheology: Experimental analysis of fine-grained slurries. Water Resour Res (1992) 28(3):841–57. doi:10.1016/0148-9062(92)92700-m

CrossRef Full Text | Google Scholar

42. Schatzmann M, Bezzola GR, Minor HE, Windhab EJ, Fischer P. Rheometry for large-particulated fluids: Analysis of the ball measuring system and comparison to debris flow rheometry fluids: Analysis of the ball measuring system and comparison to debris flow rheometry. Rheol Acta (2009) 48:715–33. doi:10.1007/s00397-009-0364-x

CrossRef Full Text | Google Scholar

43. Jeong SW. Shear rate-dependent rheological properties of mine tailings: Determination of dynamic and static yield stresses. Appl Sci (2019) 9(22):4744. doi:10.3390/app9224744

CrossRef Full Text | Google Scholar

44. Radhakrishnan R, Divoux T, Manneville S, Fielding SM. Understanding rheological hysteresis in soft glassy materials. Soft Matter (2017) 13:1834–52.

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Mujumdar A, Beris AN, Metzner AB. Transient phenomena in thixotropic systems. J Non-Newtonian Fluid Mech (2002) 102(2):157–78. doi:10.1016/s0377-0257(01)00176-8

CrossRef Full Text | Google Scholar

46. Luckham PF, Rossi S. The colloidal and rheological properties of bentonite suspensions. Adv Colloid Interf Sci (1999) 82(1–3):43–92. doi:10.1016/S0001-8686(99)00005-6

CrossRef Full Text | Google Scholar

47. Besq A, Malfoy C, Pantet A, Monnet P, Righi D. Physicochemical characterisation and flow properties of some bentonite muds. Appl Clay Sci (2003) 23(5–6):275–86. doi:10.1016/S0169-1317(03)00127-3

CrossRef Full Text | Google Scholar

48. Cheng DC. Further observations on the rheological behaviour of dense suspensions. Powder Technol (1984) 37:255–73. doi:10.1016/0032-5910(84)80022-4

CrossRef Full Text | Google Scholar

49. Cheng CH. Yield stress: A time-dependent property and how to measure it. Rheol Acta (1986) 25(5):542–54. doi:10.1007/bf01774406

CrossRef Full Text | Google Scholar

50. Assaad J, Khayat KH. Assessment of thixotropy of self-consolidating concrete and concrete-equivalent-mortar- effect of binder composition and content. ACI Mater J (2004) 101.

Google Scholar

51. Assaad J, Khayat KH, Mesbah H. Assessment of thixotropy of flowable and self-consolidating concrete. ACI Mater J (2003) 100.

Google Scholar

52. De Larrard F, Ferraris C, Sedran T. Fresh concrete: A herschel-bulkley material. Mater Struct (1998) 31:494–8. doi:10.1007/bf02480474

CrossRef Full Text | Google Scholar

53. Schippa L. Modeling the effect of sediment concentration on the flow-like behavior of natural debris flow. Int J Sediment Res (2020) 35(4):315–27.

CrossRef Full Text | Google Scholar

54. O'Brien J. S, & Julien, P. Y. (1998) Laboratory analysis of mudflow properties. Journal of Hydraulic Engineering, 114(8), 877–887.

Google Scholar