Relationship Between Nematicity, Antiferromagnetic Fluctuations, and Superconductivity in FeSe1−xSx Revealed by NMR

The S-substituted FeSe, FeSe_1−xS_x, under pressure (p), provides a versatile platform for studying the relationship among nematicity, antiferromagnetism, and superconductivity. Here we present a short review of the recent experimental evidence showing that nematicity has a remarkable impact on the relationship between antiferromagnetic fluctuations and superconductivity. This has been revealed by several ⁷⁷Se nuclear magnetic resonance studies that have tracked the variability of antiferromagnetic fluctuations and superconducting transition temperature (T_c) as a function of x and p. T_c is roughly proportional to antiferromagnetic fluctuations in the presence or absence of nematic order suggesting the importance of antiferromagnetic fluctuations in the Cooper pairing mechanism in FeSe_1−xS_x. However, the antiferromagnetic fluctuations are more effective in enhancing superconductivity in the absence of nematicity as compared to when it is present. These experimental observations give renewed insights into the interrelationships between nematicity, magnetism, and superconductivity in Fe-based superconductors.

1 Introduction

Suppressing the transition temperatures of long-range orders with a tuning parameter has led to the discovery of superconductivity (SC) in the associated quantum phase transition (QPT) regions of several classes of materials such as heavy-Fermion systems [1–3], itinerant ferromagnets [4, 5], high T_c cuprates and Fe-based superconductors [3, 6]. The quantum critical fluctuations of the suppressed long-range order parameter(s) could thus be responsible for the elusive Cooper pairing mechanism in those unconventional superconductors.

In most Fe-based superconductors, SC appears close to the quantum phase transitions of two long-range orders: the nematic order, which is an electronically driven structural transition from high-temperature tetragonal (C4 symmetry) to low-temperature orthorhombic (C2 symmetry), and the antiferromagnetic (AFM) order with spontaneously oriented electronic spins characterized by a wave vector [q = (π,0) or (0,π)] [3, 7–9]. In those systems, the nematic transition temperature (T_s) is at or just above the Néel temperature (T_N), and both phases are simultaneously suppressed with carrier doping and/or the application of pressure (p), leading to two QPTs originating from the nematic and the AFM states. As SC in these compounds emerges around the two QPTs, AFM and nematic phases are believed to play important roles for the appearance of SC. However, the individual contribution to SC from these two phases becomes difficult to separate due to the close proximity of the two orders [10–12].

In this sense, the sulfur-substituted FeSe system, FeSe_1−xS_x, provides a favorable platform for the study of the role of nematicity or antiferromagnetism on SC independently [13]. FeSe_1−xS_x has the simplest of crystal structures among the Fe-based superconductors, with a quasi-two dimensional FeSe(S) layer in the ab plane, stacked along the c axis. At x = 0, FeSe undergoes a nematic transition at T_s ∼ 90 K followed by a superconducting transition at T_c ∼ 8.5 K, but it does not show a long range AFM order at ambient p [13–16]. This allows the study of AFM fluctuations inside the nematic order and its relationship with SC [17]. The nematic phase in FeSe can be suppressed by pressure application, with T_s decreased down to 32 K at p = 1.5 GPa [18]. T_c shows a complex multi-domed structure with p, reaching a maximum T_c ∼ 37 K at p ∼ 6 GPa [19–21]. At the same time, an AFM ordered state appears above p = 0.8 GPa [22, 23], and T_s merges with T_N above p = 1.7 GPa [24], limiting the range for studying the effects of nematicity on SC without AFM state.

The nematic phase in FeSe can also be suppressed with the isovalent S substitution for Se in FeSe_1−xS_x as shown in Figure 1A taken from Ref. [25] based on data from Refs. [26, 27], where T_s decreases to zero at the critical x value, x_c ∼ 0.17. As no long-range AFM order appears in FeSe_1−xS_x at ambient p, one can study the variability of T_c including near a nematic QPT without an AFM order. At x_c, diverging nematic fluctuations were reported from elasto-resistivity measurements [28], and a temperature- (T-) linear behavior of the resistivity was seen under high magnetic fields (H) [29]. As shown in Figure 1A, T_c first increases up to 10 K around x = 0.09 making a maximum and then decreases gradually at higher x without showing any clear change in T_c around x_c [18, 26, 30]. Nevertheless, the considerable change in the size and anisotropy of the SC gap is observed at the nematic QPT in spectroscopic-imaging scanning tunneling microscopy [26, 30, 31], thermal conductivity [32], and specific heat [33] measurements, implying different SC states inside (SC1) and outside (SC2) nematic states [25]. In addition, signatures of the crossover between Bardeen-Cooper-Schrieffer and Bose-Einstein-Condensate superconductivities at the nematic QPT were recently reported by laser-excited angle-resolved photoemission spectroscopy (ARPES) measurements [34].

FIGURE 1

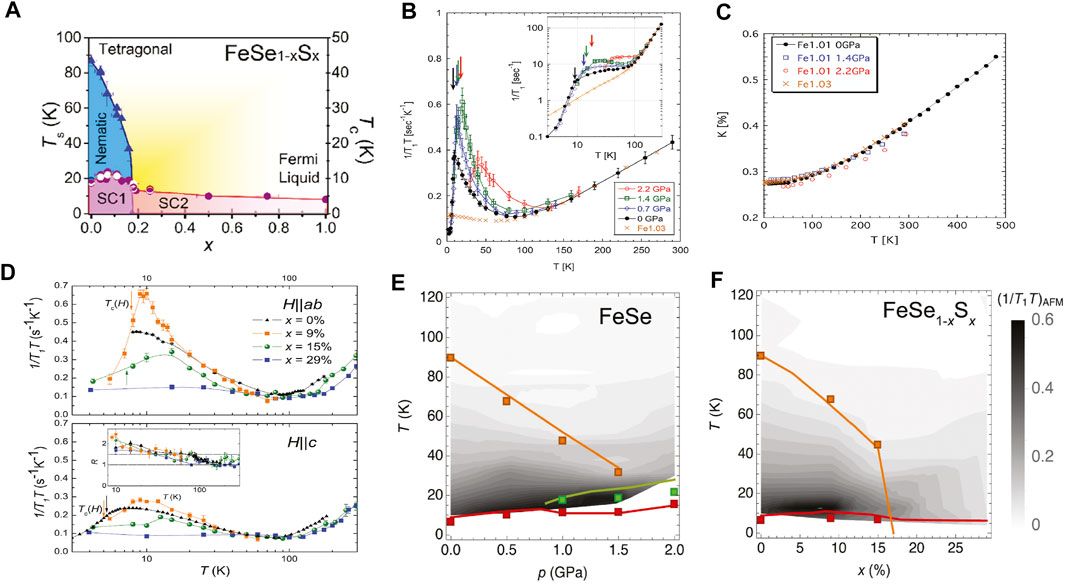
FIGURE 1. (A) Electronic phase diagram of FeSe_1−xS_x taken from Ref. [25] based on data from Refs. [26, 27]. (B) T dependence of 1/T₁T under various p in polycrystalline FeSe. The arrows show the corresponding T_c. The inset show the T dependence of 1/T₁ under p. Reprinted with permission from T. Imai et al., Physical Review Letters 102, 177005, 2009 [17]. Copyright (2009) by the American Physical Society. (C) p dependence of the Knight shift K as a function of T. Reprinted with permission from Ref. [17]. Copyright (2009) by the American Physical Society. (D) T-dependence of 1/T₁T in single crystalline FeSe_1−xS_x for H‖ab (top) and H‖c (bottom) at ambient p. The arrows show the corresponding T_c. The inset shows inset the T dependence of the ratio R = T_1,c/T_1,ab. Reprinted with permission from P. Wiecki et al., Physical Review B 98, 020507(R), 2018 [18]. Copyright (2018) by the American Physical Society. (E, F) The contour plots of the amplitude of the AFM fluctuations defined as ${(1/T_{1}T)}_{\text{AFM}}$ (see text for derivation) in single crystal: FeSe under p (E) and FeSe_1−xS_x at ambient p (F) taken from Ref. [18] which includes data reported in Refs. [58, 60]. The orange, red and green symbols show T_s, T_c, and T_N, respectively, determined by NMR measurements under H ∼ 7.4 T [18]. The colored curves are the corresponding values from literatures [58, 60]. Reprinted with permission from Ref. [18]. Copyright (2018) by the American Physical Society.

The nematic phase in the S-substituted FeSe system is also controlled by pressure application and an AFM state appears at higher p [35–38]. The three-dimensional T-p-x phase diagram of FeSe_1−xS_x up to p = 8 GPa has been reported by Matsuura et al. [35] in which the AFM ordered phase shifts to higher p with increasing x. A typical p-T phase is shown in Figure 2A for the case of x = 0.09 [37]. In this case, with increasing p, the nematic phase disappears around p ∼ 0.5 GPa corresponding to a putative nematic QPT, and the AFM state appears above p ∼ 3.5 GPa. In addition to the nematic, AFM, and SC states, Fermi liquid behaviors were reported at low temperatures in x = 0.09 (see Figure 2A) [37] and 0.11 [39] after the suppression of the nematic order by applying p. The Fermi liquid phase was recently attributed to the presence of a quantum griffiths phase close to the nematic QPT [40]. Similar to the T-x phase diagram of FeSe_1−xS_x, SC phase was shown to have two different states (SC1 and SC2) separated by the nematic QPT as shown in Figure 2A. Such two different SC states under p were also reported in x = 0.11 [39] and 0.12 [41], which is more apparent under H [41]. The presence of a series of nematic quantum phase transitions in the x-p phase diagram [35] allows the study of the correlation between T_c and AFM fluctuations in the presence and absence of the nematic order [37].

FIGURE 2

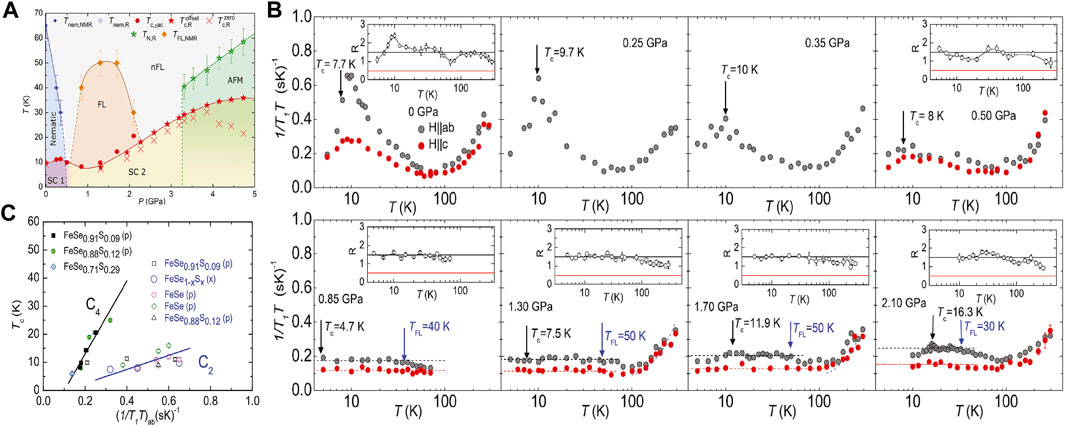
FIGURE 2. (A) Electronic phase diagram of FeSe_0.91S_0.09 under pressure. Reprinted with permission from K. Rana et al., Physical Review B 101, 180503(R), 2020 [37]. Copyright (2020) by the American Physical Society. (B) Temperature- (T-) dependence of 1/T₁T in single crystalline FeSe_0.91S_0.09 measured at the indicated pressures under H‖ab (black) and H‖c (red). Black arrows indicate the superconducting transition temperatures under H = 7.4089 T parallel to the ab plane and blue arrows correspond to the Fermi liquid temperature below which 1/T₁T = constant is observed. The insets show the ratio, R, of 1/T₁T values measured for H‖ab and H‖c at the indicated p. The black and red lines in the insets are at 1.5 and 0.5. Reprinted with permission from Ref. [37]. Copyright (2020) by the American Physical Society. (C) Superconducting transition temperature (T_c) as a function of AFM fluctuations determined by the maximum of 1/T₁T under H‖ab in FeSe_1−xS_x under p, taken from Ref. [37] which provided the original data for x = 0.09 (open and closed black boxes). The data for x = 0 were taken from Ref. [17] (open dark green circles) and Refs. [58, 60] (open magenta circles). Values for x = 0.12 were taken from Ref. [41] (closed green circles and open triangles), and that for FeSe_1−xS_x at ambient p (closed blue diamond and open blue circles) were taken from Ref. [18]. Black and blue lines fit the data with and without nematicity respectively. Reprinted with permission from Ref. [37]. Copyright (2020) by the American Physical Society.

In this mini review, we show the positive correlation between AFM fluctuations and SC and the impact of nematicity on the relationship based on the nuclear magnetic resonance (NMR) studies of the FeSe_1−xS_x system under p. After briefly introducing some basics of NMR which are used in ⁷⁷Se NMR studies to characterize the AFM fluctuations, we review the relationship between AFM fluctuations and SC in the presence of nematic order in FeSe under p and in FeSe_1−xS_x at ambient p. Then, we show the studies of FeSe_1−xS_x system under p, where we review the relationship between AFM fluctuations and SC in the absence of nematic order. Finally, we end with a summary including the current research gaps and potential future developments in the field.

2 Nuclear Magnetic Resonance and Antiferromagnetic Fluctuations

NMR is one of the powerful techniques to study the magnetic and electronic properties of materials from a microscopic point of view and has been utilized to investigate the physical properties of Fe-based superconductors. Nuclei with finite angular momentum undergo Zeeman splitting in the presence of a magnetic field at the nuclear site (H_nuc). The energy difference between the nearest nuclear spin levels is given as ΔE = γ_NℏH_nuc where γ_N is the nuclear gyromagnetic ratio. In the NMR technique, nuclei are excited from lower energy states to higher ones by applying electromagnetic wave whose energy is equal to ΔE.

The resonance frequency is determined by H_nuc which is a sum of the external magnetic field (H) and the hyperfine field (H_hf) due to the interaction between nuclei and electrons. The shift of the resonance line due to the hyperfine interaction is defined by K = H_hf/H which is the so-called Knight shift in metals. In general, the shift K has the T-independent orbital component, K_orb, and T-dependent spin component, K_s, which can be expressed as K = K_orb + K_s. K_s is proportional to the static and uniform magnetic susceptibility (χ_s) with the wave vector q = 0 and the frequency ω = 0:

$K_{\mathrm{s}}\sim A_{hf}{\chi }_{\text{s}}\left(\mathbf{q}=0,\omega =0\right).(1)$

The T dependence of K_s gives us information of the magnetic properties of compounds at q = 0. On the other hand, the nuclear relaxation rate (1/T₁) divided by T, 1/T₁T, is sensitive to the q-sum of the imaginary part of susceptibility (χ′′(q, ω_N)) at the NMR frequency (ω_N) [42] and is given as

$1/T_{1}T\sim {\gamma }_{\text{N}}^2{k}_{\text{B}}\sum _{\mathbf{q}}|A\left(\mathbf{q}\right){|}^2{\chi }^{\prime \prime }\left(\mathbf{q},{\omega }_{\text{N}}\right)/{\omega }_{\text{N}}(2)$

where A(q) is the q-dependent hyperfine form factor. 1/T₁T gives us information about the total magnetic correlations at all q values. Therefore, one can obtain important insights about q dependent magnetic correlations by comparing K_s and 1/T₁T data.

In simple metals, K_s is related to the density of states at the Fermi energy $[\mathcal{N}(E_{\text{F}})]$ where $K_{\text{s}}=A_{\text{hf}}{(g{\mu }_{\text{B}})}^2\mathcal{N}(E_{\mathrm{F}})/2$, and 1/T₁T is proportional to the square of $\mathcal{N}(E_{\mathrm{F}})$ as $1/T_{1}T=\pi \hslash A_{\text{hf}}^2{(g{\mu }_{\text{B}})}^2{\gamma }_{\text{N}}^2{\mathcal{N}}^2(E_{\mathrm{F}})k_{\text{B}}$ [43]. In a Fermi liquid picture, the ratio $S\equiv T_{1}T{K}_{\text{s}}^2$ becomes a constant [42, 44] which is called the Korringa relation. In real materials, an experimentally determined value of $T_{1}T{K}_{\text{s}}^2$ may deviate from S due to electron correlations. Thus, the deviation parameter defined as α = $S/(T_{1}T{K}_{\text{s}}^2)$ provides information about electron correlations in materials. When AFM fluctuations are present, χ”(q, ω_N) with q ≠ 0 is enhanced with little or no effect on K_s which probes only the q = 0 component of χ_s. Therefore, 1/T₁T is enhanced much higher than K_s and α becomes greater than unity. On the other hand, α < unity is expected for ferromagnetic correlations.

When the Korringa relation does not hold due to strong magnetic fluctuations (non-Fermi liquid picture), the T dependence of 1/T₁T could be different from that of K. When strong AFM fluctuations exist in systems, the contribution to 1/T₁T from AFM fluctuations will be the source of the different T dependence, and the experimentally observed 1/T₁T is sometimes decomposed as $1/T_{1}T={(1/T_{1}T)}_{\text{AFM}}+{(1/T_{1}T)}_{\mathbf{q}=0}$ [18, 45, 46]. Here ${(1/T_{1}T)}_{\mathrm{A}\mathrm{F}\mathrm{M}}$ denotes the AFM contributions from χ(q ≠ 0, ω_N) and ${(1/T_{1}T)}_{\mathbf{q}=0}$ represents the contributions from q = 0 components. By assuming ${(1/T_{1}T)}_{\mathbf{q}=0}=C{K}_{\text{s}}^2$, where C is the empirically determined proportionality constant, one can extract the AFM contribution to 1/T₁T by subtracting ${(1/T_{1}T)}_{\mathbf{q}=0}$ from the observed 1/T₁T, providing insights into the magnetic fluctuations.

In the case of Fe-based superconductors, Kitagawa et al. proposed that anisotropy in 1/T₁ at the chalcogen or pnictogen sites provides more detailed information about AFM fluctuations [47]. According to them, the ratio of 1/T₁ values measured under H parallel to c axis (1/T_1,c) and parallel to ab plane (1/T_1,ab) [R ≡ T_1,c/T_1,ab] can determine the dominant q for AFM fluctuations. In the case of isotropic AFM fluctuations, R = 1.5 is expected for stripe-type AFM fluctuations with q = (π, 0) or (0, π), whereas when Néel type AFM fluctuations with q = (π, π) are present, R = 0.5. Such analysis has been extensively used in Fe-based superconductors [18, 37, 47–51] and related materials [52, 53] to characterize the AFM fluctuations in those systems.

3 Antiferromagnetic Fluctuations and Superconductivity With Nematicity

Soon after the discovery of the Fe-based superconductors [54, 55], ⁷⁷Se (I = 1/2, γ_N/2π = 8.1432 MHz) NMR studies on polycrystalline FeSe were carried out [17, 56] and the importance of AFM fluctuations for superconductivity has been pointed out. Figure 1B shows the T dependence of 1/T₁T values in FeSe under various pressures reported by Imai et al. [17]. At higher temperatures above T ∼ 100 K, 1/T₁T at all pressures decreases with decreasing T. This behavior is similar to the T-dependence of K shown in Figure 1C where K shows a monotonic decrease when cooling from 480 to ∼ 100 K. The variations in both 1/T₁T and K above ∼ 100 K were explained in terms of spin gap formation or a peculiar band structure near the Fermi level [57]. However, upon cooling below T ∼ 100 K, the T dependences of 1/T₁T and K show quite different behaviors. Although K is nearly independent of both T and p below 50 K, 1/T₁T shows strong enhancements at all measured pressures at low temperatures where peaks are observed at the p-dependent T_c or T_N. As described above, K is proportional to χ(0, 0) and 1/T₁T reflects the T dependence of q-summed χ”(q, ω_N). Therefore, the enhancements of 1/T₁T at low temperatures unequivocally establish the presence of AFM fluctuations at the T region, suggesting that the AFM fluctuations are relevant to the SC in FeSe. In fact, a close relationship between the AFM fluctuations and SC has been pointed out from the p dependences of T_c and 1/T₁T data: the maximum of 1/T₁T increases along with T_c as shown in Figure 1B where T_cs at different p are marked by downward arrows [17]. Broad humps in 1/T₁T observed at temperatures much higher than their respective T_c values at p = 1.4 and 2.2 GPa are due to magnetic orderings. It should be noted that, due to the occurrence of the AFM order under high pressures in FeSe, the relationship between T_c and the maximum of 1/T₁T can only be compared at low pressures in this system. A later single crystalline ⁷⁷Se NMR studies under H‖ab and H‖c characterized the AFM order and the AFM fluctuations at higher pressures to be of stripe type [51, 58].

A⁷⁷Se NMR study of single crystalline FeSe_1−xS_x by Wiecki et al. [18] at ambient p also provided clear experimental evidence of the close relationship between the AFM fluctuations and SC in this system. Figure 1D show the T dependence of 1/T₁T in FeSe_1−xS_x for H‖ab (upper) and H‖c (lower), respectively, at ambient p [18], which includes the data from Ref. [58]. As in FeSe, K for all x shows monotonic decreases when lowering T from room T down to ∼ 100 K, before leveling off at constant values [18] for both H‖ab and H‖c. Although 1/T₁T showed a similar T dependence as K in all cases above 100 K, 1/T₁T shows a strong upturn below T ∼ 100 K due to the growth of AFM fluctuations. The AFM fluctuations appear below 100 K for all samples of x = 0, 0.09, 0.15, and 0.29, however, the enhancement of the AFM fluctuations shows a strong x dependence. For x less than x_c ∼ 0.17, 1/T₁T increases with decreasing T showing a Curie-Wiess-like behavior expected for two-dimensional AFM fluctuations from the self-consistent renormalization theory [42]. On the other hand, for x = 0.29 greater than x_c, a subtle upturn on cooling below T ∼ 100 K is observed, suggesting the tiny growth of the AFM fluctuations, followed by a nearly T independent behavior below T ∼ 25 K without showing clear Curie-Weiss-like behaviors. At all measured x values, the ratios R ≡ T_1,c/T_1,ab are found to be ∼ 1.5 below T ∼ 100 K shown in the inset of the lower panel of Figure 1D, indicating that the AFM fluctuations are characterized to be stripe type and do not change with x.

The x-T phase diagram (Figure 1A) of FeSe_1−xS_x at ambient p allowed Wiecki et al. to examine the correlation between AFM fluctuations and T_c, and it was shown to persist, despite the presence of a nematic QPT isolated from an AFM order. The maximum values of 1/T₁T first increased when x was changed from 0 to 0.09, then decreased for x = 0.15 and higher, similar to the x dependence of T_c shown in Figure 1A. Figures 1E,F taken from Ref. [18] are contour plots of the magnitude of AFM fluctuations determined by 1/T₁T data in FeSe under p (E) and in FeSe_1−xS_x at ambient p (F), respectively, along with their respective phase diagrams. It can be seen that T_c is enhanced at the p or x values where AFM fluctuations are stronger. This indicates the correlation between T_c and AFM fluctuations in both cases and also demonstrates the primary importance of AFM fluctuations to SC in FeSe_1−xS_x. It was also pointed out that, although nematic fluctuations are most strongly enhanced near the nematic QCP at x ∼ 0.17 in the case of FeSe_1−xS_x, no clear correlation with T_c was observed [18].

4 Antiferromagnetic Fluctuations and Superconductivity Without Nematicity

With the firm establishment of the correlation between AFM fluctuations and SC in FeSe_1−xS_x, the question then arose about the role of nematicity on the relationship. As described above, FeSe_1−xS_x provides a suitable platform for the study of the role of nematicity on the relationship by changing samples as reported by Wiecki et al. [18]. The application of pressure on FeSe_1−xS_x also provides a versatile opportunity to study the effect of nematicity on the relationship. This has an advantage because p is known as one of the clean tuning parameters which control the ground state without changing the composition avoiding any additional effects of S substitutions such as homogeneity by changing x. Several ⁷⁷Se NMR studies on single crystalline FeSe_1−xS_x under pressure have been carried out [37, 38, 41, 59]. Here we show the results of NMR measurements under pressure up to 2.1 GPa on x = 0.09 whose p-T phase diagram is shown in Figure 2A reported in Ref. [37]. With p, the nematic phase is suppressed and disappears around the critical pressure p_c ∼ 0.5 GPa, and an AFM state appears above 3 GPa with a dome-shaped Fermi-liquid phase between nematic and AFM phases. T_c shows a clear p dependence with a double dome structure with and without long-range nematicity, making the system suitable in investigating the role of nematicity on the relationship.

Figure 2B shows the T dependence of 1/T₁T for x = 0.09 under H‖ab (black) and H‖c (red) at several pressures, taken from the study by Rana et al [37]. Below p_c = 0.5 GPa, with decreasing T, 1/T₁T increases below ∼70 K showing Curie-Weiss like behavior originating from two dimensional AFM fluctuations and starts to decrease around T_c (T_c for H‖ab are shown by black arrows in the figures). On the other hand, above 0.5 GPa, 1/T₁T exhibits quite different temperature dependences in comparison with those observed at low pressures. Although 1/T₁T is slightly enhanced below ∼70 K, indicating the existence of the AFM spin fluctuations, 1/T₁Ts are nearly constant exhibiting the so-called Korringa behavior, expected for Fermi-liquid state below the temperature (defined as T_FL) marked by blue arrows. Thus the results indicate that the nature of AFM fluctuations changes below and above p_c = 0.5 GPa in FeSe_0.91S_0.09.

Similar T dependences of 1/T₁T have also been reported in ⁷⁷Se NMR studies of FeSe_1−xS_x by Kuwayama et al. [38, 41] under p up to 3.9 GPa. The authors pointed out that AFM fluctuations with different q vectors may be responsible for the two distinct SC domes [41]. However, Rana et al found that the AFM fluctuations are characterized to be stripe type and p independent by showing the fact that the ratios R are close to ∼ 1.5 at low temperatures for all measured p shown in the insets of Figure 2B.

Then what is the difference in the nature of AFM fluctuations in the presence and absence of nematic order? The idea that nematicity changes the relationship between T_c and AFM fluctuations was proposed by Rana et al [37] and can be clearly seen in Figure 2C taken from that study. Here, in the x axis, the maximum values of 1/T₁T with H‖ab were taken as a representative of the magnitude of AFM fluctuations for different values of x and p in FeSe_1−xS_x. The corresponding x and p dependent T_c values were plotted in the y axis. The data included for x = 0, 0.12 and 0.29 were taken from Refs. [17, 58, 60], Ref. [41] and Ref. [18], respectively, while those for x = 0.09 were reported by Ref. [37]. These experimental data were classified into two groups: one that includes the data points where T_c and AFM fluctuations are in the nematic order, and another that includes those measured in the absence of nematic order. The slope for the linear fitting of the data points in the absence of nematicity was higher by a factor of ∼ 5 compared to the slope for the linear fitting of those in the presence of nematicity. The results indicate that, for example, T_c is less sensitive to the strength of spin fluctuations in the tetragonal phase of FeSe_1−xS_x at ambient pressure for x < 0.17 while it is largely enhanced in the orthorhombic phase of FeSe_0.91S_0.09 above 0.5 GPa even with a small increase in AFM fluctuations. When nematicity is absent, the AFM fluctuations in this system are present at both the wave vectors q = (π, 0) and q = (0, π) due to the four-fold rotational symmetry (C4) of the tetragonal state. However, in the presence of nematicity, the rotational symmetry is reduced to two-fold rotational symmetry (C2) and the AFM fluctuations are present at only one of the wave vectors, either vector q = (π, 0) or q = (0, π) [61, 62]. Based on those results, Rana et al. pointed out that the AFM fluctuations with C4 symmetry are more effective in enhancing T_c for the FeSe_1−xS_x system.

5 Summary

We presented a brief overview of ⁷⁷Se NMR studies in FeSe_1−xS_x at ambient pressure and under pressure, especially focusing on the role of nematicity on the relationship between superconducting transition temperature T_c and antiferromagnetic (AFM) fluctuations. It was shown that T_c has a positive relationship with AFM fluctuations, suggesting the importance of AFM fluctuations in the pairing mechanism of superconducting electrons in FeSe_1−xS_x. Furthermore, nematicity is found to play a central role on the positive relationship. In the absence of nematic order, T_c can be greatly enhanced by AFM fluctuations. When the nematic order is present, this enhancement decreases by a factor of ∼ 5. The evidence of the impact of nematicity on the relationship between superconductivity and AFM fluctuations has emerged from various ⁷⁷Se NMR studies in the FeSe_1−xS_x system under pressure.

Although the findings provide a renewed insight on the relationships between nematicity, magnetism, and unconventional superconductivity in Fe-based superconductors, the origin for the strong impact of nematicity on the relationship between T_c and AFM fluctuations is still an open question. Further detailed experimental as well as theoretical investigations of the underlying reason behind the impact of nematicity on the relationships between superconductivity and AFM fluctuations would bring us a step towards understanding the physical mechanism behind unconventional superconductivity.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The work at Ames Laboratory was supported by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Division of Materials Sciences and Engineering. Ames Laboratory is operated for the U.S. DOE by Iowa State University under Contract No. DE-AC02-07CH11358.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with the authors KR and YF.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge precious collaborations and fruitful discussions with Paul Wiecki, Anna E. Böhmer, Paul C. Canfield, Sergey L. Bud’ko, Raphael Fernandes, Raquel A. Riberio, G. G. Lesseux, Yongbin Lee, and Qing-Ping Ding.

References

1. Curro NJ, Caldwell T, Bauer ED, Morales LA, Graf MJ, Bang Y, et al. Unconventional Superconductivity in PuCoGa₅. Nature (2005) 434:622–5. doi:10.1038/nature03428

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Hattori T, Ihara Y, Nakai Y, Ishida K, Tada Y, Fujimoto S, et al. Superconductivity Induced by Longitudinal Ferromagnetic Fluctuations in UCoGe. Phys Rev Lett (2012) 108:066403. doi:10.1103/PhysRevLett.108.066403

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Scalapino DJ. A Common Thread: the Pairing Interaction for Unconventional Superconductors. Rev Mod Phys (2012) 84:1383–417. doi:10.1103/RevModPhys.84.1383

CrossRef Full Text | Google Scholar

4. Canfield PC, Bud’ko SL. Preserved Entropy and Fragile Magnetism. Rep Prog Phys (2016) 79:084506. doi:10.1088/0034-4885/79/8/084506

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Brando M, Belitz D, Grosche FM, Kirkpatrick TR. Metallic Quantum Ferromagnets. Rev Mod Phys (2016) 88:025006. doi:10.1103/RevModPhys.88.025006

CrossRef Full Text | Google Scholar

6. Bertel E, Menzel A. Fluctuating Charge Order: a Universal Phenomenon in Unconventional Superconductivity. Symmetry (2016) 8:45. doi:10.3390/sym8060045

CrossRef Full Text | Google Scholar

7. Johnston DC. The Puzzle of High Temperature Superconductivity in Layered Iron Pnictides and Chalcogenides. Adv Phys (2010) 59:803–1061. doi:10.1080/00018732.2010.513480

CrossRef Full Text | Google Scholar

8. Canfield PC, Bud'ko SL. FeAs-Based Superconductivity: A Case Study of the Effects of Transition Metal Doping on BaFe₂As₂. Annu Rev Condens Matter Phys (2010) 1:27–50. doi:10.1146/annurev-conmatphys-070909-104041

CrossRef Full Text | Google Scholar

9. Stewart GR. Superconductivity in Iron Compounds. Rev Mod Phys (2011) 83:1589–652. doi:10.1103/RevModPhys.83.1589

CrossRef Full Text | Google Scholar

10. Kuo H-H, Chu J-H, Palmstrom JC, Kivelson SA, Fisher IR. Ubiquitous Signatures of Nematic Quantum Criticality in Optimally Doped Fe-Based Superconductors. Science (2016) 352:958–62. doi:10.1126/science.aab0103

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lederer S, Schattner Y, Berg E, Kivelson SA. Enhancement of Superconductivity Near a Nematic Quantum Critical Point. Phys Rev Lett (2015) 114:097001. doi:10.1103/PhysRevLett.114.097001

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Lederer S, Schattner Y, Berg E, Kivelson SA. Superconductivity and Non-Fermi Liquid Behavior Near a Nematic Quantum Critical Point. Proc Natl Acad Sci USA (2017) 114:4905–10. doi:10.1073/pnas.1620651114

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Böhmer AE, Kreisel A. Nematicity, Magnetism and Superconductivity in FeSe. J Phys Condens Matter (2018) 30:023001. doi:10.1088/1361-648X/aa9caa

CrossRef Full Text | Google Scholar

14. Hsu F-C, Luo J-Y, Yeh K-W, Chen T-K, Huang T-W, Wu PM, et al. Superconductivity in the PbO-type Structure α-FeSe. Proc Natl Acad Sci (2008) 105:14262–4. doi:10.1073/pnas.0807325105

PubMed Abstract | CrossRef Full Text | Google Scholar

15. McQueen TM, Williams AJ, Stephens PW, Tao J, Zhu Y, Ksenofontov V, et al. Tetragonal-to-Orthorhombic Structural Phase Transition at 90 K in the Superconductor Fe_1.01Se. Phys Rev Lett (2009) 103:057002. doi:10.1103/PhysRevLett.103.057002

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Baek S-H, Efremov DV, Ok JM, Kim JS, van den Brink J, Büchner B. Orbital-driven Nematicity in FeSe. Nat Mater (2015) 14:210–4. doi:10.1038/nmat4138

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Imai T, Ahilan K, Ning FL, McQueen TM, Cava RJ. Why Does Undoped FeSe Become a High-T_c Superconductor under Pressure. Phys Rev Lett (2009) 102:177005. doi:10.1103/PhysRevLett.102.177005

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wiecki P, Rana K, Böhmer AE, Lee Y, Bud'ko SL, Canfield PC, et al. Persistent Correlation between Superconductivity and Antiferromagnetic Fluctuations Near a Nematic Quantum Critical Point in FeSe_1−xS_x. Phys Rev B (2018) 98:020507. doi:10.1103/PhysRevB.98.020507

CrossRef Full Text | Google Scholar

19. Mizuguchi Y, Tomioka F, Tsuda S, Yamaguchi T, Takano Y. Superconductivity at 27 K in Tetragonal FeSe under High Pressure. Appl Phys Lett (2008) 93:152505. doi:10.1063/1.3000616

CrossRef Full Text | Google Scholar

20. Margadonna S, Takabayashi Y, Ohishi Y, Mizuguchi Y, Takano Y, Kagayama T, et al. Pressure Evolution of the Low-temperature Crystal Structure and Bonding of the Superconductor FeSe (T_c=37 K). Phys Rev B (2009) 80:064506. doi:10.1103/PhysRevB.80.064506

CrossRef Full Text | Google Scholar

21. Medvedev S, McQueen TM, Troyan IA, Palasyuk T, Eremets MI, Cava RJ, et al. Electronic and Magnetic Phase Diagram of β-Fe_1.01Se with Superconductivity at 36.7 K under Pressure. Nat Mater (2009) 8:630–3. doi:10.1038/nmat2491

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Terashima T, Kikugawa N, Kasahara S, Watashige T, Shibauchi T, Matsuda Y, et al. Pressure-induced Antiferromagnetic Transition and Phase Diagram in FeSe. J Phys Soc Jpn (2015) 84:063701. doi:10.7566/JPSJ.84.063701

CrossRef Full Text | Google Scholar

23. Bendele M, Amato A, Conder K, Elender M, Keller H, Klauss H-H, et al. Pressure Induced Static Magnetic Order in Superconducting FeSe_1−x. Phys Rev Lett (2010) 104:087003. doi:10.1103/PhysRevLett.104.087003

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kothapalli K, Böhmer AE, Jayasekara WT, Ueland BG, Das P, Sapkota A, et al. Strong Cooperative Coupling of Pressure-induced Magnetic Order and Nematicity in FeSe. Nat Commun (2016) 7:12628. doi:10.1038/ncomms12728

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Coldea AI. Electronic Nematic States Tuned by Isoelectronic Substitution in Bulk FeSe_1−xS_x. Front Phys (2021) 8:594500. doi:10.3389/fphy.2020.594500

CrossRef Full Text | Google Scholar

26. Reiss P, Watson MD, Kim TK, Haghighirad AA, Woodruff DN, Bruma M, et al. Suppression of Electronic Correlations by Chemical Pressure from FeSe to FeS. Phys Rev B (2017) 96:121103. doi:10.1103/PhysRevB.96.121103

CrossRef Full Text | Google Scholar

27. Coldea AI, Blake SF, Kasahara S, Haghighirad AA, Watson MD, Knafo W, et al. Evolution of the Low-Temperature Fermi Surface of Superconducting FeSe_1−xS_x across a Nematic Phase Transition. Npj Quant Mater (2019) 4:2. doi:10.1038/s41535-018-0141-0

CrossRef Full Text | Google Scholar

28. Hosoi S, Matsuura K, Ishida K, Wang H, Mizukami Y, Watashige T, et al. Nematic Quantum Critical Point without Magnetism in FeSe_1−xS_x Superconductors. Proc Natl Acad Sci USA (2016) 113:8139–43. doi:10.1073/pnas.1605806113

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Licciardello S, Buhot J, Lu J, Ayres J, Kasahara S, Matsuda Y, et al. Electrical Resistivity across a Nematic Quantum Critical Point. Nature (2019) 567:213–7. doi:10.1038/s41586-019-0923-y

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Abdel-Hafiez M, Zhang Y-Y, Cao Z-Y, Duan C-G, Karapetrov G, Pudalov VM, et al. Superconducting Properties of Sulfur-doped Iron Selenide. Phys Rev B (2015) 91:165109. doi:10.1103/PhysRevB.91.165109

CrossRef Full Text | Google Scholar

31. Watson MD, Kim TK, Haghighirad AA, Blake SF, Davies NR, Hoesch M, et al. Suppression of Orbital Ordering by Chemical Pressure in FeSe_1−xS_x. Phys Rev B (2015) 92:121108. doi:10.1103/PhysRevB.92.121108

CrossRef Full Text | Google Scholar

32. Hanaguri T, Iwaya K, Kohsaka Y, Machida T, Watashige T, Kasahara S, et al. Two Distinct Superconducting Pairing States Divided by the Nematic End Point in FeSe_1−xS_x. Sci Adv (2018) 4:eaar6419. doi:10.1126/sciadv.aar6419

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Sato Y, Kasahara S, Taniguchi T, Xing X, Kasahara Y, Tokiwa Y, et al. Abrupt Change of the Superconducting gap Structure at the Nematic Critical point in FeSe_1−xS_x. Proc Natl Acad Sci USA (2018) 115:1227–31. doi:10.1073/pnas.1717331115

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Hashimoto T, Ota Y, Tsuzuki A, Nagashima T, Fukushima A, Kasahara S, et al. Bose-Einstein Condensation Superconductivity Induced by Disappearance of the Nematic State. Sci Adv (2020) 6:eabb9052. doi:10.1126/sciadv.abb9052

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Matsuura K, Mizukami Y, Arai Y, Sugimura Y, Maejima N, Machida A, et al. Maximizing T_c by Tuning Nematicity and Magnetism in FeSe_1−xS_x Superconductors. Nat Commun (2017) 8:1143. doi:10.1038/s41467-017-01277-x

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Xiang L, Kaluarachchi US, Böhmer AE, Taufour V, Tanatar MA, et al. Dome of Magnetic Order inside the Nematic Phase of Sulfur-Substituted FeSe under Pressure. Phys Rev B (2017) 96:024511. doi:10.1103/PhysRevB.96.024511

CrossRef Full Text | Google Scholar

37. Rana K, Xiang L, Wiecki P, Ribeiro RA, Lesseux GG, Böhmer AE, et al. Impact of Nematicity on the Relationship between Antiferromagnetic Fluctuations and Superconductivity in FeSe_0.91S_0.09 under Pressure. Phys Rev B (2020) 101:180503. doi:10.1103/PhysRevB.101.180503

CrossRef Full Text | Google Scholar

38. Kuwayama T, Matsuura K, Gouchi J, Yamakawa Y, Mizukami Y, Kasahara S, et al. Pressure-induced Reconstitution of Fermi Surfaces and Spin Fluctuations in S-Substituted FeSe. Sci Rep (2021) 11:17265. doi:10.1038/s41598-021-96277-9

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Reiss P, Graf D, Haghighirad AA, Knafo W, Drigo L, Bristow M, et al. Quenched Nematic Criticality and Two Superconducting Domes in an Iron-Based Superconductor. Nat Phys (2019) 16:89–94. doi:10.1038/s41567-019-0694-2

CrossRef Full Text | Google Scholar

40. Reiss P, Graf D, Haghighirad AA, Vojta T. Signatures of a Quantum Griffiths Phase Close to an Electronic Nematic Quantum Phase Transition. Phys Rev Lett (2021) 127:246402. doi:10.1103/PhysRevLett.127.246402

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Kuwayama T, Matsuura K, Mizukmami Y, Kasahara S, Matsuda Y, Shibauchi T, et al. ⁷⁷Se-NMR Study under Pressure on 12%-S Doped FeSe. J Phys Soc Jpn (2019) 88:033703. doi:10.7566/JPSJ.88.033703

CrossRef Full Text | Google Scholar

42. Moriya T. The Effect of Electron-electron Interaction on the Nuclear Spin Relaxation in Metals. J Phys Soc Jpn (1963) 18:516–20. doi:10.1143/JPSJ.18.516

CrossRef Full Text | Google Scholar

43. Slichter CP. Principles of Magnetic Resonance. 3rd ed. Berlin Heidelberg: Springer (1990). doi:10.1007/978-3-662-09441-9

CrossRef Full Text | Google Scholar

44. Narath A, Weaver HT. Effects of Electron-electron Interactions on Nuclear Spin-Lattice Relaxation Rates and Knight Shifts in Alkali and Noble Metals. Phys Rev (1968) 175:373–82. doi:10.1103/PhysRev.175.373

CrossRef Full Text | Google Scholar

45. Ahilan K, Ning FL, Imai T, Sefat AS, McGuire MA, Sales BC, et al. Superconductivity Near a Quantum Critical Point in Ba(Fe_1−xCo_x)₂As₂ Physica C: Superconductivity its Appl (2010) 470:S273–S275. doi:10.1016/j.physc.2009.11.124

CrossRef Full Text | Google Scholar

46. Nakai Y, Iye T, Kitagawa S, Ishida K, Kasahara S, Shibauchi T, et al. Normal-state Spin Dynamics in the Iron-Pnictide Superconductors BaFe₂(As_1−xP_x)₂ and Ba(Fe_1−xCo_x)₂As₂ probed with NMR Measurements. Phys Rev B (2013) 87:174507. doi:10.1103/PhysRevB.87.174507

CrossRef Full Text | Google Scholar

47. Kitagawa S, Nakai Y, Iye T, Ishida K, Kamihara Y, Hirano M, et al. Stripe Antiferromagnetic Correlations in LaFeAsO_1−xF_x probed by ⁷⁵As NMR. Phys Rev B (2010) 81:212502. doi:10.1103/PhysRevB.81.212502

CrossRef Full Text | Google Scholar

48. Kitagawa K, Katayama N, Ohgushi K, Takigawa M. Antiferromagnetism of SrFe₂As₂ Studied by Single-Crystal ⁷⁵As-NMR. J Phys Soc Jpn (2009) 78:063706. doi:10.1143/JPSJ.78.063706

CrossRef Full Text | Google Scholar

49. Hirano M, Yamada Y, Saito T, Nagashima R, Konishi T, Toriyama T, et al. Potential Antiferromagnetic Fluctuations in Hole-Doped Iron-Pnictide Superconductor Ba_1-xK_xFe₂As₂ Studied by ⁷⁵As Nuclear Magnetic Resonance Measurement. J Phys Soc Jpn (2012) 81:054704. doi:10.1143/JPSJ.81.054704

CrossRef Full Text | Google Scholar

50. Furukawa Y, Roy B, Ran S, Bud'ko SL, Canfield PC. Suppression of Electron Correlations in the Collapsed Tetragonal Phase of CaFe₂As₂ under Ambient Pressure Demonstrated by ⁷⁵As NMR/NQR Measurements. Phys Rev B (2014) 89:121109. (R). doi:10.1103/PhysRevB.89.121109

CrossRef Full Text | Google Scholar

51. Wang PS, Sun SS, Cui Y, Song WH, Li TR, Yu R, et al. Pressure Induced Stripe-Order Antiferromagnetism and First-Order Phase Transition in FeSe. Phys Rev Lett (2016) 117:237001. doi:10.1103/PhysRevLett.117.237001

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Pandey A, Quirinale DG, Jayasekara W, Sapkota A, Kim MG, Dhaka RS, et al. Crystallographic, Electronic, Thermal, and Magnetic Properties of Single-crystal SrCo₂As₂. Phys Rev B (2013) 88:014526. doi:10.1103/PhysRevB.88.014526

CrossRef Full Text | Google Scholar

53. Ding Q-P, Wiecki P, Anand VK, Sangeetha NS, Lee Y, Johnston DC, et al. Volovik Effect and Fermi-Liquid Behavior in the s-wave Superconductor CaPd₂As₂: As⁷⁵ NMR-NQR Measurements. Phys Rev B (2016) 93:140502. doi:10.1103/PhysRevB.93.140502

CrossRef Full Text | Google Scholar

54. Kamihara Y, Hiramatsu H, Hirano M, Kawamura R, Yanagi H, Kamiya T, et al. Iron-based Layered Superconductor: LaOFeP. J Am Chem Soc (2006) 128:10012–3. doi:10.1021/ja063355c

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Kamihara Y, Watanabe T, Hirano M, Hosono H. Iron-based Layered Superconductor La[O_1-xF_x]FeAs (x = 0.05−0.12) with T_c = 26 K. J Am Chem Soc (2008) 130:3296–7. doi:10.1021/ja800073m

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Kotegawa H, Fujita M. Magnetic Excitations in Iron Chalcogenide Superconductors. Sci Tech Adv Mater (2012) 13:054302. doi:10.1088/1468-6996/13/5/054302

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Torchetti DA, Fu M, Christensen DC, Nelson KJ, Imai T, Lei HC, et al. ⁷⁷Se NMR Investigation of the K_xFe_2−ySe₂ High-T_c superconductor (T_c = 33 K). Phys Rev B (2011) 83:104508. doi:10.1103/PhysRevB.83.104508

CrossRef Full Text | Google Scholar

58. Böhmer AE, Arai T, Hardy F, Hattori T, Iye T, Wolf T, et al. Origin of the Tetragonal-To-Orthorhombic Phase Transition in FeSe: A Combined Thermodynamic and NMR Study of Nematicity. Phys Rev Lett (2015) 114:027001. doi:10.1103/PhysRevLett.114.02700210.1103/PhysRevLett.114.027001

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Kuwayama T, Matsuura K, Mizukami Y, Kasahara S, Matsuda Y, Shibauchi T, et al. NMR Study under Pressure on the Iron-based Superconductor FeSe_1−xS_x (x = 0.12 and 0.23): Relationship between Nematicity and AF Fluctuations. Mod Phys Lett B (2020) 34:2040048. doi:10.1142/S0217984920400485

CrossRef Full Text | Google Scholar

60. Wiecki P, Nandi M, Böhmer AE, Bud'ko SL, Canfield PC, Furukawa Y. NMR Evidence for Static Local Nematicity and its Cooperative Interplay with Low-energy Magnetic Fluctuations in FeSe under Pressure. Phys Rev B (2017) 96:180502. doi:10.1103/PhysRevB.96.180502

CrossRef Full Text | Google Scholar

61. Fernandes RM, Chubukov AV, Knolle J, Eremin I, Schmalian J. Preemptive Nematic Order, Pseudogap, and Orbital Order in the Iron Pnictides. Phys Rev B (2012) 85:024534. doi:10.1103/PhysRevB.85.024534

CrossRef Full Text | Google Scholar

62. Fernandes RM, Chubukov AV, Schmalian J. What Drives Nematic Order in Iron-Based Superconductors. Nat Phys (2014) 10:97–104. doi:10.1038/nphys2877

CrossRef Full Text | Google Scholar