Abstract
Intercalated transition metal dichalcogenides have been widely used to study the magnetic and magnetoelectric transport properties in a strong anisotropic and spin–orbit coupling environments. In this study, ferromagnetic FeTa3S6 (also known as Fe1/3TaS2) single crystals were grown by using the chemical vapor transport method, and its magnetic and magnetoelectric transport properties were measured. The results show that FeTa3S6 has ferromagnetic ordered below 37K, with sharp switching of magnetization, butterfly-shaped double-peak magnetoresistance and anomalous Hall effect, and the magnetization and resistance have strong anisotropy. When a magnetic field is oriented parallel to the c-axis, the magnetoresistance exceeds 10% at a temperature of 10K, and negative magnetoresistance is generated when the magnetic field is larger than the switching field. When the direction of the magnetic field of 9T rotates from out-of-plane to in-plane, the anisotropic magnetoresistance exceeds 40%, and the angle-dependent Hall resistance presents a novel trend, which may be due to the existence of a topological Hall effect or other magnetic structures in the FeTa3S6 thin film. When the magnetic field of 9T rotates in the ab-plane of the sample, the in-plane anisotropic magnetoresistance conforms to the form of sin2φ. The experimental results of this study provide important information for the study of magnetic and magnetoelectric transport properties of intercalated transition metal dichalcogenides.
Introduction
In recent decades, transition metal dichalcogenides (TMDs) have attracted research interest due to their unique properties and potential applications in a broad range of areas [1–7]. TMDs are a class of layered materials whose crystal structures can be classified as, depending on the local coordination of chalcogen atoms around the central transition metal, 1H (trigonal prismatic), 1T (octahedral), 1T’ (distorted octahedral), 2H (hexagonal), 3R (rhombohedral), and Td (orthorhombic) phases, and most of them are two-dimensional (2D) van der Waal materials [8–11]. The intercalation or doping of atoms or molecules can cause significant changes in the physical properties of TMDs [12–22]. For example, Cu or Pd intercalation induces superconductivity in 1T-TiSe2 [18, 19], and 3d transition metal intercalation leads to different kinds of long-range magnetic order in TMDs (such as TiS2) [20]; among the compounds with Cr-intercalated NbS2, Cr1/3NbS2 is a chiral helimagnet, which confirms the strong coupling between neighboring layers [21, 22].
FexTaS2 is a transition metal dichalcogenide of magnetic element intercalation 2H-TaS2, which exhibits abundant magnetic properties [23–34]. It is in the spin glass state for x < 0.2, ferromagnetic for 0.2 ≤ x ≤ 0.4, and antiferromagnetic for x > 0.4 [23, 24]. In the ferromagnetic state, Curie temperature changes irregularly with the change in Fe concentration x. When x is equal to 1/4 or 1/3, FexTaS2 forms commensurate 2 × 2 or √3 × √3 superlattices, respectively [25, 26]. Curie temperature reaches the maximum 160K for x = 1/4 [23, 27]. The quenched crystal has a giant magnetic coercivity at a temperature of 2K [28]. Very large magnetoresistance (≈140%) is discovered in single crystal Fe0.297TaS2, attributed to the Fe concentration departure from 1/4 or 1/3, which caused misalignment of magnetic moments [27]. Recently, Dzyaloshinskii–Moriya interaction (DMI) confirmed in topological structures such as magnetic skyrmions was also confirmed in Fe0.28TaS2 nanoplates; this shows a large topological Hall effect, which confirms the DMI in a transition metal dichalcogenide by dual intercalation [29–32]. In addition, the ferromagnet FexTaS2 also exhibits many peculiar magnetic properties, such as sharp switching of magnetization [26], strong magnetocrystalline anisotropy [33], butterfly-shaped double-peak magnetoresistance [27], anomalous Hall effect [34], and anisotropic magnetoresistance effect [33].
The anisotropic magnetoresistance effect is one of the most basic properties of magnetoelectric transport; the resistivity changes with the relative angle between the magnetization direction and the current direction [35, 36]. In ferromagnets, the anisotropic magnetoresistance effect is caused by the spin–orbit interaction, which induces the mixing of spin-up and spin-down states. This mixing depends on the magnetization direction and gives rise to a magnetization direction-dependent scattering rate [37]. Although some physical properties of FexTaS2 have been studied to a certain extent, detailed studies on the magnetic properties and magnetoelectric transport properties of FeTa3S6 are still relatively lacking. There is no report about the anisotropic magnetoresistance effect of FeTa3S6 by measuring the angle-dependent magnetoresistance. Here, we successfully grew FeTa3S6 single crystals, studied their magnetic properties and magnetoelectric transport properties, and further measured their angle-dependent magnetoresistance and Hall resistance. These results show that FeTa3S6 has rich potential applications in the field of magnetic properties and spintronics, which is worthy of further theoretical and experimental research.
Experimental Section
High-quality FeTa3S6 single crystals were prepared by using the chemical vapor transport (CVT) method. High-quality pure Fe (102.1 mg, 99.9%), Ta (667.3 mg, 99.9%), and S (235.0 mg, 99.5%) were mixed (molar ratio of 1.5:3:6) and then sealed under vacuum in a quartz tube with the addition of I2 (200 mg, 99.99%) as the transport agent. Then the quartz tube was placed horizontally in a two-temperature zone tube furnace, and the raw materials were placed in the high-temperature zone. In 10 h, the temperature in the high-temperature zone increased to 1273K, and the temperature in the low-temperature zone increased to 1173K. After 7 days, FeTa3S6 single crystals were grown in the low-temperature zone [38]. The crystals were cleaned by ultrasonication in supersaturated aqueous solution of KI, deionized water, and alcohol, and finally, the single crystals are a regular polygon with a size of millimeters [39].
The structure of FeTa3S6 single crystals was characterized by using an X-ray diffractometer (XRD, Advance D8). The elemental composition of the FeTa3S6 crystals was confirmed by using an energy-dispersive spectrometer (EDS) of a scanning electron microscope (SEM, TESCAN MIRA 3). Magnetization measurements of the bulk FeTa3S6 sample and magnetoelectric transport properties of the device were performed using an integrated physical property measurement system (PPMS, EvercoolⅡ-9T, Quantum Design). The six-terminal Hall electrode is prepared on a silicon wafer by photolithography and thermal evaporation. The FeTa3S6 thin film was mechanically exfoliated by a scotch tape from a single bulk crystal FeTa3S6, and then we used polydimethylsiloxane to transfer to the electrode through a 2D material alignment transfer platform. The thickness of the thin film was measured by using an atomic force microscope (AFM) [40].
Results and Discussion
Figure 1shows the characterization and magnetization measurement results of FeTa3S6 single crystals. Figure 1A demonstrates a sharp diffraction peak in the (00l) direction in the XRD pattern (JCPDS No. 22-0360), the result shows that the sample has excellent crystallinity, the inset is an optical image of FeTa3S6 single crystal, and it is a regular polygonal flake with metallic luster. Figure 1B presents the EDS pattern of the sample, and the actual element ratio of Fe:Ta:S is 1:3:6 (FeTa3S6). Figure 1C and Figure 1D exhibit the temperature dependence of the magnetization measured at an applied magnetic field of 0.1T oriented parallel to the c-axis and along the ab-plane with both zero-field cooling (ZFC) and field cooling (FC), respectively. The huge difference in magnetization measured in the two directions is due to the strong magnetocrystalline anisotropy of FeTa3S6 (the c-axis is the magnetic easy axis) [25]. The inset in Figure 1C shows the dM/dT curve of ZFC, and the Curie temperature of FeTa3S6 is confirmed to be 37K through the minimum point in this figure, which is consistent with previous research reports [22, 41]. Figure 1E and Figure 1F display the field-dependent magnetization (M-H) at different temperatures with the magnetic field perpendicular and parallel to the ab-plane, respectively. When the temperature is 10 K, the magnetic field is along the c-axis, the magnetization of FeTa3S6 reaches saturation at about 1T magnetic field, and its large coercivity may come from its huge uniaxial anisotropy [42, 43]. While the magnetic field is along the ab-plane, the magnetization of FeTa3S6 cannot reach saturation at 5T magnetic field, and the appearing of a weak magnetic hysteresis loop may be due to the fact that the ab-plane of the sample is not completely parallel to the magnetic field [36].
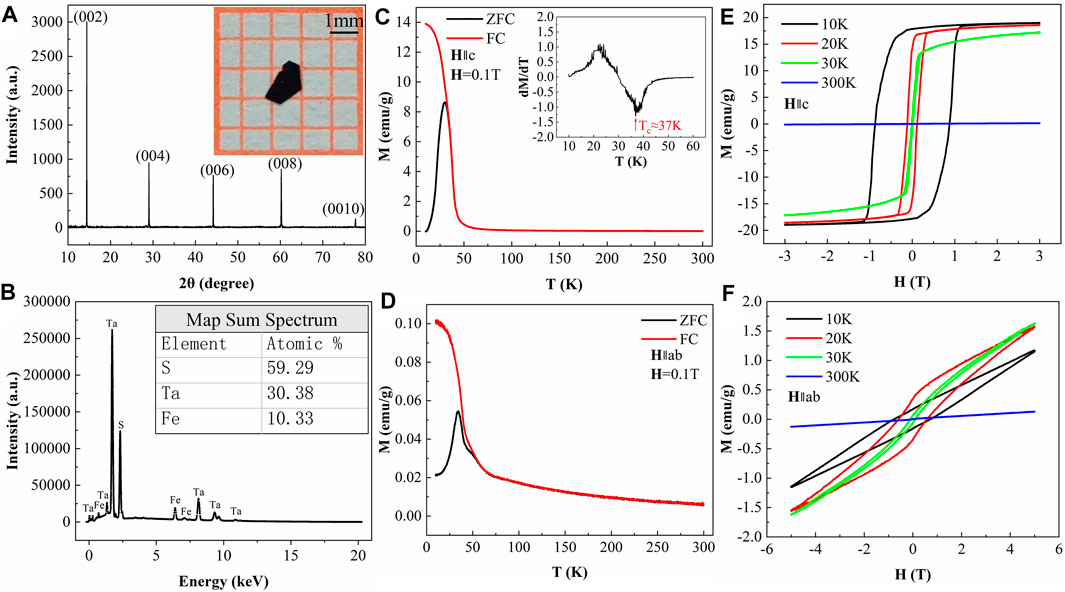
FIGURE 1
(A) XRD pattern of a FeTa3S6 single crystal, and the inset is an optical image of the FeTa3S6 single crystal; the scale is 1 mm. (B) EDS pattern of the FeTa3S6 single crystal, and the inset shows the actual atomic ratio. (C) Temperature-dependent magnetization measured of zero-field cooling (black) and field cooling (red) with H∥c, and the inset shows the dM/dT curve of zero-field cooling with H∥c. (D) Temperature dependence of the magnetization measured of zero-field cooling (black) and field cooling (red) with H∥ab. (E) Field-dependent magnetization (M-H) at different temperatures with H∥c. (F) Field-dependent magnetization (M-H) at different temperatures with H∥ab.
Figure 2 exhibits the magnetoelectric transport measurement results of the FeTa3S6 device. Figure 2A is the AFM measurement result of the thickness of a FeTa3S6 thin film on the electronic device, showing that the thickness is about 180 nm, and the inset is the optical image of the device. Figure 2B shows the temperature dependence of resistance under zero field and magnetic field of 5T. Resistance decreases with decreasing temperature, showing metallic behavior, and the resistance of the ferromagnetic state drops rapidly near the Curie temperature due to the loss of spin disorder scattering [36]; the inset is a schematic diagram of the device measurement configuration. Magnetoresistance Rxx is a crucial measurement for inferring information about the interaction between itinerant charge carriers and magnetic degrees of freedom in magnetic materials [35], defined as
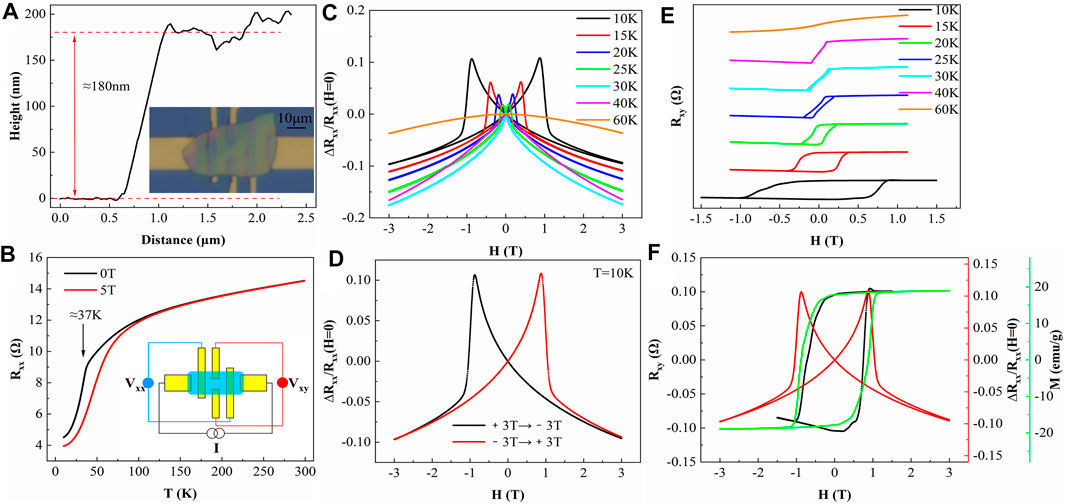
FIGURE 2
(A) Profile line information extracted from AFM image on the edge of the FeTa3S6 thin film, and the inset shows the optical image of the FeTa3S6 device. (B) Temperature-dependent resistance with zero field and 5T magnetic field, and the inset shows a schematic diagram of the device measurement configuration. (C) Magnetoresistance measured at selected temperature with applied magnetic field H∥c. (D) Magnetoresistance measured at T = 10K with applied magnetic field H∥c. (E) Hall resistance measured at selected temperature with applied magnetic field H∥c. (F) Determine the switching field of the FeTa3S6 sample by Rxy-H (black), MR (red), and M-H (green).
where is the resistance value when the magnetic field is H. Figure 2C displays the magnetoresistance of the FeTa3S6 device measured at the selected temperature by applying a magnetic field along the c-axis. Figure 2D shows the magnetoresistance at 10 K, and the magnetoresistance can reach more than 10%. When the temperature is below the Curie temperature, and the magnetic field H increases from 0T to 3T, the magnetoresistance first increases steadily and reaches the maximum value at the switching field, then decreases within a very narrow magnetic field interval, and then almost linearly decreases until the magnetic field is 3T. If the measuring magnetic field is increased, the magnetoresistance will continue to decrease. The sudden change of magnetoresistance at the switching field can be attributed to the domain reorientation parallel to the direction of the field [25], and the domain nucleation and domain wall propagation are the cause for the formation of the butterfly-shaped double-peak magnetoresistance [44]. When the magnetic field is 3T, the magnetoresistance is negative, and the negative magnetoresistance reaches a peak near the Curie temperature, which is mainly due to suppression of spin disorder resistivity with the magnetic field [45]. Figure 2E presents the Hall resistance of the FeTa3S6 device measured at the selected temperature when the magnetic field is along the c-axis (for clarify, the data are equally spaced in the vertical direction). Obvious hysteresis loops caused by the anomalous Hall effect can be observed below the Curie temperature, which originates from the spontaneous ferromagnetic order caused by the intercalation of Fe atoms [28]. When the magnetic field is larger than the switching field or the temperature is higher than the Curie temperature, only the nearly linear Hall resistance contributed by the normal Hall effect is observed. These results indicate that the spin–orbit coupling of FeTa3S6 is very strong [35]. As shown in Figure 2F, the observed switching field is very close in the magnetization measurements of FeTa3S6 and the magnetoelectric transport property measurements of the device. When the magnetic field changes, the spin direction of FeTa3S6 switches rapidly at the switching field, indicating that the crystal may be a nearly single-domain ferromagnet [25].
Figures 3A–D present the measurement results of the angle-dependent magnetoresistance of FeTa3S6 when the magnetic field H is gradually rotated in the ac and bc planes, that is, from the c-axis to the ab-plane. The current I is inputted along the a-axis, the angle between the external magnetic field and the normal of the sample plane is defined as θ, and the interval of measured angle is 2°. The angle-dependent magnetoresistance at different temperatures is measured at T = 9T, where . The magnetoresistance shows a changing trend with a period of 180°. When the magnetic field is rotated in the ac and bc planes, the magnitude of Rxx is almost the same at the same angle, and the difference may be caused by a slight misalignment of the angle. It can be seen in this figure that Rxx reaches its maximum at θ = 90° and 270°, and Rxx reaches its minimum at θ = 0°, 180°, and 360°, which means that the magnetoresistance is maximum when the magnetic field is parallel to ab-plane, and the magnetoresistance is minimum when the magnetic field is perpendicular to ab-plane, which is consistent with the property of conventional metal ferromagnets [46]. Experimental data suggest an inversion symmetry for this sample; AMR has a two-fold symmetry and is dominated by M and c-axis when field rotates in ac and bc planes [47]. At low temperatures (approximately below the Curie temperature), the curve has a sharp peak at θ = 90° and 270°, and it is caused by the sudden flip of the magnetization when the magnetic field is parallel to the sample [48], which causes the curve not to conform to the form of sin2θ. It shows that the magnetization of the sample is not strictly saturated under the magnetic field of 9T, except for magnetic field oriented parallel to the hard axis and the easy axis [49]. In addition, the largest magnetoresistance exceeding 40% was observed at T = 40 K (near the Curie temperature). As the temperature increases, the curve peak disappears and turns into a smooth curve. Figures 3E,F show the measured angle-dependent Hall resistance of FeTa3S6 by the same measurement method. The angle-dependent Hall resistance at different temperatures is measured at T = 9T, where . The Hall resistance shows a non-periodic curve that is symmetric along the axis of θ = 180°. The maximum and minimum values of Hall resistance are both around θ = 90° and 270°. The discontinuities at low temperatures are caused by the sudden flip of the magnetization across the parallel positions (θ = 90° and 270°) [48]. We found that the peak at the maximum value at the parallel position is very close to the peak of the magnetoresistance measurement; the reason may be due to the deviation of the angle between the two terminals of the Hall bar of the device. Due to the huge perpendicular magnetic anisotropy of FeTa3S6, the influence of longitudinal magnetoresistance in the measurement of Hall resistance has not been completely eliminated by data processing. The novel change trend of the angle-dependent Hall resistance may be due to the presence of other Hall effects (such as topological Hall effect) in addition to the normal Hall effect and the anomalous Hall effect [28, 48]. It is also possible that there are field-induced magnetic structures in the FeTa3S6 thin film [50], which requires further study.
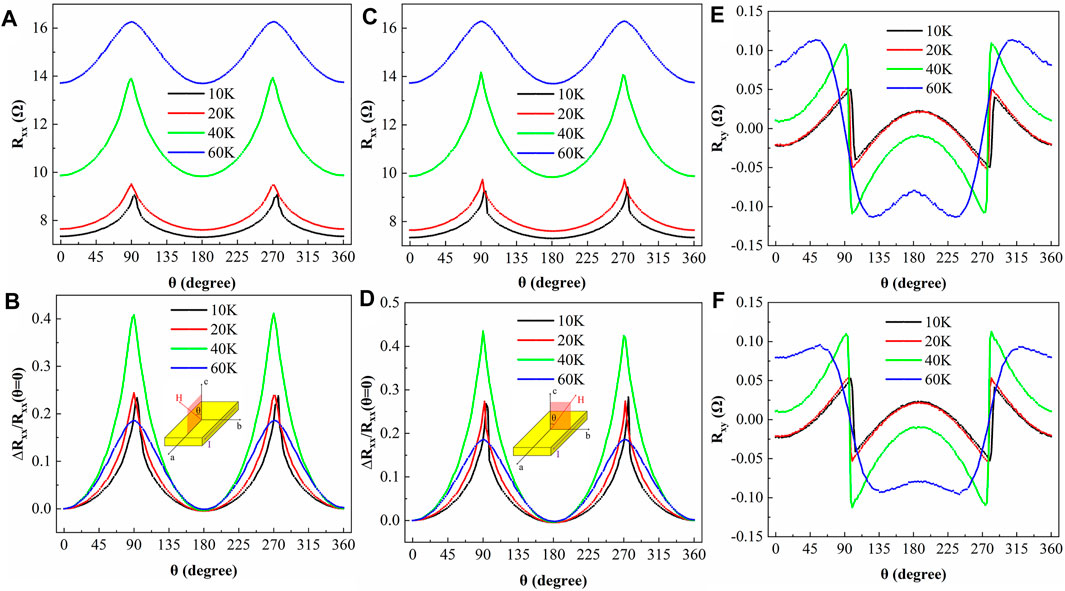
FIGURE 3
Measured angle-dependent magnetoresistance with the magnetic field rotates in the ac-plane (A,B) and bc-plane (C,D) at 10, 20, 40, 60K. The insets in (B,D) show the schematic of the corresponding measurement configuration. The measured angle-dependent Hall resistance with the magnetic field rotates in the ac-plane (E) and bc-plane (F).
Figure 4A shows the in-plane anisotropic magnetoresistance of the FeTa3S6 device measured at different temperatures with the fixed 9T magnetic field rotates in the ab-plane, where current I is applied along the a-axis, φ is defined as the angle between the direction of the b-axis and the applied magnetic field in the ab-plane, and the interval of measured angle is 2°, where . The observed AMR is dominated by magnetization when field is in the ab-plane. Thus, the AMR follows the standard cosine-square law [51]. Due to the defined angle between H and a-axis, the magnetoresistance conforms to the form of sin2φ. The maximum resistance is at φ = 90° and 270°, and the minimum resistance is at φ = 0°, 180°, and 360°, which means that the magnetoresistance is highest when the magnetic field is parallel to the current, and the magnetoresistance is the lowest when the magnetic field is perpendicular to the current. As shown in the figure, FeTa3S6 in-plane anisotropy magnetoresistance is very small, indicating that the in-plane anisotropy of this uniaxial ferromagnet is very weak. The anisotropic magnetoresistance effect comes from the interplay of the magnetic order and spin–orbit interactions [52]. The fitting formula of anisotropic magnetoresistance can described as follows:
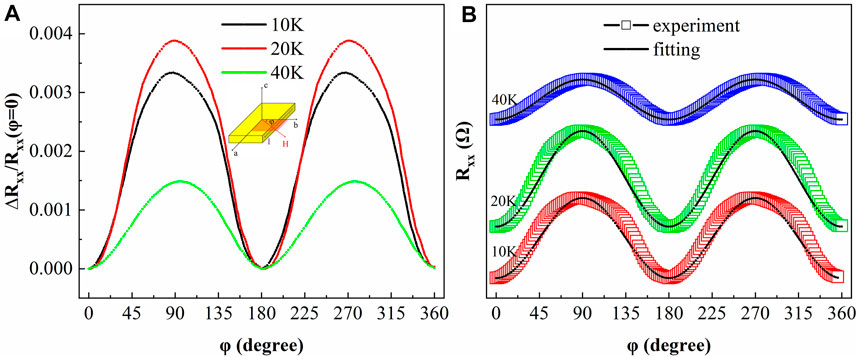
FIGURE 4
(A) Measured angle-dependent magnetoresistance at 10, 20, and 40 K with the fixed 9T magnetic field rotates in the ab-plane, and the inset shows a schematic of the measurement configuration. (B) Fitting results of in-plane anisotropic magnetoresistance.
Where and represent the magnetoresistance of the in-plane magnetic field perpendicular and parallel to the current, respectively. Figure 4B shows the fitting results of the in-plane magnetoresistance angle curve (for clarify, the data are equally spaced in the vertical direction), the hollow point curve is the experimental data, and the solid point curve is the fitting result. It can be found that the measured curve is relatively consistent with the fitting curve, and part of the slight deviation may be because the sample placement is not completely parallel to the magnetic field; therefore, the data are to be mixed with out-of-plane magnetoresistance components [53].
Conclusion
We successfully prepared ferromagnet FeTa3S6 single crystals. XRD, SEM and Curie temperature measurements prove their elemental composition. The magnetic and the magnetoelectric transport properties of the devices were measured. The results show that FeTa3S6 exhibited sharp switching of magnetization, butterfly-shaped double-peak magnetoresistance, anomalous Hall effect, and anisotropic magnetoresistance effects at low temperatures. The magnetoresistance exceeds 10% at T = 10 K, and the maximum anisotropic magnetoresistance exceeds 40% when the magnetic field of 9T rotates from out-of-plane to in-plane. The novel change in trend of the angle-dependent Hall resistance may be attributed to the existence of the topological Hall effect or the existence of other magnetic structures. The specific reasons need to be further studied. In addition, in-plane anisotropic magnetoresistance in the form of sin2φ was measured. In the future, we will explore the magnetoelectric transport properties of limit thickness FeTa3S6 films by exfoliating thinner samples, and further study the magnetoresistance and Hall effect of FeTa3S6 to provide potential application opportunities for FeTa3S6 in promising fields such as magnetoelectricity and spintronics.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
Q-LX and Y-QM conceived the idea. Y-QM and J-JG performed the experiments and conducted the characterization. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Funding
This project was financially supported by the National Science Foundation of China (Grant Nos. 61904205, 12174451, and 62174051), the Natural Science Foundation of Hunan Province (Grant No. 2020JJ4677), and the Fundamental Research Funds for the Central Universities of Central South University (Grant No. 2020zzts378). The project was also supported by the State Key Laboratory of Powder Metallurgy, Central South University, Changsha, China.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
LiJZhaoBChenPWuRLiBXiaQet alSynthesis of Ultrathin Metallic MTe2 (M = V, Nb, Ta) Single-Crystalline Nanoplates. Adv Mater (2018) 30:1801043. 10.1002/adma.201801043
2.
FazekasPTosattiE. Electrical, Structural and Magnetic Properties of Pure and Doped 1T-TaS2. Philosophical Mag B (1979) 39:229–44. 10.1080/13642817908245359
3.
FriendRHYoffeAD. Electronic Properties of Intercalation Complexes of the Transition Metal Dichalcogenides. Adv Phys (1987) 36:1–94. 10.1080/00018738700101951
4.
XuZYangHSongXChenYYangHLiuMet alTopical Review: Recent Progress of Charge Density Waves in 2D Transition Metal Dichalcogenide-Based Heterojunctions and Their Applications. Nanotechnology (2021) 32:492001. 10.1088/1361-6528/ac21ed
5.
WeiZLiBXiaCCuiYHeJXiaJ-Bet alVarious Structures of 2D Transition-Metal Dichalcogenides and Their Applications. Small Methods (2018) 2:1800094. 10.1002/smtd.201800094
6.
SuJLiuGLiuLChenJHuXLiYet alRecent Advances in 2D Group VB Transition Metal Chalcogenides. Small (2021) 17:2005411. 10.1002/smll.202005411
7.
WilsonJAYoffeAD. The Transition Metal Dichalcogenides Discussion and Interpretation of the Observed Optical, Electrical and Structural Properties. Adv Phys (1969) 18:193–335. 10.1080/00018736900101307
8.
ZhaoBShenDZhangZLuPHossainMLiJet al2D Metallic Transition‐Metal Dichalcogenides: Structures, Synthesis, Properties, and Applications. Adv Funct Mater (2021) 31:2105132. 10.1002/adfm.202105132
9.
VoiryDMohiteAChhowallaM. Phase Engineering of Transition Metal Dichalcogenides. Chem Soc Rev (2015) 44:2702–12. 10.1039/c5cs00151j
10.
YangHKimSWChhowallaMLeeYH. Structural and quantum-state phase transitions in van der Waals layered materials. Nat Phys (2017) 13:931–7. 10.1038/NPHYS4188
11.
XiaoYZhouMLiuJXuJFuL. Phase Engineering of Two-Dimensional Transition Metal Dichalcogenides. Sci China Mater (2019) 62:759–75. 10.1007/s40843-018-9398-1
12.
ObeysekeraDGamageKGaoYCheongSw.YangJ. The Magneto‐Transport Properties of Cr 1/3 TaS 2 with Chiral Magnetic Solitons. Adv Electron Mater (2021) 7:2100424. 10.1002/aelm.202100424
13.
CaiRYaoYLvPMaYXingWLiBet alEvidence for anisotropic spin-triplet Andreev reflection at the 2D van der Waals ferromagnet/superconductor interface. Nat Commun (2021) 12:6725. 10.1038/s41467-021-27041-w
14.
ParkinSSPFriendRH. 3d Transition-Metal Intercalates of the Niobium and Tantalum Dichalcogenides. I. Magnetic Properties. Philos Mag B (1980) 41:65–93. 10.1080/13642818008245370
15.
ParkinSSPFriendRH. 3d Transition-Metal Intercalates of the Niobium and Tantalum Dichalcogenides. II. Transport Properties. Philos Mag B (1980) 41:95–112. 10.1080/13642818008245371
16.
MarsegliaEA. Transition Metal Dichalcogenides and Their Intercalates. Int Rev Phys Chem (1983) 3:177–216. 10.1080/01442358309353343
17.
LuoJ-HLiBZhangJ-MZhongM-ZXiaQ-INieY-Zet alBi Doping-Induced Ferromagnetism of Layered Material SnSe2 with Extremely Large Coercivity. J Magnetism Magn Mater (2019) 486:165269. 10.1016/j.jmmm.2019.165269
18.
MorosanEZandbergenHWDennisBSBosJWGOnoseYKlimczukTet alSuperconductivity in CuxTiSe2. Nat Phys (2006) 2:544–50. 10.1038/nphys360
19.
MorosanEWagnerKEZhaoLLHorYWilliamsAJTaoJet alMultiple Electronic Transitions and Superconductivity inPdxTiSe2. Phys Rev B (2010) 81:094524. 10.1103/PhysRevB.81.094524
20.
NegishiHShoubeATakahashiHUedaYSasakiMInoueM. Magnetic Properties of Intercalation Compounds MxTiS2 (M = 3d Transition Metal). J Magnetism Magn Mater (1987) 67:179–86. 10.1016/0304-8853(87)90227-7
21.
HanHZhangLSapkotaDHaoNLingLDuHet alTricritical point and Phase Diagram Based on Critical Scaling in the Monoaxial Chiral Helimagnet Cr1/3NbS2. Phys Rev B (2017) 96:094439. 10.1103/PhysRevB.96.094439
22.
ClementsEMDasRLiLLampen-KelleyPJPhanM-HKeppensVet alCritical Behavior and Macroscopic Phase Diagram of the Monoaxial Chiral Helimagnet Cr1/3NbS2. Sci Rep (2017) 7:6545. 10.1038/s41598-017-06728-5
23.
NaritaHIkutaHHinodeHUchidaTOhtaniTWakiharaM. Preparation and Physical Properties of FexTaS2 (0.15 ≤ X ≥ 0.50) Compounds. J Solid State Chem (1994) 108:148–51. 10.1006/jssc.1994.1022
24.
EibschützMMahajanSDiSalvoFJHullGWWaszczakJV. Ferromagnetism in Metallic Intercalated Compounds FexTaS2 (0.20⩽x⩽0.34). J Appl Phys (1981) 52:2098–100. 10.1063/1.329629
25.
HoribeYYangJChoY-HLuoXKimSBOhYSet alColor Theorems, Chiral Domain Topology, and Magnetic Properties of FexTaS2. J Am Chem Soc (2014) 136:8368–73. 10.1021/ja5026134
26.
MorosanEZandbergenHWLiLLeeMCheckelskyJGHeinrichMet alSharp Switching of the Magnetization inFe1∕4TaS2. Phys Rev B (2007) 75:104401. 10.1103/PhysRevB.75.104401
27.
ChenC-WChikaraSZapfVSMorosanE. Correlations of Crystallographic Defects and Anisotropy with Magnetotransport Properties inFexTaS2single Crystals (0.23≤x≤0.35). Phys Rev B (2016) 94:054406. 10.1103/PhysRevB.94.054406
28.
ChoiYJKimSBAsadaTParkSWuWHoribeYet alGiant Magnetic Coercivity and Ionic Superlattice Nano-Domains in Fe 0.25 TaS 2. Europhys Lett (2009) 86:37012. 10.1209/0295-5075/86/37012
29.
ZhengGWangMZhuXTanCWangJAlbarakatiSet alTailoring Dzyaloshinskii-Moriya Interaction in a Transition Metal Dichalcogenide by Dual-Intercalation. Nat Commun (2021) 12:3639. 10.1038/s41467-021-23658-z
30.
ShenLXiaJZhaoGZhangXEzawaMTretiakovOAet alSpin Torque Nano-Oscillators Based on Antiferromagnetic Skyrmions. Appl Phys Lett (2019) 114:042402. 10.1063/1.5080302
31.
ShenLXiaJZhaoGZhangXEzawaMTretiakovOAet alDynamics of the Antiferromagnetic Skyrmion Induced by a Magnetic Anisotropy Gradient. Phys Rev B (2018) 98:134448. 10.1103/PhysRevB.98.134448
32.
ShenLXiaJZhangXEzawaMTretiakovOALiuXet alCurrent-Induced Dynamics and Chaos of Antiferromagnetic Bimerons. Phys Rev Lett (2020) 124:037202. 10.1103/PhysRevLett.124.0372021
33.
HardyWJChenC-WMarcinkovaAJiHSinovaJNatelsonDet alVery Large Magnetoresistance inFe0.28TaS2single Crystals. Phys Rev B (2015) 91:054426. 10.1103/PhysRevB.91.054426
34.
YuX-YFengH-LGuG-XLiuY-HLiZ-LXuT-Set alAndreev Reflection Spectroscopy of Ferromagnetic Fe0.26TaS2 with Layered Structure. Acta Phys Sin (2019) 68:247201. 10.7498/aps.68.20191221
35.
KokadoSTsunodaMHarigayaKSakumaA. Anisotropic Magnetoresistance Effects in Fe, Co, Ni, Fe4N, and Half-Metallic Ferromagnet: A Systematic Analysis. J Phys Soc Jpn (2012) 81:024705. 10.1143/JPSJ.81.024705
36.
TangWZhouZ-WNieY-ZXiaQ-IZengZ-MGuoG-H. Spin Wave Modes of Width Modulated Ni80Fe20/Pt Nanostrip Detected by Spin-Orbit Torque Induced Ferromagnetic Resonance. Appl Phys Lett (2017) 111:172407. 10.1063/1.4999818
37.
RamosRAroraSKShvetsIV. Anomalous Anisotropic Magnetoresistance in epitaxialFe3O4thin Films on MgO(001). Phys Rev B (2008) 78:214402. 10.1103/PhysRevB.78.214402
38.
SuJWangMLiuGLiHHanJZhaiT. Air‐Stable 2D Intrinsic Ferromagnetic Ta 3 FeS 6 with Four Months Durability. Adv Sci (2020) 7:2001722. 10.1002/advs.202001722
39.
ZhangHWeiWZhengGLuJWuMZhuXet alElectrical and Anisotropic Magnetic Properties in Layered Mn1/3TaS2 Crystals. Appl Phys Lett (2018) 113:072402. 10.1063/1.5034502
40.
GuoJ-JXiaQ-IWangX-GNieY-ZXiongRGuoG-H. Temperature and Thickness Dependent Magnetization Reversal in 2D Layered Ferromagnetic Material Fe3GeTe2. J Magnetism Magn Mater (2021) 527:167719. 10.1016/j.jmmm.2020.167719
41.
MangelsenSHansenJAdlerPSchnelleWBenschWMankovskySet alLarge Anomalous Hall Effect and Slow Relaxation of the Magnetization in Fe1/3TaS2. J Phys Chem C (2020) 124:24984–94. 10.1021/acs.jpcc.0c07711
42.
ZhaoGPZhaoLShenLCZouJQiuL. Coercivity Mechanisms in Nanostructured Permanent Magnets*. Chin Phys. B (2019) 28:077505. 10.1088/1674-1056/28/7/077505
43.
ZhaoGPWangXLFengYPHuangCW. Coherent Rotation and Effective Anisotropy. IEEE Trans Magn (2007) 43:2908–10. 10.1109/TMAG.2007.893629
44.
LuJWangXR. Magnetization Reversal of Single Domain Permalloy Nanowires. J Magnetism Magn Mater (2009) 321:2916–9. 10.1016/j.jmmm.2009.04.057
45.
SharmaRKarmakarSRawatR. Study of Magnetoresistance in Polycrystalline Fe Intercalated TaS2. AIP Conf Proc (2020) 2220:030001. 10.1063/5.0001191
46.
YuzhelevskiYMarkovichVJungGGorodetskyG. Anisotropic Magnetoresistance in Low-Doped La0.79Ca0.21MnO3 Crystals. J Appl Phys (2011) 109:063908. 10.1063/1.3556746
47.
WangXR. A Theory for Anisotropic Magnetoresistance in Materials with Two Vector Order Parameters. Chin Phys. Lett. (2022) 39:027301. 10.1088/0256-307X/39/2/027301
48.
JiangBWangLBiRFanJZhaoJYuDet alChirality-Dependent Hall Effect and Antisymmetric Magnetoresistance in a Magnetic Weyl Semimetal. Phys Rev Lett (2021) 126:236601. 10.1103/PhysRevLett.126.236601
49.
MiaoYChenXYangSZhengKLianZWangYet alNon-cosine Square Angular-dependent Magnetoresistance of the Face-Centered-Cubic Co Thin Films. J Magnetism Magn Mater (2020) 512:167013. 10.1016/j.jmmm.2020.167013
50.
LiuYHuZStavitskiEAttenkoferKPetrovicC. Three-dimensional ferromagnetism and magnetotransport in van der Waals Mn-intercalated tantalum disufide. Phys Rev B (2021) 103:144432. 10.1103/PhysRevB.103.144432
51.
ZhangYWangXRZhangHW. Extraordinary Galvanomagnetic Effects in Polycrystalline Magnetic Films. Epl (2016) 113:47003. 10.1209/0295-5075/113/47003
52.
HuangHGuJJiPWangQHuXQinYet alGiant Anisotropic Magnetoresistance and Planar Hall Effect in Sr0.06Bi2Se3. Appl Phys Lett (2018) 113:222601. 10.1063/1.5063689
53.
WangPHouTTangFWangPHanYRenYet alTemperature Dependent In-Plane Anisotropic Magnetoresistance in HfTe5 Thin Layers. Chin Phys. Lett. (2021) 38:017201. 10.1088/0256-307X/38/1/017201
Summary
Keywords
FeTa3S6, magnetic property, magnetoelectric transport, anomalous Hall effect, anisotropic magnetoresistance
Citation
Miao Y-Q, Guo J-J, Luo Z-Y, Zhong M-Z, Li B, Wang X-G, Nie Y-Z, Xia Q-L and Guo G-H (2022) Anisotropic Magnetoresistance Effect of Intercalated Ferromagnet FeTa3S6. Front. Phys. 10:847402. doi: 10.3389/fphy.2022.847402
Received
02 January 2022
Accepted
21 February 2022
Published
15 March 2022
Volume
10 - 2022
Edited by
Xiao-Ping Wei, Lanzhou Jiaotong University, China
Reviewed by
Xiangrong Wang, Hong Kong University of Science and Technology, Hong Kong SAR, China
Guoping Zhao, Sichuan Normal University, China
Updates
Copyright
© 2022 Miao, Guo, Luo, Zhong, Li, Wang, Nie, Xia and Guo.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qing-Lin Xia, qlxia@csu.edu.cn
This article was submitted to Condensed Matter Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.