Broadband Achromatic and Polarization Insensitive Focused Optical Vortex Generator Based on Metasurface Consisting of Anisotropic Nanostructures

Optical vortex (OV) beams are ideal carriers for high-capacity optical communication, and long-wave infrared (LWIR) is the ideal wavelength band for long-range optical communication. Here, we propose a method for the achromatic generation of focused optical vortex (FOV) beams with arbitrary homogenous polarization states in the LWIR using a single all-germanium metasurface. The chromatic aberration and polarization sensitivity are eliminated by superimposing a polarization-insensitive geometric phase and a dispersion-engineered dynamic phase. The method is validated using two broadband FOV generators with the same diameter and focal length but different topological charges. The results indicate that the FOV generators are broadband achromatic and polarization insensitive. The proposed method may pave the way for chip-scale optical communication devices.

Introduction

Optical vortex (OV) beams characterized by the Hilbert factor $\exp \left(i\ell \theta \right)$ ($\ell$ is the topological charge) can carry the orbital angular momentum (OAM) $\ell \hslash$ per photon in addition to the spin angular momentum (SAM) associated with photon spin. Unlike SAM, which is limited to $\pm 1\hslash$ per photon, the OAM per photon is theoretically unbounded. Such properties make OV beams an ideal carrier for high-capacity wireless communications [1, 2]. In addition to optical communication, OV beams have important applications in manipulating nanoparticles [3], high-security encryption [4], assembly of DNA biomolecules [5], quantum optics [6], and diffraction limit imaging [7]. In conventional optical systems, spiral phase plates [8, 9], q-waveplates [10], pitch-fork holograms [11] and spatial light modulators [12] are used to generate helical wavefronts of OV beams. For most applications, the generated vortex beam also needs to be focused by a lens to increase the light intensity. However, the bulky and high cost of such optical systems severely hinders the development of integrated focused optical vortex (FOV) generators.

Metasurfaces are two-dimensional metamaterials that possess powerful light modulation capabilities and can manipulate the phase, amplitude, and polarization of light locally, making them highly promising as a powerful platform for integrated optics. To date, a wide range of metasurfaces with sophisticated features have been demonstrated, such as beam deflector [13], metalens [14–20], cloak [21–23], polarizer [24], information encryption [25–29], analog computation [30–32], metasurface interferometry [33], and meta-holograms [34], covering a wide spectrum from visible to terahertz frequencies. Yu [35] et al. were the first to demonstrate the generation of OV beams via a metasurface consisting of a V-shaped plasmonic antenna. Owing to the intrinsic absorption loss of metals in the visible region, the efficiency of such metasurfaces is highly limited. To overcome this, all-dielectric metasurfaces composed of high-refractive-index materials have been proposed to achieve high efficiency in generating OV beams [36, 37]. Zhan [38] et al. proposed an OV generator based on a silicon nitride metasurface with an efficiency much higher than its plasmonic counterparts. By superimposing hyperbolic and helical phase profiles, Tang [39] further reduced the bulk of the optical system by generating FOV beams using only a single metasurface. Sroor et al. [40] integrated the metasurface into the laser cavity, which increased the mode purity of the generated OV beam to 92%. Although a wide variety of FOV generator metasurfaces have been developed, most of them are monochromatic. Considering the needs of practical applications, it is clear that broadband achromatic FOV generators are more desirable owing to their powerful functionalities. Recently, Ou et al. [41, 42] proposed a broadband achromatic FOV generator based on silicon metasurface in the mid-infrared region. However, such silicon metasurfaces are highly sensitive to the state of polarization (SOP) of incident light. The longwave infrared (LWIR) corresponds to an atmospheric transparent window, which makes it an ideal spectrum for optical wireless communications. However, to the best of our knowledge, no achromatic flat FOV generator for LWIR has been reported thus far.

In this study, we demonstrate a general method to achromatically generate FOV beams via a single germanium metasurface with high efficiency and high mode purity in the LWIR band. It should be noted that our metasurface is polarization-insensitive and can transform plane waves with arbitrary SOP to FOV with an arbitrary OAM state. The proposed metasurface is composed of anisotropic nanostructures, and each nanostructure behaves as a quasi-ideal half-wave plate that flips the chirality of the incident circularly polarized (CP) light. A polarization-insensitive geometric phase is imparted on the metasurface by limiting the rotation angle of each nanostructure to 0° or 90° [43]. The anisotropic geometry also allows us to finely regulate the dispersion of the dynamic phase [44, 45]. By combining the polarization-insensitive geometric phase and dispersion-engineered dynamic phase, the desired group delay and phase profile are simultaneously imparted on the metasurface, resulting in good polarization insensitivity and achromatic performance.

To validate our method, we designed and simulated two broadband achromatic flat-FOV generators. The two FOV generators have the same diameter of 200 μm, the same focal length of 300 μm, and different topological charge numbers ($\ell =0$ for metasurface Ⅰ and $\ell =-2$ for metasurface Ⅱ). The metasurface with $\ell =0$ behaves as a metalens. The metalens has a stable focus from 9.6 to 11.6 µm, and the relative focal shift is less than 4%, which indicates good achromatic performance. The average focusing efficiency under right-handed circularly polarized (RCP) incidence, left-hand circularly polarized (LCP) incidence, and linear polarized incidence along the x-axis (XLP) were 44%, 43%, and 45%, respectively, which confirms polarization-insensitive performance. Further analysis of the Strehl ratio indicates that the metalens show broadband diffraction-limited focusing ability. The metasurface with $\ell =-2$ shows a donut-shaped intensity profile and spiral-shaped phase profile from 9.6 to 11.6 µm, indicating the existence of OV at the origin in the broadband. The average efficiency of the FOV generator was 34% under RCP, LCP, and XLP incidence, which confirms polarization-insensitive functionality. The average modal purity of the desired OAM eigenstate mode under RCP, LCP, and XLP incidence were 95.5%, 95.3%, and 92.9%, respectively. The high modal purity shows that the FOV beams are of good quality, which indicates that the FOV generator is both achromatic and polarization insensitive. We believe that our results represent a substantial advance and would pave the way for applications such as chip-scale optical communication.

Materials and Methods

For most applications, intrinsic divergence of the OV beam is not preferred, and lenses are used to control the beam radius and increase the light intensity. The functionality of generating and focusing OV beams can be integrated on a single metasurface by superimposing radially hyperbolic and azimuthally linear phase profiles as follows:

$\phi =-\frac{\omega }{c}\left(\sqrt{r^2+f^2}-f\right)+\ell \theta (1)$

Where $\omega$ is the angular frequency, c is the speed of light in vacuum, r is the radial coordinate, $\theta$ is the azimuthal coordinate, $f$ is the constant focal length, and $\ell$ is the topological charge. Formula [1] can be Taylor expanded around the design frequency as follows:

$\phi \left(r,\theta ,\omega \right)=\phi \left(r,\theta ,{\omega }_d\right)+{\frac{\partial \phi }{\partial \omega }|}_{\omega ={\omega }_d}\left(\omega -{\omega }_d\right)+{\frac{{\partial }^2\phi }{\partial {\omega }^2}|}_{\omega ={\omega }_d}{\left(\omega -{\omega }_d\right)}^2+\dots (2)$

where $\phi \left(r,\theta ,{\omega }_d\right)$, ${\frac{\partial \phi }{\partial \omega }|}_{\omega ={\omega }_d}$, and ${\frac{{\partial }^2\phi }{{\partial \omega }^2}|}_{\omega ={\omega }_d}$ are the phase, group delay, and group delay dispersion that should be satisfied at the corresponding polar coordinates ($r,\theta$) at the design frequency ${\omega }_d$, respectively. It is very difficult to satisfy all derivatives in Formula [2] for the selected nanostructures at every coordinate on the metasurface. To achieve achromatic dispersion, a simple and intuitive approach is to let group delay dispersion and other higher-order derivative terms be zero; thus, the phase is linearly related to the frequency at each coordinate. In this case, the condition for achieving achromatism is simplified as follows:

${\frac{\partial \phi }{\partial \omega }|}_{\omega ={\omega }_d}=-\frac{1}{c}\left(\sqrt{r^2+f^2}-f\right)(3)$

$\phi \left(r,\theta ,{\omega }_d\right)=-\frac{{\omega }_d}{c}(\sqrt{r^2+f^2}-f)+\ell \theta (4)$

Formula [3] and Formula [4] show the group delay condition and phase condition, respectively, that need to be fulfilled by the achromatic FOV generator.

To precisely modulate the dispersion of meta-atoms, anisotropic nanopillar combinations were chosen as the archetypes of the meta-atom, as shown in the inset of Figure 2A. Moreover, each nanostructure on the metasurface is designed to be a miniature half-wave plate, which can flip the chirality of the incident CP wave. When RCP light is incident from the substrate, the metasurface converts it into an LCP converged vortex beam with a topological charge of $\ell$ and vice versa, as shown in Figure 1C. This process is called spin-orbit angular conversion [46] and can be represented by Jones calculus as follows:

$\exp \left(i{\phi }_{lens}\right)|L,\ell \rangle =\left[J_{meta}\right]|R\rangle (5)$

$\exp \left(i{\phi }_{lens}\right)|R,\ell \rangle =\left[J_{meta}\right]|L\rangle (6)$

where $\left[J_{meta}\right]$ is the Jones matrix of the metasurface, ${\phi }_{lens}=-\frac{\omega }{c}\left(\sqrt{r^2+f^2}-f\right)$ is the phase profile of a planar lens, $|R\rangle$ and $|L\rangle$ are the RCP and LCP bases, respectively. $|L,\ell \rangle$ and $|R,\ell \rangle$ are the orthonormal high-order circular polarization basis [47], which can be expressed as

$|L,\ell \rangle =\exp \left(i\ell \theta \right)(\widehat{x}-i\widehat{y})/\sqrt{2}(7)$

$|R,\ell \rangle =\exp \left(i\ell \theta \right)(\widehat{x}+i\widehat{y})/\sqrt{2}(8)$

FIGURE 1

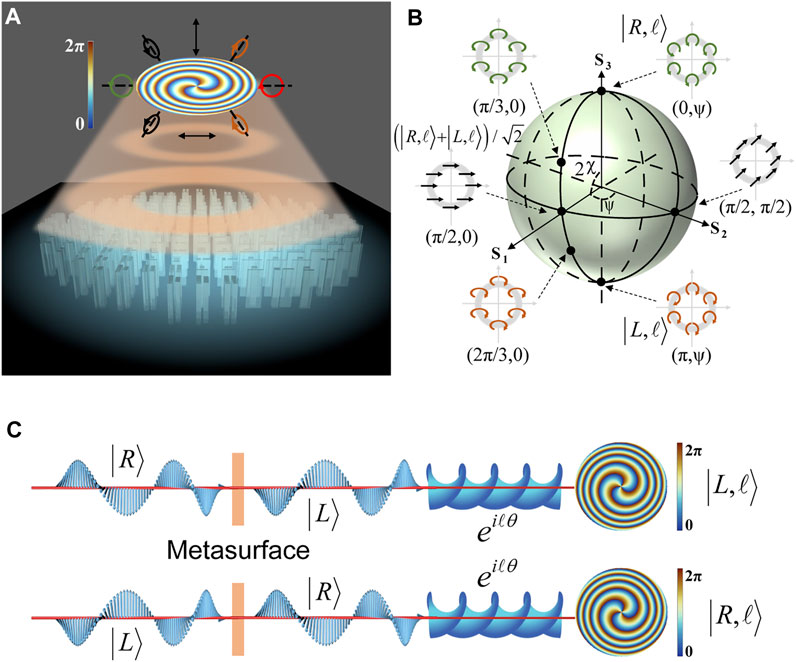
FIGURE 1. Schematic of the flat FOV generator. (A) Schematic of the metasurface consisting of anisotropic nanostructures for generating FOV beams with arbitrary SOP. (B) Schematic illustration of $HO{P}_{\ell ,\ell }$. OV beams with any scalar SOP can be obtained by superimposing the SOP corresponding to the north and south poles on the HOP sphere. (C) Spin-orbit angular momentum conversion when light passes through the proposed metasurface.

For incident light with a more general SOP $E^{in}={\psi }_L|L\rangle +{\psi }_R|R\rangle$, the corresponding outgoing light after passing through the metasurface can be expressed as

$E^{out}=\exp \left(i{\phi }_{lens}\right)\left[{\psi }_R|L,\ell \rangle +{\psi }_L|R,\ell \rangle \right](9)$

The SOP corresponding to any point on the high-order Poincaré sphere (HOP) can be decomposed into a linear combination of the SOP corresponding to the north and south poles, as shown in Figure 1B. For all possible scalar SOPs of the vortex beam, we can find the corresponding points on the corresponding $HO{P}_{\ell ,\ell }$; thus, Formula [9] shows that our method can generate an FOV with an arbitrary homogeneous SOP.

In addition, the Jones matrix of the metasurface can be expressed as

$\left[J_{meta}\right]=\exp \left(i{\phi }_{lens}\right)\exp \left(i\ell \theta \right)\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right](10)$

Formula [10] implies that a metasurface with only one wavelength thickness integrates the functions of a half-wave plate, spiral phase plate, and lens. Considering that the metasurface also has the ability to eliminate chromatic aberration, we can see that the entire optical system is highly integrated.

Although it is counterintuitive to utilize anisotropic nanostructures to form polarization-insensitive metasurfaces, this can be understood in terms of the geometric phase. For the anisotropic meta-atom shown in Figure 2A, its transmittance properties after a rotation angle α can be described by the Jones matrix as follows:

$\begin{array}{c}{E}^{out}=R{\left(\alpha \right)}^T\cdot \left[\begin{array}{cc}{t}_l& 0\\ 0& t_s\end{array}\right]\cdot R\left(\alpha \right)\cdot E^{in}\\ =\frac{1}{2}\left(t_l+t_s\right)\cdot E^{in}+\frac{1}{2}\left(t_l-t_s\right)\cdot \left(\exp \left(i2\alpha \right)\cdot {\widehat{\sigma }}_R+\exp (-i2\alpha )\cdot {\widehat{\sigma }}_L\right)\cdot E^{in}\end{array}(11)$

where $R\left(\alpha \right)=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right]$ is the rotation matrix, and $t_l$ and $t_s$ are the complex transmission coefficients for light polarized along the long and short axes of the meta-atom, respectively. ${\widehat{\sigma }}_R=\frac{1}{2}\left[\begin{array}{cc}1& -i\\ -i& -1\end{array}\right]$ and ${\widehat{\sigma }}_L=\frac{1}{2}\left[\begin{array}{cc}1& i\\ i& -1\end{array}\right]$ are chirality flip operators, and when the incident light is RCP or LCP, there exists ${\widehat{\sigma }}_R\cdot |R\rangle =0\left(\text{or }{\widehat{\sigma }}_L\cdot |L\rangle =0\right)$ and ${\widehat{\sigma }}_R\cdot |L\rangle =|R\rangle \left(\text{or }{\widehat{\sigma }}_L\cdot |R\rangle =|L\rangle \right)$. It can be observed from Formula [11] that under CP illumination, the first part represents the co-polarized component which causes unwanted scattering and can be minimized when the meta-atom is designed to be a half-wave plate, and the second part represents the cross-polarized component whose phase can be decomposed into two parts: the dynamic phase ${\phi }_d=\arg (t_l-t_s)$ and the geometric phase $2\alpha$ (for LCP incident light) and $-2\alpha$ (for RCP incident light). Generally, the geometric phase is dispersionless and polarization-sensitive, since it is only dependent on the rotation angle, and it is different for RCP and LCP light incidence. However, if the rotation angle is limited to 0° or 90°, the geometric phases of the RCP and LCP incident light will be identical, as illustrated in Figure 2C. Therefore, both the RCP and LCP incident light will experience the same phase profile imparted by the metasurface. Because any incident light can be decomposed into a combination of RCP and LCP, this property implies that the metasurface is polarization-insensitive.

FIGURE 2

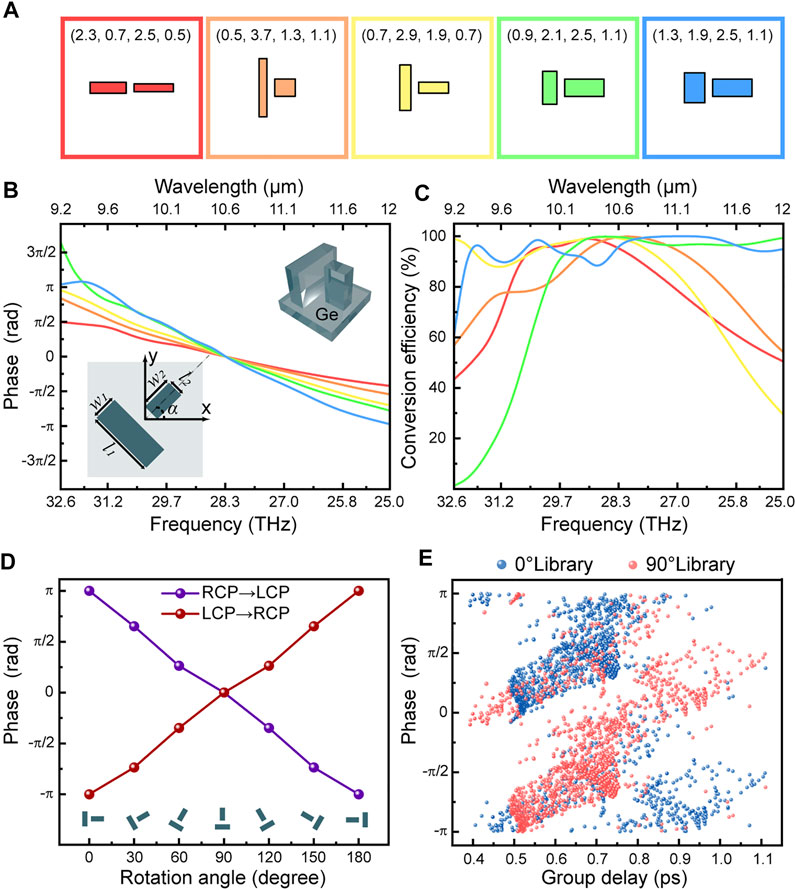
FIGURE 2. Numerical results of the meta-atoms. (A) Schematic of the five selected meta-atoms. (B,C) Phase and polarization conversion efficiency of the five selected meta-atoms. The five meta-atoms with different geometrical dimensions satisfy the screening conditions mentioned in the text, i.e. linear phase versus frequency and high polarization conversion efficiency within the designed bandwidth, but different group delays (the slope of phase with respect to the frequency). Each color curve corresponds to a meta-atom in the same colored box in (A). The parameters in the colored boxes correspond to the geometric parameters (l1, w1, l2, w2) of the nanopillars shown in the inset of (B) in microns, and the gap between nanopillars is g = 0.5 μm. (D) Geometric phase with respect to rotation angle for the same meta-atom under LCP and RCP incidence. The meta-atom has the same geometrical parameters as that in the yellow box in (A). (E) The phase and group delay for all meta-atoms in the library. Each meta-atom is represented by a blue and red point in the plot because a 90° rotation can impart a phase change of πwithout changing the group delay.

The properties of meta-atoms are also fundamentally determined by the constituent materials. Due to mature fabrication methods, silicon is widely used as the base material for metasurfaces. However, in the LWIR band, germanium has smaller absorption and higher refractive index than silicon, so the nanostructures composed of germanium materials can modulate light more efficiently. Therefore, germanium was selected as the constituent material for the meta-atom. Currently, it is still very challenging to deposit tens of microns of germanium on other materials due to material stress, so we also chose germanium as a substrate material so that in the future, we can inexpensively process metasurfaces on a single germanium wafer. We built up a meta-atoms library, and there were multiple mutually parallel nanopillars in a single meta-atom. Figure 2A shows the case of two nanopillars in one meta-atom, and a detailed discussion on the meta-atoms library is included in Supplementary Material. The nanopillars in every unit cell have the same height H = 10 μm and the same gap g = 0.5 µm, and the finest structure size is forced to be larger than 1 μm. The lattice constant P of the unit cell was chosen to be 6.2 μm to satisfy both the Nyquist law and the requirement to suppress higher-order diffraction [48].

To obtain the phase spectrum of each nanostructure, we conducted simulations using a finite-difference time-domain (FDTD) solver from Lumerical [49]. Periodic conditions were applied in the transverse direction, and the perfect matched layer (PML) condition was applied in the longitudinal direction with respect to the propagation of light, and CP illumination was applied from the substrate. After obtaining the phase spectra of all meta-atoms, we screened the meta-atoms suitable for constituting the achromatic FOV metasurface according to Formula [2]. We used a homemade linear regression program to screen the meta-atoms in the library, with an R-squared number greater than 0.98 and an avaverage conversion efficiency greater than 80%. The phase spectra and conversion efficiency spectra of the five meta-atoms meeting the above screening conditions are shown in Figure 2B,C. As shown in Figure 2E, nanostructure rotation does not affect the dispersion (group delay) of meta-atoms, but nanostructures with 0° and 90° rotation angles have a phase difference of π, which enriches the number of combinations of phase and group delays that can be implemented in our library, allowing us to meet the requirements of more achromatic FOV metasurface designs.

Results

Polarization-Insensitive and Achromatic Metalens

When the topological charge $\ell$ of the FOV beam is 0, which is considered as a special case, there is no helical component in the phase profile, as indicated in Formula [1], and the flat FOV generator behaves as a metalens.

To validate our method, we designed and simulated an achromatic metalens with a diameter of 200 μm and a numerical aperture (NA) of 0.32. We calculated the phase distribution and group delay distribution required for the achromatic metalens according to Formula [3] and Formula [4], respectively. We then discretized the required phase profile and group delay profile and selected the meta-atom in the library that best matched the required phase and group delay pairs, as shown in Figures 3B,C. Figure 3A shows the layout of a quarter of the designed metalens. Figure 4A shows the simulated intensity profile in the x-z plane under RCP, LCP, and XLP illumination. The metalens can focus light over a wide range of wavelengths, and the focal point does not shift with wavelength, indicating good achromatic performance. The metalens has the same intensity profile under three polarized incidences, which indicates good polarization insensitivity performance. We extracted the focal length of the metalens at the selected wavelengths by analyzing the intensity distribution in the x–z plane, where the focal point is defined as the position corresponding to the maximum intensity on the z-axis. Figure 5A shows the relative focal shift of the metalens, and the relative focal shift is defined as $\Delta f=\frac{f-f_0}{f_0}\times 100\%$, where $f_0$ is the focal length at the designed wavelength ($\lambda =10.6\mu m$), and $f$ is the focal length at the sampled wavelength. The relative shift of the focal length was less than 4% over the entire broadband range, confirming the excellent achromatic properties of our metalens.

FIGURE 3

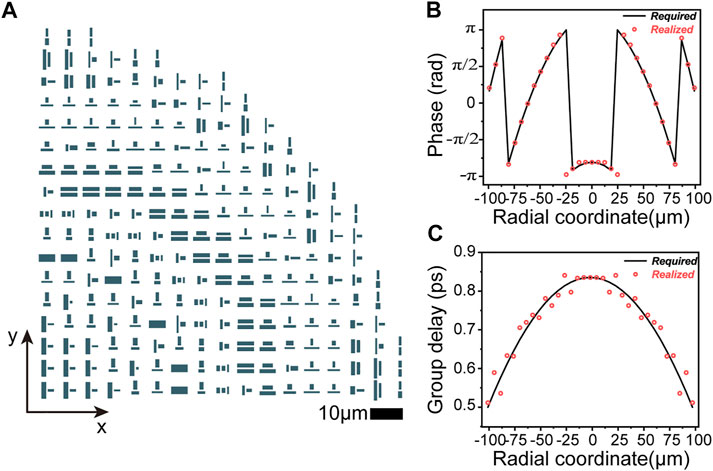
FIGURE 3. Design result of the broadband achromatic metalens. (A) Layout of the quarter of the metalens. (B,C) Realized (red circles) and required (black curves) phase and group delay at each radial coordinate on the metalens.

FIGURE 4

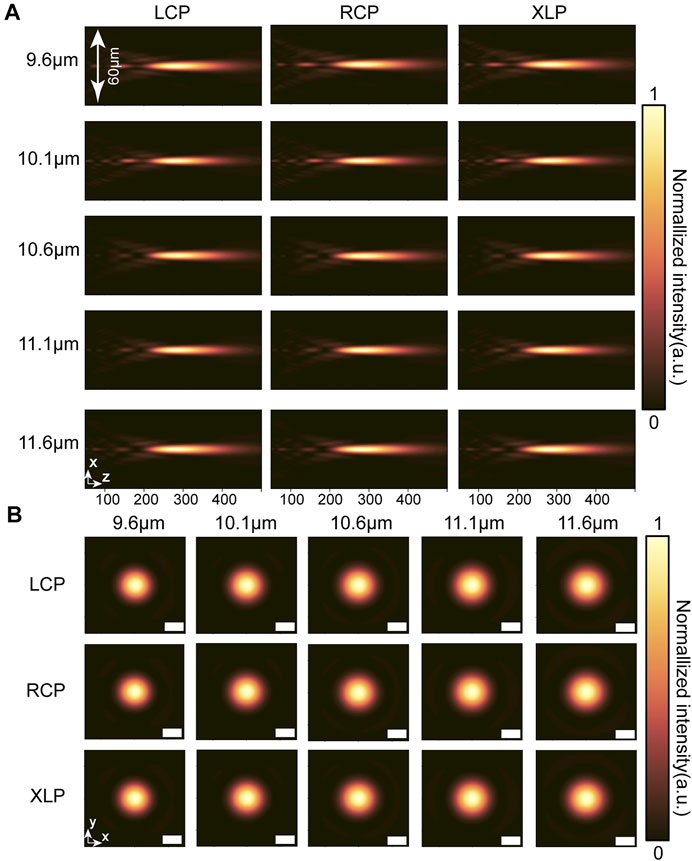
FIGURE 4. Intensity distribution of the broadband achromatic metalens. (A) Intensity profiles in the x-z plane at selected wavelengths. From left to right, each column corresponds to LCP incidence, RCP incidence, and XLP incidence. (B) Intensity distribution at the focal plane at selected wavelengths. From top to bottom, each column corresponds to LCP incidence, RCP incidence, and XLP incidence. Scale bar is 10 µm.

FIGURE 5

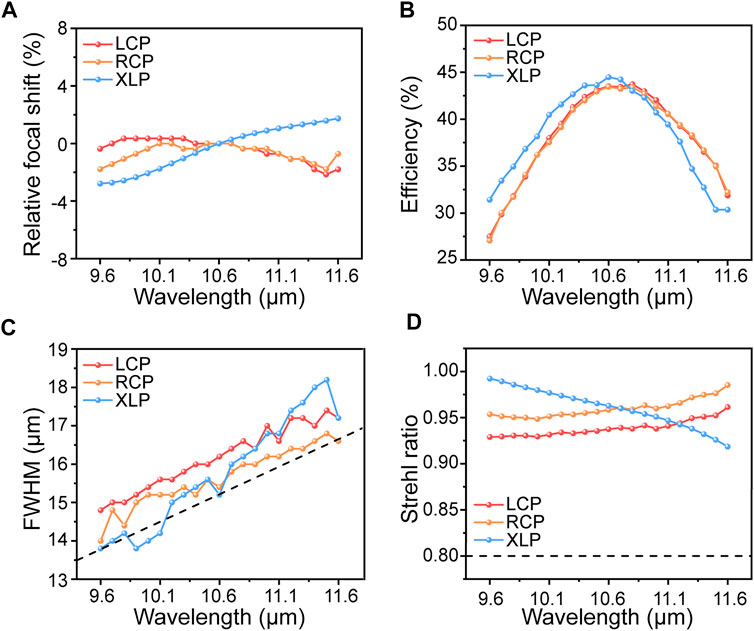
FIGURE 5. Performance characterization of the metalens. (A) Relative focal shift of the metalens. (B) Efficiency of the metalens. (C)Full-width-half-maximum of the intensity at the focal plane. (D) Strehl ratio of the metalens. The black dashed lines in (C) and (D) represent the diffraction limit.

Figure 4B shows the point spread function (PSF) of the metalens in the focal plane under RCP, LCP, and XLP illumination. The symmetric focal spot was clear, and no focal spot diffusion caused by defocusing and spherical aberration was evident at any wavelength [50]. Based on the intensity distribution in the focal plane, we extracted some metrics to quantify the performance of the metalens, such as full width half maximum (FWHM), Strehl ratio, and efficiency. Figure 5C shows the FWHM of the metalens, where the black dashed line indicates the FWHM corresponding to the ideal Airy disk. Figure 5D shows the Strehl ratio of the metalens. The Strehl ratio is defined as in Ref. [51], and the black dashed line in Figure 5D indicates the diffraction limit criterion referred to by Marehal. From the FWHM and Strehl ratio, we can conclude that our metalens is capable of diffraction-limited focusing in the continuous wavelength band. Figure 5B illustrates the efficiency of the metalens, which is defined as the power in the focal spot (circles of radius three times the FWHM spanning the center of the focal spot) compared to the power of the incident light. The efficiency of the metalens is highest around the design wavelength $\lambda =10.6\mu m$, and the decrease in efficiency at other wavelengths is mainly due to the decrease in polarization conversion efficiency of the selected meta-atoms. The average efficiency of the metalens under RCP, LCP, and XLP incidence were 44%, 43%, and 45%, respectively. It should be emphasized that these efficiency values already exceed that of the previously reported monochromatic metalens in LWIR [52]. It should be noted that the average efficiency of the metalens is much lower than the polarization conversion efficiency shown in Figure 2C. This is mainly because the polarization conversion efficiency reflects the proportion of transmitted light that is focused to the focal point without considering the reflected light. We believe that achromatic metalens will pave the way for broad applications in LWIR, such as thermal imaging and wireless communications.

Polarization-Insensitive and Achromatic FOV Generator

We designed and simulated an FOV generator based on the method proposed above. The FOV generator has a diameter of 200 μm, focal length of 300 μm, design wavelength of 10.6 μm, topological number of −2, and design operating bandwidth of 2 μm. Figure 6A shows the layout of the metasurface, which consists of mutually parallel or perpendicular nanopillars arranged in a square lattice. The design process of the FOV generator was the same as that of the metalens. First, we calculated the desired phase and group delay profiles using Formula [2] and Formula [3]. Then, we discretized the group delay and phase profiles according to the lattice constant and selected a meta-atom at each coordinate that provided the best match to the desired group delay and phase pair in the library. Figures 6B,C illustrate the group delay and phase required for the ideal achromatic FOV generator, as well as the group delay and phase that can be realized by the metasurface. The required group delay and phase exhibit small inconsistencies with the realized ones.

FIGURE 6

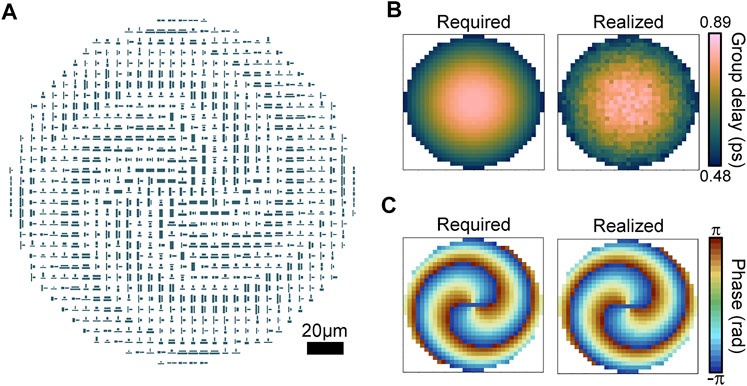
FIGURE 6. Design of the broadband achromatic and polarization insensitive flat FOV generator. (A) Layout of the flat FOV generator. (B) Required group delay (left) and realized group delay (right) of the flat FOV generator at each coordinate. (C) Required phase (left) and realized phase (right) of the flat FOV generator at each coordinate.

Figure 7A shows the intensity distribution in the x-z plane for the FOV generator under LCP, RCP, and XLP illumination. The focal length of the FOV generator is constant at all selected wavelengths, which indicates that the FOV generator has good achromatic performance, and a similar intensity distribution under LCP, RCP, and XLP incidence confirms that the FOV generator is polarization-insensitive. Figure 7B shows the intensity and phase distributions of the FOV generator in the focal plane. The donut-shaped intensity distribution and the spiral-shaped phase distribution are clear in the focal plane, both of which confirm the existence of OV at the origin. The phase distribution confirms that the transmitted beams carry an OAM of $-2\hslash$ according to the branches stemming from the origin.

FIGURE 7

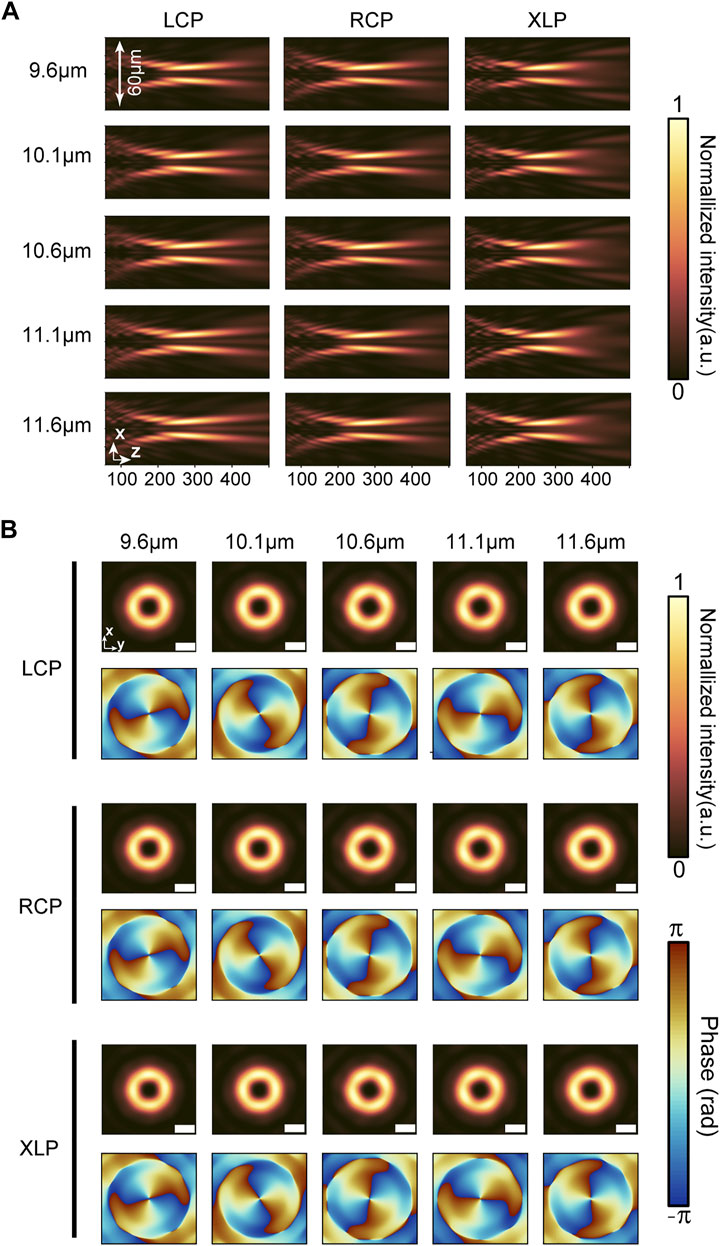
FIGURE 7. Intensity and phase distributions for the FOV generator. (A) Intensity profiles in the x-z plane at selected wavelengths. From left to right, each column corresponds to LCP incidence, RCP incidence, and XLP incidence. (B) Intensity profiles and phase profiles at the focal plane at selected wavelengths. From top to bottom, each column corresponds to LCP incidence, RCP incidence, and XLP incidence. Scale bar is 10 µm.

Figure 8D shows the efficiency of the FOV generator. Efficiency is defined as the power inside the donut ring divided by the power of the incident light, which can be expressed as follows:

$\eta =\frac{\frac{1}{2}{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_{r_0-\Delta r}^{r_0+\Delta r}\left(E_x\cdot H_y-E_y\cdot H_x\right)d\text{rd}\theta }}}{P_{in}}(12)$

where $r_0$ is the radial coordinate corresponding to the peak intensity, and $\mathrm{\Delta }r$ is the FWHM of the intensity profile. The average efficiency of the FOV was 34% for RCP, LCP, and XLP incidence, as shown in Figure 8D.

FIGURE 8

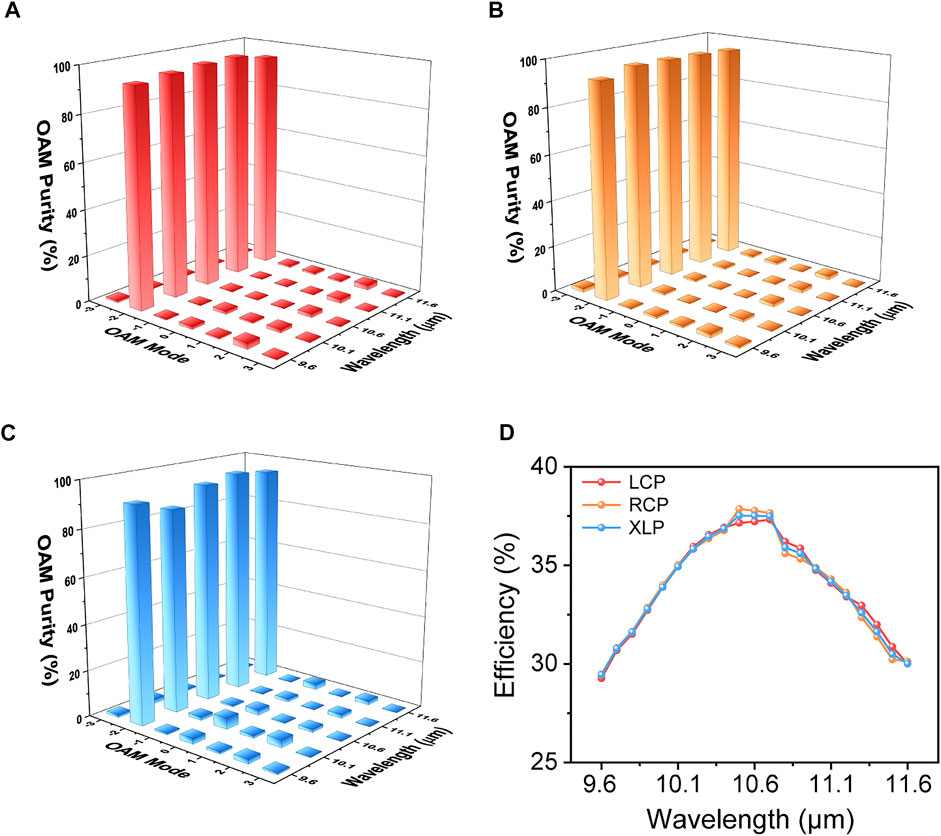
FIGURE 8. Efficiency and mode purity of the FOV generator. (A,B,C) Mode purity of the generated OV under LCP incidence, RCP incidence, and XLP incidence, respectively. (D) Efficiency of the flat FOV generator under LCP, RCP, and XLP incidence.

To quantitatively describe the modal purity of the OV beams, we performed a modal decomposition analysis of the phase in the focal plane [53]. The Fourier relationship between the OAM mode and the phase distribution can be expressed as

$A_{\ell }=\frac{1}{2\pi }{\displaystyle {\int }_0^{2\pi }\phi \left(\theta \right)}\cdot e^{-i\ell \theta }d\theta (13)$

$\phi \left(\theta \right)={\displaystyle \sum _{-\infty }^{+\infty }{A}_{\ell }}\cdot e^{i\ell \theta }(14)$

where $\phi \left(\theta \right)$ is the phase distribution of the circle corresponding to the intensity maximum in the focal plane, and $e^{i\ell \theta }$ is the harmonic related to the OAM eigenstate. Figures 8A–C show the OAM spectra of the FOV under LCP, RCP, and XLP incidence, respectively. The average purity of the modes corresponding to OAM = $-2\hslash$ is 95.5%, 95.3%, and 92.9% for LCP, RCP, and XLP incidence, respectively. The high percentage of the desired mode indicates that our FOV generator can substantially preserve the mode crosstalk at a relatively low level.

Discussion

We proposed a general method to implement a metasurface for generating FOV beams with arbitrary scalar SOPs in a broad continuous wavelength range. Although the proposed FOV generator works in the LWIR band, this design principle can be applied to arbitrary regions of the electromagnetic spectrum.

The average efficiency of the metasurfaces demonstrated in the main text is approximately 44% (metasurface Ⅰ with $\ell =0$) and 34% (metasurface Ⅱ with $\ell =-2$), respectively. The efficiency of metasurface Ⅱ is lower than that of metasurface Ⅰ because the phase distribution of metasurface Ⅱ is not rotationally symmetric, while the phase distribution of metasurface Ⅰ is rotationally symmetric. Therefore, it is more difficult to satisfy both the phase and group delay conditions for metasurface Ⅱ, which eventually leads to the selection of meta-atoms with low conversion efficiency. Considering that the germanium–air interface causes a reflection loss of 36%, the efficiency of the metasurface can be further enhanced by replacing the substrate with a low-refractive-index material. For example, by replacing the substrate with zinc sulfide (n = 2.2), the reflection loss at the interface will be reduced to 14%, which means that in this case, the efficiencies of metasurfaces Ⅰ and Ⅱ can reach 59% and 46%, respectively. Another factor limiting the efficiency of our metasurface is that the polarization conversion efficiency cannot maintain high values over a wide bandwidth, as shown in Figure 2C. This can be solved by using a three-dimensional structure such as a stacked cross to form a broadband achromatic half-wave plate [54]. It should be noted that our results are based on simulations, and the dimensional errors in the samples during fabricating can lead to lower measured efficiency and mode purity than simulated results.

A comparison between this study and previously reported flat FOV generators is presented in Table 1. Compared to previously reported works, our metasurfaces have the advantage of broadband achromatic, high mode purity and polarization insensitivity.

TABLE 1

TABLE 1. Comparison between this work and previously reported flat FOV generators.

Conclusion

In summary, we theoretically proposed two broadband achromatic polarization-insensitive FOV generators in the LWIR range based on an all-germanium metasurface. Metasurface Ⅰ with $\ell$ = 0 shows broadband achromatic diffraction-limited focusing ability with an average efficiency of 44%. Metasurface Ⅱ with $\ell$ = -2 can achromatically transform a planewave with an arbitrary SOP to a high-purity FOV beam with an average efficiency of 34%. We believe that the metasurfaces demonstrated here will pave the way for a broad range of applications, such as chip-scale optical communication and quantum optics.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JG and XJ proposed the idea and supervised the entire work. NS and NX performed the simulation and wrote the original manuscript. HL and XC deduced the theory method. QS conducted the design work and reviewed the manuscript. YT and DS discussed the results and analyzed the data.

Funding

This research was funded by the National Natural Science Foundation of China (NSFC), grant number 61901437.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.846718/full#supplementary-material

References

1. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical Communications Using Orbital Angular Momentum Beams. Adv Opt Photon (2015) 7(1):66–106. doi:10.1364/AOP.7.000066

CrossRef Full Text | Google Scholar

2. Shen Y, Wang X, Xie Z, Min C, Fu X, Liu Q, et al. Optical Vortices 30 Years on: OAM Manipulation from Topological Charge to Multiple Singularities. Light Sci Appl (2019) 8:90. doi:10.1038/s41377-019-0194-2

PubMed Abstract | CrossRef Full Text | Google Scholar

3. He H, Friese MEJ, Heckenberg NR, Rubinsztein-Dunlop H. Direct Observation of Transfer of Angular Momentum to Absorptive Particles from a Laser Beam with a Phase Singularity. Phys Rev Lett (1995) 75(5):826–9. doi:10.1103/PhysRevLett.75.826

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Fang X, Ren H, Gu M. Orbital Angular Momentum Holography for High-Security Encryption. Nat Photon (2020) 14(2):102–8. doi:10.1038/s41566-019-0560-x

CrossRef Full Text | Google Scholar

5. Zhuang X. Unraveling DNA Condensation with Optical Tweezers. Science (2004) 305(5681):188–90. doi:10.1126/science.1100603

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Stav T, Faerman A, Maguid E, Oren D, Kleiner V, Hasman E, et al. Quantum Entanglement of the Spin and Orbital Angular Momentum of Photons Using Metamaterials. Science (2018) 361(6407):1101–4. doi:10.1126/science.aat9042

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Tamburini F, Anzolin G, Umbriaco G, Bianchini A, Barbieri C. Overcoming the Rayleigh Criterion Limit with Optical Vortices. Phys Rev Lett (2006) 97(16):163903. doi:10.1103/PhysRevLett.97.163903

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Sueda K, Miyaji G, Miyanaga N, Nakatsuka M. Laguerre-Gaussian Beam Generated with a Multilevel Spiral Phase Plate for High Intensity Laser Pulses. Opt Express (2004) 12(15):3548–53. doi:10.1364/OPEX.12.003548

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Turnbull GA, Robertson DA, Smith GM, Allen L, Padgett MJ. The Generation of Free-Space Laguerre-Gaussian Modes at Millimetre-Wave Frequencies by Use of a Spiral Phaseplate. Opt Commun (1996) 127(4):183–8. doi:10.1016/0030-4018(96)00070-3

CrossRef Full Text | Google Scholar

10. Karimi E, Piccirillo B, Nagali E, Marrucci L, Santamato E. Efficient Generation and Sorting of Orbital Angular Momentum Eigenmodes of Light by Thermally Tuned Q-Plates. Appl Phys Lett (2009) 94(23):231124. doi:10.1063/1.3154549

CrossRef Full Text | Google Scholar

11. Wang X, Nie Z, Liang Y, Wang J, Li T, Jia B. Recent Advances on Optical Vortex Generation. Nanophotonics (2018) 7(9):1533–56. doi:10.1515/nanoph-2018-0072

CrossRef Full Text | Google Scholar

12. Liu J, Wang J. Demonstration of Polarization-Insensitive Spatial Light Modulation Using a Single Polarization-Sensitive Spatial Light Modulator. Sci Rep (2015) 5(1):9959. doi:10.1038/srep09959

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang D, Hwang Y, Dai Y, Si G, Wei S, Choi DY, et al. Broadband High‐Efficiency Chiral Splitters and Holograms from Dielectric Nanoarc Metasurfaces. Small (2019) 15(20):1900483. doi:10.1002/smll.201900483

PubMed Abstract | CrossRef Full Text | Google Scholar

14. McClung A, Mansouree M, Arbabi A. At-will Chromatic Dispersion by Prescribing Light Trajectories with Cascaded Metasurfaces. Light Sci Appl (2020) 9:93. doi:10.1038/s41377-020-0335-7

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhao M, Chen MK, Zhuang Z-P, Zhang Y, Chen A, Chen Q, et al. Phase Characterisation of Metalenses. Light Sci Appl (2021) 10(1):52. doi:10.1038/s41377-021-00492-y

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Chung H, Miller OD. High-NA Achromatic Metalenses by Inverse Design. Opt Express (2020) 28(5):6945–65. doi:10.1364/OE.385440

PubMed Abstract | CrossRef Full Text | Google Scholar

17. She A, Zhang S, Shian S, Clarke DR, Capasso F. Large Area Metalenses: Design, Characterization, and Mass Manufacturing. Opt Express (2018) 26(2):1573–85. doi:10.1364/OE.26.001573

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Huang L, Coppens Z, Hallman K, Han Z, Böhringer KF, Akozbek N, et al. Long Wavelength Infrared Imaging under Ambient thermal Radiation via an All-Silicon Metalens. Opt Mater Express (2021) 11(9):2907–14. doi:10.1364/OME.434362

CrossRef Full Text | Google Scholar

19. Zhou H, Chen L, Shen F, Guo K, Guo Z. Broadband Achromatic Metalens in the Midinfrared Range. Phys Rev Appl (2019) 11(2):024066. doi:10.1103/PhysRevApplied.11.024066

CrossRef Full Text | Google Scholar

20. Ding X, Kang Q, Guo K, Guo Z. Tunable GST Metasurfaces for Chromatic Aberration Compensation in the Mid-infrared. Opt Mater (2020) 109:110284. doi:10.1016/j.optmat.2020.110284

CrossRef Full Text | Google Scholar

21. Chu H, Li Q, Liu B, Luo J, Sun S, Hang ZH, et al. A Hybrid Invisibility Cloak Based on Integration of Transparent Metasurfaces and Zero-index Materials. Light Sci Appl (2018) 7(1):50. doi:10.1038/s41377-018-0052-7

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Xu H-X, Hu G, Wang Y, Wang C, Wang M, Wang S, et al. Polarization-insensitive 3D Conformal-Skin Metasurface Cloak. Light Sci Appl (2021) 10(1):75. doi:10.1038/s41377-021-00507-8

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wang C, Yang Y, Liu Q, Liang D, Zheng B, Chen H, et al. Multi-frequency Metasurface Carpet Cloaks. Opt Express (2018) 26(11):14123–31. doi:10.1364/OE.26.014123

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Wang S, Deng Z-L, Wang Y, Zhou Q, Wang X, Cao Y, et al. Arbitrary Polarization Conversion Dichroism Metasurfaces for All-In-One Full Poincaré Sphere Polarizers. Light Sci Appl (2021) 10(1):24. doi:10.1038/s41377-021-00468-y

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Cui T-J, Liu S, Li L-L. Information Entropy of Coding Metasurface. Light Sci Appl (2016) 5(11):e16172. doi:10.1038/lsa.2016.172

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Deng Y, Wang M, Zhuang Y, Liu S, Huang W, Zhao Q. Circularly Polarized Luminescence from Organic Micro-/nano-structures. Light Sci Appl (2021) 10(1):76. doi:10.1038/s41377-021-00516-7

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Jang J, Badloe T, Rho J. Unlocking the Future of Optical Security with Metasurfaces. Light Sci Appl (2021) 10(1):144. doi:10.1038/s41377-021-00589-4

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhao R, Sain B, Wei Q, Tang C, Li X, Weiss T, et al. Multichannel Vectorial Holographic Display and Encryption. Light Sci Appl (2018) 7(1):95. doi:10.1038/s41377-018-0091-0

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Deng ZL, Tu QA, Wang Y, Wang ZQ, Shi T, Feng Z, et al. Vectorial Compound Metapixels for Arbitrary Nonorthogonal Polarization Steganography. Adv Mater (2021) 33(43):2103472. doi:10.1002/adma.202103472

CrossRef Full Text | Google Scholar

30. Mohammadi Estakhri N, Edwards B, Engheta N. Inverse-designed Metastructures that Solve Equations. Science (2019) 363(6433):1333–8. doi:10.1126/science.aaw2498

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Silva A, Monticone F, Castaldi G, Galdi V, Alù A, Engheta N. Performing Mathematical Operations with Metamaterials. Science (2014) 343(6167):160–3. doi:10.1126/science.1242818

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Qian C, Lin X, Lin X, Xu J, Sun Y, Li E, et al. Performing Optical Logic Operations by a Diffractive Neural Network. Light Sci Appl (2020) 9(1):59. doi:10.1038/s41377-020-0303-2

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Georgi P, Massaro M, Luo K-H, Sain B, Montaut N, Herrmann H, et al. Metasurface Interferometry toward Quantum Sensors. Light Sci Appl (2019) 8(1):70. doi:10.1038/s41377-019-0182-6

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Overvig AC, Shrestha S, Malek SC, Lu M, Stein A, Zheng C, et al. Dielectric Metasurfaces for Complete and Independent Control of the Optical Amplitude and Phase. Light Sci Appl (2019) 8(1):92. doi:10.1038/s41377-019-0201-7

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, et al. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science (2011) 334(6054):333–7. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yan C, Li X, Pu M, Ma X, Zhang F, Gao P, et al. Generation of Polarization-Sensitive Modulated Optical Vortices with All-Dielectric Metasurfaces. ACS Photon (2019) 6(3):628–33. doi:10.1021/acsphotonics.8b01119

CrossRef Full Text | Google Scholar

37. Zhang F, Zeng Q, Pu M, Wang Y, Guo Y, Li X, et al. Broadband and High-Efficiency Accelerating Beam Generation by Dielectric Catenary Metasurfaces. Nanophotonics (2020) 9(9):2829–37. doi:10.1515/nanoph-2020-0057

CrossRef Full Text | Google Scholar

38. Zhan A, Colburn S, Trivedi R, Fryett TK, Dodson CM, Majumdar A. Low-Contrast Dielectric Metasurface Optics. ACS Photon (2016) 3(2):209–14. doi:10.1021/acsphotonics.5b00660

CrossRef Full Text | Google Scholar

39. Tang S, Ding F. High-efficiency Focused Optical Vortex Generation with Geometric gap-surface Plasmon Metalenses. Appl Phys Lett (2020) 117(1):011103. doi:10.1063/5.0014822

CrossRef Full Text | Google Scholar

40. Sroor H, Huang Y-W, Sephton B, Naidoo D, Vallés A, Ginis V, et al. High-purity Orbital Angular Momentum States from a Visible Metasurface Laser. Nat Photon (2020) 14(8):498–503. doi:10.1038/s41566-020-0623-z

CrossRef Full Text | Google Scholar

41. Ou K, Yu F, Li G, Wang W, Miroshnichenko AE, Huang L, et al. Mid-infrared Polarization-Controlled Broadband Achromatic Metadevice. Sci Adv (2020) 6(37):eabc0711. doi:10.1126/sciadv.abc0711

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Ou K, Yu F, Li G, Wang W, Chen J, Miroshnichenko AE, et al. Broadband Achromatic Metalens in Mid‐Wavelength Infrared. Laser Photon Rev (2021) 15:2100020. doi:10.1002/lpor.202100020

CrossRef Full Text | Google Scholar

43. Chen WT, Zhu AY, Sisler J, Bharwani Z, Capasso F. A Broadband Achromatic Polarization-Insensitive Metalens Consisting of Anisotropic Nanostructures. Nat Commun (2019) 10(1):355. doi:10.1038/s41467-019-08305-y

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Wang S, Wu PC, Su V-C, Lai Y-C, Hung Chu C, Chen J-W, et al. Broadband Achromatic Optical Metasurface Devices. Nat Commun (2017) 8(1):187. doi:10.1038/s41467-017-00166-7

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Chen WT, Zhu AY, Sanjeev V, Khorasaninejad M, Shi Z, Lee E, et al. A Broadband Achromatic Metalens for Focusing and Imaging in the Visible. Nat Nanotech (2018) 13(3):220–6. doi:10.1038/s41565-017-0034-6

CrossRef Full Text | Google Scholar

46. Devlin RC, Ambrosio A, Rubin NA, Mueller JPB, Capasso F. Arbitrary Spin-To-Orbital Angular Momentum Conversion of Light. Science (2017) 358(6365):896–901. doi:10.1126/science.aao5392

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Milione G, Sztul HI, Nolan DA, Alfano RR. Higher-Order Poincaré Sphere, Stokes Parameters, and the Angular Momentum of Light. Phys Rev Lett (2011) 107(5):053601. doi:10.1103/PhysRevLett.107.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Khorasaninejad M, Shi Z, Zhu AY, Chen WT, Sanjeev V, Zaidi A, et al. Achromatic Metalens over 60 Nm Bandwidth in the Visible and Metalens with Reverse Chromatic Dispersion. Nano Lett (2017) 17(3):1819–24. doi:10.1021/acs.nanolett.6b05137

PubMed Abstract | CrossRef Full Text | Google Scholar

49.Lumerical. Lumerical Is Now Part of the Ansys Family (2022). Available from: https://www.lumerical.com/ (Accessed January 31, 2022).

Google Scholar

50. Song N, Xu N, Shan D, Zhao Y, Gao J, Tang Y, et al. Broadband Achromatic Metasurfaces for Longwave Infrared Applications. Nanomaterials (2021) 11(10):2760. doi:10.3390/nano11102760

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Aieta F, Kats MA, Genevet P, Capasso F. Multiwavelength Achromatic Metasurfaces by Dispersive Phase Compensation. Science (2015) 347(6228):1342–5. doi:10.1126/science.aaa2494

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Fan Q, Liu M, Yang C, Yu L, Yan F, Xu T. A High Numerical Aperture, Polarization-Insensitive Metalens for Long-Wavelength Infrared Imaging. Appl Phys Lett (2018) 113(20):201104. doi:10.1063/1.5050562

CrossRef Full Text | Google Scholar

53. Jack B, Padgett MJ, Franke-Arnold S. Angular Diffraction. New J Phys (2008) 10(10):103013. doi:10.1088/1367-2630/10/10/103013

CrossRef Full Text | Google Scholar

54. Zhao Y, Belkin MA, Alù A. Twisted Optical Metamaterials for Planarized Ultrathin Broadband Circular Polarizers. Nat Commun (2012) 3:870. doi:10.1038/ncomms1877

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Karimi E, Schulz SA, De Leon I, Qassim H, Upham J, Boyd RW. Generating Optical Orbital Angular Momentum at Visible Wavelengths Using a Plasmonic Metasurface. Light Sci Appl (2014) 3(5):e167. doi:10.1038/lsa.2014.48

CrossRef Full Text | Google Scholar

56. Shi Z, Khorasaninejad M, Huang Y-W, Roques-Carmes C, Zhu AY, Chen WT, et al. Single-Layer Metasurface with Controllable Multiwavelength Functions. Nano Lett (2018) 18(4):2420–7. doi:10.1021/acs.nanolett.7b05458

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Zhou T, Liu Q, Liu Y, Zang X. Spin-independent Metalens for Helicity-Multiplexing of Converged Vortices and Cylindrical Vector Beams. Opt Lett (2020) 45(21):5941–4. doi:10.1364/OL.404436

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Zhang F, Song Q, Yang G-M, Jin Y-Q. Generation of Wideband Vortex Beam with Different OAM Modes Using Third-Order Meta-Frequency Selective Surface. Opt Express (2019) 27(24):34864–75. doi:10.1364/OE.27.034864

PubMed Abstract | CrossRef Full Text | Google Scholar