Multiple One-Way Edge Modes in Sonic Crystals With Large Chern Numbers

The quantum Hall effect (QHE) associated with Chern insulators reveals the non-trivial topological properties of two-dimensional electronic systems subject to strong magnetic field, which features finite Chern number $C$ and chiral edge states. The latter promise robust electron transport and have received tremendous attention in both the condensed matter physics and classical systems including photonics and acoustics. In acoustics, circulating air flow has been introduced to create an effective gauge magnetic field, which breaks the time-reversal symmetry and leads to chiral edge states for acoustic waves. While the robust edge states may offer possible routes towards acoustic devices yielding unidirectional sound propagation, e.g., acoustic diodes, the mode density at the interfaces is limited by small Chern numbers of $\pm 1$. Here, we realize acoustic Chern insulators with large Chern numbers, i.e., $\left|C\right|\ge$ 1 ($\left|C\right|$ = 1, 2, 3, 4). The system is based on circulating air flow in a sonic crystal (SC) with fourfold rotational symmetry. The large Chern numbers are obtained by breaking multiple accidental degeneracies at (non-)high-symmetric points. Based on these Chern insulators, acoustic diodes are realized by joining structures of different Chern numbers. Up to eight propagation modes are supported on the interfaces, greatly improving the mode density and hence the propagation efficiency. Our design offers possible routes towards high-efficient and topologically robust acoustic diodes, which may further inspire acoustic non-reciprocal devices based on topological Chern insulators. Experimentally, our proposals can be realized based on angular-momentum-biased resonator arrays.

Introduction

The concept of topology has generated great research interest in the last few decades [1–10]. It was first introduced into the field of condensed matter physics to explain many phenomena beyond the scope of the traditional Landau symmetry breaking theory [11], for example, the QHE with broken time-reversal symmetry [12–15] and the quantum spin Hall effect based on spin-orbit coupling [16–19]. Thouless et al. found that band structures of certain materials, determined by the wave vector k in momentum space, have nontrivial topological properties, and materials in different topological phases cannot change smoothly into one another [20]. At their interfaces, topological interface states emerge where the electrons can only propagate at the interfaces and do not enter the bulk [21]. Such interface states exhibit the characteristics of robustness, immunity to defects, and one-way transport, and therefore promise unprecedented applications in dissipationless electronics [22]. Later, the band topology theory was introduced into the fields of photonics and phononics, and quickly became a hot topic in recent years [23–36]. In electronics and photonics, external magnetic fields are applied to break the time-reversal symmetry. However, in acoustics, due to the lack of interactions between sound waves and magnetic fields, breaking the time-reversal symmetry faces considerable challenges. Recently, it was proposed that circulating air flow can act as an equivalent magnetic field for sound and therefore provides an effective technique to break the time-reversal symmetry in acoustics [37]. By using this technique, acoustic Chen insulators are realized, as an analogy of the QHE, supporting robust and unidirectional interface states for sound [27, 28, 30, 31].

The Chern number (denoted as $C$), a type of topological invariants, is often used to describe the topological properties of the QHE systems [38, 39]. When the Chern number is non-zero, the system is topologically nontrivial and can be referred to as a Chern insulator. The value of the Chen number determines the number of the one-way edge modes. In the previous studies for QHE, the Chern number has been limited to $\left|C\right|=$ 1, while realizing large Chern numbers has many practical meanings, such as increasing the mode density to reduce the contact resistance of circuit interconnections and to improve the coupling efficiency, in a similar way as reducing the potential for traffic congestion by expanding the roadways. In acoustics, similar properties are required for unidirectional sound control with large mode density and high efficiency. However, Chern insulators with Chern number lager than one were only discussed in electronic materials [40–45] and photonic crystals [46–48]. In acoustics, such an advance has been absent.

In this work, we realize acoustic Chern insulators with large Chern numbers up to four in a SC with circulating air flow. Our system has a fourfold rotational symmetry. Such a reduced symmetry from the previously adopted $C_{6v}$ symmetry of the graphene-like honeycomb lattices [28] offers a more efficient way to construct multiple linear (Dirac) and quadratic degeneracies. By applying air flow, these degeneracies can be simultaneously lifted, leading to band gaps with large Chern numbers. By tuning the geometric parameters, we realize multiple Chern insulators with $\left|C\right|\ge$ 1 ($\left|C\right|=1,$ 2, 3, 4). Based on these Chern insulators, acoustic diodes with large mode density are realized by joining structures of different Chern numbers, forming a diode network, where up to eight unidirectional sound “roadways” are obtained for each diode channel.

Designs and Results

Acoustic Chern Insulators With Circulating Air Flow

The proposed SC is schematically shown in Figure 1A. Each unit cell with a lattice constant $a$ consists of a rigid cylinder of radius $r_i$ at its center. A ring cavity of $r_i<r<r_o$ is filled with an anticlockwise circulating air flow and outside the cavity (i.e., $r>r_o$) is the stationary air. The ring cavity and the outside region are separated by a thin impedance-matched layer at radius $r_o$. This layer has two functions. One is to avoid the interaction between fluids in different regions, and the other is to guarantee full sound transmission from the cavity to the outside region and vice versa [30].

FIGURE 1

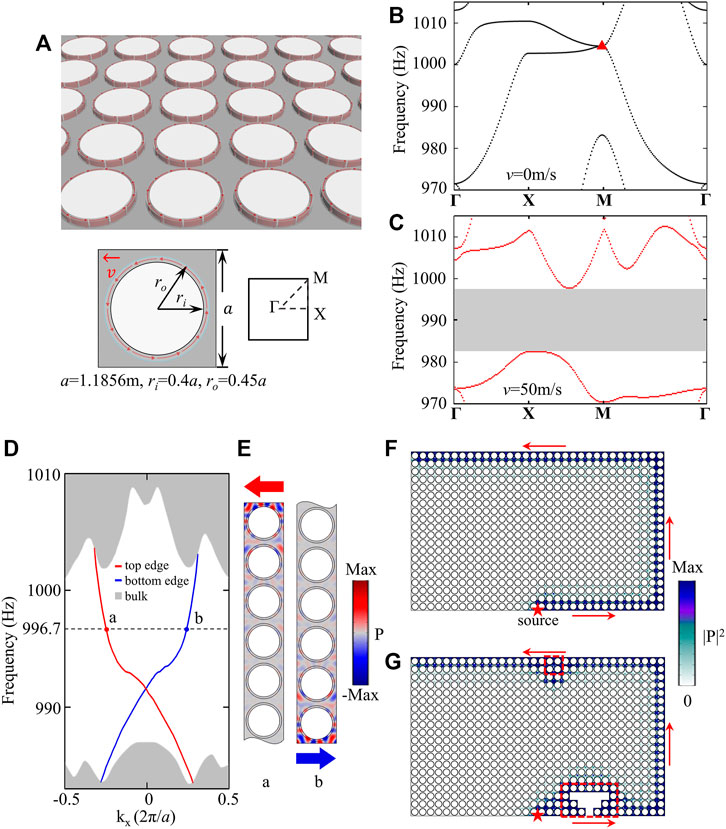
FIGURE 1. An acoustic Chern insulator with $C$ = 1. (A) Schematics of the proposed SC with $C_{4v}$ symmetry. The anticlockwise air flow is depicted by red arrows in each unit cell. The inset in the lower right corner is the first Brillion zone (BZ). Geometric parameters for the SC are also listed. (B) Bulk band structure of the SC without air flow, showing one quadratic degeneracy at the M point (marked by a red triangle). (C) The same as (B), only with a non-zero anticlockwise air flow ($\overrightarrow{v}=50$ m/s). The quadratic degeneracy is lifted and a full band gap is opened ranging from 982.5 to 997.75 Hz, as indicated by the grey shading. (D) Projected band structure of a ribbon supercell of the SC enclosed in the lower and upper directions by rigid boundaries. (E) Pressure field distributions of the lower and upper edge modes at 996.7 Hz, corresponding to those marked in (D). Note that for the sake of clarity, only partial of the supercell is presented. The red and blue arrows indicate the opposite directions of the energy flow for these two edge modes. (F) The intensity field distributions of the one-way edge modes excited at 996.7 Hz by a point source. The red star indicates the position of the source and the red arrows indicate the propagation direction. (G) The same as (F), only with local perturbations deliberately introduced on the edges (as highlighted by the red dashed boxes).

As discussed above, in electronics and photonics, external magnetic fields break the time-reversal symmetry, while in acoustics, circulating air flow acts as an equivalent magnetic field to break the time-reversal symmetry for sound, which leads to band gaps of non-zero Chern numbers. To see this, we first present in Figure 1B the band structure of the SC in Figure 1A (here, we refer to it as SC1), without air flow. A quadratic degeneracy is observed at the high symmetric point M (marked by a red triangle), which, upon introducing the air flow with a velocity of $\overrightarrow{v}=50$ m/s, is lifted and a full band gap is opened, as shown by the grey shading in Figure 1C. This gap carries a Chern number of $C$ = 1 (as will be further discussed later). The non-zero Chern number promises robust one-way edge states at interfaces between materials of different topological phases, i.e., materials with different Chern numbers. As shown in Figure 1D, the projected band structures of a ribbon supercell of SC1 consisting of $1\times 20$ unit cells are presented. The upper and lower boundaries of the supercell are enclosed by hard boundaries which can be considered as topologically trivial with $C$ = 0. It can be seen from the figure that two dispersion curves emerge in the band gap, connecting the lower and upper bulk states. These dispersion curves correspond to the one-way edge states, which counter-propagate at the bottom (blue) and upper (red) boundaries, as exemplified by the pressure field distributions for two marked modes (Figure 1E).

A smoking-gun feature of the edge states in QHE systems is their unidirectionality and topologically protection. In Figure 1F, we conduct simulations on the propagation of the edge states in a finite structure made of $32\times 20$ SC1 unit cells, which are enclosed by hard boundaries in the lower, upper and right directions while the left boundary is imposed by an absorbing boundary. The excitation is launched by a point source at the center of the lower boundary (denoted by the red star) with a frequency of 996.7 Hz (the same frequency as the marked eigen-states in Figure 1D). It is seen that despite the central position, the point source only excites the rightward edge states, which travel anticlockwise, consistent with the unidirectionality identified in Figures 1D,E. To further see the robustness of the one-way edge states, some local perturbations, including defects with several missing cells and disorders of reversed air flow, are deliberately introduced on the propagation route of the edge states. Surprisingly, it is shown that the edge states can go around these perturbations, as well as the sharp bends of ${90}^{°}$, and maintain their propagation without backscattering (Figure 1G).

Multiple Degeneracies at Non-High-Symmetric Points and Large Chern Numbers

The calculation of Chern numbers relies on the integration of Berry curvature over the entire BZ and has been a well-developed technique in studying the QHE systems [49–51]. Here, instead of conducting such a calculation, we can obtain the Chern numbers for each acoustic band gap intuitively from the bulk band structures. Specifically, for the linear degeneracies (i.e., the Dirac points), each of the two upper and lower bands connecting a pair of Dirac points can acquire a non-zero quantized Berry flux when gapped by breaking the time-reversal symmetry, i.e., one Dirac point contributes a $\pi$ Berry flux and a pair sums to $2\pi$ [38, 47]. A $2\pi$ Berry flux change across the band gap indicates a Chern number of $\pm 1$. This means when $n$ ($n\ge 1$) pairs of Dirac degeneracies are gapped by the circulating air flow, the Chern numbers of the target gap is $n$ or $-n$, depending on the air flow direction (an anticlockwise air flow induces positive Chern numbers while the clockwise air flow induces negative Chern numbers). For the quadratic degeneracies, since each quadratic point consists of two Dirac points [52], it singly contributes a Chern number of $\pm 1$. Take the example in Figures 1B,C, where a quadratic point at the high-symmetric point M (at the BZ corner) is gapped by the air flow. Considering its distribution over the entire BZ, four $\frac{1}{4}$-quadratic points count to one complete quadratic point, giving rise to $C$ = 1 for anticlockwise air flow and $C=-1$ for clockwise air flow.

From above analyses, it is seen that in order to obtain large Chern numbers, a straightforward way is to construct as many degenerate points as possible. In the following, we demonstrate that this can be realized in our system by tuning the geometric parameters, which can help to construct degenerate points not only at high-symmetric points but also at non-high-symmetric points. In Figure 2, we show the Chern insulator with $C=2$. The SC (referred to in the following as SC2) still has the same design as that in Figure 1A, only the geometric parameters are slightly changed. As a result, a linear Dirac point on the XM line is formed, as shown in Figure 2A where the Dirac point is marked by a red circle. After introducing air flow, this degeneracy is lifted and a full band gap is opened (Figure 2B). Applying the rule that we discussed above, eight $\frac{1}{2}$-Dirac points on the BZ boundary count to four complete Dirac points, suggesting a Chern number of $\pm 2$. The projected band structures for a ribbon supercell enclosed in the lower and upper directions by rigid walls indeed provide evidence. As shown in Figure 2C, there are two pairs of edge states emerging in the band gap, with each corresponding to the lower or upper edge. The mode profiles of the pressure field distributions in Figure 2D further show that one of the two pairs is localized on the lower boundary with an energy flow in the forward direction while the other pair is localized on the upper boundary with an energy flow in the backward direction, consistent with the predictions.

FIGURE 2

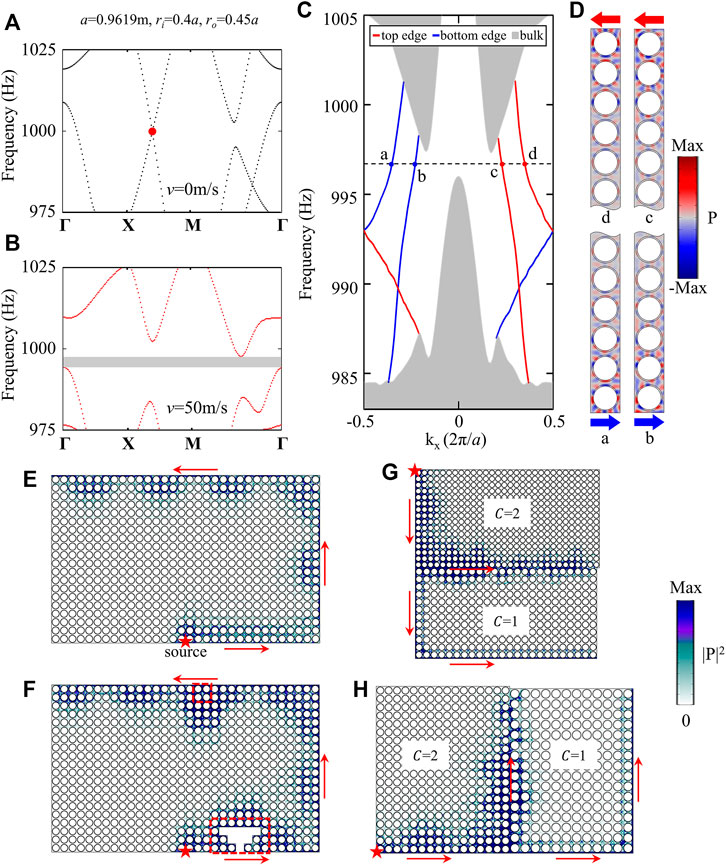
FIGURE 2. Band structures and one-way edge modes in SC2 with $C=2$. SC2 has the same design as SC1, only that the geometric parameters are slightly changed (as listed in the figure). (A,B) Bulk band structures of the SC2 with and without air flow. The red circle marks a Dirac point on the XM line. The grey region indicates the band gap for SC2, ranging from 994.25 to 997.5 Hz. (C) Projected band structure of a ribbon supercell of SC2 enclosed in the lower and upper directions by rigid boundaries. (D) Mode profiles for the eigen-states marked in (C) at 996.7 Hz. (E) The intensity field distributions of the one-way edge modes for $C=2$ excited at 996.7 Hz. (F) The same as (E), only with local perturbations. (G,H) Edge modes propagation in structures joined by SC1 with $C=1$ and SC2 with $C=2$.

We also conduct simulations to verify the one-way propagation for the edge states and their robustness against local perturbations. As shown in Figure 2E, a finite structure made of SC2 with $32\times 20$ unit cells and enclosed by rigid walls is constructed where a point source is placed at the center of the lower boundary. The excitation is launched at 996.7 Hz. Similar as the edge states for $C=1$, only the rightward propagation is excited, indicating the unidirectional properties. Differently, in this structure, due to the increased Chern number, each edge supports two edge modes with a broader “roadway” than that in Figure 1F. This can be seen from the apparently widened mode profiles in the perpendicular (to the propagation direction) direction. Further simulations on the edge state propagation with the presence of local perturbations also confirm that the edge modes for $C=2$ are robust (Figure 2F).

As mentioned above, the number of edge states on an interface made of different materials is determined by the difference between their Chern numbers. This, combined with the unidirectionality, suggests by joining different Chern insulators, the edge modes can be effectively controlled for how many edge modes can be supported and which direction the edge modes propagate. For example, when we join a Chern insulator with $C=2$ to the one with $C=1$, at their interface, there will be $2-1=1$ edge mode. Depending on different joining directions, the edge mode also propagates in different directions. As shown in Figures 2G,H, where two Chern insulators with $C=1$ and 2 are glued respectively in the y-direction and in the x-direction, they present interesting propagation behaviors. When the gluing is in the y-direction (Figure 2G), a point source from the upper-left port-entrance launches downward edge modes carrying two sound channels. Upon reaching to the gluing interface, these two channels are split into two directions, with one continuous in the downward direction while the other propagating in the rightward direction. When the gluing is in the x-direction (Figure 2H), signals from the lower-left port-entrance initially travel in the two rightward “roadways” and after a distance, they partially continue travelling rightward with the rest split into the upward “roadway”.

The above results demonstrate that using insulators with large Chern numbers, versatile unidirectional sound control can be realized, which motivates us to search for even larger Chern numbers. In the following, we report the realization of Chern insulators of $C=3$ (referred to as SC3) and $C=4$ (referred to as SC4). Figure 3A presents the bulk band structure for SC3 without air flow, showing a quadratic point (red triangle) at the high symmetric point M and a linear Dirac point (red circle) on the M $\text{Γ}$ line, which are simultaneously gapped upon introduction of air flow (Figure 3B). According to the rule to determine the Chern number, these degenerate points lead to $C=3$. The projected band structures for the ribbon supercell in Figure 3C and the corresponding mode profiles in Figure 3D indicate that indeed a Chern insulator with three edge states on each boundary is realized. In Figures 3E–H, similar studies as that in Figures 3A–D are conducted, only the geometric parameters are again modulated, giving rise to two Dirac points (red circles in Figure 3E) at the BZ boundaries, which contribute a Chern number of $C=4$ in SC4. The projected band structures for the ribbon supercell and the associated mode profiles verify the existence of four one-way edge modes on each boundary in this type of Chern insulator.

FIGURE 3

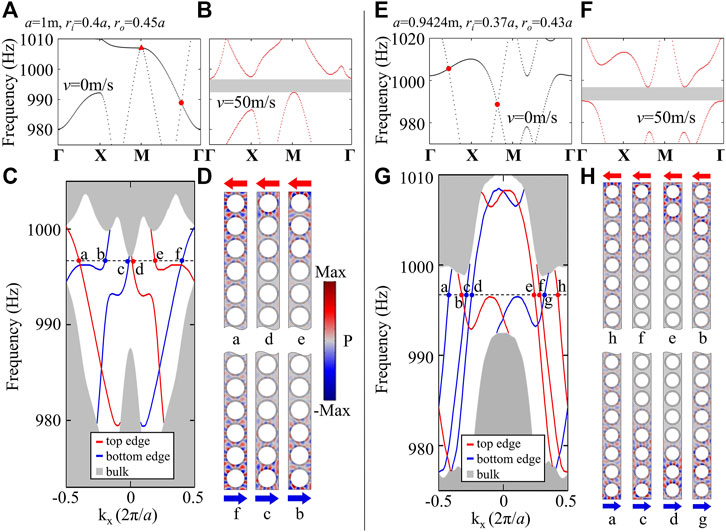
FIGURE 3. Band structures and one-way edge modes in SC3 with $C=3$ and SC4 with $C=4$. (A–D) Respectively the bulk band structures for SC3 without air flow, with air flow, the projected band structure of the ribbon supercell and the associated mode profiles of the one-way edge modes. The geometric parameters for SC3 are listed in (A). (E–H) The same as that in (A–D), only for SC4 with $C=4$. The geometric parameters of SC4 are listed in (E). All marked edge modes are at 996.7 Hz.

Here, we briefly discuss the non-Hermitian properties in the systems with circulating air flow. In general, there are two sources that can introduce non-Hermiticity into the system. One is the viscous dissipation induced by the friction between the acoustic waves and the high-speed circulating air flow. The other comes from the energy exchange between the system and the environment that drives the circulating motions [53]. In our studies, we neglect the viscous dissipation for simplicity (which essentially is another form of energy exchange, i.e., that of sound and heat). For the latter source, the aerodynamics is adopted to characterize the energy exchange, which is implemented by the Aeroacoustics module in the commercial finite element software COMSOL. We find that the one-way edge states exhibit interesting behaviors. It is shown that the edge-state bands can be folded and consequently the edge states within the same band can have two opposite propagation directions (Figure 3C). Such a band folding, according to Ref. [53], is resulted from the anti-resonances induced by the circulating air flow. This phenomenon becomes especially visible when the filling fraction of the air flow gets larger and the edge states can be folded more than once, as shown in Figure 3G. These results offer an interesting perspective on active non-Hermiticity (i.e., non-Hermiticity induced by sources, external fields, external motions, etc.,) and its possible novel phenomena, yielding further explorations.

Acoustic Diodes Created by Joining Structures of Different Chern Numbers

As discussed above, the sign of $C$ can be changed when the air flow is reversed. This means with our designs, there are up to eight types of Chern insulators with $C=\pm 1, \pm 2, \pm 3, \pm 4$, where the four positive numbers are enabled by the anticlockwise air flow while the four negative numbers are induced by the clockwise air flow. By joining these Chern insulators, we realize an acoustic diode network containing multiple interface channels and ports that support various types of “roadways” with different “lanes”. As schematically illustrated in Figures 4A,B, the diode network consists of a Sudoku-like structure with the outer eight sections filled with the Chern insulators with $C=\pm 1, \pm 2, \pm 3, \pm 4$ while the center section is a rigid void offering rigid walls for the outer sections (the rigid walls are highlighted by the thick red lines). The number labeled in each section represents the corresponding Chern number and the green numbers on the interfaces indicate the “lane” numbers. Eight output ports are created, which provide versatile unidirectionalities with different channel directions and up to 8 “lanes” (as indicated by the diode nodes and the red thick numbers labeled in each diode).

FIGURE 4

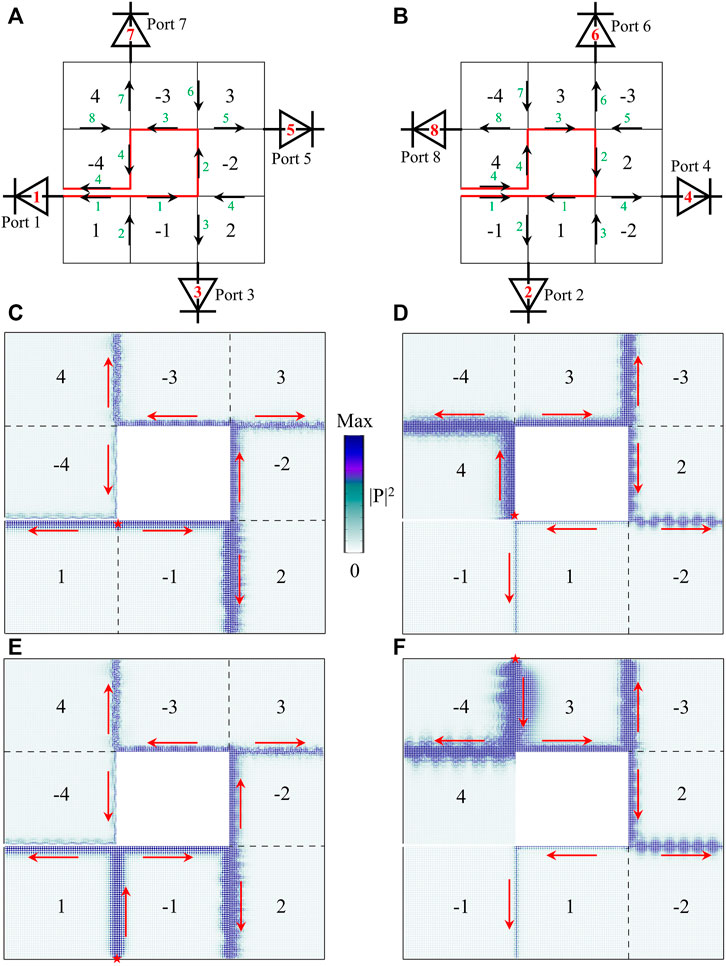
FIGURE 4. Acoustic diode networks constructed by joining structures of different $C$. (A,B) Schematics of the acoustic diode networks. Numbers in black indicate the Chern number for each Sudoku section and the green numbers illustrate the number of edge modes in each channel. Black arrows depict the unidirectionality for the sound propagation. Thick red lines represent rigid walls while the rest boundaries are imposed by absorbing boundaries. The output ports are marked by the diode icons with the red thick numbers inside them indicating how many modes are outputted from the corresponding port. (C,D) Acoustic intensity field distributions for point source excitations in the diode networks shown in (A,B). The source locations are marked by red stars and the excitation frequency is chosen as 996.25 Hz (E,F) The same as (C,D), only that the excitations are launched by two outside-coming signals (indicated by red stars).

To visualize how this diode network works, we conduct excitation simulations. In Figure 4C, a point source is placed at the interface between $C=1$ and $-1$ (indicated by a red star), which excites both leftward and rightward edge modes. The leftward one directly goes to the Port 1 while the energy carried by the rightward edge mode splits into two directions upon reaching to the interface between $C=2$ and $-1$, with a substantial amount of energy flowing into the downward output channel (to Port 3) as it supports three edge modes and can carry more energy. The upward energy continuously flows, eventually going out from Port 5 when reaching to the interface between $C=3$ and $-2$ and from Port 7 when reaching to the interface between $C=4$ and $-3$. When we reverse the air flow direction, on the other hand, different functions can be obtained. As shown in Figure 4D, the point source is located at the lower-right corner of the section with $C=4$. Its excitation now travels upwards and sends substantial amount of energy into the output channel of Port 8 which carries 8 “lanes” and is a considerably wide “roadway” for energy flowing. The rest energy is split into the rightward direction and successively goes out from Port 6, Port 4 and Port 2.

In addition to the excitations from a point source inside the network, these eight unidirectional sound channels can be launched from outside signals. As shown in Figures 4E,F, the input signals from the bottom of the $-1/1$ interface (Figure 4E) and from the top of the $-4/3$ interface (Figure 4F) also excite similar unidirectional one-way edge modes as that in Figures 4C,D, which eventually also go out from the Port 1 to Port 8. By further controlling the input signals, we can also turn off certain output ports. For example, if we have an input signal from the right of the $-2/2$ interface in Figure 4A, the Port 1 will be disabled as no energy is allowed in the left direction due to the unidirectionality. Similarly, if the input signal is from the right of the $-3/2$ interface in Figure 4B (with reversed air flow), the Port 8 will be disabled. Using similar ways, a flexible topological switch for these unidirectional diodes can be realized.

It should be pointed out that within each port, the multiple one-way edge transport suffers certain mode beating effect, i.e., different modes can crosstalk with each other via interferences. A direct evidence is the change of modal pattern. As shown in Figure 2E, when the launched edge states from the bottom edge go across the lower-right ${90}^{°}$ bend into the right edge, the modal pattern changes. When the edge states go into the upper edge, the modal pattern changes again. This is different from the single edge state propagation shown in Figure 1F where the modal pattern maintains the same across the bottom, right and upper edges. This beating effect also exists in the acoustic diodes with multiple propagation channels, as shown in Figures 4C–F. This is a common phenomenon when multi-modes are travelling in close proximity to each other [54]. While the mode beating analysis is out the scope of this work, it can be performed using several methods, e.g., interferometry [55], correlation filtering [56] and spectral imaging [57]. By implementing these methods, how each mode in a multiple-modal system contributes to its neighbors in terms of profiles and weights, as well as their relative phases that determine the output focal spots, can be determined.

Conclusion and Discussion

In conclusion, we have realized acoustic Chern insulators with large Chern numbers in SCs based on circulating air flow. We identify a simple rule to obtain large Chern numbers, which relies on the number and type of dispersion degeneracies in the bulk bands. More degenerate points suggest larger Chern number. Based on such a rule, we tune the geometric parameters of our SCs to construct multiple degenerate points, which accordingly give rise to large Chern numbers up to 4. This rule is universal in QHE systems and therefore can guide the designs of large Chern numbers in other systems. By joining structures of different Chern numbers, we design an acoustic diode network, which, further facilitated by controlling air flows, exhibits robust and versatile unidirectionalities with controllable directions and up to 8 flowing “lanes” that can carry great amount of energy due to the high mode density. Our results demonstrate the high potential of Chern insulators with large Chern numbers, which can inspire a wide range of applications in nonreciprocal (integrated) acoustics and photonics, such as diodes, unidirectional sound/light control and directional topological lasing. These results can be experimentally tested in angular-momentum-biased resonator arrays, which recently are found to be experimentally feasible [58].

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

M-HL conceived the idea. XZ proposed the acoustic diodes. HZ and TZ conducted the numerical simulations. XZ and HZ wrote the manuscript. All authors have given approval to the final version of the manuscript.

Funding

This work is supported by the National Key R&D Program of China (2017YFA0303702, 2018YFA0306200), the National Natural Science Foundation of China (Grant Numbers 51902151, 11625418, and 51732006), and the Natural Science Foundation of Jiangsu Province (Grant Number BK20190284).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Xu Ni, who has left academic employments, for his hard work to obtain the preliminary results of this research.

References

1. Zak J. Berry's Phase for Energy Bands in Solids. Phys Rev Lett (1989) 62:2747–50. doi:10.1103/PhysRevLett.62.2747

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yao W, Xiao D, Niu Q. Valley-dependent Optoelectronics from Inversion Symmetry Breaking. Phys Rev B (2008) 77:235406. doi:10.1103/PhysRevB.77.235406

CrossRef Full Text | Google Scholar

3. Zhang H, Liu C-X, Qi X-L, Dai X, Fang Z, Zhang S-C. Topological Insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a Single Dirac Cone on the Surface. Nat Phys (2009) 5:438–42. doi:10.1038/nphys1270

CrossRef Full Text | Google Scholar

4. Hasan MZ, Kane CL. Colloquium: Topological Insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/RevModPhys.82.3045

CrossRef Full Text | Google Scholar

5. Qi X-L, Zhang S-C. Topological Insulators and Superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

6. Wan X, Turner AM, Vishwanath A, Savrasov SY. Topological Semimetal and Fermi-Arc Surface States in the Electronic Structure of Pyrochlore Iridates. Phys Rev B (2011) 83:205101. doi:10.1103/PhysRevB.83.205101

CrossRef Full Text | Google Scholar

7. Asorey M. Space, Matter and Topology. Nat Phys (2016) 12:616–8. doi:10.1038/nphys3800

CrossRef Full Text | Google Scholar

8. He C, Sun X-C, Liu X-P, Lu M-H, Chen Y, Feng L, et al. Photonic Topological Insulator with Broken Time-Reversal Symmetry. Proc Natl Acad Sci USA (2016) 113:4924–8. doi:10.1073/pnas.1525502113

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhang X, Xiao M, Cheng Y, Lu M-H, Christensen J. Topological Sound. Commun Phys (2018) 1:97. doi:10.1038/s42005-018-0094-4

CrossRef Full Text | Google Scholar

10. Zhang X, Wang H-X, Lin Z-K, Tian Y, Xie B, Lu M-H, et al. Second-order Topology and Multidimensional Topological Transitions in Sonic Crystals. Nat Phys (2019) 15:582–8. doi:10.1038/s41567-019-0472-1

CrossRef Full Text | Google Scholar

11. Kosterlitz JM, Thouless DJ. Ordering, Metastability and Phase Transitions in Two-Dimensional Systems. J Phys C: Solid State Phys (1973) 6:1181–203. doi:10.1088/0022-3719/6/7/010

CrossRef Full Text | Google Scholar

12. Klitzing Kv., Dorda G, Pepper M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys Rev Lett (1980) 45:494–7. doi:10.1103/PhysRevLett.45.494

CrossRef Full Text | Google Scholar

13. Haldane FDM. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the "Parity Anomaly". Phys Rev Lett (1988) 61:2015–8. doi:10.1103/PhysRevLett.61.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Novoselov KS, Geim AK, Morozov SV, Jiang D, Katsnelson MI, Grigorieva IV, et al. Two-dimensional Gas of Massless Dirac Fermions in Graphene. Nature (2005) 438:197–200. doi:10.1038/nature04233

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhang Y, Tan Y-W, Stormer HL, Kim P. Experimental Observation of the Quantum Hall Effect and Berry's Phase in Graphene. Nature (2005) 438:201–4. doi:10.1038/nature04235

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kane CL, Mele EJ. Z2Topological Order and the Quantum Spin Hall Effect. Phys Rev Lett (2005) 95:146802. doi:10.1103/PhysRevLett.95.146802

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Kane CL, Mele EJ. Quantum Spin Hall Effect in Graphene. Phys Rev Lett (2005) 95:226801. doi:10.1103/PhysRevLett.95.226801

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Bernevig BA, Hughes TL, Zhang S-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum wells. Science (2006) 314:1757–61. doi:10.1126/science.1133734

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bernevig BA, Zhang S-C. Quantum Spin Hall Effect. Phys Rev Lett (2006) 96:106802. doi:10.1103/PhysRevLett.96.106802

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Thouless DJ, Kohmoto M, Nightingale MP, den Nijs M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys Rev Lett (1982) 49:405–8. doi:10.1103/PhysRevLett.49.405

CrossRef Full Text | Google Scholar

21. Hatsugai Y. Chern Number and Edge States in the Integer Quantum Hall Effect. Phys Rev Lett (1993) 71:3697–700. doi:10.1103/PhysRevLett.71.3697

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Castro Neto AH, Guinea F, Peres NMR, Novoselov KS, Geim AK. The Electronic Properties of Graphene. Rev Mod Phys (2009) 81:109–62. doi:10.1103/RevModPhys.81.109

CrossRef Full Text | Google Scholar

23. Haldane FDM, Raghu S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys Rev Lett (2008) 100:013904. doi:10.1103/PhysRevLett.100.013904

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Wang Z, Chong YD, Joannopoulos JD, Soljačić M. Reflection-free One-Way Edge Modes in a Gyromagnetic Photonic crystal. Phys Rev Lett (2008) 100:013905. doi:10.1103/PhysRevLett.100.013905

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Wang Z, Chong Y, Joannopoulos JD, Soljačić M. Observation of Unidirectional Backscattering-Immune Topological Electromagnetic States. Nature (2009) 461:772–5. doi:10.1038/nature08293

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Khanikaev AB, Hossein Mousavi S, Tse W-K, Kargarian M, MacDonald AH, Shvets G. Photonic Topological Insulators. Nat Mater (2013) 12:233–9. doi:10.1038/nmat3520

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Khanikaev AB, Fleury R, Mousavi SH, Alù A. Topologically Robust Sound Propagation in an Angular-Momentum-Biased Graphene-like Resonator Lattice. Nat Commun (2015) 6:8260. doi:10.1038/ncomms9260

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ni X, He C, Sun X-C, Liu X-p., Lu M-H, Feng L, et al. Topologically Protected One-Way Edge Mode in Networks of Acoustic Resonators with Circulating Air Flow. New J Phys (2015) 17:053016. doi:10.1088/1367-2630/17/5/053016

CrossRef Full Text | Google Scholar

29. Wu L-H, Hu X. Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material. Phys Rev Lett (2015) 114:223901. doi:10.1103/PhysRevLett.114.223901

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yang Z, Gao F, Shi X, Lin X, Gao Z, Chong Y, et al. Topological Acoustics. Phys Rev Lett (2015) 114:114301. doi:10.1103/PhysRevLett.114.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Chen Z-G, Wu Y. Tunable Topological Phononic Crystals. Phys Rev Appl (2016) 5:054021. doi:10.1103/PhysRevApplied.5.054021

CrossRef Full Text | Google Scholar

32. He C, Ni X, Ge H, Sun X-C, Chen Y-B, Lu M-H, et al. Acoustic Topological Insulator and Robust One-Way Sound Transport. Nat Phys (2016) 12:1124–9. doi:10.1038/nphys3867

CrossRef Full Text | Google Scholar

33. Chen C, Ding X, Qin J, He Y, Luo Y-H, Chen M-C, et al. Observation of Topologically Protected Edge States in a Photonic Two-Dimensional Quantum Walk. Phys Rev Lett (2018) 121:100502. doi:10.1103/PhysRevLett.121.100502

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Ozawa T, Price HM, Amo A, Goldman N, Hafezi M, Lu L, et al. Topological Photonics. Rev Mod Phys (2018) 91:015006. doi:10.1103/RevModPhys.91.015006

CrossRef Full Text | Google Scholar

35. Chen H, Yao LY, Nassar H, Huang GL. Mechanical Quantum Hall Effect in Time-Modulated Elastic Materials. Phys Rev Appl (2019) 11:044029. doi:10.1103/PhysRevApplied.11.044029

CrossRef Full Text | Google Scholar

36. Chen Z-G, Zhu W, Tan Y, Wang L, Ma G. Acoustic Realization of a Four-Dimensional Higher-Order Chern Insulator and Boundary-Modes Engineering. Phys Rev X (2021) 11:011016. doi:10.1103/PhysRevX.11.011016

CrossRef Full Text | Google Scholar

37. Fleury R, Sounas DL, Sieck CF, Haberman MR, Alù A. Sound Isolation and Giant Linear Nonreciprocity in a Compact Acoustic Circulator. Science (2014) 343:516–9. doi:10.1126/science.1246957

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Raghu S, Haldane FDM. Analogs of Quantum-Hall-Effect Edge States in Photonic Crystals. Phys Rev A (2008) 78:033834. doi:10.1103/PhysRevA.78.033834

CrossRef Full Text | Google Scholar

39. Lu L, Joannopoulos JD, Soljačić M. Topological Photonics. Nat Photon (2014) 8:821–9. doi:10.1038/nphoton.2014.248

CrossRef Full Text | Google Scholar

40. Yang S, Gu Z-C, Sun K, Das Sarma S. Topological Flat Band Models with Arbitrary Chern Numbers. Phys Rev B (2012) 86:241112. doi:10.1103/PhysRevB.86.241112

CrossRef Full Text | Google Scholar

41. Wang J, Lian B, Zhang H, Xu Y, Zhang S-C. Quantum Anomalous Hall Effect with Higher Plateaus. Phys Rev Lett (2013) 111:136801. doi:10.1103/PhysRevLett.111.136801

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Fang C, Gilbert MJ, Bernevig BA. Large-Chern-number Quantum Anomalous Hall Effect in Thin-Film Topological Crystalline Insulators. Phys Rev Lett (2014) 112:046801. doi:10.1103/PhysRevLett.112.046801

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Xiong T-S, Gong J, An J-H. Towards Large-Chern-Number Topological Phases by Periodic Quenching. Phys Rev B (2016) 93:184306. doi:10.1103/PhysRevB.93.184306

CrossRef Full Text | Google Scholar

44. Chen G, Sharpe AL, Fox EJ, Zhang Y-H, Wang S, Jiang L, et al. Tunable Correlated Chern Insulator and Ferromagnetism in a Moiré Superlattice. Nature (2020) 579:56–61. doi:10.1038/s41586-020-2049-7

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Ge J, Liu Y, Li J, Li H, Luo T, Wu Y, et al. High-Chern-number and High-Temperature Quantum Hall Effect without Landau Levels. Natl Sci Rev (2020) 7:1280–7. doi:10.1093/nsr/nwaa089

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Skirlo SA, Lu L, Soljačić M. Multimode One-Way Waveguides of Large Chern Numbers. Phys Rev Lett (2014) 113:113904. doi:10.1103/PhysRevLett.113.113904

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Skirlo SA, Lu L, Igarashi Y, Yan Q, Joannopoulos J, Soljačić M. Experimental Observation of Large Chern Numbers in Photonic Crystals. Phys Rev Lett (2015) 115:253901. doi:10.1103/PhysRevLett.115.253901

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Chan H-C, Guo G-Y. Tuning Topological Phase Transitions in Hexagonal Photonic Lattices Made of Triangular Rods. Phys Rev B (2018) 97:045422. doi:10.1103/PhysRevB.97.045422

CrossRef Full Text | Google Scholar

49. Berry MV. Quantal Phase Factors Accompanying Adiabatic Changes. Proc R Soc Lond A (1984) 392:45–57. doi:10.1098/rspa.1984.0023

CrossRef Full Text | Google Scholar

50. Wang H-X, Guo G-Y, Jiang J-H. Band Topology in Classical Waves: Wilson-loop Approach to Topological Numbers and Fragile Topology. New J Phys (2019) 21:093029. doi:10.1088/1367-2630/ab3f71

CrossRef Full Text | Google Scholar

51. Wang C, Zhang H, Yuan H, Zhong J, Lu C. Universal Numerical Calculation Method for the Berry Curvature and Chern Numbers of Typical Topological Photonic Crystals. Front Optoelectron (2020) 13:73–88. doi:10.1007/s12200-019-0963-9

CrossRef Full Text | Google Scholar

52. Chong YD, Wen X-G, Soljačić M. Effective Theory of Quadratic Degeneracies. Phys Rev B (2008) 77:349–54. doi:10.1103/PhysRevB.77.235125

CrossRef Full Text | Google Scholar

53. Zhao D, Wang Y-T, Fung K-H, Zhang Z-Q, Chan CT. Acoustic Metamaterials with Spinning Components. Phys Rev B (2020) 101:054107. doi:10.1103/PhysRevB.101.054107

CrossRef Full Text | Google Scholar

54. Travagnin M, Sartori F, Ruzzier M. Mode Beating Analysis by Sample Stretching and Wavelength Sweeping in a Few-Mode Fiber. J Lightwave Technol (2014) 32:494–504. doi:10.1109/JLT.2013.2294475

CrossRef Full Text | Google Scholar

55. Fontaine NK, Ryf R, Mestre MA, Guan B, Palou X, Randel S, et al. Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), 2013. Anaheim, CA, United States (2013). doi:10.1364/OFC.2013.OW1K.2Characterization of Space-Division Multiplexing Systems Using a Swept-Wavelength Interferometer

CrossRef Full Text | Google Scholar

56. Kaiser T, Flamm D, Schröter S, Duparré M. Complete Modal Decomposition for Optical Fibers Using CGH-Based Correlation Filters. Opt Express (2009) 17:9347–56. doi:10.1364/OE.17.009347

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Nicholson JW, Yablon AD, Ramachandran S, Ghalmi S. Spatially and Spectrally Resolved Imaging of Modal Content in Large-Mode-Area Fibers. Opt Express (2008) 16:7233–43. doi:10.1364/OE.16.007233

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Ding Y, Peng Y, Zhu Y, Fan X, Yang J, Liang B, et al. Experimental Demonstration of Acoustic Chern Insulators. Phys Rev Lett (2019) 122:014302. doi:10.1103/PhysRevLett.122.014302

PubMed Abstract | CrossRef Full Text | Google Scholar