The Magnetic and Thermally-Induced Spin-Related Transport Features Using Germanene Nanoribbons With Zigzag and Klein Edges

The current work employs the first-principles computations and non-equilibrium Greens function to investigate the magnetic and thermally-induced spin-related transport features using germanene nanoribbons with zigzag and Klein edges (ZKGeNRs). It was demonstrated that the ZKGeNRs with various widths (N) are placed in various spin-resolved electronic states. By increasing the width parameter N from 4 to 9, the ZKGeNRs moves from an indirect-gap bipolar magnetic semiconducting state (BMS) to bipolar spin gapless semiconductor (BSGS), and finally to ferromagnetic metal (FM). Moreover, since the right and the left temperatures of the ZKGeNRs device are different, the spin-up and spin-down currents flow in reverse orientations, demonstrating the spin-dependent Seebeck effect (SDSE). Besides, the threshold temperature decreases as N increases and then disappears, while the spin currents increase as N increases. Simulation results indicated that the ZKGeNRs could be an appropriate choice for spin caloritronic devices and could be utilized in future low-power consumption applications.

Introduction

Spin caloritronics, concentrating on the interaction between the spin and heat currents, is one of the hot topics in condensed matter physics because it plays an essential role in the growth of primary sciences and advanced low-power-consumption technologies (1–6). Recently, Slachter et al. (7) experimentally discovered the spin-dependent Seebeck effect (SDSE) through the heat transfer within the interface between a ferromagnet and a non-magnetic metal. After that, various studies have been reported concerning the SDSE in one-dimensional nanoribbons with armchair or zigzag edges, such as graphene, silicene, black phosphorus and germanene nanoribbons (8–10). For example, Majidi et al. (11) demonstrated that spin-up and spin-down currents flow in reverse orientations with two various threshold temperatures in hydrogen-terminated zigzag-edge germanene nanoribbons with a temperature difference among the source and the drain. Zheng et al. (12) found electric fields to improve spin thermoelectric efficiency of germanene nanoribbon. As we know, germanene honeycomb lattice can be sliced along <1 $\overline{1}$ 10> and <2 $\overline{1} \overline{1}$ 0 > orientations to generate armchair and zigzag/Klein edges, respectively. However, the works performed on the electronic structure and SDSE on zigzag GeNRs (ZGeNRs) with Klein edge are rare. Indeed, these two kinds of reconstructed edges for zigzag graphene nanoribbons (GNRs) have been found through experimenters (13, 14), and their significant impact on the ZGNRs’ band structures and magnetic states have been proved theoretically (15, 16). Therefore, in the current research, ab initio computations are incorporated with the nonequilibrium Green’s function technique to investigate the electronic structures and thermal spin-related transport characteristics of ZKGeNRs. Moreover, it is indicated that the ZKGeNRs can have stable ferromagnetic states, and the SDSE can also be achieved. The obtained results confirm that ZKGeNRs can be utilized in spin caloritronic devices.

Calculation Method and Model

Here we turn to introduce the device designs and theoretical method briefly. The N-ZKGeNRs in the present designs have one zigzag edge and one Klein edge (see Figure 1A,B), while two H atoms saturate both edges. N stands for the number of Ge atoms rows through the ZGeNR width, which changes from four to 9. Two probe spin caloritronic devices were then constructed using N-ZKGeNRs (say N = 4), as presented in Figure 1C. The left and right contacts are semi-infinite ZKGeNRs, while the mid scattering area involves five modules of ZKGeNRs. We concentrate on the spin currents generated through a temperature gradient, ΔT, between the left temperature T_L and the right 1 T_R, i.e., ΔT = T_L-T_R.

FIGURE 1

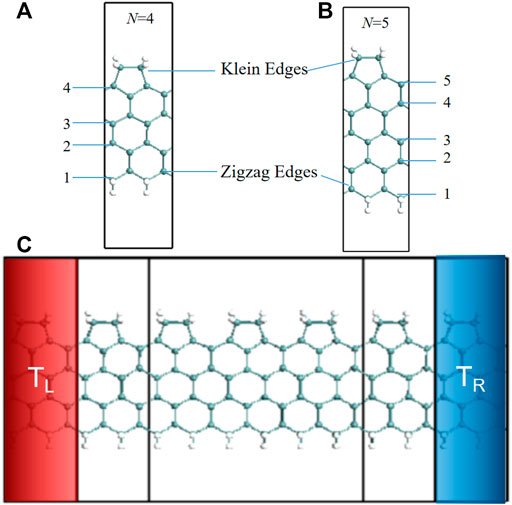
FIGURE 1. (A), (B) Optimal structure of the N-ZKGeNRs (say N = 4, 5), in which Ge and hydrogen atoms are described by the dark green and white balls, respectively. (C) Schematic description of the thermal spin device using N-ZKGeNRs (say N = 4).

The computations were accomplished with the Atomistix Toolkit (ATK) package (17, 18), incorporating the spin density functional theory with the nonequilibrium Green’s function strategy. The Double-Zeta-Polarized (DZP) basis set was utilized to accomplish the geometry optimization and electronic structure computations, while the Generalized-Gradient-Approximation method (19, 20) adopts the exchange-correlation potential. The cut-off energy was 120 Hartree, while a Monkhorst–Pack 1 × 1×100 k-mesh was adopted. In the LandauerBüttiker formulation, the spin-related currents of the devices were determined through the upcoming Eq. 21:

$I^{\uparrow (\downarrow )}=\frac{e}{h}{\displaystyle \underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\left\{T^{\uparrow (\downarrow )}\left(E\right)\left[f_L\left(E,T_L\right)-f_R\left(E,T_R\right)\right]\right\}}dE(1)$

where e stands for the electron charge, h describes the Planck constant, and T_L(R) stands for the left (right) electrode’s temperature. f_{L(R) (}E,T_L(R)) indicates the left (right) electrode’s mean Fermi–Dirac distribution:

$f_{L\left(R\right)}\left(E,T_{L\left(R\right)}\right)={\left\{1+\exp \left[E-{\mu }_{L\left(R\right)}/k_B{T}_{L\left(R\right)}\right]\right\}}^{-1}(2)$

where ${\mu }_{\text{L}\left(\text{R}\right)}$ describe the left (right) electrode’s chemical potential, $k_B$ stands for the Boltzmann constant, and T^{↑(↓) (}E) describes the spin-related transport coefficient:

$T^{\uparrow (\downarrow )}\left(E\right)=Tr\left[{\Gamma }_L{G}^r{\Gamma }_R{G}^a\right](3)$

where G^r(a) stands for the Green’s function retarded in the mid area, while Γ_L(R) describes the left (right) electrode’s coupling matrix. In addition, the calculation methods of the spin figures of merit (Z_sT) can be found in our and others previous studies (22, 23).

Results and Discussion

At first, the band structures of the N-ZKGeNRs (N = 4–9) were verified, as presented in Figure 2. The nanoribbons’ band structures vary significantly by increasing the value of N. For N = 4, the conduction band minimum (CBM) is related to the spin-down state and located at the Γ point, which is above the Fermi level (E_F), while the spin-up state below E_F was considered the valence band maximum (VBM) and placed in the line of Γ-Z. The valence and conduction bands have reverse spin polarities while approaching E_F. Furthermore, the spin-related bands of 4-ZKGeNRs are equal to 0.158 eV. These characteristics indicate that the 4-ZKGeNR is an indirect-gap BMS (24–26). The ferromagnetic shape is kept unchanged by increasing the nanoribbon width, while the band structures around the Fermi level vary significantly. For N = five to six, the CBM and VBM of the spin-down and spin-up channels are located at Γ and Γ-Z points, respectively, while the bandgaps are equal to 0.071 and 0.018 eV. Based on Wang and Hu’s works (27–29), the bandgap of about 0.1 eV or lower than 0.1 eV can be described as “gapless”. Therefore, the band structure can be considered gapless, indicating that 5-ZKGeNR and 6-ZKGeNR exhibit a BSGS behavior. For N = seven to nine, the spin-up and spin-down bands are across the E_f. These ZKGeNRs are intrinsically FM. In short, ZKGeNRs can have three states while increasing the width, including indirect-gap BMS state, BSGS state, and FM state.

FIGURE 2

FIGURE 2. Spin-dependent band structures of the N-ZKGeNRs (N = 4–9).

The transmission spectrums of ZKGeNRs should be verified to identify the induced spin-related current in the presented ZKGeNRs and illustrate the transport carriers’ behavior. Figure 3 presents the spin-related transmission spectrums. It can be observed that all the ZKGeNRs have similar characteristics, except for different transport channels. In the energy interval of [-0.3, 0.3] eV, the transmission coefficient is 2, while there exist peak values for spin-up and spin-down electrons in transmission spectrums. The mentioned peak values are caused by the band structure, as Figure 2 shows. Because the right and left electrodes have similar material and density of state, the Fermi-Dirac distribution (f_R (E, T_R) − f_L (E, T_L)) determines the carrier behavior and concentration using the constructed device, depending on the electrons temperature at two leads. Fermi-Dirac distribution function is described by Eq. 2, in which µ stands for the chemical potential and is chosen as zero in the performed computations. The number of electrons with energies higher than the Fermi level, flow from the hotter electrode (left) to the lower one (right), because the electron distribution of hotter electrode is higher than that of the lower one, causing in a spin-down current. For the same reason, the number of holes with energies lower than the Fermi energy flow from the hotter electrode to the lower one, too, causing the spin-up current. Figure 3 shows that since the transmission for spin-down electrons is more than spin-up ones in a domain of energies greater than the Fermi level, there exists a spin-down negative current for the mentioned domain. Moreover, since the spin-up current’s behavior is precisely opposite to the spin-down one, a spin-up positive current can be generated.

FIGURE 3

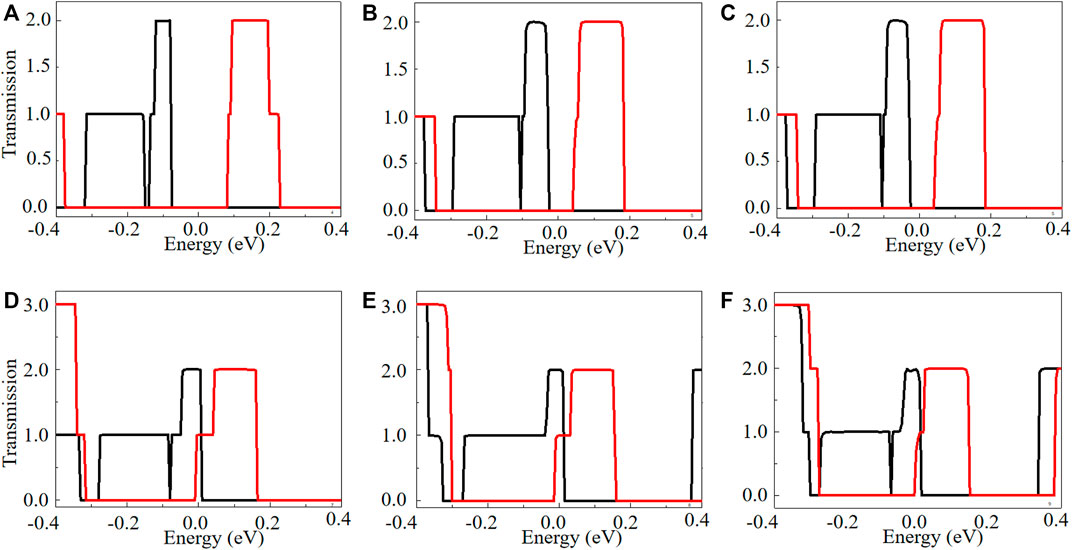
FIGURE 3. Spin-related transmission spectrums of the N-ZKGeNRs (N = 4–9) devices, (A) N = 4, (B) N = 5, (C) N = 6, (D) N = 7, (E) N = 8, (F) N = 9, in which spin-up and spin-down are described by the solid black and red lines.

The thermal spin transport features of the proposed ZKGeNRs should be verified to go through their spin-dependent currents. Figure 4 shows the spin-related currents through the N-ZKGeNRs devices versus T_L. For the 4-ZKGeNRs device, there are no spin-up currents (I_up) when T_L < 100 K and no spin-down currents (I_dn) when T_L < 120 K for three values of ΔT, demonstrating that no thermal-induced spin-related currents can be produced in these ranges of T_L, while the temperature difference (ΔT) is not important. This means that there exists a threshold temperature Tth at around 100 K for I_up and 120 K for I_dn, respectively. When T_L > Tth, both I_up and I_dn grow significantly with the increase of T_L. Nevertheless, they move in the reverse orientations, i.e., I_up is negative, while I_dn is positive. Certainly, this is induced by the SDSE (10). Moreover, the greater the ΔT, the higher the spin-related currents. The spin-related currents in terms of ΔT curves are presented in Figure 5, for T_L = 300, 350, and 400 K. These curves demonstrate that the spin-related currents are nearly symmetric around the zero-current axis and robust within a wide domain of temperature gradients. This confirms the generation of the SDSE through the spin-related currents in terms of ΔT curves. The devices of 5-ZKGeNRs and 6-ZKGeNRs have the same rules with 4-ZKGeNRs, but have smaller Tth and lager I_up and I_dn, as shown in Figures 4B,C. In addition, as shown in Figures 4D–F, I_dn of N-ZKGeNRs (N = 7–9) devices have similar rules with 4-ZKGeNRs, while Tth for I_up is equal to zero.

FIGURE 4

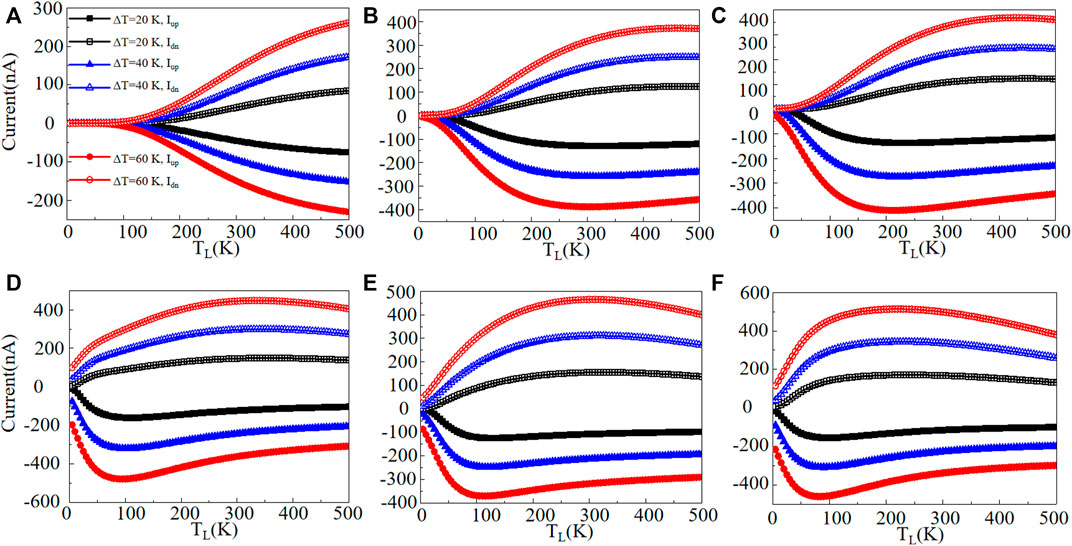
FIGURE 4. Spin-up currents (I_up) and spin-down currents (I_dn) in terms of T_L for the N-ZKGeNRs (N = 4–9) devices at selected temperature gradients, (A) N = 4, (B) N = 5, (C) N = 6, (D) N = 7, (E) N = 8, (F) N = 9.

FIGURE 5

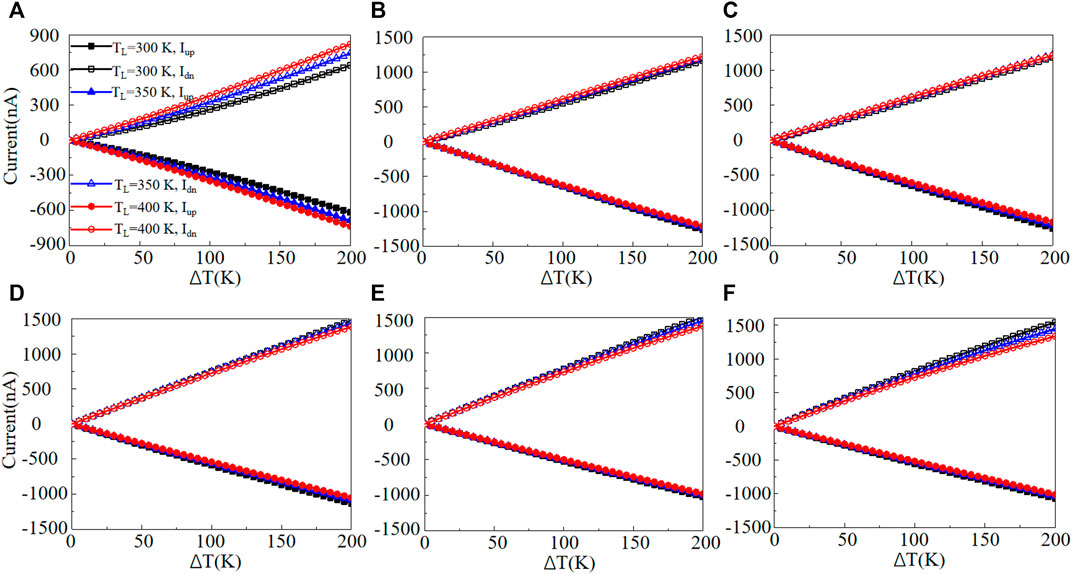
FIGURE 5. I_up and I_dn in terms of ΔT for selected values of T_L, (A) N = 4, (B) N = 5, (C) N = 6, (D) N = 7, (E) N = 8, (F) N = 9.

Finally, we turn to investigate the thermoelectric conversion efficiency of these ZKGeNRs devices. First, we plot the calculated results of spin thermopower (S_s) versus the chemical potential (μ) at T = 300 K for the ZKGeNRs (N = 4–9) in Figure 6A. It is obvious that the S_s decrease with increasing N for N = four to six, while the S_s are approximately equal for N = 7–9. Next, we plot the calculated results of spin figures of merit (Z_sT) versus the chemical potential (μ) at T = 300 K for the ZKGeNRs (N = 4–9) in Figure 6B. The maximum values related to N-ZKGeNRs are about 47.9, 25.3, 18.7, 9.6, 6.5, and 4.7 for N = four to nine, respectively. Apparently, the 4-ZKGeNRs has the largest value of Z_sT because it has the largest spin thermopower and near-linear increase of thermal conductance due to the increasing the ribbon width (30, 31). Interesting, these values are comparable with the results obtained for devices based on GeNRs (12), much larger than them at room temperature. Similar behavior was also found in sawtooth GNRs (31), edge-defected GNRs (32) and armchair GNRs with triangular antidots (33). Generally, a large Z_sT value supports a higher thermoelectric conversion performance in materials. These results confirm that ZKGeNRs are suitable candidate materials for spin caloritronic devices.

FIGURE 6

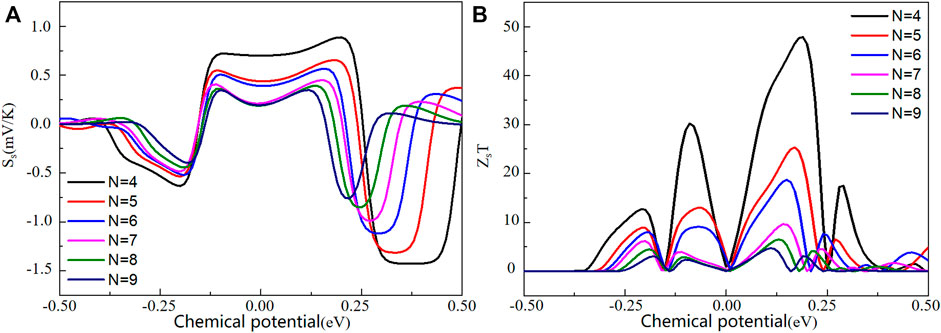
FIGURE 6. (A) The spin thermopower (S_s), (B) spin figure of merit (Z_sT) versus chemical potential for the N-ZKGeNRs (N = 4–9).

Conclusion

The current research incorporated the first-principles computations with the nonequilibrium Green’s function to evaluate the electronic structures and thermally-induced spin-related transport features of various N-ZKGeNRs. Firstly, it was demonstrated that the N-ZKGeNRs move from an indirect-gap BMS to SGS state and finally to FM state by increasing the nanoribbon width variable N. Secondly, the SDSE could be observed by generating a temperature gradient across the mentioned ZKGeNRs. In addition, the threshold temperature decreases as N increases and then disappears, while the spin currents increase as N increases. Generally, the mentioned discoveries strongly demonstrate the potential of N-ZKGeNRs for application in thermal spin nanodevices.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by the National Natural Science Foundation of China with grant No. 11864011, in part by the Science and Technology Research Program of Chongqing Municipal Education Commission (KJQN202101204) and in part by the Educational Commission of Hubei Province of China (T201914).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher

Acknowledgments

The authors would like to thank all the reviewers who participated in the review and MJEditor (www.mjeditor.com) for its linguistic assistance during the preparation of this manuscript.

References

1. Bauer GEW, Saitoh E, van Wees BJ. Spin Caloritronics. Nat Mater (2012) 11(5):391–9. doi:10.1038/nmat3301

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Boona SR, Myers RC, Heremans JP. Spin Caloritronics. Energy Environ. Sci. (2014) 7(3):885–910. doi:10.1039/c3ee43299h

CrossRef Full Text | Google Scholar

3. Borlenghi S, Wang W, Fangohr H, Bergqvist L, Delin A. Designing a Spin-Seebeck Diode. Phys Rev Lett (2014) 112(4):047203. doi:10.1103/physrevlett.112.047203

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Fu H-H, Yao KL. Perfect thermal Spin Filter and Pure Spin Thermoelectric Generator Based on a Laterally Coupled Double Quantum-Dot Array. Epl (2013) 103(5):57011. doi:10.1209/0295-5075/103/57011

CrossRef Full Text | Google Scholar

5. Uchida K, Takahashi S, Harii K, Ieda J, Koshibae W, Ando K, et al. Observation of the Spin Seebeck Effect. Nature (2008) 455(7214):778–81. doi:10.1038/nature07321

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Uchida K, Xiao J, Adachi H, Ohe J, Takahashi S, Ieda J, et al. Spin Seebeck Insulator. Nat Mater (2010) 9(11):894–7. doi:10.1038/nmat2856

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Slachter A, Bakker FL, Adam J-P, van Wees BJ. Thermally Driven Spin Injection from a Ferromagnet into a Non-magnetic Metal. Nat Phys (2010) 6(11):879–82. doi:10.1038/nphys1767

CrossRef Full Text | Google Scholar

8. Yang Y-R, Zhang Z-Q, Gu L, Fu HH. Spin-dependent Seebeck Effect in Zigzag Black Phosphorene Nanoribbons. RSC Adv (2016) 6(50):44019–23. doi:10.1039/c6ra04069a

CrossRef Full Text | Google Scholar

9. Tang X-Q, Ye X-M, Tan X-Y, Ren DH. Metal-Free Magnetism, Spin-Dependent Seebeck Effect, And Spin-Seebeck Diode Effect In Armchair Graphene Nanoribbons. Scientific Rep (2018) 8:927. doi:10.1038/s41598-018-19632-3

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Fu H-H, Gu L, Wu DD. A Spin-Seebeck Diode with a Negative Differential Spin-Seebeck Effect in a Hydrogen-Terminated Zigzag Silicene Nanoribbon Heterojunction. Phys Chem Chem Phys (2016) 18(18):12742–7. doi:10.1039/c6cp00876c

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Majidi D, Faez R. Thermally Induced Spin-dependent Current Based on Zigzag Germanene Nanoribbons. Physica E: Low-dimensional Syst Nanostructures (2017) 86:175–83. doi:10.1016/j.physe.2016.09.017

CrossRef Full Text | Google Scholar

12. Zheng J, Chi F, Guo Y. Exchange and Electric fields Enhanced Spin Thermoelectric Performance of Germanene Nano-Ribbon. J Phys Condens Matter (2015) 27:295302. doi:10.1088/0953-8984/27/29/295302

CrossRef Full Text | Google Scholar

13. Girit CO, Meyer JC, Erni R, Rossell MD, Kisielowski C, Yang L, et al. Graphene at the Edge: Stability and Dynamics. Science (2009) 323(5922):1705–8. doi:10.1126/science.1166999

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Suenaga K, Koshino M. Atom-by-atom Spectroscopy at Graphene Edge. Nature (2010) 468(7327):1088–90. doi:10.1038/nature09664

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Koskinen P, Malola S, Hakkinen H. Self-Passivating Edge Reconstructions Of Graphene. Phys Rev Lett (2008) 101(11):115502. doi:10.1103/physrevlett.101.115502

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wagner P, Ewels CP, Adjizian J-J, Magaud L, Pochet P, Roche S, et al. Band Gap Engineering via Edge-Functionalization of Graphene Nanoribbons. J Phys Chem C (2013) 117(50):26790–6. doi:10.1021/jp408695c

CrossRef Full Text | Google Scholar

17. Smidstrup S, Markussen T, Vancraeyveld P, Wellendorff J, Schneider J, et al. QuantumATK: An Integrated Platform of Electronic and Atomic-Scale Modelling Tools. J Phys: Condens Matter (2020) 32:36. doi:10.1088/1361-648X/ab4007

CrossRef Full Text | Google Scholar

18. Brandbyge M, Mozos JL, Ordejon P, Taylor J, Stokbro K. Density-Functional Method For Nonequilibrium Electron Transport. Phys Rev B (2002) 65(16), 165401. doi:10.1103/physrevb.65.165401

CrossRef Full Text | Google Scholar

19. Perdew JP, Wang Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys Rev B (1992) 45(23):13244–9. doi:10.1103/physrevb.45.13244

CrossRef Full Text | Google Scholar

20. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett (1996) 77(18):3865–8. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Imry Y, Landauer R. Conductance Viewed as Transmission. Rev Mod Phys (1999) 71(2):S306–S312. doi:10.1103/revmodphys.71.s306

CrossRef Full Text | Google Scholar

22. Xiao J, Tan X, Ye X, Tang X, Ren D. Spin-dependent Seebeck Effect, Spin-dependent Seebeck Diode, thermal Spin Filtering and Figure of merit of Nitrophenyl Diazonium Functionalized Graphene. Org Electron (2018) 63:1–6. doi:10.1016/j.orgel.2018.09.001

CrossRef Full Text | Google Scholar

23. Zakerian F, Fathipour M, Faez R, Darvish G. Near-room-temperature Spin Caloritronics in a Magnetized and Defective Zigzag MoS2 Nanoribbon. J Comput Electron (2020) 19:137–46. doi:10.1007/s10825-019-01406-3

CrossRef Full Text | Google Scholar

24. Li X, Wu X, Li Z, Yang J, Hou JG. Bipolar Magnetic Semiconductors: a New Class of Spintronics Materials. Nanoscale (2012) 4(18):5680–5. doi:10.1039/c2nr31743e

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Bannikov VV, Ivanovskii AL. Ab Initio search for Novel Bipolar Magnetic Semiconductors: Layered YZnAsO Doped with Fe and Mn. Jetp Lett (2013) 96(11):735–8. doi:10.1134/s0021364012230038

CrossRef Full Text | Google Scholar

26. Zhang JH, Li XX, Yang JL. Sin-Sic Nanofilm: A Nano-Functional Ceramic With Bipolar Magnetic Semiconducting Character. Appl Phys Lett (2014) 104(17):172403. doi:10.1063/1.4874335

CrossRef Full Text | Google Scholar

27. Wang XL. Proposal For A New Class Of Materials: Spin Gapless Semiconductors. Phys Rev Lett (2008) 100(15), 156404. doi:10.1103/physrevlett.100.156404

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hu X, Zhang W, Sun L, Krasheninnikov AV. Gold-Embedded Zigzag Graphene Nanoribbons As Spin Gapless Semiconductors. Phys Rev B (2012) 86(19), 195418. doi:10.1103/physrevb.86.195418

CrossRef Full Text | Google Scholar

29. Wang XL. Dirac Spin-Gapless Semiconductors: Promising Platforms for Massless and Dissipationless Spintronics and New (Quantum) Anomalous Spin Hall Effects. Natl Sci Rev (2017) 4(2):252–7. doi:10.1093/nsr/nww069

CrossRef Full Text | Google Scholar

30. Chen X, Xu Y, Zou X, Gu B-L, Duan W. Interfacial thermal Conductance of Partially Unzipped Carbon Nanotubes: Linear Scaling and Exponential Decay. Phys Rev B (2013) 87:155438. doi:10.1103/physrevb.87.155438

CrossRef Full Text | Google Scholar

31. Chen X, Liu Y, Gu B-L, Duan W, Liu F. Giant Room-Temperature Spin Caloritronics in Spin-Semiconducting Graphene Nanoribbons. Phys Rev B (2014) 90:121403. doi:10.1103/physrevb.90.121403

CrossRef Full Text | Google Scholar

32. Liu Q-B, Wu D-D, Fu HH. Edge-defect Induced Spin-dependent Seebeck Effect and Spin Figure of merit in Graphene Nanoribbons. Phys Chem Chem Phys (2017) 19:27132–9. doi:10.1039/c7cp05621d

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Shirdel-Havar M, Farghadan R. Armchair Graphene Nanoribbons with Giant Spin Thermoelectric Efficiency. Phys Chem Chem Phys (2018) 20:16853–60. doi:10.1039/c8cp02264j

PubMed Abstract | CrossRef Full Text | Google Scholar