- 1State Key Laboratory of Chemo/Biosensing and Chemometrics, Institute of Chemical Biology and Nanomedicine (ICBN), College of Chemistry and Chemical Engineering, Hunan University, Changsha, China
Two-dimensional transition metal dichalcogenides (2D-TMDs) have sparked immense interest, resulting from their unique structural, electronic, mechanical, and thermal properties. The band structures, effective mass, electron mobility, valley degeneracy, and the interactions between phonons and heat transport properties in 2D-TMDs can be efficiently tuned via various approaches. Moreover, the interdependent electrical and thermal conductivity can be modulated independently to facilitate the thermoelectric (TE)-based energy conversion process, which enables optimization of TE properties and promising TE applications. This article briefly reviews the recent development of TE properties in 2D-TMDs. First, the advantages of 2D-TMDs for TE applications are introduced. Then, the manipulations of electrical and thermal transport in 2D-TMDs are briefly discussed, including various influencing factors such as thickness effect, structural defects, and mechanical strain. Finally, the recent advances in the study of electrical, thermal transport, and TE properties of 2D-TMDs, TE-related applications, the challenges, and the future prospects in this field are reviewed.
Introduction
With the growing energy demand in recent decades, thermoelectric (TE) materials and devices have attracted extensive attention (Figure 1A). TE materials offer a promising route to convert waste heat into electrical power based on the Seebeck effect [1]. The conversion efficiency of TE material is defined by the dimensionless figure of merit ZT. In 1993, Hicks and Dresselhaus pointed out that low dimensional materials were beneficial for TE applications due to their sharp features in the density of states (DOS) [2]. The presence of sharp DOS was caused by quantum confinement in two-dimensional (2D, thin films), one-dimensional (1D, wires), and zero-dimensional (0D, quantum dots) structures, which enhanced the Seebeck coefficient. In 2001, 2D Bi2Te3/Sb2Te3 superlattice was the first reported TE material with an ultrahigh ZT value exceeding 2.0 [3]. Hereafter, researchers refocused on how to further enhance the TE performance of 2D layered material (2DLMs) system. Bi2Te3 and its derivatives were typical 2DLMs, which have been established as promising p- and n-type TE materials with high ZT at room temperatures [4–6]. However, the manufacture of these materials has been limited by their toxicity and poor chemical stability at high temperatures.

FIGURE 1. (A) Schematic illustration of the TE device base on Seebeck effect. (B) Schematic representation of a layered TMD structure with the formula MX2, where M is the transition metal atom and X is the chalcogen atom. (C) Interdependent relation of Seebeck coefficient (S), electrical conductivity (σ), and the electronic (κel) and lattice (κlat) thermal conductivity for different charge carrier concentrations.
Recently, researchers have tried to develop other 2D TE materials and suitable processes to enhance their TE properties. The 2D materials such as graphene [7], black phosphorus [8], MXenes [9], and transition metal dichalcogenides (TMDs) [10] have been widely studied theoretically and experimentally. Among them, as a novel class of 2DLMs, 2D-TMDs, such as MX2 (M = transition metal; and X = S, Se, Te), have attracted extensive attention (Figure 1B). Their outstanding chemical stability and mechanical and physical properties facilitated wide applications in electronics [11], optoelectronics [12], bio-application energy storage [13], topological spintronics [14], and energy conversion devices [15]. Moreover, mono-layer or few-layer TMDs have been considered as potential candidates for TE energy generation, owing to the favorable electrical and phonon transport properties, such as the wide tunability of inherent TE parameters [16]. MoS2 is a good example that exhibits higher Seebeck coefficient and relatively lower thermal conductivity than that of graphene [17]. As a benefit of the 2D nature, TMDs had an extra-large surface-to-bulk ratio, thus realizing efficient surface chemical functionalization [16,17]. In addition, mono-layer MoS2 was highly conducive to forming defects, which played an essential role in tuning the electronic and phonon transport properties in various ways [18].
Understanding the electronic and phonon transport properties in the 2D crystals has been significant for the design of novel devices integrated with 2D-TMDs. This article aims to provide an in-depth insight into the structure-property relationship of 2D-TMDs, with a focus on their electronic and phonon transport properties. Further, various manipulation strategies on electrical and thermal transport properties of typical 2D-TMDs have been discussed, as well as corresponding TE applications. Finally, the challenges and the prospects in this field are also presented.
2D-Transition Metal Dichalcogenides for Thermoelectrics
Thermoelectric Figure of Merit (ZT)
Three physical quantities, Seebeck coefficient, electrical conductivity, and thermal conductivity, determine the ZT of materials as shown in Equation 1.
where S, σ, κ, and T represent Seebeck coefficient, electrical conductivity, total thermal conductivity, and temperature, respectively. A good TE material should simultaneously meet the following requirements: a high σ to minimize the internal Joule loss; a high S to produce high voltage; and a low κ to maintain the temperature gradient [19]. For semiconductors, if temperature did not affect carrier scattering, according to Mott relationship, Seebeck coefficient can be expressed as the following Equation 2 [20],
where e is the elementary charge, kB is the Boltzmann constant, σ(E) = n(E)eμ(E) is the conductivity at Fermi energy (EF), μ(E) is the energy dependent mobility of the carriers, and n(E) is the energy dependent carrier density. n(E) can be established as
In a typical degenerate semiconductor, the electrical properties are closely related to carrier density, effective mass, and mean free path, which in turn play key roles in TE performance. Hence the Seebeck coefficient can be modified as shown in Equation 3 [21],
where h is the Planck constant and m* is the effective mass of carriers. The effective mass of the carrier is also related to the DOS. It is well accepted that a larger carrier effective mass leads to a larger value of the Seebeck coefficient.
Another important contributing parameter is σ. From the above equations, σ and S are coupled. It is difficult to enhance one of the properties alone without compromising the other. In 2D materials, if the Fermi level fell in a steep region where DOS varied rapidly with energy, there will be a large asymmetry between hot carriers (E > EF) and cold (E < EF) carriers. Therefore, it is possible to improve the S by shifting the local DOS, without affecting the carrier concentration and meanwhile making a minimal effect on σ [22].
The thermal conductivity κ of semiconductors generally contains the contributions from electrical (κel) and lattice (κlat) thermal conductivities (
where L is temperature dependent Lorentz number and T is the temperature. Heat in a crystalline solid is primarily transported by the collective vibrations of the lattice, known as phonons. From kinetic theory, κlat in crystalline solids can be expressed as Equation 5,
where Cv is the specific heat, υg is the phonon group velocity, and τ is the phonon relaxation time [26]. In most cases, the κ of semiconductor materials is mainly determined by the thermal conductivity of the phonons. τ can be suppressed by various phonon scatterings that are introduced in materials. Phonon scattering is strongly dependent on phonon frequency, i.e., high frequency phonons can be scattered by point defects, mid-frequency phonons can be effectively scattered by nanoprecipitates/2D interfaces, and low-frequency phonons get scattered by grain boundaries [27,28]. However, these effects also have an impact on carrier mobility as the formula,
Interdependent relation of S, σ, κel, and κlat for different charge carrier concentrations [29] are demonstrated in Figure 1C. High TE performance in material requires a high power factor (PF = S2σ) while retaining a low lattice thermal conductivity (κlat). Unlike the conventional materials, the anisotropic crystal structure and chemical bonding of layered materials allows one to modulate the phonon (κlat) and electronic transport properties (σ) individually. The common approach is changing the size of material grains and making it close to the wavelengths of phonons and/or electrons. On one hand, power factor is mostly enhanced by modulating the electronic structure of materials, such as band convergence and resonant level creation [21,25]. On the other hand, lattice thermal conductivity is generally reduced by various manipulations of phonon transport [26–28].
Advantages of 2D-Transition Metal Dichalcogenides for TE
The 2D-TMDs have been investigated as good candidates for TE materials in past years. One advantage of 2D-TMDs was that their 2D crystal nature led to sharp features in DOS [30,31]. Another advantage was that the interdependent electrical and thermal conductivity can be optimized individually for maximizing energy conversion. Generally, 2D sheets of materials could be stacked to form weakly bonded layered structures. The intralayer atoms in each layer were conjugated by strong chemical bonds, while neighboring layers were combined by weak van der Waals (vdWs) interactions [32,33]. Thus, it was feasible to isolate, mix, and match dissimilar atomic layers to create a wide range of vdWs heterostructures, without the constraints of lattice matching and processing compatibility [33]. The crystal structure and chemical bonding of 2D-TMDs make themself have low thermal conductivity in the out-of-plane direction, and extremely high thermal conductivity in the in-plane direction. Therefore, these structures have a large anisotropy, which are promising for designing TE materials with high ZT. From the aspect of application, 2D-TMDs in the out-of-plane direction are good for TE or thermionic applications, while 2D-TMDs in the in-plane direction are more suitable for heat dissipation related applications.
Besides, it was also possible to tune the band gap and carrier density of 2D-TMDs by changing the number of layers [34,35], strain [36,37], electric field [34,38], and the structural composition of the materials (by hydrogenation [13,39] or oxidation [13,40]). A smooth transition from semi-metallic to the semi-conductive state has been demonstrated by varying the number of layers in 2D-TMDs [35]. Applying strain or electric field to 2D-TMDs can also influence the band structure. For instance, by applying 1% tension stress, direct band gap of mono-layer MoS2 was turned to an indirect band gap [37]. The valley degeneracy in mono-layer MoS2 could be observed under an external electric field [34]. The manipulation of electrical and thermal transport in 2D-TMDs will be discussed in Section 3 detailedly. Section 4 is devoted to the discussion of the recent advances in the study of electrical, thermal transport, TE properties of some typical 2D-TMDs, and TE-related applications.
Manipulation of Electrical and Thermal Transport in 2D-Transition Metal Dichalcogenides
The manipulation of electrical and thermal transport in 2D-TMDs is crucial for the design of high-performance TE devices. It has been reported that the electrical and thermal conductivity of low dimensional materials could be modulated by material thickness [34,35,37,41–56], defect engineering [57–64], chemical functionalization [59,65–70], and strain engineering [71–94]. In the past decade, the TE performance of MoS2 has been theoretically predicted and the samples have been experimentally fabricated. In this section, by mainly considering MoS2 as a reference compound, a brief introduction about the above impact factors will be simply discussed.
Thickness Effect
The energetically degenerated valence/conduction valleys in monolayer TMDs leads to significant thickness effect on electrical properties and power factor in 2D materials (Hong et al. [34]). The calculated electrical properties and power factor in mono- and multi-layer MoS2 are shown in Figures 2A–F. For both p-type and n-type MoS2, the Seebeck coefficients are almost independent of layer number (Figures 2A,D), while the electrical conductivity (Figures 2B,E) and power factor PF/τ (Figures 2C,F) are dependent of layer number. It indicates that the Seebeck coefficient and electrical conductivity can be separately modulated by varying thickness, thus tuning valley degeneracy. The thickness dependence of valley degeneracy can be understood from the hybridization strength of different orbitals. The valence/conduction valleys at the K point are dominated by the localized Mo 4d orbital, thus the corresponding energy levels are not sensitive to the layer thickness. However, S 3p and Mo 4d orbitals are strongly hybridized, thus valence/conduction valleys at Γ and Σmin points can be varied. Hence, the energy levels of valence/conduction valleys at Γ and Σmin points are sensitive to thickness [43]. The so-called band convergence has also been proved to enhance the power factor of bulk TE materials. Similar effect of thickness on the power factors can be also observed in multi-layer MoSe2, WS2, and WSe2 [37,41,42]. A general principle for these four TMDs was that the maximum ZT coincided with the greatest near-degeneracy within kBT (kB was the Boltzmann constant, and T was temperature) of the band edge, and the optimal thickness for maximum ZT was generally not the monolayer [43].
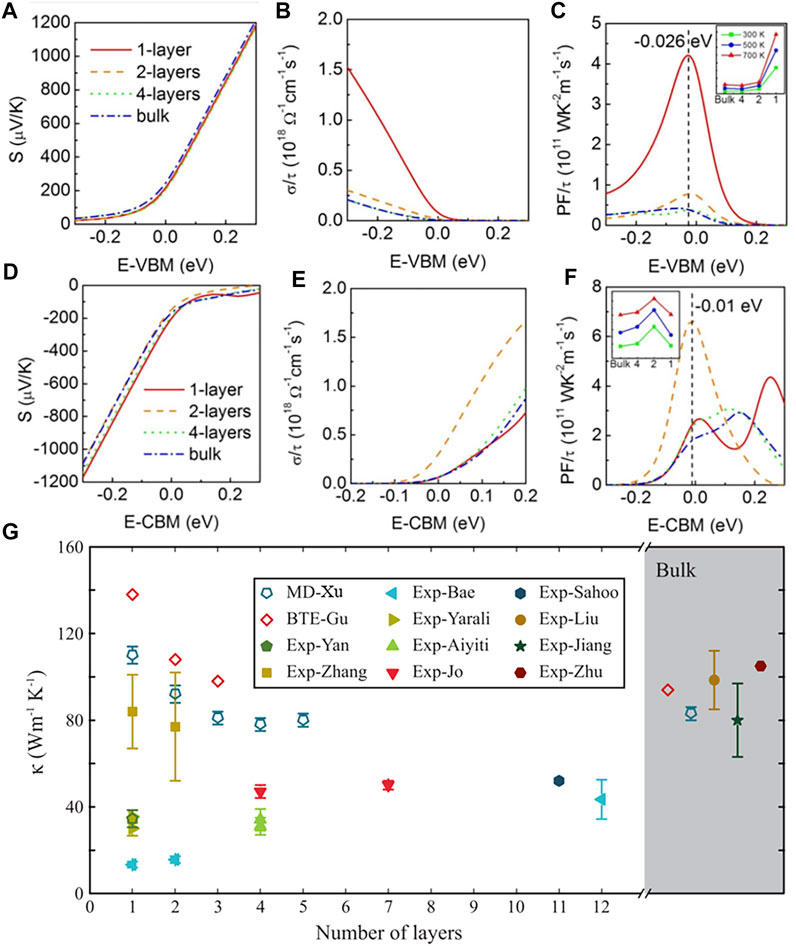
FIGURE 2. In-plane Seebeck coefficient (S), electrical conductivity (σ/τ) and power factor (PF/τ) of MoS2 at 300 K are plotted with variation of their thickness and chemical potential. (A–C) show the properties of p-type MoS2 and (D–F) show the properties of n-type MoS2. The chemical potential 0.0 refers to the edges of valence and conduction band for p- and n-types, respectively. The insets of (C,F) show the maximum power factor change with the temperature. Reprinted with permission from Ref. [34], Copyright 2016, American Physical Society. (G) Thermal conductivity as a function of the number of layers for MoS2 at 300 K and zero pressure. Sources of reference data: Gu [45]; Aiyiti [47]; Bae [48]; Liu [49]; Zhu [50]; Jiang [51]; Sahoo [52]; Jo [53]; Yan [54]; Zhang [55]; Yarali [56]. Reprinted with permission from Ref. [46], Copyright 2019, American Physical Society.
Apart from the electrical properties, the thickness effects on thermal conductivity have also been studied by different groups theoretically and experimentally [44–56]. However, the physical mechanisms are complex and the results are inconsistent. According to the non-equilibrium molecular dynamics (NEMD) method, the thermal conductivity of MoS2 was insensitive to layer number. The finite energy gap of MoS2 in the phonon spectrum made the phonon-phonon scattering channel almost unchanged with increased layer number [44]. Gu et al. [45] (Boltzmann transport equation method) and Xu et al. [46] (NEMD) reported a reduced thermal conductivity with increasing layer number from monolayer to trilayer. It could be attributed to the change of phonon dispersion and the thickness-induced anharmonicity, which was associated with the breakdown of a mirror symmetry in monolayer MoS2. These conclusions qualitatively agreed with the experimental results performed on suspended single crystal MoS2 [47], while it contradicted with those obtained from MoS2 grown with chemical vapor deposition [48]. Such conflicts can be attributed to the difference in MoS2 quality, the presence of dangling bonds at MoS2/substrate interface, and other experimental variations. The relevant results are presented and visualized in Figure 2G.
Defect Engineering
Defects in TMDs can be categorized into intrinsic defects such as vacancies and interstitials, substitution dopants, and alloy atoms, which are often applied to modify the charge carrier concentration [57,63,64]. Basically, point defect such as vacancies inevitably resides in samples during the preparation of 2D-TMDs. It is well known that defective states formed within band gap were able to affect electronic mobilities [58,59] and excitons [40,60]. In the presence of S vacancies (VS), donors (acceptors) induce carrier accumulation (depletion) around the VS center, which in turn strongly affect the screening and binding of excitons within MoS2. Consequently, the HOMO and LUMO states for donor and acceptor are shifted downwards. Thanks to that, carrier density, polarity and Seebeck coefficient can be modulated by properly introducing dopants and VS (Cai et al. [59]). Other types of defects, such as Mo vacancies, have not been studied in detail. Recently, Sharma et al. [18] studied four types of atomic defects, including VS (one S vacancy), VMo (one Mo vacancy), VMoS (one Mo and one S vacancy), and VMoS2 (one Mo and two S vacancies). The effects of various atomic defects on structure, electronic, and TE properties of MoS2 were explored by using density functional theory (DFT). It found that the electronic structure of mono-layer MoS2 showed tunable band gap with the atomic defects. Moreover, the room temperature ZT of MoS2 with VS and VMoS2 defects was as high as 6.24 and 1.30, respectively.
Vacancies can also offer an efficient way to tune the thermal conductivity and TE properties of materials, since the phonon scattering depends on the density of defects [61–63]. In experiment, Aiyiti et al. [47] used oxygen plasma treatment to controllably introduce point defects to suspended few-layer MoS2, and then studied their effects on thermal conductivity. Experiments show that, as expected, with the increase of defect concentration, the thermal conductivity decreased. Apart from vacancy defects, isotopic doping also had a considerable effect on thermal transport. For example, in MoS2, Mo isotopes had a larger impact on thermal conductivity than that of S isotopes. The reason was that S isotopes influenced high-frequency phonon modes, while Mo (heavier atomic mass) isotopes influenced low-frequency range. In thermal transport, low-frequency phonons played a more significant role [64].
Chemical Functionalization
In general, chemical functionalization for 2D materials is realized by two strategies: (1) substitutional doping, which replaces the structure composition with other elemental atoms; and (2) charge transfer doping, which exchanges charge with physical adsorbents, acids, and specific solutions. Both strategies can modify the TE performance of materials by modulating the local DOS, carrier concentration, and carrier mobility [59,65–70]. For substitutional doping, Jenisha et al. [67] recently reported the TE properties in Ni-doped MoS2. At a 7.5% Ni-doping concentration, interlayer distance was reduced and a lower thermal conductivity was confirmed. However, because of the formation of NiS phase, the electrical conductivity in Ni-doped MoS2 was increased, which resulted in a decrease in ZT value.
For 2D materials, charge transfer doping is more efficient than substitutional doping. To date, charge transfer doping for 2D materials is realized through various approaches by introducing different groups. Cai et al. [59] investigated the effect of chemical molecular doping on the TE properties of monolayer MoS2. Tetrathiafulvalene (TTF) and dimethyl-p-phenylenediamine molecules (DMPD) are effective donors (Figures 3A,B), whereas tetracyanoethylene (TCNE) and tetracyanoquinodimethane (TCNQ) are effective acceptors (Figures 3C,D). The molecular doping is found to be able to change the energetic positions of defective states in the band gap. Although the maximal Seebeck coefficient is almost insensitive to molecular doping, it can be adjusted by the molecular doping induced chemical potential variation. Thus, it is possible to switch the carrier type via doping different organic molecules. Guo et al. [68] reported in-situ grown Au-decorated MoS2-assembled heterojunction (Figure 3E), as well as the TE performance of this material. The Seebeck coefficient and electrical conductivity were increased simultaneously. The first reason was the occurrence of p-type doping of the MoS2 2H phase. The second reason was the injection energy filtering of dopant-originated carriers around the local band bending at the interface. In addition, doping also can reduce the rate of thermally activated hopping, thus lowering the thermal conductivity. Kong et al. [69] prepared oxygen doped MoS2 by heating the sample in air. A low thermal conductivity value of 3.1 Wm−1·K−1 was obtained at 327K. Abinaya et al. [70] presented an ultralow thermal conductivity of 0.248 Wm−1·K−1 in MoS2/polyaniline nanocomposites, with variable range hopping property. Nevertheless, the available experimental data on TE transport properties of doped MoS2 have been quite scarce. Most experiments have focused on the electrical transport properties and failed to measure the thermal properties. Some merely worked on the thermal conductivity. Based on those incomplete experimental data, it remains a big challenge to experimentally find a proper dopant and evaluate the TE efficiency after doping in a wide range. Thus, the ZT cannot be optimized.
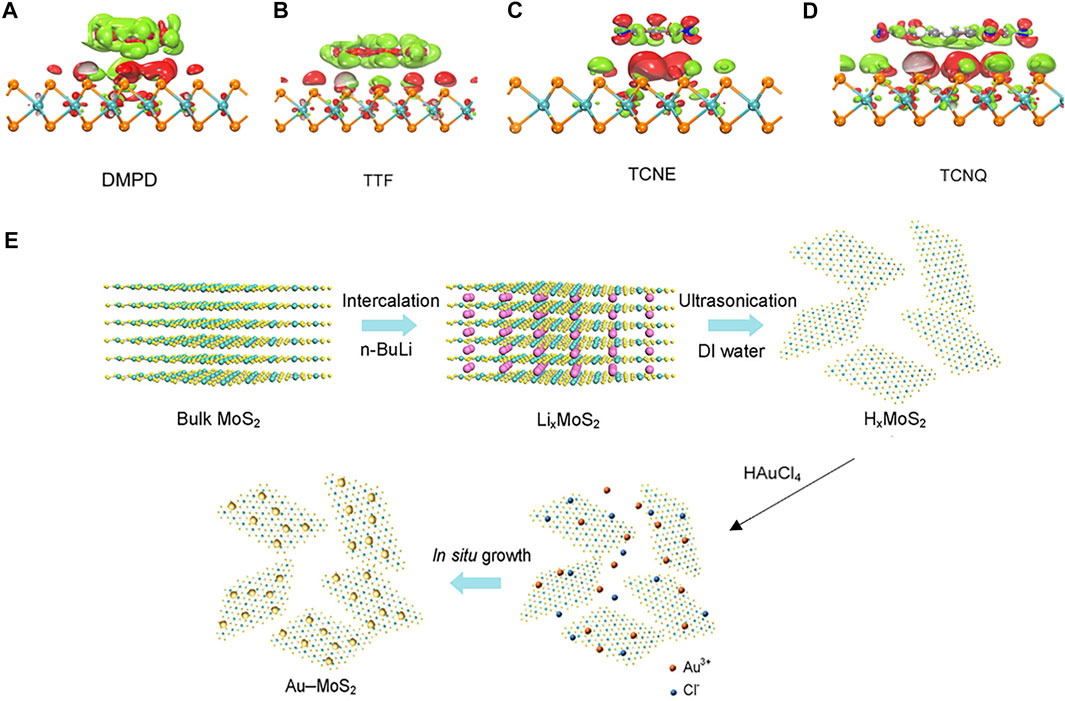
FIGURE 3. The side views of charge transfer between the molecular acceptors/donors and MoS2. (A,B) are molecular donors DMPD and TTF, respectively. (C,D) are molecular acceptors TCNE and TCNQ, respectively. The isosurface at value of 0.002 Å-3 of differential charge density is plotted. The green (red) denotes depletion (accumulation) of electrons. Reprinted with permission from Ref. [59], Copyright 2016, American Chemical Society. (E) The Au-MoS2 hybrid nanomaterials are formed by growing Au nanoparticles on 2D MoS2. Reprinted with permission from Ref. [68], Copyright 2018, American Chemical Society.
Strain Engineering
Strain engineering is a common method that has been widely applied to tune the physical properties of 2D-TMDs (Figure 4). In experiment, in-plane strain can be applied by several approaches, such as bending the TMDs prepared on a flexible substrate, introducing winkles and puddles to 2D-TMDs, indending the layer with AFM, substrate thermal expansion, and so on [71–81]. The out-of-plane strain could be applied using diamond anvil cells set up [72,73]. One of the most important phenomena is direct-to-indirect band gap transition induced by tensile strain [82–88] (in the case of WSe2, tensile strain induces an indirect-to-direct band gap transition [87,88]). In the meantime, strain also modulated the band gap, effective mass, and valley degeneracy at conduction/valance band edges of TMDs, leading to strain-tunable electrical conductivity and correlated TE properties [89,90]. For n-type WS2, the relaxation time scaled power factor (S2σ/τ) was increased by the application of compressive strain, whereas for p-type WS2, it was increased with the application of tensile strain due to valley degeneracy [91].
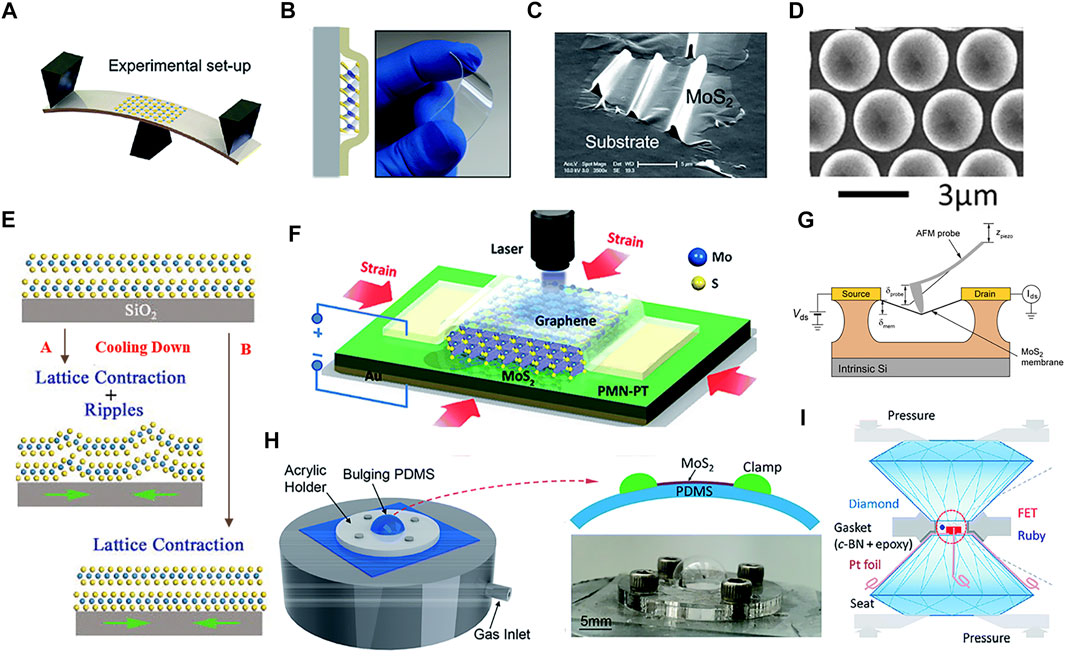
FIGURE 4. The schematic diagram of approaches for introducing external strain. (A) The three-point bending apparatus. Reprinted with permission from Ref. [74], Copyright 2013, American Physical Society. (B) Large strain magnitude can be introduced in polymer encapsulated mono-layer WSe2 by bending apparatus. Reprinted with permission from Ref. [75], Copyright 2018, American Chemical Society. (C) Wrinkled mono-layer MoS2 fabricated by prestretching an elastomeric substrate. Reprinted with permission from Ref. [76], Copyright 2013, American Chemical Society. (D) The top-view scanning electron microscopy (SEM) image of the patterned sapphire substrate (PSS). Reprinted with permission from Ref. [77], Copyright 2019, American Chemical Society. (E) Schematic diagrams showing the mismatch of thermal expansion coefficient on the formation of strain in WS2 flakes. During cooling process, the SiO2 substrate contracts and exerts compression stress on the WS2 flakes. Reprinted with permission from Ref. [78], Copyright 2016, American Institute of Physics. (F) Schematic diagram of optical measurements on strained trilayer MoS2 which is sandwiched between a piezoelectric substrate and a graphene electrode. Reprinted with permission from Ref. [79], Copyright 2013, American Chemical Society. (G) SEM image of typical MoS2 devices with suspended channels and contact electrodes. Reprinted with permission from Ref. [81], Copyright 2015, American Chemical Society. (H) Experimental setup for blown-bubble bulge measurement, high strain can be achieved in suspended MoS2 films by slowly diffusing N2 gas through the PDMS substrate to pressurize the cavity. Reprinted with permission from Ref. [80], Copyright 2017, American Chemical Society. (I) Schematic of the electrical conductance measurements of few-layer MoS2 in a diamond anvil cells. Reprinted with permission from Ref. [73], Copyright 2017, American Chemical Society.
Apart from electrical properties, the effect of strain on phonon transport properties also assists in tuning the thermal conductivity of 2D-TMDs. In general, while the tensile strain becomes large, the appearance of phonon softening lowered the phonon group velocity, leading to a reduced thermal conductivity of 2D planer nanostructures [92]. The thermal conductivity of MoS2 was monotonically decreased with the increase of tensile strain (Jiang et al. [93]). Additionally, the analysis of lattice dynamics and phonon spectroscopy revealed that the thermal conductivity was dramatically increased with pressure in the out-of-plane direction. It was mainly due to the interlayer force strengthening and the group velocity enhancing of longitudinal acoustic phonons. When the pressure was over 15 Gpa, the thermal conductivity tended to be saturated. This was due to the combined effect of increased group velocity and reduced phonon lifetime. The phenomena were observed in most vdWs heterostructures. A 9% compressive strain can cause a 7-fold increase of the thermal conductivity in the out-of-plane direction for the multilayer MoS2 (Meng et al. [94]).
Typical 2D-Transition Metal Dichalcogenides TE Materials and Applications
TMDs consist of a hexagonal structure, in which a metal atom (M) layer is sandwiched between two chalcogen (X) layers, denoted by the formula MX2 (M = transition metal; X = S, Se, Te) (Figure 1B). The anisotropic layered structure of material facilitates a low thermal conductivity in the out-of-plane direction. Furthermore, both the Seebeck coefficient and carrier mobility are high in 2D-TMDs, because of the large effective mass and valley degeneracy, as well as the confinement of carriers in 2D planes. In this section, some typical 2D-TMDs TE materials and their applications based on 2D-TMDs will be introduced.
MX2 (M = Mo, W, Ti; X = S, Se) Materials
The most common 2D-TMDs (such as MoS2, MoSe2, WS2, and WSe2) exhibit very similar electronic properties. The band structures of the 2D-TMDs show a similar transition from the direct band gap to the indirect band gap when the atomic layer increased from a mono-layer to a bilayer [95,96]. The theoretically predicted ZT values of MoS2, MoSe2, WS2, and WSe2 along the in-plane direction are displayed in Figures 5A–D. Few-layer TMDs (bilayer or trilayer) show larger increase in ZT values compared to that of bulk materials [42]. Many theoretical works on the TE properties of 2D-TMDs have also been reported. For example, Chen et al. [97] studied the TE properties of mono-layer MoS2, MoSe2, WS2, and WSe2 by the first principles calculations. The ZT value of small nanotubes was lower than that of monolayers due to the lower Seebeck coefficient. It was predicted that the highest ZT of mono-layer WSe2 was 0.91 at room temperature, which was much higher than that of zigzag WSe2 nanotube. Kumar et al. [98] explored the TE properties of bulk and monolayer MoSe2 and WSe2 by using the first principles calculations and the semiclassical Boltzmann transport theory. It proved that the electrical conductivity, the Seebeck coefficient, and the thermal conductivity of the mono-layer materials were extremely different from those of bulk materials. It indicated that much effort could be done to optimize the TE properties of unit material. Jia et al. [99] predicted the TE performance of pure MoS2, MoS2/MoSe2 lateral heterostructures (LHS), and MoS2/MoSe2 vdWs by using DFT calculations and nonequilibrium Green function (NEGF) method. Compared to pure MoS2, the ZT value of MoS2/MoSe2 LHS has been improved by the introduction of lateral interface. Moreover, the room-temperature ZT value of MoS2/MoSe2 vdWs stacking reached 3.5, which was ∼3 and ∼6 times higher than MoS2/MoSe2 LHS and pure MoS2, respectively. The results suggested that MoS2/MoSe2 vdWs can be used to construct efficient TE devices.
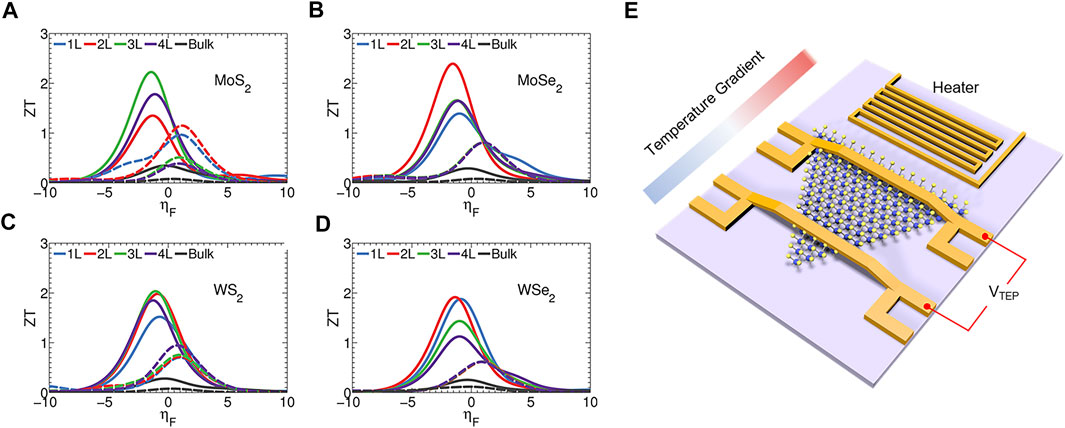
FIGURE 5. ZT at 300 K for (A) MoS2, (B) MoSe2, (C) WS2, and (D) WSe2 with bulk (black), 1 L (blue), 2 L (red), 3 L (green), and 4 L (purple) structures. The n-type ZT is plotted with a solid line and p-type ZT is plotted with a dashed line, as a function of the reduced Fermi energy, ηF. Reprinted with permission from Ref. [42], Copyright 2014, American Institute of Physics. (E) The typical structure of the thermoelectric micro-device platform.
Apart from these theoretical studies, the experimental results of 2D-TMDs have also been implemented. The typical structure of the thermoelectric micro-nano devices is shown in Figure 5E, which is used to measure the TE performance of a mono-layer or multi-layer 2D material in the in-plane direction. The temperature gradient through the nanosample one is generated by building one or two heaters at both sides. The metal electrodes are deposited onto the sample via an electron beam lithography. The Au/Cr metal contacted with the sample serves as an electrode as well as a thermometer. The TE properties of an exfoliated MoS2 fake with different thicknesses were studied by Hippalgaonkar [35]. Because of the high electron concentration n = 1.06 × 1013 cm−2 at a high external electric field, the bilayer MoS2 exhibited a high power factor of 8.5 mWmK−2. Although many theoretical researchers predicted that the 2D-TMDs should exhibit an outstanding TE performance, these results have not been proven by experimental data.
TiS2 is another typical and widely studied 2D-TMD material. In 2001, it was reported to provide a large power factor of 37.1 mW K−2·cm−1 and a low resistivity of 1.7 mΩ cm. In addition, the Seebeck coefficient was -251 mV K−1 at 300 K in the in-plane direction [100]. These values of TiS2 were comparable to that of the best TE material, i.e., Bi2Te3 alloy. In spite of the large power factor, TiS2 exhibited a relatively large thermal conductivity of 68 mW K−1·cm−1, which comes from the reducible lattice thermal conductivity. Thus, the TE performance of TiS2 can be further improved by decreasing the lattice thermal conductivity. The main strategies to maximize the TE performance of TiS2 are nonstoichiometry, intercalation, substitution, and the block layer concept [101]. Instead of stoichiometric TiS2, it was prone to obtain Ti-rich Ti1+xS2, where excessive Ti atoms intercalated between the vdWs gap [101,102]. According to a study of the effect of Ti/S stoichiometry on the TE properties of Ti1+xS2, the S was decreased with increasing x in the system (Beaumale et al. [102]). A maximum power factor of 1.7 mW m−1·K−2 in x = 0.015 was obtained at 300 K by manipulating Ti/S stoichiometry. For optimizing the TE performance of TiS2, various heavy atoms (Au, Cu) were intercalated in the vdWs gap between the S-Ti-S layers [103,104]. The methods to minimize lattice thermal conductivity have been performed by substituting Ti atom with Ta and Nb atoms in solid solution alloy [105,106]. Recently, Zhou et al. [107] employed a novel chemical welding method, in which chemically exfoliated TiS2 nanosheets bridged with multivalent cationic metal Al3+ to crosslink the nearby sheets, thus achieving a high TE performance. It is worth mentioning that all the strategies which have been employed to optimize the TE performance of TiS2 can also be applicable to TiSe2.
Misfit Layered Materials
Recently, a series of synthetic misfit compounds have been intensively studied. These misfit compounds involve two sub-lattices with different lattice constants, which hold together in an alternating fashion with weak vdWs forces. The structural summary of misfit layer compounds is shown in Figure 6A. The empirical formula can be denoted as (MX)1+x (TX2)m, where M = Pb, Bi, Sn, Sb; T = Cr, Ta, Ti, V, Nb; X = Se, S; m = l-3 and 0.08 < x < 0.28 [108–111]. The TX2 layer in the misfit compounds allows high mobility of charge carriers, and the intercalated MS layer can suppress the transport of phonons by the interaction between the TX2 layers. The misfit compounds show a phonon-glass like behavior due to the lattice mismatch between the MX and TX2 layers. These attractive properties make (MX)1+x (TX2)m an ideal class of compounds for TE energy conversion applications [112–115]. The powder of misfit compounds is often prepared by using a solid-liquid-vapor reaction method. However, although many known misfit compounds are in the sulfide space, the fabrication of kinetically controlled sulfide superlattices is still challenging due to the experimental challenges during sulfur deposition. Very recently, Roberts et al. [116] demonstrated the preparation of nanoscale SnS-TaS2 superlattices with independent sulfur source from designed amorphous precursors, which were deposited by using a radio-frequency (RF) co-sputtering technique. It is the first report of artificial sulfide misfit superlattices with kinetically controlled architectures (Figure 6B).
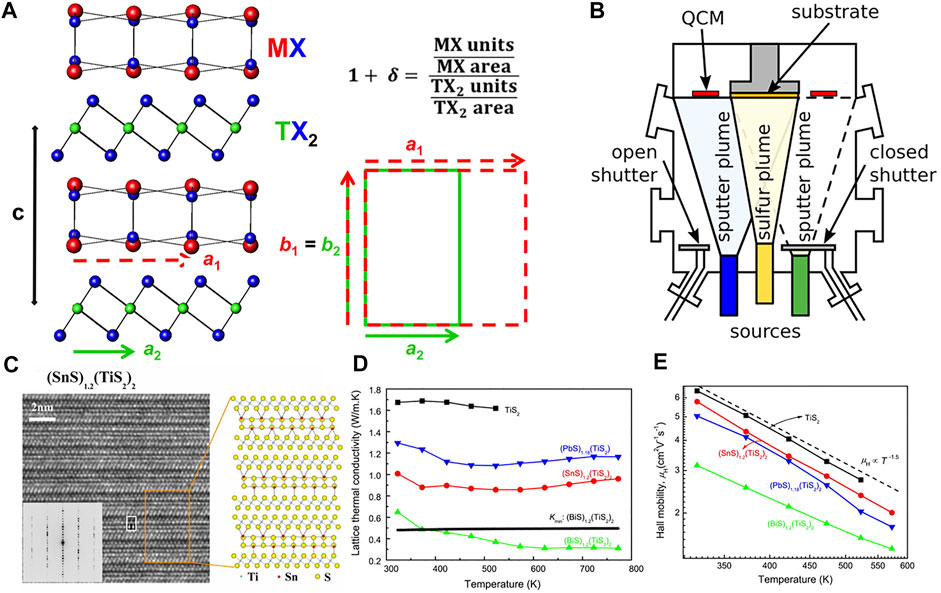
FIGURE 6. (A) Structural summary of misfit layer compounds. General Superlattice structure (left) with in-plane lattice depiction (bottom right) and calculation of misfit parameter based on difference in in-plane packing density (top right). Reprinted with permission from ref. [109], Copyright 2015, Multidisciplinary Digital Publishing Institute. (B) Side view of sputter chamber geometry used to deposit precursor films. Orthogonal shuttered sputter cathodes (green and blue) and a non-shuttered elemental sulfur cell are used as atom sources; rates are monitored by quartz crystal microbalances (QCMs) (red squares). Reprinted with permission from Ref. [116], Copyright 2020, American Chemical Society. (C) Transmission electron microscope image (left), and simulated crystal structure (right) of (SnS)1.2(TiS2)2 along the [100] zone axis. The electron diffraction patterns are also shown in the inset of HRTEM image. (D) In-plane lattice thermal conductivity and (E) Hall mobility of TiS2 (PbS)1.18(TiS2)2 (SnS)1.2(TiS2)2, and (BiS)1.2(TiS2)2 as a function of temperature. Reprinted with permission from Ref. [110], Copyright 2012, American Institute of Physics.
Many researchers have focused on the TE properties of (MX)1+x (TX2)m materials. Since 2004, a very low total thermal conductivity of 0.80 Wm−1 K−1 at 300 K was reported in misfit layered chalcogenide (Yb0.95S)1.24NbS2 along the out-of-plane direction [117]. A even lower thermal conductivity of 0.17 Wm−1·K−1 was reported in the out-of-plane direction of misfit (SnSe)m (TiSe2)n [118]. However, the electronic transport of this material was poor, manifested with low electrical conductivity and Seebeck coefficient. The reason was the sequential positioning of n-type and p-type layers. Wan et al. [110] investigated the (MS)1+x (TiS2)2 TE materials by intercalating one layer of MS (M = Pb, Sn, Bi) into the vdWs gap of the TiS2 layers, which established a natural superlattice structure in a bulk material. Compared to pristine TiS2, these stacking faults significantly reduce the lattice thermal conductivity along the layers, without deteriorating the electron mobility (Figures 6C–E).
To improve the TE performance in (MX)1+x (TX2)m materials, various strategies have been proposed to promote their electrical transport properties [114,119–121], including improving carrier mobility, optimizing carrier concentration, and enhancing DOS distortion. Alternatively, thermal conductivity could be minimized by softening lattice or introducing planar defects (such as translational displacement and stacking faults) [110,115,122]. Among all the misfit compounds (SnS)1.2(TiS2)2 showed the highest ZT of 0.5 at 625 K [123]. However, the above-mentioned highest possible ZT mainly existed in the in-plane direction while the out-of-plane properties have gathered less attention. More importantly, it is unknown to what extent anisotropic tuning can improve TE performance in the misfit-layered chalcogenide, which hinders us from maximizing the ZT value.
Solid-State Thermionic Power Generators Based on 2D-TMDs
TE materials could be applied to realize thermionic coolers and power generators in solid-state (proposed by Mahan et al. [124] and Shakouri et al. [125]). In solid-state thermionic power generators, a semiconductive layer was sandwiched between metallic electrodes as an potential barrier for carrier transport, which lowered the work function from a few eVs to less than 1 eV [126]. The working principle was described as follows: when electrons in the hot side were heated to gain enough velocity, they would overcome the energy barrier (material’s work function) and move along the out-of-plane direction. Eventually, some of these electrons were collected at another side, and then flowed through the outer circuit [125–127]. The current flow was referred to as thermionic current. It should be noted that the efficiency of a thermionic device was almost always smaller than the efficiency of a TE device with similar parameters. It was due to the size effects and Kapitza resistances at the interface [128]. The biggest challenge for a solid-state thermionic power generator is the back flow of the heat from the hot side to the cold side, due to the significant thermal conductance of the semiconductor layer [126]. The overcome solution is to reduce the thermal conductivity to a very low value, so that a large temperature drop can be established in a very small length range.
It is well known that 2D-TMDs exhibit a high anisotropy along the in-plane and out-of-plane directions. Van der Waals heterostructures based on 2D-TMDs are good candidates for the barrier layers in solid-state thermionic power generator. Their low thermal conductivity in the out-of-plane direction is originated from the weak vdWs bonds. In addition, the band gap, which plays a key role of a barrier, can be easily tuned via changing the layer number of the 2D-TMDs. It provides the opportunity to optimize the barrier heights for thermionic transport. Furthermore, Zebarjadi [127] developed an analytical model to investigate the performance of the device and suggested that the ideal thermal conductance values should be as low as 1 mW m−2·K−1. Thus, vdWs heterostructures meet both needs for designing high performance solid-state thermionic power generators. Sadeghi et al. studied the TE performance of mono-layer MoS2 sandwiched between two graphene monolayers. The out-of-plane ZT of graphene/MoS2/graphene heterostructure was 2.8, much higher than that of mono-layer MoS2 (0.3) and mono-layer graphene (negligible) [129]. Liang et al. [130] proposed a solid-state thermionic power generator where vdWs heterostructure sandwiched between two graphene electrodes. The vdWs heterostructure was composed of suitable multi-layer TMDs, such as MoS2, MoSe2, WS2, and WSe2. The device was expected to harvest waste heat at 400 K with efficiency of about 7–8%.
Although several theoretical studies have highlighted the potential of 2D-TMDs in thermionic applications and predict large ZT values [129,131], there is still no successful experimental result to confirm the high TE performance in solid-state thermionic power generators. In fact, it is difficult to measure the thermal conductivity, the Seebeck coefficient, and the electrical conductivity of single-layer and multi-layer 2D materials along the out-of-plane direction. To overcome this technical challenge, Li et al. [118] developed a specific platform. Figure 7 shows the schematic diagram of device fabrication process and an optical photo of completed device. Using the device, the out-of-plane TE properties of SnSe2 and (SnSe)n (TiSe2)n (n = 1, 3, 4, 5) layered film are measured. The out-of-plane Seebeck coefficient was decreased from -31 to -2.5 μV K−1, while the out-of-plane effective thermal conductivity was reduced by a factor of two when n decreased from five to 1. It was due to the enhanced interfacial phonon scattering.
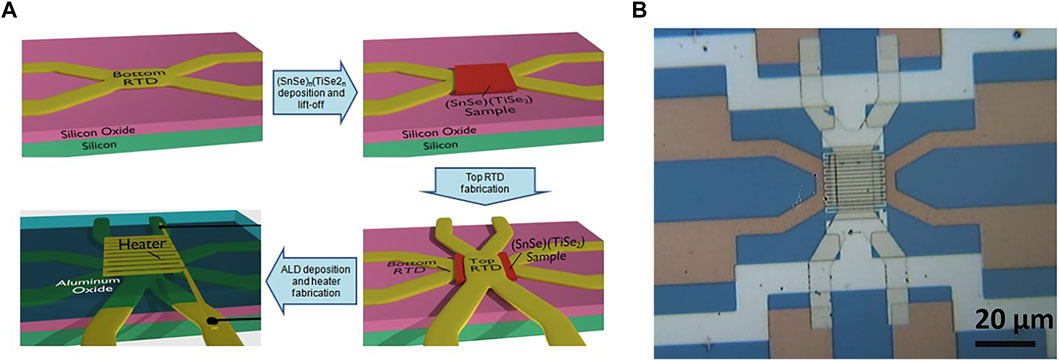
FIGURE 7. (A) Schematic diagrams illustrating the device fabrication process, and (B) Optical microscope image of an established device. Reprinted with permission from Ref. [118], Copyright 2017, American Chemical Society.
Thin-Film Thermoelectric Materials Based on 2D-Transition Metal Dichalcogenides
With the increase in the demand for wearable and portable flexible devices, thin-film TE materials have received wide attention. Besides of high TE performance, there are many other criteria for flexible TE materials, like low cost, light weight, flexibility, stability, scalable, and easy preparation [132]. Inorganic materials have high TE performance, but they are inflexible [133,134]. In contrast, organic TE materials (mainly polymers) have several advantages, such as intrinsically low thermal conductivity, mechanical flexibility, and easy processability over a large scale [135,136]. Besides of the investigations on polymer-based thin-film TE materials, recent researchers have mainly focused on the integration of 2D-TMDs such as MoS2, TiS2, WS2, and NbSe2, which exhibit promising TE properties and facile preparation. Huang et al. [137] studied the TE properties of metallic 1T-phase MoS2 nanosheets. The MoS2 nanosheets were synthesized via a chemically exfoliated process, and the thin films were fabricated via a simple vacuum-assisted filtration process. The power factor of the MoS2 film reached 73.1 μW mK−2, which was much higher than that of pristine graphene or single wall carbon nanotubes. Moreover, the TE performance of MoS2 can be further enhanced by various functionalization [65,68]. Decorating the MoS2 surface with Au nanoparticles allowed composite TE films to achieve a power factor value up to 166.3 μW mK−2 at room temperature [68]. It had great potential for harvesting heat from human body. Flexible n-type TiS2 films have provided a power factor of ∼216.7 μW mK−2 at room temperature. This value was the highest among chemically exfoliated 2D-TMDs based films, and it was comparable to the best flexible n-type TE films. Specifically, the neighboring TiS2 sheets were bridged with multivalent cationic metal Al3+, which highlighted the importance of chemical functionalization [107]. Chemically exfoliated 1T-phase WS2 and NbSe2 nanosheets are used as TE based self-powered wearable electronics (Figures 8A,B), which can constantly produce an output power up to 38 nW at a temperature gradient of 60 K [138]. Near room temperature, the power factors of WS2 (n-type) and NbSe2 (p-type) nanosheets films were evaluated to be 5–7 mW mK−2 and 26–34 mW mK−2, respectively.
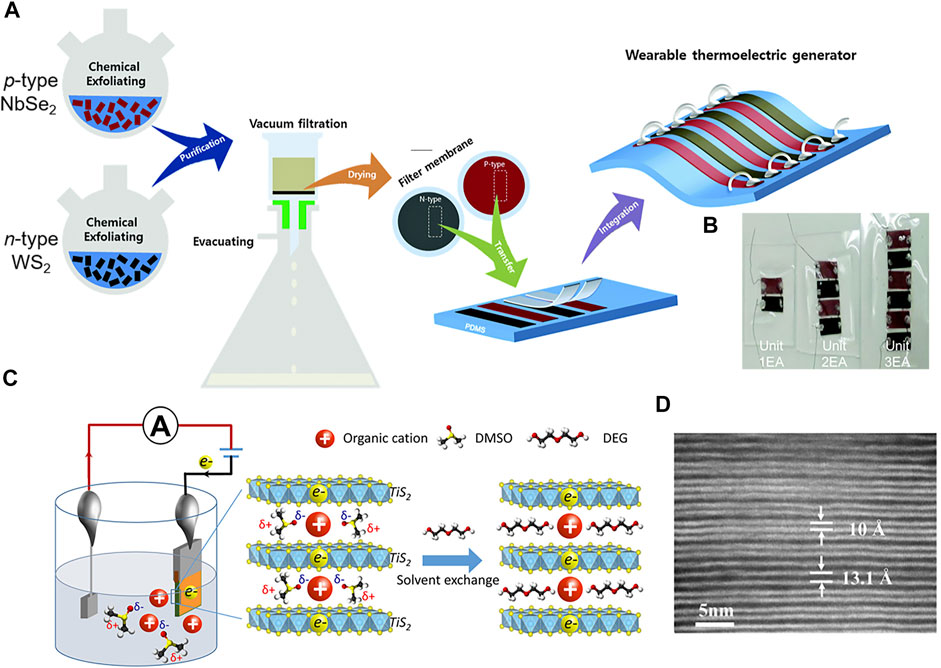
FIGURE 8. (A) Schematic illustration of overall fabrication process of the nearable thermoelectric generator based on chemically exfoliated TMD nanosheets (n-type WS2 and p-type NbSe2). (B) Photographic images of series- and parallel-connected thermoelectric generator units. Reprinted with permission from Ref. [138], Copyright 2015, Royal Society of Chemistry. (C) The facile chemical process used to synthesize TiS2-based hybrid inorganic/organic superlattices, which includes two-step electrochemical intercalation and solvent exchange processes. (D) HAADF-STEM images of one representative composition (TiS2(HA)0.097(PEG1000)0.028), where the bright area represents the inorganic TiS2 layer and the dark area represents the organic molecules. Reprinted with permission from Ref. [145], Copyright 2015, American Chemical Society.
Apart from the purely inorganic materials, organic/2D-TMDs hybrids have emerged as a new class of flexible TE materials [139–145]. A novel electrochemical intercalation and solvent exchange process to synthesize n-type hybrid organic/inorganic materials (Figures 8C,D), where TiS2 is intercalated by organic cations and polar molecules (such as DMSO, Hexylammonium, DEG, PEG1000, H2O) were reported by Wan et al. [141,145]. The organic cations were distributed on two sides of each TiS2 layer. As a result, an electrical conductivity of 790 S cm−1 and a very high power factor of 0.45 mW mK−1 were obtained in the case of the TiS2/[(Hexylammonium)x (H2O)y (DMSO)z] hybrid superlattice [141]. Moreover, the measured in-plane lattice thermal conductivity was about 0.12 W mK−1, which was two orders of magnitude lower than that of single-layer and bulk TiS2. Recently, a solution-printable and flexible n-type TE materials C60/TiS2 hybrid film is demonstrated [144]. A ZT of 0.3 at 400 K has been obtained. Most importantly, the solution of C60/TiS2 hybrid can be used as an ink for printing large-area flexible and spatial TE devices with an outstanding output power of 1.68 W m−2 at a temperature gradient of 20 K, suggesting a facile fabrication process for manufacture.
Photo-Thermoelectric Materials Based on 2D-Transition Metal Dichalcogenides
Solar energy is clean and abundant, which is considered as an ideal energy source. However, 80% of solar radiation is unexploited, which can be converted into thermal energy. Hence, capturing solar energy has become an attractive research hotspot. The concept of solar TE generators was first proposed by Telkes in 1954 [146]. Different from current solar photovoltaic and solar thermal power generation, the photo-thermoelectric generator (Photo-TEG) has been developed for converting photo-energy into electricity based on the photo-thermal effect and the Seebeck effect [147–152]. The Photo-TEG enables generating a photocurrent due to the temperature gradient induced by the absorbed light on an electric voltage (Figure 9A). A fascinating advantage of Photo-TEG was that the device could convert the whole solar spectrum into electricity including infrared (IR) light, while conventional solar photovoltaic device only utilized the ultraviolet-visible light [151]. Photo-TEG is a promising technique for energy harvesting, however, the research in this field is limited so far, compared to photovoltaics and thermoelectrics. The key challenge was to create a significant temperature difference across the device that acted as a driving force of TE generators and improved the conversion efficiency of materials and devices.
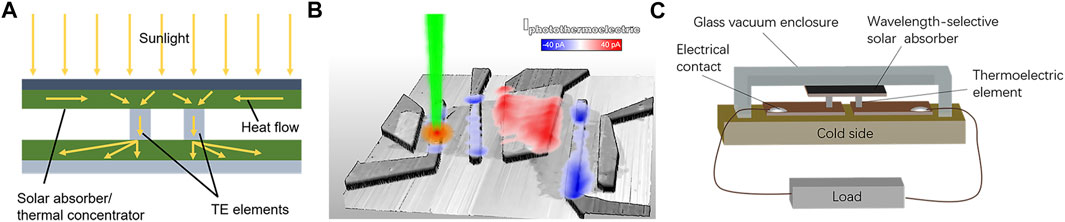
FIGURE 9. (A) Illustration of thermal absorber and cross-section of thermoelectric elements. (B) Illustration of photocurrent generation via a giant photo-thermoelectric effect in MoS2 and not due to optically induced electron-hole pairs. Reprinted with permission from Ref. [152], Copyright 2013, American Chemical Society. (C) Illustration of a Photo-TEG device made of a pair of p- and n-type thermoelectric elements, a flat-panel selective absorber, and two bottom electrodes and radiation shields. The device is surrounded by a glass vacuum enclosure.
Atomic thin semiconductors, such as 2D-TMDs, have excellent electronic and optoelectronic applications attributed to the large band gap. MoS2 was an excellent photothermal material with higher absorbance in the IR region than graphene oxide and gold nanorods [153]. Upon the absorption of light (even at energies below the bandgap of MoS2), a temperature gradient is produced in a mono-layer MoS2 device, which generates a thermovoltage (Seebeck) to drive the photocurrent through the circuit [152] (Figure 9B). Very recently, Li et al. [154] reported a stable Photo-TEG by integrating a new 2D Cu2S-phenol superlattice (CP-SL) and carbon nanotubes composites. It had a maximum output power of 534.7 nW at a temperature gradient of 39.7 K. The maximum open-circuit voltage and short-circuit current measured in the experiments are 6.86 mV and 0.31 mA, respectively.
The conventional Photo-TEG device (Figure 9C) contains many bulky components, such as a vacuum enclosure, condenser lens, and heat sink, which increase the weight and size of the device [154,155]. The huge size of the device limits its application environment. However, 2D materials based flexible Photo-TEGs can be easily mounted on various surfaces exposed to sunlight, such as clothes, windows, and the outer walls of a building [156–158]. A flexible Photo-TEG based on MoS2/polyurethane photothermal film and Te/PEDOT thermoelectric layer has been demonstrated for harvesting environmental IR light [158]. When the infrared lamp is turned on and lasting for 50 s, the open-circuit voltage of Photo-TEG is rapidly increased and plateaued at 1.2 mV. The device is expected to be useful in applications such as self-powered wearable electronic devices.
Conclusion and Outlooks
The fundamental research and recent developments on TE of 2D-TMDs have been described in this article. Key achievements to improve TE performance via various approaches such as modulation of electron and phonon transport properties, band structure tuning, and chemical functionalization have been introduced. State-of-the-art theoretical and experimental data have been presented to clarify the effects of various factors on TE properties of 2D-TMDs. The relevant theoretical and experimental results of TE properties of typical 2D-TMDs such as MX2 (M = Mo,W, Ti; X = S, Se) materials and misfit layer materials are highlighted. In addition, the solid-state thermionic power generators, thin-film TE materials, and photo-thermoelectric application based on 2D-TMDs that possesses great potential for self-powered flexible and wearable devices applications are also reviewed. However, there remain some challenges: (1) Current knowledge on the interfacial electron and phonon transport effects on the TE performance is still limited. (2) Although the calculation predictions show that the 2D-TMDs should exhibit outstanding TE performance, it still lacks of the experimental confirmation. (3) The TE performance of 2D-TMDs is still much lower than that of conventional bulk TE materials, while the thermal conductivity is much higher. The measured Seebeck coefficient is much lower than the calculation suggested data. (4) A robust and reliable fabrication and characterization platform for 2D-TMDs based TE materials is underdeveloped. (5) The facile and scalable production of high-quality 2D-TMDs based materials is still challenging. To finally achieve good TE performances in 2D-TMDs and realize practical TE based energy harvesting system, a deep understanding of the physics behind TE is needed, which requires further and continuous theoretical and experimental studies in the future.
Author Contributions
WZ, HG, XJ, YC, HL, and SL performed literature retrieval, conceived, prepared, and wrote the manuscript. All authors contributed to the article and approved the submitted version.
Funding
The work gratefully acknowledges financial support from the National Natural Science Foundation of China (No. 22175060, 21,975,067) and Natural Science Foundation of Hunan Province of China (2021JJ10014, 2021JJ30092).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Shakouri A. Recent Developments in Semiconductor Thermoelectric Physics and Materials. Annu Rev Mater Res (2011) 41:399–431. doi:10.1146/annurev-matsci-062910-100445
2. Hicks LD, Dresselhaus MS. Thermoelectric Figure of merit of a One-Dimensional Conductor. Phys Rev B (1993) 47:16631–4. doi:10.1103/physrevb.47.16631
3. Venkatasubramanian R, Siivola E, Colpitts T, O'Quinn B. Thin-Film Thermoelectric Devices with High Room-Temperature Figures of merit. Nature (2001) 413:597–602. doi:10.1038/35098012
4. Poudel B, Hao Q, Ma Y, Lan Y, Minnich A, Yu B, et al. High-thermoelectric Performance of Nanostructured Bismuth Antimony telluride Bulk Alloys. Science (2008) 320:634–8. doi:10.1126/science.1156446
5. Pan Y, Wei T-R, Cao Q, Li J-F. Mechanically Enhanced P- and N-type Bi2Te3-Based Thermoelectric Materials Reprocessed from Commercial Ingots by ball Milling and Spark Plasma Sintering. Mater Sci Eng B (2015) 197:75–81. doi:10.1016/j.mseb.2015.03.011
6. Hong M, Chasapis TC, Chen Z-G, Yang L, Kanatzidis MG, Snyder GJ, et al. n-Type Bi2Te3-xSex Nanoplates with Enhanced Thermoelectric Efficiency Driven by Wide-Frequency Phonon Scatterings and Synergistic Carrier Scatterings. ACS Nano (2016) 10:4719–27. doi:10.1021/acsnano.6b01156
8. Li L, Yu Y, Ye GJ, Ge Q, Ou X, Wu H, et al. Black Phosphorus Field-Effect Transistors. Nat Nanotech (2014) 9:372–7. doi:10.1038/nnano.2014.35
9. Lukatskaya MR, Mashtalir O, Ren CE, Dall’Agnese Y, Rozier P, Taberna PL, et al. Cation Intercalation and High Volumetric Capacitance of Two-Dimensional Titanium Carbide. Science (2013) 341:1502–5. doi:10.1126/science.1241488
10. Chhowalla M, Shin HS, Eda G, Li L-J, Loh KP, Zhang H. The Chemistry of Two-Dimensional Layered Transition Metal Dichalcogenide Nanosheets. Nat Chem (2013) 5:263–75. doi:10.1038/nchem.1589
11. Wang QH, Kalantar-Zadeh K, Kis A, Coleman JN, Strano MS. Electronics and Optoelectronics of Two-Dimensional Transition Metal Dichalcogenides. Nat Nanotech (2012) 7:699–712. doi:10.1038/nnano.2012.193
12. Wang H, Li C, Fang P, Zhang Z, Zhang JZ. Synthesis, Properties, and Optoelectronic Applications of Two-Dimensional MoS2 and MoS2-Based Heterostructures. Chem Soc Rev (2018) 47:6101–27. doi:10.1039/C8CS00314A
13. Cho B, Hahm MG, Choi M, Yoon J, Kim AR, Lee Y-J, et al. Charge-transfer-based Gas Sensing Using Atomic-Layer MoS2. Sci Rep (2015) 5:8052. doi:10.1038/srep08052
14. Alidoust N, Bian G, Xu S-Y, Sankar R, Neupane M, Liu C, et al. Observation of Monolayer Valence Band Spin-Orbit Effect and Induced Quantum Well States in MoX2. Nat Commun (2014) 5:4673. doi:10.1038/ncomms5673
15. Singh R, Giri A, Pal M, Thiyagarajan K, Kwak J, Lee J-J, et al. Perovskite Solar Cells with an MoS2 Electron Transport Layer. J Mater Chem A (2019) 7:7151–8. doi:10.1039/C8TA12254G
16. Wu J, Liu Y, Liu Y, Cai Y, Zhao Y, Ng HK, et al. Large Enhancement of Thermoelectric Performance in MoS2/h-BN Heterostructure Due to Vacancy-Induced Band Hybridization. Proc Natl Acad Sci U.S.A (2020) 117:13929–36. doi:10.1073/pnas.2007495117
17. Seol JH, Jo I, Moore AL, Lindsay L, Aitken ZH, Pettes MT, et al. Two-Dimensional Phonon Transport in Supported Graphene. Science (2010) 328:213–6. doi:10.1126/science.1184014
18. Sharma M, Kumar A, Ahluwalia PK. Electron Transport and Thermoelectric Performance of Defected Monolayer MoS2. Physica E: Low-Dimens Syst Nanostruct (2019) 107:117–23. doi:10.1016/j.physe.2018.11.011
19. Tan G, Zhao L-D, Kanatzidis MG. Rationally Designing High-Performance Bulk Thermoelectric Materials. Chem Rev (2016) 116:12123–49. doi:10.1021/acs.chemrev.6b00255
20. Mao J, Liu Z, Ren Z. Size Effect in Thermoelectric Materials. Npj Quant Mater (2016) 1:16028. doi:10.1038/npjquantmats.2016.28
21. Cutler M, Mott NF. Observation of Anderson Localization in an Electron Gas. Phys Rev (1969) 181:1336–40. doi:10.1103/PhysRev.181.1336
22. Heremans JP, Jovovic V, Toberer ES, Saramat A, Kurosaki K, Charoenphakdee A, et al. Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States. Science (2008) 321:554–7. doi:10.1126/science.1159725
23. Koga T, Sun X, Cronin SB, Dresselhaus MS. Carrier Pocket Engineering to Design superior Thermoelectric Materials Using GaAs/AlAs Superlattices. Appl Phys Lett (1998) 73:2950–2. doi:10.1063/1.122640
24. Koga T, Sun X, Cronin SB, Dresselhaus MS. Carrier Pocket Engineering Applied to “Strained” Si/Ge Superlattices to Design Useful Thermoelectric Materials. Appl Phys Lett (1999) 75:2438–40. doi:10.1063/1.125040
25. Sootsman JR, Chung DY, Kanatzidis MG. New and Old Concepts in Thermoelectric Materials. Angew Chem Int Ed (2009) 48:8616–39. doi:10.1002/anie.200900598
26. Jana MK, Biswas K. Crystalline Solids with Intrinsically Low Lattice Thermal Conductivity for Thermoelectric Energy Conversion. ACS Energ Lett. (2018) 3:1315–24. doi:10.1021/acsenergylett.8b00435
27. Biswas K, He J, Blum ID, Wu C-I, Hogan TP, Seidman DN, et al. High-Performance Bulk Thermoelectrics with All-Scale Hierarchical Architectures. Nature (2012) 489:414–8. doi:10.1038/nature11439
28. Chen Z, Zhang X, Pei Y. Manipulation of Phonon Transport in Thermoelectrics. Adv Mater (2018) 30:1705617. doi:10.1002/adma.201705617
29. Wood C. Materials for Thermoelectric Energy Conversion. Rep Prog Phys (1988) 51:459–539. doi:10.1088/0034-4885/51/4/001
30. Hicks LD, Harman TC, Sun X, Dresselhaus MS. Experimental Study of the Effect of Quantum-Well Structures on the Thermoelectric Figure of merit. Phys Rev B (1996) 53:R10493–R10496. doi:10.1103/PhysRevB.53.R10493
31. Dresselhaus MS, Chen G, Tang MY, Yang RG, Lee H, Wang DZ, et al. New Directions for Low-Dimensional Thermoelectric Materials. Adv Mater (2007) 19:1043–53. doi:10.1002/adma.200600527
32. Geim AK, Grigorieva IV. Van der Waals heterostructures. Nature (2013) 499:419–25. doi:10.1038/nature12385
33. Liu Y, Weiss NO, Duan X, Cheng H-C, Huang Y, Duan X. Van der Waals Heterostructures and Devices. Nat Rev Mater (2016) 1:16042. doi:10.1038/natrevmats.2016.42
34. Hong J, Lee C, Park J-S, Shim JH. Control of valley Degeneracy inMoS2 by Layer Thickness and Electric Field and its Effect on Thermoelectric Properties. Phys Rev B (2016) 93:35445. doi:10.1103/PhysRevB.93.035445
35. Hippalgaonkar K, Wang Y, Ye Y, Qiu DY, Zhu H, Wang Y, et al. High Thermoelectric Power Factor in Two-Dimensional Crystals of MoS2. Phys Rev B (2017) 95:115407. doi:10.1103/PhysRevB.95.115407
36. Chen Y, Deng W, Chen X, Wu Y, Shi J, Zheng J, et al. Carrier Mobility Tuning of MoS2 by Strain Engineering in CVD Growth Process. Nano Res (2021) 14:2314–20. doi:10.1007/s12274-020-3228-4
37. Shi H, Pan H, Zhang Y-W, Yakobson BI. Quasiparticle Band Structures and Optical Properties of Strained Monolayer MoS2 and WS2. Phys Rev B (2013) 87:155304. doi:10.1103/PhysRevB.87.155304
38. Dobusch L, Furchi MM, Pospischil A, Mueller T, Bertagnolli E, Lugstein A. Electric Field Modulation of Thermovoltage in Single-Layer MoS2. Appl Phys Lett (2014) 105:253103. doi:10.1063/1.4905014
39. Liu B, Chen L, Liu G, Abbas AN, Fathi M, Zhou C. High-Performance Chemical Sensing Using Schottky-Contacted Chemical Vapor Deposition Grown Monolayer MoS2 Transistors. ACS Nano (2014) 8:5304–14. doi:10.1021/nn5015215
40. Nan H, Wang Z, Wang W, Liang Z, Lu Y, Chen Q, et al. Strong Photoluminescence Enhancement of MoS2 through Defect Engineering and Oxygen Bonding. ACS Nano (2014) 8:5738–45. doi:10.1021/nn500532f
41. Huang W, Luo X, Gan CK, Quek SY, Liang G. Theoretical Study of Thermoelectric Properties of Few-Layer MoS2 and WSe2. Phys Chem Chem Phys (2014) 16:10866–74. doi:10.1039/C4CP00487F
42. Wickramaratne D, Zahid F, Lake RK. Electronic and Thermoelectric Properties of Few-Layer Transition Metal Dichalcogenides. J Chem Phys (2014) 140:124710. doi:10.1063/1.4869142
43. Zhang G, Zhang Y-W. Thermoelectric Properties of Two-Dimensional Transition Metal Dichalcogenides. J Mater Chem C (2017) 5:7684–98. doi:10.1039/C7TC01088E
44. Ding Z, Jiang J-W, Pei Q-X, Zhang Y-W. In-plane and Cross-Plane thermal Conductivities of Molybdenum Disulfide. Nanotechnology (2015) 26:065703. doi:10.1088/0957-4484/26/6/065703
45. Gu X, Li B, Yang R. Layer Thickness-dependent Phonon Properties and thermal Conductivity of MoS2. J Appl Phys (2016) 119:085106. doi:10.1063/1.4942827
46. Xu K, Gabourie AJ, Hashemi A, Fan Z, Wei N, Farimani AB, et al. Thermal Transport in MoS2 from Molecular Dynamics Using Different Empirical Potentials. Phys Rev B (2019) 99:54303. doi:10.1103/PhysRevB.99.054303
47. Aiyiti A, Hu S, Wang C, Xi Q, Cheng Z, Xia M, et al. Thermal Conductivity of Suspended Few-Layer MoS2. Nanoscale (2018) 10:2727–34. doi:10.1039/C7NR07522G
48. Bae JJ, Jeong HY, Han GH, Kim J, Kim H, Kim MS, et al. Thickness-dependent In-Plane thermal Conductivity of Suspended MoS2 Grown by Chemical Vapor Deposition. Nanoscale (2017) 9:2541–7. doi:10.1039/C6NR09484H
49. Liu J, Choi G-M, Cahill DG. Measurement of the Anisotropic thermal Conductivity of Molybdenum Disulfide by the Time-Resolved Magneto-Optic Kerr Effect. J Appl Phys (2014) 116:233107. doi:10.1063/1.4904513
50. Zhu G, Liu J, Zheng Q, Zhang R, Li D, Banerjee D, et al. Tuning thermal Conductivity in Molybdenum Disulfide by Electrochemical Intercalation. Nat Commun (2016) 7:13211. doi:10.1038/ncomms13211
51. Jiang P, Qian X, Gu X, Yang R. Probing Anisotropic Thermal Conductivity of Transition Metal Dichalcogenides MX2 (M = Mo, W and X = S, Se) Using Time‐Domain Thermoreflectance. Adv Mater (2017) 29:1701068. doi:10.1002/adma.201701068
52. Sahoo S, Gaur APS, Ahmadi M, Guinel MJ-F, Katiyar RS. Temperature-Dependent Raman Studies and Thermal Conductivity of Few-Layer MoS2. J Phys Chem C (2013) 117:9042–7. doi:10.1021/jp402509w
53. Jo I, Pettes MT, Ou E, Wu W, Shi L. Basal-plane thermal Conductivity of Few-Layer Molybdenum Disulfide. Appl Phys Lett (2014) 104:201902. doi:10.1063/1.4876965
54. Yan R, Simpson JR, Bertolazzi S, Brivio J, Watson M, Wu X, et al. Thermal Conductivity of Monolayer Molybdenum Disulfide Obtained from Temperature-dependent Raman Spectroscopy. ACS Nano (2014) 8:986–93. doi:10.1021/nn405826k
55. Zhang X, Sun D, Li Y, Lee G-H, Cui X, Chenet D, et al. Measurement of Lateral and Interfacial Thermal Conductivity of Single- and Bilayer MoS2 and MoSe2 Using Refined Optothermal Raman Technique. ACS Appl Mater Inter (2015) 7:25923–9. doi:10.1021/acsami.5b08580
56. Yarali M, Wu X, Gupta T, Ghoshal D, Xie L, Zhu Z, et al. Effects of Defects on the Temperature‐Dependent Thermal Conductivity of Suspended Monolayer Molybdenum Disulfide Grown by Chemical Vapor Deposition. Adv Funct Mater (2017) 27:1704357. doi:10.1002/adfm.201704357
57. Zheng Y, Slade TJ, Hu L, Tan XY, Luo Y, Luo Z-Z, et al. Defect Engineering in Thermoelectric Materials: what Have We Learned? Chem Soc Rev (2021) 50:9022–54. doi:10.1039/D1CS00347J
58. Qiu H, Xu T, Wang Z, Ren W, Nan H, Ni Z, et al. Hopping Transport through Defect-Induced Localized States in Molybdenum Disulphide. Nat Commun (2013) 4:2642. doi:10.1038/ncomms3642
59. Cai Y, Zhou H, Zhang G, Zhang Y-W. Modulating Carrier Density and Transport Properties of MoS2 by Organic Molecular Doping and Defect Engineering. Chem Mater (2016) 28:8611–21. doi:10.1021/acs.chemmater.6b03539
60. Cunningham PD, McCreary KM, Hanbicki AT, Currie M, Jonker BT, Hayden LM. Charge Trapping and Exciton Dynamics in Large-Area CVD Grown MoS2. J Phys Chem C (2016) 120:5819–26. doi:10.1021/acs.jpcc.6b00647
61. Ding Z, Pei Q-X, Jiang J-W, Zhang Y-W. Manipulating the Thermal Conductivity of Monolayer MoS2 via Lattice Defect and Strain Engineering. J Phys Chem C (2015) 119:16358–65. doi:10.1021/acs.jpcc.5b03607
62. Yan Z, Yoon M, Kumar S. Influence of Defects and Doping on Phonon Transport Properties of Monolayer MoSe2. 2d Mater (2018) 5:031008. doi:10.1088/2053-1583/aabd54
63. Zhao Y, Zheng M, Wu J, Guan X, Suwardi A, Li Y, et al. Modification of thermal Transport in Few-Layer MoS2 by Atomic-Level Defect Engineering. Nanoscale (2021) 13:11561–7. doi:10.1039/D1NR01832A
64. Wu X, Yang N, Luo T. Unusual Isotope Effect on thermal Transport of Single Layer Molybdenum Disulphide. Appl Phys Lett (2015) 107:191907. doi:10.1063/1.4935603
65. Ding W, Li X, Jiang F, Liu P, Liu P, Zhu S, et al. Defect Modification Engineering on a Laminar MoS2 Film for Optimizing Thermoelectric Properties. J Mater Chem C (2020) 8:1909–14. doi:10.1039/C9TC06012J
66. Aryeetey F, Pourianejad S, Ayanbajo O, Nowlin K, Ignatova T, Aravamudhan S. Bandgap Recovery of Monolayer MoS2 Using Defect Engineering and Chemical Doping. RSC Adv (2021) 11:20893–8. doi:10.1039/D1RA02888J
67. Jenisha MA, Kavirajan S, Harish S, Archana J, Kamalabharathi K, Kumar ES, et al. Interfacial Engineering Effect and Bipolar Conduction of Ni- Doped MoS2 Nanostructures for Thermoelectric Application. J Alloys Compd (2022) 895:162493. doi:10.1016/j.jallcom.2021.162493
68. Guo Y, Dun C, Xu J, Li P, Huang W, Mu J, et al. Wearable Thermoelectric Devices Based on Au-Decorated Two-Dimensional MoS2. ACS Appl Mater Inter (2018) 10:33316–21. doi:10.1021/acsami.8b10720
69. Kong S, Wu T, Yuan M, Huang Z, Meng Q-L, Jiang Q, et al. Dramatically Enhanced Thermoelectric Performance of MoS2 by Introducing MoO2 Nanoinclusions. J Mater Chem A (2017) 5:2004–11. doi:10.1039/C6TA10219K
70. Abinaya R, Archana J, Harish S, Navaneethan M, Muthamizhchelvan C, Ponnusamy S, et al. Interface Driven Energy-Filtering and Phonon Scattering of Polyaniline Incorporated Ultrathin Layered Molybdenum Disulphide Nanosheets for Promising Thermoelectric Performance. J Colloid Interf Sci (2021) 584:295–309. doi:10.1016/j.jcis.2020.09.061
71. Harats MG, Kirchhof JN, Qiao M, Greben K, Bolotin KI. Dynamics and Efficient Conversion of Excitons to Trions in Non-Uniformly Strained Monolayer WS2. Nat Photon (2020) 14:324–9. doi:10.1038/s41566-019-0581-5
72. Yan Y, Ding S, Wu X, Zhu J, Feng D, Yang X, et al. Tuning the Physical Properties of Ultrathin Transition-Metal Dichalcogenides via Strain Engineering. RSC Adv (2020) 10:39455–67. doi:10.1039/D0RA07288E
73. Chen Y, Ke F, Ci P, Ko C, Park T, Saremi S, et al. Pressurizing Field-Effect Transistors of Few-Layer MoS2 in a Diamond Anvil Cell. Nano Lett (2017) 17:194–9. doi:10.1021/acs.nanolett.6b03785
74. Zhu CR, Wang G, Liu BL, Marie X, Qiao XF, Zhang X, et al. Strain Tuning of Optical Emission Energy and Polarization in Monolayer and Bilayer MoS2. Phys Rev B (2013) 88:121301. doi:10.1103/PhysRevB.88.121301
75. Dadgar AM, Scullion D, Kang K, Esposito D, Yang EH, Herman IP, et al. Strain Engineering and Raman Spectroscopy of Monolayer Transition Metal Dichalcogenides. Chem Mater (2018) 30:5148–55. doi:10.1021/acs.chemmater.8b01672
76. Castellanos-Gomez A, Roldán R, Cappelluti E, Buscema M, Guinea F, van der Zant HSJ, et al. Local Strain Engineering in Atomically Thin MoS2. Nano Lett (2013) 13:5361–6. doi:10.1021/nl402875m
77. Chang C-Y, Lin H-T, Lai M-S, Yu C-L, Wu C-R, Chou H-C, et al. Large-Area and Strain-Reduced Two-Dimensional Molybdenum Disulfide Monolayer Emitters on a Three-Dimensional Substrate. ACS Appl Mater Inter (2019) 11:26243–9. doi:10.1021/acsami.9b05082
78. Meng L, Zhang Y, Hu S, Wang X, Liu C, Guo Y, et al. Two Dimensional WS2 Lateral Heterojunctions by Strain Modulation. Appl Phys Lett (2016) 108:263104. doi:10.1063/1.4954991
79. Hui YY, Liu X, Jie W, Chan NY, Hao J, Hsu Y-T, et al. Exceptional Tunability of Band Energy in a Compressively Strained Trilayer MoS2 Sheet. ACS Nano (2013) 7:7126–31. doi:10.1021/nn4024834
80. Yang R, Lee J, Ghosh S, Tang H, Sankaran RM, Zorman CA, et al. Tuning Optical Signatures of Single- and Few-Layer MoS2 by Blown-Bubble Bulge Straining up to Fracture. Nano Lett (2017) 17:4568–75. doi:10.1021/acs.nanolett.7b00730
81. Manzeli S, Allain A, Ghadimi A, Kis A. Piezoresistivity and Strain-Induced Band Gap Tuning in Atomically Thin MoS2. Nano Lett (2015) 15:5330–5. doi:10.1021/acs.nanolett.5b01689
82. Conley HJ, Wang B, Ziegler JI, Haglund RF, Pantelides ST, Bolotin KI. Bandgap Engineering of Strained Monolayer and Bilayer MoS2. Nano Lett (2013) 13:3626–30. doi:10.1021/nl4014748
83. Johari P, Shenoy VB. Tuning the Electronic Properties of Semiconducting Transition Metal Dichalcogenides by Applying Mechanical Strains. ACS Nano (2012) 6:5449–56. doi:10.1021/nn301320r
84. Lu P, Wu X, Guo W, Zeng XC. Strain-dependent Electronic and Magnetic Properties of MoS2 Monolayer, Bilayer, Nanoribbons and Nanotubes. Phys Chem Chem Phys (2012) 14:13035–40. doi:10.1039/C2CP42181J
85. Zhang Q, Cheng Y, Gan L-Y, Schwingenschlögl U. Giant valley Drifts in Uniaxially Strained monolayerMoS2. Phys Rev B (2013) 88:245447. doi:10.1103/PhysRevB.88.245447
86. Kumar A, Ahluwalia PK. Mechanical Strain Dependent Electronic and Dielectric Properties of Two-Dimensional Honeycomb Structures of MoX2 (X=S, Se, Te). Physica B: Condensed Matter (2013) 419:66–75. doi:10.1016/j.physb.2013.03.029
87. Wang Y, Cong C, Yang W, Shang J, Peimyoo N, Chen Y, et al. Strain-induced Direct-Indirect Bandgap Transition and Phonon Modulation in Monolayer WS2. Nano Res (2015) 8:2562–72. doi:10.1007/s12274-015-0762-6
88. Desai SB, Seol G, Kang JS, Fang H, Battaglia C, Kapadia R, et al. Strain-Induced Indirect to Direct Bandgap Transition in Multilayer WSe2. Nano Lett (2014) 14:4592–7. doi:10.1021/nl501638a
89. Bilc DI, Benea D, Pop V, Ghosez P, Verstraete MJ. Electronic and Thermoelectric Properties of Transition-Metal Dichalcogenides. J Phys Chem C (2021) 125:27084–97. doi:10.1021/acs.jpcc.1c07088
90. Zhao X, Tang G, Li Y, Zhang M, Nie Y. Biaxial Strain Improving the Thermoelectric Performance of a Two-Dimensional MoS2/WS2 Heterostructure. ACS Appl Electron Mater (2021) 3:2995–3004. doi:10.1021/acsaelm.1c00187
91. Bera J, Sahu S. Strain Induced valley Degeneracy: a Route to the Enhancement of Thermoelectric Properties of Monolayer WS2. RSC Adv (2019) 9:25216–24. doi:10.1039/C9RA04470A
92. Wei N, Xu L, Wang H-Q, Zheng J-C. Strain Engineering of thermal Conductivity in Graphene Sheets and Nanoribbons: a Demonstration of Magic Flexibility. Nanotechnology (2011) 22:105705. doi:10.1088/0957-4484/22/10/105705
93. Jiang J-W, Park HS, Rabczuk T. Molecular Dynamics Simulations of Single-Layer Molybdenum Disulphide (MoS2): Stillinger-Weber Parametrization, Mechanical Properties, and thermal Conductivity. J Appl Phys (2013) 114:064307. doi:10.1063/1.4818414
94. Meng X, Pandey T, Jeong J, Fu S, Yang J, Chen K, et al. Thermal Conductivity Enhancement in MoS2 under Extreme Strain. Phys Rev Lett (2019) 122:155901. doi:10.1103/PhysRevLett.122.155901
95. Yun WS, Han SW, Hong SC, Kim IG, Lee JD. Thickness and Strain Effects on Electronic Structures of Transition Metal Dichalcogenides: 2H-MX2semiconductors (M=Mo, W;X=S, Se, Te). Phys Rev B (2012) 85:33305. doi:10.1103/PhysRevB.85.033305
96. Splendiani A, Sun L, Zhang Y, Li T, Kim J, Chim C-Y, et al. Emerging Photoluminescence in Monolayer MoS2. Nano Lett (2010) 10:1271–5. doi:10.1021/nl903868w
97. Chen K-X, Wang X-M, Mo D-C, Lyu S-S. Thermoelectric Properties of Transition Metal Dichalcogenides: From Monolayers to Nanotubes. J Phys Chem C (2015) 119:26706–11. doi:10.1021/acs.jpcc.5b06728
98. Kumar S, Schwingenschlögl U. Thermoelectric Response of Bulk and Monolayer MoSe2 and WSe2. Chem Mater (2015) 27:1278–84. doi:10.1021/cm504244b
99. Jia P-Z, Zeng Y-J, Wu D, Pan H, Cao X-H, Zhou W-X, et al. Excellent thermoelectric performance induced by interface effect in MoS2/MoSe2 van der Waals heterostructure. J Phys Condens Matter (2019) 32:055302. doi:10.1088/1361-648x/ab4cab
100. Imai H, Shimakawa Y, Kubo Y. Large Thermoelectric Power Factor in TiS2 crystal with Nearly Stoichiometric Composition. Phys Rev B (2001) 64:241104. doi:10.1103/PhysRevB.64.241104
101. Guilmeau E, Maignan A, Wan C, Koumoto K. On the Effects of Substitution, Intercalation, Non-stoichiometry and Block Layer Concept in TiS2 Based Thermoelectrics. Phys Chem Chem Phys (2015) 17:24541–55. doi:10.1039/C5CP01795E
102. Beaumale M, Barbier T, Bréard Y, Guelou G, Powell AV, Vaqueiro P, et al. Electron Doping and Phonon Scattering in Ti1+ x S2 Thermoelectric Compounds. Acta Mater (2014) 78:86–92. doi:10.1016/j.actamat.2014.06.032
103. Barbier T, Lebedev OI, Roddatis V, Bréard Y, Maignan A, Guilmeau E. Silver Intercalation in SPS Dense TiS2: Staging and Thermoelectric Properties. Dalton Trans (2015) 44:7887–95. doi:10.1039/C5DT00551E
104. Guilmeau E, Bréard Y, Maignan A. Transport and Thermoelectric Properties in Copper Intercalated TiS2 Chalcogenide. Appl Phys Lett (2011) 99:052107. doi:10.1063/1.3621834
105. Beaumale M, Barbier T, Bréard Y, Hébert S, Kinemuchi Y, Guilmeau E. Thermoelectric Properties in the Series Ti1-xTaxS2. J Appl Phys (2014) 115:043704. doi:10.1063/1.4863141
106. Beaumale M, Barbier T, Bréard Y, Raveau B, Kinemuchi Y, Funahashi R, et al. Mass Fluctuation Effect in Ti1−x Nbx S2 Bulk Compounds. J Elec Materi (2014) 43:1590–6. doi:10.1007/s11664-013-2802-x
107. Zhou Y, Wan J, Li Q, Chen L, Zhou J, Wang H, et al. Chemical Welding on Semimetallic TiS2 Nanosheets for High-Performance Flexible N-type Thermoelectric Films. ACS Appl Mater Inter (2017) 9:42430–7. doi:10.1021/acsami.7b15026
108. Meerschaut A. Misfit Layer Compounds. Curr Opin Solid State Mater Sci (1996) 1:250–9. doi:10.1016/S1359-0286(96)80092-1
109. Merrill D, Moore D, Bauers S, Falmbigl M, Johnson D. Misfit Layer Compounds and Ferecrystals: Model Systems for Thermoelectric Nanocomposites. Materials (2015) 8:2000–29. doi:10.3390/ma8042000
110. Wan C, Wang Y, Norimatsu W, Kusunoki M, Koumoto K. Nanoscale Stacking Faults Induced Low thermal Conductivity in Thermoelectric Layered Metal Sulfides. Appl Phys Lett (2012) 100:101913. doi:10.1063/1.3691887
111. Hamann DM, Bauers SR, Miller AM, Ditto J, Moore DB, Johnson DC. Synthesis and Characterization of [(PbSe)1+δ]4[TiSe2]4 Isomers. Inorg Chem (2020) 59:10928–37. doi:10.1021/acs.inorgchem.0c01416
112. Yin C, Guo X, Liu H, Chen Z, Hu Q, Ang R. Strong Anisotropic Thermal Conductivity in Polycrystalline Layers of (Agx Sn1‐ x S)1.2 (TiS2 )2 with Prospects toward Improved Thermoelectric Performance. Annalen Der Physik (2020) 532:1900551. doi:10.1002/andp.201900551
113. Wan C, Wang Y, Wang N, Koumoto K. Low-Thermal-Conductivity (MS)1+x(TiS2)2 (M = Pb, Bi, Sn) Misfit Layer Compounds for Bulk Thermoelectric Materials. Materials (2010) 3:2606–17. doi:10.3390/ma3042606
114. Yin C, Hu Q, Tang M, Liu H, Chen Z, Wang Z, et al. Boosting the Thermoelectric Performance of Misfit-Layered (SnS)1.2(TiS2)2 by a Co- and Cu-Substituted Alloying Effect. J Mater Chem A (2018) 6:22909–14. doi:10.1039/C8TA08426B
115. Gannon RN, Hamann DM, Ditto J, Mitchson G, Bauers SR, Merrill DR, et al. Defects in Layered van der Waals Heterostructures: Implications for Thermoelectrics. ACS Appl Nano Mater (2021) 4:7943–53. doi:10.1021/acsanm.1c01272
116. Roberts DM, Bardgett D, Gorman BP, Perkins JD, Zakutayev A, Bauers SR. Synthesis of Tunable SnS-TaS2 Nanoscale Superlattices. Nano Lett (2020) 20:7059–67. doi:10.1021/acs.nanolett.0c02115
117. Miyazaki Y, Ogawa H, Kajitani T. Preparation and Thermoelectric Properties of Misfit-Layered Sulfide [Yb1.90S2]0.62NbS2. Jpn J Appl Phys (2004) 43:L1202–L1204. doi:10.1143/jjap.43.l1202
118. Li Z, Bauers SR, Poudel N, Hamann D, Wang X, Choi DS, et al. Cross-Plane Seebeck Coefficient Measurement of Misfit Layered Compounds (SnSe)n(TiSe2)n (N = 1,3,4,5). Nano Lett (2017) 17:1978–86. doi:10.1021/acs.nanolett.6b05402
119. Jood P, Ohta M. Effect of Sulfur Substitution on the Thermoelectric Properties of (SnSe)1.16NbSe2: Charge Transfer in a Misfit Layered Structure. RSC Adv (2016) 6:105653–60. doi:10.1039/C6RA20542A
120. Putri YE, Wan C, Zhang R, Mori T, Koumoto K. Thermoelectric Performance Enhancement of (BiS)1.2(TiS2)2 Misfit Layer Sulfide by Chromium Doping. J Adv Ceram (2013) 2:42–8. doi:10.1007/s40145-013-0040-6
121. Yin C, Hu Q, Wang G, Huang T, Zhou X, Zhang X, et al. Intriguing Substitution of Conducting Layer Triggered Enhancement of Thermoelectric Performance in Misfit-Layered (SnS)1.2(TiS2)2. Appl Phys Lett (2017) 110:043507. doi:10.1063/1.4975228
122. Yin C, Liu H, Hu Q, Tang J, Pei Y, Ang R. Texturization-Induced In-Plane High-Performance Thermoelectrics and Inapplicability of the Debye Model to Out-Of-Plane Lattice Thermal Conductivity in Misfit-Layered Chalcogenides. ACS Appl Mater Inter (2019) 11:48079–85. doi:10.1021/acsami.9b17964
123. Ramakrishnan A, Raman S, Chen L-C, Chen K-H. Enhancement in Thermoelectric Properties of TiS2 by Sn Addition. J Elec Materi (2018) 47:3091–8. doi:10.1007/s11664-017-5913-y
124. Mahan GD, Woods LM. Multilayer Thermionic Refrigeration. Phys Rev Lett (1998) 80:4016–9. doi:10.1103/PhysRevLett.80.4016
125. Shakouri A, Bowers JE. Heterostructure Integrated Thermionic Coolers. Appl Phys Lett (1997) 71:1234–6. doi:10.1063/1.119861
126. Wang X, Zebarjadi M, Esfarjani K. First principles calculations of solid-state thermionic transport in layered van der Waals heterostructures. Nanoscale (2016) 8:14695–704. doi:10.1039/C6NR02436J
127. Zebarjadi M. Solid-State Thermionic Power Generators: An Analytical Analysis in the Nonlinear Regime. Phys Rev Appl (2017) 8:14008. doi:10.1103/PhysRevApplied.8.014008
128. Vining CB, Mahan GD. The B Factor in Multilayer Thermionic Refrigeration. J Appl Phys (1999) 86:6852–3. doi:10.1063/1.371762
129. Sadeghi H, Sangtarash S, Lambert CJ. Cross-plane enhanced thermoelectricity and phonon suppression in graphene/MoS2 van der Waals heterostructures. 2d Mater (2016) 4:015012. doi:10.1088/2053-1583/4/1/015012
130. Liang S-J, Liu B, Hu W, Zhou K, Ang LK. Thermionic Energy Conversion Based on Graphene van der Waals Heterostructures. Sci Rep (2017) 7:46211. doi:10.1038/srep46211
131. Wang X, Zebarjadi M, Esfarjani K. High-Performance Solid-State Thermionic Energy Conversion Based on 2D van der Waals Heterostructures: A First-Principles Study. Sci Rep (2018) 8:9303. doi:10.1038/s41598-018-27430-0
132. Jia Y, Jiang Q, Sun H, Liu P, Hu D, Pei Y, et al. Wearable Thermoelectric Materials and Devices for Self‐Powered Electronic Systems. Adv Mater (2021) 33:2102990. doi:10.1002/adma.202102990
133. Gayner C, Kar KK. Recent Advances in Thermoelectric Materials. Prog Mater Sci (2016) 83:330–82. doi:10.1016/j.pmatsci.2016.07.002
134. Ma Z, Wei J, Song P, Zhang M, Yang L, Ma J, et al. Review of Experimental Approaches for Improving zT of Thermoelectric Materials. Mater Sci Semicond Process (2021) 121:105303. doi:10.1016/j.mssp.2020.105303
135. Cappai A, Antidormi A, Bosin A, Narducci D, Colombo L, Melis C. Impact of Synthetic Conditions on the Anisotropic thermal Conductivity of Poly(3,4-Ethylenedioxythiophene) (PEDOT): A Molecular Dynamics Investigation. Phys Rev Mater (2020) 4:35401. doi:10.1103/PhysRevMaterials.4.035401
136. Li X, Liu C, Zhou W, Duan X, Du Y, Xu J, et al. Roles of Polyethylenimine Ethoxylated in Efficiently Tuning the Thermoelectric Performance of Poly(3,4-Ethylenedioxythiophene)-Rich Nanocrystal Films. ACS Appl Mater Inter (2019) 11:8138–47. doi:10.1021/acsami.9b00298
137. Huang H, Cui Y, Li Q, Dun C, Zhou W, Huang W, et al. Metallic 1T Phase MoS2 Nanosheets for High-Performance Thermoelectric Energy Harvesting. Nano Energy (2016) 26:172–9. doi:10.1016/j.nanoen.2016.05.022
138. Oh JY, Lee JH, Han SW, Chae SS, Bae EJ, Kang YH, et al. Chemically Exfoliated Transition Metal Dichalcogenide Nanosheet-Based Wearable Thermoelectric Generators. Energy Environ. Sci. (2016) 9:1696–705. doi:10.1039/C5EE03813H
139. Tian R, Wan C, Wang Y, Wei Q, Ishida T, Yamamoto A, et al. A Solution-Processed TiS2/organic Hybrid Superlattice Film towards Flexible Thermoelectric Devices. J Mater Chem A (2017) 5:564–70. doi:10.1039/C6TA08838D
140. Ding W, Jiang Q, Liu G, Xu L, Liu P, Liu J, et al. Pre-Protection Strategy Performed in Processable Aqueous Dispersions of TiS2 Nanosheets to Fabricate Laminar Films with Improved Electric Properties. 2d Mater (2020) 8:015008. doi:10.1088/2053-1583/abbac0
141. Wan C, Gu X, Dang F, Itoh T, Wang Y, Sasaki H, et al. Flexible N-type Thermoelectric Materials by Organic Intercalation of Layered Transition Metal Dichalcogenide TiS2. Nat Mater (2015) 14:622–7. doi:10.1038/nmat4251
142. Jiang F, Xiong J, Zhou W, Liu C, Wang L, Zhao F, et al. Use of Organic Solvent-Assisted Exfoliated MoS2 for Optimizing the Thermoelectric Performance of Flexible PEDOT:PSS Thin Films. J Mater Chem A (2016) 4:5265–73. doi:10.1039/C6TA00305B
143. Wang T, Liu C, Jiang F, Xu Z, Wang X, Li X, et al. Solution-Processed Two-Dimensional Layered Heterostructure Thin-Film with Optimized Thermoelectric Performance. Phys Chem Chem Phys (2017) 19:17560–7. doi:10.1039/C7CP02011B
144. Wang L, Zhang Z, Geng L, Yuan T, Liu Y, Guo J, et al. Solution-printable fullerene/TiS2 Organic/inorganic Hybrids for High-Performance Flexible N-Type Thermoelectrics. Energ Environ. Sci. (2018) 11:1307–17. doi:10.1039/C7EE03617E
145. Wan C, Kodama Y, Kondo M, Sasai R, Qian X, Gu X, et al. Dielectric Mismatch Mediates Carrier Mobility in Organic-Intercalated Layered TiS2. Nano Lett (2015) 15:6302–8. doi:10.1021/acs.nanolett.5b01013
147. Gabor NM, Song JCW, Ma Q, Nair NL, Taychatanapat T, Watanabe K, et al. Hot Carrier-Assisted Intrinsic Photoresponse in Graphene. Science (2011) 334:648–52. doi:10.1126/science.1211384
148. Groenendijk DJ, Buscema M, Steele GA, Michaelis De Vasconcellos S, Bratschitsch R, van der Zant HSJ, et al. Photovoltaic and Photothermoelectric Effect in a Double-Gated WSe2 Device. Nano Lett (2014) 14:5846–52. doi:10.1021/nl502741k
149. Léonard F, Song E, Li Q, Swartzentruber B, Martinez JA, Wang GT. Simultaneous Thermoelectric and Optoelectronic Characterization of Individual Nanowires. Nano Lett (2015) 15:8129–35. doi:10.1021/acs.nanolett.5b03572
150. Limpert S, Burke A, Chen I-J, Anttu N, Lehmann S, Fahlvik S, et al. Bipolar Photothermoelectric Effect across Energy Filters in Single Nanowires. Nano Lett (2017) 17:4055–60. doi:10.1021/acs.nanolett.7b00536
151. Zhou H, Tao P, Lin Y, Chen Z, Zhao Y, Zeng W, et al. A Flexible In-Plane P-N Heterojunction Nano-Generator with Phonon-Enhanced Photothermoelectric Effect to Harvest Solar Energy. J Mater Chem A (2021) 9:14958–68. doi:10.1039/D1TA02946K
152. Buscema M, Barkelid M, Zwiller V, van der Zant HSJ, Steele GA, Castellanos-Gomez A. Large and Tunable Photothermoelectric Effect in Single-Layer MoS2. Nano Lett (2013) 13:358–63. doi:10.1021/nl303321g
153. Chou SS, Kaehr B, Kim J, Foley BM, De M, Hopkins PE, et al. Chemically Exfoliated MoS2as Near-Infrared Photothermal Agents. Angew Chem Int Ed (2013) 52:4160–4. doi:10.1002/anie.201209229
154. Li K, Xu L, Li Z, Wang Y, Wang J, Qi X, et al. Enhanced Thermoelectric Performance and Tunable Polarity in 2D Cu2S-Phenol Superlattices Composites for Solar Energy Conversion. Nano Energy (2021) 84:105902. doi:10.1016/j.nanoen.2021.105902
155. Kraemer D, Poudel B, Feng H-P, Caylor JC, Yu B, Yan X, et al. High-performance Flat-Panel Solar Thermoelectric Generators with High thermal Concentration. Nat Mater (2011) 10:532–8. doi:10.1038/nmat3013
156. Jung YS, Jeong DH, Kang SB, Kim F, Jeong MH, Lee K-S, et al. Wearable Solar Thermoelectric Generator Driven by Unprecedentedly High Temperature Difference. Nano Energy (2017) 40:663–72. doi:10.1016/j.nanoen.2017.08.061
157. Feng K, Xu L, Xiong Y, Sun L, Yu H, Wu M, et al. PEDOT:PSS and Ni-Based Thermoelectric Generator for Solar thermal Energy Conversion. J Mater Chem C (2020) 8:3914–22. doi:10.1039/C9TC06277G
Keywords: two-dimensional, transition metal dichalcogenides, thermoelectrics, electrical transport, thermal transport
Citation: Zhou W, Gong H, Jin X, Chen Y, Li H and Liu S (2022) Recent Progress of Two-Dimensional Transition Metal Dichalcogenides for Thermoelectric Applications. Front. Phys. 10:842789. doi: 10.3389/fphy.2022.842789
Received: 24 December 2021; Accepted: 20 January 2022;
Published: 11 March 2022.
Edited by:
Jian Sun, Central South University, ChinaReviewed by:
Yongji Gong, Beihang University, ChinaFayong Liu, Japan Advanced Institute of Science and Technology, Japan
Copyright © 2022 Zhou, Gong, Jin, Chen, Li and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Zhou, c3N6aG91d2VpQGhudS5lZHUuY24=; Song Liu, bGl1c29uZ0BobnUuZWR1LmNu
 Wei Zhou
Wei Zhou Huimin Gong1
Huimin Gong1