Quantum Cooperative Multicast in a Quantum Hybrid Topology Network

Quantum multicast is a significant transmission mode in a multiparty communication scenario. Multisource collaboration can further enhance the efficient multicast. However, it remains a challenge to realize quantum multicast with a cooperative way in a complex topology network. In this article, we propose a scheme of quantum cooperative multicast in a hybrid topology network. It provides information aggregation and simultaneous multipoint transmission services. First, collaborative information aggregation allows central network data to be integrated into the aggregation node. By exploiting the quantum multicast mode, the aggregation node can simultaneously deliver integrated quantum states to multiple targets. Second, our scheme is feasible for dynamic network expansion. It is capable of extending the network architecture iteratively, while the peer network requests can be handled in parallel. Finally, the new scheme shows great application potential in the distributed quantum network. It is a promising candidate for the implementation of quantum data disaster backup in future.

1 Introduction

Quantum communication [1–3] is a new subject in quantum information science. With a special network [4–10] dedicated to quantum communication, the quantum technique enables new features which cannot be achieved by its classical counterpart. With the rapid development of quantum technology, the application of quantum communication [11–19] has gradually changed with the trends of networking and globalization.

As one of the essential studies involved in large-scale quantum communication networks, quantum multicast between multiple users is an excellent group transmission technique. Quantum multicast uses a one-to-many or many-to-many association, in which quantum information is delivered simultaneously in a single transmission to many recipients. Compared with the point-to-point transmission, quantum multicast significantly improves the system performance in distributed network communication. In 2006, Shi and Soljanin [20] first investigated multicast in quantum networks and proposed a many-to-many quantum multicast scheme, in which quantum states generated by multiple sources can be simultaneously delivered to multiple targets. They focus on bottlenecks in a multicast scenario and studied lossless compression in a quantum network to reduce the edge capacity requirements. However, it should be under the condition that source nodes can generate enough copies of quantum states. Since the quantum no-cloning theorem [21] forbids the quantum information to be copied as the classical information, the quantum approximate cloning technique [13, 22, 23] has been proposed for preparing sufficient target states. In 2015, Wang et al. [23] utilized an asymmetric quantum cloning mechanism to achieve point-to-multipoint multicast communication, but the fidelity loss remains a problem. Under the quantum cloning mechanism, no matter what approach is taken to copy unknown quantum states, the output must differ from the initial state, resulting in lower fidelity.

Quantum cooperative multicast (QCM) is a novel method to realize many-to-many quantum network multicast. Compared with the quantum cloning mechanism in multicast, it contributes to high fidelity. In QCM, each source has partial information about the quantum state to be transmitted, and they cooperate with each other to achieve accurate multicast. In 2015, Xu et al first proposed the QCM protocol over the butterfly network. As the representative topology with bottleneck problems, butterfly networks here can provide a more general solution for non-trivial networks. Different from common cross-transmission, the goal of QCM is that two source nodes S₁, S₂ jointly send the integrated state $a_0{b}_0\left|0\right.⟩+a_1{b}_1\left|1\right.⟩$ to both targets T₁, T₂. Suppose S₁, S₂ own information about $a_0\left|0\right.⟩+a_1\left|1\right.⟩$, $b_0\left|0\right.⟩+b_1\left|1\right.⟩$, respectively, they adopt a cooperative manner to achieve information integration and reconstruct the integrated state $a_0{b}_0\left|0\right.⟩+a_1{b}_1\left|1\right.⟩$ at source nodes. Then they complete simultaneous multipoint transmission through the butterfly network. Finally, each target node can obtain the same integrated state, which contains both source nodes’ information. The whole process does not involve quantum approximate cloning and will not cause loss of fidelity. This work reflects the characteristics of quantum cooperative communication in a multicast scenario, but it does not cover all possible types of networks.

As the real communication occurs mostly in basic network topologies, like ring [24, 25], star [26], and hybrid topologies [27], it is necessary to extend the adaption of QCM in a typical network topology. The ring–star hybrid topology is one of the most popular network setups for a distributed network. In this configuration, the central network is set with the ring topology, whereas the peripheral networks connect the central network with the star topology. The central ring topologies allow messages to travel in one direction, which alleviates packet collision. When requesting messages from the server, data packets are delivered from one node to another until they reach the destination. The peripheral star topologies can be regarded as centralized management structures, where the central device responds to the request from the peripheral devices. This hybrid topology offers the advantages of both ring and star topologies, and it is feasible enough for network expansion.

In this study, we propose a quantum cooperative multicast scheme in a hybrid topology network. This hybrid topology [27] integrates the advantages of ring [24, 25] and star [26] networks to be consistent with a practical communication environment. Specifically, the central ring network provides an information aggregation server, whereas the peripheral star network responds to multipoint simultaneous transmission. Finally, the new scheme shows great potential in terms of expandability and applicability. We find it is a promising candidate for quantum data disaster backup in future.

2 Methods and Materials

We propose a quantum cooperative multicast scheme in a quantum hybrid topology network. Figure 1 shows the quantum hybrid network topology. In this configuration, our network architecture includes the central aggregation network and the peripheral multicast network. Here, each node $n_i,i\in \left\{0,\dots ,k-1\right\}$ in the central network has its information ${\alpha }_i,{\alpha }_i\in \left[0,\frac{\pi }{2}\right]$. Suppose the peripheral star network nodes n_s1, n_s2 ⋯ n_st request for aggregated information of the central network. The goal is that the information from all the nodes $n_i,i\in \left\{0,\dots ,k-1\right\}$ in the central network can be aggregated in the form of the quantum state:

$\left|\psi \right.⟩=\cos \left({\alpha }_0+{\alpha }_1\dots +{\alpha }_{k-1}\right)\left|0\right.⟩+\sin \left({\alpha }_0+{\alpha }_1\dots +{\alpha }_{k-1}\right)\left|1\right.⟩(1)$

at the aggregation node n_s, 0 ≤ s ≤ k − 1 and multicast to t subnodes n_s1, n_s2 ⋯ n_st in the peripheral star network.

FIGURE 1

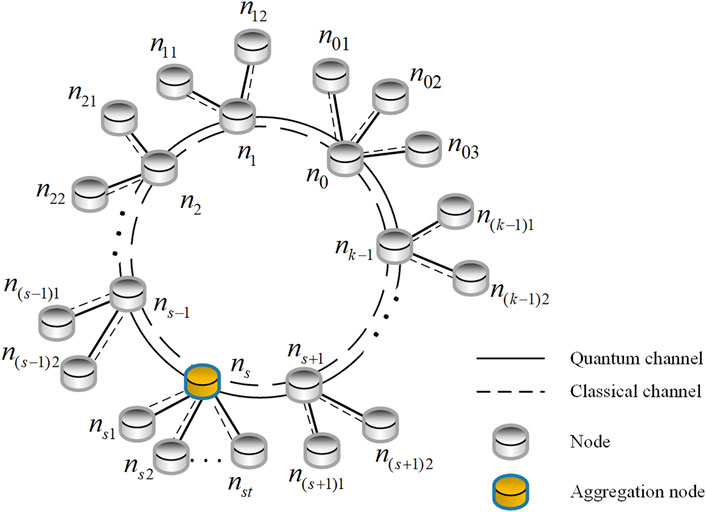
FIGURE 1. Quantum hybrid network topology. Each node $n_i,i\in \left\{0,\dots ,k-1\right\}$ in the central network is connected with a ring topology. Moreover, n_i is the central node of the peripheral star topology consisting of nodes $n_{ij},i\in \left\{1,\dots ,k\right\},j\in \left\{1,\dots ,t\right\}$. Dashed lines represent classical channels, while solid lines represent quantum channels. The node n_s, 0 ≤ s ≤ k − 1 marked in yellow is the aggregation node.

This state in Eq. 1 is called the integrated state. The amplitude of the integrated state corresponds to the trigonometric function of the finite k source’s information sum. It can be generated by local rotation operations $R_{{\alpha }_i}=\left[\begin{array}{cc}\hfill \cos {\alpha }_i\hfill & \hfill -\sin {\alpha }_i\hfill \\ \hfill -\sin {\alpha }_i\hfill & \hfill -\cos {\alpha }_i\hfill \end{array}\right]$ on the k pairs’ pre-shared Bell state $\left|{\mathrm{\Phi }}^{-}\right.⟩=\left(\frac{\left|00\right.⟩-\left|11\right.⟩}{\sqrt{2}}\right)$. When the rotation operation $R_{{\alpha }_i}$ is performed on the qubit i in the Bell state ${\left|{\mathrm{\Phi }}^{-}\right.⟩}_{{(i-1)}^{\prime }i}i\in \left\{0,\dots ,k-1\right\}$, it can be

$\left(I\otimes R_{{\alpha }_i}\right){\left|{\mathrm{\Phi }}^{-}\right.⟩}_{{\left(i-1\right)}^{\prime }i}=\frac{1}{\sqrt{2}}{\left(\left|0\right.⟩C_{{\alpha }_i}+\left|1\right.⟩D_{{\alpha }_i}\right)}_{{\left(i-1\right)}^{\prime }i}=\frac{1}{\sqrt{2}}{\left(A_{{\alpha }_i}\left|0\right.⟩-B_{{\alpha }_i}\left|1\right.⟩\right)}_{{\left(i-1\right)}^{\prime }i}.(2)$

Here, $A_{{\alpha }_i}=\cos {\alpha }_i\left|0\right.⟩+\sin {\alpha }_i\left|1\right.⟩$, $B_{{\alpha }_i}=\sin {\alpha }_i\left|0\right.⟩-\cos {\alpha }_i\left|1\right.⟩$, $C_{{\alpha }_i}=\cos {\alpha }_i\left|0\right.⟩-\sin {\alpha }_i\left|1\right.⟩$, and $D_{{\alpha }_i}=\sin {\alpha }_i\left|0\right.⟩+\cos {\alpha }_i\left|1\right.⟩$. Particularly, the addition and subtraction algorithms for i in this study are modular k addition and modular k subtraction.

The complete scheme of QCM in a quantum hybrid topology network includes two parts: information aggregation and multicast transmission. The following Steps 1-4 implements information aggregation, while Step 5 executes multicast transmission.

Step 1. The k pairs of the Bell state ${\left|{\mathrm{\Phi }}^{-}\right.⟩}_{i^{\prime }(i+1)}={\left(\frac{\left|00\right.⟩-\left|11\right.⟩}{\sqrt{2}}\right)}_{i^{\prime }(i+1)}$ are distributed among adjacent nodes (n_i, n_i+1) in the central ring network. Each node n_i has two qubits, in which the first qubit i is entangled with the previous node n_i−1 and the second qubit i′ is entangled with the next node n_i+1.

Step 2. Each node n_i performs the operation $R_{{\alpha }_i}=\left[\begin{array}{cc}\hfill \cos {\alpha }_i\hfill & \hfill -\sin {\alpha }_i\hfill \\ \hfill -\sin {\alpha }_i\hfill & \hfill -\cos {\alpha }_i\hfill \end{array}\right]$ on its first qubit i.

Step 3. Each node n_i executes the encoding process.The node n_s+1 (the next node of the aggregation node n_s) executes the encoding process. n_s+1 performs the local Bell measurement on its qubits (s + 1)′(s + 1) and transmits the Bell measurement result (BMR) to the next node n_s+2 by the classical channel. When the BMR is ${\left|{\mathrm{\Phi }}^{+}\right.⟩}_{{(s+1)}^{\prime }(s+1)}={\left(\frac{\left|00\right.⟩+\left|11\right.⟩}{\sqrt{2}}\right)}_{{(s+1)}^{\prime }(s+1)}$, the source node n_s+2 performs I on its first particle (s + 2); when the BMR is ${\left|{\mathrm{\Phi }}^{-}\right.⟩}_{{(s+1)}^{\prime }(s+1)}={\left(\frac{\left|00\right.⟩-\left|11\right.⟩}{\sqrt{2}}\right)}_{{(s+1)}^{\prime }(s+1)}$, the source node n_s+2 performs $R_{2{\alpha }_{i+1}}$ on its first particle (s + 2); when the BMR is ${\left|{\mathrm{\Psi }}^{+}\right.⟩}_{{(s+1)}^{\prime }(s+1)}={\left(\frac{\left|01\right.⟩+\left|10\right.⟩}{\sqrt{2}}\right)}_{{(s+1)}^{\prime }(s+1)}$, the source node n_s+2 performs $R_{2{\alpha }_{i+1}}XZ$ on its first particle (s + 2); and when the BMR is ${\left|{\mathrm{\Psi }}^{-}\right.⟩}_{{(s+1)}^{\prime }(s+1)}={\left(\frac{\left|01\right.⟩-\left|10\right.⟩}{\sqrt{2}}\right)}_{{(s+1)}^{\prime }(s+1)}$, the source node n_s+2 performs XZ on its first particle (s + 2).Then n_s+2 repeats the Bell measurement on its qubits (s + 2)′(s + 2) and transmits the BMR to the next node n_s+3. According to n_s+2’s BMR, n_s+3 performs corresponding unitary transformation (I, $R_{2{\alpha }_{i+1}}$, $R_{2{\alpha }_{i+1}}XZ$ or XZ) on its first qubit (s + 3). Similarly, along the counterclockwise direction around the central ring network, the nodes n_s+3, n_s+4,…,n_k−1, n₀,…,n_s−1 then repeat the encoding process in sequence.

Step 4. The aggregation node n_s performs the Z-basis measurement on qubit s. If the measurement result is $\left|0\right.⟩$, n_s performs I on qubit s′. If the measurement result is $\left|1\right.⟩$, n_s performs ZX on qubit s′. The final integrated state $\left|\psi \right.⟩$ can be obtained by the aggregation node n_s.

Step 5. Through t times circulation of Steps 1–4, the aggregation node n_s obtains t copies of the integrated states $\left|\psi \right.⟩$. The aggregation node n_s multicasts t copies of $\left|\psi \right.⟩$ to n_s1, n_s2 ⋯ n_st, respectively.The following summarizes Steps 1-4 for the information aggregation algorithm. The additive operation for i in this algorithm is modular k addition.

Algorithm 1. Information aggregation of QCM in a quantum hybrid topology network.The information aggregation algorithm runs t times to generate t copies of the integrated state $\left|\psi \right.⟩$, since the aggregation node has t subnodes in the peripheral star network. The information aggregation algorithm is implemented by utilizing the quantum circuit given in Figure 2.

FIGURE 2

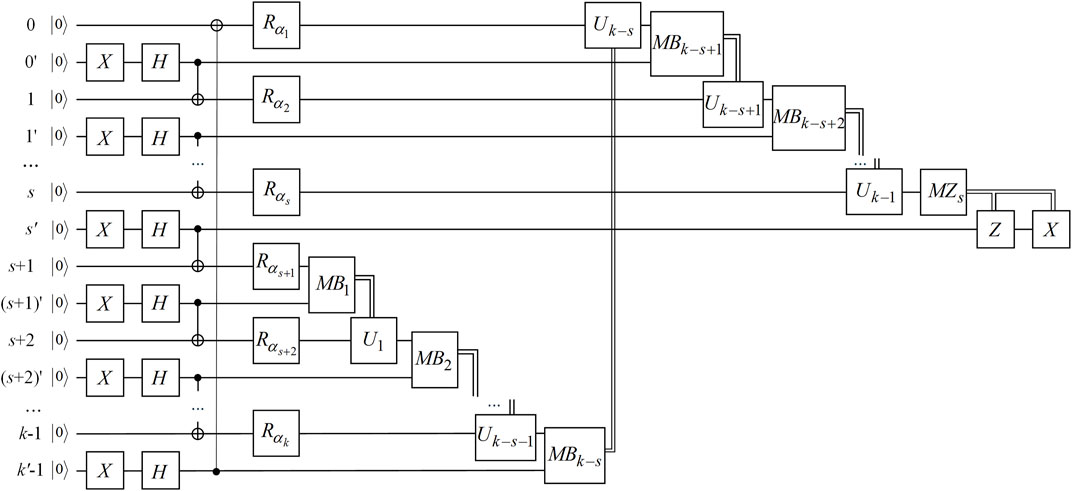
FIGURE 2. Quantum circuit for generating the integrated state $\left|\psi \right.⟩$. Here, $M{B}_i,i\in \left\{1,\dots ,k-1\right\}$ represents the ith Bell measurement result (BMR). U_i represents the unitary operation (I, $R_{2{\alpha }_{i+1}}$, $R_{2{\alpha }_{i+1}}XZ$ or XZ) according to MB_i. MZ_s represents the Z-basis measurement result on qubit s.

3 Results

The scheme pre-shares k pairs of the Bell states ${\left|{\mathrm{\Phi }}^{-}\right.⟩}_{i^{\prime }(i+1)}$ between adjacent nodes (n_i, n_i+1) in step 1. For example, (n₀, n₁) pre-share the Bell state ${\left|{\mathrm{\Phi }}^{-}\right.⟩}_{0^{\prime }1}$; (n₁, n₂) pre-share the Bell state ${\left|{\mathrm{\Phi }}^{-}\right.⟩}_{1^{\prime }2}$;…; and (n_k−1, n₀) pre-share the Bell state ${\left|{\mathrm{\Phi }}^{-}\right.⟩}_{{(k-1)}^{\prime }0}$. The whole initial quantum system is shown as follows:

$\left|{\psi }_{initial}\right.⟩={\left|{\mathrm{\Phi }}^{-}\right.⟩}_{0^{\prime }1}\otimes {\left|{\mathrm{\Phi }}^{-}\right.⟩}_{1^{\prime }2}\otimes {\left|{\mathrm{\Phi }}^{-}\right.⟩}_{2^{\prime }3}\otimes \cdots \otimes {\left|{\mathrm{\Phi }}^{-}\right.⟩}_{{\left(k-2\right)}^{\prime }\left(k-1\right)}\otimes {\left|{\mathrm{\Phi }}^{-}\right.⟩}_{{\left(k-1\right)}^{\prime }0}.(3)$

Each node n_i implements the rotation operation $R_{{\alpha }_i}$ to encode information α_i into the quantum state ${\left|{\mathrm{\Phi }}^{-}\right.⟩}_{{(i-1)}^{\prime }i}$. According to Eq. 2, the whole quantum system in step 2 becomes

$\left|{\psi }_0\right.⟩=\frac{1}{2^{\frac{k}{2}}}{\left(A_{{\alpha }_{s+1}}\left|0\right.⟩-B_{{\alpha }_{s+1}}\left|1\right.⟩\right)}_{s^{\prime }\left(s+1\right)}\underset{\begin{array}{c}i=0,\\ i\ne s\end{array}}{\overset{k-1}{\otimes }}{\left(\left|0\right.⟩C_{{\alpha }_{i+1}}+\left|1\right.⟩D_{{\alpha }_{i+1}}\right)}_{i^{\prime }\left(i+1\right)}.(4)$

Then, beginning with the node n_s+1 (the next node of the aggregation node n_s), the local Bell measurement (BM) is performed on (s + 1) (s + 1)′ and the Bell measurement result (BMR) is transmitted to the next node n_s+2 by the classical channel. After performing the corresponding unitary operation (I, $R_{2{\alpha }_{i+1}}$, $R_{2{\alpha }_{i+1}}XZ$ or XZ) on qubit s + 2, the quantum state becomes

$\left|{\psi }_1\right.⟩=\frac{1}{2^{\frac{k-1}{2}}}{\left(A_{{\alpha }_{s+1}+{\alpha }_{s+2}}\left|0\right.⟩-B_{{\alpha }_{s+1}+{\alpha }_{s+2}}\left|1\right.⟩\right)}_{s^{\prime }\left(s+2\right)}\underset{\begin{array}{c}i=0,\\ i\ne s,s+1\end{array}}{\overset{k-1}{\otimes }}{\left(\left|0\right.⟩C_{{\alpha }_{i+1}}+\left|1\right.⟩D_{{\alpha }_{i+1}}\right)}_{i^{\prime }\left(i+1\right)}.(5)$

Along the counterclockwise direction around the central ring network, the node n_s−1 finally finishes the encoding process, and the quantum state in step 3 becomes

$\left|{\psi }_{k-1}\right.⟩=\frac{1}{\sqrt{2}}{\left(A_{{\alpha }_0+{\alpha }_1+\cdots +{\alpha }_{k-1}}\left|0\right.⟩-B_{{\alpha }_0+{\alpha }_1+\cdots +{\alpha }_{k-1}}\left|1\right.⟩\right)}_{s^{\prime }s}.(6)$

Consequently, the information of each node n_i can be aggregated at the aggregation node n_s. The aggregation node n_s measures the qubit s with Z-basis to get the final integrated state in step 4:

$\begin{array}{c}|\psi >=A_{{\alpha }_0+{\alpha }_1+\cdots +{\alpha }_{k-1}}\hfill \\ =\cos \left({\alpha }_0+{\alpha }_1+\cdots +{\alpha }_{k-1}\right)\left|0\right.⟩+\sin \left({\alpha }_0+{\alpha }_1+\cdots +{\alpha }_{k-1}\right)\left|1\right.⟩.\hfill \end{array}(7)$

Up to this step, a round of information aggregation for the integrated state $\left|\psi \right.⟩$ is completed. Since the aggregation node has t subnodes in the peripheral star network, it should prepare t copies of the quantum state $\left|\psi \right.⟩$. According to Algorithm 1, it can be achieved by running t times of information aggregation. In total, it costs (kt + t) Bell pairs as the communication resource.

While the channel capacity is large enough, adjacent nodes in a central ring network can also pre-share t pairs of Bell states $\left|{\mathrm{\Phi }}^{-}\right.⟩$. Each node encodes and measures its qubits in parallel before one-off transmission of BMRs. In this case, the aggregation node n_s can also obtain t copies of the quantum state $\left|\psi \right.⟩$. By reducing the transmission delay, this synchronous measurement method makes a significant contribution to quantum networks. Finally, in Step 5, the aggregation node n_s multicasts quantum states ${\left|\psi \right.⟩}_{n_{s1}}$, ${\left|\psi \right.⟩}_{n_{s1}},\cdots$, ${\left|\psi \right.⟩}_{n_{st}}$ to peripheral nodes n_s1, n_s2 ⋯ n_st, respectively.

4 Discussion

We now discuss the performance comparison, the extendibility, and the application scenario for the proposed quantum cooperative multicast scheme in a quantum hybrid topology network.

4.1 Performance Comparison and Analysis

Existing quantum multicast protocols [14, 20, 23, 28] introduce quantum information technologies widely. Apart from our scheme, Xu’s protocol [28] is the first quantum cooperative multicast scheme, while Shi’s protocol [20] is about the lossless compression of special multicast quantum states. Kobayashi’s protocol [14] represents the quantum simulation of a classical linear network coding scheme in the N-to-N multicast model, and Wang’s protocol [23] involves quantum approximate cloning technology.

We make a comparison between the multiple aspects of our scheme and the existing quantum multicast protocols in Table 1. In Table 1, our scheme and Refs. [14, 20, 23] have the same perfect success probability to obtain the desired information, which is better than the determinacy in Ref. [28]. The fidelity of most schemes can reach 1, except for the quantum cloning method [23]. In terms of the number of communicating parties, our scheme and Refs. [20, 23] enable an arbitrary number of parties to quantum multicast, while [14, 28] are bound by the same amount of senders and receivers. Only lossless compression technology [20] can hardly multicast arbitrary quantum states. However, the network topology in our schemes is quite unique among the quantum multicast protocols [14, 20, 23]. This is determined by the information aggregation and multicast mode in our scheme. The information aggregation is dedicated to ring topology, while the multicast transmission occurs in the peripheral star topology. In addition, compared with the baseline scheme, for example, which directly distributes NM Bell pairs from N sources to M targets at a distance, our scheme distributes entangled resources among neighbor nodes to reduce decoherence.

TABLE 1

TABLE 1. Performance comparison between our scheme and previous quantum multicast protocols.

4.2 Extendibility

As the worldwide demand for quantum communication rises, a large-scale, distributed and complicated quantum network should be studied. The topology with better extendibility will further improve multicast efficiency and meet the demands of complicated network applications. The proposed quantum cooperative multicast scheme has strong scalability. It is implemented in a hybrid network topology, which could be part of a larger network.

4.2.1 Iterative Network

The hybrid topology in our scheme enables networks to be extended iteratively, which can cover a larger communication range. Based on the coverage of the local area network (LAN), there are strict differences in network levels. Here, we use “network level” to indicate the affiliation of networks within the LAN. As shown in Figure 3, we present three levels of network scenarios in an iterative network. The outmost networks are regarded as the level 3 network, which is denoted by the light blue area. These aggregation nodes of the level 3 network can contribute to a level 2 network marked with the dark blue area. This level 2 network is also equipped with aggregation nodes, contributing to a level 1 network marked with the gray area. This proves that our network is efficient in expanding the topology iteratively. We can observe that each level of the network conforms to the hybrid topology, satisfying the characteristics of a fractal network.

FIGURE 3

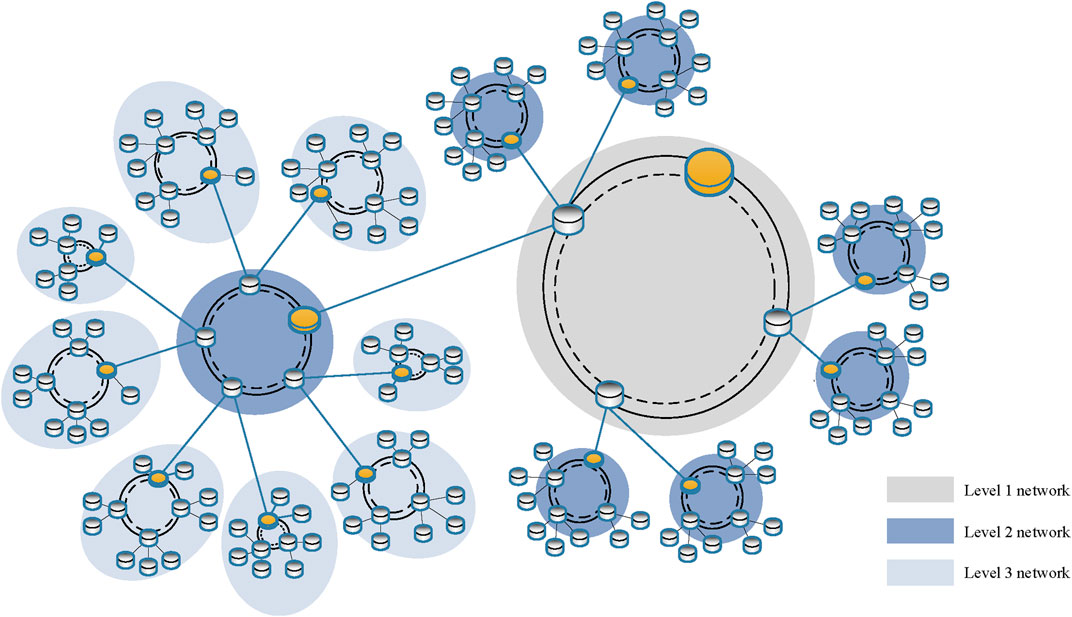
FIGURE 3. Iterative network. Networks with the same background color are peer networks. The aggregation node in the lower level network (marked in yellow) is connected to the central network of the upper level network.

Due to this topological feature, the higher level network can aggregate all the information of the connected lower level network. For example, each aggregation node of the level 3 network aggregates the information from its central network and multicasts it to the subnode which is located on the central ring of the level 2 network. Once the aggregation node of the level 2 network performs information aggregation, it does aggregate all the connected level 3 network information. Hence, the highest level network can aggregate the information of the whole iterative network.

Meanwhile, instead of being transmitted to a specific local area network, the aggregate information is spread to a vast distributed network. Each node in the central ring network of the level 1 network can be an aggregation node to aggregate the information and multicast it toward the aggregation nodes in level 2 networks. Similarly, other nodes in the central network of the level 2 network can also be aggregation nodes. While they aggregate the information over the level 2 central network, these nodes perform operation I, instead of the rotation operation $R_{{\alpha }_i}$, in Algorithm 1. In this way, each node in the central network of the level 2 network obtains the aggregated information from the level 1 network. Therefore, the aggregate information of the highest level network can be transmitted iteratively over the whole network.

This hierarchical iterative network coincides with the practical network environment. If the whole country is regarded as a local area network, the level 1 network refers to the “provincial backbone line,” which is generally set up in the provincial capital of each region and the secondary trunk line generally with the province to cover the scope. Therefore, all network nodes set in the province belong to the level 2 network. The level 3 network is actually the local network, which is divided by the city as the region. Each level of the network itself conforms to the hybrid topology, and the upper and lower level networks are connected by a star mode. At the highest level of the network, provincial capitals will be able to collect and aggregate information from all their cities. Conversely, the corresponding aggregated information can spread from provincial capitals to cities. Compared with a larger single circle or several star networks, this hierarchical iterative network benefits the entire network information management.

4.2.2 Side-by-Side Network

A side-by-side network [29] is also possibly derived from our hybrid topology structure. Here, the side-by-side network means that multiple quantum networks are connected at the same level of the network. The situation is shown in Figure 4. It is worth noting that the side-by-side network allows peer networks to share central ring network nodes. This type of collaborative multicast architecture can handle requests on peer networks in parallel. If new clients or devices are added, our network allows parallel expansion to be a side-by-side network. In this case, a large number of clients on different networks can participate in information aggregation simultaneously.

FIGURE 4

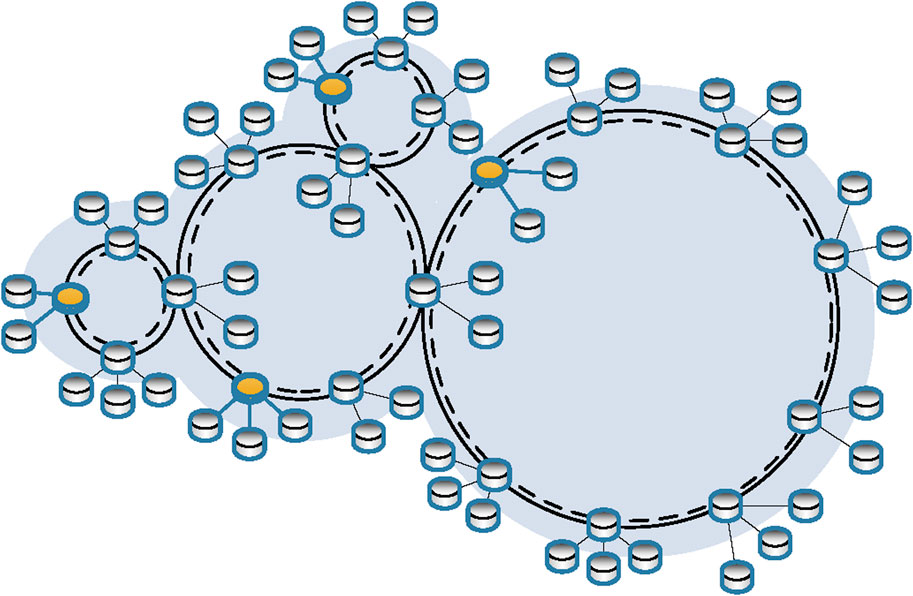
FIGURE 4. Side-by-side network. Several peer networks with the same background color are connected by a side-by-side network, which allows these peer networks to share central ring network nodes.

The extensibility of our scheme is significantly meaningful for large-scale network communication. It can not only effectively divide the network to refine the communication scale but also iteratively expand the network scope. Hence, this extensibility is sufficient for the dynamic network requirements.

4.3 Application Scenario

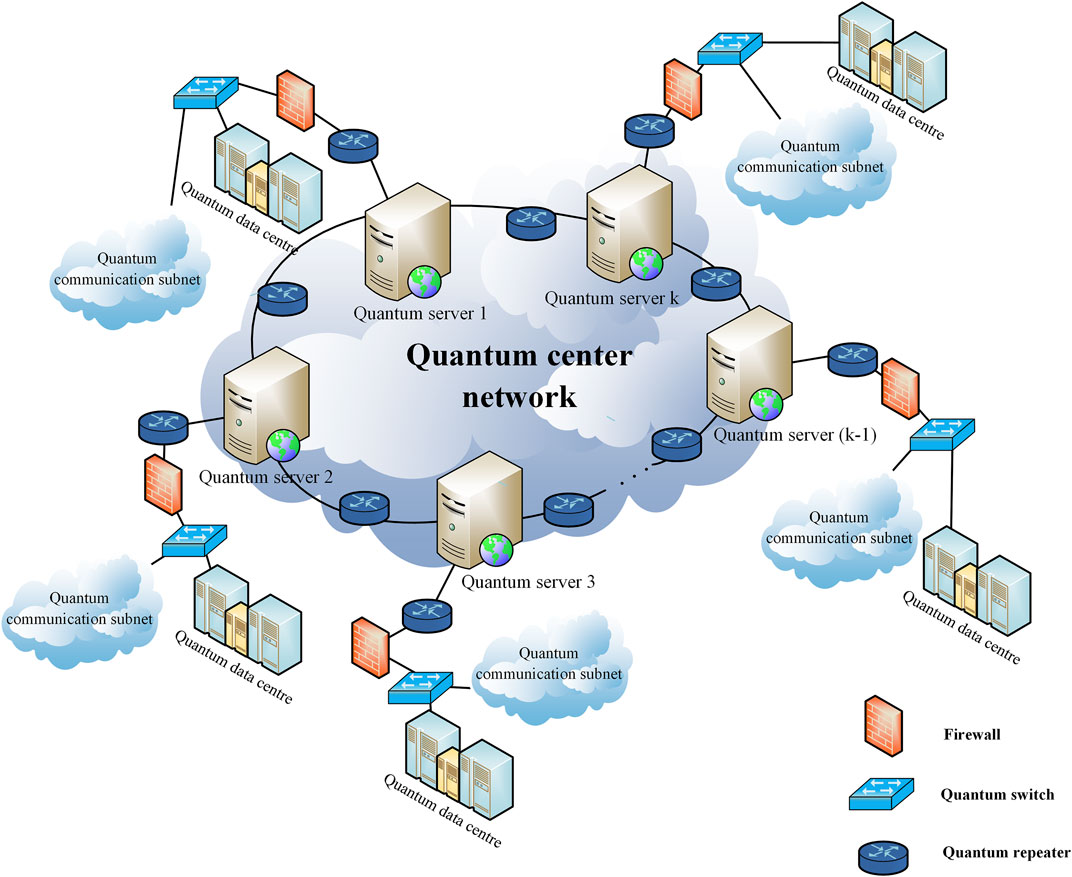
Our quantum cooperative multicast scheme is implemented in a hybrid topology network. In this scheme, the central ring network provides an information aggregation server, while the peripheral star network responds to multicast transmission. This solution pattern could be employed in various application scenarios of large-scale quantum networks in future, such as a backup system for disaster recovery. In this section, we describe a quantum disaster recovery plan in a hybrid topology network. As an application of the present scheme, this plan offers risky node information aggregation and multipoint simultaneous backup services.

We first introduce three basic network configurations in this plan: quantum repeaters, quantum switches, and firewall. With the ability of the entanglement generation, quantum repeaters [30–32] are the most popular devices in the quantum network. It is also a promising technology for enabling multicast over long distances. Quantum switches [33, 34] provide network interfaces to connect quantum communication networks. If quantum clients in a peripheral network request for aggregating information of the central network, the quantum switch is responsible for generating the adjacency of the clients to which they connect. In addition, we use the symbol of the firewall to represent the security defense. Since each node n_i is associated with partial information about the integrated state, it might reduce the security level. In general, many quantum information security technologies, such as quantum identity authentication [35] and quantum homomorphic encryption [36], can also be applied to maintain internet security. Specifically, we implement quantum distillations [37] on entanglement resources over the central network. Even if potential risks exist in the network equipment, secure communications can be established. Now, we describe a plan of quantum data disaster backup based on the proposed scheme. The preliminary design is plotted in Figure 5.

FIGURE 5

FIGURE 5. Plan of quantum data disaster backup.

Suppose each quantum server S_i, i = {1, 2, … , k} in the central network administers local database, which is represented as ${\alpha }_i,{\alpha }_i\in \left[0,\frac{\pi }{2}\right]$. Assume that some servers $S_{f_1},S_{f_2},\dots ,S_{f_n}(f_1,f_2,\dots ,f_n\in \{\mathrm{1,2},\dots ,k\})$ in the quantum central network pose potential risks of failure. This plan aims to aggregate information in the form of a quantum state $\left|\psi \right.⟩=\cos \left({\alpha }_{f_1}+{\alpha }_{f_2}\dots +{\alpha }_{f_n}\right)\left|0\right.⟩+\sin \left({\alpha }_{f_1}+{\alpha }_{f_2}\dots +{\alpha }_{f_n}\right)\left|1\right.⟩$ from these servers to a reliable node S_a, a ∈ {1, 2, … , k} and backup to its secure subnet. The following summarizes the steps of the plan.

1) The center network checks the high-risk servers $S_{f_1},S_{f_2},\dots ,S_{f_n}$ and identifies a reliable node as the aggregation node S_a.

2) The Bell pairs are distributed between adjacent nodes via quantum repeaters, forming a ring central network. Here, the Bell state needs to be distilled before entanglement distribution.

3) Algorithm 1 is adopted to aggregate information about potential faulty nodes $S_{f_1},S_{f_2},\dots ,S_{f_n}$ to the aggregation node S_a. To be specific, the nodes at risk perform the rotation operation $R_{{\alpha }_i}$ to encode their information into the entanglement resource, while other secure nodes implement the I operation, instead of the rotation operation.

4) Once the facilities are broken down, the aggregation node S_a multicasts the aggregated information securely to the peripheral star subnet through quantum switches.

Overall, the proposed quantum cooperative multicast scheme can achieve non-local information aggregation and multipoint backup, satisfying the basic demand of a quantum data disaster backup.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by the NSFC (Grant Nos. 92046001, 61671087, 61962009, 62176273, and 61971021), the Fundamental Research Funds for the Central Universities (Grant No. 2019XD-A02), the Fundamental Research Funds for Beijing Municipal Commission of Education, the Open Foundation of Guizhou Provincial Key Laboratory of Public Big Data (Grant Nos. 2018BDKFJJ018, 2019BDKFJJ010, and 2019BDKFJJ014), the BUPT Excellent Ph.D. Students Foundation (Grant No. CX2021223), the Scientific Research Launch Funds of North China University of Technology, and Beijing Urban Governance Research Base of North China University of Technology.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Dynes JF, Wonfor A, Tam WWS, Sharpe AW, Takahashi R, Lucamarini M, et al. Cambridge Quantum Network. Npj Quan Inf (2019) 5:101. doi:10.1038/s41534-019-0221-4

CrossRef Full Text | Google Scholar

2. Yu Y, Ma F, Luo XY, Jing B, Sun PF, Fang RZ, et al. Entanglement of Two Quantum Memories via Fibres over Dozens of Kilometres. Nature (2020) 578:240–5. doi:10.1038/s41586-020-1976-7

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Bhaskar MK, Riedinger R, Machielse B, Levonian DS, Nguyen CT, Knall EN, et al. Experimental Demonstration of Memory-Enhanced Quantum Communication. Nature (2020) 580:60–4. doi:10.1038/s41586-020-2103-5

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lloyd S, Shapiro JH, Wong FNC, Kumar P, Shahriar SM, Yuen HP. Infrastructure for the Quantum Internet. SIGCOMM Comput Commun Rev (2004) 34:9–20. doi:10.1145/1039111.1039118

CrossRef Full Text | Google Scholar

5. Kimble HJ. The Quantum Internet. Nature (2008) 453:1023–30. doi:10.1038/nature07127

PubMed Abstract | CrossRef Full Text | Google Scholar

6. VanMeter R. Quantum Networking. Hoboken, NJ, USA: Wiley (2014).

Google Scholar

7. Hahn F, Pappa A, Eisert J. Quantum Network Routing and Local Complementation. npj Quan Inf (2019) 76(5). doi:10.1038/s41534-019-0191-6

CrossRef Full Text | Google Scholar

8. Shi S, Qian C. Modeling and Designing Routing Protocols in Quantum Networks (2019).

Google Scholar

9. Pirker A, Dur W. A Quantum Network Stack and Protocols for Reliable Entanglement-Based Networks. New J Phys (2018) 21(3):033003.

Google Scholar

10. Pant M, Krovi H, Towsley D, Tassiulas L, Jiang L, Basu P, et al. Routing Entanglement in the Quantum Internet. npj Quan Inf (2019) 25(5). doi:10.1038/s41534-019-0139-x

CrossRef Full Text | Google Scholar

11. Peev M, Pacher C, Alleaume R, Barreiro C, Bouda J, Boxleitner W, et al. The Secoqc Quantum Key Distribution Network in vienna. New J Phys (2009) 11:075001. doi:10.1364/ofc.2009.othl2

CrossRef Full Text | Google Scholar

12. Sasaki M, Fujiwara M, Ishizuka H, Klaus W, Wakui K, Takeoka M, et al. Field Test of Quantum Key Distribution in the Tokyo Qkd Network. Opt Express (2011) 19:10387–409. doi:10.1364/oe.19.010387

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hayashi M, Iwama K, Nishimura H, Raymond R, Yamashita S Quantum Network Coding. Annu Symp Theor Aspects Comput Sci (2007) 4393:610–21.

Google Scholar

14. Kobayashi H, LeGall F, Nishimura H, Roetteler M. Perfect Quantum Network Communication Protocol Based on Classical Network Coding. Proc IEEE Int Symp Inf Theor (2010) 41:2686–90. doi:10.1109/isit.2010.5513644

CrossRef Full Text | Google Scholar

15. Satoh T, Gall FL, Imai H. Quantum Network Coding for Quantum Repeaters. Phys Rev A (2012) 86(3):032331. doi:10.1103/physreva.86.032331

CrossRef Full Text | Google Scholar

16. Satoh T, Ishizaki K, Nagayama S, Van Meter R. Analysis of Quantum Network Coding for Realistic Repeater Networks. Phys Rev A (2016) 93(3):32302. doi:10.1103/physreva.93.032302

CrossRef Full Text | Google Scholar

17. Takaaki M, Takahiko S, Shota N, Rodney VM. Analysis of Measurement-Based Quantum Network Coding over Repeater Networks under Noisy Conditions. Phys Rev A (2018) 97(6):062328.

Google Scholar

18. Iwama k., Nishimura H, Raymond R, Yamashita S. Quantum Network Coding for General Graphs. Physics (2006) 2006:0611039.

Google Scholar

19. Leung D, Oppenheim J, Winter A. Quantum Network Communication-The Butterfly and beyond. IEEE Trans Inform Theor (2010) 56:3478–90. doi:10.1109/tit.2010.2048442

CrossRef Full Text | Google Scholar

20. Shi Y, Soljanin E. On Multicast in Quantum Networks. In: 2006 40th Annual Conference on Information Sciences and Systems (2006). doi:10.1109/ciss.2006.286589

CrossRef Full Text | Google Scholar

21. Wootters WK, Zurek WH. A Single Quantum Cannot Be Cloned. Nature (1982) 299:802–3. doi:10.1038/299802a0

CrossRef Full Text | Google Scholar

22. Bruß D, Divincenzo DP, Ekert A, Fuchs CA, Macchiavello C, Smolin JA. Optimal Universal and State-dependent Quantum Cloning. Phys Rev A (1998) 57(4):2368–78. doi:10.1103/physreva.57.2368

CrossRef Full Text | Google Scholar

23. Wang XJ, An LX, Meng FX, Yu XT, Zhang ZC. A Multicast Scheme Based on Fidelity Metrics in Quantum Networks. IEEE Access (2019) 7:65703–13. doi:10.1109/access.2019.2915931

CrossRef Full Text | Google Scholar

24. Ganguly S, Varsou AC, Izmailov R. Waveband Routing on Logical Topologies Constructed over a Ring Network. In: Workshop on High Performance Switching and Routing (2004).

Google Scholar

25. Shirichian M, Sara T. Protocol for Routing Entanglement in the Quantum Ring Network. In: 2018 9th International Symposium on Telecommunications (IST) (2018). p. 658–63. doi:10.1109/istel.2018.8661126

CrossRef Full Text | Google Scholar

26. Dietzfelbinger M, Madhavapeddy S, Sudborough IH. Three Disjoint Path Paradigms in star Networks. In: Proc.ieee Symp.parallel and Distributed Processing (1991). p. 400–6.

Google Scholar

27. Das G, Parthiban R, Tucker RS, Leckie C. Traffic Aggregation in Hybrid Ring-star Optical Networks. In: TENCON 2005 2005 IEEE Region 10 (2005). doi:10.1109/tencon.2005.301054

CrossRef Full Text | Google Scholar

28. Xu G, Chen XB, Li J, Wang C, Yang YX, Li Z. Network Coding for Quantum Cooperative Multicast. Quan Inf Process (2015) 14:4297–322. doi:10.1007/s11128-015-1098-6

CrossRef Full Text | Google Scholar

29. Pirker A, Wallnöfer J, Dür W. Modular Architectures for Quantum Networks. New J Phys (2018) 20:053054–87. doi:10.1088/1367-2630/aac2aa

CrossRef Full Text | Google Scholar

30. Briegel HJ, Dür W, Cirac JI, Zoller P. Quantum Repeaters: The Role of Imperfect Local Operations in Quantum Communication. Phys Rev Lett (1998) 81:5932–5. doi:10.1103/physrevlett.81.5932

CrossRef Full Text | Google Scholar

31. Dür W, Briegel HJ, Cirac JI, Zoller P. Quantum Repeaters Based on Entanglement Purification. Phys Rev A (1999) 59:169–81. doi:10.1103/physreva.59.169

CrossRef Full Text | Google Scholar

32. Pant M, Krovi H, Englund D, Guha S. Rate-distance Tradeoff and Resource Costs for All-Optical Quantum Repeaters. Phys Rev A (2017) 95:012304. doi:10.1103/physreva.95.012304

CrossRef Full Text | Google Scholar

33. Davidovich L, Maali A, Brune M, Raimond JM, Haroche S. Quantum Switches and Nonlocal Microwave fields. Phys Rev Lett (2018) 71(15):2360–3. doi:10.1103/PhysRevLett.71.2360

CrossRef Full Text | Google Scholar

34. Ahufinger V, Mebrahtu A, Corbalan R, Sanpera A. Quantum Switches and Quantum Memories for Matter-Wave Lattice Solitons. New J Phys (2006) 9(1):284–7.

Google Scholar

35. Zhang Z, Zeng G, Zhou N, Xiong J. Quantum Identity Authentication Based on Ping-Pong Technique for Photons. Phys Lett A (2006) 356(3):199–205. doi:10.1016/j.physleta.2006.03.048

CrossRef Full Text | Google Scholar

36. Broadbent A, Jeffery S. Quantum Homomorphic Encryption for Circuits of Low T-Gate Complexity. In: Crypto 2015 (2014).

Google Scholar

37. Krastanov S, Albert VV, Jiang L. Optimized Entanglement Purification. Quantum (2019) 3:123. doi:10.22331/q-2019-02-18-123

CrossRef Full Text | Google Scholar