Giant Panda Video Image Sequence and Application in 3D Reconstruction

Giant panda 3D reconstruction technology plays an important role in the research of giant panda protection. Through the analysis of giant panda video image sequence (GPVS), we prove that it has the long-range–dependent characteristics. This article proposes an algorithm to accurately reconstruct the giant panda 3D model by using the long-range–dependent characteristics of GPVS. First, the algorithm uses a skinned multi-animal linear model (SMAL) to obtain the initial 3D model of giant panda, and the 3D model of the single-frame giant panda image is reconstructed by controlling shape parameters and attitude parameters; then, we use the coherence information contained in the long-range–dependent characteristics between video sequence images to construct a smooth energy function to correct the error of the 3D model. Through this error, we can judge whether the 3D reconstruction result of the giant panda is consistent with the real structural characteristics of the giant panda. The algorithm solves the problem of low 3D reconstruction accuracy and the problem that 3D reconstruction is easily affected by occlusion or interference. Finally, we realize the accurate reconstruction of the giant panda 3D model.

1 Introduction

In recent years, in the field of animal protection, computer three-dimensional reconstruction methods are more and more used in the study of animal morphology. Giant pandas are China’s national treasures and first-class protected animals. China has established giant panda breeding research bases in many places for the protection and research of giant pandas. Through the research on the three-dimensional reconstruction of giant pandas, we can not only carry out non-contact body size measurement of giant pandas, including the measurement of giant pandas’ body height, body length, chest circumference, and weight, but also the protection workers can better understand the growth status of giant pandas, such as height, obesity, weight gain and loss, and body length increase and decrease, so as to further analyze the living environment and health status of giant pandas and to better protect giant panda species and improve the protection level of giant pandas. At the same time, through flexible and diversified forms such as rapid three-dimensional reconstruction and three-dimensional display, people can have a more intuitive and comprehensive understanding of the species of giant panda and further enhance people’s awareness of animal protection. This is not only helpful for animal protection but also beneficial to the whole society.

Since the giant panda is a nonrigid target, the traditional rigid body–based 3D reconstruction algorithm (Structure-from-Motion‐SFM [1], etc.) is not suitable for its 3D modeling. NRSFM (non-rigid structure-from-motion) is an extended SFM method. In 2000, Bregler first proposed the scientific question of how to recover the 3D nonrigid shape model [2] from the video sequence of single view. In 2013, Grag, Ravi, and other scholars used a variant algorithm for dense 3D reconstruction of nonrigid surfaces from monocular video sequences [3], which formulate the nonrigid structure of NRSFM into a global variational energy minimization problem. This method can reconstruct highly deformed smooth surfaces. In reference [4], a method for observing the dynamic motion of nonrigid objects from long monocular video sequences is adopted. This method makes use of the fact that many deformed shapes will repeat over time and simplifies NRSFM to a rigid problem.

In 2015, Matthew Loper and other scholars proposed a three-dimensional SMPL (skinned multi-person linear) model of human body using human shape and position [5]. In 2018, Angjoo Kanazawa et al. utilized a network framework for recovering a 3D human model from a 2D human image by the end-to-end method [6]. This method directly infers 3D-mesh parameters from image features and combines the 3D reconstruction method with deep learning.

Due to the uncontrollable behavior of giant pandas and other animals, the three-dimensional modeling algorithm suitable for human body cannot obtain high three-dimensional modeling accuracy. In 2017, Silvia Zuff et al. designed a 3D modeling method of animals based on a single image, using the 3D shape [7] and pose of animals to build the same statistical shape model as SMPL, called SMAL (skinned multi-animal linear model) [8, 9]. At present, the model has achieved satisfactory results in the application of three-dimensional reconstruction of several kinds of quadrupeds, such as three-dimensional reconstruction of dogs, horses, and cattle.

In the study, we found that the accuracy of the 3D giant panda model based on the single image is related to the results of 3D giant panda pose modeling based on the SMAL model. Because the temporal relationship between frames is not considered in the giant panda 3D model of single frame image data, the motion sequence composed of the results of single-frame pose modeling will be uneven and not smooth. Such errors are difficult to be automatically corrected in the single-frame algorithm. Therefore, the 3D reconstruction effect is usually unsatisfactory.

This article is organized as follows: in Section 2, we define the autocorrelation coefficient of GPVS (giant panda video image sequence) and discuss the long-range dependent of GPVS by analyzing the H index. In Section 3, we propose the giant panda 3D model. In Section 4, we took advantage of the new motion smoothing constraint to improve 3D accuracy by using frame-to-frame relationships. In Section 5, the experimental results of 3D modeling are presented, and in Section 6, we give the conclusion.

2 Long-Range Dependent of GPVS

2.1 ACF of GPVS

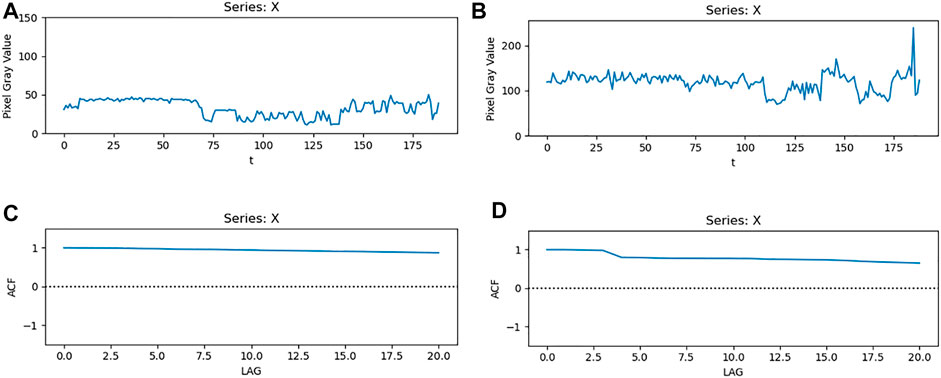
If the ACF value of a sequence is not zero or has a tailing phenomenon, we believe that the sequence may be long-range–dependent sequence [10].

Theorem: Let $X(i,j)$ be a sequence composed of pixel values at the coordinates of each image $(i,j)$ in GPVS, and let $x_t(t=\mathrm{1,2},\cdots ,n)$ is the gray value of the coordinates of frame t picture $(i,j)$ in sequence $X$, then,

$\mathit{acf}\left(\mathit{k}\right)=\frac{\mathit{n}}{\mathit{n}-\mathit{k}}\times \frac{{{\displaystyle \sum }}_{\mathit{t}=\mathit{k}+1}^{\mathit{n}}\left({\mathit{x}}_{\mathit{t}}-\mathit{\mu }\right)\left({\mathit{x}}_{\mathit{t}-\mathit{k}}-\mathit{\mu }\right)}{{{\displaystyle \sum }}_{\mathit{t}=1}^{\mathit{n}}\left({\mathit{x}}_{\mathit{t}}-\mathit{\mu }\right)\left({\mathit{x}}_{\mathit{t}}-\mathit{\mu }\right)},$(2.1)

where $\mathit{k}$ is the lag order ($\mathit{k}=\mathrm{0,1},\cdots ,\mathit{n}-1$), and $\mathit{\mu }$ is the mean of sequence $\mathit{X}$.

Proof. Let the mean $\mathit{\mu }$ of sequence $\mathit{X}$ be:

$\mathit{\mu }=\mathit{{\rm E}}\left(\mathit{X}\right).$(2.2)

Let the autocovariance ${\mathit{c}}_{\mathit{k}}$ of sequence $\mathit{X}$ be:

${\mathit{c}}_{\mathit{k}}=\frac{1}{\mathit{n}-\mathit{k}}{\displaystyle \sum }_{\mathit{t}=\mathit{k}+1}^{\mathit{n}}\left({\mathit{x}}_{\mathit{t}}-\mathit{\mu }\right)\left({\mathit{x}}_{\mathit{t}-\mathit{k}}-\mathit{\mu }\right),$(2.3)

where $\mathit{k}$ is the lag order ($\mathit{k}=\mathrm{0,1},\cdots ,\mathit{n}-1$).The ACF of sequence $\mathit{X}$ is:

$\mathit{acf}\left(\mathit{k}\right)=\frac{{\mathit{c}}_{\mathit{k}}}{{\mathit{c}}_0}.$(2.4)

Bring Eq. 2.3 into Eq. 2.4, we get

$\mathit{acf}\left(\mathit{k}\right)=\frac{\mathit{n}}{\mathit{n}-\mathit{k}}\times \frac{{{\displaystyle \sum }}_{\mathit{t}=\mathit{k}+1}^{\mathit{n}}\left({\mathit{x}}_{\mathit{t}}-\mathit{\mu }\right)\left({\mathit{x}}_{\mathit{t}-\mathit{k}}-\mathit{\mu }\right)}{{{\displaystyle \sum }}_{\mathit{t}=1}^{\mathit{n}}\left({\mathit{x}}_{\mathit{t}}-\mathit{\mu }\right)\left({\mathit{x}}_{\mathit{t}}-\mathit{\mu }\right)}.$(2.5)

This finishes the proof.Figure 1 is a first frame, a 60th frame, and a 1,800th frame image in the GPVS. Figure 2 shows that the ACF value of the GPVS is not equal to 0, and the ACF curve has a tailing effect, which indicates that the GPVS may be the long-range–dependent sequence.

FIGURE 1

FIGURE 1. Giant panda video image sequence. (A) First frame, (B) 60th frame, and (C) 1800th frame.

FIGURE 2

FIGURE 2. Pixel value and ACF value of GPVS. (A,C) GPVS of (300,400) and (B,D) GPVS of (600,800).

2.2 Hurst Exponent of GPVS

A Hurst exponent ($\mathit{H}$) is an index established by H.E. Hurst, a British hydrologist. Its essence is a judgment index, which can be used to judge whether the time series data are a random walk form or a biased random walk process.

When $0.5<\text{H}<1$, according to the model of fractional Gaussian noise, the time series data has long-range dependent (persistence), indicating that the time series has the characteristics of long-range dependent. If the sequence goes up in the previous period, it will continue to go up in the next period. When the $\mathit{H}$ value is close to 1, this trend is stronger [11, 12].

Through the analysis in Section 2.1, we can see that the GPVS sequence may have long-range–dependent characteristics. Next, we use the $\mathit{H}$ exponent to further judge that the GPVS has long-range–dependent characteristics, and use the $\mathit{H}$ exponent analysis method of [13] to calculate the $\mathit{H}$ exponent. The calculation process is as follows:

(1) Divide the sequence $\mathit{X}$ into $\mathit{G}$ groups of nonoverlapping subsequences with length $\mathit{n}$:

${\mathit{x}}_{11},{\mathit{x}}_{12},\dots ,{\mathit{x}}_{1\mathit{r}}{\mathit{x}}_{21},{\mathit{x}}_{22},\dots ,{\mathit{x}}_{2\mathit{r}}\mathit{ }\dots {\mathit{x}}_{\mathit{g}1},{\mathit{x}}_{\mathit{g}2},\dots ,{\mathit{x}}_{\mathit{gr}}.$

(2) Calculate the mean value ${\overline{\mathit{x}}}_{\mathit{i}}$ of each group of subsequences${\mathit{x}}_{\mathit{g}1},{\mathit{x}}_{\mathit{g}2},\dots ,{\mathit{x}}_{\mathit{gr}}\left(\mathit{i}=\mathrm{1,2},\cdots ,\mathit{g}\right)$.

${\overline{\mathit{x}}}_{\mathit{i}}=\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{n}}{\mathit{x}}_{\mathit{ij}}\mathit{ }\mathit{i}=\mathrm{1,2},\dots ,\mathit{g }\mathit{j}=\mathrm{1,2},\dots ,\mathit{n}\mathit{.}$(2.6)

(3) Calculated deviation ${\mathit{y}}_{\mathit{ij}}$:

${\mathit{y}}_{\mathit{ij}}={\mathit{x}}_{\mathit{ij}}-{\overline{\mathit{x}}}_{\mathit{i}}\mathit{i}=\mathrm{1,2},\dots ,\mathit{g}\mathit{j}=\mathrm{1,2},\dots ,\mathit{n}\mathit{.}$(2.7)

(4) Calculate cumulative deviation ${\mathit{z}}_{\mathit{ij}}$:

${\mathit{z}}_{\mathit{ij}}={\displaystyle \sum }_{\mathit{k}=1}^{\mathit{j}}{\mathit{y}}_{\mathit{ik}}\mathit{i}=\mathrm{1,2},\dots ,\mathit{g}\mathit{j}=\mathrm{1,2},\dots ,\mathit{n}\mathit{.}$(2.8)

(5) Calculate range ${\mathit{R}}_{\mathit{i}}$:

${\mathit{R}}_{\mathit{i}}=\mathbf{max}\left({\mathit{z}}_{\mathit{ij}}\right)-\mathbf{min}\left({\mathit{z}}_{\mathit{ij}}\right)\mathit{i}=\mathrm{1,2},\dots ,\mathit{g}\mathit{j}=\mathrm{1,2},\dots ,\mathit{n}\mathit{.}$(2.9)

(6) Calculate standard deviation ${\mathit{S}}_{\mathit{i}}$:

${\mathit{S}}_{\mathit{i}}=\sqrt{\frac{1}{\mathit{n}-1}{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{n}}{\mathit{y}}_{\mathit{ij}}^{\mathit{2}}}\mathit{i}=\mathrm{1,2},\dots ,\mathit{g}\mathit{.}$(2.10)

(7) Get value $\mathit{R}{\mathit{S}}_{\mathit{i}}$:

$\mathit{R}{\mathit{S}}_{\mathit{i}}=\frac{{\mathit{R}}_{\mathit{i}}}{{\mathit{S}}_{\mathit{i}}} \mathit{i}=\mathrm{1,2},\dots ,\mathit{g}\mathit{.}$(2.11)

The average value $\overline{\mathit{RS}}$ of each subsequence was obtained:

$\overline{\mathit{RS}}=\frac{1}{\mathit{g}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{g}}\mathit{R}{\mathit{S}}_{\mathit{i}}.$(2.12)

Finally, $\mathbf{log}\overline{\mathit{RS}}$ as the explained variable $\mathit{Y}$ and $\text{log}n$ as the explanatory variable $\mathit{X}$, the data pair ($\mathbf{log}\mathit{n}$, $\mathbf{log}\overline{\mathit{RS}}$) is obtained for each grouping ${\mathit{X}}_{\mathit{n}}\left(\mathit{k}=\mathrm{1,2},\cdots ,\mathit{m}\right)$, and the slope $\mathit{H}$ is estimated by linear regression, that is, the Hurst index.

Figure 3A shows the sequence $\mathit{H}$ value composed of the values of (300,400) in 190 giant panda video images, $\mathit{H}=0.906348$. Figure 3B shows the $\mathit{H}$ value distribution of all pixels in 190 giant panda video images.

FIGURE 3

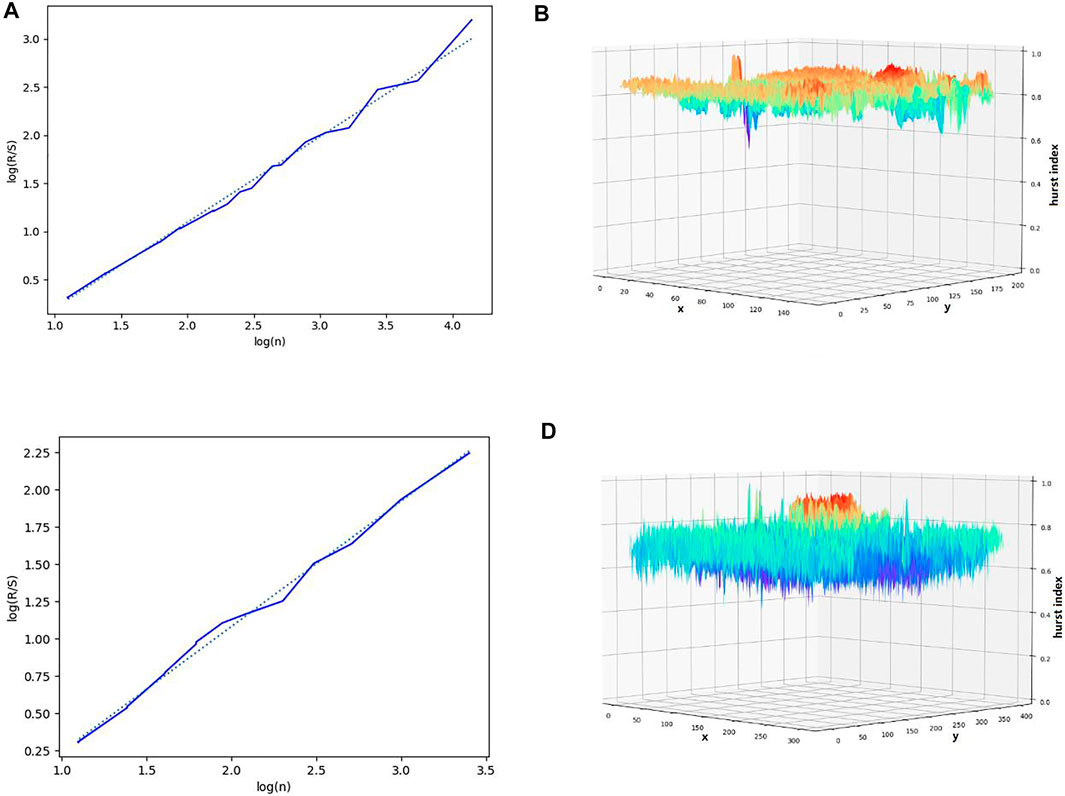
FIGURE 3. Hurst exponent. (A) Hurst exponent of GPVS1 (300,400), (B) Hurst exponent of GPVS1, (C) Hurst exponent of GPVS2 (600,800), and (D) Hurst exponent of GPVS2.

Figure 3C shows the sequence $\mathit{H}$ value composed of the values of (600,800) in 127 giant panda video images, $\mathit{H}=0.840534$. Figure 3D shows the $H$ distribution of all pixels in 127 giant panda video images.

From Figure 3, we can see that the $\mathit{H}$ value of the giant panda video image sequence is far greater than 0.5, close to 1, indicating that GPVS has long-range–dependent characteristics.

3 Giant Panda 3D Modeling

3.1 Giant Panda Skeleton

The structure formed by a series of joints and bones is called the skeleton. Each joint can correspond to one or more bones and can have multiple subjoints. A correct skeleton structure can ensure that the giant panda has a real and correct motion structure after three-dimensional modeling, which is one of the important links of the giant panda model.

The selection of bones and joints will affect the deformation of the three-dimensional model of the giant panda. Therefore, the analysis of the skeleton structure of the giant panda plays a very important role in the three-dimensional model of the giant panda. Figure 4A shows the detailed skeleton system of the giant panda. In the SMAL model, we usually use 33 joints to represent five kinds of quadrupeds with different attributes, such as cats, dogs, equines, cattle, and hippopotamuses [9, 14]. Compared with these five kinds of quadrupeds, the giant panda has certain similarities, so most of the bones and joints in the whole skeleton can be used for reference, such as head, spine, and leg bone structures.

FIGURE 4

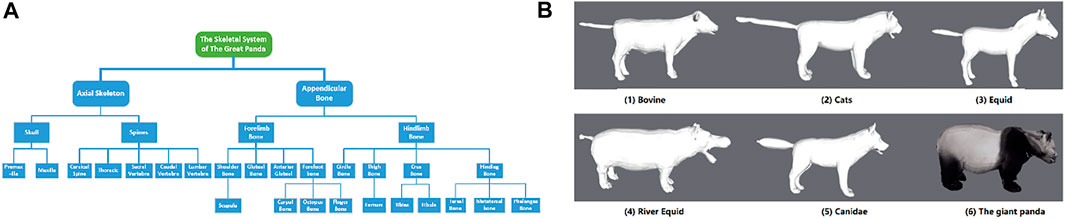
FIGURE 4. Giant panda skeleton. (A) Giant panda skeleton system. (B) Differences between giant panda skeleton and other animals.

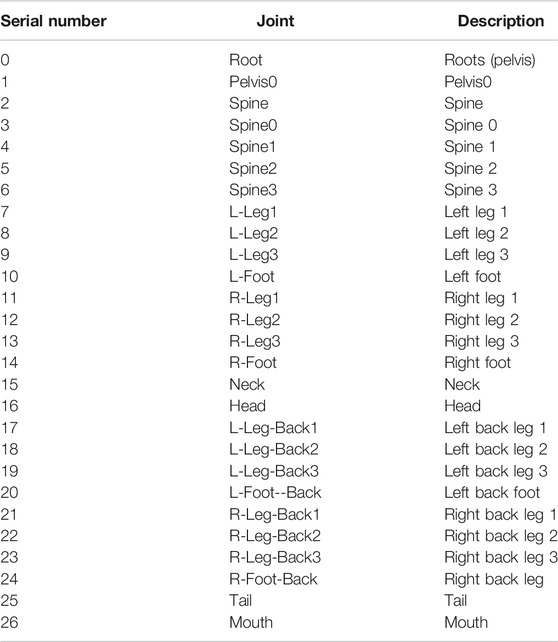
However, the characteristics of giant panda and other quadrupeds are also different in the skeleton structure, as shown in Figure 4B. The tail of the adult giant panda is very short. The body length of the giant panda is about 120–180 cm, while the tail length is only about 10–12 cm. Some tails are shorter than the tail of the rabbit, so we cannot feel the existence of the tail of the giant panda intuitively. In the whole movement structure, we combined the structural characteristics of the giant panda and combined the seven joints of the tail. We used 27 joints as the basic skeleton structure of the giant panda, as shown in Table 1.

TABLE 1

TABLE 1. Joint description of the giant panda skeleton.

3.2 Giant Panda SMAL Model

Since it is impossible to obtain the three-dimensional model of giant panda by scanning the living body of giant panda, this article uses the designed three-dimensional model of giant panda to bind the skeleton [15], as shown in Figure 5. The SMAL model is shown in Formula 3.1. Linear blending skinning (LBS) is used to generate giant panda models with different shapes and postures, so as to build the giant panda shape data set and attitude data set, as shown in Figure 6.

$\begin{array}{c}\{\begin{array}{c}\mathit{S}\left(\mathit{\beta }\right)=\overline{\mathit{S}}+{\mathit{B}}_{\mathit{S}}\mathit{\beta }\\ {\mathit{T}}_{\mathit{p}}^{\mathit{\prime }}={\overline{\mathit{T}}}_{\mathit{p}}+{\mathit{B}}_{\mathit{p}}\left(\mathit{\theta }\right)\end{array}\end{array},$(3.1)

where $\mathit{S}\left(\mathit{\beta }\right)$ is the deformation shape parameter of giant panda, $\overline{\mathit{S}}$ is the giant panda average model, $\mathit{\beta }$ is the shape parameter, and ${\mathit{B}}_{\mathit{S}}$ is the shape basis matrix of the eigenvector.

FIGURE 5

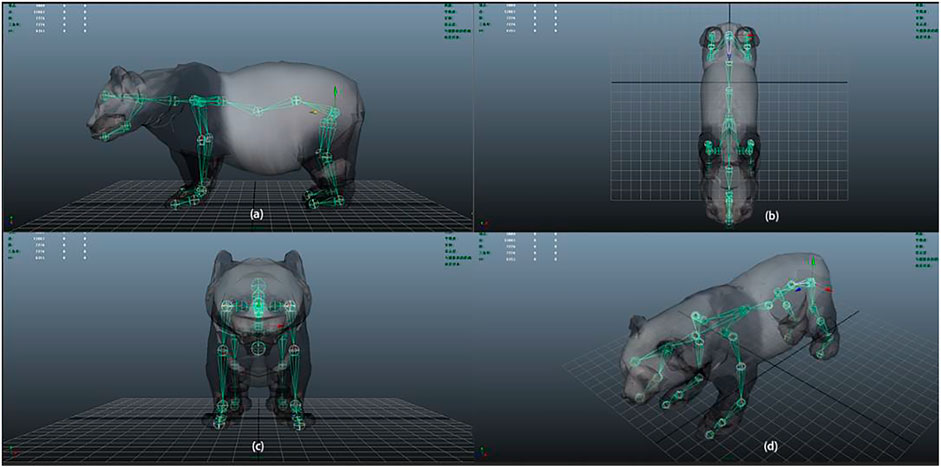
FIGURE 5. 3D model of a giant panda is bound by a giant panda skeleton. (A) Side view, (B) top view, (C) front view, and (D) oblique view.

FIGURE 6

FIGURE 6. Giant panda SMAL model. (A) Giant panda shapes obtained by SMAL. (B) Panda poses obtained by SMAL.

$\mathit{P}$ is a matrix composed of 243 attitude vectors ${\mathit{P}}_{\mathit{i}}$, ${\mathit{T}}_{\mathit{P}}^{\text{'}}$ is a giant panda posture model, ${\overline{\mathit{T}}}_{\mathit{P}}$ is the average posture model, $\mathit{\theta }$ is the joint rotation angle, and ${\mathit{B}}_{\mathit{P}}\left(\mathit{\theta }\right)$ is the vertex offset between the posture model at angle $\mathit{\theta }$ and the average attitude model.

4 Motion Smoothing Process

The 3D model of giant panda reconstructed from a single-frame video image does not take into account the time relationship between frames and the long-range–dependent characteristics of the video image sequence. When the target is obscured or has large noise, there will be relatively large 3D reconstruction errors, such as left leg matching to right leg and right leg matching to left leg. Moreover, the motion sequence composed of the results of single-frame 3D modeling will be not smooth [16].

For video image sequences, the long-distance dependent between data is used to capture the correlation between pixels of distant frames in the sequence, which is more conducive to the recognition and judgment of image information. In Section 2.2, we have analyzed that the GPVS has long-distance–dependent characteristics, so we will use the characteristics of the GPVS to improve the giant panda 3D modeling.

In order to improve the accuracy of the single-frame pose modeling algorithm, we fully consider that the RGB video sequence has long-range–dependent characteristics. That is, the movement and limb rotation angle of the giant panda in the video sequence shall not change too much. We use this characteristic to correct the error of 3D modeling results, so as to make the 3D modeling results of giant panda more smooth and accurate.

First, the body shape parameters β and attitude parameters θ of giant pandas in each frame of the video are solved by Eq. 3.1. Then, the energy function formula 4.1 is used to construct the time-smoothing term to improve the motion fluency and 3D reconstruction accuracy.

${\mathit{E}}_{\mathit{n}}\left(\mathit{\beta },\mathit{\theta }\right)={\mathit{\lambda }}_{3\mathit{d}}{\mathit{E}}_{3\mathit{d}}\left(\mathit{\beta },\mathit{\theta }\right)+{\mathit{\lambda }}_{\mathit{sm}}{\mathit{E}}_{\mathit{sm}}\left(\mathit{\beta },\mathit{\theta }\right),$(4.1)

where ${\mathit{\lambda }}_{3\mathit{d}}$ ${\mathit{\lambda }}_{\mathit{sm}}$ is the weight parameter of the corresponding energy term, ${\mathit{E}}_{3\mathit{d}}$ is the three-dimensional error energy, and ${\mathit{E}}_{\mathit{sm}}$ is the motion-smoothing energy.

(1) 3D attitude error

$\{\begin{array}{c}{\mathit{E}}_{3\mathit{d}}={\displaystyle \sum }_{\mathit{n}}{\mathit{w}}_{\mathit{n}}\mathit{dist}\left({\mathit{\theta }}_{\mathit{n}},{\widehat{\mathit{\theta }}}_{\mathit{n}}\right)\\ {\mathit{w}}_{\mathit{n}}=\mathbf{exp}\left(-{\mathit{\delta }}_{\mathit{n}}\right)\\ {\mathit{\delta }}_{\mathit{n}}={\displaystyle {\sum }_{\mathit{j}}{\mathit{C}}_{\mathit{n},\mathit{j}}\Vert {\mathit{x}}_{\mathit{n,j}}-{{\widehat{\mathit{x}}}_{\mathit{n},\mathit{j}}\Vert }_2^2}\end{array},$(4.2)

where dist is the distance between the SMAL 3D model and the 3D model after rotation. ${\mathit{x}}_{\mathit{n},\mathit{j}}$ and ${\mathit{C}}_{\mathit{n},\mathit{j}}$ is the two-dimensional coordinates of the joint in the nth frame of the video and its confidence, and ${\mathit{x}}_{\mathit{n},\mathit{j}}$ is the two-dimensional joint coordinates projected from the three-dimensional joint of the model to the image.

The main function of this item is to slightly adjust the first three-dimensional vector of the attitude parameters of the SMAL model to adjust the rotation angle of the model while maintaining the consistency between the projection of the three-dimensional attitude of the model and the results of the two-dimensional joint points, so as to improve the accuracy of attitude modeling and restrain some problems of incorrect pose estimation of the model, so as to ensure the accuracy of the attitude modeling algorithm.

(2) Motion smoothing

${\mathit{E}}_{\mathit{sm}}={\displaystyle \sum }_{\mathit{n}}{\displaystyle \sum }_{\mathit{j}}{\begin{array}{c}\Vert {\mathit{J}}_{\mathit{i}}\left({\mathit{\beta }}_{\mathit{n}},\mathit{\theta }\right)-{\mathit{J}}_{\mathit{i}}\left({\mathit{\beta }}_{\mathit{n}+1},\mathit{\theta }\right)\Vert \end{array}}_2^2,$(4.3)

where ${\mathit{J}}_{\mathit{i}}$ is the function of the coordinates of the three-dimensional joint numbered I of the SMAL model given the shape and attitude parameters of the SMAL model.

This item uses the similarity of giant panda actions in adjacent frames of the video to constrain the changes of three-dimensional bone joints of the model. The greater the change of model posture from the previous frame, the greater the energy value of this item. In case of large errors, due to image feature mismatch or over-fitting, this item can be constrained to correct some large errors such as leg exchange or posture inversion.

5 Discussion

Our experimental work is based on the prior information of the giant panda SMAL model. According to two-dimensional images of the giant panda, the algorithm uses Formula 3.1 to obtain the shape, pose, and other parameters of the three-dimensional model of the giant panda and reconstructs a 3D model of the giant panda. Then, the 3D reconstruction accuracy is improved by Eq. 4.1, and the motion fluency of the 3D model is improved, and the 3D reconstruction results of giant panda are shown in Figures 7–10.

FIGURE 7

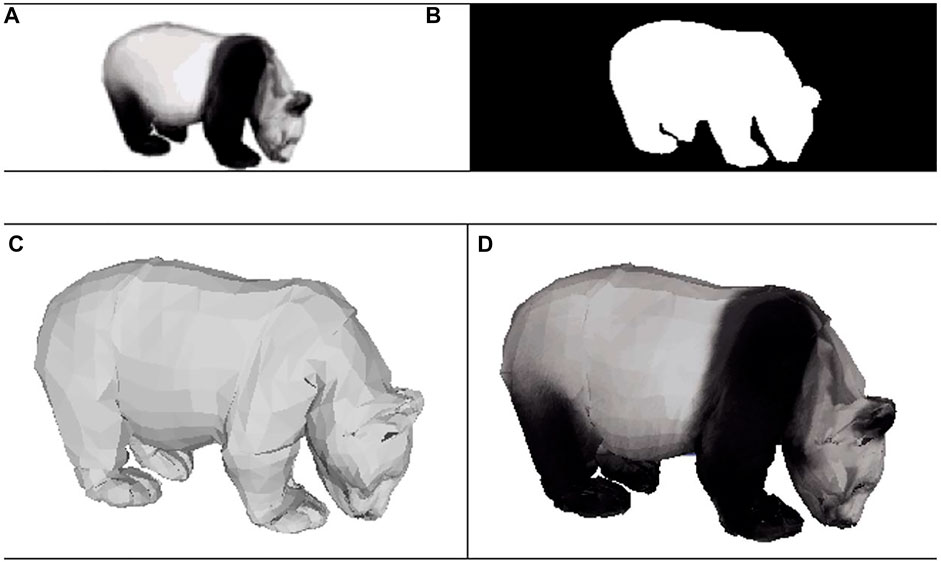
FIGURE 7. 3D reconstruction of GPVS in frame 10. (A) Original image, (B) contour silhouette after segmentation, (C) reconstruction effect of the 3D model of the giant panda without skin texture, and (D) reconstruction effect of the 3D model of the giant panda with skin texture.

FIGURE 8

FIGURE 8. 3D reconstruction of GPVS in frame 30. (A) Original image, (B) contour silhouette after segmentation, (C) reconstruction effect of the 3D model of the giant panda without skin texture, and (D) reconstruction effect of the 3D model of the giant panda with skin texture.

FIGURE 9

FIGURE 9. 3D reconstruction of GPVS in frame 60. (A) Original image, (B) contour silhouette after segmentation, (C) reconstruction effect of the 3D model of the giant panda without skin texture, and (D) reconstruction effect of the 3D model of the giant panda with skin texture.

FIGURE 10

FIGURE 10. 3D reconstruction of GPVS in frame 100. (A) Original image, (B) contour silhouette after segmentation, (C) reconstruction effect of the 3D model of the giant panda without skin texture, and (D) reconstruction effect of the 3D model of the giant panda with skin texture.

Figures 7–10 show the experimental results of the algorithm in restoring the SMAL giant panda 3D model from the image. The upper left figure of each group of images is the original image, the upper right figure is the segmented contour silhouette, and the lower left corner and lower right corner are the reconstruction effects of the giant panda 3D model without skin texture and with skin texture, respectively. It is obvious that there is a good fit between the image and the restored three-dimensional model of giant panda.

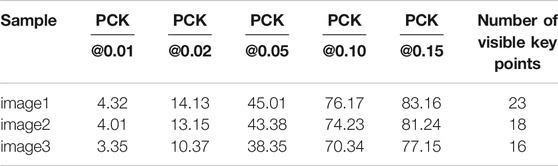
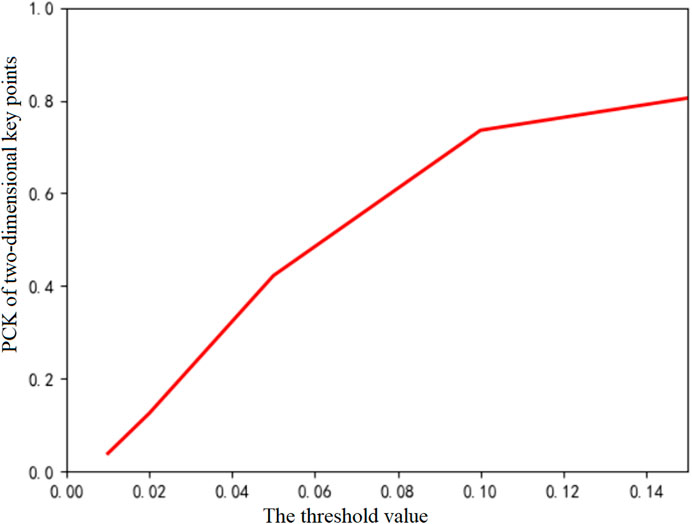
Table 2 shows the PCK indicators under different thresholds for some image examples. Figure 11 shows the visualization results of the mean value of the evaluation index PCK between the projection key points obtained after the restoration of the three-dimensional model of the giant panda and the truly marked key points of the input image. When the threshold of key point detection is PCK@0.15 (corresponding to 0.15 times of image pixels), the accuracy can reach 80.51%. Therefore, experiments show that our method can also obtain a 3D model of giant panda with a good reconstruction effect in the presence of occlusion or insufficient key points.

TABLE 2

TABLE 2. PCK results table of different thresholds.

FIGURE 11

FIGURE 11. PCK indicators.

6 Conclusion

Through the analysis of GPVS, we prove that it has the long-range–dependent characteristics [17, 18]. We propose a method to use the coherent information contained in the long-range–dependent characteristics between video sequence images to construct a smooth energy function to correct the 3D model error. Through this error, we can judge that the 3D reconstruction result of giant panda is different from the real structure of giant panda. Finally, the experimental results show that our algorithm can obtain a more accurate 3D reconstruction model of giant panda.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials; further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research is supported by the Chengdu Research Base of Giant Panda Breeding (NOs. 2020CPB-C09 and CPB2018-01).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Schönberger JL, Frahm JM. Structure-from-Motion Revisited[C]. In: IEEE Conference on Computer Vision & Pattern Recognition; 2016 Jun 27–30; Las Vegas, Nevada (2016).

Google Scholar

2. Bregler C, Hertzmann A, Biermann H. Recovering Non-Rigid 3D Shape from Image Streams[C]. In: IEEE Conference on Computer Vision & Pattern Recognition; 2000 Jun 13–15; Hilton Head, SC. IEEE (2000).

Google Scholar

3. Garg R, Roussos A, Agapito L. Dense Variational Reconstruction of Non-Rigid Surfaces from Monocular Video[C]. In: IEEE Conference on Computer Vision and Pattern Recognition; 2013 Jun 23–28; NW Washington, DC. IEEE (2013).

Google Scholar

4. Li X, Li H, Joo H, Liu Y, Sheikh Y. Structure from Recurrent Motion: From Rigidity to Recurrency[J] (2018). Salt Lake City, UT: IEEE CVPR.

Google Scholar

5. Loper M, Mahmood N, Romero J, Black MJ. SMPL: A Skinned Multi-Person Linear model[J]. Kobe, Japan: ACM Transactions on Graphics TOG (2015).

Google Scholar

6. Kanazawa A, Black MJ, Jacobs DW, Malik J. End-to-end Recovery of Human Shape and Pose[J] (2017). Salt Lake City, UT: IEEE CVPR, 2018.

Google Scholar

7. Zuffi S, Kanazawa A, Jacobs D, Black MJ. 3D Menagerie: Modeling the 3D Shape and Pose of Animals. In: IEEE Conf. on Computer Vision and Pattern Recognition(CVPR); 2017 Jul 21–26; Hawaii Convention Center, Hawaii (2017). doi:10.1109/cvpr.2017.586

CrossRef Full Text | Google Scholar

8. Vicente S, Agapito L. Balloon Shapes: Reconstructing and Deforming Objects with Volume from Images[C]. In: International Conference on 3d Vision-3dv; 2013 Jun 29–Jul 01; Seattle, WA. IEEE (2013).

Google Scholar

9. Biggs B, Roddick T, Fitzgibbon A, Cipolla R. Creatures Great and SMAL: Recovering the Shape and Motion of Animals from Video. In: Asian Conference on Computer Vision; 2018 Dec 04–06; Perth, Australia (2018).

Google Scholar

10. Li M. Fractal Time Series—A Tutorial Review. Math Probl Eng (2010) 2010:157264. doi:10.1155/2010/157264

CrossRef Full Text | Google Scholar

11. Li M. Modified Multifractional Gaussian Noise and its Application. Physica Scripta (2021) 96(12):125002. doi:10.1088/1402-4896/ac1cf6

CrossRef Full Text | Google Scholar

12. Li M. Generalized Fractional Gaussian Noise and its Application to Traffic Modeling. Physica A (2021) 579(22):126138. doi:10.1016/j.physa.2021.126138

CrossRef Full Text | Google Scholar

13. Peltier RF, Levy-Vehel J. Multifractional Brownian Motion: Definition and Preliminaries Results. INRIA TR 2645 (1995).

Google Scholar

14. Zuffi S, Kanazawa A, Black M. Lions and Tigers and Bears: Capturing Non-Rigid 3D. Salt Lake City, UT: Articulated Shape from Images (2018).

Google Scholar

15. Bogo F, Kanazawa A, Lassner C, Gehler P, Romero J, Black MJ. Keep it SMPL: Automatic Estimation of 3D Human Pose and Shape from a Single Image. In: European Conference on Computer Vision; 2016 Oct 11–14; Amsterdam, Netherlands (2016).

CrossRef Full Text | Google Scholar

16. Zhang H. Research on 3D Human Modeling and its Application Based on SML Model. Xian, Shaanxi, China: Shaanxi University of Science & Technology (2020).

Google Scholar

17. He J, George C, Wu J, Li M, Leng J. Spatiotemporal BME Characterization and Mapping of Sea Surface Chlorophyll in Chesapeake Bay (USA) Using Auxiliary Sea Surface Temperature Data. Sci Total Environ (2021) 794(1):148670. doi:10.1016/j.scitotenv.2021

PubMed Abstract | CrossRef Full Text | Google Scholar

18. He J. Application of Generalized Cauchy Process on Modeling the Long-Range Dependence and SelfSimilarity of Sea Surface Chlorophyll Using 23 Years of Remote Sensing Data. Front Phys (2021) 9:750347. doi:10.3389/fphy.2021.750347

CrossRef Full Text | Google Scholar