- 1International Academic Center of Complex Systems, Beijing Normal University, Zhuhai, China
- 2School of Systems Science, Beijing Normal University, Beijing, China
- 3Institute for Theoretical Physics, University of Cologne, Köln, Germany
Characterizing the reputation of an evaluator is particularly significant for consumers to obtain useful information from online rating systems. Furthermore, overcoming the difficulties of spam attacks on a rating system and determining the reliability and reputation of evaluators are important topics in the research. We have noticed that most existing reputation evaluation methods rely only on using the evaluator’s rating information and abnormal behaviour to establish a reputation system, which disregards the systematic aspects of the rating systems, by including the structure of the evaluator-object bipartite network and nonlinear effects. In this study, we propose an improved reputation evaluation method by combining the structure of the evaluator-object bipartite network with rating information and introducing penalty and reward factors. The proposed method is empirically analyzed on a large-scale artificial data set and two real data sets. The results have shown that this method has better performance than the original correlation-based and IARR2 in the presence of spamming attacks. Our work contributes a new idea to build reputation evaluation models in sparse bipartite rating networks.
1 Introduction
The flourishing development of e-commerce has broad and far-reaching impacts on our daily lives, leading consumers to increasingly rely on using the internet to obtain information about products and services that help them decide how to consume [1–4]. However, with an overwhelming amount of products and services available, potential users may overloaded with information such as that from big data of the quality attributes, performance attributes, and previous reviews [5, 6]. To solve the information overload of users, some e-commerce platforms have implemented online rating systems to help users fuse information, where evaluators are encouraged to present reasonable ratings for the objects [7]. These ratings are representations of the inherent quality of objects and reflections of evaluators’ credibility. In reality, current rating systems face many challenges. Unobjective ratings may be given simply because some users are unacquainted with the relevant field or due to their poor judgments [8]. However, unreliable evaluators even deliberately give maximal/minimal ratings for various psychosocial reasons [9–11]. These ubiquitous noises and distorted information purposefully mislead evaluators’ choices and decisions and have a wicked effect on the reliability of the online rating systems [12, 13]. Therefore, establishing a reliable and efficient reputation evaluation system is an extremely urgent task for an online rating system, which has a huge impact not only against spam attacks but also on the economy and society [14, 15].
In various evaluation systems, the reputation management of evaluators contributes to social governance. For instance, as an important platform for providing health services, online health communities are favoured by both physicians and patients as these communities establish an effective service channel between them [16]. In the evaluation of research funding applications, peer reviewers must distinguish the best applications from relatively weaker ones to appropriately allocate funding. Only peer reviewers with a good reputation can correctly guide the highly competitive allocation of limited resources [17, 18]. Moreover, the online reputation system for job seekers helps employers better understand job seekers and decide whether to hire them [19]. Similar problems exist in other scenarios, e.g., recommendations, selection, and voting, in which the credibility of the evaluators will affect the final result. One of the most important ways to solve this problem is by building reputation-evaluation systems [20–23].
Over the past decades, researchers have been increasingly interested in modelling reputations on web-based rating platforms [24, 25]. The earlier method of measuring the reputation of online evaluators is the iterative refinement (IR) algorithm designed by Laureti [26]. The correlation-based ranking (CR) method proposed in [27] by Zhou et al. is the most representative method, and it is robust against spam attacks. Very recently, the IARR2 algorithm was proposed by introducing two penalty factors to improve the CR method [28]. These aforementioned methods are based on the assumption that each rating given by the evaluators is the most objective reflection of the quality of the objects. Another kind of thinking is to consider the behavioural features of the evaluators in bipartite networks. Gao et al. proposed group-based ranking (GR) and iterative group-based ranking (IGR) algorithms, which group evaluators according to their ratings [29, 30] and measure the evaluators’ reputation according to the sizes of the corresponding groups [31]. Other scholars employed the deviation-based ranking (DR) method to model evaluators’ reputation [32], and Sun et al. combined this method with GR to construct the iterative optimization ranking (IOR) [33]. In addition, there are some other methods, such as the Bayesian-based method [7, 34] and others [35]. One can also read the review literature on reputation systems [36] for further insight.
Nevertheless, most existing reputation evaluation algorithms neglect the systematic aspects of the rating systems, especially the structural information of the evaluator-object bipartite network and nonlinear effects, both of which are core factors in complex systems. Considering that these factors lead to some new ideas to improve the classical CR method, in this paper, we introduce a new reputation evaluation method by combining the CR method with the clustering coefficient of evaluators in the evaluator-object bipartite network. Meanwhile, we also believe that if an evaluator has a relatively high reputation, he should receive some rewards to enhance his reputation further, and vice versa. Therefore, we construct a penalty reward function to update the weight of the evaluator’s reputation. Extensive experiments on artificial data and two well-known real-world datasets suggest that the proposed method has higher accuracy and recall score of spammer identification. Its overall performance exceeds that of the classical CR method.
The remainder of this paper is organized as follows. The proposed reputation-evaluation method is described in detail in Section 2. Section 3 introduces the data and evaluation metrics. The experimental study and results are discussed and analysed in Section 4. Finally, conclusions are given in Section 5.
2 Methods
We first briefly introduce some basic notations for online rating systems, which can be naturally represented as a weighted evaluator-object bipartite network. The set of evaluators is denoted E, and the set of objects is denoted O. The numbers of evaluators and objects are recorded as |E| and |O|, respectively. We use Latin and Greek letters for evaluator-related and object-related indices, respectively. The degree of evaluator i and object α are indicated by ki and kα, respectively. The weight of the link in the bipartite network is the rating given by evaluator i to object α, denoted by riα, and riα ∈ (0, 1). The set Eα describes the evaluators who rate object α, and the set Oi defines the objects rated by evaluator i.
A reputation value Ri should be assigned to each evaluator i by a reputation evaluation method. This value measures the evaluator’s ability to reflect the intrinsic quality of the objects or items accurately, known as credibility. Similarly, each object α has a true quality that most objectively reflects its character. However, in practice, it is extremely challenging for us to determine the intrinsic quality of an object, and we usually estimate quality Qα with the weighted average of the ratings that object α has obtained. It is shown as
where the initial reputation of each evaluator is set as Ri = ki/|O|.
Second, the CR method defines that the reputation is measured by the correlation between the rating vector from the evaluator and the corresponding quality vectors of the objects. We calculate the evaluator’s temporary reputation as
where
Next, we expect to refine the evaluator’s reputation. In principle, when an evaluator rates the objects that are also familiar by the other evaluators, this evaluator is more likely to have a high reputation due to the popularity of these objects. As we mentioned in the introduction section, the clustering coefficient in the bipartite graph network are employed to refine the reputation of evaluators. Despite the one-mode projection network providing the interaction between each group member, it should be noted that substantial information may disappear after projection [37]. This paper adopts the concept of the clustering coefficient extended by Latapy et al. [37], who first defines the clustering coefficient for pairs of nodes cc (ei, ej). Mathematically, it reads
Here, N (ei) denotes the objects evaluated by evaluator i, i.e., the neighbours of node i, and |⋅| denotes the number of elements in the set. Then, the clustering coefficient for one node is expressed as
We now refine the reputation of evaluators according to the clustering coefficient of each evaluator. This modified method is referred to as CRC, and can be expressed as follows:
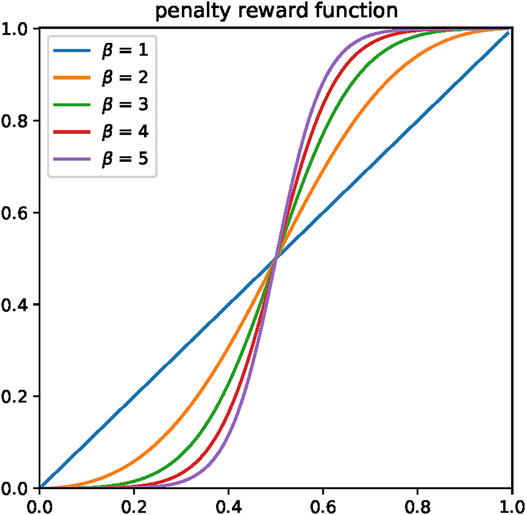
For evaluators with different reputation values, their credibility is different, so we rescale their reputation by nonlinear recovery. The penalty-reward function is used to update evaluators’ reputation, which will allocate higher reputation as a reward to evaluators with a high reputation. In contrast, a penalty is given to further reduce the reputation of evaluators with a low reputation. The function is
This enhanced method is referred to as CRCN, and the function image is shown in Figure 1. The CRCN method will degrade to CRC when β = 1.
The evaluator reputation Ri and the quality of object Qα are iteratively updated using eqs. (1) to (6) until the change of the quality |Q − Q″| is less than the threshold value, and it is calculated in Eq. 7. In the process of reputation updating, the reputation of evaluators with higher clustering coefficient will be more rewards through nonlinear recovery, and vice versa. The effects of refining the reputation and estimating the quality are gradually accumulated in each step of the recurring algorithm.
where Q″ is the quality from the previous step, and the threshold is set as 10–6.
Finally, we sort evaluators in ascending order according to their reputation value, and the evaluators with L smallest reputation values are identified as spammers.
3 Data and Metrics
3.1 Artificial Rating Data
To generate the artificial dataset, we generate a bipartite network with 6,000 evaluators and 4,000 objects, i.e., |E| = 6,000 and |O| = 4,000. The network sparsity is set as η = 0.02, which means that the total number of weighted links (ratings) is 0.02 ×|E‖O| = 4.8 × 105. We employ the preferential attachment mechanism [38] to choose a pair of evaluator and object and add a link between them. At each time step t, the probabilities of selecting evaluator i and object α are
where ki(t) and kα(t) are the degrees of evaluator i and object α at time step t.
We suppose that the rating riα given by evaluator i to object α is composed of the intrinsic quality of object
Both evaluators’ ratings and objects’ qualities are limited to the range (0, 1).
3.2 Real Rating Data
We consider two commonly studied datasets in real online rating systems—MovieLens and Netflix, which contain ratings for movies provided by GroupLens (www.grouplens.org) and Netflix Prize (www.netflixprize.com), respectively—to investigate the effectiveness and accuracy of the proposed methods. These two datasets are given by integer ratings scaling from 1 to 5, with 1 being the worst and 5 being the best. Herein, we sample a subset from the original datasets in which each evaluator has at least 20 ratings. Table 1 presents some basic statistical properties for these two datasets.

TABLE 1. Basic statistical properties of the real datasets used in this paper, where
It is well known that ranking all evaluators and comparing them with the ground truth is an effective way to measure the performance of different evaluation algorithms. However, in real systems, there are no ground-truth ranks for evaluators. We manipulate the real dataset by randomly selecting some evaluators and assigning them as artificial spammers to test the proportion of these spammers detected by an evaluation method. In the implementation, we randomly select ρ fractions of evaluators and turn them into spammers by replacing their original ratings with distorted ratings: random integers in the set (1, 2, 3, 4, 5) for random spammers or integer 1 or 5 for malicious spammers. Thus, the number of spammers is d = ρ|E|. We also set ω = k/|O| as the activity of spammers; here, k is the degree of each spammer and is a tuneable parameter. If a spammer’s original degree ki ≥ k, then k ratings are randomly selected and replaced with distorted ratings, and the unselected ki − ω|O| ratings are ignored; if ki < k, we first replace all the spammer’s original ratings and randomly select k − ki of his/her unrated ratings and assign them with distorted ratings.
3.3 Evaluation Metrics
To evaluate the robustness and effectiveness of the reputation-evaluation methods, we adopt four widely used metrics: Kendall’s tau [39], AUC (the area under the ROC curve) [40], recall [41], and ranking score [42].
Kendall’s tau (τ) measures the rank correlation between the estimated quality of objects Q and their intrinsic quality Q′:
where
AUC measures the accuracy of the reputation evaluation methods. In artificial datasets, one can select a part of high-quality objects as benchmark objects, and the remaining objects are regarded as nonbenchmark objects. Here, we select 5% of the highest-quality objects as the benchmark objects. Nevertheless, in empirical datasets, as mentioned above, we randomly designate some evaluators as spammers. When the reputation of all evaluators is provided, the AUC value can essentially be interpreted as the probability that the reputation of a randomly chosen normal evaluator is higher than the reputation of a randomly selected spammer. To calculate the AUC values, we control N independent comparisons of the reputations of a pair of normal evaluator and spammer and record N′ as the number of times the spammer has a lower reputation and N″ as the number of times the spammer has the same reputation. Then, the value of AUC is defined as
Therefore, the higher the AUC is, the more accurate the evaluation method is. If the AUC value is 0.5, it indicates that the method is randomly ranked for all evaluators.
The recall describes the proportion of spammers that can be identified among L evaluators with the lowest reputation. Mathematically, it can be defined as
where d′(L) is the number of detected spammers in the L lowest ranking list, and the range of Rc is [0, 1]. A higher Rc indicates a higher accuracy for reputation ranking.
The ranking score (RS) characterizes the effect of evaluation methods by focusing more on the influence of ranking position. Given the ranking of all evaluators, we measure the position of all spammers in the evaluator ranking list. The ranking score is obtained by averaging the rankings of all spammers, and the specific formula is as follows:
where li indicates the rank of spammer i in the evaluator ranking list, and Es denotes the set of spammers. Accordingly, RS has the range [0, 1]. A good evaluation algorithm is expected to give the spammer a higher rank, which causes a small ranking score. The smaller the RS is, the higher the ranking accuracy, and vice versa.
4 Results and Discussion
We analyse the performance of the two proposed algorithms for the artificial dataset and two commonly studied empirical datasets and compare them with the classical CR algorithm and IARR2 algorithm.
4.1 Results From Artificial Rating Data
A well-performing evaluation algorithm should defend against any distorted information. We first calculate the values of Kendall’s tau τ and AUC on the generated artificial rating data, including spammers, to investigate the robustness of the proposed two methods and the original CR method in protecting against different spammers. We suppose there are two types of distorted ratings: random ratings and malicious ratings. Random ratings mainly come from mischievous evaluators who provide arbitrary and meaningless rating values, and malicious ratings indicate that spammers always give maximum or minimum allowable rating values to push the target object’s rating up or down.
To create noisy information for the artificial datasets, we randomly switch p fractions of the links with the distorted ratings The larger the value of p is, the less true information there is in the dataset, while p = 1 means there is no true information. In the following analysis, we set p ∈ [0, 0.6]. We report the effectiveness of the two proposed algorithms and the CR method as the ratio of spammers increases. Figure 2 shows the dependence of AUC and τ on different values of p for random ratings and malicious ratings. For both spammer cases, one can easily observe that the AUC value and τ of the CRC method are only slightly higher than those of the classical CR algorithm. However, the CRCN method is significantly better than the CR method, especially when the ratio of spammers is high. Thus, we conclude that both of our proposed algorithms, CRC and CRCN, have more advantages than the CR method.
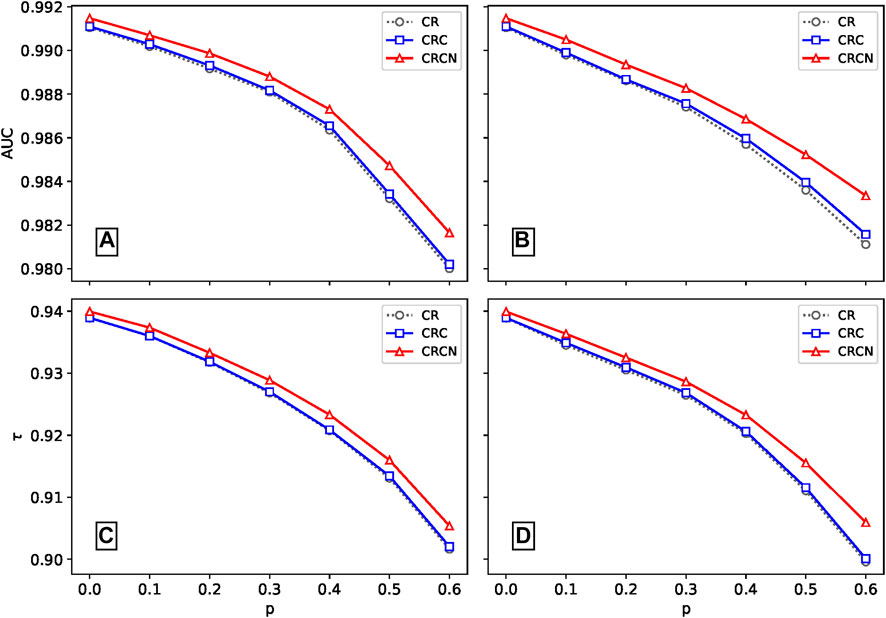
FIGURE 2. Comparison of the robustness of the three algorithms. Panels (A) and (C) are the AUC and τ for different fractions p for random rating spamming, and panels (B) and (D) show the same for malicious rating spamming. The results are averaged over ten independent realizations.
We also investigated the effect of β on AUC and τ in the CRCN method, and the results are shown in Appendix A. It is obvious that the parameter β improves the effectiveness of the algorithm since CRCN degenerates to the CRC method when β = 1. Moreover, the difference in the AUC value between β = 2 and β = 3 is negligible, but τ is optimal when β = 2, which implies that the overall performance of the CRCN algorithm is better when β = 2. In the following analysis, we adopt β = 2. Please see Appendix A for the dependence of AUC and τ on the parameter β.
4.2 Results From Real Rating Data
We naturally consider the performance of the proposed algorithms on real datasets. The reputation values of all evaluators in each dataset are calculated and sorted in ascending order to detect the proportion of the top L evaluators who are spammers. At the same time, the CR and IARR2 methods are compared with the proposed CRC and CRCN methods. We first turn 5% of evaluators in each real dataset to two types of spammers to test the effectiveness of the evaluation method, i.e., ρ = 5%. Figure 3 presents the recall score of different methods calculated according to the length L of the spammer list. Regardless of the type of spamming, the CRCN method has a significant advantage over the CR method, and the CRC method is essentially an improvement over the CR method. In particular, this enhancement of CRCN is more remarkable for both datasets in the case of malicious spammers, which indicates that it is more challenging to detect random spammers.
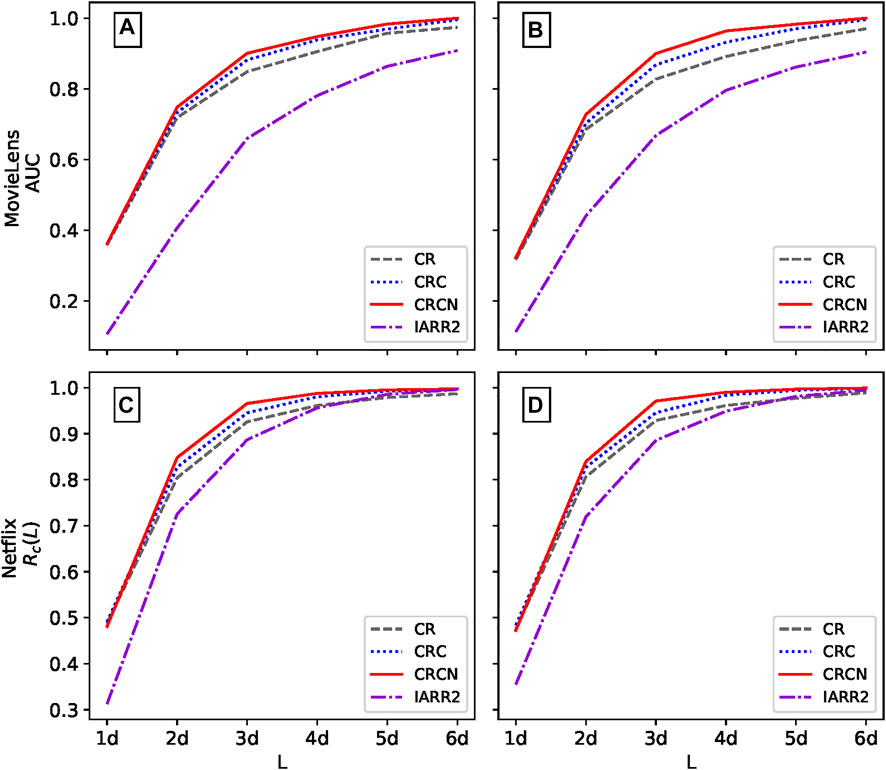
FIGURE 3. The recall score Rc of different methods varies with length L in MovieLens and Netflix. Panels (A) and (C) represent random spammers, and panels (B) and (D) represent malicious spammers. The parameter ρ in both datasets is 0.05, and the parameter ω is 0.05 and 0.01 for MovieLens and Netflix, respectively. The results are averaged over ten independent realizations.
The AUC and RS values are reported in Table 2. One can find that for both types of spammers, the AUC values of the CRC and CRCN methods are higher than those of the CR method for every dataset, which implies that the two methods have more advantages in accuracy. However, it is worth mentioning that the improvement of the CRC method over the CR method is very considerable. Moreover, RS verifies the effectiveness of CRC and CRCN from another aspect. The smaller the RS is, the higher the ranking of spammers. As shown in Table 2, we easily note that the RS of CRCN is the smallest for both types of spammers in both datasets. From the above analysis, we can find that the qualitative results of these methods for both types of spammers are very similar, so we will only consider the case of random spammers in the following analysis.
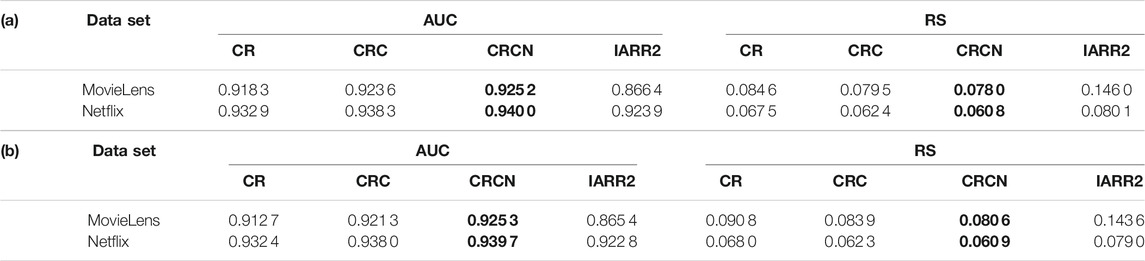
TABLE 2. AUC and RS values of different methods on two real datasets (A) with random spammers and (B) with malicious spammers. The parameters ω and ρ are the same as those in Figure 3. The results are averaged over ten independent realizations. The most remarkable value in each row is emphasized in bold.
Next, we will analyse whether the performance of the proposed methods is still outstanding while varying ω and ρ; here, ω and ρ are the ratio of objects rated by spammers and the ratio of spammers, respectively. In the following, we set ρ ∈ [0.05, 0.2] to test the robustness changing with the number of spammers in the ground truth and set the length of the detected spam list to twice the number of spammers, namely, L = 2d. The parameter ω is selected according to the sparsity of the datasets, and ω of the Netflix dataset is smaller than that of the MovieLens dataset since the Netflix dataset is sparser. Figure 4 shows how the AUC, Rc, and RS values change under different methods when there are different proportions of spammers in the two datasets. Please see Appendix B for more details of different ω. It is worth noting that, as a whole, the performance of the CRCN method is better than other methods, especially when ρ is small. Moreover, the Rc values of all methods are positively correlated to the number of spammers. In contrast, the RS value of the CRCN method is always lower than that of the other methods, regardless of the number of spammers. Therefore, we conclude that the performance of the proposed CRCN method is stable and accurate.

FIGURE 4. The AUC, Rc and RS values of different methods with different ρ in the random spammer case for (A-C) MovieLens and (D-F) Netflix datasets. The parameter ω is 0.05 and 0.01 for MovieLens and Netflix, respectively. The results are averaged over 10 independent realizations.
One of the motivations of the IARR2 method is that evaluators should have a high reputation only when they have a high degree. From Figure 4, we can find that the performance of IARR2 method is not satisfactory compared with other methods in the two data sets, especially in the MovieLens data set. This fully demonstrates that the simple structural information, such as degree, cannot make a reliable correction to the original CR algorithm. It is indispensable to discuss the relationship between the clustering coefficients of evaluators and their degree in the bipartite network, as shown in Figure 5. As the evaluators’ degrees are continuous and with different scales, we take the log of the degrees for both datasets and divide them into ten bins. It is not surprising that, similar to the conclusions of many studies [43], there is no relatively positive correlation between the evaluators’ degree and the clustering coefficient in the two real datasets. To be sure, the introduction of the clustering coefficient in the reputation evaluation process considers the network association from systematic aspects, which effectively improves the classical CR algorithm.
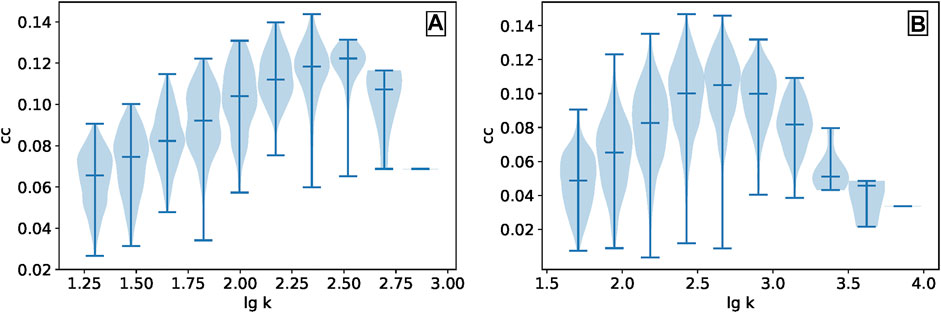
FIGURE 5. The relationship between the evaluators’ degree and the clustering coefficient in (A) MovieLens and (B) Netflix are presented by a violin plot. The evaluators in each dataset are divided into ten bins according to their degrees. The extreme value and median are marked with short bars, and the probability density is represented by shadows.
5 Conclusion
Building a sound reputation evaluation system for online rating systems is a crucial issue that has great commercial value in e-commerce systems and has guiding significance for a wide range of systematic evaluations. In this paper, we propose a robust reputation evaluation algorithm that considers network association and nonlinear recovery from the systematic aspects of rating systems by combining the structural information of the evaluator-object bipartite network and the penalty reward function with the original correlation-based ranking method. More specifically, in the iterations, we introduced the clustering coefficient of evaluators in the bipartite network to refine their reputations and then used the penalty-reward function to strengthen the high-reputation evaluators further and weaken the impact of low-reputation evaluators. Extensive experiments on artificial data and two real-world datasets show that the proposed CRC and CRCN methods have better performance than the originally proposed CR and IARR2 algorithms. These two newly proposed methods outperform the previous ones in evaluating evaluator reputation, and their accuracy and recall scores are remarkably improved and can effectively identify spammers.
The proposed CRCN method has a similar framework as the previous IARR2 algorithm, but the new method focuses more on the core system factors in complex systems, and the CRCN method demonstrates its effectiveness and stability compared to the unsatisfying performance of IARR2. The results show that introducing the clustering coefficient as the most basic network association feature and nonlinear recovery in the iterative process can capture more profound evaluator behaviour characteristics to improve the CR method. This novel method has also been applied in related studies on the nonlinear behaviors of the earth systems [44, 45]. In future work, we can focus on more systematic factors to build a reputation evaluation system, such as the interactions among evaluators. We can also consider the impact of time on building a reputation system because normal evaluators rarely generate a large number of ratings in a short time, whereas spammers may do so. Additionally, we should also pay attention to the emotional language in the text comments of the evaluation system, which can provide more meaningful information to individuals [46].
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found in Section 3.2.
Author Contributions
ML, CH and ZD contributed to conception and design of the study. ML and YJ performed the analysis and validated the analysis. ML and CH wrote the first draft of the manuscript. ZD designed the research and reviewed the manuscript. All authors have read and approved the content of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China through Grant No.71 731 002.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
CH gratefully acknowledges support from the German Federal Ministry of Education and Research under Grant No. 03EK3055B.
References
1. Muchnik L, Aral S, TaylorTaylor SJ. Social Influence Bias: A Randomized experiment. Science (2013) 341(6146):647–51. doi:10.1126/science.1240466
2. Linyuan L, Medo M, Yeung CH, Zhang Y-C, Zhang Z-K, Zhou T. Recommender Systems. Phys Rep (2012) 519(1):1–49.
3. Wang D, Liang Y, Dong X, Feng X, Guan R. A Content-Based Recommender System for Computer Science Publications. Knowledge-Based Syst (2018) 157(1–9). doi:10.1016/j.knosys.2018.05.001
4. Ureña R, Kou G, Dong Y, Chiclana F, Herrera-Viedma E. A Review on Trust Propagation and Opinion Dynamics in Social Networks and Group Decision Making Frameworks. Inf Sci (2019) 478:461–75. doi:10.1016/j.ins.2018.11.037
5. Zeng A, Vidmer A, Medo M, Zhang Y-C. Information Filtering by Similarity-Preferential Diffusion Processes. Epl (2014) 105(5):58002. doi:10.1209/0295-5075/105/58002
6. Zhang F, Zeng A. Improving Information Filtering via Network Manipulation. Epl (2012) 100(5):58005. doi:10.1209/0295-5075/100/58005
7. Liu X-L, Liu J-G, Yang K, Guo Q, Han J-T. Identifying Online User Reputation of User-Object Bipartite Networks. Physica A: Stat Mech its Appl (2017) 467:508–16. doi:10.1016/j.physa.2016.10.031
8. Zeng A, Cimini G. Removing Spurious Interactions in Complex Networks. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85(3):036101. doi:10.1103/PhysRevE.85.036101
9. Chung C-Y, Hsu P-Y, Huang S-H. A Novel Approach to Filter Out Malicious Rating Profiles from Recommender Systems. Decis Support Syst (2013) 55(1):314–25. doi:10.1016/j.dss.2013.01.020
10. Yang Z, Zhang Z-K, Zhou T. Anchoring Bias in Online Voting. Epl (2013) 100(6):68002. doi:10.1209/0295-5075/100/68002
11. Zhang Y-L, Guo Q, Ni J, Liu J-G. Memory Effect of the Online Rating for Movies. Physica A: Stat Mech its Appl (2015) 417:261–6. doi:10.1016/j.physa.2014.09.012
12. Toledo RY, Mota YC, Martínez L. Correcting Noisy Ratings in Collaborative Recommender Systems. Knowledge-Based Syst (2015) 76:96–108. doi:10.1016/j.knosys.2014.12.011
13. Zhang Q-M, Zeng A, Shang M-S. Extracting the Information Backbone in Online System. PLoS One (2013) 8(5):e62624. doi:10.1371/journal.pone.0062624
14. Allahbakhsh M, Ignjatovic A, Motahari-Nezhad HR, Benatallah B. Robust Evaluation of Products and Reviewers in Social Rating Systems. World Wide Web (2015) 18(1):73–109. doi:10.1007/s11280-013-0242-4
15. Dhingra K, Yadav SK. Spam Analysis of Big Reviews Dataset Using Fuzzy Ranking Evaluation Algorithm and Hadoop. Int J Mach Learn Cyber (2019) 10(8):2143–62. doi:10.1007/s13042-017-0768-3
16. Qiao W, Yan Z, Wang X. Join or Not: The Impact of Physicians' Group Joining Behavior on Their Online Demand and Reputation in Online Health Communities. Inf Process Manage (2021) 58(5):102634. doi:10.1016/j.ipm.2021.102634
17. Gallo SA, SullivanSullivan JH, GlissonGlisson SR. The Influence of Peer Reviewer Expertise on the Evaluation of Research Funding Applications. PLoS One (2016) 11(10):e0165147. doi:10.1371/journal.pone.0165147
18. Pier EL, Brauer M, Filut A, Kaatz A, Raclaw J, Nathan MJ, et al. Low Agreement Among Reviewers Evaluating the Same Nih grant Applications. Proc Natl Acad Sci USA (2018) 115(12):2952–7. doi:10.1073/pnas.1714379115
19. Alexander N, Spiekermann S. Oblivion of Online Reputation: How Time Cues Improve Online Recruitment. Int J Electron Business (2017) 13(2-3):183–204.
20. Fouss F, Achbany Y, Saerens M. A Probabilistic Reputation Model Based on Transaction Ratings. Inf Sci (2010) 180(11):2095–123. doi:10.1016/j.ins.2010.01.020
21. Jian Q, Li X, Wang J, Xia C. Impact of Reputation Assortment on Tag-Mediated Altruistic Behaviors in the Spatial Lattice. Appl Maths Comput (2021) 396:125928. doi:10.1016/j.amc.2020.125928
22. Xia C, Gracia-Lázaro C, Moreno Y. Effect of Memory, Intolerance, and Second-Order Reputation on Cooperation. Chaos (2020) 30(6):063122. doi:10.1063/5.0009758
23. Li X, Hao G, Wang H, Xia C, Perc M. Reputation Preferences Resolve Social Dilemmas in Spatial Multigames. J Stat Mech (2021) 2021(1):013403. doi:10.1088/1742-5468/abd4cf
24. Wang S, Zheng Z, Wu Z, Lyu MR, Yang F. Reputation Measurement and Malicious Feedback Rating Prevention in Web Service Recommendation Systems. IEEE Trans Serv Comput (2014) 8(5):755–67.
25. Chang MK, Cheung W, Tang M. Building Trust Online: Interactions Among Trust Building Mechanisms. Inf Manage (2013) 50(7):439–45. doi:10.1016/j.im.2013.06.003
26. Laureti P, Moret L, Zhang Y-C, Yu Y-K. Information Filtering via Iterative Refinement. Europhys Lett (2006) 75(6):1006–12. doi:10.1209/epl/i2006-10204-8
27. Zhou Y-B, Lei T, Zhou T. A Robust Ranking Algorithm to Spamming. Epl (2011) 94(4):48002. doi:10.1209/0295-5075/94/48002
28. Liao H, Zeng A, Xiao R, Ren Z-M, Chen D-B, Zhang Y-C. Ranking Reputation and Quality in Online Rating Systems. PLoS One (2014) 9(5):e97146. doi:10.1371/journal.pone.0097146
29. Gao J, Dong Y-W, Shang M-S, Cai S-M, Zhou T. Group-based Ranking Method for Online Rating Systems with Spamming Attacks. Epl (2015) 110(2):28003. doi:10.1209/0295-5075/110/28003
30. Gao J, Zhou T. Evaluating User Reputation in Online Rating Systems via an Iterative Group-Based Ranking Method. Physica A: Stat Mech its Appl (2017) 473:546–60. doi:10.1016/j.physa.2017.01.055
31. Lu D, Guo Q, Liu X-L, Liu J-G, Zhang Y-C. Identifying Online User Reputation in Terms of User Preference. Physica A: Stat Mech its Appl (2018) 494:403–9.
32. Lee D, Lee MJ, Kim BJ. Deviation-based Spam-Filtering Method via Stochastic Approach. Epl (2018) 121(6):68004. doi:10.1209/0295-5075/121/68004
33. Sun H-L, Liang K-P, Liao H, Chen D-B. Evaluating User Reputation of Online Rating Systems by Rating Statistical Patterns. Knowledge-Based Syst 219:1068952021.
34. Zhang J, Cohen R. A Framework for Trust Modeling in Multiagent Electronic Marketplaces with Buying Advisors to Consider Varying Seller Behavior and the Limiting of Seller Bids. ACM Trans Intell Syst Technol (2013) 4(2):1–22. doi:10.1145/2438653.2438659
35. Liu X-L, Guo Q, Hou L, Cheng , Liu J-G. Ranking Online Quality and Reputation via the User Activity. Physica A: Stat Mech its Appl (2015) 436:629–36. doi:10.1016/j.physa.2015.05.043
36. Linyuan L, Chen D, Ren X-L, Zhang Q-M, Zhang Y-C, Zhou T. Vital Nodes Identification in Complex Networks. Phys Rep (2016) 650:1–63.
37. Latapy M, Magnien C, Del Vecchio N. Basic Notions for the Analysis of Large Two-Mode Networks. Social Networks (2008) 30(1):31–48. doi:10.1016/j.socnet.2007.04.006
38. Barabási A-L, Albert R. Emergence of Scaling in Random Networks. Science (1999) 286(5439):509–12. doi:10.1126/science.286.5439.509
39. Kendall MG. A New Measure of Rank Correlation. Biometrika (1938) 30(1/2):81–93. doi:10.2307/2332226
40. James AH, McNeil BJ. The Meaning and Use of the Area under a Receiver Operating Characteristic (Roc) Curve. Radiology (1982) 143(1):29–36. doi:10.1148/radiology.143.1.7063747
41. Herlocker JL, Konstan JA, Terveen LG, Riedl JT. Evaluating Collaborative Filtering Recommender Systems. ACM Trans Inf Syst (Tois) (2004) 22(1):5–53. doi:10.1145/963770.963772
42. Zhou T, Ren J, Medo M, Zhang Y-C. Bipartite Network Projection and Personal Recommendation. Phys Rev E (2007) 76(4):046115. doi:10.1103/PhysRevE.76.046115
43. Ravasz E, Barabási A-L. Hierarchical Organization in Complex Networks. Phys Rev E (2003) 67(2):026112. doi:10.1103/PhysRevE.67.026112
44. Fan J, Meng J, Ludescher J, Chen X, Yosef A, Kurths J, et al. Statistical Physics Approaches to the Complex Earth System. Phys Rep (2021) 1–84. doi:10.1016/j.physrep.2020.09.005
45. Zhang Y, Yosef A, Havlin S. Asymmetry in Earthquake Interevent Time Intervals. J Geophys Res Solid Earth (2021) 126(9):e2021JB022454. doi:10.1029/2021jb022454
Appendix A.
The dependence of parameter β in CRCN method. Here, we show the effect of β on AUC and τ in the CRCN method. We set the ratio of spammers to 0.6, and the results are shown in Figure 6. As mentioned in the main, the parameter β improves the effectiveness of the algorithm since CRCN degenerates to the CRC method when β = 1. Moreover, the difference in AUC value between β = 2 and β = 3 is negligible, but τ is optimal when β = 2, which implies that the overall performance of the CRCN algorithm is better when β = 2. Therefore, in the following analysis, we adopt β = 2.
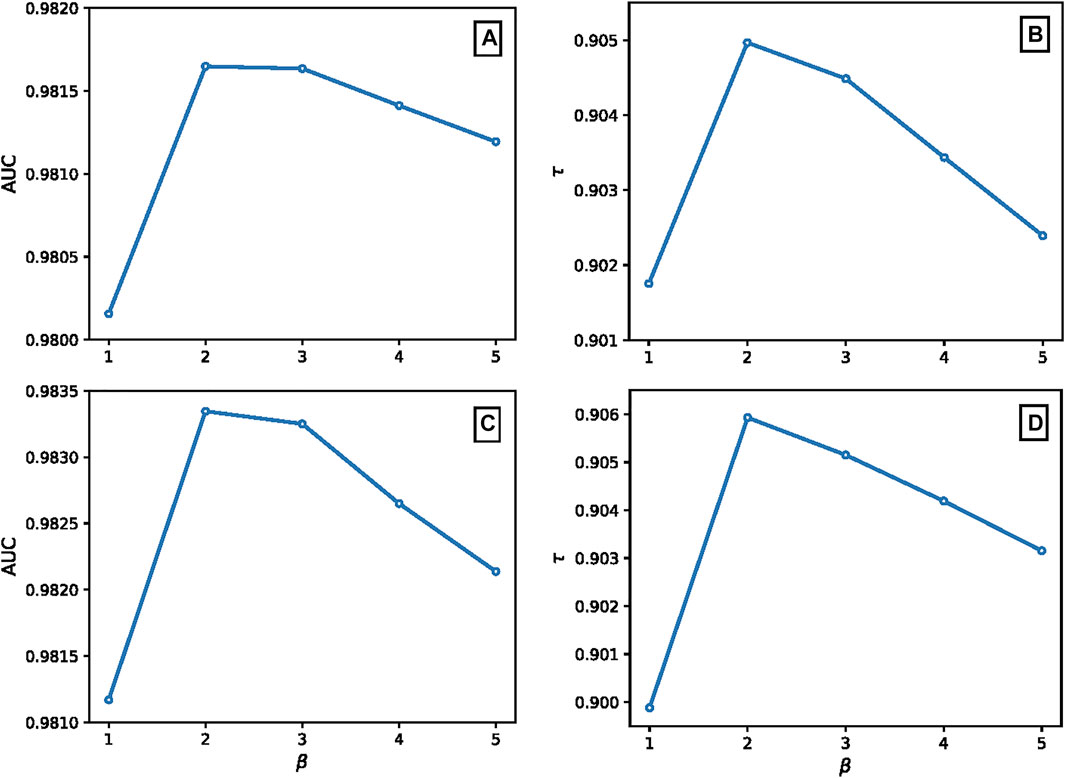
FIGURE 6. The dependence of AUC and τ on the parameter β in CRCN method. Panels (A) and (B) show the AUC and τ values for different β with random-rating spamming, and panels (C) and (D) show the same for push-rating spamming. The results are averaged over ten independent realizations.
Appendix B.
We also compared the performance of the proposed method with the classical CR method and the IARR2 method while varying ω and ρ. The results are shown in Figure 7. We can find that the performance of the CRCN method is better than other methods.
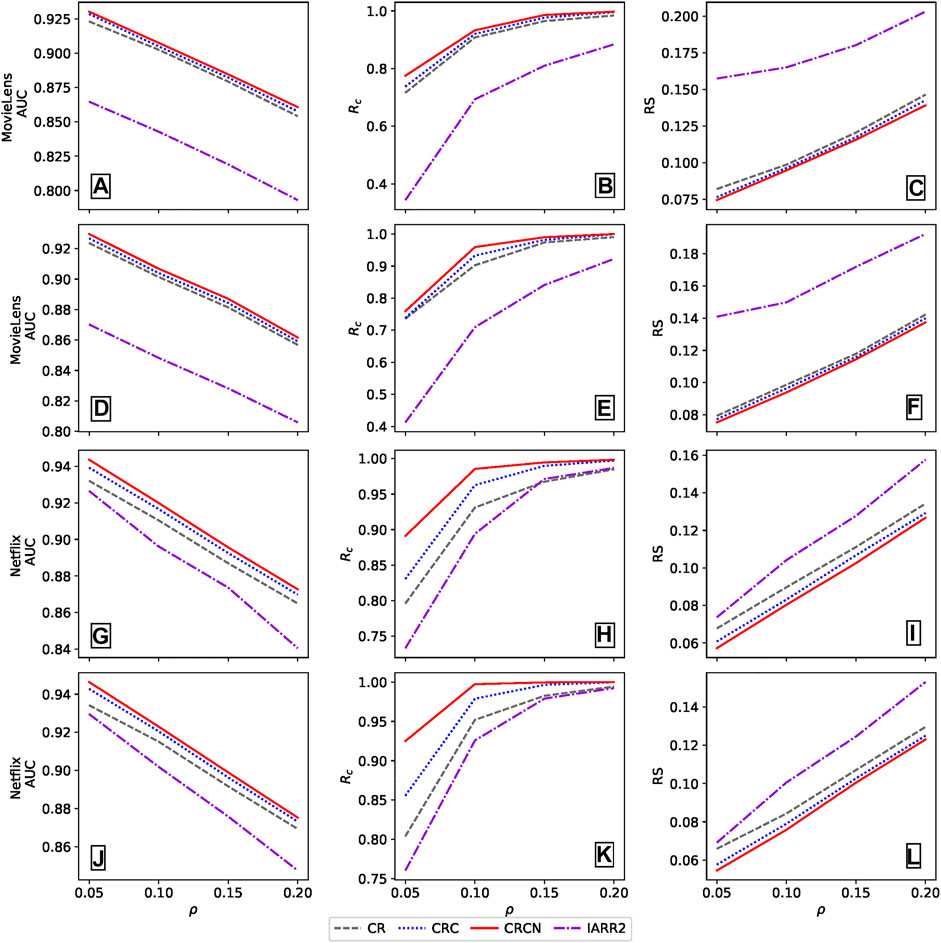
FIGURE 7. The AUC, Rc and RS values of different methods with different ω and ρ in the random spammers for (A-F) MovieLens and (G-L) Netflix data sets, respectively. Each row represents a different parameter ω: a-c (ω = 0.75); d-f (ω = 0.1); g-i (ω = 0.02); j-l (ω = 0.03). The results are averaged over 10 independent realizations.
Keywords: reputation evaluation, spam attack, online rating system, systematic factors, network structure
Citation: Li M, Han C, Jiang Y and Di Z (2022) Improving the Performance of Reputation Evaluation by Combining a Network Structure With Nonlinear Recovery. Front. Phys. 10:839462. doi: 10.3389/fphy.2022.839462
Received: 20 December 2021; Accepted: 14 January 2022;
Published: 22 February 2022.
Edited by:
Gaogao Dong, Jiangsu University, ChinaReviewed by:
Chengyi Xia, Tianjin University of Technology, ChinaYongwen Zhang, Kunming University of Science and Technology, China
Copyright © 2022 Li, Han, Jiang and Di. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zengru Di, emRpQGJudS5lZHUuY24=
 Meng Li
Meng Li Chengyuan Han3
Chengyuan Han3 Zengru Di
Zengru Di