Effect of Nonequilibrium Transient Electronic Structures on Lattice Stability in Metals: Density Functional Theory Calculations

The electronic structures of metals undergo transient nonequilibrium states during the photoexcitation process caused by isochoric heating of X-ray free-electron laser, and their lattice stability is, thus, significantly affected. By going beyond frozen core approximation, we manually introduced nonequilibrium electron distribution function in finite-temperature density functional theory with the framework of Kohn–Sham–Mermin to investigate such transient states, and their effect on lattice stability in metals is demonstrated by phonon dispersion calculated using the finite displacement method. We found that the perfect lattice of a metal collapses due to the exotic electronic structure of nonequilibrium transient state created by isochoric heating of X-ray free-electron laser. Further increase of the number of holes created in the sample (i.e., an increase of laser fluence) still results in lattice instability for aluminum, while for copper, it results in phonon hardening. The potential energy surface is calculated for the extreme case of both Al and Cu with exactly one hole created in its inner shell for each one of the atoms. A double-well structure is clearly observed for Al, while the potential energy surface becomes steeper for Cu.

1 Introduction

Lattice dynamics are of fundamental importance in a variety of fields, including phase transition [1], superconductivity [2], and thermal conductivity [3] It is reported that under intense laser radiation, the melting of the semiconductor will be athermal due to softening of interatomic bonds, which takes place long before the conventional thermal melting due to the process of energy transfer from electrons to ionic lattice [4]. For metals, however, the phenomenon of structural instability, phonon hardening, and phonon softening has been reported [4–11]. Recently, the lattice dynamics of Au–Cu alloys at warm dense state (WDM) have also been investigated [12]. More interestingly, the chemical bond hardening in warm dense gold [13] is observed in experiment, which provides helpful information for understanding the generation process of warm dense matter [14, 15]. WDM is of great importance to bridge the gap between atomic physics, condensed matter physics, and plasma physics. The equation of states, transport properties such as electrical and thermal conductivity, etc., as well as the lattice dynamics are fundamental properties of WDM, which are helpful in understanding the process of inertial confinement fusion [16–18] and the formation of celestial bodies [19–22]. With the development of laser technology, the nonequilibrium state of WDM has been realized by the techniques of isochoric heating using the X-ray free-electron laser (XFEL) [23–26], optical lasers [27–31] and ion beams [32–34] in experiment [35]. Although some recent progresses of theoretical studies and experiments about lattice dynamics of WDM have been reported, it is still a long-standing challenge to understand the effect of electron excitation on lattice stability.

As a crude but useful model, the generation of WDM via isochoric heating usually can be studied using the two-temperature model [36–39] where the energy is delivered to the valence electrons within several tens of femtoseconds, while the ions remain unmoved. The electron excitation can be considered as nonthermal process, and the electronic subsystem reaches local equilibrium by electron–electron collisions, described by Fermi–Dirac distribution [40]. In the next step, the crystalline structure will be rearranged after laser excitation, and the energy will be transferred from the excited electrons to the lattice by electron–phonon coupling [41–43].The whole system is in a nonequilibrium state until the electron–phonon equilibration is reached [40, 44, 45]. During this period, the lattice temperature is lower than the electron temperature. By calculating phonon dispersion, we can understand lattice stability and predict the macroscopic thermal properties, which are dependent on the microscopic description of ionic vibrational dynamics [46]. The calculation is usually performed using density functional perturbation theory (DFPT) [47] or finite displacement method [48]. In addition, electronic structures, potential energy surface (PES), and formation enthalpies, etc. are also helpful tools to study lattice stability [46, 49, 50]. In addition to the nonequilibrium between ions and electrons, the electronic subsystem also moves away from equilibrium because of the excitation process. It is very difficult to fully account for the photoexcitation due to XFEL. For example, even the expensive time-depedent density functional theory (TDDFT) calculation cannot include the Auger process. As a small step forward, the variation of occupation number of excited electrons is a good candidate to study the nonequilibrium states within the framework of finite-temperature density functional theory (FTDFT) with less computational cost and has been successfully applied in studying 2D material as well as WDM [51, 52].

In this study, we investigate the effect of electron excitation in the inner shell orbitals on the lattice stability of metals at solid density by isochoric heating of XFEL. The electron excitation can be realized using FTDFT simulations by changing the occupation number of electrons in the specific Kohn–Sham orbitals, which does not rely on any fitting parameters and is simpler and much faster than that of more advanced approaches, such as constrained DFT [53]. The phonon dispersions are calculated using the finite displacement method. Density of states (DOSs) and local densities of states (LDOS), the radial electron density of valence electrons in real space, and the PES along the direction of mode eigenvectors are also calculated. This study provides an exploration to understand the effect of nonequilibrium transient electronic excitation on crystal structural stability, which may shed light on intrinsic physics of lattice dynamics.

2 Methodology and Numerical Details

In this section, we will describe the methodology and numerical details of this study. The population of electrons in the self-consistent field (SCF) cycle is controlled manually in the FTDFT calculations to create holes in inner shell orbitals. Then, we calculate the phonon dispersion by using the forces acting on atoms obtained by the finite displacement method. We also obtain the PES by moving the atoms along the corresponding phonon mode eigenvectors.

2.1 Finite Temperature Density Functional Theory

In the Kohn–Sham–Mermin scheme [54, 55], the occupation numbers of electrons follow the Fermi–Dirac distribution, and the electrons are considered to be in thermal equilibrium. When the electrons were excited by laser, the time scale of energy transfer between the electrons and the ions is much slower than that of the relaxation process of the electron subsystem. Thus, the electrons and the lattice can be considered to be in a transient state of nonequilibrium before the electron–phonon equilibration is completed. This justifies the application of the two-temperature model, and the electrons can be described by FTDFT with fixed ionic configuration according to Born–Oppenheimer approximation. There is yet another nonequilibrium process involved because the electron subsystem is also away from equilibrium. In fact, only electrons with specific energy can be photoionized during isochoric heating by the XFEL. To calculate such a complex nonequilibrium system, we use the plane-wave pseudopotential open-source package QUANTUM ESPRESSO (QE) [56, 57] with minor modifications to realize nonequilibrium distribution of electrons in the FTDFT calculations. The occupation number in the relevant inner shell Kohn–Sham orbitals is set as zero in every SCF step to create holes, and the same number of electrons as that of holes was added to the chemical potential to study the nonequilibrium transient state after laser excitation so that the total number of electrons remains unchanged in the system. This could be realized experimentally by carefully choosing the XFEL energy. The new chemical potential is decided self-consistently like in the original SCF process, which also determines the occupation numbers of all orbitals in return, except for those that were forced to be zero. In this way, we can go beyond the frozen core approximation and create holes directly in our FTDFT calculations for real materials, contrary to the common practice of creating holes in atomic calculation during the generation of pseudopotentials and treating the corresponding atom as an impurity in the FTDFT calculations [58, 59].

2.2 Phonon Dispersion Calculation

The DFPT and finite displacement method for calculating phonons are by now two different well-established tools for investigating vibrational properties. Here, we use both the DFPT and the finite displacement method to calculate the phonon dispersion relations of two metals, Al and Cu, at room temperature for benchmark. For nonequilibrium calculations, only the finite displacement method is used due to its straightforwardness.

For DFPT, the calculations are performed using the QE code; the pseudopotential takes the projector augmented wave (PAW) formalism [60] and the exchange-correlation functional takes the Perdew–Burke–Ernzerhof (PBE) parameterization [61]. For Al, we use a pseudopotential including both L-shell and M-shell electrons (i.e., 2s²2p⁶3s²3p¹) as valence electrons. For Cu, we use the pseudopotential which considers both M-shell and N-shell electrons (i.e., 3s²3p⁶3d¹⁰4s¹) as valence electrons. The plane wave cutoff energy is set to 170 Ry, a 16 × 16 × 16 Monkhorst-Pack K-point mesh [62] is used for the sampling of the Brillouin zone, and the grid of q-point of lattice dynamical matrices is 4 × 4 × 4. The lattice constant is relaxed to be 7.639 Bohr for Al and 6.848 for Cu. The convergence with respect to plane-wave cutoff energy, k-point, and q-point meshes is carefully checked for all our calculations.

For the finite displacement method, the calculations for Al and Cu are performed on a 3 × 3 × 3 supercell (108 atoms) using the ALAMODE [63, 64] as a postprocessing code for QE using the same pseudopotential as DFPT. Before isochoric heating with the XFEL, the samples are supposed to be at ambient conditions, which mean that the electron temperature of 300 K is used for the metallic system. The benchmark between the DFPT and finite displacement method for such a case is shown in Figures 3A,B (green triangles versus black curves) with perfect agreement. The advantage of the finite displacement method is that we can relate the calculations of electron excitation from multiatomic system to the excitation of electrons of metals in the experiments. As a result, we only use the finite displacement method to calculate phonon dispersions for photoexcitation cases rather than DFPT. The shifted Monkhorst-Pack k-point meshes are 6 × 6 × 6 for Al and 4 × 4 × 4 for Cu. The atomic displacement of 3 × 10⁻² Å and the plane-wave cutoff energy of 60 Ry are used for both Al and Cu. The convergence of plane-wave cutoff energy and the size of k-point mesh are also carefully checked in our calculations.

2.3 Potential Energy Surface Calculation

In the lattice dynamic calculations, we use the finite displacement method to calculate the second-order interatomic force constants and the phonon frequencies under quasi-harmonic approximation. To include the anharmonicity, we calculate the PES with excited electrons and illustrate the origin of lattice stability. The PES can be obtained by moving the atomic positions far away from their equilibrium positions along the eigenvector of different modes at specific high-symmetry points. The displacement of the j^th atom in the l^th unit cell along a phonon mode amplitude Q is denoted by d_jl and defined as

$d_{jl}=\frac{Q}{\sqrt{N_a{m}_j}}\mathrm{R}\mathrm{e}\left[\exp (\mathrm{i}\mathrm{\Phi }){\mathbf{e}}_{\mathit{\text{j}}}\exp (\mathbf{q}\cdot {\mathbf{r}}_{\mathit{\text{jl}}})\right],(1)$

where Q is the normal-mode coordinate, N_a is the total number of atoms in the supercell, and m_j and r_jl are the mass and position of the j^th atom in the lth unit cell, respectively. e_j is the j^th component of the unit normal coordinate eigenvector. Φ is an arbitrary phase factor and is set to zero by default. If the expansion of the supercell is commensurate with the wavevector q, the total energy should not change when a nonzero Φ is used because the displacement corresponds to a part of the wave period [65]. The unit normal eigenvector can be obtained from the QE code, and then, we can manage to move the atoms accordingly. The total energy can be calculated by FTDFT with new atomic positions, and then, we can obtain the PES by summarizing the data along different directions.

3 Results and Disccussions

3.1 Electronic Structure

The absorption of photon by isochoric heating with the XFEL can change the electronic structure of metals to a transient exotic state. Experimentally, the XFEL which has tunable photon energy with pulse duration on the order of 10 fs and high intensity as much as 10¹⁷ W/cm² can heat and excite the electrons of metals and create a nonequilibrium electronic structure [66]. The L_I edge of Al is 117.8 eV and the M_I edge of Cu is 122.5 eV, both of which are in the soft X-ray range of an XFEL [67]. The specific holes can be created by predominant photoionization of 2s electrons of Al or 3s electrons of Cu to their Fermi surface, with other transitions being of minor importance. The electrons which are excited to higher energies are also found to relax to the chemical potential within a few femtoseconds [66]. Thus, this transient state could exist in a time scale longer than the time scale of the pulse and shorter than the time scale of Auger decay.

With the excitation of valence electrons in the inner shell, the reduced screening of core electrons [52] results in localization of the valence band. The DOS of electrons in such nonequilibrium transient states is plotted in Figures 1A,B, and we see similar change of the DOS as in [52], which shows small change for Al but considerable localization of valence bands for Cu. This is mainly due to the semilocal d band in Cu. The black curves show the calculated DOS without a hole, the red and blue ones, respectively, represent the DOS with a hole and two holes of every atom in the system. Due to the deeper Coulomb potential which the remaining electrons feel [52], it is clear that these atom-like features shift toward lower energy. The rise of chemical potential is also observed when the excited electrons are increased. In Figures 1C,D, the local density of states (LDOSs) is calculated by projecting the one-electron eigenstates onto the local atomic orbitals, which illustrates the contribution of different orbitals to the electronic structure of a specific atom.

FIGURE 1

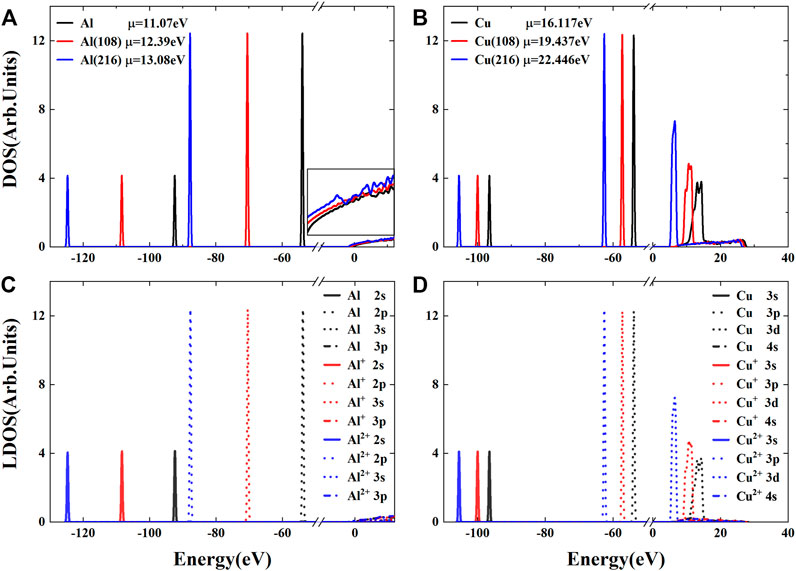
FIGURE 1. Density of states of Al and Cu and the local density of states of Al and Cu with perfect lattice structure at room temperature. The black solid curves correspond to the DOS or LDOS without a hole in the system. (A) DOS of atoms of Al with one (red color) hole and two (blue color) holes in the 2s orbital. Their corresponding chemical potentials are labeled in the legends as well. (B) DOS of atoms of Cu with a (red color) hole and two (blue color) holes in the 3s orbital. Their corresponding chemical potentials are labeled in the legends as well. (C) LDOS for Al. (D) LDOS for Cu.

To show the charge transfer process in real space, we plot the radial electron density for Al and Cu, as shown in Figures 2A,B, respectively. The black curve corresponds to the atoms without holes, and the red curve represents every atom with a hole in the system. For Al, the electrons of the 2s orbital are excited to the conduction band. As a result, the electron density is reduced near the nucleus and increased away from the nucleus, showing an increase in ionization degree. For Cu, the electrons of the 3s orbital are excited to the conduction band, and a similar trend is observed. This picture is in agreement with the shift of the DOS in Figure 1.

FIGURE 2

FIGURE 2. Radial valence electron density (A) of Al atom without (black curve) and with (red curve) a hole in the 2s orbital, and radial valence electron density (B) of Cu atom without (black curve) and with (red curve) a hole in the 3s orbital.

3.2 Phonon Dispersion

First, we calculate the phonon dispersion with the DFPT and finite displacement method using Al and Cu as illustrating examples. As shown in Figure 3, the result calculated at ambient condition is in perfect agreement with the experimental measurements by using the abovementioned two methods.

FIGURE 3

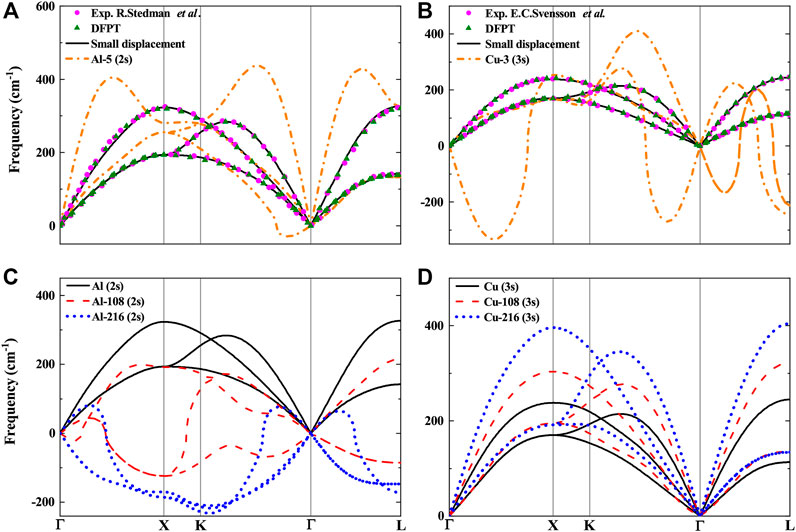
FIGURE 3. Calculated phonon dispersion of Al and Cu placed in their perfect lattice structure at room temperature with variable method and variable number of holes in their inner shell. Experimental measurements are plotted as purple dots for comparison [72, 73]; the green triangles correspond to the DFPT method, and the black lines correspond to the finite displacement method. (A) Al: the orange dash-dotted lines represent the atoms with five electrons removed from the 2s orbital. (B) Cu: the orange dash-dotted lines represent the atoms with three electrons removed from the 3s orbital. (C) Al: the red dashed lines and blue dotted lines correspond to the atoms with a hole and two holes in the 2s orbital, respectively. (D) Cu: the red dashed lines and blue dotted lines correspond to the atoms with a hole and two holes in the 3s orbital, respectively.

As shown in Figures 3A,C, the imaginary frequencies of phonon dispersions of Al can be observed along the direction of k-path Γ-X-K-Γ-L in the Brillouin zone of the FCC lattice [68] when there are more than four holes in the 2s orbital, which suggests that the lattice becomes unstable. In our calculation, we increase the number of excited electrons one by one until the electrons of the 2s orbital are all excited in the system. We found that the change of the system from the state of stable to unstable will happen with the increased excited electrons and the stability of lattice cannot recover when the lattice symmetry is satisfied again. For instance, the state of the system is still stable when the four electrons are excited; however, it becomes unstable when five or more electrons are excited. This suggests a process of lattice collapse for Al. It is to be noted that due to the incompleteness of our model, this picture is qualitatively right, but the number mentioned here is not quantitatively accurate.

For Cu, however, as shown in Figures 3B,D, we found that the lattice becomes unstable when the symmetry is broken, and the lattice becomes stable again when the symmetry is satisfied. We also found that the change of the system from the state of stable to unstable will happen when we increase the number of excited electrons of the 3s orbital gradually. For instance, the state of the system is stable when the two electrons are excited; however, it becomes unstable when three or more electrons are excited. It is possibly related to the symmetry breaking of the perfect lattice since the holes are randomly located within the atom in the sample. However, it is surprising that the lattice stability recovers when each atom excites one electron or two electrons from the 3s orbital. It may suggest that the Cu lattice becomes more stable when laser fluence is increased, which corresponds to the increased phonon frequencies. We suspect that the lattice might undergo a process of phase transition in this case. As for Cu, the phenomenon of phonon hardening in all three acoustic branches is observed significantly and which means the perfect lattice becomes harder to break when the inner shell electrons of every atom are excited. It is very different from aluminum.

3.3 Potential Energy Surface

Phonon dispersion with quasi-harmonic approximation might not be persuasive, especially for cases far away from equilibrium. Focusing on the crystal instability and phonon hardening [46, 51, 65, 69–71] cases, we plotted the potential energy surface (PES) of Al and Cu in the normal coordinates for the transverse acoustic (TA) and longitudinal acoustic (LA) modes at the high-symmetry point $L(\frac{1}{2},\frac{1}{2},\frac{1}{2})$ in the first Brillouin zone to include anharmonicity effect. The scaling factor Q₁ of the lowest TA mode and the scaling factor Q₂ of the LA mode are applied in the calculation, and the PES is a function of scaled coordinates E = E(Q₁, Q₂); we do not show the second-lowest TA mode because it is degenerate with the lowest TA mode. The finite displacements are imposed along the corresponding mode eigenvectors so that we can obtain the shape of the PES around the equilibrium position. To compare the curve of the potential surface, we both set the potential energy as zero in the equilibrium position.

The PES is plotted in Figures 4A,B, and the PES of Al without a hole and with a hole in the 2s orbital is represented, respectively. In Figure 4A, the PES of atoms which vibrate along the corresponding eigenvector in the system is plotted, and the potential energy curve of Al along the Q₁ direction and Q₂ direction is plotted using the black lines in Figures 4C,D. In Figure 4B, the PES of atoms with a hole is also plotted, and the potential energy curve of Al along the Q₁ direction and Q₂ direction is plotted using the red lines in Figures 4C,D. We can see that the slope of the TA mode is lower than that of the LA mode in the two cases by associating the PES and potential energy curve along different directions with the phonon dispersions, which is shown in Figure 3C. The transition from a single-well to double-well potential along the Q₁ direction and the phonon softening along the Q₂ direction shown in Figures 4C,D indicates probable softening of chemical bonds or displacive phase transition. So, we can know that the dynamic instability of aluminum originates from the fact that it is the local maximum of the double-well, which results in the negative curvature $\frac{{\partial }^{2}E}{\partial Q_1^2}<0$ and the eigenvalue of the TA mode ω² is also negative with the excitation of electrons in the inner shell of aluminum. Meanwhile, the potential energy curve of the LA mode along the vibration direction becomes much smoother when electrons are excited to the conduction band, while for Cu, as shown in Figure 5, the phonon hardening originates from the steeper potential energy curve along both Q₁ and Q₂ direction. From the PES of Cu, we can intuitively observe the increased trends of energy of both the LA and TA mode in three dimensions, corresponding to the increased frequencies in phonon dispersions shown in Figure 3D. The evidence indicates the reduced screening of orbitals and an increase of the effective ion–ion potential, which results in the localized electron of the d orbital being closer to the nucleus in real space and phonon hardening as a whole.

FIGURE 4

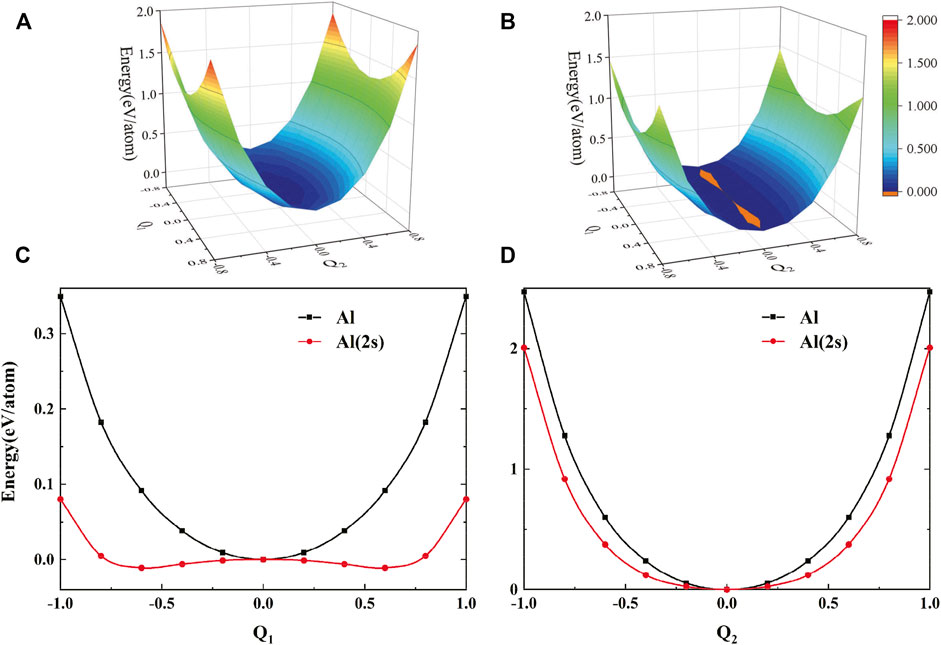
FIGURE 4. PES of Al in the direction of the eigenvectors at high-symmetry point L. Q₁ and Q₂ correspond to dimensionless normal coordinates of the lowest TA mode and LA mode without (A) and with (B) a hole in the 2s orbital, respectively. (C) PES along the Q₁ direction with Q₂ = 0. (D) PES along the Q₂ direction with Q₁ = 0. The lattice energy is set as zero in the equilibrium position.

FIGURE 5

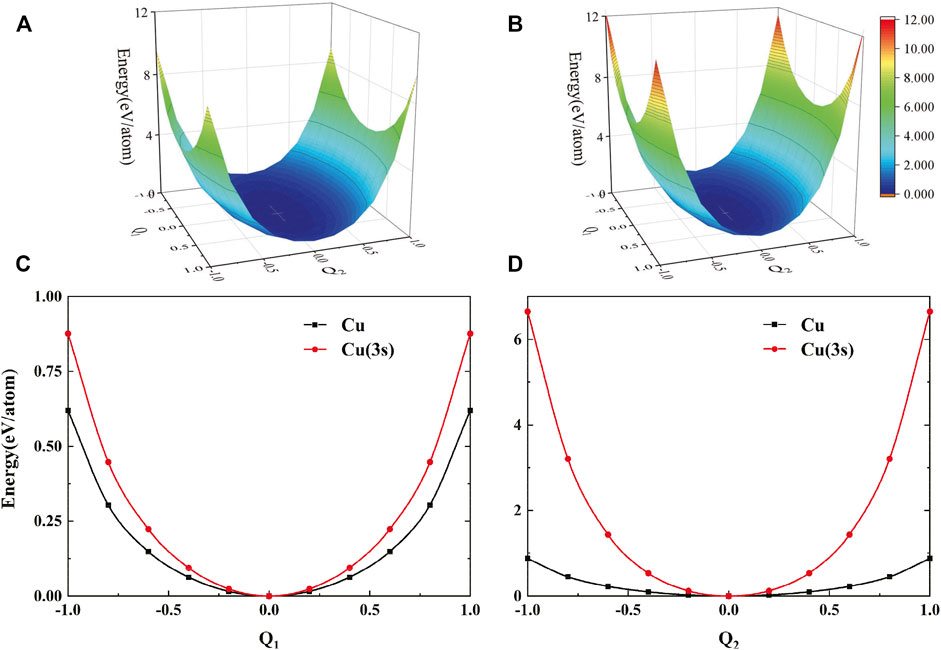
FIGURE 5. PES of Cu in the direction of the eigenvectors at high-symmetry point L. Q₁ and Q₂ correspond to dimensionless normal coordinates of the lowest TA mode and LA mode without (A) and with (B) a hole in the 3s orbital, respectively. (C) PES along the Q₁ direction with Q₂ = 0. (D) PES along the Q₂ direction with Q₁ = 0. The lattice energy is set as zero in the equilibrium position.

4 Conclusion

In summary, the effect of nonequilibrium electronic structures created by the photoexcitation of an XFEL on lattice stability is studied by a modified FTDFT method. We find lattice instability for Al but phonon hardening for Cu with a hole or two holes in every atom using the finite displacement method. Their electron structure, phonon dispersion, and PES are obtained in this study.

When electrons are excited to the conduction band, the screening of core electrons is reduced, and the forces and the interactional potential of atoms also change quickly, which changes the lattice stability of metals. The process is much faster than the time scale of several picoseconds required to convert the electronic energy to the lattice by electron–phonon coupling. At first, the change of the system from the state of stable to unstable will happen for both Al and Cu, possibly due to the asymmetric distribution of electrons. Then, the lattice stability cannot recover for Al when symmetry is satisfied again, while for Cu, the lattice stability can recover when symmetry is satisfied again and the process of excitation probably corresponds to the phase transition in specific cases. We show that the instability of Al with a hole in the 2s orbital originates from the double-well shape of the PES and the phonon hardening of Cu with a hole in the 3s orbital originates from the steeper PES.

We note that our study is qualitatively different from earlier calculations of excited electrons by either increasing the electron temperature or using the impurity model. Though missing the relax of wavefunction compared to more advanced calculations, such as TDDFT, our method is more computationally efficient and can give insight into the physical processes that can be expected in related XFEL experiments. Our result could arouse interests in understanding the effect of nonequilibrium on lattice dynamics.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the study and approved it for publication.

Funding

This study was supported by the National Key RD Program of China under Grant No. 2017YFA0403200, the National Natural Science Foundation of China under Grant Nos. 11 774 429, 11 874 424, 11 904 401, and 12 047 561, the NSAF under Grant No. U1830206, the Science Challenge Project under Grant No. TZ2016001, and the Science and Technology Innovation Program of Hunan Province under Grant Nos. 2020RC2038 and 2021RC4026.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank Prof. Z. X. Zhao and Prof. J. M. Yuan for the insightful discussions. All calculations were carried out at the Research Center of Supercomputing Application at NUDT.

References

1. Shirane G, Yamada Y. Lattice-Dynamical Study of the 110°K Phase Transition in SrTiO3. Phys Rev (1969) 177:858–63. doi:10.1103/physrev.177.858

CrossRef Full Text | Google Scholar

2. Bardeen J, Cooper LN, Schrieffer JR. Theory of Superconductivity. Phys Rev (1957) 108:1175–204. doi:10.1103/physrev.108.1175

CrossRef Full Text | Google Scholar

3. Feng T, Lindsay L, Ruan X. Four-phonon Scattering Significantly Reduces Intrinsic thermal Conductivity of Solids. Phys Rev B (2017) 96:161201. doi:10.1103/physrevb.96.161201

CrossRef Full Text | Google Scholar

4. Recoules V, Clérouin J, Zérah G, Anglade PM, Mazevet S. Effect of Intense Laser Irradiation on the Lattice Stability of Semiconductors and Metals. Phys Rev Lett (2006) 96:055503. doi:10.1103/PhysRevLett.96.055503

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Yan G-Q, Cheng X-L, Zhang H, Zhu Z-Y, Ren D-H. Different Effects of Electronic Excitation on Metals and Semiconductors. Phys Rev B (2016) 93:214302. doi:10.1103/physrevb.93.214302

CrossRef Full Text | Google Scholar

6. Harbour L, Dharma-Wardana MWC, Klug DD, Lewis LJ. Equation of State, Phonons, and Lattice Stability of Ultrafast Warm Dense Matter. Phys Rev E (2017) 95:043201. doi:10.1103/PhysRevE.95.043201

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ono S. Lattice Dynamics for Isochorically Heated Metals: A Model Study. J Appl Phys (2019) 126:075113. doi:10.1063/1.5099165

CrossRef Full Text | Google Scholar

8. Medvedev N, Milov I. Nonthermal Phase Transitions in Metals. Sci Rep (2020) 10:12775–9. doi:10.1038/s41598-020-69604-9

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ono S, Kobayashi D. Phonon Softening in Sodium with a Stepwise Electron Distribution. J Appl Phys (2020) 127:165105. doi:10.1063/5.0004523

CrossRef Full Text | Google Scholar

10. Bouchet J, Bottin F. High-temperature and High-Pressure Phase Transitions in Uranium. Phys Rev B (2017) 95:054113. doi:10.1103/physrevb.95.054113

CrossRef Full Text | Google Scholar

11. Ben-Mahfoud L, Silaeva EP, Stoian R, Colombier JP. Structural Instability of Transition Metals upon Ultrafast Laser Irradiation. Phys Rev B (2021) 104:104104. doi:10.1103/physrevb.104.104104

CrossRef Full Text | Google Scholar

12. Ono S, Kobayashi D. Lattice Stability of Ordered Au-Cu Alloys in the Warm Dense Matter Regime. Phys Rev B (2021) 103:094114. doi:10.1103/physrevb.103.094114

CrossRef Full Text | Google Scholar

13. Ernstorfer R, Harb M, Hebeisen CT, Sciaini G, Dartigalongue T, Miller RJD. The Formation of Warm Dense Matter: Experimental Evidence for Electronic Bond Hardening in Gold. Science (2009) 323:1033–7. doi:10.1126/science.1162697

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Graziani F, Desjarlais MP, Redmer R, Trickey SB. Frontiers and Challenges in Warm Dense Matter. Berlin, Germany: Springer Science & Business (2014).

Google Scholar

15. Bonitz M, Dornheim T, Moldabekov ZA, Zhang S, Hamann P, Kählert H, et al. Ab Initio simulation of Warm Dense Matter. Phys Plasmas (2020) 27:042710. doi:10.1063/1.5143225

CrossRef Full Text | Google Scholar

16. Hu S, Collins L, Boehly T, Kress J, Goncharov V, Skupsky S, et al. First-principles thermal Conductivity of Warm-Dense Deuterium Plasmas for Inertial Confinement Fusion Applications. Phys Rev E (2014) 89:043105. doi:10.1103/PhysRevE.89.043105

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhang S, Zhao S, Kang W, Zhang P, He XT. Link between K Absorption Edges and Thermodynamic Properties of Warm Dense Plasmas Established by an Improved First-Principles Method. Phys Rev B (2016) 93:115114. doi:10.1103/physrevb.93.115114

CrossRef Full Text | Google Scholar

18. Kang D, Hou Y, Zeng Q, Dai J. Unified First-Principles Equations of State of Deuterium-Tritium Mixtures in the Global Inertial Confinement Fusion Region. Matter Radiat Extremes (2020) 5:055401. doi:10.1063/5.0008231

CrossRef Full Text | Google Scholar

19. Bethkenhagen M, Witte BB, Schörner M, Röpke G, Döppner T, Kraus D, et al. Carbon Ionization at Gigabar Pressures: An Ab Initio Perspective on Astrophysical High-Density Plasmas. Phys Rev Res (2020) 2:023260. doi:10.1103/physrevresearch.2.023260

CrossRef Full Text | Google Scholar

20. Schlanges M, Bonitz M, Tschttschjan A. Plasma Phase Transition in Fluid Hydrogen-Helium Mixtures. Contrib Plasma Phys (1995) 35:109–25. doi:10.1002/ctpp.2150350203

CrossRef Full Text | Google Scholar

21. Zhang S, Wang H, Kang W, Zhang P, He X. Extended Application of Kohn-Sham First-Principles Molecular Dynamics Method with Plane Wave Approximation at High Energy—From Cold Materials to Hot Dense Plasmas. Phys Plasmas (2016) 23:042707. doi:10.1063/1.4947212

CrossRef Full Text | Google Scholar

22. Lu B, Kang D, Wang D, Gao T, Dai J. Towards the Same Line of Liquid–Liquid Phase Transition of Dense Hydrogen from Various Theoretical Predictions. Chin Phys Lett (2019) 36:103102. doi:10.1088/0256-307x/36/10/103102

CrossRef Full Text | Google Scholar

23. Naghilou A, Armbruster O, Kautek W. “Laser-induced Non-thermal Processes.” in Handbook of Laser Micro-and Nano-Engineering, Berlin, Germany: Springer (2020) 1–23. doi:10.1007/978-3-319-69537-2_63-1

CrossRef Full Text | Google Scholar

24. Vinko S, Ciricosta O, Cho B, Engelhorn K, Chung HK, Brown C, et al. Creation and Diagnosis of a Solid-Density Plasma with an X-ray Free-Electron Laser. Nature (2012) 482:59–62. doi:10.1038/nature10746

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Hau-Riege SP, Graf A, Döppner T, London RA, Krzywinski J, Fortmann C, et al. Ultrafast Transitions from Solid to Liquid and Plasma States of Graphite Induced by X-ray Free-Electron Laser Pulses. Phys Rev Lett (2012) 108:217402. doi:10.1103/physrevlett.108.217402

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Kraus D, Bachmann B, Barbrel B, Falcone R, Fletcher L, Frydrych S, et al. Characterizing the Ionization Potential Depression in Dense Carbon Plasmas with High-Precision Spectrally Resolved X-ray Scattering. Plasma Phys Controlled Fusion (2018) 61:014015. doi:10.1088/1361-6587/aadd6c

CrossRef Full Text | Google Scholar

27. Saemann A, Eidmann K, Golovkin I, Mancini R, Andersson E, Förster E, et al. Isochoric Heating of Solid Aluminum by Ultrashort Laser Pulses Focused on a Tamped Target. Phys Rev Lett (1999) 82:4843. doi:10.1103/physrevlett.82.4843

CrossRef Full Text | Google Scholar

28. Chen Z, Holst B, Kirkwood S, Sametoglu V, Reid M, Tsui Y, et al. Evolution of Ac Conductivity in Nonequilibrium Warm Dense Gold. Phys Rev Lett (2013) 110:135001. doi:10.1103/physrevlett.110.135001

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Sentoku Y, Kemp A, Presura R, Bakeman M, Cowan T. Isochoric Heating in Heterogeneous Solid Targets with Ultrashort Laser Pulses. Phys Plasmas (2007) 14:122701. doi:10.1063/1.2816439

CrossRef Full Text | Google Scholar

30. Chen Z, Mo M, Soulard L, Recoules V, Hering P, Tsui Y, et al. Interatomic Potential in the Nonequilibrium Warm Dense Matter Regime. Phys Rev Lett (2018) 121:075002. doi:10.1103/PhysRevLett.121.075002

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Holst B, Recoules V, Mazevet S, Torrent M, Ng A, Chen Z, et al. Ab Initio model of Optical Properties of Two-Temperature Warm Dense Matter. Phys Rev B (2014) 90:035121. doi:10.1103/physrevb.90.035121

CrossRef Full Text | Google Scholar

32. Patel P, Mackinnon A, Key M, Cowan T, Foord M, Allen M, et al. Isochoric Heating of Solid-Density Matter with an Ultrafast Proton Beam. Phys Rev Lett (2003) 91:125004. doi:10.1103/physrevlett.91.125004

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Roth M, Alber I, Bagnoud V, Brown C, Clarke R, Daido H, et al. Proton Acceleration Experiments and Warm Dense Matter Research Using High Power Lasers. Plasma Phys Controlled Fusion (2009) 51:124039. doi:10.1088/0741-3335/51/12/124039

CrossRef Full Text | Google Scholar

34. Mancic A, Robiche J, Antici P, Audebert P, Blancard C, Combis P, et al. Isochoric Heating of Solids by Laser-Accelerated Protons: Experimental Characterization and Self-Consistent Hydrodynamic Modeling. High Energ Density Phys (2010) 6:21–8. doi:10.1016/j.hedp.2009.06.008

CrossRef Full Text | Google Scholar

35. Falk K. Experimental Methods for Warm Dense Matter Research. High Power Laser Sci Eng (2018) 6. doi:10.1017/hpl.2018.53

CrossRef Full Text | Google Scholar

36. Zeng Q, Dai J. Structural Transition Dynamics of the Formation of Warm Dense Gold: From an Atomic Scale View. SCIENCE CHINA PhysicsMechanics Astron (2020) 63:1–9. doi:10.1007/s11433-019-1466-2

CrossRef Full Text | Google Scholar

37. Lin Z, Zhigilei LV, Celli V. Electron-phonon Coupling and Electron Heat Capacity of Metals under Conditions of strong Electron-Phonon Nonequilibrium. Phys Rev B (2008) 77:075133. doi:10.1103/physrevb.77.075133

CrossRef Full Text | Google Scholar

38. Anisimov S, Kapeliovich B, Perelman T. Electron Emission from Metal Surfaces Exposed to Ultrashort Laser Pulses. Zh Eksp Teor Fiz (1974) 66:375–7.

Google Scholar

39. Minakov D, Levashov P. Melting Curves of Metals with Excited Electrons in the Quasiharmonic Approximation. Phys Rev B (2015) 92:224102. doi:10.1103/physrevb.92.224102

CrossRef Full Text | Google Scholar

40. Rethfeld B, Ivanov DS, Garcia ME, Anisimov SI. Modelling Ultrafast Laser Ablation. J Phys D: Appl Phys (2017) 50:193001. doi:10.1088/1361-6463/50/19/193001

CrossRef Full Text | Google Scholar

41. Rethfeld B, Kaiser A, Vicanek M, Simon G. Ultrafast Dynamics of Nonequilibrium Electrons in Metals under Femtosecond Laser Irradiation. Phys Rev B (2002) 65:214303. doi:10.1103/physrevb.65.214303

CrossRef Full Text | Google Scholar

42. Mueller B, Rethfeld B. Relaxation Dynamics in Laser-Excited Metals under Nonequilibrium Conditions. Phys Rev B (2013) 87:035139. doi:10.1103/physrevb.87.035139

CrossRef Full Text | Google Scholar

43. Weber ST, Rethfeld B. Phonon-induced Long-Lasting Nonequilibrium in the Electron System of a Laser-Excited Solid. Phys Rev B (2019) 99:174314. doi:10.1103/physrevb.99.174314

CrossRef Full Text | Google Scholar

44. Lin Z, Zhigilei LV. Time-resolved Diffraction Profiles and Atomic Dynamics in Short-Pulse Laser-Induced Structural Transformations: Molecular Dynamics Study. Phys Rev B (2006) 73:184113. doi:10.1103/physrevb.73.184113

CrossRef Full Text | Google Scholar

45. Ma Q, Dai J, Kang D, Murillo M, Hou Y, Zhao Z, et al. Extremely Low Electron-Ion Temperature Relaxation Rates in Warm Dense Hydrogen: Interplay between Quantum Electrons and Coupled Ions. Phys Rev Lett (2019) 122:015001. doi:10.1103/PhysRevLett.122.015001

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Qian X, Yang R. Temperature Effect on the Phonon Dispersion Stability of Zirconium by Machine Learning Driven Atomistic Simulations. Phys Rev B (2018) 98:224108. doi:10.1103/physrevb.98.224108

CrossRef Full Text | Google Scholar

47. Baroni S, De Gironcoli S, Dal Corso A, Giannozzi P. Phonons and Related crystal Properties from Density-Functional Perturbation Theory. Rev Mod Phys (2001) 73:515. doi:10.1103/revmodphys.73.515

CrossRef Full Text | Google Scholar

48. Kresse G, Furthmüller J, Hafner J. Ab Initio force Constant Approach to Phonon Dispersion Relations of diamond and Graphite. EPL (Europhysics Letters) (1995) 32:729. doi:10.1209/0295-5075/32/9/005

CrossRef Full Text | Google Scholar

49. Bottin F, Zérah G. Formation Enthalpies of Monovacancies in Aluminum and Gold under the Condition of Intense Laser Irradiation. Phys Rev B (2007) 75:174114. doi:10.1103/physrevb.75.174114

CrossRef Full Text | Google Scholar

50. Zijlstra ES, Tatarinova LL, Garcia ME. Laser-induced Phonon-Phonon Interactions in Bismuth. Phys Rev B (2006) 74:220301. doi:10.1103/physrevb.74.220301

CrossRef Full Text | Google Scholar

51. Peng B, Zhang H, Chen W, Hou B, Qiu ZJ, Shao H, et al. Sub-picosecond Photo-Induced Displacive Phase Transition in Two-Dimensional Mote 2. npj 2D Mater Appl (2020) 4:1–8. doi:10.1038/s41699-020-0147-x

CrossRef Full Text | Google Scholar

52. Zhang H, Zhang S, Kang D, Dai J, Bonitz M. Finite-temperature Density-Functional-Theory Investigation on the Nonequilibrium Transient Warm-Dense-Matter State Created by Laser Excitation. Phys Rev E (2021) 103:013210. doi:10.1103/PhysRevE.103.013210

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Mauri F, Car R. First-principles Study of Excitonic Self-Trapping in diamond. Phys Rev Lett (1995) 75:3166. doi:10.1103/physrevlett.75.3166

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Kohn W, Sham LJ. Self-consistent Equations Including Exchange and Correlation Effects. Phys Rev (1965) 140:A1133. doi:10.1103/physrev.140.a1133

CrossRef Full Text | Google Scholar

55. Mermin ND. Thermal Properties of the Inhomogeneous Electron Gas. Phys Rev (1965) 137:A1441. doi:10.1103/physrev.137.a1441

CrossRef Full Text | Google Scholar

56. Giannozzi P, Baroni S, Bonini N, Calandra M, Car R, Cavazzoni C, et al. Quantum Espresso: a Modular and Open-Source Software Project for Quantum Simulations of Materials. J Phys Condensed matter (2009) 21:395502. doi:10.1088/0953-8984/21/39/395502

CrossRef Full Text | Google Scholar

57. Giannozzi P, Andreussi O, Brumme T, Bunau O, Nardelli MB, Calandra M, et al. Advanced Capabilities for Materials Modelling with Quantum Espresso. J Phys Condensed matter (2017) 29:465901. doi:10.1088/1361-648x/aa8f79

CrossRef Full Text | Google Scholar

58. Taillefumier M, Cabaret D, Flank AM, Mauri F. X-ray Absorption Near-Edge Structure Calculations with the Pseudopotentials: Application to the K Edge in diamond and α-quartz. Phys Rev B (2002) 66:195107. doi:10.1103/physrevb.66.195107

CrossRef Full Text | Google Scholar

59. Kang D, Dai J, Sun H, Hou Y, Yuan J. Quantum Simulation of Thermally-Driven Phase Transition and Oxygen K-Edge X-ray Absorption of High-Pressure Ice. Scientific Rep (2013) 3:1–7. doi:10.1038/srep03272

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Blöchl PE. Projector Augmented-Wave Method. Phys Rev B (1994) 50:17953. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

61. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett (1996) 77:3865. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Monkhorst HJ, Pack JD. Special Points for Brillouin-Zone Integrations. Phys Rev B (1976) 13:5188. doi:10.1103/physrevb.13.5188

CrossRef Full Text | Google Scholar

63. Tadano T, Gohda Y, Tsuneyuki S. Anharmonic Force Constants Extracted from First-Principles Molecular Dynamics: Applications to Heat Transfer Simulations. J Phys Condensed Matter (2014) 26:225402. doi:10.1088/0953-8984/26/22/225402

CrossRef Full Text | Google Scholar

64. Tadano T, Tsuneyuki S. Self-consistent Phonon Calculations of Lattice Dynamical Properties in Cubic Srtio 3 with First-Principles Anharmonic Force Constants. Phys Rev B (2015) 92:054301. doi:10.1103/physrevb.92.054301

CrossRef Full Text | Google Scholar

65. Rahim W, Skelton JM, Savory CN, Evans IR, Evans JS, Walsh A, et al. Polymorph Exploration of Bismuth Stannate Using First-Principles Phonon Mode Mapping. Chem Sci (2020) 11:7904–9. doi:10.1039/d0sc02995e

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Nagler B, Zastrau U, Faustlin RR, Vinko SM, Whitcher T, Nelson A, et al. Turning Solid Aluminium Transparent by Intense Soft X-ray Photoionization. Nat Phys (2009) 5:693.

Google Scholar

67. Henke BL, Gullikson EM, Davis JC. X-ray interactions: photoabsorption, scattering, transmission, and reflection at e= 50-30,000 ev, z= 1-92. At Data Nucl Data tables (1993) 54:181–342. doi:10.1006/adnd.1993.1013

CrossRef Full Text | Google Scholar

68. Setyawan W, Curtarolo S. High-throughput Electronic Band Structure Calculations: Challenges and Tools. Comput Mater Sci (2010) 49:299–312. doi:10.1016/j.commatsci.2010.05.010

CrossRef Full Text | Google Scholar

69. Grigoryan NS, Zier T, Garcia ME, Zijlstra ES. Ultrafast Structural Phenomena: Theory of Phonon Frequency Changes and Simulations with Code for Highly Excited Valence Electron Systems. JOSA B (2014) 31:C22–C27. doi:10.1364/josab.31.000c22

CrossRef Full Text | Google Scholar

70. Tadano T, Tsuneyuki S. Quartic Anharmonicity of Rattlers and its Effect on Lattice thermal Conductivity of Clathrates from First Principles. Phys Rev Lett (2018) 120:105901. doi:10.1103/physrevlett.120.105901

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Peng B, Hu Y, Murakami S, Zhang T, Monserrat B. Topological Phonons in Oxide Perovskites Controlled by Light. Sci Adv (2020) 6:eabd1618. doi:10.1126/sciadv.abd1618

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Stedman R, Nilsson G. Dispersion Relations for Phonons in Aluminum at 80 and 300 K. Phys Rev (1966) 145:492. doi:10.1103/physrev.145.492

CrossRef Full Text | Google Scholar

73. Svensson E, Brockhouse B, Rowe J. Crystal Dynamics of Copper. Phys Rev (1967) 155:619. doi:10.1103/physrev.155.619

CrossRef Full Text | Google Scholar