Spatial Manipulation via Four-Wave Mixing in Five-Level Cold Atoms

In a recent publication [S. Gan, Laser Phys. 31, 055401 (2021)], a scheme for controlling the vortex four-wave mixing (FWM) in a five-level atomic system has been put forward. Based on this work, we propose a new scheme for the spatial manipulation via four-wave mixing in a five-level atomic system when the radial index is considered. It is found that the phase and intensity of the FWM field can be spatially manipulated. More importantly, we show the superposition modes created by the interference between the FWM field and a same-frequency Gaussian beam, which can also be controlled via the corresponding parameters. Our research is helpful to understand and manipulate optical vortices and can be widely used in quantum computation and communication.

1 Introduction

The Laguerre–Gaussian (LG) light carrying orbital angular momentum (OAM) [1] has attracted a lot of interest due to its unique amplitude and phase structures. In particular, the four-wave mixing (FWM) based on OAM light has emerged as a hot topic in recent years. For instance, Qiu et al. proposed a scheme to demonstrate the manipulation of space-dependent four-wave mixing (FWM) in a four-level atomic system [2]. By adjusting the detuning of the control field, one can effectively control the FWM output field. Yu et al. described a theoretical investigation of a FWM scheme in a six-level atomic system driven by a field with OAM and making use of two electromagnetically induced transparency (EIT) control fields [3]. The obtained results allow one to control the helical phase of the output FWM field by varying the intensities of the two EIT control fields as well as the detuning of the probe field. Quite recently, Wang et al. have also proposed some schemes to control vortex FWM carrying OAM in different nanostructures [4–6].

In this paper, we investigated the spatial manipulation via four-wave mixing in a five-level atomic system. Quite recently, we have proposed a scheme for modulating the spatial vortex FWM in a five-level atomic system [7]. However, different from this previous study, the major features of applying our considered scheme are as follows. First, the main difference between our scheme and the one in [7] is that we have shaped the LG field as a double-ring LG mode with the radial index p = 1 while in [7] the radial index is 0. This scheme has many advantages for controlling the FWM in comparison with the publication [7]. For example, the double-ring LG mode provides two FWM channels, and in different channels the spatial variation of the FWM are different. Second, in this scheme more physical parameters (e.g., the radial index p = 1) can be manipulated and hence one can select suitable radial index p to explore singularity characteristics of helical phase wavefront in nonlinear processes. Third, we display the superposition modes created by the interference between the FWM field and a same-frequency Gaussian beam, which show a more flexible intensity control or phase control for the superposition modes.

2 Theoretical Model and Equations

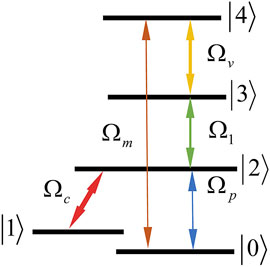
We consider an atomic system as shown in Figure 1. A probe field with Rabi frequency ${\mathrm{\Omega }}_p={\mathrm{\Omega }}_{p0}{e}^{-{(r/R_p)}^2}\sqrt{\pi /(2\ln 2)}\exp [-t^2/(2\ln 2/{\pi }^2)]$ (Ω_p0 and R_p are the amplitude and transverse radius with t being the time) is applied to the transition |2⟩ ↔|0⟩. A control field with Rabi frequency Ω_c drives the transition |2⟩ ↔|1⟩. A pump field with Rabi frequency Ω₁ drives the transition |3⟩ ↔|2⟩, while a LG field with Rabi frequency Ω_v drives the transition |4⟩ ↔|3⟩. Here Ω_v is defined as

${\mathrm{\Omega }}_v={\mathrm{\Omega }}_{v0}\mathrm{\Omega }\left(r\right)e^{-il\varphi }\text{,}(1)$

where $\mathrm{\Omega }(r)=\frac{\sqrt{2p!/\pi (p+\left|l\right|)!}}{{\omega }_0}{\left(\frac{\sqrt{2}r}{{\omega }_0}\right)}^{|l|}{L}_p^{\left|l\right|}\left(\frac{2r^2}{{\omega }_0^2}\right)e^{-r^2/{\omega }_0^2}$, Ω_v0 is the initial Rabi frequency, r is the radius and the beam waist is ω₀. ϕ is the azimuthal angle and $L_p^{\left|l\right|}$ is the Laguerre polynomial. The radial index and azimuthal index are defined by p and l, respectively.

FIGURE 1

FIGURE 1. Schematic of a five-level atomic system.

Making use of the Schrödinger equation, the dynamical equations for the atomic probability amplitudes A_j(j = 1–4) in the interaction picture are given by [8].

$\begin{array}{ll}\hfill \dot{A_1}& =\left[i\left({\mathrm{\Delta }}_p-{\mathrm{\Delta }}_c\right)-{\gamma }_1\right]A_1+i{\mathrm{\Omega }}_c^{\ast }{A}_2\text{,}\hfill \end{array}(\mathrm{2a})$

$\begin{array}{ll}\hfill \dot{A_2}& =i{\mathrm{\Omega }}_p{A}_0+\left(i{\mathrm{\Delta }}_p-{\gamma }_2\right)A_2+i{\mathrm{\Omega }}_c{A}_1+i{\mathrm{\Omega }}_1^{\ast }{A}_3\text{,}\hfill \end{array}(\mathrm{2b})$

$\begin{array}{ll}\hfill \dot{A_3}& =i{\mathrm{\Omega }}_1{A}_2+i{\mathrm{\Omega }}_v^{\ast }{e}^{i\delta \vec{k}\cdot \vec{r}}{A}_4+\left[i\left({\mathrm{\Delta }}_p+{\mathrm{\Delta }}_3\right)-{\gamma }_3\right]A_3\text{,}\hfill \end{array}(\mathrm{2c})$

$\begin{array}{lll}\hfill \dot{A_4}& =i{\mathrm{\Omega }}_m{A}_0+i{\mathrm{\Omega }}_v{e}^{-i\delta \vec{k}\cdot \vec{r}}{A}_3+\hfill & \hfill \\ \hfill & \hfill & \hfill \left[i\left({\mathrm{\Delta }}_p+{\mathrm{\Delta }}_3+{\mathrm{\Delta }}_4\right)-{\gamma }_4\right]A_4\text{,}\end{array}(\mathrm{2d})$

where Δ_p, Δ_c, Δ₃ and Δ₄ are the detunings of the fields. The $\delta \vec{k}={\vec{k}}_m-({\vec{k}}_p+{\vec{k}}_1+{\vec{k}}_v)$ is phase mis-matching condition, and ${\vec{k}}_i(i=p,1,v,m)$ are the wave vectors of the corresponding fields. The γ_n (n = 1–4) are decay rates.

Under the slowly varying envelope approximation, the propagation equations of the probe and FWM fields are governed by the Maxwell equations

$\frac{\partial {\mathrm{\Omega }}_{p\left(m\right)}}{\partial z}+\frac{\partial {\mathrm{\Omega }}_{p\left(m\right)}}{c\partial t}=\frac{i}{2k_{p\left(m\right)}}{\nabla }_{\perp }^2{\mathrm{\Omega }}_{p\left(m\right)}+i{\kappa }_{02\left(04\right)}a{A}_{2\left(4\right)}{A}_0^{\ast }\text{,}(3)$

where k_p(m) is the wave number of the probe field (FWM field). κ₀₂₍₀₄₎ = 2Nω_p(m)|D₀₂₍₀₄₎|²/(cℏ) is the propagation constant, which is related to the frequently used oscillator strengths of the transition |0⟩ ↔|2⟩ (|4⟩). N and D₀₂₍₀₄₎ are the atomic density and dipole moment between states |0⟩ and |2⟩ (|4⟩), respectively.

We assume all the atoms are in the ground state |0⟩ i.e. ${\left|A_0\right|}^2\approx 1$ and use the condition of phase matching $\delta \vec{k}=0$. By applying Fourier transformations $A_j(t)=\int {\tilde{A}}_j(\omega )e^{-i\omega t}d\omega (j=1-4)$ to Eqs 2a, 3 and obtain [9].

$\begin{array}{lll}\hfill & \hfill & \hfill f_1{\tilde{A}}_1+{\mathrm{\Omega }}_c^{\ast }{\tilde{A}}_2=0\text{,}\end{array}(\mathrm{4a})$

$\begin{array}{lll}\hfill & \hfill & \hfill {\mathrm{\Omega }}_c{\tilde{A}}_1+f_2{\tilde{A}}_2+{\mathrm{\Omega }}_1^{\ast }{\tilde{A}}_3=-{\tilde{\mathrm{\Omega }}}_p\text{,}\end{array}(\mathrm{4b})$

$\begin{array}{lll}\hfill & \hfill & \hfill {\mathrm{\Omega }}_1{\tilde{A}}_2+f_3{\tilde{A}}_3+{\mathrm{\Omega }}_v^{\ast }{\tilde{A}}_4=0\text{,}\end{array}(\mathrm{4c})$

$\begin{array}{lll}\hfill & \hfill & \hfill {\mathrm{\Omega }}_v{\tilde{A}}_3+f_4{\tilde{A}}_4=-{\tilde{\mathrm{\Omega }}}_m\text{\hspace{0.17em},}\end{array}(\mathrm{4d})$

and the Maxwell’s equations Ω_p(m) obeyed as follows

$\frac{\partial {\tilde{\mathrm{\Omega }}}_{p\left(m\right)}}{\partial z}-{\frac{i\omega }{c}\tilde{\mathrm{\Omega }}}_{p\left(m\right)}=\frac{i}{2k_{p\left(m\right)}}{\nabla }_{\perp }^2{\tilde{\mathrm{\Omega }}}_{p\left(m\right)}+i{\kappa }_{02\left(04\right)}{\tilde{A}}_{2\left(4\right)}\text{,}(5)$

where ω is the Fourier frequency. f₁ = ω + Δ_p − Δ_c + iγ₁, f₂ = ω + Δ_p + iγ₂, f₃ = ω + Δ_p + Δ₃ + iγ₃, f₄ = ω + Δ_p + Δ₃ + Δ₄ + iγ₄, and ${\tilde{\mathrm{\Omega }}}_{p(m)}$ are the Fourier transformations of Ω_p(m). The first terms on the right-hand sides of the Eq. 5 accounts for light diffraction. Light diffraction can be neglected if the propagation distance is much smaller than the Rayleigh ranges of the probe pulse or the generated FWM field [10, 11], i.e. $\pi {\omega }_0^2/\lambda \gg L$. We take the propagation distance z = 15 mm, the transverse characteristic dimension w_T = ω₀ = 0.18 mm and the wavelength of the FWM field λ ≈ 300 nm, obtaining $\pi {\omega }_0^2/\lambda \approx 339.12$ mm ≫ 15 mm. So it is safe to ignore diffraction in this work.

Using the initial condition ${\tilde{\mathrm{\Omega }}}_m(z=0,\omega )=0$, the generated FWM field is given by

${\tilde{\mathrm{\Omega }}}_m\left(z,\omega \right)=\frac{{\tilde{\mathrm{\Omega }}}_p\left(z=0,\omega \right){\kappa }_{04}{\beta }_1{\mathrm{\Omega }}_1{\mathrm{\Omega }}_v}{M\left[K_{+}\left(\omega \right)-K_{-}\left(\omega \right)\right]}\left(e^{i{K}_{-}\left(\omega \right)z}-e^{i{K}_{+}\left(\omega \right)z}\right)\text{,}(6)$

where $K_{\pm }(\omega )=\frac{\omega }{c}+\frac{F_p+F_m}{2}\pm \sqrt{{\left[\frac{F_p-F_m}{2}\right]}^2+G}$, $F_p=-(f_3{f}_4-{\left|{\mathrm{\Omega }}_v\right|}^2)f_1{\kappa }_{02}/M,$ $F_m=-[M+(f_1{f}_2-|{\mathrm{\Omega }}_c{|}^2){\left|{\mathrm{\Omega }}_v\right|}^2]{\kappa }_{04}/M{f}_4$, $G=f_1^2|{\mathrm{\Omega }}_1{|}^2|{\mathrm{\Omega }}_v{|}^2{\kappa }_{02}{\kappa }_{04}/M^2$, M = (f₁f₂ − |Ω_c|²) (f₃f₄ − |Ω_v|²) − |Ω₁|²f₁f₄, with ${\tilde{\mathrm{\Omega }}}_p(z=0,\omega )={\mathrm{\Omega }}_{p0}{e}^{-{(r/{\omega }_{p0})}^2}\exp [-{\omega }^2/(2{\pi }^2/\ln 2)]$. We can see that there exist two modes K₊(ω) and K₋(ω) described by the dispersion relation K(ω) = K₊(ω) + K₋(ω) in Eq. 6, the real part Re[K(ω)] reflects the phase while the imaginary part Im[K(ω)] represents the absorption [12].

3 Results and Discussion

In this section, we aim to study the effects of the different parameters on phase and intensity of the FWM field ${\tilde{\mathrm{\Omega }}}_m(z,\omega )$. In order to clearly show the spatial-dependent mechanism, the superposition modes created by the interference between the FWM field and a same-frequency Gaussian beam are also provided.

In Figure 2, we plot the phase and the normalized intensity patterns of the FWM field versus the (x, y) for different probe detuning Δ_p. As we expected, both the phase (Figures 2A1–A7) and intensity (Figures 2B1–B7) patterns are divided into two parts. From this figure, one can find that, upon increasing Δ_p from 1 MHz to ±5 MHz, the value of intensity decrease progressively while the phase twist is suppressed. The key factor is that the azimuthal dependent absorption and dispersion properties of the FWM field are modulated, which lead to the corresponding results. Moreover, the real (Figures 2C1–C7) part and imaginary (Figures 2D1–D7) part of dispersion relation K(ω) are shown in Figure 2, which have given the physical reason for the phase and the intensity patterns of the FWM field being changed in Figure 2.

FIGURE 2

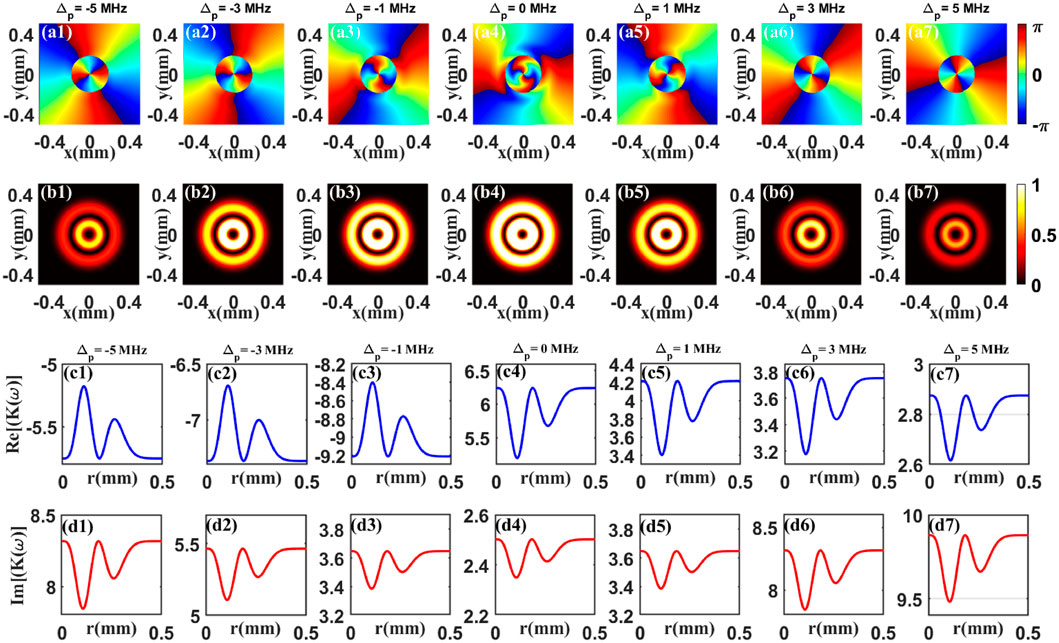
FIGURE 2. Phase (A1–A7) and normalized intensity (B1–B7) patterns of the FWM field for different probe detuning Δ_p. The real (C1–C7) and imaginary (D1–D7) parts of dispersion relation K(ω) versus radius r for different probe detuning Δ_p. The other parameters are ω₀ = 0.18 mm, R_p = 3ω₀, ω = 3 MHz, z = 15 mm, p = 1, l = 2, γ₁ = 1 × 10^–4 MHz, γ₂ = 6 MHz, γ₃ = 0.66 MHz, γ₄ = 0.08 MHz, Ω₁ = 12 MHz, Ω_v0 = 2.5 MHz, Ω_c = 5.5 MHz, Ω_p0 = 0.55 MHz, Δ_c = Δ₃ = Δ₄ = 0, κ₀₂ = 200 MHz/mm, κ₀₄ = 0.01κ₀₂.

In Figure 3, we present the phase and the normalized intensity patterns of the FWM field for different detuning Δ₃. By direct comparison in Figures 2, 3, we obtain that the situation in Figure 3 is nearly the same as the Figure 2. Such results indicate that the OAM phase is transferred to the FWM field and is modulated via detuning Δ₃. Here, we also provide the real part and imaginary part of dispersion relation in Figures 3C1–C7 and Figures 3D1–D7. By increasing the detuning Δ₃, both the imaginary part and real part are changing. So we can see the varying phase and intensity of the FWM field.

FIGURE 3

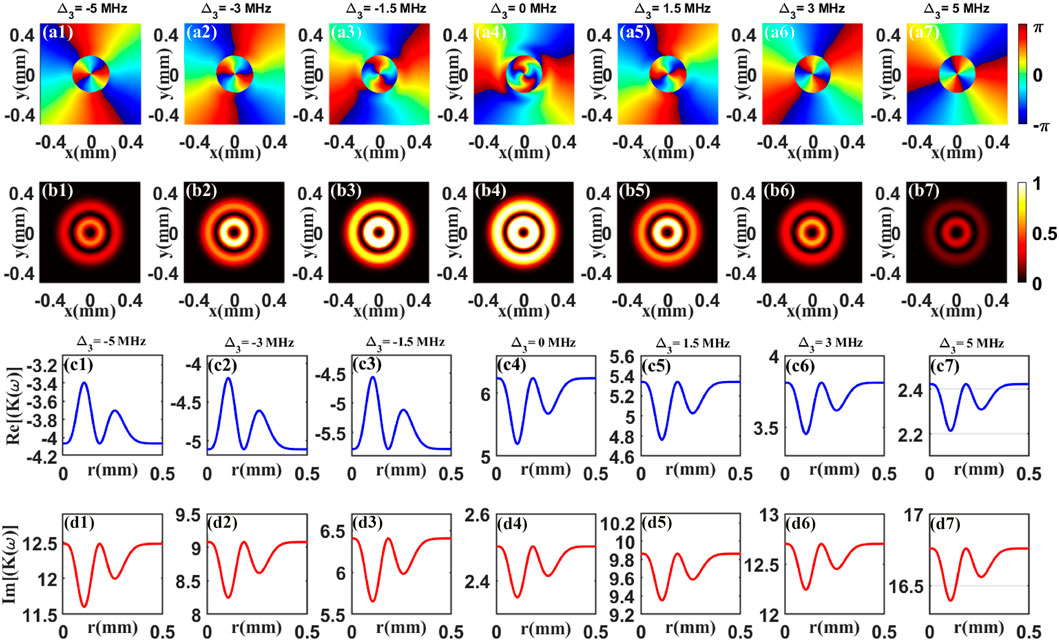
FIGURE 3. Phase (A1–A7) and normalized intensity (B1–B7) patterns of the FWM field for different detuning Δ₃. The real (C1–C7) and imaginary (D1–D7) parts of dispersion relation K(ω) versus radius r for different detuning Δ₃. The other parameters are the same as in Figure 2.

Next, to obtain a better understanding of the vortex modulation, we show the superposition patterns of the FWM field and a same-frequency Gaussian beam in Figure 4. As illustrated in Figure 4, the superposition patterns are extremely rotated for different detunings Δ_p and Δ₃. The reason for this is that, due to the equiphase surface of Gaussian beam is a plane, azimuthally phase difference between the FWM field and Gaussian beam is very sensitive to detunings (Δ_p, Δ₃), which reflects the different superposition patterns. The findings in Figure 4 imply that the OAM phase is indeed transferred to the FWM field and has a spatial dependency, which is originated from the spatial-sensitive absorption and dispersion properties induced by the three fields in the present system.

FIGURE 4

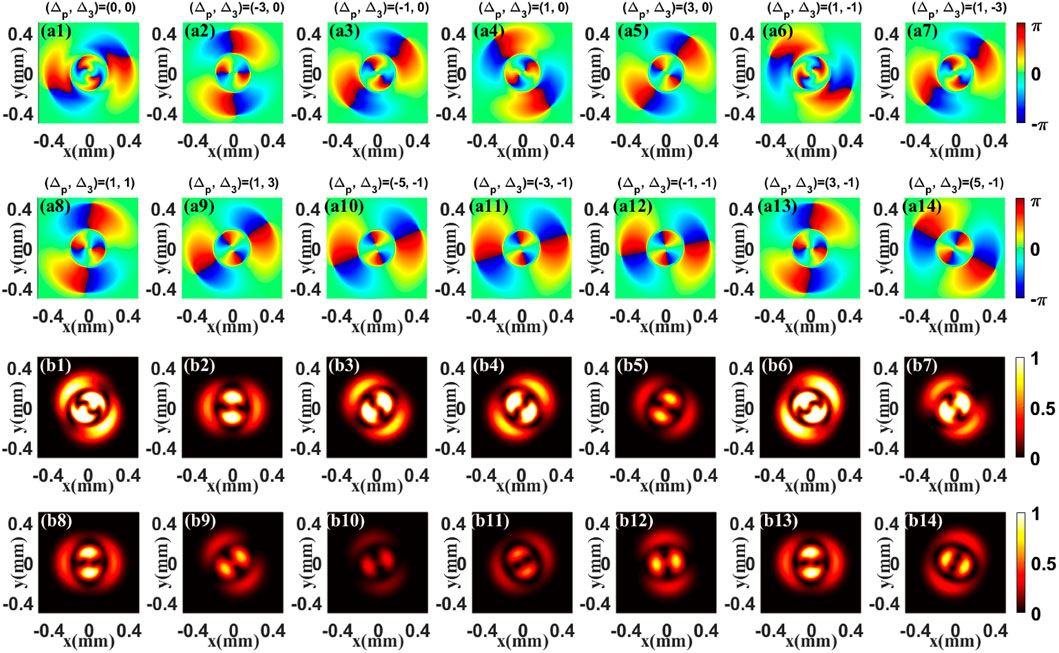
FIGURE 4. Superposition phase (A1–A14) and intensity (B1–B14) patterns of FWM field and the same-frequency Gaussian beam ${\mathrm{\Omega }}_G=e^{-{(r/2{\omega }_0)}^2}$ for different Δ_p and Δ₃. The other parameters are the same as in Figure 2.

We note that, very recently, some theoretical schemes for controlling the space-dependent FWM in atoms [2, 3] or in semiconductor quantum wells [4–6] have been proposed. Comparing with those schemes, the major features of our proposal are the following. First, we have utilized the EIT induced by a additional control beam Ω_c. The EIT scheme has many advantages for controlling the FWM in comparison with the one in [2]. For example, the coherent optical FWM with the EIT condition mediated by detunings Δ_p or Δ₃ will lead to many orders of magnitude enhancement in the amplitude of the generated wave (e.g., see Figures 2, 3). Second, Different from the results obtained in [3], we display the superposition modes created by the interference between the FWM field and a same-frequency Gaussian beam. It is found that the superposition modes can be spatially manipulated via the corresponding parameters, which show a more flexible intensity control or phase control for the superposition modes. Third, unlike in solid-state systems [4–6], nonlinear effects are highly efficient and require only low light intensities in atomic vapors, which is convenient for the experimental realization of our scheme.

Before ending this section, it is worthwhile to briefly discuss the possible experimental realization of our scheme. Such an atomic structure can be realized in cold ⁸⁵Rb atoms. The designated states can be chosen as: |0⟩ = |5S_1/2, F = 1⟩, |1⟩ = |5S_1/2, F = 2⟩, |2⟩ = |5P_3/2⟩, |3⟩ = |5D_5/2⟩ and |4⟩ = |nP_3/2⟩ (n > 10). Three transitions are |5S_1/2, F = 1⟩ ↔|5P_3/2⟩ at 780 nm, |5P_3/2⟩ ↔|5D_5/2⟩ at 776 nm, |5D_5/2⟩ ↔|63P_3/2⟩ at 1260 nm, and a Rydberg transition generated the FWM field |5S_1/2, F = 1⟩ ↔|63P_3/2⟩ at 300 nm.

4 Conclusion

In summary, we have studied the spatial manipulation via four-wave mixing (FWM) in a five-level atomic system. Interestingly, by adjusting the detunings, one can effectively modulate the phase and intensity of the FWM field when the radial index is considered. More importantly, we show the superposition modes created by the interference between the FWM field and a same-frequency Gaussian beam, which show many interesting properties. So our results may be helpful to investigate the interactions between OAM light and quantum media [13, 14].

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work is supported by the key project of continuing education and teaching reform of Department of Education of Anhui Province (2019jxjj39) and the key project of research and development of Anhui Province (NO. 202004a05020043).

References

1. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Qiu J, Wang Z, Ding D, Huang Z, Yu B. Control of Space-dependent Four-Wave Mixing in a Four-Level Atomic System. Phys Rev A (2020) 102:033516. doi:10.1103/physreva.102.033516

CrossRef Full Text | Google Scholar

3. Yu C, Wang Z. Engineering Helical Phase via Four-Wave Mixing in the Ultraslow Propagation Regime. Phys Rev A (2021) 103:013518. doi:10.1103/physreva.103.013518

CrossRef Full Text | Google Scholar

4. Zhang Y, Wang Z, Qiu J, Hong Y, Yu B. Spatially Dependent Four-Wave Mixing in Semiconductor Quantum wells. Appl Phys Lett (2019) 115:171905. doi:10.1063/1.5121275

CrossRef Full Text | Google Scholar

5. Wang Z, Zhang Y, Paspalakis E, Yu B. Efficient Spatiotemporal-Vortex Four-Wave Mixing in a Semiconductor Nanostructure. Phys Rev A (2020) 102:063509. doi:10.1103/physreva.102.063509

CrossRef Full Text | Google Scholar

6. Qiu J, Wang Z, Ding D, Li W, Yu B. Highly Efficient Vortex Four-Wave Mixing in Asymmetric Semiconductor Quantum wells. Opt Express (2020) 28(3):2975–86. doi:10.1364/oe.379245

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gan S. Spatial Vortex Four-Wave Mixing in a Five-Level Atomic System. Laser Phys (2021) 31:055401. doi:10.1088/1555-6611/abee8e

CrossRef Full Text | Google Scholar

8. Wu Y, Payne MG, Hagley EW, Deng L. Efficient Multiwave Mixing in the Ultraslow Propagation Regime and the Role of Multiphoton Quantum Destructive Interference. Opt Lett (2004) 29:2294. doi:10.1364/ol.29.002294

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wu Y, Saldana J, Zhu Y. Large Enhancement of Four-Wave Mixing by Suppression of Photon Absorption from Electromagnetically Induced Transparency. Phys Rev A (2003) 67:013811. doi:10.1103/physreva.67.013811

CrossRef Full Text | Google Scholar

10. Hong Y, Wang Z, Ding D, Yu B. Ultraslow Vortex Four-Wave Mixing via Multiphoton Quantum Interference. Opt Express (2019) 27:29863. doi:10.1364/oe.27.029863

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chen J, Wang Z, Yu B. Spatially Dependent Hyper-Raman Scattering in Five-Level Cold Atoms. Opt Express (2021) 29(7):10914–22. doi:10.1364/oe.420015

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wu Y, Yang X. Highly Efficient Four-Wave Mixing in Double-Λsystem in Ultraslow Propagation Regime. Phys Rev A (2004) 70:053818. doi:10.1103/physreva.70.053818

CrossRef Full Text | Google Scholar

13. Qiu J, Wang Z, Yu B. Generation of New Structured Beams via Spatially Dependent Transparency. Quan Inf Process (2019) 18:1. doi:10.1007/s11128-019-2278-6

CrossRef Full Text | Google Scholar

14. Zhang K, Wang W, Liu S, Pan X, Du J, Lou Y, et al. Reconfigurable Hexapartite Entanglement by Spatially Multiplexed Four-Wave Mixing Processes. Phys Rev Lett (2020) 124:090501. doi:10.1103/physrevlett.124.090501

PubMed Abstract | CrossRef Full Text | Google Scholar