Experimental Study and DEM Simulation of Size Effects on the Dry Density of Rockfill Material

The initial dry density has a significant effect on the mechanical behavior of rockfill material (RFM). The size effects on the minimum/maximum dry density (referred to as dry density, ρ_d) of RFM still need further study. To investigate the relationship between ρ_d and d_M, a series of surface vibration compaction tests and DEM simulations are performed on the samples with different maximum particle sizes d_M. Both the physical and numerical results exhibit that ρ_d increases fast when d_M ranges from 10 to 40 mm. When d_M exceeds 40 mm, ρ_d increases slowly and tends to be a constant. Results indicate that ρ_d is affected by the gradation. To consider the gradation effect, a normalized parameter λ is introduced, and the relation between ρ_d and d_M can be characterized by an empirical equation.

1 Introduction

Rockfill material (RFM) has been widely used in the construction of dams and railway embankments due to its inherent flexibility, capacity to cope with large seismic actions, and adaptability to various foundation conditions. Nowadays, the maximum diameter d_M of rockfill particles used in the field can be up to 1,200 mm [1]. However, the d_M allowable in laboratory is usually not more than 60 mm because of the limitation of apparatus size [2]. Therefore, several scaling techniques have been proposed to prepare the scaled samples. The scaling techniques include the scalping technique [3], the parallel gradation technique [4], the quadratic grain size distribution technique [5], the replacement technique [6], the hybrid method [7, 8], etc. Although the scaling techniques have been widely applied, the size effects on the properties of RFM have still not been fully understood [9–11].

Many researchers have studied the size effects on the mechanical behavior of RFM via large-scale triaxial tests [1, 12–14]. However, most of the studies neglect the size effects on the density of rockfill samples. Limited literature on the size effects of density can be found [15, 16]. Experimental results show that the mechanical behavior of RFM is directly related to its initial density (or void ratio) [17, 18]. Hence, the size effects on the density of RFM need further investigation. In contrast, the discrete element method (DEM) is a good tool to simulate granular materials because of their discontinuous and heterogeneous natures [19]. In practice, the DEM has been widely used to reproduce the laboratory tests on granular materials (e.g., soil, sand, and RFM) [20–22]. The responses of the granular materials can be understood in the particle scale.

Generally, the minimum dry density ρ_d, min/maximum dry density ρ_d, max (referred to as dry density, ρ_d) is mainly controlled by the gradation and particle shape [23–28]. There are few analytical models for predicting the minimum/maximum dry densities. Kezdi [29] proposed an analytical method to estimate the ρ_d, max of sand-silt mixtures. The method is based on the ideal situation that the void space among sand grains can be effectively filled by silt particles without altering the packing structure of sand. Hence, this method usually overestimates the realistic ρ_d, max [30]. In combination with the liquefaction potential of silty sand, Lade et al. [31] also proposed a formula to predict the ρ_d, max. The formula is also based on the ideal situation used by Kezdi [29] and thus overestimates the ρ_d, max. Korfiatis and Manikopoulos [32] proposed a piecewise linear relationship between the particle size distribution (PSD) curve and the ρ_d, max of granular soils based on the theoretical formulations. The basic assumption in the model is that the log-normal gradation is expected to be a straight line and is determined by two parameters, i.e., a center point and a slope. Chang et al. [33] also proposed an analytical method for predicting the ρ_d, max of sand-silt mixtures. The analytical methods mentioned here have been focused on sand-silt mixtures. Therefore, these models can not be applied to soils with a wide range of particle sizes, like RFM.

In this study, the size effects on the dry density of RFM are investigated by a series of surface vibration compaction tests and numerical simulations. The relationship between ρ_d and d_M is discussed. An empirical equation is proposed to describe the relation between ρ_d and d_M considering the effect of gradation.

2 Experiments

2.1 Test Materials

The studied materials were obtained from the Shuangjiangkou rockfill material resources field in western China. The rockfill particles of sizes from 1 to 100 mm are shown in Figure 1A. The rock is a granite mainly composed of feldspar, quartz, and biotite, with an angular/sub-angular shape (as shown in Figure 1B). Field emission scanning electron microscope (FE-SEM) and energy-dispersive X-ray spectroscopy (EDS) were used to identify the mineral compositions (Figure 1C). The specific gravity of rockfill particles is 2.68. The d_M of the studied RFM is 600 mm, which is greater than the limit of the conventional test apparatus in laboratory. Therefore, the prototype gradation of RFM should be scaled down by scaling techniques.

FIGURE 1

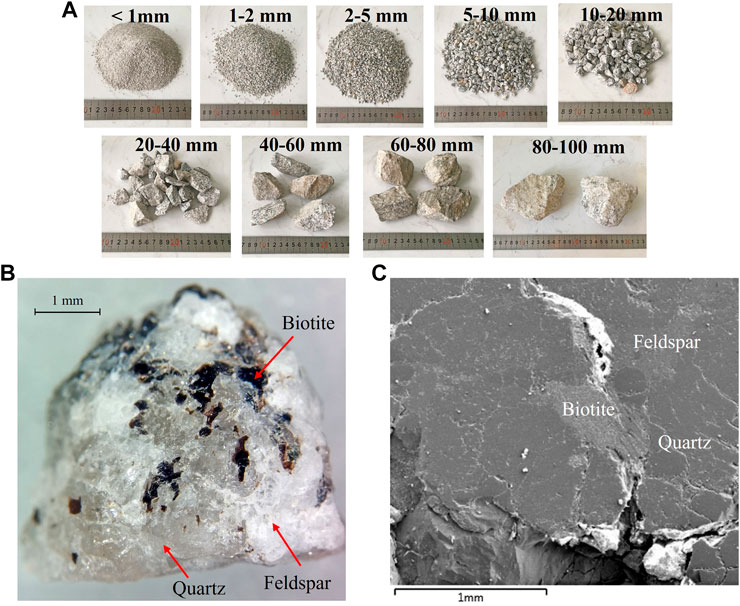
FIGURE 1. Macroscopic observations on (A) Shuangjiangkou rockfill particles of sizes 1–100 mm. Microscopic observations on Shuangjiangkou rockfill particles: (B) surface view with different mineral compositions; (C) FE-SEM image of one typical rockfill particle.

The hybrid method [7, 8] is adopted in the present study. In practice, it is a combination of the parallel gradation and replacement techniques. The method is popular in China as it has both the advantages of these two scaling techniques. In this method, the gradation is first scaled parallelly by an appropriate ratio to ensure that the percentage of fine fraction (i.e., d < 5 mm) is less than 30%. After that, if the oversized fraction (i.e., d > d_M) still remains, it will be replaced proportionally by the coarse fraction (i.e., 5 mm $<d<d_M$). As a result, the scaled gradation curve has a similar shape compared to the prototype, and the content of fine fraction is also limited to a low value.

Six different values of d_M (10, 20, 40, 60, 80, and 100 mm) are adopted for the dry density tests. The chosen values of d_M are in the range of the commonly used maximum particle sizes in laboratory. In practice, the diameter of triaxial samples can be 61.8, 101, and 300 mm while the maximum particle size allowable is 1/5 of the sample diameters [7, 8, 34], i.e., 10, 20, and 60 mm.

The particle size distribution (PSD) curves for prototype and scaled RFMs are shown in Figure 2. The PSD curves are labeled by the letter H and a number. The letter H represents the hybrid method and the number indicates the value of d_M. Prior to the usage in the experiment, the soil is sieved into different fractions, and each individual fraction is then mixed according to the given PSD to prepare laboratory samples. In the dry density tests, the specimen is not divided into layers before compaction.

FIGURE 2

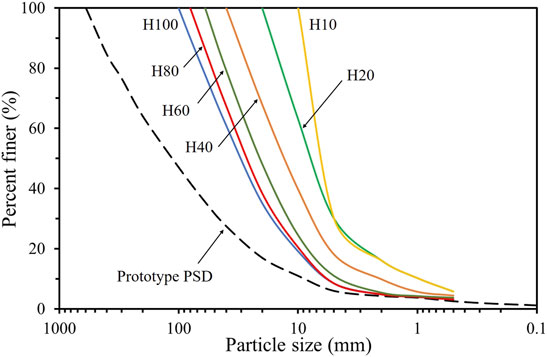
FIGURE 2. Particle size distribution (PSD) curves for the prototype and scaled rockfill materials (RFMs).

2.2 Dry Density Tests

The ρ_d, min (or maximum void ratio e_M) is obtained by the loose-fill method [8, 35]. The ρ_d, max (or minimum void ratio e_m) is determined using the surface vibration compaction test [8, 36].

The surface vibration test device includes a steel mold, a steel plate, and a surface vibrator. The steel mold (diameter 303 mm and height 418 mm) is used to hold the soil samples. The surface vibrator has an exciting force of 4.2 kN with a motor frequency of 50 Hz and an amplitude of 2 mm. The steel plate is positioned on the top of the sample to ensure a uniform distribution of vertical stress applied to the samples. The steel plate is 280 mm in diameter and 20 mm in height. The static pressure applied on the samples by the vibration hammer is 14 kPa.

In the loose-fill method, the soil sample is filled into a container by using a small shovel. To ensure that the soil sample slowly slides into the container, the small shovel should touch close to the surface of soil during filling. The filling process is stopped until the filled soil is above the top of the container. The top surface of the container is then leveled by the shovel, and the weight of the container and soil sample is measured. Then, the ρ_d, min can be obtained. In the surface vibration test, a soil sample of 40 kg are carefully prepared and filled into the steel mold by the small shovel. The steel plate is then placed on the surface of the sample, on which the surface vibrator is placed. The vibration time is 15 min for the densest state. The ρ_d, max can then be determined by measuring the sample height. The tests are repeated two times and an average value is adopted for a more reliable result.

3 Numerical Modeling

3.1 DEM Modeling of Rockfill Material

To better understand the size effects on the ρ_d, max of RFM, a series of DEM simulations of dry density tests are conducted. The DEM is performed by YADE, an open source framework [37]. The particles are generated according to the PSD curves in Figure 2. For the samples with d_M = 120 − 150 mm, the parallel gradation technique is used for scaling. For a compromise between the computational efficiency and a relatively realistic reconstruction of samples, the fine fractions (i.e., d < 5 mm) are all replaced by particles with size d = 5 mm.

The rigid container for holding the sample with d_M = 60 mm is 303 mm in diameter and 600 mm in height. For the rest of samples with a given d_M, the corresponding container diameter and height are scaled by a factor f = d_M/60 to ensure the same sample-size ratio (SSR), which is the ratio of the sample diameter to d_M [38–40]. The rigid container is constructed by rigid facet units. Linear contact model [19] in DEM is used with the Young’s modulus of 60 MPa and Poisson’s ratio of 0.45. Both the friction angles of walls and balls are 0, i.e., the friction angles of all contacts are set as 0 for a dense state of soil samples. The density of particles is 2.68 (g/cm³). No calibration is made here, and the model parameters are chosen considering an appropriate computational time. The aim of the DEM simulation is to provide more data for the study of relationship between ρ_d, max and d_M. The d_M is not more than 100 mm in physical tests due to the limitation of apparatus size, while the d_M can be up to 150 mm in DEM simulation. Typical numerical samples with d_M = 10 mm, 60 mm, and 100 mm are given in Figure 3.

FIGURE 3

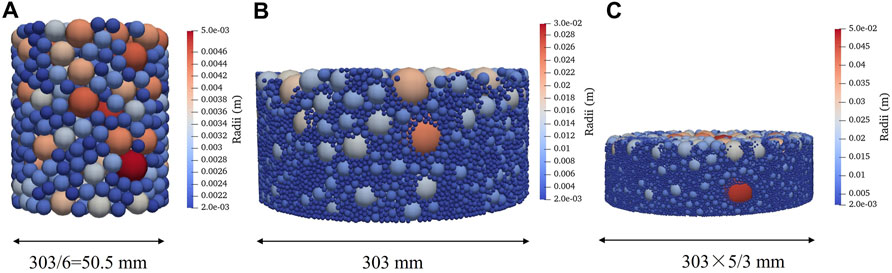
FIGURE 3. DEM samples with three maximum particle sizes: (A) d_M = 10 mm; (B) d_M = 60 mm; (C) d_M = 100 mm.

3.2 Simulation of Compaction Process

In the physical tests, the dense soil samples are obtained by surface vibration tests. However, a dense sample in DEM can be easily obtained by setting the friction angle as 0 [41, 42], which is adopted in the present study. The particles are first deposited into the container under gravity. After that, a rigid wall is generated above the sample and then moved downward until a vertical pressure of 14 kPa is reached. The pressure of 14 kPa is same to the static pressure applied by the vibration hammer in physical tests. The simulation is terminated when a steady state is reached.

4 Results and Discussion

Figure 4A shows the relationship between the ρ_d and d_M in the physical dry density tests. Both the ρ_d, min and ρ_d, max increase with the increase of d_M. The ρ_d increases rapidly when d_M ranges from 10 to 40 mm. When d_M exceeds 40 mm, the ρ_d increases slowly and tends to be a constant. These results can be explained by the gradation: with a wide range of particle sizes, the sample with a large d_M is better graded than that with a small d_M. This observation is consistent with the previous laboratory test results [27, 40, 43, 44].

FIGURE 4

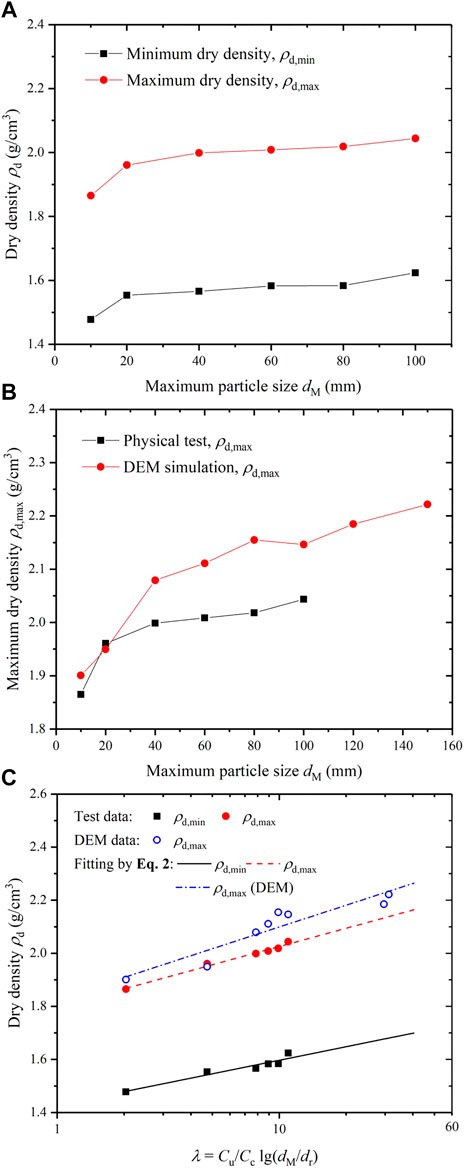
FIGURE 4. (A) Relationship between the dry density ρ_d and maximum particle size d_M in physical dry densty tests; (B) comparison of dry density results in physical tests and DEM simulations; (C) relationship between the dry density ρ_d and normalized parameter λ in physical tests and DEM simulations.

Figure 4B shows the comparison of the ρ_d, max − d_M relations in physical tests and numerical simulations. The ρ_d, max − d_M relation in the physical tests can be generally reproduced by the DEM simulations: the ρ_d, max increases fast when d_M ranges from 10 to 40 mm and then increases slowly and tends to be a constant. The high value of ρ_d, max in DEM simulation should be partly attributed to the chosen assumptions (spherical particle and friction angle of 0). The use of complex particle shapes and non-zero friction angles would be more faithful to the facts. However, the choice of friction angle of 0 and spherical particles in the present study is in consideration of computational time. In DEM, the bonded particle model (BPM) or polyhedron is used to describe the irregular particle shape. The BPM needs many elementary balls to generate an agglomerate [45], and the polyhedron needs complex contact detection methods [46]. The effect of particle shape on the ρ_d has been seldom studied by DEM. Jensen et al. [47] used a 2D BPM to study the effect of particle shape on the void ratio. They confirmed that the void ratio of a particle mass increased as the angularity or roughness of the particle increased. Deng et al. [45] used a 3D BPM to simulate the dynamic process of particle packing with different particle aspect ratios. The above studies verify the important effect of particle shape on ρ_d. However, the numerical samples reported in the literature are usually uniformly graded, and the particle packing with a wide gradation is not considered due to the high computational cost.

Based on the work of Zhu et al. [48], the normalized parameter λ can be used to describe the relationship between dry density, gradation, and maximum particle size, which can be expressed as

$\lambda =C_u/C_c\lg \left(d_M/d_r\right)(1)$

where C_u = coefficient of uniformity, C_c = coefficient of curvature, d_r = 1 mm, i.e., reference size. The maximum particle size d_M is the value of maximum particle size in a PSD. The C_u and C_c are defined as [49]

$C_u=d_{60}/d_{10}(2)$

$C_c=d_{30}^2/\left(d_{10}\times d_{60}\right)(3)$

where d₁₀, d₃₀, and d₆₀ are the particle diameter corresponding to 10, 30, and 60%, respectively, passing on the cumulative PSD curve. Therefore, the values of C_u and C_c are related to the width and shape of PSD curve. The relationship between ρ_d and λ is given in a semi-logarithmic scale (Figure 4C). The data points can be well fitted by a linear function

${\rho }_d={\rho }_w\left(a\lg \left(\lambda \right)+b\right)(4)$

where a and b are the fitting parameters; ρ_w is the density of water, 1 g/cm³. In the present study, a and b are 0.10 and 1.80, 0.07 and 1.43, for the ρ_d, max and ρ_d, min of the studied RFM, respectively. For the prototype gradation (i.e., d_M = 600 mm, C_u = 19.61, C_c = 1.35, λ = 40.4), the ρ_d, max and ρ_d, min are estimated to be 2.164 and 1.700 g/cm³ by Eq. 4, increasing by 7.74 and 7.37% compared to the corresponding value of H60 sample, respectively.

DEM simulation results are also illustrated in Figure 4C. The data points can also be linearly fitted, shown as a dash-dotted line. The applicability of Eq. 4 has been verified by the numerical simulation when the d_M is in the range of 10—150 mm.

5 Conclusion

The size effects on the minimum/maximum dry density (referred to as dry density, ρ_d) of rockfill material are studied by a series of surface vibration compaction tests and DEM simulations. Both physical and numerical results show that the ρ_d increases fast when the d_M ranges from 10 to 40 mm and then increases slowly and tends to be a constant. By introducing the nominal parameter λ, an empirical equation is proposed to describe the relation between ρ_d and d_M considering the effect of gradation. A more accurate predictive formula considering particle shape needs further investigation. This study can provide a valuable reference to understand the size effects on the dry density of rockfill material.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

Funding acquisition and formal writing of the work, XZ and JZ; investigation and data analysis of the work, XZ, YW, and NB; review and editing of the work, JZ, YJ, J-BC, and HB. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (No. U1865104), the Key project from NSFC of the Yangtze River Water Science Research Joint Fund (No. U2040221), and the 111 Project (No. B13024). The first author gratefully acknowledges the financial support from China Scholarship Council (No. 201806710020).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The DEM simulations in this paper have been done on the HPC Computing Mésocentre of University of Lille.

References

1. Varadarajan A, Sharma KG, Venkatachalam K, Gupta AK. Testing and Modeling Two Rockfill Materials. J Geotech Geoenviron Eng (2003) 129:206–18. doi:10.1061/(asce)1090-0241(2003)129:3(206)

CrossRef Full Text | Google Scholar

2. Xiao Y, Liu H, Chen Y, Jiang J, Zhang W. Testing and Modeling of the State-dependent Behaviors of Rockfill Material. Comput Geotechnics (2014) 61:153–65. doi:10.1016/j.compgeo.2014.05.009

CrossRef Full Text | Google Scholar

3. Zeller J, Wullimann R. The Shear Strength of the Shell Materials for the Go-Schenenalp Dam, switzerland. In: Proceedings of the 4th International Conference on Soil Mechanics and Foundation Engineering, Held in London, 1957. London: Butterworths Scientific Publications, 2 (1957). p. 399–415.

Google Scholar

4. Lowe J. Shear Strength of Coarse Embankment Dam Materials. In: Proceedings of the 8th International Congress on Large Dams, 3. Paris: International Commission on Large Dams (1964). p. 745–61.

Google Scholar

5. Fumagalli E. Tests on Cohesionless Materials for Rockfill Dams. J Soil Mech Found Div (1969) 92:313–32. doi:10.1061/jsfeaq.0001223

CrossRef Full Text | Google Scholar

6. Frost R. Some Testing Experiences and Characteristics of boulder-gravel Fill in Earth Dams. In: Evaluation of Relative Density and its Role in Geotechnical Projects Involving Cohesionless Soils. West Conshohocken: ASTM International (1973).

Google Scholar

7. Trujillo-Gonzalez JM. Standard Test Methods for Soils (1999). sl237-1999.

Google Scholar

8.Standard Code. Code for Coarse-Grained Soil Tests for Hydropower and Water Conservancy Engineering (2006). DL/T 5356-2006.

Google Scholar

9. Alonso EE, Tapias M, Gili J. Scale Effects in Rockfill Behaviour. Géotechnique Lett (2012) 2:155–60. doi:10.1680/geolett.12.00025

CrossRef Full Text | Google Scholar

10. Xiao Y, Liu H, Chen Y, Zhang W. Particle Size Effects in Granular Soils under True Triaxial Conditions. Géotechnique (2014) 64:667–72. doi:10.1680/geot.14.t.002

CrossRef Full Text | Google Scholar

11. Ovalle C, Dano C. Effects of Particle Size-Strength and Size-Shape Correlations on Parallel Grading Scaling. Géotechnique Lett (2020) 10:191–7. doi:10.1680/jgele.19.00095

CrossRef Full Text | Google Scholar

12. Varadarajan A, Sharma KG, Abbas SM, Dhawan AK. The Role of Nature of Particles on the Behaviour of Rockfill Materials. Soils and Foundations (2006) 46:569–84. doi:10.3208/sandf.46.569

CrossRef Full Text | Google Scholar

13. Hu W, Dano C, Hicher PY, Le Touzo JY, Derkx F, Merliot E. Effect of Sample Size on the Behavior of Granular Materials. Geotech Test J (2011) 34:186–97.

Google Scholar

14. Ovalle C, Frossard E, Dano C, Hu W, Maiolino S, Hicher P-Y. The Effect of Size on the Strength of Coarse Rock Aggregates and Large Rockfill Samples through Experimental Data. Acta Mech (2014) 225:2199–216. doi:10.1007/s00707-014-1127-z

CrossRef Full Text | Google Scholar

15. Ham T-G, Nakata Y, Orense RP, Hyodo M. Influence of Gravel on the Compression Characteristics of Decomposed Granite Soil. J Geotech Geoenviron Eng (2010) 136:1574–7. doi:10.1061/(asce)gt.1943-5606.0000370

CrossRef Full Text | Google Scholar

16. Wang J-J, Cheng Y-Z, Zhang H-P, Deng D-P. Effects of Particle Size on Compaction Behavior and Particle Crushing of Crushed sandstone-mudstone Particle Mixture. Environ Earth Sci (2015) 73:8053–9. doi:10.1007/s12665-014-3961-7

CrossRef Full Text | Google Scholar

17. Xiao Y, Liu H, Chen Y, Jiang J. Strength and Deformation of Rockfill Material Based on Large-Scale Triaxial Compression Tests. I: Influences of Density and Pressure. J Geotech Geoenviron Eng (2014) 140:04014070. doi:10.1061/(asce)gt.1943-5606.0001176

CrossRef Full Text | Google Scholar

18. Wang L, Zhu J, Zhang Z, Zheng H. Effects of Dry Density on Shear Behavior and Particle Breakage for Slate Rockfill Material. Bull Eng Geol Environ (2021) 80:1181–92. doi:10.1007/s10064-020-01971-z

CrossRef Full Text | Google Scholar

19. Cundall PA, Strack ODL. A Discrete Numerical Model for Granular Assemblies. Géotechnique (1979) 29:47–65. doi:10.1680/geot.1979.29.1.47

CrossRef Full Text | Google Scholar

20. Anandarajah A. On Influence of Fabric Anisotropy on the Stress-Strain Behavior of Clays. Comput Geotechnics (2000) 27:1–17. doi:10.1016/s0266-352x(00)00005-7

CrossRef Full Text | Google Scholar

21. Cil MB, Alshibli KA. 3d Evolution of Sand Fracture under 1d Compression. Géotechnique (2014) 64:351–64. doi:10.1680/geot.13.p.119

CrossRef Full Text | Google Scholar

22. Wang Y, Song E-x., Zhao Z. Particle Mechanics Modeling of the Effect of Aggregate Shape on Creep of Durable Rockfills. Comput Geotechnics (2018) 98:114–31. doi:10.1016/j.compgeo.2018.02.013

CrossRef Full Text | Google Scholar

23. Miura K, Maeda K, Furukawa M, Toki S. Mechanical Characteristics of Sands with Different Primary Properties. Soils and Foundations (1998) 38:159–72. doi:10.3208/sandf.38.4_159

CrossRef Full Text | Google Scholar

24. Cubrinovski M, Ishihara K. Maximum and Minimum Void Ratio Characteristics of Sands. Soils and Foundations (2002) 42:65–78. doi:10.3208/sandf.42.6_65

CrossRef Full Text | Google Scholar

25. Rousé PC, Fannin RJ, Shuttle DA. Influence of Roundness on the Void Ratio and Strength of Uniform Sand. Géotechnique (2008) 58:227–31. doi:10.1680/geot.2008.58.3.227

CrossRef Full Text | Google Scholar

26. Chang CS, Deng Y, Yang Z. Modeling of Minimum Void Ratio for Granular Soil with Effect of Particle Size Distribution. J Eng Mech (2017) 143:04017060. doi:10.1061/(asce)em.1943-7889.0001270

CrossRef Full Text | Google Scholar

27. Kuei KC, DeJong JT, Martinez A. Particle Size Effects on the Strength and Fabric of Granular media. In: Geo-Congress 2020: Modeling, Geomaterials, and Site Characterization. VA: American Society of Civil Engineers Reston (2020). p. 349–58. doi:10.1061/9780784482803.038

CrossRef Full Text | Google Scholar

28. Maroof MA, Mahboubi A, Vincens E, Noorzad A. Effects of Particle Morphology on the Minimum and Maximum Void Ratios of Granular Materials. Granul Matter (2022) 24:1–24. doi:10.1007/s10035-021-01189-0

CrossRef Full Text | Google Scholar

29. Kézdi A. Soil Physics. Amsterdam, Netherlands: Elsevier (1979).

Google Scholar

30. Vallejo LE. Interpretation of the Limits in Shear Strength in Binary Granular Mixtures. Can Geotech J (2001) 38:1097–104. doi:10.1139/t01-029

CrossRef Full Text | Google Scholar

31. Chaney RC, Demars KR, Lade PV, Liggio CD, Yamamuro JA. Effects of Non-plastic Fines on Minimum and Maximum Void Ratios of Sand. Geotech Test J (1998) 21:336. doi:10.1520/gtj11373j

CrossRef Full Text | Google Scholar

32. Korfiatis GP, Manikopoulos CN. Correlation of Maximum Dry Density and Grain Size. J Geotech Engrg Div (1982) 108:1171–6. doi:10.1061/ajgeb6.0001341

CrossRef Full Text | Google Scholar

33. Chang CS, Wang J-Y, Ge L. Modeling of Minimum Void Ratio for Sand-silt Mixtures. Eng Geology (2015) 196:293–304. doi:10.1016/j.enggeo.2015.07.015

CrossRef Full Text | Google Scholar

34.ASTM international. Standard Test Method for Consolidated Drained Triaxial Compression Test for Soils. West Conshohocken: ASTM International (2020). annual book of astm standards. ASTM D 7181-20.

Google Scholar

35.ASTM international. Standard Test Methods for Minimum index Density and Unit Weight of Soils and Calculation of Relative Density. West Conshohocken: ASTM International (2016). ASTM D 4254-16.

Google Scholar

36.ASTM international. Standard Test Methods for Determination of Maximum Dry Unit Weight of Granular Soils Using a Vibrating Hammer. West Conshohocken: ASTM International (2020). ASTM D 7382-20.

Google Scholar

37. Kozicki J, Donzé FV. A New Open-Source Software Developed for Numerical Simulations Using Discrete Modeling Methods. Comput Methods Appl Mech Eng (2008) 197:4429–43. doi:10.1016/j.cma.2008.05.023

CrossRef Full Text | Google Scholar

38. Holtz WG, Gibbs HJ. Triaxial Shear Tests on Pervious Gravelly Soils. J Soil Mech Found Div (1956) 82:1–22. doi:10.1061/jsfeaq.0000004

CrossRef Full Text | Google Scholar

39. Marachi N. Strength and Deformation Characteristics of Rockfill Materials. Berkeley, USA: University of California (1969). Ph.D. thesis.

40. Stoeber JN. Effects of Maximum Particle Size and Sample Scaling on the Mechanical Behavior of Mine Waste Rock; a Critical State Approach. Libraries: Colorado State University (2012). Ph.D. thesis.

41. Yan WM, Dong J. Effect of Particle Grading on the Response of an Idealized Granular Assemblage. Int J Geomech (2011) 11:276–85. doi:10.1061/(asce)gm.1943-5622.0000085

CrossRef Full Text | Google Scholar

42. Fu R, Hu X, Zhou B. Discrete Element Modeling of Crushable Sands Considering Realistic Particle Shape Effect. Comput Geotechnics (2017) 91:179–91. doi:10.1016/j.compgeo.2017.07.016

CrossRef Full Text | Google Scholar

43. Pike D. Compactability of Graded Aggregates: 1. In: Standard Laboratory Tests. Wokingham: Transport and Road Research Laboratory (1972).

Google Scholar

44. Verdugo R, de la Hoz K. Strength and Stiffness of Coarse Granular Soils. In: Soil Stress-Strain Behavior: Measurement, Modeling and Analysis. Heidelberg: Springer (2007). p. 243–52. doi:10.1007/978-1-4020-6146-2_9

CrossRef Full Text | Google Scholar

45. Deng XL, Davé RN. Dynamic Simulation of Particle Packing Influenced by Size, Aspect Ratio and Surface Energy. Granular Matter (2013) 15:401–15. doi:10.1007/s10035-013-0413-0

CrossRef Full Text | Google Scholar

46. Cantor D, Azéma E, Sornay P, Radjai F. Three-dimensional Bonded-Cell Model for Grain Fragmentation. Comp Part Mech (2017) 4:441–50. doi:10.1007/s40571-016-0129-0

CrossRef Full Text | Google Scholar

47. Jensen RP, Edil TB, Bosscher PJ, Plesha ME, Kahla NB. Effect of Particle Shape on Interface Behavior of DEM‐Simulated Granular Materials. Int J Geomechanics (2001) 1:1–19. doi:10.1061/(asce)1532-3641(2001)1:1(1)

CrossRef Full Text | Google Scholar

48. Zhu J, Weng H, Wu X, Liu H. Experimental Study of Compact Density of Scaled Coarse-Grained Soil. Rock Soil Mech (2010) 31:2394–8. doi:10.16285/j.rsm.2010.08.046

CrossRef Full Text | Google Scholar

49.ASTM International. Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System)1. West Conshohocken: ASTM International (2017). 2487-17e1.

Google Scholar