- 1Max Planck Institute for Solid State Research, Stuttgart, Germany
- 2Yusuf Hamied Department of Chemistry, University of Cambridge, Cambridge, United Kingdom
The discovery of superconductivity in hole-doped infinite-layer NdNiO2 — a transition metal (TM) oxide that is both isostructural and isoelectronic to cuprate superconductors—has lead to renewed enthusiasm in the hope of understanding the origin of unconventional superconductivity. Here, we investigate the electron-removal states in infinite-layered Ni1+ oxide, NdNiO2, which mimics hole doping, with the state-of-the-art many-body multireference quantum chemistry methods. From the analysis of the many-body wavefunction we find that the hole-doped d8 ground state of NdNiO2 is very different from the d8 ground state in isostructural cuprate analog CaCuO2, although the parent d9 ground states are for the most part identical. We show that the doped hole in NdNiO2 mainly localizes on the Ni 3
1 Introduction
For more than 3 decades, understanding the mechanism of superconductivity observed at high critical temperature (HTC) in strongly correlated cuprates [1] has been the “holy grail” of many theoretical and experimental condensend matter researchers. In this context, the observation of superconductivity in nickelates LnNiO2, Ln = {La, Nd and Pr} [2–4] upon doping with holes is remarkable. These superconducting nickelates are isostructural as well as isoelectronic to HTC cuprate superconductors and thus enable the comparison of the essential physical features that may be playing a crucial role in the mechanism driving superconductivity.
LnNiO2 family of compounds are synthesized in the so-called infinite-layer structure, where NiO2 and Ln layers are stacked alternatively [2]. The NiO2 planes are identical to the CuO2 planes in HTC cuprates which host much of the physics leading to superconductivity [5]. A simple valence counting of the these nickelates reveals a 1+ oxidation state for Ni (2- for O and 3+ for Ln) with nine electrons in the 3d manifold. In the cuprates, the Cu2+ oxidation state gives rise to the same 3d9 electronic configuration. Contrary to many nickel oxides where the Ni atom sits in an octahedral cage of oxygens, in the infinite-layered structure, square planar NiO4 plaques are formed without the apical oxygens. The crystal field due to square-planar oxygen coordination stabilizes the
Several electronic structure calculations based on density-functional theory (DFT) have shown that in monovalent nickelates the Ni 3
In the cuprate charge-transfer insulators, the strong hybridization of the Cu 3
Despite the efforts to discern the similarities and differences between the monovalent nickelates and superconducting cuprates, there is no clear understanding on the nature of doped holes in NdNiO2. Particularly, there is no reliable parameter-free ab initio analysis of the hole-doped situation. In this work, we investigate the hole‐doped ground state in NdNiO2 and draw parallels to the hole‐doped ground state of cuprate analogue CaCuO2. We use fully ab initio many-body wavefunction-based quantum chemistry methodology to compute the ground state wavefunctions for the hole‐doped NdNiO2 and CaCuO2. We find that the doped hole in NdNiO2 mainly localizes on the Ni 3
In what follows, we first describe the computational methodology we use in this work where we highlight the novel features of the methods and provide all the computational details. We then present the results of our calculations and conclude with a discussion.
2 The Wavefunction Quantum Chemistry Method
Ab initio configuration interaction (CI) wavefunction-based quantum chemistry methods, particularly the post Hartree-Fock (HF) complete active space self-consistent field (CASSCF) and the multireference perturbation theory (MRPT), are employed. These methods not only facilitate systematic inclusion of electron correlations, but also enable to quantify different types of correlations, static vs. dynamic [18]. These calculations do not use any ad hoc parameters to incorporate electron-electron interactions unlike other many-body methods, instead, they are computed fully ab initio from the kinetic and Coulomb integrals. Such ab initio calculations provide techniques to systematically analyze electron correlation effects and offer insights into the electronic structure of correlated solids that go substantially beyond standard DFT approaches, e.g., see Refs. [7, 19–22] for the 3d TM oxides and Refs. [23–27] for 5d compounds.
2.1 Embedded Cluster Approach
Since strong electronic correlations are short-ranged in nature [28], a local approach for the calculation of the N and N ± 1 –electron wavefunction is a very attractive option for transition metal compounds. In the embedded cluster approach, a finite set of atoms, we call quantum cluster (QC), is cut out from the infinite solid and many-body quantum chemistry methods are used to calculate the electronic structure of the atoms within the QC. The cluster is “embedded” in a potential that accounts for the part of the crystal that is not treated explicitly. In this work, we represent the embedding potential with an array of point charges (PCs) at the lattice positions that are fitted to reproduce the Madelung crystal field in the cluster region [29]. Such procedure enables the use of quantum chemistry calculations for solids involving transition-metal or lanthanide ions, see Refs. [23, 30, 31].
2.2 Complete Active Space Self-Consistent Field
CASSCF method [18] is a specific type of multi-configurational (MC) self-consistent field technique in which a complete set of Slater determinants or configuration state functions (CSFs) that is used in the expansion of the CI wavefunction is defined in a constrained orbital space, called the active space. In the CASSCF(n,m) approach, a subset of n active electrons are fully correlated among an active set of m orbitals, leading to a highly multi-configurational (CAS) reference wavefunction. CASSCF method with a properly chosen active space guarantees a qualitatively correct wavefunction for strongly correlated systems where static correlation [18] effects are taken into account.
We consider active spaces as large as CAS(24,30) in this work. Because the conventional CASSCF implementations based on deterministic CI space (the Hilbert space of all possible configurations within the active space) solvers are limited to active spaces of 18 active electrons in 18 orbitals, we use the full configuration interaction quantum Monte Carlo (FCIQMC) [32–34] and density matrix renormalization group (DMRG) theory [35, 36] algorithms to solve the eigenvalue problem defined within the active space.
2.3 Multireference Perturbation Theory
While the CASSCF calculation provides a qualitatively correct wavefunction, for a quantitative description of a strongly correlated system, dynamic correlations [18] (contributions to the wavefunction from those configurations related to excitations from inactive to active and virtual, and active to virtual orbitals) are also important and must be accounted for. A natural choice is variational multireference CI (MRCI) approach where the CI wavefunction is extended with excitations involving orbitals that are doubly occupied and empty in the reference CASSCF wavefunction [18]. An alternative and computationally less demanding approach to take into account the dynamic correlations is based on perturbation theory in second- and higher-orders. In multireference perturbation theory (MRPT) MC zeroth-order wavefunction is employed and excitations to the virtual space are accounted by means of perturbation theory. If the initial choice of the MC wavefunction is good enough to capture the large part of the correlation energy, then the perturbation corrections are typically small. The most common variations of MRPT are the complete active space second-order perturbation theory (CASPT2) [37] and the n-electron valence second-order perturbation theory (NEVPT2) [38] which differ in the type of zeroth-order Hamiltonian H0 employed.
3 The Ab Initio model
Before we describe the ab initio model we consider, let us summarize the widely used and prominent model Hamiltonian to study the nature of doped hole in HTC cuprates and also employed for monovalent nickelates lately. It is the three-band Hubbard model [39] with three orbital degrees of freedom (bands) which include the d orbital of Cu with x2−y2 symmetry and the in-plane oxygen p orbitals aligned in the direction of the nearest Cu neighbours. These belong to the b1 irreducible representation (irrep) of the D4h point group symmetry realized at the Cu site of the CuO4 plaque, the other Cu d orbitals belong to a1
Within the embedded cluster approach described earlier, we consider a QC of five NiO4 (CuO4) plaques that includes five Ni (Cu) atoms, 16 oxygens and 8 Nd (Ca) atoms, see Figure 1. The 10 Ni (Cu) ions neighbouring to the cluster are also included in the QC, however, these are considered as total ion potentials (TIPs). The QC is embedded in point charges that reproduce the electrostatic field of the solid environment. We used the crystal structure parameters for the thin film samples reported in Refs. [2, 42–44].
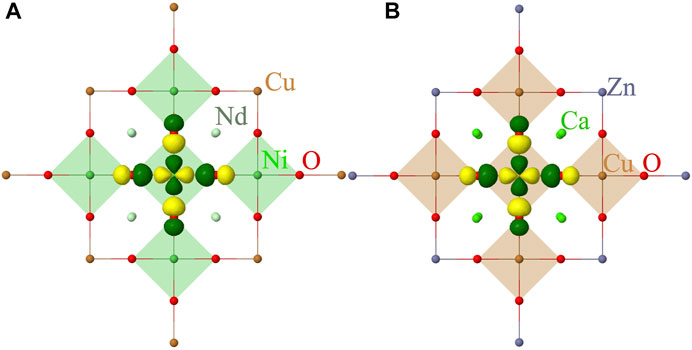
FIGURE 1. Quantum cluster of five NiO4 (A) and CuO4 (B) plaques considered in our calculations. The point-charge embedding is not shown. The symmetry adapted localized 3
We used effective core potentials [45] and correlation consistent basis sets of triple-ζ quality with additional polarization functions—[4s3p3d1f]—for Ni (Cu) [46] and double-ζ quality—[ 3s2p1d ]—for oxygens [47]. For the eight Nd (Ca) atoms large core effective potentials [48–50] and associated [3s2p2d] basis functions were used. In the case of Nd, the f-electrons were incorporated in the core. Cu1+ (Zn2+) total ion potentials (TIPs) with [2s1p] functions were used for the 10 Ni1+ (Cu2+) [51, 52] peripheral ions of the QC.
To investigate the role of different interactions in the d8 ground state, two different active spaces were considered. In the first active space, CAS-1 in Table 1, only the orbitals in the b1 and a1 irreps are active. These are

TABLE 1. The different active spaces (CAS) considered in this work. NEL is number of active electrons and NORB is the number of active orbitals. The numbers in parenthesis indicate the orbital numbers in Figure 2.
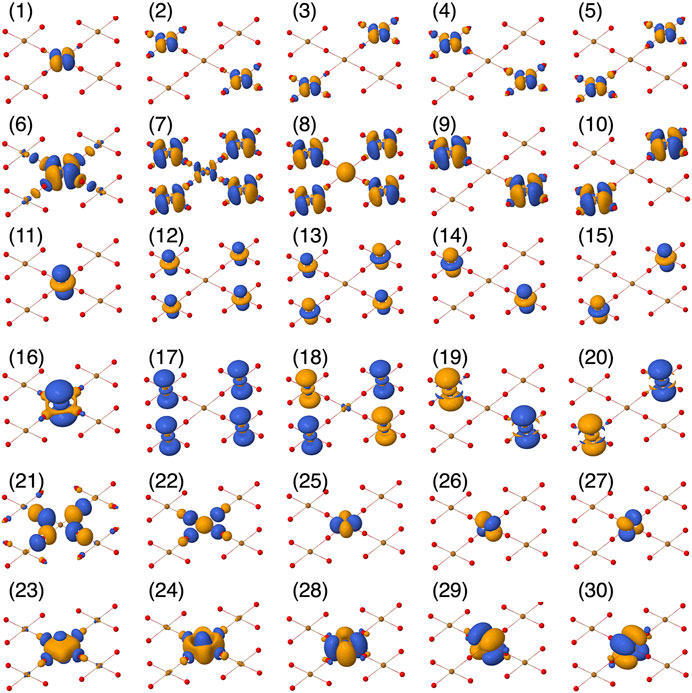
FIGURE 2. Active orbital basis used in the CASSCF calculations, plotted using Jmol [54].
The two active spaces considered in this work not only describe all the physical effects included in the above mentioned three-band Hubbard model but go beyond. More importantly, we do not have any ad-hoc input parameters for the calculation as all the physical interactions are implicitly included in the ab initio Hamiltonian describing the actual scenario in the real materials. We employed OpenMolcas [53] quantum chemistry package for all the calculations.
4 Results
4.1 Ground State of the d8 Configuration
Starting from the electronic structure of the parent compounds, where each Ni (Cu) is in the d9 configuration, we compute the electron-removal (in the photoemission terminology) d8 state to investigate the hole-doped quasiparticle state. Since the parent compounds in d9 configuration have strong nearest neighbour antiferromagnetic (AF) correlations [7], the total spin of our QC in undoped case, with five Ni (Cu) sites, in the AF ground state is SQC = 3/2. By introducing an additional hole (or removing an electron) from the central Ni (Cu) in our QC, the SQC values range from 0 to 3. To simplify the analysis of the distribution of the additional hole, we keep the spins on the four neighbouring Ni (Cu) sites parallelly aligned in all our calculations and from now on we only specify the spin multiplicity of the central Ni (Cu)O4 plaque. The multiplet structure of the d8 configuration thus consists of only spin singlet and triplet states, spanned by the four irreps of the 3d manifold. The active spaces we consider in this work allow us to compute accurately the excitations only within the b1 and a1 irreps [55] and we address the full multiplet structure elsewhere.
When computing the local excitations, a local singlet state on the central Ni (Cu) corresponds to a total spin on the cluster SQC = 2. However, a local triplet state, with central spin aligned parallel to the neighboring spins, corresponds to SQC = 3 and do not satisfy the AF correlations. To avoid the spin coupling between the central d8 Ni (Cu) with the neighbouring d9 Ni (Cu) ions, we replace the latter with closed shell, Cu (Zn) d10, ions and freeze them at the mean-field HF level. Such a simplification is justified, as the local excitation energy we compute is an order of magnitude larger than the exchange interaction [7].
In Table 2, the relative energies of the lowest local spin singlets 1A1g, 1B1g and spin triplet 3B1g states are shown. These are obtained from CASSCF + CASPT2 calculations with CAS(12,14) active space (CAS-3 in Table 1) which includes the 3d and 4d orbitals of the central Ni (Cu) ion and the in-plane O 2p and 3p orbitals in the b1 irrep. In the CASPT2 calculation, the remaining doubly occupied O 2p, the central Ni (Cu) 3s and 3p orbitals and all the unoccupied virtual orbitals are correlated.

TABLE 2. Relative energies (in eV) of the electron removal d8 states in NdNiO2 and the iso-structural CaCuO2 obtained from CAS(12,14)SCF and CASSCF + CASPT2 calculations.
It can be seen that the ground state is of 1A1g symmetry and the lowest triplet excited state, with 3B1g symmetry, is around 1.88 and 2.5 eV for NdNiO2 and CaCuO2 respectively. The AF magnetic exchange in these two compounds is 76 and 208 meV respectively [7], and thus we expect that our simplification of making the neighbouring d9 ions closed shell do not over/underestimate the excitation energies. At the CASSCF level, the 1A1g-3B1g excitation energy is 1.35 eV in NdNiO2 while it is 2.26 eV in CaCuO2. Interestingly, the inclusion of dynamical correlations via the CASPT2 calculation, the 1A1g in NdNiO2 is stabilized by 0.53 eV compared to 3B1g state. However, in CaCuO2, the 1A1g state is stabilized by only 0.24 eV. This indicates that the dynamical correlations are more active in the 1A1g state in NdNiO2 than in CaCuO2. We note that the hole excitations within the 3d orbitals in the irreps b2 and e, calculated with this limited active space (CAS-3) results in energies lower than the 3B1g and 1B1g states. However, an accurate description of those states requires an enlarged active space that includes not only the same symmetry oxygen 2p and 3p orbitals from the central NiO4 plaque but also the 3d, 4d manifold of the neighbouring Ni (Cu) ions, making the active space prohibitively large. Here, we concentrate on the analysis of the 1A1g ground state and address the complete d8 multiplet spectrum elsewhere.
4.2 Wavefunction of the d8 Ground State
The 1A1g ground wavefunction in terms of the weights of the four leading Slater determinants (SD) (in the case of CaCuO2) is shown in Table 3. The wavefunctions corresponding to the CASSCF calculations with the active spaces CAS-1 and CAS-2 are shown. The basis in which the wavefunctions are represented is constructed in two steps: 1) A set of natural orbitals are generated by diagonalising the CASSCF one-body reduced density matrix. 2) To obtain a set of atomic-like symmetry-adapted localized orbital basis, we localize the Ni (Cu) 3d and O 2p orbitals on the central NiO4 (CuO4) plaque through a unitary transformation. Such partial localization within the active space keeps the total energy unchanged. The resulting 3
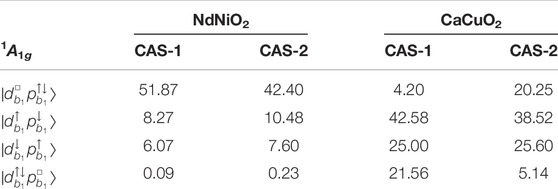
TABLE 3. Ni and Cu 3d8 1A1g ground state wavefunction: Weights (%) of the leading configurations in the wavefunction computed for NdNiO2 and CaCuO2 with active spaces CAS-1 and CAS-2 (see Table 1).
From Table 3 it can be seen that the electron-removal d8 ground state wavefunction for the two compounds is mostly described by the four configurations spanned by the localized 3
We note that the four configurations shown in Table 3 encompass almost 90% of the d8 wavefunction (with CAS-2 active space) in CaCuO2. Thus, the use of a three-band Hubbard model [39, 40] to investigate the role of doped holes in CuO2 planes is a reasonable choice. However, for NdNiO2 these configurations cover only 60% of the d8 wavefunction, hence a three-band Hubbard model is too simple to describe the hole-doped monovalent nickelates.
In Table 4 and Table 5, we show the first ten dominant SD configurations by weight in the d8 wavefunction of NdNiO2 and CaCuO2 respectively. Interestingly, the configurations with two holes in the out-of-plane d-orbitals

TABLE 4. Dominant ten Slater derterminants and their weights (in %) in the d8 wavefunction for NdNiO2 (we also show the 11th which is the same as the fourth configuration in Table 3). The wavefunction is represented in the same basis as the wavefunction in Table 3. However, for convenience we use the orbital numbers from Figure 2 in the first row to express the basis. These orbitals are visually very close to the actual basis. The doubly occupied orbitals are shown as ↑↓, the singly occupied ones with ↑(↓) for spin
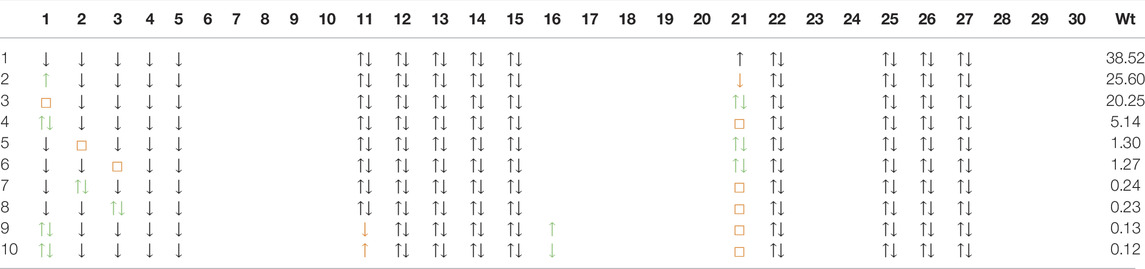
TABLE 5. Dominant ten SD configurations and their weights (in %) in the d8 wavefunction for CaCuO2. See the caption of Table 4 for details of the wavefunction representation.
A more intuitive and visual understanding of the distribution of the additional hole can be obtained by plotting the difference of the d8 and the d9 ground state electron densities as shown in Figure 3. Electron density of a multi-configurational state can be computed as a sum of densities arising from the natural orbitals and corresponding (well-defined) occupation numbers. We used Multiwfn program [56] to perform this summation. The negative values of the heat map of the electron density difference (blue color) and the positive values (in red) represent respectively the extra hole density and additional electron density in d8 state compared to the d9 state. From Figure 3A/Figure 3C that show the density difference in the NiO2/CuO2 planes (xy-plane), we conclude the following:
1. The hole density is concentrated on the Ni site (darker blue) with b1 (
2. In NdNiO2, the hole density is spread out around the Ni ion with larger radius, and otherwise in CaCuO2. This demonstrates that the 3d manifold in Cu is much more localized than in Ni and therefore the onsite Coulomb repulsion U is comparatively smaller for Ni.
3. The darker red regions around the Ni site in NdNiO2 indicate stronger d8 multiplet effects that result in rearrangement of electron density compared to d9 configuration.
4. In CaCuO2, we see darker red regions on the oxygen ions instead, which shows that the significant presence of a hole on these ions results in noticeable electron redistribution.
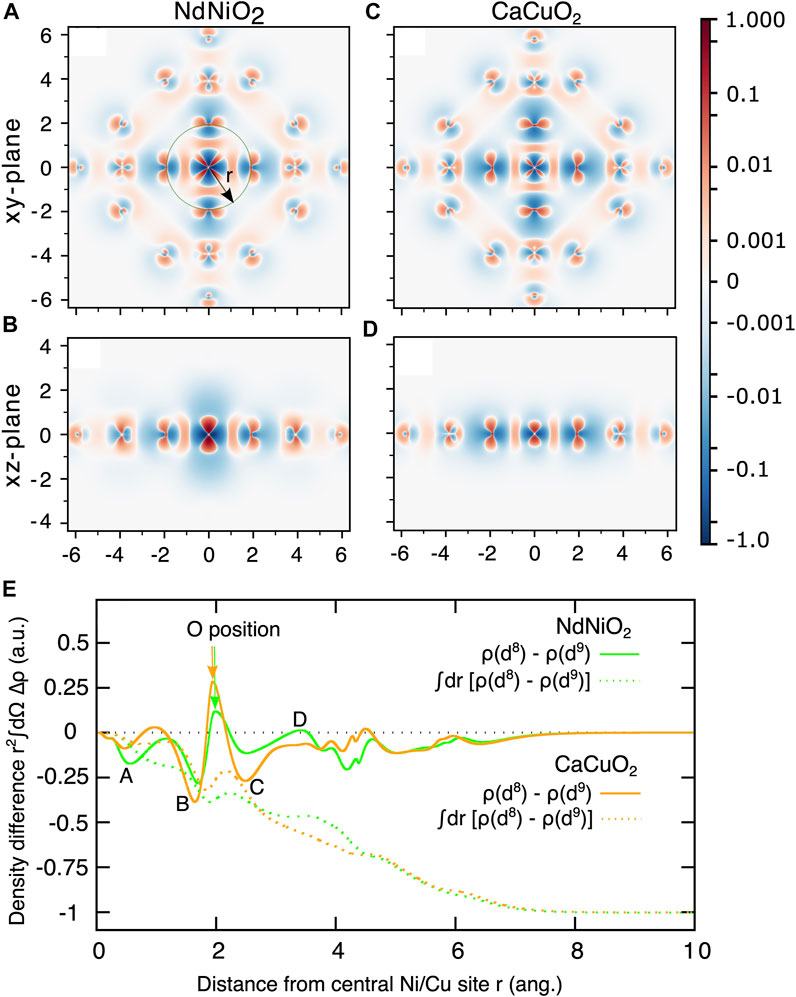
FIGURE 3. Electron density difference of the d8 and d9 ground states (ρ(d8)− ρ(d9)) for NdNiO2 in the xy-plane (A) and xz-plane (B), and for CaCuO2 xy-plane (C) and xz-plane (D). The coordinates of the central Ni (Cu) d8 ion are set to (0,0). The scale of the heat-bar is logarithmic between ±0.001 to ±1.0 and is linear between 0 and ±0.001. (E) Electron density difference integrated over a sphere centered on the central Ni(Cu) atoms (full curves) as a function of the radius r shown in (A). The result of an additional radial integration (dashed curves) as a function of the upper integration limit.
The electron density difference in the xz-plane (which is perpendicular to the NiO2/CuO2 planes) is quite different in the two compounds. The hole density in NdNiO2 is spread out up to 2 Å in the z-direction, unlike in CaCuO2, where it is confined to within 1 Å. We attribute this to the strong radial-type correlations in NdNiO2. With the creation of additional hole on the 3
To obtain a quantitative understanding of the charge density differences for the two compounds, in Figure 3E we plot the electron density difference integrated over a sphere centered on the central Ni(Cu) atom as a function of the radius r shown in Figure 3A. Four features, which we marked A-D, clearly demonstrate the contrast in the charge density differences in the two compounds. From the feature A at r close to Ni (Cu), it is evident that the extent of hole density around Ni in NdNiO2 is larger than around Cu in CaCuO2. The features B and C that are on either side of the position of oxygen ions show that the hole density is significantly larger on oxygen atoms in CaCuO2 than in NdNiO2. It is interesting to note that we see a jump (feature D) in the electron density above zero at r close to the position of Nd ions in NdNiO2, while in CaCuO2 the curve is flat in the region of Ca ions. This shows that there is some electron redistribution happening around the Nd ions. The hole density within a solid sphere (SS) around the central Ni (Cu) atom obtained by additional integration over the radius r is also shown in Figure 3E with dashed curves. It can be seen that the total hole density within the SS of r ∼4 Å, where the neighboring Ni (Cu) ions are located, is only ∼0.5 in both the compounds, with slight differences related to the feature D. This is due to the screening of the hole with the electron density pulled in from the farther surroundings. As one would expect, a SS with r of the size of the cluster, the total hole density is one in both the compounds.
4.3 Orbital Entanglement Entropy
To analyse the different type of correlations active in the two compounds in d8 configuration, we compute the entanglement entropy [57–59]. While the single orbital entropy, s(1)i, quantifies the correlation between ith orbital and the remaining set of orbitals, the mutual information, Ii,j is the two-orbital entropy between i and j [60, 61], and illustrates the correlation of an orbital with another, in the embedded environment comprising of all other orbitals. We used QCMaquis [63] embedded in OpenMolcas [54] package to compute the entropies.
In Figure 4, s(1)i and Ii,j extracted from the d8 ground state CASSCF calculations with CAS-2 active space for NdNiO2 and CaCuO2 are shown. The orbital basis for which the entropy is computed is the same as the basis in which the wavefunction presented in Table 3 is expanded. As mentioned previously, this orbital basis is obtained from partial localization of the natural orbitals in a way that only the 3
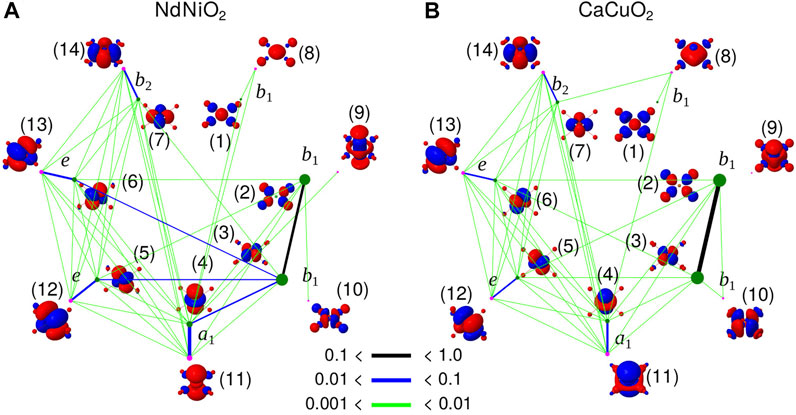
FIGURE 4. Single orbital entanglement entropy, s(i)i (dots) and mutual orbital entanglement entropy, Ii,j (colored lines) of the orbital basis used to expand the d8 wavefunction in Table 3 for NdNiO2 (A) and CaCuO2 (B). Entanglement entropy of the orbitals centred on the central NiO4/CuO4 plaque are only shown. The irrep to which the orbitals belong to are also shown. The green and magenta colors represent the two different set of orbitals, occupied (at the HF level) and the corresponding double-shell (virtual), respectively. The thickness of the black, blue and green lines denote the strength of Ii,j, and the size of the dots is proportional to s (1)i. The raw data is presented in Supplementary Tables S1, S2.
5 Conclusion and Discussion
In conclusion, our ab initio many-body quantum chemistry calculations for the electron removal (d8) states find a low-spin closed-shell singlet ground state in NdNiO2 and that the additional hole is mainly localized on the Ni 3
It was recently proposed that nickelates could be a legitimate realization of the single-band Hubbard model [65]. However, our analysis shows that even the three-band Hubbard model [66], which successfully describes the hole-doped scenario in cuprates, falls short to describe hole-doped nickelates and additional orbital degrees of freedom are indeed necessary for the description of the strong multiplet effects we find. Much has been discussed about the importance of rare-earth atoms for the electronic structure of superconducting nickelates, e.g. see [67]. The three-dimensional nature of the hole density we find in NdNiO2 might also be hinting at the importance of out-of-plane Nd ions. It would be interesting to compare the hole density of NdNiO2 with other iso-structural nickelates such as LaNiO2 where La 5d states are far from the Fermi energy. Since the infinite-layered monovalent nickelates are thin films that are grown on substrates, one could ask the question of how the electronic structure of the undoped and doped compounds changes with varying Ni-O bond length. Would this influence the role of electronic correlations in d9 nickelates? We will address these in the near future.
Data Availability Statement
The data supporting the conclusions of this study can be made available upon reasonable request.
Author Contributions
VK and AA designed the project. VK and NB performed the calculations. All the authors analysed the data. VK wrote the paper with inputs from NB and AA.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
VK would like to acknowledge Giovanni Li Manni and Oskar Weser for fruitful discussions. We gratefully acknowledge the Max Plank Society for financial support.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.836784/full#supplementary-material
References
1. Bednorz JG, Müller KA. Possible High Tc Superconductivity in the Ba-La-Cu-O System. Z Physik B - Condensed Matter (1986) 64:189–93. doi:10.1007/bf01303701
2. Li D, Lee K, Wang BY, Osada M, Crossley S, Lee HR, et al. Superconductivity in an Infinite-Layer Nickelate. Nature (2019) 572:624–7. doi:10.1038/s41586-019-1496-5
3. Osada M, Wang BY, Goodge BH, Lee K, Yoon H, Sakuma K, et al. A Superconducting Praseodymium Nickelate with Infinite Layer Structure. Nano Lett (2020) 20:5735–40. doi:10.1021/acs.nanolett.0c01392
4. Osada M, Wang BY, Goodge BH, Harvey SP, Lee K, Li D, et al. Nickelate Superconductivity without Rare‐Earth Magnetism: (La,Sr)NiO2. Adv Mater (2021) 33:2104083. doi:10.1002/adma.202104083
5. Keimer B, Kivelson SA, Norman MR, Uchida S, Zaanen J. From Quantum Matter to High-Temperature Superconductivity in Copper Oxides. Nature (2015) 518:179–86. doi:10.1038/nature14165
6. Rossi M, Lu H, Nag A, Li D, Osada M, Lee K, et al. Orbital and Spin Character of Doped Carriers in Infinite-Layer Nickelates. Phys. Rev. B (2021). 104:L220505. doi:10.1103/PhysRevB.104.L220505
7. Katukuri VM, Bogdanov NA, Weser O, van den Brink J, Alavi A. Electronic Correlations and Magnetic Interactions in Infinite-Layer NdNiO2. Phys Rev B (2020) 102:241112. doi:10.1103/physrevb.102.241112
8. Moretti Sala M, Bisogni V, Aruta C, Balestrino G, Berger H, Brookes NB, et al. Energy and Symmetry of d-d Excitations in Undoped Layered Cuprates Measured by CuL3 Resonant Inelastic X-ray Scattering. New J Phys (2011) 13:043026. doi:10.1088/1367-2630/13/4/043026
9. Lee K-W, Pickett WE. Infinite-Layer LaNiO2: Ni1+ is not Cu2+. Phys Rev B (2004) 70:165109. doi:10.1103/physrevb.70.165109
10. Liu Z, Ren Z, Zhu W, Wang Z, Yang J. Electronic and Magnetic Structure of Infinite-Layer NdNiO2: Trace of Antiferromagnetic Metal. Npj Quan Mater (2020) 5:31. doi:10.1038/s41535-020-0229-1
11. Zhang H, Jin L, Wang S, Xi B, Shi X, Ye F, et al. Effective Hamiltonian for Nickelate Oxides Nd1−xSrxNiO2. Phys Rev Res (2020) 2:013214. doi:10.1103/physrevresearch.2.013214
12. Zaanen J, Sawatzky GA, Allen JW. Band Gaps and Electronic Structure of Transition-Metal Compounds. Phys Rev Lett (1985) 55:418–21. doi:10.1103/physrevlett.55.418
13. Hepting M, Li D, Jia CJ, Lu H, Paris E, Tseng Y, et al. Electronic Structure of the Parent Compound of Superconducting Infinite-Layer Nickelates. Nat Mater (2020) 19:381–5. doi:10.1038/s41563-019-0585-z
14. Goodge BH, Li D, Lee K, Osada M, Wang BY, Sawatzky GA, et al. Doping Evolution of the Mott–Hubbard Landscape in Infinite-Layer Nickelates. Proc Natl Acad Sci (2021) 118:e2007683118. doi:10.1073/pnas.2007683118
15. Zhang FC, Rice TM. Effective Hamiltonian for the Superconducting Cu Oxides. Phys Rev B (1988) 37:3759–61. doi:10.1103/physrevb.37.3759
16. Jiang M, Berciu M, Sawatzky GA. Critical Nature of the Ni Spin State in Doped NdNiO2. Phys Rev Lett (2020) 124:207004. doi:10.1103/physrevlett.124.207004
17. Plienbumrung T, Schmid MT, Daghofer M, Oleś AM. Character of Doped Holes in Nd1−xSrxNiO2. Condensed Matter (2021) 6:33. doi:10.3390/condmat6030033
18. Helgaker T, Jørgensen P, Olsen J. Molecular Electronic-Structure Theory. Chichester: Wiley (2000).
19. Muñoz D, Illas F, de P. R. Moreira I. Accurate Prediction of Large Antiferromagnetic Interactions in High-Tc HgBa2Ca{n–1}CunO{2n+2+} (n=2,3) Superconductor Parent Compounds. Phys Rev Lett (2000) 84:1579–82. doi:10.1103/physrevlett.84.1579
20. Hozoi L, Siurakshina L, Fulde P, van den Brink J. Ab Initio determination of Cu 3d Orbital Energies in Layered Copper Oxides. Sci Rep (2011) 1:65. doi:10.1038/srep00065
21. Hozoi L, Fulde P. Computational Methods for Large Systems: Electronic Structre Approaches for Biotechnology and Nanotechnology. Hoboken: John Wiley & Sons (2011). Chap. 6.
22. Bogdanov NA, van den Brink J, Hozoi L. Ab Initio Computation of d-d Excitation Energies in Low-Dimensional Ti and V Oxychlorides. Phys Rev B (2011) 84:235146. doi:10.1103/physrevb.84.235146
23. Katukuri VM, Stoll H, van den Brink J, Hozoi L. Ab Initio Determination of Excitation Energies and Magnetic Couplings in Correlated Quasi-Two-Dimensional Iridates. Phys Rev B (2012) 85:220402. doi:10.1103/physrevb.85.220402
24. Bogdanov NA, Maurice R, Rousochatzakis I, van den Brink J, Hozoi L. Magnetic State of Pyrochlore Cd2Os2O7 Emerging from Strong Competition of Ligand Distortions and Longer-Range Crystalline Anisotropy. Phys Rev Lett (2013) 110:127206. doi:10.1103/physrevlett.110.127206
25. Gretarsson H, Clancy JP, Liu X, Hill JP, Bozin E, Singh Y, et al. Crystal-field Splitting and Correlation Effect on the Electronic Structure of A2IrO3. Phys Rev Lett (2013) 110:076402. doi:10.1103/PhysRevLett.110.076402
26. Katukuri VM, Yushankhai V, Siurakshina L, Brink JVD, Hozoi L, Rousochatzakis I. Mechanism of Basal-Plane Antiferromagnetism in the Spin-Orbit Driven Iridate Ba2IrO4. Phys Rev X (2014) 4:021051. doi:10.1103/physrevx.4.021051
27. Katukuri VM, Nishimoto S, Yushankhai V, Stoyanova A, Kandpal H, Choi S, et al. Kitaev Interactions Between j= 1/2 Moments in Honeycomb Na2IrO3 are Large and Ferromagnetic: Insights From Ab Initio Quantum Chemistry Calculations. New J Phys (2014) 16:013056. doi:10.1088/1367-2630/16/1/013056
29. Klintenberg M, Derenzo SE, Weber MJ. Accurate crystal fields for Embedded Cluster Calculations. Comput Phys Commun (2000) 131:120–8. doi:10.1016/s0010-4655(00)00071-0
30. Katukuri VM, Roszeitis K, Yushankhai V, Mitrushchenkov A, Stoll H, van Veenendaal M, et al. Electronic Structure of Low-Dimensional 4d5 Oxides: Interplay of Ligand Distortions, Overall Lattice Anisotropy, and Spin-Orbit Interactions. Inorg Chem (2014) 53:4833–9. doi:10.1021/ic402653f
31. Babkevich P, Katukuri VM, Fåk B, Rols S, Fennell T, Pajić D, et al. Magnetic Excitations and Electronic Interactions in Sr2CuTeO6: A Spin-1/2 Square Lattice Heisenberg Antiferromagnet. Phys Rev Lett (2016) 117:237203. doi:10.1103/physrevlett.117.237203
32. Booth GH, Thom AJW, Alavi A. Fermion Monte Carlo without Fixed Nodes: a Game of Life, Death, and Annihilation in Slater Determinant Space. J Chem Phys (2009) 131:054106. doi:10.1063/1.3193710
33. Cleland D, Booth GH, Alavi A. Communications: Survival of the Fittest: Accelerating Convergence in Full Configuration-Interaction Quantum Monte Carlo. J Chem Phys (2010) 132:041103. doi:10.1063/1.3302277
34. Guther K, Anderson RJ, Blunt NS, Bogdanov NA, Cleland D, Dattani N, et al. NECI: N-Electron Configuration Interaction with an Emphasis on State-Of-The-Art Stochastic Methods. J Chem Phys (2020) 153:034107. doi:10.1063/5.0005754
35. Chan GK-L, Sharma S. The Density Matrix Renormalization Group in Quantum Chemistry. Annu Rev Phys Chem (2011) 62:465–81. doi:10.1146/annurev-physchem-032210-103338
36. Sharma S, Chan GK-L. Spin-adapted Density Matrix Renormalization Group Algorithms for Quantum Chemistry. J Chem Phys (2012) 136:124121. doi:10.1063/1.3695642
37. Andersson K, Malmqvist PÅ, Roos BO. Second‐order Perturbation Theory with a Complete Active Space Self‐consistent Field Reference Function. J Chem Phys (1992) 96:1218–26. doi:10.1063/1.462209
38. Angeli C, Cimiraglia R, Evangelisti S, Leininger T, Malrieu J-P. Introduction Of N-Electron Valence States for Multireference Perturbation Theory. J Chem Phys (2001) 114:10252–64. doi:10.1063/1.1361246
39. Emery VJ. Theory of High-Tc superconductivity in Oxides. Phys Rev Lett (1987) 58:2794–7. doi:10.1103/physrevlett.58.2794
40. Jiang M, Moeller M, Berciu M, Sawatzky GA. Relevance of Cu-3d Multiplet Structure in Models of High-Tc Cuprates. Phys Rev B (2020) 101:035151. doi:10.1103/physrevb.101.035151
41. Plienbumrung T, Daghofer M, Oleś AM. Interplay between Zhang-Rice Singlets and High-Spin States in a Model for Doped NiO2 Planes. Phys Rev B (2021) 103:104513. doi:10.1103/physrevb.103.104513
42. Hayward MA, Rosseinsky MJ. Synthesis of the Infinite Layer Ni(I) Phase NdNiO2+x by Low Temperature Reduction of NdNiO3 with Sodium Hydride. Solid State Sci (2003) 5:839–50. doi:10.1016/s1293-2558(03)00111-0
43. Kobayashi N, Hiroi Z, Takano M. Compounds and Phase Relations in the SrO-CaO-CuO System under High Pressure. J Solid State Chem (1997) 132:274–83. doi:10.1006/jssc.1997.7442
44. Karpinski J, Mangelschots I, Schwer H, Conder K, Morawski A, Lada T, et al. Single crystal Growth of HgBaCaCuO and Infinite Layer CaCuO2 at High Gas Pressure. Physica C: Superconductivity (1994) 235-240:917–8. doi:10.1016/0921-4534(94)91683-7
45. Dolg M, Wedig U, Stoll H, Preuss H. Energy-adjusted ab Initio Pseudopotentials for the First Row Transition Elements. J Chem Phys (1987) 86:866–72. doi:10.1063/1.452288
46. Martin JML, Sundermann A. Correlation Consistent Valence Basis Sets for Use with the Stuttgart-Dresden-Bonn Relativistic Effective Core Potentials: The Atoms Ga-Kr and In-Xe. J Chem Phys (2001) 114:3408–20. doi:10.1063/1.1337864
47. Roos BO, Lindh R, Malmqvist P-Å, Veryazov V, Widmark P-O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J Phys Chem A (2004) 108:2851–8. doi:10.1021/jp031064+
48. Dolg M, Stoll H, Savin A, Preuss H. Energy-adjusted Pseudopotentials for the Rare Earth Elements. Theoret Chim Acta (1989) 75:173–94. doi:10.1007/bf00528565
49. Dolg M, Stoll H, Preuss H. A Combination of Quasirelativistic Pseudopotential and Ligand Field Calculations for Lanthanoid Compounds. Theoret Chim Acta (1993) 85:441–50. doi:10.1007/bf01112983
50. Kaupp M, Schleyer Pv. R, Stoll H, Preuss H. Pseudopotential Approaches to Ca, Sr, and Ba Hydrides. Why Are Some Alkaline Earth MX2 Compounds Bent? J Chem Phys (1991) 94:1360–6. doi:10.1063/1.459993
51. Igel-Mann G. Ph.D. thesis. Stuttgart: University of Stuttgart (1987). Untersuchungen an Hauptgruppenelementen und Nebengruppenelementen mit abgeschlossener d-Schale
52.University of Cologne. Energy-consistent Pseudopotentials of Stuttgart/Cologne Group (2014). Available at: http://www.tc.uni-koeln.de/cgi-bin/pp.pl?language=en,format=molpro,element=Zn,job=getecp,ecp=ECP28SDF (Accessed Sept 15, 2021).
53. Fdez. Galván I, Vacher M, Alavi A, Angeli C, Aquilante F, Autschbach J, et al. OpenMolcas: From Source Code to Insight. J Chem Theor Comput. (2019) 15:5925–64. doi:10.1021/acs.jctc.9b00532
54.Jmol. Jmol: An Open-source Java Viewer for Chemical Structures in 3D (2001). Available from: http://www.jmol.org/.
55..For an accurate quantitative description of the multiplet structure spanned by the other two irreps b1 and e, one would need to extend the active space and include the 3d and 4d manifolds of the four neighbouring Ni (Cu) atoms as well as the O 2p orbitals of the same symmetry, resulting in a gigantic 68 electrons in 74 orbitals active space.
56. Lu T, Chen F. Multiwfn: A Multifunctional Wavefunction Analyzer. J Comput Chem (2012) 33:580–92. doi:10.1002/jcc.22885
57. Boguslawski K, Tecmer P, Legeza Ö, Reiher M. Entanglement Measures for Single- and Multireference Correlation Effects. J Phys Chem Lett (2012) 3:3129–35. doi:10.1021/jz301319v
58. Boguslawski K, Tecmer P, Barcza G, Legeza Ö, Reiher M. Orbital Entanglement in Bond-Formation Processes. J Chem Theor Comput. (2013) 9:2959–73. doi:10.1021/ct400247p
59. Boguslawski K, Tecmer P. Orbital Entanglement in Quantum Chemistry. Int J Quan Chem. (2015) 115:1289–95. doi:10.1002/qua.24832
60. Legeza Ö, Sólyom J. Optimizing the Density-Matrix Renormalization Group Method Using Quantum Information Entropy. Phys Rev B (2003) 68:195116. doi:10.1103/physrevb.68.195116
61. Rissler J, Noack RM, White SR. Measuring Orbital Interaction Using Quantum Information Theory. Chem Phys (2006) 323:519–31. doi:10.1016/j.chemphys.2005.10.018
62. Keller S, Dolfi M, Troyer M, Reiher M. An Efficient Matrix Product Operator Representation of the Quantum Chemical Hamiltonian. J Chem Phys (2015) 143:244118. doi:10.1063/1.4939000
63. Gunnarsson O, Andersen OK, Jepsen O, Zaanen J. Density-functional Calculation of the Parameters in the Anderson Model: Application to Mn in CdTe. Phys Rev B (1989) 39:1708–22. doi:10.1103/physrevb.39.1708
64. Bogdanov NA, Li Manni G, Sharma S, Gunnarsson O, Alavi A. Enhancement of Superexchange Due to Synergetic Breathing and Hopping in Corner-Sharing Cuprates. Nat Phys (2021) 18:190–5. doi:10.1038/s41567-021-01439-1
65. Kitatani M, Si L, Janson O, Arita R, Zhong Z, Held K. Nickelate Superconductors – a Renaissance of the One-Band Hubbard Model. npj Quan Mater (2020) 5:59. doi:10.1038/s41535-020-00260-y
66. Eskes H, Sawatzky GA. Single-, Triple-, or Multiple-Band Hubbard Models. Phys Rev B (1991) 44:9656–66. doi:10.1103/physrevb.44.9656
Keywords: nickelates, superconductors, wavefunction quantum chemistry, doped-holes, ab initio
Citation: Katukuri VM, Bogdanov NA and Alavi A (2022) Ab Initio Wavefunction Analysis of Electron Removal Quasi-Particle State of NdNiO2 With Fully Correlated Quantum Chemical Methods. Front. Phys. 10:836784. doi: 10.3389/fphy.2022.836784
Received: 15 December 2021; Accepted: 14 March 2022;
Published: 11 May 2022.
Edited by:
Danfeng Li, City University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
Frank Lechermann, European X-Ray Free Electron Laser, GermanyBaiYang Wang, Stanford University, United States
Copyright © 2022 Katukuri, Bogdanov and Alavi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vamshi M. Katukuri, Vi5LYXR1a3VyaUBma2YubXBnLmRl
 Vamshi M. Katukuri
Vamshi M. Katukuri Nikolay A. Bogdanov
Nikolay A. Bogdanov Ali Alavi1,2
Ali Alavi1,2