Coexistence of Multiple Attractors in a Novel Simple Jerk Chaotic Circuit With CFOAs Implementation

A novel, simple Jerk chaotic circuit with three current feedback operational amplifiers included (CFOA-JCC) is proposed, which has a simpler circuit structure, fewer components, but higher frequency characteristics. The dynamic behaviors of CFOA-JCC are analyzed, including equilibrium, stability, Lyapunov exponent, bifurcation diagram, offset boosting, and phase diagram. Furthermore, the frequency spectrum characteristic of the ordinary op-amps Jerk chaotic circuit was compared with CFOA-JCC under the same circuit parameters, and the chaotic attractor frequency of CFOA-JCC can reach about 650 kHz, much better than that of ordinary op-amps (12 kHz). Numerical simulation shows that CFOA-JCC has coexisting attractors, verified by hardware circuit experiments.

Introduction

Chaos is a complex nonlinear phenomenon with special dynamical properties, and various chaotic systems are found and widely used in the fields of electronic communication systems, control systems, and so on [1–6]. Chaotic circuits have become an important tool for studying chaos theory due to easy observation. Proposed by Sprott based on the method of computer exhaustive, the Jerk chaotic system (a class of third-order autonomous chaotic systems) has attracted much attention because it is easy to achieve complex dynamical behavior with a simple structure. The general mathematical expression is $\stackrel{\cdot \cdot \cdot }{x}=J\left(\stackrel{\cdot \cdot }{x},\stackrel{\cdot }{x},x\right)$ [7–10]. In 2011, Sprott proposed a novel chaotic circuit of Jerk, which realizes a chaotic system with only resistance, capacitance, operational amplifier, and diode. The three first-order differential equation is as follows [11]:

$\stackrel{\cdot \cdot \cdot }{x}+\stackrel{\cdot \cdot }{x}+x+f\left(\stackrel{\cdot }{x}\right)=0(1)$

The nonlinear term in the chaotic circuit can be nonlinear functions, piecewise linear functions, and mersister generation [12–14]. However, most Jerk circuit implementations use traditional voltage mode op-amps as active devices, and the gain of the designed circuit must be decreased to increase bandwidth. For the current feedback operational amplifier (CFOA), there is almost no such relationship between gain and bandwidth. Therefore, it is not necessary to design a circuit to balance the gain and bandwidth as a voltage feedback amplifier [15–17]. Therefore, using CFOA to realize chaotic circuits has become a hotspot because CFOA has better frequency gain characteristics [18–24]. It makes the circuit structure simpler and more flexible due to its good port characteristics [25–29]. There have been many reports about the coexistence attractors in recent years, but all the reports did not pay much attention to the simpler topology of the chaotic circuit. For example, in 2011, Sprott proposed a Jerk chaotic circuit with traditional voltage feedback operational amplifiers (VFOA). He did not discuss the coexistence of attractors of his system, and the circuit was not the simplest one. In 2016, Kengene et al. proposed a novel chaotic Jerk circuit, which can realize the coexistence of multiple attractors [30]. Five amplifiers and two diodes had been used in the circuit, and they discussed the frequency of the circuit. In their circuit, the center frequency can be obtained at about 4 Hz. In 2020, Xu et al. proposed a memristive Chua’s circuit with attractors with two stable foci [14]. A one-dimensional multi-scroll chaotic circuit is designed with CFOA [26], but the circuit structure is complex, and there are many active devices. A grid multi-scroll chaotic circuit is designed using CFOA [27, 28], but more active devices are used with lower operating frequency. Wu proposed a chaotic circuit only using CFOA [29], but the center frequency of the chaotic signal is 250 kHz.

In this article, a novel Jerk chaotic circuit with three CFOAs (called CFOA-JCC) was designed to realize a chaotic system in Description of the CFOA-JCC. In Equilibrium Point Analysis, based on the equation of state of CFOA-JCC, the equilibrium point and the system dissipation are analyzed by solving the dimensionless equation. In Dynamical Behaviors, numerical analysis and description were done using MATLAB R2018b to perform the numerical simulation. Lyapunov exponent spectra and bifurcation diagram are plotted in adjusting the parameter regions to reveal the dynamical behaviors. The occurrence of coexisting attractors at deferent initial conditions is also discussed using phase diagrams and bifurcation. Single parameter-controlled offset boosting for variable $x$ is simulated. In Circuit Implementation and Spectrum Characteristics, hardware experiments are performed, the phase and offset boosting diagrams in the x-y plane captured by the UNI-T2102CM oscilloscope strongly confirm the previous theoretical analysis, and then the spectrum of CFOA-JCC is compared with that of the VFOA circuit in adjusting the parameter regions of capacitance under the same value of the resistor. The conclusions are summarized in the last section.

Description of the CFOA-JCC

AD844AN is a typical CFOA with better frequency properties. Its circuit symbol is shown in Figure 1A. Under ideal conditions, the port characteristics of AD844AN are satisfied:

$\{\begin{array}{c}{\mathit{I}}_{\mathit{3}}\mathit{=0}\\ {\mathit{V}}_{\mathit{2}}\mathit{=}{\mathit{V}}_{\mathit{3}}\\ {\mathit{I}}_{\mathit{2}}\mathit{=\pm }{\mathit{I}}_{\mathit{3}}\\ {\mathit{V}}_{\mathit{5}}\mathit{=}{\mathit{V}}_{\mathit{6}}\end{array}(2)$

With the current output port, the current state of CFOA is easy to observe. As can be seen from the characteristic curve in Figure 1B, the gain of both op-amps is stable when the frequency is within 100 kHz. AD844AN has a better high-frequency performance than VFOA. The closed-loop bandwidth frequency at −3 dB can be expressed as ${\mathit{f}}_{\mathit{cl}}\mathit{=}\frac{\mathit{1}}{\mathit{2\pi }{\mathit{C}}_{\mathit{P}}{\mathit{R}}_{\mathit{f}}}$. The closed-loop bandwidth of the CFOA is determined by the feedback resistor R_f and the internal circuit C_p. It illustrates the importance of the feedback resistance R_f of the CFOA, so $$ R_f can be used to adjust the frequency response of the amplifier [31].

FIGURE 1

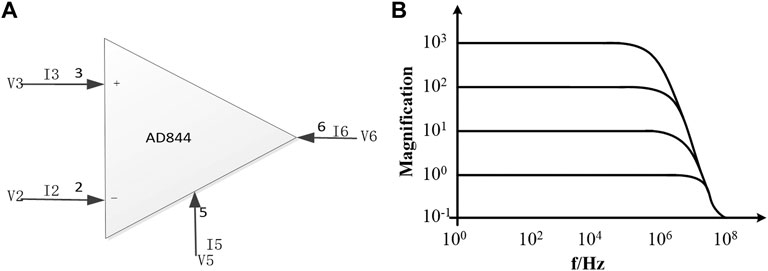
FIGURE 1. AD844AN circuit symbol and its frequency characteristic. (A) AD844AN circuit symbol. (B) Magnification frequency characteristic curve of AD844AN.

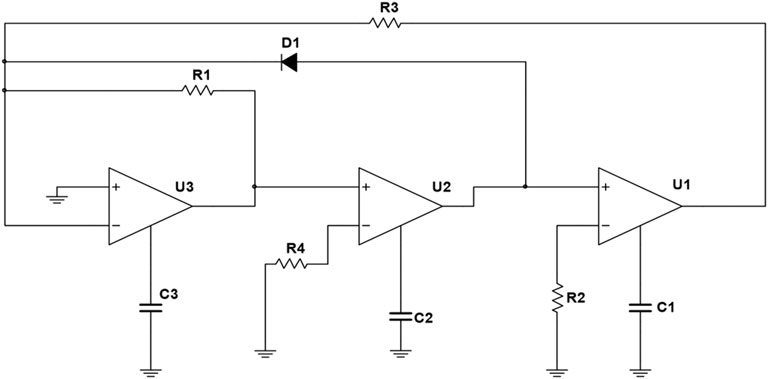
This designed circuit configuration is shown in Figure 2, which includes three CFOAs; three capacitors C₁, C₂, C₃; four resistors R₁, R₂, R₃, R₄, and a silicon diode named D₁. This circuit is derived from the CFOAs-based sinusoidal oscillator [32], and a nonlinear function is obtained according to volt-ampere characteristics of the diode.

FIGURE 2

FIGURE 2. The novel Jerk circuit with three CFOAs AD844AN.

Equilibrium Point Analysis

According to Kirchhoff’s Current Law and Kirchhoff’s Voltage Law, the port characteristics of CFOA, and the current-voltage relations of each circuit component of the novel circuit in Figure 2, in terms of the three-node voltage of u₁, u₂, u₃, three coupled first-order autonomous nonlinear differential equations can be attained to express the nonlinear dynamics of the circuit. The differential equations of the proposed system can be written as

$\{\mathit{ }\begin{array}{c}\frac{\mathit{d}{\mathit{u}}_{\mathit{1}}}{\mathit{dt}}\mathit{=}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{2}}{\mathit{C}}_{\mathit{1}}}{\mathit{u}}_{\mathit{2}}\mathit{ }\\ \frac{\mathit{d}{\mathit{u}}_{\mathit{2}}}{\mathit{dt}}\mathit{=}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{4}}{\mathit{C}}_{\mathit{2}}}{\mathit{u}}_{\mathit{3}}\\ \frac{\mathit{d}{\mathit{u}}_{\mathit{3}}}{\mathit{dt}}\mathit{=-}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{3}}{\mathit{C}}_{\mathit{3}}}{\mathit{u}}_{\mathit{1}}\mathit{-}\frac{\mathit{1}}{{\mathit{C}}_{\mathit{3}}}\cdot {\mathit{I}}_{\mathit{S}}\left({\mathit{e}}^{\frac{{\mathit{u}}_{\mathit{2}}}{{\mathit{V}}_{\mathit{T}}}}\mathit{-1}\right)\mathit{-}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{1}}{\mathit{C}}_{\mathit{3}}}{\mathit{u}}_{\mathit{3}}\end{array}\mathit{ }(3)$

The voltage signals u₁, u₂, u₃ and time variable t are non-dimensional to obtain $x$, $y$, $z$ through the following relationship [33]:

$\mathit{x}\cdot \mathit{1V=}{\mathit{u}}_{\mathit{1}}\mathit{,y}\cdot \mathit{1V=}{\mathit{u}}_{\mathit{2}}\mathit{,z}\cdot \mathit{1V=}{\mathit{u}}_{\mathit{3}},$

$\mathit{\alpha =}\frac{{\mathit{R}}_{\mathit{2}}{\mathit{C}}_{\mathit{1}}}{{\mathit{R}}_{\mathit{2}}{\mathit{C}}_{\mathit{1}}}\mathit{,\beta =}\frac{{\mathit{R}}_{\mathit{2}}{\mathit{C}}_{\mathit{1}}}{{\mathit{R}}_{\mathit{4}}{\mathit{C}}_{\mathit{2}}},\mathit{\gamma =}\frac{{\mathit{R}}_{\mathit{2}}{\mathit{C}}_{\mathit{1}}}{{\mathit{R}}_{\mathit{3}}{\mathit{C}}_{\mathit{3}}},\mathit{\delta =}\frac{{\mathit{R}}_{\mathit{2}}{\mathit{C}}_{\mathit{1}}}{{\mathit{C}}_{\mathit{3}}},\epsilon \mathit{=}\frac{{\mathit{R}}_{\mathit{2}}{\mathit{C}}_{\mathit{1}}}{{\mathit{R}}_{\mathit{1}}{\mathit{C}}_{\mathit{3}}},\mathit{\tau =}\frac{\mathit{t}}{{\mathit{R}}_{\mathit{2}}{\mathit{C}}_{\mathit{1}}}(4)$

When it is at room temperature 300 K, the diode reverse saturation current $I_S$ = 10⁻⁹ A and the voltage equivalent of temperature $V_T$ = 26 mV [34]. Therefore, Eq. 3 can be written as

$\{ \begin{array}{c}\stackrel{\cdot }{x}=\alpha y \\ \stackrel{\cdot }{y}=\beta z\\ \stackrel{\cdot }{z}=-\gamma x-\delta \cdot {10}^{-9}\left(e^{\frac{y}{0.026}}-1\right)-\epsilon z\end{array}(5)$

Assuming $\stackrel{\cdot }{x} =0$, $\stackrel{\cdot }{y}=0$, and $\stackrel{\cdot }{z}=0$ to analyze the equilibrium point and stability, Eq. 3 has a zero equilibrium point P₀ = (0,0,0) [35].

$\{\begin{array}{c}\alpha y=0 \\ \beta z=0\\ -\gamma x-\delta \cdot {10}^{-9}\left(e^{\frac{y}{0.026}}-1\right)-\epsilon z=0\end{array} (6)$

The Jacobin matrix at the equilibrium point can be derived as

$J_{\left(P_0\right)}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& \beta \\ -\gamma & -0.026\times {10}^{-9}\delta & -\epsilon \end{array}\right](7)$

The characteristic equation at the equilibrium is yielded as

$Det\left(\mathit{E}\mathbf{\lambda }-{\mathit{J}}_{P_0}\right)={\lambda }^3+\epsilon {\lambda }^2+2.6\times {10}^{-11}\beta \delta \cdot \lambda +\beta \gamma =0(8)$

The Routh–Hurwitz conditions for the above cubic polynomial Eq. 8 are given by [36–39]

$\{\begin{array}{c}\gamma >0\\ \beta \gamma >0\\ E\times 2.6\times {10}^{-11}\beta \delta -\beta \epsilon >0\end{array}.(9)$

Obviously, the first and second conditions are satisfied in this system, but the third condition is only satisfied when ε and δ take very large values. Then, the system can be stable. Nevertheless, the system is unstable when the value of ε and δ is small, and the above characteristic equation has both positive and negative roots.

The circuit parameters in Figure 2 are given as $$ R₁ = R₂ = R₃ = R₄ = 1 kΩ and C₁ = C₂ = C₃ = 100nF. Therefore, the normalized parameters can be calculated by Eq. 4 as α = 1, β = 1, γ = 1, δ = 1, and ε = 1, so that the characteristic equation at the equilibrium is yielded as

$\mathit{Det}\left(\mathit{E\lambda -}{\mathit{J}}_{{\mathit{P}}_{\mathit{0}}}\right)\mathit{=}{\mathit{\lambda }}^{\mathit{3}}\mathit{+}{\mathit{\lambda }}^{\mathit{2}}\mathit{+2}\mathit{.6}\cdot \mathit{1}{\mathit{0}}^{\mathit{-11}}\cdot \mathit{\lambda +1=0}(10)$

Three eigenvalues can be obtained from Eq. 10: λ1 = −1.4665571, λ2 = 0.232786 + 0.792552i, and λ3 = 0.232786 + 0.792552i. Among them, λ2 and λ3 are complex roots, and λ1 is a negative real root. From the three eigenvalues, it can be seen that P0 (0, 0, 0) is an unstable saddle point. Consequently, system (3) may produce chaotic behaviors [40–42]. System (3) is a three-dimensional system, and the divergence of its vector field can be described as

$\nabla \mathit{V=}\frac{\partial \dot{\mathit{x}}}{\partial \mathit{x}}\mathit{+}\frac{\partial \dot{\mathit{y}}}{\partial \mathit{y}}\mathit{+}\frac{\partial \dot{\mathit{z}}}{\partial \mathit{z}}\mathit{=-\epsilon =-1}(11)$

It shows that the system is dissipative. When t→∞, each volume element of the trajectory of the system shrinks to 0 at an exponential rate of −1, and its gradual motion will be fixed on an attractor [43–46].

Dynamical Behaviors

With fixed parameters α = 1, β = 1, γ = 1, δ = 1, and the initial values (x0, y0, z0) = (0, 0.4, 0) and (x0, y0, z0) = (0, −0.4, 0) lying close to the equilibrium point, the Lyapunov exponent (LE) spectrum and bifurcation diagram of the system varying with parameter ε∊ [0.001, 2] can be obtained as shown in Figures 3A,B,D. In this article, all the numerical simulations are made in MATLAB R2018b, the simulation step size is 0.01, the ode45 numerical solver is used, and the simulation time is 500 s.

FIGURE 3

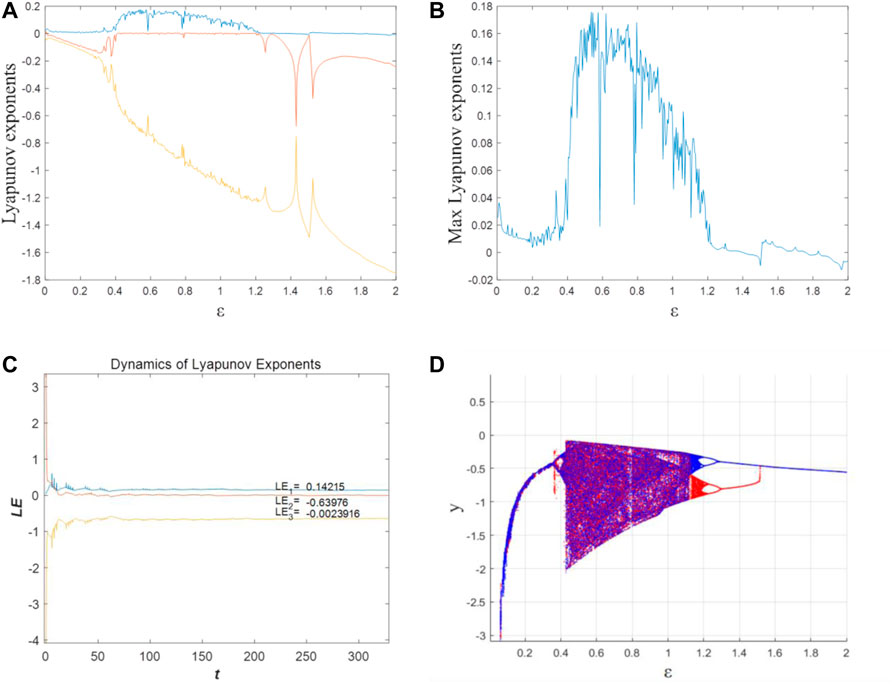
FIGURE 3. Lyapunov exponent spectrum and bifurcation diagram at different initial values. (A) Lyapunov exponents at (x₀, y₀, z₀) = (0, 0.4, 0). (B) Max Lyapunov exponent at (x₀, y₀, z₀) = (0, 0.4, 0). (C) LEs when ε = 0.5 at (x₀, y₀, z₀) = (0, 0.4, 0). (D) Bifurcation diagram at (x₀, y₀, z₀) = (0, 0.4, 0) (red) and (x₀, y₀, z₀) = (0, −0.4, 0) (blue).

The system can maintain a chaotic state when the parameter ε changes within a certain range. The value of the max LE of the system is approximately 0 when ε ∊ [0.001, 0.394), which means the system is in a period state. The bifurcation diagram shown in Figure 3D is represented by one or several curves. When ε ∊ [0.0.39, 0.394), the system produces a bifurcation, which evolves from period 1 to period 2, respectively. When ε ∊ [0.394, 1.2), there is one positive LE, which means the system is in a chaotic state. For instance, as Figure 3C shows, when ε = 0.5, the LEs can be calculated as LE₁ = 0.14215, LE₂ = −0.63976, LE₃ = −0.0023916. LE₁ is positive, and LE₂ and LE₃ are negative, meaning the system’s phase volume is exponentially shrinking. According to the Kaplan–York dimension ($D_{KY}$), an integer j must satisfy the following requirement, ${\displaystyle {\sum }_{i=1}^{j}L{E}_i}\ge \mathrm{0}$, ${\displaystyle {\sum }_{i=1}^{j+1}L{E}_i}\mathrm{<0}$, so D_KY of the chaotic state can be calculated as follows:

${\mathit{D}}_{\mathit{KY}}\mathit{=j+ }\frac{{\displaystyle {\sum }_{i=1}^{j}L{E}_i}}{\left|\mathit{L}{\mathit{E}}_{\mathit{j+1}}\right|}\mathit{= 1 + }\frac{{\displaystyle {\sum }_{i=1}^{1}L{E}_i}}{\left|\mathit{L}{\mathit{E}}_{\mathit{2}}\right|}\mathit{=2}\mathit{.56308}(12)$

In Figure 3D, the bifurcation diagram also proves the system is chaotic when ε ∊ [0.394, 1.2). With the increase in ε, the system returns to the periodic state when ε ≥ 1.2. From Figure 3D, we also can obtain that there are two different attractors when the initial value is fixed (x₀, y₀, z₀) = (0, 0.4, 0) and (x₀, y₀, z₀) = (0, −0.4, 0). That means there are coexisting attractors in this system.

Figure 4 shows the phase diagram of the system corresponding to different ε values. The process of the system from period bifurcation to chaos and then back to the periodic state can be clearly seen from the diagrams. The trajectories colored in red start from the initial condition (x₀, y₀, z₀) = (0, 0.4, 0) and those colored in blue correspond to (x₀, y₀, z₀) = (0, −0.4, 0). For the two initial conditions, it can be observed from Figure 4 that when ε = 0.5, the chaotic attractor is obtained, as shown in Figures 4A1, A2. Then as ε increases, the system returns to the periodic state, but the period attractors are different under two initial conditions, which are shown in Figures 4B1,B2,C1,C2.

FIGURE 4

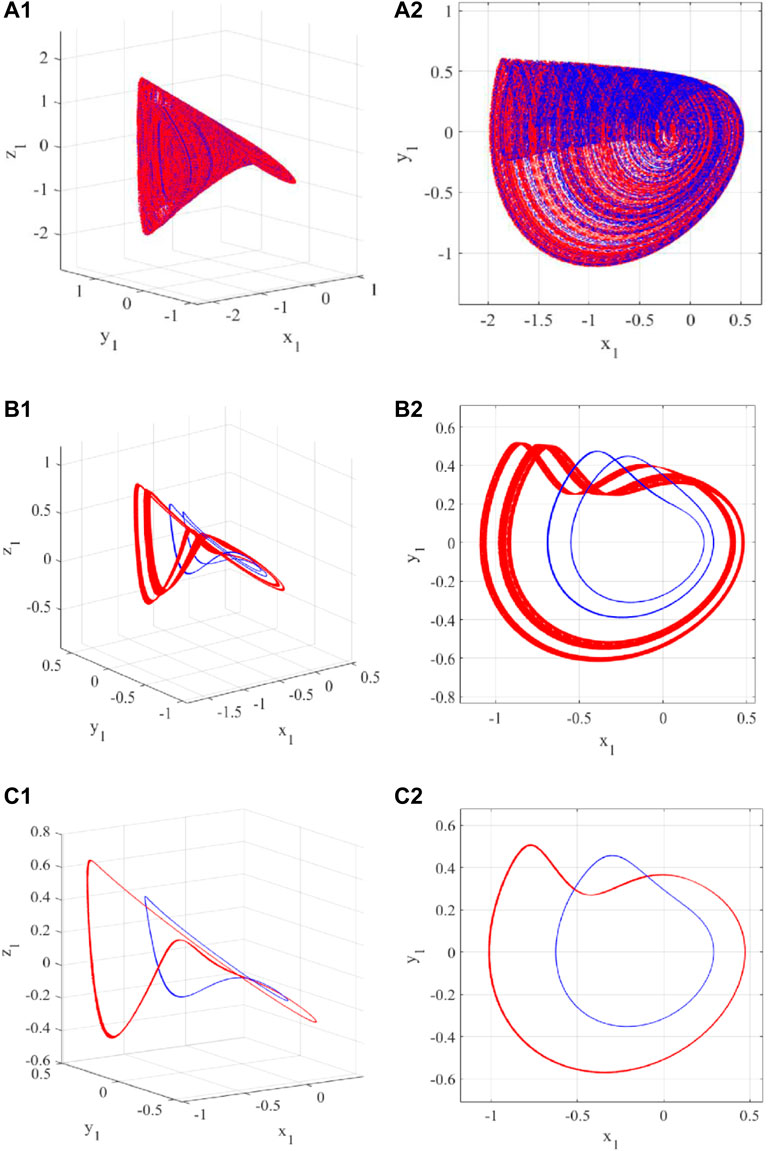
FIGURE 4. The phase diagrams in 3D and 2D (x-y plane) with the initial conditions of (x₀, y₀, z₀) = (0, 0.4, 0) (red) and (x₀, y₀, z₀) = (0, −0.4, 0) (blue), and different values of ε: (A) 0.5; (B) 1.2; (C) 1.3.

The state variable $x$ appears once in the second equation of Eq. 6. Consequently, the state variable $x$ can be easily boosted. In system (5) [47, 48], we fixed the parameters as α = 1, β = 1, γ = 1, δ = 1, and ε = 1 and added a parameter k, which can realize the offset boosting without changing the basic dynamics as the substitution of x → x + k transforms it to its original form at k = 0. Then, the equation can be written as

$\{\begin{array}{c}\stackrel{\cdot }{x}=y \\ \stackrel{\cdot }{y}=z\\ \stackrel{\cdot }{z}=-\left(x+k\right)-{10}^{-9}\left(e^{\frac{y}{0.026}}-1\right)-\epsilon z\end{array}(13)$

To better clarify the variable-boostable phenomenon, different k was selected to plot the phase diagrams. For the dimensionless system (13), the fixed time step of 0.001 was used for numerical simulations. The projections of attractors in the x-y plane are given in Figures 5A,B, where the blue, red, and yellow orbits correspond to k = 2 for (x₀, y₀, z₀) = (−2, 0.4, 0), k = 0 for (x₀, y₀, z₀) = (0, 0.4, 0), and k = −2 for (x₀, y₀, z₀) = (2, 0.4, 0). It is found that the attractor is linearly boosted towards the x direction. Besides, we choose a relatively long time interval τ ∊ [1000,5000] to compute the average and amplitude of each variable [49–51]. The average and amplitude (maximum and minimum size) of x, y, and z are plotted in Figures 5C,D, respectively. The results show that both the average and amplitude of the variable x are boosted when adjusting k, whereas the other three variables almost keep unchanging.

FIGURE 5

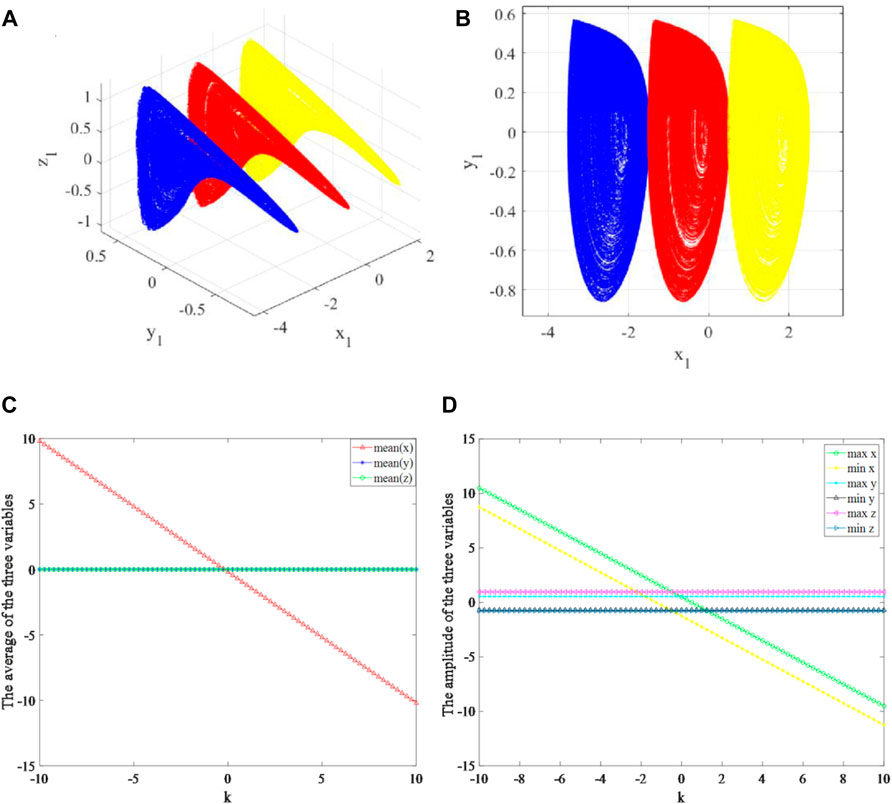
FIGURE 5. Offset boosting behaviors of the system (13) for the constant k. (A) 3D phase diagram of the boosted attractors for k = 2 (blue), k = 0 (red), k = −2 (yellow). (B) x-y plane phase diagrams of the boosted attractors for k = 2 (blue), k = 0 (red), k = −2 (yellow). (C) The average of each variable x, y, and z. (D) the amplitude of variables x, y, and z.

Circuit Implementation and Spectrum Characteristics

Circuit Implementation

To verify the authenticity of the simulation results, the real circuit was made to physically implement the system shown in Figures 6A,B, in which one precision potentiometer, three monolithic ceramic capacitors, one silicon diode 1N4148, three carbon film resistors with the error of ±5%, and three CFOAs AD844AN with operating voltages of ±12 V are utilized. The circuit parameters are listed in Table 1. The experiment results of x-y plane phase diagrams and spectrum can be captured by the UNI-T UTD2102CM and UNI-T UPO9504Z, respectively.

FIGURE 6

FIGURE 6. Actual circuit implementation with COFAs. (A) Etched circuit board. (B) Actual experimental test with UNI-TUTD2102CM and UNI-T UPO9504Z.

TABLE 1

TABLE 1. Linear element parameters for experiments.

According to the previous normalization formula Eq. 4, when the component parameters in the circuit are fixed, the value of ε depends on R₁. When R₁ = 34.48 kΩ, the value of ε is 0.29, and the system is in a period one state. Moreover, the value of R₁ continues to decrease when R₁ is adjusted to correspond to the value of ε in Figure 4, respectively, and the phase diagrams are captured by UNI-T UTD2102CM as shown in Figure 7. According to the phase diagrams, it is found that when R₁ is adjusted to a certain fixed value, the phase diagrams can be consistent with the numerical simulation results. For example, R₁ = 19.8 kΩ and ε = 0.5, and its phase diagram is shown in Figure 7C. The system is in a chaotic state and is in the same state in Figure 4A. Meanwhile, it is found that when R₁ is in the range of [10.1, 12.58] kΩ, the system shows periods corresponding to another period attractor, which also fully proves that the system has the phenomenon of attractors coexistence, as shown in Figures 7D,F.

FIGURE 7

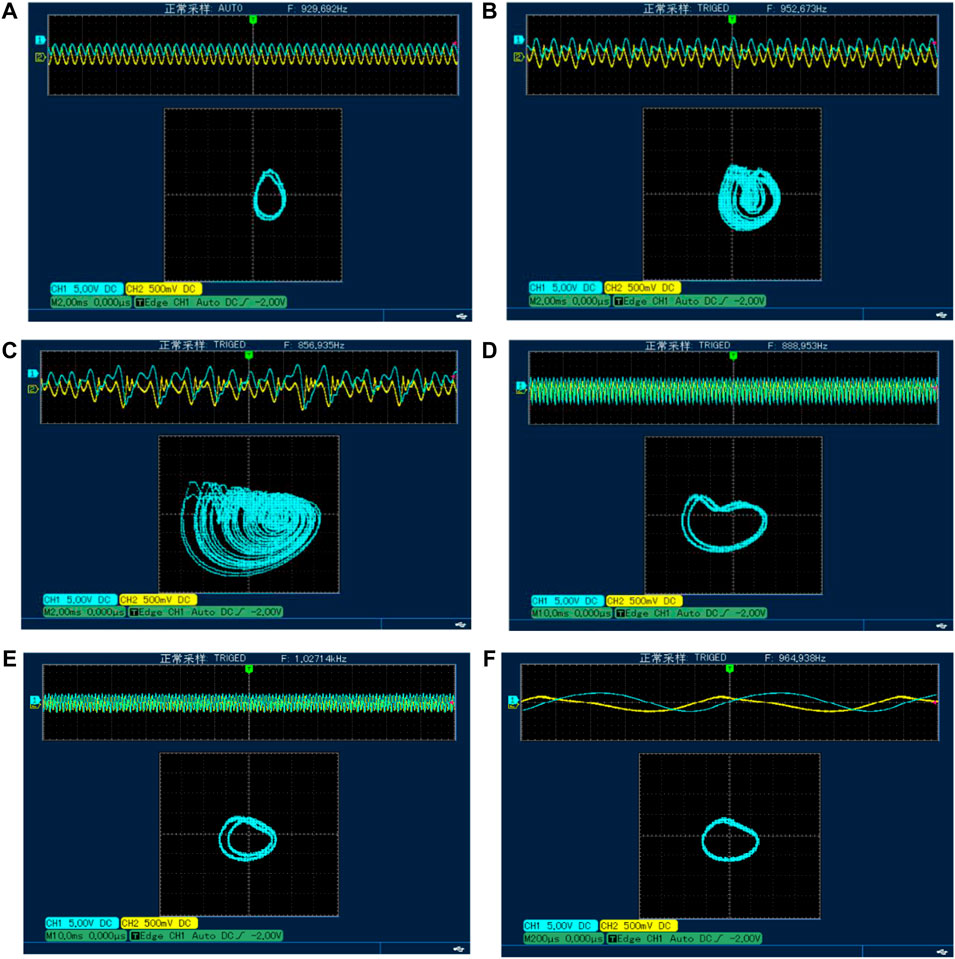
FIGURE 7. Experiment results at different values of R1. (A) R1 = 34.48 kΩ. (B) R1 = 26.35 kΩ. (C) R1 = 19.8 kΩ. (D) R1 = 10.59 kΩ. (E) R1 = 8.32 kΩ. (F) R1 = 7.67 kΩ.

Offset Boosting Implementation

Rewrite Eq. 13 as follows:

$\{\begin{array}{c}\frac{\mathit{d}{\mathit{u}}_{\mathit{1}}}{\mathit{dt}}\mathit{=}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{2}}{\mathit{C}}_{\mathit{1}}}{\mathit{u}}_{\mathit{2}}\mathit{ }\\ \frac{\mathit{d}{\mathit{u}}_{\mathit{2}}}{\mathit{dt}}\mathit{=}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{4}}{\mathit{C}}_{\mathit{2}}}{\mathit{u}}_{\mathit{3}}\\ \frac{\mathit{d}{\mathit{u}}_{\mathit{3}}}{\mathit{dt}}\mathit{=-}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{3}}{\mathit{C}}_{\mathit{3}}}\mathit{(}{\mathit{u}}_{\mathit{1}}\mathit{+}{\mathit{V}}_{\mathit{k}}\mathit{)-}\frac{\mathit{1}}{{\mathit{C}}_{\mathit{3}}}\cdot {\mathit{I}}_{\mathit{S}}\left({\mathit{e}}^{\frac{{\mathit{u}}_{\mathit{2}}}{{\mathit{V}}_{\mathit{T}}}}\mathit{-1}\right)\mathit{-}\frac{\mathit{1}}{{\mathit{R}}_{\mathit{1}}{\mathit{C}}_{\mathit{3}}}{\mathit{u}}_{\mathit{3}}\end{array}(14)$

According to the circuit diagram of Figure 2 and Eq. 14, the simple Jerk circuit is built in NI Multisim 14.0, as shown in Figure 8A. A circuit in the red dashed box, containing a precision potentiometer, a common discharge constituting a voltage follower, and a resistor forming DC current $I_k$, is incorporated into the reverse port of $u_1$. Adjusting for R7 to 35, 50, and 65%, respectively, when V_k = −4.5 V, V_k = 0 V, and V_k = 4.5 V, its chaotic attractors correspond to the blue, red, and yellow attractors in Figure 8B.

FIGURE 8

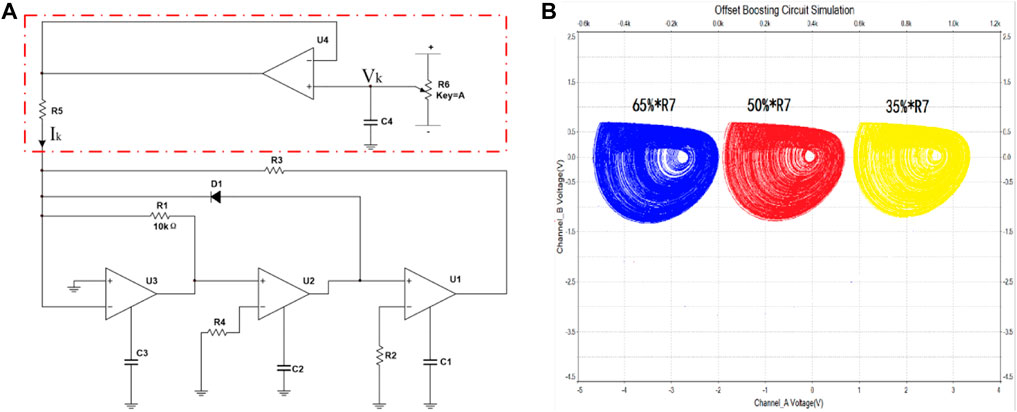
FIGURE 8. The circuit simulation of offset boosting. (A) The circuit of offset boosting for variable x. (B) The attractors of offset boosting when adjusting for R7 to 35% (blue), 50% (red), and 65% (yellow).

To verify the implementation ability of the simulation, we performed the experimental test as shown in Figure 9A. Adjusting the precision potentiometer to correspond the voltage of $V_k$ to 4.5 , 0 , and −4.5 V, respectively, the attractor phase diagrams can be captured by the oscilloscope as shown in Figures 9B–D.

FIGURE 9

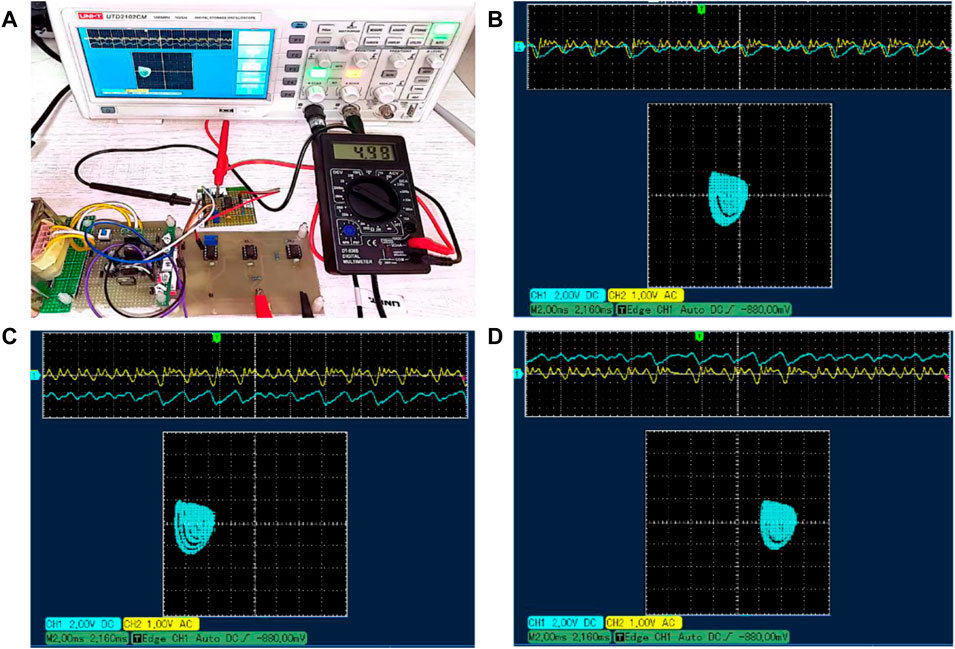
FIGURE 9. Offset boosting with actual circuit implementation and its x-y plane phase diagrams in oscilloscope. (A) Actual experimental test. (B) V_k = −4.5 V. (C) V_k = 0 V. (D) V_k = 4.5 V.

Frequency Spectrum Characteristics

The frequency spectrum is one of the most important characteristics of the chaotic signal. The frequency-domain characteristics of chaos are of great significance in chaotic encryption communication and automatic control [52]. In the integrator circuit, the time constant τ = RC, when R is determined to be unchanged, changing the value of the capacitor C, different time constants can be obtained [53].

For comparison, an experimental circuit using four ordinary op-amps to realize the chaotic system [11] was made as Figure 10 shows which includes four VFOAs AD711AN; three capacitors C₁, C₂, C₃; five resistors R₁, R₂, R₃, R₄, R₅; one precision potentiometer R₆; and one silicon diode D₁ 1N4148, which provides the nonlinear function.

FIGURE 10

FIGURE 10. VFOA circuit experimental test. (A) The experimental circuit board with AD711AN. (B) Actual experimental test with UNI-TUTD2102CM and UNI-T UPO9504Z.

The specific parameters are that all the resistances are 10 kΩ in both of the two kinds of the chaotic circuit, and all capacitors are changed according to the experimental requirements at the same time. The frequency spectrums of the chaotic attractor under different time constants are obtained, as shown in Figure 11, during changing the value of integrating capacitors. It can be seen that when C = 100 nF, the center frequency of the two chaotic circuits is about 1.5 kHz. When C = 10 nF, the center frequency is about 12 kHz. Continuously, when C = 1 nF, the circuit with VFOAs is no longer chaotic. It can be seen from the frequency spectrum and the phase diagram that it is in a periodic state. However, CFOA-JCC is still in chaos and the center frequency of the chaotic attractor is about 120 kHz. What is more, the center frequency can be improved to about 650 kHz when C = 200 pF in the CFOA-JCC. Compared with the chaotic circuit based on VFOA, it can generate a high-frequency chaotic signal. Consequently, the CFOA-JCC is not only simple in structure but also can increase the operating frequency of the circuit and broaden its spectrum range.

FIGURE 11

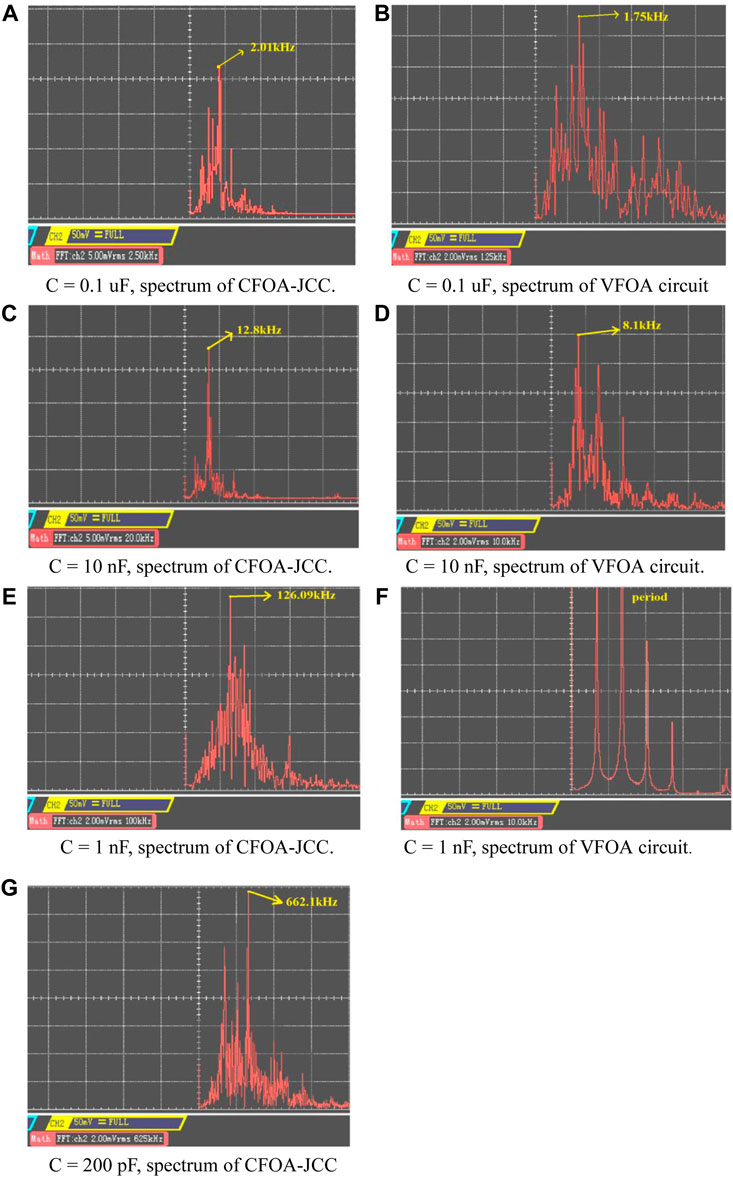
FIGURE 11. Spectrums of the CFOA-JCC and VFOA circuit when capacitors take different values. (A) C = 0.1 uF, spectrum of CFOA-JCC. (B) C = 0.1 uF, spectrum of VFOA circuit. (C) C = 10 nF, spectrum of CFOA-JCC. (D) C = 10 nF, spectrum of VFOA circuit. (E) C = 1 nF, spectrum of CFOA-JCC. (F) C = 1 nF, spectrum of VFOA circuit. (G) C = 200 pF, spectrum of CFOA-JCC

In ideal conditions, the dominant frequency of oscillation is expected to be $\mathit{f=}\frac{\mathit{\omega }}{\mathit{2\pi RC}}$ and $\omega$ is the imaginary part of λ₂ and λ₃¹¹. The values of f can be obtained as shown in Table 2 in the case of different capacitances when all resistance values are 10 kΩ. Compering with Figure 8, the value of fin Table 2 is extremely similar to the value in Figure 8 experimentally observed.

TABLE 2

TABLE 2. The theoretical values of fin deferent capacitances.

Conclusion

The dynamics of CFOA-JCC and the electronic circuit implementation have been discussed extensively in terms of its parameters using standard nonlinear analysis techniques such as bifurcation diagrams, Lyapunov exponent plots, offset boosting, and frequency spectra. The bifurcation analysis suggests that chaos that arises in the CFOA-JCC follows the classical period-doubling when adjusting the bifurcation control parameters slowly. It is also found that the proposed CFOA-JCC exhibits the asymmetrical and striking feature of multiple coexistence attractors for a wide range of circuit parameters. A numerical simulation and circuit experimental test verified the coexistence of multiple attractors of this system. The voltage slew rate of the feedback amplifier is almost independent of frequency and has better high-frequency characteristics. Consequently, the CFOA-JCC has better high-frequency performance than the chaotic circuit designed by ordinary VFOAs, so that higher frequency chaotic attraction can be obtained. At the same time, compared with the VFOA chaotic circuit, the CFOA-JCC has a simpler topology and fewer components, conducive to system integration.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

QW: system analysis, circuit design, and draft writing. ZT: checking the whole analysis and manuscript revision. XW: numerical analysis, circuit implementation. WT: checking the whole analysis.

Funding

This work was supported by the Natural Science Foundation of China (nos. 51660115, U1612442, 62061008, and 61264004), the Guizhou Province Science and Technology Plan Project (no. 20185769), and Research Projects of Innovation Group of Guizhou Provincial Department of Education (QianJiaoHeKY(2021)022).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lü J., Murali K., Sinha S., Leung H., Aziz-Alaoui M. Generating Multi-Scroll Chaotic Attractors by Thresholding. Phys Lett A (2008) 372(18):3234–9. doi:10.1016/j.physleta.2008.01.065

CrossRef Full Text | Google Scholar

2. Li Z., Peng C., Tan W., Li L. An Efficient Plaintext-Related Chaotic Image Encryption Scheme Based on Compressive Sensing. Sensors (2021) 21(3):758. doi:10.3390/s21030758

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Yu F., Zhang Z., Shen H., Huang Y., Cai S., Du S. FPGA Implementation and Image Encryption Application of a New PRNG Based on a Memristive Hopfield Neural Network with a Special Activation Gradient. Chin Phys. B (2021). doi:10.1088/1674-1056/ac3cb2

CrossRef Full Text | Google Scholar

4. Xu Q., Tan X., Zhu D., Bao H., Bao B. Bifurcations to Bursting and Spiking in the Chay Neuron and Their Validation in a Digital Circuit. Chaos, Solitons & Fractals (2020) 141(927):110353. doi:10.1016/j.chaos.2020.110353

CrossRef Full Text | Google Scholar

5. Ma C., Mou J., Li P., Liu T. Dynamic Analysis of a New Two-Dimensional Map in Three Forms: Integer-Order, Fractional-Order and Improper Fractional-Order. Eur Phys J Spec Top (2021) 230:1945–57. doi:10.1140/epjs/s11734-021-00133-w

CrossRef Full Text | Google Scholar

6. Lu T., Chen G., Xing H. Doubling the Coexisting Attractors. Chaos (2019) 29:051102–2. doi:10.1063/1.5097998

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sprott J. C. Some Simple Chaotic Jerk Functions. Am J Phys (1997) 65:537–43. doi:10.1119/1.18585

CrossRef Full Text | Google Scholar

8. Sprott J. C. A New Class of Chaotic Circuit. Phys Lett A (2000) 266:19–23. doi:10.1016/s0375-9601(00)00026-8

CrossRef Full Text | Google Scholar

9. Sprott J. C. Simple Chaotic Systems and Circuits. Am J Phys (2000) 68:758–63. doi:10.1119/1.19538

CrossRef Full Text | Google Scholar

10. Kiers K., Klein T., Kolb J., Price S., Sprott J. C. Chaos in a Nonlinear Analog Computer. Int J Bifurcation Chaos (2004) 14:2867–73. doi:10.1142/s0218127404010898

CrossRef Full Text | Google Scholar

11. Sprott J. C. A New Chaotic Jerk Circuit. IEEE Trans Circuits Syst (2011) 58:240–3. doi:10.1109/tcsii.2011.2124490

CrossRef Full Text | Google Scholar

12. Ma X., Mou J., Liu J., Ma C., Zhao X. A Novel Simple Chaotic Circuit Based on Memristor–Memcapacitor. Nonlinear Dyn (2020) 100:2859–76. doi:10.1007/s11071-020-05601-x

CrossRef Full Text | Google Scholar

13. Xu Q., Ju Z., Ding S., Feng C., Chen M. Electromagnetic Induction Effects on Electrical Activity within a Memristive Wilson Neuron Model. Cogn Neurodynamics (2021). doi:10.1007/s11571-021-09764-0

CrossRef Full Text | Google Scholar

14. Xu Q., Lin Y., Bao B., Chen M. Multiple Attractors in a Non-ideal Active Voltage-Controlled Memristor Based Chua's Circuit. Chaos, Solitons & Fractals (2016) 83:186–200. doi:10.1016/j.chaos.2015.12.007

CrossRef Full Text | Google Scholar

15. Elwakil A. S., Soliman A. M. Current Conveyor Chaos Generators. IEEE Trans Circuits Syst (1999) 46:393–8. doi:10.1109/81.751313

CrossRef Full Text | Google Scholar

16. Devices A. AD844 Data Sheet (1990). p. I990.

Google Scholar

17. Wang C., Zhang J., Wang L., Shi W., Jing D. A Novel Nth-Order Voltage-Mode Universal Filter Based on CMOS CFOA. Optik (2016) 127:2226–30. doi:10.1016/j.ijleo.2015.11.127

CrossRef Full Text | Google Scholar

18. Kilic R. On Current Feedback Operational Amplifier-Based Realization of Chua's Circuit. Circuits Syst Signal Process (2003) 22:475–91. doi:10.1007/s00034-003-0920-z

CrossRef Full Text | Google Scholar

19. Kilic R., Yildirim F. Current-Feedback Operational Amplifier-Based Inductorless Mixed-Mode Chua’s Circuits. Int J Bifurcation chaos (2006) 16:709–14. doi:10.1142/S0218127406015076

CrossRef Full Text | Google Scholar

20. Bao B.-C., Xu J.-P., Liang Y. Inductor Current Sampled Feedback Control of Chaos in Current-Mode Boost Converter. J Electron Sci Technology (2008) 6:52–5.

Google Scholar

21. Tan Ping-An T., Zhang Bo Z., Qiu Dong-Yuan Q. Stabilization of Chaotic Behaviour and Spiking Current in Thyristor with Time-Delayed Feedback Control. wlxb (2010) 59:5299–306. doi:10.7498/aps.59.5299

CrossRef Full Text | Google Scholar

22. Ji X., Ren W., Yuan W. The Design of Multi-Scroll Chaotic Circuit Based on Current Conveyor. Sci Technology Eng (2013) 17.

Google Scholar

23. Lin Y., Wang C. H., Xu H. Generation of Grid Multiscroll Chaotic Attractors Using a Current Conveyor. J Math Sci (2014) 201:350–60. doi:10.1007/s10958-014-1995-8

CrossRef Full Text | Google Scholar

24. Joshi M., Ranjan A. Current-Controlled Chaotic Chua’s Circuit Using CCCII. In: Advances in Communication and Computational Technology. Lecture Notes in Electrical Engineering, 668. Singapore: Springer (2020).

Google Scholar

25. Shepherd L., et al. Towards Ultra-low Power Bio-Inspired Processing. London: Springer (2006).

Google Scholar

26. Prasad S. R. A New High Frequency Realization of Chua’s Chaotic Circuit Using Current Feedback Operational Amplifiers (CFOA’s). Int J Electron Comput Sci Eng (2012) 1 (02), 223–229.

Google Scholar

27. Wand C.-H., Yin J.-W., Lin Y. Design and Realization of Grid Multi-Scroll Chaotic Circuit Based on Current Conveyers. Acta Phys Sin (2012) 61. doi:10.7498/aps.61.210507

CrossRef Full Text | Google Scholar

28. Lin Y., Wang C. H., Xu H. Grid Multi-Scroll Chaotic Attractors in Hybrid Image Encryption Algorithm Based on Current Conveyor. Acta Physica Sinica (2012) 61:514–8. doi:10.7498/aps.61.240503

CrossRef Full Text | Google Scholar

29. Wu X. M., He Y. G., Yu W. X. Design and Implementation of Grid Multi-Scroll Chaotic Circuit Based on Current Feedback Operational Amplifier. Acta Physica Sinica (2014) 63. doi:10.7498/aps.63.180506

CrossRef Full Text | Google Scholar

30. Kengne J., Njitacke Z. T., Nguomkam Negou A., Fouodji Tsostop M., Fotsin H. B. Coexistence of Multiple Attractors and Crisis Route to Chaos in a Novel Chaotic Jerk Circuit. Int J Bifurcation Chaos (2016) 26:1650081. doi:10.1142/s0218127416500814

CrossRef Full Text | Google Scholar

31. Topaloglu S., Sagbas M., Anday F. Three-input Single-Output Second-Order Filters Using Current-Feedback Amplifiers. AEU - Int J Electronics Commun (2012) 66:683–6. doi:10.1016/j.aeue.2011.12.009

CrossRef Full Text | Google Scholar

32. Elwakil A. S., Kennedy M. P. Chaotic Oscillators Derived from Sinusoidal Oscillators Based on the Current Feedback Op Amp. Analog Integrated Circuits Signal Process. (2000) 24:239–51. doi:10.1023/a:1008369810214

CrossRef Full Text | Google Scholar

33. Qiwei T., et al. A Simple Inductor-free Memristive Circuit with Three Line Equilibria. Nonlinear Dyn (2018) 94:1585–602.

Google Scholar

34. Se Hwan Kim S. H., Seung Hoon Lee S. H., Jang J. Fabrication and Characterization of Low-Temperature Poly-Silicon Lateral P-I-N Diode. IEEE Electron Device Lett (2010) 31:443–5. doi:10.1109/led.2010.2043047

CrossRef Full Text | Google Scholar

35. Yan-ning F., Yi-sui S., Ji-lin Z. Non-linear Stability of the Equilibrium of a System of Mass Points. Chin Astron Astrophysics (2002) 26:354–62. doi:10.1016/s0275-1062(02)00077-2

CrossRef Full Text | Google Scholar

36. Erawaty N., Kasbawati K., Amir A. K. Stability Analysis for Routh-Hurwitz Conditions Using Partial Pivot. J Phys Conf Ser (2019) 1341:062017. doi:10.1088/1742-6596/1341/6/062017

CrossRef Full Text | Google Scholar

37. Peña J. M. Characterizations and Stable Tests for the Routh-Hurwitz Conditions and for Total Positivity. Linear Algebra its Appl (2004) 393:319–32. doi:10.1016/j.laa.2003.11.013

CrossRef Full Text | Google Scholar

38. Dharma Rao N. Routh-Hurwitz Conditions and Lyapunov Methods for the Transient-Stability Problem. Proc Inst Electr Eng UK (1969) 116:539–47. doi:10.1049/piee.1969.0112

CrossRef Full Text | Google Scholar

39. Bottema O. The Routh-Hurwitz Condition for the Biquadratic Equation. Indagationes Mathematicae (Proceedings) (1956) 59:403–6. doi:10.1016/s1385-7258(56)50054-6

CrossRef Full Text | Google Scholar

40. Bnzar T., Lzureanu C. A NEW 3-DIMENSIONAL SYSTEM WITH CHAOTIC BEHAVIOR (2014).

Google Scholar

41. Lü J., Chen G., Zhang S. Dynamical Analysis of a New Chaotic Attractor. Int J Bifurcation Chaos (2002) 12:1001–15. doi:10.1142/s0218127402004851

CrossRef Full Text | Google Scholar

42. Marsden J. E., Ratiu T. S. Introduction to Mechanics and Symmetry. New York: Springer-Verlag (1999).

Google Scholar

43. Pehlivan İ., Uyaroğlu Y. A New 3D Chaotic System with golden Proportion Equilibria: Analysis and Electronic Circuit Realization. Comput Electr Eng (2012) 38:1777–84. doi:10.1016/j.compeleceng.2012.08.007

CrossRef Full Text | Google Scholar

44. Teng L., Iu H. H. C., Wang X., Wang X. Chaotic Behavior in Fractional-Order Memristor-Based Simplest Chaotic Circuit Using Fourth Degree Polynomial. Nonlinear Dyn (2014) 77:231–41. doi:10.1007/s11071-014-1286-4

CrossRef Full Text | Google Scholar

45. Zhang X., Chen M., Wang Y., Tian H., Wang Z. Dynamic Analysis and Degenerate Hopf Bifurcation-Based Feedback Control of a Conservative Chaotic System and its Circuit Simulation. Complexity (2021) 2021:1–15. doi:10.1155/2021/5576353

CrossRef Full Text | Google Scholar

46. Joshi M., Ranjan A. Investigation of Dynamical Properties in Hysteresis-Based a Simple Chaotic Waveform Generator with Two Stable Equilibrium. Chaos, Solitons & Fractals (2020) 134:109693 doi:10.1016/j.chaos.2020.109693

CrossRef Full Text | Google Scholar

47. Li C., Sprott J. C., Liu Y., Gu Z., Zhang J. Offset Boosting for Breeding Conditional Symmetry. Int J Bifurcation Chaos (2018) 28(14):1850163. doi:10.1142/s0218127418501638

CrossRef Full Text | Google Scholar

48. Ma C., Mou J., Xiong L., Banerjee S., Han X. Dynamical Analysis of a New Chaotic System: Asymmetric Multistability, Offset Boosting Control and Circuit Realization. Nonlinear Dyn (2021) 103:1–14. doi:10.1007/s11071-021-06276-8

CrossRef Full Text | Google Scholar

49. Li C., Lei T., Wang X., Chen G. Dynamics Editing Based on Offset Boosting. Chaos (2020) 30:063124. doi:10.1063/5.0006020

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Li C., Gu Z., Liu Z., Jafari S., Kapitaniak T. Constructing Chaotic Repellors. Chaos, Solitons & Fractals (2021) 142:110544. doi:10.1016/j.chaos.2020.110544

CrossRef Full Text | Google Scholar

51. Li C., Peng Y., Tao Z., Sprott J. C., Ja Fari S. Coexisting Infinite Equilibria and Chaos. Int J Bifurcation Chaos (2021) 31. doi:10.1142/s0218127421300147

CrossRef Full Text | Google Scholar

52. Zemlyanyi O. V. KEYING OF THE BROADBAND CHAOTIC SIGNAL SPECTRUM FOR DATA TRANSMISSION. Telecommunications Radio Eng (2016) 75 (05), 401–411. doi:10.1615/TelecomRadEng.v75.i5.20

CrossRef Full Text | Google Scholar

53. Sansen W. M. C., Van Peteghem P. M. An Area-Efficient Approach to the Design of Very-Large Time Constants in Switched-Capacitor Integrators. IEEE J Solid-State Circuits (2003) 19:772–80. doi:10.1109/JSSC.1984.1052220

CrossRef Full Text | Google Scholar