
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 21 February 2022
Sec. Condensed Matter Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.834682
This article is part of the Research TopicAdvances in Superconducting Infinite-Layer and Related NickelatesView all 16 articles
We study the magnetic and spectral properties of a single-band Hubbard model for the infinite-layer nickelate compound LaNiO2. As spatial correlations turn out to be the key ingredient for understanding its physics, we use two complementary extensions of the dynamical mean-field theory to take them into account: the cellular dynamical mean-field theory and the dynamical vertex approximation. Additionally to the systematic analysis of the doping dependence of the non-Curie-Weiss behavior of the uniform magnetic susceptibility, we provide insight into its relation to the formation of a pseudogap regime by the calculation of the one-particle spectral function and the magnetic correlation length. The latter is of the order of a few lattice spacings when the pseudogap opens, indicating a strong-coupling pseudogap formation in analogy to cuprates.
With the discovery of superconductivity in Sr-doped NdNiO2 in 2018 [1] it is likely that a new branch of the family of unconventional superconductors (i.e. with non-phonon mediated pairing) was revealed. At this time nickelates, as bulk materials and heterostructures, have already been in the focus of an intense search for high-Tc cuprate anaolgue oxides for a while (see e.g. [2–9]). One of the current challenges is therefore to understand similarities and/or differences between nickelate and other unconventional superconductors like, e.g., cuprate-, organic-, iron pnictide-, and heavy-fermion compounds. While there is currently no consensus if these materials could be covered by a single theory, there are strong indications that for all of them purely electronic (in particular magnetic) fluctuations are at least part of the key to understand their pairing mechanism. Such fluctuations are also expected to be responsible for unusual observations above the critical temperature which for the high-Tc cuprates include non-Fermi liquid behaviour in 1) temperature dependence of resistivity (universal in all cuprates, e.g. [10, 11], and found also in organic- and iron pnictide-SC [12, 13] 2) magnetic susceptibilities which are neither Pauli- nor Curie-like but exhibit sharp drops at a new temperature scale commonly denoted T* [14], and 3) partially (i.e. momentum dependently) gapped quasi-particle Fermi surfaces [15–17]. The region of these phenomena in the temperature/hole-doping phase diagram is commonly referred to as the “pseudogap” region.
Motivated by our recent combined experiment/theory multi-method study of the static uniform magnetic susceptibility χ in LaNiO2 [18] and other recent experimental studies [19–21], in this manuscript we investigate deeper how the two-particle magnetic response is linked to one-particle spectra A(k, ω) for different temperatures and different doping levels. With the help of complementary quantum many-body techniques, we show that the emergence of a maximum in χ is concomitant with a significant drop in the antinodal weight of A(k ≈ (π, 0), ω = ɛF) at the Fermi level. On the basis of these results we argue that - like cuprates - also nickelate superconductors feature a pseudogap region in their phase diagram.
The paper is organized as follows: in Section 2 we introduce the effective single-band model of infinite-layer nickelates and a brief overview of the numerical methods used to analyze it. In Section 3 we present our results starting with the temperature/doping phase diagram obtained from the maxima of χ (Section 3.1). Afterwards we show the one-particle spectral functions (Section 3.2) and provide magnetic correlation lengths as a function of temperature (Section 3.3). We conclude the paper in Section 4 by commenting on the relevance of our findings to infinite-layer nickelates and their cuprate analogues.
For our study we use the single-band repulsive Hubbard model [22–27] on a two-dimensional square lattice:
where σ is the spin of the electron,
Such models has already been successfully applied in the description of the superconducting phase in NdNiO2 [28–30] and the non-Curie-Weiss behavior of the magnetic susceptibility in LaNiO2 [18]. The material realistic hopping parameters, resulting from a Wannier- and tight-binding projection are t = 395meV, t′ = − 0.25t = − 95 meV, and t″ = 0.12t = 47 meV as well as the local Hubbard interaction U = 8t = 3.16 eV from a cRPA calculation [28]. All energies are given in units of eV except for temperatures, which are given in Kelvin. The chemical potential μ is adjusted to an average filling of n = 1 − δ, where δ indicates the hole-doping of the single
We investigate the properties of the model in Eq. 1 as a function of temperature T and doping δ by applying three numerical methods. Besides dynamical mean-field theory (DMFT) [31–34], which includes all temporal onsite-correlations of the lattice problem, we use two complementary extensions of it: cellular dynamical mean-field theory (CDMFT) [35] and the dynamical vertex approximation (DΓA) [36, 37], a diagrammatic extension of DMFT [38]. The combination of complementary numerical methods (“multi-method approach” [39, 40]) turned out to be very useful and versatile recently for both purely model- [39, 41] and material-based [18] studies.
For the present work we make use of this approach in order to study the influence of (non-local) magnetic fluctuations captured by the different approximations on different length scales. CDMFT is a conceptually simple real-space cluster extension of DMFT and controlled in the sense that it recovers the exact solution for infinite cluster sizes (Nc → ∞). For finite Nc (for the present study we use Nc = 4 × 4) it captures correlations up to the characteristic length scale of the cluster. For the DΓA we employ its ladder-version in the particle-hole (magnetic) channel with Moriyaesque λ-corrections in the spin channel [42–44]. This choice of the scattering channel greatly simplifies the algorithm (as it bypasses the general, but complicated, parquet treatment) and is justified in the pseudogap regime of the Hubbard model, where fluctuation diagnostics methods could demonstrate unequivocally the dominance of the spin channel on the single-particle spectrum [45–48].
Different from CDMFT, DΓA captures short- and long-range fluctuations in the magnetic channel on equal footing which, as previous studies have shown, is indispensable in the vicinity of second order phase transitions [49–52]. Moreover, DΓA respects the Mermin-Wagner theorem [53, 54] and shows no ordering instability at finite temperatures for our two-dimensional model Eq. 1. This is not the case for DMFT and CDMFT where the finite cluster size (for DMFT Nc = 1) leads to an antiferromagnetic phase transition at a finite Néel temperature TNéel. We therefore restrict ourselves to results obtained at temperatures above TNéel for these methods.
As impurity solver we use the latest generation of a continuous time quantum Monte-Carlo solver in its interaction expansion (CT-INT [55]) which is an application of the TRIQS package [56].
We start the presentation of our results by discussing the phase diagram of Figure 1, a summary of the data obtained by our different numerical techniques applied to Eq. 1 as a function of doping (δ as the bottom horizontal axis, Sr-doping as the top one). In the left panel the black triangles represent the temperatures T* where the static uniform magnetic susceptibility χ := Re χm (q = (0, 0), iΩn = 0) displays a maximum in DΓA. This temperature scale T* is highest in the half-filled case and monotonously decreases with increasing doping. Interestingly, for the doped system, this line follows to very good agreement the magnetic ordering temperature of CDMFT
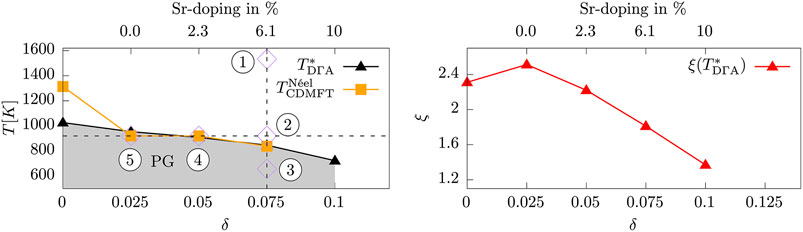
FIGURE 1. Left: phase diagram of the Hubbard model given by Eq. 1 as a function of temperature T and doping δ. T* indicates the maximum of χ calculated in DΓA (black triangles). The orange squares indicate the magnetic ordering temperature in CDMFT
For the determination of T* we turn to Figure 2, which shows χ calculated by DMFT (blue circles), CDMFT (orange squares) and DΓA (black triangles) for three representative levels of doping. The shaded areas indicate magnetically ordered phases of DMFT (below
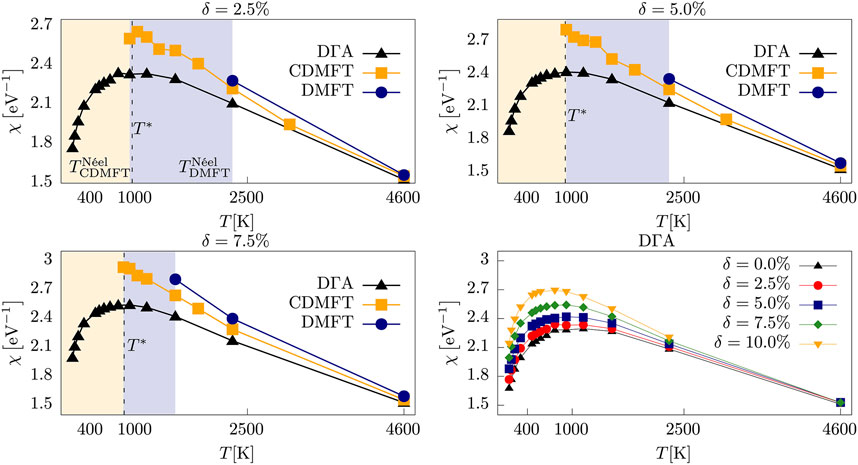
FIGURE 2. Static uniform magnetic susceptibilities χ as a function of T for 2.5% (upper left panel), 5% (upper right panel) and 7.5% (lower left panel) hole doping. The transition temperature of DMFT
For all hole dopings considered in our nickelate model the flat maximum χmax := χ(T*) is a clear indicator of non-Curie-Weiss (and non-Pauli) behavior [18, 58, 60–62]. In high-Tc cuprates such behavior is also seen in the suppression of the nuclear magnetic resonance (NMR) Knight shift [63], which is the original hallmark of the onset of the pseudogap phase [14]. Its second hallmark, observed in angle-resolved photoemission spectroscopy (ARPES [17]) is the non-isotropic suppression of spectral weight and emergence of Fermi arcs in the one-particle spectrum, which we investigate in the next section.
For the analysis of the one-particle spectral function
where ɛ(k) is the non-interacting dispersion relation and Σ(k, iωn) the self-energy from DΓA (which is zero in the non-interacting case).
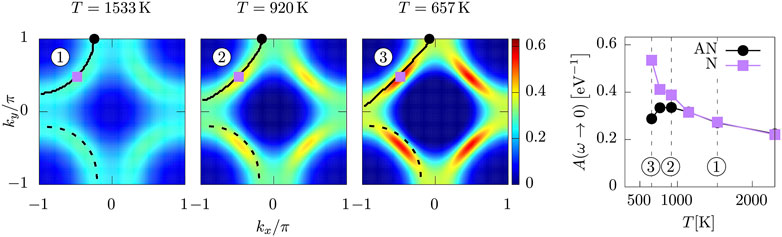
FIGURE 3. Spectral intensities A(k, ω = 0) for a constant doping of 7.5% and temperatures of 1533K, 920K, and 657K, calculated by DΓA. The black lines indicate the Fermi surfaces of the non-interacting case (dashed) and interacting case (solid) [for increased readability, these are only shown for one quadrant of the Brillouin zone]. The nodal (purple square)-antinodal (black circle) differentiation of the spectral weight together with the suppression of it at the antinode (right-hand panel) is a clear indication of a pseudogap.
Cooling the system across T*, and passing 920 and 657 K, one first notices that the shape of the Fermi surface starts to deviate strongly from the non-interacting case. This can be attributed to self-energy effects stemming from non-local correlations. This behaviour is also in qualitative agreement with recent numerically exact diagrammatic Monte Carlo calculations [64] for smaller interactions. Second, at low temperatures, one can observe a clear Fermi arc structure of the spectral intensity. Third, the temperature dependence of the spectral weight at the antinode (black circle) starts to differ strongly from that of the node (purple square): At high temperatures, both values increase when the system is cooled. After reaching T*, however, only the spectral weight at the node continues to grow, whereas at the antinode it starts to decrease. Together with the decrease in the uniform static magnetic susceptibility (see Section 3.1) this is an unequivocal indication of the onset of a pseudogap regime. Topologically at T* the Fermi surface is hole-like, i.e.
In Figure 4 we show the complementary evolution of the spectral intensity across the T* line at fixed T = 920 K following the horizontal dashed line in phase diagram Figure 1. On can observe here that the progressive reduction of the doping from 7.5 to 2.5% leads to a significant drop of spectral intensity at both the node and the antinode and, eventually, to a mitigation of the nodal-antinodal differentiation. Furthermore, there is a strong tendency visible toward a reconstruction of the topology of the Fermi surface from hole-like [
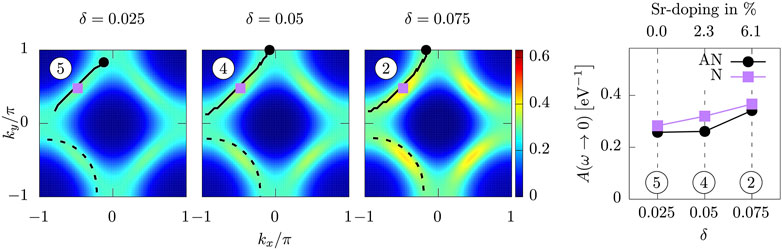
FIGURE 4. Analogous plots to Figure 3 at fixed T = 920 K for dopings 2.5%, 5%, and 7.5%.
In order to investigate more closely the nature of the emerging pseudogap, in the next section we analyse the magnetic correlation length and the momentum-dependent magnetic response.
We first calculate the fully momentum-dependent static magnetic susceptibility χm (q, iΩn = 0) within DΓA. The top leftmost panel of Figure 5 shows results for (δ = 7.5% and T = 960 K), which is slightly above T* for this doping. The maximum value of χm (q, iΩn = 0) is assumed at q = Q = (π, π) at T*. We note in passing that also incommensurate Néel order with Q ≠ (π, π) may occur in different parameter regimes of the model [50, 62, 67, 68]. For obtaining the correlation length ξ we perform an Ornstein-Zernike fit with [39, 49, 69, 70].
where Q denotes the momentum vector where the susceptibility assumes its maximum value. Assuming this functional form for the fit is justified by two exemplary fits in the momentum directions q = (qx, π) and q = (qx, qx) shown in the upper center and right panels of Figure 5. The so-obtained temperature dependence of ξ for several dopings is plotted in the lower panel of Figure 5. For small dopings we fit this dependence with
(with ρS being the spin stiffness), characteristic of a low-T gapped regime in two dimensions. The fit works reasonably well for temperatures T < T*, hinting towards a magnetically ordered ground state in DΓA for the dopings investigated.
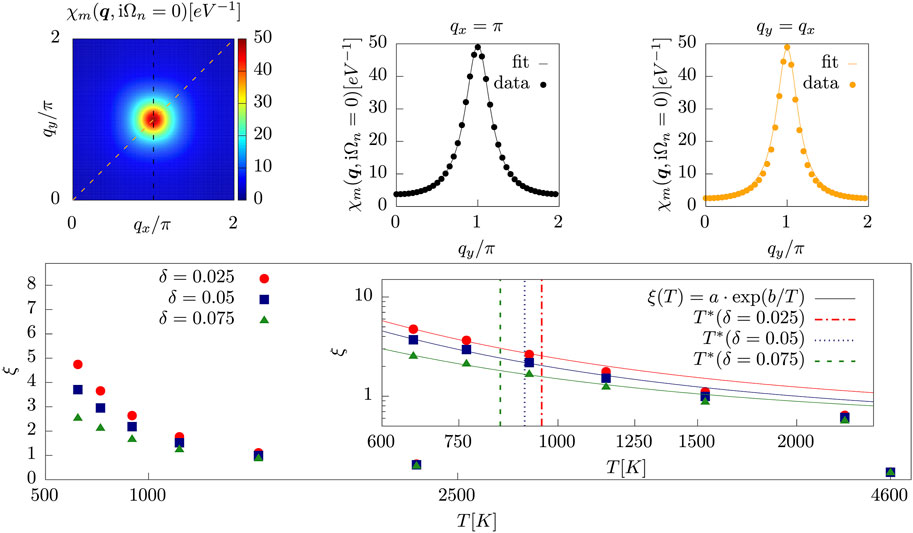
FIGURE 5. Top, from left to right: χm (q, iΩn = 0), χm (q = (qx, π), iΩn = 0), and χm (q = (qx, qx), iΩn = 0) for a doping of δ = 7.5% and a temperature of 960K, calculated by DΓA. Circles denote calculated points, the solid line an Ornstein-Zernike fit by Eq. 3. Bottom: Correlation lengths ξ of DΓA plotted over the temperature for different dopings. The insets shows a double-logarithmic plot and temperature fits [see text and Eq. 4].
As already commented in the discussion of Figure 1, the correlation lengths at the pseudogap temperature T* range from 1.2 to about 2 lattice spacings. This is a clear indicator that the pseudogap mechanism in our case is not the one observed in the weak coupling regime of the Hubbard model [39, 70–76]: there, in contrast, the pseudogap is opened when the magnetic correlation length exceeds the thermal de Broglie wavelength of the quasiparticles ξ ≫ vF/(πT) (Vilk criterion), where vF is the Fermi velocity. Hence, in the weak coupling regime, large correlation lengths have to be present for opening the (pseudo-)gap. This, however, does not need to be the case for stronger coupling: here, already the treatment of short-ranged (spin) fluctuations allows for the development of a pseudogap as momentum-differentiated gap, which is the reason for the successful description of this regime by cluster extensions of DMFT (like CDMFT and DCA [45, 60, 61, 77–79]).
To summarize, we analyzed a material-realistic single-band Hubbard model for the infinite-layer nickelate compound LaNiO2. By a combination of cellular dynamical mean-field theory and dynamical vertex approximation calculations we could trace the temperatures sufficiently low to determine a flat maximum in the uniform static magnetic susceptibility for the hole-doped system at T*. This temperature marks the onset of the pseudogap regime which manifests on the one-particle level as Fermi arcs in the spectral function. Concomitant on the two-particle level, the momentum-resolved magnetic susceptibility shows short-ranged magnetic fluctuations, which is characteristic of a strong coupling pseudogap. The exact location of the change from a weak-coupling to a strong-coupling pseudogap regime is a matter of current debate. Three indicators for this change can be mentioned: 1) a sudden increase in electronic correlations leading to a change in Fermi surface topology [65], 2) this strong correlation regime hosts relatively short-ranged correlations with the occurrence of (partial) localization [45, 68] and 3) the electron-boson coupling vertex develops a significant imaginary part [80, 81]. Our investigations of 1) and 2) in this manuscript by means of the DΓA, hence, allow us to characterize the found pseudogap as driven by strong coupling (Mott) physics.
In conclusion, our results for LaNiO2 support the idea that the infinite-layer nickelates and new nickelate superconductors are indeed close relatives of other unconventional superconductors and, in particular, high-Tc cuprates. This is a most promising perspective as contrasting nickelates with cuprates might lead to a much deeper understanding of non-phonon mediated pairing. Indeed future research should focus on apparent differences between the two material classes. Specifically, the absence of magnetic order in the infinite-layer nickelate compounds as well as their reduced covalency with oxygen [3, 82] compared to the cuprates is remarkable. Whether this means that also pairing mechanisms are distinct remains to be investigated.
For applying DΓA with Moriyaesque λ-corrections we solve the Bethe-Salpeter equations in Matsubara frequency space with Niω = 90 positive fermionic and NiΩ = 89 positive bosonic Matsubara frequencies for the two-particle Green function at all temperature shown, as well as 200 linear momentum grid points. To converge the DMFT calculation self-consistently we used the continuous-time quantum Monte Carlo solver in an interaction expansion (CT-INT) as part of an application of the TRIQS package. Every iteration was done using 256 ⋅ 105 cycles and roughly 6,200 core hours per temperature. For all shown spectral function plots over the Brillouin Zone we used a momentum resolution of 3,000 k-points.
In order to extract the magnetic susceptibility in a CDMFT approach we apply a ferromagnetic field on each lattice site with field strengths HF = 0.02, 0.04, 0.06 to get the slope of a linear fit which enables us to calculate the magnetic susceptibility:
For each doping/temperature point we checked that all the applied fields are still within the linear response regime. All CDMFT calculations are again performed using the CT-INT quantum Monte Carlo solver in a continuous-time approach. For every data point we used twenty self-consistency steps, each using 6.4 million Monte Carlo cycles.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
MK performed the numerical calculations and the post-processing of the data. The manuscript has been written by MK, PH, and TS. TS initiated and supervised the project. All authors provided critical feedback and shaped the research, analysis and manuscript.
The Max Planck Society is acknowledged for funding of the open access fee.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank K. Held, M. Kitatani, L. Si, P. Worm, M. Hepting, M. Ferrero, A. Georges, F. Šimkovic, and A. Toschi for insightful discussions and F. Šimkovic and E. König for critically reading the manuscript. We thank the computing service facility of the MPI-FKF for their support and we gratefully acknowledge use of the computational resources of the Max Planck Computing and Data Facility.
1. Li D, Lee K, Wang BY, Osada M, Crossley S, Lee HR, et al. Superconductivity in an Infinite-Layer Nickelate. Nature (2019) 572:624–7. doi:10.1038/s41586-019-1496-5
2. Anisimov VI, Bukhvalov D, Rice TM Electronic Structure of Possible Nickelate Analogs to the Cuprates. Phys Rev B (1999) 59:7901–6. doi:10.1103/physrevb.59.7901
3. Lee K-W, Pickett WE Infinite-layerLaNiO2: Ni1+is notCu2+. Phys Rev B (2004) 70:165109. doi:10.1103/physrevb.70.165109
4. Chaloupka Jc. v., Khaliullin G Phys Rev Lett (2008) 100:016404. doi:10.1103/physrevlett.100.016404
5. Hansmann P, Yang X, Toschi A, Khaliullin G, Andersen OK, Held K Phys Rev Lett (2009) 103:016401. doi:10.1103/physrevlett.103.016401
6. Hansmann P, Toschi A, Yang X, Andersen OK, Held K Electronic Structure of Nickelates: From Two-Dimensional Heterostructures to Three-Dimensional Bulk Materials. Phys Rev B (2010) 82:235123. doi:10.1103/physrevb.82.235123
7. Benckiser E, Haverkort MW, Brück S, Goering E, Macke S, Frañó A, et al. Orbital Reflectometry of Oxide Heterostructures. Nat Mater (2011) 10:189–93. doi:10.1038/nmat2958
8. Han MJ, Wang X, Marianetti CA, Millis AJ Dynamical Mean-Field Theory of Nickelate Superlattices. Phys Rev Lett (2011) 107:206804. doi:10.1103/physrevlett.107.206804
9. Disa AS, Kumah DP, Malashevich A, Chen H, Arena DA, Specht ED, et al. Phys Rev Lett (2015) 114:026801. doi:10.1103/physrevlett.114.026801
10. Takagi H, Batlogg B, Kao HL, Kwo J, Cava RJ, Krajewski JJ, et al. Systematic Evolution of Temperature-dependent Resistivity inLa2−xSrxCuO4. Phys Rev Lett (1992) 69:2975–8. doi:10.1103/physrevlett.69.2975
11. Daou R, Doiron-Leyraud N, LeBoeuf D, Li SY, Laliberté F, Cyr-Choinière O, et al. Linear Temperature Dependence of Resistivity and Change in the Fermi Surface at the Pseudogap Critical point of a High-Tc Superconductor. Nat Phys (2009) 5:31–4. doi:10.1038/nphys1109
12. Doiron-Leyraud N, Auban-Senzier P, René de Cotret S, Bourbonnais C, Jérome D, Bechgaard K, et al. Correlation between Linear Resistivity andTcin the Bechgaard Salts and the Pnictide superconductorBa(Fe1−xCox)2As2. Phys Rev B (2009) 80:214531. doi:10.1103/physrevb.80.214531
13. Taillefer L Scattering and Pairing in Cuprate Superconductors. Annu Rev Condens Matter Phys (2010) 1:51–70. doi:10.1146/annurev-conmatphys-070909-104117
14. Alloul H, Ohno T, Mendels P Y89NMR Evidence for a Fermi-Liquid Behavior inYBa2Cu3O6+x. Phys Rev Lett (1989) 63:1700–3. doi:10.1103/physrevlett.63.1700
15. Shen KM, Ronning F, Lu DH, Baumberger F, Ingle NJC, Lee WS, et al. Nodal Quasiparticles and Antinodal Charge Ordering in Ca 2-x Na X CuO 2 Cl 2. Science (2005) 307:901–4. doi:10.1126/science.1103627
16. Kanigel A, Norman MR, Randeria M, Chatterjee U, Souma S, Kaminski A, et al. Evolution of the Pseudogap from Fermi Arcs to the Nodal Liquid. Nat Phys (2006) 2:447–51. doi:10.1038/nphys334
17. Damascelli A, Hussain Z, Shen Z-X Angle-resolved Photoemission Studies of the Cuprate Superconductors. Rev Mod Phys (2003) 75:473–541. doi:10.1103/revmodphys.75.473
18. Ortiz RA, Puphal P, Klett M, Hotz F, Kremer RK, Trepka H, et al. Magnetic Correlations in Infinite-Layer Nickelates: An Experimental and Theoretical Multi-Method Study (2021). arXiv:2111.13668 [cond-mat.str-el].
19. Zhao D, Zhou YB, Fu Y, Wang L, Zhou XF, Cheng H, et al. Intrinsic Spin Susceptibility and Pseudogaplike Behavior in Infinite-Layer LaNiO2. Phys Rev Lett (2021) 126:197001. doi:10.1103/physrevlett.126.197001
20. Lu H, Rossi M, Nag A, Osada M, Li DF, Lee K, et al. Magnetic Excitations in Infinite-Layer Nickelates. Science (2021) 373:213–6. doi:10.1126/science.abd7726
21. Fowlie J, Hadjimichael M, Martins MM, Li D, Osada M, Wang BY, et al. Intrinsic Magnetism in Superconducting Infinite-Layer Nickelates. arXiv (2022). arXiv:2201.11943.
24. Kanamori J Electron Correlation and Ferromagnetism of Transition Metals. Prog Theor Phys (1963) 30:275–89. doi:10.1143/ptp.30.275
25. Gutzwiller MC Effect of Correlation on the Ferromagnetism of Transition Metals. Phys Rev Lett (1963) 10:159–62. doi:10.1103/physrevlett.10.159
26. Qin M, Schäfer T, Andergassen S, Corboz P, Gull E The Hubbard Model: A Computational Perspective. Annu Rev Condens Matter Phys (2022) 13:033948. doi:10.1146/annurev-conmatphys-090921-033948
27. Arovas DP, Berg E, Kivelson SA, Raghu S The Hubbard Model. Annu Rev Condens Matter Phys (2022) 13:null. doi:10.1146/annurev-conmatphys-031620-102024
28. Kitatani M, Si L, Janson O, Arita R, Zhong Z, Held K Nickelate Superconductors-A Renaissance of the One-Band Hubbard Model. Npj Quan Mater. (2020) 5:59. doi:10.1038/s41535-020-00260-y
29. Held K, Si L, Worm P, Janson O, Arita R, Zhong Z, et al. Phase Diagram of Nickelate Superconductors Calculated by Dynamical Vertex Approximation. Front Phys (2022) 9:810394. doi:10.3389/fphy.2021.810394
30. Karp J, Hampel A, Millis AJ Superconductivity and Antiferromagnetism in NdNiO2 and CaCuO2: A Cluster DMFT Study. arXiv (2022). arXiv:2201.10481.
31. Georges A, Kotliar G, Krauth W, Rozenberg MJ Dynamical Mean-Field Theory of Strongly Correlated Fermion Systems and the Limit of Infinite Dimensions. Rev Mod Phys (1996) 68:13–125. doi:10.1103/revmodphys.68.13
32. Georges A, Kotliar G Hubbard Model in Infinite Dimensions. Phys Rev B (1992) 45:6479–83. doi:10.1103/physrevb.45.6479
33. Metzner W, Vollhardt D Correlated Lattice Fermions ind=∞Dimensions. Phys Rev Lett (1989) 62:324–7. doi:10.1103/physrevlett.62.324
34. Chen H, Hampel A, Karp J, Lechermann F, Millis AJ Dynamical Mean Field Studies of Infinite Layer Nickelates: Physics Results and Methodological Implications. Front Phys (2022) 10:835942. doi:10.3389/fphy.2022.835942
35. Maier T, Jarrell M, Pruschke T, Hettler MH Quantum Cluster Theories. Rev Mod Phys (2005) 77:1027–80. doi:10.1103/revmodphys.77.1027
38. Rohringer G, Hafermann H, Toschi A, Katanin AA, Antipov AE, Katsnelson MI, et al. Rev Mod Phys (2018) 90:025003. doi:10.1103/revmodphys.90.025003
39. Schäfer T, Wentzell N, Šimkovic F, He Y-Y, Hille C, Klett M, et al. Phys Rev X (2021) 11:011058. doi:10.1103/physrevx.11.011058
40. LeBlanc JPF, Antipov AE, Becca F, Bulik IW, Chan GK-L, Chung C-M, et al. Simons Collaboration on the Many-Electron Problem. Phys Rev X (2015) 5:041041. doi:10.1103/physrevx.5.041041
41. Wietek A, Rossi R, Šimkovic F, Klett M, Hansmann P, Ferrero M, et al. Phys Rev X (2021) 11:041013. doi:10.1103/physrevx.11.041013
42. Rohringer G, Katanin A, Schäfer T, Hausoel A, Held K, Toschi A, ladderDGA. Available from: github.com/ladderDGA (2018).
43. Rohringer G New Routes towards a Theoretical Treatment of Nonlocal Electronic Correlations. Ph.D. thesis. Vienna, Austria: TU Wien (2013).
44. Schäfer T Classical and Quantum Phase Transitions in Strongly Correlated Electron Systems. Ph.D. thesis. Vienna, Austria: TU Wien (2016).
45. Gunnarsson O, Schäfer T, LeBlanc JPF, Gull E, Merino J, Sangiovanni G, et al. Fluctuation Diagnostics of the Electron Self-Energy: Origin of the Pseudogap Physics. Phys Rev Lett (2015) 114:236402. doi:10.1103/physrevlett.114.236402
47. Rohringer G Spectra of Correlated many-electron Systems: From a One- to a Two-Particle Description. J Electron Spectrosc Relat Phenomena (2020) 241:146804. doi:10.1016/j.elspec.2018.11.003
49. Rohringer G, Toschi A, Katanin A, Held K Critical Properties of the Half-Filled Hubbard Model in Three Dimensions. Phys Rev Lett (2011) 107:256402. doi:10.1103/physrevlett.107.256402
50. Schäfer T, Katanin AA, Held K, Toschi A Phys Rev Lett (2017) 119:046402. doi:10.1103/physrevlett.119.046402
51. Schäfer T, Katanin AA, Kitatani M, Toschi A, Held K Quantum Criticality in the Two-Dimensional Periodic Anderson Model. Phys Rev Lett (2019) 122:227201. doi:10.1103/physrevlett.122.227201
52. Kitatani M, Schäfer T, Aoki H, Held K Phys Rev B (2019) 99:041115(R). doi:10.1103/physrevb.99.041115
53. Mermin ND, Wagner H Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys Rev Lett (1966) 17:1307. doi:10.1103/physrevlett.17.1307
54. Hohenberg PC Existence of Long-Range Order in One and Two Dimensions. Phys Rev (1967) 158:383–6. doi:10.1103/physrev.158.383
55. Gull E, Millis AJ, Lichtenstein AI, Rubtsov AN, Troyer M, Werner P Continuous-time Monte Carlo Methods for Quantum Impurity Models. Rev Mod Phys (2011) 83:349–404. doi:10.1103/revmodphys.83.349
56. Parcollet O, Ferrero M, Ayral T, Hafermann H, Krivenko I, Messio L, et al. TRIQS: A Toolbox for Research on Interacting Quantum Systems. Comput Phys Commun (2015) 196:398–415. doi:10.1016/j.cpc.2015.04.023
57. Fratino L, Charlebois M, Sémon P, Sordi G, Tremblay A-MS Effects of Interaction Strength, Doping, and Frustration on the Antiferromagnetic Phase of the Two-Dimensional Hubbard Model. Phys Rev B (2017) 96:241109. doi:10.1103/physrevb.96.241109
59. Klett M, Wentzell N, Schäfer T, Šimkovic F, Parcollet O, Andergassen S, et al. Phys Rev Res (2020) 2:033476. doi:10.1103/physrevresearch.2.033476
60. Huscroft C, Jarrell M, Maier T, Moukouri S, Tahvildarzadeh AN Pseudogaps in the 2D Hubbard Model. Phys Rev Lett (2001) 86:139–42. doi:10.1103/physrevlett.86.139
61. Macridin A, Jarrell M, Maier T, Kent PRC, D’Azevedo E Phys Rev Lett (2006) 97:036401. doi:10.1103/physrevlett.97.036401
62. Wietek A, He Y-Y, White SR, Georges A, Stoudenmire EM Phys Rev X (2021) 11:031007. doi:10.1103/physrevx.11.031007
63. Chen X, Leblanc JPF, Gull E Simulation of the NMR Response in the Pseudogap Regime of the Cuprates. Nat Commun (2017) 8:14986. doi:10.1038/ncomms14986
64. Rossi R, Šimkovic F, Ferrero M Renormalized Perturbation Theory at Large Expansion Orders. Epl (2020) 132:11001. doi:10.1209/0295-5075/132/11001
65. Wu W, Scheurer MS, Chatterjee S, Sachdev S, Georges A, Ferrero M Phys Rev X (2018) 8:021048. doi:10.1103/physrevx.8.021048
66. Scheurer MS, Chatterjee S, Wu W, Ferrero M, Georges A, Sachdev S Topological Order in the Pseudogap Metal. Proc Natl Acad Sci USA (2018) 115:E3665–E3672. doi:10.1073/pnas.1720580115
67. Huang EW, Mendl CB, Jiang H-C, Moritz B, Devereaux TP Stripe Order from the Perspective of the Hubbard Model. Npj Quant Mater (2018) 3:22. doi:10.1038/s41535-018-0097-0
68. Šimkovic F, Rossi R, Ferrero M The Weak, the Strong and the Long Correlation Regimes of the Two-Dimensional Hubbard Model at Finite Temperature (2021). arXiv:2110.05863 [cond-mat.str-el].
70. Schäfer T, Geles F, Rost D, Rohringer G, Arrigoni E, Held K, et al. Fate of the False Mott-Hubbard Transition in Two Dimensions. Phys Rev B (2015) 91:125109. doi:10.1103/physrevb.91.125109
71. Vilk YM, Tremblay A-MS Destruction of Fermi-Liquid Quasiparticles in Two Dimensions by Critical Fluctuations. Europhys Lett (1996) 33:159–64. doi:10.1209/epl/i1996-00315-2
72. Vilk YM, Tremblay A-MS Non-Perturbative Many-Body Approach to the Hubbard Model and Single-Particle Pseudogap. J Phys France (1997) 7:1309–68. doi:10.1051/jp1:1997135
73. Schäfer T, Toschi A, Held K Dynamical Vertex Approximation for the Two-Dimensional Hubbard Model. J Magnetism Magn Mater (2016) 400:107–11. doi:10.1016/j.jmmm.2015.07.103
74. Šimkovic F, LeBlanc JPF, Kim AJ, Deng Y, Prokof’ev NV, Svistunov BV, et al. Phys Rev Lett (2020) 124:017003.
75. Kim AJ, Šimkovic F, Kozik E Spin and Charge Correlations across the Metal-To-Insulator Crossover in the Half-Filled 2D Hubbard Model. Phys Rev Lett (2020) 124. doi:10.1103/physrevlett.124.117602
76. Hille C, Rohe D, Honerkamp C, Andergassen S Phys Rev Res (2020) 2:033068. doi:10.1103/physrevresearch.2.033068
77. Kyung B, Kancharla SS, Sénéchal D, Tremblay A-MS, Civelli M, Kotliar G Pseudogap Induced by Short-Range Spin Correlations in a Doped Mott Insulator. Phys Rev B (2006) 73:165114. doi:10.1103/physrevb.73.165114
78. Gull E, Parcollet O, Millis AJ Superconductivity and the Pseudogap in the Two-Dimensional Hubbard Model. Phys Rev Lett (2013) 110:216405. doi:10.1103/physrevlett.110.216405
79. Fratino L, Bag S, Camjayi A, Civelli M, Rozenberg MJ Doping-driven Pseudogap-Metal-To-Metal Transition in Correlated Electron Systems (2021). arXiv:2109.06572 [cond-mat.str-el].
80. Krien F, Worm P, Chalupa P, Toschi A, Held K Spin Scattering Turns Complex at strong Coupling: The Key to Pseudogap and Fermi Arcs in the Hubbard Model (2021). arXiv:2107.06529 [cond-mat.str-el].
81. van Loon EGCP, Krien F, Hafermann H, Lichtenstein AI, Katsnelson MI Fermion-boson Vertex within Dynamical Mean-Field Theory. Phys Rev B (2018) 98:205148. doi:10.1103/physrevb.98.205148
Keywords: nickelates, magnetism, pseudogap, hubbard model, dynamical mean-field theory (DMFT), dynamical vertex approximation, cellular dynamical mean field theory
Citation: Klett M, Hansmann P and Schäfer T (2022) Magnetic Properties and Pseudogap Formation in Infinite-Layer Nickelates: Insights From the Single-Band Hubbard Model. Front. Phys. 10:834682. doi: 10.3389/fphy.2022.834682
Received: 13 December 2021; Accepted: 14 January 2022;
Published: 21 February 2022.
Edited by:
Danfeng Li, City University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
Sergio Ciuchi, University of L'Aquila, ItalyCopyright © 2022 Klett, Hansmann and Schäfer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marcel Klett, bS5rbGV0dEBma2YubXBnLmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.