- 1The Niels Bohr Institute, University of Copenhagen, Copenhagen Ø, Denmark
- 2Nordita, KTH Royal Institute of Technology and Stockholm University, Stockholm, Sweden
We review recent developments on nonrelativistic string theory. In flat spacetime, the theory is defined by a two-dimensional relativistic quantum field theory with nonrelativistic global symmetries acting on the worldsheet fields. This theory arises as a self-contained corner of relativistic string theory. It has a string spectrum with a Galilean dispersion relation, and a spacetime S-matrix with nonrelativistic symmetry. This string theory also gives a unitary and ultraviolet complete framework that connects different corners of string theory, including matrix string theory and noncommutative open strings. In recent years, there has been a resurgence of interest in the non-Lorentzian geometries and quantum field theories that arise from nonrelativistic string theory in background fields. In this review, we start with an introduction to the foundations of nonrelativistic string theory in flat spacetime. We then give an overview of recent progress, including the appropriate target-space geometry that nonrelativistic strings couple to. This is known as (torsional) string Newton–Cartan geometry, which is neither Lorentzian nor Riemannian. We also give a review of nonrelativistic open strings and effective field theories living on D-branes. Finally, we discuss applications of nonrelativistic strings to decoupling limits in the context of the AdS/CFT correspondence.
1 Introduction
It has long been known that different string theories are limits of M-theory. While the various corners in this web that are described by perturbative string theories are fairly well understood, we are still far from a complete understanding of nonperturbative regimes in the full M-theory. For example, exploring nonperturbative aspects of string/M-theory is important for understanding the information paradox for black holes, which are fundamentally nonperturbative objects. One nonperturbative approach to M-theory stems from taking a subtle limit of the compactification on a spacelike circle. This notably leads to Matrix theory [1–6], which serves as a powerful tool for understanding the full M-theory in a simple system of D0-branes.
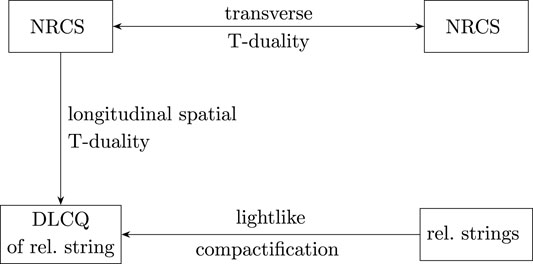
Similarly, by taking an infinite boost limit of the compactification of string theory on a spacelike circle, we are led to the discrete light cone quantization (DLCQ) of strings, which has a Matrix string theory description [7–9]. The infinite boost limit along a spacelike circle can be interpreted as a compactification on a lightlike circle, which leads to nonrelativistic (NR) behavior in the resulting frame (see for example [10]). From a different perspective, it is known that the DLCQ of string theory arises from a T-duality transformation along a compactified spacelike circle in a genuine NR theory [11–13]. This theory is a unitary and ultraviolet (UV) complete string theory described by a two-dimensional quantum field theory (QFT) with a Galilean-like global symmetry in flat spacetime. This NR symmetry is realized by introducing extra one-form worldsheet fields in addition to the ones that are target-space coordinates. The theory has a spectrum of string excitations that satisfy a ‘string’ Galilean-invariant dispersion relation, and hence it has a spacetime S-matrix with NR symmetries. For these reasons, such a theory is referred to as nonrelativistic string theory in the literature [12].1 Via T-duality, NR string theory provides a microscopic definition of string theory in the DLCQ, which is otherwise only defined as a subtle limit. In the formalism of NR string theory, the exotic physics of string/M-theory in the DLCQ with compactification on a lightlike circle is now translated to the more familiar language of NR physics.
There are no massless physical states in NR string theory, and the associated low-energy effective theory is described by a Newton-like theory of gravity, instead of General Relativity [12, 13]. Since it is UV finite, NR string theory provides a UV completion of the associated theory of gravity in the same way that relativistic string theory provides a UV completion of Einstein’s gravity [12–14]. In this sense, NR string theory defines a NR theory of quantum gravity. As such, it provides us with a novel approach towards understanding relativistic quantum gravity, orthogonal and hopefully complementary to the usual paths towards quantum gravity that start from relativistic classical gravity or relativistic QFT.
Recently, there has been renewed interest in NR string theory, based for a large part on understanding the precise notion of its target space geometry, starting with the early work in [15]. The appropriate geometry that NR strings couple to is now known as string Newton–Cartan geometry, which is neither Riemannian nor Lorentzian. The original notion of Newton–Cartan geometry was introduced to geometrize Newtonian gravity, and hence only distinguishes a single direction which is associated to time. In contrast, string Newton–Cartan geometry generalizes this notion to distinguish two directions that are longitudinal to the string.
We start this review in Section 2 by introducing the defining action of NR string theory in flat spacetime. We review how this string theory is embedded in relativistic string theory as a decoupling limit, where parts of the spectrum decouple and the remaining states satisfy a Galilean-invariant dispersion relation. This is achieved by coupling winding relativistic string states to a background Kalb-Ramond field, which is fine tuned such that its energy cancels the string tension. We elaborate on basic ingredients of NR closed and open strings, and review how they are related to relativistic strings in the DLCQ via T-duality. In Section 3, we review recent progress on classical NR strings in curved spacetime. This leads to (torsional) string Newton-Cartan geometry in the target space. In Section 4, we discuss quantum aspects of the sigma model for NR strings in curved spacetime. We will also review different target-space effective theories that arise from imposing the worldsheet Weyl invariance at quantum level. Next, in Section 5, we discuss applications of NR strings to the AdS/CFT correspondence. We focus on a limit of NR string theory that results in sigma models with a NR worldsheet. These theories are related to decoupling limits of AdS/CFT that lead to Spin Matrix theories. In Section 6, we conclude the review and comment on other interesting lines of research in the field.
Finally, it is important to point out that several different limits of string theory that lead to NR symmetries have been considered in the literature. We will always use the term ‘nonrelativistic string theory’ to refer to the theory we mentioned above, but some of the other approaches are sketched in Section 6.
2 What Is Nonrelativistic String Theory?
We start with reviewing the sigma model describing nonrelativistic (NR) string theory in flat spacetime with a NR global symmetry that was first introduced in [12]. We will review its basic ingredients, how it arises from relativistic string theory, and its relation to other corners of string theory.
2.1 Nonrelativistic String Theory in Flat Spacetime
In this review, we work with a Euclidean worldsheet corresponding to a Riemann surface Σ, parametrized by σα = (σ1, σ2), where σ2 is the Euclidean time. We denote the worldsheet metric and the worldsheet zweibein by hαβ and eαa, with a = 1, 2, such that hαβ = δab eαa eβb. The worldsheet fields consist of the scalars Xμ = (X0, … , Xd−1) that map S to a d-dimensional spacetime manifold
where α′ is the Regge slope and h = det hαβ. Transverse indices are lowered using the flat Euclidean metric δA′B′, whereas the longitudinal directions contain a Minkowski structure. We introduced the light-cone coordinates X and
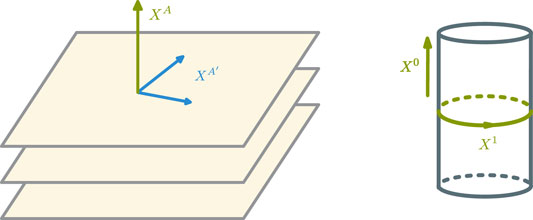
FIGURE 1. A schematic illustration of the longitudinal and transverse fields XA and XA′ in the NR string action. The green arrows represent the two longitudinal directions XA. Each horizontal slice represents the (d − 2)-dimensional transverse directions XA′.
Here, the worldsheet Levi-Civita symbol ϵαβ is defined by ϵ12 = +1. In conformal gauge, we set hαβ = δαβ so that
which is also known as the Gomis–Ooguri string theory [12].
In conformal gauge, the fields λ and
on the longitudinal directions.2 The global symmetry algebra of the NR string action Eq. 2.3 consists of an infinite number of spacetime isometries [19]. This algebra contains two copies of the Witt algebra, which are related to the (anti-)holomorphic reparametrizations associated to the constraints Eq. 2.4. It also includes a Galilei-like boost symmetry that acts on the worldsheet fields Xμ as,
which is referred to as the string Galilei boost symmetry. This is a natural generalization of the Galilei boost symmetry for NR particles: while the Galilei boost acts differently on space and time directions, string Galilei boosts act differently on the directions longitudinal and transverse to the string. Additionally, for the action Eq. 2.3 to be invariant under string Galilei boosts, the one-form fields are required to transform as follows:
This implies that the two-dimensional QFT defined by the action Eq. 2.3 has a NR global symmetry that acts on worldsheet fields. Consequently, as we will see in Section 2.2, this theory has a string spectrum that contains both open and closed string states with a (string-)Galilean-invariant dispersion relation. The BRST structure NR string theory is the same as in relativistic string theory, so its critical dimensions are d = 26 for bosonic string theory and d = 10 for superstring theories [12]. Intriguingly, in order for NR string theory to have a nonempty string spectrum that contains propagating degrees of freedom, it turns out that we have to compactify the longitudinal spatial direction X1 over a circle, as we will see in the following.
2.2 Nonrelativistic String Theory as a Low-Energy Limit
Although NR string theory can be studied from first principles using the action Eq. 2.3, it is useful to understand how this theory is embedded in relativistic string theory. In fact, historically, NR string theory was initially introduced as a zero Regge slope limit of relativistic string theory in a near-critical B-field [11–13]. Our starting point is the sigma model that describes relativistic string theory,
with the following Riemannian (or Lorentzian) metric and Kalb-Ramond background fields:
Here and in the following, we use hats to distinguish variables in relativistic string theory, while variables in NR string theory are unhatted. On this background, the relativistic string action Eq. 2.7 is
This action seems to be singular in the
which reproduces the action Eq. 2.9 upon integrating out the auxiliary fields λ and
We now examine the closed string states. The constant B-field in Eq. 2.7 has a nontrivial effect if the X1 direction is compactified over a circle of radius R. In the relativistic string theory described by Eq. 2.7, closed string states with a nonzero winding number w in X1 and momentum Kμ satisfy the following mass-shell condition (see for example [26]):
together with the level-matching condition
Finiteness of the dispersion relation Eq. 2.12 imposes the condition that w ≠ 0. Therefore, all asymptotic states in the closed string spectrum necessarily carry a nonzero string winding number along the compact X1 direction [12, 14]. Note that the Kaluza-Klein momentum number n does not show up explicitly in the dispersion relation, but only enters via the level-matching condition.
As is evident from the rewriting Eq. 2.9 of relativistic string theory, the free theory Eq. 2.3 that describes NR string theory can be deformed towards relativistic string theory by reintroducing the operator
When U0 ≠ 0, there are asymptotic states in the zero-winding sector with w = 0 that satisfy the relativistic dispersion relation,
In contrast, as we have seen earlier, only states corresponding to strings that have nonzero winding around the longitudinal target space circle X1 survive in the NR string theory limit
2.3 Nonrelativistic Closed Strings
Having reviewed how NR string theory arises as a zero Regge slope limit in string theory, we return to the defining action Eq. 2.3 for NR string theory, focusing on the sector of nonrelativistic closed string (NRCS) theory. We already learned from the α′ → 0 limit that, in order to have a nonempty closed string spectrum, we have to compactify the longitudinal spatial direction X1 over a spatial circle of radius R. We will now see that the Galilean-invariant dispersion relation Eq. 2.12 can be derived directly from the NR string action Eq. 2.3, without performing any limits, by constructing the BRST-invariant vertex operators in NRCS. For this, we first discuss a physical interpretation of the λ and
We first consider a T-duality transformation along the compact longitudinal target space direction X1. For this, we introduce the parent action
Integrating out Y1 imposes
This is the action of relativistic string theory in a flat background, with spatial directions XA′ and lightlike directions X0 and Y1. However, since it is dual to X1, which is a circle with radius R, the lightlike direction Y1 is a circle with effective radius α′/R. Therefore, the closed string described by the action Eq. 2.16 describes the DLCQ of relativistic string theory [12, 14]. As such, NRCS provides a NR covariant definition of DLCQ in relativistic string theory, which is normally defined using a subtle limit of the compactification of relativistic strings on a spacelike circle [4–6].
A T-duality transformation of NRCS along a compact transverse direction acts in the same way as in relativistic string theory, resulting in NRCS on a background with the corresponding dual compact transverse direction. The complete curved-spacetime Buscher rules can be found in [17, 26, 27], see also [28–32] for related works. These T-duality relations of NRCS are displayed in Figure 2.
In addition, we consider a T-duality transformation along a lightlike longitudinal direction in the action Eq. 2.16 that describes the DLCQ of relativistic string theory. To do this, we Wick rotate and compactify the X0 direction in the original action Eq. 2.3. Following the same procedure as before, we start from the action Eq. 2.16 and exchange the X0 direction for a dual Y0, which leads to
where Y = Y0 + Y1 and
These equations map the NRCS one-forms λ and
While the relation Eq. 2.18 is technically only valid for compact X0, we can still use λ = −∂Y and
The closed string tachyon vertex operator then takes the form
where Q0 = 0 and Q1 = − 2wR/α′ parametrizes the longitudinal winding. We have omitted a cocycle factor, which is needed for the single-valuedness of the OPEs and contributes a sign to string amplitudes. Higher-order vertex operators are constructed from the tachyon vertex operator Eq. 2.20 by dressing it up with derivatives of Xμ and YA. The BRST invariance of such vertex operators then leads to the dispersion relation Eq. 2.12 [12, 34].
The string amplitudes between winding closed strings represented by such vertex operators have been considered in [12]. The tree-level string amplitudes have poles corresponding to excited closed string states carrying nonzero winding. There is no graviton in the spectrum of NRCS. However, in the special case where the winding number is not exchanged among the asymptotic states, the amplitudes gains a contribution from exchanging off-shell states in the zero winding sector. The leading long-range contribution is proportional to 1/(KA′KA′). These zero-winding states become of measure zero in the asymptotic limit, and therefore only arise as intermediate states [14]. These intermediate states give rise to a Newton-like potential after a Fourier transform, and induce an instantaneous gravitational force between winding strings.
As in relativistic string theory, NRCS has a perturbative expansion with respect to the genera of the worldsheet Riemann surfaces. However, at loop level, there are nontrivial constraints that restrict the moduli space to a lower dimensional manifold [12]. This is because the one-form fields (λ,
Here, m denotes the winding number in X0. From Eq. 2.21, it is manifest that the integral over the fundamental domain for the moduli space of the torus in the evaluation of one-loop amplitudes is now localized to be a sum over discrete points. The fact that the one-loop moduli space for NR strings lies within the fundamental domain for relativistic string theory, implies that the NR string free energy is finite. The constraint Eq. 2.21 is also generalized to higher-loop and general N-point amplitudes [12], in such a way that holomorphic maps from the worldsheet to the target space exist. Such localization theorems in the moduli space suggest that the computation of NR string amplitudes may simplify significantly compared to the case in relativistic string theory.6 The free energy and N-point amplitudes at one-loop order match the ones in the DLCQ of string theory [14, 38]7.
2.4 Nonrelativistic and Noncommutative Open Strings
We now consider open strings, whose worldsheet Σ has a boundary ∂Σ. At tree level, Σ is a strip with σ1 ∈ [0, π] and the Euclidean time
First, consider open strings that satisfy the Dirichlet boundary condition δX1 = 0 on ∂Σ, by anchoring the ends of an open string on D(d − 2)-branes transverse to X1. In this case, the variation of the action Eq. 2.3 with respect to XA vanishes only if
where w is the fractional winding number of open strings stretched between transverse D-branes located along X1. Therefore, imposing Dirichlet boundary conditions in X1 defines the NROS sector. On the D-brane, the global symmetry of the sigma model is broken down to be the Bargmann symmetry. In the zero winding sector, the effective field theory living on a stack of n coinciding D-branes is Galilean Yang—Mills theory [33],
with D0 and DA′ are covariant derivatives with respect to the U(n) gauge group. The electric and magnetic field strengths EA′ and FA′B′ are associated to the gauge fields A0 and AA′ on the D-brane. The scalar field N is in the adjoint representation of U(n), and perturbs around the solitonic D(d − 2)-brane. In the U(1) case, this gives rise to Galilean electrodynamics (GED) [44–46]9.
Next, consider open strings that satisfy the Neumann boundary condition ∂X1/∂σ1 = 0 on ∂Σ. In this case, open strings reside on spacetime filling D-branes. For the theory to be well-defined, a nonzero electric field strength E (or a nonzero B-field) is introduced. The resulting theory has a relativistic string spectrum and noncommutativity between the longitudinal space and time directions, with
Nonrelativistic and noncommutative open strings are related via T-duality [51], as illustrated in Figure 3. In NROS, the geometry of the longitudinal sector in the target space is taken to be a spacetime cylinder, wrapping around the compactified longitudinal spatial direction X1. Performing a T-duality transformation along X1 in NROS leads to the DLCQ of relativistic open string theory on spacetime filling D-branes. To make the connection to NCOS, one needs to introduce a twist in the compactification of X1 by shifting one end of the longitudinal cylinder along the time direction, before gluing back. This shift does not change the nature of the T-duality transformation and still leads to the DLCQ of relativistic open strings, unless the shift equals the circumference of the longitudinal circle. In the latter case, the T-dual theory is NCOS on a spacetime-filling brane and with a compact longitudinal lightlike circle. The background electric field in NCOS corresponds to a rescaling factor of the X1 circle in NROS. It is also interesting to consider a T-duality transformation along X1 in NCOS. In the T-dual frame, there arises relativistic open string theory on a D(d − 2)-brane in the DLCQ description. Such a D(d − 2)-brane is infinitely boosted along a spatial circle [23]. Generalizations of the above T-duality transformations in arbitrary background fields are studied in [51].
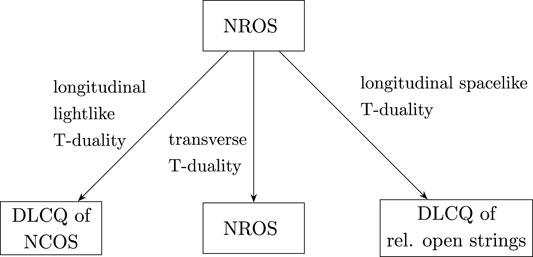
FIGURE 3. T-duality relations for NR open string theory (NROS). The transverse T-duality swaps Dirichlet and Neumann boundary conditions in the usual way.
3 Nonrelativistic Strings in Curved Spacetime
After reviewing the basic ingredients of NR string theory in flat spacetime, we now consider generalizations to curved spacetime. In the following, we will restrict to string states with zero winding along the compact longitudinal direction. Such states are not part of the physical spectrum, but they serve to mediate the instantaneous forces between the physical asymptotic states with nonzero winding. As a result, the low-energy effective theory that arises from the nonwinding sectors of closed and open strings that we consider in the following play a similar role to the instantaneous force in Newtonian gravity or the Coulomb force in electrostatics. Exponentiating the vertex operators associated with such zero winding states in the path integral gives rise to various background fields. These background fields are functional couplings in the nonlinear sigma model that generalizes the free worldsheet theory Eq. 2.1 by including arbitrary marginal deformations that are conformally invariant.
We have seen in Section 2.2 that the marginal operator
The remaining background fields give rise to a general framework for studying the appropriate spacetime geometry coupled to NR string theory. The resulting target space geometry is known as torsional string Newton—Cartan (TSNC) geometry [31, 52–54], since it generically allows for nonzero torsion. In contrast to Newton–Cartan geometry, which is related to particle probes, string Newton–Cartan geometry contains not one but two distinguished directions that are longitudinal to the string. In the free worldsheet action Eq. 2.1, these directions are represented by the longitudinal lightlike coordinates X and
3.1 Strings in Torsional String Newton—Cartan Geometry
The curved spacetime generalization of the free NR string theory action Eq. 2.1 is obtained by turning on all allowed marginal local interactions in the sigma model, which leads to the classically-conformal action [16, 17] (see also [34] for the inclusion of the
Here, hαβ is the worldsheet metric, R(h) is its Ricci scalar, and λ and
The background fields in this action consist of the symmetric and antisymmetric two-tensors Sμν and Aμν, the one-forms τμ and
One of the remarkable features of the resulting target-space geometry is that it contains the one-forms
In addition, the worldsheet couplings contain the symmetric and antisymmetric two-tensors Sμν and Aμν. However, the action Eq. 3.1 is invariant under a set of Stückelberg-type transformations [17],
together with appropriate shifts of the Lagrange multipliers λ and
We can fix this Stückelberg symmetry by requiring Sμν to be fully transverse with respect to the longitudinal directions. For this, we introduce a set of inverse vielbeine
Here, Mμν is still an arbitrary antisymmetric tensor, which generically contains both transverse and longitudinal components, but Eμν is now purely transverse. For this reason, we have introduced the transverse vielbeine
The resulting geometry is referred to as torsional string Newton—Cartan (TSNC) geometry [31, 52–54]. In contrast to the usual Lorentzian geometry of general relativity, nonzero ‘intrinsic’ torsion related to dτA arises naturally in these geometries for connections that are compatible with the NR geometric data. Additionally, TSNC geometry has a codimension-two foliation structure, with leaves being the transverse sector. See Figure 4 for an illustration of such a foliation structure. For this to be the case, the Frobenius integrability condition needs to hold, which in terms of the target-space one-forms τA = τμA dxμ is
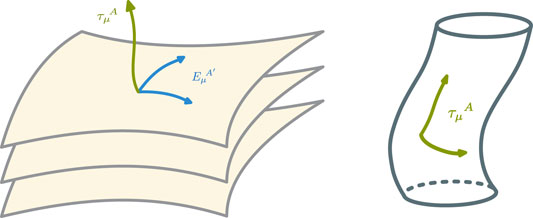
FIGURE 4. A schematic illustration of a stringy generalization of Newton–Cartan geometry. The green arrows represent the two longitudinal directions along the worldsheet, whose geometry is encoded in the vielbein fields τμA. Each horizontal slice represents the (d − 2)-dimensional transverse directions, parametrized by the vielbein fields EμA′.
This generalizes ‘regular’ Newton–Cartan geometry with a single clock one-form
As we will see later on, such foliation conditions play a role in the quantum consistency of the worldsheet theory10. More generally, conditions on dτA (which is related to torsion) are sometimes also referred to as torsion conditions in the literature. In particular, introducing a longitudinal spin connection
has been proposed [15], which implies in particular that the foliation condition Eq. 3.6 holds.
After fixing the Stückelberg symmetry as in Eq. 3.4, the sigma model action Eq. 3.1 that describes NR strings becomes [31].
In the flat limit with
Similar to how Lorentzian geometry can be seen as the gauging of the Poincaré algebra, we can use the resulting gauge symmetries to define the TSNC target space geometry. The vielbein fields τμA and EμA′ can be seen as gauge fields associated with the longitudinal translations HA and transverse translations PA′. The longitudinal Lorentz boost JAB = ϵABJ and the transverse rotations JA′B′ act on τμA and EμA′ in the standard way. In particular, the string Galilei boost, with generators GAB′ and Lie group parameters
In addition, the string Galilei boost symmetry acts nontrivially on λ and
The target-space fields also transform under diffeomorphisms as usual, and the antisymmetric field Mμν transforms under a one-form gauge symmetry,
Finally, the sigma model Eq. 3.9 is invariant under a dilatation symmetry [17, 53] that rescales the longitudinal vielbeine
In the absence of the dilaton field, the Nambu-Goto form of the action can be obtained by integrating out the worldsheet zweibein eαa in the path integral, which leads to [15].
Here, ταβ = ∂αXμ ∂βXντμν is the pullback of τμν = τμA τνB ηAB, corresponding to the induced metric on the worldsheet, and ταβ is its inverse.
An alternative formulation of the Polyakov form of the action Eq. 3.9 can be obtained by splitting off the longitudinal components in Mμν in terms of an additional gauge field mμA,
In doing so, we have absorbed the boost transformations in mμA, so that the remaining antisymmetric tensor Bμν is invariant under boosts. This results in the action [17].
Here, we introduced the combination
3.2 Torsional String Newton—Cartan Geometry From a Limit
In Section 2.2, we reviewed how NR string theory in flat spacetime arises as a zero Regge slope limit of relativistic string theory. This limiting procedure can be directly generalized to strings propagating in arbitrary background fields. For this, we start from the sigma model for relativistic string theory,
Next, we introduce a set of longitudinal vielbeine τμA. We then parametrize the relativistic Lorentzian background metric
where
where we have identified U = 1/c2. We then promote U to be a functional coupling depending on Xμ. This corresponds precisely to the action Eq. 3.1 with general marginal couplings that we introduced at the beginning of this section. As a result, we see that sending c → ∞ in the relativistic theory Eq. 3.16 using the parametrization Eq. 3.17 of the background fields removes the
While we are able to make sense of the c → ∞ limit on the worldsheet, this limit seems singular from the perspective of the relativistic NS-NS geometric data
3.2.1 Algebra Gauging
From an algebraic perspective, Lorentzian geometry can be obtained from a gauging of the Poincaré algebra. This gauging associates the Lorentzian vielbeine
The Lorentzian tangent space metric
While the
To implement the NR limit, we split the frame indices
The transverse vielbeine correspond to EμA′ and πμA′ = ΠμA′. Using the parametrizations in Eq. 3.20, this results in the following expansions,11
Here, we recover the transverse metric Eμν = δA′B′ EμA′ EνB′ and the antisymmetric tensor Mμν that were introduced in Eq. 3.4. The latter is now parametrized as
In the c → ∞ limit, the redefinition Eq. 3.21 corresponds to an
3.2.2 Double Field Theory
An alternative approach to parametrizing non-Lorentzian geometries comes from double field theory (DFT) [35, 36, 57]. This formalism was originally intended to provide a manifestly T-duality covariant description of the geometry that relativistic strings couple to (see for example [58] for a review). In relativistic string theory, the DFT formalism unifies the Lorentzian metric and the Kalb–Ramond field into a single generalized metric,
The indices M, N are 2d-dimensional and they are raised and lowered using the O(d, d) metric
The doubled coordinates
Remarkably, the particular combinations of the Lorentzian metric and Kalb–Ramond field that enter in the parametrization Eq. 3.24 combine in such a way that its c → ∞ limit using the expansion (Eq. 3.22) is nonsingular. In this limit, we obtain [36, 60].
Clearly, this generalized metric no longer corresponds to a Lorentzian metric, since its top left block Eμν is now degenerate. However, if one considers the doubled description of the target space geometry as fundamental, one can take Eq. 3.26 as the defining relations of the geometry. From this perspective, the parametrization Eq. 3.27 in terms of TSNC variables therefore constitutes a valid generalized metric in the doubled actions, since these defining relations still hold, even though the generalized metric can no longer be related to relativistic NS-NS geometry.
The most general solution of the defining Eq. 3.26 for
3.3 Torsional String Newton—Cartan Geometry From Null Reduction
NR string actions can also be obtained from a null reduction in a relativistic background with a lightlike isometry [28]. Starting from a d-dimensional Lorentzian manifold with a lightlike isometry, we choose adapted coordinates xμ = (u, xi) such that the lightlike isometry is generated by ∂u. Then we can write the associated metric as
Together with u, the d − 1 coordinates xi form a chart of the target-space manifold. Additionally, we decompose the Kalb–Ramond field in the components bi = Bui and Bij. In such a background, the relativistic Polyakov action is given bry
As we have discussed in Section 3.1, Xu and Xi are worldsheet functions that parametrize the embedding of the worldsheet in terms of the target space coordinates u and xi. Pullbacks such as τα = ∂αXiτi are constructed using the embedding coordinates Xi. To implement a null reduction, we also require that the momentum of the string in the u-direction is conserved off shell. For this, we introduce a Lagrange multiplier Aα that imposes a relation between the momentum current
In this action, the equations of motion for η imply that the one-form Aα dσα is closed. As a result, we can recover the original lightlike direction through Aα = ∂αXu and we see that our action is equivalent to the relativistic string action Eq. 3.29. Alternatively, we can interpret η itself as an embedding coordinate that is dual to Xu. We work in a sector of fixed total momentum in the u-direction, and interpret η as a compact target-space direction along which the string has a fixed winding mode. Then the constraint imposed by the Lagrange multipliers Aα imply that the total momentum of the string in the u-direction is mapped to the string winding in η. For this reason, the dual NR string winds exactly once in η, and the periodicity of this direction is determined by the original lightlike momentum in Xu.
The action Eq. 3.30 describes strings coupled to a torsional Newton–Cartan geometry, described by the fields τi, Eij, together with the background fields mi, Bij and bi as well as the η direction along which the string winds. It is equivalent to the worldsheet action Eq. 3.9 introduced above after the following identifications [30, 31, 52].
The last line defines the antisymmetric tensor Mμν, where xi and v form a chart of the dual target space manifold. Similarly, the symmetric tensor Eij is extended to Eμν by setting Evv = Eiv = 0. The Lagrange multipliers Aα are related to the one-forms λ and
In the above, we have considered a single lightlike momentum sector of strings in the relativistic background Eq. 3.28. The lightlike isometry in the relativistic background corresponds to an isometry of the spatial longitudinal direction v in the dual TSNC geometry, and the momentum mode of the string along u is translated to a single winding mode of the nonrelativistic string along v. For related constructions of nonrelativistic particle or field theory actions through null reduction, the lightlike direction u is typically taken to be noncompact. On the other hand, the T-duality relation between NR strings and the DLCQ of relativistic strings that was discussed in Section 2.3 would require that u is a compact lightlike direction.
4 Effective Field Theories From Nonrelativistic Strings
Next, we review the RG analysis of the sigma model Eq. 3.9 where the classical value for the background field associated with the
We discuss different proposals for symmetry algebras that have been used to construct renormalizable interacting worldsheet QFTs that describe NR strings in background fields. Imposing Weyl invariance at the quantum level, the vanishing beta-functionals of background fields determine the spacetime equations of motion that govern the dynamics of the target-space TSNC geometry. This is analogous to how the (super)gravity equations of motion arise in relativistic string theory. With such worldsheet symmetries, NR string theory can be studied in a self-contained way, without referring to the full relativistic string theory. We also comment on recent progress on supersymmetrizations of NR string theory and its relation to the modified symmetry algebras. Finally, we review recent progress on the RG calculation of the worldsheet theory for NR open strings. This analysis of conformal anomalies gives the NR analog of Dirac-Born-Infeld (DBI) action that describes the low energy dynamics of D-branes. The distinction between different NR limits considered in the literature that lead to extended p-brane objects in NR string/M-theory will also be discussed.
4.1 Beta Functions of the Worldsheet Theory
After reviewing classical aspects of NR string sigma models and the associated target-space geometry, we now investigate the quantum behavior of the worldsheet QFT. We first approach this by taking a limit of the beta functionals of relativistic string theory. Next, we review different constructions of self-contained NR string theories in curved spacetime that are defined by renormalizable sigma models.
4.1.1 Target-Space Gravity From a Limit
The self-consistency of string theory requires the classical worldsheet Weyl invariance to be preserved at the quantum level. This sets all beta-functionals of the background fields in the string sigma model to zero. The vanishing beta-functionals determine the target-space equations of motion that govern the dynamics of the target-space geometry. In relativistic string theory, this procedure leads to the spacetime supergravity equations of motion.
We already learned that the bosonic string sigma model Eq. 3.16 describes strings propagating in NR geometries only if U = 0, corresponding to the limit c = U−1/2 → ∞. This limit has been applied to the spacetime equations of motion determined by the vanishing beta-functionals [53]. It is shown that the dynamics of the NR target space arises from the c → ∞ limit of the NS-NS gravity in relativistic string theory. At the lowest order in α′, this defines the so-called dilatation-invariant string Newton-Cartan gravity [53]. The associated target-space gravity action has been studied in [53] and also from a DFT point of view in [54]. Since these results are rather involved, we will only show them in a simplified model where the torsion is set to zero, which is discussed in Section 4.1.3.
The supersymmetric generalization of the parametrization Eq. 3.17 has been studied in various works. See [16, 68–70] for examples, and we will follow closely the recent paper [70] for the state of the art. In addition to the reparametrization of the metric, Kalb-Ramond, and dilaton field in Eq. 3.17, one also needs to reparametrize the fermionic fields, including the gravitino
where ψ± and λ± are worldsheet chirality projected spinors. The c → ∞ limit is nonsingular if the following geometric constraints hold:
One can choose whether these constraints are imposed on dτ or
4.1.2 Quantum Corrections and Renormalizability
It is also insightful to apply the U = c−2 → 0 limit to the beta-functionals of the sigma model Eq. 3.16 that describes relativistic strings propagating in Lorentzian geometries, before committing to the conformal fixed point [34]. This leads to the RG structure of the sigma model action Eq. 3.9, evaluated around the physical value U = 0. Moreover, the Weyl invariance of sigma models in torsional Newton–Cartan backgrounds that we discussed in Section 3.3 has also been studied directly using the worldsheet QFT in [71]. It is shown in [18, 71] that the
Here, we defined
At the lowest order in α′ Eqs. 4.3 and 4.4 lead to the geometric constraints
These constraints are the lightlike components of the foliation condition Eq. 3.7 and coincide with the first condition in Eq. 4.2 obtained from requiring the supersymmetry transformations to be finite. The resulting NR gravity is therefore a zero U solution to the (super)gravity equations of motion in relativistic string theory.
There are two perspectives on how Eq. 4.4 should be treated [34]. In the first perspective [28, 30, 31, 53, 71], we solve Eq. 4.4 together with other target-space equations of motion perturbatively, order by order in α′. This defines target-space non-Lorentzian gravity with higher derivative corrections, but with the potential problem that solutions to the target-space equations of motion at lower orders in α′ might not be extendable to higher orders without introducing a nonzero U. In the second perspective [17, 18, 26, 72], we are interested in identifying the conditions under which quantum corrections to
4.1.3 Extensions of String Galilei Symmetries
In the following, we review several proposals for extended worldsheet global symmetry algebras, whose realization on the sigma model Eq. 3.15 results in different constraints on the longitudinal vielbein field τμA that restrict the torsion of the TSNC geometry. Once such constraints are imposed, the sigma model Eq. 3.9 is protected against any
In Section 3.1, we showed that the sigma model Eq. 3.9 is invariant under the symmetry transformations that form the string Galilei algebra (Eq. 3.11), which arises as a contraction of the Poincaré algebra. Recall that the string Galilei algebra consists of generators associated with longitudinal and transverse translations that we refer to as HA and PA′ , respectively, as well as the string Galilei boosts GAA′ . Notably, PA′ and GAA′ commute in Eq. 3.11.
In analogy to how the Galilei algebra can be extended to the Bargmann algebra in the particle case, it is shown in [15, 56, 73] that the string Galilei algebra can be extended to the string Bargmann algebra by introducing a generator ZA such that
This new generator ZA is the stringy version of the central charge corresponding to the conserved particle number in the Bargmann algebra. In contrast, because ZA carries a longitudinal index and hence does not commute with the longitudinal Lorentz boost, ZA is noncentral in the string Bargmann algebra. One way to close the algebra is by including an additional generator Y that arises from the commutator of GAA′ and GBB′. This second extension will not play any important role in the following discussions, and we refer the readers to [26, 30] for discussions on the Y extension and its generalizations.12
The target-space gauge transformations corresponding to the string Bargmann algebra are most naturally realized on the variables τμA, EμA′, mμA and Bμν in the action Eq. 3.15. In terms of these variables, the boost transformations remain the same as in Eq. 3.14, and the ZA symmetry only acts nontrivially on mμA,
where we have used σA to denote the parameter for ZA gauge transformations.13 Additionally, the derivative Dμ is covariant with respect to the spin connection ΩμAB associated with the longitudinal Lorentz boost. Recall that without imposing the condition
Requiring that the NR string sigma model is invariant under the background field transformations generated by the string Bargmann symmetries reproduces the action Eq. 3.15, which we repeat below for convenience:
Here,
While part of the components in Eq. 4.9 can be used to solve for the longitudinal spin connection ΩμAB, the rest give rise to the geometric constraints,
The first condition in Eq. 4.10 coincides with the integrability condition Eq. 3.7 in the codimension-two foliation structure, which sets the torsion associated to dτA to zero. The target-space geometry coupled to NR strings described by the worldsheet action Eq. 4.8 with string Bargmann symmetries is referred to as string Newton-Cartan (SNC) geometry, which has zero torsion [15]. As desired, it is shown in [72] that this action does not receive quantum correction to the
The beta-functionals of the background fields Hμν, Bμν, and Φ in Eq. 4.8 have been studied in [18, 72], which we review below. In the path integral, the Stückelberg symmetries Eq. 3.3 that mix Hμν and Bμν are recast in the form of Ward identities. The physical beta-functionals are therefore manifestly invariant under the Stückelberg symmetries in Eq. 3.3. It has been proven in [72] that there is a nonrenormalization theorem for τμA. We can therefore define the beta-functionals with respect to the remaining variables Eμν, Mμν, and Φ that enter in the action Eq. 3.9 where the Stückelberg symmetries are fixed,
Here, t is the renormalization ‘time’ and et defines the renormalization scale. In terms of the variables Hμν and Bμν, we have
The subscripts A and A′ of the beta-functionals denote contractions with the inverse vielbeine
A compatible connection can be constructed using these boost-invariant objects (but not uniquely, see for example [26]),
Using this connection, the Riemann curvature
Where
We denoted the Kalb-Ramond field strength as
Here, G = det(τμA, EμA′). These one-loop beta-functionals have been derived first from analyzing the OPEs in [18], and they were later corroborated by the background field method in [72]. The same result was also derived as a NR limit of the relativistic beta-functionals in [26]. The overlap of these results with the beta-functionals derived in [71] for the sigma models in torsional Newton–Cartan geometry from Section 3.3 is confirmed using double field theory methods in [54].
In Section 3.1, we noted that the sigma model Eq. 4.8 is also invariant under a dilatational symmetry, namely,
Nevertheless, this dilatational symmetry is not preserved by the zero-torsion constraint Eq. 4.9, unless ∂A′Δ = 0 [26]. Intriguingly, one can still obtain a renormalizable worldsheet QFT that is compatible with the dilatational symmetry if one breaks half of the ZA symmetry [34]. In order to preserve the longitudinal Lorentz symmetry, the only possibility is to break a lightlike component of the ZA symmetry. We choose to break
where σ is the Lie group parameter associated with the Z generator. Requiring that Eq. 4.8 is invariant under the Z symmetry leads us to the condition
This condition leads to the geometric constraints
Here,
This halved ZA symmetry leads to attractive features. First, it is shown in [34] that the geometric constraints Eq. 4.21 are sufficient for eliminating at all loops the quantum corrections that generate the
4.2 Nonrelativistic Open Strings and Dirac-Born-Infeld Action
We already learned in Section 2.4 that, in flat spacetime, open strings ending on a D(d − 2)-brane that is transverse to the longitudinal spatial direction X1 enjoy a Galilean-invariant dispersion relation. In a curved spacetime, we consider the boundary condition
Varying λ and
The beta-functionals of N and Ai have been derived in [33] using the covariant background field method. Imposing Weyl invariance at the quantum level requires that these beta-functionals vanish. These are target-space equations that arise from a D(d − 2)-brane action, which has a straightforward generalization to Dp-branes,
where F = dA is the field strength on the Dp-brane. A related worldvolume action for D-branes also appears in [75, 76], where the embedding spacetime is taken to be torsional Newton–Cartan spacetime extended with a periodic space direction, as discussed in Section 3.3. In the flat limit, at the quadratic order in the field strength Fμν, the Dp-brane action Eq. 4.23 in the broken phase reproduces Galilean electrodynamics, which is the U(1) case of Eq. 2.23, with the scalar N receiving the natural interpretation as a NG boson.
The DBI-like action Eq. 4.23 continues to hold in the case that the D-brane extends in the compactified longitudinal X1 direction. In the flat limit, open strings residing on such a D-brane configuration satisfy the Neumann boundary condition in the X1 circle. As reviewed in Section 2.4, such open strings are in the NCOS sector and enjoy a relativistic dispersion relation. It is shown in [51] that dualizing the DBI-like action Eq. 4.23 that describes a D-brane localized in a longitudinal lightlike circle gives rise to the DLCQ of NCOS. This is in contrast to the fact that the T-dual of a NR Dp-brane localized in a longitudinal spatial circle is T-dual to relativistic DBI action in the DLCQ [51].
4.3 Generalized Nonrelativistic p-branes
In [33], it is shown that the Galilean DBI action Eq. 4.23 arises as the c → ∞ limit of the relativistic DBI action,
where the background fields are parametrized as in Eq. 3.17, and
Instead of the ‘stringy’ parametrization Eq. 3.17, we now consider a ‘p-brane’ parametrization,
Here, u = 0, … , p, and γμu are the vielbein fields that encode the geometry of the induced (p + 1)-dimensional foliation in spacetime. In the limit c → ∞, the p-brane action Eq. 4.25 gives rise to a nonsingular low-energy action,
where γαβ = ∂αXμ ∂βXν γμν and γ = det γαβ. In the case of p = 1, the p-brane action Eq. 4.27 is the Nambu-Goto action Eq. 3.13 of NR string theory. For the Polyakov description of the p-brane limit, see, e.g., [68, 69], where κ-symmetries of the p-brane actions are also discussed. Also see [16] for discussions on κ-symmetry in the Green-Schwarz formalism of NR string theory in AdS background.
The p-brane limit of relativistic p-branes differs in nature from the stringy limit of relativistic DBI action. The NR DBI action Eq. 4.23 that arises as the stringy limit describes Dp-branes coupled to SNC geometry, equipped with a two-dimensional foliation structure. In contrast, the NR p-branes described by Eq. 4.27 are coupled to the so-called p-brane Newton-Cartan geometry, equipped with a (p + 1)-dimensional foliation structure. The two-brane limit that induces a three-dimensional foliation structure has been applied to (super) M2-branes [68, 80]. Also see [81, 82] for a theory of light Open Membranes (OM) on an M5-brane near a critical three-form field strength. This OM theory arises in the two-brane limit of M-theory and describes five-dimensional NCOS at strong coupling. Such an (open) membrane limit of M2-and M5-brane actions has been studied in [83]. Moreover, the two-brane limit of the bosonic sector of eleven-dimensional supergravity has recently been investigated in [67]. S-dualities of light (super) Dp-branes that arise from performing the general p-brane limits in relativistic string/M-theory are studied in [12, 84].
5 Nonrelativistic Holographic Dualities
As was mentioned in Section 1, one of the hopes in studying NR string theory is that it will allow us to obtain a better understanding of previously inaccessible corners of relativistic string theory. We will now briefly discuss particular applications of these ideas in the context of the AdS/CFT correspondence. Other directions will be mentioned in Section 6.
Specifically, we focus on a decoupling limit that was originally introduced in the context of
5.1 Decoupling Limits of the AdS/CFT Correspondence
In the strongest form of the AdS/CFT correspondence [88], four-dimensional
Here, Δ is the anomalous dimension of the corresponding operator, and Q is a particular combination of the R-charge and S3 Cartan generators (J1, J2, J3) and (S1, S2), which is usually taken to be equal to J1. Other choices of Q would lead to different coordinates on the pp-wave. In this limit, the field theory spectrum can be matched perturbatively to the spectrum obtained from quantizing the string on the pp-wave background.
NR string theory can be viewed as another example where a decoupled sector of string theory is analysed in a self-contained way. In this case, the decoupled sector only contains winding string states that satisfy a Galilean-invariant dispersion relation. As a first example, an NR limit of string theory on AdS5 × S5 has been studied in [16], where it was shown to be equivalent to a supersymmetric two-dimensional sigma model of free particles propagating on AdS2. The T-dual of this NR string theory leads to relativistic strings on a time-dependent pp-wave with a compactified lightlike circle and hence DLCQ. This NR string theory was subsequently given a dual interpretation in terms of a conformal quantum mechanics theory [90]. See also [91, 92] for more recent work in this direction.
Another decoupling limit that allows us to probe particular subsectors of
Here, Q is again a particular combination of S3 and R-charge Cartan generators. Fields in SMT have ‘matrix’ indices that are inherited from the SU(N) gauge symmetry of the parent
The field theory SMT limit Eq. 5.2 has been mapped to the relativistic string sigma model on AdS5 × S5 [28]. It results in a NR string similar to the ones we discussed before, but in this case not only the target space geometry but also the worldsheet geometry is nonrelativistic. As a result, instead of the usual Virasoro symmetry, this Spin Matrix string theory has a Galilean conformal algebra (GCA) of reparametrization symmetries on the worldsheet [30]. Its target-space geometry, known as U(1)-Galilean geometry, is closely related to the TSNC geometry that we have discussed in Section 3.2, and we will discuss its local symmetries below.
In the following, we give a brief review of the construction of the sigma model for SMT strings from the sigma model for NR strings in general backgrounds. Additionally, we show how the U(1)-Galilean geometries associated to particular BPS bounds can be constructed from an appropriate limit of the AdS geometry [28, 30, 94]. We also review how, after gauge fixing the GCA worldsheet symmetry, the classical string sigma model reproduces known effective continuum spin chain actions obtained from field theory. Finally, we discuss their interaction with the Penrose limits mentioned above.
5.2 Spin Matrix Theory Limit of Nonrelativistic String Theory
We first consider the tensionless limit of the NR string sigma model Eq. 3.9 that was introduced in [28, 30]. This limit results in a NR string with a NR worldsheet structure. For simplicity, we will set the dilaton to zero in the following discussion. Additionally, following the discussion in Section 3.3, we assume the existence of a lightlike Killing vector in the original Lorentzian target space, which results in a TSNC geometry with a longitudinal spatial isometry. Correspondingly, we split the embedding coordinates as Xμ = (Xi, η), where the worldsheet scalar η parametrizes the longitudinal spatial isometry, and i is a (d − 1)-dimensional index that contains a timelike component. Here, following the literature, we now consider a Lorentzian worldsheet. Using the parametrization Eq. 3.31 together with bi = 0 and Mij = 0, this leads to the worldsheet action
We have introduced a set of worldsheet vielbeine eαa with a = 0, 1 such that hαβ = ηab eαaeβb. As discussed in Section 3.3, this sigma model describes strings propagating in a TNC geometry that is extended with a spatial circle direction parametrized by η. The TNC geometry is described by the clock one-form τi, the transverse vielbeine EiA′, and the U(1) gauge field mi corresponding to the remaining antisymmetric couplings.
Next, we perform a zero tension limit of the sigma model Eq. 5.3. This is implemented by sending c → ∞ after taking the following rescalings:
while EiA′ and mi remain unchanged. In this limit, the action Eq. 5.3 becomes
Similar to the previous action, this sigma model is invariant under global worldsheet transformations corresponding to Galilean boosts ΛA′ and U(1) symmetries σ,
which correspond to gauge symmetries in the target space geometry. Unlike in TNC geometry, the U(1) gauge field mi field no longer transforms under Galilei boosts after the limit, which is why the resulting geometry is referred to as U(1)-Galilean geometry. We can also clearly see that the worldsheet vielbeine eα0 and
where f parametrizes Weyl transformations and g corresponds to local Galilei boosts. We can choose flat gauge on the worldsheet to fix these local symmetries, up to the residual gauge transformations
which correspond to a Galilei conformal algebra. Classically, its Lie brackets are given by
This algebra corresponds to a contraction of the usual two Virasoro algebras.
5.3 Spin Matrix Strings From a Limit on AdS5 × S5
We now consider the SMT limit of strings in AdS5 × S5 [28], which can be implemented using the previous tensionless limit. If we denote the AdS5 and S5 radius by ℓ, the associated effective string tension is given by
where gs is the string coupling and N denotes the total number of coinciding extremal black D3-branes. Recall that the AdS/CFT dictionary relates field theory and string theory parameters through 4π gs = λ/N and ℓ/ℓs = λ1/4, where λ is the ’t Hooft coupling in
The energy Δ and the charge Q are now associated to target space isometries of the AdS5 × S5 metric, which, in global coordinates, is given by
where
The u coordinate will be lightlike on a particular submanifold M of AdS5 × S5 and, as we will see in more detail below, the SMT limit restricts the dynamics of the string to this submanifold. We can parametrize the metric on M as
From this parametrization, we obtain a TNC geometry (τi, mi, Eij), which allows us to construct the nonrelativistic bosonic TNC string action in Eq. 5.3. Note that the dimension of this geometry will depend on the choice of Q. In this construction, the momentum along the u-direction is interpreted as a winding number in the η direction, as discussed in Section 3.3. Additionally, it turns out that the clock one-form τi dxi = dx0 + ⋯ always contains a component along the X0 direction.
The SMT field theory limit Eq. 5.11 can then be implemented using the tensionless string limit. For this, we scale the conserved charge associated to the X0 direction as T2,
Note that, in this limit, the momentum along the u direction (and hence the winding along the η direction) is given by J, which corresponds to the length of the spin chain in the dual field theory.
Going to flat worldsheet gauge, solving the constraints imposed by the Lagrange multipliers ω and ψ, and fixing the residual GCA transformations, the action Eq. 5.5 reduces to
As we will see below, this allows us to recover several known sigma models arising from spin chains. So far, this gauge fixing of the SMT string has only been implemented classically.
5.3.1 The SU(2) Spin Matrix String and the Landau–Lifshitz Model
Now let us illustrate the SMT string construction with the concrete example of Q = J1 + J2, which allows us to zoom in the SU(2) sector [28, 30, 94]. From the bulk perspective, this charge involves two of the three commuting S5 isometries, so we can parametrize it using Hopf coordinates on an S3 ⊂ S5. In these coordinates, the S5 metric is given by
where γ parametrizes the Hopf fiber, and (θ, ϕ) parametrize the base S2 of the S3 ⊂ S5. Correspondingly, we have −i∂γ = J1 + J2. Together with the global AdS time t from Eq. 5.12, we can then define the adapted coordinates X0 and u,
The length of the ∂u vector is then given by
Hence, we see that the u-direction is lightlike when ρ = 0 and α = 0. As a result, in the SMT limit zooming in on Q = J1 + J2, the dynamics of the string is restricted to the center of AdS5 and the Hopf S3 inside S5. The SU(2) spin group then arises from the isometries of this S3. The corresponding U(1)-Galilean background geometry is given by
On this background, the gauge fixed action Eq. 5.16 corresponds to
where
5.3.2 General Spin Matrix Theory String Backgrounds and Penrose Limits
The most general SMT limit comes from zooming in on the BPS bound
which involves all Cartan generators of the S3 ⊂ AdS5 and the S5 isometries. The resulting U(1)-Galilean target-space geometry is given by
Here,
They arise from the S5, and from the S3 in AdS5 (corresponding to the barred quantities

TABLE 1. The Spin Matrix theories arising from the near-BPS limit Δ ≥ Q for charge combinations with integer coefficients, the 2n spatial dimensions of their target space in the bulk and their AdS5 × S5 origin. The associated U(1)-Galilean geometry can be obtained from appropriate restrictions of the PSU(1, 2|3) result in Eq. 5.23.
The resulting sigma models match with the SU(1, 1) sigma model and the bosonic part of the PSU(1, 1|2) sigma model that were obtained (following [95] for the SU(2) sector) from a coherent state representation in [96–98]. Spinning string solutions of the SMT string sigma models have been considered in [99].
To simplify the resulting sigma models, we set J → ∞, focusing on long spin chains or long strings, and hence zooming in on the region around a particular point of the U(1)-Galilean target space. For example, in the SU(2) Landau–Lifshitz sigma model Eq. 5.21, we can take
with x and y fixed. Then the action Eq. 5.21 becomes
corresponding to the free magnon limit of the Landau–Lifshitz model. This action can then be quantized exactly and its spectrum matches the result of the corresponding decoupling limit on the field theory side [100].
Geometrically, the large charge limit is similar to the Penrose limit discussed above. There, one zooms in on the neighborhood of a lightlike geodesic on AdS5 × S5, which results in a pp-wave geometry. This is a maximally supersymmetric solution of IIB supergravity. The solution is unique, but, depending on the choice of lightlike geodesic, one obtains the same geometry in different coordinates, analogous to how different u-coordinates correspond to different SMT limits. The most general form of the pp-wave metric we need is
Here, k, l = 1, … , n are ‘flat’ directions, while the string feels a quadratic potential in the p, q = 1, … , 8 − 2n directions. The SMT limit then suppresses the dynamics in the p′ directions, and results in the sigma model (5.16) coupled to the U(1)-Galilean geometry
The number of surviving spatial directions 2n is determined by the choice of SMT limit as listed in Table 1. These U(1)-Galilean geometries were referred to as ‘flat-fluxed’ or FF backgrounds in [94], since they contain only the minimum requisite flux mi in order to make the resulting SMT sigma model Eq. 5.5 nontrivial.
Supplemented with the appropriate five-form field strength, IIB strings can be quantized on the general pp-wave background Eq. 5.27, and the SMT limit of the resulting spectrum can be matched to the field theory result [101]. To further establish this corner of NR strings in the holographic correspondence, this result should also be obtained from a direct quantization of the SMT string sigma model on the FF U(1)-Galilean backgrounds Eq. 5.28. Finally, a new approach has recently been developed for the explicit construction of Spin Matrix theories using a classical reduction of
6 Outlook
We have reviewed recent developments in several aspects of NR string theory. We discussed how this theory arises from a decoupling limit of relativistic string theory. Starting from the free theory, we showed that this limit gives rise to a self-consistent, unitary and UV-complete string theory with a Galilean-invariant spectrum. The resulting NR string theory provides a first-principles definition of the discrete light cone quantization (DLCQ) of relativistic strings that is covariant under nonrelativistic symmetries. In general backgrounds, with appropriate symmetries imposed on the worldsheet theory, NR string theory can be studied in a self-contained way, without referring to the parent relativistic string theory. Several aspects of the geometry, the quantization and the dualities of this theory have already been explored, but much work remains to be done.
In particular, the supersymmetrization of NR string theory is still relatively unexplored. In our discussion, we have exclusively discussed the bosonic sector of NR string theory, which has so far been the main focus of current research. Nevertheless, there already have been studies of NR superstring analogs of the Ramond-Neveu-Schwarz [65, 106, 107], the Green-Schwarz formalism [16, 64], and κ-symmetries [16, 68]. Likewise, a Dirac equation for spacetime fermions has been obtained from the quantization of a supersymmetric free NR string action [106], and the NR limit of the target space supergravity action has also recently been studied [70]. It is of imminent importance to extend these works to map out a more complete picture of NR superstring theories. This would not only improve our understanding of the DLCQ of string/M-theory, in a formalism that is covariant with respect to NR target-space gauge symmetries, but also enable us to develop a top-down view of NR holographic dualities. Moreover, it would be intriguing to explore NR superstring amplitudes and generalizing the higher-genus results in [12] to superstrings.
As a concrete example of such NR holographic dualities, the Spin Matrix theory (SMT) limits of AdS/CFT that we discussed in Section 5 are expected to provide a fertile testing ground. Immediate goals include quantizing the SMT string sigma model, including its Galilean Conformal algebra (GCA) of residual reparametrization symmetries (see also [29, 108]), and obtaining its beta functions. Since we can deduce the effects of the SMT limit on the AdS geometry, a set of proposed consistent backgrounds already exists. Also for these SMT strings, the supersymmetrization of the theory is still underdeveloped. It should be noted that another sigma model with nonrelativistic worldsheet geometry and GCA symmetries exist, which is likewise obtained from a tensionless limit [20–22]. While the resulting strings are fundamentally different, the developments in the quantization [109, 110] and supersymmetrization [111] of this latter tensionless string can perhaps be of use for SMT strings. Additionally, it would be very interesting to revisit the NR string theory obtained in [16, 90] from a limit on AdS5 × S5. See for example [91, 112] for recent discussions of uniform light-cone gauge fixing.
More generally, it would be intriguing to complete the program of building up a duality web in NR string theory, which would provide a new window on studying various nonperturbative sectors in M-theory. This analysis can be approached both using Dp-branes as probes (see for example [113]), whose analogs in NR string theory have been discussed in this review, or using supergravity. For this purpose, it is essential to include Ramond-Ramond charges in the framework of NR string theory and to further explore the different p-brane limits generalizing the NR string limit that were discussed in Section 4.3. It would also be interesting to understand the relation to the recent construction of NR theories from null reduction of M5-branes [114–116].
We have also seen that the T-duality-invariant framework of double field theory (DFT) appears to be particularly suited for studying NR string theory, as it incorporates both the limit and null reduction/duality approach. As we mentioned in Section 3.2.2, the formalism of DFT naturally incorporates several notions of non-Riemannian geometry. As a result, many DFT-covariant constructions that were originally developed for relativistic string theory can be efficiently applied to NR string theory, including the target-space actions [54, 62] and supersymmetric worldsheet actions [64, 65]. Similar results can be obtained in exceptional field theory [66, 67], and both frameworks are expected to be useful in building a broader understanding of NR strings and their related theories.
So far, we have focused on string theories obtained from NR limits. However, building on recent work on the NR expansion of general relativity [117–120], a similar NR expansion of string theory using a small but nonzero Regge slope has been considered [55]. This expansion would allow us to consider relativistic corrections to the NR limit order by order.
There also exist other notions of NR strings and membranes that are not covered by this review. For example, a particle limit of relativistic strings has been studied in [19, 121, 122]. This limit gives rise to non-vibrating Galilean strings described by a NR worldsheet, propagating in a target-space geometry that is Newton-like, equipped with a codimension-one foliation structure. For another example, sigma models with various Lifshitz scalings have been applied to construct the worldvolume theories for membranes [123] and strings [124], in the absence of any worldvolume (Lorentzian nor Galilean) boost symmetries. Such endeavours beyond the relativistic framework may eventually lead to an alternative route towards the unification of different string theories, as well as a larger class of holographic dualities. Additionally, there exist several ‘bottom-up’ constructions of NR holography, many of which arise from explicit symmetry breaking in relativistic parent theories, see for example the review [125].
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The work of GO is supported in part by the project “Towards a deeper understanding of black holes with non-relativistic holography” of the Independent Research Fund Denmark (grant number DFF-6108-00 340) and also by the Villum Foundation Experiment project 00 023 086.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Eric Bergshoeff, Chris Blair, Stephen Ebert, Domingo Gallegos, Umut Gürsoy, Troels Harmark, Niels Obers, Jeong-Hyuck Park, Peter Schupp and Natale Zinnato for useful discussions and comments on this review. Nordita is supported in part by NordForsk.
Footnotes
1Also see [13], where NR string theory is referred to as ‘wound string theory.’ In [12], a no-ghost theorem similar to the one in relativistic string theory has been put forward for NR string theory, showing unitarity of the theory. Moreover, tree-level and one-loop NR closed string amplitudes have been studied in [12, 13], showing that NR string theory is a self-consistent, UV-finite perturbation theory in the genus. Higher-genus amplitudes have also been discussed in [12]. We will not focus on string amplitudes in this review, but a brief discussion can be found at the end of Section 2.3.
2The quantum mechanical implementation of the constraints Eq. 2.4 in string loops will be reviewed in Section 2.3.
3Although this limit is the main focus of this review, several other limits of the relativistic string Eq. 2.1 can be considered. For example, a different NR limit of relativistic string theory has been explored in [19], where only the time direction instead of the two-dimensional longitudinal sector is treated differently. This limit leads to NR strings that do not vibrate. Additionally, a tensionless limit of relativistic string theory has been considered [20–22], which leads to a sigma model with non-Riemannian worldsheet structure, similar to the further limit of NR strings we will discuss in Section 5.
4The field redefinition Eq. 2.18 involves time derivatives and contributes nontrivially to the path-integral measure. However, in the operator formalism, the substitution Eq. 2.18 is always valid.
5A further reparametrization of worldsheet fields that mix XA and YA has been considered in [34], where the resulting OPEs take the same form as in relativistic string theory. It is therefore possible to evaluate string amplitudes in NR string theory by borrowing results directly from relativistic string theory.
6See [37] for generalizations of such localization theorems at one-loop to NR open strings. In this paper, KLT relations between tree-level NR string amplitudes are also studied.
7It is also shown in [39] that the thermodynamic partition function of the finite temperature type IIA string theory in the DLCQ is equivalent to the partition function of matrix string theory.
8This space/time noncommutativity is tied to the stringy nature of the theory. In contrast, introducing noncommutativity between space and time in field theories typically leads to inconsistencies [40–42]. Also see [43] for theories with lightlike noncommutativity.
9Note that this theory contains no propagating degrees of freedom. However, in [47], it is shown that coupling GED to Schrödinger scalars in 2 + 1 dimensions affects the renormalization group (RG) structure nontrivially and leads to a family of NR conformal fixed points.
10String foliation constraints also arise from the 1/c2 expansion of the relativistic string action [55], which we do not consider in this review.
11A related expansion also appears in [26].
12Another way of including a ZA generator in the string Galilei algebra is provided by the F-string Galilei algebra mentioned in Section 3.2.1. This algebra also includes generators corresponding to the one-form gauge transformations, and because of that it evades the need for introducing the additional extension Y. However, its realization on the worldsheet does not impose any constraints on the torsion, and it is therefore less suitable for the purposes of the current discussion.
13This should not be confused with the worldsheet coordinates σα.
14See [74] for an example where the zero-torsion condition Eq. 4.9 arises as an equation of motion from a spacetime action.
References
1. Banks T, Fischler W, Shenker SH, Susskind L. M Theory as a Matrix Model: A Conjecture. Phys Rev D (1997) 55:5112. [hep-th/9610043]. doi:10.1103/physrevd.55.5112
3. Seiberg N. Why Is the Matrix Model Correct. Phys Rev Lett (1997) 79:3577. [hep-th/9710009]. doi:10.1103/physrevlett.79.3577
4. Sen A. D0-branes on TnAnd Matrix Theory. Adv Theor Math Phys (1998) 2:51. [hep-th/9709220]. doi:10.4310/atmp.1998.v2.n1.a2
5. Hellerman S, Polchinski J. Compactification in the Lightlike Limit. Phys Rev D (1999) 59:125002. [hep-th/9711037]. doi:10.1103/physrevd.59.125002
6. de Wit B, Hoppe J, Nicolai H. On the Quantum Mechanics of Supermembranes. Nucl Phys B (1988) 305:545. doi:10.1016/0550-3213(88)90116-2
8. Banks T, Seiberg N. Strings from Matrices. Nucl Phys B (1997) 497:41. [hep-th/9702187]. doi:10.1016/s0550-3213(97)00278-2
9. Dijkgraaf R, Verlinde EP, Verlinde HL. Matrix String Theory. Nucl Phys B (1997) 500:43. [hep-th/9703030]. doi:10.1016/s0550-3213(97)00326-x
10. Bigatti D, Susskind L. Review of Matrix Theory. NATO Sci Ser C (1999) 520:277. [hep-th/9712072]. doi:10.1007/978-94-011-4730-9_11
11. Klebanov IR, Maldacena JM. 1+1)-dimensional NCOS and its U(N) Gauge Theory Dual. Adv Theor Math Phys (2000) 4:283. [hep-th/0006085]. doi:10.4310/atmp.2000.v4.n2.a3
12. Gomis J, Ooguri H. Nonrelativistic Closed String Theory. J Math Phys (2001) 42:3127. [hep-th/0009181]. doi:10.1063/1.1372697
13. Danielsson UH, Guijosa A, Kruczenski M. IIA/B, Wound and Wrapped. JHEP (2000) 10:020. [hep-th/0009182]. doi:10.1088/1126-6708/2000/10/020
14. Danielsson UH, Guijosa A, Kruczenski M. Newtonian Gravitons and D-Brane Collective Coordinates in Wound String Theory. JHEP (2001) 03:041. [hep-th/0012183]. doi:10.1088/1126-6708/2001/03/041
15. Andringa R, Bergshoeff E, Gomis J, de Roo M. ’Stringy’ Newton-Cartan Gravity. Class Quant Grav (2012) 29:235020. [arXiv:1206.5176]. doi:10.1088/0264-9381/29/23/235020
16. Gomis J, Gomis J, Kamimura K. Non-relativistic Superstrings: A New Soluble Sector of AdS5×S5. JHEP (2005) 12:024. [hep-th/0507036]. doi:10.1088/1126-6708/2005/12/024
17. Bergshoeff E, Gomis J, Yan Z. Nonrelativistic String Theory and T-Duality. JHEP (2018) 11:133. [arXiv:1806.06071]. doi:10.1007/jhep11(2018)133
18. Gomis J, Oh J, Yan Z. Nonrelativistic String Theory in Background fields. JHEP (2019) 10:101. [arXiv:1905.07315]. doi:10.1007/jhep10(2019)101
19. Batlle C, Gomis J, Not D. Extended Galilean Symmetries of Non-relativistic Strings. JHEP (2017) 02:049. [arXiv:1611.00026]. doi:10.1007/jhep02(2017)049
21. Isberg J, Lindstrom U, Sundborg B, Theodoridis G. Classical and Quantized Tensionless Strings. Nucl Phys B (1994) 411:122. [hep-th/9307108]. doi:10.1016/0550-3213(94)90056-6
22. Bagchi A. Tensionless Strings and Galilean Conformal Algebra. JHEP (2013) 05:141. [arXiv:1303.0291]. doi:10.1007/jhep05(2013)141
23. Seiberg N, Susskind L, Toumbas N. Strings in Background Electric Field, Space/Time Noncommutativity and a New Noncritical String Theory. JHEP (2000) 06:021. [hep-th/0005040]. doi:10.1088/1126-6708/2000/06/021
24. Gopakumar R, Maldacena JM, Minwalla S, Strominger A. S Duality and Noncommutative Gauge Theory. JHEP (2000) 06:036. [hep-th/0005048]. doi:10.1088/1126-6708/2000/06/036
25. Grignani G, Orselli M, Semenoff GW. Matrix Strings in a B Field. JHEP (2001) 07:004. [hep-th/0104112]. doi:10.1088/1126-6708/2001/07/004
26. Bergshoeff EA, Gomis J, Rosseel J, Şimşek C, Yan Z. String Theory and String Newton-Cartan Geometry. J Phys A (2020) 53:014001. [arXiv:1907.10668]. doi:10.1088/1751-8121/ab56e9
27. Klusoň J. Note about T-Duality of Non-relativistic String. JHEP (2019) 08:074. [arXiv:1811.12658].
28. Harmark T, Hartong J, Obers NA. Nonrelativistic Strings and Limits of the AdS/CFT Correspondence. Phys Rev D (2017) 96:086019. [arXiv:1705.03535]. doi:10.1103/physrevd.96.086019
29. Klusoň J. Remark about Non-relativistic String in Newton-Cartan Background and Null Reduction. JHEP (2018) 05:041. [arXiv:1803.07336].
30. Harmark T, Hartong J, Menculini L, Obers NA, Yan Z. Strings with Non-relativistic Conformal Symmetry and Limits of the AdS/CFT Correspondence. JHEP (2018) 11:190. [arXiv:1810.05560]. doi:10.1007/jhep11(2018)190
31. Harmark T, Hartong J, Menculini L, Obers NA, Oling G. Relating Non-relativistic String Theories. JHEP (2019) 11:071. [arXiv:1907.01663]. doi:10.1007/jhep11(2019)071
32. Klusoň J. T-duality of Non-relativistic String in Torsional Newton-Cartan Background. JHEP (2020) 05:024. [arXiv:1909.13508].
33. Gomis J, Yan Z, Yu M. Nonrelativistic Open String and Yang—Mills Theory. JHEP (2021) 03:269. [arXiv:2007.01886]. doi:10.1007/jhep03(2021)269
35. Ko SM, Melby-Thompson C, Meyer R, Park JH. Dynamics of Perturbations in Double Field Theory & Non-relativistic String Theory. JHEP (2015) 12:144. [arXiv:1508.01121]. doi:10.1007/jhep12(2015)144
36. Morand K, Park JH. Classification of Non-riemannian Doubled-Yet-Gauged Spacetime. Eur Phys J C (2017) 77:685. [arXiv:1707.03713]. doi:10.1140/epjc/s10052-017-5257-z
38. Bilal A. A Comment on Compactification of M Theory on an (Almost) Lightlike circle. Nucl Phys B (1998) 521:202. [hep-th/9801047]. doi:10.1016/s0550-3213(98)00203-x
39. Grignani G, Semenoff GW. Thermodynamic Partition Function of Matrix Superstrings. Nucl Phys B (1999) 561:243. [hep-th/9903246]. doi:10.1016/s0550-3213(99)00519-2
40. Seiberg N, Susskind L, Toumbas N. Space-time Noncommutativity and Causality. JHEP (2000) 06:044. [hep-th/0005015]. doi:10.1088/1126-6708/2000/06/044
41. Barbon JLF, Rabinovici E. Stringy Fuzziness as the Custodian of Time-Space Noncommutativity. Phys Lett B (2000) 486:202. [hep-th/0005073]. doi:10.1016/s0370-2693(00)00735-8
42. Gomis J, Mehen T. Space-time Noncommutative Field Theories and Unitarity. Nucl Phys B (2000) 591:265. [hep-th/0005129]. doi:10.1016/s0550-3213(00)00525-3
43. Aharony O, Gomis J, Mehen T. On Theories with Lightlike Noncommutativity. JHEP (2000) 09:023. [hep-th/0006236]. doi:10.1088/1126-6708/2000/09/023
44. Le Bellac M, Lévy-Leblond JM. Galilean Electromagnetism. Il Nuovo Cimento B (1973) 14:217. 1971-1996.
45. Santos ES, de Montigny M, Khanna FC, Santana AE. Galilean Covariant Lagrangian Models. J Phys A (2004) 37:9771. doi:10.1088/0305-4470/37/41/011
46. Festuccia G, Hansen D, Hartong J, Obers NA. Symmetries and Couplings of Non-relativistic Electrodynamics. JHEP (2016) 11:037. [arXiv:1607.01753]. doi:10.1007/jhep11(2016)037
47. Chapman S, Di Pietro L, Grosvenor KT, Yan Z. Renormalization of Galilean Electrodynamics. JHEP (2020) 10:195. [arXiv:2007.03033]. doi:10.1007/jhep10(2020)195
48. Connes A, Douglas MR, Schwarz AS. Noncommutative Geometry and Matrix Theory: Compactification on Tori. JHEP (1998) 02:003. [hep-th/9711162]. doi:10.1088/1126-6708/1998/02/003
49. Douglas MR, Hull CM. D-branes and the Noncommutative Torus. JHEP (1998) 02:008. [hep-th/9711165]. doi:10.1088/1126-6708/1998/02/008
50. Seiberg N, Witten E. String Theory and Noncommutative Geometry. JHEP (1999) 09:032. [hep-th/9908142]. doi:10.1088/1126-6708/1999/09/032
51. Gomis J, Yan Z, Yu M. T-duality in Nonrelativistic Open String Theory. JHEP (2021) 02:087. [arXiv:2008.05493]. doi:10.1007/jhep02(2021)087
52. Bidussi L, Harmark T, Hartong J, Obers NA, Oling G. Torsional String Newton-Cartan Geometry for Non-relativistic Strings. p. 00642.arXiv:2107.
53. Bergshoeff EA, Lahnsteiner J, Romano L, Rosseel J, Şimşek C. A Non-relativistic Limit of NS-NS Gravity. JHEP (2021) 06:021. [arXiv:2102.06974]. doi:10.1007/jhep06(2021)021
54. Gallegos AD, Gürsoy U, Verma S, Zinnato N. Non-Riemannian Gravity Actions from Double Field Theory. JHEP (2021) 06:173. [arXiv:2012.07765]. doi:10.1007/jhep06(2021)173
55. Hartong J, Have E. On the Non-relativistic Expansion of Closed Bosonic Strings. arXiv:2107.00023.
56. Brugues J, Curtright T, Gomis J, Mezincescu L. Non-relativistic Strings and Branes as Non-linear Realizations of Galilei Groups. Phys Lett B (2004) 594:227. [hep-th/0404175]. doi:10.1016/j.physletb.2004.05.024
57. Lee K, Park JH. Covariant Action for a String in ”doubled yet Gauged” Spacetime. Nucl Phys B (2014) 880:134. [1307.8377]. doi:10.1016/j.nuclphysb.2014.01.003
58. Aldazabal G, Marques D, Nunez C. Double Field Theory: A Pedagogical Review. Class Quant Grav (2013) 30:163001. [arXiv:1305.1907]. doi:10.1088/0264-9381/30/16/163001
59. Angus S, Cho K, Park JH. Einstein Double Field Equations. Eur Phys J C (2018) 78:500. [arXiv:1804.00964]. doi:10.1140/epjc/s10052-018-5982-y
60. Blair CDA, Oling G, Park JH. Non-Riemannian Isometries from Double Field Theory. JHEP (2021) 04:072. [arXiv:2012.07766]. doi:10.1007/jhep04(2021)072
61. Park JH, Sugimoto S. String Theory and Non-riemannian Geometry. Phys Rev Lett (2020) 125:211601. [arXiv:2008.03084]. doi:10.1103/physrevlett.125.211601
62. Cho K, Park JH. Remarks on the Non-riemannian Sector in Double Field Theory. Eur Phys J C (2020) 80:101. [arXiv:1909.10711]. doi:10.1140/epjc/s10052-020-7648-9
63. Blair CDA. Non-relativistic Duality and T _ T Deformations. JHEP (2020) 07:069. [arXiv:2002.12413].
64. Park JH. Green-schwarz Superstring on Doubled-Yet-Gauged Spacetime. JHEP (2016) 11:005. [arXiv:1609.04265]. doi:10.1007/jhep11(2016)005
65. Blair CDA. A Worldsheet Supersymmetric Newton-Cartan String. JHEP (2019) 10:266. [arXiv:1908.00074]. doi:10.1007/jhep10(2019)266
66. Berman DS, Blair CDA, Otsuki R. Non-Riemannian Geometry of M-Theory. JHEP (201901867) 07175:1902. doi:10.1007/jhep07(2019)175
67. Blair CDA, Gallegos D, Zinnato N. A Non-relativistic Limit of M-Theory and 11-dimensional Membrane Newton-Cartan. p. 07579. arXiv:2104.
68. Gomis J, Kamimura K, Townsend PK. Non-relativistic Superbranes. JHEP (2004) 11:051. [hep-th/0409219]. doi:10.1088/1126-6708/2004/11/051
69. Gomis J, Passerini F, Ramirez T, Van Proeyen A. Non Relativistic Dp Branes. JHEP (2005) 10:007. [hep-th/0507135]. doi:10.1088/1126-6708/2005/10/007
70. Bergshoeff EA, Lahnsteiner J, Romano L, Rosseel J, Simsek C. Non-relativistic Ten-Dimensional Minimal Supergravity. arXiv:2107.14636.
71. Gallegos AD, Gürsoy U, Zinnato N. Torsional Newton Cartan Gravity from Non-relativistic Strings. JHEP (2020) 09:172. [arXiv:1906.01607]. doi:10.1007/jhep09(2020)172
72. Yan Z, Yu M. Background Field Method for Nonlinear Sigma Models in Nonrelativistic String Theory. JHEP (2020) 03:181. [arXiv:1912.03181]. doi:10.1007/jhep03(2020)181
73. Brugues J, Gomis J, Kamimura K. Newton-hooke Algebras, Non-relativistic Branes and Generalized Pp-Wave Metrics. Phys Rev D (2006) 73:085011. [hep-th/0603023]. doi:10.1103/physrevd.73.085011
74. Bergshoeff EA, Grosvenor KT, Simsek C, Yan Z. An Action for Extended String Newton-Cartan Gravity. JHEP (2019) 01178:1810. doi:10.1007/jhep01(2019)178
75. Klusoň J. Non-Relativistic D-Brane from T-Duality along Null Direction. JHEP (2019) 10153:05662. 1907.
76. Klusoň J. Unstable D-Brane in Torsional Newton-Cartan Background. JHEP (2020) 09:19111543. 2001.
77. Roychowdhury D Probing Tachyon Kinks in Newton-Cartan Background. Phys Lett B (2019) 795:225. [arXiv:1903.05890]. doi:10.1016/j.physletb.2019.06.031
78. Pereñiguez D. p-Brane Newton–Cartan Geometry. J Math Phys (2019) 60:112501. [arXiv:1908.04801]. doi:10.1063/1.5126184
79. Kluson J. Stable And Unstable Dp-Branes in P-Brane Newton–Cartan Background. J Phys A (2021) 54:215401. [arXiv:2003.14037].
81. Gopakumar R, Minwalla S, Seiberg N, Strominger A, OM. Theory in Diverse Dimensions. JHEP (2000) 08:008. [hep-th/0006062]. doi:10.1088/1126-6708/2000/08/008
82. Bergshoeff E, Berman DS, van der Schaar JP, Sundell P. Critical fields on the M5-Brane and Noncommutative Open Strings. Phys Lett B (2000) 492:193. [hep-th/0006112]. doi:10.1016/s0370-2693(00)01081-9
83. Garcia JA, Guijosa A, Vergara JD. A Membrane Action for OM Theory. Nucl Phys B (2002) 630:178. [hep-th/0201140].
84. Kamimura K, Ramirez T. Brane Dualities in Non-relativistic Limit. JHEP (2006) 03:058. [hep-th/0512146]. doi:10.1088/1126-6708/2006/03/058
85. Harmark T, Orselli M. Spin Matrix Theory: A Quantum Mechanical Model of the AdS/CFT Correspondence. JHEP (2014) 11:134. [arXiv:1409.4417]. doi:10.1007/jhep11(2014)134
86. Blau M, Figueroa-O’Farrill JM, Hull C, Papadopoulos G Penrose Limits and Maximal Supersymmetry. Class Quant Grav (2002) 19:L87. [hep-th/0201081]. doi:10.1088/0264-9381/19/10/101
87. Berenstein DE, Maldacena JM, Nastase HS. Strings in Flat Space and Pp Waves from N=4 Super Yang-Mills. JHEP (2002) 04:013. [hep-th/0202021]. doi:10.1088/1126-6708/2002/04/013
88. Maldacena JM. The Large N Limit of Superconformal Field Theories and Supergravity. Adv Theor Math Phys (1998) 2:231. [hep-th/9711200]. doi:10.4310/atmp.1998.v2.n2.a1
89. Blau M, Figueroa-O’Farrill JM, Hull C, Papadopoulos G. A New Maximally Supersymmetric Background of IIB Superstring Theory. JHEP (2002) 01:047. [hep-th/0110242]. doi:10.1088/1126-6708/2002/01/047
90. Sakaguchi M, Yoshida K. Holography Of Non-relativistic String on AdS5×S5. JHEP (2008) 02:092. [arXiv:0712.4112]. doi:10.1088/1126-6708/2008/02/092
91. Fontanella A, Nieto García JM, Torrielli A. Light-Cone Gauge In Non-relativistic AdS5 ×S5String Theory (2102). p. 00008.
92. Fontanella A, García JMN. Classical String Solutions in Non-relativistic AdS5 ×S5: Closed And Twisted Sectors. arXiv:2109.13240.
93. Gutowski JB, Reall HS. General Supersymmetric AdS(5) Black Holes. JHEP (2004) 04:048. [hep-th/0401129]. doi:10.1088/1126-6708/2004/04/048
94. Harmark T, Hartong J, Obers NA, Oling G. Spin Matrix Theory String Backgrounds and Penrose Limits of AdS/CFT. JHEP (2021) 03:129. [arXiv:2011.02539]. doi:10.1007/jhep03(2021)129
95. Kruczenski M. Spin Chains and String Theory. Phys Rev Lett (2004) 93:161602. [hep-th/0311203]. doi:10.1103/physrevlett.93.161602
96. Stefanski B, Tseytlin AA. Large Spin Limits of AdS/CFT and Generalized Landau-Lifshitz Equations. JHEP (2004) 05:042. [hep-th/0404133]. doi:10.1088/1126-6708/2004/05/042
97. Bellucci S, Casteill PY, Morales JF, Sochichiu C. SL(2) Spin Chain and Spinning Strings on AdS(5) X S**5. Nucl Phys B (2005) 707:303. [hep-th/0409086]. doi:10.1016/j.nuclphysb.2004.11.020
98. Bellucci S, Casteill PY. Sigma Model from SU(1,1| 2) Spin Chain. Nucl Phys B (2006) 741:297. [hep-th/0602007]. doi:10.1016/j.nuclphysb.2006.02.021
99. Roychowdhury D. Decoding the Spin-Matrix Limit of Strings on AdS5×S5. Phys Lett B (2021) 820:136499. [arXiv:2101.06513]. doi:10.1016/j.physletb.2021.136499
100. Harmark T, Kristjansson KR, Orselli M. Matching Gauge Theory and String Theory in a Decoupling Limit of AdS/CFT. JHEP (2009) 02:027. [arXiv:0806.3370]. doi:10.1088/1126-6708/2009/02/027
101. Grignani G, Harmark T, Marini A, Orselli M. New Penrose Limits and AdS/CFT. JHEP (2010) 06:034. [arXiv:0912.5522]. doi:10.1007/jhep06(2010)034
102. Harmark T, Wintergerst N. Nonrelativistic Corners of
103. Baiguera S, Harmark T, Wintergerst N. Nonrelativistic Near-BPS Corners of
104. Baiguera S, Harmark T, Lei Y, Wintergerst N. Symmetry Structure of the Interactions in Near-BPS Corners of
105. Baiguera S, Harmark T, Lei Y. Spin Matrix Theory in near
106. Kim BS. Non-relativistic Superstring Theories. Phys Rev D (2007) 76:126013. [arXiv:0710.3203]. doi:10.1103/physrevd.76.126013
107. Kim BS. World Sheet Commuting Beta Gamma CFT and Non-relativistic String Theories. Phys Rev D (2007) 76:106007. [arXiv:0708.4261]. doi:10.1103/physrevd.76.106007
108. Kluson J. Canonical Analysis of Non-relativistic String with Non-relativistic World-Sheet. arXiv:2101.03758.
109. Bagchi A, Banerjee A, Chakrabortty S, Dutta S, Parekh P. A Tale of Three — Tensionless Strings and Vacuum Structure. JHEP (2020) 04:061. [arXiv:2001.00354].
110. Bagchi A, Mandlik M, Sharma P. Tensionless Tales: Vacua and Critical Dimensions. JHEP (2021) 08:054. [arXiv:2105.09682]. doi:10.1007/jhep08(2021)054
111. Bagchi A, Chakrabortty S, Parekh P. Tensionless Superstrings: View from the Worldsheet. JHEP (2016) 10:113. [arXiv:1606.09628]. doi:10.1007/jhep10(2016)113
112. Kluson J. Canonical Analysis of New Non-relativistic String Action and Uniform Light-Cone Gauge Formulation. arXiv:2108.13804.
114. Lambert N, Lipstein A, Mouland R, Richmond P. Five-dimensional Non-lorentzian Conformal Field Theories and Their Relation to Six-Dimensions. JHEP (2021) 03:053. [arXiv:2012.00626]. doi:10.1007/jhep03(2021)053
115. Mouland R. Non-Lorentzian Supersymmetric Models and M-Theory Branes, Ph.D. Thesis, 9. King’s College London (2021). arXiv:2109.04416.
117. Van den Bleeken D. Torsional Newton–Cartan Gravity from the Large C Expansion of General Relativity. Class Quant Grav (2017) 34:185004. [arXiv:1703.03459]. doi:10.1088/1361-6382/aa83d4
118. Hansen D, Hartong J, Obers NA. Action Principle for Newtonian Gravity. Phys Rev Lett (2019) 122:061106. [arXiv:1807.04765]. doi:10.1103/PhysRevLett.122.061106
119. Hansen D, Hartong J, Obers NA. Non-relativistic Gravity and its Coupling to Matter. JHEP (2020) 06:145. [arXiv:2001.10277]. doi:10.1007/jhep06(2020)145
120. Ergen M, Hamamci E, Van den Bleeken D. Oddity in Nonrelativistic, strong Gravity. Eur Phys J C (2020) 80:563. [arXiv:2002.02688]. doi:10.1140/epjc/s10052-020-8112-6
121. Gomis J, Townsend PK. The Galilean Superstring. JHEP (2017) 02:105. [arXiv:1612.02759]. doi:10.1007/jhep02(2017)105
122. Batlle C, Gomis J, Mezincescu L, Townsend PK. Tachyons in the Galilean Limit. JHEP (2017) 04:120. [arXiv:1702.04792]. doi:10.1007/jhep04(2017)120
Keywords: string theory, sigma models, D-branes, AdS/CFT correspondence, string Newton-Cartan geometry
Citation: Oling G and Yan Z (2022) Aspects of Nonrelativistic Strings. Front. Phys. 10:832271. doi: 10.3389/fphy.2022.832271
Received: 09 December 2021; Accepted: 18 January 2022;
Published: 09 June 2022.
Edited by:
Jan Rosseel, University of Vienna, AustriaReviewed by:
Joaquim Gomis, University of Barcelona, SpainMarika Taylor, University of Southampton, United Kingdom
Copyright © 2022 Oling and Yan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gerben Oling, Z2VyYmVuLm9saW5nQHN1LnNl; Ziqi Yan, emlxaS55YW5Ac3Uuc2U=
 Gerben Oling
Gerben Oling Ziqi Yan
Ziqi Yan