Abstract
Given the worldwide pandemic of the novel coronavirus disease 2019 (COVID-19) and its continuing threat brought by the emergence of virus variants, there are great demands for accurate surveillance and monitoring of outbreaks. A valuable metric for assessing the current risk posed by an outbreak is the time-varying reproduction number (). Several methods have been proposed to estimate using different types of data. We developed a new tool that integrated two commonly used approaches into a unified and user-friendly platform for the estimation of time-varying reproduction numbers. This tool allows users to perform simulations and yield real-time tracking of local epidemic of COVID-19 with an R package.
Introduction
The novel coronavirus disease 2019 (COVID-19) pandemic caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has led to 257 million confirmed cases and 5.15 million deaths worldwide by November 22, 2021 [1]. The COVID-19 pandemic continues to pose substantial risks to public health, and the situation is worsened by the emergence of SARS-CoV-2 variants with potentially higher transmissibility [2].
Quantification of the transmissibility during epidemics is fundamental for designing and adjusting public health responses. The time-varying reproduction number , defined as the expected number of secondary cases of disease caused by a single infected individual at time , is a key epidemiological measure of transmissibility, with indicating that incidence is in decline because of either successful control measures or population immunity having reached a sufficiently high level to limit further transmission. The real-time monitoring of provides feedback on the effectiveness of interventions and on the need to intensify control efforts [3, 4].
A large number of methods have been proposed to estimate from surveillance data [5–12]. There are generally two categories. One is based on fitting mechanistic transmission models to incidence data, and the other is a statistical approach requiring case incidence data and the distribution of the serial interval (the time between symptom onsets in a primary case and secondary case) [13]. The mechanistic models are often complicated to deal with because of the potential for biases in the reported incidence data and the context-specific assumptions made. The statistical method proposed by Wallinga and Teunis [13] is relatively simpler but still has drawbacks. Estimates of can vary considerably over a short period when the data aggregation time step is small. To overcome these limits, Cori et al. [14] developed a generic tool for estimating with a ready-to-use R software package EpiEstim, which has been frequently used to analyze the recent outbreaks of COVID-19. After searching CRAN package data which retrieve package download information from the RStudio mirror, we found that the most popular packages providing estimation of time-varying reproduction number include EpiEstim, EpiNow2, R0, epidemia, and nbTransmission. All of these tools use statistical methods to estimate from surveillance data and are widely adopted to study COVID-19.
Recently, a new method was proposed by Hay et al. [15] using information inherent in cycle threshold (Ct) values from reverse transcription quantitative polymerase chain reaction (RT-qPCR) tests to estimate the time-varying reproduction number from positive samples. Ct values are semiquantitative results provided by RT-qPCR tests. It is common when testing for infectious diseases to use this quantification of sample viral load. Lower Ct values indicate higher viral loads, and a Ct value below 40 gives a positive result. Based on cross-sectional virologic surveys (observed viral loads), this method overcomes the biases in traditional approaches resulting from testing constraint, unrepresentative sampling, and reporting delays. They also developed the R package virosolver to infer epidemic dynamics including estimation of .
In this study, we chose EpiEstim and virosolver as the representatives of traditional and new methods, respectively. Although the accuracies of the two approaches have been separately demonstrated, there is still a lack of comparison between the two methods to the best of our knowledge. Therefore, we quantify the accuracies of EpiEstim and virosolver in different transmission scenarios by individual-based simulations and develop a ready-to-use R package for researchers to compare different methods with the synthetic truth.
Methods
SEIR-based simulation
To assess the performance of the methods, we simulate outbreaks in three scenarios with different basic reproduction numbers (, respectively) using SEIR-based simulations as the baselines. The three scenarios could represent the situations of wild type, Delta variants, and potential variants of SARS-CoV-2 with higher transmissibility, according to estimates given by previous studies [16, 17]. The model parameters were determined on the basis of existing literature and epidemiological characteristics of COVID-19 in Hong Kong in early 2020 [14, 15, 18]. In particular, we adopted the prior distributions for the parameters of the SEIR model given by Hay et al. [15]. The SEIR model is a compartmental model which assumes that the growth rate of new infections depends on the current prevalence of infectious and susceptible individuals by modeling the proportion of the population who are susceptible (S), exposed not infectious (E), infectious (I), and recovered (R) with respect to disease over time, as illustrated in Figure 1. A stochastic SEIR model is implemented, and the R package odin is used to solve the model and obtain true infections over time. The true value of is estimated as , where is the proportion of susceptible population, is the transmission rate at time derived from the compartmental transition equations, and is the average infectious period.
FIGURE 1
The SEIR structure model used to describe the transmission of infections.
EpiEstim and virosolver methods were run separately on the same simulations for comparison. For EpiEstim, it relies on two inputs: incidence time series and the serial interval distribution. Incidence data by days since the start of outbreak were generated from the simulated SEIR epidemic. We used an empirical serial interval distribution informed by a previous outbreak of COVID-19 in Hong Kong in early 2020 [18], and we also used the simulated serial interval distribution for comparison, denoted by EpiEstim (empirical SI) and EpiEstim (simulated SI) in Figure 2. We assumed that the simulated serial interval distribution has the same standard variation as that of the empirical serial interval distribution and inferred the mean of the simulated serial interval distribution by conducting numerical experiments on a range of means from 1 to 10 with a step of 0.1 and chose the one yielding the least root mean square error (RMSE). For virosolver, the input data include population-level Ct values over days since the start of outbreak, and individual-level viral kinetics model over days since the infection. The Ct values were generated for all exposed, infectious, and recovered individuals when they were samples based on the Ct value model proposed by Hay et al. [15], and the viral kinetics parameters were also given in their study. We assumed that the Ct values were observed from randomized samples of the population at selected testing days, and Figure 2 shows the simulated Ct values of the sampled people every 14 days. Each panel presents the distribution of observed Ct values among sampled infected individuals on that testing day. Day 14 and Day 28 had no data because there was no infection among the samples at the early stage of the epidemic.
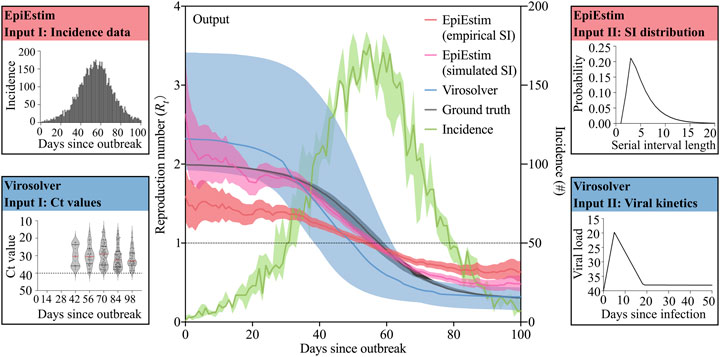
FIGURE 2
A schematic illustrating how our simulation platform generates a comparison of the estimated from EpiEstim and virosolver. Incidence data and ground truth were generated from 100 simulations based on the SEIR model (green/gray line and shaded ribbon show mean and the range). Estimates of were obtained using EpiEstim (red line and shaded ribbon show posterior median and 95% CrI using mean incidence data) and virosolver (blue line and shaded ribbon show posterior mean and 95% CrI using Ct value model), respectively. EpiEstim using the empirical value of serial interval distribution [18] and the simulated serial interval distribution are denoted by EpiEstim (empirical SI) and EpiEstim (simulated SI), respectively.
EpiEstim
The framework of EpiEstim is based on statistical assumptions and Bayesian estimation. Transmission is modeled by a Poisson process so that the rate, at which individuals infected between infection and symptom onset generate new infections, is equal to , where is the time postinfection; is the time post symptom onset; is the time-varying reproduction number at time ; and is a probability distribution describing the average infectiousness profile after infection. The incidence at time is assumed to be Poisson distributed with mean , and the likelihood of the incidence given the reproduction number is:where . is estimated in a time window , under the assumption that the time-varying reproduction number is constant within that time window. Therefore, over time period , the likelihood of the incidence during this time period given the reproduction number , conditional on the previous incidences, is as follows:
Using a Bayesian framework with a Gamma distributed prior with parameters of shape a and scale b for , the posterior distribution of is assumed to be a Gamma distribution with parameters . Hence, inference of is straightforward from the posterior distribution. Note that the choice of the time window size has an impact on the estimates of : small values of lead to a more rapid detection of changes in transmission but also more statistical noise; large values lead to more smoothing and reductions in statistical noise. By conducting simulation experiments on respectively, we found that exhibited the best compromise between high accuracy and easy interpretation, so the window size was set to be 14 in this study. Readers can refer to Gostic et al. [19] for a detailed discussion on the sliding window of the EpiEstim method.
Virosovler
The R package virosolver was developed by Hay et al. [15] using virological data and Ct values, to infer epidemic dynamics. Ct values are inversely correlated with viral loads, which depend on the time since infection. The distribution of Ct values across positive specimens at a single time point reflects the epidemic trajectory: a growing epidemic will have a high proportion of recently infected individuals with high viral loads, whereas a declining epidemic will have more individuals with older infections and thus lower viral loads. Using a mathematical model for population-level viral load distributions calibrated to known features of the SARS-CoV-2 viral load kinetics, we can use Ct values from a single random cross section of virologic testing to estimate the time-varying reproduction number in a population. For individual sampled on day , the Ct value is assumed to follow the Gumbel distribution aswhere is the time of infection, and and are the location and scale parameters, respectively. The details of the parameterization are found in [15]. In practice, virosolver takes an input data frame of Ct values with associated sample collection dates from RT-qPCR testing and reconstructs the incidence curve that gave rise to those measurements. By capturing this logic in a mathematical model, we can obtain a probabilistic estimate of the underlying incidence curve, thus time-varying reproduction number having observed a set of Ct values at some point in time. Noting that the sampling scheme has an impact on the estimate of incidence, we set the population number to be 8,000 and sampled 1,000 (1/8) of the population to fit the local prevalence data of COVID-19 in Hong Kong in early 2020 as a case study [20].
Results
We assessed the performance of EpiEstim and virosovler in three scenarios where , respectively, in which can serve as a demonstration of the outbreak of COVID-19 in Hong Kong in early 2020. For each scenario, we generated the incidence data over 100 days based on the SEIR model from 100 stochastic simulations and estimated the mean incidence. Figure 3 gives the estimated with the uncertainties (95% credible intervals) across 100 simulations using EpiEstim and virosolver, respectively, and the ground truths for the values are presented for comparison. EpiEstim with the empirical serial interval distribution [18] would underestimate . In contrast with EpiEstim, virosovler provided less biased estimates but exhibited wider intervals of uncertainty. However, both approaches performed well in detecting the timing point when .
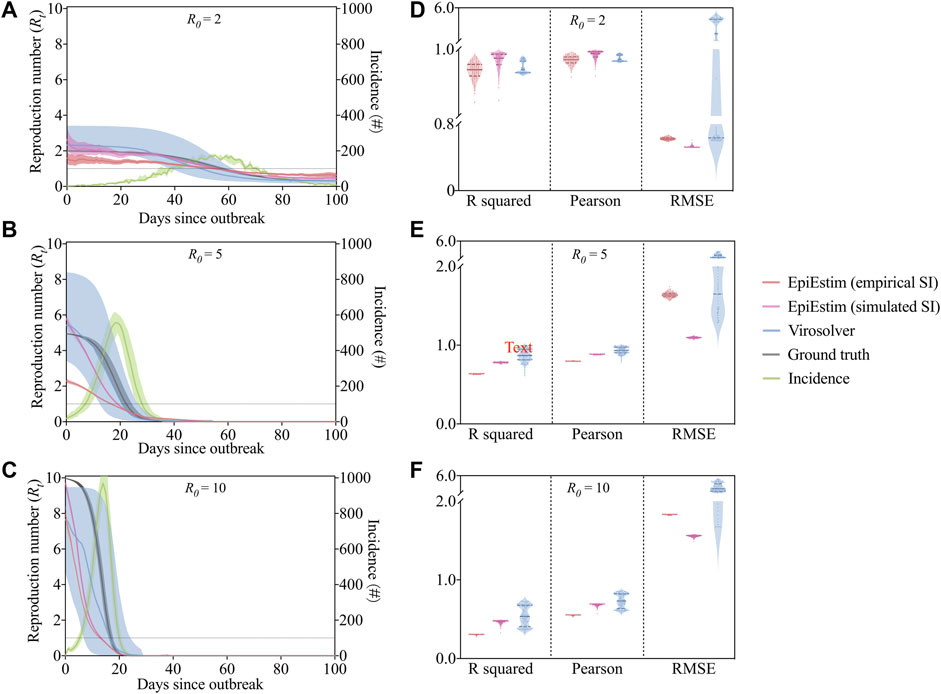
FIGURE 3
The output of estimates in three designed scenarios and the corresponding outcomes of accuracy assessment. (A–C) The graphical interface by setting , respectively. We parameterized the serial interval distribution used by EpiEstim with the empirical study [18] and the simulated serial interval distribution, which are denoted by EpiEstim (empirical SI) and EpiEstim (simulated SI) in figure legends. (D–F) Results of R squared, Pearson correlation coefficient, and RMSE for both methods in scenarios with , respectively.
To quantify and compare the accuracies of the methods, we used multiple metrics including coefficient of determination (), Pearson correlation coefficient, and root mean square error (RMSE). As Figures 3D–F show, in all scenarios, virosolver almost had the highest and Pearson correlation coefficient with the ground truth of , suggesting that virosolver had the highest accuracy and strongest correlation with the synthetic epidemic growth. In terms of RMSE, the performance of EpiEstim with the simulated serial interval distribution was the best (lowest RMSE), and virosolver had the largest RMSE due to its large estimation uncertainties. We noted that EpiEstim with simulated SI always performed better than EpiEstim with empirical SI. In conclusion, virosovler provided more accurate estimates of , and EpiEstim relied on the adjustment of serial interval distribution for better performance.
Discussion
Quantifying disease transmissibility during outbreaks is crucial for designing effective control measures and assessing their effectiveness once implemented. In the situation where the incidence is still increasing while the time-varying reproduction number is actually dropping, there might be a very different outlook compared to if the incidence and the reproduction number are both increasing. The platform for estimating provided here can therefore help epidemiologists and policymakers to monitor temporal changes in the transmissibility of COVID-19. The key contributions of our platform are as follows: 1) our software package integrates the most popular method (EpiEstim) and the newest approach (virosolver) into a unified framework, allowing users to infer real-time viral transmissibility from different perspectives; 2) by setting the value of , users can conduct simulation experiments on our platform to study the epidemic development and compare the performances of two approaches accordingly; 3) this platform is easy enough for nonspecialists to apply by simply inputting the required data and is also flexible for specialists to use by changing the parameters setting if needed.
The estimation tools we used here have several limitations and thus may result in potential bias. For EpiEstim, a preexisting estimate of serial interval distribution is required as the input data, which may account for the underestimation of reproduction number in our simulation study (Figure 3). If data on pairs of infector-infected individuals are available, the serial interval distribution can be estimated jointly, which leads to more precise estimates of transmissibility [21]. In addition, the inevitable delay between infection and case reporting (the incubation period) could also result in biased estimation of . If data on the incubation period are available, a possible strategy would be to use the incubation period distribution to back-calculate the incidence of infections from the incidence of symptoms and then apply EpiEstim to estimate the reproduction number from those inferred data.
The virologic data-based method, virosolver, as mentioned above, exhibits greater uncertainty of estimated than EpiEstim. This is probably caused by insufficient information on Ct value distribution and viral kinetics model. The viral load kinetics model used in virosolver was generated on the basis of observed properties of measured viral loads in the literature, and these results were applied to inform priors on key parameters when estimating reproduction numbers. The estimates can therefore be improved by choosing more precise, accurate priors relevant to the observations used during model fitting. For example, the model should be adjusted by specifying different distributions if results come from multiple testing platforms. Results may also be improved if individual-level features such as symptom status, age, antiviral treatment, and vaccination record are available and incorporated into the Ct value model.
Apart from the two methods presented in our study, many other approaches are still available, which we will include in this platform in the future to track disease transmissibility by using other data sources (e.g., hospitalization and death). Additionally, genomic data are also of great importance in the inference of transmissibility of COVID-19 considering recent emergence of virus variants [22]. We only provide incidence and estimates as the outputs; other epidemiological metrics such as prevalence, hospitalization, admission to ICU, death, and the economic analysis, such as net monetary benefit (NMB), are not included in our platform. Besides, we used the SEIR model for simulation in our package, because Hay et al. [15] had studied four other epidemic models for fitting cross-sectional viral load data, namely, the SEIR model, exponential growth model, SEEIRR model, and Gaussian process model, and they also made a comparison of these models. They found that the SEIR model was the most appropriate as it consistently provided unbiased, constrained estimates of transmissibility during the epidemic growth. We may explore these models and other individual-based models (branching process, for example) in future studies.
Our tool can also be applied to the new variants of SARS-CoV-2 as long as incidence data and Ct values of the infected people are available. Users can obtain a more accurate estimation by adopting the updated parameters of serial interval distribution and viral kinetics model for objective variants informed by recent studies [23–26]. In conclusion, we have established a platform for simulation and inference of time-varying reproduction numbers by incorporating two commonly used approaches. We would ensure our tool to epidemiologists and public health organizations in a wide range of future outbreak response scenarios.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
CL, LX, ZD, and BC: conceived the study, designed statistical and modeling methods, conducted analyses, interpreted results, and wrote and revised the manuscript; YB, XX, and EL: interpreted the results and revised the manuscript.
Acknowledgments
We acknowledge the financial support from the Collaborative Research Fund (Project No. C7123-20G) of the Research Grants Council of the Hong Kong SAR Government.
Conflict of interest
BC reports honoraria from AstraZeneca, GSK, Moderna, Pfizer, Roche, and Sanofi Pasteur.
CL, LX, YB, EL, BC, and ZD were employed by the company Laboratory of Data Discovery for Health, Hong Kong Science and Technology Park.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
Home - Johns Hopkins Coronavirus Resource center. Available from: https://coronavirus.jhu.edu/. Accessed 22 November 2021.
2.
Sars-CDC. CoV-2 Variant Classifications and Definitions (2021). Available from: https://www.cdc.gov/coronavirus/2019-ncov/variants/variant-info.html?CDC_AA_refVal=https%3A%2F%2Fwww.cdc.gov%2Fcoronavirus%2F2019-ncov%2Fcases-updates%2Fvariant-surveillance%2Fvariant-info.html (Accessed November 3, 2021).
3.
AndersonRMMayRM. Infectious Diseases of Humans: Dynamics and Control. Oxford: OUP Oxford (1992).
4.
FergusonNMCummingsDATFraserCCajkaJCCooleyPCBurkeDS. Strategies for Mitigating an Influenza Pandemic. Nature (2006) 442:448–52. 10.1038/nature04795
5.
RileySFraserCDonnellyCAGhaniACAbu-RaddadLJHedleyAJet alTransmission Dynamics of the Etiological Agent of SARS in Hong Kong: Impact of Public Health Interventions. Science (2003) 300:1961–6. 10.1126/science.1086478
6.
FraserCDonnellyCACauchemezSHanageWPVan KerkhoveMDHollingsworthTDet alPandemic Potential of a Strain of Influenza A (H1N1): Early Findings. Science (2009) 324:1557–61. 10.1126/science.1176062
7.
FergusonNMDonnellyCAAndersonRM. Transmission Intensity and Impact of Control Policies on the Foot and Mouth Epidemic in Great Britain. Nature (2001) 413:542–8. 10.1038/35097116
8.
AmundsenEJStigumHRøttingenJ-AAalenOO. Definition and Estimation of an Actual Reproduction Number Describing Past Infectious Disease Transmission: Application to HIV Epidemics Among Homosexual Men in Denmark, Norway and Sweden. Epidemiol Infect (2004) 132:1139–49. 10.1017/s0950268804002997
9.
BettencourtLMARibeiroRM. Real Time Bayesian Estimation of the Epidemic Potential of Emerging Infectious Diseases. PLoS One (2008) 3:e2185. 10.1371/journal.pone.0002185
10.
Cintrón-AriasACastillo-ChávezCBettencourtLMLloydALBanksHT. The Estimation of the Effective Reproductive Number from Disease Outbreak Data. Math Biosci Eng (2009) 6:261–82. 10.3934/mbe.2009.6.261
11.
HowardSCDonnellyCA. Estimation of a Time-Varying Force of Infection and Basic Reproduction Number with Application to an Outbreak of Classical Swine Fever. J Epidemiol Biostat (2000) 5:161–8.
12.
KellyHAMercerGNFieldingJEDowseGKGlassKCarcioneDet alPandemic (H1N1) 2009 Influenza Community Transmission Was Established in One Australian State when the Virus Was First Identified in North America. PLoS One (2010) 5:e11341. 10.1371/journal.pone.0011341
13.
WallingaJTeunisP. Different Epidemic Curves for Severe Acute Respiratory Syndrome Reveal Similar Impacts of Control Measures. Am J Epidemiol (2004) 160:509–16. 10.1093/aje/kwh255
14.
CoriAFergusonNMFraserCCauchemezS. A New Framework and Software to Estimate Time-Varying Reproduction Numbers during Epidemics. Am J Epidemiol (2013) 178:1505–12. 10.1093/aje/kwt133
15.
HayJAKennedy-ShafferLKanjilalSLennonNJGabrielSBLipsitchMet alEstimating Epidemiologic Dynamics from Cross-Sectional Viral Load Distributions. Science (2021) 373:373. 10.1126/science.abh0635
16.
AlimohamadiYTaghdirMSepandiM. Estimate of the Basic Reproduction Number for COVID-19: A Systematic Review and Meta-Analysis. J Prev Med Public Health (2020) 53:151–7. 10.3961/jpmph.20.076
17.
LiuYRocklövJ. The Reproductive Number of the Delta Variant of SARS-CoV-2 Is Far Higher Compared to the Ancestral SARS-CoV-2 Virus. J Trav Med (2021) 28. 10.1093/jtm/taab124
18.
ZhaoSGaoDZhuangZChongMKCCaiYRanJet alEstimating the Serial Interval of the Novel Coronavirus Disease (COVID-19): A Statistical Analysis Using the Public Data in Hong Kong from January 16 to February 15, 2020. Front Phys (2020) 8:347. 10.3389/fphy.2020.00347
19.
GosticKMMcGoughLBaskervilleEBAbbottSJoshiKTedijantoCet alPractical Considerations for Measuring the Effective Reproductive Number, Rt. Plos Comput Biol (2020) 16:e1008409. 10.1371/journal.pcbi.1008409
20.
Real-time Dashboard. Available from: https://covid19.sph.hku.hk/. Accessed 10 November 2021.
21.
ThompsonRNStockwinJEvan GaalenRDPolonskyJAKamvarZNDemarshPAet alImproved Inference of Time-Varying Reproduction Numbers during Infectious Disease Outbreaks. Epidemics (2019) 29:100356. 10.1016/j.epidem.2019.100356
22.
LeungKShumMHLeungGMLamTTWuJT. Early Transmissibility Assessment of the N501Y Mutant Strains of SARS-CoV-2 in the United Kingdom, October to November 2020. Eurosurveillance (2021) 26:2002106. 10.2807/1560-7917.es.2020.26.1.2002106
23.
RyuSKimDLimJ-SAliSTCowlingBJ. Serial Interval and Transmission Dynamics during SARS-CoV-2 Delta Variant Predominance, South Korea. Emerg Infect Dis (2022) 28:407–10. 10.3201/eid2802.211774
24.
PungRMakTMKucharskiAJLeeVJCMMID COVID-19 working group. Serial Intervals in SARS-CoV-2 B.1.617.2 Variant Cases. The Lancet (2021) 398:837–8. 10.1016/s0140-6736(21)01697-4
25.
SinganayagamAHakkiSDunningJ, Community Transmission and Viral Load Kinetics of the SARS-CoV-2 delta (B. 1.617. 2) Variant in Vaccinated and Unvaccinated Individuals in the UK: a Prospective, Longitudinal, Cohort Study. Lancet Infect Dis (2021) 22(2):183–195. 10.1016/s1473-3099(21)00648-4
26.
ChiaPYOngSWXChiewCJ, Virological and Serological Kinetics of SARS-CoV-2 Delta Variant Vaccine Breakthrough Infections: a Multicentre Cohort Study. Clin Microbiol Infect (2021). 10.1016/j.cmi.2021.11.010
Summary
Keywords
epidemics (covid 19), surveillance, infectious disease, package, modeling
Citation
Liu C, Xu L, Bai Y, Xu X, Lau EHY, Cowling BJ and Du Z (2022) Local Surveillance of the COVID-19 Outbreak. Front. Phys. 10:824369. doi: 10.3389/fphy.2022.824369
Received
29 November 2021
Accepted
13 January 2022
Published
03 March 2022
Volume
10 - 2022
Edited by
Huijia Li, Central University of Finance and Economics, China
Reviewed by
Yongxing Li, Beijing University of Technology, China
Xueyan Liu, Jilin University, China
Updates
Copyright
© 2022 Liu, Xu, Bai, Xu, Lau, Cowling and Du.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhanwei Du, duzhanwei0@gmail.com
†These authors have contributed equally to this work and share first authorship
This article was submitted to Social Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.