Superconductor Meissner Effects for Gravito-Electromagnetic Fields in Harmonic Coordinates Due to Non-Relativistic Gravitational Sources

There is much discrepancy in the literature concerning the possibility of a superconductor expelling gravito-electromagnetic fields just as it expels electromagnetic fields in the Meissner effect. Contradicting results are found in at least 18 papers written collectively by more than 20 authors and published over the course of more than 55 years (from 1966 to the present year of 2022). The primary purpose of this paper is to carefully explain the reason for the discrepancies, and provide a single conclusive treatment which may bring coherence to the subject. The analysis begins with a covariant Lagrangian for spinless charged particles (Cooper pairs) in the presence of electromagnetic fields in curved space-time. It is known that such a Lagrangian can lead to a vanishing Hamiltonian. Alternatively, it is shown that using a “space + time” Lagrangian leads to an associated Hamiltonian with a canonical momentum and minimal coupling rule. Discrepancies between Hamiltonians obtained by various authors are resolved. The canonical momentum leads to a modified form of the London equations and London gauge that includes the effects of gravity. A key result is that the gravito-magnetic field is expelled from a superconductor with a penetration depth on the order of the London penetration depth only when an appropriate magnetic field is also present. The gravitational flux quantum (fluxoid) in the body of a superconductor, and the quantized supercurrent in a superconducting ring, are also derived. Lastly, the case of a superconducting ring in the presence of a charged rotating mass cylinder is used as an example of applying the formalism developed.

1 Introduction

Over the course of many decades, researchers have investigated a wide variety of new theoretical gravitational effects and the possibility of experiments that can detect these effects. Many of these include the use of superconductors [1–3], [11–27], [30–35], [38–47], [49, 50, 58, 59, 62], [63–66], [71–78], [80], [83–91], [100, 101, 104, 105], [109–111]. Some of the earliest interest in this topic is exhibited by the founding of the Gravity Research Foundation (GRF) in 1949 by Roger Babson. “His views were reflected by the wording in the announcement of the first essay competition that said the awards were to be given for suggestions for anti-gravity devices, for partial insulators, reflectors, or absorbers of gravity, or for some substance that can be rearranged by gravity to throw off heat - although not specifically mentioned in the announcement, he was thinking of absorbing or reflecting gravity waves.” [1]

Yet by 1953, the winning GRF essay by Bryce DeWitt dispensed with such endeavors as unrealizable. DeWitt expressed doubt that a material which absorbs or reflects gravity exists [2]. He states, “... first fix our sights on those grossly practical things, such as ‘gravity reflectors’ or ‘insulators,’ or magic ‘alloys’ which can change ‘gravity’ into heat, which one might hope to find as the usual by-products of new discoveries in the theory of gravitation... Of primary importance is the extreme weakness of gravitation coupling between material bodies ... The weakness of this coupling has the consequence that schemes for achieving gravitational insulation, via methods involving fanciful devices such as oscillation or conduction, would require masses of planetary magnitude.”

However, in 1966 DeWitt’s viewpoint apparently changed when he published a highly influential paper predicting the gravito-magnetic field (also known as frame-dragging or Lense-Thirring field) is expelled from superconductors in a Meissner effect [3]. It is evident DeWitt considered quantum mechanical systems (such as superconductors) may possess properties that were not previously considered when the statement was made barring the possibility of gravitational reflectors or insulators.

In [3], DeWitt begins with the Lagrangian for a relativistic spinless charged particle in an electromagnetic field in curved space-time and develops the associated Hamiltonian. He identifies a minimal coupling rule involving a gravitational vector potential and concludes this result implies the associated gravitational field must be expelled from a superconductor, just as the magnetic field is expelled from a superconductor in the Meissner effect.

DeWitt’s novelty and intuition is highly commendable, and his paper in [3] has been extremely influential in the field of gravity and superconductors. However, it will be shown that there may be some technical shortcomings in his treatment. Also, his interpretation of the flux quantization condition, and his order of magnitude calculation for an induced electric current, are questioned. In particular, the following items will be demonstrated.

• In [3], the Hamiltonian for a relativistic spinless charged particle in curved space-time is given by DeWitt as

$\begin{array}{ll}\hfill H_{DW}& =c{\left(g^{jk}{g}_{0j}{g}_{0k}-g_{00}\right)}^{1/2}{\left[m^2{c}^2+g^{jk}\left(P_j-e{A}_j\right)\left(P_k-e{A}_k\right)\right]}^{1/2}\hfill \\ \hfill & -c{g}^{jk}{g}_{0k}\left(P_j-e{A}_j\right)-ce{A}_0\hfill \end{array}(1)$

where g^μν is stated as the inverse metric, and $\vec{P}$ is the canonical momentum. However, it will be shown that g^jk is the inverse metric only if g⁰ⁱ = 0, or if the Hamiltonian is kept to first order in the perturbation.

• In [3], the weak field, low velocity limit of the Hamiltonian is written as

$H_{DW}=\frac{1}{2m}{\left(\vec{P}-e\vec{A}-m{\vec{h}}_0\right)}^2+V(2)$

where

$V=-e{A}_0-\frac{1}{2}m{h}_{00}\text{and}{\vec{h}}_0=c\left(h_{01,}{h}_{02,}{h}_{03}\right)(3)$

Here e and m are the charge and mass of an electron, respectively. The appearance of $m{\vec{h}}^2$ in this Hamiltonian is not consistent with a linear approximation in the metric perturbation. Also, the term involving P_iAⁱ will be shown to be absent. Furthermore, several other terms of comparable order are missing in Eq. 2.

• The Hamiltonian in Eq. 2 implies a minimal coupling rule given by $\vec{P}\to \vec{P}-e\vec{A}-m{\vec{h}}_0$. However, this coupling rule is missing other terms of comparable order. The missing terms impact the associated London equations, London gauge, and penetration depths for the magnetic field and the gravito-magnetic field.

• It is also stated in [3] that the flux of $\vec{G}=e\nabla \times \vec{A}+m\nabla \times {\vec{h}}_0$ must be quantized in units of h/2. In actuality, there is an additional term in the flux condition which involves the flux of ${\vec{E}}_G\times \vec{A}$, where ${\vec{E}}_G=\frac{c^2}{2}\nabla h_{00}$.

• The gravito-magnetic field used in [3] is coordinate-dependent. With an appropriate coordinate transformation, the field can be made to vanish. Therefore, the corresponding gravitational Meissner-like effect is also coordinate-dependent and can be made to vanish as well. By contrast, a coordinate invariant formulation can be used which does not vanish by a coordinate transformation (to linear order in the perturbation).

• Lastly, it is claimed in [3] that a magnetic flux must arise in a superconducting ring that is concentric with a massive cylinder that begins rotating since it will produce a gravito-magnetic flux in the ring. It is predicted that the ring will remain in the n = 0 state, and an electric current will therefore be induced with an order-of-magnitude given by

$I_{DW}\sim \frac{GmMV}{ed}(4)$

where V is the rim speed, M is the mass, and d is the diameter of the rotating cylinder. However, it will be shown that the electric current predicted by Eq. 4 is actually limited to $I<h/\left(2eL\right)$, where L is the self-inductance. Furthermore, it will be shown that if there is no external magnetic field present, and the system remains in the n = 0 state, then the flux of the gravito-magnetic field will produce an electric current with a different form compared to Eq. 4.

1.1 A Summary of the Sections in This Paper

Section 2 begins with a covariant Lagrangian for a relativistic spinless charged particle in an electromagnetic field in curved space-time. The Euler-Lagrange equation of motion leads to the geodesic equation of motion modified by the Lorentz four-force in curved space-time. Although the equation of motion correctly describes the dynamics of the particle, the associated Hamiltonian is identically zero and therefore cannot be used to describe a quantum mechanical system such as a superconductor.

Alternatively, a “space + time” Lagrangian is used to obtain a canonical three-momentum and Hamiltonian valid to all orders in the metric. The result is compared to DeWitt’s in Eq. 1. Some relevant metric relationships will be used to match the Hamiltonian with that of other authors for confirmation of its validity. The Hamiltonian is then expanded to first order in the metric to show the lowest order coupling of the momentum, electromagnetic fields, and gravity. Again, the result is compared to DeWitt’s result in Eq. 2. The Hamiltonian is further simplified by introducing the trace-reversed metric perturbation and assuming non-relativistic gravitational sources. Alternative Hamiltonians are also discussed as well as the conditions necessary for a Hamiltonian to be quantized.

In Section 3, gravito-electric and gravito-magnetic fields are defined in terms of the metric perturbation. Using the stress tensor of a non-relativistic ideal fluid, and the linearized Einstein field equation in harmonic coordinates, leads to gravito-electromagnetic field equations. In addition, the canonical momentum is used to develop constitutive equations for the supercurrent. These lead to a modified set of London equations describing the interaction of electromagnetic and gravito-electromagnetic fields with a superconductor. A modification to the London gauge condition is also identified.

In Section 4, the constitutive equations are used in the field equations to identify a penetration depth associated with the magnetic field and the gravito-magnetic field. It is found that the usual London penetration depth for the magnetic field is modified by the presence of a gravito-magnetic field, however, the modification is miniscule. It is also found that in the absence of a magnetic field, the superconductor demonstrates a paramagnetic effect rather than a diamagnetic (Meissner) effect for the gravito-magnetic field. In other words, the gravito-magnetic field is not expelled. However, when the magnetic field and the gravito-magnetic field are both present, it is possible for the gravito-magnetic field to be expelled with a penetration depth on the same order as the London penetration depth. However, it is demonstrated that the gravito-magnetic field is a coordinate-dependent quantity and therefore effects associated with it can be made to vanish with an appropriate coordinate transformation.

In Section 5, it is found that the usual London penetration depth for the electric field is modified by the presence of a gravito-magnetic field, however, again the modification is miniscule. In the process of developing these results, a penetration depth is also found for a field defined as the linear combination of the magnetic and gravito-magnetic vector potentials. However, since the gravito-magnetic vector potential is time-independent in this approximation, then it is shown not to have an associated penetration depth. This is expected since it is known that the Newtonian gravitational field generally cannot be shielded.

In Section 6, the new minimal coupling rule obtained in Section 2 will be used to write the Ginzburg-Landau supercurrent with coupling to electromagnetism and gravity. The complex order parameter must be single-valued around a closed path according to the Byers-Yang theorem. Then using the fact that all the fields vanish within the body of the superconductor leads a quantization condition for the flux of the magnetic and gravitational fields.

Lastly, in Section 7, the canonical momentum is used to develop an expression for the Ginzburg-Landau phase around a superconducting ring. Once again, using the fact that the wave function is single-valued around a closed path leads to a quantization condition involving the flux of the magnetic and gravitational fields, as well as the supercurrent around a superconducting ring. A charged, rotating mass cylinder is introduced as a source for electromagnetic and gravitational fields. The effect of placing the rotating cylinder coaxial with the superconducting ring is carefully analyzed. It is argued that the electric current predicted by DeWitt in Eq. 4 is not induced. Rather, the supercurrent in the ring is quantized along with the flux of electromagnetic and gravitational fields through the ring.

2 The “Space + Time” Hamiltonian for a Charged Spinless Particle in Curved Space-Time

Using an action of the form $S={\int }_{{\tau }_1}^{{\tau }_2}\tilde{L}d\tau$, where τ is proper time, leads to a Lagrangian for a relativistic spinless charged particle in an electromagnetic field in curved space-time that can be written as¹

$\tilde{L}=-mc\sqrt{-g_{\mu \nu }{u}^{\mu }{u}^{\nu }}-q{g}_{\mu \nu }{A}^{\mu }{u}^{\nu }(5)$

where u^μ = dx^μ/dτ is the four-velocity, $A^{\mu }=\left(\phi /c,A^i\right)$ is the electromagnetic four-potential, and m and q are the rest mass and charge of the test particle, respectively. It is well known that using Eq. 5 in the Euler-Lagrange equation of motion

$\frac{\partial \tilde{L}}{\partial x^{\mu }}-\frac{d}{d\tau }\frac{\partial \tilde{L}}{\left(\partial x^{\mu }/d\tau \right)}=0(6)$

leads to the geodesic equation of motion modified by the Lorentz four-force in curved space-time

$\frac{d{p}^{\mu }}{d\tau }+m{\mathrm{\Gamma }}_{\sigma \rho }^{\mu }{u}^{\sigma }{u}^{\rho }=q{g}_{\nu \alpha }{u}^{\alpha }{F}^{\mu \nu }(7)$

where ${\mathrm{\Gamma }}_{\sigma \rho }^{\mu }$ are the metric connections (Christoffel symbols).² This demonstrates that the Lagrangian in Eq. 5 correctly characterizes the dynamics in a covariant form. Evaluating a canonical four-momentum, $P_{\mu }=\partial \tilde{L}/\partial u^{\mu }$, and using q = −e leads to p_μ = P_μ − eA_μ. This implies a covariant minimal coupling rule given by P^μ → P^μ − eA^μ.

However, it is known that using Eq. 5 in a covariant Legendre transformation, $\tilde{H}=P_{\mu }{u}^{\mu }-\tilde{L}$, leads to a Hamiltonian that is identically zero and therefore cannot have the interpretation of energy. This issue of a vanishing Hamiltonian is discussed in Jackson [7] and Barut [8] in the context of flat space-time, and by Bertschinger [9, 10] in curved space-time. The problem stems from the fact that u^μu_μ = −c² imposes an additional constraint on the Lagrangian in Eq. 5. This issue is discussed in further detail in the subsection, “Alternative methods of obtaining the Hamiltonian” found further below.

For the purposes of this paper, we will take an approach similar to [3, 11] by reparametrizing the action for the Lagrangian in Eq. 5 in terms of coordinate time rather than proper time.³ Note that the four-velocity can be written as u^μ = γv^μ, where the Lorentz factor is γ = dt/dτ, the coordinate velocity is $v^{\mu }=d{x}^{\mu }/dt=\left(c,v^i\right)$, and t is the coordinate time. Then the action for the Lagrangian in Eq. 5 can be written as

$S={\int }_{{\tau }_1}^{{\tau }_2}\left(-mc\sqrt{-g_{\mu \nu }{u}^{\mu }{u}^{\nu }}-q{g}_{\mu \nu }{A}^{\mu }{u}^{\nu }\right)d\tau (8)$

$\begin{array}{ll}\hfill & \hfill \\ \hfill & ={\int }_{{\tau }_1}^{{\tau }_2}\left(-mc\sqrt{-g_{\mu \nu }\left(v^{\mu }\frac{dt}{d\tau }\right)\left(v^{\nu }\frac{dt}{d\tau }\right)}-q{g}_{\mu \nu }{A}^{\mu }{v}^{\nu }\frac{dt}{d\tau }\right)d\tau \hfill \end{array}(9)$

$\begin{array}{ll}\hfill & \hfill \\ \hfill & ={\int }_{t_1}^{t_2}\left(-mc\sqrt{-g_{\mu \nu }{v}^{\mu }{v}^{\nu }}-q{g}_{\mu \nu }{A}^{\mu }{v}^{\nu }\right)dt\hfill \end{array}(10)$

Therefore the action can be written as $S={\int }_{t_1}^{t_2}Ldt$, where the “space + time” Lagrangian is

$L=-mc\sqrt{-g_{\mu \nu }{v}^{\mu }{v}^{\nu }}-q{g}_{\mu \nu }{A}^{\mu }{v}^{\nu }(11)$

This is the Lagrangian used by DeWitt [3] except he uses the notation $v^{\mu }={\dot{x}}^{\mu }$ and sets c = 1. DeWitt and other authors such as [11] leave the electromagnetic field in the Lagrangian Eq. 11 as A_μv^μ instead of qg_μνA^μv^ν which masks the explicit coupling of gravity to the electromagnetic field. Using g_μνu^μu^ν = −c², the Lorentz factor in curved space-time can be evaluated as

$\begin{array}{ll}\hfill \gamma & =\sqrt{-g_{\mu \nu }{v}^{\mu }{v}^{\nu }}={\left(-g_{00}-\frac{2v^j}{c}{g}_{0j}-\frac{v^i{v}^j}{c^2}{g}_{ij}\right)}^{-1/2}\hfill \\ \hfill & \hfill \end{array}(12)$

Then the canonical three-momentum, P_i = ∂L/∂vⁱ, can be found from Eq. 11 to be

$P_i=\gamma m\left(c{g}_{0i}+g_{ij}{v}^j\right)-q\left(g_{0i}{A}^0+g_{ij}{A}^j\right)(13)$

Note that p_μ = g_μνp^ν and $p^{\nu }=\gamma m\left(c,v^i\right)$ lead to $p_i=\gamma m\left(c{g}_{0i}+g_{ij}{v}^j\right)$ which is the first term on the right side of Eq. 13. Also note that A_μ = g_μνA^ν leads to

$A_i=g_{0i}{A}^0+g_{ij}{A}^j\text{and}{A}_0=g_{00}{A}^0+g_{0i}{A}^i(14)$

Therefore Eq. 13 can be written as simply p_i = P_i − eA_i which is consistent with the covariant canonical momentum relationship, p_μ = P_μ − eA_μ. Similarly, in [10] a covariant canonical momentum of the form P_μ = mg_μνv^ν + qA_μ appears. In [13], a canonical momentum is shown as P_i = mg_iju^j − eA_i, where u^j = γv^j. This form is missing the term involving γmcg_0i in Eq. 13 which may be because the canonical momentum in [13] is not formally derived from a Lagrangian but obtained by replacing the canonical momentum in flat space-time with a form proposed for curved space-time. Also [14, 15], have a result similar to Eq. 13 but without the terms involving A⁰ and Aⁱ. This is due to starting from a Lagrangian similar to Eq. 11 but without the electromagnetic field.

Using g_μν = η_μν + h_μν, where η_μν is the Minkowski metric of flat space-time, and h_μν is a perturbation, makes Eq. 13 become

$\gamma m{v}_i=P_i-\gamma m\left(c{h}_{0i}+h_{ij}{v}^j\right)+q\left({\eta }_{ij}{A}^j+h_{0i}{A}^0+h_{ij}{A}^j\right)(15)$

In [16], a result similar to Eq. 15 is obtained but with h_0i = 0 and γ = 1 due to using transverse-traceless coordinates $\left(h_{\mu 0}=0\right)$ and remaining to lowest order in vⁱ. Likewise, a result similar to Eq. 15 appears in [17–27], but the terms involving h_ijv^j, h_0iA⁰, and h_ijA^j are all missing⁴.

Note that in the absence of electromagnetism and gravity, the canonical momentum reduces to P_i = γmv_i. Therefore, Eq. 15 implies that the presence of electromagnetism and gravity leads to a minimal coupling rule given by

$\begin{array}{l}\hfill P_i\to P_i-\gamma m\left(c{h}_{0i}+h_{ij}{v}^j\right)+q\left({\eta }_{ij}{A}^j+h_{0i}{A}^0+h_{ij}{A}^j\right)\end{array}(16)$

For an electron $\left(q=-e\right)$ this is the usual minimal coupling rule, P_i → P_i − eA_i. As previously stated, the first term on the right side of Eq. 13 can be identified as

$\begin{array}{ll}\hfill p_i& =\gamma m\left(c{g}_{0i}+g_{ij}{v}^j\right)\hfill \\ \hfill & \hfill \end{array}(17)$

Using a Legendre transformation, H = P_kv^k − L, requires solving Eq. 17 for vⁱ which requires constructing the inverse of g_ik. This is shown in $\left(209\right)$ of Supplementary Appendix SA to be

${\tilde{g}}^{jk}\equiv g^{jk}-\frac{g^{0j}{g}^{0k}}{g^{00}}(18)$

which satisfies ${\tilde{g}}^{jk}{g}_{ik}={\delta }_i^j$. Then the velocity and the Lorentz factor can be expressed as, respectively,

$\begin{array}{ll}\hfill v^j& =\frac{{\tilde{g}}^{jk}{p}_k}{\gamma m}-c{\tilde{g}}^{jk}{g}_{0k}\text{and}\gamma =\frac{1}{mc}\sqrt{\frac{m^2{c}^2+{\tilde{g}}^{jk}{p}_j{p}_k}{{\tilde{g}}^{jk}{g}_{0j}{g}_{0k}-g_{00}}}\hfill \\ \hfill & \hfill \end{array}(19)$

Expressions equivalent to Eq. 19 can also be found in [11, 14, 15]. Inserting Eq. 19 into Eq. 17, and making use of Eq. 13 with q = −e, makes the Hamiltonian become

$\begin{array}{cc}\hfill H& =c{\left({\tilde{g}}^{jk}{g}_{0j}{g}_{0k}-g_{00}\right)}^{1/2}\hfill \\ \hfill & \times {\left[m^2{c}^2+{\tilde{g}}^{jk}\left(P_j-e{g}_{0j}{A}^0-e{g}_{jl}{A}^l\right)\left(P_k-e{g}_{0k}{A}^0-e{g}_{km}{A}^m\right)\right]}^{1/2}\hfill \\ \hfill & -c{\tilde{g}}^{jk}{g}_{0k}\left(P_j-e{g}_{0j}{A}^0-e{g}_{jl}{A}^l\right)-ec\left(g_{00}{A}^0+g_{0j}{A}^j\right)\hfill \end{array}(20)$

This can be considered a “space + time” Hamiltonian for a relativistic spinless charged particle in an electromagnetic field in curved space-time⁵. The result is exact in the metric perturbation and particle velocity. To compare with DeWitt’s result in Eq. 1, we can use Eq. 14 to write the Hamiltonian as

$\begin{array}{ll}\hfill H& =c{\left({\tilde{g}}^{jk}{g}_{0j}{g}_{0k}-g_{00}\right)}^{1/2}{\left[m^2{c}^2+{\tilde{g}}^{jk}\left(P_j-e{A}_j\right)\left(P_k-e{A}_k\right)\right]}^{1/2}\hfill \\ \hfill & \hfill \\ \hfill & -c{\tilde{g}}^{jk}{g}_{0k}\left(P_j-e{A}_j\right)-ec{A}_0\hfill \end{array}(21)$

This matches DeWitt’s result in Eq. 1 except that DeWitt uses g^jk instead of ${\tilde{g}}^{jk}$. The same issue also appears in [30] where a Legendre transformation is applied to the same Lagrangian used in Eq. 11. The Hamiltonian in Eq. 1 is also quoted and utilized in [31]. However, it is shown in Supplementary Appendix SA that ${\tilde{g}}^{jk}\approx g^{jk}$ is only true to first order in the metric perturbation. This issue is properly recognized in [11].

In the literature, the “space + time” Hamiltonian appears in several other forms. To compare with Eq. 20, the following metric relationships developed in Supplementary Appendix SA can be used:

$\begin{array}{ll}\hfill {\tilde{g}}^{jk}{g}_{0k}& =-\frac{g^{0j}}{g^{00}}\text{and}{\tilde{g}}^{jk}{g}_{0j}{g}_{0k}-g_{00}=-\frac{1}{g^{00}}\hfill \\ \hfill & \hfill \end{array}(22)$

Using Eq. 22 in Eq. 20 leads to a form that matches Cognola, Vanzo, and Zerbini [11].

$\begin{array}{ll}\hfill H_{\mathit{CV\; Z}}& =c{\left[\frac{m^2{c}^2+{\tilde{g}}^{jk}{p}_j{p}_k}{-g^{00}}\right]}^{1/2}+c\frac{g^{0j}}{g^{00}}{p}_j-ec{A}_0\hfill \\ \hfill & \hfill \end{array}(23)$

It is stated in [11] that Eq. 23 and DeWitt’s result in Eq. 1 are not equivalent when there is a nonvanishing g_0i. However, it is demonstrated here that Eq. 20, which is the corrected form of DeWitt’s approach, is indeed equivalent to Eq. 23 via the use of Eq. 22. Also, substituting Eq. 18 into Eq. 23 leads to a result that matches Bertschinger [9], except [9] does not include electromagnetic fields.

$\begin{array}{ll}\hfill H_B& =c\frac{g^{0j}}{g^{00}}{p}_j+c{\left[\frac{m^2{c}^2+g^{jk}{p}_j{p}_k}{-g^{00}}+{\left(\frac{g^{0j}{p}_j}{g^{00}}\right)}^2\right]}^{1/2}\hfill \\ \hfill & \hfill \end{array}(24)$

With some algebraic manipulation, this Hamiltonian also matches the result derived by Piyakis, Papini, and Rystephanick [32].

$H_{\mathit{PPR}}=\frac{c}{g^{00}}\left\{{\left[{\left(g^{0j}{p}_j\right)}^2-g^{00}\left(m^2{c}^2+g^{jk}{p}_j{p}_k\right)\right]}^{1/2}+g^{0j}{p}_j\right\}(25)$

Therefore, the discrepancies between all of the authors stated above are resolved.

2.1 The Weak-Field, Low-Velocity Limit of the Hamiltonian

The lowest order expansion of Eq. 20 is now considered. As discussed below Eq. 7, the canonical four-momentum is found to be P_μ = p_μ + eA_μ. Using the metric perturbation leads to

$\begin{array}{ll}\hfill P_i& ={\eta }_{ij}\left(p^j+e{A}^j\right)+h_{ij}\left(p^j+e{A}^j\right)+h_{0i}\left(p^0+e{A}^0\right)\hfill \\ \hfill & \hfill \end{array}(26)$

This shows that to lowest order, $P_i\sim {\eta }_{ij}\left(p^j+e{A}^j\right)$. It can also be assumed that pⁱ ∼ eAⁱ since the vector potential drives the supercurrent. Then for approximation purposes, P_i can be treated the same as pⁱ.

Following the procedure of Supplementary Appendix SB, but remaining to first order in the perturbation and second order in momentum, leads to

$\begin{array}{ll}\hfill H& =m{c}^2+\frac{1}{2m}{\left(P_i-e{\eta }_{ij}{A}^j\right)}^2-\frac{1}{2}{h}_{00}m{c}^2+ec{A}^0-ec{h}_{00}{A}^0-ec{h}_{0i}{A}^i\hfill \\ \hfill & \hfill \\ \hfill & -c{h}_{0i}\left(P_i-e{\eta }_{ij}{A}^j\right)-\frac{e}{m}\left(h_{ij}{A}^j+h_{0i}{A}^0\right)\left(P_i-e{\eta }_{ik}{A}^k\right)\hfill \\ \hfill & \hfill \\ \hfill & -\frac{h_{00}}{4m}{\left(P_i-e{\eta }_{ij}{A}^j\right)}^2-\frac{h_{ij}}{2m}\left(P_i-e{\eta }_{ik}{A}^k\right)\left(P_j-e{\eta }_{jl}{A}^l\right)\hfill \\ \hfill & \hfill \end{array}(27)$

To compare with DeWitt’s result in Eq. 2, the indices of the electromagnetic potentials can be lowered using Eq. 14. Remaining to first order in the perturbation leads to

$\begin{array}{ll}\hfill H& =m{c}^2+\frac{1}{2m}{\left(P_i-e{A}_i\right)}^2-c{h}_{0i}\left(P_i-e{A}_i\right)-\frac{1}{2}{h}_{00}m{c}^2-ec{A}_0\hfill \\ \hfill & \hfill \\ \hfill & -\frac{h_{00}}{4m}{\left(P_i-e{A}_i\right)}^2-\frac{h_{ij}}{2m}\left(P_i-e{A}_i\right)\left(P_j-e{A}_j\right)-\frac{h_{0i}}{2m}e{A}^0\left(P_i-e{A}_i\right)\hfill \\ \hfill & \hfill \end{array}(28)$

Although Eq. 28 has the benefit of being more compact than Eq. 27, it can be misleading due to the fact that A_i and A₀ contain metric perturbation terms as demonstrated by Eq. 14. In fact, terms that are second order in $\left(P_i-e{A}_i\right)$ could be falsely interpreted as containing the metric perturbation to second order which is inconsistent with the first order expansion used to obtain the Hamiltonian. Therefore, it can be argued that Eq. 27 is preferred since all metric perturbations are explicitly shown to first order

The following are comparisons between DeWitt’s result in Eq. 2 and the result obtained in Eq. 28.

• The Hamiltonian in Eq. 28 contains the scalar, vector, and tensor parts of the metric perturbation which are, respectively, h₀₀, h_0i, and h_ij. The tensor part of the perturbation is still first order in the perturbation⁶ but is missing in Eq. 2. In fact, all the terms after ecA₀ in Eq. 28 are missing from Eq. 2. It is shown in Supplementary Appendix SB that the terms involving $h_{00}{P}_i^2$ and h_ijP_iP_j are generally many orders of magnitude larger than ch_0iP_i which is kept in Eq. 2. Therefore, it is inconsistent to drop $h_{00}{P}_i^2$ and h_ijP_iP_j but keep ch_0iP_i.

• The expression appearing as ${\left(\vec{P}-e\vec{A}-m\vec{h}\right)}^2$ in Eq. 2 leads to couplings of the form h_0iP_i and h_0iA_i. The first is a coupling between gravity and the test particles which is common to Eq. 28. The second is a coupling between gravity and electromagnetism, and is common to Eq. 28 as well. However, returning to Eq. 27, it is evident that the coupling of the form h_0iAⁱ cancels⁷ when combining the terms appearing as ech_0iAⁱ and $c{h}_{0i}\left(P_i-e{\eta }_{ik}{A}^k\right)$. Although there is no coupling of the form h_0iAⁱ, there are still several other couplings between gravity and electromagnetism that appear in Eq. 27, such as h_0iA⁰Aⁱ, h_ijAⁱA^j, and h₀₀A².

• The expression appearing as ${\left(\vec{P}-e\vec{A}-m\vec{h}\right)}^2$ in Eq. 2 also leads to a coupling of the form $m{h}_{0i}^2$. This coupling is absent in Eq. 28 since $m{h}_{0i}^2$ is second order in the perturbation and therefore does not belong in a first order expansion. It is shown in Supplementary Appendix SB that a second order expansion does lead to a term of the form $m{h}_{0i}^2$. However, it is shown that there are 24 other terms that are many orders of magnitude larger than $m{h}_{0i}^2$ and therefore must also be kept to justify keeping $m{h}_{0i}^2$ in the Hamiltonian.⁸

• The Hamiltonian in Eq. 2 implies a minimal coupling rule given by $\vec{P}\to \vec{P}-e\vec{A}-m\vec{h}$, rather than the full minimal coupling rule found in Eq. 16. In fact, errors in the Hamiltonian and the coupling rule are related since starting with a Hamiltonian of the form $H=\frac{1}{2m}{P}^2+V$, and assuming $\vec{P}\to \vec{P}-e\vec{A}-m\vec{h}$, leads directly to the result $H=\frac{1}{2m}{\left(\vec{P}-e\vec{A}-m\vec{h}\right)}^2+V$. This Hamiltonian appears in a multitude of papers, some of which are [14, 15, 19, 25, 26, 30, 32, 35], [40–50].

The Hamiltonian in Eq. 31 can also be written using the trace-reversed metric perturbation, ${\bar{h}}_{\mu \nu }$, where $h_{\mu \nu }={\bar{h}}_{\mu \nu }-\frac{1}{2}{\eta }_{\mu \nu }\bar{h}$ and $\bar{h}={\eta }^{\mu \nu }{\bar{h}}_{\mu \nu }$. It will be shown in the following section that using the harmonic coordinate condition, ${\partial }^{\nu }{\bar{h}}_{\mu \nu }=0$, leads to ${\bar{h}}_{ij}=0$ for non-relativistic gravitational sources. Then the components of the perturbation are

$h_{00}=\frac{1}{2}{\bar{h}}_{00},h_{0i}={\bar{h}}_{0i},h_{ij}=\frac{1}{2}{\bar{h}}_{00}{\delta }_{ij}(29)$

A gravito-scalar potential and gravito-vector potential can also be defined as, respectively,

${\phi }_G\equiv -\frac{c^2}{4}{\bar{h}}_{00}\text{and}{h}^i\equiv \frac{c}{4}{\bar{h}}_{0i}(30)$

For brevity, a minimally coupled canonical momentum can be defined as ${\tilde{P}}_i\equiv P_i-e{\eta }_{ij}{A}^j$, where ${\tilde{P}}^2={\tilde{P}}_i{\tilde{P}}_i$. Also using A⁰ = φ/c in Eq. 27 leads to

$H=m{c}^2+e\phi +\left(\frac{{\tilde{P}}^2}{2m}+m{\phi }_G\right)+\frac{2e\phi {\phi }_G}{c^2}+\left(\frac{3{\phi }_G{\tilde{P}}^2}{2m{c}^2}+\frac{2e{\phi }_G{A}^i{\tilde{P}}_i}{m{c}^2}\right)-4h^i{P}_i-\frac{4e\phi h^i{\tilde{P}}_i}{m{c}^2}(31)$

Terms are listed from largest to smallest magnitude based on the order-of-magnitude analysis found in Supplementary Appendix SB. Terms within an order of magnitude are grouped in parentheses. It is shown that using the maximum momentum permitted for Cooper pairs (which requires keeping the kinetic energy below the BCS energy gap), and estimating the largest value for hⁱ that can be reasonably produced in a lab, then hⁱP_i ∼ 10^–47 J while $e\phi h^i{P}_i/\left(m_e{c}^2\right)\sim 10^{-50}$ J. Therefore the last term in Eq. 31 can be dropped and still maintain consistency. However, it is also shown in Supplementary Appendix SB that an expansion to second order in the perturbation, and fourth order in the momentum, introduces seven more terms that are several orders of magnitude larger than hⁱP_i. Therefore, a consistent approximation leads to the following result for the weak-field, low-velocity limit of the Hamiltonian.

$\begin{array}{cc}\hfill H& =m{c}^2+e\phi +\left(\frac{{\tilde{P}}^2}{2m}+m{\phi }_G\right)+\frac{2e{\phi }_G\phi }{c^2}+\left(\frac{3{\phi }_G{\tilde{P}}^2}{2m{c}^2}+\frac{2e{\phi }_G{A}^i{\tilde{P}}_i}{m{c}^2}-\frac{m{\phi }_G^2}{2c^2}-\frac{{\tilde{P}}^4}{8m^3{c}^2}\right)\hfill \\ \hfill & +\left(\frac{11{\phi }_G^2{\tilde{P}}^2}{4m{c}^4}+\frac{2e^2{A}^2{\phi }_G^2}{m{c}^4}-\frac{e{A}^i{\phi }_G{\tilde{P}}_i{\tilde{P}}^2}{m^3{c}^4}-\frac{5{\phi }_G{\tilde{P}}^4}{8m^3{c}^4}+\frac{6e{\phi }_G^2{A}^i{\tilde{P}}_i}{m{c}^4}\right)-4h^i{P}_i\hfill \end{array}(32)$

where A² = AⁱAⁱ. Note that the terms involving ${\phi }_G^2$, ${\tilde{P}}^3$ and ${\tilde{P}}^4$ (which come from a second order expansion) are all larger than hⁱP_i (which comes from a first order expansion). We can attempt to eliminate these terms to obtain a result similar to DeWitt’s Eq. 2. However, it is shown in Supplementary Appendix SB that keeping hⁱP_i and eφ, while eliminating other terms that do not appear in Eq. 2, is only possible if the electromagnetic potentials are reduced to absurdly small (but non-zero) values: A ∼ 10^–32 T⋅m and φ ≪ 10^–44 V. Then the second order Hamiltonian found in Supplementary Appendix SB is

$H=m{c}^2+m{\phi }_G-\frac{m{\phi }_G^2}{2c^2}+e\phi +\frac{{\left(P_i-e{\eta }_{ij}{A}^j\right)}^2}{2m}-4h^i{P}_i+8m{h}^2(33)$

Again, terms are listed from largest to smallest magnitude. Notice the term involving $m{\phi }_G^2$ still remains since it is many orders of magnitude larger than hⁱP_i. This is due to the fact that φ_G is produced by earth and hence is outside experimental control. Note that the last three terms cannot be combined into a single expression of the form $\frac{1}{2m}{\left(P_i-e{\eta }_{ij}{A}^j-4m{h}^i\right)}^2$ since 4ehⁱAⁱ does not appear in the Hamiltonian. Therefore Eq. 33 is arguably the closest to DeWitt’s Hamiltonian in Eq. 2 that can be obtained.

2.2 Alternative Methods of Obtaining the “Space + Time” Hamiltonian

The following is a discussion of the various covariant Hamiltonians that describe the same particle dynamics, and the differing ways that a “space + time” Hamiltonian has been derived by various authors. It is emphasized that all of these approaches found throughout the literature are shown here to be equivalent. The issue of a vanishing covariant Hamiltonian, and the issue of singular Lagrangians is also discussed.

It was stated after Eq. 7 that using a Lagrangian, ${\tilde{L}}_1$, in the form shown in Eq. 5, and applying a covariant Legendre transformation, ${\tilde{H}}_1=P_{\mu }{u}^{\mu }-{\tilde{L}}_1$, leads to a vanishing Hamiltonian. This occurs due to the constraint u^μu_μ = −c². Therefore, ${\tilde{H}}_1$ cannot have the interpretation of energy.⁹ The problem is recognized in [11] where it is stated that instead of dealing with the constrained system, the choice is made to give up the general covariance of ${\tilde{L}}_1$ and instead use the reparametrized Lagrangian, L₁ in Eq. 11 which is claimed to be nonsingular. Then [11] obtains the “space + time” Hamiltonian in Eq. 23 and claims that it is a correction to DeWitt’s result in [3] .

However, it is demonstrated in [51] that even L₁ is singular due to the constraint u^μu_μ = −c². It is also shown in this paper that the Hamiltonians in Eq. 20 and Eq. 23 are equivalent. Therefore, contrary to the statement in [11], it is demonstrated here that both Eq. 20 and Eq. 23 are valid expressions of the “space + time” Hamiltonian despite the fact that they are both derived from a singular Lagrangian, L₁.

Furthermore [9], shows that a covariant Lagrangian of the form ${\tilde{L}}_2=\frac{1}{2}{g}_{\mu \nu }{u}^{\mu }{u}^{\nu }$ will lead to ${\tilde{H}}_2=\frac{1}{2}{g}^{\mu \nu }{P}_{\mu }{P}_{\nu }$. This demonstrates that abandoning covariance is not necessary to obtain a non-vanishing Hamiltonian. Also, both ${\tilde{H}}_1$ and ${\tilde{H}}_2$ lead to equivalent covariant Hamilton canonical equations of motion. Therefore they are equivalent means of describing the same particle dynamics. It will also be shown below that ${\tilde{H}}_2$ leads to the same “space + time” Hamiltonian as ${\tilde{H}}_1$.

As an extension to this approach, it was shown in [12] that electromagnetic fields can also be included by writing ${\tilde{L}}_2=\frac{m}{2}{g}_{\mu \nu }{u}^{\mu }{u}^{\nu }+e{A}_{\mu }{u}^{\mu }$. Like the case of ${\tilde{L}}_1$, this leads to a covariant minimal coupling rule given by p_μ → P_μ − eA_μ. However, unlike ${\tilde{H}}_1$ which vanishes, it is found that ${\tilde{H}}_2=\frac{1}{2m}{g}_{\mu \nu }\left(P^{\mu }-e{A}^{\mu }\right)\left(P^{\nu }-e{A}^{\nu }\right)$ which further confirms the validity of the covariant minimal coupling rule.

This topic is also discussed in [8] where two covariant Hamiltonians are shown. One of them is ${\tilde{H}}_2=-\frac{1}{2m}{\left(p^{\mu }-f^{\mu }\right)}^2$ and the other can be described as ${\tilde{H}}_3=-c{\left[{\left(p^{\mu }-f^{\mu }\right)}^2\right]}^{1/2}$. They both obey the constraint ${\left(p^{\mu }-f^{\mu }\right)}^2=m^2{c}^2$, where f^μ is a function of the external fields and velocities.¹⁰ Furthermore, it is shown that ${\tilde{H}}_2=-\frac{1}{2}m{c}^2$ and ${\tilde{H}}_3=-m{c}^2$. Both Hamiltonians lead to the same canonical equations of motion but with the added feature of including f^μ for external fields.

Lastly, note that the method used in this paper to obtain the “space + time” Hamiltonian in Eq. 20 is different from the method used by [12] to obtain the “space + time” Hamiltonian in Eq. 23. In this paper, ${\tilde{L}}_1$ is used to obtain the canonical momentum. The velocity is also solved in terms of the inverse metric in Eq. 19. Then the velocity and canonical momentum are both substituted into a Legendre transformation¹¹ to obtain Eq. 20. However [12], starts from ${\tilde{L}}_2$ and reparametrizes in terms of coordinate time to obtain L₂ = mv^μp_μ + eA^μv_μ. A Legendre transformation, H₂ = P_ivⁱ − L₂, is again used. However, rather than substituting for the velocity, instead the Lagrangian and kinetic four-momentum, p_μ = P_μ − eA_μ, are used to write the Hamiltonian as H₂ = −cP₀. Then using $g^{\mu \nu }\left(P_{\mu }-e{A}_{\mu }\right)\left(P_{\nu }-e{A}_{\nu }\right)=-m^2{c}^2$, solving algebraically for P₀, and substituting back into H₂ leads to Eq. 23. The key feature of this approach is that the constraint p^μp_μ = −m²c² is utilized explicitly due to ${\tilde{H}}_2=-\frac{1}{2}m{c}^2$, versus the case of ${\tilde{H}}_1$ which vanishes.¹² All of these examples demonstrate that there are numerous ways of obtaining the same “space + time” Hamiltonian appearing in Eq. 20 and equivalently Eq. 23-Eq. 25.

2.3 Quantization of the Canonical Momentum and Hamiltonian

Concerning the quantization of a classical Hamiltonian, it is common to simply promote canonical quantities to quantum operators. Then xⁱ and P_j are replaced with ${\widehat{x}}^i$ and ${\widehat{P}}_j$ which satisfy the canonical quantization condition $\left[{\widehat{x}}^i,{\widehat{P}}_j\right]=i\hslash {\delta }_j^i$. However, the canonical quantization rule developed by Dirac [52–54] involves a formal procedure to go from Poisson brackets to commutators, $\left\{x^i,P_j\right\}\to \frac{1}{i\hslash }\left[{\widehat{x}}^i,{\widehat{P}}_j\right]$.

In [8], it is shown that the general theory of canonical transformations and Poisson brackets in Hamilton-Jacobi theory can be put in covariant form for a single particle. However, it is noted that a relativistic theory of multiple interacting particles introduces the complication that we cannot assume a common proper time for all particles.

In the case of Eq. 32, the issue of proper time is avoided by using a “space + time” approach, as well as the Lorentz factor obtained in Eq. 19. The Lorentz factor essentially removes proper time in favor of coordinate time and the metric. Therefore, Eq. 32 can be generalized to a collection of particles which are assumed to be embedded in the same space-time metric, with velocities measured by an observer in terms of a single coordinate time. This is particularly relevant to the fact that DeWitt states in [3], “For the Hamiltonian of the ensemble of free electrons inside a superconductor, Eq. 2 is replaced by

$H_{DW}=\sum \left\{\frac{1}{2m}{\left[\left({\vec{P}}_n-e\vec{A}\left({\vec{x}}_n\right)-m{\vec{h}}_0\left({\vec{x}}_n\right)\right)\right]}^2\right\}+V_{\text{int}}(34)$

where ${\vec{x}}_n$ and ${\vec{P}}_n$ are the canonical variables of the nth electron and V_int includes the electron-phonon interaction and the phonon energy.”

In [8], it is also pointed out that using $H_3={\left[{\left(p^{\mu }-f^{\mu }\right)}^2\right]}^{1/2}$ versus $H_2=\frac{1}{2mc}{\left(p^{\mu }-f^{\mu }\right)}^2$ in a quantum theory leads to the additional complication of taking the square root of operators, as in the case of Dirac theory (involving anti-commuting matrices). This would seem to favor H₂ for the purposes of describing a quantum system. However, using a “space + time” approach, both H₂ and H₃ lead to Eq. 20 and Eq. 23, which still involve square roots. Therefore, dealing with the issue of square roots (without resorting to anti-commuting matrices) is generally achieved by expanding the Hamiltonian in powers of h_μν and P_i, as is done to obtain Eq. 28. It is assumed in the remainder of this paper that P_i and H can be promoted to the usual quantum mechanical operators, ${\widehat{P}}_i=-i\hslash {\partial }_i$ and $\widehat{H}=i\hslash {\partial }_t$, respectively. However, for a formal treatment of quantizing manifestly Lorentz-invariant Lagrangians, see [55, 56].

Lastly, a modified Schrödinger equation can be obtained from Eq. 33. Dropping the rest mass energy and acting the Hamiltonian on a wave function, $\psi \left(x,t\right)$, leads to

$i\hslash {\partial }_t\psi \left(x,t\right)=\left[\frac{1}{2m}{\left(-\hslash {\partial }_i-e{\eta }_{ij}{A}^j\right)}^2+4i\hslash h^i{\partial }_i+8m{h}^2+m{\phi }_G-\frac{m{\phi }_G^2}{2c^2}+e\phi \right]\psi \left(x,t\right)(35)$

In the absence of gravity, this reduces to the usual Schrödinger equation in the presence of an electromagnetic field. In that case, the solution could be written as $\psi \left(x,t\right)=e^{i\varphi }{\psi }_0\left(x,t\right)$, where ${\psi }_0\left(x,t\right)$ is the solution to the field-free Schrödinger equation, and the phase is $\varphi =\frac{e}{\hslash }\int A^{i}d{x}^i$. If the presence of gravity introduced a modification to the Hamiltonian given by ${\left({\widehat{P}}_i-e{\eta }_{ij}{A}^j\right)}^2\to {\left({\widehat{P}}_i-e{\eta }_{ij}{A}^j-4m{\eta }_{ij}{h}^j\right)}^2$, then the phase would become

$\varphi =\frac{1}{\hslash }\int {\eta }_{ij}\left(e{A}^j+4m{h}^j\right)d{x}^i(36)$

similar to what is shown in [14, 15, 30, 35, 40, 42, 44, 47]. However, this is not how the presence of gravity appears in Eq. 35. Rather, gravity enters as a multiplicative factor to a first derivative term, hⁱ∂_i, not an additive factor inside the second derivative term. In fact, attempting to use ψ = e^iϕψ₀, with a phase given by Eq. 36, leads to ${\left(-i\hslash {\partial }_i-e{\eta }_{ij}{A}^j\right)}^2{\psi }_0={\left(-i\hslash {\partial }_i+4m{\eta }_{ij}{h}^j\right)}^2{\psi }_0$ and $i\hslash h^i{\partial }_i{\psi }_0=\left(i\hslash h^i{\partial }_i-e{\eta }_{ij}{h}^i{A}^j-4m{h}^2\right){\psi }_0$. Substituting these into Eq. 35 does not lead to the field-free Schrödinger equation.

This topic can be understood in the context of a covariant Ginzburg-Landau model [50, 57–63]. The transformations of a complex scalar field and the four-potential can be written, respectively, as $\psi \to e^{\frac{iq\chi }{\hslash }}\psi$ and A_μ → A_μ + ∂_μχ, where χ is an arbitrary scalar function. In flat space-time, the gauge covariant derivative is $D_{\mu }={\partial }_{\mu }-\frac{iq}{\hslash }{A}_{\mu }$ which also transforms as $D_{\mu }\to e^{\frac{iq\chi }{\hslash }}{D}_{\mu }$. Therefore, the gauge freedom of ψ and A_μ can be unified in a fully covariant approach. Notice that the gauge freedom of A_μ leads effectively to a phase factor e^iqχ in D_μ. This is analogous to the presence of Aⁱ in Eq. 35 leading to a phase factor e^iϕ in $\psi \left(x,t\right)$.

In curved space-time, the gauge covariant derivative becomes $D_{\mu }={\nabla }_{\mu }-\frac{iq}{\hslash }{A}_{\mu }$, where ∇_μ is the covariant derivative involving Christoffel symbols [10, 11, 47, 58, 59, 62], [64–66]. However, the gauge covariant derivative still transforms as $D_{\mu }\to e^{\frac{iq\chi }{\hslash }}{D}_{\mu }$ even in curved space-time. This means that the phase factor e^iqχ is unaffected by the presence of gravity. This is because in General Relativity (or any metric theory of gravity), the gravitational “field” is not an additional field on the same footing as electromagnetism, rather it introduces curvature to the otherwise flat space-time that all other fields live in.¹³ This is represented by the fact that ∂_μ → ∇_μ. Furthermore, the spatial part of the gauge covariant derivative is $D_i={\nabla }_i-\frac{iq}{\hslash }{A}_i$, where ∇_i is intended to denote a derivative involving Christoffel symbols, not just a gradient. Notice that the covariant derivative is not $D_i={\partial }_i-\frac{i}{\hslash }\left(q{A}_i+m{h}_i\right)$ as stated in [25], [71–75].

In fact, since the gauge covariant derivative transforms as $D_{\mu }\to e^{\frac{iq\chi }{\hslash }}{D}_{\mu }$, and the wave function transforms as $\psi \to e^{\frac{iq\chi }{\hslash }}\psi$, then incorrectly assuming the solution to Eq. 35 is ψ = e^iϕψ₀, where the phase is Eq. 36, gives the false impression that $\left(e\vec{A}+4m\vec{h}\right)$ transforms as $\left(e\vec{A}+4m\vec{h}\right)\to \left(e\vec{A}+4m\vec{h}\right)+\nabla \chi$. However, $\vec{A}$ and $\vec{h}$ do not have identical transformation properties. To linear order, the gauge (coordinate) freedom of the perturbation is h_μν → h_μν + ∂_μξ_ν + ∂_νξ_μ, where ξ^μ is associated with a coordinate transformation such as x^μ → x^μ + ξ^μ. This is contrary to what is shown in [40] where the gauge freedom of $\vec{h}$ is written as $\vec{h}\to \vec{h}+\nabla \mu$, where μ is an arbitrary scalar function.¹⁴

A possible cause for confusion is the fact that quantizing the canonical momentum Eq. 16 leads to

$-i\hslash {\partial }_i\to -i\hslash {\partial }_i-\gamma m\left(c{h}_{0i}+h_{ij}{v}^j\right)+q\left({\eta }_{ij}{A}^j+h_{0i}{A}^0+h_{ij}{A}^j\right)(37)$

This seems to imply that $D_i={\partial }_i-\frac{i}{\hslash }\left(q{\eta }_{ij}{A}^j+mc{h}_{0i}\right)+\cdots$ is the gauge covariant derivative to be used in the Schrödinger equation, $\widehat{H}\psi =\frac{{\hslash }^2}{2m}{D}_i^2\psi +V\psi$. However, Eq. 35 demonstrates that this is not the case.

In fact, since Eq. 35 involves a second order spatial derivative, then this issue can be further understood by starting from a second order covariant derivative acting on a scalar wave function in the absence of electromagnetic fields: g^μν∇_μ∇_νψ. Since ψ is a scalar, then the first covariant derivative of ψ is just a partial derivative: ∇_νψ = ∂_νψ. However, since ∂_νψ is a vector, then acting the second covariant derivative brings in the Christoffel symbol: $g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }\psi =g^{\mu \nu }{\partial }_{\mu }{\partial }_{\nu }\psi +g^{\mu \nu }{\mathrm{\Gamma }}_{\mu \nu }^{\sigma }\left({\partial }_{\sigma }\psi \right)$. Using g_μν = η_μν + h_μν, choosing harmonic coordinates, $g^{\mu \nu }{\mathrm{\Gamma }}_{\mu \nu }^{\sigma }=0$, and remaining to first order in the perturbation leads to

$g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }\psi =-\frac{1}{c^2}\left(1-h_{00}\right)\ddot{\psi }-\frac{2}{c}{h}_{0i}{\partial }_i\acute{\psi }+\left({\partial }_i^2+h_{ij}{\partial }_i{\partial }_j\right)\psi (38)$

Similar to Eq. 35, it is found that h_0i multiplies a first derivative term, rather than appearing as an additive factor inside the second derivative term. Furthermore, Eq. 38 can be used to write the Klein-Gordon equation in curved space-time as $\left(g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }-k_c^2\right)\psi =0$, where k_c = mc/ℏ is the Compton wave number [15, 65, 66, 76]. Since the Klein-Gordon equation is $g^{\mu \nu }{\widehat{P}}_{\mu }{\widehat{P}}_{\nu }=-m^2{c}^4$, with ${\widehat{P}}^{\mu }=\left(\widehat{E}/c,{\widehat{P}}^i\right)$, then the Schrödinger equation can be obtained by taking the non-relativistic limit. Using g_μν = η_μν + h_μν and ${\widehat{P}}_i=g_{i\mu }{\widehat{P}}^{\mu }$ leads to

$\widehat{E}=\left(1+\frac{1}{2}{h}_{00}\right)m{c}^2+\frac{{\widehat{P}}_i^2}{2m}+2c{h}_{0i}{\widehat{P}}_i+\frac{h_{00}{\widehat{P}}_i^2}{4m}+\frac{3h_{ij}{\widehat{P}}_i{\widehat{P}}_j}{2m}(39)$

Again, notice that h_0i is multiplying ${\widehat{P}}_i$ which is consistent with Eq. 35 and Eq. 38.

In summary, the distinction between the way gravity and electromagnetism couple to a quantum field is fundamentally the reason for the difference in the way they appear in the modified Schrödinger equation Eq. 35, and the reason why it is not the case that ψ = e^iϕψ₀, where ψ₀ is the solution to the field-free Schrödinger equation if the phase is assumed to be Eq. 36. However, it will be shown in Sections 6, 7 that the canonical momentum Eq. 13 can be used to obtain a quantum phase with terms that include those appearing in Eq. 36.

2.4 Alternative Hamiltonians and Methods of Coupling Gravity to a Superconductor

On a more fundamental level, ${\tilde{H}}_1$ and ${\tilde{H}}_2$ are derived respectively from Lagrangians, ${\tilde{L}}_1$ and ${\tilde{L}}_2$, which are both associated with the geodesic equation of motion Eq. 7. However, the geodesic equation of motion is subject to the Equivalence Principle which makes it possible to transform into a frame of reference where all gravitational effects vanish. Stated another way, there is no unique absolute motion of a test particle since the observed motion of a particle depends on the frame of reference of the observer.

However, the relative motion between a particle and an observer is uniquely described by the geodesic deviation equation. Therefore, it is argued in [77, 78] that a Hamiltonian based on the geodesic deviation equation is preferred (which involves the Riemann curvature tensor) versus a Hamiltonian based on the geodesic equation (which involves the Christoffel symbols). A similar approach was used by Weber¹⁵ in the context of gravitational wave detection [79].

In fact, it is shown in [78] that for the case of gravitational waves (in the weak field, low velocity limit), the Lagrangian leading to the geodesic deviation equation is $L=\frac{1}{2}m\left(v^2-{\dot{h}}_{ij}{v}^i{x}^j\right)$, where xⁱ is the coordinate distance of the test particle from the observer. The associated interaction Hamiltonian is $H_{\mathit{int}}={\dot{h}}_{ij}{p}^i{x}^j/2$. This result clearly differs from Eq. 31 which predicts the interaction Hamiltonian is $H_{\mathit{int}}=h_{ij}{p}^i{p}^j/\left(2m\right)$. This discrepancy in Hamiltonians is directly parallel to the fact that the geodesic equation of motion (for the same conditions) is $\frac{d^2{x}^i}{d{t}^2}=-{\dot{h}}_{ij}{v}^j$, while the geodesic deviation equation is $\frac{d^2{x}^i}{d{t}^2}={\ddot{h}}_{ij}{x}^j/2$. Note that the latter is what is physically observed by a gravitational wave detector such as LIGO [36]. The former gives the false impression that a detector must be in motion to interact with the gravitational wave. This further highlights the importance of carefully considering the approach to formulating a Hamiltonian that correctly describes the physically observed effects of gravity on a quantum system.¹⁶

Another approach is the use of Fermi normal coordinates¹⁷ which also expresses the Hamiltonian in terms of the Riemann curvature tensor (which is coordinate invariant) rather than Christoffel symbols (which are coordinate dependent) [16, 34], [83–86]. There are also other approaches that depart entirely from the use of a Lagrangian associated with either the geodesic equation of motion or the geodesic deviation equation. For example [87], uses a Ginzburg-Landau free energy density that includes a coupling to gravity via a term involving the Ricci scalar.

On the other hand [88], uses a Hamiltonian derived from an effective field theory describing a system of quantum oscillators coupled to a stochastic gravitational radiation background, where the coupling to gravity occurs via a parameter associated with an Ohmic bath spectral density. Although [88] does not consider a superconductor, it is possible that a similar treatment could be used to describe the coupling of the stochastic gravitational wave background to a superconductor. Fundamentally, the coupling of the quantum system to gravity is obtained via the action for a scalar field stress tensor coupled to the curved space-time background [89].

On a related note, it should be emphasized that the action in Eq. 8 only describes the particle dynamics but treats electromagnetism and gravity as fixed background fields with no dynamics. This means that any fields produced by the motion of test particles (which are Cooper pairs leading to a supercurrent) are neglected. However, in Section 4 it is evident that the supercurrent does indeed produce fields which can lead to a Meissner effect. Therefore, a complete action should also include the dynamics of the fields by including terms for electromagnetism and gravity which are, respectively, $S_{EM}=-\frac{1}{4{\mu }_0}\int F^{\mu \nu }{F}_{\mu \nu }\sqrt{-g}{d}^{4}x$ and $S_G=\frac{1}{2\kappa }\int R\sqrt{-g}{d}^{4}x$, where R is the Ricci scalar, and g is the determinant of the metric [50, 74, 75]. In fact, the action associated with particle dynamics could be replaced by an action describing the current density, $S_C=\int J^{\mu }{A}_{\mu }\sqrt{-g}{d}^{4}x$.

It is also shown in [10] that a Ginzburg-Landau Lagrangian density in curved space-time can be used to obtain a quantum current density and quantum stress tensor. The action has the form $S_{GL}=-\frac{1}{2}\int \left[g^{\mu \nu }{\left(D_{\mu }\varphi \right)}^{*}\left(D_{\nu }\varphi \right)-{\mu }^2{\left|\varphi \right|}^2+\frac{\lambda }{2}{\left|\varphi \right|}^4\right]\sqrt{-g}{d}^{4}x$, where ϕ is a complex scalar field, and μ and λ are coupling parameters. This action is effectively “phi-fourth” field theory due to the quartic self-interaction term [60, 61]. Other treatments for embedding phi-fourth (covaraint Ginzburg-Landau) theory in curved space-time are found in [62, 64], [90–93]. All of the treatments described above demonstrate there is a great diversity in the approaches that can be taken to couple gravity to superconductors and quantum systems in general. However, the remainder of this paper will focus on the coupling described by quantizing the canonical momentum in Eq. 13.

3 Modified London Equations and Gauge Condition

In this section, gravito-electromagnetic field equations are introduced, and constitutive equations are developed from the canonical momentum and combined with the field equations to obtain a modified form of the London equations [94–96]. Using harmonic coordinates, ${\partial }^{\nu }{\bar{h}}_{\mu \nu }=0$, makes the linearized Einstein equation, G^μν = κT^μν, become $\square {\bar{h}}^{\mu \nu }=-2\kappa T^{\mu \nu }$, where κ = 8πG/c⁴. For a non-relativistic ideal fluid, the components of the stress tensor are

$T^{00}\approx {\rho }_M{c}^2,T^{0i}\approx {\rho }_{M}c{V}^i,T^{ij}\approx 0(40)$

where ρ_M is mass density, and Vⁱ is the velocity, of the gravitational sources. Note that in the presence of electromagnetic fields, the full stress tensor should also include

$T_{\left(EM\right)}^{\mu \nu }=\frac{1}{{\mu }_0}\left(g_{\alpha \beta }{F}^{\mu \alpha }{F}^{\nu \beta }-\frac{1}{4}{g}^{\mu \nu }{g}_{\alpha \rho }{g}_{\beta \sigma }{F}^{\rho \sigma }{F}^{\alpha \beta }\right)(41)$

where the components of the electromagnetic strength tensor are

$F^{0i}=\frac{1}{c}{E}^i,F^{ij}={\epsilon }^{\mathit{ijk}}{B}^k,F^{\mu \nu }=-F^{\nu \mu },F^{\mu \mu }=0(42)$

To lowest order, using E = cB, the components of Eq. 41 are

$T_{\left(EM\right)}^{00}\approx B^2/{\mu }_0,T_{\left(EM\right)}^{0i}\approx {\epsilon }^{\mathit{ijk}}{B}^j{B}^k/{\mu }_0,T_{\left(EM\right)}^{ij}\approx \left({\eta }^{ij}{B}^2-2B^j{B}^i\right)/{\mu }_0(43)$

Comparing Eq. 43 to Eq. 40, it is evident that the contribution of electromagnetic fields to the total stress tensor can be neglected provided B²/μ₀ ≪ ρ_McV. For a superconductor such as niobium, we can use ρ_M ∼ 10⁴ kg/m³. It is also shown in Supplementary Appendix SB that a maximum of v ∼ 10⁴ m/s will preserve the superconducting state¹⁸. This leads to B ≪ 10⁵ T which is certainly satisfied in a laboratory setting.

Since T^ij ≈ 0, then ${\bar{h}}^{ij}\approx 0$ in this approximation. A time-independent gravito-electric field (the Newtonian gravitational field) and a gravito-magnetic (Lense-Thirring) field can also be defined respectively as¹⁹

$\begin{array}{ll}\hfill {\vec{E}}_G& \equiv -\nabla {\phi }_G\text{and}{\vec{B}}_G\equiv \nabla \times \vec{h}\hfill \\ \hfill & \hfill \end{array}(44)$

Defining the mass current density as $J_M^i=T^{0i}/c={\rho }_M{V}_i$, leads to non-homogeneous field equations given by

$\nabla \cdot {\vec{E}}_G=-\frac{{\rho }_M}{{\epsilon }_G}\text{and}\nabla \times {\vec{B}}_G=-{\mu }_G{\vec{J}}_M+\frac{1}{c^2}{\partial }_t{\vec{E}}_G(45)$

where ${\epsilon }_G\equiv 1/\left(4\pi G\right)$ and μ_G ≡ 4πG/c². The field equations in Eq. 45 can be described as a gravito-Gauss law (Newton’s law of gravitation), and a gravito-Ampere law, respectively.

To develop constitutive equations for a superconductor, we begin by promoting the canonical momentum in Eq. 13 to a quantum mechanical operator, ${\widehat{P}}_i=-i\hslash {\partial }_i$, and act on the Ginzburg-Landau complex order parameter, $\mathrm{\Psi }\left(r\right)=\psi \left(r\right)e^{i\vec{p}\cdot \vec{r}}$, where ψ² = n_s is the number density of Cooper pairs. This gives

${\widehat{P}}_i\mathrm{\Psi }=\left[\gamma m\left(c{g}_{0i}+g_{ij}{\widehat{v}}^j\right)-q\left(g_{0i}{\widehat{A}}^0+g_{ij}{\widehat{A}}^j\right)\right]\mathrm{\Psi }(46)$

This can be considered a semiclassical approach where the gravitational field, h_μν, is still a classical field while $\widehat{P}$, $\widehat{v}$, and $\widehat{A}$ are quantum operators that act on the Cooper pair state, Ψ. Since the bulk of the superconductor is in the zero-momentum eigenstate, then ${\widehat{P}}_i\mathrm{\Psi }=p_0\mathrm{\Psi }=0$. Then taking the expectation value gives

$0=\gamma m\left(c{g}_{0i}+g_{ij}⟨{\widehat{v}}^j⟩\right)-q\left(g_{0i}⟨{\widehat{A}}^0⟩+g_{ij}⟨{\widehat{A}}^j⟩\right)(47)$

Applying Ehrenfest’s theorem allows this equation to return to a classical equation of motion once again. To first order in the metric perturbation, and first order in test mass velocity, Eq. 12 becomes γ ≈ 1 + h₀₀/2 + h_0jv^j/c. Then using Eq. 29 and Eq. 30 in Eq. 47, remaining to first order in the metric perturbation, and using q = −e and m = m_e for electrons, leads to

$\vec{v}=-\left(1+\frac{{\phi }_G}{c^2}\right)\frac{e}{m_e}\vec{A}-4\left(1+\frac{e\phi }{m_e{c}^2}\right)\vec{h}(48)$

A similar expression appears in [19] but the scalar potentials, φ and φ_G, are absent. The charge and mass supercurrent densities are, respectively²⁰

${\vec{J}}_c=-n_{s}q\vec{v}\text{and}{\vec{J}}_m=n_{s}m\vec{v}(49)$

where n_s is the number density of Cooper pairs. Inserting Eq. 48 into Eq. 49

${\vec{J}}_c=-{\mathrm{\Lambda }}_L\left(\alpha \vec{A}+\beta \vec{h}\right)(50)$

and

${\vec{J}}_m=-n_{s}e\left(\alpha \vec{A}+\beta \vec{h}\right)(51)$

where Λ_L ≡ n_se²/m_e can be defined as the London constant, and

$\alpha \equiv 1+\frac{{\phi }_G}{c^2},\beta \equiv \frac{4\left(m_e{c}^2+e\phi \right)}{e{c}^2}(52)$

The expressions in Eq. 50 and Eq. 51 are the London constitutive equations for a non-relativistic supercurrent in the presence of electromagnetism and gravity (from non-relativistic gravitational sources in harmonic coordinates). Similar expressions can be found in [22–24], [26], however, with α = 1 and β = m_e/e which is a special case where φ_G = 0 and φ = 0. Notice that if $\vec{h}=0$, then Eq. 50 becomes the standard London constitutive equation, ${\vec{J}}_c=-{\mathrm{\Lambda }}_L\vec{A}$. Also notice that setting the charge to zero in Eq. 51 gives ${\vec{J}}_m=-4n_s{m}_e\vec{h}$ which is the constitutive equation for a neutral superfluid in the presence of a gravito-vector potential. Taking a time derivative of Eq. 50 and Eq. 51, and using the fact that ∇φ = 0 inside a superconductor²¹ and ${\partial }_t\vec{h}=0$ in this approximation, leads to

${\partial }_t{\vec{J}}_c={\mathrm{\Lambda }}_L\left(\alpha \vec{E}-\frac{1}{c^2}{\dot{\phi }}_G\vec{A}-\frac{4}{c^2}\dot{\phi }\vec{h}\right)(53)$

and

${\partial }_t{\vec{J}}_m=e{n}_s\left(\alpha \vec{E}-\frac{1}{c^2}{\dot{\phi }}_G\vec{A}-\frac{4}{c^2}\dot{\phi }\vec{h}\right)(54)$

Equations similar to Eq. 53 and Eq. 54 are also obtained in [17, 21, 22, 24, 71, 72], but with the absence of the gravitational and electric scalar potentials which means α = 1, ${\dot{\phi }}_G=0$, and $\dot{\phi }=0$. Also, these authors include a term involving ${\vec{E}}_G=-{\partial }_t\vec{h}$ which is not valid since it was shown that ${\partial }_t\vec{h}\approx 0$ for non-relativistic gravitational sources. Notice that Eq. 53 is the usual electric London equation, ${\partial }_t{\vec{J}}_c={\mathrm{\Lambda }}_L\vec{E}$, but with correction terms due to gravity. Also, Eq. 54 is a redundant equation since ${\vec{J}}_c={\vec{J}}_m\left(e/m_e\right)$, however, for a neutral superfluid, only Eq. 54 would be relevant.

Taking the curl of Eq. 50 and Eq. 51, and using Eq. 44, leads to, respectively,

$\nabla \times {\vec{J}}_c=-{\mathrm{\Lambda }}_L\left(\alpha \vec{B}+\beta {\vec{B}}_G-\frac{1}{c^2}{\vec{E}}_G\times \vec{A}\right)(55)$

and

$\nabla \times {\vec{J}}_m=-n_{s}e\left(\alpha \vec{B}+\beta {\vec{B}}_G-\frac{1}{c^2}{\vec{E}}_G\times \vec{A}\right)(56)$

Similar expressions can be found in [17, 20, 71, 72], however, with α = 1 and β = m_e/e. Notice that Eq. 55 is the usual magnetic London equation, $\nabla \times {\vec{J}}_c=-{\mathrm{\Lambda }}_L\vec{B}$, but with correction terms due to gravity. For the case of a neutral superfluid, setting the charge to zero makes Eq. 56 become

$\nabla \times {\vec{J}}_m=-4n_s{m}_e{\vec{B}}_G(57)$

The same result is obtained in [26, 27, 62, 73, 100]. A result similar to Eq. 57 is also obtained in [74, 75], however, it will be shown later that there is a critical sign difference which impacts whether a gravito-magnetic Meissner effect is predicted to occur in the absence of a magnetic field.

Concerning the gauge condition, note that the usual London gauge, $\nabla \cdot \vec{A}=0$, follows from the London constitutive equation, ${\vec{J}}_c=-{\mathrm{\Lambda }}_L\vec{A}$, with the requirement $\nabla \cdot {\vec{J}}_c=0$. By the continuity equation, this means ∂_tρ_c = 0 which is consistent with a static Cooper pair density $\left({\rho }_c=2n_{s}e\right)$ in the interior of the superconductor. Applying the same condition, $\nabla \cdot {\vec{J}}_c=0$, to the modified London constitutive equation in Eq. 50 leads to a new gauge condition given by $\nabla \cdot \left(\alpha \vec{A}+\beta \vec{h}\right)=0$. Using Eq. 52 and ∇φ = 0 yields

$\alpha \nabla \cdot \vec{A}-\frac{1}{c^2}\left({\vec{E}}_G\cdot \vec{A}\right)+\beta \nabla \cdot \vec{h}=0(58)$

This is the modified gauge condition associated with the London equations developed above. It is similar to the gauge condition shown in [74, 75] as $\left({\vec{A}}_e+\frac{m}{e}{\vec{A}}_g\right)=0$, except Eq. 58 has an additional term involving ${\vec{E}}_G\cdot \vec{A}$ is absent. On the other hand [19, 20, 23], set $\nabla \cdot \vec{A}=0$ and $\nabla \cdot {\vec{A}}_g=0$ as independent gauge conditions. Note that due to the use of harmonic coordinates, ${\partial }_{\nu }{\bar{h}}^{\mu \nu }=0$, the last term in Eq. 58 can also be expressed using $\nabla \cdot \vec{h}=-{\dot{\phi }}_G/c^2$. This means that for a static gravitational scalar potential, the last term in Eq. 58 vanishes from the gauge condition.

Lastly, taking the curl of Eq. 55, using $\nabla \times \left(\nabla \times {\vec{J}}_c\right)=\nabla \left(\nabla \cdot {\vec{J}}_c\right)-{\nabla }^2{\vec{J}}_c$, where $\nabla \cdot {\vec{J}}_c=0$, and making use of Eq. 52 and Eq. 45, as well as ∇φ = 0 and ${\vec{J}}_c={\vec{J}}_m\left(e/m_e\right)$ leads to

${\nabla }^2{\vec{J}}_c-\left(\alpha {\mu }_0{\mathrm{\Lambda }}_L-\beta {\mu }_G{n}_{s}e\right){\vec{J}}_c+\frac{{\mathrm{\Lambda }}_L}{c^2}\left[E_G\times \vec{B}+\nabla \times \left({\vec{E}}_G\times \vec{A}\right)\right]=0(59)$

It will be shown in the following section that αμ₀Λ_L ≫ βμ_Gn_se and α ≈ 1. Also, using $\alpha {\mu }_{0}J\gg {\vec{E}}_{G}B/c^2$ makes Eq. 59 reduce to a Yukawa-like equation,

${\nabla }^2{\vec{J}}_c-{\lambda }_L^{-2}{\vec{J}}_c\approx 0(60)$

where the London penetration depth is

${\lambda }_L^2={\left({\mu }_0{\mathrm{\Lambda }}_L\right)}^{-1}=\frac{m_e}{{\mu }_0{n}_s{e}^2}(61)$

Notice that Eq. 59 contains a quantity which can be defined as

$k^2\equiv \alpha {\mu }_0{\mathrm{\Lambda }}_L-\beta {\mu }_G{n}_{s}e(62)$

As explained in the following section, this quantity can be understood as leading to a modified London penetration depth, ${\lambda }_L^{\prime }\equiv 1/k$.

4 Meissner Effects and Penetration Depths for Magnetic and Gravito-Magnetic Fields

The Maxwell equation (with sources) in curved space-time is

${\nabla }_{\nu }{F}^{\mu \nu }={\mu }_0{J}_c^{\mu }(63)$

where $J_c^{\mu }$ is the charge four-current [4]. The covariant derivative of the strength tensor is

$\begin{array}{l}\hfill {\nabla }_{\nu }{F}^{\mu \nu }={\partial }_{\nu }{F}^{\mu \nu }+{\mathrm{\Gamma }}_{\nu \sigma }^{\nu }{F}^{\sigma \mu }+{\mathrm{\Gamma }}_{\nu \sigma }^{\mu }{F}^{\nu \sigma }\end{array}(64)$

Since ${\mathrm{\Gamma }}_{\nu \sigma }^{\mu }$ is symmetric in νσ, and F^νσ is anti-symmetric in νσ, then the last term above is zero. The linearized Christoffel symbols are

${\mathrm{\Gamma }}_{\nu \gamma }^{\mu }=\frac{1}{2}{\eta }^{\mu \rho }\left({\partial }_{\gamma }{h}_{\rho \nu }+{\partial }_{\nu }{h}_{\gamma \rho }-{\partial }_{\rho }{h}_{\nu \gamma }\right)(65)$

Then Eq. 63 becomes

$\begin{array}{ll}\hfill {\partial }_{\nu }{F}^{\mu \nu }+\frac{1}{2}{\eta }^{\nu \rho }\left({\partial }_{\sigma }{h}_{\rho \nu }+{\partial }_{\nu }{h}_{\sigma \rho }-{\partial }_{\rho }{h}_{\nu \sigma }\right)F^{\sigma \mu }& ={\mu }_0{J}_c^{\mu }\hfill \\ \hfill & \hfill \end{array}(66)$

Setting μ = i, and using Eq. 30, Eq. 44, and Eq. 42 leads to

$\nabla \times \vec{B}={\mu }_0{\vec{J}}_c+\frac{1}{c^2}{\partial }_t\vec{E}+\frac{2}{c^2}\left(\frac{{\dot{\phi }}_G}{c^2}\vec{E}+{\vec{E}}_G\times \vec{B}\right)(67)$

This is the usual Ampere law but with added corrections due to the presence of gravity.

Assume a steady-state supercurrent so that ${\partial }_t\vec{E}=0$, and a static gravitational scalar potential so that ${\dot{\phi }}_G=0$. Taking the curl of Eq. 67, using the identity $\nabla \times \left(\nabla \times \vec{B}\right)=\nabla \left(\nabla \cdot \vec{B}\right)-{\nabla }^2\vec{B}$, where $\nabla \cdot \vec{B}=0$, and using Eq. 55 leads to

${\nabla }^2\vec{B}={\mu }_0{\mathrm{\Lambda }}_L\left(\alpha \vec{B}+\beta {\vec{B}}_G-\frac{1}{c^2}{\vec{E}}_G\times \vec{A}\right)+\frac{2}{c^2}\left[\vec{B}\left(\nabla \cdot {\vec{E}}_G\right)-\left(\vec{B}\cdot \nabla \right){\vec{E}}_G+\left({\vec{E}}_G\cdot \nabla \right)\vec{B}\right](68)$

Since ${\vec{E}}_G$ is primarily due to earth, then the spatial variation of ${\vec{E}}_G$ over the dimensions of the superconductor is negligible. Therefore $\left(\vec{B}\cdot \nabla \right){\vec{E}}_G\approx 0$. Also, if ${\vec{E}}_G=E_G\widehat{z}$, and the magnetic field is arranged in the x- or y-direction, then $\left({\vec{E}}_G\cdot \nabla \right)\vec{B}=0$. Lastly using $\nabla \cdot {\vec{E}}_G=-{\rho }_M/{\epsilon }_G$ leads to

${\nabla }^2\vec{B}={\mu }_0{\mathrm{\Lambda }}_L\left({\alpha }^{\prime }\vec{B}+\beta {\vec{B}}_G-\frac{1}{c^2}{\vec{E}}_G\times \vec{A}\right)(69)$

where

${\alpha }^{\prime }\equiv 1+\frac{{\phi }_G}{c^2}-\frac{2{\rho }_M}{{\mu }_0{\mathrm{\Lambda }}_L{c}^2{\epsilon }_G}(70)$

Notice that α′ differs from α in Eq. 52 by an additional factor given by $2{\rho }_M/\left({\mu }_0{\mathrm{\Lambda }}_L{c}^2{\epsilon }_G\right)\sim 10^{-40}$, assuming the mass density of earth and the superconducting sample are $\sim 10^4$ kg/m³, and ${\mu }_0{\mathrm{\Lambda }}_L={\lambda }_L^{-2}\sim 10^{18}$ m^-2, where λ_L ∼ 10⁻⁹ m is the London penetration depth of a superconductor such as niobium. Note that at the surface of earth, ${\phi }_G/c^2\approx G{M}_E/\left(c^2{R}_E\right)\sim 10^{-9}$, where M_E and R_E are the mass and radius of earth, respectively. Since the last term in Eq. 70 is 31 orders of magnitude smaller than the second term, then α′ ≈ α.

A similar treatment can be applied to the gravito-Ampere law in Eq. 45 which is $\nabla \times {\vec{B}}_G=-{\mu }_G{\vec{J}}_m$ for the case of a steady-state supercurrent. Taking the curl, using $\nabla \times \left(\nabla \times {\vec{B}}_G\right)=\nabla \left(\nabla \cdot {\vec{B}}_G\right)-{\nabla }^2{\vec{B}}_G$, where $\nabla \cdot {\vec{B}}_G=0$, and using Eq. 56 leads to

${\nabla }^2{\vec{B}}_G=-{\mu }_G{n}_{s}e\left(\alpha \vec{B}+\beta {\vec{B}}_G-\frac{1}{c^2}{\vec{E}}_G\times \vec{A}\right)(71)$

Coupled differential equations similar to Eq. 69 and Eq. 71 can also be found in [18–22]. In the absence of gravity, α = 1 and ${\vec{B}}_G=0$. Then Eq. 69 becomes a Yukawa-like equation²², ${\nabla }^2\vec{B}-{\lambda }_L^{-2}\vec{B}=0$, where the London penetration depth is given in Eq. 61. The general solution for the magnetic field is

$\vec{B}={\vec{c}}_1{e}^{-{\lambda }_L^{-1}z}+{\vec{c}}_2{e}^{{\lambda }_L^{-1}z}+{\vec{c}}_3(72)$

where ${\vec{c}}_1$, ${\vec{c}}_2$, ${\vec{c}}_3$ are constant vectors.

For a superconducting slab occupying the region z > 0, where z is the distance from the surface to the interior of the superconductor, then the boundary conditions for the magnetic field are

$\vec{B}\left(0\right)={\vec{B}}_0\text{and}\underset{z\to \infty }{\lim }\vec{B}\left(z\right)\to 0(73)$

where ${\vec{B}}_0$ is the magnetic field at the surface of the superconductor. These conditions require ${\vec{c}}_2^{\prime },{\vec{c}}_3^{\prime }=0$ , and ${\vec{c}}_1^{\prime }={\vec{B}}_0$ . Then Eq. 72 reduces to $\vec{B}={\vec{B}}_0{e}^{-z/{\lambda }_L}$ . This is the standard Meissner effect which predicts that the magnetic field vanishes within the superconductor at depths beyond the London penetration depth.

Three other cases are now considered which involve gravity:

1. The presence of only ${\vec{B}}_G$

2. The effect of ${\vec{B}}_G$ on the penetration depth of $\vec{B}$

3. The effect of $\vec{B}$ on the penetration depth of ${\vec{B}}_G$

4.1 The Presence of Only ${\vec{B}}_G$

If ${\vec{B}}_G$ is the only field present (or equivalently, a neutral superfluid is used), then Eq. 71 becomes ${\nabla }^2{\vec{B}}_G=-4{\mu }_G{n}_s{m}_e{\vec{B}}_G$ which is a Helmholtz-like differential equation (rather than a Yukawa-like differential equation), and therefore only allows sinusoidal solutions, not exponential solutions. Since there is no exponential decay of the field then there is no penetration depth and no associated Meissner effect. The reason can be traced back to the difference in the sign appearing in the magnetic field equation, $\nabla \times \vec{B}={\mu }_0{\vec{J}}_c$ , and the gravito-magnetic field equation, $\nabla \times {\vec{B}}_G=-{\mu }_G{\vec{J}}_m$ . The negative sign in the gravito-Ampere law eliminates a gravitational Meissner effect for a neutral superfluid. Physically speaking, this implies a paramagnetic effect instead of a diamagnetic (Meissner) effect.

In fact, for a maximum gravito-magnetic field at the surface of the superconductor $\left(z=0\right)$ , the solution to the gravito-Ampere field equation would have the form ${\vec{B}}_G={\vec{B}}_{G,0}\cos \left(2\pi z/\tilde{\lambda }\right)$ , where ${\vec{B}}_{G,0}$ is the gravito-magnetic field at the surface of the superconductor, and the spatial periodicity in the field is

${\lambda }_{\left(\text{periodicity\hspace{0.17em}of\hspace{0.17em}}{\vec{B}}_G\right)}\equiv \frac{2\pi }{\sqrt{4{\mu }_G{n}_s{m}_e}}(74)$

Note that Eq. 74 can also be written in the following alternative forms using μ _G = 4πG/c ² and Eq. 61.

${\lambda }_{\left(\text{periodicity\hspace{0.17em}of\hspace{0.17em}}{\vec{B}}_G\right)}=\sqrt{\frac{\pi c^2}{4G{n}_s{m}_e}}=\frac{\pi e}{m_e}\sqrt{\frac{{\mu }_0}{{\mu }_G}}{\lambda }_L(75)$

To obtain a numerical estimate for this quantity, consider a superconductor such as niobium which has a London penetration depth of λ _L ∼ 10⁻⁹ m. Then Eq. 75 gives approximately 10²² λ _L ∼ 10¹³ m which is clearly not observable on a terrestrial scale.

The absence of a gravito-magnetic Meissner effect (when $\vec{B}=0$ ) is in agreement with [20, 49, 71, 72], but in disagreement with [19, 26, 27, 62], [73–75], [100]. In most of the papers that predict a gravito-magnetic Meissner effect (with $\vec{B}=0$ ), it is due to a minus sign error somewhere in the calculation. In some cases, finding the error requires careful analysis, but in others it is straight forward. For example, in [100], the minus sign error occurred while using the vector identity $\nabla \times \left(\nabla \times {\vec{B}}_G\right)=\nabla \left(\nabla \cdot {\vec{B}}_G\right)-{\nabla }^2{\vec{B}}_G$ .

However, in the case of [19], the issue is more subtle. The gravito-vector potential is defined as $A_g^i\equiv \frac{1}{4}{h}^{0i}$ . Notice the metric perturbation has upper indices compared to the lower indices in Eq. 30. This leads to a sign difference $\left({\vec{A}}_g=-\vec{h}\right)$ and therefore the mass current density is written in [19] as ${\vec{j}}_m=8m_e{\vec{A}}_g+\cdots$ rather than ${\vec{J}}_m=-4n_s{m}_e\vec{h}$ as obtained from Eq. 51. The use of a different convention is not problematic, however, the error occurs in the use of the Einstein equation, G ^μν = κT ^μν . Using the convention of [19] should lead to a gravito-Ampere law with a positive sign on the source term contrary to Eq. 45. However [19], has a negative sign. The net result is a Yukawa-like differential equation is incorrectly obtained for ${\vec{B}}_g$ , rather than a Helmholtz-like differential equation. Also, an expression similar to Eq. 74 is obtained, with a value on the order of 10¹³ m, but is interpreted as a penetration depth rather than a spatial periodicity.

In the case of [74, 75], the gravito-vector potential is defined as $A_g^i\equiv \frac{1}{4}{\bar{h}}_{0i}$ similar to Eq. 30. The same approach as [71–73] is used with a “generalized vector potential” defined as $\vec{A}\equiv {\vec{A}}_e+\frac{m}{e}{\vec{A}}_g$ , and an associated covariant derivative, $\tilde{\nabla }=\nabla -i\tilde{g}\vec{A}$ , where $\tilde{g}=e^2$ . This leads to a current density given by $\vec{j}=-\frac{\tilde{g}}{m}\left({\vec{A}}_e+\frac{m}{e}{\vec{A}}_g\right)n_s+\cdots$ which matches Eq. 51. Furthermore, it is shown that setting $\vec{B}=0$ leads to ${\vec{B}}_g=-{\mu }_0{\lambda }_e^2\nabla \times {\vec{j}}_g$ which appears to match Eq. 57. However, the authors defined the mass current density as ${\vec{j}}_g={\rho }_g\vec{v}$ , where ρ _g ≡ − T ₀₀. This introduces an additional minus sign which leads to ${\vec{B}}_g={\mu }_0{\lambda }_e^2{T}_{00}\nabla \times \vec{v}$ . This is is in disagreement with Eq. 57 which can be written as $4{\vec{B}}_G=-\nabla \times \vec{v}$ . This difference in sign is the reason why [74, 75] obtain a Yukawa-like differential equation rather than a Helmholtz-like differential equation for ${\vec{B}}_g$ . Then the gravito-magnetic penetration depth is given as λ _G ≈ 10²¹ λ _L . This is similar to the result obtained from Eq. 75 but it is interpreted in [74, 75] as a penetration depth rather than a spatial periodicity.

In the case of [26, 27], the presence of a gravito-magnetic Meissner effect is argued on the basis of spontaneous symmetry breaking. A Lagrangian is written in the form $L=\frac{1}{2}{\left(\nabla \mathrm{\Psi }\right)}^{*}\nabla \mathrm{\Psi }-\frac{1}{4}\beta {\left({\left|\mathrm{\Psi }\right|}^2-\frac{\alpha }{\beta }\right)}^2-\frac{1}{2}{\vec{B}}_g^2$ , where ${\left|\mathrm{\Psi }\right|}^2=-\alpha /\beta$ and β > 0. The associated field equation is found to be ${\nabla }^2{\vec{B}}_g-\frac{16m^2}{{\hslash }^2}\frac{\alpha }{\beta }{\vec{B}}_g=0$ , with ${\lambda }^2=\frac{\hslash }{4m}\left(\frac{\alpha }{\beta }\right)$ . It is stated that α < 0 and α > 0 correspond to the presence and absence of spontaneous symmetry breaking, respectively. Therefore, the sign of α determines the sign of ${\left|\mathrm{\Psi }\right|}^2$ which determines the sign in the field equation for ${\vec{B}}_g$ . This distinguishes whether the equation is a Yukawa-like or a Helmholtz-like differential equation. However, it is shown in 4.1 of Tinkham [94] that if α < 0, then ${\left|\mathrm{\Psi }\right|}^2=0$ , which means there is no superconducting state. Also, the minimum energy is ${\left|\mathrm{\Psi }\right|}^2=-\alpha /\beta$ only when α < 0. This means that ${\left|\mathrm{\Psi }\right|}^2$ is always positive, which corresponds to the fact that in Ginzburg-Landau theory, ${\left|\mathrm{\Psi }\right|}^2=n_s$ , the number density of Cooper pairs which can only be positive. Lastly, notice that if α < 0, then the field equation for ${\vec{B}}_g$ is actually a Helmholtz-like differential equation, and the expression for λ ² is negative which therefore cannot be interpreted as a penetration depth.

In the case of [73], there is discussion about whether the “covariant derivative” is $\bar{\nabla }=\nabla +ig{\vec{A}}_g$ or $\bar{\nabla }=\nabla -ig{\vec{A}}_g$ , where g is a coupling constant. Using $\bar{\nabla }=\nabla +ig{\vec{A}}_g$ leads to a Yukawa-like differential equation for ${\vec{B}}_g$ , and an associated Meissner effect. Using $\bar{\nabla }=\nabla -ig{\vec{A}}_g$ leads to a Helmholtz-like differential equation for ${\vec{B}}_g$ , and the absence of a Meissner effect. However, there is no statement concerning which is the correct approach. The reason may be because the canonical momentum Eq. 13, which determines the sign, is not formally derived in [73]. Instead, the discussion is based on the concept of spontaneous symmetry breaking. As previously explained, the Ginzburg-Landau theory of superconductivity does not permit ${\left|\mathrm{\Psi }\right|}^2$ to be negative which is associated with $\bar{\nabla }=\nabla +ig{\vec{A}}_g$ . Acting the canonical momentum Eq. 13 on Ψ leads to $\bar{\nabla }=\nabla -ig{\vec{A}}_g$ which [73] describes as the “classical” covariant derivative since it is associated with the absence of spontaneous symmetry breaking.

4.2 The Effect of ${\vec{B}}_G$ on the Penetration Depth of $\vec{B}$

For a charged supercurrent in the presence of both magnetic and gravito-magnetic fields, the differential equations Eq. 69 and Eq. 71 need to be decoupled to obtain solutions. For simplicity, consider a system arranged such that ${\vec{E}}_G\times \vec{A}=0$ . Then solving Eq. 69 for ${\vec{B}}_G$ , substituting the result into Eq. 71, and canceling common terms gives ²³

${\nabla }^4\vec{B}-k^2{\nabla }^2\vec{B}=0(76)$

where k matches Eq. 62 which is

$k^2\equiv \alpha {\mu }_0{\mathrm{\Lambda }}_L-\beta {\mu }_G{n}_{s}e(77)$

The modified London penetration depth can be defined as ${\lambda }_L^{\prime }\equiv 1/k$ . Using ${\lambda }_L^{-2}={\mu }_0{\mathrm{\Lambda }}_L$ gives

${\lambda }_L^{\prime -2}=\alpha {\lambda }_L^{-2}-\beta {\mu }_G{n}_{s}e(78)$

Notice that the first term in Eq. 78 encodes a correction due to the gravitational scalar potential, while the second term encodes a correction due to the electric scalar potential. An order of magnitude can be calculated for each term in Eq. 78 using Eq. 52. The first term on the right side of Eq. 78 implies a correction to the London penetration depth given by ${\lambda }_L^{\prime }={\left(1+{\phi }_G/c^2\right)}^{-1/2}{\lambda }_L$ . At the surface of earth, ${\phi }_G/c^2\approx G{M}_E/\left(c^2{R}_E\right)\sim 10^{-9}$ , where M _E and R _E are the mass and radius of earth, respectively. Then ${\lambda }_L^{\prime }\approx \left(1-10^{-9}\right){\lambda }_L$ . For a superconductor such as niobium, the London penetration depth is λ _L ∼ 10⁻⁹ m. This means the correction due to the scalar potential of earth is $\sim 10^{-18}$ m which would not be observable.

For the second term in Eq. 78, note that if m _e c ² ≫ eφ, then β ≈ 4m _e /e ∼ 10⁻¹¹ kg/C. Also using n _s ∼ 10²⁶ m⁻³ means the second term in Eq. 78 is $\sim 10^{-30}$ m⁻². Since the first term is $\alpha {\lambda }_L^{-2}\sim 10^{18}$ m⁻², then the second term is completely negligible. Hence we find that the presence of a Newtonian and/or gravito-magnetic field will not likely have a measurable effect on the penetration depth of the magnetic field.

Since $\alpha {\lambda }_L^{\prime -2}>\beta {\mu }_G{n}_{s}e$ , then ${\lambda }_L^{\prime -2}$ is positive and therefore the general solution to Eq. 76 is

$\vec{B}={\vec{c}}_1{e}^{-{\lambda }_L^{\prime -1}z}+{\vec{c}}_2{e}^{{\lambda }_L^{\prime -1}z}+{\vec{c}}_{3}z+{\vec{c}}_4(79)$

Using the boundary conditions in Eq. 73 leads to ${\vec{c}}_2$ , ${\vec{c}}_3$ , ${\vec{c}}_4=0$ , and ${\vec{c}}_1={\vec{B}}_0$ . Therefore, the solution is reduced to

$\vec{B}={\vec{B}}_0{e}^{-z/{\lambda }_L^{\prime }}(80)$

This is the standard Meissner effect but with a modified London penetration depth given by Eq. 78. Notice that the first term in Eq. 78 encodes a correction due to the gravitational scalar potential since α = 1 + φ _G /c ². The second term in Eq. 78 encodes a correction due to the gravito-magnetic field since it can be traced back to the terms involving $\beta {\vec{B}}_G$ in Eq. 69 and Eq. 71.

4.3 The Effect of $\vec{B}$ on the Penetration Depth of $\vec{B}$ _G

Again, for simplicity, consider a system arranged such that ${\vec{E}}_G\times \vec{A}=0$ . Solving Eq. 71 for $\vec{B}$ , substituting the result into Eq. 69, and canceling common terms gives ²⁴

${\nabla }^4{\vec{B}}_G-k^2{\nabla }^2{\vec{B}}_G=0(81)$

where k is given by Eq. 77. For a neutral superfluid (or in the absence of a magnetic field), Eq. 77 reduces to k ² = −4μ _G n _s m _e and therefore Eq. 81 leads to a paramagnetic effect, as stated before. However, for a charged supercurrent in the presence of both $\vec{B}$ and ${\vec{B}}_G$ , both terms in Eq. 77 must be considered. Since ${\mu }_0{\mathrm{\Lambda }}_L={\lambda }_L^{-2}$ , then the first term in Eq. 77 can be expressed in terms of the London penetration depth which gives $\alpha {\lambda }_L^{-2}\sim 10^{18}$ m⁻². An order of magnitude can be calculated for the second term in Eq. 77 using β ≈ 4m _e /e ∼ 10⁻¹¹ kg/C and n _s ∼ 10²⁶ m⁻³ which gives $\sim 10^{-30}$ m⁻². Since αμ ₀Λ _L ≫ μ _G n _s eβ, then k ² is positive and the general solution to Eq. 81 is

${\vec{B}}_G={\vec{c}}_1^{\prime }{e}^{-kz}+{\vec{c}}_2^{\prime }{e}^{kz}+{\vec{c}}_3^{\prime }z+{\vec{c}}_4^{\prime }(82)$

The general form of the solutions in Eq. 79 and Eq. 82 are also found in [20]. Using the boundary conditions in Eq. 73 leads to ${\vec{c}}_2^{\prime }$ , ${\vec{c}}_3^{\prime }$ , ${\vec{c}}_4^{\prime }=0$ , and ${\vec{c}}_1^{\prime }={\vec{B}}_{G,0}$ . Therefore, the solution reduces to

${\vec{B}}_G={\vec{B}}_{G,0}{e}^{-kz}(83)$

This result predicts a diamagnetic (Meissner) effect for the gravito-magnetic field when a magnetic field is also present. In fact, the gravito-magnetic field is expelled with approximately the same penetration depth as the magnetic field. Defining the gravitational penetration depth as λ _G ≡ 1/k, and using Eq. 77 gives

$\begin{array}{l}\hfill {\lambda }_{\left(\text{penetration\hspace{0.17em}depth\hspace{0.17em}of\hspace{0.17em}}{\vec{B}}_G\right)}^{-2}=\alpha {\lambda }_L^2-\beta {\mu }_G{n}_{s}e\approx {\lambda }_L^{-2}\end{array}(84)$

Therefore, it is found that ${\vec{B}}_G$ is expelled from the superconductor with a penetration depth on the order of the London penetration depth, provided a magnetic field is also present. This observation is being taken into account for guiding experimental work [101].

This effect can be understood by comparing how the physics contained in Eq. 77 applies to the magnetic field versus the gravito-magnetic field. As it applies to the magnetic field, Eq. 77 predicts a diamagnetic (Meissner) effect with only a miniscule modification due to the presence of the gravito-magnetic field. However, as it applies to the gravito-magnetic field, Eq. 77 predicts a paramagnetic effect which is drastically altered by the presence of the magnetic field. In fact, the alteration is so substantial that it switches a paramagnetic effect into a diamagnetic (Meissner) effect for the gravito-magnetic field.

This can be further understood by returning to Eq. 71 and noticing that when $\alpha \vec{B}+\beta {\vec{B}}_G<0$ , or equivalently, $\alpha \vec{B}<-\beta {\vec{B}}_G$ , then the differential equation switches from a Helmholtz-like equation, to a Yukawa-like equation. Physically speaking, this mechanism can be understood by the following example. Consider a case where the superconductor is in the presence of a gravito-magnetic field but no magnetic field. According to Eq. 55, there will be a small supercurrent given by $\nabla \times {\vec{J}}_c=-{\mathrm{\Lambda }}_L\beta {\vec{B}}_G$ . Now introduce an opposing magnetic field, $\alpha \vec{B}<-\beta {\vec{B}}_G$ , which will cause an opposing supercurrent given by $\nabla \times {\vec{J}}_c=-{\mathrm{\Lambda }}_L\alpha \vec{B}$ . Since the supercurrent will switch direction, then the gravito-Ampere law, $\nabla \times {\vec{B}}_G=-{\mu }_G{\vec{J}}_m$ , predicts that a gravito-magnetic field will be produced inside the superconductor which opposes the incident gravito-magnetic field and therefore cancels it. This is effectively a gravito-magnetic Meissner effect. The key feature of this concept is that the magnetic field and gravito-magnetic field must be generated by independent sources so that their strength and direction can be independently adjusted. This key feature may be missing from formulations such as [71, 72, 74, 75] which work in terms of a single field defined as $\vec{B}={\vec{B}}_e+\frac{m}{e}{\vec{B}}_g$ or $\vec{B}={\vec{B}}_g+\frac{q}{m}{\vec{B}}_e$ .

This description also demonstrates that there is a threshold value for the minimum magnetic field necessary to produce a Meissner effect for the gravito-magnetic field. It is given by $\alpha \left|\vec{B}\right|>\beta \left|{\vec{B}}_G\right|$ . For a numerical estimate describing this condition, again use φ _G /c ² ∼ 10^–9 so that α = 1 + φ _G /c ² ≈ 1, and assume m _e c ² ≫ eφ so that β ≈ 4m _e /e ∼ 10⁻¹¹ kg/C. Then $\left|\vec{B}\right|>\left|{\vec{B}}_G\right|\left(10^{-11}\text{\hspace{0.17em}kg/C}\right)$ . Therefore, it takes an extremely small magnetic field (relative to the gravito-magnetic field) to produce a gravito-magnetic Meissner effect.

Hence the findings above are summarized as follows:

• A supercurrent in the presence of only $\vec{B}$ : magnetic Meissner effect.

• A supercurrent in the presence of only ${\vec{B}}_G$ : no gravito-magnetic Meissner effect.

• A supercurrent in the presence of both ${\vec{B}}_G$ and $\vec{B}<-{\vec{B}}_G\left(\beta /\alpha \right)$ : both magnetic and gravito-magnetic Meissner effects.

• A neutral superfluid in the presence of ${\vec{B}}_G$ : no gravito-magnetic Meissner effect ²⁵

These results demonstrate an important interaction between electromagnetism, gravitation, and a quantum mechanical system that only occurs when all three are present. The superconductor provides the quantum mechanical system which is necessary to have any kind of Meissner effect. The gravito-magnetic field is required to create a novel gravitational effect. Lastly, the magnetic field is necessary to mediate the interaction. In the absence of a magnetic field, the novel gravito-magnetic Meissner effect would not take place.

Note that the conclusion that both $\vec{B}$ and ${\vec{B}}_G$ penetrate together to the same depth given by Eq. 84 was also found in [18–22, 71, 72, 74, 75]. In the case of [19], the exponential decay solutions in Eq. 80 and Eq. 83 are also obtained, but with the assumption ${\vec{B}}_{G,0}=\left(m_e/e\right){\vec{B}}_0$ . In the case of [19, 20], the Meissner effect is shown for the combined field, $e\vec{B}+4m_e{\vec{B}}_G$ . Similarly [21, 22], show a Meissner effect for $\vec{B}+\frac{m}{e}{\vec{B}}_G$ . In [20], screening currents are taken into account by introducing the following boundary conditions in addition to those shown in Eq. 73.

$B_0-B={\mu }_0{\int }_0^z{J}_{c}dz\text{and}{B}_{G,0}-B_G=-{\mu }_G{\int }_0^z{J}_{m}dz(85)$

Using Eq. 60 and $J_c=J_m\left(e/m_e\right)$ leads to a solution for both J _c and J _m of the form $J\approx J_0{e}^{-z/{\lambda }_L}$ , where J ₀ is the current density at the surface. Therefore, Eq. 85 becomes

$B_0-B\approx -{\mu }_0{\sigma }_{c,0}\left(e^{-z/{\lambda }_L}-1\right)\text{and}{B}_{G,0}-B_G\approx {\mu }_G{\sigma }_{m,0}\left(e^{-z/{\lambda }_L}-1\right)(86)$

where σ _c,0 ≡ λ _L J _c,0 and σ _m,0 ≡ λ _L J _m,0 are charge and mass surface current densities, respectively. Similarly, the solutions for $\vec{B}$ and ${\vec{B}}_G$ in [21, 22] contain σ _c,0 and σ _m,0. The combined “screening” current also decays exponentially so that ${\mu }_0{\sigma }_e-\frac{m_e}{e}{\mu }_G{\sigma }_m\approx 0$ for z ≫ λ _L .

The use of Eq. 86 leads to solutions for $\vec{B}$ and ${\vec{B}}_G$ in [20–22] that contain an exponential decay term plus a constant term. Due to the constant term, [22] states that a “constant residual magnetic and gravito-magnetic fields will exist within a pure superconductor.” When z ≫ λ, the residual fields are

${\vec{B}}_G\approx {\vec{B}}_{G,0}+\frac{{\mu }_g{m}_e}{\mu e}{\vec{B}}_0\text{and}\vec{B}\approx -\frac{m_e^2{\mu }_g}{e^2\mu }{\vec{B}}_0-\frac{m_e}{e}{\vec{B}}_{G,0}\text{for\hspace{0.17em}\hspace{0.17em}}z\gg {\lambda }_L(87)$

The following observations can be made about Eq. 87.

• It is noted in [20–22] that $\vec{B}+\frac{m_e}{e}{\vec{B}}_G\approx 0$ is still satisfied even for the residual fields. This means the Meissner effect for the combined field still occurs despite the existence of these residual fields.

• It is also noted in [20] that the absence of an external magnetic field, ${\vec{B}}_0=0$ , makes Eq. 87 become

${\vec{B}}_G\approx {\vec{B}}_{G,0}\text{and}\vec{B}\approx -\frac{m_e}{e}{\vec{B}}_{G,0}(88)$

The first expression is consistent with the absence of a gravito-magnetic Meissner effect when there is no magnetic field. The second expression means that a gravito-magnetic field will generate a very small magnetic field in the interior of the superconductor.

• It is noted in [21] that the absence of an external gravito-magnetic field, ${\vec{B}}_{G,0}=0$ , makes Eq. 87 become

${\vec{B}}_G\approx \frac{{\mu }_g{m}_e}{\mu e}{\vec{B}}_0\text{and}\vec{B}\approx -\frac{m_e^2{\mu }_g}{e^2\mu }{\vec{B}}_0(89)$

The first expression can be understood as a result of the magnetic field generating screening currents which produce a gravito-magnetic field. Therefore, ${\vec{B}}_0$ produces ${\vec{B}}_G$ in the superconductor. This leads to an interpretation of the second expression as a second order effect where ${\vec{B}}_G$ produces an additional screening current with then produces an additional $\vec{B}$ in the superconductor. The net result is that the magnetic field exists slightly deeper in the superconductor than it would otherwise be expected to. A similar explanation is given in [20] .

• The expressions in Eq. 89 both involve μ _g /μ. Based on this, it is stated in [22] that the material properties of the superconductor will determine the residual fields which could lead to experimentally observable gravitational effects.

• Lastly, the residual fields in Eq. 87 can be interpreted as expressions associated with ${\vec{c}}_4$ and ${\vec{c}}_4^{\prime }$ in Eq. 79 and Eq. 82. Recall that the boundary conditions in Eq. 73 assume that the fields vanish for z → ∞. This leads to setting ${\vec{c}}_4$ and ${\vec{c}}_4^{\prime }$ to zero in Eq. 79 and Eq. 82, respectively. This is similar to setting ${\vec{c}}_3=0$ in Eq. 72 to obtain the usual Meissner effect. However [20–22], uses the less restrictive requirement that the fields are finite (but not necessarily zero) for z → ∞. Combining this with the use of the screening currents in Eq. 86 ultimately leads to the residual fields in Eq. 87. However, consider if this same approach is used with the usual Meissner effect. If ${\vec{c}}_3$ is not assumed to be zero, and the first condition in Eq. 86 is used, the solution is found to be

$B={\mu }_0{\sigma }_{c,0}{e}^{-z/{\lambda }_L}-{\mu }_0{\sigma }_{c,0}+B_0(90)$

Notice there are residual terms remaining when z ≫ λ _L . However, setting B ₀ = μ ₀ σ _c,0 leads to the usual solution, $B=B_0{e}^{-z/{\lambda }_L}$ . This corresponds to setting ${\vec{c}}_3=0$ in Eq. 72. Therefore, it can be argued that the residual fields in Eq. 87 are an artifact of using boundary conditions that are not consistent with the standard Meissner effect.

In the case of [71, 72], a “generalized field” is defined as $\vec{B}=\frac{q}{m}{\vec{B}}_e+{\vec{B}}_g$ . The associated field equation is found to be

${\nabla }^2\vec{B}-\left(\frac{1}{{\lambda }_e^2}-\frac{1}{{\lambda }_g^2}\right)\vec{B}=0(91)$

where λ _e is the London penetration depth, and λ _g is essentially the expression found in Eq. 75. It is recognized that Eq. 91 becomes a Yukawa-like equation when λ _g > λ _e which leads to a “generalized Meissner effect.” Since λ _g ∼ 10¹³ m and λ _e ∼ 10⁻⁸ m, then the condition for a “generalized Meissner effect” is clearly satisfied. In fact, since λ _g ≫ λ _e , then and the “generalized penetration depth” from Eq. 91 becomes $\lambda ={\left({\lambda }_e^{-2}-{\lambda }_g^{-2}\right)}^{-1}\approx {\lambda }_e$ . This demonstrates that the penetration depth of the gravito-magnetic field becomes the same as the London penetration depth as indicated by Eq. 84.

In [74, 75], the same approach is used except the combined field is defined as $\vec{B}={\vec{B}}_e+\frac{m}{e}{\vec{B}}_g$ . As previously explained, using ${\vec{j}}_g={\rho }_g\vec{v}$ , where ρ _g ≡ − T ₀₀, leads to ${\vec{B}}_g={\mu }_0{\lambda }_e^2{T}_{00}\nabla \times \vec{v}$ . This result for the gravito-magnetic case has the same sign as $\vec{B}={\mu }_0{\lambda }_e^2\nabla \times \vec{v}$ for the magnetic case. As a result, the “generalized penetration depth” becomes $\lambda ={\left({\lambda }_e^{-2}+{\lambda }_g^{-2}\right)}^{-1}$ which has a plus rather than the minus seen in Eq. 91. Since λ _g ≫ λ _e , then the result is still λ ≈ λ _e for the generalized field. However, in the absence of a magnetic field, this difference in sign is the reason why [74, 75] still find a gravito-magnetic Meissner effect, while [71] does not.

A final important consideration is the issue of coordinate-freedom in linearized General Relativity. The gravito-magnetic field, ${\vec{B}}_G=\nabla \times \vec{h}$ , is a coordinate-dependent quantity which can be made to vanish by a linear coordinate transformation, x′ ^μ = x ^μ − ξ ^μ . Since the linearized metric perturbation transforms as $h_{\mu \nu }^{\prime }=h_{\mu \nu }+{\partial }_{\mu }{\xi }_{\nu }+{\partial }_{\nu }{\xi }_{\mu }$ , then ${\vec{B}}_G$ and ${\vec{E}}_G$ transform, respectively, as [12]

${\vec{B}}_G^{\prime }={\vec{B}}_G+\frac{1}{4}\nabla \times \stackrel{\cdot }{\vec{\xi }}\text{and\hspace{0.17em}}{\vec{E}}_G^{\prime }={\vec{E}}_G-\stackrel{\cdot \cdot }{\vec{\xi }}(92)$

Therefore, the effects associated with ${\vec{B}}_G$ and ${\vec{E}}_G$ can be made to vanish by a coordinate transformation. Alternatively, a coordinate-invariant approach can be used which also applies to gravitational waves. This is discussed in [12, 38, 39].

5 Electric Field Penetration Depth, and Absence of Meissner Effect for the Gravito-Electric Field

Using $\vec{B}=\nabla \times \vec{A}$ in $\nabla \times \vec{B}={\mu }_0{\vec{J}}_c$ , and using ${\vec{B}}_G=\nabla \times \vec{h}$ in $\nabla \times {\vec{B}}_G=-{\mu }_G{\vec{J}}_m$ , leads to, respectively,

$\nabla \times \nabla \times \vec{A}={\mu }_0{\vec{J}}_c\text{and}\nabla \times \nabla \times \vec{h}=-{\mu }_G{\vec{J}}_m(93)$

On the left side of both equations, we can use the identity $\nabla \times \nabla \times \vec{V}=\nabla \left(\nabla \cdot \vec{V}\right)-{\nabla }^2\vec{V}$ . On the right sides, we can use Eq. 50 and Eq. 51 in each equation respectively. This gives

${\nabla }^2\vec{A}={\mu }_0{\mathrm{\Lambda }}_L\left(\alpha \vec{A}+\beta \vec{h}\right)+\nabla \left(\nabla \cdot \vec{A}\right)(94)$

and

${\nabla }^2\vec{h}=-{\mu }_G{n}_{s}e\left(\alpha \vec{A}+\beta \vec{h}\right)+\nabla \left(\nabla \cdot \vec{h}\right)(95)$

Since ${\partial }_t\vec{h}=0$ in this approximation, then taking a time derivative of Eq. 95 will have a vanishing result and therefore eliminates a Meissner effect for the time-independent gravito-electric field (which is the Newtonian field). This is expected since it is known that the Newtonian field generally cannot be shielded. This conclusion is in agreement with [20, 24], but in disagreement with [71–73].

In the case of [20, 24], the gravitational sources are non-relativistic $\left(T^{ij}\approx 0\right)$ and harmonic coordinates are used $\left({\partial }_{\nu }{\bar{h}}^{\mu \nu }=0\right)$ . However, it is not recognized that this leads to ${\partial }_t\vec{h}=0$ . Then [20] sets ∇φ _G = 0 (by assuming the Newtonian gravitational field of the superconductor is negligible) which leads to a “transverse gravito-electric field” written as ${\vec{E}}_g=-{\partial }_t{A}_g$ . As a result of this error, coupled differential equations for $\vec{E}$ and ${\vec{E}}_g$ are obtained which have a similar form to Eq. 69 and Eq. 71. Also, solutions for ${\vec{E}}_g$ and $\vec{E}$ have the same form as Eq. 79 and Eq. 82. Once again, the requirement that the fields are finite (but not necessarily zero) for z → ∞ leads to solutions which contain an exponential decay term plus a constant term. Then it is stated that when z ≫ λ, the residual fields are given in a form identical to Eq. 87 but with $\vec{B}\to \vec{E}$ and ${\vec{B}}_G\to {\vec{E}}_G$ . It follows that the entire discussion concerning Eq. 87 would apply, including the claim that $\vec{E}+\frac{m_e}{e}{\vec{E}}_G\approx 0$ is satisfied for the residual fields. This would imply a Meissner effect for the combined field. However, since ${\vec{E}}_g=-{\partial }_t{A}_g=0$ for non-relativistic gravitational sources, then the entire discussion becomes moot.

In the case of [71–73], the exact same problem is at the root of the analysis. Again the gravitational sources are non-relativistic $\left(T^{ij}\approx 0\right)$ . The use of harmonic coordinates is not explicitly stated, but it is clearly implied based on the Maxwell-like field equations appearing, and the references cited in the paper. Again it is overlooked that ${\partial }_t\vec{h}=0$ in this approximation. As discussed in [12, 28], this eliminates the gravito-Faraday law since ${\partial }_t\nabla \times \vec{h}={\partial }_t{\vec{B}}_G=0$ . However [71–73], include the gravito-Faraday law and use it (in differing notation) to obtain ${\vec{E}}_G=-{\partial }_t\vec{h}$ . Then the usual approach of taking the time derivative of Eq. 60 and using Eq. 53 leads to a Yukawa-like equation. In the case of [73], only gravity is considered, so the result is ${\nabla }^2{\vec{E}}_G-{\lambda }_g^{-2}{\vec{E}}_G=0$ , where λ _g is the gravitational penetration depth. In the case of [71–73], a generalized field is defined as $\vec{E}={\vec{E}}_G+\frac{q}{m}\vec{E}$ , and a field equation identical to Eq. 91 is obtained. Again, it follows that a “generalized penetration depth” becomes $\lambda ={\left({\lambda }_e^{-2}-{\lambda }_g^{-2}\right)}^{-1}\approx {\lambda }_e$ . However, since ${\vec{E}}_G=-{\partial }_t\vec{h}=0$ for non-relativistic gravitational sources, then once again then the entire discussion becomes moot.

Returning to Eq. 94, an expression for the electric field can be obtained by taking a time derivative and using $\nabla \left(\nabla \cdot \vec{E}\right)=\nabla {\rho }_c/{\epsilon }_0=0$ for a uniform charge density. ²⁶

${\nabla }^2\vec{E}={\mu }_0{\mathrm{\Lambda }}_L\left(\alpha \vec{E}-\frac{1}{c^2}{\dot{\phi }}_G\vec{A}-\frac{4}{c^2}\dot{\phi }\vec{h}\right)(96)$

In the absence of gravity, Eq. 96 becomes ${\nabla }^2\vec{E}={\lambda }_L^{-2}\vec{E}$ . For a superconducting slab occupying z ≥ 0, the solution is $\vec{E}={\vec{E}}_0{e}^{-z/{\lambda }_L}$ which predicts the electric field vanishes within the superconductor at depths beyond the London penetration depth. However, if gravity is present, then the associated penetration depth must be modified. If φ _G and φ are static, then the solution to Eq. 96 is $\vec{E}={\vec{E}}_0{e}^{-z/{\lambda }_L^{\prime }}$ where

$\begin{array}{ll}\hfill {\lambda }_L^{\prime }& ={\alpha }^{-1/2}{\lambda }_L\approx \left(1-\frac{{\phi }_G}{2c^2}\right){\lambda }_L\hfill \end{array}(97)$

However, if φ _G and φ are time-dependent, then Eq. 96 requires obtaining solutions for $\vec{A}$ and $\vec{h}$ found in the coupled equations Eq. 94 and Eq. 95. We can use the gauge condition Eq. 58 in Eq. 94 to eliminate $\nabla \cdot \vec{A}$ in favor of $\nabla \cdot \vec{h}$ which gives

$\begin{array}{ll}\hfill {\nabla }^2\vec{A}& ={\mu }_0{\mathrm{\Lambda }}_L\left(\alpha \vec{A}+\beta \vec{h}\right)-\frac{\beta }{\alpha }\nabla \left(\nabla \cdot \vec{h}\right)+\frac{1}{\alpha c^2}\nabla \left({\vec{E}}_G\cdot \vec{A}\right)\hfill \\ \hfill & \hfill \end{array}(98)$

Multiplying Eq. 95 by β/α, adding the result to Eq. 98, and using a field defined as $\vec{D}\equiv \alpha \vec{A}+\beta \vec{h}$ gives

$\begin{array}{ll}\hfill {\nabla }^2\vec{D}-k^2\vec{D}-\frac{1}{c^2}\nabla \left({\vec{E}}_G\cdot \vec{A}\right)& =0\hfill \\ \hfill & \hfill \end{array}(99)$

where k is given by Eq. 77. Consider a system where $\nabla \left({\vec{E}}_G\cdot \vec{A}\right)/c^2=0$ . Since ∇φ = 0, and φ _G due to earth has miniscule variation over the length scale of a superconductor, then the solution to Eq. 99 is $\vec{D}={\vec{D}}_0{e}^{-z/{\lambda }_L^{\prime }}$ , where ${\lambda }_L^{\prime }$ is given by Eq. 78. This solution can be written as

$\begin{array}{ll}\hfill \alpha \vec{A}+\beta \vec{h}& =\left(\alpha {\vec{A}}_0+\beta {\vec{h}}_0\right)e^{-z/{\lambda }_L^{\prime }}\hfill \end{array}(100)$

Taking a time derivative gives

$\begin{array}{ll}\hfill \alpha \vec{E}-\frac{1}{c^2}{\dot{\phi }}_G\vec{A}-\frac{4}{c^2}\dot{\phi }\vec{h}& =\left(\alpha {\vec{E}}_0-\frac{1}{c^2}{\dot{\phi }}_G{\vec{A}}_0-\frac{4}{c^2}\dot{\phi }{\vec{h}}_0\right)e^{-z/{\lambda }_L^{\prime }}\hfill \\ \hfill & \hfill \end{array}(101)$

Inserting Eq. 101 into Eq. 96 gives

$\begin{array}{ll}\hfill {\nabla }^2\vec{E}-{\mu }_0{\mathrm{\Lambda }}_L\vec{H}{e}^{-z/{\lambda }_L^{\prime }}& =0\hfill \end{array}(102)$

where $\vec{H}\equiv \alpha {\vec{E}}_0-\frac{1}{c^2}\left({\dot{\phi }}_G{\vec{A}}_0-4\dot{\phi }{\vec{h}}_0\right)$ . The general solution is

$\vec{E}={\mu }_0{\mathrm{\Lambda }}_L\vec{H}{\lambda }_L^{\prime 2}{e}^{-z/{\lambda }_L^{\prime }}+{\vec{C}}_{1}z+{\vec{C}}_2(103)$

where ${\vec{C}}_1,{\vec{C}}_2$ are constant vectors. Using the same boundary conditions as Eq. 73 requires C ₁, ${\vec{C}}_2=0$ . Therefore, the solution reduces to $\vec{E}={\mu }_0{\mathrm{\Lambda }}_L\vec{H}{\lambda }_L^{\prime 2}{e}^{-z/{\lambda }_L^{\prime }}$ . An explicit function for $\vec{H}$ will depend on the particular time-dependence of $\dot{\phi }$ and ${\dot{\phi }}_G$ , however, the penetration depth for $\vec{E}$ will still be ${\lambda }_L^{\prime }$ .

6 Flux Quantum (Fluxoid) in the Body of a Superconductor

In Ginzburg-Landau theory, the minimal coupling rule, ${\widehat{P}}_i\to {\widehat{P}}_i-q{\widehat{A}}_i$ , makes the supercurrent become

$\vec{J}=\frac{e}{2m}\left[{\mathrm{\Psi }}^{\ast }\left(-i\hslash \nabla \right)\mathrm{\Psi }-\mathrm{\Psi }\left(-i\hslash \nabla \right){\mathrm{\Psi }}^{\ast }-2e\vec{A}{\left|\mathrm{\Psi }\right|}^2\right](104)$

where $\mathrm{\Psi }\left(r\right)$ is the complex order parameter [94, 103]. Using Eq. 29 and Eq. 30 in Eq. 16, and promoting the canonical momentum to a quantum mechanical operator makes the minimal coupling rule become

${\widehat{P}}_i\to {\widehat{P}}_i-\gamma m\left(4h^i-\frac{2}{c^2}{\phi }_G{v}_i\right)+q\left({\eta }_{ij}{A}^j+\frac{4}{c^2}\phi h^i-\frac{2}{c^2}{\phi }_G{A}_i\right)(105)$

Staying to first order in the metric perturbation, and first order in test mass velocity, requires using γ ≈ 1 in Eq. 105. For convenience, the entire coupling vector can be defined as

$\vec{C}\equiv -m\left(4\vec{h}-\frac{2}{c^2}{\phi }_G\vec{v}\right)+q\left(\vec{A}+\frac{4}{c^2}\phi \vec{h}-\frac{2}{c^2}{\phi }_G\vec{A}\right)(106)$

Then the corresponding supercurrent becomes

$\vec{J}=\frac{e}{2m}\left[{\mathrm{\Psi }}^{\ast }\left(-i\hslash \nabla \right)\mathrm{\Psi }-\mathrm{\Psi }\left(-i\hslash \nabla \right){\mathrm{\Psi }}^{\ast }+\vec{C}{\left|\mathrm{\Psi }\right|}^2\right](107)$

which reduces to Eq. 104 in the absence of gravity. Using $\mathrm{\Psi }\left(r\right)=\sqrt{n_s}{e}^{i\varphi \left(r\right)}$ , where ϕ is the phase, leads to

$\vec{J}=\frac{e{n}_s}{2m}\left(2\hslash \nabla \varphi +\vec{C}\right)(108)$

An expression similar to Eq. 108 is found in [18, 19, 21, 23, 24, 26, 49], [71–75], [104, 105], however, the terms involving φ and φ _G in Eq. 106 are missing. In the previous section, it was shown that inside the body of the superconductor (much deeper than the London penetration depth), all the fields in Eq. 48 vanish and therefore the supercurrent velocity is zero. Therefore, using J _i = 0 in Eq. 108 and v _i = 0 in Eq. 106 makes Eq. 108 become

$\hslash \nabla \varphi =4m\vec{h}-q\vec{A}-\frac{4q}{c^2}\phi \vec{h}+\frac{2q}{c^2}{\phi }_G\vec{A}(109)$

Integrating around a closed loop gives

${\oint }_C\left(4m\vec{h}-q\vec{A}-\frac{4q}{c^2}\phi \vec{h}+\frac{2q}{c^2}{\phi }_G\vec{A}\right)\cdot d\vec{l}=\hslash {\oint }_C\left(\nabla \varphi \right)\cdot d\vec{l}(110)$

Since the order parameter is single-valued, then it must return to the same value when the line integral returns to the same point. Therefore, the right side must be 2πn, where n is an integer. ²⁷

Applying Stokes’ theorem on the left side gives

$\underset{S}{\int }\nabla \times \left(4m\vec{h}-q\vec{A}-\frac{4q}{c^2}\phi \vec{h}+\frac{2q}{c^2}{\phi }_G\vec{A}\right)\cdot d\vec{S}=\hslash 2\pi n(111)$

where S is the surface bounded by the curve C. Using ∇φ = 0 within the body of the superconductor, and q = −2e and m = 2m _e for Cooper pairs, gives

$e\left(1-\frac{2{\phi }_G}{c^2}\right){\mathrm{\Phi }}_B+4m_e\left(1+\frac{e\phi }{m_e{c}^2}\right){\mathrm{\Phi }}_{B_G}+\frac{2e}{c^2}\underset{S}{\int }\left({\vec{E}}_G\times \vec{A}\right)\cdot d\vec{S}=n\frac{h}{2}(112)$

where Φ _B and ${\mathrm{\Phi }}_{B_G}$ are the flux of $\vec{B}$ and ${\vec{B}}_G$ , respectively. Since φ _G ≪ c ² and eφ ≪ m _e c ², then the result can be approximated to

$\begin{array}{l}\hfill e{\mathrm{\Phi }}_B+4m_e{\mathrm{\Phi }}_{B_G}+\frac{2e}{c^2}\underset{S}{\int }\left({\vec{E}}_G\times \vec{A}\right)\cdot d\vec{S}=n\frac{h}{2}\end{array}(113)$

In the absence of electromagnetism, the gravito-magnetic flux condition can be written as ${\mathrm{\Phi }}_{B_G}=n{\mathrm{\Phi }}_{B_G,0}$ , where ${\mathrm{\Phi }}_{B_G,0}\equiv h/\left(8m_e\right)$ is a gravito-magnetic flux quantum (fluxoid). This result is also found in [27, 50, 73]. The total flux quantum in Eq. 113 is found in [17, 19, 62], and is consistent with DeWitt’s statement in [3] that “the total flux of $\vec{G}$ linking a superconducting circuit must be quantized in units of $\frac{1}{2}h$ ,” where $\vec{G}=e\nabla \times \vec{A}+m\nabla \times \vec{h}$ . However, none of these authors have the additional term in Eq. 113 involving the flux of ${\vec{E}}_G\times \vec{A}$ . This may be due to applying the approximation φ _G ≪ c ² before taking the curl in Eq. 111.

In the absence of gravity, Eq. 113 gives the usual magnetic flux condition, Φ _B = nΦ _B,0, where ${\mathrm{\Phi }}_{B,0}\equiv h/\left(2e\right)$ . This has been experimentally verified, even for the n = 1 state [107, 108]. Using ${\mathrm{\Phi }}_B=\int \vec{A}\cdot d\vec{l}$ around a closed loop surrounding the fluxoid, implies that the n = 1 state leads to

$A=\frac{h}{4\pi er}(114)$

where r = r ₀ is the radius of a fluxoid. Then Eq. 113 in the n = 1 state can be written as

$e{\mathrm{\Phi }}_B+4m_e{\mathrm{\Phi }}_{B_G}+\frac{2e}{c^2}\underset{S_0}{\int }\left({\vec{E}}_G\times \vec{A}\right)\cdot d\vec{S}=\frac{h}{2}(115)$

where S ₀ is the area of a single fluxoid. Since the dominant source of ${\vec{E}}_G$ is due to earth, consider a system arranged so that $\vec{A}$ is parallel to the surface of earth. Since ${\vec{E}}_G$ is approximately uniform over the area of a fluxoid, then using Eq. 114 in Eq. 115, and integrating, leads to

$e{\mathrm{\Phi }}_B+4m_e{\mathrm{\Phi }}_{B_G}+\frac{h{E}_G{r}_0}{c^2}=\frac{h}{2}(116)$

Since ${\mathrm{\Phi }}_{B,0}=\int {\vec{A}}_0\cdot d{\vec{l}}_0=A_{0}2\pi r_0$ , then $r_0={\mathrm{\Phi }}_{B,0}/\left(A_{0}2\pi \right)$ which means Eq. 116 can also be expressed as

$\left(1+\frac{h{E}_G}{2\pi c^{2}e{A}_0}\right){\mathrm{\Phi }}_B+\frac{4m_e}{e}{\mathrm{\Phi }}_{B_G}=\frac{h}{2e}(117)$

The two terms involving gravity are small corrections. Therefore, solving for Φ _B and keeping only lowest order terms involving E _G and B _G leads to

${\mathrm{\Phi }}_B=\frac{h}{2e}-\frac{4m_e}{e}{\mathrm{\Phi }}_{B_G}-\frac{h^2{E}_G}{4\pi c^2{e}^2{A}_0}(118)$

This result can be interpreted as a modified magnetic fluxoid in the presence of gravity. Since [107] used r ₀ ∼ 10⁻⁵ m, then Eq. 114 gives A ₀ ∼ 10⁻³⁰ T⋅m. Therefore, the last term in Eq. 118 becomes $\sim 10^{-54}$ Wb which is hopelessly too small to be observed.

For the term involving ${\mathrm{\Phi }}_{B_G}$ to be comparable to Φ _B , we need $\frac{m_e}{e}{\mathrm{\Phi }}_{B_G,0}\gtrsim \frac{h}{2e}\sim 10^{-15}$ Wb. It is shown in Supplementary Appendix SB that the gravito-vector potential of a large flywheel can be $\left|\vec{h}\right|\sim 10^{-21}$ m/s. Using ${\mathrm{\Phi }}_{B_G}=\int \vec{h}\cdot d{\vec{l}}_0=h2\pi r_0$ and r ₀ ∼ 10⁻⁵ m gives $\frac{m_e}{e}{\mathrm{\Phi }}_{B_G}\sim 10^{-36}$ Wb. Again, this is hopelessly too small. A more promising approach might be to use a low Earth orbit (LEO) satellite. It is found in Supplementary Appendix SB that the gravito-vector potential due to earth as observed by the satellite would be ${\left|\vec{h}\right|}_{\text{LEO}}\sim 10^{-3}$ m/s. This leads to $\frac{m_e}{e}{\mathrm{\Phi }}_{B_G}\sim 10^{-18}$ Wb which implies that an experiment would still need extreme sensitivity that can measure ${\mathrm{\Phi }}_{B,0}-\frac{m_e}{e}{\mathrm{\Phi }}_{B_G,0}\sim \frac{h}{2e}\left(1-10^{-18}\right)$ to demonstrate the presence of a gravito-magnetic fluxoid.

7 Supercurrent in a Closed Loop

Promoting the canonical momentum in Eq. 13 to a quantum mechanical operator and acting on the complex order parameter gives

$\begin{array}{ll}\hfill {\widehat{P}}_i\mathrm{\Psi }& =\gamma m\left(c{g}_{0i}+g_{ij}{\widehat{v}}^j\right)-q\left(g_{0i}{\widehat{A}}^0+g_{ij}{\widehat{A}}^j\right)\mathrm{\Psi }\hfill \\ \hfill & \hfill \end{array}(119)$

Again use Ψ = ψe ^iϕ , but now let $\psi =\sqrt{n_s}$ be a uniform number density around a ring. Therefore, ${\widehat{P}}_i\mathrm{\Psi }=\hslash \mathrm{\Psi }{\partial }_i\varphi$ . Then using Eq. 119 and taking the expectation value gives

$\begin{array}{ll}\hfill \hslash ⟨{\partial }_i\varphi ⟩& =\gamma m\left(c{g}_{0i}+g_{ij}⟨{\widehat{v}}^j⟩\right)-q\left(g_{0i}⟨{\widehat{A}}^0⟩+g_{ij}⟨{\widehat{A}}^j⟩\right)\hfill \end{array}(120)$

Applying Ehrenfest’s theorem allows this equation to return to a classical equation. Staying to first order in the metric perturbation and test mass velocity, and using Eq. 29 and Eq. 30 leads to

$\begin{array}{ll}\hfill \hslash \nabla \varphi & =\left(1-\frac{3{\phi }_G}{c^2}\right)m\vec{v}-\left(1-\frac{2{\phi }_G}{c^2}\right)q\vec{A}+4\left(1-\frac{q\phi }{m{c}^2}\right)m\vec{h}\hfill \end{array}(121)$

This expression can be written in terms of the supercurrent density, J ⁱ = −qn _s v ⁱ . Then integrating around a closed loop gives

$\begin{array}{ll}\hfill {\oint }_C\left[-\frac{m}{q{n}_s}\left(1-\frac{3{\phi }_G}{c^2}\right)\vec{J}-\left(1-\frac{2{\phi }_G}{c^2}\right)q\vec{A}+4\left(1-\frac{q\phi }{m{c}^2}\right)m\vec{h}\right]\cdot d\vec{l}& =\hslash {\oint }_C\left(\nabla \varphi \right)\cdot d\vec{l}\hfill \end{array}(122)$

Since the order parameter is single-valued, then it must return to the same value when the line integral returns to the same point. Therefore, the right side must be 2πn, where n is an integer. Applying Stokes’ theorem on the left side, and using q = −2e and m = 2m _e for Cooper pairs, gives

$\begin{array}{ll}\hfill & \frac{m_e}{2e{n}_s}{\oint }_C\left(1-\frac{3{\phi }_G}{c^2}\right)\vec{J}\cdot d\vec{l}+e\left(1-\frac{2{\phi }_G}{c^2}\right){\mathrm{\Phi }}_B+4m_e\left(1+\frac{e\phi }{m_e{c}^2}\right){\mathrm{\Phi }}_{B_G}\hfill \\ \hfill & +\frac{2e}{c^2}\underset{S}{\int }\left({\vec{E}}_G\times \vec{A}-2\vec{E}\times \vec{h}\right)\cdot d\vec{S}=n\frac{h}{2}\hfill \end{array}(123)$

Since φ _G ≪ c ² and eφ ≪ m _e c ², then the expression can be approximated to

$\frac{m_e}{2e{n}_s}{\oint }_C\vec{J}\cdot d\vec{l}+e{\mathrm{\Phi }}_B+4m_e{\mathrm{\Phi }}_{B_G}+\frac{2e}{c^2}\underset{S}{\int }\left({\vec{E}}_G\times \vec{A}-2\vec{E}\times \vec{h}\right)\cdot d\vec{S}=n\frac{h}{2}(124)$

This result is similar to Eq. 113 which applies to the bulk of the superconductor. However, Eq. 124 contains additional terms involving $\vec{J}$ and $\vec{E}$ which can be non-zero on the surface of the ring (shallower than the penetration). An expression similar to Eq. 124 also appears in [17] [35, 109, 110], except the terms involving ${\vec{E}}_G\times \vec{A}$ and $\vec{E}\times \vec{h}$ are absent.

7.1 Supercurrent Quantization for a Superconducting Ring Coaxial With a Rotating Massive Cylinder

As a practical example, consider a superconducting ring in the presence of a rotating massive cylinder of length ℓ and radius R. The cylinder rotates at a constant non-relativistic angular velocity and hence has a stationary mass current (See Figure 1).

FIGURE 1

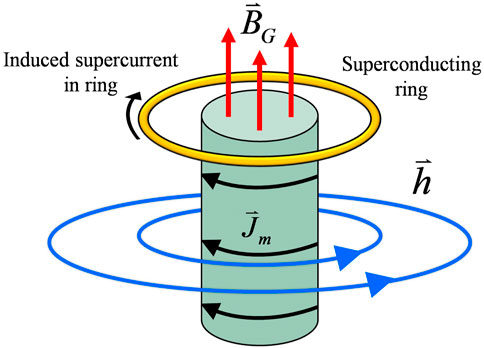
FIGURE 1. A rotating massive cylinder carries a mass current, ${\vec{J}}_m$ , which creates a gravito-vector potential, $\vec{h}$ , and a corresponding gravito-magnetic field, ${\vec{B}}_G$ . Note that $\vec{h}$ points in the opposite direction of ${\vec{J}}_m$ as a result of the negative sign in $\nabla \times \left(\nabla \times \vec{h}\right)=-{\mu }_G{\vec{J}}_m$ . A superconducting ring is coaxial to the cylinder so that a gravito-magnetic flux exists through the ring. As the flux of ${\vec{B}}_G$ increases with time, a supercurrent is induced in the superconducting ring.

This is effectively the same system that was considered by DeWitt [3]. He states, “Now consider an experiment in which the superconductor is a uniform circular ring surrounding a concentric, axially symmetric, quasirigid mass. Suppose the mass, initially at rest, is set in motion until a constant final angular velocity is reached. This produces a Lense-Thirring field which, in a coordinate system for which the metric is time-independent, takes the form

$\vec{\nabla }\times {\vec{h}}_0=16\pi \kappa {\nabla }^{-2}\vec{\nabla }\times \left(\rho \vec{V}\right)(125)$

where κ is the gravitation constant, and ρ and $\vec{V}$ are, respectively, the mass density and velocity field of the rotating mass.” For a steady-state current, the gravito-Ampere equation in Eq. 45 can indeed be written as ${\nabla }^2\vec{h}=\left(4\pi G/c^2\right){\rho }_m\vec{V}$ . This matches Eq. 125 up to a factor of 4 (which is due to DeWitt’s ${\vec{h}}_0$ being related to $\vec{h}$ used in this paper by ${\vec{h}}_0=4\vec{h}$ .) Also note that DeWitt sets c = 1.

Neglecting terms that are $\mathcal{O}\left(c^{-2}\right)$ in Eq. 124, and using DeWitt’s notation, $\vec{G}=e\vec{H}+m\nabla \times {\vec{h}}_0$ , where $\vec{H}=\nabla \times \vec{A}$ , gives

$\frac{m_e}{2e{n}_s}{\oint }_C\vec{J}\cdot d\vec{l}+\underset{S}{\int }\left(e\vec{H}+m\nabla \times {\vec{h}}_0\right)\cdot d\vec{S}=n\frac{h}{2}(126)$

DeWitt states, “If $\vec{H}$ is initially zero then so is $\vec{G}$ . Because of the flux quantization condition, the flux of $\vec{G}$ through the superconducting ring must remain zero. But since $\vec{\nabla }\times {\vec{h}}_0$ is nonvanishing in the final state, a magnetic field must be induced.” This implies that DeWitt is considering a system where every term in Eq. 126 is zero in the initial state. Then in the final state, he requires that $\vec{J}$ and n are still zero, but the flux of $\nabla \times {\vec{h}}_0$ is non-zero. Therefore, he concludes that the flux of $\vec{H}$ must become non-zero as well.

A similar statement is found in Papini’s paper [111] which is a follow up to DeWitt’s paper [3]. Papini states, “The main result of this [DeWitt’s] work is that whenever a Lense-Thirring field is present, it is not the magnetic field which vanishes inside a superconductor, but a combination of magnetic and gravitational fields. Similarly, the flux which is quantized is the total flux of magnetic and gravitational fields... It is important that initially the total flux linking the loop be zero. The total flux is in fact quantized in units of π and if it vanishes in the initial state, it also vanishes in the final state. It then follows that the magnetic flux equals in absolute value the flux of the gravitational field.” Using Eq. 124, this condition can be written as

$\begin{array}{ll}\hfill {\mathrm{\Phi }}_B& =-\frac{4m_e}{e}{\mathrm{\Phi }}_{B_G}\hfill \\ \hfill & \hfill \end{array}(127)$

DeWitt states, “Suppose the rotating mass is kept electromagnetically neutral... Then the magnetic field must arise from a current induced in the ring. The magnitude of this current will be

$I=-\frac{4m_e}{eL}\underset{S}{\int }\left(\vec{\nabla }\times {\vec{h}}_0\right)\cdot d\vec{S}=-\frac{16\pi \kappa m_e}{eL}\oint \left({\nabla }^{-2}\rho \vec{V}\right)\cdot d\vec{r}(128)$

where S is the area spanned by the ring, L is its self-inductance, and the final integral is taken around the ring.” Since a static flux does not generate a current, and the presence of inductance in Eq. 128 implies a changing current, then Faraday’s law and Eq. 127 must have been used to obtain

$\frac{dI}{dt}=-\frac{1}{L}\frac{d{\mathrm{\Phi }}_B}{dt}=\frac{4m_e}{eL}\frac{d{\mathrm{\Phi }}_{B_G}}{dt}(129)$

Integrating with respect to time gives $\mathrm{\Delta }I=\frac{4m_e}{eL}\mathrm{\Delta }{\mathrm{\Phi }}_{B_G}$ . Then letting the current and flux be initially zero, and using Eq. 125 leads to Eq. 128. Applying Stokes’ theorem to Eq. 128, integrating around the perimeter of the ring with a diameter of d = 2R, and using $M={\rho }_m\left(\pi R^2\ell \right)$ , where ℓ and M are the length and mass of the cylinder, respectively, gives

$I=-\frac{64\pi G{m}_e}{e{c}^2}\frac{M{\nabla }^{-2}\vec{V}}{L\ell d}(130)$

Evidently DeWitt assumes $\frac{64\pi }{L\ell }{\nabla }^{-2}\sim 1$ to obtain a result of ²⁸

$I_{DW}\sim \frac{G{m}_e}{e{c}^2}\frac{MV}{d}(131)$

except he sets c = 1. However, a more accurate estimate for Eq. 128 can be obtained using the gravito-magnetic flux evaluated in Supplementary Appendix SB as

${\mathrm{\Phi }}_{B_G}=\frac{{\mu }_{G}M{R}^2\omega }{2\ell }(132)$

where $4{\mathrm{\Phi }}_{B_G}=\int \left(\vec{\nabla }\times {\vec{h}}_0\right)\cdot d\vec{S}$ since ${\vec{h}}_0=4\vec{h}$ . For the case of a large flywheel (as described in Supplementary Appendix SB), we can use M ∼ 4 × 10³ kg, R ∼ ℓ ∼ 1 m, and ω ∼ 6 × 10² rad/s. For a 1 m length of 0.25 mm diameter superconducting wire well below its transition temperature, the inductance is on the order of L ∼ 10⁻¹⁰ H [112]. Then the order of magnitude predicted by Eq. 128 is ²⁹

$I_{DW}=\frac{32\pi G{m}_e}{e{c}^2}\frac{M{R}^2\omega }{\ell L}\sim 10^{-23}\text{\hspace{0.17em}A}(133)$

The following objections can be raised concerning DeWitt’s treatment summarized above.

• The expression in Eq. 127 was obtained using an initial state with every term in Eq. 126 set to zero, then letting ${\vec{h}}_0$ be non-zero in the final state, but requiring that $\vec{J}$ and n still remain zero in the final state. However, recall that Eq. 126 was fundamentally derived from the canonical momentum in Eq. 119 which shows that the presence of fields drives supercurrents. In fact, this same canonical momentum led to the London constitutive equations Eq. 50 and Eq. 51 which show explicitly the linear relationship between the fields and the supercurrent. Therefore, making ${\vec{h}}_0$ become non-zero will have the effect of introducing a supercurrent.

• When ${\vec{h}}_0$ is made non-zero, and a current is generated, the combined expression on the left side of Eq. 126 will remain quantized in units of h/2. However, this does not require the system to remain in the n = 0 state. Other states are also permitted. For example, in the body of a superconductor where $\vec{J}=0$ (and gravity is neglected), Eq. 126 reduces to just ${\mathrm{\Phi }}_B=nh/\left(2e\right)$ . States other than n = 0 are certainly observed [107, 108]. The only difference with Eq. 126 is that the presence of a supercurrent extends the quantization condition to include the sum total of fluxes, $e{\mathrm{\Phi }}_B+4m_e{\mathrm{\Phi }}_{B_G}$ , as well as the current, $\oint \vec{J}\cdot d\vec{l}$ .

• Since a static flux does not generate a current, then Eq. 129 must be used to obtain an induced current. However, it was also stated that Eq. 125 was obtained “in a coordinate system for which the metric is time-independent.” Since the right side of Eq. 129 is zero for a time-independent metric, then no electric current would be predicted.

With these considerations in mind, it is suggested that a correct interpretation of Eq. 126 would be described as follows. Introducing a non-zero B _G can generate a mass current in the ring via a gravito-Faraday flux rule. Because the mass current consists of Cooper pairs, then there will be an associated electric current, $J_c=J_m\left(m_e/e\right)$ . The electric current will produce an associated magnetic field and thereby a magnetic flux in the ring. The sum total of fluxes, $e{\mathrm{\Phi }}_B+4m_e{\mathrm{\Phi }}_{B_G}$ , and current, $\oint \vec{J}\cdot d\vec{l}$ , will be quantized according to Eq. 126. If the total on the left side of Eq. 126 is kept smaller than h/2, then the system will remain in the n = 0 state.

In this sense, Eq. 126 plays the role of a constraint equation describing the quantization of the current, rather than a field equation that can generate a flux. To elaborate on this, we can return to the more general expression Eq. 124 and write it as

$\frac{m_e}{2e{n}_s}{\oint }_C\vec{J}\cdot d\vec{l}+F=n\frac{h}{2}(134)$

where the total flux through the ring is

$F\equiv e{\mathrm{\Phi }}_B+4m_e{\mathrm{\Phi }}_{B_G}+\frac{2e}{c^2}\underset{S}{\int }\left({\vec{E}}_G\times \vec{A}-2\vec{E}\times \vec{h}\right)\cdot d\vec{S}(135)$

If the current density is assumed to be uniform and only occupies the skin of the superconducting ring (no deeper than the penetration depth), then $J=I/\left(\pi {\lambda }_L^2\right)$ . Therefore, using Eq. 61 and Eq. 134 leads to a quantization condition on the electric current given by

$I+\frac{2}{{\mu }_{0}e}\frac{F}{d}=I_{0}n(136)$

where

$I_0\equiv \frac{h}{{\mu }_{0}ed}(137)$

is an “electric current quantum” analogous to the magnetic flux quantum, ${\mathrm{\Phi }}_0=h/\left(2e\right)$ . Similar to DeWitt, the fluxes in Eq. 135 can be expressed in terms of the properties of the massive cylinder (such as mass density, rotation speed, etc). However, rather than applying ∇⁻² to both sides of the gravito-Ampere law as DeWitt did in Eq. 125, we can use the expressions derived in Supplementary Appendix SC for the potentials, fields, and associated fluxes. This makes Eq. 135 become ³⁰

$\begin{array}{ll}\hfill F& =-\frac{1}{2}\pi e\mu R^4\omega {\rho }_c+2\pi m_e{\mu }_G{R}^4\omega {\rho }_m-\frac{\pi R^{6}e{\rho }_m{\rho }_c\omega }{2{\epsilon }_G{\epsilon }_0{c}^4}\left[\frac{2-{\epsilon }_r{\mu }_r}{4{\epsilon }_r}+\ln \left(\frac{d}{2R}\right)\right]\hfill \\ \hfill & \hfill \end{array}(138)$

Here the relative electric permittivity and magnetic permeability of the massive cylinder are, respectively, ɛ _r = ɛ/ɛ ₀ and μ _r = μ/μ ₀. Also d is the diameter of the ring. Notice from Eq. 138 that F is a continuous function of ω, however, the entire left side of Eq. 136 is discretized and can only increase by increments of I ₀. This means that even though F can change gradually, the smallest change in F that can change the state of the system is ΔF = μ ₀ eI ₀ d/2, and each change by ΔF will move the system between n states. (If F changes by an amount smaller than μ ₀ eI ₀ d/2, the quantum “rigidity” of the Cooper pair wave function will preserve the state of the system.) However, since $h/\left({\mu }_{0}e\right)\sim 10^{-9}$ m⋅A, then macroscopic values for d will make I ₀ extremely small relative to the other terms in Eq. 136. Thus for macroscopic experiments, Eq. 136 becomes $I+\frac{2}{{\mu }_{0}e}\frac{F}{d}\approx 0$ which does not involve Planck’s constant, in accordance with the Correspondence Principle.

For simplicity, consider if the diameter of the ring is similar to the diameter of the solenoid $\left(d\approx 2R\right)$ , and the solenoid is electrically neutral $\left({\rho }_c=0\right)$ . This corresponds to setting the flux of ${\vec{E}}_G\times \vec{A}$ and $\vec{E}\times \vec{h}$ to zero in Eq. 135. Consider if ${\mathrm{\Phi }}_{B_G}$ increases with time due to either enlarging the ring with time, or spinning up the massive cylinder from rest. The changing gravito-magnetic flux will induce a current in the ring which points in the direction shown in Figure 1. This is in agreement with DeWitt [3] who states, “The current I arises from an induced motion of electrons on the surface of the superconductor. This motion is in the same direction as the motion of the rotating mass.” This current will produce a magnetic field that points downward in Figure 1. Therefore, Φ _B will be subtracted from ${\mathrm{\Phi }}_{B_G}$ in Eq. 135. For simplicity, we can approximate $B_{\text{ring}}\approx {\mu }_{0}I/\left(2\pi R\right)$ over the entire area of the ring ³¹ Then using Eq. 132 makes Eq. 135 become

$F=-\frac{e{\mu }_{0}IR}{2}+\frac{8\pi G{m}_{e}M{R}^2\omega }{c^2\ell }(139)$

and Eq. 136 becomes

$I+\frac{16\pi G{m}_e}{{\mu }_{0}e{c}^2}\frac{MR\omega }{\ell }=2I_{0}n(140)$

This is the quantization condition for the superconducting ring in the configuration of Figure 1. Again, it is emphasized that we cannot set n = 0 and claim that

$I\sim \frac{16\pi G{m}_e}{{\mu }_{0}e{c}^2}\frac{MR\omega }{\ell }(141)$

is generated in the ring. Rather, Eq. 141 should be interpreted as simply the smallest non-zero current that can exist in the ring. However, next we proceed to calculate the current that will be generated.

7.2 Induced Supercurrent in the Ring Due to a Motional Gravitational emf

The current generated in the superconducting ring can be evaluated by developing a gravitational version of the Faraday flux rule. In Supplementary Appendix SD it is shown that the Lorentz four-force in curved space-time Eq. 7 can be evaluated to first order in the perturbation and test mass velocity to obtain

$\vec{F}={\vec{F}}_{EM}+{\vec{F}}_G+{\vec{F}}_{\text{coupled}}(142)$

where the electromagnetic force is

${\vec{F}}_{EM}=q\left(\vec{E}+\vec{v}\times \vec{B}\right)(143)$

the gravitational force is

${\vec{F}}_G=m\left({\vec{E}}_G+4\vec{v}\times {\vec{B}}_G+3\vec{v}{\dot{\phi }}_G/c^2\right)(144)$

and the electromagnetic force coupled to gravity is

${\vec{F}}_{\text{coupled}}=q\left[\frac{{\phi }_G}{c^2}\left(\vec{E}-3\vec{v}\times \vec{B}\right)+\frac{4}{c^2}\left(\vec{E}\cdot \vec{h}\right)\vec{v}-4\vec{h}\times \vec{B}\right](145)$

The electromagnetic emf is given by

${\epsilon }_{EM}\equiv \frac{1}{q}\oint {\vec{F}}_{EM}\cdot d\vec{l}(146)$

which leads to the usual Faraday flux rule,

${\epsilon }_{EM}=-\frac{d{\mathrm{\Phi }}_B}{dt}=\oint \left(\vec{E}+{\vec{v}}_b\times \vec{B}\right)\cdot d\vec{l}(147)$

where ${\vec{v}}_b$ is the velocity of the moving boundary. In Supplementary Appendix SD, a “gravitational emf” is also defined as

${\epsilon }_G\equiv \frac{1}{m}\oint {\vec{F}}_G\cdot d\vec{l}(148)$

which leads to an associated “gravitational Faraday flux rule” given by

${\epsilon }_G=-4\underset{\text{constant\hspace{0.17em}}{B}_G}{\left(\frac{d{\mathrm{\Phi }}_{B_G}}{dt}\right)}+3\oint \left(\nabla \times {\partial }_t{\vec{B}}_G\right)\cdot d\vec{l}+\frac{3}{c^2}\oint {\dot{\phi }}_G{\vec{v}}_b\cdot d\vec{l}(149)$

where the notation “constant B _G ” indicates that the term in parentheses involves a time-varying boundary, not a time-varying B _G (which is accounted for in the next term). The emf generated by a time-varying boundary can be referred to as a motional gravitational emf, while the emf generated by a time-varying B _G can be referred to as a transformer gravitational emf. Lastly, a “coupled emf” associated with Eq. 145 can be defined as

${\epsilon }_{\text{coupled}}\equiv \frac{1}{q}\oint {\vec{F}}_{\text{coupled}}\cdot d\vec{l}(150)$

which becomes

$\begin{array}{ll}\hfill {\epsilon }_{\text{coupled}}& =\oint \left[\frac{{\phi }_G}{c^2}\left(\vec{E}-3{\vec{v}}_b\times \vec{B}\right)+\frac{4}{c^2}\left(\vec{E}\cdot \vec{h}\right){\vec{v}}_b-4\vec{h}\times \vec{B}\right]\cdot d\vec{l}\hfill \end{array}(151)$

The total emf associated with the total force Eq. 142 is

$\epsilon =\oint \left(\frac{1}{q}{\vec{F}}_{EM}+\frac{1}{m}{\vec{F}}_G+\frac{1}{q}{\vec{F}}_{\text{coupled}}\right)\cdot d\vec{l}(152)$

For the system in Figure 1, there is no electric field. Also, the gravito-scalar potential is primarily due to earth, therefore ${\dot{\phi }}_G=0$ . Lastly, $\vec{h}\times \vec{B}$ points radially inward while $d\vec{l}$ circulates around the ring, so $\left(\vec{h}\times \vec{B}\right)\cdot d\vec{l}=0$ . It was also previously explained that Φ _B must be subtracted from ${\mathrm{\Phi }}_{B_G}$ . With all of these considerations, the total emf becomes

$\epsilon =-\frac{d{\mathrm{\Phi }}_B}{dt}\left(1-\frac{3{\phi }_G}{c^2}\right)+\frac{4m_e}{e}\underset{\text{constant\hspace{0.17em}}{B}_G}{\left(\frac{d{\mathrm{\Phi }}_{B_G}}{dt}\right)}(153)$

Since φ _G is primarily due to earth, then 1 − 3φ _G /c ² ≈ 1 − 10⁻⁹ ∼ 1. For simplicity, again we can approximate $B_{\text{ring}}\approx {\mu }_{0}I/\left(2\pi R\right)$ over the entire interior area of the ring. Applying the definition of inductance, $L=-\frac{\epsilon }{dI/dt}$ , and using Eqs 132, 153 gives

$\frac{d}{dt}\left[\left(\frac{{\mu }_{0}I}{2\pi R}-\frac{8G{m}_e}{e{c}^2}\frac{M\omega }{\ell }\right)\pi r^2\right]=-L\frac{dI}{dt}(154)$

where r is the time-varying radius of the ring. Consider if the ring is expanding at a constant rate, r = v _b t, and define

$a\equiv \frac{{\mu }_0{v}_b^2}{LR}\text{and}b\equiv \frac{16\pi G{m}_e{v}_b^2}{e{c}^2}\frac{M\omega }{L\ell }(155)$

where a characterizes electromagnetic effects, and b characterizes gravitational effects. Then Eq. 154 becomes

$\left(1+2a{t}^2\right)\frac{dI}{dt}+aIt=bt(156)$

In the absence of gravity $\left(b=0\right)$ , the equation describes the induced changes in the current of a superconducting ring if the ring already has a current and the size of the ring changes at a constant rate. Therefore gravity introduces an additional driving term, bt, to the system. If the rotating cylinder is a large flywheel (as described in Supplementary Appendix SB), we can use M ∼ 4 × 10³ kg, R ∼ ℓ ∼ 1 m, and ω ∼ 6 × 10² rad/s. This leads to a characteristic value for the current given by

$I_0=\frac{b}{2a}=\frac{32\pi G{m}_e{\epsilon }_0}{e}\frac{MR\omega }{\ell }\sim 10^{-24}\text{\hspace{0.17em}A}(157)$

which is indicative of the fact that gravity has a miniscule effect on the induced changes in the current. In superconductors, L ∼ 10⁻¹⁰ H at most [112]. Also, if v _b ∼ 1 m/s, then a ∼ 10⁴ s⁻². Therefore, 1 + 2at ² ≈ 1 for $t\ll {\left(2a\right)}^{-1/2}\sim 10^{-2}$ s. In that case, if I = 0 at t = 0, the solution to Eq. 156 is

$I\approx I_0\left(1-e^{-a{t}^2}\right)\text{for\hspace{0.17em}}t\ll {\left(2a\right)}^{-1/2}(158)$

Note that the values of L and v _b are not relevant until t ≪ 10⁻² s is no longer satisfied.

7.3 Induced Supercurrent in the Ring Due to a Transformer Gravitational emf

As previously stated, Eq. 129 implies DeWitt was considering a situation associated with a transformer emf (not a motional emf) since he states, “Suppose the mass, initially at rest, is set in motion until a constant final angular velocity is reached.” It has been emphasized throughout this paper that the use of non-relativistic gravitational sources and harmonic coordinates leads to ${\partial }_t\vec{h}=0$ , as shown in Section 3. This implies the absence of a gravito-Faraday law and a gravitational transformer emf.

However, to treat the system DeWitt was considering, we can relax this requirement and permit ${\partial }_t\vec{h}\ne 0$ . This has the effect of turning ${\nabla }^2\vec{h}={\mu }_G{\vec{J}}_m$ into $\square \vec{h}={\mu }_G{\vec{J}}_m$ . There are other modifications to the gravito-electromagnetic field equations which are discussed in [28], however, for our purposes here, the only relevant change is the presence of a gravito-Faraday law, $\nabla \times {\vec{E}}_G=-d{\vec{B}}_G/dt$ . Therefore, the emf induced in the ring now involves the second term on the right side of Eq. 149. Using Stokes’ theorem on this term and including the electromagnetic flux leads to a total flux given by

$\epsilon =-\frac{d{\mathrm{\Phi }}_B}{dt}\left(1-\frac{3{\phi }_G}{c^2}\right)+\frac{3m_e}{e}\underset{\text{constant\hspace{0.17em}boundary}}{\left(\frac{d{\mathrm{\Phi }}_{B_G}}{dt}\right)}(159)$

where the notation “constant boundary” indicates that the term in parentheses involves a time-varying B _G , not a time-varying boundary. Again, 1 − 3φ _G /c ² ∼ 1. This leads to a result similar to Eq. 154 but this time r = R (which is constant) but ω varies with time. Therefore we have

$\frac{{\mu }_{0}A}{2\pi R}\frac{dI}{dt}-\frac{6G{m}_e}{e{c}^2}\frac{MA}{\ell }\alpha \left(t\right)=-L\frac{dI}{dt}(160)$

where $\alpha \left(t\right)=d\omega /dt$ . Defining

$a^{\prime }\equiv \frac{{\mu }_{0}R}{2L}\text{and}{b}^{\prime }\equiv \frac{6\pi G{m}_e}{eL{c}^2}\frac{M{R}^2}{\ell }(161)$

leads to

$\frac{dI}{dt}-\frac{b^{\prime }}{1+a^{\prime }}\alpha \left(t\right)=0(162)$

Again a′ characterizes electromagnetic effects, and b′ characterizes gravitational effects. Letting I = 0 at t = 0, and t = T when the mass cylinder reaches ω _max, leads to the following solution to Eq. 162.

$I\left(t\right)=\frac{b^{\prime }}{1+a^{\prime }}{\int }_0^T\alpha \left(t\right)(163)$

If α is constant, then ω _max = αT. For the case of a large flywheel, again we can use M ∼ 4 × 10³ kg, R ∼ ℓ ∼ 1 m, and ω _max ∼ 6 × 10² rad/s. Since L ∼ 10^–10 H at most in superconductors [112], then 1 + a′ ≈ a′ ∼ 10⁴ and Eq. 163 becomes

$I\approx \frac{b^{\prime }{\omega }_{\max }}{a^{\prime }}=\frac{12\pi G{m}_e{\epsilon }_0}{e}\frac{MR{\omega }_{\max }}{\ell }\sim 10^{-25}\text{\hspace{0.17em}A}(164)$

Note that the electric current produced by a motional gravitational emf Eq. 157 and transformer gravitational emf Eq. 164 are not unique to a superconductor since the London equations were not utilized anywhere in the analysis. The only feature in the calculation unique to superconductors is the value of the inductance, however, the inductance cancels in both calculations.

Alternatively, a treatment involving the London equations could begin with Eq. 53. When we permit ${\partial }_t\vec{h}\ne 0$ and use ${\vec{E}}_G=-{\partial }_t\vec{h}$ for the non-conservative gravito-electric field, then Eq. 53 becomes

${\partial }_t{\vec{J}}_c={\mathrm{\Lambda }}_L\left[\left(1+\frac{{\phi }_G}{c^2}\right)\vec{E}+\frac{4m_e}{e}{\vec{E}}_G\right](165)$

where we set ${\dot{\phi }}_G=0$ and φ = 0. An expression for ${\vec{E}}_G$ can be obtained by using the gravito-Faraday law in integral form

$\int {\vec{E}}_G\cdot d\vec{l}=-\frac{d{\mathrm{\Phi }}_{B_G}}{dt}(166)$

Applying this to the ring and using Eq. 132 leads to a magnitude given by

$E_G=\frac{GMR\alpha \left(t\right)}{c^2\ell }(167)$

where $\alpha \left(t\right)=d\omega /dt$ . Likewise, an expression for $\vec{E}$ can be obtained using Faraday’s law in integral form and approximating $B_{\text{ring}}\approx {\mu }_{0}I/\left(2\pi R\right)$ over the entire interior area of the ring. This leads to a magnitude given by

$E=\frac{{\mu }_0}{4\pi }\frac{dI}{dt}(168)$

As previously stated, the effect of Eqs 167, 168 are in opposite directions. Therefore, using Eq. 165 as well as $J=I/\left(\pi {\lambda }_L^2\right)$ and Eq. 61, and approximating 1 + φ _G /c ² ≈ 1 leads to

$\frac{dI}{dt}=\frac{16\pi G{m}_e{\epsilon }_0}{5e}\frac{MR\alpha \left(t\right)}{\ell }(169)$

This has the same form as Eq. 162 and therefore has a solution similar to Eq. 163.

$I\left(t\right)=\frac{16\pi G{m}_e{\epsilon }_0}{5e}\frac{MR}{\ell }{\int }_0^T\alpha \left(t\right)(170)$

Assuming α is constant, and using the same parameters for a large flywheel again leads to

$I=\frac{16\pi G{m}_e{\epsilon }_0}{5e}\frac{MR{\omega }_{\max }}{\ell }\sim 10^{-26}\text{\hspace{0.17em}A}(171)$

Again, the result is not dependent on the inductance, and the value is comparable to Eq. 164. It is arguable that the result obtained in Eq. 171 is more reliable since it is calculated using the London equation which is derived from the canonical momentum. Therefore, it stems from a quantum mechanical approach (since the canonical momentum operator acting on the Ginzburg-Landau order parameter leads to the London equations). In contrast, Eq. 171 is derived from a purely classical equation of motion (the geodesic equation of motion with a Lorentz four-force). ³²

7.4 Gravitational Hall Effect in the Ring

Due to the current in the ring and the presence of magnetic and gravito-magnetic fields, there will be a corresponding Hall effect as shown in Figure 2.

FIGURE 2

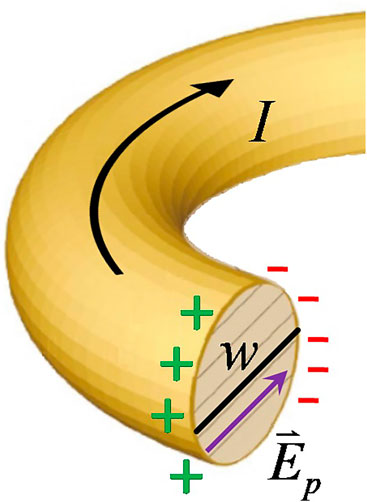
FIGURE 2. A polarization electric field, $\vec{E}p$ , occurs as a result of the supercurrent I in the presence of ${\vec{B}}_G$ . The width of the cross-section of the ring is w, and a corresponding Hall potential, V _H = wE _p , would exist between the inner and outer surface of the ring.

Following the usual derivation of the Hall effect, we begin with the total force on the charge carriers. As previously stated, ${\dot{\phi }}_G=0$ for the gravito-scalar potential of earth. However, now we let $\vec{E}\ne 0$ since charge carriers will accumulate on opposite sides of a cross-section of the ring, as shown in Figure 3. Therefore Eq. 142 becomes

$\vec{F}=q\left({\vec{E}}_p+{\vec{v}}_s\times \vec{B}\right)+m\left({\vec{E}}_G+4{\vec{v}}_s\times {\vec{B}}_G\right)+q\left[\frac{{\phi }_G}{c^2}\left({\vec{E}}_p-3\vec{v}\times \vec{B}\right)+\frac{4}{c^2}\left({\vec{E}}_p\cdot \vec{h}\right)\vec{v}-4\vec{h}\times \vec{B}\right](172)$

where v _s is the velocity of the supercurrent around the ring, and ${\vec{E}}_p$ is the electric field produced due to the polarization across the cross-section of the ring. The current on one side of the ring will generate a magnetic field that points downward on the other side of the ring. This will generate a magnetic force that points radially inward on Cooper pairs which are negative charge carriers $\left(q=-2e\right)$ . Meanwhile, the gravito-magnetic field will produce a force that also points radially inward on Cooper pairs which are mass carriers $\left(m=2m_e\right)$ . For simplicity, assume $\vec{B}$ points directly down through the ring, and ${\vec{B}}_G$ points directly up so that $\left|{\vec{v}}_s\times \vec{B}\right|=v_{s}B$ and $\left|{\vec{v}}_s\times {\vec{B}}_G\right|=v_s{B}_G$ .

FIGURE 3

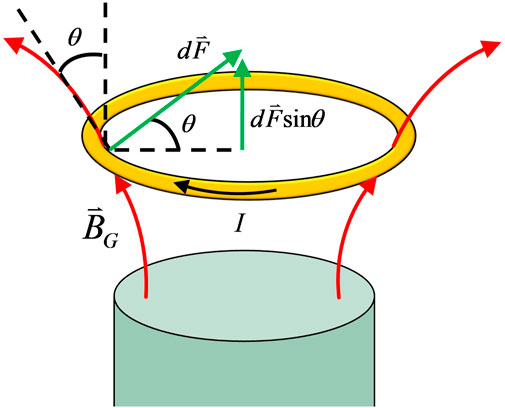
FIGURE 3. A superconducting ring placed above a rotating mass cyldiner. At the location of the ring, ${\vec{B}}_G$ makes an angle θ with respect to the vertical line. The differential force in the vertical direction is $d\vec{F}\sin \theta$ .

The net effect of the magnetic and gravito-magnetic forces is to cause Cooper pairs to accumulate on the inner perimeter of the ring. As a result, there will be an electric field pointing radially inward. There will not be any ${\vec{E}}_G$ in the radial direction since ${\vec{E}}_G$ due to earth points downward, and ${\vec{E}}_G$ due to $d{\mathrm{\Phi }}_{B_G}/dt$ is azimuthal. Also note that ${\vec{E}}_p\cdot \vec{h}=0$ since $\vec{h}$ is azimuthal but ${\vec{E}}_p$ is radial. However, $\vec{h}\times \vec{B}$ points in the radially inward direction. Therefore, the radial component of Eq. 172 becomes

$F_r=2e{E}_p\left(1+\frac{{\phi }_G}{c^2}\right)-2e{v}_{s}B\left(1-\frac{3{\phi }_G}{c^2}\right)-8m_e{v}_s{B}_G-8e\left|\vec{h}\right|B(173)$

Following the usual derivation of the Hall effect, the total radial force on the charge carriers will be zero for a steady-state current. Also using $\vec{J}=n_{s}e{\vec{v}}_s$ and $J=I/\left(\pi {\lambda }_L^2\right)$ , as well as Eq. 61, leads to

$I=\frac{\pi m_e{v}_s}{{\mu }_{0}e}(174)$

Then approximating 1 − 3φ _G /c ² ∼ 1 makes Eq. 173 become

$E_p=\frac{{\mu }_{0}I}{\pi }\left(\frac{e}{m_e}B+4B_G\right)+4\left|\vec{h}\right|B(175)$

We can approximate $B_{\text{ring}}\approx \frac{{\mu }_{0}I}{2\pi R}$ and use $B_G=\frac{{\mu }_{G}M\omega }{2\pi \ell }$ and $\left|\vec{h}\right|=\frac{{\mu }_{G}MR\omega }{4\pi \ell }$ from Supplementary Appendix SB. Also writing the hall potential as V _H = wE _p , where w is the width of the cross-section of the ring, leads to

$V_H=\frac{{\mu }_0^{2}e}{2{\pi }^2{m}_e}\frac{I^2}{wR}+\frac{10G{\mu }_0}{\pi c^2}\frac{M\omega I}{\ell w}(176)$

The first term is purely electromagnetic and quadratic in the current, while the second term involves gravitational effects and is linear in the current. In fact, for the case of a large flywheel (M ∼ 4 × 10³ kg, R ∼ ℓ ∼ 1 m, ω ∼ 6 × 10² rad/s), the two terms become comparable when

$I=\frac{20\pi {\epsilon }_{0}G{m}_e}{e}\frac{M\omega R}{\ell }\sim 10^{-23}\text{\hspace{0.17em}A}(177)$

This is similar to the result obtained in Eq. 157. Using Eq. 177 and ω ∼ 10⁻⁴ m in Eq. 176 gives

$V_H=\frac{20G{\mu }_0}{\pi c^2}\frac{M\omega I}{\ell w}\sim 10^{-23}\text{\hspace{0.17em}V}(178)$

A gravitational Hall effect for a superfluid is also considered in [27], however, no Hall potential value is obtained.

7.5 Induced Force on the Ring

Lastly, consider if the ring is raised some distance above the massive cylinder so that ${\vec{B}}_G$ at the ring is not completely in the vertical direction, as shown in Figure 3.

A vertical force on the ring will exist due to the current in the ring and the gravito-magnetic field of the mass cylinder. This effect is analogous to the “jumping ring” experiment where a magnetic force is evaluated using $\vec{F}=I\int d\vec{l}\times \vec{B}$ and is found to be F = 2πRIB sin θ, where B is an external magnetic field, and θ is the angle shown in Figure 3. However, to deal with the gravitational case, we can start with the total force in Eq. 142 and set $\vec{E}=0$ and ${\dot{\phi }}_G=0$ . Neglecting the weight of the ring gives

$\vec{F}=q\vec{v}\times \vec{B}+m\left({\vec{E}}_{G,\text{ind}}+4\vec{v}\times {\vec{B}}_G\right)-\frac{3q{\phi }_G}{c^2}\vec{v}\times \vec{B}-4q\vec{h}\times \vec{B}(179)$

where ${\vec{E}}_{G,\text{ind}}$ is the gravito-electric field induced by the time-varying gravito-magnetic flux. Since ${\vec{E}}_{G,\text{ind}}$ is azimuthal, it only serves to drive the supercurrent and does not contribute to any vertical force on the ring. Likewise, $\vec{h}\times \vec{B}$ and ${\vec{v}}_s\times \vec{B}$ also do not contribute to a vertical force since $\vec{B}$ points downward, but v _s and $\vec{h}$ are azimuthal.

Recall that the differential magnetic force in a current segment, $d\vec{F}=Id\vec{l}\times \vec{B}$ , is obtained from $\vec{F}=q\vec{v}\times \vec{B}$ by using qv → Idl. Similarly, for the gravitational force, we can use mv → I _m dl, where I _m is the mass current which is related to the electric current by $I=I_m\left(m_e/e\right)$ . Since $d\vec{l}$ is azimuthal and B _G has no azimuthal component, then $\left|d\vec{l}\times {\vec{B}}_G\right|=B_{G}dl$ . However, the component of dF in the vertical direction is dF sin θ, as can be seen from Figure 3. Therefore, the differential force in the vertical direction for each differential segment is

$dF=\frac{4m_e}{e}I{B}_G\sin \theta dl(180)$

In Supplementary Appendix SB, the gravito-magnetic field along the axis of the mass cylinder is found as $B_G={\mu }_{G}M\omega /\left(2\pi \ell \right)$ . Since the field near the end of a solenoid is approximately half of that at the center. Then the total force around the ring can be approximated as

$F=\frac{8\pi G{m}_e}{c^{2}e}\frac{MRI\omega }{\ell }\sin \theta (181)$

Approximating θ ≈ 30⁰, using the case of a large flywheel (M ∼ 4 × 10³ kg, R ∼ ℓ ∼ 1 m, ω ∼ 6 × 10² rad/s), and I ∼ 10⁻²⁶ A obtained in Eq. 171 leads to F ∼ 10⁻⁵⁷ N which is completely negligible. To get a more substantial effect, an electric current can be driven in the ring prior to introducing B _G from the massive cylinder. It is shown in Supplementary Appendix SB that the maximum supercurrent velocity that preserves the superconducting state is v ∼ 10⁴ m/s. Then using Eq. 174 leads to

$I=\frac{\pi m_e{v}_s}{{\mu }_{0}e}\sim 10^{-1}\text{\hspace{0.17em}A}(182)$

This is a factor of 10²⁵ larger than the current induced by B _G . Furthermore, it was previously mentioned that in a low Earth orbit (LEO) satellite, the gravito-vector potential due to earth (as observed by the satellite) is h _LEO ∼ 10⁻³ m/s. Compared to the large flywheel (h ∼ 10⁻²¹ m/s) this leads to another factor of 10¹⁸ increase for B _G . As a result, the force on a ring could be F ∼ 10⁻¹⁴ N.

On a related note, the factor of 10¹⁸ increase in $\vec{h}$ would also increase the electric current produced by a motional emf Eq. 157 and by a transformer emf Eq. 171 so that they become I ∼ 10⁻⁶ A and I ∼ 10⁻⁸ A, respectively. Also, using h _LEO ∼ 10⁻³ m/s makes Eq. 177 become I ∼ 10⁻⁵ A and the Hall potential in Eq. 178 becomes V _H ∼ 10⁻¹ V.

Since the gravito-vector potential of the earth cannot be controlled (unlike that of a spinning flywheel), an option for controlling the exposure of the system to $\vec{h}$ would be to place the system in an enclosure surrounded by superconducting material. The gravitational Meissner effect described in Section 4 could be used to shield the system from $\vec{h}$ by controlling the temperature of the enclosure material such that it can transition above and below the critical temperature for the superconducting state.

8 Conclusion

The following are key results demonstrated uniquely in this paper.

• The canonical momentum for a relativistic spinless charged particle in curved space-time is obtained in Eq. 13 as

$P_i=\gamma m\left(c{g}_{0i}+g_{ij}{v}^j\right)-q\left(g_{0i}{A}^0+g_{ij}{A}^j\right)(183)$

where the Lorentz factor in curved space-time is $\gamma =\sqrt{-g_{\mu \nu }{v}^{\mu }{v}^{\nu }}$ . This result is valid to all orders in the metric and particle velocity. It can also be written as simply p _i = P _i − eA _i which is consistent with the covariant minimal coupling rule, P _μ → P _μ − eA _μ .

• A corrected version of DeWitt’s Hamiltonian Eq. 1 is given by the “space + time” Hamiltonian shown in Eq. 20 as

$\begin{array}{ll}\hfill H& =c{\left({\tilde{g}}^{jk}{g}_{0j}{g}_{0k}-g_{00}\right)}^{1/2}{\left[m^2{c}^2+{\tilde{g}}^{jk}\left(P_j-e{g}_{0j}{A}^0-e{g}_{jl}{A}^l\right)\left(P_k-e{g}_{0k}{A}^0-e{g}_{km}{A}^m\right)\right]}^{1/2}\hfill \\ \hfill & -c{\tilde{g}}^{jk}{g}_{0k}\left(P_j-e{g}_{0j}{A}^0-e{g}_{jl}{A}^l\right)-ec\left(g_{00}{A}^0+g_{0j}{A}^j\right)\hfill \end{array}(184)$

where ${\tilde{g}}^{jk}\equiv g^{jk}-g^{0j}{g}^{0k}/g^{00}$ . This is shown to be equivalent to the “space + time” Hamiltonian derived by multiple other authors in Eq. 23, Eq. 24, and Eq. 25.

• The Hamiltonian that is first order in the metric perturbation and second order in momentum is found in Eq. 28 to be

$\begin{array}{ll}\hfill H& =m{c}^2+\frac{1}{2m}{\left(P_i-e{A}_i\right)}^2-c{h}_{0i}\left(P_i-e{A}_i\right)-\frac{1}{2}{h}_{00}m{c}^2-ec{A}_0\hfill \\ \hfill & -\frac{h_{00}}{4m}{\left(P_i-e{A}_i\right)}^2-\frac{h_{ij}}{2m}\left(P_i-e{A}_i\right)\left(P_j-e{A}_j\right)-\frac{h_{0i}}{2m}e{A}^0\left(P_i-e{A}_i\right)\hfill \end{array}(185)$

The last three terms in Eq. 185 are missing from DeWitt’s result in Eq. 2 which is

$H_{DW}=\frac{1}{2m}{\left(\vec{P}-e\vec{A}-m{\vec{h}}_0\right)}^2-e{A}_0-\frac{1}{2}m{h}_{00}(186)$

It is also shown that contrary to Eq. 186, a coupling of the form h _0i A ⁱ is absent in Eq. 185, and a coupling of the form $m{h}_{0i}^2$ is second order in the perturbation and therefore absent. It is pointed out that Eq. 186 is quoted by a multitude of authors, or obtained by authors by starting from $H=\frac{1}{2m}{P}^2+V$ and using $\vec{P}\to \vec{P}-e\vec{A}-m\vec{h}$ instead of the full canonical momentum in Eq. 183.

• A consistent approach to obtaining the weak-field, low-velocity Hamiltonian requires an expansion to second order in the perturbation and fourth order in the momentum. For non-relativistic gravitational sources in harmonic coordinates, the Hamiltonian is found in Eq. 32 to be

$\begin{array}{ll}\hfill H& =m{c}^2+e\phi +\left(\frac{{\tilde{P}}^2}{2m}+m{\phi }_G\right)+\frac{2e{\phi }_G\phi }{c^2}+\left(\frac{3{\phi }_G{\tilde{P}}^2}{2m{c}^2}+\frac{2e{\phi }_G{A}^i{\tilde{P}}_i}{m{c}^2}-\frac{m{\phi }_G^2}{2c^2}-\frac{{\tilde{P}}^4}{8m^3{c}^2}\right)\hfill \\ \hfill & +\left(\frac{11{\phi }_G^2{\tilde{P}}^2}{4m{c}^4}+\frac{2e^2{A}^2{\phi }_G^2}{m{c}^4}-\frac{e{A}^i{\phi }_G{\tilde{P}}_i{\tilde{P}}^2}{m^3{c}^4}-\frac{5{\phi }_G{\tilde{P}}^4}{8m^3{c}^4}+\frac{6e{\phi }_G^2{A}^i{\tilde{P}}_i}{m{c}^4}\right)-4h^i{P}_i.\hfill \end{array}(187)$

$\text{where}{\stackrel{\sim }{P}}_i\equiv P_i-{\eta }_{ij}{A}^j,{\stackrel{\sim }{P}}_i^2={\stackrel{\sim }{P}}_i{\stackrel{\sim }{P}}_i\mathrm{a}\mathrm{n}\mathrm{d}{A}_i^2=A_i{A}_i$ . It is shown that the closest form to a Hamiltonian similar to DeWitt’s in Eq. 2 is obtained only if the electromagnetic potentials are reduced to absurdly small (but non-zero) values: A ∼ 10⁻³² T⋅m and φ ≪ 10⁻⁴⁴ V. Then the result is found in Eq. 31 to be

$\begin{array}{ll}\hfill H& =m{c}^2+m{\phi }_G-\frac{m{\phi }_G^2}{2c^2}+e\phi +\frac{{\left(P_i-e{\eta }_{ij}{A}^j\right)}^2}{2m}-4h^i{P}_i+8m{h}^2\hfill \\ \hfill & \hfill \end{array}(188)$

• Quantizing the Hamiltonian in Eq. 188 leads to a modified Schrödinger equation:

$i\hslash {\partial }_t\psi \left(x,t\right)=\left[\frac{1}{2m}{\left(-\hslash {\partial }_i-e{\eta }_{ij}{A}^j\right)}^2+4i\hslash h^i{\partial }_i+8m{h}^2+m{\phi }_G-\frac{m{\phi }_G^2}{2c^2}+e\phi \right]\psi \left(x,t\right)(189)$

It is shown that using a solution of the form $\psi \left(x,t\right)=e^{i\varphi }{\psi }_0\left(x,t\right)$ , where ${\psi }_0\left(x,t\right)$ is the solution to the field-free Schrödinger equation, does not lead to a phase given by $\varphi =\frac{1}{\hslash }\int {\eta }_{ij}\left(e{A}^j+4m{h}^j\right)d{x}^i$ , as commonly found in the literature.

• The canonical momentum Eq. 183 is used to develop modified London equations Eq. 53–Eq. 56, and a modified gauge condition Eq. 58 .

• The gravito-magnetic field, ${\vec{B}}_G$ , is expelled from a superconductor in a Meissner effect only if there is also a magnetic field satisfying $\vec{B}<-{\vec{B}}_G\left(m_e/e\right)$ . This observation is being taken into account for guiding experimental work [101]. The associated penetration depth is found in Eq. 84 to be on the order of the London penetration depth:

${\lambda }_L^{\prime -2}=\alpha {\lambda }_L^2-\beta {\mu }_G{n}_{s}e\approx {\lambda }_L^{-2}(190)$

where α ≡ 1 + φ _G /c ² and $\beta \equiv 4\left(m_e{c}^2+e\phi \right)/\left(e{c}^2\right)$ . Also, the presence of gravity leads to a slightly modified penetration depth for $\vec{B}$ which is also given by Eq. 190.

• In the absence of $\vec{B}$ , there is no Meissner effect for ${\vec{B}}_G$ . Instead, the field has an oscillatory solution with spatial periodicity found in Eq. 74 to be

$\begin{array}{ll}\hfill {\lambda }_{\left(\text{periodicity\hspace{0.17em}of\hspace{0.17em}}{\vec{B}}_G\right)}& \equiv \frac{2\pi }{\sqrt{4{\mu }_G{n}_s{m}_e}}\hfill \end{array}(191)$

• For non-relativistic gravitational sources (in harmonic coordinates), the gravito-electric field, ${\vec{E}}_G$ , is time-independent (which is just the Newtonian field) and is not expelled from a superconductor. However, the presence of ${\vec{E}}_G$ leads to a small correction to the penetration depth of $\vec{E}$ which becomes Eq. 190. The general solution is

$\vec{E}={\mu }_0{\mathrm{\Lambda }}_L\vec{H}{\lambda }_L^{\prime 2}{e}^{-z/{\lambda }_L^{\prime }}(192)$

where $\vec{H}\equiv \alpha {\vec{E}}_0-\frac{1}{c^2}\left({\dot{\phi }}_G{\vec{A}}_0-4\dot{\phi }{\vec{h}}_0\right)$ , and ${\vec{E}}_0$ , ${\vec{A}}_0$ , ${\vec{h}}_0$ are the fields at the surface of the superconductor $\left(z=0\right)$ .

• The flux quantum (fluxoid) in the body of a superconductor is found in Eq. 113 to be

$e{\mathrm{\Phi }}_B+4m_e{\mathrm{\Phi }}_{B_G}+\frac{2e}{c^2}\underset{S}{\int }\left({\vec{E}}_G\times \vec{A}\right)\cdot d\vec{S}=n\frac{h}{2}(193)$

The first two terms involving eΦ _B and $m_e{\mathrm{\Phi }}_{B_G}$ are common in the literature, but the flux of ${\vec{E}}_G\times \vec{A}$ is not. In the absence of electromagnetism, the gravito-magnetic flux condition can be written as ${\mathrm{\Phi }}_{B_G}=n{\mathrm{\Phi }}_{B_G,0}$ , where ${\mathrm{\Phi }}_{B_G,0}\equiv h/\left(8m_e\right)$ is a gravito-magnetic flux quantum (fluxoid). For a low Earth orbit (LEO) satellite, ${\left|\vec{h}\right|}_{\text{LEO}}\sim 10^{-3}$ m/s which implies that demonstrating the presence of a gravito-magnetic fluxoid would require an experiment with sensitivity that can measure ${\mathrm{\Phi }}_{B,0}-\frac{m_e}{e}{\mathrm{\Phi }}_{B_G,0}\sim \frac{h}{2e}\left(1-10^{-18}\right)$ , where h is Planck’s constant.

• Similarly, the quantized supercurrent in a superconducting ring is found in Eq. 124 to be

$\frac{m_e}{2e{n}_s}{\oint }_C\vec{J}\cdot d\vec{l}+e{\mathrm{\Phi }}_B+4m_e{\mathrm{\Phi }}_{B_G}+\frac{2e}{c^2}\underset{S}{\int }\left({\vec{E}}_G\times \vec{A}-2\vec{E}\times \vec{h}\right)\cdot d\vec{S}=n\frac{h}{2}(194)$

Again, the terms involving eΦ _B and $m_e{\mathrm{\Phi }}_{B_G}$ are common in the literature, but the flux of ${\vec{E}}_G\times \vec{A}$ and $\vec{E}\times \vec{h}$ are not. This can also be written as a quantization condition on the electric current given by Eq. 136 as

$I+\frac{2}{{\mu }_{0}e}\frac{F}{d}=I_{0}n(195)$

where d is the diameter of the ring, F is the total flux of fields through the ring as shown in Eq. 194, and

$I_0\equiv \frac{h}{{\mu }_{0}ed}(196)$

is an “electric current quantum” analogous to the magnetic flux quantum, ${\mathrm{\Phi }}_0=h/\left(2e\right)$ .

• For the case of a superconducting ring coaxial with a rotating massive cylinder (flywheel), the induced supercurrent predicted by DeWitt is found using Eq. 195. Using a large flywheel (M ∼ 4 × 10³ kg, R ∼ ℓ ∼ 1 m, ω ∼ 6 × 10² rad/s), and assuming the diameter of the ring is d ≈ 2R, leads to

$I_{DW}=\frac{32\pi G{m}_e}{e{c}^2}\frac{M{R}^2\omega }{\ell L}\sim 10^{-23}\text{\hspace{0.17em}A}(197)$

This result depends on L ∼ 10⁻¹⁰ H for the inductance of the superconductor. In comparison, using a motional gravitational emf (a time-varying boundary of the ring) leads to an electric current in the ring given by Eq. 157 as

$I=\frac{32\pi G{m}_e{\epsilon }_0}{e}\frac{MR\omega }{\ell }\sim 10^{-24}\text{\hspace{0.17em}A}(198)$

For a transformer gravitational emf (a time-varying ${\vec{B}}_G$ ), using an inductance approach leads to Eq. 164 which gives

$I=\frac{12\pi G{m}_e{\epsilon }_0}{e}\frac{MR{\omega }_{\max }}{\ell }\sim 10^{-25}\text{\hspace{0.17em}A}(199)$

This result does not depend on inductance because it cancels out in the analysis. Alternatively, using a gravito-Faraday law and London equation approach leads to Eq. 171 which gives

$I=\frac{16\pi G{m}_e{\epsilon }_0}{5e}\frac{MR{\omega }_{\max }}{\ell }\sim 10^{-26}\text{\hspace{0.17em}A}(200)$

It is argued that Eq. 197 is not a valid result since it is based on setting n = 0 and I = 0 in Eq. 195 which contradicts I ≠ 0 in Eq. 197. It is also argued that for a transformer gravitational emf, the result in Eq. 200 is likely more valid than Eq. 199 because Eq. 199 is based on a purely classical analysis (not unique to a superconductor) while Eq. 200 employs the London equation which is fundamentally quantum mechanical.

• A gravitational Hall effect is found to occur between the inner radius and outer radius of the superconducting ring with a Hall potential given by

$V_H=\frac{20G{\mu }_0}{\pi c^2}\frac{M\omega I}{\ell w}\sim 10^{-23}\text{\hspace{0.17em}V}(201)$

• If the ring is positioned above the mass cylinder, a vertical force is induced in the ring which is found in Eq. 181 to be

$F=\frac{8\pi G{m}_e}{c^{2}e}\frac{MRI\omega }{\ell }\sin \theta (202)$

where θ is the angle of ${\vec{B}}_G$ relative to the vertical line through the plane of the ring. Using the current induced by the large flywheel mentioned above leads to F ∼ 10⁻⁵⁷ N. Alternatively, using the maximum supercurrent that preserves the superconducting state (I ∼ 10⁻¹ A), and using ${\left|\vec{h}\right|}_{\text{LEO}}\sim 10^{-3}$ m/s for a low Earth orbit (LEO) satellite, leads to F ∼ 10⁻¹⁴ N.

• Since ${\left|\vec{h}\right|}_{\text{LEO}}\sim 10^{-3}$ m/s is a factor of 10¹⁸ larger than $\left|\vec{h}\right|\sim 10^{-21}$ m/s produced by the large flywheel, then the electric current produced by a motional gravitational emf Eq. 157 and a transformer gravitational emf Eq. 164 become I ∼ 10⁻⁶ A and I ∼ 10⁻⁸ A, respectively. Also, the Hall potential in Eq. 201 becomes V _H ∼ 10⁻¹ V.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author would like to thank Professor Raymond Chiao, Professor Gerardo Muñoz, Professor Douglas Singleton, Dr. Ahmed Farag Ali, and Dr. Lance Williams for very helpful discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.823592/full#supplementary-material

Footnotes

¹ The signature of the Minkowski metric used here is diag $\left(-1,+1,+1,+1\right)$ . Greek space-time indices μ, ν, … run from 0 to 3. Latin spatial indices i, j, … run from 1 to 3. The notation $\tilde{L}$ in Eq. 5 is used to distinguish the Lagrangian parametrized in proper time, $\tilde{L}=\tilde{L}\left(u^{\mu }\right)$ , from the “space+time” Lagrangian, $L=L\left(v^{\mu }\right)$ , in Eq. 11 which is parametrized in coordinate time. Likewise, the corresponding Hamiltonians that follow from $\tilde{L}=\tilde{L}\left(u^{\mu }\right)$ and $L=L\left(v^{\mu }\right)$ will be denoted as $\tilde{H}\left(x^{\mu },p_{\mu }\right)$ and $H\left(x^i,p_i\right)$ , respectively.

² See Box 13.3 in MTW [4], 3.3 in Wald [5], or 3.6 and 4.4 in Weber [6].

³ For a more detailed discussion of the reparametrization of the action from proper time to coordinate time, see [9,10], and Appendix M of [12].

⁴ The missing terms are due to the fact that [21–27] uses a Lorentz-like force equation written as $\vec{F}=q\left(\vec{E}+\vec{v}\times \vec{B}\right)+m({\vec{E}}_g+\vec{v}\times {\vec{B}}_g)$ , which has an associated Lagrangian given by $L=\frac{1}{2}m{v}^2-q\left(\varphi -\vec{v}\cdot \vec{A}\right)-m\left({\varphi }_g-\vec{v}\cdot {\vec{A}}_g\right)$ . The canonical momentum is found from this Lagrangian to be $\vec{P}=m\vec{v}+q\vec{A}+m{\vec{A}}_g$ , where $\vec{P}=-i\hslash \nabla$ . However, it is shown in [12,28] that the Lorentz-like equation of motion used in [21–27] stems from a faulty approximation applied to the geodesic equation of motion which is very common in the literature. In particular, it is not consistent to retain $\vec{v}\times {\vec{B}}_g$ while eliminating other terms involving h ₀₀ and h _ij . Also, for non-relativistic gravitational sources, it is not valid to use ${\vec{E}}_g=-\nabla {\varphi }_g-{\partial }_t{\vec{A}}_g$ which is required for the Lagrangian used by [21–27] to lead to the Lorentz-like equation of motion.

⁵ The result in Eq. 20 can be related to the standard result in flat space-time shown in Chaper 12 of Jackson [7]. First, the action in (12.29) of Jackson must be reparametrized using $S=\int \tilde{L}d\tau =\int Ldt$ so that the Lagrangian is again Eq. 11. In the absence of gravity, the canonical momentum is $P_i=\frac{\partial L}{\partial v^i}={\eta }_{ij}\left(\gamma m{v}^j-q{A}^j\right)$ and the Hamiltonian is $H=c{\left[m^2{c}^2+{\left(P_i-e{\eta }_{ij}{A}^j\right)}^2\right]}^{1/2}+ec{A}^0$ . This result matches Eq. 20 when g _μν = η _μν , which leads to the Hamiltonian of a relativistic spinless charged particle in the presence of electromagnetic fields in flat space-time. This also matches (16.8) of Landau and Lifshitz [29].

⁶ The coupling term involving the tensor part of the perturbation, $h_{ij}{P}_i{P}_j/\left(2m\right)$ , is also found in [14,16,30,33–35]. In [16,34], an interaction Lagrangian density, ${\mathcal{L}}_{\mathit{int}}=\frac{1}{2}{h}_{\mu \nu }{T}^{\mu \nu }$ , leads to an interaction Hamiltonian density, ${\mathcal{H}}_{\mathit{int}}=\frac{1}{2}{h}_{\mu \nu }{T}^{\mu \nu }$ , with an associated interaction Hamiltonian for a particle given as $H_{\mathit{int}}=h_{ij}{P}_i{P}_j/\left(2m\right)$ . Since [36,37] show that the transverse-traceless part of h _ij , isolates the propagating degrees of freedom for gravitational waves, then [12,38,39] investigate how this interaction term describes the lowest order interaction of gravitational waves with a superconductor. However, in the context of this paper, using Eq. 29 and Eq. 30 leads to h _ij P _i P _j becoming ${\phi }_G{\tilde{P}}^2$ in Eq. 31.

⁷ Yet another way of observing the cancellation is by returning to the Legendre transformation, H = P _i v ⁱ − L. Using the canonical momentum Eq. 15 and velocity Eq. 19 in P _i v ⁱ leads to a factor of h _0i A ⁱ . The Lagrangian Eq. 11 also contains a factor of h _0i A ⁱ . Therefore, the two factors cancel by subtraction in the Legendre transformation.

⁸ The coupling terms in DeWitt’s Hamiltonian are discussed in detail in [40]. In particular, it is stated that A ⁱ h ⁱ predicts an interaction between electromagnetic and gravitational fields mediated by the quantum system, h ⁱ P _i predicts an interaction of the quantum system with gravity, and mh ² predicts a gravitational Landau-diamagnetism interaction of the quantum system.

⁹ It is mentioned in [8] that an alternative approach is to use a symmetric tensor H ^μν = p ^μ u ^ν − g ^μν L, where the canonical equatons are ∂H ^μν /∂x ^μ = −p ^ν and ∂H ^μν /∂p ^μ = u ^ν . Although this produces the correct equation of motion, H ^μν is clearly not a scalar quantity which can be interpreted as an energy.

¹⁰ In the context of this paper, f ^μ = eA ^μ . Also note [8] uses the notation M and M′ which are relatated to the notation used here by H ₂ = −cM and H ₃ = −cM′.

¹¹ This same method involving a Legendre transformation applied to ${\tilde{L}}_1$ is used by [3,14,30] to arrive at Eq. 1. This is also the method used by [11] to arrive at Eq. 23.

¹² This method used in [12] was an adaptation of the treatment in [9] but with the inclusion of electromagnetic fields.A similar approach is shown in [32], however, it is stated that Hamilton’s equations are used to identify H ₂ = −cP ₀. The result is equivalent to Eq. 23 but without A ⁰ and A ⁱ appearing.

¹³ For a discussion of the contrast between gravity described by a geometrical perturbation tensor $\left(g_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu }\right)$ versus gravity described by a quantum tensor field $\left(f_{\mu \nu }={\eta }_{\mu \nu }+{\psi }_{\mu \nu }\right)$ , see [67] which expounds on Feynman’s work in [68,69,70].

¹⁴ Note that if ${\vec{h}}^{\prime }=\vec{h}+\nabla \mu$ , then taking the curl would lead to ${\vec{B}}_G^{\prime }={\vec{B}}_G$ , where ${\vec{B}}_G\equiv \nabla \times \vec{h}$ . This implies that ${\vec{B}}_G$ is gauge (coordinate) invariant. However, using h′ ^μν = h ^μν + ∂ ^μ ξ ^ν + ∂ ^ν ξ ^μ and $h^i\equiv \frac{c}{4}{h}_{0i}$ means the actual transformation is given by $h^{\prime i}=h^i+\frac{1}{4}{\dot{\xi }}^i-\frac{c}{4}{\partial }^i{\xi }^0$ , and the corresponding transformation for ${\vec{B}}_G$ is ${\vec{B}}_G^{\prime }={\vec{B}}_G+\frac{1}{4}\nabla \times \stackrel{\cdot }{\vec{\xi }}$ as shown in Eq. 92.

¹⁵ It is stated in [77] that the Hamiltonian developed by Weber [79] differs from that of [77], despite the fact that both are derived based on the geodesic deviation equation. It is also stated that the difference is due to the fact that Weber first linearizes the equation of motion, and that Weber’s Hamiltonian is not valid if the test particle is charged.

¹⁶ Detailed treatments of the Lagrangian and Hamiltonian formulation of geodesic deviation can be found in [80,81,82].

¹⁷ It is argued in [83] that Fermi normal coordinates are appropriate for a problem involving energy levels, in contrast to Riemann normal coordinates.

¹⁸ This value assumes the maximum kinetic energy must be below the BCS energy gap since the supercurrent effectively consists of Cooper pairs in a BCS condensate. Using the BCS energy gap leads to a non-relativistic supercurrent velocity. However, if an observer were to be moving at a relativistic speed with respect to the superconductor, then the Cooper pairs would be observed as relativistic. This concept is considered in [19]. For further discussion of the possibility of relativistic superconductivity, see [63,97,98].

¹⁹ Note that the harmonic coordinate condition, ${\partial }_{\nu }{\bar{h}}^{\mu \nu }=0$ , leads to ${\partial }_0{\bar{h}}^{i0}+{\partial }_j{\bar{h}}^{ij}=0$ . Since non-relativistic sources led to ${\bar{h}}^{ij}=0$ , then ${\partial }_t{\bar{h}}^{i0}=0$ which means that $\vec{h}$ is time-independent in this approximation. Therefore, we cannot use ${\vec{E}}_G\equiv -\nabla {\phi }_G-{\partial }_t\vec{h}$. For a discussion of this topic, see [12] or [28].

²⁰Note that a negative is used in ${\vec{J}}_c=-n_{s}q\vec{v}$ so that when q = −e is used, then ${\vec{J}}_c$ becomes positive and hence represents the conventional current.

²¹In standard London theory, the requirement that ∇φ = 0 inside a superconductor follows from inserting $\vec{E}=-\nabla \phi -{\partial }_t\vec{A}$ into the electric London equation, ${\partial }_t{\vec{J}}_c={\mathrm{\Lambda }}_L\vec{E}$ which gives ${\partial }_t\left({\vec{J}}_c+{\mathrm{\Lambda }}_L\vec{A}\right)=-{\mathrm{\Lambda }}_L\nabla \phi$. Since ${\vec{J}}_s=-{\mathrm{\Lambda }}_L\vec{A}$ is the London constitutive equation, then it follows that ∇φ = 0. However, this assumption is not taken for granted and is widely discussed in the literature, as summarized in [99]. In the treatment used here, we can also insert $\vec{E}=-\nabla \phi -{\partial }_t\vec{A}$ into Eq. 53 to obtain ${\partial }_t\left[{\vec{J}}_c+{\mathrm{\Lambda }}_L\left(\alpha \vec{A}-\beta \vec{h}\right)\right]=-{\mathrm{\Lambda }}_L\alpha \nabla \phi$. Then using Eq. 50 requires the bracket to be zero and therefore ∇φ = 0.

²²More formally, the field equation should be written ${\nabla }^2\vec{B}={\lambda }_L^{-2}\vec{B}$ ^(external) , where $\vec{B}$ is the magnetic field produced by the superconductor while $\vec{B}$^(external) is produced by some source external to the superconductor. However, the common approach in London theory is to view $\vec{B}$ as taking into account all the fields, including those produced by the material of the superconductor as well as those introduced externally.

²³Note that if the system is not arranged so as to make ${\vec{E}}_G\times \vec{A}=0$ in Eq. 69 and Eq. 71, then Eq. 76 would have the more complicated form ${\nabla }^4\vec{B}-k^2{\nabla }^2\vec{B}+\frac{{\mu }_0{\mathrm{\Lambda }}_L}{c^2}{\nabla }^2\left({\vec{E}}_G\times \vec{A}\right)=0$.

²⁴Note that if the system is not arranged so as to make ${\vec{E}}_G\times \vec{A}=0$ in Eq. 69 and Eq. 71, then Eq. 81 would have the more complicated form ${\nabla }^4{\vec{B}}_G+k^2{\nabla }^2{\vec{B}}_G-\frac{{\mu }_G{n}_{s}e}{c^2}{\nabla }^2\left({\vec{E}}_G\times \vec{A}\right)=0$.

²⁵The presence of $\vec{B}$ would be irrelevant to a neutral superfluid since there is no net charge to couple to the magnetic field.

²⁶In 9.4 of Griffiths [102], it is shown that any free charge density in the interior of a normal conductor dissipates on time scales such as 10⁻¹⁹ s for copper. Therefore, it is also reasonable to assume ∇ρ_c = 0 for the interior of a superconductor.

²⁷This can also be identified as an extended application of the Byers-Yang theorem [106] which ordinarily applies only to a wave function in the presence of a magnetic vector potential.

²⁸Dimensionally, $\frac{64\pi }{L\ell }{\nabla }^{-2}$ has units of $\frac{A^2\cdot s^2}{kg\cdot m}$, therefore Eq. 131 is not in units of electrical current.

²⁹An expression similar to Eq. 133 is obtained in [111] using the gravito-magnetic field of the earth. The electric current is given by $I=\frac{8\pi }{5}\frac{MG}{c^{2}R}\frac{m{a}^2\omega }{eL}$, where M, R and ω are, respectively the mass, radius and angular velocity of the earth, and L and a are, respectively, the self-inductance and radius of the loop.

³⁰The result for F is obtained by evaluating the following expression.

³¹Note that $B_{\text{ring}}={\mu }_{0}I/\left(2\pi R\right)$ is the magnetic field only at the center of the ring $\left(r=0\right)$. At any other location in the plane of the ring, the magnetic field is

where $K\left(k\right)$ and $E\left(k\right)$ are the complete elliptic integral functions of the first and second kind, respectively, with $k\equiv \sqrt{\frac{4a}{1+a^2}}$ and a ≡ r/R.

³²This is analogous to the fact that in the absence of gravity, the correct London equation cannot be derived using the total Lorentz force on Cooper pairs. Specifically, using $m_e{\partial }_t\vec{v}=e\left(\vec{E}+\vec{v}\times \vec{B}\right)$ and $\vec{J}=n_{s}e\vec{v}$ would imply ${\partial }_t\vec{J}={\mathrm{\Lambda }}_L\left(\vec{E}+\vec{v}\times \vec{B}\right)$ which is incorrect. The correct London equation is obtained from the Lorentz force only when $\vec{v}\times \vec{B}$ is neglected which demonstrates that a classical approach using a force equation is questionable.

References

1. George R. Gravity Research Foundation (1949). Available at: www.gravityresearchfoundation.org.

Google Scholar

2. DeWitt B. New directions for research in the theory of gravitation. In: Reprinted in cécile DeWitt-morette, the pursuit of quantum gravity: Memoirs of Bryce DeWitt from 1946 to 2004. New York: Springer (2011). p. 61–8. 1953available in GRF Box 2, Folder 8, and at Available at: www.gravityresearchfoundation.org.

Google Scholar

3. DeWitt B. Superconductors and gravitational drag. Phys Rev Lett (1966) 16:1092–3. doi:10.1103/physrevlett.16.1092

CrossRef Full Text | Google Scholar

4. Misner C, Thorne K, Wheeler J. Gravitation. San Francisco: Freeman (1972).

Google Scholar

5. Wald R. General relativity. Chicago: University of Chicago Press (1984).

Google Scholar

6. Weber J. General relativity and gravitational waves. Dover Publications (2004).

Google Scholar

7. Jackson J. Classical electrodynamics. 3rd ed. John Wiley & Sons (1998).

8. Barut A. Electrodynamics and classical theory of fields and particles. New York: Macmillian (1964). Dover reprint.

Google Scholar

9. Bertschinger E. Physics 8.962 notes, “Hamiltonian dynamics of particle motion (1999).

Google Scholar

10. Bertschinger E. Physics 8.962 notes, “Symmetry transformations, the Einstein-Hilbert action, and gauge invariance (2002).

Google Scholar

11. Cognola G, Vanzo L, Zerbini S. Relativistic wave mechanics of spinless particles in a curved space-time. Gen Relativ Gravit (1986) 18(9):971–82. doi:10.1007/bf00773561

CrossRef Full Text | Google Scholar

12. Inan N. Formulations of General Relativity and their applications to quantum mechanical systems (with an emphasis on gravitational waves interacting with superconductors). Open Access Publications from the University of California (2018). PhD Dissertation, eScholarshipProQuest ID: Inan_ucmerced_1660D_10366, Merritt ID: ark:/13030/m5jb13w2.

Google Scholar

13. Hirakawa H. Superconductors in gravitational field. Phys Lett (1975) 53A:number 5.

Google Scholar

14. Papini G. In: PG Bergmann, and V de Sabbata, editors. Quantum systems in weak gravitational fieldsAdvances in the interplay between quantum and gravity physics, 60. Dordrecht: Springer (2002). NATO Science Series. doi:10.1007/978-94-010-0347-6_13

CrossRef Full Text | Google Scholar

15. Lambiase G, Papini G. The interaction of spin with gravity in particle physics. Heidelberg, Germany: Springer Nature (2021).

Google Scholar

16. Rothman T, Boughn S. Can gravitons be detected. Found Phys (2006) 36:1801–25. doi:10.1007/s10701-006-9081-9

CrossRef Full Text | Google Scholar

17. Ross D. The London equations for superconductors in a gravitational field. J Phys A: Math Gen (1983) 16:1331–5. doi:10.1088/0305-4470/16/6/026

CrossRef Full Text | Google Scholar

18. Peng H, Torr D. Effects of a superconductor on spacetime and the potential effect on the gyroscope experiment. Nucl Phys B - Proc Supplements (1989) 6:411–3. doi:10.1016/0920-5632(89)90485-4

CrossRef Full Text | Google Scholar

19. Peng H. A new approach to studying local gravitomagnetic effects on a superconductor. Gen Relativ Gravit (1990) 22(6):609–17. doi:10.1007/bf00755981

CrossRef Full Text | Google Scholar

20. Peng H, Lind G, Chin Y. Interaction Between Gravity and Moving Superconductors. Gen Relativ Gravit (1991) 23(11):1231–50. doi:10.1007/bf00756846

CrossRef Full Text | Google Scholar

21. Li N. A magnetically induced gravitomagnetic field inside a superconductor,” Essays on Gravitation. Gravity Research Foundation (1990). arxiv.org/abs/2201.12969v1.

Google Scholar

22. Li N, Torr D. Effects of a gravitomagnetic field on pure superconductors. Phys Rev D (1991) 43:457–9. Number 2. doi:10.1103/PhysRevD.43.457

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Li N, Torr D. Gravitational effects on the magnetic attenuation of superconductors. Phys Rev B (1992) 46:5489–95. doi:10.1103/PhysRevB.46.5489

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Torr D, Li N. Gravitoelectric-electric coupling via superconductivity. Found Phys Lett (1993) 6:371–83. doi:10.1007/BF00665654

CrossRef Full Text | Google Scholar

25. Ho V, Morgan M. An experiment to test the gravitational Aharonov-Bohm effect. Aust J Phys (1994) 47(3):245–52. doi:10.1071/ph940245

CrossRef Full Text | Google Scholar

26. Agop M, Gh Buzea C, Griga V, Ciubotariu C, Buzea C, Stan C, et al. Gravitational paramagnetism, diamagnetism and gravitational superconductivity. Aust J Phys (1996) 49:1063–22. doi:10.1071/ph961063

CrossRef Full Text | Google Scholar

27. Agop M. Gravitomagnetic field, spontaneous symmetry breaking and a periodical property of space. Il Nuovo Cimento Gennaio (1998) 11.

Google Scholar

28. Williams L, Inan N. Maxwellian mirages in general relativity. New J Phys (2021) 23:053019. doi:10.1088/1367-2630/abf322

CrossRef Full Text | Google Scholar

29. Landau L, Lifshitz E. The classical theory of fields. 3rd ed., 2. Butterworth-Heinemann (2000).

Google Scholar

30. Papini G. Particle wave functions in weak gravitational fields. Nuov Cim B (1967) 52:136–41. doi:10.1007/bf02710658

CrossRef Full Text | Google Scholar

31. Cabrera B, Gutfreund H, Little W. Relativistic mass corrections for rotating superconductors. Phys Rev B (1982) 25:6644–54. 11. doi:10.1103/physrevb.25.6644

CrossRef Full Text | Google Scholar

32. Piyakis K, Papini G, Rystephanick R. Static paramagnetic response of thin soft superconductors. Can J Phys (1980) 58(6):812–9. doi:10.1139/p80-111

CrossRef Full Text | Google Scholar

33. Dyson F. Seismic response of the Earth to a gravitational wave in the 1-Hz Band. Astrophys J (1969) 156:529. doi:10.1086/149986

CrossRef Full Text | Google Scholar

34. Boughn S, Rothman T. Aspects of graviton detection: Graviton emission and absorption by atomic hydrogen. Class Quan Gravity (2006) 23:5839–52. doi:10.1088/0264-9381/23/20/006

CrossRef Full Text | Google Scholar

35. Gallerati A, Modanese G, Ummarino G. Interaction between macroscopic quantum systems and gravity. Front Phys (2022) 10. doi:10.3389/fphy.2022.941858

CrossRef Full Text | Google Scholar

36. Flanagan É, Hughes S. The basics of gravitational wave theory. New J Phys (2005) 7:204. doi:10.1088/1367-2630/7/1/204

CrossRef Full Text | Google Scholar

37. Poisson E, Will C. Gravity: Newtonian, post-Newtonian, relativistic. Cambridge University Press (2014).

Google Scholar

38. Inan N, Thompson J, Chiao R. Interaction of gravitational waves with superconductors. Fortschr Phys (2016) 65:1600066. doi:10.1002/prop.201600066

CrossRef Full Text | Google Scholar

39. Inan N. A new approach to detecting gravitational waves via the coupling of gravity to the zero-point energy of the phonon modes of a superconductor. Int J Mod Phys D (2017) 26(12):1743031. doi:10.1142/S0218271817430313

CrossRef Full Text | Google Scholar

40. Chiao R, Haun R, Inan N, Kang B, Martinez L, Minter S, et al. “A gravitational Aharonov-Bohm effect, and its connection to parametric oscillators and gravitational radiation,” in Quantum theory: A two-time success story (yakir aharonov festschrift), 213–46. (Springer-Verlag Italia) (2014). doi:10.1007/978-88-470-5217-8

CrossRef Full Text | Google Scholar

41. Papini G. London Moment of Rotating Superconductors and Lense-Thirring Fields of General Relativity. Nuov Cim B (1966) 45(1):66–8. doi:10.1007/bf02710584

CrossRef Full Text | Google Scholar

42. Papini G. Detection of Inertial Effects with Superconducting Interferometers. Phys Lett A (1967) 24(1):32–3. doi:10.1016/0375-9601(67)90178-8

CrossRef Full Text | Google Scholar

43. Papini G. Gravity-induced electric fields in superconductors. Nuov Cim B (1969) 63(2):549–59. doi:10.1007/bf02710706

CrossRef Full Text | Google Scholar

44. Papini G. Inertial potentials in classical and quantum mechanics. Nuov Cim B (1970) 68:1–10. doi:10.1007/bf02710354

CrossRef Full Text | Google Scholar

45. Leung M, Papini G, Rystephanick R. Gravity-induced electric fields in metals. Can J Phys (1971) 49(22):2754–67. doi:10.1139/p71-334

CrossRef Full Text | Google Scholar

46. Papini G. The transport of electricity in superconductors subject to gravitational or inertial forces. Phys Lett A (1975) 53(4):331–2. doi:10.1016/0375-9601(75)90089-4

CrossRef Full Text | Google Scholar

47. Cai Y, Papini G. Particle interferometry in weak gravitational fields. Class Quan Gravity (1989) 6:407–18. doi:10.1088/0264-9381/6/3/017

CrossRef Full Text | Google Scholar

48. Bertschinger E. Cosmological dynamics,” cosmology and large scale structure. In: R Schaeffer, J Silk, M Spiro, and J Zinn-Justin, editors. Proc. Les houches summer school, session LX. Amsterdam: Elsevier Science (1995).

Google Scholar

49. Ciubotariu C, Agop M. Absence of a gravitational analog to the Meissner effect. Gen Relativ Gravit (1996) 28(4):405–12. doi:10.1007/bf02105084

CrossRef Full Text | Google Scholar

50. Agop M, Ciubotariu C, Gh Buzea C, Buzea C, Ciobanu B. Physical implications of the gravitational fluxoid. Aust J Phys (1996) 49(3):613–22. doi:10.1071/PH960613

CrossRef Full Text | Google Scholar

51. Cisneros-Parra J. On singular Lagrangians and Dirac’s method. Revista Mexicana de Fısica (2012) 58:61–8.

Google Scholar

52. Dirac P. Generalized Hamiltonian dynamics. Can J Math (1950) 2:129–48. doi:10.4153/cjm-1950-012-1

CrossRef Full Text | Google Scholar

53. Dirac P. The theory of gravitation in Hamiltonian form. Proc Roy Soc Lond A (1958) 246:326.

Google Scholar

54. Dirac P. “Lectures on quantum mechanics,” in Belfer Graduate School of Science, Yeshiva University. New York, NY: Dover Publications Inc. (1964).

Google Scholar

55. Castellani L, Dominion D, Longhi G. Quantization rules and Dirac’s correspondence. Nuov Cim A (1978) 48A:359–68. N.1. doi:10.1007/bf02781602

CrossRef Full Text | Google Scholar

56. Roberts M. The quantization of geodesic deviation. Gen Relativ Gravit (1996) 28:1385–92. doi:10.1007/bf02109528

CrossRef Full Text | Google Scholar

57. Nielsen H, Olesen P. Vortex-line models for dual strings. Nucl Phys B (1973) 61(24):45–61. doi:10.1016/0550-3213(73)90350-7

CrossRef Full Text | Google Scholar

58. Meyer V, Salier N. Generally relativistic phenomenological theory of superconductivity. Theor Math Phys (1979) 38:270–5. doi:10.1007/bf01018547

CrossRef Full Text | Google Scholar

59. Dinariev O, Mosolov A. Relativistic generalization of the Ginzburg-Landau theory. Soviet Phys J (1989) 32:315–9. doi:10.1007/bf00897278

CrossRef Full Text | Google Scholar

60. Peskin M, Schroeder D. Introduction to quantum field theory. Boca Raton, FL: CRC Press (1995).

Google Scholar

61. Ryder L. Quantum field theory. 2nd ed. Cambridge University Press (1996).

Google Scholar

62. Lano R. Gravitational phase transition in neutron stars (1996). arXiv:gr-qc/9611023v1.

Google Scholar

63. Bertrand D. A relativistic BCS theory of superconductivity: An experimentally motivated study of electric fields in superconductors. Dissertation, Université catholique de Louvain (2005). Available at: http://hdl.handle.net/2078.1/5380

Google Scholar

64. Cai Q, Papini G. Applying Berry's phase to problems involving weak gravitational and inertial fields. Class Quan Gravity (1990) 7:269–75. doi:10.1088/0264-9381/7/2/021

CrossRef Full Text | Google Scholar

65. Papini G. Quantum physics in inertial and gravitational fields. In: Relativity in rotating frames (fundamental theories of physics), 135. Dordrecht: Springer (2004). doi:10.1007/978-94-017-0528-8_18

CrossRef Full Text | Google Scholar

66. Papini G. On gravitational fields in superconductors. Front Phys (2022) 10. doi:10.3389/fphy.2022.920238

CrossRef Full Text | Google Scholar

67. Baryshev Y. Einstein’s geometrical versus Feynman’s quantum-field approaches to gravity physics: Testing by modern multimessenger astronomy. Universe (2020) 6(11):212. doi:10.3390/universe6110212

CrossRef Full Text | Google Scholar

68. Feynman R. Quantum theory of gravitation. Acta Phys Pol (1963) 24:697–722.

Google Scholar

69. Feynman R. Lectures on Gravitation. Pasadena, CA, USA: California Institute of Technology (1971).

Google Scholar

70. Feynman R, Morinigo F, Wagner W. Feynman Lectures on Gravitation. Boston, MA, USA: Addison-Wesley Publishing Company (1995).

Google Scholar

71. Agop M, Buzea C, Ciobanu B. On gravitational shielding in electromagnetic fields (1999). arXiv:physics/9911011.

Google Scholar

72. Agop M, Buzea C, Nica P. Local gravitoelectromagnetic effects on a superconductor. Physica C: Superconductivity (2000) 339(2):120–8. doi:10.1016/S0921-4534(00)00340-3

CrossRef Full Text | Google Scholar

73. Agop M, Iaonnoi P, Diaconu F. Some implications of gravitational superconductivity. Prog Theor Phys (2000) 104:733–42. doi:10.1143/ptp.104.733

CrossRef Full Text | Google Scholar

74. Ummarino G, Gallerati A, Superconductor . Superconductor in a weak static gravitational field. Eur Phys J C (2017) 778:549. doi:10.1140/epjc/s10052-017-5116-y

CrossRef Full Text | Google Scholar

75. Gallerati A, Ummarino G. Superconductors and gravity. Symmetry (2022) 14(3):554. doi:10.3390/sym14030554

CrossRef Full Text | Google Scholar

76. Cai Q, Papini G. The effect of space-time curvature on Hilbert space. Gen Relativ Gravit (1990) 22:259–67. doi:10.1007/bf00756276

CrossRef Full Text | Google Scholar

77. Speliotopoulos A. Quantum mechanics and linearized gravitational waves. Phys Rev D (1995) 51:1701–9. doi:10.1103/physrevd.51.1701

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Speliotopoulos A, Chiao R. Differing calculations of the response of matter-wave interferometers to gravitational waves (2004). arXiv:gr-qc/0406096v1.

Google Scholar

79. Weber J. Gravitational radiation and relativity. In: J Weber, and TM Karade, editors. Proceedings of the sir arthur eddington centenary symposium, nagpur, India, 3. Singapore: World Scientific (1986). 1984.

Google Scholar

80. Speliotopoulos A, Chiao R. Coupling of linearized gravity to nonrelativistic test particles: Dynamics in the general laboratory frame. Phys Rev D (2004) 69:084013. doi:10.1103/physrevd.69.084013

CrossRef Full Text | Google Scholar

81. Cariglia M, Houri T, Krtous P, Kubiznak D. On integrability of the geodesic deviation equation. Eur Phys J C (2018) 78:661. doi:10.1140/epjc/s10052-018-6133-1

CrossRef Full Text | Google Scholar

82. Kerner R. Generalized geodesic deviations: A lagrangean approach. Banach Cent Publications (2003) 59(N 1):173–88. doi:10.4064/bc59-0-9

CrossRef Full Text | Google Scholar

83. Parker L. One-electron atom in curved space-time. Phys Rev Lett (1980) 44:1559–62. doi:10.1103/PhysRevLett.44.1559

CrossRef Full Text | Google Scholar

84. Parker L. One-electron atom as a probe of spacetime curvature. Phys Rev D (1980) 22(8):1922–34. doi:10.1103/PhysRevD.22.1922

CrossRef Full Text | Google Scholar

85. Parker L, Pimentel L. Gravitational perturbation of the hydrogen spectrum. Phys Rev D (1982) 25:3180–90. doi:10.1103/PhysRevD.25.3180

CrossRef Full Text | Google Scholar

86. Minter S. On the implications of incompressibility of the quantum mechanical wavefunction in the presence of tidal gravitational fields,” doctoral dissertation. Merced: Department of Physics, University of California (2010). ProQuest ID: 2010_sminter. Merritt ID: ark:/13030/m5f77sm2.

Google Scholar

87. Atanasov V. The geometric field (gravity) as an electro-chemical potential in a Ginzburg-Landau theory of superconductivity. Physica B: Condensed Matter (2017) 517(15):53–8. doi:10.1016/j.physb.2017.05.006

CrossRef Full Text | Google Scholar

88. Blencowe M. Effective field theory approach to gravitationally induced decoherence. Phys Rev Lett (2013) 111:021302. doi:10.1103/physrevlett.111.021302

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Arteaga D, Parentani R, Verdaguer E. Propagation in a thermal graviton background. Phys Rev D (2004) 70:044019. doi:10.1103/PhysRevD.70.044019

CrossRef Full Text | Google Scholar

90. Gregorash D, Papini G. A unified theory of gravitation and electromagnetism for charged superfluids. Phys Lett A (1981) 82(2):67–9. doi:10.1016/0375-9601(81)90939-7

CrossRef Full Text | Google Scholar

91. Callan C, ColemanJackiw SR. A new improved energy-momentum tensor. Ann Phys (1970) 59(1):42–73. doi:10.1016/0003-4916(70)90394-5

CrossRef Full Text | Google Scholar

92. Birrell N, Davies P. Quantum fields in curved space. Cambridge University Press (1982).

Google Scholar

93. Parker L, Toms D. Quantum field theory in curved spacetime. Cambridge University Press (2009).

Google Scholar

94. Tinkham M. Introduction to superconductivity. 2nd ed. Mineola, N.Y.: Dover Publications (2004).

Google Scholar

95. London F, London H. The electromagnetic equations of the supraconductor. Proc Roy Soc (London) (1935) 149:866. doi:10.1098/rspa.1935.0048

CrossRef Full Text | Google Scholar

96. London F. Superfluids, 1. Dover Publications (1950).

Google Scholar

97. Bailin D, Love A. Superconductivity for Relativistic Electrons. J Phys A: Math Gen (1982) 15:3001–5. doi:10.1088/0305-4470/15/9/046

CrossRef Full Text | Google Scholar

98. Govaerts J, Bertrand D. Superconductivity and electric fields: A relativistic extension of BCS superconductivity. In: Proceedings of the fourth international workshop on contemporary problems in mathematical physics. World Scientific (2006). arxiv.org/pdf/cond-mat/0608084.

CrossRef Full Text | Google Scholar

99. Lipavsky P. Bernoulli potential in superconductors. Springer (2007).

Google Scholar

100. Lano R. Gravitational meissner effect (1996). arXiv:hep-th/9603077v1.

Google Scholar

101. Tajmar M, Neunzig O, Kößling M. Measurement of anomalous forces from a Cooper-pair current in high-T_c superconductors with nano-Newton precision. Front Phys (2022) 10. doi:10.3389/fphy.2022.892215

CrossRef Full Text | Google Scholar

102. Griffiths D. Introduction to electrodynamics. 3rd ed.. Upple Saddle River, NJ: Prentice-Hall (1999).

Google Scholar

103. Ginzburg V, Landau L. On superconductivity and superfluidity. Berlin, Heidelberg: Springer (2009). doi:10.1007/978-3-540-68008-6_4

CrossRef Full Text | Google Scholar

104. Ummarino G, Gallerati A. Exploiting weak field gravity-Maxwell symmetry in superconductive fluctuations regime. Symmetry (2019) 11(11):1341. doi:10.3390/sym11111341

CrossRef Full Text | Google Scholar

105. Ummarino G, Gallerati A. Possible alterations of local gravitational field inside a superconductor. Entropy (2021) 23(2):193. doi:10.3390/e23020193

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Byers N, Yang C. Theoretical considerations concerning quantized magnetic flux in superconducting cylinders. Phys Rev Lett (1961) 7:46–9. doi:10.1103/PhysRevLett.7.46

CrossRef Full Text | Google Scholar

107. Deaver B, Fairbank W. Experimental evidence for quantized flux in superconducting cylinders. Phys Rev Lett (1961) 7:43–6. doi:10.1103/PhysRevLett.7.43

CrossRef Full Text | Google Scholar

108. Doll R, Näbauer M. Experimental proof of magnetic flux quantization in a superconducting ring. Phys Rev Lett (1961) 7:51–2. doi:10.1103/PhysRevLett.7.51

CrossRef Full Text | Google Scholar

109. Tajmar M, de Matos C. Gravitomagnetic field of a rotating superconductor and of a rotating superfluid. Physica C: Superconductivity (2003) 385(4):551–4. doi:10.1016/S0921-4534(02)02305-5

CrossRef Full Text | Google Scholar

110. Tajmar M, de Matos C. Extended Analysis of Gravitomagnetic Fields in Rotating Superconductors and Superfluids. Physica C: Superconductivity its Appl (2005) 420(1–2):56–60. doi:10.1016/j.physc.2005.01.008

CrossRef Full Text | Google Scholar

111. Papini G. A test of General Relativity by means of superconductors. Phys Lett (1966) 23:418–9. number 7. doi:10.1016/0031-9163(66)91071-7

CrossRef Full Text | Google Scholar

112. Meservery R, Tedrow P. Measurements of the kinetic inductance of superconducting linear structures. J Appl Phys (1969) 40:2028–34. doi:10.1063/1.1657905

CrossRef Full Text | Google Scholar

113. Güllü I, Şişman TÇ, Tekin B. Unitarity analysis of general Born-Infeld gravity theories. Phys Rev D (2010) 82:124023. doi:10.1103/PhysRevD.82.124023

CrossRef Full Text | Google Scholar

114. Hinterbichler K. Theoretical aspects of massive gravity. Rev Mod Phys (2012) 84:671–710. doi:10.1103/RevModPhys.84.671

CrossRef Full Text | Google Scholar

115. Atlas E, Tekin B. Second order perturbation theory in general relativity: Taub charges as integral constraints. Phys Rev D (2019) 99:104078. doi:10.1103/PhysRevD.99.104078

CrossRef Full Text | Google Scholar