Thermoelectric Conversion From Interface Thermophoresis and Piezoelectric Effects

Piezoelectric effect has proved itself to be a promising energy conversion mechanism that can convert mechanical energy into electricity. Here, we propose an indirect thermoelectric conversion mechanism based on a combination of the thermophoresis and piezoelectric effects. We first analyze this thermally driven mechanism using a simplified theoretical model and then numerically analyze a molecular dynamics (MD) simulation of a hybrid system constructed of a single-layer MoS₂ nanoribbon and a concentric carbon nanotube. We show that the thermophoresis-induced piezoelectric output voltage can reach 3.5 V, and this value can be tuned using a temperature difference. The output voltage obtained using this mechanism is significantly higher than that obtained by heating piezoelectric materials directly. Given the generality of the thermophoresis effect in Van der Waals structures, this mechanism has potential applications in the conversion of thermal energy into electrical energy at the nanoscale level.

Introduction

The thermoelectric and piezoelectric effects, which, respectively, convert heat and mechanical energy into electricity, have attracted tremendous attention in the past few decades. Significant efforts have been devoted to improving thermoelectric conversion efficiency by suppressing lattice thermal conductivity [1–8] or engineering electronic band structures [9–17] to enhance the power factor. However, thermoelectric conversion efficiency is still limited by the complex coupling relations between phonons and electrons [18–20]. The piezoelectric effect converts mechanical energy into electricity directly and has been applied in nanowires [21–23], thin films [24], and organic–inorganic perovskites [25]. However, the piezoelectric effect generally converts artificial or ambient mechanical energy rather than heat energy into electrical power. Although piezoelectric materials can also realize thermoelectric conversion via the pyroelectric effect, this relies on a constantly changing temperature [26]. There is still a challenge when it comes to converting heat energy into electrical energy through the piezoelectric effect when the system is at a constant temperature difference. Encouragingly, the experimental observation of the piezoelectric effect in 2D materials suggests an opportunity for thermoelectric conversion based on piezoelectric materials [27].

Recently, thermally driven piezoelectric conversion has attracted extensive attention in energy conversion [28]. Our previous study has demonstrated that output voltages as large as 0.34 V can be obtained by thermally induced deflection of GaN nanowires [29]. A similar conversion mechanism has also been observed in 2D materials such as h-BN nanoribbons [30]. This conversion mechanism depends on direct heating to trigger the deflection of piezoelectric materials. Another promising mechanism called the thermophoresis effect, which converts thermal energy into mechanical energy, has also been confirmed by theory [31, 32] and experiment [33] and has shown great potential for application in energy conversion [34]. According to the motion style, thermophoretic motion can be classified into two major categories. One is linear motion, in which the mover undergoes translational motion relative to the stator. The other one is known as rotation, in which the rotor rotates along the axis of the stator. The thermophoresis effect has been identified in many different materials that are connected by Van der Waals (vdW) interactions, such as bilayer graphene [35], h-BN/graphene vdW heterostructures [36], and concentric double-walled carbon nanotubes (CNTs) [37–40].

Here, we theoretically propose a thermoelectric conversion mechanism based on a combination of interface thermophoresis and piezoelectric effects. This allows for energy conversion from heat to mechanical to electrical energy, by combining the thermophoresis and piezoelectric effects into one system. The key point here is the generation of a considerable low-frequency periodic strain in the piezoelectric material via a thermophoresis oscillator (mover CNT). Generally, large vibrational amplitude can be effectively induced through a resonance effect, with the frequency of an external excitation (such as the temperature gradient and/or external force) being equal to or close to the natural (eigen) frequency of the material [41]. However, the vibrations are composed of many different high-frequency lattice waves when a temperature difference is directly applied to piezoelectric materials [42]. Such high-frequency vibrations are hardly harvested by piezoelectric materials.

Since the mover and stator of the thermophoretic system are bonded by vdW interactions, the dynamical properties of the thermophoretic mover are dependent not only on the thermal properties of the stator but also on the strength of the vdW interactions between the stator and mover. Recently, theoretical studies have shown that the vibration induced by the thermophoresis effect can be periodic and tuned by a temperature difference [38, 40, 43]. Therefore, the thermophoresis effect is a promising way to realize thermally induced piezoelectric conversion. Based on the thermophoresis effect, we have designed a composite structure made of a concentric CNT network and a suspended MoS₂ nanoribbon with two fixed leads, as depicted in Figure 1. The mover CNT (outer tube) will be pushed to move when a temperature difference is established between both ends of the stator CNT (inner tube). The mover CNT then serves as the strain source for the 2D piezoelectric material to realize the thermally driven piezoelectric conversion.

FIGURE 1

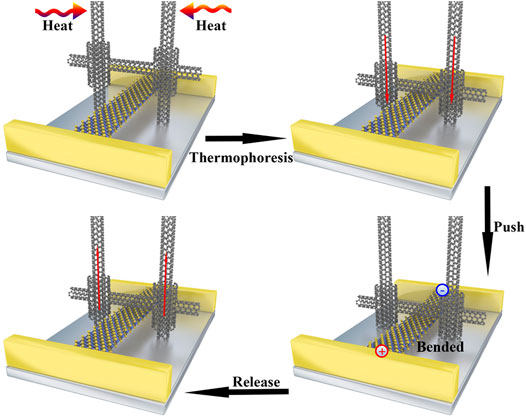
FIGURE 1. Sketch of the thermoelectric conversion process driven by thermophoresis and piezoelectric effects. The concentric carbon nanotube is made of an [4, 4] inner tube and [8, 8] outer tube with the length of 36.9 and 3.3 nm, respectively. An armchair edge MoS₂ nanoribbon with the length of 21.9 nm is adopted, and the different widths of the nanoribbon (1.58, 2.21, and 2.84 nm) are investigated for comparison.

Results and Discussion

The entire piezoelectric vibration system can be simplified into an oscillator model with an external driving force. We first present an atomic chain model with two fixed leads to illustrate the dynamical properties of the system, shown in Figure 2A. Considering the mover CNT mainly acts on the central region of the nanoribbon, a similar periodic driving force is applied to the central area of the atomic chain to serve as the non-equilibrium phonon-transport-induced thermal driving force. Considering the wave nature of the lattice vibrations, the assumption of a periodic thermal driving force is reasonable. We also provide a phonon wave-packet simulation [44] for the phonon-transport-induced thermal driving force to illustrate our assumption (see Supplementary Material). Here, we consider only the nearest neighbor atomic interactions and the internal damping force acting on the oscillator. Then, the equation of motion of the oscillators can be written as follows:

$\mathit{m}\ddot{\mathit{r}}+\mathit{\lambda }\dot{\mathit{r}}+\mathit{k}\mathit{r}-{\displaystyle \sum }_{\mathit{i}}{\mathit{F}}_{\mathit{i}}\mathbf{cos}{\mathit{\omega }}_{\mathit{i}}\mathit{t}=\mathbf{0},$

where k is the spring constant of the harmonic oscillator, r is the position of the atoms, m is the atomic mass, and λ is the damping factor (λ = 0.1). The external driving forces are a linear combination of forces with different frequencies (ω_i) and amplitudes (F_i).

FIGURE 2

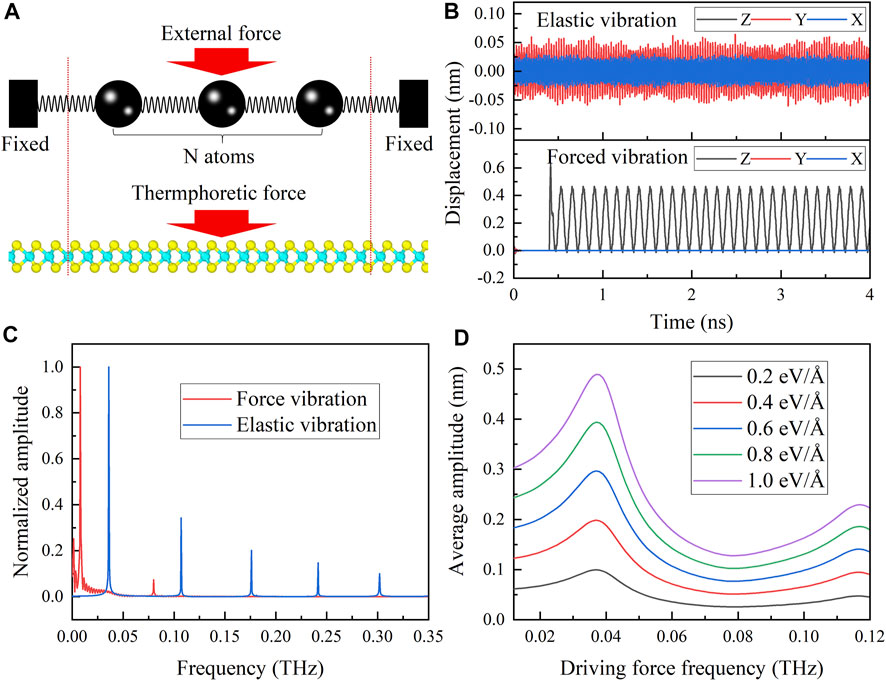
FIGURE 2. (A) Model of the atomic chain and MoS₂ nanoribbon with a periodic thermal driving force. Here, atom number N = 21. (B) Vibration trajectory of the center atom in the range of 0–4 ns and 10–12 ns (inset), where the driving force amplitude F_i = 1, 0.5, 0.25 eV/Å and the corresponding frequency ω_i = 0.008, 0.08, and 0.8 THz, respectively. (C) Vibration frequency distribution of forced vibration and elastic vibration (without external driving force and damping force). (D) Vibration amplitude of atomic chain versus the driving force frequency when the driving force amplitude F₁ = 0.2, 0.4, 0.6, 0.8, and 1.0 eV/Å, respectively.

As we can see in Figure 2B, in the case of forced vibration, the amplitude of the system in all directions is very small until the driving force is applied. Subsequently, the out-of-plane vibration fluctuates significantly but soon converges to a stable state (with an amplitude of around 0.4 nm), and the in-plane vibrations (in the x and y directions) are still very small. In contrast, the amplitude of the elastic vibration is around one magnitude less than that of the forced vibration, and the frequency of the elastic vibration is much higher than that of the forced vibration. We further analyze the vibrational properties in the frequency domain with and without the external driving force. As we can see in Figure 2C, the natural vibration of the oscillator (without the driving force) displays multi-frequency peaks (blue solid line). By contrast, the vibrational frequency of the oscillator is significantly reduced in the presence of an external driving force (red solid line). There are only two obvious vibration frequencies that can be observed. We further change the driving force frequency to calculate the amplitude of the oscillator (from 0.008 THz to 0.12 THz). As shown in Figure 2D, when the driving force frequency approaches the natural frequency of the oscillator, the amplitude of the oscillator is significantly enhanced. These results suggest that the vibrational amplitude and frequency of the oscillator can be effectively controlled as long as we can tune the driving force.

The toy model gives positive results for the realization of thermally driven deflection. However, the actual system is far more complex than this toy model. One may wonder whether the thermophoretic driving force is sufficient to induce a considerable low-frequency vibration on the actual piezoelectric material. For this purpose, we further adopt a molecular dynamics (MD) simulation to investigate the thermally driven vibration of the MoS₂ nanoribbon in two cases (1): the temperature difference is directly applied at both ends of the suspended MoS₂ nanoribbon to trigger the lattice vibrations (2); the temperature difference is applied to both ends of the stator CNT (the inner tube in Figure 1) to induce the thermophoretic motion of the mover CNT (the outer layer CNT in Figure 1), thereby triggering the deflection of the nanoribbon. In both cases, the entire system is first relaxed at the NPT ensemble for 0.2 ns. Next, Nose–Hoover thermostats are applied at both ends of the CNT. The time step is set to 0.1 fs. The vibrational trajectory of the MoS₂ nanoribbon is collected every 2 ps to characterize the vibration state. The original and modified AIREBO potentials are adopted for the MoS₂ and CNT, respectively [45, 46]. The vdW interactions between the MoS₂ and CNT are described by the Lenard–Jones potential with parameters σ_C-Mo = 3.075, ε_C-Mo = 3.32 meV, σ_C-S = 3.513, and ε_C-S = 7.35 meV [47]. All of the MD simulations were performed using the LAMMPS code.

We first discuss the vibrational properties of the MoS₂ nanoribbon in the case of direct heating. As shown in Figure 3A, a temperature difference ΔT = 210 K (around 9.6 K/nm) is established at both ends of the suspended nanoribbon to induce lattice vibration. The vibrational trajectory of the MoS₂ nanoribbon is shown in Figure 3B, and we can see that the average amplitude is around 0.1 nm in the out-of-plane direction and around 0.2 nm in the in-plane direction. In addition, as shown in Figure 3C, the frequency domain clearly shows three obvious vibration states at 0.049, 0.065, and 0.122 THz. This is in qualitative agreement with the results of the elastic vibration model in theoretical analysis. It is worth noting that the in-plane deflection of the nanoribbon can reach 0.2 nm. This seems to suggest that the direct heating method is a promising way to trigger piezoelectric effects. However, a theoretical study has pointed out that high-frequency vibration reduces the conversion efficiency of piezoelectric materials [48].

FIGURE 3

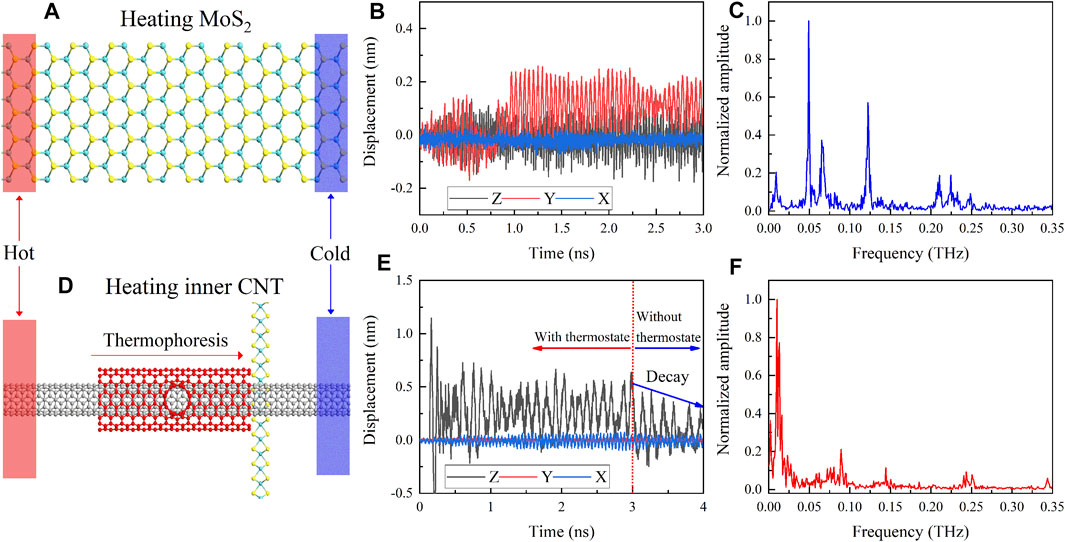
FIGURE 3. (A) Heated bath at both ends of the MoS₂ nanoribbon: (B) the vibration trajectory and (C) the vibration frequency distribution when observed from the center area of the MoS₂ nanoribbon. (D) Heated bath on both ends of the inner CNT. (E) Vibration trajectory of the MoS₂ nanoribbon. The left/right side of the red dashed line corresponded to the situation of with and without the heated bath, respectively. (F) Vibration frequency distribution of the MoS₂ nanoribbon when the inner CNT is heated.

As a comparison, we establish the same temperature difference at both ends of the stator CNT (a temperature gradient of around 5.8 K/nm), as shown in Figure 3D. It should be mentioned that this temperature gradient is reasonable. Both theoretical [31, 38] and experimental [33, 49] studies suggest that a maximum thermal gradient of around 10 K/nm can be imposed on the CNT. The vibrational trajectory of the MoS₂ is shown in Figure 3E. We can see that the amplitude of the out-of-plane vibration is around 0.5 nm, while the amplitude of the in-plane vibration is almost negligible. The out-of-plane vibrational amplitude is significantly enhanced, and the in-plane vibrational amplitude is suppressed in comparison with direct heating of the nanoribbon. More importantly, the vibration of the nanoribbon also exhibits good periodicity. This is equivalent to applying a periodic strain in the out-of-plane direction of the nanoribbon. This result is consistent with the simplified model and satisfactorily proves the feasibility of our core idea.

To be prudent, the presence of damping forces in this system should be further verified to exclude false periodicity caused by elastic vibration. As shown on the right side of Figure 3E, we remove the temperature difference after 3 ns, and thus, the whole system is at room temperature (300 K). The vibration of the MoS₂ nanoribbon is damped without external energy input. This proves the reliability of the thermally induced periodic vibration. On another hand, it also suggests that the switching state of the system can be flexibly controlled by applying/removing the temperature difference. More importantly, as shown in Figure 3F, the frequency domain shows a major vibration peak at about 0.01 THz. The vibrational frequency of out-of-plane modes is suppressed by up to 5 times compared to the direct heating method, and the amplitude is increased by up to 2 times. For piezoelectric materials, a lower vibrational frequency usually means a higher energy conversion efficiency [48]. This means that the hybrid system driven by the thermophoresis effect will obtain a higher conversion efficiency and output voltage.

Another question is whether the thermophoretic driving force can be effectively regulated in such a system. Recent studies have shown that the natural frequency of materials will be shifted when the ambient temperature is changed [50–53]. This suggests that the frequency of the thermophoretic force can be tuned by changing the temperature difference between the left and right leads. For this reason, we further investigate the temperature-dependent average amplitude of the MoS₂ nanoribbon. As shown in Figure 4A, the average amplitude of the MoS₂ nanoribbon is increased with increasing temperature difference when ΔT < 270 K. There is a maximum amplitude at ΔT = 270 K, which is qualitatively consistent with the amplitude increase as predicted by the theoretical analysis. This effect illustrates that the temperature difference can effectively regulate the driving force frequency and then tune the thermally induced vibrational amplitude.

FIGURE 4

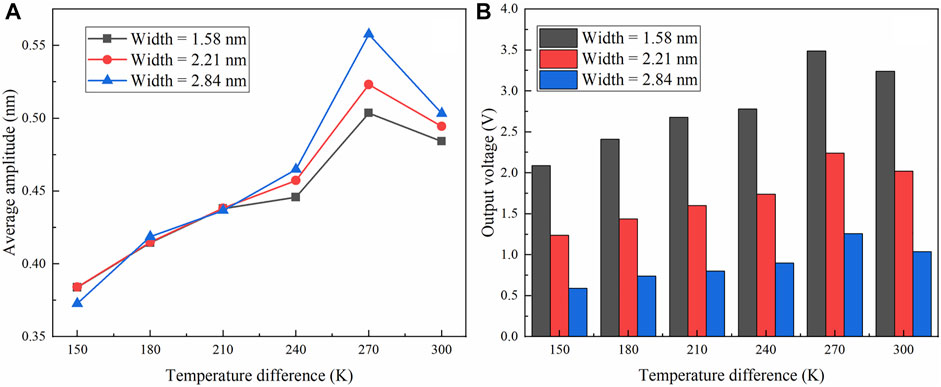
FIGURE 4. (A) Average amplitude and (B) open-circuit voltage of the MoS₂ nanoribbon with different widths as a function of temperature difference.

To confirm the piezoelectric performance, the size-dependent piezoelectric constant of the MoS₂ is calculated using a density functional theory (DFT) calculation, as shown in Table 1. The piezoelectric potential distribution under a periodic strain is calculated with the help of the finite element method. The parameters of the MoS₂ used for the simulation are as follows: Poisson ratio 0.32 [54], Young’s modulus 330 GPa [55], mass density 4,800 kg/m³, and relative permittivity 3.5 [56]. Here, the piezoelectric constant and elastic constant of the MoS₂ with different widths are obtained from a DFT calculation as implemented in the ATK package. The generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) functional and the revised PBE functional with double-zeta polarization (DZP) orbital basis sets was used. The cut-off energy is set to 250 Ry. The tolerance of the stress error, force, and energy for structural optimization are 0.1 GPa, 10⁻² eV/Å, and 10⁻⁵ eV, respectively. A density of k-mesh points of 1 × 1×7 was used for the electronic self-consistent calculation of the nanoribbon. The piezoelectric constant of the MoS₂ is calculated assuming homogeneous strains (the step of the strain is 0.01). The model sizes were limited to one lattice constant along the polar axis of the nanoribbon with periodic boundary conditions applied. The vacuum layer in the lateral and out-of-plane direction of the nanoribbon is set to 20 Å to ensure non-interaction between two mirror atomic layers.

TABLE 1

TABLE 1. Piezoelectric and elastic constant of MoS₂ when normalized by a layer thickness of 0.7 nm.

The experimental observation gives 0.5 C/m² and 52 GPa for the piezoelectric [57] and elastic constants [58] of the bulk MoS₂, which is consistent with our DFT calculation (shown in Table 1). In addition, the piezoelectric constant of the nanoribbon is almost one magnitude larger than that of bulk MoS₂, and the piezoelectric constant tends to decay exponentially with the nanoribbon width. Such size-dependent piezoelectricity has also been reported in GaN and ZnO nanowires [59]. This suggests that the output piezoelectric potential can be further improved by reducing the size of the materials. For this purpose, we calculated the width-dependent output voltage using the finite element simulation. As shown in Figure 4B, the peak output voltage of 3.5 V can be obtained when the deflection of the nanoribbon is 0.5 nm. In addition, the output voltage can still reach around 0.5 V, even when the piezoelectric constants approach the bulk value when the width of the nanoribbon is increased. It is still superior to the maximum output voltage that can be obtained in nanowires via the direct heating method.

From the perspective of the experiment, this result is comparable with the previous experimental observation (0.19 V voltage and 28 pA currents with 0.64% strain) for a single-layer MoS₂ nanoribbon with a length of 10 μm and a width of 5 μm. As mentioned before, the DFT calculation suggests that the piezoelectric constant of a small-size nanoribbon has a giant size effect. Therefore, an almost one order of magnitude enhancement in the output voltage has been achieved in this work. Correspondingly, a larger current can be obtained when the MoS₂ nanoribbon is connected to the load. This demonstrates the great potential of nanoscale piezoelectric materials in harvesting thermal energy. In addition, it has been experimentally demonstrated that the Curie temperature of MoS₂ can be effectively boosted by up to 395 K via a phase-transition strategy [60]. This proves the feasibility of the hybrid system above room temperature. Other 2D piezoelectric materials with high Curie temperatures can also serve as choices for the piezoelectric sensor of this system [61]. For structural fabrication, the concentric cross-shaped CNT network seems very complex, but similar structures have been experimentally synthesized [62, 63]. The major difficulty is that the hybrid system is not easy to fabricate. However, the state-of-the-art practice of cutting, folding, bending, and twisting objects into versatile shapes, called nano-kirigami, has recently been identified as a feasible method for manufacturing 3D nanostructures [64]. For this reason, we believe that the hybrid structure proposed in this work will not be difficult to realize in the future.

Conclusion

In conclusion, we have proposed a promising mechanism for converting heat energy into electrical energy by connecting the thermophoresis effect with the piezoelectric effect. We show that the thermophoretic motion of the CNT can effectively trigger the periodic vibration of 2D piezoelectric materials, and the vibrational amplitude can be quantitatively controlled by the temperature difference. Moreover, the thermophoresis-effect-induced vibration of piezoelectric materials has a lower vibrational frequency than thermally induced lattice vibrations, and the size-dependent piezoelectric constant provides another way to further improve the energy conversion efficiency for this mechanism. All these features ensure a relatively high-energy conversion. This may open up a new approach for developing thermally induced nanodevices for actuation and energy conversion.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

K-QC and Y-JZ conceived this work. Y-JZ, Y-YL, HP, and Z-KD performed the numerical simulations. W-XZ, L-MT, and BL reviewed and discussed the manuscript. All authors discussed the results and contributed to the final manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (No. 11974106).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.823284/full#supplementary-material

References

1. Gu X, Wei Y, Yin X, Li B, Yang R. Colloquium: Phononic thermal Properties of Two-Dimensional Materials. Rev Mod Phys (2018) 90:041002. doi:10.1103/revmodphys.90.041002

CrossRef Full Text | Google Scholar

2. Xiong S, Sääskilahti K, Kosevich YA, Han H, Donadio D, Volz S. Blocking Phonon Transport by Structural Resonances in alloy-based Nanophononic Metamaterials Leads to Ultralow thermal Conductivity. Phys Rev Lett (2016) 117:025503. doi:10.1103/PhysRevLett.117.025503

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zeng Y-J, Wu D, Cao X-H, Feng Y-X, Tang L-M, Chen K-Q. Significantly Enhanced Thermoelectric Performance of Molecular Junctions by the Twist Angle Dependent Phonon Interference Effect. J Mater Chem A (2020) 8(23):11884–91. doi:10.1039/d0ta02423f

CrossRef Full Text | Google Scholar

4. Zhang X-R, Peng X-F, Tan S-H, Long M-Q. Ballistic Electrical-thermal Transport Properties and Their Applications in Graphene-Nanoribbon-Stacked Heterojunctions. Physica E: Low-dimensional Syst Nanostructures (2021) 136:115025. doi:10.1016/j.physe.2021.115025

CrossRef Full Text | Google Scholar

5. Chen X-K, Zeng Y-J, Chen K-Q. Thermal Transport in Two-Dimensional Heterostructures. Front Mater (2020) 427:578791. doi:10.3389/fmats.2020.578791

CrossRef Full Text | Google Scholar

6. Jia P-Z, Zeng Y-J, Wu D, Pan H, Cao X-H, Zhou W-X, et al. Excellent thermoelectric performance induced by interface effect in MoS2/MoSe2 van der Waals heterostructure. J Phys Condensed Matter (2019) 32:055302. doi:10.1088/1361-648x/ab4cab

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Chen X-K, Hu X-Y, Jia P, Xie Z-X, Liu J. Tunable Anisotropic thermal Transport in Porous Carbon Foams: The Role of Phonon Coupling. Int J Mech Sci (2021) 206:106576. doi:10.1016/j.ijmecsci.2021.106576

CrossRef Full Text | Google Scholar

8. Zeng Y-J, Feng Y-X, Tang L-M, Chen K-Q. Effect of Out-Of-Plane Strain on the Phonon Structures and Anharmonicity of Twisted Multilayer Graphene. Appl Phys Lett (2021) 118(18):183103. doi:10.1063/5.0047539

CrossRef Full Text | Google Scholar

9. Pei Y, Shi X, LaLonde A, Wang H, Chen L, Snyder GJ. Convergence of Electronic Bands for High Performance Bulk Thermoelectrics. Nature (2011) 473(7345):66–9. doi:10.1038/nature09996

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Pei Y, Wang H, Snyder GJ. Band Engineering of Thermoelectric Materials. Adv Mater (2012) 24(46):6125–35. doi:10.1002/adma.201202919

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yang K, Perfetto E, Kurth S, Stefanucci G, D'Agosta R. Density Functional Theory of the Seebeck Coefficient in the Coulomb Blockade Regime. Phys Rev B (2016) 94:081410. doi:10.1103/physrevb.94.081410

CrossRef Full Text | Google Scholar

12. Yang J-H, Yuan Q, Deng H, Wei S-H, Yakobson BI. Earth-Abundant and Non-toxic SiX (X = S, Se) Monolayers as Highly Efficient Thermoelectric Materials. J Phys Chem C (2017) 121(1):123–8. doi:10.1021/acs.jpcc.6b10163

CrossRef Full Text | Google Scholar

13. Wu D, Cao X-H, Jia P-Z, Zeng Y-J, Feng Y-X, Tang L-M, et al. Excellent Thermoelectric Performance in Weak-Coupling Molecular Junctions with Electrode Doping and Electrochemical Gating. Sci China Phys Mech Astron (2020) 63(7):276811. doi:10.1007/s11433-019-1528-y

CrossRef Full Text | Google Scholar

14. Liu Q, Li J-J, Wu D, Deng X-Q, Zhang Z-H, Fan Z-Q, et al. Gate-controlled Reversible Rectifying Behavior Investigated in a Two-Dimensional MoS 2 Diode. Phys Rev B (2021) 104:045412. doi:10.1103/physrevb.104.045412

CrossRef Full Text | Google Scholar

15. Wang J, Wu D, Huang L, Cao X-H, Ding Z-K, Zeng Y-J, et al. Thermoelectric Performance Enhanced by Destructive Quantum Interference in Nanoporous Carbon Nanotube Based Junctions. Phys Status Solidi RRL (2021) 15:2100400. doi:10.1002/pssr.202100400

CrossRef Full Text | Google Scholar

16. Fan Z-Q, Jiang X-W, Chen J, Luo J-W. Improving Performances of In-Plane Transition-Metal Dichalcogenide Schottky Barrier Field-Effect Transistors. ACS Appl Mater Inter (2018) 10(22):19271–7. doi:10.1021/acsami.8b04860

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Fan Z-Q, Zhang Z-H, Yang S-Y. High-performance 5.1 Nm In-Plane Janus WSeTe Schottky Barrier Field Effect Transistors. Nanoscale (2020) 12(42):21750–6. doi:10.1039/d0nr05269h

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Narducci D. Do we Really Need High Thermoelectric Figures of merit? A Critical Appraisal to the Power Conversion Efficiency of Thermoelectric Materials. Appl Phys Lett (2011) 99(10):102104. doi:10.1063/1.3634018

CrossRef Full Text | Google Scholar

19. Zeng YJ, Wu D, Cao XH, Zhou WX, Tang LM, Chen KQ. Nanoscale Organic Thermoelectric Materials: Measurement, Theoretical Models, and Optimization Strategies. Adv Funct Mater (2020) 30(8):1903873. doi:10.1002/adfm.201903873

CrossRef Full Text | Google Scholar

20. Zeng Y-J, Liu Y-Y, Zhou W-X, Chen K-Q. Nanoscale thermal Transport: Theoretical Method and Application. Chin Phys B (2018) 27:036304. doi:10.1088/1674-1056/27/3/036304

CrossRef Full Text | Google Scholar

21. Wang ZL, Song J. Piezoelectric Nanogenerators Based on Zinc Oxide Nanowire Arrays. Science (2006) 312(5771):242–6. doi:10.1126/science.1124005

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yang R, Qin Y, Dai L, Wang ZL. Power Generation with Laterally Packaged Piezoelectric fine Wires. Nat Nanotech (2009) 4(1):34–9. doi:10.1038/nnano.2008.314

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Goktas N, Wilson P, Ghukasyan A, Wagner D, McNamee S, LaPierre R. Nanowires for Energy: A Review. Appl Phys Rev (2018) 5:041305. doi:10.1063/1.5054842

CrossRef Full Text | Google Scholar

24. Matloub R, Hadad M, Mazzalai A, Chidambaram N, Moulard G, Sandu CS, et al. Piezoelectric Al1−xScxN Thin Films: A Semiconductor Compatible Solution for Mechanical Energy Harvesting and Sensors. Appl Phys Lett (2013) 102(15):152903. doi:10.1063/1.4800231

CrossRef Full Text | Google Scholar

25. You Y-M, Liao W-Q, Zhao D, Ye H-Y, Zhang Y, Zhou Q, et al. An Organic-Inorganic Perovskite Ferroelectric with Large Piezoelectric Response. Science (2017) 357(6348):306–9. doi:10.1126/science.aai8535

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sebald G, Guyomar D, Agbossou A. On Thermoelectric and Pyroelectric Energy Harvesting. Smart Mater Struct (2009) 18(12):125006. doi:10.1088/0964-1726/18/12/125006

CrossRef Full Text | Google Scholar

27. Wu W, Wang L, Li Y, Zhang F, Lin L, Niu S, et al. Piezoelectricity of Single-Atomic-Layer MoS2 for Energy Conversion and Piezotronics. Nature (2014) 514(7523):470–4. doi:10.1038/nature13792

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ikuno T, Honda S-i., Yasuda T, Oura K, Katayama M, Lee JG, et al. Thermally Driven Nanomechanical Deflection of Hybrid Nanowires. Appl Phys Lett (2005) 87(21):213104. doi:10.1063/1.2133919

CrossRef Full Text | Google Scholar

29. Liu Y-Y, Li B-L, Zhou W-X, Chen K-Q. Triggering Piezoelectricity Directly by Heat to Produce Alternating Electric Voltage. Appl Phys Lett (2016) 109(11):113107. doi:10.1063/1.4962904

CrossRef Full Text | Google Scholar

30. López-Suárez M, Abadal G, Gammaitoni L, Rurali R. Noise Energy Harvesting in Buckled BN Nanoribbons from Molecular Dynamics. Nano Energy (2015) 15:329–34. doi:10.1016/j.nanoen.2015.04.021

CrossRef Full Text | Google Scholar

31. Schoen PAE, Walther JH, Arcidiacono S, Poulikakos D, Koumoutsakos P. Nanoparticle Traffic on Helical Tracks: Thermophoretic Mass Transport through Carbon Nanotubes. Nano Lett (2006) 6(9):1910–7. doi:10.1021/nl060982r

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Schoen PAE, Walther JH, Poulikakos D, Koumoutsakos P. Phonon Assisted Thermophoretic Motion of Gold Nanoparticles inside Carbon Nanotubes. Appl Phys Lett (2007) 90(25):253116. doi:10.1063/1.2748367

CrossRef Full Text | Google Scholar

33. Barreiro A, Rurali R, Hernández ER, Moser J, Pichler T, Forró L, et al. Subnanometer Motion of Cargoes Driven by thermal Gradients along Carbon Nanotubes. Science (2008) 320(5877):775–8. doi:10.1126/science.1155559

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Guo Z, Zhang H, Li J, Leng J, Zhang Y, Chang T. An Intrinsic Energy Conversion Mechanism via Telescopic Extension and Retraction of Concentric Carbon Nanotubes. Nanoscale (2018) 10(10):4897–903. doi:10.1039/c7nr07971k

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Chang T, Zhang H, Guo Z, Guo X, Gao H. Nanoscale Directional Motion towards Regions of Stiffness. Phys Rev Lett (2015) 114:015504. doi:10.1103/PhysRevLett.114.015504

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wang D, Chen G, Li C, Cheng M, Yang W, Wu S, et al. Thermally Induced Graphene Rotation on Hexagonal boron Nitride. Phys Rev Lett (2016) 116(12):126101. doi:10.1103/physrevlett.116.126101

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Takagi Y, Uda T, Ohno T. Carbon Nanotube Motors Driven by Carbon Nanotube. J Chem Phys (2008) 128(19):194704. doi:10.1063/1.2918287

CrossRef Full Text | Google Scholar

38. Coluci VR, Timóteo VS, Galvão DS. Thermophoretically Driven Carbon Nanotube Oscillators. Appl Phys Lett (2009) 95(25):253103. doi:10.1063/1.3276546

CrossRef Full Text | Google Scholar

39. Guo Z, Chang T, Guo X, Gao H. Thermal-induced Edge Barriers and Forces in Interlayer Interaction of Concentric Carbon Nanotubes. Phys Rev Lett (2011) 107(10):105502. doi:10.1103/physrevlett.107.105502

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Leng J, Guo Z, Zhang H, Chang T, Guo X, Gao H. Negative Thermophoresis in Concentric Carbon Nanotube Nanodevices. Nano Lett (2016) 16(10):6396–402. doi:10.1021/acs.nanolett.6b02815

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Liu Y-Y, Zhou W-X, Tang L-M, Chen K-Q. An Important Mechanism for thermal Rectification in Graded Nanowires. Appl Phys Lett (2014) 105(20):203111. doi:10.1063/1.4902427

CrossRef Full Text | Google Scholar

42. McGaughey AJ, Larkin JM. Predicting Phonon Properties from Equilibrium Molecular Dynamics Simulations. Annu Rev Heat Transfer (2014) 17:6915. doi:10.1615/annualrevheattransfer.2013006915

CrossRef Full Text | Google Scholar

43. de Miguel R, Rubí JM. Negative Thermophoretic Force in the strong Coupling Regime. Phys Rev Lett (2019) 123(20):200602. doi:10.1103/physrevlett.123.200602

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Schelling PK, Phillpot SR, Keblinski P. Phonon Wave-Packet Dynamics at Semiconductor Interfaces by Molecular-Dynamics Simulation. Appl Phys Lett (2002) 80(14):2484–6. doi:10.1063/1.1465106

CrossRef Full Text | Google Scholar

45. Liang T, Phillpot SR, Sinnott SB. Parametrization of a Reactive many-body Potential for Mo-S Systems. Phys Rev B (2009) 79(24):245110. doi:10.1103/physrevb.79.245110

CrossRef Full Text | Google Scholar

46. Stuart SJ, Tutein AB, Harrison JA. A Reactive Potential for Hydrocarbons with Intermolecular Interactions. J Chem Phys (2000) 112(14):6472–86. doi:10.1063/1.481208

CrossRef Full Text | Google Scholar

47. Ding Z, Pei Q-X, Jiang J-W, Huang W, Zhang Y-W. Interfacial thermal Conductance in graphene/MoS2 Heterostructures. Carbon (2016) 96:888–96. doi:10.1016/j.carbon.2015.10.046

CrossRef Full Text | Google Scholar

48. Zhou Y, Liu W, Huang X, Zhang A, Zhang Y, Wang ZL. Theoretical Study on Two-Dimensional MoS2 Piezoelectric Nanogenerators. Nano Res (2016) 9(3):800–7. doi:10.1007/s12274-015-0959-8

CrossRef Full Text | Google Scholar

49. Begtrup GE, Ray KG, Kessler BM, Yuzvinsky TD, Garcia H, Zettl A. Probing Nanoscale Solids at thermal Extremes. Phys Rev Lett (2007) 99(15):155901. doi:10.1103/physrevlett.99.155901

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Kong LT. Phonon Dispersion Measured Directly from Molecular Dynamics Simulations. Comp Phys Commun (2011) 182(10):2201–7. doi:10.1016/j.cpc.2011.04.019

CrossRef Full Text | Google Scholar

51. Dorado B, Bottin F, Bouchet J. Phonon Spectra of Plutonium at High Temperatures. Phys Rev B (2017) 95(10):104303. doi:10.1103/physrevb.95.104303

CrossRef Full Text | Google Scholar

52. Qian X, Yang R. Temperature Effect on the Phonon Dispersion Stability of Zirconium by Machine Learning Driven Atomistic Simulations. Phys Rev B (2018) 98(22):224108. doi:10.1103/physrevb.98.224108

CrossRef Full Text | Google Scholar

53. Zhou WX, Cheng Y, Chen KQ, Xie G, Wang T, Zhang G. Thermal Conductivity of Amorphous Materials. Adv Funct Mater (2020) 30(8):1903829. doi:10.1002/adfm.201903829

CrossRef Full Text | Google Scholar

54. Singer IL, Bolster RN, Wegand J, Fayeulle S, Stupp BC. Hertzian Stress Contribution to Low Friction Behavior of Thin MoS2coatings. Appl Phys Lett (1990) 57(10):995–7. doi:10.1063/1.104276

CrossRef Full Text | Google Scholar

55. Li T. Ideal Strength and Phonon Instability in Single-Layer MoS2. Phys Rev B (2012) 85(23):235407. doi:10.1103/physrevb.85.235407

CrossRef Full Text | Google Scholar

56. Lee G-H, Yu Y-J, Cui X, Petrone N, Lee C-H, Choi MS, et al. Flexible and Transparent MoS2 Field-Effect Transistors on Hexagonal boron Nitride-Graphene Heterostructures. ACS nano (2013) 7(9):7931–6. doi:10.1021/nn402954e

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Zhu H, Wang Y, Xiao J, Liu M, Xiong S, Wong ZJ, et al. Observation of Piezoelectricity in Free-Standing Monolayer MoS2. Nat Nanotech (2015) 10(2):151–5. doi:10.1038/nnano.2014.309

CrossRef Full Text | Google Scholar

58. Feldman JL. Elastic Constants of 2H-MoS2 and 2H-NbSe2 Extracted from Measured Dispersion Curves and Linear Compressibilities. J Phys Chem Sol (1976) 37(12):1141–4. doi:10.1016/0022-3697(76)90143-8

CrossRef Full Text | Google Scholar

59. Agrawal R, Espinosa HD. Giant Piezoelectric Size Effects in Zinc Oxide and Gallium Nitride Nanowires. A First Principles Investigation. Nano Lett (2011) 11(2):786–90. doi:10.1021/nl104004d

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Cai L, He J, Liu Q, Yao T, Chen L, Yan W, et al. Vacancy-induced Ferromagnetism of MoS2 Nanosheets. J Am Chem Soc (2015) 137(7):2622–7. doi:10.1021/ja5120908

CrossRef Full Text | Google Scholar

61. Pan L, Wen H, Huang L, Chen L, Deng H-X, Xia J-B, et al. Two-dimensional XSe2 (X= Mn, V) Based Magnetic Tunneling Junctions with High Curie Temperature*. Chin Phys. B (2019) 28(10):107504. doi:10.1088/1674-1056/ab3e45

CrossRef Full Text | Google Scholar

62. Romo-Herrera JM, Terrones M, Terrones H, Dag S, Meunier V. Covalent 2D and 3D Networks from 1D Nanostructures: Designing New Materials. Nano Lett (2007) 7(3):570–6. doi:10.1021/nl0622202

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Ma L, Peng J, Wu C, He L, Ni Y. Sphere-To-Tube Transition toward Nanotube Formation: A Universal Route by Inverse Plateau-Rayleigh Instability. ACS nano (2017) 11(3):2928–33. doi:10.1021/acsnano.6b08248

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Chen S, Liu Z, Du H, Tang C, Ji CY, Quan B, et al. Electromechanically Reconfigurable Optical Nano-Kirigami. Nat Commun (2021) 12(1):1299–8. doi:10.1038/s41467-021-21565-x

PubMed Abstract | CrossRef Full Text | Google Scholar