Study on the Insulation Performance of SF6 Gas Under Different Environmental Factors

During the long-term operation of electrical equipment, the insulation performance of applied SF₆ gas may be affected by humidity, pressure, and temperature. In this study, the collision cross sections of SF₆ and H₂O are considered, including ionization, attachment, excitation, and elastic collision. In order to analyze the influencing factors of SF₆ insulation performance, discharge parameters are computed by the Boltzmann equation under different environmental conditions, including humidity, pressure, and temperature. It is concluded that with the conditions of 0.1 MPa and 300 K, the critical breakdown electric field increases by 1.23 kV/cm as the relative humidity increases from 0% to 80%. As the pressure increases from 0.1 to 0.6 MPa, the critical breakdown electric field increases by 451.07 kV/cm. However, temperature also has little effect on the insulation performance of SF₆ gas. The conclusions of this study have reference value for safe and stable operation of SF₆ insulated power equipment.

Introduction

UHV gas-insulated switchgear (GIS) is an important component for the UHV transmission network to ensure safe and stable operation. Since the1960s, SF₆ gas has been widely used in high-pressure GIS equipment. During the operation of high-voltage GIS equipment, many factors affect its safe and stable operation, such as pressure, temperature, humidity, and discharge by-products [1, 2]. The electron transport parameters of gas discharge are an important basis for studying the insulation performance. Experimental and numerical calculation methods are applied to obtain electron transport parameters of SF₆ gas. Steady-state Thompson experiment (SST) and pulse Thompson experiment (PT) are the two main experimental methods. Numerical methods include the fluid dynamics hybrid model, PIC-Monte Carlo collision model, and model of Boltzmann equation. Since the solving process of PIC-Monte Carlo is too complicated and mainly used at low pressure, it is not suitable for SF₆ gas [3]. Since the Boltzmann equation is of great significance in the study of transport theory, it has attracted the attention of many scholars. The Boltzmann equation is to solve the electron energy distribution function (EEDF) and the important parameters of gas discharge under known section data. Compared with the other two numerical calculation methods, the Boltzmann equation can improve the calculation accuracy with a shorter calculation time [4].

for SF₆ is a strong electronegative gas with good arc extinguishing performance and insulation performance, SF₆ gas is widely used as an insulation medium in GIS power equipment. The pressure and electric field are much higher in GIS equipment. Therefore, the discharge parameters of SF₆ gas can vary sensitively under different environmental conditions. In 1988, H Itoh et al. [5, 6] studied the electron group behavior by using three Boltzmann equation methods and determined a set of uniform electron collision cross sections. The calculated results are compared with the Boltzmann equation with a two-term approximation, and the electron group parameters are completely effective. In 1993, H Itoh et al. [7] modified the cross-sectional data and added the elastic momentum transfer cross section on the basis of the abovementioned literature. The electron transport parameters calculated by the Boltzmann equation are very consistent with those calculated by the Monte Carlo method. Phelps and Van Brunt [8] studied the electron transport parameters of SF₆ by the Boltzmann equation and predicted the critical breakdown field strength and electron drift velocity of SF₆ and N₂, O₂, and Ne gas mixtures. A set of cross-sectional data of SF₆ at lower and higher energies are summarized, which are different from the previous data. The electric field when the ionization coefficient is equal to the attachment coefficient is defined as the critical effective breakdown field (E/N)_cr. MJ Pinheiro et al. [9] calculated the effective ionization coefficient and electron drift velocity of SF₆ and He, Xe, CO_2, and N₂ gas mixtures by Boltzmann equation analysis, which proved the validity of using the Boltzmann equation with two-term approximation to calculate the transport parameters of SF₆. Feng Li et al. [10] analyzed the influence of temperature on the insulation performance of SF₆/N₂ gas mixture by the experimental method and concluded that the critical breakdown field strength changed little in the temperature range of −20–20°C. Bin Li et al. [11] used an SF₆ circuit breaker to test the relationship between temperature and SF₆ humidity and the influence on the insulation performance of the product. It is verified that temperature and humidity have little effect on the ability of the SF₆ circuit breaker to withstand high voltage. Tang et al. [12] studied the effect of micro-water on SF₆ discharged products under an overheating fault by the experimental method. The abovementioned literature focuses on the study of the insulation performance of SF₆ gas and its mixture, and the influence of humidity, pressure, and temperature is mostly through experimental methods. However, the influence of humidity, pressure, and temperature on the insulation performance of SF₆ gas is rarely analyzed by numerical calculation.

The aim of this study is to analyze the influence of humidity, pressure, and temperature on the insulation performance of SF₆ gas by the Boltzmann equation. The role of different environmental factors is dissected by the introduction of electron energy distribution function, and the effects of humidity, pressure, and temperature on the effective ionization coefficient are analyzed as well.

Basic Model and Theory

Boltzmann Equation

When the fluid-chemical model is used to simulate the hydrodynamic simulation of gas, the electron transport parameters are important requirements for solving the electron continuity equation, energy equation, and momentum equation. Electron transport parameters calculated by the Boltzmann equation are the premise of hydrodynamic simulation of the discharge process.

The plasma discharge process can be explained by the plasma dynamics theory, and the Boltzmann equation shown in Eq. 1 can represent the distribution function of electrons in the six-dimensional phase space [13–16].

$\frac{\partial f}{\partial t}+v\cdot {\nabla }_{r}f-\frac{e}{m}\cdot \left(E\cdot {\nabla }_{v}f\right)=C\left[f\right],(1)$

where f is an electron energy distribution function, including 6D phase-space coordinates and time coordinates; v is the electron velocity vector; e is the charge of electrons; m is the mass of electrons; E is the electric field intensity vector; and C[f] is the change rate of the electron energy distribution function during the collision.

It can be seen that the Boltzmann equation is a multidimensional partial differential equation. Because of the high-dimensional characteristics of the Boltzmann equation, it is very complex to directly solve the Boltzmann equation, so the classical two-term approximation theory is used to simplify it [17]. The electron distribution function is symmetrical along the electric field direction in the velocity space and only changes along the electric field direction in the coordinate space. Therefore, using spherical coordinates in velocity space, Eq. 1 can be simplified to as follows:

$\frac{\partial f}{\partial t}+v\cos \theta \frac{\partial f}{\partial z}-\frac{e}{m}E\left(\cos \theta \frac{\partial f}{\partial v}+\frac{{\sin }^2\theta }{v}\frac{\partial f}{\partial \cos \theta }\right)=C\left[f\right],(2)$

where θ is the angle between the direction of electron velocity and the direction of electric field intensity.

And the electron energy distribution function can be expanded by the spherical harmonic function, as shown in the following equation:

$f\left(v,r,t\right)={\displaystyle \sum _{n=0}^{\infty }{f}_n\left(v,r,t\right)P_n\left(\cos \theta \right)}.(3)$

When applied to gas discharge, elastic collision plays a leading role due to the small electric field intensity and the small anisotropy caused by an electric field. At the same time, the electron mass is small, and the energy loss is less when the elastic collision with the molecule and the thermal motion under the electric field is dominant. Even if the electric field intensity is large, the anisotropy of the electron velocity distribution function is weak. Just keep the second item of the spherical harmonic expansion (to first order), as shown in the following equation:

$f\left(v\right)=f_{\mathit{0}}\left(v\right)+f_1\left(v\right)\cos \theta ,\cos \theta =v\times \frac{E}{vE},(4)$

where f₀ and f₁ are isotropic and anisotropic components of the electron energy distribution function, respectively; θ is the angle between the direction of electron velocity and the direction of electric field intensity.

The calculation results in Reference [18] show that the useful transport parameters can be calculated by using the first-order spherical harmonic expansion. The difference between the calculated transport parameters retained in the first order and the calculated transport parameters retained in the sixth order is less than 10%.

Substitute Eq. 4 into Eq. 2, respectively, multiplying Legendre polynomials (1 and cosθ) and integrating cosθ, the following two first-order partial differential equations are obtained as follows:

$\frac{\mathit{\partial }{f}_0}{\mathit{\partial }t}+\frac{\gamma }{3}{\epsilon }^{1/2}\frac{\mathit{\partial }{f}_1}{\mathit{\partial }t}-\frac{\gamma }{3}{\epsilon }^{-1/2}\frac{\mathit{\partial }}{\partial \epsilon }\epsilon E{f}_1=C_0,(5)$

$\frac{\mathit{\partial }{f}_1}{\mathit{\partial }t}+\gamma {\epsilon }^{1/2}\frac{\mathit{\partial }{f}_0}{\mathit{\partial }t}-E\gamma {\epsilon }^{1/2}\frac{\mathit{\partial }{f}_0}{\mathit{\partial }\epsilon }=-N{\sigma }_m\gamma {\epsilon }^{1/2}{f}_1.(6)$

${\sigma }_m={\displaystyle \sum _k{x}_k{\sigma }_k},(7)$

where γ=(2e/m)^1/2 is a constant, ε=(v/γ)² is electronic energy, and σ_m and σ_k are total collision cross sections and reaction k collision cross sections, respectively.

Eqs 5, 6 are combined by the separation variable method to obtain a second-order partial differential equation about f₀ and f₁ equation about f₀:

$\frac{\partial }{\partial \epsilon }\left[\frac{\epsilon }{3{\sigma }_m}\frac{\mathit{\partial }{f}_0}{\partial \epsilon }{\left(\frac{E}{N}\right)}^2+{\epsilon }^2\left(f_0+\frac{k_{b}T}{e}\frac{\mathit{\partial }{f}_0}{\partial \epsilon }\right)\right]=\mathit{S},(8)$

$f_1=\frac{E}{N}\frac{1}{{\sigma }_m}\frac{\mathit{\partial }{f}_0}{\partial \epsilon },(9)$

${\sigma }_{\epsilon }={\displaystyle \sum 2\frac{m_e}{M}{\sigma }_k},(10)$

$S={\displaystyle \sum _{k=inelastic}{C}_k-\gamma \lambda {\epsilon }^{1/2}f},(11)$

where σ_ε is the total cross section of elastic collision; N represents air density; M represents particle mass; k_B represents the Boltzmann constant; T is gas temperature; S is the energy loss source term representing inelastic collisions; and C_k is the term of type k inelastic collisions between electrons and other particles, solving f₀ and f₁ to obtain the electron energy distribution function.

The electron transport parameters can be obtained, including the reduced ionization coefficient α/N, the reduced attachment coefficient η/N, and the reduced effective ionization coefficient (α−η)/N. As (α−η) = 0, the reduced electric field intensity is the critical reduced electric field strength (E/N)_cr.

The reduced ionization coefficient and the reduced attachment coefficient can be calculated according to Eqs 12, 13, respectively.

$\frac{\alpha }{\mathit{N}}=\sqrt{\frac{2\mathit{e}}{\mathit{m}}}\frac{1}{\mathit{W}}{\displaystyle {\int }_{{\epsilon }_{\mathit{i}}}^{\infty }\epsilon {\mathit{Q}}_{\mathit{i}}}\left(\epsilon \right){\mathit{F}}_0\left(\epsilon \right)\mathit{d}\epsilon ,(12)$

$\frac{\eta }{\mathit{N}}=\sqrt{\frac{2\mathit{e}}{\mathit{m}}}\frac{1}{\mathit{W}}{\displaystyle {\int }_{{\epsilon }_{\mathit{a}}}^{\infty }\epsilon {\mathit{Q}}_{\mathit{a}}}\left(\epsilon \right){\mathit{F}}_0\left(\epsilon \right)\mathit{d}\epsilon ,(13)$

where N is the number density of neutral particles; W is the electron diffusion velocity; Q_i is the electron collision ionization cross section; Q_a is the electron attachment cross section; F₀ is the electron energy distribution function that remains unchanged in time and space after expanding f through two-term approximation; ε is the electron energy; ε_i is the critical energy of collision ionization; and ε_a is the critical energy of adsorption reaction.

Electron Collision Reaction

Elastic collision, excitation, attachment, and ionization occur during discharge processes. The electron collision cross section is the basic data for solving the Boltzmann equation. The accuracy of the calculation depends on the cross-section set. The cross-section sets of different electron collision reactions selected in this study are all from the LXCat database [19, 20]. In order to simplify the calculation, this study only considers electron collisions. The collision types mainly include ionization, attachment, elastic collision, and excitation. As shown in Table 1.

TABLE 1

TABLE 1. Cross-section set of the considered electron collision reactions.

Analysis of Discharge Characteristics of SF₆ Gas

In this study, the BOLSIG+ is used to solve the Boltzmann equation with the two-term approximation method [13]. The electron energy distribution function, reduced ionization coefficient, reduced attachment coefficient, and reduced effective ionization coefficient are all calculated.

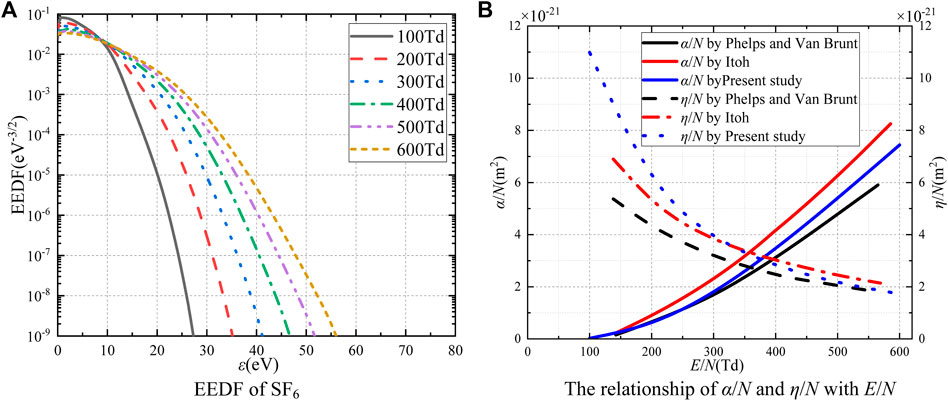
Figure 1A shows the electron energy distribution functions of reduced electric fields (E/N) of 100, 200, 300, 400, 500, and 600 Td (1Td = 10⁻²¹ V·m²) in SF₆ gas at 300 K. As the electron energy is below 10 eV, the electron energy distribution function decreases with the reduced electric field. This is caused by the strong electronegative property of SF₆. It can attach electrons in the mean free path and make a large number of electrons gather around the SF₆ molecule. The smaller the reduced electric field is, the larger the proportion of low-energy electrons is. As the electron energy exceeds 10 eV, the electron energy distribution function increases with the reduced electric field. The increasing electric field will increase the electron kinetic energy, resulting in a larger proportion of high-energy electrons. The aforementioned results are basically consistent with the conclusions in Reference [21].

FIGURE 1

FIGURE 1. (A) EEDF of SF₆; (B) the relationship of α/N and η/N with E/N.

The reduced ionization coefficient mainly reflects the probability of collision ionization between electrons and SF₆ molecules, while the reduced attachment coefficient mainly reflects the ability of SF₆ molecules to attach electrons. The reduced electric field has a great influence on the ionization and attachment reactions between electrons and gas molecules. As shown in Figure 1B, the reduced ionization coefficient increases with the reduced electric field. The results of the present study are between those of Phelps and Van Brunt [8] and Itoh [22]. And the relationship between SF₆ attachment coefficient and reduced electric field. It can be seen that the attachment capacity decreases with the increase of the reduced electric field, and the calculation results are basically consistent with those of Phelps and Van Brunt [8] and Itoh [22]. SF₆ has a strong attachment ability that will inhibit the collision ionization process in SF₆ gas.

Effect of Different Environment Factors on the Insulation Performance of SF₆ Gas

Gas Humidity

The EEDF of SF₆ gas with a relative humidity of 0% and 80% is shown in Figure 2A. As E/N = 100 Td, the electron energy distribution function curve of dry SF₆ is slightly higher than that of wet SF₆. This is because H₂O can capture free electrons to form negative ions, inhibiting the collision ionization process. However, when the E/N is 300 Td, the kinetic energy obtained by electrons also increases, and the movement of electrons is accelerated, making it difficult for water vapor molecules to capture electrons. The increasing number of high-energy electrons makes it easy for electron collision ionization. Therefore, the electron energy distribution function curve of dry SF₆ is slightly lower than that of wet SF₆.

FIGURE 2

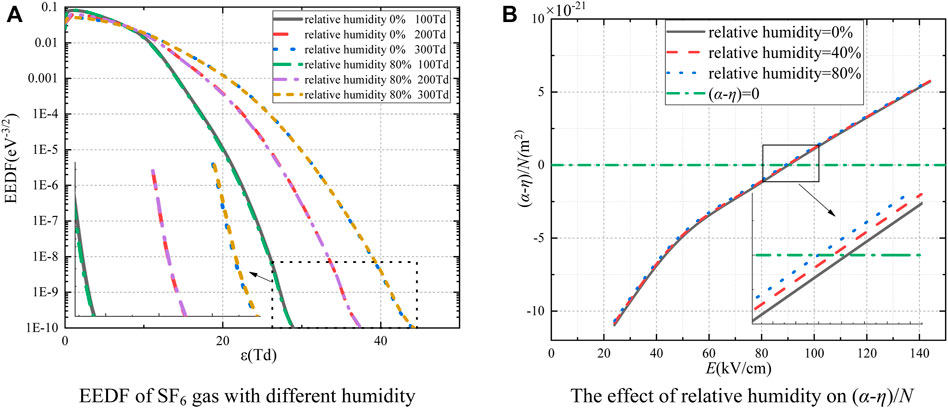
FIGURE 2. (A) EEDF of SF₆ gas with different humidity; (B) the effect of relative humidity on (α-η)/N.

To study the effect of humidity on the critical electric field of SF₆ gas, the discharge transport parameters are calculated under different relative humidity from 0 to 80% at the E/N of 100, 200, 300, 400, 500, and 600 Td under the condition of 0.1 MPa and 300 K. Figure 2B shows the relationship between (α-η)/N and E. With the relative humidity increases from 0% to 80%, the critical breakdown electric field of SF₆ gas increases by 1.23 kV/cm. Therefore, humidity has little effect on the insulation performance of SF₆ gas, which has no effect on the insulation performance of SF₆ when the relative humidity is 30% in Reference [11].

Gas Pressure

The variation of pressure can affect the number of SF₆ particles per unit volume, which can be described by the ideal gas law as follows:.

$PV=NRT,(14)$

where P is the pressure, V is the gas volume, T is the temperature, N is the amount of gas material, and R is the molar gas constant.

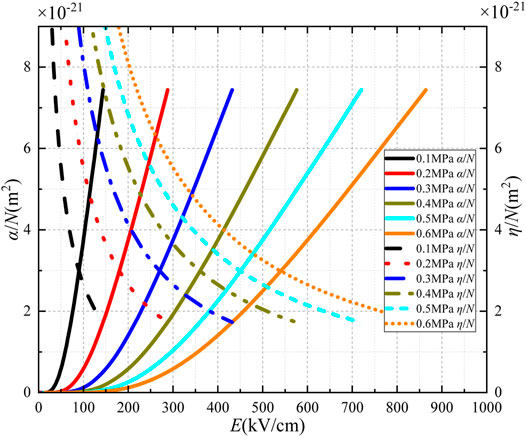
SF₆ gas generally works at high pressure in electrical equipment. With the increasing pressure, the SF₆ molecule's density increases. At 300 K, the relationships of α/N, η/N with E are calculated at a pressure of 0.1–0.6 MPa, as shown in Figure 3. With the increasing electric field, α/N increases, while η/N does not change significantly. Therefore, the pressure mainly affects the α/N of SF₆ gas. When (α-η)/N = 0, the electric field strength corresponding to the transverse coordinates of the intersection point is defined as the critical breakdown electric field. As the pressure increases from 0.1 to 0.6 MPa, the critical breakdown electric field increases by 451.07 kV/cm.

FIGURE 3

FIGURE 3. The relationships of α/N and η/N with E under 0.1–0.6 MPa.

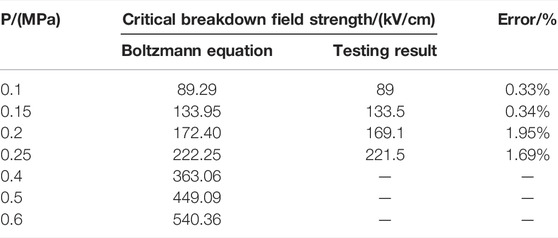
Table 2 shows the comparison between the calculation results in this study and testing results in Reference [23], with the maximum error not exceeding 2%. Since the pressure value of SF₆ gas applied in gas-insulated switchgear (GIS) equipment is generally 0.4–0.6 MPa, Table 2 also shows the relationship between (α-η)/N and E at 0.4–0.6 MPa.

TABLE 2

TABLE 2. Critical breakdown field at (α-η)/N = 0.

With the increase of pressure, the critical breakdown field strength increases, and the insulation performance is enhanced. The increase in air pressure can reduce the free path length of electrons and the number of collision ionization between electrons and SF₆ molecules, thus inhibiting collision ionization.

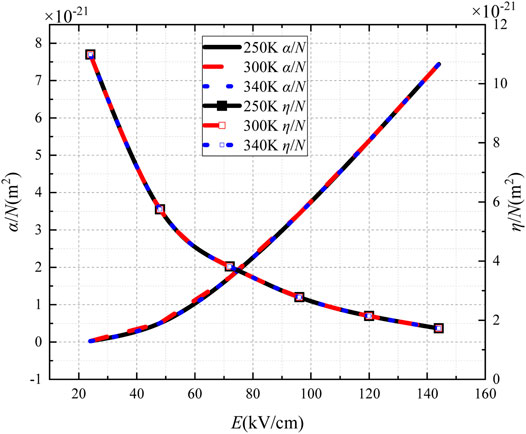
Gas Temperature

To study the effect of gas temperature, α/N and η/N of SF₆ gas at 250 K, 300 K, and 340 K were calculated, as shown in Figure 4. The gas temperature has little effect on α/N and η/N.

FIGURE 4

FIGURE 4. α/N and η/N versus E with the temperature of 250–340 K.

With the increasing temperature, the critical breakdown electric field changes slightly. Therefore, the effect of temperature on the discharge characteristics of SF₆ gas is very small and can be approximately ignored.

Conclusion

This study uses BOLSIG+ to solve the Boltzmann equation with the two-term approximation method. The accurate cross-sectional data are selected to solve the electron energy distribution function and discharge transport parameters of SF₆ gas. The accuracy of the model is verified by comparing the results with the known literature.

1) EEDF is mainly affected by the E/N. As the electron energy is below 10 eV, the EEDF decreases with the reduced electric field. And the EEDF increases with the reduced electric field when the electron energy exceeds 10 eV.

2) Humidity has a slight impact on the insulation performance of SF₆. Collision reactions of H₂O are considered in this study. As the relative humidity is increased from 0% to 80%, the critical breakdown electric field increases by 1.23 kV/cm.

3) Pressure effects a lot on the insulation performance of SF₆. Through comparing the calculation results in this study and testing results, verify the accuracy of the model. The critical breakdown electric field increases by 451.07 kV/cm as the pressure is increased from 0.1 to 0.6 MPa.

4) Gas temperature has little effect on α/N and η/N. Also, the critical breakdown electric field changes slightly.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YA: conceptualization, writing—original draft preparation, and software; KY: software; YH: funding acquisition and validation; KY: project administration; TH: supervision; CM: revision; MY: supervision; BA: validation; and DC: figures.

Funding

This work was supported in part by the Natural Science Foundation of China under grant 51807113 and in part by the Natural Science Foundation of Shandong Province under grant ZR202103040796 and the Natural Science Foundation of Jiangsu Province under grant BK20200111.

Conflict of Interest

Author TH is employed by Construction Branch of State Grid Jiangsu Electric Power Co., Ltd., Nanjing, China. Author CM, BA, and DC are employed by Jining Huayuan Thermal Power Plant, Jining, China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Christophorou LG, Olthoff JK, Brunt R Sulfur Hexafluoride and the Electric Power Industry[J]. IEEE Electr. Insul. Mag. (1997) 13(5):20–24. doi:10.1109/57.620514

CrossRef Full Text | Google Scholar

2. Christophorou LG, Brunt RJV. SF₆/N₂ Mixtures: Basic and HV Insulation Properties. IEEE Trans Dielectr Electr Insulation (2002) 2(5):952–1003.

Google Scholar

3. Li X. Researches on Discharge Mechanism and Circuit Breaker Dielectric Recovery Characteristics of SF₆/N₂ and SF₆/CF₄. PhD thesis. Shenyang: Shenyang University of Technology (2017).

Google Scholar

4. Liu X, He W, Fan Y, Xiao HG. Simulation and Analysis of Electron Transport Parameters in Air Discharge. High Volt Eng (2011) 37(07):1614–9.

Google Scholar

5. Itoh H, Miura Y, Ikuta N, Nakao Y, Tagashira H. Electron Swarm Development in SF6. I. Boltzmann Equation Analysis. J. Phys. D Appl. Phys. (1988) 21(6):922–30. doi:10.1088/0022-3727/21/6/010

CrossRef Full Text | Google Scholar

6. Yan W, An Y, Hu Y, Jiang Z, Gao X, Zhou L. Research on Cylinder Flexible Graphite Earth Electrode (FGEE) Used to Reduce Tower Earth Resistance. Electr Power Syst Res (2021) 196(3):107268. doi:10.1016/j.epsr.2021.107268

CrossRef Full Text | Google Scholar

7. Itoh H, Matsumura T, Satoh K, Date H, Nakao Y, Tagashira H. Electron Transport Coefficients in SF₆. J Phys D Appl Phys (1993) 26(11):1975. doi:10.1088/0022-3727/26/11/020

CrossRef Full Text | Google Scholar

8. Phelps AV, Van Brunt RJ. Electron‐transport, Ionization, Attachment, and Dissociation Coefficients in SF6 and its Mixtures. J Appl Phys (1988) 64(9):4269–77. doi:10.1063/1.341300

CrossRef Full Text | Google Scholar

9. Pinheiro MJ, Loureiro J. Effective Ionization Coefficients and Electron Drift Velocities in Gas Mixtures of SF6with He, Xe, CO2and N2from Boltzmann Analysis. J. Phys. D Appl. Phys. (2002) 35(23):3077–84. doi:10.1088/0022-3727/35/23/307

CrossRef Full Text | Google Scholar

10. Li F, Zhang X, Zhang Z. Effect of Temperature Variation on Discharge Characteristics of SF₆/N₂ Gas Mixtures. High Volt Eng (2017) 43(03):736–42.

Google Scholar

11. Li B, Shen D, Yang J. Influence of Environmental Temperature and Humidity of SF₆ on Insulating Properties of SF₆ Circuit Breaker. High Volt Appar (2010) 46(01):97–8+102.

Google Scholar

12. Tang J, Zeng F, Sun H. The Influence and Correction of Micro H₂O on SF₆ Decomposition Characteristics under Overheating Fault. Proc CSEE (2015) 35(09):2342–50.

Google Scholar

13. Hagelaar GJM, Pitchford LC. Solving the Boltzmann Equation to Obtain Electron Transport Coefficients and Rate Coefficients for Fluid Models. Plasma Sources Sci. Technol. (2005) 14(4):722–33. doi:10.1088/0963-0252/14/4/011

CrossRef Full Text | Google Scholar

14. Zhou Q, Dong Z. Theoretical Study on the Electron Energy Distribution Function of Weakly Ionized Air Plasma. Acta Phys Sin (2013) 62(1):709–12. doi:10.7498/aps.62.205201

CrossRef Full Text | Google Scholar

15. Hu Y, Lin Y, An Y, Wen X, Li H, Su M, et al. Laboratory Study on Negative Spark Inception Direction and Breakdown Characteristics in Rod–Rod Air Gaps. Electr Power Syst Res (2021) 201:107498. doi:10.1016/j.epsr.2021.107498

CrossRef Full Text | Google Scholar

16. Amorim J. Kinetics and Spectroscopy of Low Temperature Plasmas[M]. Springer International Publishing (2016).

17. White RD, Robson RE, Schmidt B, Morrison MA. Is the Classical Two-Term Approximation of Electron Kinetic Theory Satisfactory for Swarms and Plasmas? J. Phys. D Appl. Phys. (2003) 36(24):3125–31. doi:10.1088/0022-3727/36/24/006

CrossRef Full Text | Google Scholar

18. Pitchford LC, Oneil SV, Rumble JR. Extended Boltzmann Analysis of Electron Swarm Experiments. Phys. Rev. A (1981) 23(1):294–304. doi:10.1103/physreva.23.294

CrossRef Full Text | Google Scholar

19.MORGAN database.SF₆ (2010). Available from: http://www.lxcat.net (accessed on Dec, 2020).

Google Scholar

20.TRINITI database.H₂O (2017). Available from: http://www.lxcat.net (accessed on Dec, 2020).

Google Scholar

21. Cai X, Wang X, Xiaobing Z, Zhiwei L Effect of Attachment on Electron Transport Properties[J]. Proc CSEE (2016) 36(11):3126–3132.

Google Scholar

22. Itoh H, Matsumura T, Satoh K, Date H, Nakao Y, Tagashira H. Electron Transport Coefficients in SF₆. J. Phys. D Appl. Phys (1975) 26(11):1839–52. doi:10.1088/0022-3727/26/11/020

CrossRef Full Text | Google Scholar

23. Cheng Y, Wang C, Zhou F, Tu Y. Breakdown Characteristics of SF₆ and CF₃I as Well as Their Binary and Ternary Gas Mixtures from 0.1MPa to 0.25MPa Gas Pressures. High Volt Eng (2017) 43(03):795–800. doi:10.13336/j.1003-6520.hve.20170303014

CrossRef Full Text | Google Scholar