Polarimetric Imaging Through Scattering Media: A Review

Imaging in scattering media has been a challenging and important subject in optical science. In scattering media, the image quality is often severely degraded by the scattering and absorption effects owing to the small particles and the resulting nonuniform distribution of the intensity or polarization properties. This study reviews the recent development in polarimetric imaging techniques that address these challenges. Specifically, based on the polarization properties of the backscattering light, polarimetric methods can estimate the intensity level of the backscattering and the transmittance of the media. They can also separate the target signal from the undesired ones to achieve high-quality imaging. In addition, the different designs of the polarimetric imaging systems offer additional metrics, for example, the degree/angle of polarization, to recover images with high fidelity. We first introduce the physical degradation models in scattering media. Secondly, we apply the models in different polarimetric imaging systems, such as polarization difference, Stokes vector, Mueller matrix, and deep learning-based systems. Lastly, we provide a model selection guideline and future research directions in polarimetric imaging.

1 Introduction

Optical imaging through scattering media, including turbid water [1, 2], haze [3, 4], fog [5], and biological tissue [6–8], enjoys a wide range of applications in areas such as underwater rescue [9], automatic driving [10], underwater archaeology [11], and biomedical imaging [12]. Therefore, the realization of clear visions in scattering media is of great interest and significance. However, the visibility and identifiability of the target scene are usually compromised as the radiance observed from a scene is scattered and absorbed by aerosols and particles existing in the environment [13]. The optical performance is thus limited in many practical applications [14]. In other words, the image quality captured by a camera deteriorates significantly, resulting in low image contrast [15], distorted color [16], and poor visibility [17].

Various dehazing or de-scattering techniques that have been developed to restore the image quality can be classified into two categories, non-physical and physical model-based methods, as shown in Figure 1. The non-physical methods, based on the image enhancement method, aim to highlight the target of interest and improve the contrast. The simplest non-physical method is the histogram equalization (HE) method, which enhances the overall image contrast by increasing the dynamic range of the gray value. Depending on the difference in the computing region of an image, HE can be divided into global HE (GHE) and local HE (LHE). The advantage of GHE lies in its higher efficiency and lower computation requirement, which is particularly suitable for enhancing excessively dark or bright images. This method does not fit images with high local brightness values, which often cause the “halo” effect. Such an issue can be addressed by applying the LHE method, for example, contrast limited adaptive histogram equalization (CLAHE) [18]. However, the “blocking effect” accompanied by increased computation complexity [19] cannot be avoided. Besides, HE methods may amplify noises during dehazing. Retinex-based algorithms [20, 21] are models based on the color perception of human eyes, with the main concept of obtaining an object’s reflection property to model the color invariance. Thus, the Retinex-based algorithms have been widely applied in the field of image enhancement to remove haze and scattered light. In addition, this method helps increase an image’s contrast and brightness and regulate the dynamic range of its gray level. Nevertheless, the Retinex-based algorithms do not preserve edges well, which may lead to the halo phenomena in sharp boundary regions [21, 22]. Finally, with regard to the dehazing technique, the frequency domain filtering (FDF) method proves to be another popular solution for image enhancement. More details can be found in the previous works [23–25].

FIGURE 1

FIGURE 1. Classification of dehazing/de-scattering methods.

The physical model-based dehazing and de-scattering methods are based on the knowledge related to the scene’s physical features. To successfully restore an image, one of the key factors is to acquire an accurate depth of the scene [26], that is, the physical distance between the camera and target scene. However, the depth map is always unattainable for practical applications [27]. Therefore, a fundamental challenge in optical de-scattering techniques is to accurately estimate the depth map, that is, the transmission of scattering media [28]. Various methods have been proposed to overcome the challenge. For example, Fattal et al. [27] proposed a method that inferred the medium transmission map by estimating the albedo of the scene. However, such a method assumes that the transmission and surface shading are locally uncorrected and thus may fail when handling dense haze. Hautiere et al. [29] estimated the depth by determining the relationship between the road visibility and the contrast in the foggy image. Based on the analysis of the side geographical information obtained via an onboard optical sensor system, a 3D geographical model was established to remove the fog. Upon observing the property of haze-free outdoor images, He et al. [3] proposed the dark channel prior (DCP), based on the premise that “dark pixels” had a very low intensity in at least one-color channel except in the sky region. His method included three steps: air-light/scattered light estimation, transmission map estimation and refinement, and the final image reconstruction. Thanks to its effectiveness in dehazing, DCP has been adopted by most of the recent physical model-based techniques.

Almost all methods above are implemented based on the input of a single image, where certain assumptions or prior knowledge are necessary. The other physical model-based methods are based on multiple images corresponding to the same scene, that is, the images obtained under different visibility [30], images obtained with visible and near-infrared cameras [31], and images acquired with different polarization angles [15, 32, 33]. While images under different visibilities render the estimation of the depth map and scene structures to significantly enhance the image contrast, it remains challenging to handle real-time scenes [34]. Thanks to the excellent “long-distance transmission capacity” of the near-infrared light, the visible and near-infrared fusion methods improve the image quality by combining the rich color information of the visible image and the high visibility of the near-infrared image. However, the major obstacle is to acquire the visible and near-infrared images simultaneously, where expensive equipment and accurate optical alignment are both required. As opposed to the above methods, polarimetric imaging [35–37] is more effective because the scattered light is partially polarized [35] and the polarization information of the object and the turbid medium is different. Therefore, in principle, obtaining the polarization information of the scene and then processing them can effectively suppress the scattered light and extract the light coming from the object light [15, 32, 38]. A series of studies have shown that polarization-based imaging is a physical, low-cost, and applicable way to enhance the image quality, especially in highly scattering environments [2, 39, 40].

The typical polarimetric imaging systems include the polarization difference (PD) imaging [1, 41, 42], Stokes-based polarimetric (SP) imaging [43], and Mueller matrix (MM) imaging [44, 45]. The PD imaging is based on two orthometric polarized sub-images to estimate the transmittance by analyzing the degree of linear polarization. The SP imaging, especially the full-SP imaging, leverages the robustness of the polarization angle [38] or the “memory effect” of circular polarization to achieve the backscatter removal [39, 46, 47]. The MM imaging benefits from its complete polarization characterization. These three basic models are built upon different optical systems that offer flexible options subject to different application requirements. Besides, the polarization-based methods can be further improved by integrating with computer-vision-based and learning-based methods [2, 15, 48]. In other words, by introducing the polarization information into the traditional vision or learning-based method, greater application possibilities can be explored due to enhanced performance in image quality [2, 49–52].

This study first introduces the basic principles of the common polarimetric imaging models in scattering media and provides a comprehensive and up-to-date review for both traditional and advanced works. We explore topics that include the progress in model optimization and parameter estimation and the analysis of different methods from the perspectives of their limitations and potential solutions, with application-based recommendations for readers in optics and engineering communities. Section 2 introduces the imaging model through the scattering media and the related optical imaging systems. Section 3 demonstrates the polarimetric methods for imaging through turbid media based on different imaging systems. Section 4 provides a conclusion and an overlook for future development.

2 Imaging Model in Scattering Media

2.1 Physical Imaging Model in Scattering Media

The particles existing in the scattering media, such as in the atmosphere during hazy or foggy weather and under turbid water or sea, generally absorb and scatter light, resulting in the decay of image contrast, saturation attenuation, and color-shifting in the detected images [39, 46]. Therefore, image dehazing or de-scattering plays an important role in various practical applications, such as traffic surveillance systems, security systems, object recognition, medical imaging, and remote sensing. Studies related to the image degradation mechanism, imaging systems, and recovery algorithms are receiving much attention.

Koschmieder et al. [53] proposed the first atmospheric scattering model, which was further modified by Narasiman and Nayar [54, 55]. Based on their model, the image signal received by the camera is composed of two components: 1) direct transmission D(x, y), which represents the effect of scattering of light and the eventual decay of light before it reaches the camera, and 2) backscattered light A(x, y), which denotes the undesired backscattered lights from the particles in the object line of sight (LOS) [1, 32]:

$I\left(x,y\right)=D\left(x,y\right)+A(x,y).(1)$

As the light from the target progresses towards the camera, its energy is lost due to scattering and absorption. The fraction that does reach the camera is the direct transmission given by

$D\left(x,y\right)=L_{object}\left(x,y\right)e^{-\beta z(x,y)},(2)$

where $z(x,y)$ is the distance between the object and the camera and depends on the pixel coordinates x and y; $\beta$ is the attenuation coefficient; and $L_{object}\left(x,y\right)$ is the object radiance not scattered and absorbed along the LOS [1, 35]. The attenuation coefficient is given by $\beta$, and the term $e^{-\beta z(x,y)}$ is also called the transmittance of light t $\left(x,y\right)$.

$A(x,y)$ denotes the undesired lights received by the camera mainly due to scattering by particles. It does not originate from the object on the LOS but varies with the horizontal distance by

$A\left(x,y\right)=A_{\infty }\left(x,y\right)\left[1-t(x,y)\right],(3)$

where $A_{\infty }$ refers to the intensity value of backscattered light from infinity in the turbid medium. In most works, it is assumed to be a global constant independent of the location (x, y). Figure 2A shows the image formation and visual illumination components through the scattering medium. According to Eq. 2 and Eq. 3, we can observe that $L_{object}\left(x,y\right)$ and, thus, the recovered image could be obtained as far as the transmittance and backscattering are estimated accurately and the attenuation of the object light is compensated. Combining Eq. 1 and Eq. 2, one can recover $L_{object}\left(x,y\right)$ as follows:

$L_{object}\left(x,y\right)=\frac{I\left(x,y\right)-A(x,y)}{1-A(x,y)/A_{\infty }}.(4)$

FIGURE 2

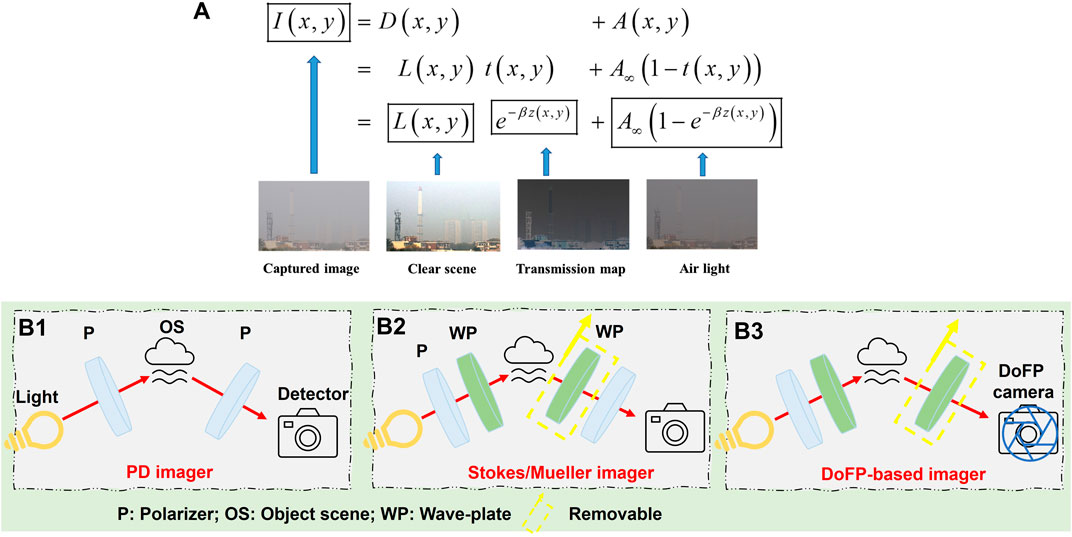
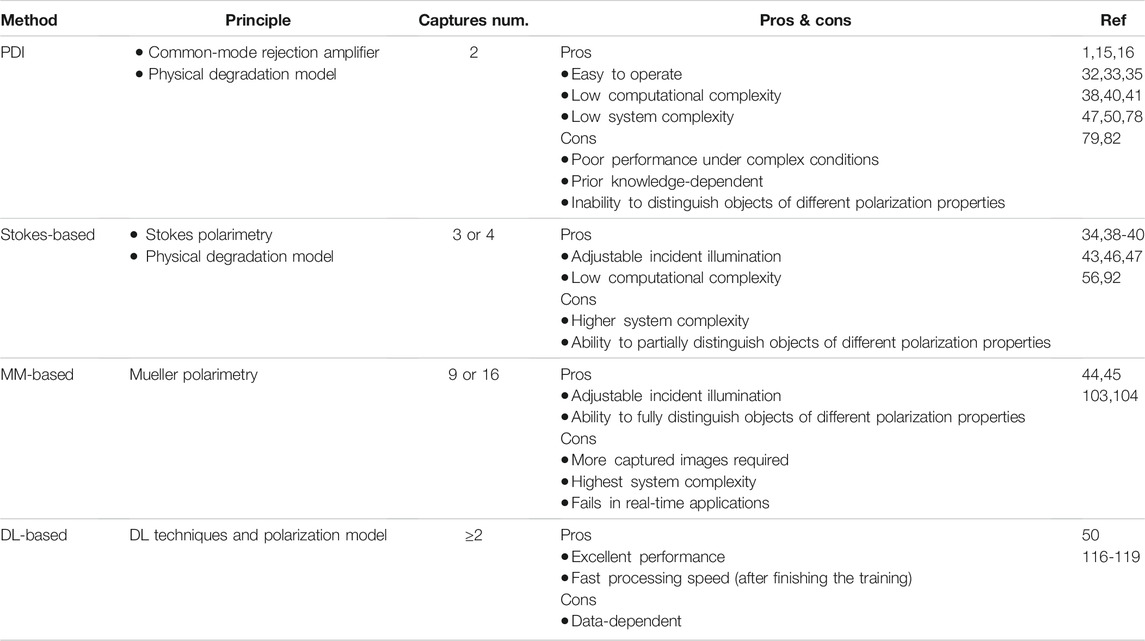
FIGURE 2. (A) Image formation and visual example of illumination components through the turbid media (reprinted from Springer Nature: Scientific Reports [2], copyright 2018). (B) Different polarimetric imaging systems: (B1) PD imager, (B2) Stokes/Mueller imager, and (B3) DoFP camera-based imager.

The currently reported polarimetric imaging-based dehazing methods are based on the above physical model and the scattered light’s polarization property. The published results in various works show the high information restoration capacity and computational efficiency [56]. For the recovered image in Eq. 4, many quantitative criteria are used to characterize the quality of results, including the visibility range or distance [56, 57], Michelson contrast (MC) [43], peak-to-correlation energy (PCE) [58], mean gradient [51], measure of enhancement (EME) [2, 17, 48], blind-reference-less image spatial quality evaluator (BRISQUE) [2], natural image quality evaluator (NIQE) [17], entropy [2], and peak signal-to-noise ratio (PSNR) [19, 27, 54]. Among the above criteria, PCE and PSNR describe the similarity between the restoration and clear image, EME and entropy describe the image contrast, and BRISQUE and NIQE quantify the distortion indicator of quality.

The superiority of the polarimetric methods also embodies the robustness of polarization parameters in various complex scattering conditions. Many works study the propagating light’s physical characteristics and polarization properties in scattering media [59–61]. For example, with the aid of the Monte Carlo simulations, Xu et al. [62] demonstrated that the intensity of the polarized light after being transmitted underwater sharply decreases as the transmission distance increases, but the degree of polarization (DoP) of the transmitted lights remains above 0.75. It means that compared with the traditional imaging encoded with intensity information (in which the intensity will be significantly lost), the polarization encoding by DoP has overpowering advantages. Besides, Shen et al. [61] demonstrated that the depolarization behavior of light is sensitive to the mixing ratio or the distribution state of particles. Tao et al. [60] also found that the polarization properties provide additional information for the imaging, and the contrast of the polarization image can be significantly enhanced compared to the simplex intensity image in the turbid media. Moreover, the circular polarization images offer better contrast and higher visibility than linear ones under the same circumstance. All these reported results make the polarimetric methods and polarization control more promising for imaging in scattering media.

To date, whether it is on the basis of two images [15, 32], three or four images [38, 46], and nine or 16 images [44, 45], various polarization recovery methods have been developed by modifying the basic model in Eq. 1. These methods are related to different polarization information, such as the PD, Stokes vector, DoP, angle of polarization (AoP), and MM. The following section introduces the related imaging systems and configurations.

2.2 Polarimetric Imaging Systems

Based on different polarization information, various polarimetric imaging systems have been developed. Early works in polarimetric imaging applications mainly focused on cases with linearly polarized light. This cross-polarization imagery, also called the PD imagery, was commonly used to enhance image contrast and minimize the blurring light in media with relatively low concentrations. The main element of this system is shown in Figure 2B1. In the setup, a light source, such as a light-emitting diode or a laser, is expanded with a beam expander. The light is polarized with a linear polarizer and hits on the target scene. A camera is positioned normal to the target scene to avoid most of the glare created by the interface. Finally, a rotating analyzer, always a linear polarizer, is placed in front of the camera to filter the back-reflected polarized light. By this configuration, two images $(I_{\parallel },I_{\perp })$ with orthogonal polarization states are acquired, from which one can calculate the degree of linear polarization (DoLP) as

$P=\frac{I_{\parallel }-I_{\perp }}{I_{\parallel }+I_{\perp }}.(5)$

Stokes parameters have played a prominent part in the optical literature on polarized light [63, 64]. As early as 1947, Chandrasekhar [65] used the Stokes vector to formulate the radiative transfer equations for scattering partially polarized light. Furthermore, the Stokes parameters give a complete description of any polarization state of light:

$\mathbf{S}={\left[S_0, S_1, S_2, S_3\right]}^{\text{T}},(6)$

where the first three parameters are linear components of the Stokes, while the last one is the circular component [49, 63]. From this formalism, other parameters can be deduced, such as the DoP (P), the DoLP $\left(P_l\right)$, the degree of circular polarization (DoCP), that is, $P_c$, and the AoP $\left(\alpha \right)$. They are defined as follows:

$P=\frac{\sqrt{S_1^2+S_2^2+S_3^2}}{S_0}, P_l=\frac{\sqrt{S_1^2+S_2^2}}{S_0}, P_c=\frac{S_3}{S_0}, \text{and} \alpha =\frac{1}{2}{\text{tan}}^{-1}\left[\frac{S_2}{S_1}\right].(7)$

A more detailed description of Stokes vector can be found in the books about polarized light [63].

Unlike the PD imagery for linear polarized light, the Stokes vector contains the ellipticity of the beam. Hence, the complete imaging system for the Stokes vector requires an extension of the instrumentation. Optical retarders or wave plates (WP) are usually introduced into the system to generate or measure elliptical or circular states. Four intensity measurements are needed to calculate the complete Stokes vector parameters. Figure 2B2 shows a typical Stokes vector imagery, consisting of two sections: the polarization state generation (PSG) and the polarization analysis (PSA). In PSG, a WP and a linear polarizer are used to generate polarized illumination with an arbitrary state. The reflected intensity from the target scene is measured by adjusting the WP and/or polarizer’s states in PSA. Based on these captured intensities, one can estimate the Stokes vector of the reflected light. In practice, the measurement of $S_0$, $S_1$, and $S_2$ is conducted by removing the WP in PSA. Only the last term, $S_3$, requires this element to measure an elliptical/circular state. Moreover, with the development of nano-structures fabrication, a snapshot imaging solution has recently gained much attention using a division of focal plane (DoFP) polarization camera [66, 67]. It can simultaneously capture four polarization angles from each video frame without image mismatch [68]. Besides, by adding a rotated WP, one can measure the full Stokes with only two shots [69]. The polarization camera makes real-time polarimetric imaging a reality and its applications possible.

The MM, proposed by Hans Mueller in the early 1940s [63, 70], is another common parameter in addition to the Stokes vector in polarization imaging technology. The Stokes vector is a parameter describing the characteristics of the incident and the outgoing light when interacting with the materials, while the Mueller matrix is a “bridge” between the light and the material and describes the modulation of the incident light by the material [71, 72]. The Stokes vector’s description of a light beam requires four parameters. The modulation relationship between the incident and outgoing light can be fully described using a 4 × 4 matrix [73]. This matrix is called the MM. When a beam of light is incident on objects, the polarization properties of the reflected or transmitted light generally change [74, 75]. Assuming that the Stokes vector of the incident light is $\mathrm{S}$, the Stokes vector of the outgoing light after interaction with the medium is ${\mathrm{S}}^{\text{'}}$, and the MM can express their relationship as follows:

$\left(\begin{array}{c}{S}_0^{\prime }\\ S_1^{\prime }\\ S_2^{\prime }\\ S_3^{\prime }\end{array}\right)=\left(\begin{array}{cccc}{m}_{00}& m_{01}& m_{02}& m_{03}\\ m_{10}& m_{11}& m_{12}& m_{13}\\ m_{20}& m_{21}& m_{22}& m_{23}\\ m_{30}& m_{31}& m_{32}& m_{33}\end{array}\right)\left(\begin{array}{c}{S}_0\\ S_1\\ S_2\\ S_3\end{array}\right).(8)$

That is,

${\mathbf{S}}^{\prime }=\text{M}\cdot \mathbf{S}\mathrm{.}(9)$

In practice, the MM can be obtained using some possible PSG and PSA combinations in Figure 2B2. A straightforward implementation includes setting the light source at three linear states and the right circular state. Finally, 16 intensity measurements are needed to calculate the full 4 × 4 MM. By removing the WPs in PSG and PSA, the configuration becomes the same as that of the Stokes imager (Figure 2B2). Then, by respectively rotating the directions of the two polarizers three times and obtaining a total of nine intensities, one can calculate a linear or incomplete MM with a size of 3 × 3.

In addition, according to the light sources’ properties or the selected optical elements, the configurations can be categorized into different types as follows:

(1) Depending on the existence of light sources, it can be categorized into “active illumination type” (with additional source) and “passive illumination type” (with nature light).

(2) Depending on PSG’s composition, it can be categorized into “unpolarized illumination type” and “polarized illumination type.” In particular, the “polarized illumination type” can be further divided into “linearly polarized illumination” and “circularly polarized illumination.”

(3) To match the type of illumination, the PSA will contain a polarizer with “linearly polarized illumination” or a polarizer together with a retarder if it is “circularly polarized illumination.”

Choosing the configuration types depends not only on the polarization parameters being used but also on the environment in reality. For example, in the atmospheric environment, “passive illumination type” with sunlight is recommended, while in underwater, undersea, or low-light surroundings, the “polarized active illumination type” is preferred. In addition, for different target scenes, one needs to switch between linear and circular polarized illuminations. In the following section, we introduce well-established polarimetric methods in accordance with the above-mentioned configurations for imaging in scattering media.

3 Models of Polarimetric Imaging in Scattering Media

3.1 Polarization Difference Imaging

3.1.1 Basic Model and Configuration

Inspired by the polarization-sensitive vision of some animals, PD imaging systems are proposed and developed to improve the visibility of objects in scattering media. This model is served as a common-mode rejection amplifier that can reduce the effects of background scattering and amplify the signal from targets where the PD magnitude is distinct from the background [41, 76]. Based on the images captured for the same scene at two orthogonal linear polarization states ($I_{\parallel }\left(x,y\right)$ and $I_{\perp }(x,y)$), the traditional PD system, proposed by Tyo et al. in 1995 [76], generates the PD and polarization-sum (PS) images as

$I_{PD}=I_{\parallel }\left(x,y\right)-I_{\perp }\left(x,y\right), I_{PS}=I_{\parallel }\left(x,y\right)+I_{\perp }\left(x,y\right) ,(10)$

where the PS image is equivalent to a polarization blind image obtained by a conventional imaging system. The PD image clearly depends on the choice of polarization axes, whereas the PS image does not. Such a relationship with the choice of axes can be used to minimize the effects of a partially polarized background in a PD image [42]. Notably, the scattered light is partially polarized and has the orthogonal and the same polarization components to the incident light at the same time. The performance of the PD method depends on the ratio of different components, which may be determined by the properties of scattering media, the incident polarization, the incident and observed angles, and so on.

Unlike Tyo’s PD model, which is based on the theory of common-mode rejection, Schechner et al. [32, 35] proposed a novel de-scattering method based on the atmospheric scattering model in Eq. 1, as shown in Figure 3. Similarly, this method captures two orthogonal polarized images composed of two unknown components (the scene radiance in the absence of haze and air-light). Because the air-light is usually partially polarized, these two images can be described by

$I_i\left(x,y\right)=\frac{D(x,y)}{2}+A_i\left(x,y\right), i\in [\parallel ,\perp ] .(11)$

FIGURE 3

FIGURE 3. Polarization-based atmospheric scattering model (reprint from OSA: Applied Optics [32], copyright 2003).

This model considers the natural polarization effects in imaging through the haze and builds the relationship of atmospheric properties, polarization properties, and imaging formalism. It does not require modeling the scattering particles’ size or the precise scattering mechanisms. In general, such methods based on Schechner’s model need to estimate two critical global parameters: air-light at infinity $A_{\infty }$ and DoP p. Then, the air-light and the transmittance can be calculated by

$\widehat{A}\left(x,y\right)=\frac{I_{\parallel }\left(x,y\right)-I_{\perp }\left(x,y\right)}{p}, \widehat{ t}\left(x,y\right)=1-\frac{\widehat{A}\left(x,y\right)}{A_{\infty }},(12)$

respectively. Here, $A_{\infty }$ and p rely on the choice of background or sky region $\text{Ω}$ and are usually calculated by

$p=\frac{I_{\text{Ω}}^{\parallel }-I_{\text{Ω}}^{\perp }}{A}, A_{\infty }=I_{\text{Ω}}^{\parallel }+I_{\text{Ω}}^{\perp } .(13)$

Finally, all these parameters are involved in the polarimetric model to obtain the recovered image as

$L(x,y)=\frac{I(x,y)-A(x,y)}{1-A(x,y)/A_{\infty }}=\frac{I^{\mathrm{\Vert }}(x,y)+I^{\perp }(x,y)-A(x,y)}{1-A(x,y)/A_{\infty }}.(14)$

The PD-based methods share the same configuration shown in Figure 2B1. The polarizer in front of the camera or other intensity detectors is a must to capture two orthogonal polarized images. In contrast, the polarizer behind the light illumination source is optional and depends on the actual scene, active or passive illumination.

3.1.2 Representative Methods

As the first attempt, Tyo et al. [41, 76] designed a special sample, an aluminum target containing two abraded patches with orthogonal directions, to verify the effectiveness of PD imaging systems. This sample is placed in a tank with inside dimensions of 30 × 30 × 15 cm³. This tank is filled with water and milk to simulate the scattering environments. PS and PD images after being transformed for optimal display are shown in Figure 4A. We can see that the abraded patches are clearly visible in the transformed PD image but practically invisible in the transformed PS image. The key factor contributing to the enhanced visibility of the two patches in the PD image is the common-mode rejection feature intrinsic to PD. Based on a series of validation, Tyo et al. [76] found that the PD imaging model is quite sensitive to intrinsically small signals and possesses valuable qualities of being passive, simple, and potentially fast.

FIGURE 4

FIGURE 4. The comparison results by (A) Tyo’s imaging method (reprint from OSA: Applied Optics [41], copyright 1996) and (B) Guan’s methods (reprint from OSA: Optics Express [42], copyright 2013). (C1) Imaging recovery example in air-environment (reprint from OSA: Applied Optics [32], copyright 2003), (C2) and (C3) underwater based on Schechner’s model (reprint from IEEE: Transactions on Pattern Analysis and Machine Intelligence [35], copyright 2008).

This method does not employ polarized illumination, which makes it constantly suffer from a reduced signal-to-noise ratio (SNR) because light reflected from the target and diffusive light backscattered from the turbid medium are superposed. Guan et al. [42] developed the traditional model and added a linear polarizer behind the light source to generate a polarized illumination. By measuring the co-polarization (parallel to the incident light’s polarization state) and cross-polarization (perpendicular to the incident light’s polarization state) images, they obtain an improved PD image, expressed as $I_{PDI}=I_{\parallel }-I_{\perp }$. Figure 4B presents the comparison between PS and PD images. The result shows that the proposed method significantly suppresses the background noise, and the image contrast is improved approximately 1.7 times [42].

However, the biggest challenge of the common-mode rejection-based method is that it cannot process scenes with complex conditions and objects because it does not consider the degradation mechanism in the scattering media. To solve this problem, Schechner et al. [32, 35, 77, 78] combined both polarized optics and the typical atmospheric scattering model and showed how the polarization tool boosts the vision clarity in scattering media. An example in the air environment is shown in Figure 4C1. The dehazed image has much better contrast and color, especially in the distant regions of the scene noted as the green forest and the red roofs [32]. Unlike such applications in the air environment, which rely on natural sun illumination, active illumination is necessary for underwater applications. In 2004, Schechner et al. [57] developed their original model for the de-scattering in turbid water by introducing a polarized illumination, as shown in Figure 4C2. The corresponding results are shown in Figure 4C3. From the results, we may observe that the objects (i.e., the iron box) are well restored in both contrast and color. However, we must point out that their model is based on three assumptions:

(1) Only the backscattering light/air-light is polarized, while the objects are unpolarized.

(2) The total attenuation for objects at infinity also equals inhomogeneous haze; that is, $t_{\infty }=0$.

(3) The multiple scattering (which affects the angular scattering distribution) is dominated by single scattering.

The first assumption does not apply to all practical cases because the object radiance could also contribute to polarization. When the depolarization degree of target objects is low, the light scattered or reflected by objects could contribute considerably to polarization. As a result, the previous methods may cause significant estimation errors. Huang et al. [59] found that the estimation produces negative values of t (as shown in Figures 5A–D) at the pixels corresponding to the low-depolarizing material if one assumes that the light emanated from objects in the scene is unpolarized. To solve this problem, they modified the traditional model by estimating the PD image of the target signal with feasible region fitting. Figure 5E shows that the recovered results reveal the details, which are not visible in the intensity images, regardless of the area corresponding to the objects having a high depolarization degree (plastic cube) or a low depolarization degree (metal coin).

FIGURE 5

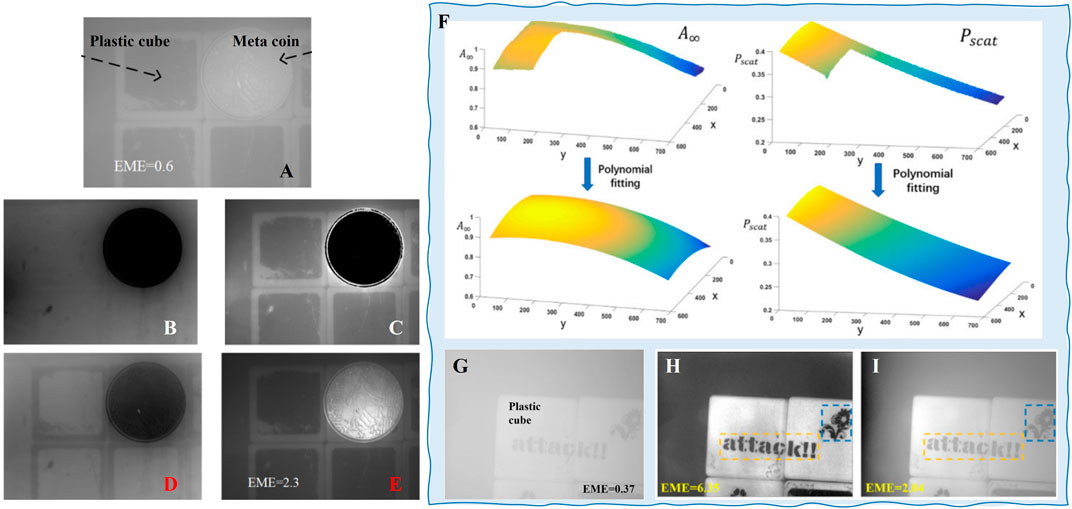
FIGURE 5. (A) Raw image. The deduced (B) transmittance and the recovered (C) radiance of the objects when the light emanating from objects in the scene is unpolarized. The retrieved (D) transmittance and (E) radiance of the objects by Huang’s method (reprint from OSA: Optics Express [59], copyright 2016). (F) The fitting spatial distribution of A_∞ and p. (G) Raw intensity image of the scene. (H) Recovered image by Hu’s and (I) Schechner’s methods [32] (reprint from IEEE: Photonics Journal [79], copyright 2018).

To overcome the limitation caused by the second assumption and improve the recovery performance in complex conditions, such as that in the non-uniform optical field, Hu et al. [79] proposed a method of retrieving the radiance of the object based on estimating the spatial distributions of the DoP and the intensity of backscatter light by extrapolation fitting. For example, the progress of fitting spatial distribution is shown in Figure 5F, and the corresponding results are also shown for comparison. It shows that this method reveals the details of the scene (in orange and blue rectangles) that decay significantly in the intensity image, and it has better quality than the image recovered by Schechner’s method because, under the non-uniform optical field, the DoP of backscatter A_∞, represented by p, on the right side of the background region is considerably higher than that on the left side. Suppose we recover the image with Schechner’s method, which considered the backscatter and its DoP to be constants; the transmittance can be considerably overestimated because of the improper estimations of A_∞ and p. In that case, it will lead to incomplete haze removal, thus a less clear recovered image [79].

The third assumption makes the traditional methods perform poorly in the case of dense haze [2, 39]. To overcome this issue, Li et al. [2] proposed to combine the polarization-based model and the computational processing method, such as histogram stretching (HS). Their main idea is to reduce the density of haze computationally. Specifically, this method stretches the histograms of the orthogonal polarization images while maintaining the polarization relation in between. Based on the processed orthogonal polarization images, the recovered image with higher quality can be obtained by the traditional polarimetric recovery method. Figure 6A presents an example in the dense turbid medium. The results show that the method significantly removes the scattered light and restores more details than Schechner’s method. This method opens a door and verifies the feasibility and effectiveness of combining computer vision and polarimetric methods for image recovery in scattering media. Although the HS method and Schechner’s polarimetric recovery method involved in this work are both old methods, the core idea of this combination has many perspectives. For example, Brosseau et al. [80] combined the low-pass polarization filter and DCP method and demonstrated the ability to significantly improve visibility and reduce runtime by a factor of about 50 for a 4K image. Figure 6B shows the natural imaging experiments at sea.

FIGURE 6

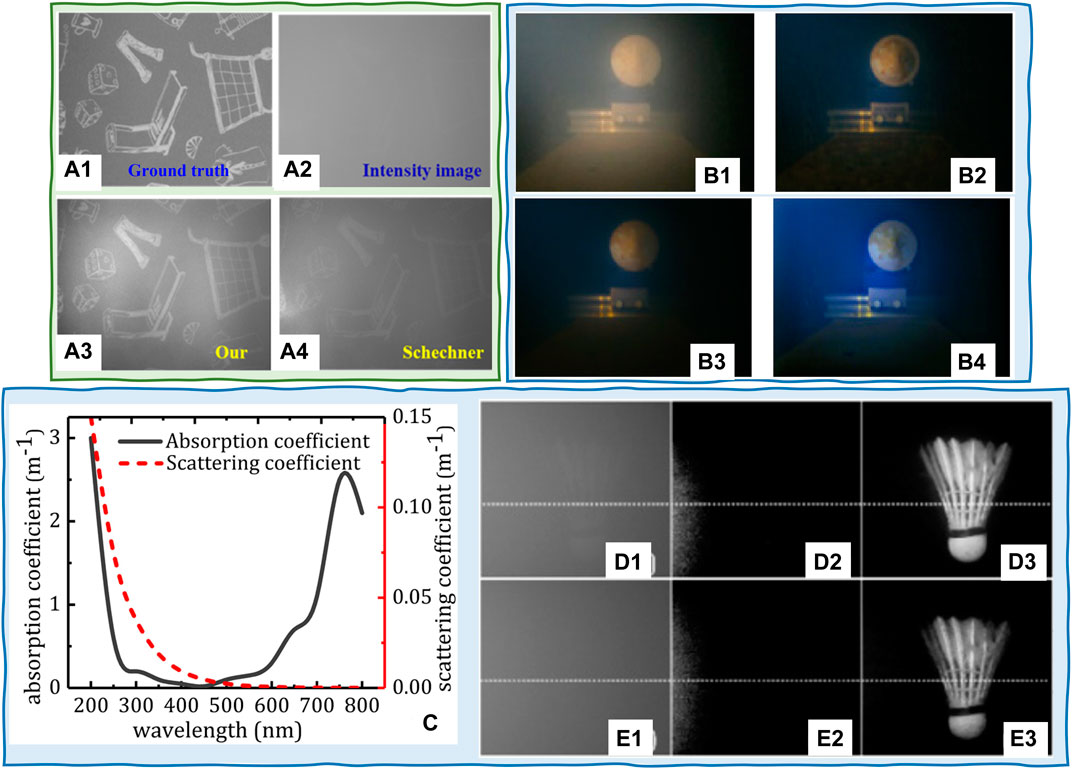
FIGURE 6. (A) (A1) Ground truth and (A2) the raw intensity image under water. Comparison of recovered scenes by using (A3) Li’s [2] (labeled as “Our”) and (A4) Schechner’s [32] methods (reprinted from Springer Nature: Scientific Reports [2], copyright 2018). Comparison of the recovered images when the raw image is (B1): using (B2) DCP, (B3) DCP with transmission map by soft matting, and (B4) Brosseau’s method (reprint from OSA: Optics Express [80], copyright 2019). (C) Measured absorption and scattering coefficients of pure seawater (reprint from OSA: Optics Letters [82], copyright 2018). (D1) and (E1) Directly captured images in 41 NTU and 70 NTU turbid water; (D2) and (E2) results from traditional polarization imaging method; (D3) and (E3) finally detected images by the Liu’s method (reprint from OSA: Optics Letters [82], copyright 2018).

It is worth noting that the wavelength of the active illumination also affects the imaging performance because the scattered light caused by both water and particles is wavelength-dependent. Smith and Baker [81] measured the absorption coefficients and scattering coefficients of pure seawater on the wavelength ranging from 200 to 800 nm and validated the dependence of scattering on wavelength. Liu et al. [82] plotted the measured absorption and scattering coefficients of pure seawater in the visible-light range, as shown in Figure 6C. Results show that scattering decreases with wavelength increase. Based on this wavelength-dependent fact, they proposed a wavelength-selection-based polarization imaging method to image through highly turbid water with red light illumination. This method makes a good balance between range and vision and can turn targets from “undetectable” into “detectable,” as shown in Figures 6D,E.

In fact, as one of the earliest polarimetric imaging techniques, the PD-based methods have received a great deal of attention for image dehazing/de-scattering in scattering media. This makes them enjoy fast development in terms of scientific research and engineering applications. However, the PD-based methods only contain two polarized images, which means that the freedom degree of information is limited to two. A complete polarization characterization of the scattered light and objects is helpful in further enhancing the recovery performance. Naturally, possible solutions include capturing more images and obtaining polarization parameters with high information freedom degrees, such as Stokes vector and MM [64, 83].

3.2 Stokes-Based Polarimetric Imaging

3.2.1 Basic Model and Configuration

As the information dimension (number of polarization sub-images) in Stokes vector configurations is higher (i.e., three for linear Stokes and four for complete Stokes) than two in the PD imaging system, the Stokes vector is more suited for characterizing polarization properties of scattered light. In contrast, as the two important parameters (AoP and DoP), which are highly relevant to the scattered lights’ properties [66, 84], can be directly deduced from the Stokes parameters, introducing Stokes analysis into the scattering removal is promising.

According to the fundamental model in Eq. 1, we know that the estimation of transmittance $t(x,y)$ depends on the scattering section $A(x,y)$, where the polarization property can be characterized by the Stokes vector ${\mathrm{S}}^A(x,y)$. Here, $S_0^A$ is the captured intensity corresponding to $A(x,y)$. In this way, Eq. 1 can be rewritten as

$\mathbf{S}\left(x,y\right)={\mathbf{S}}^D\left(x,y\right)+{\mathbf{S}}^A\left(x,y\right),(15)$

where ${\mathrm{S}}^D(x,y)$ denotes the Stokes vector related to the direct transmission D(x, y). If the target objects are assumed unpolarized, ${\mathrm{S}}^D(x,y)$ equals ${[D\left(x,y\right), 0, 0, 0]}^T;$ conversely, ${\mathrm{S}}^D\left(x,y\right)={[D\left(x,y\right),S_1^D\left(x,y\right),S_1^D\left(x,y\right),S_1^D\left(x,y\right)]}^T$, and the last three polarization parameters cannot be ignored. Based on the intensity measurements in different polarization states, we can estimate ${\mathrm{S}}^A$. Accordingly, we can obtain the $A_{\infty }$ and $t(x,y)$. In other words, the Stokes-based methods remove the veiling light by building the model between Stokes vectors (or the related polarization parameters) and ($A_{\infty }, t(x,y)$); that is,

$\left(A_{\infty }, t\left(x,y\right)\right)=f(P, P_l, P_c, \alpha ),(16)$

where the parameters in Eq. 16 (i.e., $P, P_l, P_c, \text{and} \alpha$) are defined in Eq. 7. The basic configuration of the Stokes-based methods can refer to that in Figure 2B2, and the specific choice depends on the used algorithm and realistic environments. According to the number of the used Stokes parameters, the methods can be classified as the linear-Stokes (LS) and the circular-Stokes (CS) based methods. In particular, for the LS-based methods, the PSA contains a fixed linear polarizer to generate polarized illumination, while the PSG contains a rotating linear polarizer. By adjusting the polarizer in PSG at least three times, we can obtain polarization sub-images. Based on these images, we can obtain a 1 × 3 linear Stokes vector. In contrast, in the CS-based methods, both PSG and PSA contain a linear polarizer and a retarder (e.g., QWP or liquid crystal variable retarders). By adjusting PSG’s states at least four times and obtaining the related intensity images, we can get a 1 × 4 complete Stokes vector. The difference between the two systems is whether the circular component of the Stokes vector (i.e., $S_3$) is considered.

However, the CS-based methods do not depend on the scattering angle and can survive more multi-scattering events than linearly polarized light [47, 85, 86]. Figures 7A,B present the DoP as a function of optical depth in water with different diameter particles, from which we can observe that the CP light maintains better polarization characteristics than linear polarization (LP) [47]. This property, the so-called circular polarization (CP) memory effect, can be explained by the Mie scattering phase functions of LP and CP. The phase function in the circular case possesses a marked forward lobule that permits the photons to propagate around the beam axis with a higher probability than in the linear case [87, 88]. Figure 1B presents the effects of size on the DoP. Results show that when the size parameter is large, the DOP for CP is greater than that for LP [85]. The characteristics in Figure 7B attest to the superiority of CS-based methods in dense turbid water or underwater environments with large-sized particles. Besides, Sara et al. [89] quantitively demonstrated the superiority of circularly polarized light in foggy environments. The experiments are carried out at CEREMA’s 30 m fog chamber under controlled fog density conditions. Figure 7C compares the ratio of CO channels (probe the prevalence of the input polarized light through the fog) with respect to the intensity signal as a function of the radius of the intensity profile of the source image for circular (solid lines) and linear (dashed lines) polarizations at three visibilities. The results imply that circular polarization has a larger signal-to-noise ratio in transmission at deeper layers, whereas the signal from the linearly polarized light carries some noise due to its higher depolarization ratio when propagating in scattering media.

FIGURE 7

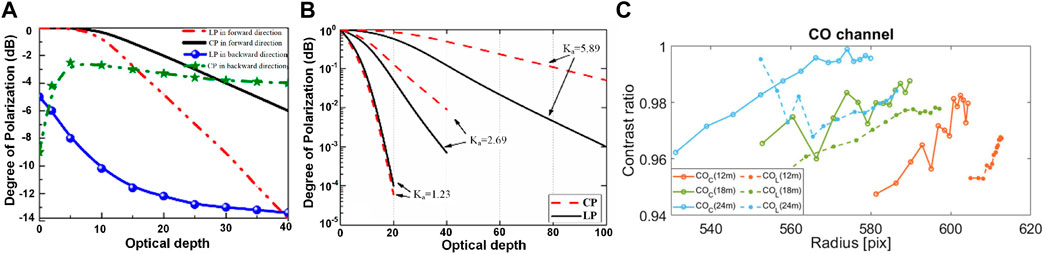
FIGURE 7. DoP as a function of optical depth in water with different diameter particles; (A) 2 μm particle; (B) the size parameter (ka) varies (reprint from Elsevier: Applied Sciences [47], copyright 2021). (C) Comparison of the ratio of Co channel with respect to the intensity signal as a function of the radius of the intensity profile of the source image for circular (solid lines) and linear (dashed lines) polarizations at three visibilities: 12, 18, and 24 m (reprint from OSA: Optics Letters [89], copyright 2022).

3.2.2 Representative Methods

To enhance the contrast, the two orthogonal polarized images in the traditional PD imaging model must be strictly selected to make the projections of the veiling light onto the two orthogonal axis directions equal [41]. However, this selection is time-consuming and inconvenient by rotating the polarizer mechanically, which is unsuitable for rapid imaging applications. Tian et al. optimized the traditional PD model to deal with this limitation. They proposed a modified PD imaging method (M-PDI) based on the Stokes vector analysis of the veiling light [90]. The output image after removing the veiling light is expressed by

$I_{M-PDI}=S_1\text{sin}2\alpha -S_2\text{cos}2\alpha ,(17)$

where $\alpha$ is the polarization orientation angle of the veiling light. The optimal value of $\alpha$ corresponds to the highest image contrast. A linear Stokes vector is calculated by capturing three images in polarizer’s directions of 0, 45, and 90° and searching the optimal $\alpha$. The significant advantage of this method is that the recovery performance can be updated automatically by the computation program when obtaining the Stokes parameters, which makes the implementation of PD imaging ideal for rapid imaging. Figures 8A–D show the recovery results of this method. The result shows the background noise is significantly suppressed, and the contrast of the target “Z” is significantly improved.

FIGURE 8

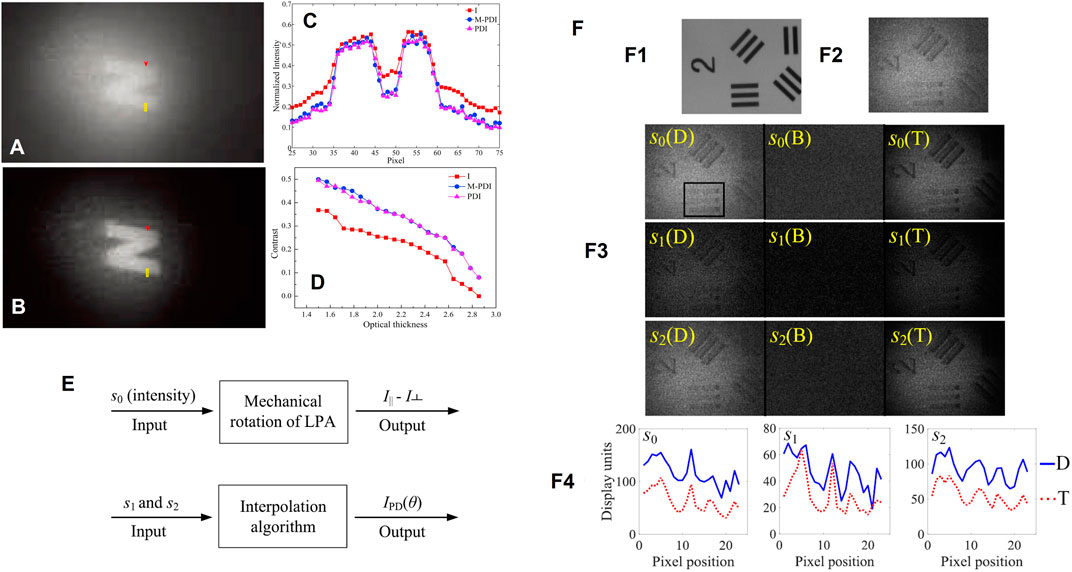
FIGURE 8. (A) Raw intensity. (B) Imaging results by M-PDI. (C) Intensity profiles by raw intensity, traditional PI, and M-PDI. (D) Contrast distributions of the object obtained by raw intensity, traditional PI, and M-PDI versus optical thickness (reprint from Elsevier: Optics and Laser Technology [90], copyright 2018). (E) Comparison of traditional and interpolation method-based PDI systems. (F) Images corresponding to target in (F1) clear water and (F2) turbid conditions. (F3) Stokes vector elements for the direct measurement (D), separated scatter (B), and target (T). (F4) Generation of numerical plots for the direct measurement and separated target (reprint from IOP: Journal of Physics D: Applied Physics [91], copyright 2018).

In 2018, Guan et al. [91] modified the above method and proposed another M-PDI method via the Stokes vector-based interpolation method. Figure 8E compares the traditional and the modified polarization filtering methods in PD imaging. The principle of this method is shown in Figure 8F [91]. From the image results, the object’s contrast is significantly enhanced, and the background noise is significantly decreased. More details of this method and the comparison with the traditional PD method can be found in [91].

Although the M-PDI method has partially addressed certain inherent drawbacks of the traditional model based on Stokes analysis, the determination of crucial parameters, based on the computational searching, makes the model performance unstable and sensitive to noise [38]. To overcome this issue, Liang et al. [38] further explored the relationship between the Stokes vector and veiling light and estimated the backscattering/air-light using the AoP analysis. Based on the three captured images on different polarizer directions (i.e., 0, 45, and 90°), the Stokes vector is calculated by the expressions in [38]

$\begin{array}{c}{S}_0=I\left(0\right)+I\left(90\right)\\ S_1=I\left(0\right)-I\left(90\right)\\ S_2=2I\left(45\right)-S_0\end{array} ,(18)$

where I(i) denotes the captured image when the direction of the polarizer is set to i degree. Then, we can calculate the intensity level of air-light as

$A_p=\frac{2I\left(0\right)}{{\text{cos}}^2\theta }-S_0,(19)$

where $\theta =1/2actan(S_2/S_1)$ denotes the AoP of air-light. Then, the output with a clear vision can be obtained by the typical physical model in Eq. 14. In this method, the noise in the sky area can be eliminated without any imaging-processing algorithm, which makes this method much more convenient and reliable in practical applications. Based on the technique, Liang et al. developed a series of algorithms to further enhance the recovery performance. For example, in 2015, they optimized the estimation of critical parameters (e.g., AoP and the intensity level of the air-light) to accommodate dense haze and achieved a 74% enhancement in the range of visibility (ROV) [43]. In 2016, as the infrared radiance has a better capacity for traveling through the haze, they modified the model by merging visible and infrared images. The ROV was thus improved by 100% [43]. In 2021, they introduced low-pass filtering into the AoP-based polarimetric imaging model and overcame the drawback of “noise sensitivity” in estimating the AoP value. The final imaging performance of these methods is shown in Figure 9. We can observe from the results that the faint information in hazy images is well preserved, and the contrast of the recovered image is increased significantly [92].

FIGURE 9

FIGURE 9. Recovery performance for Liang’s methods in Refs. (A) Ref1 (reprint from Chinese Laser Press: Photonics Research [38], copyright 2014). (B) Ref2 (reprint from OSA: Optics Express [43], copyright 2015). (C) Ref3 (reprint from OSA: Optics Express [40], copyright 2021). (D) Ref4 (reprint from OSA: Applied Optics [56], copyright 2016).

Such works based on AoP analysis accelerate the development of polarimetric imaging in specific scattering media. However, all these methods are based on the linear Stokes vector, which only includes three parameters and merely reflects the interaction of target objects with the linearly polarized light without considering the response to circularly polarized light. In particular, in some special scattering media requiring active illumination, the circularly polarized light tends to maintain its original polarization property better than the linearly polarized light, namely, the “circular polarization memory” effect [93, 94]. Therefore, using circularly polarized light can improve the recovery performance in dense turbid media more than linearly polarized light. Therefore, Hu et al. [46] proposed a new polarimetric image recovery method in dense turbid media with the illumination light featuring circular polarization. In this method, the active illumination is modulated by a polarizer and an additional retarder to generate circularly polarized light. The estimated Stokes vector is decomposed into linear polarization, circular polarization, and un-polarization parts as follows:

$\mathbf{S}={\mathbf{S}}_{l-\text{polarized}}+{\mathbf{S}}_{c-\text{polarized}}+{\mathbf{S}}_{\text{unpolarized}},(20)$

where the subscripts of l and c indicate the linearly and circularly polarized light, respectively. According to this decomposition, the linear and circular components of the veiling light are removed by solving the DoLP and DoCP of the backscattering. Figure 10A shows the difference between these two degrees of polarization, while the circular one is always missed in most methods. This is the first polarimetric imaging system and algorithm considering circularly polarized lighting. The recovered result and its comparison with the linear one are as shown in Figure 10B and further evidenced by experimental results for the scenes with different polarization properties, for example, a rough wooden board with patterns and words on its surface and the non-flat plastic toy.

FIGURE 10

FIGURE 10. (A) Intensity image of the scene, DoLP, and DoCP. (B) Recovery comparison for methods in [46] and [32] (reprint from OSA: Optics Express [46], copyright 2018). (C) Flowchart of underwater polarization reconstruction utilizing polarimetric calculation method of the global pixel. (D) Comparison results of three classical restoration methods (PD: polarization difference [41], ML: Schechner’s method [35], VLC: Vanderlugt correlator) and this method in different turbidity (reprint from IEEE: Photonics Journal [52], copyright 2021).

With the improvement in the theoretical model, the trend of Stokes-based polarimetric imaging in scattering media continues to optimize the estimation of key parameters and render more accurate values, such as the polarization information of object and scattering signals. For example, Jin et al. [52] proposed a scattering removal method from the perspective of global estimation of polarization information to realize polarimetric calculation of global pixels for automatically estimating the DoP. This global pixel calculation is accomplished by utilizing the gradient prior information of the total intensity image. Figure 10C shows the flowchart of this method, and (Figure 10D) shows the comparison results of three classical recovery methods and this method in different turbidity [32, 41, 82]. Apparently, as opposed to methods with the assumption of constant DoP of target light, this method can retrieve the DoP of the target light of each pixel in the image. As a result, it has a better performance of recovering the scene’s details even though the water is turbid [52].

In short, the Stokes-based methods outperform the PD-based methods because the Stokes vector renders more useful polarization information, such as DoP and AoP, which are closely related to the backscattering/veiling light caused by the existing particles. Improving the information dimension and estimating key parameters are two effective ways to boost imaging performance. However, we must remember that, unlike MM, the Stokes vector is not a complete polarization characterization [63, 95]. Therefore, the trial based on the MM has become the preferred approach to improve the information dimension, an exciting solution to enhance imaging performance in scattering media further.

3.3 MM-Based Polarimetric Imaging in Scattering Medium

3.3.1 Basic Model and Configuration

Unlike the Stokes vector, which is usually used to characterize the polarization properties of the light beam, the MM contains all the polarization information of the target materials. Therefore, the MM is always applied to distinguish different materials [8, 96–98] and 3D physical imaging [99–101]. According to the basic model in Section 2, the received signal or images can be classified into the target and scattered signals. The Stokes-based methods build the relationship between the Stokes vector and the scattered light. However, they fail to distinguish objects with different polarization properties. These methods are unsuitable for objects whose reflected light has a similar Stokes vector with the backscattering light.

With the information provided by MM, the operational space for polarization image processing is greatly improved, making it possible to distinguish objects in a high degree of freedom for the polarization information [102]. In addition, the MM-based configuration opens the door to modulate the incident illumination with a significant polarization space. In other words, the MM-based scattering suppression imaging technology modulates the illumination and analysis parts simultaneously. The basic configuration of MM-based methods is as shown in Figure 2B2, and one can remove the WPs in accordance with the type of MM (incomplete or complete) that is desired.

3.3.2 Representative Methods

The MM-based polarimetric suppression method for the imaging in scattering media is mainly based on modulating the polarization state of the active illumination. The earliest attempts focused on imaging linear MM and required nine intensity images [44, 45, 103]. In the related configurations, the WPs in PSG and PSA in Figure 2B2 are removed, and the polarizers in PSG and PSA are rotated to three different positions to capture nine images, respectively.

In 2019, Guan et al. [44] found that the illumination polarization angle and the MM difference between the medium and the object could affect the SNR of recovered results obtained by the rotation orthogonal polarization imaging method. They designed a linear MM-based polarimetric method to precisely control the illumination polarization angle and achieve a rapid imaging process. In 2021, Wang et al. [45] plotted backscattered light and target reflected light in the point cloud diagram in Figure 11A by establishing a differential imaging model. According to Figure 11A, on the premise that the angle between the polarizer’s direction and the backscattering light’s polarization direction is 45°, the backscattering light can be removed by the PD method to achieve scattering suppression. By analyzing the principle of polarization difference, the output result under ideal conditions is given by

$I_{out}\left(x,y\right)=\left(I_{P{B}_{\parallel }}\left(x,y\right)-I_{P{B}_{\perp }}\left(x,y\right)\right)+\left(I_{P{T}_{\parallel }}\left(x,y\right)-I_{P{T}_{\perp }}\left(x,y\right)\right)=\left|I_{PT}\left(x,y\right)\right|\cdot \sin \left(2\theta \right),(21)$

where $I_{PB\parallel }(x,y)$, $I_{PB\perp }(x,y)$, $I_{PT\parallel }(x,y)$, and $I_{PT\perp }(x,y)$ represent the horizontal and vertical projection of the polarized part of the backscattering and target light, respectively. It can be seen from the above formula that the output result of the differential image will be affected by the polarization angle between the target and backscattered light. Therefore, by modulating the incident light and changing $\theta$, the performance of the traditional PD method can be improved. Figure 11B presents the comparison results of this method with the traditional PD method and other classical methods. We see that the modulation of incident light has a significant influence on polarization differential scattering suppression.

FIGURE 11

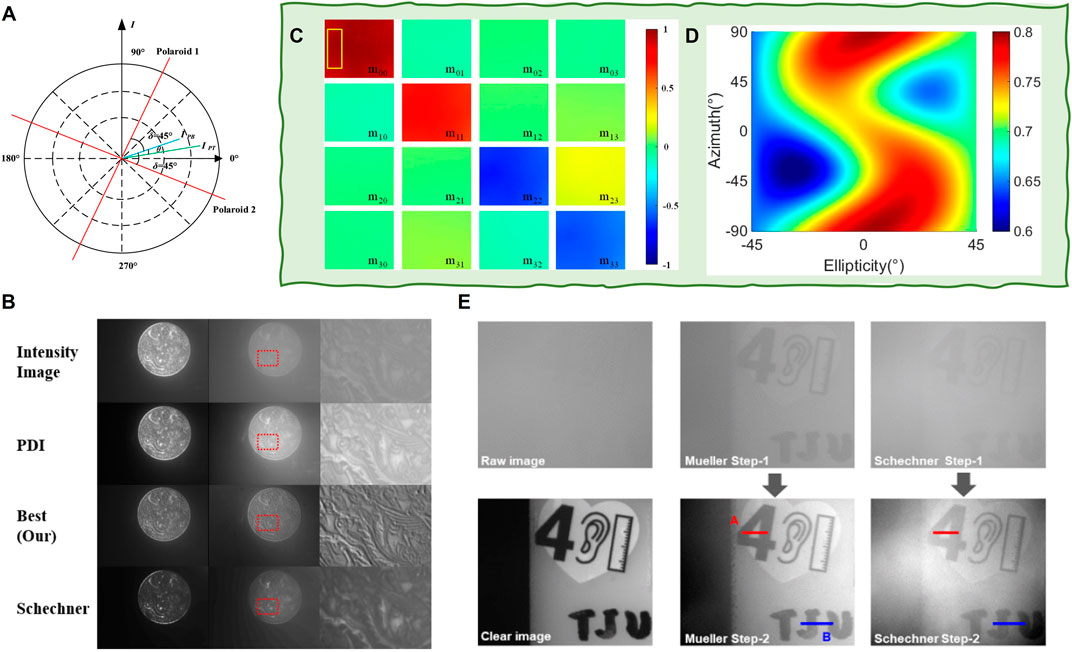
FIGURE 11. (A) Principal diagram of polarization difference method based on MM. (B) Comparison results of scattering suppression by different methods and different scattering medium concentration, where Wang’s method is labeled by “Best (Our)” (reprint from Elsevier: Optics Communications [103], copyright 2021). (C) MM image of the scene in turbid water. (D) Variation of DoP with the azimuth and the ellipticity of PSG. (E) Underwater image restoration results and the histograms in different turbidities of water (reprint from IEEE: Photonics Journal [45], copyright 2021).

In other work, the authors disregard the traditional PD method and instead directly process the image according to the MM⁴⁵. By modulating the polarization state of the incident active illumination light, the DoP of the backscattered light is directly maximized, thus achieving the best suppression of the backscattered light. Based on the configuration in Figure 2B2, one can obtain any specific polarized incident light by adjusting the PSG. The Stokes vector of the incident light ${\mathrm{S}}^{\mathit{in}}$ can be expressed by its DoP value P, azimuth $\alpha ,$ and ellipticity $\epsilon$ as follows:

${\mathbf{S}}^{in}={\mathbf{S}}_0^{in}{\left[\begin{array}{cc}1& P{\mathrm{S}}^{\text{T}}\end{array}\right]}^{\text{T}}=S_0^{in}\left[\begin{array}{c}1\\ P\cos 2\alpha \cos 2\epsilon \\ P\sin 2\alpha \cos 2\epsilon \\ P\sin 2\epsilon \end{array}\right],(22)$

where $S_0^{in}$ denotes the intensity of the illustration light and $\mathrm{S}=\left[\begin{array}{ccc}{S}_1^{in},& S_2^{in},& S_3^{in}\end{array}\right]$ is the normalized Stokes vector. When the DoP of backscattered light $P_{back}$ is higher, more backscattered light can be blocked by the PSA. Therefore, to suppress the backscattered light optimally, one must maximize the DoP of the backscattered light by choosing an optimal set of azimuths and ellipticities $\left({\alpha }_{opt},{\epsilon }_{opt}\right)$. This optimization problem can be expressed by

$\left({\alpha }_{opt},{\epsilon }_{opt}\right)=\begin{array}{cc}\underset{\left({\alpha }_{opt},{\epsilon }_{opt}\right)}{\text{arg}}& \max \left\{P_{back}\left(M,\alpha ,\epsilon \right)\right\}\end{array},(23)$

where

$P_{back}\left(M,\alpha ,\epsilon \right)=\frac{1}{{{\displaystyle \sum }}_{j=0}^3{M}_{0j}{s}_j^{in}\left(\alpha ,\epsilon \right)}{\left\{{\displaystyle \sum }_{i=1}^3{\displaystyle \sum }_{j=0}^3{\left[M_{ij}{s}_j^{in}\left(\alpha ,\epsilon \right)\right]}^2\right\}}^{\frac{1}{2}}.(24)$

Figure 11C presents the MM image of the target scene, and the corresponding optimal set of azimuths and ellipticities can be found by a global search shown in Figure 11D. The imaging results and the comparison with the traditional PD method are shown in Figure 11E. The results demonstrate that this method is stable and can be implemented with any digital image processing to achieve a more scattering suppression performance.

In 2022, Liu et al. [104] developed an MM-based de-scattering method and introduced the depolarization (Dep) index into the de-scattering algorithm. Dep is derived from the MM and is defined by

$De{p}_M(x,y)=\frac{\sqrt{\text{tr}\left(M^{T}M\right)-m_{00}^2(x,y)}}{\sqrt{3m_{00}^2(x,y)}}.(25)$

By studying the backscattering distribution in different NTU turbidities, it is found that the background intensity correlates linearly with Dep in a remarkable way, as shown in Figures 12A–B. Therefore, Dep is used to characterize scattering media. By quantifying the light attenuation with the transmittance map, a clear vision of targets can be recovered using the information of scattering media. An example of recovery performance is shown in Figures 12C1,C2. The results demonstrate that the image contrast is significantly improved after recovery. In particular, the paper stripe and metal ruler are both clearly visible. From the zoomed-in view in Figures 12C3,C4, the ruler in the intensity image blurs, especially the tick mark and edges. In contrast, the edges of the ruler are visible after recovery, even with distinguishable tick marks.

FIGURE 12

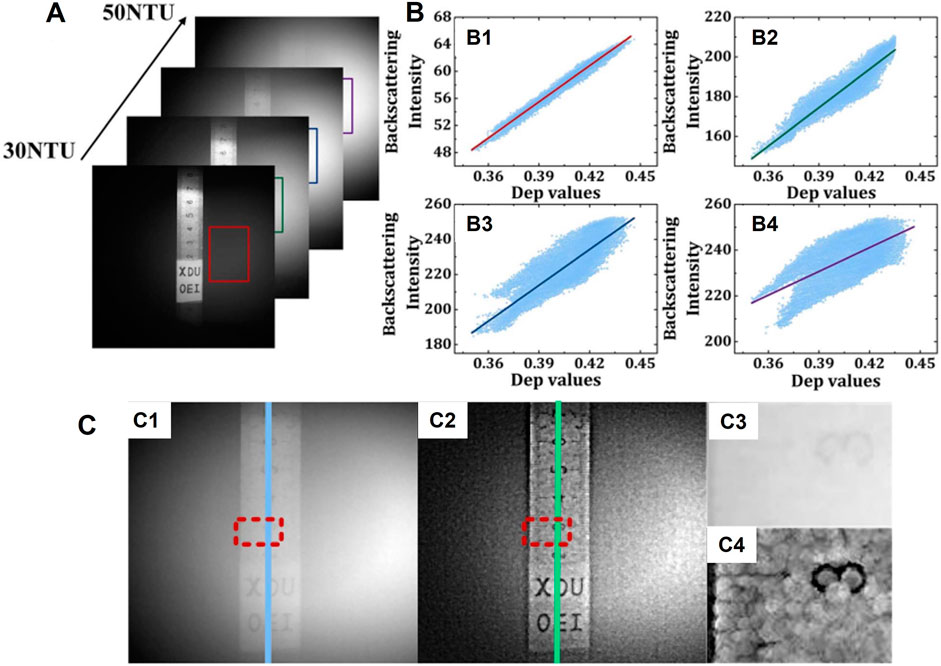
FIGURE 12. (A) Four measured intensity images at different values of NTU. (B1–B4) Fitting results of backscattering intensity as a function of Dep values. (C1) Intensity image; (C2) recovered image with the proposed de-scattering method; (C3) and (C4) the zoomed-in view of the region of interest in (C1) and (C2) marked out with red rectangle (reprint from Chinese Laser Press: Chinese Optics Letters [104], copyright 2022).

The MM-based methods have many advantages. For example, they provide more helpful information by increasing the degree of freedom for polarization and making a clear differentiation among objects with similar intensity appearance but different polarization properties. However, it should be noted that a very scarce amount of works, less than five to the best of our knowledge, has placed the focus on MM-based de-scattering. Indeed, making full use of the MM decomposition and other MM-related parameters is promising and needs more attention.

3.4 Learning-Based Polarimetric Imaging

As discussed in Section 2, one of the dehazing methods is based on a physical model where prior knowledge is applied to extract physical parameters related to the scattering media and then recover the targeted signal. In this case, the estimation accuracy of these key parameters determines the final performance. Therefore, almost every developed method strives to optimize the accuracy of parameter estimation to make it as close as possible to the physical values in the scene. However, the optimizations come at the cost of increased computation complexity and reduced universality. In contrast, the methods not directly based on a physical model aim to improve the image quality by enhancing the image contrast and the difference between different image structures. This kind of method handles different scenarios indiscriminately but can perform poorly, especially with complex conditions.

The deep learning- (DL-) based method is data-driven and thus capable of extracting the hidden relationship and physical properties between/in the raw and target data. This makes it a promising choice for de-scattering. In some ways, the traditional “end-to-end” network corresponds to methods that are not based on the physical model, while the “physical embodiment” network is based on physical models. The following section introduces learning-based polarimetric imaging in scattering media from the basic concepts to well-established applications.

3.4.1 Basic Concepts of the DL and Neural Network

In 1943, psychologist Warren McCulloch and mathematical logician Walter Pitts proposed the concept of the artificial neural network and the mathematical model of the artificial neuron, thus prompting the era of artificial neural network research [105]. They abstracted the entire working process of neurons into the model shown in Figure 13A. In the model, input data $x_i$ are given to the network processed with weights and bias parameters. Then, a nonlinear activation function $\phi (\ast )$ is applied to obtain the final output $Y$. The whole process is called forward propagation. The weights $w_i$ and bias $b$ are the parameters to be learned, which can be seen as the memory of the neural network. The final output is the prediction result obtained by the network according to the input data, which may be different from the ground truth. Therefore, it is necessary to calculate the deviation between the predicted result and the ground truth, or the network loss, to update network parameters. The process of updating weights is usually via some variant of a gradient descent algorithm. The training process of the network repeats the forward propagation and backpropagation process until the loss is minimal so that when we put in input data, we obtain an output nearly the same as the ground truth [106].

FIGURE 13

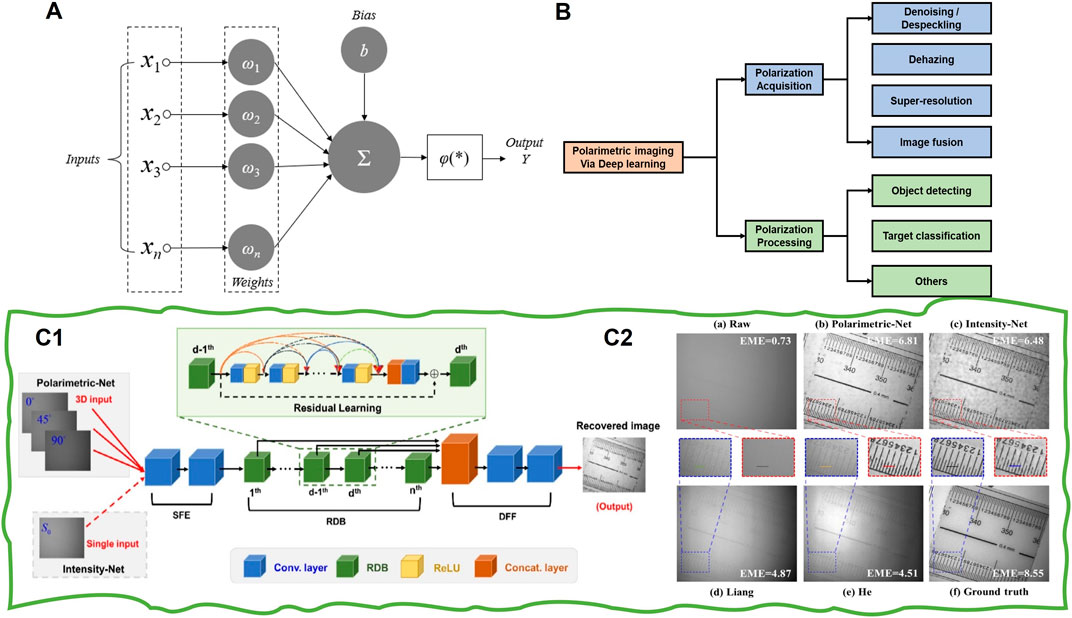
FIGURE 13. (A) Schematic diagram of neural network structure. (B) Classification of polarimetric imaging via DL. (C1) The architecture of polarimetric dense network (PDN) and (C2) recovered image (reprint from Elsevier: Optics and Lasers in Engineering [50], copyright 2020).

To boost the network performance and suitability for various tasks, different advanced network structures have been developed, such as LeNet [107], AlexNet [108], GoogleNet [109], ResNet [110], and DenseNet [111]. In the field of computer vision, learning-based solutions have become the hottest topic. Particularly, various learning-based works focus on improving imaging quality in scattering media. For example, Chen et al. [112] proposed an “end-to-end” dehazing network. In their review, a generative adversarial network (GAN) is used to realize end-to-end image dehazing. The work focuses on solving the problem of grid artifacts and has greatly improved the indexes of peak signal-to-noise ratio (PSNR) and Structural Similarity Index Measure (SSIM). In 2019, Pan [113] proposed a physics-based feature dehazing network for image dehazing network. In contrast to most existing end-to-end trainable network-based dehazing methods, they explicitly considered the physical model of the hazing process in the network design and removed haze in a deep feature space. However, all these de-scattering methods are based on a single intensity image. In recent years, DL has been successfully applied to polarimetric imaging [49, 66, 114]. Such works develop mainly from two parts: polarization acquisition and polarization processing. The related applications include denoising, dehazing, image fusion, targets detection and classification, and super-resolution (a brief classification is shown in Figure 13B). In the following, we focus on the learning-based de-scattering works.

3.4.2 Representative Methods

The currently popular neural network ResNet was first proposed by He et al. [110] in 2015 and is widely used in many scenarios of DL. This structure can solve the problem of gradient disappearance when the network is deep. Huang et al. [111] proposed DenseNet in 2017, which can alleviate gradient disappearance, strengthen feature propagation, encourage feature reuse, and significantly reduce the number of parameters through the dense connections between layers. Based on these two networks, Hu et al. [50] first proposed a polarimetric dense network (PDN) and applied it to underwater polarization image restoration. The network structure of PDN is shown in Figure 13C1. This network includes three main components (shallow feature extraction, residual dense block, and dense feature fusion) to deeply extract shallow features of polarization information from three polarization images and then fuse them. The loss function used is defined as

$l\left(\text{Θ}\right)=\frac{1}{2N}{\displaystyle \sum }_{i=1}^N\left|\right|I_i^{pred}(x,y;\text{Θ})-I_i^{gt}{(x,y)}_F^2\left|\right|,(26)$

where $I_i^{pred}(x,y)$ and $I_i^{gt}(x,y)$ refer to predicted and ground truth images, respectively, with their polarization information. Because the polarization is considered, the recovered image in Figure 13C2 has more detailed features than the intensity image used alone. Besides, there are more artifacts in the recovered result by “intensity-Net” than “Polarimetric-Net.” These results demonstrate that embedding polarization information and constraints into the network helps improve performance.

In 2021, Zhang et al. [115] studied how to optimize the network structure and loss function to improve the suitable model performance. They found that, by adding polarized information along with the light intensity information to the model at the very front of the model structure, a better-recovered image can be obtained. The model structure proposed can be used for image recovery in turbid water or other scattering environments. It should be noted that both the above methods are “end-to-end” and depend on paired training data. Although the application of neural networks has significantly improved image de-scattering performance compared with traditional methods, its disadvantages are also easily recognizable. DL networks, especially end-to-end networks, have poor interpretability as the neural networks are more like a black box. It is difficult to explain and understand the inner operation process. To solve this problem, Ren et al. [116] integrated the polarimetric imaging model with the DL-based method and proposed a lightweight network structure, which can restore underwater images with different turbidity. This method makes the image restoration through neural networks more in line with the physical principle and achieves good results.

To complete the physical meaning in the network and reduce the degree of freedom of the model, Zhou et al. [117] proposed a generalized physical formation model of hazy images and a robust polarization-based dehazing pipeline without the assumptions in traditional polarimetric methods. The designed network includes sub-networks to estimate different parameters, as shown in Figure 14A. The network divides the whole image de-scattering process into two steps. At the end of each step, semantic and contextual information is used to refine the output of the corresponding sub-network. This method provides a new perspective for the fusion of physical models and neural networks. However, the generalization ability on the real dataset is still limited for utilizing computer-synthesized datasets. In order to get rid of the paired data’s dependence and make the learning-based methods applicable in practice, the unsupervised model-based and untrained model-based solutions are proposed. For example, Yang et al. [118] designed an end-to-end unsupervised generative network to remove the backscattering light, as shown in Figure 14B1. This method produces an adversarial loss with the discriminative network to improve the performance. In addition to using GAN to remove the backscattering light, they also modified the underwater imaging model based on several physical priors. The DoP of backscatter is the same as that of background light. This new model can be applied in a variety of non-uniform optical fields. Figure 14B2 shows its recovered results by different methods. Besides, they also verified that this unsupervised solution could adapt to the non-uniform optical field with different incident angles. In 2021, Zhu et al. [119] proposed a non-GAN unsupervised method by combining the polarization physics model and DL technology. Figure 14C1 presents the network’s architecture. Rather than using atmospheric scattering model directly, they input the polarimetric hazy images into U-Net to obtain the corresponding de-scattered images, added haze to the output of the network through the model proposed by Liang et al. [43], and finally calculated the loss between the generated hazy images and corresponding captured images. Figure 14C2 presents a visual comparison among different de-scattering methods. From the results, we may observe that the background area with the homogeneous scattering effects is removed using this method, but the object information is preserved. In short, the unsupervised image de-scattering through U-Net does not need paired datasets or even haze-free images.

FIGURE 14

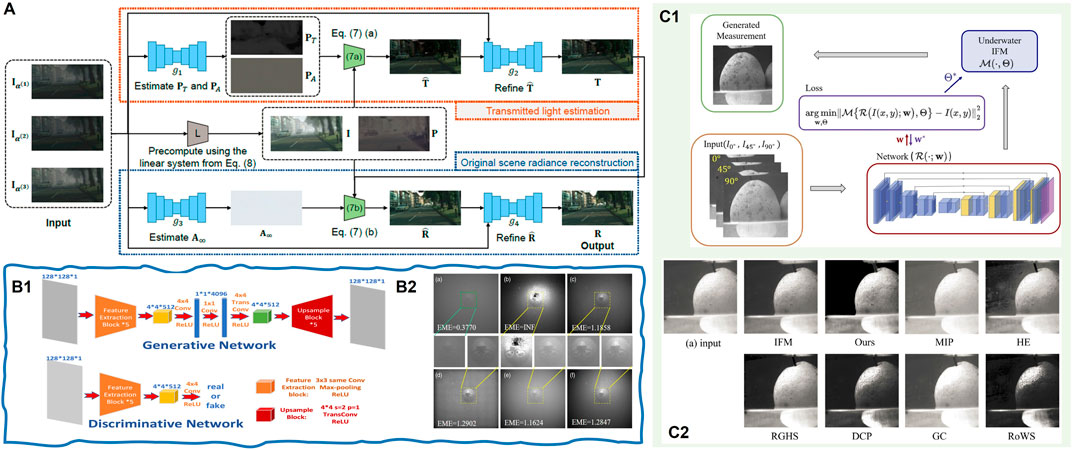
FIGURE 14. (A) Schematic diagram of neural network structure proposed by Zhou et al. (reprint from MIT Press: Advances in Neural Information Processing Systems [117], copyright 2021). (B1) The architecture of the GAN-based polarization network and (B2) the recovered images (reprint from OSA: Applied Optics [118], copyright 2021). (C1) The architecture of untrained network in [119] and (C2) visual comparison among different de-scattering methods: our method, i.e., Zhu’s method [119], IFM, MIP [120], HE [121], RGHS [122], DCP [3], GC [123], and RoWS [124] (reprint from OSA: Optics Express [119], copyright 2021).

All the above works can be considered strong evidence that learning-based, especially the physics-embedded learning-based method, can resolve the limitations of traditional methods and provide an irreplaceable solution for imaging tasks in scattering media. It should be noted that the reported DL models and research largely depend on a particular dataset, and it is hard to guarantee similar performance from other datasets. This is where this method falls short if compared with other common traditional models. Nevertheless, we firmly believe that DL techniques hold a crucial place in this field.

3.5 Polarimetric Imaging Through Scattering Tissues

In the above sections, we have reviewed the polarimetric imaging through such scattering media as fog, haze, and turbid water. Meanwhile, biological tissues as another important scattering media and the related polarimetric imaging techniques have gained great attention in the biomedical field. To be more specific, the biological tissues contain fiber-like macromolecules (e.g., the collagen fibers in the skin and tendons, muscle fibers, and myofibrils in skeletal muscles), which exhibit a certain degree of structural anisotropy and anisotropy in dielectric response. These properties manifest themselves via birefringence [125, 126], which can be observed using polarization measurement or polarimetric imaging [127]. For example, many works have shown that the depolarization, retardance, and diattenuation induced by the birefringent tissues can be considered indicators to assess macromolecules’ microstructure, thus being conducive to diagnosis and the study of pathological alterations [128, 129]. However, the scattering (especially the multiple scattering) in thick tissues often results in the depolarization of light, which makes detection of the remaining information-carrying polarization signals challenging. Therefore, various polarimetry or polarimetric imaging techniques have been developed to maximize measurement sensitivity to assist in analyzing useful tissue information [97, 127, 130, 131].

In fact, the polarimetric imaging through the biological tissues often shares the same basic polarization configurations as mentioned in Section 2: polarization difference, Stokes vector, and Mueller matrix polarimeters. However, the focus and methods of the related research are significantly different from those in Section 3. Here, the main focus is to study the properties of scattering media, namely, the tissues themselves. For example, the emphasis will be placed on modeling the polarized light transport and the depolarization of multiply scattered light in tissues by both Monte Carlo simulation and the real experiments [132–135] or the study of the mechanism of depolarization and its dependence on the different tissue or media parameters (e.g., the density, size, distribution, shape, and refractive index) [131, 136–140]. On the contrary, for the reviewed physical degradation mode-based polarimetric recovery methods in Section 3, the properties of scattering media do not directly impact the recovery performance. This is because these techniques aim to remove the scattered light (i.e., A(x, y) in Eq. 1) and recover the direct transmission (i.e., D(x, y) in Eq. 1). The critical step is to calculate media transmittance (i.e., t(x, y)) and the intensity level of scattered light (i.e., $A_{\infty }$) by estimating polarization properties (i.e., DoP and AoP). In short, the recovery performance mainly relies on the accuracy of the estimation polarization properties. More details can be found in the related works in Refs. [130, 141].

4 Conclusion and Outlooks

In this review, we have presented an overview of the polarimetric imaging methods through scattering media from the perspectives of the basic model, imaging system, and representative works. Table 1 provides a brief summary and comparison across these methods.

TABLE 1

TABLE 1. Summary of polarimetric de-scattering methods.

Thanks to the property of polarized light propagated in scattering media, polarimetric methods outperform traditional intensity-based methods, particularly under complex conditions such as high-density turbid media, non-ideal illumination environments, and scenes with multi-material objects. We have demonstrated that the increase in polarization information dimension can constantly improve the imaging performance and the polarimetric methods. However, the complexity in both the imaging systems and computations is inevitably increased. It is worth noting that to achieve the balance between performance and complexity, advanced optical equipment and innovation in imaging systems must come into play. In addition, the demand for practical applications will certainly drive the development of polarimetric imaging methods. As such, we propose several topics of interest for future studies:

4.1 Multispectral-Polarization Systems and Fusion Algorithms

The combination of multi-spectral and polarization is often applied in the field of remote sensing [142, 143]. They found that more complex and accurate indices and models can be developed to reveal more information when the polarization information is supplemented [144, 145]. Therefore, combining multi-spectral and polarization into an integrated imaging system and fusing multi-parameters are two possible directions to enhance the image quality in complex scattering media.

As mentioned in Section 3, the long-wave light is more robust for transmitting through the haze than visible light. Another powerful example is using a long-wave infrared DoFP polarization in road detection, as shown in Figure 15A [146]. The fusion of short and long wavelengths effectively increases the visual range at the cost of decreased resolution. Therefore, an optimal tradeoff is helpful for this solution [147, 148]. Besides, in the realistic underwater scene, seawater appears in different colors because the scattering and absorption depend on both the wavelength and the physical properties of the particles. It seems that a tunable wavelength source will make the imaging system have a wide range of application scenarios. On the contrary, the existing polarimetric methods mainly focus on recovering information only related to the intensity, that is, “to see it.” However, the most significant advantage of polarization is that it can see what human eyes cannot (in the intensity condition), such as information related to DoP [149], AoP [150], or the index of polarization pure (IPP) [151, 152]. These parameters help distinguish different materials and different optical responses. For example, the DoP and AoP have been successfully applied in self-driving. They can provide additional information in complicated meteorological environments (fog and rain), as shown in Figure 15B [153].

FIGURE 15

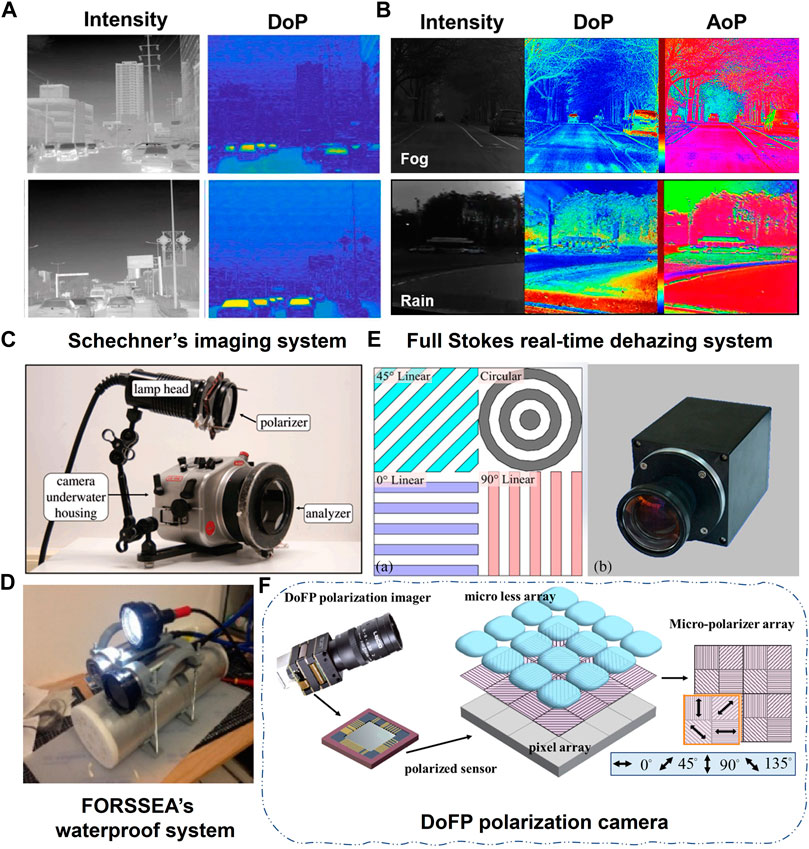
FIGURE 15. (A) Images by LWI-DoFP camera (reprint from Elsevier: ISPRS Journal of Photogrammetry and Remote Sensing [146], copyright 2021). (B) Polarimetric imaging in the field of self-driving [153]. Different systems of polarimetric underwater imaging were developed for realistic applications. (C) Schechner’s imaging system (reprint from IEEE: Transactions on Pattern Analysis and Machine Intelligence [35], copyright 2008). (D) FOREEEA’s waterproof system (reprint from OSA: Optics Express [80], copyright 2019). (E) Full Stokes real-time dehazing system (reprint from OSA: Applied Optics [34], copyright 2017). (F) DoFP polarization camera (reprint from OSA: Optics Express [49], copyright 2020).

Fusing multiple polarization parameters and intensity into a frame, further increasing the information dimension, may open a new door for the imaging in scattering media and take a transform from “could be seen” to “see far” and from “see clearly” to “see more.”

4.2 Real-Time, Real-Scenario, and Robust (3R) Solution for Polarimetric Imaging

Most reported polarimetric imaging methods for scattering media have been demonstrated under laboratory conditions. Although some were implemented in real-life scenarios, the imaging process was static, and the analysis was completed afterward. To achieve real-time, real-scenario, and robust (3R) solutions for polarimetric methods, advanced algorithms for optical information processing need to be developed and an improved collaborative imaging system is also required.

Schechner et al. first developed an underwater polarimetric imaging system, as shown in Figure 15C. This system is designed based on their basic PD imaging model and performs better in real-life scenarios by combining necessary post-processes [35]. In 2019, Khadidja et al. used the waterproof imaging system designed by FORSSEA Robotics Company, as shown in Figure 15D, to carry out the experiments under more realistic conditions [80]. Compared with the preceding imaging system, their setup is improved and can be integrated into underwater detectors, such as the underwater robot and autonomous underwater vehicles. However, these two systems are based on linear polarized light, and there are only two images with orthogonal polarization states. Zhang et al. designed an aperture-division polarimetric camera, as shown in Figure 15E, to capture four polarization images in the atmosphere via methods based on the full Stokes vector. It successfully achieves real-time image haze removal with an output rate of 25 fps [34]. However, the dehazing performance can be significantly affected by the registration accuracy. With the development of the DoFP polarization camera, as shown in Figure 15F, real-time processing is made possible without registration error. Our team has integrated this DoFP camera with a watertight device and an adjustable polarized illumination to create the underwater polarimetric imaging system (UPIS). The corresponding configuration is shown in Figure 2B3 to perform de-scattering (in air and undersea) tasks in real-life scenarios. Using custom dehazing algorithms, the visual range is increased by about 8.5 times, and the processing speed reaches 15–25 fps for images with a resolution of approximately 1000 × 1000 [154]. In other words, this custom-made system has fulfilled the “3R-criterion” to a much greater extent. However, compared with traditional solutions with a single image and advanced computer-vision-based algorithms, there remains room for further improvement in the 3R-polarimetric imaging system.

A possible approach going forward is to further exploit integrated polarimetric imaging systems based on the DoFP polarization camera and automatic rotating devices in PSG and PSA [155–159]. As such, the polarization modulations in both illumination and detector can be controlled simultaneously to handle multifunctional applications.

In the review, we have covered some, if not all, of the established works in the fields of polarimetric imaging in scattering media, and we are keen to see more studies in the area as further understanding in polarimetric imaging will undoubtedly benefit both the academic and industrial communities in a significant way.

Author Contributions

XL, YH, and HW prepared the references and data. XL wrote the manuscript with input from all authors. TL reviewed and improved the writing. S-CC and HH supervised the project.

Funding

National Natural Science Foundation of China (62075161, 61775163); HKSAR Research Grants Council, General Research Fund (14206517); Innovation and Technology Commission, Innovation Technology Fund (ITS/428/17FP); and Guangxi Innovation-Driven Development Project (GuikeAA21077008).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Schechner YY, Karpel N. Recovery of Underwater Visibility and Structure by Polarization Analysis. IEEE J Oceanic Eng (2005) 30:570–87. doi:10.1109/joe.2005.850871

CrossRef Full Text | Google Scholar

2. Li X, Hu H, Zhao L, Wang H, Yu Y, Wu L, et al. Polarimetric Image Recovery Method Combining Histogram Stretching for Underwater Imaging. Sci Rep (2018) 8:12430–10. doi:10.1038/s41598-018-30566-8

PubMed Abstract | CrossRef Full Text | Google Scholar

3. He K, Sun J, Tang X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans Pattern Anal Mach Intell (2011) 33:2341–53. doi:10.1109/TPAMI.2010.168

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Tarel J-P, Hautiere N. Fast Visibility Restoration from a Single Color or gray Level Image. In: in 2009 IEEE 12th international conference on computer vision. 2201-2208. IEEE (2009).

CrossRef Full Text | Google Scholar

5. Davis GB, Carley KM. Clearing the FOG: Fuzzy, Overlapping Groups for Social Networks. Social Networks (2008) 30:201–12. doi:10.1016/j.socnet.2008.03.001

CrossRef Full Text | Google Scholar

6. Chenault DB, Pezzaniti JL. In Polarization Analysis, Measurement, and Remote Sensing III. International Society for Optics and Photonics (2018). p. 124–33.

Google Scholar

7. Dang X, Bardhan NM, Qi J, Gu L, Eze NA, Lin CW, et al. Deep-tissue Optical Imaging of Near Cellular-Sized Features. Sci Rep (2019) 9:3873–12. doi:10.1038/s41598-019-39502-w

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ghosh N, Wood MF, Vitkin IA. Mueller Matrix Decomposition for Extraction of Individual Polarization Parameters from Complex Turbid media Exhibiting Multiple Scattering, Optical Activity, and Linear Birefringence. J Biomed Opt (2008) 13:044036. doi:10.1117/1.2960934

CrossRef Full Text | Google Scholar

9. Piazza P, Cummings V, Guzzi A, Hawes I, Lohrer A, Marini S, et al. Underwater Photogrammetry in Antarctica: Long-Term Observations in Benthic Ecosystems and Legacy Data rescue. Polar Biol (2019) 42:1061–79. doi:10.1007/s00300-019-02480-w

CrossRef Full Text | Google Scholar

10. Nowosielski A, Małecki K, Forczmański P, Smoliński A. Spoofing 2D Face Recognition Systems with 3D Masks. In: International Conference on Computer Recognition Systems. Springer (2013). p. 174–83.

Google Scholar

11. Drap P, Papini O, Sourisseau J-C, Gambin T. Mining the Semantic Web. In: European semantic web conference. Springer (2012). 3–6.

Google Scholar

12. Sheng W. Photonics. 34. Multidisciplinary Digital Publishing Institute (2022).

Google Scholar

13. Singh D, Kumar V. A Comprehensive Review of Computational Dehazing Techniques. Arch Computat Methods Eng (2019) 26:1395–413. doi:10.1007/s11831-018-9294-z

CrossRef Full Text | Google Scholar

14. Tyo JS, Goldstein DL, Chenault DB, Shaw JA. Review of Passive Imaging Polarimetry for Remote Sensing Applications. Appl Opt (2006) 45:5453–69. doi:10.1364/ao.45.005453

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Li X, Hu H, Zhao L, Wang H, Han Q, Cheng Z, et al. Pseudo-polarimetric Method for Dense Haze Removal. IEEE Photon J. (2019) 11:1–11. doi:10.1109/jphot.2018.2890771

CrossRef Full Text | Google Scholar

16. Liu T, Guan Z, Li X, Cheng Z, Han Y, Yang J, et al. Polarimetric Underwater Image Recovery for Color Image with Crosstalk Compensation. Opt Lasers Eng (2020) 124:105833. doi:10.1016/j.optlaseng.2019.105833

CrossRef Full Text | Google Scholar

17. Hu H, Qi P, Li X, Cheng Z, Liu T. Underwater Imaging Enhancement Based on a Polarization Filter and Histogram Attenuation Prior. J Phys D: Appl Phys (2021) 54:175102. doi:10.1088/1361-6463/abdc93

CrossRef Full Text | Google Scholar

18. Reza AM. Realization of the Contrast Limited Adaptive Histogram Equalization (CLAHE) for Real-Time Image Enhancement. J VLSI Signal Processing-Systems Signal, Image, Video Tech (2004) 38:35–44. doi:10.1023/b:vlsi.0000028532.53893.82

CrossRef Full Text | Google Scholar

19. Wang W, Yuan X. Recent Advances in Image Dehazing. Ieee/caa J Autom Sinica (2017) 4:410–36. doi:10.1109/jas.2017.7510532

CrossRef Full Text | Google Scholar

20. Land EH. The Retinex Theory of Color Vision. Sci Am (1977) 237:108–28. doi:10.1038/scientificamerican1277-108

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Land EH, McCann JJ. Lightness and Retinex Theory. J Opt Soc Am (1971) 61:1–11. doi:10.1364/josa.61.000001

CrossRef Full Text | Google Scholar

22. Zhongli M, Jie W. Single-scale Retinex Sea Fog Removal Algorithm Fused the Edge Information. J Computer-Aided Des Comp Graphics (2015) 27:217–25.

Google Scholar

23. Seow M-J, Asari VK. Ratio Rule and Homomorphic Filter for Enhancement of Digital Colour Image. Neurocomputing (2006) 69:954–8. doi:10.1016/j.neucom.2005.07.003

CrossRef Full Text | Google Scholar

24. Yong Du Y, Guindon B, Cihlar J. Haze Detection and Removal in High Resolution Satellite Image with Wavelet Analysis. IEEE Trans Geosci Remote Sensing (2002) 40:210–7. doi:10.1109/36.981363

CrossRef Full Text | Google Scholar

25. Starck J-L, Murtagh F, Candès EJ, Donoho DL. Gray and Color Image Contrast Enhancement by the Curvelet Transform. IEEE Trans Image Process (2003) 12:706–17. doi:10.1109/tip.2003.813140

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Guan L. Model-based Neural Evaluation and Iterative Gradient Optimization in Image Restoration and Statistical Filtering. J Electron Imaging (1995) 4:407–12. doi:10.1117/12.217268

CrossRef Full Text | Google Scholar

27. Fattal R. Single Image Dehazing. ACM Trans Graph (2008) 27:1–9. doi:10.1145/1360612.1360671

CrossRef Full Text | Google Scholar

28. Lu H, Li Y, Nakashima S, Serikawa S. Single Image Dehazing through Improved Atmospheric Light Estimation. Multimed Tools Appl (2016) 75:17081–96. doi:10.1007/s11042-015-2977-7

CrossRef Full Text | Google Scholar

29. Hautiére N, Tarel J-P, Lavenant J, Aubert D. Automatic Fog Detection and Estimation of Visibility Distance through Use of an Onboard Camera. Machine Vis Appl (2006) 17:8–20. doi:10.1007/s00138-005-0011-1

CrossRef Full Text | Google Scholar

30. Narasimhan SG, Nayar SK. Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001. In: Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001. II-II. IEEE (2001).

Google Scholar

31. Feng C, Zhuo S, Zhang X, Shen L, Süsstrunk S. ICDAR 2013 Document Image Binarization Contest (DIBCO 2013). In: 2013 IEEE International Conference on Image Processing. IEEE (2013). 2363–7.

Google Scholar

32. Schechner YY, Narasimhan SG, Nayar SK. Polarization-based Vision through Haze. Appl Opt (2003) 42:511–25. doi:10.1364/ao.42.000511

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Fade J, Panigrahi S, Carré A, Frein L, Hamel C, Bretenaker F, et al. Long-range Polarimetric Imaging through Fog. Appl Opt (2014) 53:3854–65. doi:10.1364/ao.53.003854

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zhang W, Liang J, Ren L, Ju H, Qu E, Bai Z, et al. Real-time Image Haze Removal Using an Aperture-Division Polarimetric Camera. Appl Opt (2017) 56:942–7. doi:10.1364/ao.56.000942

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Treibitz T, Schechner YY. Active Polarization Descattering. IEEE Trans Pattern Anal Mach Intell (2008) 31:385–99. doi:10.1109/TPAMI.2008.85

CrossRef Full Text | Google Scholar

36. Seow KLC, Török P, Foreman MR. Single Pixel Polarimetric Imaging through Scattering media. Opt Lett (2020) 45:5740–3. doi:10.1364/ol.399554

PubMed Abstract | CrossRef Full Text | Google Scholar

37. El Ketara M, Breugnot S. Polarization: Measurement, Analysis, and Remote Sensing XIII. 106550N. International Society for Optics and Photonics (2018).

Google Scholar

38. Liang J, Ren L, Qu E, Hu B, Wang Y. Method for Enhancing Visibility of Hazy Images Based on Polarimetric Imaging. Photon Res (2014) 2:38–44. doi:10.1364/prj.2.000038

CrossRef Full Text | Google Scholar

39. Li X, Wang H, Hu H, Liu T. AOPC 2019. In: Optical Sensing and Imaging Technology. 113382O. International Society for Optics and Photonics (2019).

Google Scholar

40. Liang J, Ren L, Liang R. Low-pass Filtering Based Polarimetric Dehazing Method for Dense Haze Removal. Opt Express (2021) 29:28178–89. doi:10.1364/oe.427629

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Tyo JS, Rowe MP, Pugh EN, Engheta N. Target Detection in Optically Scattering media by Polarization-Difference Imaging. Appl Opt (1996) 35:1855–70. doi:10.1364/ao.35.001855

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Guan J, Zhu J. Target Detection in Turbid Medium Using Polarization-Based Range-Gated Technology. Opt Express (2013) 21:14152–8. doi:10.1364/oe.21.014152

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Liang J, Ren L, Ju H, Zhang W, Qu E. Polarimetric Dehazing Method for Dense Haze Removal Based on Distribution Analysis of Angle of Polarization. Opt Express (2015) 23:26146–57. doi:10.1364/oe.23.026146

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Guan J, Ma M, Sun P. Optimization of Rotating Orthogonal Polarization Imaging in Turbid media via the Mueller Matrix. Opt Lasers Eng (2019) 121:104–11. doi:10.1016/j.optlaseng.2019.04.001

CrossRef Full Text | Google Scholar

45. Wang H, Li J, Hu H, Jiang J, Li X, Zhao K, et al. Underwater Imaging by Suppressing the Backscattered Light Based on Mueller Matrix. IEEE Photon J. (2021) 13:1–6. doi:10.1109/jphot.2021.3094359

CrossRef Full Text | Google Scholar

46. Hu H, Zhao L, Li X, Wang H, Yang J, Li K, et al. Polarimetric Image Recovery in Turbid media Employing Circularly Polarized Light. Opt Express (2018) 26:25047–59. doi:10.1364/oe.26.025047

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Liu F, Li X, Han P, Shao X. Advanced Visualization Polarimetric Imaging: Removal of Water Spray Effect Utilizing Circular Polarization. Appl Sci (2021) 11:2996. doi:10.3390/app11072996

CrossRef Full Text | Google Scholar

48. Hu H, Zhao L, Huang B, Li X, Wang H, Liu T. Enhancing Visibility of Polarimetric Underwater Image by Transmittance Correction. IEEE Photon J. (2017) 9:1–10. doi:10.1109/jphot.2017.2698000

CrossRef Full Text | Google Scholar

49. Li X, Li H, Lin Y, Guo J, Yang J, Yue H, et al. Learning-based Denoising for Polarimetric Images. Opt Express (2020) 28:16309–21. doi:10.1364/oe.391017

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Hu H, Zhang Y, Li X, Lin Y, Cheng Z, Liu T. Polarimetric Underwater Image Recovery via Deep Learning. Opt Lasers Eng (2020) 133:106152. doi:10.1016/j.optlaseng.2020.106152

CrossRef Full Text | Google Scholar

51. Liu F, Cao L, Shao X, Han P, Bin X. Polarimetric Dehazing Utilizing Spatial Frequency Segregation of Images. Appl Opt (2015) 54:8116–22. doi:10.1364/ao.54.008116

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Jin H, Qian L, Gao J, Fan Z, Chen J. Polarimetric Calculation Method of Global Pixel for Underwater Image Restoration. IEEE Photon J (2020) 13:1–15.

Google Scholar

53. Koschmieder H. Theorie der horizontalen Sichtweite. Beitrage zur Physik der freien Atmosphare (1924) 33-53.

Google Scholar

54. Koranga P, Kumawat S. Face Mask Detection Classifier and Model Pruning with Keras-Surgeon. In: 2020 5th IEEE International Conference on Recent Advances and Innovations in Engineering (ICRAIE). IEEE (2020). 1–6.

Google Scholar

55. Narasimhan SG, Nayar SK. Vision and the Atmosphere. Int J Comp Vis (2002) 48:233–54. doi:10.1023/a:1016328200723

CrossRef Full Text | Google Scholar

56. Liang J, Zhang W, Ren L, Ju H, Qu E. Polarimetric Dehazing Method for Visibility Improvement Based on Visible and Infrared Image Fusion. Appl Opt (2016) 55:8221–6. doi:10.1364/ao.55.008221

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Schechner YY, Karpel N. Component-Based Face Recognition with 3D Morphable Models. In: Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2004. I-IIEEE (2004).

Google Scholar

58. Han P, Liu F, Wei Y, Shao X. Optical Correlation Assists to Enhance Underwater Polarization Imaging Performance. Opt Lasers Eng (2020) 134:106256. doi:10.1016/j.optlaseng.2020.106256

CrossRef Full Text | Google Scholar

59. Huang B, Liu T, Hu H, Han J, Yu M. Underwater Image Recovery Considering Polarization Effects of Objects. Opt Express (2016) 24:9826–38. doi:10.1364/oe.24.009826

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Tao Q, Sun Y, Shen F, Xu Q, Gao J, Guo Z. Active Imaging with the Aids of Polarization Retrieve in Turbid media System. Opt Commun (2016) 359:405–10. doi:10.1016/j.optcom.2015.09.109

CrossRef Full Text | Google Scholar

61. Shen F, Zhang B, Guo K, Yin Z, Guo Z. The Depolarization Performances of the Polarized Light in Different Scattering media Systems. IEEE Photon J (2017) 10:1–12.

Google Scholar

62. Xu Q, Guo Z, Tao Q, Jiao W, Wang X, Qu S, et al. Transmitting Characteristics of Polarization Information under Seawater. Appl Opt (2015) 54:6584–8. doi:10.1364/ao.54.006584

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Goldstein DH. Polarized Light. CRC Press (2017).

Google Scholar

64. Li X, Liu T, Huang B, Song Z, Hu H. Optimal Distribution of Integration Time for Intensity Measurements in Stokes Polarimetry. Opt Express (2015) 23:27690–9. doi:10.1364/oe.23.027690

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Chandrasekhar S. Radiative Transfer. Courier Corporation (2013).

Google Scholar

66. Hu H, Lin Y, Li X, Qi P, Liu T. IPLNet: a Neural Network for Intensity-Polarization Imaging in Low Light. Opt Lett (2020) 45:6162–5. doi:10.1364/ol.409673

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Shibata S, Hagen N, Otani Y. Robust Full Stokes Imaging Polarimeter with Dynamic Calibration. Opt Lett (2019) 44:891–4. doi:10.1364/ol.44.000891

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Qiu S, Fu Q, Wang C, Heidrich W. Polarization Demosaicking for Monochrome and Color Polarization Focal Plane Arrays. In: International Symposium on Vision, Modeling and Visualization. The Eurographics Association (2019).

Google Scholar

69. Li X, Hu H, Boffety M, Roussel S, Liu T, Goudail F. Optimal Tradeoff between Precision and Sampling Rate in DoFP Imaging Polarimeters. Opt Lett (2019) 44:5900–3. doi:10.1364/ol.44.005900

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Mueller H. On the Theory of Scattering of Light. Proceedings of the Royal Society of London. Series A. Math Phys Sci (1938) 166:425–49.

Google Scholar

71. Gil JJ. Polarimetric Characterization of Light and media. Eur Phys J Appl Phys (2007) 40:1–47. doi:10.1051/epjap:2007153

CrossRef Full Text | Google Scholar

72. Ghosh N, Wood MFG, Li S-h., Weisel RD, Wilson BC, Li R-K, et al. Mueller Matrix Decomposition for Polarized Light Assessment of Biological Tissues. J Biophoton (2009) 2:145–56. doi:10.1002/jbio.200810040

CrossRef Full Text | Google Scholar

73. Spandana K, Sindhoora K, Mahato K, Banik S, Mazumder N. Frontiers in Optics. In: FTu8B. 3. Optical Society of America (2022).

Google Scholar

74. Sindhoora K. Journal of Physics. In: Conference Series. 012045. IOP Publishing (2022).

Google Scholar

75. Spandana K, Mahato K, Mazumder N. Polarization-resolved Stokes-Mueller Imaging: a Review of Technology and Applications. Lasers Med Sci (2019) 34:1283–93.

PubMed Abstract | Google Scholar

76. Rowe MP, Tyo JS, Engheta N, Pugh EN. Polarization-difference Imaging: a Biologically Inspired Technique for Observation through Scattering media. Opt Lett (1995) 20:608–10. doi:10.1364/ol.20.000608

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Horvath H. On the Applicability of the Koschmieder Visibility Formula. Atmos Environ (1967) 5(1971):177–84.

Google Scholar

78. Schechner YY, Narasimhan SG, Nayar SK. In: Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001. I-I. IEEE (2001).

79. Hu H, Zhao L, Li X, Wang H, Liu T. Underwater Image Recovery under the Nonuniform Optical Field Based on Polarimetric Imaging. IEEE Photon J. (2018) 10:1–9. doi:10.1109/jphot.2018.2791517

CrossRef Full Text | Google Scholar

80. Amer KO, Elbouz M, Alfalou A, Brosseau C, Hajjami J. Enhancing Underwater Optical Imaging by Using a Low-Pass Polarization Filter. Opt Express (2019) 27:621–43. doi:10.1364/oe.27.000621

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Smith RC, Baker KS. Optical Properties of the Clearest Natural Waters (200-800 Nm). Appl Opt (1981) 20:177–84. doi:10.1364/ao.20.000177

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Liu F, Han P, Wei Y, Yang K, Huang S, Li X, et al. Deeply Seeing through Highly Turbid Water by Active Polarization Imaging. Opt Lett (2018) 43:4903–6. doi:10.1364/ol.43.004903

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Li X, Hu H, Wu L, Liu T. Optimization of Instrument Matrix for Mueller Matrix Ellipsometry Based on Partial Elements Analysis of the Mueller Matrix. Opt Express (2017) 25:18872–84. doi:10.1364/oe.25.018872

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Li X, Hu H, Wu L, Yu Y, Liu T. Impact of Intensity Integration Time Distribution on the Measurement Precision of Mueller Polarimetry. J Quantitative Spectrosc Radiative Transfer (2019) 231:22–7. doi:10.1016/j.jqsrt.2019.04.021

CrossRef Full Text | Google Scholar

85. Ishimaru A, Jaruwatanadilok S, Kuga Y. Polarized Pulse Waves in Random Discrete Scatterers. Appl Opt (2001) 40:5495–502. doi:10.1364/ao.40.005495

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Singh MD, Vitkin IA. Discriminating Turbid media by Scatterer Size and Scattering Coefficient Using Backscattered Linearly and Circularly Polarized Light. Biomed Opt Express (2021) 12:6831–43. doi:10.1364/boe.438631

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Ramella-Roman JC, Prahl SA, Jacques SL. Three Monte Carlo Programs of Polarized Light Transport into Scattering media: Part I. Opt Express (2005) 13:4420–38. doi:10.1364/opex.13.004420

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Ramella-Roman JC, Prahl SA, Jacques SL. Three Monte Carlo Programs of Polarized Light Transport into Scattering media: Part II: Part II. Opt Express (2005) 13:10392–405. doi:10.1364/opex.13.010392

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Peña-Gutiérrez S, Ballesta-Garcia M, García-Gómez P, Royo S. Quantitative Demonstration of the Superiority of Circularly Polarized Light in Fog Environments. Opt Lett (2022) 47:242–5. doi:10.1364/ol.445339

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Tian H, Zhu J, Tan S, Zhang Y, Zhang Y, Li Y, et al. Rapid Underwater Target Enhancement Method Based on Polarimetric Imaging. Opt Laser Tech (2018) 108:515–20. doi:10.1016/j.optlastec.2018.07.057

CrossRef Full Text | Google Scholar

91. Guan J, Ren W, Cheng Y. Stokes Vector Based Interpolation Method to Improve the Efficiency of Bio-Inspired Polarization-Difference Imaging in Turbid media. J Phys D: Appl Phys (2018) 51:145402. doi:10.1088/1361-6463/aab28f

CrossRef Full Text | Google Scholar

92. Wei Y, Han P, Liu F, Shao X. Enhancement of Underwater Vision by Fully Exploiting the Polarization Information from the Stokes Vector. Opt Express (2021) 29:22275–87. doi:10.1364/oe.433072

PubMed Abstract | CrossRef Full Text | Google Scholar

93. MacKintosh FC, Zhu JX, Pine DJ, Weitz DA. Polarization Memory of Multiply Scattered Light. Phys Rev B (1989) 40:9342–5. doi:10.1103/physrevb.40.9342

CrossRef Full Text | Google Scholar

94. Ni X, Alfano RR. Time-resolved Backscattering of Circularly and Linearly Polarized Light in a Turbid Medium. Opt Lett (2004) 29:2773–5. doi:10.1364/ol.29.002773

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Pérez JJG, Ossikovski R. Polarized Light and the Mueller Matrix Approach. CRC Press (2017).

Google Scholar

96. Sun M, He H, Zeng N, Du E, Guo Y, Liu S, et al. Characterizing the Microstructures of Biological Tissues Using Mueller Matrix and Transformed Polarization Parameters. Biomed Opt Express (2014) 5:4223–34. doi:10.1364/boe.5.004223

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Du E, He H, Zeng N, Sun M, Guo Y, Wu J, et al. Mueller Matrix Polarimetry for Differentiating Characteristic Features of Cancerous Tissues. J Biomed Opt (2014) 19:76013. doi:10.1117/1.JBO.19.7.076013

CrossRef Full Text | Google Scholar

98. Kudenov MW, Escuti MJ, Hagen N, Dereniak EL, Oka K. Snapshot Imaging Mueller Matrix Polarimeter Using Polarization Gratings. Opt Lett (2012) 37:1367–9. doi:10.1364/ol.37.001367

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Carnicer A, Bosch S, Javidi B. Mueller Matrix Polarimetry with 3D Integral Imaging. Opt Express (2019) 27:11525–36. doi:10.1364/oe.27.011525

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Kobata T, Nomura T. Digital Holographic Three-Dimensional Mueller Matrix Imaging. Appl Opt (2015) 54:5591–6. doi:10.1364/ao.54.005591

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Ellingsen PG, Aas LM, Hagen VS, Kumar R, Lilledahl MB, Kildemo M. Mueller Matrix Three-Dimensional Directional Imaging of Collagen Fibers. J Biomed Opt (2014) 19:026002. doi:10.1117/1.JBO.19.2.026002

CrossRef Full Text | Google Scholar

102. Gil JJ, Ossikovski R. Polarized Light and the Mueller Matrix Approach. CRC Press (2017).

Google Scholar

103. Wang H, Hu H, Jiang J, Li J, Li X, Zhang W, et al. Polarization Differential Imaging in Turbid Water via Mueller Matrix and Illumination Modulation. Opt Commun (2021) 499:127274. doi:10.1016/j.optcom.2021.127274

CrossRef Full Text | Google Scholar

104. Liu F. Depolarization index from Mueller Matrix Descatters Imaging in Turbid Water. Chin Opt Lett. 20 (2022) 022601.

CrossRef Full Text | Google Scholar

105. McCulloch WS, Pitts W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull Math Biophys (1943) 5:115–33. doi:10.1007/bf02478259

CrossRef Full Text | Google Scholar

106. Bishop CM. Neural Networks for Pattern Recognition. (Oxford University Press,(1995).

Google Scholar

107. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based Learning Applied to Document Recognition. Proc IEEE (1998) 86:2278–324. doi:10.1109/5.726791

CrossRef Full Text | Google Scholar

108. Krizhevsky A, Sutskever I, Hinton GE. Imagenet Classification with Deep Convolutional Neural Networks. Adv Neural Inf Process Syst (2012) 25:1097–105.

Google Scholar

109. Szegedy C. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. (2016). 1–9.

110. He K, Zhang X, Ren S, Sun J. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. (2021). 770–8.

111. Huang G, Liu Z, Van Der Maaten L, Weinberger KQ. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. (2016). 4700–8.

112. Chen D. In: 2019 IEEE Winter Conference on Applications of Computer Vision (WACV). IEEE (2019). 1375–83.

113. Pan J. Physics-based Generative Adversarial Models for Image Restoration and beyond. IEEE Trans Pattern Anal Machine Intelligence (2020) 43:2449–62.

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Zhang J, Shao J, Chen J, Yang D, Liang B, Liang R. PFNet: an Unsupervised Deep Network for Polarization Image Fusion. Opt Lett (2020) 45:1507–10. doi:10.1364/ol.384189

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Zhang R, Gui X, Cheng H, Chu J. Underwater Image Recovery Utilizing Polarimetric Imaging Based on Neural Networks. Appl Opt (2021) 60:8419–25. doi:10.1364/ao.431299

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Ren Q, Xiang Y, Wang G, Gao J, Wu Y, Chen R-P. The Underwater Polarization Dehazing Imaging with a Lightweight Convolutional Neural Network. Optik (2022) 251:168381. doi:10.1016/j.ijleo.2021.168381

CrossRef Full Text | Google Scholar

117. Zhou C, Teng M, Han Y, Xu C, Shi B. Learning to Dehaze with Polarization. Adv Neural Inf Process Syst (2021) 34.

Google Scholar

118. Yang S, Qu B, Liu G, Deng D, Liu S, Chen X. Unsupervised Learning Polarimetric Underwater Image Recovery under Nonuniform Optical fields. Appl Opt (2021) 60:8198–205. doi:10.1364/ao.432994

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Zhu Y, Zeng T, Liu K, Ren Z, Lam EY. Full Scene Underwater Imaging with Polarization and an Untrained Network. Opt Express (2021) 29:41865–81. doi:10.1364/oe.444755

CrossRef Full Text | Google Scholar

120. Carlevaris-Bianco N, Mohan A, Eustice RM. In Oceans 2010 Mts/IEEE Seattle. IEEE (2010). 1–8.

Google Scholar

121. Hummel R. Image Enhancement by Histogram Transformation (1975). Unknown.

Google Scholar

122. Huang D, Wang Y, Song W, Sequeira J, Mavromatis S. In: International Conference on Multimedia Modeling. Springer (2022). p. 453–65.

123. Huang SC, Cheng FC, Chiu YS. Efficient Contrast Enhancement Using Adaptive Gamma Correction with Weighting Distribution. IEEE Trans Image Process (2012) 22:1032–41. doi:10.1109/TIP.2012.2226047

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Chao L, Wang M. In: 2010 2nd international conference on computer engineering and technology. V2-35-V32-39. IEEE (2010).

125. Courtney T, Sacks MS, Stankus J, Guan J, Wagner WR. Design and Analysis of Tissue Engineering Scaffolds that Mimic Soft Tissue Mechanical Anisotropy. Biomaterials (2006) 27:3631–8. doi:10.1016/j.biomaterials.2006.02.024

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Jain A, Maurya AK, Ulrich L, Jaeger M, Rossi RM, Neels A, et al. Polarimetric Imaging in Backscattering for the Structural Characterization of Strongly Scattering Birefringent Fibrous media. Opt Express (2020) 28:16673–95. doi:10.1364/oe.390303

PubMed Abstract | CrossRef Full Text | Google Scholar

127. Tuchin VV. Polarized Light Interaction with Tissues. J Biomed Opt (2016) 21:71114. doi:10.1117/1.JBO.21.7.071114

CrossRef Full Text | Google Scholar

128. Yakovlev DD, Shvachkina ME, Sherman MM, Spivak AV, Pravdin AB, Yakovlev DA. Quantitative Mapping of Collagen Fiber Alignment in Thick Tissue Samples Using Transmission Polarized-Light Microscopy. J Biomed Opt (2016) 21:71111. doi:10.1117/1.JBO.21.7.071111

CrossRef Full Text | Google Scholar

129. He H, Zeng N, Li D, Liao R, Ma H. Quantitative Mueller Matrix Polarimetry Techniques for Biological Tissues. J Innov Opt Health Sci (2012) 05:1250017. doi:10.1142/s1793545812500174

CrossRef Full Text | Google Scholar

130. Ghosh N, Vitkin AI. Tissue Polarimetry: Concepts, Challenges, Applications, and Outlook. J Biomed Opt (2011) 16:110801. doi:10.1117/1.3652896

CrossRef Full Text | Google Scholar

131. Sankaran V, Walsh JT, Maitland DJ. Comparative Study of Polarized Light Propagation in Biologic Tissues. J Biomed Opt (2002) 7:300–6. doi:10.1117/1.1483318

CrossRef Full Text | Google Scholar

132. Wang X, Wang LV. Propagation of Polarized Light in Birefringent Turbid media: a Monte Carlo Study. J Biomed Opt (2002) 7:279–90. doi:10.1117/1.1483315

CrossRef Full Text | Google Scholar

133. Nishizawa N, Hamada A, Takahashi K, Kuchimaru T, Munekata H. Monte Carlo Simulation of Scattered Circularly Polarized Light in Biological Tissues for Detection Technique of Abnormal Tissues Using Spin-Polarized Light Emitting Diodes. Jpn J Appl Phys (2020) 59:SEEG03. doi:10.35848/1347-4065/ab69db

CrossRef Full Text | Google Scholar

134. Yun T, Zeng N, Li W, Li D, Jiang X, Ma H. Monte Carlo Simulation of Polarized Photon Scattering in Anisotropic media. Opt Express (2009) 17:16590–602. doi:10.1364/oe.17.016590

PubMed Abstract | CrossRef Full Text | Google Scholar

135. Wang X, Wang LV, Sun C-W, Yang C-C. Polarized Light Propagation through Scattering media: Time-Resolved Monte Carlo Simulations and Experiments. J Biomed Opt (2003) 8:608–17. doi:10.1117/1.1606462

CrossRef Full Text | Google Scholar

136. Sankaran V, Schönenberger K, Walsh JT, Maitland DJ. Polarization Discrimination of Coherently Propagating Light in Turbid media. Appl Opt (1999) 38:4252–61. doi:10.1364/ao.38.004252

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Shukla P, Sumathi R, Gupta S, Pradhan A. Influence of Size Parameter and Refractive index of the Scatterer on Polarization-Gated Optical Imaging through Turbid media. J Opt Soc Am A (2007) 24:1704–13. doi:10.1364/josaa.24.001704

CrossRef Full Text | Google Scholar

138. Schilders SP, Gan XS, Gu M. Resolution Improvement in Microscopic Imaging through Turbid media Based on Differential Polarization Gating. Appl Opt (1998) 37:4300–2. doi:10.1364/ao.37.004300

PubMed Abstract | CrossRef Full Text | Google Scholar

139. Morgan SP, Khong MP, Somekh MG. Effects of Polarization State and Scatterer Concentration on Optical Imaging through Scattering media. Appl Opt (1997) 36:1560–5. doi:10.1364/ao.36.001560

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Rodríguez C. Polarized Light and Optical Angular Momentum for Biomedical Diagnostics. 116460P. International Society for Optics and Photonics (2021).

Google Scholar

141. Ghosh N, Pradhan A, Gupta PK, Gupta S, Jaiswal V, Singh RP. Depolarization of Light in a Multiply Scattering Medium: Effect of the Refractive index of a Scatterer. Phys Rev E Stat Nonlin Soft Matter Phys (2004) 70:066607. doi:10.1103/PhysRevE.70.066607

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Li S, Jiao J, Wang C. Research on Polarized Multi-Spectral System and Fusion Algorithm for Remote Sensing of Vegetation Status at Night. Remote Sensing (2021) 13:3510. doi:10.3390/rs13173510

CrossRef Full Text | Google Scholar

143. Chowdhary J, Cairns B, Waquet F, Knobelspiesse K, Ottaviani M, Redemann J, et al. Sensitivity of Multiangle, Multispectral Polarimetric Remote Sensing over Open Oceans to Water-Leaving Radiance: Analyses of RSP Data Acquired during the MILAGRO Campaign. Remote Sensing Environ (2012) 118:284–308. doi:10.1016/j.rse.2011.11.003

CrossRef Full Text | Google Scholar

144. Dubovik O, Li Z, Mishchenko MI, Tanré D, Karol Y, Bojkov B, et al. Polarimetric Remote Sensing of Atmospheric Aerosols: Instruments, Methodologies, Results, and Perspectives. J Quantitative Spectrosc Radiative Transfer (2019) 224:474–511. doi:10.1016/j.jqsrt.2018.11.024

CrossRef Full Text | Google Scholar

145. Yan L, Li Y, Chandrasekar V, Mortimer H, Peltoniemi J, Lin Y. General Review of Optical Polarization Remote Sensing. Int J Remote Sensing (2020) 41:4853–64. doi:10.1080/01431161.2020.1724350

CrossRef Full Text | Google Scholar

146. Li N, Zhao Y, Pan Q, Kong SG, Chan JC-W. Illumination-invariant Road Detection and Tracking Using LWIR Polarization Characteristics. ISPRS J Photogrammetry Remote Sensing (2021) 180:357–69. doi:10.1016/j.isprsjprs.2021.08.022

CrossRef Full Text | Google Scholar

147. Bu Y. Hyperspectral and Multispectral Image Fusion via Graph Laplacian-Guided Coupled Tensor Decomposition. IEEE Trans Geosci Remote Sensing (2020) 59:648–62.

Google Scholar

148. Xue J, Zhao Y-Q, Bu Y, Liao W, Chan JC-W, Philips W. Spatial-spectral Structured Sparse Low-Rank Representation for Hyperspectral Image Super-resolution. IEEE Trans Image Process (2021) 30:3084–97. doi:10.1109/tip.2021.3058590

PubMed Abstract | CrossRef Full Text | Google Scholar

149. Wang Hui 王. 辉., Wang Jin 王. 进., Li Xiaobo 李., Hu Haofeng 胡., Liu Tiegen 刘. Optimization for a Polarimetic Dehazing Method Based on the Circularly Polarized Light. 红外与激光工程 (2019) 48:1126001. doi:10.3788/irla201948.1126001

CrossRef Full Text | Google Scholar

150. Wang H, Hu H, Li X, Guan Z, Zhu W, Jiang J, et al. An Angle of Polarization (AoP) Visualization Method for DoFP Polarization Image Sensors Based on Three Dimensional HSI Color Space. Sensors (2019) 19:1713. doi:10.3390/s19071713

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Van Eeckhout A, Lizana A, Garcia-Caurel E, Gil JJ, Ossikovski R, Campos J. Synthesis and Characterization of Depolarizing Samples Based on the Indices of Polarimetric Purity. Opt Lett (2017) 42:4155–8. doi:10.1364/ol.42.004155

PubMed Abstract | CrossRef Full Text | Google Scholar

152. Sheppard CJ, Bendandi A, Gratiet AL, Diaspro A. Photonics. 88. Multidisciplinary Digital Publishing Institute (2022).

Google Scholar

153.Biosensors Lab. Bioinspired Camera Could Help Self-Driving Cars See Better (2022). <https://biosensors.web.engr.illinois.edu/events-view/bioinspired-camera-could-help-self-driving-cars-see-better/>.

Google Scholar

154. Li J. Research of Underwater Image Recovery Based on Mueller Matrix and Stokes Vector. Master Thesis. Tianjin University (2020).

Google Scholar

155. Li X, Goudail F, Qi P, Liu T, Hu H. Integration Time Optimization and Starting Angle Autocalibration of Full Stokes Imagers Based on a Rotating Retarder. Opt Express (2021) 29:9494–512. doi:10.1364/oe.418399

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Gottlieb D, Arteaga O. Mueller Matrix Imaging with a Polarization Camera: Application to Microscopy. Opt Express (2021) 29:34723–34. doi:10.1364/oe.439529

PubMed Abstract | CrossRef Full Text | Google Scholar

157. Goudail F, Li X, Boffety M, Roussel S, Liu T, Hu H. Precision of Retardance Autocalibration in Full-Stokes Division-Of-Focal-Plane Imaging Polarimeters. Opt Lett (2019) 44:5410–3. doi:10.1364/ol.44.005410

PubMed Abstract | CrossRef Full Text | Google Scholar

158. Huang T, Meng R, Qi J, Liu Y, Wang X, Chen Y, et al. Fast Mueller Matrix Microscope Based on Dual DoFP Polarimeters. Opt Lett (2021) 46:1676–9. doi:10.1364/ol.421394

PubMed Abstract | CrossRef Full Text | Google Scholar

159. Li X, Le Teurnier B, Boffety M, Liu T, Hu H, Goudail F. Theory of Autocalibration Feasibility and Precision in Full Stokes Polarization Imagers. Opt Express (2020) 28:15268–83. doi:10.1364/oe.390882

PubMed Abstract | CrossRef Full Text | Google Scholar