Abstract
Diffusion-weighted magnetic resonance imaging (DW-MRI) is a non-invasive technique to probe tissue microstructure. Conventional Stejskal–Tanner diffusion encoding (i.e., encoding along a single axis), is unable to disentangle different microstructural features within a voxel; If a voxel contains microcompartments that vary in more than one attribute (e.g., size, shape, orientation), it can be difficult to quantify one of those attributes in isolation using Stejskal–Tanner diffusion encoding. Multidimensional diffusion encoding, in which the water diffusion is encoded along multiple directions in q-space (characterized by the so-called “b-tensor”) has been proposed previously to solve this problem. The shape of the b-tensor can be used as an additional encoding dimension and provides sensitivity to microscopic anisotropy. This has been applied in multiple organs, including brain, heart, breast, kidney and prostate. In this work, we discuss the advantages of using b-tensor encoding in different organs.
1 Introduction
1.1 Background
Diffusion magnetic resonance imaging (dMRI) sensitizes the signal to the random motion of the water molecules in the tissue [1]. By probing the water motion in the tissue, one can infer information about the underlying microstructure [2–6]. Some basic features of the tissue, such as fiber orientation or anisotropy can be captured using the diffusion weighted signal. In tissue that is highly ordered on the micron-scale, water molecules experience fewer boundaries along one direction and travel further per unit time than along other directions [7,8]. Altered microstructure is the hallmark of many diseases, which manifests itself in altered diffusion properties. [9] showed the reduction in the apparent diffusivity by increase in cell density in tumors. The first clinical application of diffusion MRI was on detection of early stage cerebral ischemia [10,11], which at that time could not be depicted with computed tomography (CT) or other MRI contrasts. Since then, diffusion MRI has been used in diagnosis of other diseases, such as epilepsy, stroke, tumors in central nervous system, breast and prostate, as well as surgical planning [12–22]. Diffusion MRI has also been invaluable in the study of brain development [23], learning [24,25], and connectivity [26,27]. More recently, diffusion MRI of the heart has regained some significant interest, enabled by advances in MR scanner hardware and experimental design [28–31]. Diffusion MRI has been also used in the imaging of other organs with skeletal muscle such as breast [32,33], kidney [34,35], and prostate [36,37]. In this review, we briefly explain different diffusion encoding schemes and the advantages of using advanced diffusion encoding in brain and body imaging are discussed.
1.2 Different Acquisition Schemes
In this section, we briefly explain single, double, and triple diffusion encoding (SDE, DDE, and TDE), as well as free gradient waveforms and b-tensor encoding with the special cases of linear, planar, and spherical tensor encoding (LTE, PTE, and STE).
Most diffusion MRI studies in the literature are based on conventional Stejskal–Tanner acquisitions [38], which has one pair of pulsed field gradients that encode diffusion along a single axis. In the nomenclature proposed by [39] this is referred to as Single Diffusion Encoding (SDE). A drawback of this technique is that the effect of microscopic anisotropy, orientation dispersion, and isotropic variance are entangled. This means different combinations of these factors lead to the same signal attenuation with SDE-so one may need to change the signal attenuation properties to separate them [40–47].
Double Diffusion Encoding (DDE) which contains two pairs of pulsed-field gradients that are separated from each other with a mixing time τ [39,48] has been used to disentangle the effect of microscopic anisotropy from orientation dispersion [46,47,49–55]. The encoding direction of each pair can be controlled independently and therefore facilitates measuring the diffusivity along two directions using a single preparation of the signal. The principles of DDE-based approaches have been described in several studies [45,56–59].
Varying the relative gradient directions of the two SDE blocks, one can estimate microscopic diffusion anisotropy [44,46,52,60,61] whereas varying the gradients’ strengths while keeping them orthogonal to each other reveals compartmental kurtosis [62,63]. To estimate exchange, e.g., through the membrane between extra-cellular and intra-cellular spaces, parallel gradients with variable mixing time can be used [64–69]. Another application of DDE is the estimation of compartment size using parallel and antiparallel gradients with a short mixing time [61,70].
Triple Diffusion Encoding (TDE) allows for disentangling microscopic anisotropy from isotropic diffusion, which is not feasible using SDE alone and also the advantage of TDE over DDE is that the isotropic diffusivity can be obtained from TDE using a single measurement [40,71–74].
Isotropic diffusion encoding was introduced by [75] and [71] for fast measurement of mean diffusivity. [76] used the combination of SDE and spherical/isotropic diffusion encoding to probe microscopic anisotropy, while [77] developed the method to quantify it (See Figure 1 as an example). The difference between the signals from SDE and isotropic diffusion encoding is related to the microscopic anisotropy. The non-monoexponential decay of the diffusion weighted signal as a function of b-value from isotropic diffusion encoding can show the presence of multiple compartments within a voxel [42,43,77,78].
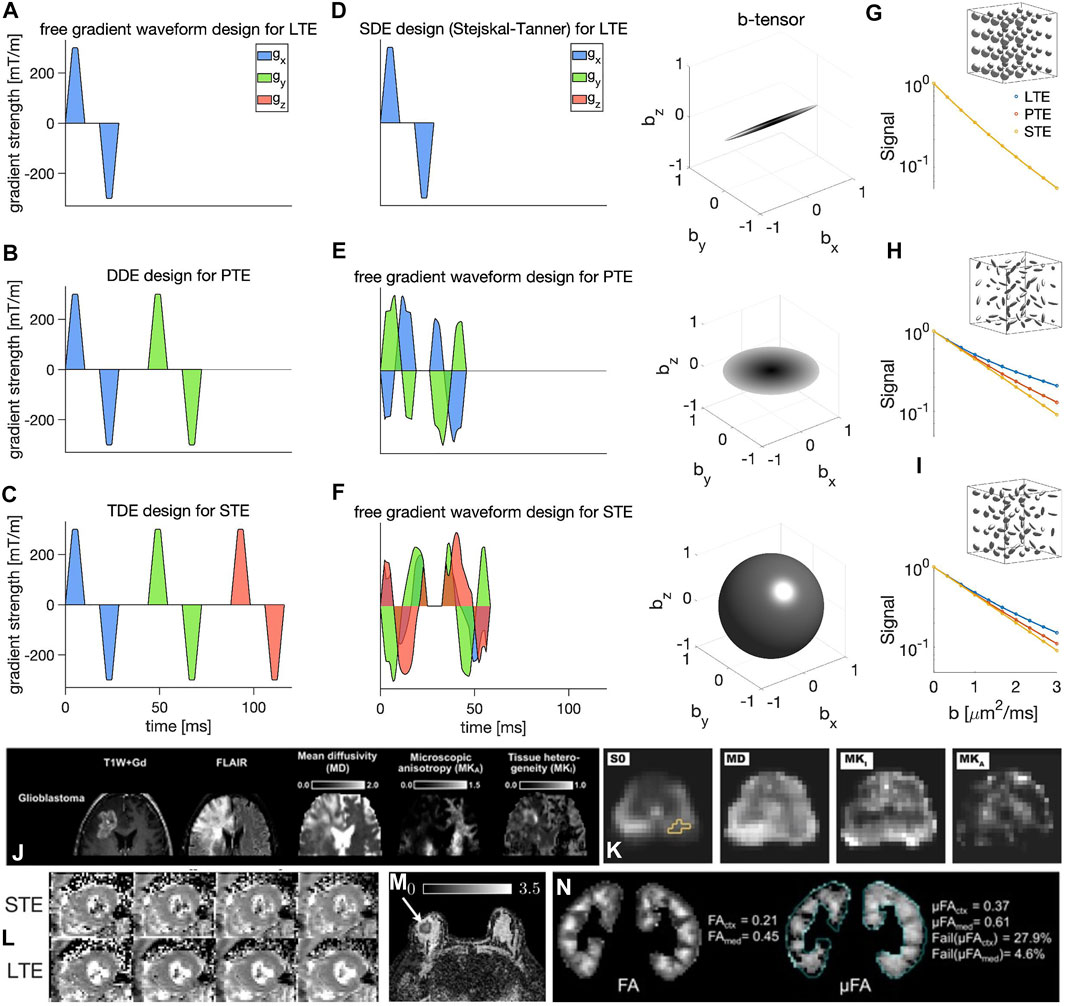
FIGURE 1
Illustration of various diffusion encoding schemes (A–F) (all waveforms are effective). In each row, an exemplary diffusion weighting gradient waveform is shown on the left (x, y, and z components are shown in blue, green, and red, respectively) and its corresponding b-tensor shape is shown on the right. The diffusion encoding schemes shown here include: (A) SDE design by Stejskal and Tanner [38] for LTE, (B) DDE [48] design for PTE, (C) TDE [71] design for isotropic/spherical diffusion encoding, (D–F) free gradient waveform encoding [86,87], (D), LTE, (E) PTE, and (F) STE. Subfigures (G–I) show the plots of the MR signal versus b-value measured in three synthetic environments; (G) fast and slow isotropic compartments, (H) randomly oriented anisotropic compartments, and (I) randomly oriented anisotropic compartments with different anisotropies using linear, planar, and spherical b-tensors (the microenvironments are all assumed Gaussian components and therefore time dependence and microkurtosis (μK) [62,102–104] are considered negligible). Subfigures (J–N) show examples of brain [92], prostate [37], cardiac [96], breast [33], and kidney [35] images. (The images (J–N) are taken with permission from [33,35,92,96,98]).
Although SDE, DDE, and TDE are the most common gradient waveforms there is no reason to limit the shape of the gradient to a rectangular/trapezoidal waveform. Free gradient waveforms may be more useful than the trapezoidal ones, as explained below [79–81].
[82] proposed a general framework to describe diffusion encoding for arbitrary gradient waveforms. In this framework, the b-value and encoding direction were replaced by the “b-tensor”, which includes the shape of the diffusion encoding [74,82–85]. In this framework, SDE is just a special realization of linear tensor encoding (LTE) where the b-tensor has only one non-zero eigenvalue as all gradients are in the same orientations. DDE can yield encoding with up to two non-zero eigenvalues and can be designed to be Planar Tensor Encoding (PTE), some asymmetric rank-2 b-tensor or LTE. In spherical tensor encoding (STE) the gradients point in all directions at some time giving rise to a rank-3 b-tensor.
Optimization of gradient waveforms in terms of echo time (providing the maximum b-value in a given echo time) has allowed for b-tensor encoding to be used across many clinical systems [86,87]. It has been used to study the tissue microstructure in the healthy brain [43,88–91], brain tumors [78,92], multiple sclerosis [93,94], epilepsy [95], as well as other organs such as breast [33], heart [96], kidney [35], and prostate [36,37]. It has shown the improvement of parameter estimates in biophysical models [91,97–100] and fiber dispersion quantification [101]. The extra dimensionality provided by b-tensor encoding helps to improve model fitting in situations where the analysis based on LTE alone has resulted in ambiguities in model parameters.
1.3 Diffusion Biomarkers
Each imaging voxel contains an ensemble of microenvironments (over a million cells for brain tissue). The diffusion within each microenvironment can be modeled by a microscopic diffusion tensor (assuming R1.1 multiple Gaussian components (MGC), i.e. no time dependence and microscopic kurtosis, μK = 0 [62,102–104]) and therefore the whole voxel has a distribution of diffusion tensors [46,77,83,105,106]. Single diffusion tensor [3] from a voxel is equivalent to the average of the microscopic tensors. Although the voxel level diffusion tensor has a lot of applications [107], it does not provide information about the underlying distribution of microscopic diffusion tensors. To obtain such information, the distribution of the microscopic diffusion tensors can be parametrized in terms of mean diffusivity (MD) and two components of diffusional variance; anisotropic and isotropic variance [43,77]. Isotropic and anisotropic mean kurtosis (MKI and MKA) are proportional to isotropic and anisotropic variances respectively (for more details see [78,106]). Fractional anisotropy (FA) reflects the average anisotropy of the voxel [108] whereas microscopic fractional anisotropy (μFA) is not influenced by the orientational order of the tissue [43,46,49,77]. Apparent diffusion coefficient (ADC) can show the macro heterogeneity (across many voxels) or the local average (in one voxel) [109,110], however, it cannot capture microheterogeneity within a voxel.
Figures 1A–F provides an overview of various diffusion encoding schemes. As shown in this figure, b-tensor encoding allows for the data to be acquired in a shorter echo time compared to DDE and TDE. Figures 1G–I shows the plots of the MR signal versus b-value measured in three synthetic environments using linear, planar, and spherical b-tensors. The three synthetic cases represent three distinct scenarios with different distributions of microenvironments (fast and slow isotropic compartments, randomly oriented anisotropic compartments, and randomly oriented anisotropic compartments with different anisotropies). Fitting a diffusion tensor to the signal from these examples will lead to a spherical diffusion tensor on the macroscopic level for all of them, while the difference between the LTE, PTE, and STE signal shows the difference in the underlying microstructure [74,77]. Figure 1 (j-R1.4n) show examples of brain [92], prostate [37], cardiac [96], breast [33], and kidney [35] images (The images (j-n) are taken with permission from [33,35,92,96,98]).
2 Tensor-Valued Diffusion Encoding: Application in the Brain
In this section, the advantages of using tensor-valued diffusion encoding in healthy brain, schizophrenia, brain tumor, epilepsy, multiple sclerosis, and Parkinson’s disease will be reviewed.
2.1 Healthy Brain
Tensor-valued diffusion encoding has been used to study the tissue microstructure in healthy brain [43,88,91,97,98,111–116]. Because of fiber crossings and the orientation dispersion, the FA measure extracted from conventional diffusion MRI is not able to show the changes in the microscopic level properly. Therefore microscopic anisotropy can be used to show the changes in the underlying microstructure independent of fiber architecture. In the normal brain, microscopic anisotropy is high in white matter and low in cortex [41,99,113,117,118].
2.2 Schizophrenia
[83] used tensor-valued diffusion encoding and extracted the scalar maps representing the mean and variance of the diffusion tensor distribution, to study the changes in schizophrenia compared to normal brains. An increase in the variance of mean diffusivity (VMD, the variance in mean diffusivities between local microenvironments) was observed. This cannot be explained by a homogeneous increase in the local mean diffusivity but it shows a higher fraction of free water (water molecules that diffuse freely, only likely to be found in the extracellular space). This indicated the elevated extracellular water content due to the neuro-inflammatory process, which is the porposed primary mechanism to explain the changes in the white matter diffusion in schizophrenia [119]. Reduction in the microscopic anisotropy in schizophrenia patients could indicate axonal degeneration at the microscopic level. The advantage of using tensor-valued diffusion encoding for the study of Schizophrenia is that the changes in the microstructure of the tissue, such as axonal degeneration can be reflected in the microscopic anisotropy while this was not necessarily clear in the macroscopic anisotropy.
2.3 Tumor
[78] used the combination of LTE and STE to investigate the link between diffusional variance and tissue heterogeneity in meningiomas and gliomas. The eccentric cells in meningiomas lead to high structural anisotropy which can be captured by anisotropic mean kurtosis (MKA) [78]. These structures are not present in gliomas. Normal white matter has high microscopic anisotropy and low tissue heterogeneity, while tumours have low to intermediate microscopic anisotropy and low to high tissue heterogeneity (Meningioma contains microscopically anisotropic tissue [78]). High tissue heterogeneity can be captured by the variation of the diffusivity (MKI) within the voxel. This can be explained by partial necrosis within the voxel which means in some parts of the voxel there is high cell density and low apparent diffusivity while other parts are necrotic with high diffusivity. [92] extended the exploration to other tumour types and with better waveforms and a shorter acquisition scheme.
2.4 Epilepsy
One of the main causes of drug-resistant epilepsy is malformations of cortical development (MCD) [120]. It can produce seizures that are mostly treated through surgical resection. [95] used tensor-valued dMRI to obtain information about tissue microstructure on MCD. In MCD, the variation in microscopic anisotropy is consistent with variations in axonal content reported in the previous studies [121–125].
2.5 Multiple Sclerosis
[94] and [93] showed that microscopic fractional anisotropy (μFA) improves the microstructural imaging of cerebral white matter in multiple sclerosis (MS) compared to standard diffusion tensor imaging. MS lesions are areas with demyelination and axonal degeneration. A considerable reduction in μFA was reported by [94] in the MS patients compared to healthy controls. In the presence of crossing fibers, the degeneration in one set of fibers may cause an increase in the FA value [126] while the anisotropy is decreased microscopically. Reduced μFA suggests a change in the volume fraction of the cellular spaces due to demyelination or axonal degeneration. In addition, more supporting cells such as glial cells in the microstructural environment may cause a decrease in μFA [127] (however, if we have glial processes, these will be picked up as microscopic anisotropic domains).
2.6 Parkinson Disease
[128] used DDE to investigate white matter degeneration in Parkinson disease (PD). In PD, mean diffusivity (MD) increases, while FA, mean kurtosis (MK), anisotropic mean kurtosis (MKA) and μFA decrease [128–134]. Some features of the neurodegeneration in PD include neuroinflammation, degeneration of myelin sheath, axonal swelling/beading, and axonal loss [135,136]. The analysis of kurtosis in [128] shows that the reductions of MK in PD are likely from the reduction in microscopic anisotropy. The increase of isotropic mean kurtosis (MKI) and decrease of MKA have different time trajectories during PD progression. [137] suggest that the increase in MKI is related to early neuroinflammation and the decrease of MKA is associated with the subsequent degeneration, so MK may have a non-monotonical trajectory, increasing in the beginning followed by a decrease. A large free-water fraction reported by [137] can explain the decrease in microscopic anisotropy although this is not the only reason and other factors such as axonal loss and demyelination may have the same effect on μFA.
3 Tensor-Valued Diffusion Encoding: Application in Body Imaging
In this section, we describe some advantages of using tensor-valued diffusion encoding in the imaging of the heart, breast, prostate, and kidney.
3.1 Breast Imaging
Diffusion weighted imaging is increasingly used in breast cancer imaging [14,33]. In the presence of pathology, microstructural features of tissue such as cellular density, membrane permeability, shape and orientation may change. These alterations are reflected in the diffusion weighted signal that is obtained from tissue. [33] studied the feasibility of non-invasive microstructural characterization of normal and neoplastic breast tissue using b-tensor encoding. They aimed for potential use of b-tensor encoding in the clinic to disentangle the fibroglandular breast tissue (FGT) from breast cancer. Their findings show that the breast cancer tissue has low isotropic diffusivity and high anisotropy, while normal FGT exhibited a low amount of anisotropy and high isotropic diffusivity which means the normal breast tissue has non-hindered isotropic environment where the water molecules can diffuse fast.The average of isotropic diffusivities in a voxel is equivalent to some conventional imaging biomarkers such as ADC that is useful to disentangle healthy tissue from benign and malignant lesions [138]. Previous studies in breast lesions showed that the tissue cellularity is inversely correlated with MD. [33] showed that isotropic diffusivity in FGT [139–141] were significantly higher than cancers which is in agreement with previous findings on MD [142–145].[33] reported that the fractional anisotropy and microscopic anisotropy values in FGT were significantly lower than tumors, in line with the previous literature [139,146].In healthy breast tissue, there are elongated structures such as lobules, ducts, and stroma in FGT that have large diameters compared to the mean displacement of water molecules during the diffusion time [139]. This may lead to low microscopic anisotropy and FA values in healthy breast tissue. The limitations of this work are the low resolution of images that may affect the delineation of small lesions and the contrast injection which may cause bias in the estimated diffusivity values.
3.2 Prostate Imaging
ADC and FA have been used as common biomarkers in detection of prostate cancer [147,148]. However, there is contradiction in the reported results by different groups as some found higher and others reported lower FA in normal glandular tissue compared to the cancerous one [148–150]. This can be explained by different factors, such as echo time, diffusion time or the spatial resolution in different studies which all may affect the estimated FA. Especially the low resolution causes each voxel of image to include cells with different orientations and leads to lower FA value due to orientation dispersion [43,108]. This is common in prostate images because of high orientation dispersion [151]. [37] and [36] used tensor-valued diffusion encoding to scan the prostate in patients with cancer. They showed that the tissue with more elongated cell structures has higher microscopic diffusion anisotropy (microscopic anisotropic kurtosis (MKA)) and isotropic heterogeneity (microscopic isotropic kurtosis (MKI)) compared to normal tissue.In the prostate, regions with stromal smooth muscle have high microscopic anisotropy [151]. This can be detected as high FA if the image resolution is high enough to avoid the orientation dispersion inside a voxel which is not usually feasible in in vivo clinical scans. As cancer progresses from Gleason pattern 3 to pattern 4 the well-formed glands are replaced by fused glands [152]. This leads to a disorganized and heterogeneous tissue that has high MKI. Low resolution of the imaging protocol may prevent the accurate delineation of the lesions. In addition, it may cause partial volume effect. There is a lack of voxel-to-voxel histology to match with each voxel of MRI data [153].
3.3 Kidney Imaging
FA has been used in the kidney as a measure of tubular integrity [154,155]. Several studies have shown higher FA in the kidney medulla compared to the kidney cortex [156–158]. Comparing FA in patients and healthy controls showed that FA is reduced in kidney disease patients [159]. However, FA is not able to disentangle different pathophysiological features that cause renal dysfunction [154]. Therefore, more specific biomarkers of renal microstructure are desirable. [35] used the combination of LTE and STE to extract the microscopic FA in the human kidney in vivo. The lower bound for the b-value range that is required to provide microstructural information about kidney tissue is around 500 s/mm2 [35]. Clear divergence between LTE and STE curves by increasing the b-value (due to microscopic anisotropy) in the cortex and medulla of the kidney was observed without the need for any model fitting [35].
3.4 Cardiac Imaging
Cardiac diffusion weighted imaging is one of the most challenging medical imaging techniques because of the macroscopic motion of the beating heart and of respiration, which are several orders of magnitude larger than the length scale of displacement of water molecules during the diffusion time. Motion-compensated diffusion encoding overcomes this limitation [160–163]. Most of the cardiac dMRI studies are based on single diffusion encoding, which has already led to interesting insights in the healthy [28,90,96,161,162] and diseased heart, including myocardial infarction [29], hypertrophic and dilated cardiomyopathy [164], amyloidosis [165] and athlete’s heart [166]. Isotropic diffusion encoding can be used to estimate mean diffusivity (MD) in a shorter time compared to conventional single diffusion encoding [71,75]. First order nulling of isotropic encoding was proposed by [71]. [96] proposed b-tensor encoding with arbitrary order nulling to compensate the higher order motion in cardiac dMRI [28,90,167]. The nulling of concomitant field was also considered, this is done in numerical optimization.
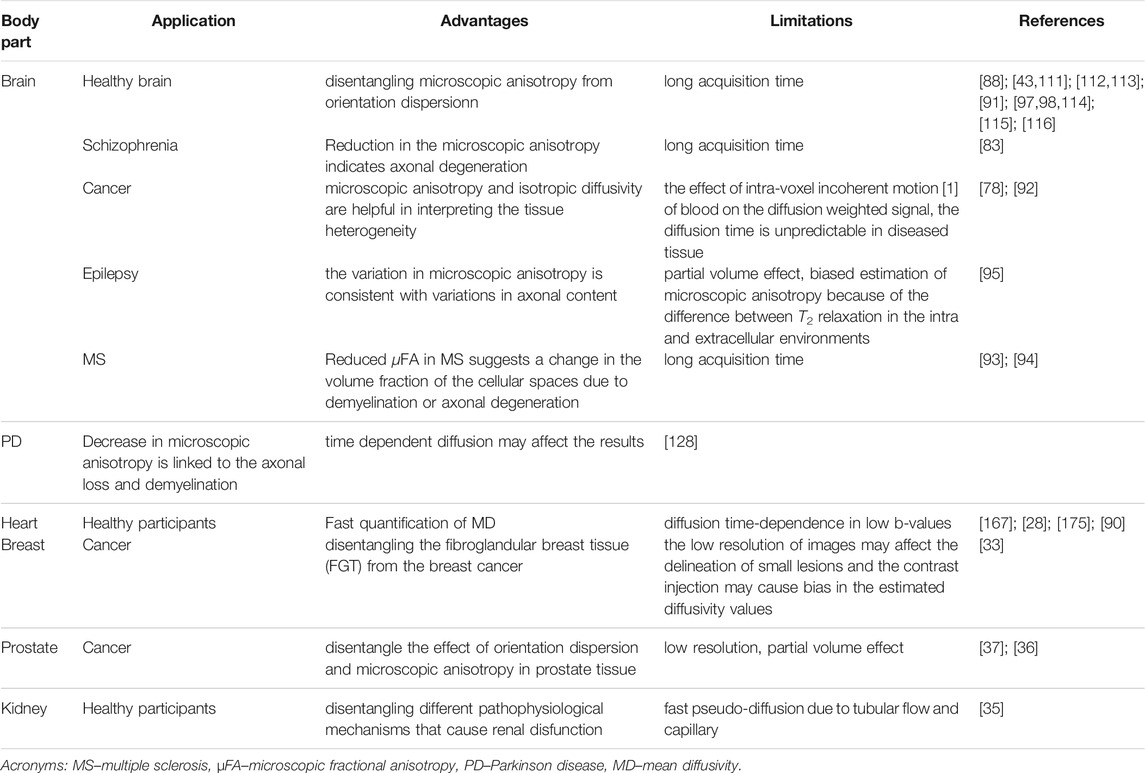
Table 1 represents a summary of the application of tensor-valued diffusion encoding in the neuro and non-neuro applications.
TABLE 1
| Body part | Application | Advantages | Limitations | References |
|---|---|---|---|---|
| Brain | Healthy brain | disentangling microscopic anisotropy from orientation dispersionn | long acquisition time | [88]; [43,111]; [112,113]; [91]; [97,98,114]; [115]; [116] |
| Schizophrenia | Reduction in the microscopic anisotropy indicates axonal degeneration | long acquisition time | [83] | |
| Cancer | microscopic anisotropy and isotropic diffusivity are helpful in interpreting the tissue heterogeneity | the effect of intra-voxel incoherent motion [1] of blood on the diffusion weighted signal, the diffusion time is unpredictable in diseased tissue | [78]; [92] | |
| Epilepsy | the variation in microscopic anisotropy is consistent with variations in axonal content | partial volume effect, biased estimation of microscopic anisotropy because of the difference between T2 relaxation in the intra and extracellular environments | [95] | |
| MS | Reduced μFA in MS suggests a change in the volume fraction of the cellular spaces due to demyelination or axonal degeneration | long acquisition time | [93]; [94] | |
| PD | Decrease in microscopic anisotropy is linked to the axonal loss and demyelination | time dependent diffusion may affect the results | [128] | |
| Heart | Healthy participants | Fast quantification of MD | diffusion time-dependence in low b-values | [167]; [28]; [175]; [90] |
| Breast | Cancer | disentangling the fibroglandular breast tissue (FGT) from the breast cancer | the low resolution of images may affect the delineation of small lesions and the contrast injection may cause bias in the estimated diffusivity values | [33] |
| Prostate | Cancer | disentangle the effect of orientation dispersion and microscopic anisotropy in prostate tissue | low resolution, partial volume effect | [37]; [36] |
| Kidney | Healthy participants | disentangling different pathophysiological mechanisms that cause renal disfunction | fast pseudo-diffusion due to tubular flow and capillary | [35] |
Summary of application of tensor-valued diffusion encoding in brain and body imaging.
Acronyms: MS–multiple sclerosis, μFA–microscopic fractional anisotropy, PD–Parkinson disease, MD–mean diffusivity.
3.5 Practical Considerations for Use of B-Tensor Encoding
To use b-tensor encoding, optimized waveforms in terms of echo time are necessary [86]. However, some hardware limits such as slew rate, maximum gradient amplitude and Peripheral Nerve Stimulation (PNS) are the limiting factors, especially in designing the motion compensated waveforms [79,96]. In addition, the effect of Maxwell terms should be considered. These may cause an extra gradient term, proportional to the G2 (G–gradient strength), which can lead to a signal loss and bias in the metrics of interest [87,168,169]. Timing of the linear and spherical encodings are sometimes different (in the design of the waveforms) which may cause differences in the effective diffusion time for the two b-tensor encoding schemes, and therefore confound the measurements [79,103,104,113,170,171,172,173] and introduce parameter bias.
3.6 Other Approaches for Quantifying Microstructure
There are approaches other than tensor valued diffusion encoding for quantifying microstructure such as SDE with different diffusion times, correlation tensor imaging (CTI) [62], oscillationg gradient spin echo (OGSE) [174]. Using CTI, one can disentangle three sources of kurtosis; isotropic, anisotropic, and intra-component kurtosis [62]. OGSE is useful to investigate small sizes in the tissue.
4 Conclusion
In conclusion, tensor-valued diffusion encoding requires bespoke waveforms that can be optimized based on the hardware limits. The results reported in the previous studies show that one of the main factors in the imaging of the body parts such as heart, prostate, etc. is the motion that should be considered in designing the waveform. In most of the diseases studied using tensor-valued diffusion encoding, a decrease in the microscopic anisotropy is reported compared to the healthy controls. Tensor-valued diffusion encoding can provide useful information about tissue microstructure which is not achievable using conventional diffusion MRI.
Statements
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research was funded in whole, or in part, by a Wellcome Trust Investigator Award (219 536/Z/19/Z, 096 646/Z/11/Z) and a Wellcome Trust Strategic Award (104 943/Z/14/Z). For the purpose of open access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission. This work was also supported by the British Heart Foundation, United Kingdom (SI/14/1/30 718), EPSRC (EP/M029778/1), and The Wolfson Foundation. F. Szczepankiewicz is supported by the Swedish Prostate Cancer Federation. The authors aknowledge BHF Project Grant, PG/17/28/32943 and BHF Project Grant PG/19/1/34076.
Conflict of interest
FS is the inventor on patents related to gradient waveform design.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
Le BihanDBretonELallemandDGrenierPCabanisELaval-JeantetM. Mr Imaging of Intravoxel Incoherent Motions: Application to Diffusion and Perfusion in Neurologic Disorders. Radiology (1986) 161:401–7. 10.1148/radiology.161.2.3763909
2.
BasserPJ. Inferring Microstructural Features and the Physiological State of Tissues from Diffusion-Weighted Images. NMR Biomed (1995) 8:333–44. 10.1002/nbm.1940080707
3.
BasserPJMattielloJLeBihanD. Estimation of the Effective Self-Diffusion Tensor from the Nmr Spin echo. J Magn Reson Ser B (1994) 103:247–54. 10.1006/jmrb.1994.1037
4.
ChengHCalhounV. Exploring Microstructure with Diffusion-Weighted Imaging: from Acquisition to Modeling. J Neurosci Methods (2021) 363:109335. 10.1016/j.jneumeth.2021.109335
5.
NovikovDSFieremansEJespersenSNKiselevVG. Quantifying Brain Microstructure with Diffusion MRI: Theory and Parameter Estimation. NMR Biomed (2019) 32:e3998. 10.1002/nbm.3998
6.
JelescuIOPalomboMBagnatoFSchillingKG. Challenges for Biophysical Modeling of Microstructure. J Neurosci Methods (2020). 10.1016/j.jneumeth.2020.108861
7.
StaniszGJWrightGAHenkelmanRMSzaferA. An Analytical Model of Restricted Diffusion in Bovine Optic Nerve. Magn Reson Med (1997) 37:103–11. 10.1002/mrm.1910370115
8.
BeaulieuC. The Basis of Anisotropic Water Diffusion in the Nervous System - a Technical Review. NMR Biomed (2002) 15:435–55. 10.1002/nbm.782
9.
ChenLLiuMBaoJXiaYZhangJZhangLet alThe Correlation between Apparent Diffusion Coefficient and Tumor Cellularity in Patients: a Meta-Analysis. PloS one (2013) 8:e79008. 10.1371/journal.pone.0079008
10.
WarachSDasheJFEdelmanRR. Clinical Outcome in Ischemic Stroke Predicted by Early Diffusion-Weighted and Perfusion Magnetic Resonance Imaging: a Preliminary Analysis. J Cereb Blood Flow Metab (1996) 16:53–9. 10.1097/00004647-199601000-00006
11.
MoseleyMECohenYMintorovitchJChileuittLShimizuHKucharczykJet alEarly Detection of Regional Cerebral Ischemia in Cats: Comparison of Diffusion- and T2-Weighted MRI and Spectroscopy. Magn Reson Med (1990) 14:330–46. 10.1002/mrm.1910140218
12.
SundgrenPCDongQGmez-HassanDMukherjiSKMalyPWelshR. Diffusion Tensor Imaging of the Brain: Review of Clinical Applications. Neuroradiology (2004) 46:339–50. 10.1007/s00234-003-1114-x
13.
TsienCCaoYChenevertT. Clinical Applications for Diffusion Magnetic Resonance Imaging in Radiotherapy. In: Seminars in Radiation Oncology, 24. Elsevier (2014). p. 218–26. 10.1016/j.semradonc.2014.02.004
14.
PartridgeSCNissanNRahbarHKitschAESigmundEE. Diffusion-weighted Breast Mri: Clinical Applications and Emerging Techniques. J Magn Reson Imaging (2017) 45:337–55. 10.1002/jmri.25479
15.
AfzaliMSoltanian-ZadehHElisevichKV. Tract Based Spatial Statistical Analysis and Voxel Based Morphometry of Diffusion Indices in Temporal Lobe Epilepsy. Comput Biol Med (2011) 41:1082–91. 10.1016/j.compbiomed.2011.05.006
16.
PadhaniARLiuGMu-KohDChenevertTLThoenyHCTakaharaTet alDiffusion-weighted Magnetic Resonance Imaging as a Cancer Biomarker: Consensus and Recommendations. Neoplasia (2009) 11:102–25. 10.1593/neo.81328
17.
NilssonMEnglundESzczepankiewiczFvan WestenDSundgrenPC. Imaging Brain Tumour Microstructure. Neuroimage (2018) 182:232–50. 10.1016/j.neuroimage.2018.04.075
18.
HorsfieldMAJonesDK. Applications of Diffusion-Weighted and Diffusion Tensor MRI to white Matter Diseases - a Review. NMR Biomed (2002) 15:570–7. 10.1002/nbm.787
19.
JellisonBJFieldASMedowJLazarMSalamatMSAlexanderAL. Diffusion Tensor Imaging of Cerebral white Matter: a Pictorial Review of Physics, Fiber Tract Anatomy, and Tumor Imaging Patterns. AJNR Am J Neuroradiol (2004) 25:356–69.
20.
TaouliBBeerAJChenevertTCollinsDLehmanCMatosCet alDiffusion-weighted Imaging outside the Brain: Consensus Statement from an Ismrm-Sponsored Workshop. J Magn Reson Imaging (2016) 44:521–40. 10.1002/jmri.25196
21.
BuddeMDSkinnerNP. Diffusion MRI in Acute Nervous System Injury. J Magn Reson (2018) 292:137–48. 10.1016/j.jmr.2018.04.016
22.
AssafYJohansen-BergHThiebaut de SchottenM. The Role of Diffusion MRI in Neuroscience. NMR Biomed (2019) 32:e3762. 10.1002/nbm.3762
23.
LebelCTreitSBeaulieuC. A Review of Diffusion MRI of Typical white Matter Development from Early Childhood to Young Adulthood. NMR Biomed (2019) 32:e3778. 10.1002/nbm.3778
24.
ZatorreRJFieldsRDJohansen-BergH. Plasticity in gray and white: Neuroimaging Changes in Brain Structure during Learning. Nat Neurosci (2012) 15:528–36. 10.1038/nn.3045
25.
ThomasCBakerCI. Teaching an Adult Brain New Tricks: a Critical Review of Evidence for Training-dependent Structural Plasticity in Humans. Neuroimage (2013) 73:225–36. 10.1016/j.neuroimage.2012.03.069
26.
JonesD. Studying Connections in the Living Human Brain with Diffusion MRI. cortex (2008) 44:936–52. 10.1016/j.cortex.2008.05.002
27.
TournierJ-D. Diffusion MRI in the Brain - Theory and Concepts. Prog Nucl Magn Reson Spectrosc (2019) 112-113:1–16. 10.1016/j.pnmrs.2019.03.001
28.
TehILasicSLundellHWereszczyńskaBBuddeMDall’ArmellinaEet alMultidimensional Diffusion MRI in the Ex Vivo Mouse Heart. In: Proceedings of the 29th Annual Meeting of ISMRM (2021).
29.
DasAKellyCTehIStoeckCTKozerkeSChowdharyAet alAcute Microstructural Changes after St-Segment Elevation Myocardial Infarction Assessed with Diffusion Tensor Imaging. Radiology (2021) 299:86–96. 10.1148/radiol.2021203208
30.
MoonJCCLorenzCHFrancisJMSmithGCPennellDJ. Breath-hold Flash and Fisp Cardiovascular Mr Imaging: Left Ventricular Volume Differences and Reproducibility. Radiology (2002) 223:789–97. 10.1148/radiol.2233011181
31.
StoeckCTKalinowskaAVon DeusterCHarmerJChanRWNiemannMet alDual-phase Cardiac Diffusion Tensor Imaging with Strain Correction. PLoS One (2014) 9:e107159. 10.1371/journal.pone.0107159
32.
GalonsJ-PAltbachMIPaine-MurrietaGDTaylorCWGilliesRJ. Early Increases in Breast Tumor Xenograft Water Mobility in Response to Paclitaxel Therapy Detected by Non-invasive Diffusion Magnetic Resonance Imaging. Neoplasia (1999) 1:113–7. 10.1038/sj.neo.7900009
33.
NaranjoIDReymbautABrynolfssonPLo GulloRBryskheKTopgaardDet alMultidimensional Diffusion Magnetic Resonance Imaging for Characterization of Tissue Microstructure in Breast Cancer Patients: A Prospective Pilot Study. Cancers (2021) 13:1606. 10.3390/cancers13071606
34.
RiesMJonesRABasseauFMoonenCTWGrenierN. Diffusion Tensor Mri of the Human Kidney. J Magn Reson Imaging (2001) 14:42–9. 10.1002/jmri.1149
35.
NeryFSzczepankiewiczFKerkeläLHallMGKadenEGordonIet alIn Vivo demonstration of Microscopic Anisotropy in the Human Kidney Using Multidimensional Diffusion MRI. Magn Reson Med (2019) 82:2160–8. 10.1002/mrm.27869
36.
LangbeinBJSzczepankiewiczFWestinC-FBayCMaierSEKibelASet alA Pilot Study of Multidimensional Diffusion Mri for Assessment of Tissue Heterogeneity in Prostate Cancer. Invest Radiol (2021). 10.1097/rli.0000000000000796
37.
NilssonMEklundGSzczepankiewiczFSkorpilMBryskheKWestinC-Fet alMapping Prostatic Microscopic Anisotropy Using Linear and Spherical B-Tensor Encoding: a Preliminary Study. Magn Reson Med (2021).
38.
StejskalEOTannerJE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time‐Dependent Field Gradient. J Chem Phys (1965) 42:288–92. 10.1063/1.1695690
39.
ShemeshNJespersenSNAlexanderDCCohenYDrobnjakIDyrbyTBet alConventions and Nomenclature for Double Diffusion Encoding NMR and MRI. Magn Reson Med (2016) 75:82–7. 10.1002/mrm.25901
40.
MitraPP. Multiple Wave-Vector Extensions of the Nmr Pulsed-Field-Gradient Spin-echo Diffusion Measurement. Phys Rev B (1995) 51:15074–8. 10.1103/physrevb.51.15074
41.
NovikovDSVeraartJJelescuIOFieremansE. Rotationally-invariant Mapping of Scalar and Orientational Metrics of Neuronal Microstructure with Diffusion MRI. NeuroImage (2018) 174:518–38. 10.1016/j.neuroimage.2018.03.006
42.
HenriquesRNJespersenSNShemeshN. Microscopic Anisotropy Misestimation in Spherical-Mean Single Diffusion Encoding MRI. Magn Reson Med (2019) 81:3245–61. 10.1002/mrm.27606
43.
SzczepankiewiczFLasičSvan WestenDSundgrenPCEnglundEWestinC-Fet alQuantification of Microscopic Diffusion Anisotropy Disentangles Effects of Orientation Dispersion from Microstructure: Applications in Healthy Volunteers and in Brain Tumors. NeuroImage (2015) 104:241–52. 10.1016/j.neuroimage.2014.09.057
44.
ÖzarslanE. Compartment Shape Anisotropy (Csa) Revealed by Double Pulsed Field Gradient Mr. J Magn Reson (2009) 199:56–67. 10.1016/j.jmr.2009.04.002
45.
FinsterbuschJ. Multiple-wave-vector Diffusion-Weighted Nmr. Annu Rep NMR Spectrosc (2011) 72:225–99. 10.1016/b978-0-12-385857-3.00006-2
46.
JespersenSNLundellHSønderbyCKDyrbyTB. Orientationally Invariant Metrics of Apparent Compartment Eccentricity from Double Pulsed Field Gradient Diffusion Experiments. NMR Biomed (2013) 26:1647–62. 10.1002/nbm.2999
47.
CallaghanPTKomloshME. Locally Anisotropic Motion in a Macroscopically Isotropic System: Displacement Correlations Measured Using Double Pulsed Gradient Spin-echo Nmr. Magn Reson Chem (2002) 40:S15–S19. 10.1002/mrc.1122
48.
CoryDGarrowayAMillerJ. Applications of Spin Transport as a Probe of Local Geometry. In: Abstracts of Papers of the American Chemical Society, 199. WASHINGTON, DC: AMER CHEMICAL SOC 1155 16TH ST, NW (1990). p. 20036. 105–POLY.
49.
ÖzarslanEBasserPJ. Microscopic Anisotropy Revealed by Nmr Double Pulsed Field Gradient Experiments with Arbitrary Timing Parameters. J Chem Phys (2008) 128:154511. 10.1063/1.2905765
50.
LawrenzMKochMAFinsterbuschJ. A Tensor Model and Measures of Microscopic Anisotropy for Double-Wave-Vector Diffusion-Weighting Experiments with Long Mixing Times. J Magn Reson (2010) 202:43–56. 10.1016/j.jmr.2009.09.015
51.
JensenJHHuiESHelpernJA. Double-pulsed Diffusional Kurtosis Imaging. NMR Biomed (2014) 27:363–70. 10.1002/nbm.3094
52.
ShemeshNÖzarslanEAdiriTBasserPJCohenY. Noninvasive Bipolar Double-Pulsed-Field-Gradient Nmr Reveals Signatures for Pore Size and Shape in Polydisperse, Randomly Oriented, Inhomogeneous Porous media. J Chem Phys (2010) 133:044705. 10.1063/1.3454131
53.
KomloshMEHorkayFFreidlinRZNevoUAssafYBasserPJ. Detection of Microscopic Anisotropy in gray Matter and in a Novel Tissue Phantom Using Double Pulsed Gradient Spin echo Mr. J Magn Reson (2007) 189:38–45. 10.1016/j.jmr.2007.07.003
54.
NajacCLundellHBulkMKanHWebbARonenI. Estimating Compartment-And Cell-specific Microscopic Anisotropy in the Human Brain Using Double-Diffusion Encoding Spectroscopy at 7t. Proc Int Soc Magn Reson Med (2019) 27:56.
55.
IanuşADrobnjakIAlexanderDC. Model-based Estimation of Microscopic Anisotropy Using Diffusion MRI: a Simulation Study. NMR Biomed (2016) 29:672–85. 10.1002/nbm.3496
56.
ÖzarslanE. Compartment Shape Anisotropy (CSA) Revealed by Double Pulsed Field Gradient MR. J Magn Reson (2009) 199:56–67. 10.1016/j.jmr.2009.04.002
57.
ShemeshNÖzarslanEKomloshMEBasserPJCohenY. From Single-Pulsed Field Gradient to Double-Pulsed Field Gradient Mr: Gleaning New Microstructural Information and Developing New Forms of Contrast in MRI. NMR Biomed (2010) 23:757–80. 10.1002/nbm.1550
58.
CallaghanPT. Translational Dynamics and Magnetic Resonance: Principles of Pulsed Gradient Spin echo NMR. Oxford University Press (2011).
59.
JespersenSN. Equivalence of Double and Single Wave Vector Diffusion Contrast at Low Diffusion Weighting. NMR Biomed (2012) 25:813–8. 10.1002/nbm.1808
60.
ChengYCoryDG. Multiple Scattering by NMR. J Am Chem Soc (1999) 121:7935–6. 10.1021/ja9843324
61.
FinsterbuschJ. The Parallel-Antiparallel Signal Difference in Double-Wave-Vector Diffusion-Weighted Mr at Short Mixing Times: A Phase Evolution Perspective. J Magn Reson (2011) 208:114–21. 10.1016/j.jmr.2010.10.012
62.
HenriquesRNJespersenSNShemeshN. Correlation Tensor Magnetic Resonance Imaging. Neuroimage (2020) 211:116605. 10.1016/j.neuroimage.2020.116605
63.
PaulsenJLÖzarslanEKomloshMEBasserPJSongY-Q. Detecting Compartmental Non-gaussian Diffusion with Symmetrized Double-PFG MRI. NMR Biomed (2015) 28:1550–6. 10.1002/nbm.3363
64.
FuróIDvinskikhSV. Nmr Methods Applied to Anisotropic Diffusion. Magn Reson Chem (2002) 40:S3–S14. 10.1002/mrc.1123
65.
ÅslundINowackaANilssonMTopgaardD. Filter-exchange Pgse Nmr Determination of Cell Membrane Permeability. J Magn Reson (2009) 200:291–5. 10.1016/j.jmr.2009.07.015
66.
LasičSNilssonMLättJStåhlbergFTopgaardD. Apparent Exchange Rate Mapping with Diffusion MRI. Magn Reson Med (2011) 66:356–65. 10.1002/mrm.22782
67.
SønderbyCKLundellHDyrbyTB. Assessing Exchange between Multiple Compartments Using Multi-Directional Double Wave Diffusion Sequences. Proc Int Soc Magn Reson Med (2012) 352.
68.
NilssonMvan WestenDStåhlbergFSundgrenPCLättJ. The Role of Tissue Microstructure and Water Exchange in Biophysical Modelling of Diffusion in white Matter. Magn Reson Mater Phy (2013) 26:345–70. 10.1007/s10334-013-0371-x
69.
NingLNilssonMLasičSWestinC-FRathiY. Cumulant Expansions for Measuring Water Exchange Using Diffusion MRI. J Chem Phys (2018) 148:074109. 10.1063/1.5014044
70.
KochMAFinsterbuschJ. Compartment Size Estimation with Double Wave Vector Diffusion-Weighted Imaging. Magn Reson Med (2008) 60:90–101. 10.1002/mrm.21514
71.
WongECCoxRWSongAW. Optimized Isotropic Diffusion Weighting. Magn Reson Med (1995) 34:139–43. 10.1002/mrm.1910340202
72.
ValetteJGiraudeauCMarchadourCDjemaiBGeffroyFGhalyMAet alA New Sequence for Single-Shot Diffusion-Weighted Nmr Spectroscopy by the Trace of the Diffusion Tensor. Magn Reson Med (2012) 68:1705–12. 10.1002/mrm.24193
73.
TopgaardD. Isotropic Diffusion Weighting Using a Triple-Stimulated echo Pulse Sequence with Bipolar Gradient Pulse Pairs. Microporous Mesoporous Mater (2015) 205:48–51. 10.1016/j.micromeso.2014.08.023
74.
ErikssonSLasičSNilssonMWestinC-FTopgaardD. Nmr Diffusion-Encoding with Axial Symmetry and Variable Anisotropy: Distinguishing between Prolate and Oblate Microscopic Diffusion Tensors with Unknown Orientation Distribution. J Chem Phys (2015) 142:104201. 10.1063/1.4913502
75.
MoriSVan ZijlPCM. Diffusion Weighting by the Trace of the Diffusion Tensor within a Single Scan. Magn Reson Med (1995) 33:41–52. 10.1002/mrm.1910330107
76.
ErikssonSLasicSTopgaardD. Isotropic Diffusion Weighting in Pgse Nmr by Magic-Angle Spinning of the Q-Vector. J Magn Reson (2013) 226:13–8. 10.1016/j.jmr.2012.10.015
77.
LasičSSzczepankiewiczFErikssonSNilssonMTopgaardD. Microanisotropy Imaging: Quantification of Microscopic Diffusion Anisotropy and Orientational Order Parameter by Diffusion MRI with Magic-Angle Spinning of the Q-Vector. Front Phys (2014) 2:11.
78.
SzczepankiewiczFvan WestenDEnglundEWestinC-FStåhlbergFLättJet alThe Link between Diffusion MRI and Tumor Heterogeneity: Mapping Cell Eccentricity and Density by Diffusional Variance Decomposition (DIVIDE). Neuroimage (2016) 142:522–32. 10.1016/j.neuroimage.2016.07.038
79.
SzczepankiewiczFWestinC-FNilssonM. Gradient Waveform Design for Tensor-Valued Encoding in Diffusion MRI. J Neurosci Methods (2021b10900). 10.1016/j.jneumeth.2020.109007
80.
DrobnjakIAlexanderDC. Optimising Time-Varying Gradient Orientation for Microstructure Sensitivity in Diffusion-Weighted Mr. J Magn Reson (2011) 212:344–54. 10.1016/j.jmr.2011.07.017
81.
DrobnjakISiowBAlexanderDC. Optimizing Gradient Waveforms for Microstructure Sensitivity in Diffusion-Weighted Mr. J Magn Reson (2010) 206:41–51. 10.1016/j.jmr.2010.05.017
82.
WestinC-FSzczepankiewiczFPasternakOÖzarslanETopgaardDKnutssonHet alMeasurement Tensors in Diffusion MRI: Generalizing the Concept of Diffusion Encoding. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer (2014). p. 209–16. 10.1007/978-3-319-10443-0_27
83.
WestinC-FKnutssonHPasternakOSzczepankiewiczFÖzarslanEvan WestenDet alQ-space Trajectory Imaging for Multidimensional Diffusion MRI of the Human Brain. Neuroimage (2016) 135:345–62. 10.1016/j.neuroimage.2016.02.039
84.
TopgaardD. Multidimensional Diffusion MRI. J Magn Reson (2017) 275:98–113. 10.1016/j.jmr.2016.12.007
85.
MattielloJBasserPJLe BihanD. The B Matrix in Diffusion Tensor echo-planar Imaging. Magn Reson Med (1997) 37:292–300. 10.1002/mrm.1910370226
86.
SjölundJSzczepankiewiczFNilssonMTopgaardDWestinC-FKnutssonH. Constrained Optimization of Gradient Waveforms for Generalized Diffusion Encoding. J Magn Reson (2015) 261:157–68. 10.1016/j.jmr.2015.10.012
87.
SzczepankiewiczFWestinCFNilssonM. Maxwell‐compensated Design of Asymmetric Gradient Waveforms for Tensor‐valued Diffusion Encoding. Magn Reson Med (2019) 82:1424–37. 10.1002/mrm.27828
88.
NingLSzczepankiewiczFNilssonMRathiYWestinC-F. Probing Tissue Microstructure by Diffusion Skewness Tensor Imaging. Scientific Rep (2021) 11:1–10. 10.1038/s41598-020-79748-3
89.
LiSZhengYSunWLasičSSzczepankiewiczFWeiQet alGlioma Grading, Molecular Feature Classification, and Microstructural Characterization Using Mr Diffusional Variance Decomposition (divide) Imaging. Eur Radiol (2021) 1–11. 10.1007/s00330-021-07959-x
90.
SzczepankiewiczFSjölundJDall’ArmellinaEPleinSSchneiderJETehIet alMotion‐compensated Gradient Waveforms for Tensor‐valued Diffusion Encoding by Constrained Numerical Optimization. Magn Reson Med (2021) 85:2117–26. 10.1002/mrm.28551
91.
LampinenBSzczepankiewiczFNovénMWestenDHanssonOEnglundEet alSearching for the Neurite Density with Diffusion MRI: Challenges for Biophysical Modeling. Hum Brain Mapp (2019) 40:2529–45. 10.1002/hbm.24542
92.
NilssonMSzczepankiewiczFBrabecJTaylorMWestinCFGolbyAet alTensor‐valued Diffusion MRI in under 3 minutes: an Initial Survey of Microscopic Anisotropy and Tissue Heterogeneity in Intracranial Tumors. Magn Reson Med (2020) 83:608–20. 10.1002/mrm.27959
93.
YangGTianQLeuzeCWintermarkMMcNabJA. Double Diffusion Encoding Mri for the Clinic. Magn Reson Med (2018) 80:507–20. 10.1002/mrm.27043
94.
AndersenKWLasičSLundellHNilssonMTopgaardDSellebjergFet alDisentangling white-matter Damage from Physiological Fibre Orientation Dispersion in Multiple Sclerosis. Brain Commun (2020) 2:fcaa077. 10.1093/braincomms/fcaa077
95.
LampinenBZampeliABjörkman‐BurtscherIMSzczepankiewiczFKällénKCompagno StrandbergMet alTensor‐valued Diffusion MRI Differentiates Cortex and white Matter in Malformations of Cortical Development Associated with Epilepsy. Epilepsia (2020) 61:1701–13. 10.1111/epi.16605
96.
LasičSSzczepankiewiczFDall'ArmellinaEDasAKellyCPleinSet alMotion-compensated B-Tensor Encoding for In Vivo Cardiac Diffusion-Weighted Imaging. NMR Biomed (2020) 33:e4213. 10.1002/nbm.4213
97.
AfzaliMPalomboMMuellerLZhangHAlexanderDCNilssonMet alImproving Neural Soma Imaging Using the Power Spectrum of the Free Gradient Waveforms. Proc Intl Soc Mag Reson Med (2020) 204.
98.
AfzaliMNilssonMPalomboMJonesDK. Spheriously? the Challenges of Estimating Sphere Radius Non-invasively in the Human Brain from Diffusion MRI. NeuroImage (2021) 237:118183. 10.1016/j.neuroimage.2021.118183
99.
LampinenBSzczepankiewiczFMårtenssonJWestenDHanssonOWestinCFet alTowards Unconstrained Compartment Modeling in white Matter Using Diffusion‐relaxation MRI with Tensor‐valued Diffusion Encoding. Magn Reson Med (2020) 84:1605–23. 10.1002/mrm.28216
100.
ReisertMKiselevVGDhitalB. A Unique Analytical Solution of the white Matter Standard Model Using Linear and Planar Encodings. Magn Reson Med (2019) 81:3819–25. 10.1002/mrm.27685
101.
CottaarMSzczepankiewiczFBastianiMHernandez-FernandezMSotiropoulosSNNilssonMet alImproved Fibre Dispersion Estimation Using B-Tensor Encoding. NeuroImage (2020) 215:116832. 10.1016/j.neuroimage.2020.116832
102.
MitraPPSenPNSchwartzLM. Short-time Behavior of the Diffusion Coefficient as a Geometrical Probe of Porous media. Phys Rev B (1993) 47:8565–74. 10.1103/physrevb.47.8565
103.
de SwietTMSenPN. Time Dependent Diffusion Coefficient in a Disordered Medium. J Chem Phys (1996) 104:206–9. 10.1063/1.470890
104.
JespersenSNOlesenJLIanuşAShemeshN. Effects of Nongaussian Diffusion on "isotropic Diffusion" Measurements: An Ex-Vivo Microimaging and Simulation Study. J Magn Reson (2019) 300:84–94. 10.1016/j.jmr.2019.01.007
105.
JianBVemuriBCÖzarslanECarneyPRMareciTH. A Novel Tensor Distribution Model for the Diffusion-Weighted Mr Signal. NeuroImage (2007) 37:164–76. 10.1016/j.neuroimage.2007.03.074
106.
TopgaardD. Director Orientations in Lyotropic Liquid Crystals: Diffusion MRI Mapping of the Saupe Order Tensor. Phys Chem Chem Phys (2016) 18:8545–53. 10.1039/c5cp07251d
107.
AlexanderALLeeJELazarMFieldAS. Diffusion Tensor Imaging of the Brain. Neurotherapeutics (2007) 4:316–29. 10.1016/j.nurt.2007.05.011
108.
PierpaoliCJezzardPBasserPJBarnettADi ChiroG. Diffusion Tensor Mr Imaging of the Human Brain. Radiology (1996) 201:637–48. 10.1148/radiology.201.3.8939209
109.
RyuYJChoiSHParkSJYunTJKimJ-HSohnC-H. Glioma: Application of Whole-Tumor Texture Analysis of Diffusion-Weighted Imaging for the Evaluation of Tumor Heterogeneity. PloS one (2014) 9:e108335. 10.1371/journal.pone.0108335
110.
WangSKimSZhangYWangLLeeEBSyrePet alDetermination of Grade and Subtype of Meningiomas by Using Histogram Analysis of Diffusion-Tensor Imaging Metrics. Radiology (2012) 262:584–92. 10.1148/radiol.11110576
111.
SzczepankiewiczFSjölundJStåhlbergFLättJNilssonM. Tensor-valued Diffusion Encoding for Diffusional Variance Decomposition (divide): Technical Feasibility in Clinical MRI Systems. PLoS One (2019) 14:e0214238. 10.1371/journal.pone.0214238
112.
DhitalBKellnerEKiselevVGReisertM. The Absence of Restricted Water Pool in Brain white Matter. Neuroimage (2018) 182:398–406. 10.1016/j.neuroimage.2017.10.051
113.
DhitalBReisertMKellnerEKiselevVG. Intra-axonal Diffusivity in Brain white Matter. NeuroImage (2019) 189:543–50. 10.1016/j.neuroimage.2019.01.015
114.
AfzaliMAja‐FernándezSJonesDK. Direction‐averaged Diffusion‐weighted MRI Signal Using Different Axisymmetric B‐tensor Encoding Schemes. Magn Reson Med (2020) 84:1579–91. 10.1002/mrm.28191
115.
de Almeida MartinsJPTaxCMWReymbautASzczepankiewiczFChamberlandMJonesDKet alComputing and Visualising Intra‐voxel Orientation‐specific Relaxation-Diffusion Features in the Human Brain. Hum Brain Mapp (2021) 42:310–28. 10.1002/hbm.25224
116.
ReymbautACaronAVGilbertGSzczepankiewiczFNilssonMWarfieldSKet alMagic diamond: Multi-Fascicle Diffusion Compartment Imaging with Tensor Distribution Modeling and Tensor-Valued Diffusion Encoding. Med Image Anal (2021) 70:101988. 10.1016/j.media.2021.101988
117.
LampinenBSzczepankiewiczFMårtenssonJvan WestenDSundgrenPCNilssonM. Neurite Density Imaging versus Imaging of Microscopic Anisotropy in Diffusion MRI: a Model Comparison Using Spherical Tensor Encoding. Neuroimage (2017) 147:517–31. 10.1016/j.neuroimage.2016.11.053
118.
JespersenSNBjarkamCRNyengaardJRChakravartyMMHansenBVosegaardTet alNeurite Density from Magnetic Resonance Diffusion Measurements at Ultrahigh Field: Comparison with Light Microscopy and Electron Microscopy. Neuroimage (2010) 49:205–16. 10.1016/j.neuroimage.2009.08.053
119.
PasternakOWestinC-FDahlbenBBouixSKubickiM. The Extent of Diffusion MRI Markers of Neuroinflammation and white Matter Deterioration in Chronic Schizophrenia. Schizophrenia Res (2015) 161:113–8. 10.1016/j.schres.2014.07.031
120.
DalicLCookM. Managing Drug-Resistant Epilepsy: Challenges and Solutions. Ndt (2016) Vol. 12:2605–16. 10.2147/ndt.s84852
121.
HannanAJServotteSKatsnelsonASisodiyaSBlakemoreCSquierMet alCharacterization of Nodular Neuronal Heterotopia in Children. Brain (1999) 122:219–38. 10.1093/brain/122.2.219
122.
Alonso-NanclaresLGarbelliRSolaRGPastorJTassiLSpreaficoRet alMicroanatomy of the Dysplastic Neocortex from Epileptic Patients. Brain (2005) 128:158–73. 10.1093/brain/awh331
123.
JudkinsARMartinezDFerreiraPDobynsWBGoldenJA. Polymicrogyria Includes Fusion of the Molecular Layer and Decreased Neuronal Populations but normal Cortical Laminar Organization. J Neuropathol Exp Neurol (2011) 70:438–43. 10.1097/nen.0b013e31821ccf1c
124.
ColomboNSalamonNRaybaudCÖzkaraÇBarkovichAJ. Imaging of Malformations of Cortical Development. Epileptic Disord (2009) 11:194–205. 10.1684/epd.2009.0262
125.
ErikssonSHSymmsMRRugg-GunnFJBoulbyPAWheeler-KingshottCAMBarkerGJet alExploring white Matter Tracts in Band Heterotopia Using Diffusion Tractography. Ann Neurol (2002) 52:327–34. 10.1002/ana.10295
126.
DouaudGJbabdiSBehrensTEJMenkeRAGassAMonschAUet alDTI Measures in Crossing-Fibre Areas: Increased Diffusion Anisotropy Reveals Early white Matter Alteration in MCI and Mild Alzheimer's Disease. Neuroimage (2011) 55:880–90. 10.1016/j.neuroimage.2010.12.008
127.
LynchAMMurphyKJDeighanBFO'ReillyJAGun'koYKCowleyTRet alThe Impact of Glial Activation in the Aging Brain. Aging Dis (2010) 1:262–78.
128.
KamiyaKKamagataKOgakiKHatanoTOgawaTTakeshige-AmanoHet alBrain white-matter Degeneration Due to Aging and Parkinson Disease as Revealed by Double Diffusion Encoding. Front Neurosci (2020) 14:584510. 10.3389/fnins.2020.584510
129.
MaddenDJBennettIJBurzynskaAPotterGGChenN-k.SongAW. Diffusion Tensor Imaging of Cerebral white Matter Integrity in Cognitive Aging. Biochim Biophys Acta (Bba) - Mol Basis Dis (2012) 1822:386–400. 10.1016/j.bbadis.2011.08.003
130.
CoutuJ-PChenJJRosasHDSalatDH. Non-gaussian Water Diffusion in Aging white Matter. Neurobiol Aging (2014) 35:1412–21. 10.1016/j.neurobiolaging.2013.12.001
131.
BillietTVandenbulckeMMädlerBPeetersRDhollanderTZhangHet alAge-related Microstructural Differences Quantified Using Myelin Water Imaging and Advanced Diffusion MRI. Neurobiol Aging (2015) 36:2107–21. 10.1016/j.neurobiolaging.2015.02.029
132.
BenitezAJensenJHFalangolaMFNietertPJHelpernJA. Modeling white Matter Tract Integrity in Aging with Diffusional Kurtosis Imaging. Neurobiol Aging (2018) 70:265–75. 10.1016/j.neurobiolaging.2018.07.006
133.
GuerreriMPalomboMCaporaleAFasanoFMacalusoEBozzaliMet alAge-related Microstructural and Physiological Changes in normal Brain Measured by MRI γ-metrics Derived from Anomalous Diffusion Signal Representation. Neuroimage (2019) 188:654–67. 10.1016/j.neuroimage.2018.12.044
134.
LawrenzMBrassenSFinsterbuschJ. Microscopic Diffusion Anisotropy in the Human Brain: Age-Related Changes. Neuroimage (2016) 141:313–25. 10.1016/j.neuroimage.2016.07.031
135.
TagliaferroPKarevaTOoTFYaryginaOKholodilovNBurkeRE. An Early Axonopathy in a hLRRK2(R1441G) Transgenic Model of Parkinson Disease. Neurobiol Dis (2015) 82:359–71. 10.1016/j.nbd.2015.07.009
136.
CollierTJKanaanNMKordowerJH. Aging and Parkinson's Disease: Different Sides of the Same coin?Mov Disord (2017) 32:983–90. 10.1002/mds.27037
137.
AndicaCKamagataKHatanoTSaitoAUchidaWOgawaTet alFree-Water Imaging in White and Gray Matter in Parkinson's Disease. Cells (2019) 8:839. 10.3390/cells8080839
138.
BaltzerPMannRMMannRMIimaMSigmundEEClauserPet alDiffusion-weighted Imaging of the Breast-A Consensus and mission Statement from the EUSOBI International Breast Diffusion-Weighted Imaging Working Group. Eur Radiol (2020) 30:1436–50. 10.1007/s00330-019-06510-3
139.
NissanNFurman-HaranEFeinberg-ShapiroMGrobgeldDEyalEZehaviTet alTracking the Mammary Architectural Features and Detecting Breast Cancer with Magnetic Resonance Diffusion Tensor Imaging. J Vis Exp (2014) e52048. 10.3791/52048
140.
PlazaMJMorrisEAThakurSB. Diffusion Tensor Imaging in the normal Breast: Influences of Fibroglandular Tissue Composition and Background Parenchymal Enhancement. Clin Imaging (2016) 40:506–11. 10.1016/j.clinimag.2015.12.001
141.
EyalEShapiro-FeinbergMFurman-HaranEGrobgeldDGolanTItzchakYet alParametric Diffusion Tensor Imaging of the Breast. Invest Radiol (2012) 47:284–91. 10.1097/rli.0b013e3182438e5d
142.
JiangRMaZDongHSunSZengXLiX. Diffusion Tensor Imaging of Breast Lesions: Evaluation of Apparent Diffusion Coefficient and Fractional Anisotropy and Tissue Cellularity. Bjr (2016) 89:20160076. 10.1259/bjr.20160076
143.
CakirOArslanAInanNAnıkYSarısoyTGumustasSet alComparison of the Diagnostic Performances of Diffusion Parameters in Diffusion Weighted Imaging and Diffusion Tensor Imaging of Breast Lesions. Eur J Radiol (2013) 82:e801–e806. 10.1016/j.ejrad.2013.09.001
144.
WangKLiZWuZZhengYZengSELet alDiagnostic Performance of Diffusion Tensor Imaging for Characterizing Breast Tumors: a Comprehensive Meta-Analysis. Front Oncol (2019) 9:1229. 10.3389/fonc.2019.01229
145.
TagliaficoARescinitoGMonettiFVillaAChiesaFFisciEet alDiffusion Tensor Magnetic Resonance Imaging of the normal Breast: Reproducibility of Dti-Derived Fractional Anisotropy and Apparent Diffusion Coefficient at 3.0 T. Radiol Med (2012) 117:992–1003. 10.1007/s11547-012-0831-9
146.
LuoJHippeDSRahbarHParsianSRendiMHPartridgeSC. Diffusion Tensor Imaging for Characterizing Tumor Microstructure and Improving Diagnostic Performance on Breast MRI: a Prospective Observational Study. Breast Cancer Res (2019) 21:102–16. 10.1186/s13058-019-1183-3
147.
KozlowskiPChangSDJonesECBereanKWChenHGoldenbergSL. Combined Diffusion-Weighted and Dynamic Contrast-Enhanced MRI for Prostate Cancer Diagnosis-Correlation with Biopsy and Histopathology. J Magn Reson Imaging (2006) 24:108–13. 10.1002/jmri.20626
148.
LiLMargolisDJADengMCaiJYuanLFengZet alCorrelation of gleason Scores with Magnetic Resonance Diffusion Tensor Imaging in Peripheral Zone Prostate Cancer. J Magn Reson Imaging (2015) 42:460–7. 10.1002/jmri.24813
149.
ManentiGCarlaniMMancinoSColangeloVDi RomaMSquillaciEet alDiffusion Tensor Magnetic Resonance Imaging of Prostate Cancer. Invest Radiol (2007) 42:412–9. 10.1097/01.rli.0000264059.46444.bf
150.
Uribe MuñozCF. In-vivo 3T and Ex-Vivo 7T Diffusion Tensor Imaging of Prostate Cancer: Correlation with Histology. Ph.D. thesis. Vancouver: University of British Columbia (2012).
151.
BourneRMBongersAChatterjeeASvedPWatsonG. Diffusion Anisotropy in Fresh and Fixed Prostate Tissue Ex Vivo. Magn Reson Med (2016) 76:626–34. 10.1002/mrm.25908
152.
EpsteinJI. Prostate Cancer Grading: a Decade after the 2005 Modified System. Mod Pathol (2018) 31:47–63. 10.1038/modpathol.2017.133
153.
BourneRMBaileyCJohnstonEWPyeHHeaveySWhitakerHet alApparatus for Histological Validation of In Vivo and Ex Vivo Magnetic Resonance Imaging of the Human Prostate. Front Oncol (2017) 7:47. 10.3389/fonc.2017.00047
154.
CaroliASchneiderMFriedliILjimaniADe SeigneuxSBoorPet alDiffusion-weighted Magnetic Resonance Imaging to Assess Diffuse Renal Pathology: a Systematic Review and Statement Paper. Nephrol Dial Transplant (2018) 33:ii29–ii40. 10.1093/ndt/gfy163
155.
GaudianoCClementiVBusatoFCorcioniBFerramoscaEMandreoliMet alRenal Diffusion Tensor Imaging: Is it Possible to Define the Tubular Pathway? a Case Report. Magn Reson Imaging (2011) 29:1030–3. 10.1016/j.mri.2011.02.032
156.
KataokaMKidoAYamamotoANakamotoYKoyamaTIsodaHet alDiffusion Tensor Imaging of Kidneys with Respiratory Triggering: Optimization of Parameters to Demonstrate Anisotropic Structures on Fraction Anisotropy Maps. J Magn Reson Imaging (2009) 29:736–44. 10.1002/jmri.21669
157.
KidoAKataokaMYamamotoANakamotoYUmeokaSKoyamaTet alDiffusion Tensor MRI of the Kidney at 3.0 and 1.5 Tesla. Acta Radiol (2010) 51:1059–63. 10.3109/02841851.2010.504741
158.
ChanRWVon DeusterCStoeckCTHarmerJPunwaniSRamachandranNet alHigh-resolution Diffusion Tensor Imaging of the Human Kidneys Using a Free-Breathing, Multi-Slice, Targeted Field of View Approach. NMR Biomed (2014) 27:1300–12. 10.1002/nbm.3190
159.
LiuZXuYZhangJZhenJWangRCaiSet alChronic Kidney Disease: Pathological and Functional Assessment with Diffusion Tensor Imaging at 3t Mr. Eur Radiol (2015) 25:652–60. 10.1007/s00330-014-3461-x
160.
PipeJGChenevertTL. A Progressive Gradient Moment Nulling Design Technique. Magn Reson Med (1991) 19:175–9. 10.1002/mrm.1910190116
161.
GamperUBoesigerPKozerkeS. Diffusion Imaging of the In Vivo Heart Using Spin Echoes-Considerations on Bulk Motion Sensitivity. Magn Reson Med (2007) 57:331–7. 10.1002/mrm.21127
162.
StoeckCTVon DeusterCGenetMAtkinsonDKozerkeS. Second-order Motion-Compensated Spin echo Diffusion Tensor Imaging of the Human Heart. Magn Reson Med (2016) 75:1669–76. 10.1002/mrm.25784
163.
WelshCLDiBellaEVRHsuEW. Higher-order Motion-Compensation for In Vivo Cardiac Diffusion Tensor Imaging in Rats. IEEE Trans Med Imaging (2015) 34:1843–53. 10.1109/tmi.2015.2411571
164.
Nielles-VallespinSKhaliqueZFerreiraPFde SilvaRScottADKilnerPet alAssessment of Myocardial Microstructural Dynamics by In Vivo Diffusion Tensor Cardiac Magnetic Resonance. J Am Coll Cardiol (2017) 69:661–76. 10.1016/j.jacc.2016.11.051
165.
GotschyAvon DeusterCvan GorkumRJHGastlMVintschgerESchwotzerRet alCharacterizing Cardiac Involvement in Amyloidosis Using Cardiovascular Magnetic Resonance Diffusion Tensor Imaging. J Cardiovasc Magn Reson (2019) 21:56–9. 10.1186/s12968-019-0563-2
166.
DasAChowdharyAKellyCTehIStoeckCTKozerkeSet alInsight into Myocardial Microstructure of Athletes and Hypertrophic Cardiomyopathy Patients Using Diffusion Tensor Imaging. J Magn Reson Imaging (2021) 53:73–82. 10.1002/jmri.27257
167.
LundellHLasicSSzczepankiewiczFWereszczyńskaBBuddeMDall’ArmellinaEet alInvestigating Time Dependent Diffusion, Microscopic Anisotropy and T2 Effects in the Mouse Heart. In: Proceedings of the 29th Annual Meeting of ISMRM (2021).
168.
MeierCZwangerMFeiweierTPorterD. Concomitant Field Terms for Asymmetric Gradient Coils: Consequences for Diffusion, Flow, and echo-planar Imaging. Magn Reson Med (2008) 60:128–34. 10.1002/mrm.21615
169.
BaronCALebelRMWilmanAHBeaulieuC. The Effect of Concomitant Gradient fields on Diffusion Tensor Imaging. Magn Reson Med (2012) 68:1190–201. 10.1002/mrm.24120
170.
de SwietTMMitraPP. Possible Systematic Errors in Single-Shot Measurements of the Trace of the Diffusion Tensor. J Magn Reson Ser B (1996) 111:15–22. 10.1006/jmrb.1996.0055
171.
LundellHNilssonMDyrbyTParkerGHubbardPZhouFet alMicroscopic Anisotropy with Spectrally Modulated Q-Space Trajectory Encoding. Proc Intl Soc Mag Reson Med (2017) 25.
172.
LundellHNilssonMDyrbyTBParkerGJMCristinaccePLHZhouFLet alMultidimensional Diffusion MRI with Spectrally Modulated Gradients Reveals Unprecedented Microstructural Detail. Sci Rep (2019) 9:9026–12. 10.1038/s41598-019-45235-7
173.
IanuşAJespersenSNSerradas DuarteTAlexanderDCDrobnjakIShemeshN. Accurate Estimation of Microscopic Diffusion Anisotropy and its Time Dependence in the Mouse Brain. Neuroimage (2018) 183:934–49. 10.1016/j.neuroimage.2018.08.034
174.
BaronCABeaulieuC. Oscillating Gradient Spin-echo (Ogse) Diffusion Tensor Imaging of the Human Brain. Magn Reson Med (2014) 72:726–36. 10.1002/mrm.24987
175.
LasicSLundellHWereszczyńskaBBuddeMYuldashevaNSzczepankiewiczFet alTime-dependent Anisotropic Diffusion in the Mouse Heart: Feasibility of Motion Compensated Tensor-Valued Encoding on a 7t Preclinical Scanner. In: Proceedings of the 29th Annual Meeting of ISMRM (2021).
Summary
Keywords
diffusion weighted imaging, b-tensor encoding, microstructure, brain, heart, body, microscopic anisotropy
Citation
Afzali M, Mueller L, Szczepankiewicz F, Jones DK and Schneider JE (2022) Quantification of Tissue Microstructure Using Tensor-Valued Diffusion Encoding: Brain and Body. Front. Phys. 10:809133. doi: 10.3389/fphy.2022.809133
Received
04 November 2021
Accepted
24 January 2022
Published
11 February 2022
Volume
10 - 2022
Edited by
Mustapha Bouhrara, National Institute on Aging (NIH), United States
Reviewed by
Noam Shemesh, Champalimaud Foundation, Portugal
Updates
Copyright
© 2022 Afzali, Mueller, Szczepankiewicz, Jones and Schneider.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Maryam Afzali, M.Afzali1@leeds.ac.uk
This article was submitted to Medical Physics and Imaging, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.